( ) ( ) ( ) El producto escalar de dos vectores puede ser negativo. La información que se obtiene del signo del producto escalar es:
|
|
|
- María Josefa Cruz Peña
- hace 5 años
- Vistas:
Transcripción
1 . Hll el pdct escl de ls ectes ( ) y ( ). Slción. P est definids en l se cnónic ( ) ( ) ( ) El pdct escl de ds ectes pede se negti. L infmción qe se tiene del sign del pdct escl es > 0 El ángl ente ls ectes es gd < 0 El ángl ente ls ectes es ts. Hll si ( ) y el ángl qe fmn ls ectes y es de 0º. Slción. Teniend en cent el tip de dts qe ns dn el pdct escl l hcems p l definición. cs Siend el ángl qe fmn ls ectes. El módl de ( ) 0 cs 0 cs 0º. Hll el pdct escl y el ángl qe fmn ls ectes ( ) y w ( ) Slción. w 0 Si w 0 w w 0 Si sn pependicles el ángl qe fmn es de 90º ( ) ( ) ( ) 0. Clcl ls ángls y l lngitd de ls lds del tiángl ABC siend qe ls cdends de ss étices sn ls pnts A(00) B() y C(). Slción. P clcl el ángl cespndiente n étice es pecis tm ls ectes cn igen en dich étice. AB AB )  80º A AC CA Vectes necesis AB ( 0 0) ( ) BA ( ) AC c 0 0 CA BC c ( ) ( ) BA ( ) Ángls cs  AB AC AB AC ( ) ( ) ( ) ( ) ( ) 0 ( ) ( ) 0 0  ccs º. cs Bˆ BA BC BA BC ( ) (. ) ( ) (. ) ( ) ( ) ( ) ( ) ( ) ( ) Bˆ 0º Teniend en cent el l de l sm de ls ángls de en n tiángl ) Ĉ 80º A Bˆ 0º º 90º ( ) ( ) º
2 Lds Ld ( AB) AB ( ) 0 Ld Ld ( AC) AC ( ) 0 ( BC) BC (. ) ( ) 0. Hll n pnt B de l pependicl OX qe ps p A( ) de tl fm qe ls ectes de psición de ms pnts fmen ente sí n ángl de 0º. Slción. Se pide detemin ls cdends de n pnt y p ell ns dn ds dts El pnt B p petenece l pependicl OX qe ps p A (x ) tendá l fm ( y). El ángl () qe fmn ls ectes de psición de ls pnts es de 0º p plicción l definición de pdct escl de ds ectes cs OA ( ) Siend OB ( y) Aplicnd l expesión nlític del pdct escl. cs cs 0 Mltiplicnd en cz p den y y ( y ) 8 y y y Elend l cdd p elimin l íz y dennd el esltd se tiene n ección de segnd gd. es de 0º. Slción. cs ( y ) ( 8 y) ( y ) y y y 0 y y 0 y 0 Existen ds psiles pnts B qe cmplen ls cndicines ppests B ( 0 ) ó B ( 0 ). Cmpe qe el ángl fmd p ls ectes ( ) y w ( ) w ( ) ( ) ( ) ( ) ( ) ( ) w ( ) ( ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) cs cs 0º
3 7. Ls cmpnentes de sn ( ). Siend qe fm n ángl de 0º cn y tienen igl módl clcl ls cmpnentes de. Slción. Se pide clcl ls cmpnentes de n ect ( ) qe cmpl ds cndicines. ( ) ( ) ( ). cs 0 cs 0 Cd n de ls cndicines gene n ección p l qe se pede plnte n sistem. S El sistem se esele p sstitción (l más sencill es despej de l ª ección y sstiti en l pime). Cncid se clcl. ( ) 8 0 ( ) ( ) 0 ( 0) 8. Clcl s de md qe ( s ) y ( s) sen pependicles. Slción. Si el pdct escl de ds ectes n nls es ce ls ectes sn pependicles. 0 s s ( ) s s 0 ( ) ( ) 0 s 0 s ± 9. Hll ls cmpnentes de n ect niti y pependicl l segment AB siend A( ) y B( ). Slción. El ect niti de AB se tiene diidiend ls cmpnentes del ect p s módl y se denmin ect nmlizd ( AB n ). ABn ± AB AB ( ) AB n AB AB ( ) ( ) ( ) ( ) ( ) ± 0 ± 0 ± 0 ± ABn Uniti de igl diección y sentid
4 0 0 AB n Uniti de igl diección y sentid pest El ect pependicl l niti (tnml) y en genel el ect pependicl n cncid se tiene intecmind ls cmpnentes de psición y n de sign ( clqie). ABn ó ABn Dds ls ectes ( ) y ( ) detemin el ángl qe fm l isectiz de ests ectes cn el eje OX. Slción. El ángl qe fm l isectiz ls ds ectes cn el eje OX () es l medi itmétic del ángl qe fm cd ect cn el eje OX. El ángl qe fm n ect cn el eje OX es el ángl qe fm cn s ect i 0 ). epesentti ( ( ) Si denminms y ls ángls qe fm cd ect cn OX i ( ) ( 0) 0 cs ccs 7'9º 7º8' i ( ) ( 0) i ( ) ( 0) 0 cs ccs 8'º 8º' i ( ) ( 0) º8' 8º' 7º'. Desems tz l tngente desde n pnt A n cicnfeenci. Siend qe ls cdends de A sn ( ) y qe l cicnfeenci está centd en el igen de dends y es de di nidd clcl ls cdends del pnt de tngenci P(x y). Slción. El pnt scd P(x y) fm ds ectes el OP y el AP. Del pime cncems s módl p se el di de l cicnfeenci y s psición elti espect l segnd sn pependicles p se di ( OP ) y tngente ( AP ). Cd n de ests cndicines pemite plnte n sistem de ds eccines cn ds incógnits. OP ( x y) OP x y x y x OP AP OP AP 0 AP p x y x y OP AP ( x y) ( x y ) 0 ( x ) y( y ) 0 x x y y 0 x x y y x y x y 0 x y 0 El sistem se esele p sstitción de l segnd ección x y Se sstitye en l ª ( ( ) ) ( )
5 ( x ) x x x x 9x x x x 0 Resliend l ección de segnd gd x y P x y P Se tienen ds psiles pnts tl y cm mest l fig.. Dds ls ectes () y () hll ) L pyección de se. ) El ect pyección de se. Slción.. P definición py py ( ) ( ) ( ) ( ) ( ) ( ). Si denminms ω l ect pyección de se ω py N Siend N el ect nmlizd de. ( ) N ( ) Cncid N y l pyección de se se clcl ω. ω py N. Hll el áe de n tiángl de étices A( ) B( ) y C(7 ). El áe de clqie tiángl A se lt se pede tene cm plicción del pdct escl. Si en el tiángl de l fig se tm cm se l lngitd del segment AC l lt seá el l slt de l pyección del segment AB se l diección tgnl (pependicl) l segment AC. AC c Áe ABC AC py AC ORT AB ( 7 ) ( ) AC ( ) Sí AC ( ) ACORT ( ) AB ( ) ( ) AB ACORT ( ) ( ) 7 ( ) py AB AC ORT ACORT
6 Áe ABC AC py ACORT AB 7 7. Si { } es n se tnml y ; hll p qe el pdct escl de. Slción. Ls ectes qe fmn n se tnml sn pependicles ente si y de módl nidd p l tnt ls pdcts escles p ells misms sn l nidd y ls pdcts czds ente ells sn nls. cs 0 cs ( ) ( ) P qe ls ectes y fmn n se tnml Hll ls cdends de ect ( ) espect de dich se. Slción. Un se tnml est fmd p ectes pependicles de módl nidd. 9 Módls 9 Pependicles 0 0 Ls ectes fmn n se tnml ó cnónic. P expes en fnción de y hy qe sc ds númes eles ( β) tles qe β ( ) β Descmpniend l igldd p cmpnentes se lleg n sistem de ds eccines cn ds incógnits. ª β β 0 ( slción) ª β β β P l tnt
7 . P qe si ( cs sin ) y ( sin cs ) sn pependicles y nitis. Slción. Un se tnml est fmd p ectes pependicles de módl nidd. Módls ( cs ) ( sin ) cs sin Pependicles 0 ( sin ) ( cs ) sin cs ( cs sin ) ( sin cs ) 0 cs sin ( sin ) cs 0 Ls ectes fmn n se tnml ó cnónic. 7. P qe ls pnts A(7)B()C(-)D() petenecen n cicnfeenci de cent O(). Slción. Si ls pnts A B C y D petenecen l cicnfeenci de cent O seá p qe tds ells están igl distnci de O y p l tnt ls módls de ls segments qe deteminn ls pnts cn el pnt O seán igles. OA OB OC c OD d OA OB OC OD ( 7 ) ( 0 ) OA 0 ( ) ( ) OB ( ) ( ) OC ( ) ( ) ( 0) OD 0 Tds ls pnts están cinc niddes de O p l tnt petenecen l cicnfeenci de cent O y di 8. Dds ls pnts A( ) B( ) C( ) clcl el ángl qe fmn AB y AC. Slción. El ángl ente ectes se clcl cm plicción del pdct escl. Si denminms l ángl qe fmn AB cn AC Sstityend ( ) ( cs ) ( ) ( ) 0 AB AC cs AB AC AB AC c 0 ( ( ) ( ) ( ( ) ) ( ) 0'99 cs ( ) ( ) ( ) ( ) ( ) ( ) 9. Hll el l de p qe ls ectes z ( ) y w ( ) ( 0'99) 7'8º 7º' fmen n ángl de º. Slción. Aplicnd l definición de ángl ente ds ectes se despej el pámet. Si denminms l ángl qe fmn ls ectes z y w 7
8 cs º ( ) ( ) ( ) ( ) cs z w z w ( ) 8 ( ) Mltiplicnd en cz se tiene n ección icinl qe se esele elend l cdd ls ds miems. ( 8) 8 8 ( ) ( ) ( 8) Resliend l ección de segnd gd se tienen ls psiles les del pámet. 9 ± 9 7 ( 8) 9 ± Hll n ect niti en l mism diección y sentid qe el ect z i j. Hll t igl pe en sentid pest. Slción. Si denminms l ect niti en l mism diección y sentid ( ) ( ) z z ( ) El ect de sentid pest ( ω ) seá el ect pest (el mism pe de sign cmid) ω. Hll n ect de módl 0 en l diección de i j. Slción. Si denminms l ect niti en l mism diección qe y de módl 0 0 N Dnde N es el ect nmlizd (de módl l nidd). ( ) ( ) ( 8 ) N. Dds ls ectes ( ) y ( m) ) Angl fmd ente y se de 0º ) se pependicl Slción.. Si llmms l ángl qe fmn ls ectes cs cs 0º Mltiplicnd en cz p den. Clcl el l de m p qe ( ) ( m) m ( ) m m 8 m m 8
9 Elend l cdd p qit l íz y dennd se tiene n ección de º gd. m 8 m ( m) 8 8m m ( 9) ± ( 9) ( m ) 9m m m m 9m ± 0. se pependicl Slción. Si ds ectes sn pependicles s pdct escl es ce. m 8 ± ( ) ( m) ( m) ( m) ( ) ( m ) ( ( ) m) ( 7 m) 9m 0 0 m ( m) ( 7 m) 0 7 ( m) ( m) 0 8 9m m 0 ( 9) ± ( 9) ( ) 0 9 ± ( ). Hll el pdct escl de ls ectes y siend qe y fmn 0º y qe y. Slción. ( ) ( ) Teniend en cent qe el pdct escl es cnmtti ( ) pecines nméics. Ls pdcts escles y se eselen p l definición. cs 0º cs 0º cs 0º cs 0º Sstityend p ss les cs 0º 0. Clcl y p qe ls ectes ( ) y ( ) Slción. dennd. ( pnt) Si ± ± Si ls ectes fmn 0º deen cmpli cs 0º ( ) ( ) ( ) y efectnd ls fmen 0º y demás 9
10 Si esliend 8 0 elend l cdd ( 8 ) 0 0 dennd 0 ( ) ± ± 70 x P tnt ds psiles slcines sn ( 70 ) ( ) ó 70 Si 8 0 esliend ( ) ( ) elend l cdd ( 8 ) 0 x 0 dennd 0 ( ) ± ( ) ( ) P tnt ls ts ds psiles slcines sn 70 ó 70. Dds ls ectes ( ) ± 70 ( ) ( ) ( ) ( ) ( x). Clcl x p qe dichs ectes fmen º. Slción. P plicción del pdct escl de ectes. Si denminms l ángl qe fmn ls ectes cs ( ) ( x) ( ) ( x) ( ) x cs ( ) x Mltiplicnd en cz dennd y simplificnd x x x Elend l cdd p qit l íz x ( x) x x x x 0 x 0 x 0
11 . Dds ls ectes ( ) ( ) c ( ) Clcl ) El ángl qe fm y ) Ls cdends de n ect pependicl c de mdl c) L pyección del ect se c d) El ect pyección de se Slción.. P plicción del pdct escl de ectes. Si denminms l ángl qe fmn ls ectes. cs ( ) ( ) ( ( cs ( ) ( ) ( ) ccs 0º. Si denminms l ect pependicl c de nódl cot c ( ) ( ) c ( ) cot ( ) py c c c ( ) ( ) c. ( ) ( ) ( ) d. py py n siend n Vect nmlizd (de módl nidd). ( ) ( ) py ( ) ( ) ( ) n Sstityend en l expesión py ( ) 7. Se tienen ls ectes ( 0) ( ). Clcl el ángl qe fmn ls ectes y. Slción. Si denminms l ángl qe fmn ls ectes ( ) ( ) cs ( ) ( ) ( ) ( 0) ( ) ( ) ( 0 ) ( ) cs ( ) ( ) ( ) ( ) ( ) 0 0 ( ) ccs 7º 7
12 8. Clcl ls les de m y de n p qe ls ectes n m ) Sen nitis ) Sen tgnles. c) Si m n clcl ls pyeccines de en de y en Slción.. Vect niti mdl nidd. m m m m ± ± n n n n ± ±. Si ds ectes sn tgnles fmn 90º y p tnt s pdct escl es ce. 0 0 n m 0 m n 0 n m Ección hmgéne cn infinits slcines. P tene n clqie de ss slcines st cn d n l n de ls incógnits y clcl l t medinte l ección. Si n m c py py 9. Ds ectes y sn tles qe 0 ; 0 ;. Hll s pdct escl el ángl qe fmn ente ells y ls ángls qe fmn cd n de ells cn el ect sm. Slción. Pdct escl ( ) El plem se esele pti de l definición de módl de n ect. Aplicnd l definición l módl de l sm y pend el pdct escl ( ) ( ) Teniend en cent qe el pdct escl es cnmtti y qe el pdct escl de n ect p si mism es el módl del ect eled l cdd cs 0
13 cs 0 Nt El ángl qe fm n ect cn el mism es ce. Sstityend en l definición de módl Elend ls ds miems l cdd se despej el pdct escl de ls ectes ( ) Ángls. Pime se clcl el ángl ente y () cm plicción del pdct escl cncid este se clcl el ángl ente n de ells y el ect sm (p ejempl ) p últim el ángl se clcl teniend en cent qe. 0 7 cs º ccs ( ) cs º ccs º 9º º 0. Si y c sn tes ectes de igl módl y c clcl el pdct escl de ls ectes y y el ángl qe fmn. Slción. Si denminms l ángl qe fmn ls ectes cs El pdct escl se tiene de l definición de módl de l sm en fnción en fnción de ls módls de ls ectes. Aplicnd l definición de módl l módl de l sm y pend el pdct escl ( ) ( ) Teniend en cent qe el pdct escl es cnmtti y qe el pdct escl de n ect p si mism es el módl del ect eled l cdd cs 0º cs 0º Sstityend en l definición de módl de l sm Elend ls ds miems l cdd se despej el pdct escl de ls ectes.
14 El módl de l sm se pede tene del enncid. Si c c (si ds ectes sn igles ss módls tmién l sn) y cm c se pede cncli Sstityend en l expesión del pdct escl Si en l expesión del ángl ente ectes sstitims td en fnción del módl de cs ccs 0º Si c y c ls tes ectes fmn n tiángl eqiláte. Se el tiángl de étices A( ) B( 0) y C( ). Clcl i. Módl de AB ii. iii. i. Ángl de AB cn AC Pyección de AB se el eje x Pyección de AB se AC. Vect niti en l diección de AC i. Vect pyección de AB se AC ii. Áe del tiángl iii. Detemin el l de p qe el ect ( ) se tgnl l ect BC ix. Vl de p qe el pnt ( ) fme cn B y C n tiángl de áe niddes cdds. Slción. AB 0 ; AB ( ) ( ) 0 i. ( ) ( ) ii. Se denminms l ángl qe fmn ls ectes AB AC AB ( ) cs AB AC AC c ( ) ( ) ( ) ( ) ( ) 0 cs ccs 70º 0 0 iii. El epesentnte del eje OX es el ect niti i ( 0) AB i ( ) ( 0) py i AB i ( ) 0 0
15 AB AC i. py AC AB AC. Vect niti nmlizd. AC N AC AC ( ) i. py AB py AB AC ( ) AC ii. ( ABC) AC N ( ) ( ) ( ) ( ) ( ) ( ) AB AC' AC Áe AC' iii. Si ds ectes sn pependicles s pdct escl es ce. ( ) BC 0 ( ) ( ) 0 ( ) 0 ix. A( ); B( 0); C( ) ( ) ( ) AB AC' AB 0 Áe( ABC) AC ( ) ( ) AC' ( ) ( ) ( ) ( ) ( ) 8 8 ± ( ) ( ) 8 ± 8 0
PRODUCTO ESCALAR. r r r
 PRODUCTO ESCALAR Defncón de pdct escl de ectes. Se denmn pdct escl de ds ectes (, ) y (, ), l núme: cs α y l epesentms p En el pdct escl se mltplcn ds ectes, pe el esltd es n núme (escl). S ls ectes petenecen
PRODUCTO ESCALAR Defncón de pdct escl de ectes. Se denmn pdct escl de ds ectes (, ) y (, ), l núme: cs α y l epesentms p En el pdct escl se mltplcn ds ectes, pe el esltd es n núme (escl). S ls ectes petenecen
2, 3 1, 3 1, 3 , 3 , 3
 . Dd el et ( ) hll t en s mism dieión qe se niti. Cll tmién t et de módl de igl dieión qe sentid pest. Slión. En l pime pte del plem se pide ll el et niti de. n ± ± ± dieión sentid pest Igl ' dieión sentid
. Dd el et ( ) hll t en s mism dieión qe se niti. Cll tmién t et de módl de igl dieión qe sentid pest. Slión. En l pime pte del plem se pide ll el et niti de. n ± ± ± dieión sentid pest Igl ' dieión sentid
VECTORES EN EL ESPACIO
 Tem Vectes Ejecicis eselts Mtemátics II º Bchillet VECTORES EN EL ESPACIO DEPENDENCIA E INDEPENDENCIA LINEAL COMBINACIÓN LINEAL BASE EJERCICIO : Dds ls vectes ( ) b( ) c ( ) d ( ): ) Fmn n bse de R? Expes
Tem Vectes Ejecicis eselts Mtemátics II º Bchillet VECTORES EN EL ESPACIO DEPENDENCIA E INDEPENDENCIA LINEAL COMBINACIÓN LINEAL BASE EJERCICIO : Dds ls vectes ( ) b( ) c ( ) d ( ): ) Fmn n bse de R? Expes
PRODUCTO ESCALAR. r r r
 PRODUCTO ESCALAR Defnón de pdt esl de vetes. Se denmn pdt esl de ds vetes ( ) y ( ) p l núme: s y l epesentms En el pdt esl se mltpln ds vetes pe el esltd es n núme (esl). S ls vetes peteneen l esp vetl
PRODUCTO ESCALAR Defnón de pdt esl de vetes. Se denmn pdt esl de ds vetes ( ) y ( ) p l núme: s y l epesentms En el pdt esl se mltpln ds vetes pe el esltd es n núme (esl). S ls vetes peteneen l esp vetl
Vectores. Bases. Producto escalar, vectorial y mixto; y aplicaciones
 Mtemátics II Geometí del espcio Vectoes. Bses. Podcto escl vectoil mixto; plicciones Obsevción: L moí de los poblems eseltos continción se hn popesto en los exámenes de Selectividd.. Ddos los vectoes (
Mtemátics II Geometí del espcio Vectoes. Bses. Podcto escl vectoil mixto; plicciones Obsevción: L moí de los poblems eseltos continción se hn popesto en los exámenes de Selectividd.. Ddos los vectoes (
TEMAS DE MATEMATICAS (Oposiciones de Secundaria)
 TEMAS DE MATEMATICAS (Opsicines de Secndi) TEMA 5 SISTEMAS DE REFERENCIA EN EL PLANO Y EN EL ESPACIO. ECUACIONES DE LA RECTA Y DEL PLANO. RELACIONES AFINES.. Espci Afín... Pln Afín... Espci Afín... Sespcis
TEMAS DE MATEMATICAS (Opsicines de Secndi) TEMA 5 SISTEMAS DE REFERENCIA EN EL PLANO Y EN EL ESPACIO. ECUACIONES DE LA RECTA Y DEL PLANO. RELACIONES AFINES.. Espci Afín... Pln Afín... Espci Afín... Sespcis
I.E.S. Mediterráneo de Málaga Septiembre 2015 Juan Carlos Alonso Gianonatti OPCIÓN DE EXAMEN Nº 1
 I.E.S. editeáneo de álg Septiembe Jn Clos lonso Ginontti OCIÓN DE EXEN Nº Considee el sigiente sistem de ecciones dependiendo del pámeto [7 UNTOS] Clcle los loes de p qe el sistem teng solción. b [ UNTOS]
I.E.S. editeáneo de álg Septiembe Jn Clos lonso Ginontti OCIÓN DE EXEN Nº Considee el sigiente sistem de ecciones dependiendo del pámeto [7 UNTOS] Clcle los loes de p qe el sistem teng solción. b [ UNTOS]
PROYECTO DE TEORIA DE MECANISMOS.
 Nmbe: Mecnism: PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemátic y dinámic de un mecnism pln ticuld cn un gd de libetd. 7. Cálcul de ls celecines cn el métd de ls celecines eltivs gáfic y nlític 7.1.
Nmbe: Mecnism: PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemátic y dinámic de un mecnism pln ticuld cn un gd de libetd. 7. Cálcul de ls celecines cn el métd de ls celecines eltivs gáfic y nlític 7.1.
teniendo en cuenta que la relación de equipolencia es una relación de igualdad: ( ) ( )
 Jni. Ejeii B. (Pntión máim pnts Ls pnts A( B( C( sn tes éties nsetis de n plelgm. Se pide (pnt Hll ls dends del t étie D ll el áe de dih plelgm. ( pnt Clsifi el plelgm p ss lds p ss ángls. Slión Si t pnts
Jni. Ejeii B. (Pntión máim pnts Ls pnts A( B( C( sn tes éties nsetis de n plelgm. Se pide (pnt Hll ls dends del t étie D ll el áe de dih plelgm. ( pnt Clsifi el plelgm p ss lds p ss ángls. Slión Si t pnts
Representar las dos proyecciones y la tercera proyección de los puntos dados a continuación:
 Repesent ls dos poyecciones y l tece poyección de los puntos ddos continución: pto. lej. cot A + 0 B + = + C + < + D 0 + E - > + F - = + G - > + H - 0 I - > - J - = - K L - 0 < - - M + < - N + = - + >
Repesent ls dos poyecciones y l tece poyección de los puntos ddos continución: pto. lej. cot A + 0 B + = + C + < + D 0 + E - > + F - = + G - > + H - 0 I - > - J - = - K L - 0 < - - M + < - N + = - + >
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
POSICIONES RELATIVAS
 POSIIONES RELTIVS i. Picine Relti e pln ii. Picine elti e te pln iii. Picine elti e ect i. Picine elti e n ect n pln Picine elti e pln. Sen l pln picine elti peen e - Secnte. - Plel. - inciente Secnte.
POSIIONES RELTIVS i. Picine Relti e pln ii. Picine elti e te pln iii. Picine elti e ect i. Picine elti e n ect n pln Picine elti e pln. Sen l pln picine elti peen e - Secnte. - Plel. - inciente Secnte.
FUNDAMENTOS FÍSICOS DE LA INFORMÁTICA PRIMER EJERCICIO GRUPO 1PV 27 de Febrero de 2002
 FUNDAMENTOS FÍSICOS DE LA INFORMÁTICA PRIMER EJERCICIO GRUPO 1PV 7 de Fee de Cuestines 1. Otén ls dimensines del fluj del cmp eléctic e indic sus uniddes en el sistem intencinl. F Q MLT IT 1 [ Φ] [ ES
FUNDAMENTOS FÍSICOS DE LA INFORMÁTICA PRIMER EJERCICIO GRUPO 1PV 7 de Fee de Cuestines 1. Otén ls dimensines del fluj del cmp eléctic e indic sus uniddes en el sistem intencinl. F Q MLT IT 1 [ Φ] [ ES
OPCIÓN A. Colegio La Presentación Granada MATEMATICAS II. Examen de Matemáticas GLOBAL DE GEOMETRÍA
 Colegio L Pesentción Gnd OPCIÓN A 1- () [1 punto] Sen u y v dos vectoes otogonles y de módulo 1 Hll los vloes del pámeto p que lo vectoes u + v y u v fomen un ángulo 60º (b) [1 punto] Hll un vecto z de
Colegio L Pesentción Gnd OPCIÓN A 1- () [1 punto] Sen u y v dos vectoes otogonles y de módulo 1 Hll los vloes del pámeto p que lo vectoes u + v y u v fomen un ángulo 60º (b) [1 punto] Hll un vecto z de
1: El producto escalar de un vector consigo mismo coincide con el cuadrado de su módulo
 UNIDAD : Geometrí eclíde. Prodcto esclr. PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores y y se not por l nº rel qe se obtiene de l sigiente form: = es decir el
UNIDAD : Geometrí eclíde. Prodcto esclr. PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores y y se not por l nº rel qe se obtiene de l sigiente form: = es decir el
CAPÍTULO 3: CAMPO MAGNÉTICO. BIBLIOGRAFÍA Tipler. "Física". Cap. 27. Reverté Campo magnético creado por cargas puntuales en movimiento. (27.
 CAPÍTULO 3: 3.. Camp magnétic cead p cagas pntales en mvimient. (7.) CAMPO MAGNÉTCO 3.3. Camp magnétic cead p cientes elécticas: Le de it Savat. (7.) 3.. Le de Gass paa el magnetism. (7.3) 3.5. Le de Ampee.
CAPÍTULO 3: 3.. Camp magnétic cead p cagas pntales en mvimient. (7.) CAMPO MAGNÉTCO 3.3. Camp magnétic cead p cientes elécticas: Le de it Savat. (7.) 3.. Le de Gass paa el magnetism. (7.3) 3.5. Le de Ampee.
TEMA II: POSICIONES RELATIVAS ENTRE ELEMENTOS
 TEA II: POSICIONES RELATIVAS ENTRE ELEENTOS..D Ente dos ects Dos ects en el espcio pueden se: ) plels (sus poecciones homónims son plels) b) secntes (tienen un único punto en común) c) o cuse Ejemplo 4
TEA II: POSICIONES RELATIVAS ENTRE ELEENTOS..D Ente dos ects Dos ects en el espcio pueden se: ) plels (sus poecciones homónims son plels) b) secntes (tienen un único punto en común) c) o cuse Ejemplo 4
- La energía potencial electrostática de una carga puntual es nula.
 1 e EXAMEN PACIAL. FÍSICA II. TEMAS 1 Y (6/04/016) ESOLUCIÓN Cuestión 1.- Cnsidéense ls siguientes distibucines de cg: () puntul; (b) supeficil unifme, sbe un esfe de di ; (c) vlúmic unifme en un esfe
1 e EXAMEN PACIAL. FÍSICA II. TEMAS 1 Y (6/04/016) ESOLUCIÓN Cuestión 1.- Cnsidéense ls siguientes distibucines de cg: () puntul; (b) supeficil unifme, sbe un esfe de di ; (c) vlúmic unifme en un esfe
UNIDAD13.PRODUCTO ESCALAR, VECTORIAL Y MIXTO. APLICACIONES
 6 Unidd. Podcto ecl ectoil mito. Apliccione en el epcio. UNIDAD.PRODUCTO ESCALAR VECTORIAL Y MIXTO. APLICACIONES. Podcto ecl de do ectoe libe.. Definición.. Intepetción geométic.. Epeión nlític. Podcto
6 Unidd. Podcto ecl ectoil mito. Apliccione en el epcio. UNIDAD.PRODUCTO ESCALAR VECTORIAL Y MIXTO. APLICACIONES. Podcto ecl de do ectoe libe.. Definición.. Intepetción geométic.. Epeión nlític. Podcto
CURVAS PLANAS DEFINIDAS PARAMÉTRICAMENTE.
 Intdcción Definición de las fncines ectiales cntinas: Si llamams M al plan métic asciad al espaci ectial eclidian de dimensines, E, R, cnsideams el sistema de efeencia tnmal en M, {, {,}}, se pede establece
Intdcción Definición de las fncines ectiales cntinas: Si llamams M al plan métic asciad al espaci ectial eclidian de dimensines, E, R, cnsideams el sistema de efeencia tnmal en M, {, {,}}, se pede establece
ESPACIO EUCLÍDEO ESPACIO EUCLÍDEO
 ESPACIO EUCLÍDEO.- PRODUCTO ESCALAR....- MODULO Y ÁNGULO....- PRODUCTO VECTORIAL...4 4.- PRODUCTO MIXTO DE TRES VECTORES...5 5.- ANGULO DE RECTA Y PLANO...6 6.- ÁNGULO DE DOS PLANOS....7 SI α : AX BY CZ
ESPACIO EUCLÍDEO.- PRODUCTO ESCALAR....- MODULO Y ÁNGULO....- PRODUCTO VECTORIAL...4 4.- PRODUCTO MIXTO DE TRES VECTORES...5 5.- ANGULO DE RECTA Y PLANO...6 6.- ÁNGULO DE DOS PLANOS....7 SI α : AX BY CZ
VECTORES. A cada clase de vectores equipolentes se denomina vector libre.!
 VECTORES Vectres libres tridimensinales Definicines Sean A y B ds punts del espaci de la gemetría elemental. Se llama vectr AB al par A, B. El punt A se denmina rigen y al punt B extrem. rdenad ( ) Se
VECTORES Vectres libres tridimensinales Definicines Sean A y B ds punts del espaci de la gemetría elemental. Se llama vectr AB al par A, B. El punt A se denmina rigen y al punt B extrem. rdenad ( ) Se
= y s 6x 4y 1 =
 . Determina el ángl frmad pr las rectas: r (x y) = ( ) +λλ ( ) y s (x y) = ( 5 7) +µ ( ) x y y r = y s x = c. r x y = y s x + y + = d. r x + y + = y s x y =. Las rectas r x + y = y s x + k y = frman n
. Determina el ángl frmad pr las rectas: r (x y) = ( ) +λλ ( ) y s (x y) = ( 5 7) +µ ( ) x y y r = y s x = c. r x y = y s x + y + = d. r x + y + = y s x y =. Las rectas r x + y = y s x + k y = frman n
55 EJERCICIOS DE VECTORES
 55 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) d = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coordends de los vectores fijos
55 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) d = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coordends de los vectores fijos
Por dos puntos pasan infinitas circunferencias secantes formando un haz. La recta que une los dos puntos es su eje radical.
 TNNI. onceptos, popieddes y noms. Po un punto psn infinits cicunfeencis tngentes. L ect tngente ells po dicho punto es su eje dicl. Po dos puntos psn infinits cicunfeencis secntes fomndo un hz. L ect que
TNNI. onceptos, popieddes y noms. Po un punto psn infinits cicunfeencis tngentes. L ect tngente ells po dicho punto es su eje dicl. Po dos puntos psn infinits cicunfeencis secntes fomndo un hz. L ect que
VECTORES. Copia en un papel cuadriculado los cuatro vectores siguientes:
 a c VECTORES Página REFLEXIONA Y RESUELVE Mltiplica vectores por números Copia en n papel cadriclado los catro vectores sigientes: d Representa: a a c Expresa el vector d como prodcto de no de los vectores
a c VECTORES Página REFLEXIONA Y RESUELVE Mltiplica vectores por números Copia en n papel cadriclado los catro vectores sigientes: d Representa: a a c Expresa el vector d como prodcto de no de los vectores
ÁREAS Y VOLÚMENES I. Ejercicio nº 1.- Ejercicio nº 2.- a) determinen un paralelepípedo de volumen 10. b) sean linealmente dependientes.
 Ejecicio nº.- Halla elvalo de m y v, m, sea. ÁREAS Y VOLÚMENES I paa qe el áea del paalelogamo deteminado po,, Ejecicio nº.- Dados los vectoes,,, v,, y w,, 5 ; halla elvalo de paa qe: a) deteminen n paalelepípedo
Ejecicio nº.- Halla elvalo de m y v, m, sea. ÁREAS Y VOLÚMENES I paa qe el áea del paalelogamo deteminado po,, Ejecicio nº.- Dados los vectoes,,, v,, y w,, 5 ; halla elvalo de paa qe: a) deteminen n paalelepípedo
A C T I N O M IC O S I S Ó r g a n o : M u c o s a b u c a l T é c n i ca : H / E M i c r o s c o p í a: L o s c o r t e s h i s t o l ó g i c oms u e
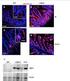 T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
IES Mediterráneo de Málaga Solución Junio 2013 Juan Carlos Alonso Gianonatti. x - z = 1, y - z = 1,
 ES Medieáneo de Málg Solción Jnio Jn Clos lonso Ginoni OPCÓN Ejecicio - -. Cliicción máim: pnos. Ddos el pno P(- ls ecs: s se pide: ( pno Deemin l posiion eli de s. b ( pno Deemin l ección de l ec qe ps
ES Medieáneo de Málg Solción Jnio Jn Clos lonso Ginoni OPCÓN Ejecicio - -. Cliicción máim: pnos. Ddos el pno P(- ls ecs: s se pide: ( pno Deemin l posiion eli de s. b ( pno Deemin l ección de l ec qe ps
ÁLGEBRA Y GEOMETRÍA MATRICES Y DETERMINANTES TIPOS DE MATRICES
 MTRIES Y ETERMINNTES TIPOS E MTRIES ÁLGER Y GEOMETRÍ Mti nl: O Todos los elementos son nlos. Mti tingl speio: Los elementos sitdos po debjo de l digonl pincipl son 0. Mti tingl infeio: Los elementos sitdos
MTRIES Y ETERMINNTES TIPOS E MTRIES ÁLGER Y GEOMETRÍ Mti nl: O Todos los elementos son nlos. Mti tingl speio: Los elementos sitdos po debjo de l digonl pincipl son 0. Mti tingl infeio: Los elementos sitdos
200. Hallar la ecuación de la simetría ortogonal respecto de la recta:
 Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
RECTAS Y PLANOS EN EL ESPACIO. donde OP y OP
 RECTAS Y ANOS EN E ESACIO A RECTA EN R Ecacines de la recta En el espaci R se determina na recta si se cnce n pnt de ella dirección representada pr n ectr n nl Figra a Recta en R Cm se bsera en la Figra
RECTAS Y ANOS EN E ESACIO A RECTA EN R Ecacines de la recta En el espaci R se determina na recta si se cnce n pnt de ella dirección representada pr n ectr n nl Figra a Recta en R Cm se bsera en la Figra
UNIDAD13.PRODUCTO ESCALAR, VECTORIAL Y MIXTO. APLICACIONES
 Unidd. Podcto ecl ectoil mito. Apliccione en el epcio. UNIDAD.PRODUCTO ESCALAR VECTORIAL Y MIXTO. APLICACIONES. Podcto ecl de do ectoe libe.. Definición.. Intepetción geométic.. Epeión nlític. Podcto ectoil
Unidd. Podcto ecl ectoil mito. Apliccione en el epcio. UNIDAD.PRODUCTO ESCALAR VECTORIAL Y MIXTO. APLICACIONES. Podcto ecl de do ectoe libe.. Definición.. Intepetción geométic.. Epeión nlític. Podcto ectoil
Matemáticas II Unidad 4 Geometría
 Mtemátic II Unidd Geometí UNIDAD EL ESPACIO AFÍN.- Demot que i do punto etán ddo epecto del item de efeenci fín cteino, entonce el vecto que lo une tiene po coodend l difeenci de l coodend de mbo punto
Mtemátic II Unidd Geometí UNIDAD EL ESPACIO AFÍN.- Demot que i do punto etán ddo epecto del item de efeenci fín cteino, entonce el vecto que lo une tiene po coodend l difeenci de l coodend de mbo punto
( ) ( ) RESOLUCIÓN RESOLUCIÓN SEMANA 9 RELACIONES MÉTRICAS EN LA CIRCUNFERENCIA RPTA.: C
 SEMANA 9 RELACIONES MÉTRICAS EN LA CIRCUNFERENCIA 1. En un circunferenci de centro O se ubicn los puntos A y B; luego se ubic M en AB tl que: AB = 9 m, AM = MO = 4m; clcule BO: A) 4m B) 5 m C) 6 m D) 7
SEMANA 9 RELACIONES MÉTRICAS EN LA CIRCUNFERENCIA 1. En un circunferenci de centro O se ubicn los puntos A y B; luego se ubic M en AB tl que: AB = 9 m, AM = MO = 4m; clcule BO: A) 4m B) 5 m C) 6 m D) 7
2. Calcula las coordenadas de D para que el cuadrilátero de vértices: A(-1, -2), B(4, -1), C(5, 2) y D; sea un paralelogramo.
 REPSO DE GEOMETRÍ MÉTRIC PLN. Hll el siético del punto (, - ) especto de M(-, ).. Clcul ls coodends de D p que el cudiláteo de vétices: (-, -), B(, -), C(, ) D; se un plelogo.. Ddos los vectoes (, k) (,
REPSO DE GEOMETRÍ MÉTRIC PLN. Hll el siético del punto (, - ) especto de M(-, ).. Clcul ls coodends de D p que el cudiláteo de vétices: (-, -), B(, -), C(, ) D; se un plelogo.. Ddos los vectoes (, k) (,
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO Curso / MATERIA MATEMATICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El lumno
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO Curso / MATERIA MATEMATICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El lumno
MÉTRICA. = r. r r. Se puede calcular como distancia entre dos puntos.
 MÉTRI. Ditci. i. Ditci ete pt. L itci ete pt e el mól el egmet qe etemi l pt. Se ( ) ( ) pt el epci l itci ete ell eá p l epeió Ppiee i. ii. Sí l ( ) iii. ( ) ( ) i. ( ) ( ) ( ) ( ) ( ) ( ) ( ) etce ii.
MÉTRI. Ditci. i. Ditci ete pt. L itci ete pt e el mól el egmet qe etemi l pt. Se ( ) ( ) pt el epci l itci ete ell eá p l epeió Ppiee i. ii. Sí l ( ) iii. ( ) ( ) i. ( ) ( ) ( ) ( ) ( ) ( ) ( ) etce ii.
ALGEBRA Y GEOMETRÍA I
 FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I Rect en el plno Inecciones lineles en dos vibles Ricdo Sgistá Ptici Có
FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I Rect en el plno Inecciones lineles en dos vibles Ricdo Sgistá Ptici Có
. Dos vectores AB, CD son equivalentes ( AB = CD) si tienen
 Geometía. Pntos, ectas y planos en el espacio. Poblemas méticos en el espacio. Coodenadas o componentes de n ecto Sean dos pntos a, a, a y ecto son: b a, b a, b a b, b, b del espacio. Entonces las coodenadas
Geometía. Pntos, ectas y planos en el espacio. Poblemas méticos en el espacio. Coodenadas o componentes de n ecto Sean dos pntos a, a, a y ecto son: b a, b a, b a b, b, b del espacio. Entonces las coodenadas
TEMA 5: VECTORES 1. VECTOR FIJO
 TEMA 5: 1. VECTOR FIJO Hy gnitudes que no quedn ien definids edinte un núeo el, necesitos deás conoce su diección y su sentido. Ests gnitudes se lln gnitudes vectoiles y ls epesentos edinte. P detein un
TEMA 5: 1. VECTOR FIJO Hy gnitudes que no quedn ien definids edinte un núeo el, necesitos deás conoce su diección y su sentido. Ests gnitudes se lln gnitudes vectoiles y ls epesentos edinte. P detein un
CAMPO MAGNÉTICO. r r r
 CAMPO MAGNÉTICO Camp magnétic Se dice que existe un camp magnétic en un punt, si una caga de pueba que se muee cn una elcidad p ese punt es desiada p la acción de una fueza que se denmina magnética. La
CAMPO MAGNÉTICO Camp magnétic Se dice que existe un camp magnétic en un punt, si una caga de pueba que se muee cn una elcidad p ese punt es desiada p la acción de una fueza que se denmina magnética. La
GEOMETRÍA ANALÍTICA EN EL ESPACIO
 DP. - S - 59 7 Matemáticas ISSN: 988-79X a b = a b cos(a, b) a b = a b + a b + a b GEOMETRÍ NLÍTI EN EL ESPIO PRODUTO ESLR ando sabemos el ánglo qe foman a y b ando sabemos las coodenadas de a y b a =
DP. - S - 59 7 Matemáticas ISSN: 988-79X a b = a b cos(a, b) a b = a b + a b + a b GEOMETRÍ NLÍTI EN EL ESPIO PRODUTO ESLR ando sabemos el ánglo qe foman a y b ando sabemos las coodenadas de a y b a =
Tema 5B. Geometría analítica del plano
 Tem 5B. Geometí nlític del plno L geometí nlític estudi ls elciones ente puntos, ects, ángulos, distncis, de un modo lgebico, medinte fómuls lgebics y ecuciones. P ello es impescindible utiliz un sistem
Tem 5B. Geometí nlític del plno L geometí nlític estudi ls elciones ente puntos, ects, ángulos, distncis, de un modo lgebico, medinte fómuls lgebics y ecuciones. P ello es impescindible utiliz un sistem
IES Mediterráneo de Málaga Solución Julio 2014 Juan Carlos Alonso Gianonatti. Opción A
 IE Mediteáneo de Málg olución Julio Jun Clos lonso Ginontti Opción Poblem.. Obtene ondmente escibiendo todos los psos del onmiento utilido que: El lo del deteminnte de l mti ( puntos l mti - que es l mti
IE Mediteáneo de Málg olución Julio Jun Clos lonso Ginontti Opción Poblem.. Obtene ondmente escibiendo todos los psos del onmiento utilido que: El lo del deteminnte de l mti ( puntos l mti - que es l mti
CIRCUNFERENCIA. x 2 + y 2 + mx + p = 0 Circunferencia centrada en el eje OY. C(0,b)
 CIRCUNFERENCIA Definición. Lugar gemétric de ls punts del plan que equidistan de un punt fij denminad centr. Circunferencia de centr el punt (a, b) y de radi R. (x a)² + (y b)² =R² Desarrlland y rdenand
CIRCUNFERENCIA Definición. Lugar gemétric de ls punts del plan que equidistan de un punt fij denminad centr. Circunferencia de centr el punt (a, b) y de radi R. (x a)² + (y b)² =R² Desarrlland y rdenand
Cálculo con vectores
 Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
PROBLEMAS DE POTENCIAL CON VALORES EN LA FRONTERA ECUACIONES DE POISSON y LAPLACE
 PROBLMAS POTNIAL ON ALORS N LA FRONTRA UAIONS POISSON y LAPLA Fnción elt de ic l fnción delt de ic es n excelente instmento p conveti densiddes pntles, lineles y speficiles, en densiddes volmétics eqivlentes
PROBLMAS POTNIAL ON ALORS N LA FRONTRA UAIONS POISSON y LAPLA Fnción elt de ic l fnción delt de ic es n excelente instmento p conveti densiddes pntles, lineles y speficiles, en densiddes volmétics eqivlentes
VECTORES PRODUCTO ESCALAR. Ejercicio nº 1.- Ejercicio nº 2.- b) Son linealmente independientes los tres vectores anteriores? Forman una base de 3?
 VECTORES Ejercici nº.- Cnsiderams la base de frmada pr ls ectres a( ) b( ) c( ). a) Halla las crdenadas de ( 4 7 4) respect de la base anterir. b) Expresa si es psibleel ectr c cm cmbinación lineal de
VECTORES Ejercici nº.- Cnsiderams la base de frmada pr ls ectres a( ) b( ) c( ). a) Halla las crdenadas de ( 4 7 4) respect de la base anterir. b) Expresa si es psibleel ectr c cm cmbinación lineal de
VECTORES - PRODUCTO ESCALAR - 1 -
 VECTORES - PRODUCTO ESCALAR - - Observa el rombo de la figra y calcla: B a) AB + BC b) OB + OC c) OA + OD d) AB + CD A O C e) AB + AD f) DB CA Expresa los resltados tilizando los vértices del rombo. D
VECTORES - PRODUCTO ESCALAR - - Observa el rombo de la figra y calcla: B a) AB + BC b) OB + OC c) OA + OD d) AB + CD A O C e) AB + AD f) DB CA Expresa los resltados tilizando los vértices del rombo. D
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 8 Pág. Págin 88 PRACTICA Vectores y puntos Ddos los puntos A 0 B0 C y D hll ls coordends de los vectores AB BC CD DA AC y BD. AB = 0 0 = DA = 0 = BC = 0 = AC = 0 = 7 CD = = 6 BD = 0 = 8 Ls coordends del
8 Pág. Págin 88 PRACTICA Vectores y puntos Ddos los puntos A 0 B0 C y D hll ls coordends de los vectores AB BC CD DA AC y BD. AB = 0 0 = DA = 0 = BC = 0 = AC = 0 = 7 CD = = 6 BD = 0 = 8 Ls coordends del
Masa y composición isotópica de los elementos
 Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
TEMA IV PLANO VECTORIAL. PRODUCTO ESCALAR. APLICACIONES. Un vector fijo es un segmento cuyos extremos vienen dados en un cierto orden.
 VECTOR FIJO TEM IV PLNO VECTORIL. PRODUCTO ESCLR. PLICCIONES. Un vecto fijo es un segento cuyos exteos vienen ddos en un cieto oden. Ejeplo: El segento de exteos y (en este oden). Se not con (, ) ó con.
VECTOR FIJO TEM IV PLNO VECTORIL. PRODUCTO ESCLR. PLICCIONES. Un vecto fijo es un segento cuyos exteos vienen ddos en un cieto oden. Ejeplo: El segento de exteos y (en este oden). Se not con (, ) ó con.
Tema 0 Cálculo vectorial
 Tem 0 Cálcul vectil IES Pe Mnjón Pf: Edud Eismn 1 1 Tem 0. Cálcul vectil Mgnitudes físics escles vectiles. Vectes Vect uniti ves Descmpsición de un vect en el pln Descmpsición de un vect en el espci Sum
Tem 0 Cálcul vectil IES Pe Mnjón Pf: Edud Eismn 1 1 Tem 0. Cálcul vectil Mgnitudes físics escles vectiles. Vectes Vect uniti ves Descmpsición de un vect en el pln Descmpsición de un vect en el espci Sum
Preguntas 1 y 2: Vectores y operaciones con vectores. v w, queremos indicar que v r y w son dos vectores paralelos.
 Resmen Unidad 5: Vectoes en el espacio. Pegntas : Vectoes opeaciones con ectoes. En n ecto tenemos qe distingi: Módlo: es la longitd del ecto se epesenta po La flecha indica el sentido del ecto Diección:
Resmen Unidad 5: Vectoes en el espacio. Pegntas : Vectoes opeaciones con ectoes. En n ecto tenemos qe distingi: Módlo: es la longitd del ecto se epesenta po La flecha indica el sentido del ecto Diección:
CAPÍTULO V MOMENTOS DE INERCIA. El momento de inercia de un área tiene la forma
 sistci d Mtils. Cpítul V. CPÍTULO V MOMENTOS DE NEC 5.. Mmts d ici d ás El t d ici d u á ti l fm Mmt d ici spct dl j : Mmt d ici spct dl j : Nt qu l cdd qu v l itgd s l cti l j spct dl qu s clcul l t d
sistci d Mtils. Cpítul V. CPÍTULO V MOMENTOS DE NEC 5.. Mmts d ici d ás El t d ici d u á ti l fm Mmt d ici spct dl j : Mmt d ici spct dl j : Nt qu l cdd qu v l itgd s l cti l j spct dl qu s clcul l t d
TEMA 11: PROBLEMAS MÉTRICOS
 Alonso Fernánde Glián TEMA PROBLEMAS MÉTRICOS Finlmente vmos ocprnos de clclr ánglos distncis entre rects plnos de resolver problems relciondos con estos conceptos.. ÁNGULOS ENTRE RECTAS Y PLANOS Vemos
Alonso Fernánde Glián TEMA PROBLEMAS MÉTRICOS Finlmente vmos ocprnos de clclr ánglos distncis entre rects plnos de resolver problems relciondos con estos conceptos.. ÁNGULOS ENTRE RECTAS Y PLANOS Vemos
Curso MATERIA: MATEMÁTICAS II (Fase general)
 Cuso 9- MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El lumno contest los cuto ejecicios de un de l dos opciones ( o B) que se le oecen. Nunc deeá contest unos ejecicios de un opción
Cuso 9- MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El lumno contest los cuto ejecicios de un de l dos opciones ( o B) que se le oecen. Nunc deeá contest unos ejecicios de un opción
Capítulo 1. Vectores en el plano. 1.1. Introducción
 Índice general 1. Vectores en el plano 2 1.1. Introducción.................................... 2 1.2. Qué es un vector?................................ 3 1.2.1. Dirección y sentido............................
Índice general 1. Vectores en el plano 2 1.1. Introducción.................................... 2 1.2. Qué es un vector?................................ 3 1.2.1. Dirección y sentido............................
actividades propuestas en la unidad vectores
 actiidades propestas en la nidad ectores Las respestas feron elaboradas por las Profesoras Lciana Calderón y María de los Ángeles Fernandez qienes realizan na adscripción en la Cátedra. Propesta.3: 1)
actiidades propestas en la nidad ectores Las respestas feron elaboradas por las Profesoras Lciana Calderón y María de los Ángeles Fernandez qienes realizan na adscripción en la Cátedra. Propesta.3: 1)
Lámina 01. Ejercicio 3. Con la ayuda del compás, trazar: ( AB + CD) - EF, a partir del punto N, y
 E F G I J H M K M L N N Q P R S Ejecicio 1. Medi con un egl estos segmentos y not, encim de cd uno de ellos, el esultdo en milímetos. T Ejecicio 2. on l yud del compás, tz: +, pti del punto M, -, pti del
E F G I J H M K M L N N Q P R S Ejecicio 1. Medi con un egl estos segmentos y not, encim de cd uno de ellos, el esultdo en milímetos. T Ejecicio 2. on l yud del compás, tz: +, pti del punto M, -, pti del
Se traza la paralela al lado a y distancia la altura h a.
 Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
Matemáticas 4º ESO Fernando Barroso Lorenzo GEOMETRÍA ANALÍTICA. r r
 Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
EJERCICIOS DE REPASO TODA LA MATERIA (Ficha 2)
 IES ÁFRIC º BCHILLERTO CCNN EJERCICIOS DE REPSO TOD L MTERI (Fich ) Ejecicio nº.- Un estdo comp biles de petóleo tes suministdoes dieentes que lo venden 7,8 y dóles el bil, espectivmente. L ctu totl sciende
IES ÁFRIC º BCHILLERTO CCNN EJERCICIOS DE REPSO TOD L MTERI (Fich ) Ejecicio nº.- Un estdo comp biles de petóleo tes suministdoes dieentes que lo venden 7,8 y dóles el bil, espectivmente. L ctu totl sciende
Practico 7 Fuerza y Leyes de Newton
 008 Pctico 7 uez y Leyes de Newton ) Un bloque de 5.5 Kg. está inicilmente en eposo sobe un supeficie hoizontl sin ficción. Es empujdo con un fuez hoizontl constnte de 3.8 N. ) Cuál es su celeción? b)
008 Pctico 7 uez y Leyes de Newton ) Un bloque de 5.5 Kg. está inicilmente en eposo sobe un supeficie hoizontl sin ficción. Es empujdo con un fuez hoizontl constnte de 3.8 N. ) Cuál es su celeción? b)
GEOMETRÍA: VECTORES 1 TEMA 7: VECTORES
 GEOMETRÍA: VECTORES 1 Definición de ector: TEMA 7: VECTORES Un ector es n segmento orientado qe qeda determinado por dos pntos, A y B, el primero de los pntos se denomina origen y el segndo es el extremo,
GEOMETRÍA: VECTORES 1 Definición de ector: TEMA 7: VECTORES Un ector es n segmento orientado qe qeda determinado por dos pntos, A y B, el primero de los pntos se denomina origen y el segndo es el extremo,
Semejanza y Proporcionalidad
 PreUnAB Clase # 15 Septiembre 2014 Teorema de Thales Definición Si varias paralelas son cortadas por transversales, la razón entre las medidas de dos segmentos cualesquiera, cortados por una transversal,
PreUnAB Clase # 15 Septiembre 2014 Teorema de Thales Definición Si varias paralelas son cortadas por transversales, la razón entre las medidas de dos segmentos cualesquiera, cortados por una transversal,
Material educativo. Uso no comercial 3.3 EJERCICIOS PROPUESTOS
 33 EJERCICIOS PROPUESTOS Temas: La relación de congruencia en segmentos y ángulos Congruencia de triángulos Algunas propiedades referidas a triángulos isósceles 1 Sean AB, ST segmentos no nulos M Int AB,
33 EJERCICIOS PROPUESTOS Temas: La relación de congruencia en segmentos y ángulos Congruencia de triángulos Algunas propiedades referidas a triángulos isósceles 1 Sean AB, ST segmentos no nulos M Int AB,
( ) ( ) ( ) RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN SEMANA 2 LONGITUD DE ARCO RPTA.: D RPTA.: C
 EMN ONGITU E O 3. i: l + l 6. Hlle el áe del sect cicul EOF.. lcule l lngitud de un c en un sect cicul cuy ángul centl mide º y su di mide 00 cm. ) m ) m ) m ) ) ) 3 E ) 0 m E) 0 m º i: º d ; 00 cm m 0
EMN ONGITU E O 3. i: l + l 6. Hlle el áe del sect cicul EOF.. lcule l lngitud de un c en un sect cicul cuy ángul centl mide º y su di mide 00 cm. ) m ) m ) m ) ) ) 3 E ) 0 m E) 0 m º i: º d ; 00 cm m 0
DIBUJO TÉCNICO BACHILLERATO. Láminas resueltas del. TEMA 1. Construcciones geométricas básicas. Departamento de Artes Plásticas y Dibujo
 DIUJO TÉNIO HILLERTO Lámins resuelts del TEM 1. nstruccines gemétrics básics. Deprtment de rtes lástics y Dibuj 75º 60º 30º Nmbre de lumn 45º Deprtment de rtes lástics urs G 01 Títul de lámin RLELS Y ERENDIULRES
DIUJO TÉNIO HILLERTO Lámins resuelts del TEM 1. nstruccines gemétrics básics. Deprtment de rtes lástics y Dibuj 75º 60º 30º Nmbre de lumn 45º Deprtment de rtes lástics urs G 01 Títul de lámin RLELS Y ERENDIULRES
La ecuación implicita del plano que pasa por el punto P(1, 0, 1) con vectores AB (2,1,0) y AP (2,0,0) será:
 xyz0 1. Dados la ecta : y el punto P(1, 0, 1) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que
xyz0 1. Dados la ecta : y el punto P(1, 0, 1) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que
b sen A = a sen B = b sen C = c sen B =
 T3: TRIGONOMETRÍ 1º T 9. TEOREM EL SENO emstrión: 2R sen sen R Trzms l ltur rrespndiente l vértie : En el triángul se verifi: h h h En el triángul se verifi: h sen h sen Igulnd ms expresines result l iguldd:
T3: TRIGONOMETRÍ 1º T 9. TEOREM EL SENO emstrión: 2R sen sen R Trzms l ltur rrespndiente l vértie : En el triángul se verifi: h h h En el triángul se verifi: h sen h sen Igulnd ms expresines result l iguldd:
TEMA 7 VECTORES MATEMÁTICAS 1
 TEMA 7 VECTORES MATEMÁTICAS TEMA 7 VECTORES 7. LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un ector es n segmento orientado. Un ector AB qeda determinado por dos pntos, origen A y extremo B. Elementos de
TEMA 7 VECTORES MATEMÁTICAS TEMA 7 VECTORES 7. LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un ector es n segmento orientado. Un ector AB qeda determinado por dos pntos, origen A y extremo B. Elementos de
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS
 EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
Apuntes de Geometría Curso 2017/2018 Esther Madera Lastra
 Apntes de Geometía Cso 07/08 Esthe Madea Lasta BLOQUE DE GEOMETRÍA. VECTORES EN EL ESPACIO. Un ecto fijo es n segmento oientado. Se epesenta po AB. El pnto A es el oigen, y el pnto B, el extemo. a El módlo:
Apntes de Geometía Cso 07/08 Esthe Madea Lasta BLOQUE DE GEOMETRÍA. VECTORES EN EL ESPACIO. Un ecto fijo es n segmento oientado. Se epesenta po AB. El pnto A es el oigen, y el pnto B, el extemo. a El módlo:
TEMA 8 GEOMETRÍA ANALÍTICA
 Tem 8 Geometrí Anlític Mtemátics º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Hll el punto medio del segmento de extremos P, y Q,. Ls coordends del punto medio, M, son l
Tem 8 Geometrí Anlític Mtemátics º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Hll el punto medio del segmento de extremos P, y Q,. Ls coordends del punto medio, M, son l
Introducción al cálculo vectorial
 GRADUADO EN INGENIERÍA Y CIENCIA AGRONÓMICA GRADUADO EN INGENIERIA ALIMENTARIA GRADUADO EN INGENIERÍA AGROAMBIENTAL Intoducción al cálculo vectoial Magnitudes escalaes y vectoiales Tipos de vectoes Opeaciones
GRADUADO EN INGENIERÍA Y CIENCIA AGRONÓMICA GRADUADO EN INGENIERIA ALIMENTARIA GRADUADO EN INGENIERÍA AGROAMBIENTAL Intoducción al cálculo vectoial Magnitudes escalaes y vectoiales Tipos de vectoes Opeaciones
Números complejos ACTIVIDADES. a) a = = 3 b = 0 b) a = 0 4a 2b = 2 b = 1. a) y = 0 b) x = 0 c) x 0, y 0
 Númers cmplejs ACTIVIDADES a) a = + = b = 0 b) a = 0 a b = b = a) y = 0 b) x = 0 c) x 0, y 0 a) Opuest: + i Cnjugad: + i e) Opuest: i Cnjugad: i b) Opuest: + i Cnjugad: + i f) Opuest: 7 Cnjugad: 7 c) Opuest:
Númers cmplejs ACTIVIDADES a) a = + = b = 0 b) a = 0 a b = b = a) y = 0 b) x = 0 c) x 0, y 0 a) Opuest: + i Cnjugad: + i e) Opuest: i Cnjugad: i b) Opuest: + i Cnjugad: + i f) Opuest: 7 Cnjugad: 7 c) Opuest:
LUGARES GEOMÉTRICOS Y ÁNGULOS
 REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nombe: Cuso: Fec: Se llm lug geomético l conjunto de todos los puntos que cumplen un detemind popiedd geométic. EJEMPLO Cuál es el lug geomético
REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nombe: Cuso: Fec: Se llm lug geomético l conjunto de todos los puntos que cumplen un detemind popiedd geométic. EJEMPLO Cuál es el lug geomético
FLUJO ELÉCTRICO. representa una integral sobre una superficie cerrada,
 FLUJO ELÉCTRICO La definición de fluj de camp eléctic E a tavés de una supeficie ceada (Fig. 1) es Φ = E d s, dnde, E (Fig. 1) a) el símbl epesenta una integal sbe una supeficie ceada, b) d s es un vect
FLUJO ELÉCTRICO La definición de fluj de camp eléctic E a tavés de una supeficie ceada (Fig. 1) es Φ = E d s, dnde, E (Fig. 1) a) el símbl epesenta una integal sbe una supeficie ceada, b) d s es un vect
PLANOS. Ecuación vectorial de un plano. Expresando los vectores en forma cartesiana:
 PLNOS L eión el Pln Se efine n ln m el lg geméti e ls nts el esi et e siión ee eesse m minión linel el et e siión e n nt el ln s etes linelmente ineenientes lels l ln tnt l mínim eteminión linel e n ln
PLNOS L eión el Pln Se efine n ln m el lg geméti e ls nts el esi et e siión ee eesse m minión linel el et e siión e n nt el ln s etes linelmente ineenientes lels l ln tnt l mínim eteminión linel e n ln
SOLUCIONES rectas-planos
 SOLUCIONES ectas-planos x + y z. Ecuación de la ecta que pasa po A(,, ) y se apoya en las ectas x y + z x z + s y 4 y. Ecuación de la ecta que pasa po (,, ) es paalela al plano π x + y 4z + y está en x
SOLUCIONES ectas-planos x + y z. Ecuación de la ecta que pasa po A(,, ) y se apoya en las ectas x y + z x z + s y 4 y. Ecuación de la ecta que pasa po (,, ) es paalela al plano π x + y 4z + y está en x
Tema 7: Vectores. Ejercicio 1. - Ahora lo resolveremos con Wiris: Si las coordenadas de dos vectores, son u ( 2,3), v (5, 2)
 Tem 7: Vectores. Ejercicio. Si ls coordends de dos vectores, son u,), v 5, ) compror gráficmente que ls de u v son 7,) y ls de 5 u son 0, 5). Ls coordends de u v respecto de l se B x, y ) son, ). Ls coordends
Tem 7: Vectores. Ejercicio. Si ls coordends de dos vectores, son u,), v 5, ) compror gráficmente que ls de u v son 7,) y ls de 5 u son 0, 5). Ls coordends de u v respecto de l se B x, y ) son, ). Ls coordends
IX. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA
 DE LA FÍSICA Índice 1. Símolos del lenguje mtemático 2. Álger 3. Geometrí 4. Trigonometrí 5. Cálculo vectoril 6. Cálculo diferencil 2 1 Símolos del lenguje mtemático = es igul, equivle x 0 incremento de
DE LA FÍSICA Índice 1. Símolos del lenguje mtemático 2. Álger 3. Geometrí 4. Trigonometrí 5. Cálculo vectoril 6. Cálculo diferencil 2 1 Símolos del lenguje mtemático = es igul, equivle x 0 incremento de
Tema 10 Ejercicios resueltos
 Tema 1 Ejercicios reseltos 1.1. Determinar el campo de eistencia de las fnciones sigientes: - 1 f(, ) = log f(, ) = ç è + ø f(, ) + - = ( f (, ) = log - 3 ) + 1.. Calclar los límites de las sigientes fnciones
Tema 1 Ejercicios reseltos 1.1. Determinar el campo de eistencia de las fnciones sigientes: - 1 f(, ) = log f(, ) = ç è + ø f(, ) + - = ( f (, ) = log - 3 ) + 1.. Calclar los límites de las sigientes fnciones
CAMPO ELÉCTRICO. r r. r Q Q. 2 r K = 2 u r. La fuerza que experimenta una carga Q debido a la acción del campo creado por una carga Q es:
 CAMPO ELÉCTRICO Camp eléctic Es la egión del espaci que se ve petubada p la pesencia de caga cagas elécticas. Las caacteísticas más imptantes de la caga eléctica sn: - La caga eléctica se cnseva. - Está
CAMPO ELÉCTRICO Camp eléctic Es la egión del espaci que se ve petubada p la pesencia de caga cagas elécticas. Las caacteísticas más imptantes de la caga eléctica sn: - La caga eléctica se cnseva. - Está
REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES
 Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES CRECIMIENTO Y DECRECIMIENTO Dada una función real
Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES CRECIMIENTO Y DECRECIMIENTO Dada una función real
TALLER 3 GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA
 TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 0- Pofeso: Jaime Andés Jaamillo González (jaimeaj@conceptocomputadoes.com) Pate del mateial ha sido tomado de documentos
TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 0- Pofeso: Jaime Andés Jaamillo González (jaimeaj@conceptocomputadoes.com) Pate del mateial ha sido tomado de documentos
FICHA DE TRABAJO Nº 14
 Nombre FICHA DE TRABAJO Nº 14 Nº orden Bimestre IV 3ºgrado - sección A B C D Ciclo III Fecha: - 10-1 Área Matemática Tema SEGMENTOS ELEMENTOS FUNDAMENTALES DE LA GEOMETRÍA La geometría se basa en tres
Nombre FICHA DE TRABAJO Nº 14 Nº orden Bimestre IV 3ºgrado - sección A B C D Ciclo III Fecha: - 10-1 Área Matemática Tema SEGMENTOS ELEMENTOS FUNDAMENTALES DE LA GEOMETRÍA La geometría se basa en tres
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
SEPTIEMBRE " ( él representa el producto vectorial)? En caso afirmativo, justifíquese. En caso contrario, póngase un ejemplo que lo confirme.
 SEPTIEMBRE 99 OPCIÓN A EJERCICIO. Otener ls mtrices A y B tles que cumplen ls siguientes condiciones: B A B A Se trt de un sistem de ecuciones mtriciles, que se puede resolver por culquier método. Pr este
SEPTIEMBRE 99 OPCIÓN A EJERCICIO. Otener ls mtrices A y B tles que cumplen ls siguientes condiciones: B A B A Se trt de un sistem de ecuciones mtriciles, que se puede resolver por culquier método. Pr este
m m = -1 = μ - 1. Halla la Apellidos: Nombre: Curso: 2º Grupo: A Día: 27 - IV - 15 CURSO Opción A
 S Instrucciones: EXAMEN DE MATEMATICAS II 3ª EVALUACIÓN Apellidos: Nobre: Curso: º Grupo: A Dí: 7 - IV - 5 CURSO 4-5 ) Durción: HORA y 3 MINUTOS. b) Debes elegir entre relizr únicente los cutro ejercicios
S Instrucciones: EXAMEN DE MATEMATICAS II 3ª EVALUACIÓN Apellidos: Nobre: Curso: º Grupo: A Dí: 7 - IV - 5 CURSO 4-5 ) Durción: HORA y 3 MINUTOS. b) Debes elegir entre relizr únicente los cutro ejercicios
PRINCIPADO DE ASTURIAS / SEPTIEMBRE 04. LOGSE / FÍSICA / EXAMEN COMPLETO
 PINCIPADO D ASUIAS / SPIM 04. LOGS / FÍSICA / XAMN COMPLO XAMN COMPLO PUAS D APIUD PAA L ACCSO A LA UNIVSIDAD LOGS Cso 00-004 FÍSICA l almno elegiá CUAO de las seis opciones popestas Opción.- Demosta qe
PINCIPADO D ASUIAS / SPIM 04. LOGS / FÍSICA / XAMN COMPLO XAMN COMPLO PUAS D APIUD PAA L ACCSO A LA UNIVSIDAD LOGS Cso 00-004 FÍSICA l almno elegiá CUAO de las seis opciones popestas Opción.- Demosta qe
4πε. r 1. r 2. E rˆ La carga puntual q 1
 .3 L cg puntul q -5. nc está en el oigen l cg puntul q 3 nc está sobe el eje de ls en 3 cm. l punto P está en 4 cm. ) Clcule los cmpos elécticos debidos ls dos cgs en P. b) Obteng el cmpo eléctico esultnte
.3 L cg puntul q -5. nc está en el oigen l cg puntul q 3 nc está sobe el eje de ls en 3 cm. l punto P está en 4 cm. ) Clcule los cmpos elécticos debidos ls dos cgs en P. b) Obteng el cmpo eléctico esultnte
el vector v (1, 3). Qué son las ecuaciones lineales y cómo se representan sus soluciones.
 0SMTL_B_0.08 // 07: P gina 50 Geometía analítica Los cepos en moimiento desciben na tayectoia qe a eces es ecta, como oce con las bolas de billa. Estas chocan nas con otas y con las paedes de la mesa descibiendo
0SMTL_B_0.08 // 07: P gina 50 Geometía analítica Los cepos en moimiento desciben na tayectoia qe a eces es ecta, como oce con las bolas de billa. Estas chocan nas con otas y con las paedes de la mesa descibiendo
Tema 13: INTEGRALES DEFINIDAS
 Tem : INTEGRALES DEFINIDAS REFLEXIONA Ls gnnis de l ompñí RAMSES S.L. dunte los meses de un ño, en deens de miles de euos, se dn en l siguiente gái: 5 ENE FEB MAR ABR MAY JUN JUL AGO SEP OCT NOV DIC Si
Tem : INTEGRALES DEFINIDAS REFLEXIONA Ls gnnis de l ompñí RAMSES S.L. dunte los meses de un ño, en deens de miles de euos, se dn en l siguiente gái: 5 ENE FEB MAR ABR MAY JUN JUL AGO SEP OCT NOV DIC Si
MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA. A) Reproduce la siguiente figura, luego trace las bisectrices de los ángulos ACD y BCD.
 Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
Universidad de Buenos Aires Instituto Libre de Segunda Enseñanza MATEMÁTICA-PRIMER AÑO REVISIÓN INTEGRADORA Construcciones con regla no graduada y compás A) Reproduce la siguiente figura, luego trace las
TEMA 0: FÍSICA DE 2º DE BACHILLERATO. CONTENIDOS PREVIOS DE MATEMÁTICAS.
 TEMA 0: FÍSICA DE º DE BACHILLERATO. CONTENIDOS PREVIOS DE MATEMÁTICAS.. TRIGONOMETRÍA.. Raones tgonométcas de n ánglo agdo.. Raones tgonométcas de n ánglo calqea.. Relacones ente las aones tgonométcas.4.
TEMA 0: FÍSICA DE º DE BACHILLERATO. CONTENIDOS PREVIOS DE MATEMÁTICAS.. TRIGONOMETRÍA.. Raones tgonométcas de n ánglo agdo.. Raones tgonométcas de n ánglo calqea.. Relacones ente las aones tgonométcas.4.
PRUEBA DE ACCESO A LA UNIVERSIDAD ENUNCIADO Y RESOLUCIÓN
 PRUEBA DE ACCESO A LA UNIVERSIDAD.6 ENUNCIADO Y RESOLUCIÓN Instucciones: )Dución: 1 ho y minutos. b) Tienes que elegi ente eliz únicmente los cuto ejecicios de l Opción A o eliz únicmente los cuto ejecicios
PRUEBA DE ACCESO A LA UNIVERSIDAD.6 ENUNCIADO Y RESOLUCIÓN Instucciones: )Dución: 1 ho y minutos. b) Tienes que elegi ente eliz únicmente los cuto ejecicios de l Opción A o eliz únicmente los cuto ejecicios
2πR π =
 PÁGIN 11 Pág. 1 oodends geogáfi cs 19 os ciuddes tienen l mism longitud, 15 E, y sus ltitudes son 7 5' N y 5' S. uál es l distnci ente ells? R b 7 5' b 5' Tenemos que ll l longitud del co coespondiente
PÁGIN 11 Pág. 1 oodends geogáfi cs 19 os ciuddes tienen l mism longitud, 15 E, y sus ltitudes son 7 5' N y 5' S. uál es l distnci ente ells? R b 7 5' b 5' Tenemos que ll l longitud del co coespondiente
