Institut Alexandre Satorras Departament de Matemàtiques. Primer de Batxillerat. (científic-tecnològic) MATEMÀTIQUES. curs 2014/15
|
|
|
- Gregorio Reyes Moya
- hace 8 años
- Vistas:
Transcripción
1 Institut Alendre Storrs Deprtment de Mtemàtiques Primer de Btillert (científic-tecnològic) MATEMÀTIQUES curs 04/5
2 ÍNDEX.- Trigonometri pàg.- Geometri pàg 4.- Circumferènci i còniques pàg 4.- Conjunts numèrics pàg Successions i progressions pàg 6.- Funcions lgebriques i polinomis pàg Funcions trnscendents pàg Continuïtt pàg Derivdes pàg 58
3 CONNEXIONS AMB ALTRES MATÈRIES FÍSICA I Aproimcions, errors i notció científic: en tot el currículum de físic i prticulrment qun es fn pràctiques quntittives o es trct el tem de l sensibilitt dels instruments de mesur. Vectors i trigonometri: cinemàtic, dinàmic, cmp grvittori, cmp elèctric, electromgnetisme. Fenòmens periòdics: moviment circulr. Còniques: cmp grvittori, cmp elèctric. Les funcions polinòmiques, de proporcionlitt invers, eponencils i trigonomètriques: en tot el currículum de físic Tes de vrició i derivdes: pràcticment en totes les prts però especilment en l cinemàtic i el moviment ondultori. Estdístic: trctment de ddes eperimentls. QUÍMICA I Aproimcions, errors i notció científic: en tot el currículum de químic i prticulrment qun es fn pràctiques quntittives o es trct el tem de l sensibilitt dels instruments de mesur. Resolució d equcions: problemes d equilibri químic Estudi de funcions prtir de tules i gràfics Funcions polinòmiques i de proporcionlitt invers: llei dels gsos de Gy-Lussc, llei de Boyle-Mriotte Logritmes: equilibri químic, ph Tes de vrició i derivdes: cinètic químic, gsos idels. Estdístic: Trctment de ddes eperimentls. Ús de l clculdor i de fulls de càlcul en bon prt del currículum BIOLOGIA I i II Aproimcions, errors i notció científic: en tot el currículum de biologi i prticulrment qun es fn pràctiques quntittives o es trct el tem de l sensibilitt dels instruments de mesur. Funció eponencil: creiements de poblció Tes de vrició: t de creiement d un poblció Combintòri: Bioquímic i reproducció cel lulr Probbilitt: genètic Estdístic: Evolució DIBUIX TÈCNIC I Geometri pln: Construccions geomètriques i resolució gràfic de problemes. CIÈNCIES DE LA TERRA I DEL MEDI AMBIENT I Trigonometri: càlcul d àrees Funcions trigonomètriques: fenòmens periòdics FÍSICA II Còniques: interferències, cmp grvittori i elèctric. Derivdes: moviment ondultori Funcions trigonomètriques: moviment hrmònic simple, pèndul simple, moviment ondultori. Funció eponencil: físic nucler ELECTROTÈCNIA Derivdes, funcions trigonomètriques i compleos: Corrent ltern
4 TRIGONOMETRIA. Els ngles i l sev mesur Un ngle és un de les meitts en què qued dividit el pl per dues semirectes (nomendes costts) mb el mtei origen (noment vèrte). Per indicr quin meitt és es f un petit senyl en form d'rc de circumferènci. Un ngle té per nom un lletr (mjúscul o greg) que s'escriu en el vèrte o l'interior. Qun un objecte gir l voltnt d'un punt descriu un ngle que s nomen ngle de gir. Els ngles de gir són ngles orientts: ngles positius si el gir és contrri l de les busques del rellotge, i ngles negtius si giren en el mtei sentit. ngle de gir positiu ngle de gir negtiu Si el gir dón més d'un volt complet l centre, l'ngle que qued finlment entre els costts és l determinció principl de l'ngle de gir. Sistemes de mesur d ngles Hi h dos sistemes de mesur d'ngles: () El sistem dels grus. Té tres unitts: gru, minut i segon. En quest sistem un ngle recte vl 90 grus. No és un sistem deciml i per tnt no es poden escriure dècimes de gru ni de minut. () El sistem dels rdins: si es trç un circumferènci que té centre l vèrte d'un ngle, entre els costts quedrà un rc. Si l rc mesur igul que el rdi tenim rdià. L mesur d un ngle qulsevol en rdins és el resultt de dividir l longitud de l'rc entre l longitud del rdi. ngle = r m rdins m r
5 En quest sistem un ngle complet (un volt sencer) vl π rdins, un ngle pl en vl π, i un ngle recte en vl π rdins. Per cnvir de grus rdins i recíprocment s'utilitz l proporció grus = 80 rdins π Representció dels ngles l circumferènci unitt L circumferènci unitt és un circumferènci mb centre l'origen de coordendes que se supos de rdi. Un ngle es represent l circumferènci unitt posnt el vèrte l'origen i el primer costt l meitt positiv de l'ei horitzontl. Llvors l'ltre costt tll l circumferènci en un punt. Els eios divideien l circumferènci en qutre qudrnts. Segons en quin estigui el punt representtiu, l'ngle és diu que "l ngle és del primer qudrnt", "l ngle és del segon qudrnt", etc. L divisió dels qudrnts en dues o en tres prts produei els ngles més importnts (que tmbé preien en figures regulrs com el tringle equilàter, el qudrt o l hegon, bé com ngles propis o bé qun es trcen les bisectrius) que estn indicts les figures següents mb l sev mesur en grus i en rdins: Si el punt representtiu d'un ngle es reflectei successivment en cd ei s'obtenen tres ngles més, un cd qudrnt, que són els ngles relcionts mb el primer. Com veurem més endvnt questes relcions sern importnts per deduir les rons trigonomètiques d un ngle prtir d un ltre. 4
6 . Les rons trigonomètriques Si per un punt d'un costt d'un ngle gut es trç un perpendiculr l'ltre costt es form un tringle rectngle. A prtir de les mesures, y i z es defineien les rons trigonomètriques de l'ngle, mb les quls relcionem els costts d un tringle rectngle mb els seus ngles. L divisió y:z s nomen el sinus de l'ngle: L divisió :z s nomen el cosinus de l'ngle: L divisió y: s nomen l tngent de l'ngle: y sin α = z cos α = z y tn α = El sinus, el cosinus i l tngent són tres nombres, generlment decimls, que són independents del punt que s hgi gft per definir-los (es comprov tenint en compte el Teorem de Tles). Si l'ngle està representt l circumferènci unitt les tres rons trigonomètriques corresponen les longituds de tres segments: Si l'ngle no és gut les rons trigonomètriques es defineien tl com s'indic l figur següent, considernt el punt situt sobre uns eios de coordendes: segon qudrnt tercer qudrnt qurt qudrnt Les longituds de i de y es compten com positives o com negtives d'cord mb l sev posició respecte dels eios, i l longitud z es compt sempre positiv. 5
7 Result doncs que els signes de les rons trigonomètriques vrien segons els qudrnts de l form que s'indic continució: sinus cosinus tngent Relcions fonmentls Entre les tres rons trigonomètriques hi h dues relcions molt importnts: sin α+cos α = sin α tn α = cos α Un conseqüènci de l primer relció és que ni el sinus ni el cosinus poden ser més grns que ni més petits que -.. Càlcul de rons trigonomètriques Càlcul directe: Consistei en pssr de l'ngle les rons. Es f mb les tecles sin, cos i tn de l clculdor. Cl tenir en compte que l'ngle es pot entrr en grus (mode DEG) o en rdins (mode RAD). Convé sber les rons d'lguns ngles que tenen un form especilment senzill: Angle grus Angle rdins 0 π 6 π 4 π π π π sinus 0 / / / 0 - cosinus / / / 0-0 tngent 0 / cp 0 cp Càlcul invers: Consistei pssr d'un de les rons l'ngle. Es f mb les tecles sin -, cos - i tn - de l clculdor. Ar bé, hi h molts ngles que tenen un mtei ró. L clculdor només en dón un, que s nomen l'rcsinus, rccosinus o rctngent segons els csos; els ltres s'hn de clculr seguint l'esquem nterior i sumnt i restnt múltiples de 60. Per donr l respost correct és necessri sber en quin qudrnt h d'estr. 6
8 Rons trigonomètriques d un ngle relcionnt-lo mb un del primer qudrnt: Si coneiem les rons trigonomètriques d un ngle α es poden deduir les dels ngles relcionts mb ell de l form següent: sin (80-α )= sin α cos (80-α )= - cos α tn (80-α )= -tn α sin (80+α )= - sin α cos (80+α )= - cos α tn (80+α )= tn α sin (60-α )= - sin α cos (60-α )= cos α tn (60-α )= -tn α Aquestes relcions quedrien ií esquemtitzdes, respecte un ngle del primer qudrnt:: segon tercer qurt sinus iguls sinus oposts sinus oposts cosinus oposts cosinus oposts cosinus iguls tngents oposdes tngents iguls tngents oposdes Importnt: Per tnt cd volt hi h dos ngles que tenen un vlor igul per un ró determind, ecepte en el cs de sin o cos igul o -. Com trobr les rons trigonomètriques prtir d un de dond: Es pot fer: - utilitznt les relcions que hi h l finl de l secció ; llvors no és necessri clculr el vlor de l'ngle i els resultts poden ser més ectes, iò sí depenent d rrels qudrdes. - clculnt l'ngle que correspon l ró dond, mb les precucions epressdes bns. 4. Resolució de tringles Un tringle té sis elements que es poden mesurr: els tres costts, b i c i els tres ngles A, B i C. Normlment l lletr d'un ngle és l mjúscul de l lletr del costt opost. Resolució de tringles rectngles Si el tringle és rectngle i A és l'ngle recte, el costt s nomen hipotenus i els costts b i c s nomenen ctets. Entre quests elements hi h les següents relcions: () entre els ngles: A+B+C = 80 () entre els costts: = b +c (teorem de Pitàgores) () entre els ngles i els costts: sin B = b ctet opost B ctet djcent C = = = cos C hipotenus hipotenus cos B = c ctet djcent B ctet opost C = = = sin C hipotenus hipotenus tn B = b ctet opost B ctet djcent C = = c ctet djcent B ctet opost C = tn C 7
9 Entre els 5 elements B, C,, b i c es poden clculr tres d'ells si es sben els ltres dos (ecepte si quests dos són B i C). Aquest càlcul és l resolució del tringle rectngle. Relció entre les rons d un ngle i les del seu complementri A prtir de les relcions nteriors i tenint en compte que B+C=90 o sigui que C=90-B, en generl podem escriure les relcions entre les rons trigonomètriques d un ngle i el del seu complementri: sin (90-α )= cos α cos (90-α )= sin α tn (90- α )= tnα Resolució de tringles no rectngles L resolució d un tringle no rectngle pot fer-se tenint com ddes els tres costts un costt i els ngles djcents dos costts i l'ngle que formen dos costts i un ngle que no formen. En quest cs el problem pot tenir dues solucions. El càlcul dels ltres elements es f prtir de les relcions: ) A+B+C = 80 ) fórmules del cosinus: ² = b² + c² - bc.cos A b² = ² + c² - c.cos B c² = ² + b² - b.cos C ) fórmul dels sinus sin A = b sin B = c sin C És interessnt pensr en l resolució geomètric mb regle i compàs dels diferents csos, prtir de les ddes que tenim, i es pot nlitzr quines ddes dónen solució, quines no i quines en donen dues. 5. Fórmules mb rons trigonomètriques No és cert que sin(+b) = sin + sin b, ni que sin = sin, ni ltres relcions simples d'quest cire. Les utèntiques relcions entre les rons trigonomètriques i les opercions de sum i producte vénen dond per les quinze fórmules següents: A) Fòrmules de l sum d'ngles. sin(+b) = sin.cos b + cos.sin b. cos(+b) = cos.cos b - sin.sin b. tn (+b)= tn + tnb tn tnb A prtir de l primer de les fórmules es poden nr deduint les ltres, per iò us donem l demostrció de l primer que és l més importnt. Aquestes fórmules més endvnt s utilitzrn per resoldre equcions trigonomètriques. 8
10 Demostrció de l fórmul trigonomètric En el tringle BOE es té sin(+b) = BE OB. Però BE = BD + DE, i per tnt BE OB = BD DE +. OB OB L primer frcció no es cnvi si es multipliquen el numerdor i el denomindor pel mtei fctor, en quest cs BD BD per BC: OB = BC BC OB. L ngle DBC és igul l ngle perquè tenen els costts perpendiculrs. En el tringle BDC es té cos = BD BC. En el tringle OBC es té sin b = BC BD. Result doncs que = cos sin b OB OB Anem l segon frcció. Aquest tmpoc no es cnvi si es multipliquen el numerdor i el denomindor pel mtei fctor, en quest cs per OC: DE DE OB = OC OC OB. El segment DE és igul l segment CF, i per iò DE CF =. Però si es mir el tringle OCF, quest divisió OC OC result ser sin = CF OC DE. En el tringle OBC es té = cos b. Result doncs que = sin cos b OC OB OB Per tnt tenim, sin(+b) = sin cos b + cos sin b B) Fòrmules de l diferènci d'ngles 4. sin(-b) = sin.cos b - cos.sin b 5. cos(-b) = cos.cos b + sin.sin b 6. tn(-b) = tn tnb + tn tnb C) Fórmules de l'ngle doble 7. sin = sin.cos 8. cos = cos² - sin² 9. tn = tn - tn D) Fórmules de l'ngle meitt 0. sin cos =. E) Fórmules de l sum i diferènci de rons. sin + sin b = sin 4. cos +cos b = cos + b b cos + b b cos cos = + cos. sin - sin b = cos 5. cos - cos b = - sin + b b sin + b b.sin 9
11 TRIGONOMETRIA EXERCICIS. Dibui ngles de 4, 55, -80, 48, -55 i.. D'un formtge circulr de rdi 7 cm tlles un sector, l circumferènci del qul mesur cm. Quin és l'ngle d'quest sector?.. Clcul l mesur en rdins d'un ngle que comprèn un rc de,4 cm de longitud en un cercle de rdi 5 cm. 4. Clcul l longitud de l'rc que comprèn un ngle de,5 rdins en un cercle de rdi 8, cm. 5. Un biciclet que té les rodes de 5 cm de rdi recorre 4 metres. Quin ngle hn girt les seves rodes?. 6. Clcul l'ngle que formen les busques d'un rellotge les: ) 7 hores i 0 minuts b) 0 hores i 0 minuts 7. Epress en grus, minuts i segons els ngles que mesuren, en rdins:,4 /5 4, 4π/9 π/5 7π/4 8. Epress en rdins els ngles que mesuren, en grus i minuts: ' 0 5' 9. Trob l determinció principl dels ngles que mesuren: π rd 5π/6 rd 5 rd 0. Dibui i clcul l mesur de tots els ngles compresos entre 0 i 60 grus relcionts mb els ngles de: ) 5 grus b) grus c) 47 grus d) 4 grus. Clcul les rons trigonomètriques de dos ngles, i després el vlor dels dos ngles, si el seu primer costt és l'ei positiu de les X i el segon pss per: ) el punt (5,8) b) el punt (,-). Dibui tres ngles que tinguin, respectivment: ) cosinus igul / b) tngent igul /5 c) sinus igul -/6 i clcul les ltres rons trigonomètriques d'quests ngles, i després el vlor dels ngles.. Clcul les rons trigonomètriques dels ngles d'un tringle rectngle en què: ) l hipotenus és 7 i un ctet b) els ctets són i 5 c) un ctet és el doble de l'ltre 4. Escriu el sinus, el cosinus i l tngent de tots els ngles superiors l primer qudrnt que divideien el cercle en 8 i en prts iguls. 5. Si un ngle és del segon qudrnt i té sinus /8, clcul'n el cosinus i l tngent. 0
12 6. Si un ngle és del tercer qudrnt i té cosinus -/5, clcul'n el sinus i l tngent. 7. Si un ngle és del primer qudrnt i té tngent 4, clcul'n el sinus i el cosinus. 8. Escriu tots els ngles α compresos entre 0 i 60 tls que: ) sin α = / b) tn α = - c) cos α = sin 40 d) sin α = 0'8 9. Si l'ngle α és l primer qudrnt i sin α = / clcul les rons trigonomètriques d'α, -α, 80 - α i 80 + α. 0. Si l'ngle ß és l tercer qudrnt i tn ß = clcul les rons trigonomètriques de ß, ß - 80, 60 - ß.. Amb regle, compàs i trnsportdor, dibui els tringles rectngles que tenen: ) ctets de cm i 6 cm b) un ctet de cm i l hipotenus de 8 cm c) un ctet de 4 cm i l'ngle entre quest ctet i l hipotenus de 5 d) un ctet de 0 cm i l'ngle opost ell de 7 e) l hipotenus de 8 cm i un ngle de 4.. Clcul l'ltur què rrib un escl de 5 metres recolzd en un pret, si form mb el pviment un ngle de 70.. Clcul l'ngle d'elevció del Sol respecte l horitzó qun un person de,7 metres project un ombr de, metres. 4. Un rmp de 0 metres de llrg està, en el seu punt més lt,, metres del sòl. Clcul quin és el seu ngle d'inclinció. 5. Un blcó està,8 metres sobre el sòl i sobresurt 49 cm de l pret. Plou i l pluj cu inclind cp l pret, mb un ngle de desvició respecte l verticl de 8. Es mullrà l pret o no?. En cs firmtiu, fins quin lçd?. En cs negtiu, fins quin distànci de l pret quedrà el terr sec?. 6. Resol i dibui els tringles rectngles en què se sp que: ) un ctet és cm i l hipotenus és 8 cm b) un ctet és 5 cm i l'ngle opost és 4 c) l hipotenus és 6 cm i un ngle és 6 d) els ctets són cm i cm e) l'àre és 0 cm² i un ngle és 40 f) un ngle és 5 i l'ltur sobre l hipotenus és 4 cm. 7. Un compàs té longitud '5 cm i està obert de form que l distànci entre les puntes és 5'8 cm. Clcul el seu ngle d'obertur. 8. Des d'un lloc del terr es veu el punt més lt d'un cs mb un ngle de. Si vncem 8 metres l'ngle pss ser de 58. Clcul l'ltur de l cs.
13 9. L'Estàtu de l Llibertt que hi h Nov York té 45 metres d'lt i és dlt d'un pedestl que en té 47. Un person se l mir des de 00 metres de l bse del pedestl. Quin és el seu ngle de visió de l'estàtu?. 0. Clcul l'mpld d'un riu de ribes prl leles si des de dos punts de l mtei rib distnts 50 metres observes un mtei punt de l'ltr mb ngles de 0 i de 60.. Clcul els ngles i els costts d'un rombe que té les digonls de 6 i 0 centímetres.. Resol i dibui els tringles no rectngles en què es conei: ) b =, c = 7, A = 76 b) A = 40, B = 6, c = c) = 0, b = 8, c = 7 d) =, b = 5, A = 48 e) =, b = 4, A = 80 f) A = 7, B = 47, = 0. Un tringle té costts, i 4. Clcul l longitud de les tres ltures. 4. Un pl de 54 cm s'inclin 50 en l direcció del Sol, qun l'ltur d'quest és. Clcul l longitud de l'ombr del pl. 5. Des d'un punt surten l'hor dos cotes per dues crreteres rectes que formen un ngle de 4. Un v 8 km/h i l'ltre 6 km/h. Clcul: ) quin seprció hi hurà entre ells l cp d'un hor? b) qunt trigrn en estr seprts per 00 km.? 6. Resol el tringle de l figur de sot l esquerr sbent que l'ngle B és 45, b = i h = 7. A h b B D B C A E C 7. En l figur de dlt l dret l distànci EC = 5, i els ngles AED = 66, AEB = 7, ACB = 68. Clcul l distànci BD. 8. En l figur següent l distànci CD = 00, i els ngles ACD = 0, BCD = 68, CDB = 88, CDA = 4. Clcul l distànci AB. B A C 9. Les tngents un circumferènci de rdi 4 trçdes per un punt eterior formen un ngle de 40. Clcul l distànci del punt l centre de l circumferènci. D
14 40. Dues rodes de rdis metre i 5 centímetres estn unides per un corretj de trnsmissió. Si els centres de les rodes estn seprts per metres, clcul l longitud de l corretj. 4.- Deduei l fórmul per clculr l àre lterl d un con prtir de l genertriu i del rdi de l bse. INDICACIÓ: Pens en quin figur qued si ho desplegues. 4. Trob les rons trigonomètriques de l ngle de 75 o sbent que 75= Sbent que sin = i que l ngle és del primer qudrnt, trob tn 44. Si α és un ngle del segon qudrnt mb sin α = 4/5 i ß un ngle del qurt qudrnt mb cos ß = /, clcul (sense decimls ni clculdor) el sinus i el cosinus dels ngles α+ß, α-ß, α/, ß/, α i ß. Determin en quin qudrnt estn quests ngles. 45. Trob un epressió per sin depenent de sin. Indicció: pos =+ 46. Demostr que pels tres ngles d un tringle qulsevol es verific que tn A+tn B+tn C= tn A tn B tn C Indicció: pos A+B=80-C i desenvolup tn (A+B)= tn (80-C) 47. Clcul les rons trigonomètriques dels ngles α i ß sbent que: ) α és gut i cos α = / b) ß és del tercer qudrnt i sin β = Reduei epressions el més senzilles possible: 4 4 sin α cos α sin α cos α + sin α cos α + sin α sin α AMPLIACIÓ Tenint en compte que un con desplegt és un sector circulr, deduei l fórmul que s utiltz per clculr l àre lterl d un con.
15 . Punts i vectors GEOMETRIA Cd punt ve identifict per dos nombres que són les seves coordendes. Hi h diversos sistemes de coordendes, però el més importnt és el de les coordendes crtesines rectngulrs: L referènci l formen dues rectes perpendiculrs (eios) que es tllen en un punt O (origen). Les coordendes de P són les distàncies de P ls eios, i es diuen bsciss i ordend. S'escriu P = (p,p ) o bé P = (,y). y P O Dos punts A i B determinen un segment AB. Un vector és un segment orientt del pl. Els seus etrems s nomenen origen i finl. Si A és l'origen i B el finl, el vector s'escriu AB i es dibui com un flet que unei A i B. Indic el cmí que s'h de fer sobre el pl per nr d'a fins B. Si les coordendes crtesines d'a i B són (, ) i (b,b ), s nomenen components d' AB les diferències de coordendes: AB = B - A = (b -,b - ) Les components són les projeccions d' AB sobre els eios. b B A b - b - b S nomen mòdul (o longitud) d' AB l distànci entre A i B. S nomen direcció d' AB l direcció de l rect determind per A i B. Els vectors AB i BA són vectors oposts: tenen els mteios mòdul i direcció, però diferent sentit. Tots els vectors que tenen les mteies components tenen el mtei mòdul, l mtei direcció i el mtei r sentit. El conjunt de les dues components s'nomen un vector lliure: v = ( v, v ) El vector lliure de components (0,0) s nomen vector nul i s'escriu 0. El mòdul d'un vector lliure v r s'escriu v r i es clcul per r v = v + v L'rgument d'un vector lliure v és l'ngle α que es clcul per tn α = v v 4
16 . Opercions mb vectors ) Sum Si u = (u, u ) i v = (v, v ) l sum és u+v = (u +v, u +v ). Gràficment, es prenen representnts d'u i v mb el mtei origen; l digonl del prl lelogrm que determinen i que té el mtei origen represent u+v. b) Diferènci Si v = (v, v ) el seu vector lliure opost és -v = (-v, -v ). L diferènci de dos vectors és u-v = (u -v, u -v ). Gràficment, u-v es f sumnt un representnt d'u l'opost un representnt de v, o bé representnt-los en el mtei origen i unint els finls de tots dos. u+v v u-v v u Per tnt si u i v determinen un prl lelogrm, les digonls d'quest representen u+v i u-v. c) Producte per un esclr Si k és un esclr (un vlor numèric) i v un vector, es definei kv = (kv, kv ). El vector kv té l direcció de v, mòdul k v r, i sentit igul o contrri l de v segons si k>0 o k<0. Els vectors u i v són dependents si u = kv per un esclr k. En tl cs els vectors tenen l u u mtei direcció i les seves components són proporcionls: =. v v Si u i v no són dependents són independents. Dos vectors independents es diu que formen un bse dels vectors del pl: Aleshores qulsevol ltre vector w pot escriure's com combinció d'u i v: w = u+bv mb i b esclrs u u w v Sempre que u i v siguin independents (tinguin diferent direcció) podrem trobr un múltiple de u i un múlitple de v que sumts ens donin w. Per fer-ho gràficment hs de construir un prl lelogrm, trçnt prl leles u i v que pssin per l etrem de w, i llrgnt els vectors u i v fins que tllin les prl leles que hs dibuit. 5
17 d) Producte esclr de vectors S nomen producte esclr dels vectors u i v l'esclr u v = u v +u v. Els vectors u i v són ortogonls si formen un ngle recte o sigui si u v = 0. Per eemple, ( v, v) és ortogonl ( v, v). Hi h infinits vectors ortogonls un dont, i tots ells són dependents. El mòdul d'un vector pot epressr-se per mitjà del producte esclr: v = v v Un vector de mòdul és un vector unitri. Per tot v, el vector v v és unitri i rep el nom de normlitzt de v. L'ngle entre dos vectors lliures u i v és l'ngle α formt per dos representnts mb el mtei u v origen. Es clcul per cos α = u v D'quí s'obté un definició lterntiv de producte esclr que no f servir les components: u v = u v cos α Si u i v són els vectors lliures representts en els costts d'un prl lelogrm, quest prl lelogrm és un rectngle si u v = 0, un rombe si u = v i un qudrt si u v = 0 i u = v. L àre del prl lelogrm que formen dos vectors v=(v, v ) i u=(u, u ) es igul v u v u que es el vlor bsolut del que s nomen el determinnt dels dos vectors.. Geometri de rectes Si A és un punt i v un vector lliure, s nomen rect determind per A i v l conjunt de punts P tls que AP és dependent de v. El vector v és el vector director de l rect. Si A = (, ), v = (v, v ) i P = (,y) es té rect. v = v L rect que pss pels punts A i B té vector director v = AB = b b, que és l'equció contínu de l i equció contínu Multiplicnt en creu l equció continu i igulnt zero tenim l equció crtesin: + by + c = 0 El vector n = (,b) formt pels coeficients de l'equció crtesin és ortogonl l vector director, i rep el nom de vector norml l rect. Si després ïllem l vrible y tenim l equció eplícit: y = m + n El coeficient m de l'equció eplícit s nomen pendent de l rect i és l tngent de l'rgument v del vector director (m=tn α = ) n P v A v 6
18 El punt mitjà entre dos punts A i B s'obté fent A + B L intersecció de dues rectes és el punt que té per coordendes les solucions del sistem formt per les equcions de les dues rectes. Dues rectes que no tenen intersecció són prl leles. En tl cs les dues rectes tenen: - vectors directors dependents - vectors normls dependents - el mtei pendent Dond un rect r, per un punt eterior P hi pss un sol rect prl lel i escriurem l sev equció en form continu posnt el mtei vector director de l rect r i posnt com coordendes del punt les del punt P. P r L'ngle entre dues rectes és el formt pels seus vectors directors o pels seus vectors normls. A prtir dels pendents de les dues rectes m i m, es pot clculr l ngle que formen ií: tnα tnβ m m' tnω = = + tnα tnβ + m m' Si l ngle que formen dues rectes és un ngle recte les rectes són perpendiculrs. En tl cs les dues rectes tenen: - vectors directors ortogonls - vectors normls ortogonls - pendents recíprocs i oposts (si un és m, l ltre és -/m) Dond un rect r, per un punt eterior P hi pss un únic rect perpendiculr i escriurem l sev equció en form continu posnt-li com vector director un vector ortogonl l de r i posnt com coordendes del punt les del punt P P r L distànci entre dos punts és el mòdul del vector que determinen: d(p,q) = PQ = (q p) + (q p ) L distànci entre un punt i un rect es clcul prtir de les coordendes del punt P = (p,p ) i l equció de l rect r: +by+c = 0 fent: p d(p,r) = + bp + b + c 7
19 GEOMETRIA EXERCICIS. Represent els punts donts en coordendes crtesines per A = (-,4); B = (0,5); C = (,) i D = (-6,0). Dibui tots els vectors que determinen, i clcul'n les components.. Desplç els punts (5,6), (-,) i (0,-7) segons el vector lliure u =(,-5).. Dibui un tringle de vèrtes (,5), (,-) i (0,6). Trslld'l de form que el primer vèrte vgi prr (-7,). On nirn els ltres dos vèrtes?. 4. Si A = (,-), B = (0,-) i C = (-5,4) trob un qurt punt que formi mb ells un prl lelogrm. Quntes solucions hi h?. 5. Si A=(,0), B=(6,) i C=(,-4) trob els punts D, E i F que compleien: ) DB = AD b) BE + AC = (5, ) c) 4 CF AB+ FA = 0 6. Essent u =(-,4), v =(,) i w = (4,-6), clcul les combincions: ) u-v-w b) (u+v)-(u-v) c) u-v-(v-(v-u)) d) u-v+ w e) u + v w f) u+v-(u-(v-w)) 7. Clcul dos vectors u i v tls que u-v = (,5) i u-v = (-,7) 8. Decidei quins dels següents prells de vectors són dependents: ) (,-) i (,-4) b), i,- c) 4 9, i, d) (, 5) i (, ) e) (, ) i ( +,) f) ( 5,0 9 5) i ( 5 +, 5) 9. Clcul per que els següents prells de vectors siguin dependents: ) (,+8) i (-,6) b) ( 4,5) i (+,) c) (-, 4) i (, -) 0. Epress com combinció, si és possible: ) (4,-7), de (,) i (-,) b) (,8), de (,) i (,) c) (,0), de (,) i (,). Si u =(,-), v = (,4) i w = (-,5), clcul: u v, (u+v) w, (u-v) (u+v), (u+v) v-w (v-4u). Clcul el mòdul i l'rgument dels vectors u = (5,) i v = (, ). Clcul l'ngle que formen els vectors,0 i (6,-), vectors (,) i (, ) i el que formen els 4. Clcul qutre vectors de mòdul 5 que siguin: ) d'rgument 80º b) de l form (+,) c) de l form (,-) d) ortogonl (6,) 5. Clcul per que el vector (,) sigui: ) de mòdul b) d'rgument 0 c) ortogonl (-4,9) 6. Clcul tres vectors ortogonls (-,8) que siguin: 8
20 ) de l form (,) b) de l form (,²) c) unitri 7. Clcul un vector que formi ngles iguls mb els vectors (4,) i (,-5) 8. Dibui un prl lelogrm que tingui representts ls costts els vectors (,) i (,5), i d'quest prl lelogrm clcul l longitud dels costts, l longitud de les digonls, l'ngle que formen els costts i l'ngle que formen les digonls. 9. Busc dos vectors u i v tls que: () u i (,) es representin en els costts d'un qudrt. (b) v i (-,5) es representin en els costts d'un rectngle d'àre De cdscun de les rectes dondes per les equcions següents escriu: tres punts, un vector director, un vector norml i el pendent. 5 y =, - + y += 0, y = 7, 0 y =, y = 0. Essent A i B punts, v un vector director, n un vector norml, i m el pendent, escriu les equcions de les rectes determindes per: ) A=(9,-7) v =(,-) b) A=(,-5) B=(,0) c) B=(-8,), n=(0,-) d) A=(4,4) m= /5. Trob el vlor que hn de tenir, b, c, d, e, f, g i h per que: ) les rectes +y-4=0, -y+4=0 i -y= pssin per un mtei punt ) els punts (,b), (b,) i (b+,5) estiguin linets ) les rectes c+y+4=0 i -7+dy-=0 es tllin en el punt (4,5) 4) l rect que pss per (,e) i (e,) tingui pendent - 5) les rectes f+(f-)y+=0 i y= siguin prl leles 6) les rectes +y-=0 i g-y+99999=0 formin un ngle de 60º 7) les rectes h+(h-)y+=0 i y=+h² siguin perpendiculrs.. Escriu l'equció de les rectes determindes per: ) és prl lel 6-y-=0 i pss per (-,) b) és prl lel y=- i pss per l intersecció de 5-y+=0 i l'ei d'bscisses c) és prl lel l rect que pss per (7,7) i (-4,0), i pss per (,-) d) és perpendiculr -y+=0 i pss per (8,9) e) és perpendiculr l vector (-5,) i pss per (0,) f) és perpendiculr l rect que pss per (,) i (5,), i pss per l'origen. 4. Si els vèrtes d'un tringle són els punts A=(4,), B=(0,) i C=(-6,), clcul: ) les equcions dels tres costts b) els punts mitjns dels tres costts (M de AB, N de BC, P de AC) c) les equcions de les rectes que uneien els punts mitjns dels costts d) les equcions de les rectes que uneien cd vèrte i el punt mitjà del costt opost (medines) 9
21 e) el punt G d'intersecció de dues de les rectes de l prt (d) (bricentre). Comprov que l A + B + C tercer tmbé pss pel punt i que les coordendes del bricentre verifiquen f) les components dels vectors AG i GN, i les dels vectors BG i GP g) els tres ngles h) les equcions de les meditrius dels tres costts i) el punt F en què es tllen les meditrius (circumcentre) j) les distàncies de F A, B i C k) les equcions de les tres ltures l) el punt O d'intersecció de les ltures (ortocentre) m) l'àre del tringle prtir de l fórmul trdicionl. Després comprov que coincidei mb l que vm donr per clculr l àre del prl lelogrm que formen dos vectors divindint-l per dos. Eercicis complementris 5. Clcul l distànci del punt P=(0,5) l rect -+y+7=0, i el punt simètric de P respecte d'quest rect. 6. Un tringle té dos dels seus vèrtes A=(,-) i B=(-5,), el seu bricentre està l'ei d'bscisses i el vèrte C és l'ei d'ordendes. Determin el punt C. 7. Un tringle té un vèrte A=(,4), el costt AB és prl lel l rect +5y+7=0, el costt AC és perpendiculr l rect 5+7y-=0, i el costt BC tll els eios de coordendes distàncies 4 i - de l'origen. Determin els vèrtes B i C. 8. Un tringle té dos vèrtes A=(,-) i B=(,), el vèrte C és l rect -y=4, i l'àre del tringle és 6. Determin el vèrte C. 9. Un rombe ABCD té el vèrte A l'origen, l digonl BD és sobre l rect +y=4, i el costt AB és prl lel l rect -6y+=0. Clcul els vèrtes B, C i D. 0. Un tringle té vèrtes A=(,) i B=(6,0), i ortocentre H =(,). Determin el vèrte C.. Dos costts d'un prl lelogrm tenen equcions y=, y=, i el seu centre és el punt (,). Determin els qutre vèrtes.. L projecció del vector u sobre el vector v, és un vector w que és dependent de v i tl que u-w és ortogonl mb v. Fes un esquem gràfic per fer-te n un ide. Clcul l projecció w del vector u = (, ) sobre el vector v = (5, 4). Clcul u v i v w. Clcul l ngle α entre u i v i comprov que w = u cos α. Comprov que el producte esclr de v u és igul v w, o sigui que el producte esclr és igul l producte del mòdul d un dels vectors pel mòdul de l projecció de l ltre sobre ell. 0
22 CIRCUMFERÈNCIES I ALTRES CÒNIQUES Un lloc geomètric és un conjunt de punts que verific un cert propiett. J n heu vist uns qunts fins r: l circumferènci, l meditriu d un segment i l bisectriu d un segment. Un superfície cònic és un figur de l espi que s obté fent girr un rect (que s nomen genertriu) l voltnt d un ltr (que és l ei de gir) que l tll en un punt. Hi h unes quntes corbes del pl que són llocs geomètrics i que s obtenen tllnt un superfície cònic mb un pl. S nomenen còniques. D elles prlrem en quest cpítol..- Geometri de l circumferènci L cònic més senzill és l circumferènci j que s obté tllnt un superfície cònic mb un pl perpendiculr l ei de gir. Un circumferènci és tmbé un lloc geomètric j que està formd per un conjunt de punts (,y) tls que l sev distànci un punt (,b) noment centre és un quntitt fi r nomend rdi. Els punts d un circumferènci verifiquen un equció de segon gru: (-) +(y-b) = r Aquest equció, desenvolupd, té l specte +y +A+By+C = 0. Recíprocment, tot equció d quest tipus correspon un circumferènci sempre que A +B -4C sigui positiu. L relció entre les dues equcions és A = -, B = -b, C = +b -r. Si l circumferènci està centrd l origen l sev equció és +y = r El segment que unei dos punts d un circumferènci és un cord. L meditriu d un cord pss pel centre. Per iò tres punts determinen un circumferènci, que té el centre en l intersecció de les meditrius entre cd prell de punts. L intersecció d un rect i un circumferènci és un sistem d'equcions de segon gru. Si té dues solucions, l rect és secnt l circumferènci i en determin un cord; si té un solució, l rect és tngent l circumferènci i tenen un punt de contcte. L tngent un circumferènci en un punt és perpendiculr l rdi en el punt de contcte. I tmbé tenim que el rdi és igul l distànci del centre l rect tngent. Per un punt eterior sempre es poden trçr dues tngents. L intersecció de dues circumferències és tmbé un sistem d'equcions de segon gru, que pot reduir-se l formt per l equció d un d elles i l diferènci de les dues equcions. Aquest diferènci correspon l rect que pss pels punts d intersecció, qun n hi h, i s'nomen ei rdicl de les dues circumferències..- L el lipse L el lipse és un cònic que s obté tllnt un superfície cònic mb un pl que tll l ei de gir de form obliqu i que no més prl lel l genertriu. És el lloc geomètric formt pels punts tls que l sum de les distàncies dos ltres punts noments focus és constnt. y L equció reduïd de l el lipse centrd l origen és + = b En quest equció i b són els semieios de l el lipse. Els focus sempre estn situts sobre el semiei grn.
23 Si c és l semidistànci focl es verific =b +c c I l ecentricitt de l el lipse és e=. Està sempre entre 0 i.si és 0 és un circumferènci. Si l el lipse està centrd en un punt (m,n) diferent de l origen l sev equció és ( m) (y n) + b =.- L hipèrbol L hipèrbol és un cònic que s obté tllnt un superfície cònic mb un pl prl lel l ei de gir. És el lloc geomètric formt pels punts tls que l diferènci de les distàncies dos ltres punts noments focus és constnt. y L equció reduïd de l hipèrbol centrd l origen és = b En quest equció és el semiei de l hipèrbol (i està sobre l ei ) i b és el semiei imginri (i està sobre l ei y). Si c és l semidistànci focl es verific c = +b L ecentricitt de l hipèrbol és e= c. L ecentricitt és sempre més grn que. Un hipèrbol té dues símptotes que tenen pendents b i b L hipèrbol que té símptotes de pendents i - es diu equilàter Si l hipèrbol està centrd en un punt (m,n) diferent de l origen l sev equció és: ( m) (y n) b 4.- L pràbol = L pràbol és un cònic que s obté tllnt un superfície cònic mb un pl prl lel l genertriu. És el lloc geomètric formt pels punts tls que l distànci un punt noment focus i un rect nomend directriu són iguls. L equció reduïd de l pràbol mb el vèrte l origen i que tingui l ei de simetri sobre l ei de les és y =p El vlor de p és l distànci del focus l directriu. Si l pràbol té el vèrte en un punt (m,n) diferent de l origen, l ei de simetri és prl lel l ei de les i l distànci del focus l directriu és p, l sev equció serà: (y-n) =p(-m) Si l pràbol té l ei de simetri l ei de les y l equció serà =py Si l pràbol té el vèrte en un punt (m,n) diferent de l origen, l ei de simetri és prl lel l ei de les y i l distànci del focus l directriu és p, l sev equció serà: (-m) =p(y-n)
24 EXERCICIS CIRCUMFERÈNCIA I CÒNIQUES. Escriu les equcions de les circumferències que tenen: ) centre (, -) i rdi b) centre (0, ) i rdi 5. Clcul el centre i el rdi de les circumferències ) +y -6+4y+5 = 0 b) +y ++y+ = 0. Escriu l equció de les circumferències determindes per les condicions següents: () (,-) i (-4,7) són punts oposts d un diàmetre (b) té el mtei centre que +y -8+y+4 = 0, i rdi doble que quest (c) pss per (0,), (-,) i (4,) (d) pss per (4,0) i (0,6) i té el centre sobre l rect y = - 4. Escriu l equció de l circumferènci de rdi 7 que pssi pel punt (0,) i tingui el seu centre sobre l rect -y = Trob els punts de l circumferènci +y -y = 0 que estn distànci màim i distànci mínim del punt (, ). 6. Clcul l longitud de l cord comun les circumferències +y +4-y+ = 0 i +y + =. 7. ) Clcul l rect tngent l circumferènci (-) +(y+) = en el punt (,-). b) Clcul les rectes tngents l circumferènci +y +4+6y = en els punts de l circumferènci en què =. 8. Clcul m per que +y +6-y+m = 0 sigui tngent y = Escriu l equció de l circumferènci de centre (,4) tngent l rect +4y =. 0. Escriu les tngents +y = que siguin: ) prl leles l rect =y b) perpendiculrs l rect y = c) pssin pel punt (,). Escriu les equcions de les circumferències determindes per: ) pss per (,6) i és tngent y = - en (0,0) b) té el centre l rect +4y = 6 i és tngent ls eios. Trob el vèrte, el focus i l directriu de l pràbol y= 4. Trob els vèrtes, els focus i l ecentricitt de les el lipses següents y y = = 4. En un el lipse l ei mjor mesur 4 cm i el menor 6 cm. Clcul l distànci focl i l ecentricitt.
25 y 5. Trob els focus, els vèrtes, l ecentricitt i les símptotes de l hipèrbol = De l pràbol y= -4+, clcul el vèrte, l ei de simetri, el focus i l directriu. 7. Identific les còniques següents, clcul n els elements crcterístiques i dibui-les 4 +9y =6 6-9y = y =5 =6y -4y =6 y =4 8. Sbent que l òrbit el líptic que descriu l Terr l voltnt del Sol (que està en un dels focus de l el lipse) té un ecentricitt e= 0 06 i que l ei mjor és molt proimdment 00 milions de km. ) Trob els semieios i l distànci focl b) Clcul les distàncies màim i mínim de l Terr mb respecte l Sol c) Escriu l equció de l òrbit de l Terr 4
26 CONJUNTS NUMÈRICS. Els nombres rels Els nombres nturls són 0,,,... S'utilitzen per comptr. Sense sortir d'ells es poden fer sumes i multipliccions. El conjunt dels nombres nturls es design per N. Podríem dir que els nombres nturls compten. Els nombres enters són els resultt d'fegir ls nturls els nombres -, -,... que s'nomenen els nombres negtius, qun hem de situr l ltre costt prtir d un referènci que és el zero. Sense sortir d'ells es poden fer sumes, restes i multipliccions. El conjunt dels nombres enters es design per Z. Podríem dir que els enters situen i ordenen un costt o un ltre d un referènci... Els nombres rcionls són el resultt d'fegir ls enters els nombres de l form /b, on i b són enters i b 0, que s'nomenen els nombres frccionris. Sense sortir d'ells es poden fer sumes, restes, multipliccions i divisions (sempre que el divisor no sigui 0!). El conjunt dels nombres rcionls es design per Q. Podríem dir que els nombres rcionls reprteien i compren... Els nombres rcionls coincideien mb els nombres decimls finits o periòdics. Per tnt prtir d un frcció es pot trobr el nombre deciml finit o periòdic i prtir d un nombre deciml finit o periòdic es pot trobr l frcció que el gener. Aquest frcció es pot representr en un rect utiltznt el Teorem de Tles, però l rect encr queden més punts, per eemple, que no són rcionls. És molt interessnt l demostrció de que no és un nombre rcionl. Els nombres rels són el resultt d'fegir ls rcionls els nombres decimls no periòdics (com r π o els rdicls), que s'nomenen els nombres irrcionls, i mb ells l rect qued completd. Sense sortir d'ells es poden fer sumes, restes, multipliccions, divisions i rrels (ecepte les d'índe prell i rdicnd negtiu). El conjunt dels nombres rels es design per R, i l sev representció se sol dir l rect rel. Són els que s'utilitzen per descriure vribles contínues. Podríem dir que els nombres rels mesuren i clculen... Es té doncs N Z Q R, on el signe signific "inclòs ". El vlor bsolut d un nombre rel és l distànci que hi h des del punt que el represent fins l origen. Serà el mtei nombre si és positiu, i serà el nombre cnvit de signe si és negtiu. Es design per. Per eemple tindrem 4 = 4, 5 = 5. El vlor bsolut del 0 és 0. L prt enter d un nombre rel és definei com el nombre rel enter immeditment inferior o igul ell. Es design per []. Per eemple tindrem [ 4'7] 4, [ 5'] = 6 =. Per ls nombres enters l prt enter coincidei mb el mtei nombre, per eemple 7 = 7, = [ ] [ ] 5
27 . Representció dels nombres rels. Intervls Els nombres de les qutre clsses nteriors poden representr-se en un ei grdut, és dir en un líni rect en què hi h mrcts el 0 i el. L representció de R és complet: els nombres rels coincideien ectment mb els punts de l'ei grdut. Per iò els nombres rels s'utilitzen per mesurr. Si α i β són dos nombres, es design per [α, β] i s nomen intervl tnct d'etrems α i β l conjunt de nombres tls que α β, i es design per (α, β) i s nomen intervl obert d'etrems α i β l conjunt de nombres tls que α <<β. Un intervl es represent en un segment de l'ei grdut, i l longitud d'quest segment és l'mpld de l'intervl. Si α és un nombre, es design per (α, + ) i s nomen semirect dret d'origen α, l conjunt de nombres tls que α<, i es design per (-, α) i s nomen semirect esquerr d'origen α, l conjunt de nombres tls que <α. Un intervl conté un nombre finit de vlors de N o de Z, i un nombre infinit de vlors de Q i de R.. Aproimcions i errors Els nombres irrcionls que no siguin rdicls es coneien només en form d intervls limitts per dos decimls finits que són les seves proimcions per defecte i per ecés. L millor d'elles és l'rrodoniment del nombre. Per eemple: el nombre π està dins els intervls (,4,,5 ) o (,45,,46 ). En el primer cs l rrodoniment és,4 (l proimció per defecte) i en el segon és,46 (l proimció per ecés). Sovint l pràctic un nombre es dón de form proimd i leshores es comet uns errors que es mesuren ií: Error bsolut= Vlor rel - Vlor proimt Com que hi h vegdes que el vlor rel és desconegut el que fem és cotr l error i diem l error bsolut és menor que... Error reltiu= Error bsolut : Vlor rel, que sovint se sol pssr percenttge multiplicnt-ho per 00 Per eemple: Si gfem,4 com vlor de π, estem cometent un error bsolut menor que 0,00 i un error reltiu de 0,00:,4=0,00066 o sigui menor que 0,0007= 0,07% 4.- L notció científic J hvíem vist en cursos nteriors que els nombres molt grns o molt petits se solen epressr en notció científic utiltznt les potències de 0, positives o negtives segons el cs. Un nombre s epress en notció científic mb un producte d un nombre d un sol ifr enter positiv diferent de zero (o sigui mjor que i menor que 0) multiplict per un potènci de 0. Aleshores per escruire el nombre mb totes les ifres hem de desplçr l com cp l esquerr o cp l dret tnts llocs com indiqui l eponent de l potènci de 0. Per eemple:, = , = 0,
28 5.- Arrels i logritmes Si tenim un igultt del tipus n = b - l bse s ïll fent un rrel-enèsim = n b - l eponent n s ïll fent un logritme n= log b Propietts de les rrels: n p n p m n mn ( ) = m n = n n m = n np p n = = Aquestes propietts poden servir per escriure de form diferent un rdicl i leshores poder simplificr determindes epressions. n n n Per multiplicr rdicls del mtei índe fem: b = b n m m n m + n Per multiplicr rdicls mb el mtei rdicnd fem: = Per multiplicr rdicls mb diferents índe i diferent rdicnd s hn de reduir l mtei índe. Per eemple, 5 = 5 = 6 5 = 5 = Només es poden sumr i restr els rdicls semblnts, que són els que tenen el mtei rdicnd i el mtei índe. Per eemple, 5 = Per estr segurs de si dos rdicls són semblnts sovint cl etreure n els fctors. Per eemple, 8 i 50 són semblnts j que 8 = i 50 = 5. Per iò es pot fer = 8 Rcionlitzr un frcció vol dir epressr-l sense rrels en el denomindor. Per rcionlitzr un epressió com n b es multiplic dlt i bi per n b n Per rcionlitzr un epressió del tipus b + l epressió del denomindor que seri b c c, es multiplic dlt i bi pel conjugt de De les propietts dels logritmes prlrem més endvnt, de moment per poder clculr, utilitznt l clculdor, heu de sber que: log b = logb log on els logritmes indicts sense bse són logritmes decimls de bse 0 i els clculem mb l tecl log de l clculdor. 6.- Els nombres compleos Amb els nombres rels encr tenim un problem j que no es poden resoldre totes les equcions. Tl com vm veure el curs psst, hi h equcions que no tenien solució qun prei un rrel d un nombre negtiu en el procés de l sev resolució. Per eemple + 4 = 0 + = = 0 Per solucionr iò, i seguint mb les mplicions que hvíem vist, es definei un conjunt nou, que és mplició de R i que es design per C i que s nomen conjunt dels nombres 7
29 compleos, i que està formt pels nombres de l form +bi, on els coeficients i b són nombres rels i l lletr i represent l unitt imginàri i verific les igultts següents: i = = i En el conjunt C, totes les equcions tenen solució, j que per eemple per resoldre les equcions nteriors frem: 4 = 6 = 4 6 = ± i = ± 6 i 7 = 7 = ± 7 i Per tnt podríem dir que els nombres compleos resolen... Les opercions mb nombres compleos es relitzen ií: Sum: (+bi)+(c+di)= (+c)+(b+d)i Rest: (+bi)-(c+di)= (-c)+(b-d)i Multiplicció: (+bi) (c+di)= (c-db)+(d+bc)i Divisió: c + + bi ( + bi) (c di) c + db bc d = = + di (c + di) (c di) c + d c + d Els nombres compleos es poden representr gràficment mitjnçnt un vector que començ l origen i cb l punt (,b). Es pot epressr tmbé en form en form polr ( r α ) i, mb el mòdul (r) que és l longitud del vector i l rgument (α ) que és l ngle que form el vector mb l prt positiv de l ei de les. Per pssr de l form binòmic l polr frem: r= b + b tgα = Per pssr de l form polr l binòmic frem: = r cos α b= r sin α Les opercions de multiplicr, dividir i les potències en form polr es relitzen ií: ( ) α r ( ) s β = ( r s) α+ β 7.- Inequcions r s α β r = s α β ( r n n α ) = (r ) nα Un inequció és un desigultt entre epressions lgebràiques. L sev solució és el conjunt de vlors que compleien l desigultt i se sol epressr mb form d intervls. Per resoldre un inequció reduïd del tipus f() 0 es fn els pssos següents: ) es resol l'equció f() = 0 b) es busquen els vlors que no pertnyen l domini de f() c) sobre un ei grdut que represent el conjunt dels nombres rels, es disposen en ordre de menor mjor tots els vlors obtinguts en els pssos nteriors i es comprov el signe de f() en un vlor situt entre cd dos d'ells d) si entre un vlor α i un vlor β és f() 0, l'intervl [α, β] form prt del domini Ens hem de fir bé si l desigultt hi h l igul inclòs o no i leshores l intervl solució hi figurrn o no els seus etrems. EXERCICIS CONJUNTS NUMÈRICS 8
30 . Escriu utilitznt intervls i semirectes: els nombres rels entre - i, inclosos quests els nombres rels que no pssin de 4 els nombres rels més grns que 7 els tls que -6 < 6 els negtius superiors - l prt comú [,7] i (,5) l prt comú (,7) i [,5]. Sobre un rect mrc l origen i l unitt. Després represent-hi utilitznt regl i compàs i 4 pensnt en el Teorem de Tles les frccions i 7.- Sobre l rect rel represent-hi els nombres 5 i utilitznt regl i compàs i pensnt en el Teorem de Pitàgores (heu de posr el nombre de dintre l rrel com sum de dos qudrts!). Després represent-hi 7, tenint en compte que quest nombre no es pot posr com sum de qudrts de dos nombres enters. 4. Clcul l àre d un cercle de rdi 7 m, rrodonint el resultt ls m i ls cm i cotnt l error que comets en cd cs.. 5. Clcul el volum de l piràmide de Kheops sbent que té un ltur de 7 m i que el costt de l bse, que és qudrngulr, mesur 0 m. Arrodonei ls m i ls dm i cot l error que comets en cd cs. 6. El llc Bikl l Sibèri té un cpcitt de.500 km d igu dolç. Tenint en compte que es consider que l despes diàri d un person en igu és de 50 l, clcul, utilitznt l notció científic, per qunt de temps hi huri per bstir tot l humnitt clculnt que l món hi h un poblció l voltnt dels 7 mil milions d hbitnts. 7. Tenint en compte que l velocitt de l llum és de km/s i que l estrell més proper, prt del Sol, és Pròim Centuri que està 4 nys llum. Clcul, utilitznt l notció científic l distànci en km de l Terr fins quest estrell. 8. Tenint en compte que el rdi proimt de l terr és de 6.70 km. I que el diàmetre d un àtom d hidrogen (rdi de Bohr) es consider que és de m, clcul qunts àtoms d hidrogen cbrien dintre l terr. 9. Escriu en form de rdicls o de logritmes els nombres que compleien les igultts: = 5 4 = = = 0,5 Després clcul, rrodonint mb dos decimls el vlor dels resultts. 0. Escriu questes potències en form de rdicls (si és necessri, combints mb frccions) sense fer cp operció: Escriu quests rdicls en form de potències mb l bse enter més petit possible: 9
31 Simplific quests rdicls, epressnt-los mb l índe més petit possible: Fes les següents multipliccions de rdicls: Treu tots els fctors possibles d quests rdicls: Introduei els fctors eteriors per formr un sol rdicl: Fes les següents multipliccions de rdicls i simplific els resultts si és possible: Fes questes divisions de rdicls: Fes les sumes i restes que siguin possibles, deint el resultt com rdicl Reduei quests rdicls l form més breu possible: Fes les opercions que siguin possibles i simplific els resultts: 5 5 ( + ) ( 7 6 ) ( 7 6 ) Rcionlitz questes frccions i simplific tot el possible els resultts: Fes els càlculs següents mb nombres compleos: (7-i) (-+i)= (4-i) = 6 i-9 (i) = i +i +4i 4 +5i 5 = 5 i + 4i. Trob el vlor que h de tenir l m per tl que 5 + mi i sigui un nombre rel + 0
32 4. Pss els dos nombres següents l form polr: -+i + i Pss els dos nombres següents l form binòmic: Donts els nombres compleos z= i i w=-+i, clcul en form polr w z 6. Trob les rrels cúbiques del nombre comple dont en form polr per 8 7 Indicció: per trobr les rrels cúbiques hs de trobr nombres que elevts l cub donin el que et donen 7. Clcul tot pssnt prèviment form polr 5 i 8. Resol les equcions següents: -6+5=0-8+6=0 9. Resol les inequcions següents, epressnt les solucions en form d intervls: ( + ) ( + ) 4 ( ) Quin vlor pot tenir un nombre rel positiu tl que si fem el seu quíntuple dón un vlor més petit que si li sumem 7 unitts?. Quines dimensions pot tenir un rectngle sbent que l bse mesur tres metres més que l ltur i que l àre és inferior 0 m?
33 .Successions SUCCESSIONS I PROGRESSIONS Un successió és un llist, possiblement infinit, de nombres rels, cd un dels quls ocup un lloc en l successió prtir del lloc. Els nombres que preien en un successió s'nomenen els seus termes. En generl el terme que ocup l posició n s'escriu n i l successió com un tot s'escriu { n }. Hi h dos procediments principls de definir un successió: ) donr un fórmul que per cd n produeii n. Aquest fórmul és el terme generl de l successió. Es pot conèier el terme que ocup un lloc determint substituint l fórmul l n pel vlor del lloc. b) donr un regl de construcció que relcioni un terme mb els nteriors i permeti obtenir-lo prtir d'ells. Aquest regl que epress n prtir d' n-, n-, etc. és un relció de recurrènci. Coneient un relció de recurrènci i el terme o els termes inicils es poden obtenir d'un en un tots els termes, però no es pot sber directment un terme sense hver obtingut els nteriors, no ser que tmbé es pugui sber el terme generl, com sol pssr en lguns csos. Les successions més corrents les ciències nturls o socils són les formdes pels vlors d'un mgnitud que vri mb el temps, i que es prenen l cp de,,,... intervls de temps iguls. En el cs de les successions definides per un relcions de recurrènci és especilment conegud l successió de Fiboncci en l qul n = n- + n-, que vol dir que cd terme s obté sumnt els dos nteriors. Si comencem per,, l successió seguiri,, 5, 8,,, 4,... Si els termes d un successió es vn proimnt tnt com es vulgui un nombre dont l, es diu que l successió tendei l, o que l és el límit de l successió. S escriu { n } l Si els termes es vn fent cd vegd més grns i supernt qulsevol nombre per grn que sigui es diu que l successió tendei +, o que el límit és + i s escriu { n } +. Si els termes es vn fent cd vegd més petits i menors que qulsevol nombre negtiu es diu que l successió tendei, o que el límit és, i s escriu { n }. Tmbé h successions que no tenen límit, per eemple { n }=(-) n+ n, en l qul els termes vn oscil lnt:, -,, -4, 5, -6, 7,... n L successió de terme generl + té per límit un nombre molt importnt dintre les n mtemàtiques que es represent mb l lletr e, i té un vlor proimt de Progressions Un successió es diu que és un progressió ritmètic si ve definid per un relció de recurrènci de l form n = n- +d, on d és constnt (positiv o negtiv) i s nomen l diferènci de l progressió. El terme generl d'un progressió ritmètic és n = +(n-)d, sent el primer terme, i d l diferènci. L sum dels termes d'un progressió ritmètic compresos entre els llocs i n rep el nom de sum prcil de lloc n i es design per S n. Es clcul fent S n ( + n)n = El fet de trobr un nombre determint de termes situts entre dos de donts d un progressió ritmètic s nomen interpolció linel.
NOMBRES REALS I RADICALS
 ESO-B NOMBRES REALS I RADICALS Nombres Rels Quins dels nombres següents no poden expressr-se com quocient de dos nombres enters? ;,; ;, ;, ; π; b Express com frcció quells que sig possible. c Quins són
ESO-B NOMBRES REALS I RADICALS Nombres Rels Quins dels nombres següents no poden expressr-se com quocient de dos nombres enters? ;,; ;, ;, ; π; b Express com frcció quells que sig possible. c Quins són
Classifica els polígons següents. a) b) c) d)
 1 FIGURES PLNES EXERIIS PER ENTRENR-SE Polígons 1.44 lssific els polígons següents. ) b) c) d) ) Pentàgon irregulr còncu. b) Heptàgon regulr convex. c) ctògon irregulr còncu. d) Hexàgon irregulr convex.
1 FIGURES PLNES EXERIIS PER ENTRENR-SE Polígons 1.44 lssific els polígons següents. ) b) c) d) ) Pentàgon irregulr còncu. b) Heptàgon regulr convex. c) ctògon irregulr còncu. d) Hexàgon irregulr convex.
TEMA 6: Trigonometria
 TEMA 6: Trigonometri L trigonometri, és l prt de l geometri dedicd l resolució de tringles, es dir, determinr els vlors dels ngles i dels costts d un tringle. 6. MESURA D ANGLES Per mesurr ngles doptrem
TEMA 6: Trigonometri L trigonometri, és l prt de l geometri dedicd l resolució de tringles, es dir, determinr els vlors dels ngles i dels costts d un tringle. 6. MESURA D ANGLES Per mesurr ngles doptrem
1.1.- Nomenclatura Matrius especials Principals operacions Rang: definició, propietats i càlcul Equacions matricials
 1.- NOCIONS ELEMENTALS 1.1.- Nomencltur 1.2.- Mtrius especils 2.- CÀLCUL MATRICIAL 2.1.- Principls opercions 2.2.- Rng: definició, propietts i càlcul 2.3.- Equcions mtricils 1.- NOCIONS ELEMENTALS 1.1.-
1.- NOCIONS ELEMENTALS 1.1.- Nomencltur 1.2.- Mtrius especils 2.- CÀLCUL MATRICIAL 2.1.- Principls opercions 2.2.- Rng: definició, propietts i càlcul 2.3.- Equcions mtricils 1.- NOCIONS ELEMENTALS 1.1.-
VECTORS. Una magnitud vectorial es representa mitjançant vectors. Des del punt de vista geomètric un vector A v (ó A)és un segment orientat amb:
 VECTORS Mgnituds esclrs i ectorils Les mgnituds físiques poden clssificr-se en esclrs i ectorils. Són mgnituds esclrs l tempertur, el trell o l energi, l mss etc., i són mgnituds ectorils l elocitt, el
VECTORS Mgnituds esclrs i ectorils Les mgnituds físiques poden clssificr-se en esclrs i ectorils. Són mgnituds esclrs l tempertur, el trell o l energi, l mss etc., i són mgnituds ectorils l elocitt, el
10 Problemes d optimització
 0 Problemes d optimitzció icrd Peiró i Estruch icrd Peiró i Estruch Problem Dont un tetredre regulr d rest inscriviu un prism regulr tringulr de volum màim que ting un bse en l bse del tetredre i els ltres
0 Problemes d optimitzció icrd Peiró i Estruch icrd Peiró i Estruch Problem Dont un tetredre regulr d rest inscriviu un prism regulr tringulr de volum màim que ting un bse en l bse del tetredre i els ltres
3.- Resolució d equacions d una variable
 3.- Resolució d equcions d un vrile 3.1. Recerc de zeros de funcions. Els lgorisme per tror zeros de funcions son mètodes numèrics que permeten tror un (o més) vlors de x tl que f(x) = 0 per un determind
3.- Resolució d equcions d un vrile 3.1. Recerc de zeros de funcions. Els lgorisme per tror zeros de funcions son mètodes numèrics que permeten tror un (o més) vlors de x tl que f(x) = 0 per un determind
SOLUCIONARI Unitat 1. Introducció al càlcul vectorial. Qüestions. 1. Dibuixeu dos vectors equipol. lents. 2. Dibuixeu dos vectors lliures iguals.
 SOLUCIONARI Unitt Introducció l càlcul vectoril Qüestions. Diuixeu dos vectors equipol. lents. Respost oert.. Diuixeu dos vectors lliures iguls. Respost oert. 3. Com són els vectors i que verifiquen questes
SOLUCIONARI Unitt Introducció l càlcul vectoril Qüestions. Diuixeu dos vectors equipol. lents. Respost oert.. Diuixeu dos vectors lliures iguls. Respost oert. 3. Com són els vectors i que verifiquen questes
Equacions polinòmiques
 EQUACIONS de r i n GRAU Hi h de molts tipus d equcions, per exemple: TEMA 7. EQUACIONS DE r I DE n GRAU I SISTEMES D EQUACIONS -Logrítmiques: -Trigonmètriques: -Rdicls: log( x + ) logx sin x cos x tgx
EQUACIONS de r i n GRAU Hi h de molts tipus d equcions, per exemple: TEMA 7. EQUACIONS DE r I DE n GRAU I SISTEMES D EQUACIONS -Logrítmiques: -Trigonmètriques: -Rdicls: log( x + ) logx sin x cos x tgx
12. Els polígons i la circumferència
 costt SLUINI 103 1. Els polígons i l circumferènci 1. PLÍGNS PENS I LUL lcul qunt f l ngle centrl mrct en els polígons següents:? costt? 4. ivideix un circumferènci de de rdi en sis prts iguls i dibuix
costt SLUINI 103 1. Els polígons i l circumferènci 1. PLÍGNS PENS I LUL lcul qunt f l ngle centrl mrct en els polígons següents:? costt? 4. ivideix un circumferènci de de rdi en sis prts iguls i dibuix
11. Triangles SOLUCIONARI 1. CONSTRUCCIÓ DE TRIANGLES 2. MITJANES I ALTURES D UN TRIANGLE
 SLUINRI 91 11. Tringles 1. NSTRUIÓ DE TRINLES PENS I LUL Justific si es poden dibuixr els tringles següents coneixent-ne les ddes: ) Tres costts les longituds dels quls són 1 cm, 2 cm i 3 cm b) Un costt
SLUINRI 91 11. Tringles 1. NSTRUIÓ DE TRINLES PENS I LUL Justific si es poden dibuixr els tringles següents coneixent-ne les ddes: ) Tres costts les longituds dels quls són 1 cm, 2 cm i 3 cm b) Un costt
TEMA 3.- Els nombres reals Correspondència amb el llibre de text: Temes 1 i 2.
 TEMA.- Els nombres rels Correspondènci mb el llibre de text: Temes i. Guió dels continguts d quest tem: Qulificció Deprtment de Mtemàtiques https://sites.google.com//slesinos.edu/deprtment-de-mtemtiques/
TEMA.- Els nombres rels Correspondènci mb el llibre de text: Temes i. Guió dels continguts d quest tem: Qulificció Deprtment de Mtemàtiques https://sites.google.com//slesinos.edu/deprtment-de-mtemtiques/
8 problemes d optimització
 8 problemes d optimitzció Problem De tots els ortoedres d àre de l bse cm i l sum de l longitud de totes les restes 0cm, determineu el de mjor àre Potpov Pàgin 5, problem 6 Problem Demostreu que de totes
8 problemes d optimitzció Problem De tots els ortoedres d àre de l bse cm i l sum de l longitud de totes les restes 0cm, determineu el de mjor àre Potpov Pàgin 5, problem 6 Problem Demostreu que de totes
SOLUCIONS ABRIL BD '. Aplicant el teorema del cosinus al triangle ABP: Pagina 1 de 14. AUTOR: Ricard Peiró i Estruch. IES Abastos.
 Pgin de OLUCION ABRIL 08 AUTOR: Ricrd Peiró i Estruch IE Abstos lènci ABRIL -8: Clculr l ngle que formen dues digonls d un cub Nivell: A prtir de EO olució: ig ABCDA B C D el cub d rest AB Aplicnt el teorem
Pgin de OLUCION ABRIL 08 AUTOR: Ricrd Peiró i Estruch IE Abstos lènci ABRIL -8: Clculr l ngle que formen dues digonls d un cub Nivell: A prtir de EO olució: ig ABCDA B C D el cub d rest AB Aplicnt el teorem
8 Geometria analítica
 Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
EQUACIONS DE SEGON GRAU AMB UNA INCÒGNITA
 EQUACIONS DE SEGON GRAU AMB UNA INCÒGNITA Un equió de segon gru mb un inògnit () és un epressió de l form : +b + 0 On, és el oefiient del terme de segon gru i és fonmentl que sigui diferent de zero. (Si
EQUACIONS DE SEGON GRAU AMB UNA INCÒGNITA Un equió de segon gru mb un inògnit () és un epressió de l form : +b + 0 On, és el oefiient del terme de segon gru i és fonmentl que sigui diferent de zero. (Si
Problemes de Geometria per a l ESO 98
 Ricrd Peiró i Estruch Problemes de Geometri per l ESO 98 97- Determineu l relció entre els volums dels dos cossos formts per l secció d un piràmide regulr qudrngulr per un plànol que pss pels punts migs
Ricrd Peiró i Estruch Problemes de Geometri per l ESO 98 97- Determineu l relció entre els volums dels dos cossos formts per l secció d un piràmide regulr qudrngulr per un plànol que pss pels punts migs
Còniques. Circumferència
 H. Helmi Còniques -1/19 Còniques Introducció Reen el nom de seccions còniques el conjunt de les diferents figures que s otenen en tllr un superfície cònic m un pl que no pssi pel vèrtex. L inclinció del
H. Helmi Còniques -1/19 Còniques Introducció Reen el nom de seccions còniques el conjunt de les diferents figures que s otenen en tllr un superfície cònic m un pl que no pssi pel vèrtex. L inclinció del
1) Enuncieu i demostreu la Regla de Barrow (2n teorema fonamental del càlcul integral). (1 punt) a) Dibuixeu el recinte limitat per aquestes corbes
 Generlitt de Ctluny Deprtment d Ensenyment Institut Jume Blmes Deprtment de Mtemàtiques n BATX MA Integrls definides i mètode de Guss Nom i Cognoms: Grup: Dt: ) Enuncieu i demostreu l Regl de Brrow (n
Generlitt de Ctluny Deprtment d Ensenyment Institut Jume Blmes Deprtment de Mtemàtiques n BATX MA Integrls definides i mètode de Guss Nom i Cognoms: Grup: Dt: ) Enuncieu i demostreu l Regl de Brrow (n
Pendents de 4t d ESO MATEMÀTIQUES
 Deures d estiu JUNY Pendents de t d ESO MATEMÀTIQUES Et recomno que durnt l estiu prepris mb temps i dedicció l emen de setembre. Us heu de presentr l emen de mtemàtiques el di que diu l ull que se us
Deures d estiu JUNY Pendents de t d ESO MATEMÀTIQUES Et recomno que durnt l estiu prepris mb temps i dedicció l emen de setembre. Us heu de presentr l emen de mtemàtiques el di que diu l ull que se us
Raons trigonomètriques d un angle agut. Denominació Definició Propietat bàsica Sinus sin α = b a. cos α = c a. tg α = tan α = b c
 Trigonometri Trigonometri Rons trigonomètriques d un ngle gut c Denominció Definició Propiett àsic Sinus sin = 0 sen 1 Cosinus Tngent cos = c tg = tn = c Propiett fonmentl sen + cos = 1 Rons trigonomètriques
Trigonometri Trigonometri Rons trigonomètriques d un ngle gut c Denominció Definició Propiett àsic Sinus sin = 0 sen 1 Cosinus Tngent cos = c tg = tn = c Propiett fonmentl sen + cos = 1 Rons trigonomètriques
Unitat 7. Rectes i angles
 Unitt 7. Rectes i ngles Pàgin 134. Reflexion Un grup de nois i noies col lboren en l rehbilitció de l cs de cultur. Observ lgunes de les eines de mesure i trçt que utilitzen: L plomd indic l direcció verticl
Unitt 7. Rectes i ngles Pàgin 134. Reflexion Un grup de nois i noies col lboren en l rehbilitció de l cs de cultur. Observ lgunes de les eines de mesure i trçt que utilitzen: L plomd indic l direcció verticl
Aplicacions del càlcul integral
 Apliccions del càlcul integrl Apliccions del càlcul integrl Càlcul de l àre d un funció Per clculr l àre tncd per un funció en un intervl [, ] m l eix X, s h de fer servir l integrl definid. Csos: 1. Si
Apliccions del càlcul integrl Apliccions del càlcul integrl Càlcul de l àre d un funció Per clculr l àre tncd per un funció en un intervl [, ] m l eix X, s h de fer servir l integrl definid. Csos: 1. Si
1.1.- Introducció Càlcul de determinants I Propietats dels determinants Càlcul de determinants II
 .- DETERMINNTS..- Introducció..- Càlcul de determinnts I..- Propietts dels determinnts..- Càlcul de determinnts II.- MTRIU INVERS.- CÀLCUL DEL RNG D UN MTRIU.- RESOLUCIÓ DE SISTEMES..- Mètode de l mtriu
.- DETERMINNTS..- Introducció..- Càlcul de determinnts I..- Propietts dels determinnts..- Càlcul de determinnts II.- MTRIU INVERS.- CÀLCUL DEL RNG D UN MTRIU.- RESOLUCIÓ DE SISTEMES..- Mètode de l mtriu
b c 2 A = : 2 = 176 m 2 A = p(p a) (p b) (p c) A = = = 47,33 m 2 a = 84 : 4 = 21 m
 117 elige Mtemátics, curso y tem. 13. Perímetres i àrees 4. Clcul l àre d un tringle rectngle en què els ctets fn m i 16 m 1. PERÍMETRE I ÀREES DELS POLÍGONS (I) PENSA I CALCULA Clcul mentlment el perímetre
117 elige Mtemátics, curso y tem. 13. Perímetres i àrees 4. Clcul l àre d un tringle rectngle en què els ctets fn m i 16 m 1. PERÍMETRE I ÀREES DELS POLÍGONS (I) PENSA I CALCULA Clcul mentlment el perímetre
Nombres enters i racionals
 1 Nombres enters i rcionls Objectius En quest quinzen prendràs : Representr i ordenr nombres enters. Operr mb nombres enters. Aplicr els conceptes reltius ls nombres enters problemes rels. Reconèixer i
1 Nombres enters i rcionls Objectius En quest quinzen prendràs : Representr i ordenr nombres enters. Operr mb nombres enters. Aplicr els conceptes reltius ls nombres enters problemes rels. Reconèixer i
DOSSIER DE RECUPERACIÓ 1r BATXILLERAT CURS MATEMÀTIQUES. Dossier recuperació 1r MAT INS Ernest Lluch i Martín 1 de 11
 DOSSIER DE RECUPERACIÓ r BATXILLERAT CURS -7 MATEMÀTIQUES Dossier recuperció r MAT INS Ernest Lluch i Mrtín de T. NOMBRES REALS. Digues de mner rond el primer conjunt numèric l qul pertnyen els següents
DOSSIER DE RECUPERACIÓ r BATXILLERAT CURS -7 MATEMÀTIQUES Dossier recuperció r MAT INS Ernest Lluch i Mrtín de T. NOMBRES REALS. Digues de mner rond el primer conjunt numèric l qul pertnyen els següents
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2011 SÈRIE 1
 Oficin d Orgnitzció de Proves d Accés l Universitt Pàgin 1 de 9 { 2x y +z = 2 1- Dond l rect r: x+z +1 = 0 : () Trobeu-ne un vector director SÈRIE 1 (b) Clculeu l equció contínu de l rect que és prl lel
Oficin d Orgnitzció de Proves d Accés l Universitt Pàgin 1 de 9 { 2x y +z = 2 1- Dond l rect r: x+z +1 = 0 : () Trobeu-ne un vector director SÈRIE 1 (b) Clculeu l equció contínu de l rect que és prl lel
DIVISIBILITAT. Amb els nombres 5, 7 i 35 podem escriure diverses expressions matemàtiques: 5x7= 35 35 5 35
 ESO Divisibilitat 1 ESO Divisibilitat 2 A. El significat de les paraules. DIVISIBILITAT Amb els nombres 5, 7 i 35 podem escriure diverses expressions matemàtiques: 5x7= 35 35 = 7 5 35 = 5 7 35 7 0 5 35
ESO Divisibilitat 1 ESO Divisibilitat 2 A. El significat de les paraules. DIVISIBILITAT Amb els nombres 5, 7 i 35 podem escriure diverses expressions matemàtiques: 5x7= 35 35 = 7 5 35 = 5 7 35 7 0 5 35
DOSSIER DE RECUPERACIÓ 1r BATXILLERAT MATEMÀTIQUES
 DOSSIER DE RECUPERACIÓ r BATXILLERAT MATEMÀTIQUES . Determin sense resoldre-l quntes solucions té l equció 9 0 mostr el ronment seguit b Resol l següent equció: 6. Resol les següents equcions: b c d 6
DOSSIER DE RECUPERACIÓ r BATXILLERAT MATEMÀTIQUES . Determin sense resoldre-l quntes solucions té l equció 9 0 mostr el ronment seguit b Resol l següent equció: 6. Resol les següents equcions: b c d 6
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Els nombres reals. Objectius. Abans de començar
 Els nomres rels Ojectius En quest quinzen prendràs : Clssificr els nomres rels en rcionls i irrcionls. Aproimr nomres rels per truncment i rrodoniment. Representr gràficment nomres rels. Comprr nomres
Els nomres rels Ojectius En quest quinzen prendràs : Clssificr els nomres rels en rcionls i irrcionls. Aproimr nomres rels per truncment i rrodoniment. Representr gràficment nomres rels. Comprr nomres
Matrius i determinants
 Mtrius i determinnts Mtrius i determinnts Mtrius Un mtriu és un grup de nombres orgnitzts en files i columnes, limitts per prèntesis: 1 2 3 n columnes 11 12 13 1 n 21 22 23 2n A= 31 32 33 3n m 1 m2 m3...
Mtrius i determinnts Mtrius i determinnts Mtrius Un mtriu és un grup de nombres orgnitzts en files i columnes, limitts per prèntesis: 1 2 3 n columnes 11 12 13 1 n 21 22 23 2n A= 31 32 33 3n m 1 m2 m3...
Iniciació a les integrals 2
 Inicició les integrls. Primitives. Regles bàsiques per l seu càlcul. Àre sot un corb. Teorem fonmentl del càlcul. Càlcul de l àre entre un corb i l ei X. Càlcul de l àre compres entre dues corbes INICIACIÓ
Inicició les integrls. Primitives. Regles bàsiques per l seu càlcul. Àre sot un corb. Teorem fonmentl del càlcul. Càlcul de l àre entre un corb i l ei X. Càlcul de l àre compres entre dues corbes INICIACIÓ
Matemàtiques 1, Editorial Castellnou
 MATEMÀTIQUES 1r BATXILLERAT Llibre utilitzat: Matemàtiques 1, Editorial Castellnou Observacions: La unitat 3 s estudia abans qua la unitat 2, per què l alumnat hagi revisat la Trigonometria abans de necessitar-la
MATEMÀTIQUES 1r BATXILLERAT Llibre utilitzat: Matemàtiques 1, Editorial Castellnou Observacions: La unitat 3 s estudia abans qua la unitat 2, per què l alumnat hagi revisat la Trigonometria abans de necessitar-la
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT CT ESTIU 2015
 EXERCICIS MATEMÀTIQUES r BATXILLERAT CT ESTIU 0 El trebll d estiu està penst per consolidr els conceptes trebllts primer de btillert que es necesten per rontr mb èit el segon curs.. Mtemàtiques Bt CT Tem:
EXERCICIS MATEMÀTIQUES r BATXILLERAT CT ESTIU 0 El trebll d estiu està penst per consolidr els conceptes trebllts primer de btillert que es necesten per rontr mb èit el segon curs.. Mtemàtiques Bt CT Tem:
Oficina d Accés a la Universitat Pàgina 1 de 11 PAU 2017 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficin d Accés l Universitt Pàgin de PAU 7 Criteris específics de correcció i qulificció per ser fets públics un cop finlitzdes Mtemàtiques SÈRIE Responeu CINC de les sis qüestions següents. En les respostes,
Oficin d Accés l Universitt Pàgin de PAU 7 Criteris específics de correcció i qulificció per ser fets públics un cop finlitzdes Mtemàtiques SÈRIE Responeu CINC de les sis qüestions següents. En les respostes,
[PAU97S1AQ3] Feu un esquema de la representació gràfica del polinomi
![[PAU97S1AQ3] Feu un esquema de la representació gràfica del polinomi [PAU97S1AQ3] Feu un esquema de la representació gràfica del polinomi](/thumbs/71/64973058.jpg) FUNCIONS [PAU97JBQ] Clculeu el límit qun i qun de l funció polinòmic n f ( ) K n, on els coeficients,,, n són nombres rels, i n > (hureu de considerr el cs que n sigui prell i el cs que sigui senr). Justifiqueu
FUNCIONS [PAU97JBQ] Clculeu el límit qun i qun de l funció polinòmic n f ( ) K n, on els coeficients,,, n són nombres rels, i n > (hureu de considerr el cs que n sigui prell i el cs que sigui senr). Justifiqueu
Com pagar una hipoteca
 IES Arquitecte Mnuel Rspll Com pgr un hipotec 3r trimestre A. ANUALITATS Com molt bé sbeu, poc gent es pot deslliurr de pgr un hipotec, sol licitr un crèdit personl o comprr terminis. Trctrem quests tipus
IES Arquitecte Mnuel Rspll Com pgr un hipotec 3r trimestre A. ANUALITATS Com molt bé sbeu, poc gent es pot deslliurr de pgr un hipotec, sol licitr un crèdit personl o comprr terminis. Trctrem quests tipus
Es important dir que, dos vectors, des del punt de vista matemàtic, són iguals quan els seus mòduls, sentits i direccions són equivalents.
 1 CÀLCUL VECTORIAL Abans de començar a parlar de vectors i ficar-nos plenament en el seu estudi, hem de saber distingir els dos tipus de magnituds que defineixen la física: 1. Magnituds escalars: magnituds
1 CÀLCUL VECTORIAL Abans de començar a parlar de vectors i ficar-nos plenament en el seu estudi, hem de saber distingir els dos tipus de magnituds que defineixen la física: 1. Magnituds escalars: magnituds
Límits i continuïtat. lim+ lim. x x. lim. lim : lim. lim. lim. lim. 2 x 5x. lim. lim. lim. lim. lim. lim. lim
 Mtemàtiques n Bt Unitt 0: Límits i continuïtt Col legi Mirsn Unitt 0: Límits i continuïtt. Clcul els següents límits: 0 : c e g 7 0 0 7 i b 0 d f h 7. Clcul els següents límits lterls: c e b d f. Clcul
Mtemàtiques n Bt Unitt 0: Límits i continuïtt Col legi Mirsn Unitt 0: Límits i continuïtt. Clcul els següents límits: 0 : c e g 7 0 0 7 i b 0 d f h 7. Clcul els següents límits lterls: c e b d f. Clcul
Apunts de Càlcul Tema 3. Integració de funcions d una variable
 Apunts de Càlcul Tem 3. Integrció de funcions d un vrible Lli Brrière, Josep M. Olm Deprtment de Mtemàtic Aplicd 4 - UPC Enginyeri de Sistemes de Telecomunicció Enginyeri Telemàtic EETAC Càlcul (EETAC-UPC)
Apunts de Càlcul Tem 3. Integrció de funcions d un vrible Lli Brrière, Josep M. Olm Deprtment de Mtemàtic Aplicd 4 - UPC Enginyeri de Sistemes de Telecomunicció Enginyeri Telemàtic EETAC Càlcul (EETAC-UPC)
Dossier preparació PAU
 Dossier preprció PAU ( AB C) XAB XC = C X AB C = C X = C AB C AB C = = = 6 AB C = 6 8 = 8 = 8 X = C ( AB C) = = = 8 5 uur uur Curs 7-8 AB = B A =,,, AC=C-A= -,-,- - - - - y- =, --y+z+= +y-z-= - z- Mtemàtiques
Dossier preprció PAU ( AB C) XAB XC = C X AB C = C X = C AB C AB C = = = 6 AB C = 6 8 = 8 = 8 X = C ( AB C) = = = 8 5 uur uur Curs 7-8 AB = B A =,,, AC=C-A= -,-,- - - - - y- =, --y+z+= +y-z-= - z- Mtemàtiques
Seccions còniques. 1 Introducció. 2 Seccions d un con per un pla. Ramon Nolla Departament de Matemàtiques IES Pons d Icart
 IES Pons d Icrt Seccions còniques 1 Seccions còniques Rmon Noll Deprtment de Mtemàtiques IES Pons d Icrt 1 Introducció S tribuei Menecm (iv C) el descobriment de les seccions còniques. No se sp de quin
IES Pons d Icrt Seccions còniques 1 Seccions còniques Rmon Noll Deprtment de Mtemàtiques IES Pons d Icrt 1 Introducció S tribuei Menecm (iv C) el descobriment de les seccions còniques. No se sp de quin
A C T I V I T A T S D E R E C U P E R A C I Ó D E M A T E M À T I Q U E S II
 A C T I V I T A T S D E R E C U P E R A C I Ó D E M A T E M À T I Q U E S II NOM... ANÀLISI. Dond l funció f() ln( ), es demn : ) Monotoni ) Curvtur c) Gràfic. ) Determin el vlor del pràmetre que f que
A C T I V I T A T S D E R E C U P E R A C I Ó D E M A T E M À T I Q U E S II NOM... ANÀLISI. Dond l funció f() ln( ), es demn : ) Monotoni ) Curvtur c) Gràfic. ) Determin el vlor del pràmetre que f que
3º A d'eso Capítol 5: Equacions de segon grau i sistemes lineals
 Mtemàtiques orientdes les ensennces plicdes : Equcions n gru i sistemes linels ºA ESO º A d'eso Cpítol : Equcions de segon gru i sistemes linels Revisors: Sergio Hernández i Mrí Molero Il lustrcions: Rquel
Mtemàtiques orientdes les ensennces plicdes : Equcions n gru i sistemes linels ºA ESO º A d'eso Cpítol : Equcions de segon gru i sistemes linels Revisors: Sergio Hernández i Mrí Molero Il lustrcions: Rquel
Potències i radicals. Objectius
 Potècies i rdicls Ojectius E est quice prederás : Clculr i operr m potècies d'epoet eter. Recoèier les prts d'u rdicl i el seu sigifict. Oteir rdicls equivlets u de dot. Epressr u rdicl com potèci d'epoet
Potècies i rdicls Ojectius E est quice prederás : Clculr i operr m potècies d'epoet eter. Recoèier les prts d'u rdicl i el seu sigifict. Oteir rdicls equivlets u de dot. Epressr u rdicl com potèci d'epoet
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
Àmbit de les Matemàtiques, de la Ciència i de la Tecnologia M14 Operacions numèriques UNITAT 1 OPERACIONS AMB ENTERS
 UNITAT 1 OPERACIONS AMB ENTERS 1 Què treballaràs? En acabar la unitat has de ser capaç de... Sumar, restar, multiplicar i dividir nombres enters. Entendre i saber utilitzar les propietats de la suma i
UNITAT 1 OPERACIONS AMB ENTERS 1 Què treballaràs? En acabar la unitat has de ser capaç de... Sumar, restar, multiplicar i dividir nombres enters. Entendre i saber utilitzar les propietats de la suma i
Problemes de Camp Magnètic 2009
 FME FÍSCA GENEAL - OBLEMES DFEN rolemes de Cmp Mgnètic 2009 ecordeu: µ 0 = 4π 10-7 Tm/A, e = 1.6 10-19 C, m p = 1.67 10-27 kg, m e = 9.11 10-31 kg, 1 T = 10 4 G 1. Clculeu l forç de Lorentz que ctu sore
FME FÍSCA GENEAL - OBLEMES DFEN rolemes de Cmp Mgnètic 2009 ecordeu: µ 0 = 4π 10-7 Tm/A, e = 1.6 10-19 C, m p = 1.67 10-27 kg, m e = 9.11 10-31 kg, 1 T = 10 4 G 1. Clculeu l forç de Lorentz que ctu sore
Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra.
 UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
EL MÈTODE DELS ELEMENTS FINITS: FONAMENTS
 Problem model EL MÈTODE DELS ELEMENTS FINITS: FONAMENTS Form fort (diferencil) EDP: en Condicions de contorn Dirichlet Lbortori de Càlcul Numèric (LCàN) Universitt Politècnic de Ctluny (Spin) http://www-lcn.upc.es
Problem model EL MÈTODE DELS ELEMENTS FINITS: FONAMENTS Form fort (diferencil) EDP: en Condicions de contorn Dirichlet Lbortori de Càlcul Numèric (LCàN) Universitt Politècnic de Ctluny (Spin) http://www-lcn.upc.es
Matemàtiques 1r d'eso Professora: Lucía Clar Tur DOSSIER DE REPÀS
 DOSSIER DE REPÀS 1. Ordena els nombres de més petit a més gran: 01 0 01 101 0 001 0 001 0 1. Converteix els nombres fraccionaris en nombres decimals i representa ls en la recta: /4 1/ 8/ 11/10. Efectua
DOSSIER DE REPÀS 1. Ordena els nombres de més petit a més gran: 01 0 01 101 0 001 0 001 0 1. Converteix els nombres fraccionaris en nombres decimals i representa ls en la recta: /4 1/ 8/ 11/10. Efectua
2.1.- Operacions bàsiques Producte Punt mitjà d un segment
 1.- VECTORS 1.1.- Cnceptes previs 1.2.- Relció entre V 2 i R 2 1.3.- Crdendes crtesines 1.4.- Mòdul d un vectr 1.5.- Cmbinció linel 1.6.- Cncepte i tipus de Bses 2.- OPERACIONS 2.1.- Opercins bàsiques
1.- VECTORS 1.1.- Cnceptes previs 1.2.- Relció entre V 2 i R 2 1.3.- Crdendes crtesines 1.4.- Mòdul d un vectr 1.5.- Cmbinció linel 1.6.- Cncepte i tipus de Bses 2.- OPERACIONS 2.1.- Opercins bàsiques
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
x x Com es pot saber si una equació de 2n grau dels tipus ax 2 +bx+c=0, té dues, una o cap solució sense resoldre-la?
 TEMA t ESO Equions e r i n gru Resol les següents equions: Com es pot ser si un equió e n gru els tipus, té ues, un o p soluió sense resolre-l? Determin per quins vlors e k l equió -k. Té: un sol soluió;
TEMA t ESO Equions e r i n gru Resol les següents equions: Com es pot ser si un equió e n gru els tipus, té ues, un o p soluió sense resolre-l? Determin per quins vlors e k l equió -k. Té: un sol soluió;
Ampliació de Matemàtiques Tema 1. Integrals dobles i triples 1 / 26
 Ampliió de Mtemàtiques Tem 1. Integrls dobles i triples Lli Brrière Deprtment de Mtemàtiques - UPC Enginyeri de Sistemes Aeroespils Enginyeri d Aeroports Enginyeri d Aeronvegió EETAC Ampliió de Mtemàtiques
Ampliió de Mtemàtiques Tem 1. Integrls dobles i triples Lli Brrière Deprtment de Mtemàtiques - UPC Enginyeri de Sistemes Aeroespils Enginyeri d Aeroports Enginyeri d Aeronvegió EETAC Ampliió de Mtemàtiques
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Trigonometria Resolució de triangles.
 Trigonometria Resolució de triangles. Raons trigonomètriques d un angle agut. Considerarem el triangle rectangle ABC on A = 90º Recordem que en qualsevol triangle rectangle Es complia el teorema de Pitàgores:
Trigonometria Resolució de triangles. Raons trigonomètriques d un angle agut. Considerarem el triangle rectangle ABC on A = 90º Recordem que en qualsevol triangle rectangle Es complia el teorema de Pitàgores:
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
7. Calcula P (x ) Q (x ): P (x ) = 5x 4 + x 3 2x 2 5 Q (x ) = 7x 4 5x 2 + 3x + 2 P (x ) Q (x ) = 2x 4 + x 3 + 3x 2 3x 7
 50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
Trigonometria. Objectius. Abans de començar.
 7 Trigonometri Objectius En quest quinzen prendreu : Clculr les rons trigonomètriques d'un ngle. Trobr totes les rons trigonomètriques d'un ngle prtir d'un d'questes. Resoldre tringles rectngles qun es
7 Trigonometri Objectius En quest quinzen prendreu : Clculr les rons trigonomètriques d'un ngle. Trobr totes les rons trigonomètriques d'un ngle prtir d'un d'questes. Resoldre tringles rectngles qun es
DE FORMA ALGEBRAICA CERTES SITUACIONS
 EXPRESSAR OBJECTIU DE FORMA ALGEBRAICA CERTES SITUACIONS NOM: CURS: DATA: LLENGUATGE NUMÈRIC I LLENGUATGE ALGEBRAIC El llenguatge en què intervenen nombres i signes d operacions l anomenem llenguatge numèric.
EXPRESSAR OBJECTIU DE FORMA ALGEBRAICA CERTES SITUACIONS NOM: CURS: DATA: LLENGUATGE NUMÈRIC I LLENGUATGE ALGEBRAIC El llenguatge en què intervenen nombres i signes d operacions l anomenem llenguatge numèric.
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
UNITAT 3: TRIGONOMETRIA
 UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
1.- Elements d una recta Vector director d una recta Vector normal d una recta Pendent d una recta
 .- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
.- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
FITXA 1: Angles consecutius i adjacents
 FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
Unitat 1. Nombres reals.
 Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
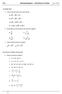 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
TEMA 4. SISTEMA MÈTRIC DECIMAL
 c s e s MATEMÀTIQUES 1r ESO o p u n i e s v e s i n c TEMA 4. SISTEMA MÈTRIC DECIMAL Un mnitud és un crcterístic que pot ser mesurd i expressd mitjnçnt un nombre. L mnitud es mesur comprnt-l mb un ptró
c s e s MATEMÀTIQUES 1r ESO o p u n i e s v e s i n c TEMA 4. SISTEMA MÈTRIC DECIMAL Un mnitud és un crcterístic que pot ser mesurd i expressd mitjnçnt un nombre. L mnitud es mesur comprnt-l mb un ptró
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
TEMA 2: Múltiples i Divisors
 TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
Dossier d Energia, Treball i Potència
 Dossier d Energia, Treball i Potència Tipus de document: Elaborat per: Adreçat a: Dossier de problemes Departament de Tecnologia (LLHM) Alumnes 4 Curs d ESO Curs acadèmic: 2007-2008 Elaborat per: LLHM
Dossier d Energia, Treball i Potència Tipus de document: Elaborat per: Adreçat a: Dossier de problemes Departament de Tecnologia (LLHM) Alumnes 4 Curs d ESO Curs acadèmic: 2007-2008 Elaborat per: LLHM
Introducció a la Trigonometria 4t ESO
 Introducció a la Trigonometria 4t ESO Índex: 1. Unitats de mesura d'angles: graus i radians.... 3. Raons trigonomètriques bàsiques: sinus, cosinus i tangent. Definicions.... 5 3. Relacions entre les raons
Introducció a la Trigonometria 4t ESO Índex: 1. Unitats de mesura d'angles: graus i radians.... 3. Raons trigonomètriques bàsiques: sinus, cosinus i tangent. Definicions.... 5 3. Relacions entre les raons
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
UNI DAD 2 TRIGONOMETRÍA ANALÍTICA. Objetivos
 UNI DAD 2 TRIGONOMETRÍA ANALÍTICA Objetivos Geometrí nlític Introducción funciones trigonométrics Vribles: dependientes independientes Constnte: numéric bsolut rbitrri, y z., b, c, Funciones: función
UNI DAD 2 TRIGONOMETRÍA ANALÍTICA Objetivos Geometrí nlític Introducción funciones trigonométrics Vribles: dependientes independientes Constnte: numéric bsolut rbitrri, y z., b, c, Funciones: función
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
5.3.- Nivells de metalls en sang
 5.3. Nivells de metlls en sng S'hn mesurt els nivells de beril li (Be), mngnès (Mn), mercuri (Hg) i lom (Pb) en les mostres de sng totl corresonents ls 8 rticints en l estudi. Les concentrcions de beril
5.3. Nivells de metlls en sng S'hn mesurt els nivells de beril li (Be), mngnès (Mn), mercuri (Hg) i lom (Pb) en les mostres de sng totl corresonents ls 8 rticints en l estudi. Les concentrcions de beril
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
MÍNIM COMÚ MULTIPLE m.c.m
 MÍNIM COMÚ MULTIPLE m.c.m Al calcular el mínim comú múltiple de dos o més nombres el que estem fent és quedar-nos amb el valor més petit de tots els múltiples que són comuns a aquests nombres. És a dir,
MÍNIM COMÚ MULTIPLE m.c.m Al calcular el mínim comú múltiple de dos o més nombres el que estem fent és quedar-nos amb el valor més petit de tots els múltiples que són comuns a aquests nombres. És a dir,
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Departament de Física i Química
 Deprtment de Físic i Químic EXERCICIS RESOLTS CINÈTICA QUÍMICA n BATXILLERAT Velocitt d un recció químic 1. Oserv l recció següent: clor (g) + igu (g) clorur d hidrogen (g) + 1/ oxigen (g) Escriu l relció
Deprtment de Físic i Químic EXERCICIS RESOLTS CINÈTICA QUÍMICA n BATXILLERAT Velocitt d un recció químic 1. Oserv l recció següent: clor (g) + igu (g) clorur d hidrogen (g) + 1/ oxigen (g) Escriu l relció
TEMA 2: Múltiples i Divisors. Activitats. 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3 ens doni 25
 TEMA 2: Múltiples i Divisors Activitats Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per
TEMA 2: Múltiples i Divisors Activitats Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per
11 Límits de funcions. Continuïtat i branques infinites
 Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
FITXA 1: Polígons. Conceptes
 FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
Tema 3: EQUACIONS I INEQUACIONS
 Tem : EQUACIONS I INEQUACIONS Full de preprció Aques full s h de lliurà el di de l prov Nom:... Curs:... 1. Resoleu: ) ( ) + = ) ( + ) = ( + 1 ) + 1 e e e c) 1 ( ) e) + ( 1 - ) =. Resoleu les equcions
Tem : EQUACIONS I INEQUACIONS Full de preprció Aques full s h de lliurà el di de l prov Nom:... Curs:... 1. Resoleu: ) ( ) + = ) ( + ) = ( + 1 ) + 1 e e e c) 1 ( ) e) + ( 1 - ) =. Resoleu les equcions
