DECLARACIÓN REAL DECRETO 1065/2007, DE 27 DE JULIO

Para consultas llamar al: 800-4722

I. Documntos ncsrios pr solicitr un préstmo hipotcrio ASALARIADOS Crt d trbjo originl Copi d cédul d idntidd prsonl Copi d l fich d Sguro Socil Copi d los dos últimos tlonrios d chqu Solicitud complt firmd

PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------

IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d

OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)

IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo

UNIVERSIDAD DE LA RIOJA JUNIO lim

IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios

F U T S W W P V F W P V G U T S P V G F P V W P V P V W. nfec. G nfe C. Energía libre y fuerza electromotriz.

nrgí libr y furz lctromotriz. Dsd un punto d vist trmodinámico, sbmos qu tmprtur constnt, l disminución d l nrgí libr d Hlmholtz, F (pr un procso rvrsibl), rprsnt l trbjo totl (W) hcho sobr los lrddors,

PROCEDIMIENTO PARA EL RECONOCIMIENTO DE CRÉDITOS POR ACREDITACIÓN PROFESIONAL

PROCEDIMIENTO PARA EL RECONOCIMIENTO DE CRÉDITOS POR ACREDITACIÓN PROFESIONAL (Aprobado por Consejo de Gobierno de 11 de febrero de 2011) En consonancia con lo aprobado en el artículo 6 del Real Decreto

Para la lectura del instructivo tenga en cuenta la descripción de las partes de la siguiente manera:

CONOCIMIENTO DEL CLIENTE Person Jurídic Fech de elorción: Nov de 2015 Código: IN-J.04-2 Págin 1 de 7 Versión: 1 OBJETIVO Estlecer el correcto diligencimiento de l informción requerid en el formto único

Sistemas de ecuaciones lineales

Sistems de ecuciones lineles º) L sum de ls tres cifrs de un número es 8, siendo l cifr de ls decens igul l medi de ls otrs dos. Si se cmbi l cifr de ls uniddes por l de ls centens, el número ument en

Impuesto sobre Sucesiones y Donaciones Adquisiciones "mortis causa"

STE MODELO SE REPRODUCE A EFECTOS MERAMENTE INFORMATIVOS. PARA SU DESCARGA, IMPRESIÓN Y CUMPLIMENTACIÓN DEBE ACUDIRSE A LA WEB DE LA AGENCIA TRIBUTARIA RELACIÓN DE BIENES QUE INTEGRAN EL CAUDAL HEREDITARIO.

CONSEJERÍA DE ECONOMÍA Y HACIENDA IMPUESTO SOBRE SUCESIONES Y DONACIONES

CÓDIGO TERRITORIAL E H CONSEJERÍA DE ECONOMÍA Y HACIENDA T ALÓN DE CARGO PAGINA 1 FECHA DEVENGO 02 DÍA MES AÑO SUJETO PASIVO (A) Espcio reservdo pr l etiquet identifictiv 05 06 07 08 FAX 15 16 FECHA NACIMIENTO

GERENCIA SECTORIAL DE REGISTRO Y CONTROL CIRCULAR TRAMITES DE PRODUCTOS COSMETICOS A PARTIR DEL 01/09/2010

Instituto Ncionl de Higiene "Rfel Rngel" Ciudd Universitri UCV, Los Chgurmos, Crcs - Republic Bolivrin de Venezuel Cod. 1041 RC-C-009/2010 CARACAS, 26/07/2010 GERENCIA SECTORIAL DE REGISTRO Y CONTROL CIRCULAR

núm. 117 lunes, 24 de junio de 2013 III. ADMINISTRACIÓN LOCAL AYUNTAMIENTO DE BRIVIESCA

III. ADMINISTRACIÓN LOCAL AYUNTAMIENTO DE BRIVIESCA C.V.E.: BOPBUR-2013-04928 Por acurdo dl Plno dl Ayuntaminto d Brivisca d fcha 29 d mayo d 2013, s adoptó l Acurdo dl tnor litral siguint: Antcdnts d

Logaritmos y exponenciales:

Logrimos ponncils: L rsolución d cucions ponncils s s n l siguin propidd d ls poncis : Dos poncis con un mism s posiiv disin d l unidd son iguls, si sólo si son iguls sus ponns. Es dcir, p. j. Si = noncs

I.E.S. Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti PROPUESTA A

I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto

DATOS GENERALES DE IDENTIFICACIÓN

DATOS GENERALES DE IDENTIFICACIÓN IDP IDENTIFICACIÓN DE LA EMPRESA SA: 01011 SL: 01012 Forma jurídica 01010 Otras: 01013 X Denominación social: 01020 Domicilio social: 01022 PZ MAYOR 1 Municipio: 01023

PROTOCOLO DE PRUEBA DE CARACTERÍSTICAS TÉCNICAS DE PORTALES DE INTERNET NT CNTI 0003-1: 2008

PROTOCOLO DE PRUEBA DE CARACTERÍSTICAS TÉCNICAS DE PORTALES DE INTERNET NT CNTI 0003-1: 2008 Introducción Este documento tiene como objetivo describir el instrumento trvés del cul se especificn, desde

Integrales impropias.

IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls

FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS

FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds

IV. POSICIONES GEODESICAS

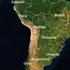IV. OICIOE GEODEIC Un d ls finlidds principls d l godsi s l cálculo d ls coordnds godésics d puntos sobr l lipsoid. Ests coordnds s dnoinn Ltitud y Longitud y stán sipr rfrids un sist godésico pr-dtrindo.

TRANSFORMADORES EN PARALELO

TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:

IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho UNIVERSIDAD DE EXTREMADURA MATEMÁTICAS II

IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un

Boletín Oficial de Castilla y León I. COMUNIDAD DE CASTILLA Y LEÓN

Boletín Oficial de Castilla y León Núm. 78 Lunes, 27 de abril de 2015 Pág. 29169 I. COMUNIDAD DE CASTILLA Y LEÓN A. DISPOSICIONES GENERALES CONSEJERÍA DE HACIENDA ORDEN HAC/318/2015, de 16 de abril, por

METODOLOGÍA PARA LOS PROYECTOS DE SUSTITUCIÓN DE COMBUSTIBLES FÓSILES POR ENERGÍA SOLAR EN UNA INSTALACIÓN DE RIEGO AISLADA NUEVA O YA EXISTENTE

METODOLOGÍA PARA LOS PROYECTOS DE SUSTITUCIÓN DE COMBUSTIBLES FÓSILES POR ENERGÍA SOLAR EN UNA INSTALACIÓN DE RIEGO AISLADA NUEVA O YA EXISTENTE Sector: Agricultur. Est metodologí plicrá los proyectos

SUBVENCIONES PARA LA MOVILIDAD DE ESTUDIANTES UNIVERSITARIOS SÉNECA Cuaderno del becario

SUBVENCIONES PARA LA MOVILIDAD DE ESTUDIANTES UNIVERSITARIOS SÉNECA Cuaderno del becario Curso académico 2012-2013 ÍNDICE 1. DOCUMENTOS PARA LA GESTIÓN DE LAS BECAS 1.1. Documentos para el alta Compromiso

Para la lectura del instructivo tenga en cuenta la descripción de las partes de la siguiente manera:

Fech de elorción: Nov de 2015 Código: IN-J.04-1 Págin 1 de 8 Versión: 2 OBJETIVO Estlecer el correcto diligencimiento de l informción requerid en el formto único de conocimiento del cliente - Person Nturl,

III.- OTRAS DISPOSICIONES Y ACTOS

AÑO XXXII Núm. 170 3 de septiembre de 2013 23655 III.- OTRAS DISPOSICIONES Y ACTOS Corrección de errores de la Orden de 26/08/2013, por la que se convocan subvenciones para el desarrollo de actividades

DECLARACIÓN DE TITULARES DE INVERSIÓN ESPAÑOLA EN EL EXTERIOR EN VALORES NEGOCIABLES. Modelo D-6. Instrucciones de Cumplimentación

Instrucciones aprobadas por Resolución de 24 de enero de 2013 (BOE Nº 31 de 5 de febrero de 2013) de la Dirección General de Comercio e Inversiones. DECLARACIÓN DE TITULARES DE INVERSIÓN ESPAÑOLA EN EL

BASES QUE HAN DE REGIR EL CONCURSO DE DISEÑO DE LOGOTIPO TOLEDO CAPITAL ESPAÑOLA DE LA GASTRONOMÍA 2016

AYUNTAMIENTO DE TOLEDO BASES QUE HAN DE REGIR EL CONCURSO DE DISEÑO DE LOGOTIPO TOLEDO CAPITAL ESPAÑOLA DE LA GASTRONOMÍA 2016 1.- OBJETO DEL CONCURSO. Con motivo de la declaración de la ciudad de Toledo

Deducción de las reglas de derivación. Partiendo de las derivadas de la función potencial, la función exponencial y la función seno, ( ) ( ) 1

dmttmtics.wordprss.com Btriz d Otto Lópz Dducción d ls rgls d drivción Prtindo d ls drivds d l función potncil, l función ponncil l función sno, = R = f = =, f = sn = cos, f,, d ls rgls d drivción pr l

BOLSAS DE TRABAJO TEMPORAL ENFERMERAS HOJA DE AUTOBAREMO

BOLSAS DE TRABAJO TEMPORAL ENFERMERAS HOJA DE AUTOBAREMO INSTRUCCIONES GENERALES PARA LA CUMPLIMENTACIÓN DE LA HOJA DE AUTOBAREMO: Todos los candidatos elaborarán su Hoja de Autobaremo, calificando sus

Ie Io. Medidas absolutas y medidas relativas

Mdids soluts y mdids rltivs Cómo otnr un mdi socición? Comprndo dos mdids d frcunci Mdids soluts (Difrnci) Mdids rltivs (Rzón) Supongmos qu un invrsión inicil d Euros s convirt n 2 Euros l co d un ño.

TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES

3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin

PROCEDIMIENTO DEVOLUCIONES CARTERA INSTITUCIONAL

OBJETIVO ALCANCE PUNTOS DE INTERÉS Pr relizr ls devoluciones se dee verificr que los dineros están consigndos en l cuent de l Universidd y que l mtrícul del estudinte se encuenr pgd en su totlidd. Relizr

MINISTERIO DE EMPLEO Y SEGURIDAD SOCIAL TESORERÍA GENERAL DE LA SEGURIDAD SOCIAL. tc. 17/11 RECONOCIMIENTO DE DEUDAS CON LA SEGURIDAD SOCIAL

MINISTERIO tc. 17/11 RECONOCIMIENTO DE DEUDAS CON LA SEGURIDAD SOCIAL INSTRUCCIONES PARA LA CUMPLIMENTACIÓN DEL MODELO GENERALES - El documento deberá cumplimentarse a máquina o con letras mayúsculas,

MANUAL DE USO PARA LA GESTIÓN ON LINE DE SU PÓLIZA COLECTIVA

IMPRIMIR PORTAL SANITAS EMPRESAS MANUAL DE USO PARA LA GESTIÓN ON LINE DE SU PÓLIZA COLECTIVA Snits pone su disposición el portl de Empress, un herrmient on line muy útil que le permitirá gestionr todos

P41. Renta disponible total del hogar (rentas menos impuestos) al mes. 5.2 Serie neta de componentes de renta en el hogar

5. Rent y gstos 5.1 Rent del hogr P41. Rent disponible totl del hogr (rents menos impuestos) l mes 5.2 Serie net de componentes de rent en el hogr P42. Indique de cuál de ls siguientes fuentes proviene

ESTADO DE ARIZONA CONDADO DE MARICOPA COMITÉ POLÍTICO INFORME DE FINANZAS DE LA CAMPAÑA

ESTADO DE ARIZONA CONDADO DE MARICOPA COMITÉ POLÍTICO INFORME DE FINANZAS DE LA CAMPAÑA SÓLO PARA USO OFICIAL 1. Complto l Comité Dirión Tléono 3. 2. Orgnizión Ptroinor (si s pli) l Cnito y Pusto qu Soliit

ÁLGEBRA Tema 1) MATRICES

MTEMÁTICS PLICDS LS CIENCIS SOCILES II ÁLGER Tema ) MTRICES Orientaciones para la PRUE DE CCESO L UNIVERSIDD en relación con este tema: Conocer el vocabulario básico para el estudio de matrices: elemento

Multiplicación algebraica

Versión01 Multiplicciónlgeric Por:SndrElviPéreMárque Lsopercioneslgericscomolmultipliccióndivisiónnecesitndelgunosconocimientosprevios, por ejemplo: ls regls de los signos, de los eponentes, por lo que

BOLETÍN OFICIAL DEL ESTADO

Núm. 289 Martes 30 de noviembre de 2010 Sec. I. Pág. 99247 I. DISPOSICIONES GENERALES MINISTERIO DE ECONOMÍA Y HACIENDA 367 Orden EHA/3061/2010, de 22 de noviembre, por la que se modifican el modelo 347

ADVERTENCIA AL ASEGURABLE

FORMULARIO PROPUESTA CENTROS COBERTURA MEDICINA SEGURO REPRODUCTIVA PARA SEGURO ESTUDIOS RESPONSABILIDAD CONTABLES FORMULARIO RECOLECCION DATOS PARA PRECOTIZACIÓN ADVERTENCIA AL ASEGURABLE En caso de que

Venta de 6 frigoríficos a 1.000 cada uno. Las ventas del ejercicio son ingresos. Banco Clientes a Ventas de mercaderías 6000

Solución Ejercicio 3: A. Registro de l vent. Vent de 6 frigoríficos 1.000 cd uno. Ls vents del ejercicio son ingresos. 5400 Bnco Clientes Vents de mercderís 0 (+) Bnco (-) (-) Resultdo Ejer (+) 0 (+) Clientes

Lectura del informe técnico del sr. Intendente Principal de la Policía Local Apertura sobres C Oferta económica.

Expediente: 2403/2014 Asunto: Contrato renting 2 vehículos policía local Día y hora de la reunión: 13 de octubre de 2014 Lugar de celebración: Salón de Sesiones de la Casa Consistorial Asistentes: Presidente:

En adelante, podrá ser también denominado el Distribuidor.

En Miami, a de octubre de 2015. REUNIDOS: A.- DE UNA PARTE: D. MIGUEL J. LAZARO MONREAL, mayor de edad, con Número Identificación 16.007.824.P, que interviene en nombre y representación, como Presidente

INSTRUCCIONES PARA CUMPLIMENTAR EL FORMULARIO ELECTRÓNICO PROGRAMA DE ESTUDIOS DE POSTGRADO EN ECONOMÍA Y FINANZAS 2006-2008

INSTRUCCIONES PARA CUMPLIMENTAR EL FORMULARIO ELECTRÓNICO PROGRAMA DE ESTUDIOS DE POSTGRADO EN ECONOMÍA Y FINANZAS 2006-2008 INSTRUCCIONES GENERALES Le tentmente ests instrucciones ntes comenzr cumplimentr

REGISTRO DE DIFENILOS POLICLORADOS AÑO 2016

RESOLUCIÓN 497 ANEXO I. SUPERINTENDENCIA DE RIESGOS DEL TRABAJO REGISTRO DE DIFENILOS POLICLORADOS AÑO 2016 Nº SIMPLIFICACIÓN REG. REGISTRO GENERAL DE ENTRADA (*) Número de entrada Fecha de entrada (*)

OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits

REGISTRO MUNICIPAL DE SOLARES Y EDIFICACIONES RUINOSAS

FINCA Nº 1048 FOLIO Nº 137 1) CLASE DE INMUEBLE INCLUIDO (1) :. Debido a (2) : Solar sin edificar. 2) CIRCUNSTANCIAS: 2.1) Nombre de la finca: Calle o plaza: Cardenal Lluch. Número actual y anteriores:

Números Racionales 1. INTRODUCCIÓN

Númros Rionls Título: Númros Rionls Trgt: PROFESORES DE MATEMÁTICAS Asigntur: Mtmátis Autor: Emilin Oliván Clz Lini n Mtmátis Prosor Mtmátis n Euión Sunri 1 INTRODUCCIÓN En l ominio intgri (DI) los númros

INTEGRAL DEFINIDA ÁREAS Y VOLUMENES

Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid

PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 28 FISICA TOMO 2. Tercera y quinta edición. Raymond A. Serway

PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3

MATRICES DE NÚMEROS REALES

MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m

a > 0 y a 1. Si la base es e se llama exponencial natural tiene la forma

INTRODUCCIÓN A LAS MATEMATICAS SUPERIORES TEMA 6 FUNCIONES LOGARÍTMICAS Un función ponncil d s tin l form f ( pr tod R > 0 y. Si l s s s llm ponncil nturl tin l form dond f (. L.- Con l informción qu cunt

DOCUMENTACION PARA FORMACIÓN BONIFICADA PARA EMPRESAS

DOCUMENTACION PARA FORMACIÓN BONIFICADA PARA EMPRESAS Adhesión al Convenio: Cumplimentar y firmar por el Representante Legal de su empresa. Ficha del alumno: Completar y firmar como alumno del curso elegido.

IMPUESTO SOBRE SOCIEDADES (Cierre fiscal ejercicio 2013) (Ajustes y conceptos a considerar)

IMPUESTO SOBRE SOCIEAES (Cierre fiscl ejercicio 2013) (Ajustes y conceptos considerr) (13) LIMITACIÓN A LAS AMORTIZACIONES FISCALMENTE EUCIBLES EN EL IMPUESTO SOBRE SOCIEAES Novedd introducid por l Ley

Debe marcar con una X el tipo de trámite que realiza.

Debe marcar con una X el tipo de trámite que realiza. X Indicar la nacionalidad del solicitante. JUAN LOPEZ LOPEZ MEXICANA 100 Anotar el apellido materno. Asentar el nombre o nombres completos del o los

Solicitud de corrección patronal. Los documentos que necesitas son:

Solicitud de corrección patronal Los documentos que necesitas son: Solicitud para adherirte al programa de corrección a través del formato CORP-01 Solicitud de Corrección Patronal. Tarjeta de Identificación

Para la lectura del instructivo tenga en cuenta la descripción de las partes así:

Fech de elorción: Noviemre de 2015 Código: IN-J.04-4 Págin 1 de 10 Versión: 1.0 OBJETIVO Diligencir de mner decud l informción requerid pr l vinculción de Persons Jurídics Intermedirios y/o Proveedores,

1.3.4 Ejercicios resueltos sobre la función exponencial y logarítmica

.. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:

PRODUCTOS NOTABLES APELLIDOS Y NOMBRES

PRODUCTOS NOTABLES APELLIDOS Y NOMBRES SECCIÓN Qué es un producto notble? L plbr "producto" hce referenci l resultdo de un multiplicción y l plbr "notble" hbl de lgo que se puede notr simple vist; por

BANCOS FORMULARIO PARA INICIO DE RELACIONES - Persona Jurídica -

FORMULARIO IVE-BA-02 BANCOS FORMULARIO PARA INICIO DE RELACIONES - Persona Jurídica - 1. LUGAR: 2. FECHA (dd/mm/aaaa): 3. 3.1 Razón Social y Nombre Comercial: DATOS DE LA PERSONA OBLIGADA 3.2 Nombre de

PARTICIPACIONES COTIZADAS, S.A.U.)

DON MIGUEL CRESPO RODRÍGUEZ, con D.N.I. nº 10.057.714-K, Secretario no consejero del Consejo de Administración de BANCO FINANCIERO Y DE AHORROS, S.A. (SOCIEDAD UNIPERSONAL), entidad de crédito de nacionalidad

Número Total Empleados: Número Total de Empleados con acceso a Ficheros que contengan Datos de Carácter Personal

SOLICITUD DE SEGURO RESPONSABILIDAD CIVIL POR PROTECCIÓN DE DATOS 1. Datos generales Tomador de la Póliza:...C.I.F.:... Domicilio Social:... Ciudad:... C.P.:... Teléfono:... Fax.. E-mail:... Fecha de creación

CONDICIONES RELATIVAS A LA APERTURA, UTILIZACIÓN Y CIERRE DE UNA CUENTA CORRIENTE EN LA OMPI

CONDICIONES RELATIVAS A LA APERTURA, UTILIZACIÓN Y CIERRE DE UNA CUENTA CORRIENTE EN LA OMPI 1. Disposiciones generales A petición de los clientes regulares de la Organización, la OMPI ofrece la posibilidad

DOCUMENTACION PARA FORMACIÓN BONIFICADA PARA EMPRESAS

DOCUMENTACION PARA FORMACIÓN BONIFICADA PARA EMPRESAS Adhesión al Convenio: Cumplimentar y firmar por el Representante Legal de su empresa. Ficha del alumno: Completar y firmar como alumno del curso elegido.

Tarea 11. Integral Impropia

Tr Intgrl Imroi Ers con l límit corrsondint cd un d ls siguints intgrls Mustr un dibujo qu indiqu l ár qu s clculrí (si ist) con l intgrl rsctiv, no clculs l intgrl d ; b) d ; c) d ; d) / cot( ) d En los

MEMORIA ANUAL RELATIVA AL DESARRROLLO DE LA INVERSIÓN EN EL EXTERIOR. Modelo D-8. Instrucciones de Cumplimentación

MEMORIA ANUAL RELATIVA AL DESARRROLLO DE LA INVERSIÓN EN EL EXTERIOR Modelo D-8 Instrucciones de Cumplimentación Normas generales de cumplimentación Corresponde utilizar este modelo D-8 para presentar

NORMATIVA DE GESTIÓN DE PROYECTOS ASOCIADOS A REMANENTES (PAR) DE LA UNIVERSIDAD DE CANTABRIA

NORMATIVA DE GESTIÓN DE PROYECTOS ASOCIADOS A REMANENTES (PAR) DE LA UNIVERSIDAD DE CANTABRIA Justificación: Los grupos de la UC cada vez se encuentran con más frecuencia con la necesidad de continuar

Cuál es su valor de CRF? Es normal? Qué enfermedad le sugiere esta valor de CRF?

1 Bloque 1 Problem 1. Un niño es conectdo, después de un espirción norml, un bols conteniendo 2 litros de 8% He, 92% O 2. Respir de l bols hst que l mezcl es complet, y en ese momento l concentrción de

SOLICITUD AVAL TECNICO PYMES NO SOCIOS RECIENTE CREACION (NO SOCIOS)

SOLICITUD AVAL TECNICO PYMES NO SOCIOS RECIENTE CREACION (NO SOCIOS) DOCUMENTACIÓN NECESARIA PARA EL ESTUDIO DE LA OPERACIÓN ESCRITURAS DE CONSTITUCIÓN FOTOCOPIA DEL PODER DE REPRESENTACIÓN DE LA PERSONA

ANEXO 1. NORMAS DE PRESENTACIÓN DEL TRABAJO FIN DE MÁSTER Máster Universitario en

ANEXO 1 NORMAS DE PRESENTACIÓN DEL TRABAJO FIN DE MÁSTER Máster Universitario en 1. El trabajo tendrá una extensión entre y 2. El texto debe estar libre de errores tipográficos y gramaticales, y utilizar

De la lectura de este párrafo podemos llegar a las mismas conclusiones detalladas anteriormente.

INFORME TÉCNICO SOBRE LA NATURALEZA CONTABLE DE LA AMORTIZACIÓN Y SU IMPLICACIÓN EN EL PROCESO DE CÁLCULO DE LOS COSTES DE LOS PRODUCTOS TERMINADOS Y EN LA CUENTA DE PÉRDIDAS Y GANANCIAS. 1.- OBJETIVO

SOLICITUD DE POLIZA POR RESPONSABILIDAD CIVIL PARA INVESTIGACIONES Y/O ENSAYOS

SOLICITUD DE POLIZA POR RESPONSABILIDAD CIVIL PARA INVESTIGACIONES Y/O ENSAYOS INSTRUCTIVO: a) Por favor, complete los datos solicitados en el formulario y adjunte toda información complementaria que se

Código Nombre Municipio. DNI/NIE/Pasaporte Núm. identificación. Fecha de nacimiento Lugar de nacimiento País Nacionalidad

. Historil cdémico Educción secundri pr ls persons dults Dtos del centro Código Nombre Municipio Dtos del lumno DNINIEPsporte Núm. identificción Fech de ncimiento Lugr de ncimiento Pís Ncionlidd Dtos cdémicos

CUESTIONARIO PRELIMINAR DE EMPRESAS

Hoja 1 de 5 1.- DATOS DE IDENTIFICACIÓN GENERALES Nombre de la Empresa: (Nombre de la empresa) (PECAL solicitada) Personal total de la empresa:... Persona de contacto con el AII/SDGINREID/DGAM: Nombre

EXPRESIONES ALGEBRAICAS

EXPRESIONES ALGEBRAICAS Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman V A R I A B L ES, I N C Ó G N I T A S o

CONTROL DE ASISTENCIA PRESENCIAL

CONTROL DE ASISTENCIA PRESENCIAL OPCIÓN A EMPRESA BONIFICADA: CIF.: OPCIÓN B ENTIDAD ORGANIZADORA: CIF.: CÓDIGO DE AGRUPACIÓN: (Se seleccionará uno de los apartados anteriores dependiendo del perfil con

I. Comunidad Autónoma

Página 22793 I. Comunidad Autónoma 3. Otras disposiciones 6858 Orden de 27 de mayo de 2015, de la Consejería de Educación, Cultura y Universidades por la que se convocan los Premios Extraordinarios de

Definición. Cualquier nombre acompañado de "Sociedad Civil" o "SCP" Escritura Pública si se aportan bienes inmuebles o derechos reales.

Sociedad Civil Contrato por el cual dos o más personas se obligan a poner en común dinero, bienes o industria, para realizar una actividad empresarial en común con ánimo de repartir entre sí las ganancias.

DOCUMENTACION PARA FORMACIÓN A TRAVÉS DEL PERMISO INDIVIDUAL DE FORMACIÓN

DOCUMENTACION PARA FORMACIÓN A TRAVÉS DEL PERMISO INDIVIDUAL DE FORMACIÓN Adhesión al Convenio: Cumplimentar y firmar por el Representante Legal de su empresa. Ficha del alumno: Completar y firmar como

1er GRADO. Resta HOJAS DE TRABAJO

1er GRADO Rest HOJAS DE TRABAJO Rest voculrio Cundo restmos, scmos un número o un cntidd de otro número o cntidd. Luke tení 9. Regló 2 su hermno. Le quedron 7 left. Escriimos esto como 9 2 = 7 1 Coloc

SOLICITUD DE PENSIÓN DE JUBILACIÓN NO CONTRIBUTIVA Texto Refundido Ley General Seguridad Social (RDL 1/1994, de 20 de junio)

SEGURIDAD SOCIAL SOLICITUD DE PENSIÓN DE JUBILACIÓN NO CONTRIBUTIVA Texto Refundido Ley General Seguridad Social (RDL 1/1994, de 20 de junio) I. DATOS DEL INTERESADO 1. Datos personales (Antes de cumplimentar

BOLETÍN OFICIAL DEL ESTADO

Núm. 247 Jueves 15 de octubre de 2015 Sec. I. Pág. 95792 I. DISPOSICIONES GENERALES MINISTERIO DE HACIENDA Y ADMINISTRACIONES PÚBLICAS 11074 Orden HAP/2118/2015, de 9 de octubre, por la que se aprueba

SOLICITUD DE SEGURO DE AERONAVES DE AVIACIÓN GENERAL. Estado: Ciudad: Zona Postal: Teléfono (Indique Código de Área): Número de Fax:

SOLICITUD DE SEGURO DE AERONAVES DE AVIACIÓN GENERAL Nº DE POLIZA: FECHA: La presente Solicitud de Seguro debe ser leída y llenada a máquina o letra de molde, en todos sus puntos, sin enmiendas y en tinta

ÍNDICE. 6.2 Evaluación de la eficacia de la Dirección

PROCEDIMIENTO OPERATIVO DEL SISTEMA DE GESTIÓN DE LA CALIDAD NMPO 02.01 Hoja 1 de 4 ÍNDICE 1. OBJETO 2. ALCANCE 3. DOCUMENTACIÓN DE REFERENCIA 4. DEFINICIONES 5. RESPONSABILIDADES 6. REALIZACIÓN 6.1. Plan

REUNIDOS ACTUAN EXPONEN. Que es su intención la de constituir una sociedad civil privada, que se regirá por las siguientes CLAUSULAS

CONTRATO DE OCIEDAD CIVIL PRIVADA En Castellé,a 29 de DIciembre de 2.010 REUNIDOS A.E.A.T. DELEGACION DE CASTELLON GESTION TRIBUT ARIA CODIGO DE IDENTIFICACION DE LAS PERSONAS JURIDICAS y ENTIDADES EN

Pruebas t para una y dos muestras independientes

Densidd Densidd AGRO 55 LAB 9 Pruebs t pr un y dos muestrs independientes 1. Clcule ls siguientes probbiliddes usndo l tbl t e InfoStt. Incluy un digrm en cd cso.. P(T>1.356) si gl=1 b. P(T

ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS MATEMÁTICAS

ESCUELA SUPEIO POLITÉCNICA DEL LITOAL INSTITUTO DE CIENCIAS MATEMÁTICAS Mtmátics d Nivl 0A Invirno 00 Sgund Evlución Ingnirís Abril d 00 Nombr: VESIÓN. Dd l gráfic d l función f qu s djunt l prsnt, idntifiqu

ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS MATEMÁTICAS

ESCUELA SUPEIO POLITÉCNICA DEL LITOAL INSTITUTO DE CIENCIAS MATEMÁTICAS Mtmátics d Nivl 0A Invirno 00 Sgund Evlución Ingnirís Abril d 00 Nombr: VESIÓN 0. Si g s un función d l n l cu gráfic stá dd por:

I. Comunidad Autónoma

Página 41592 I. Comunidad Autónoma 3. Otras disposiciones 14490 Orden de 11 de noviembre de 2014, de la Consejería de Educación, Cultura y Universidades por la que se convocan los Premios Extraordinarios

TEMA 3 POLINOMIOS NOMBRE Y APELLIDOS... HOJA 1 - FECHA...

TEMA 3 POLINOMIOS NOMBRE Y APELLIDOS... HOJA 1 - FECHA... TEMA 3 EXPRESIONES ENTERAS Y POLINOMIOS Una expresión algebraica es una combinación de letras y números con operaciones matemáticas que las unen,

p m son términos semejantes

Páin dl Colio d Mtmátics d l ENP-UNAM Ocions con monomios olinomios Auto: D. José Mnul Bc Esinos OPERACIONES CON MONOMIOS Y POLINOMIOS UNIDAD IV IV. OPERACIONES CON MONOMIOS Un vil s un lmnto d un ómul,

2. REPRESENTACIÓN ANALÍTICA Y GRÁFICA DE UN VECTOR

1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid

SOLICITUD DE FRANQUICIA

SOLICITUD DE FRANQUICIA La información registrada en este formato tendrá un uso estrictamente confidencial por parte de Grupo Inmobiliario Rentohouse de Mexico SA de CV. Por favor proporciónenos la información

AYUDA A LA PRODUCCION de ACEITE DE OLIVa Y ACEITUNa DE MESA SOLICITUD DE ALTA DE USUARIO DEL SISTEMA DE CONSULTA EN PÁGINA WEB CAMPAÑA 2001/2002

AYUDA A LA PRODUCCION de ACEITE DE OLIVa Y ACEITUNa DE MESA CAMPAÑA 2001/2002 SOLICITUD DE ALTA DE USUARIO DEL SISTEMA DE CONSULTA EN PÁGINA WEB Versión 1 26/09/2002 Dirección General del Subdirección

78217 SAN ANTONIO, TX USA

INFORMACION GENERAL: a) Nombre o denominación social: COEM HEAVY AND LIGHT EQUIPMENT TRADER LLC. Domicilio: STARCREST DR 272 8800 Calle Número y/o letra exterior Número y/o letra interior 78217 SAN ANTONIO,

PROBLEMAS DE OPTIMIZACIÓN

PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito

UN NUEVO MULTIPLICADOR MONETARIO

UN NUEVO MULTIPLICADOR MONETARIO 1. Introducción La figura del multiplicador monetario es de sobra conocida por todos los economistas. Aparece en todos los libros de importantes de economía y, aunque hoy

INFORMACIÓN SOBRE LA FUSIÓN ENTRE. GRUPO EMPRESARIAL MIGAN, S.L. (como Sociedad Absorbente)

INFORMACIÓN SOBRE LA FUSIÓN ENTRE GRUPO EMPRESARIAL MIGAN, S.L. (como Sociedad Absorbente) Y FRIGORÍFICOS MIGAN, S.A.U. LUFRI, S.A.U. (como Sociedades Absorbidas) ÍNDICE A los efectos de lo dispuesto en

1. DEFINICIÓN Y CLASIFICACIÓN DE MATRICES

Mtrices. . DEFINICIÓN Y CLSIFICCIÓN DE MTRICES Ls mtrices son utilizds por primer vez hci el ño por Jmes Joseph Sylvester. El desrrollo inicil de l teorí mtricil se debe l mtemático británico Willim Rown