Fonaments Físics de les Estructures. Tema 4.- Geometria de masses (I): Centre de gravetat de superfícies planes.
|
|
|
- Adrián Campos Botella
- hace 6 años
- Vistas:
Transcripción
1 Fonaments Físcs de les Estructures Tema 4.- eometra de masses (I): Centre de gravetat de superfíces planes.
2 Objectus: Entendre el concepte de centre de gravetat. Dferencar el centre de gravetat màssc del centre de gravetat d una superfíce. Aprendre a calcular centres de gravetat d objectes lneals, b- trdmensonals. Aprendre a calcular centres de gravetat de superfíces complexes. Conèxer saber utltzar els teoremes de Pappos-uldn.
3 stemes de vectors paral lels ón sstemes en els quals tots els vectors tenen la matexa dreccó., F F u La resultant també té la matexa dreccó que tots els vectors. R F u R
4 stemes de vectors paral lels El moment del sstema respecte d un punt qualsevol P és perpendcular a la resultant: M PA F P Axò mplca que el segon nvarant és nul: m M u P 0
5 stemes de vectors paral lels es gra tot el sstema de vectors, es defnex una nova dreccó un nou ex central del sstema: Y Y X Els exos centrals dels sstemes obtnguts grant en totes les dreccons possbles el sstema de vectors es tallen en un punt anomenat Centre del stema. X
6 stemes de vectors paral lels Per a un sstema de vectors paral lels, exstex un punt d especal mportànca, que s anomena punt central del sstema. Es troba sobre l ex central es pot calcular mtjançant l expressó: r C F r F, on r són els vectors de poscó.
7 Centre de gravetat d un sstema de partícules El centre de gravetat (cdg) d un sstema de partícules és el centre del sstema de vectors format per les forces-pes de les partícules del sstema: Y F mg F mg r r r r c.d.m. F M g F F mg mg X r F r mg r m r F m g m uposem que ens trobem en la superfíce terrestre, on el camp gravtator produex una acceleracó g constant.
8 Centre de gravetat d un sstema de partícules La resultant de totes les forces-pes està aplcada en el cdg del sstema de partícules: F mg F mg r r r Y r c.d.m. F F mg mg X F Mg F M g
9 Centre de gravetat d un sstema de partícules Les components cartesanes del vector de poscó del cdg d un sstema de partícules venen donades per mx my mz x ; y ; z ; m m m r Y F mg F mg r r r r c.d.m. F F mg mg X F M g
10 Centre de gravetat d un cos sòld Quan h ha una gran quanttat d elements xcotets, F mg F mg M g
11 Centre de gravetat d un cos sòld Quan la dstrbucó de massa no és dscreta, snó que és contínua, com succeex en un sòld qualsevol, es consderen elements nfntesmals de massa dm. df=dm g
12 Centre de gravetat d un cos sòld Les coordenades cartesanes del vector de poscó del cdg de un cos sòld (amb denstat constant) venen donades per r x V V xdm dm 1 M V xdm y V V ydm dm 1 M V ydm z V V zdm dm 1 M V zdm
13 Centre de gravetat d una dstrbucó lneal de massa X Una dstrbucó lneal de massa és sempre la que té una de les tres dmensons, per exemple el llarg, molt més gran que les altres dues (ample, alt). Z r dl Y anomena denstat lneal de massa al quocent: dm dl és. El centre de gravetat té vector de poscó: r rdm rdl rdl V L L dm dl L V M L L ( kg / m ) (dstrbucó unforme de massa)
14 Centre de gravetat d una dstrbucó lneal de massa Y /2 dl EXEMPLE: CALCULEU EL CD D UN QUART DE CIRCUMFERÈNCIA En aquest cas el paràmetre serà l angle de la fgura. d R O x y 0 X Es verfca: dl Rd x R cos y Rsen x xdl R Rd R d Rsen R dl Rd d /2 /2 /2 cos cos L y /2 /2 /2 L 0 0 0
15 Centre de gravetat d una dstrbucó lneal de massa Habtualment la corba es pot expressar com una funcó on les varables es poden expressar d acord amb un paràmetre. Per a una corba plana en el pla OXY: Z r dl Y dy dl dx dy dx dx y 1 1 ' dx 2 X
16 Centre de gravetat d una dstrbucó superfcal de massa Quan una de les dmensons de la dstrbucó de masses és molt més petta que les altres dues, es poden consderar com una dstrbucó superfcal de massa. anomena denstat superfcal de massa al quocent: dm és. El centre de gravetat té vector de poscó: r V V rdm r d rd dm d M d 2 ( kg / m ) (dstrbucó unforme de massa)
17 Centro de gravetat d una dstrbucó superfcal de massa Les coordenades cartesanes del cdg d una dstrbucó superfcal de massa en el pla OXY són: x xd yd ; y ; EXERCICI: CALCULEU EL CD D UN TRIANLE RECTANLE (pàg del llbre)
18 Centre de gravetat d una dstrbucó volumètrca de massa En el cas general d un cos trdmensonal, es du que exstex una dstrbucó volumètrca de massa. anomena denstat de massa al quocent: és. El centre de gravetat té vector de poscó: r dm dv V V V V rdm rdv rdv dm dv M V 3 ( kg / m ) V (dstrbucó unforme de massa)
19 Centre de gravetat d una dstrbucó volumètrca de massa Les coordenades cartesanes del cdg d una dstrbucó volumètrca unforme de massa són: xdv ydv zdv V V V x ; y ; z ; V V V EXERCICI: CALCULEU EL CD D UN CON RECTE (pàg del llbre)
20 Teoremes de Pappos-uldn Prmer teorema: L'àrea lateral de la fgura de revolucó engendrada en grar una lína al voltant d un ex que no talla és gual al producte de la longtud de la crcumferènca que descru el centre de gravetat de la lína per la seua longtud. L àrea de la superfíce de revolucó és: d 2 ydl 2L y L y 2 L
21 Teoremes de Pappos-uldn Aplcacons del prmer teorema: Coneguda la UPERFÍCIE Obtndre CD de la LÍNIA Conegut el CD de la LÍNIA Obtndre la UPERFÍCIE Un quart de crcumferènca en grar respecte a l ex X genera la superfíce d una semesfera. Y y 2 semesfera 2 r 2r 2 L r crcunf crcumf /4 2 2 y X
22 Teoremes de Pappos-uldn Aplcacons del prmer teorema: Coneguda la UPERFÍCIE Obtndre el CD de la LÍNIA Conegut el CD de la LÍNIA Obtndre la UPERFÍCIE clndro clndre h 2 r long. lnea recorrdo long. lína recorregut r cono h r 2 r h r long. lnea long. lína recorrdo recorregut
23 Teoremes de Pappos-uldn egon teorema: El volum de la fgura de revolucó engendrada en grar una superfíce al voltant d un ex que no talla és gual al producte de la longtud de la crcumferènca que descru el centre de gravetat de la superfíce per l àrea d aquesta superfíce. Un element d genera un volum dv=2yd El volum de revolucó és: V dv 2 yd 2 y y V 2
24 Teoremes de Pappos-uldn Aplcacons del segon teorema: Conegut el VOLUM Obtndre el CD de la UPERFÍCIE Conegut el CD de la UPERFÍCIE Obtndre el VOLUM 1 2 rh r V r h x x 3 trángulo trangle recorregut recorrdo r 4r V r x x 3 semcírculo semcercle recorrdo recorregut
25 Teoremes de Pappos-uldn Aplcacons del segon teorema: Conegut el VOLUM Obtndre el CD de la UPERFÍCIE Conegut el CD de la UPERFÍCIE Obtndre el VOLUM V a 2 2 b 2 2 a 2 b círculo cercle recorrdo recorregut
26 Càlcul sstemàtc de centres de gravetat Per a calcular el cdg d una superfíce rregular, podem dvdr-la en N trossos amb formes regulars, de les quals podem conèxer fàclment la poscó del cdg (càlcul o utltzant les taules). El cdg del conjunt serà: x y x x x... x N N 1 2 y y y... y N N 1 2 N N
27 Càlcul sstemàtc de centres de gravetat H ha moltes formes d especejar la fgura en formes regulars. la denstat superfcal és constant, són possbles especejaments en què h haja parts amb una superfíce negatva. la superfíce es compon de materals de dferents denstats, s haurà de dvdr en trossos que tnguen la matexa denstat. En aquest cas, les coordenades del cdg són: on és la denstat superfcal de cada tros. x x y ; y ;
28 Taula de fgures regulars amb els seus cdg
29 Exemple de càlcul de cdg Obtenu la dstànca a l ex X del centre de gravetat d una seccó plana trapezoïdal en funcó de les seues dmensons. El trapez sempre es pot especejar en un rectangle (1) u o dos trangles (2 3). Axí, les àrees són: 1 bc abc 2 3 /2 les coordenades vertcals dels cdg respectves són: Axí doncs la coordenada vertcal del cdg del trapez és: ; c c y1 ; y2 y3 ; 2 3. y c b a y c a 2b 3 a b
30 Aplcacó 2n teorema de Pappos Obtenu l expressó del volum del tronc de con recte. L àrea del trapez és Per a calcular la coordenada y del cdg s especeja el trapez en un rectangle (1) un trangle (2). r1 En el rectangle és en el trangle és amb àrees y1, 2 r2 r1 r2 2 r1 y 2 r1, 3 3 r h r rh /2. Axí doncs el cdg del trapez té coordenada y : trapeco trapez r r h X y h Z r 1 r 2 y y Y
31 Aplcacó 2n teorema de Pappos ubsttunt en l expressó les dades obtngudes resulta y r1 r2 2r r 1 2 r1 h r1 h r2 r1h r1 h 2 que smplfcada és y y r rr r 3 r r y y Aplcant el 2n teorema de Pappos, el volum del tronc de con és: r r h r rr r h V r rr r r1 r2 3 área trapeco àrea trapez recorrdo recorregut X h Z r 1 r 2 Y EXERCICI: CALCULEU LA UPERFÍCIE LATERAL DEL TRONC DE CON
32 Moments respecte d un ex La dstrbucó de masses en un cos determnarà el seu comportament davant l aplcacó de forces externes. La poscó del cdg té relacó drecta amb l establtat d un cos. També, la deformacó d una bga sota l accó d un sstema de forces depén del moment d nèrca de la seccó respecto a la lína de suport.
33 Moments respecte d un ex Però el centre de gravetat és el prmer ordre, el moment d nèrca és el segon ordre d una magntud més general anomenada Moment d una superfíce respecte d un ex. En general, per a una superfíce un ex E qualsevol, es defnex el moment d ordre n de la superfíce com: n n M n d M n dd (dstrbucó dscreta) (dstrbucó contínua) on d és la dstànca de la superfíce a l ex.
34 Moments respecte d un ex El moment de prmer ordre d una superfíce respecte d un ex s anomena Moment estàtc. Y y d M U d d 1 EE ' Moment de prmer ordre respecte de l ex X: O x X M U y d 1X OX Moment de prmer ordre respecte de l ex Y: M U x d 1Y OY
35 Moments respecte d un ex La relacó entre el Moment de prmer ordre el cdg és mmedata. Y y d x xd yd ; y ; O x X U OX y d U OY x d UOY UOX Resulten, x ; y ;
36 Moments respecte d un ex DEFINICION: PROPIETAT: Una superfíce és smètrca respecte d un ex EE s, per a cada punt P de la superfíce, exstex un altre P de la matexa tal que el segment PP és perpendcular a l ex EE, la superfíce està dvdda en dues parts guals per aquest ex. Una superfíce es smètrca respecte d un punt O s per a cada element d en (x,y) exstex un altre element d en (-x,-y). El moment de prmer ordre de una superfíce respecto de qualsevol lína de smetra és gual a zero. la superfíce té algun ex de smetra, el seu centre de gravetat es troba en aquex ex. una superfíce té dos exos de smetra, el seu centro de gravetat es troba en la nterseccó dels dos. El centre de gravetat d una superfíce concdex amb el seu centre de smetra.
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
POLÍGONS, CIRCUMFERÈNCIA I CERCLE
 POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ 1.2. CLASSIFICACIÓ
 GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 3 ÀREES I VOLUMS. Unitat 3 ÀREES I VOLUMS
 70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
La porció limitada per una línia poligonal tancada és un
 PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES
 OBJECTIU RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES 10 NOM: CURS: DATA: CONCEPTE DE PRISMA Un prisma és un poliedre format per dues bases iguals i paral leles, les cares laterals
OBJECTIU RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES 10 NOM: CURS: DATA: CONCEPTE DE PRISMA Un prisma és un poliedre format per dues bases iguals i paral leles, les cares laterals
Etáti Estática. 2.Centros de gravedad y 3.Momentos de inercia
 Etát Estátca.Equlbro 2.Centros de gravedad y 3.Momentos de nerca Parte de la físca que estuda el equlbro de los cuerpos Partedelafíscaqueestudalasrelaconesexstentes entre las fuerzas que actúan en un cuerpo
Etát Estátca.Equlbro 2.Centros de gravedad y 3.Momentos de nerca Parte de la físca que estuda el equlbro de los cuerpos Partedelafíscaqueestudalasrelaconesexstentes entre las fuerzas que actúan en un cuerpo
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
TRIANGLES. TEOREMA DE PITÀGORES.
 TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
j Introducció al càlcul vectorial
 FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
Políedres regulars Cossos de revolució
 Políedres regulars Cossos de revolució Políedre. Un políedre és un cos limitat per cares poligonals. Angle díedre. Angle políedre anomena angle díedre d un políedre el que està format per dues cares que
Políedres regulars Cossos de revolució Políedre. Un políedre és un cos limitat per cares poligonals. Angle díedre. Angle políedre anomena angle díedre d un políedre el que està format per dues cares que
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Deduce razonadamente en que casos los planos π 1 y π 2 son o no paralelos:
 GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
GEOMETRÍA Junio 98 Deduce razonadamente en que casos los planos y son o no paralelos: a) : x + y + z = y : x + y z = 4 b) : x y + z = 4 y : x y + z = Obtén la distancia entre los planos y cuando sean paralelos.
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
TEMA2. Dinámica I Capitulo 3. Dinámica del sólido rígido
 TEM. Dnámca I Captulo 3. Dnámca del sóldo rígdo TEM : Dnámca I Capítulo 3: Dnámca del sóldo rígdo Eje nstantáneo de rotacón Sóldo con eje fjo Momento de nerca. Teorema de Stener. Conservacón del momento
TEM. Dnámca I Captulo 3. Dnámca del sóldo rígdo TEM : Dnámca I Capítulo 3: Dnámca del sóldo rígdo Eje nstantáneo de rotacón Sóldo con eje fjo Momento de nerca. Teorema de Stener. Conservacón del momento
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
GEOMETRÍA ANALÍTICA PLANA
 GEOMETRÍA ANALÍTICA PLANA Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo). Módulo del vector : Es la longitud del segmento AB, se representa por. Dirección del
GEOMETRÍA ANALÍTICA PLANA Un vector fijo es un segmento orientado que va del punto A (origen) al punto B (extremo). Módulo del vector : Es la longitud del segmento AB, se representa por. Dirección del
Fuerzas distribuidas. 2. Momento de inercia
 Dpto. Físca y Mecánca Fuerzas dstrbudas d Centro de gravedad centro de masas. Centro de gravedad, centro de masas. Momento de nerca ntroduccón. Fuerzas dstrbudas Cálculo de centrodes y centros de gravedad
Dpto. Físca y Mecánca Fuerzas dstrbudas d Centro de gravedad centro de masas. Centro de gravedad, centro de masas. Momento de nerca ntroduccón. Fuerzas dstrbudas Cálculo de centrodes y centros de gravedad
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
CAMPS DE FORÇA CONSERVATIUS
 El treball fet per les forces del camp per a traslladar una partícula entre dos punts, no depèn del camí seguit, només depèn de la posició inicial i final. PROPIETATS: 1. El treball fet pel camp quan la
El treball fet per les forces del camp per a traslladar una partícula entre dos punts, no depèn del camí seguit, només depèn de la posició inicial i final. PROPIETATS: 1. El treball fet pel camp quan la
UN POLÍGON és una superficie plana
 UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
Tema 1. MOVIMENT ÍNDEX
 Tema 1. MOVIMENT Tema 1. MOVIMENT ÍNDEX 1.1. Les magnituds i les unitats 1.2. Moviment i repòs 1.3. Posició i trajectòria 1.4. Desplaçament i espai recorregut 1.5. Velocitat i acceleració 1.6. Moviment
Tema 1. MOVIMENT Tema 1. MOVIMENT ÍNDEX 1.1. Les magnituds i les unitats 1.2. Moviment i repòs 1.3. Posició i trajectòria 1.4. Desplaçament i espai recorregut 1.5. Velocitat i acceleració 1.6. Moviment
quaderns de matemàtiques
 1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte xevi.vb@gmail.com CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte xevi.vb@gmail.com CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos
 DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
DE S L U S RE S I V I C LES Resultat final, sense desenvolupar, dels exercicis i problemes proposats de cada unitat i de l apartat Resolució de problemes. En queden exclosos aquells exercicis que requereixen
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Sector circular i Segment circular.
 Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SISTEMES DE FORCES. La força neta actuant sobre un cos és la suma de totes les forces que hi actuen i es denomina resultant: F net =ΣF i.
 SISTEMES DE FRCES Introduccó. Lles de Newton Començarem aquest tema fent una ntroduccó a la dnàmca, que es la part de la Físca que estuda les causes del moment. Ens mantndrem sempre en l àmbt de la mecànca
SISTEMES DE FRCES Introduccó. Lles de Newton Començarem aquest tema fent una ntroduccó a la dnàmca, que es la part de la Físca que estuda les causes del moment. Ens mantndrem sempre en l àmbt de la mecànca
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
INTEGRALS. 2 a) 3-2 x 2 x 3 dx b) 5-3x 2 dx c) 5 x 2 7 x dx d) x x 4 dx. x x - 2 x2 - x 3 dx c) 1+x 2 dx.
 INTEGRALS a) 3 6 b) 2 2 c) 5 3 2 d) 7 3 e) 2 a) 3-2 2 3 b) 5-3 2 c) 5 2 7 d) 3 a) 5-2 3-7 2 +2-5 3 b) 3 2-3 + 3 +5 2-2 2-3 c) + 2 a) 3-3 2 2 b) -3 2 c) 5-3 2 5 a) 2 +7-6 +3 5 b) 7 3-2+ 3 +3 c) 5+3 7 2
INTEGRALS a) 3 6 b) 2 2 c) 5 3 2 d) 7 3 e) 2 a) 3-2 2 3 b) 5-3 2 c) 5 2 7 d) 3 a) 5-2 3-7 2 +2-5 3 b) 3 2-3 + 3 +5 2-2 2-3 c) + 2 a) 3-3 2 2 b) -3 2 c) 5-3 2 5 a) 2 +7-6 +3 5 b) 7 3-2+ 3 +3 c) 5+3 7 2
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
2.5. La mesura de les forces. El dinamòmetre
 D11 2.5. La mesura de les forces. El dinamòmetre Per mesurar forces utilitzarem el dinamòmetre (NO la balança!) Els dinamòmetres contenen al seu interior una molla que és elàstica, a l aplicar una força
D11 2.5. La mesura de les forces. El dinamòmetre Per mesurar forces utilitzarem el dinamòmetre (NO la balança!) Els dinamòmetres contenen al seu interior una molla que és elàstica, a l aplicar una força
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
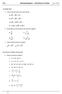 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
TEMA 1: Trigonometria
 TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
Centro de Masa. Sólido Rígido
 Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Centro de Masa Sóldo Rígdo El centro de masa de un sstema de partículas es un punto en el cual parecería estar concentrada toda la masa del sstema. En un sstema formado por partículas dscretas el centro
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
1.- Elements d una recta Vector director d una recta Vector normal d una recta Pendent d una recta
 .- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
.- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
TEMA 4 : Matrius i Determinants
 TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
TEMA 4 : Matrius i Determinants MATRIUS 4.1. NOMENCLATURA. DEFINICIÓ Una matriu és un conjunt de mxn elements distribuïts en m files i n columnes, A= Aquesta és una matriu de m files per n columnes. És
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
GEOMETRIA ANALÍTICA PLANA
 GEOMETRIA ANALÍTICA PLANA Un vector fix és un segment orientat que va del punt A (origen) al punto B (extrem). M òdul del vector AB, es representa pe r. : É s la long itud del segment Direc ció del vector
GEOMETRIA ANALÍTICA PLANA Un vector fix és un segment orientat que va del punt A (origen) al punto B (extrem). M òdul del vector AB, es representa pe r. : É s la long itud del segment Direc ció del vector
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2005
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Comprovar experimentalment les nocions bàsiques de l'estàtica de fluids: l equació fonamental de l'estàtica de fluids i el principi d Arquímedes.
 Estàtica de fluids Objectiu Comprovar experimentalment les nocions bàsiques de l'estàtica de fluids: l equació fonamental de l'estàtica de fluids i el principi d Arquímedes. Fonament teòric Quan se submergeix
Estàtica de fluids Objectiu Comprovar experimentalment les nocions bàsiques de l'estàtica de fluids: l equació fonamental de l'estàtica de fluids i el principi d Arquímedes. Fonament teòric Quan se submergeix
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Quadern de matemàtiques Decimals1
 Quadern de matemàtiques Decimals CENTENES DESENES UNITATS DECIMES CENTÈSIMES 3,5 Busca les vuit diferències que hi ha en aquests dos dibuixos Curs i grup: Data inici quadern Data acabament Seguiment Data
Quadern de matemàtiques Decimals CENTENES DESENES UNITATS DECIMES CENTÈSIMES 3,5 Busca les vuit diferències que hi ha en aquests dos dibuixos Curs i grup: Data inici quadern Data acabament Seguiment Data
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
Les Arcades. Molló del terme. Ermita la Xara. Esglèsia Sant Pere
 Les Arcades Molló del terme Ermita la Xara Esglèsia Sant Pere Pàg. 2 Monomi Un monomi (mono=uno) és una expressió algebraica de la forma: *+,-=/, 1 on R N., rep el nom d indeterminada o variable del monomi,
Les Arcades Molló del terme Ermita la Xara Esglèsia Sant Pere Pàg. 2 Monomi Un monomi (mono=uno) és una expressió algebraica de la forma: *+,-=/, 1 on R N., rep el nom d indeterminada o variable del monomi,
Cálculo de momentos de inercia
 Cálculo de momentos de nerca Cuando el cuerpo es homogéneo y unforme el cálculo de momento de nerca es una ntegral - Dvdmos el cuerpo en elementos de masa nfntesmal dm, todos a la msma dstanca r del eje
Cálculo de momentos de nerca Cuando el cuerpo es homogéneo y unforme el cálculo de momento de nerca es una ntegral - Dvdmos el cuerpo en elementos de masa nfntesmal dm, todos a la msma dstanca r del eje
Introducció als elements químics. Sessió 1
 Introducció als elements químics Sessió 1 Que tenen en comú aquests objetes? Bateria liti Microxips Vidre Etiqueta Paper Mòbils TOTS ESTAN FORMATS PER ÀTOMS Carcassa de plàstic Pantalla LCD Polímers Poliamides
Introducció als elements químics Sessió 1 Que tenen en comú aquests objetes? Bateria liti Microxips Vidre Etiqueta Paper Mòbils TOTS ESTAN FORMATS PER ÀTOMS Carcassa de plàstic Pantalla LCD Polímers Poliamides
8 Geometria analítica
 Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
TEMA 2 Revisión de mecánica del sólido rígido
 TEMA 2 Revsón de mecánca del sóldo rígdo 2.. ntroduccón SÓLDO RÍGDO SÓLDO: consderar orentacón y rotacón RÍGDO: CONDCÓN DE RGÍDEZ: - movmento: no se alteran dstancas entre puntos - se gnoran las deformacones
TEMA 2 Revsón de mecánca del sóldo rígdo 2.. ntroduccón SÓLDO RÍGDO SÓLDO: consderar orentacón y rotacón RÍGDO: CONDCÓN DE RGÍDEZ: - movmento: no se alteran dstancas entre puntos - se gnoran las deformacones
EXERCICIS PROPOSATS. 3 cm
 EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
Cinemática del movimiento rotacional
 Cnemátca del movmento rotaconal Poscón angular, θ Para un movmento crcular, la dstanca (longtud del arco) s, el rado r, y el ángulo están relaconados por: 180 s r > 0 para rotacón en el sentdo anthoraro
Cnemátca del movmento rotaconal Poscón angular, θ Para un movmento crcular, la dstanca (longtud del arco) s, el rado r, y el ángulo están relaconados por: 180 s r > 0 para rotacón en el sentdo anthoraro
TEMA 10: Cossos geomètrics
 TEMA 10: Cossos geomètrics 4tESO CB Cossos geomètrics: podem diferenciar poliedres i cossos de revolució I. Poliedre És una figura tridimensional limitat per cares que tenen forma de polígon: triangles,
TEMA 10: Cossos geomètrics 4tESO CB Cossos geomètrics: podem diferenciar poliedres i cossos de revolució I. Poliedre És una figura tridimensional limitat per cares que tenen forma de polígon: triangles,
FITXA 1: Polígons. Conceptes
 FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
16 febrer 2016 Integrals exercicis. 3 Integrals
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
Àmbit de les matemàtiques, de la ciència i de la tecnologia M14 Operacions numèriques UNITAT 2 LES FRACCIONS
 M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
ACTIVITATS SOBRE LA LLUM I EL SO
 ACTIVITATS SOBRE LA LLUM I EL SO Activitat 1: Visiona "El Meravellós món del color" i respon: a) Existeix el color? b) Per què es veuen els objectes d un color determinat, per exemple, roig o groc? c)
ACTIVITATS SOBRE LA LLUM I EL SO Activitat 1: Visiona "El Meravellós món del color" i respon: a) Existeix el color? b) Per què es veuen els objectes d un color determinat, per exemple, roig o groc? c)
La representació de la Terra
 La representació de la Terra Antigament, la realització de mapes era lenta i difícil, perquè es dibuixaven a partir d observacions sobre el terreny. Actualment, els mapes es fan a partir de fotografies
La representació de la Terra Antigament, la realització de mapes era lenta i difícil, perquè es dibuixaven a partir d observacions sobre el terreny. Actualment, els mapes es fan a partir de fotografies
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
FÍSICA NUCLEAR. En tots els àtoms trobem: Càrrega. Massa. Protons +1, C 1,0071 1, Nucli. Neutrons - 1,0085 1,
 Física n Batxillerat Tota forma de matèria que existeix a l'univers prové de la combinació de 0 àtoms diferents. El 99% de la matèria de tot l'univers està formada per àtoms d'hidrogen. L'% restant el
Física n Batxillerat Tota forma de matèria que existeix a l'univers prové de la combinació de 0 àtoms diferents. El 99% de la matèria de tot l'univers està formada per àtoms d'hidrogen. L'% restant el
, i el seu resultat és igual a la suma dels productes de les coordenades corresponents. Si u = (u 1, u 2 ) i v. , es denota u v
 Els vectors Els vectors Distància entre dos punts del pla Donats dos punts coordenats del pla, P 1 = (x 1, y 1 ) i P = (x, y ), la distància entre aquests dos punts, d(p 1,P ), es calcula de la manera
Els vectors Els vectors Distància entre dos punts del pla Donats dos punts coordenats del pla, P 1 = (x 1, y 1 ) i P = (x, y ), la distància entre aquests dos punts, d(p 1,P ), es calcula de la manera
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 2005 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 005 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 005 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
+ 1= 0 té alguna arrel real (x en radians).
 Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
DIAGRAMA DE FASES D UNA SUBSTANCIA PURA
 DIAGRAMA DE FASES D UNA SUBSTANCIA PURA Que es una fase? De forma simple, una fase es pot considerar una manera d anomenar els estats: sòlid, líquid i gas. Per exemple, gel flotant a l aigua, fase sòlida
DIAGRAMA DE FASES D UNA SUBSTANCIA PURA Que es una fase? De forma simple, una fase es pot considerar una manera d anomenar els estats: sòlid, líquid i gas. Per exemple, gel flotant a l aigua, fase sòlida
UNITAT 3: TRIGONOMETRIA
 UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
FÍSICA FÍSICA. Totes les preguntes tenen una puntuació màxima de 2 punts.
 FÍSICA FÍSICA A) CARACTERÍSTIQUES DE L EXAMEN L examen constarà de 5 qüestions senzilles, de caràcter numèric, que l estudiant ha de resoldre aplicant les lleis fonamentals de la Física en el termini màxim
FÍSICA FÍSICA A) CARACTERÍSTIQUES DE L EXAMEN L examen constarà de 5 qüestions senzilles, de caràcter numèric, que l estudiant ha de resoldre aplicant les lleis fonamentals de la Física en el termini màxim
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
MATÈRIA ÀTOMS ELEMENTS I T.PERIÒDICA
 MATÈRA ÀTOMS ELEMENTS T.PERÒDCA DEFNEX MATÈRA COM ES CLASSFCA LA MATÈRA? COM ES CLASSFQUEN LES SUBSTÀNCES PURES? COM ES CLASSFQUEN LES MESCLES? ELEMENT? COMPOST? A MESCLA HOMOGÈNA? A MESCLA HETEROGÈNA?
MATÈRA ÀTOMS ELEMENTS T.PERÒDCA DEFNEX MATÈRA COM ES CLASSFCA LA MATÈRA? COM ES CLASSFQUEN LES SUBSTÀNCES PURES? COM ES CLASSFQUEN LES MESCLES? ELEMENT? COMPOST? A MESCLA HOMOGÈNA? A MESCLA HETEROGÈNA?
Dotze problemes d optimització
 Dotze problemes d optimització Problema 1 Determineu les dimensions d un cilindre de volum màxim inscrit en un cub d aresta a tal que l eix del cilindre siga una diagonal del cub Problema En una semiesfera
Dotze problemes d optimització Problema 1 Determineu les dimensions d un cilindre de volum màxim inscrit en un cub d aresta a tal que l eix del cilindre siga una diagonal del cub Problema En una semiesfera
L ANÀLISI DE VARIÀNCIA (ANOVA) 2. Estimació de components de variància
 L ANÀLS DE VARÀNCA (ANOVA). Estmacó de components de varànca Alca Maroto, Rcard Boqué Grup de Qumometra Qualmetra Unverstat Rovra Vrgl C/ Marcel lí Domngo, s/n (Campus Sescelades) 43007-Tarragona A l artcle
L ANÀLS DE VARÀNCA (ANOVA). Estmacó de components de varànca Alca Maroto, Rcard Boqué Grup de Qumometra Qualmetra Unverstat Rovra Vrgl C/ Marcel lí Domngo, s/n (Campus Sescelades) 43007-Tarragona A l artcle
Tema 0.- Magnituds Físiques i Unitats
 Tema 0.- Magnituds Físiques i Unitats Anomenem magnituds físiques totes aquelles propietats dels cossos de l Univers que es poden mesurar, és a dir, aquelles a les quals podem atorgar un nombre o valor;
Tema 0.- Magnituds Físiques i Unitats Anomenem magnituds físiques totes aquelles propietats dels cossos de l Univers que es poden mesurar, és a dir, aquelles a les quals podem atorgar un nombre o valor;
Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure
 Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure Quim Primavera 2017 Introducció Estem a l espai (R 3 ) i els punts del domini tenen tres components: (x, y, z). El nostre domini
Definir els límits d integració en dominis 3D (R 3 ) Càlcul 2 - Aula Lliure Quim Primavera 2017 Introducció Estem a l espai (R 3 ) i els punts del domini tenen tres components: (x, y, z). El nostre domini
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Tema 3-Sistemas de partículas
 Tema 3-Sstemas de partículas Momento lneal y colsones Momento lneal de un partícula Segunda ley de Newton dp F dt p mv Impulso I tb ta Fdt Teorema del mpulso I p B p A Centro de masas 1 r M m r con M m
Tema 3-Sstemas de partículas Momento lneal y colsones Momento lneal de un partícula Segunda ley de Newton dp F dt p mv Impulso I tb ta Fdt Teorema del mpulso I p B p A Centro de masas 1 r M m r con M m
