CM2 ENRICH CREUS CARNICERO Nivel 2
|
|
|
- Inmaculada Caballero Rivero
- hace 7 años
- Vistas:
Transcripción
1 CM ENRICH CREUS CARNICERO Nivel Unidad Anexo Superficies en 3D 01 Anexo de la Unidad : Superficies en 3D Anexo 1: valor absoluto o módulo El valor absoluto o módulo de un número a, que se anota a, es la distancia de dicho valor hasta 0, en la recta numérica. Las distancias son siempre positivas (o nulas), por lo que tenemos: a si a 0 a = a si a < 0 Dados el valor absoluto de un número a una cualquiera k, se cumple que: 1) Si a a = k a ) Si a < k k < a < k 3) Si a > k k > a ó a > k Ejemplos: 1. Si x = x = - x = ; que es igual a decir: x = ±. Si x 6 = x 6 = - x 6 = x = x 0 3. Si x < 5 5 < x < 5. Si x > 3 3 > x ó x < 3 5. Si x 1 < < x 1< 10 < x < 11 Un caso importante: el valor absoluto aparece en las inecuaciones, al despejar una potencia par. Veamos algunos ejemplos ilustrativos, en los que se desea despejar x. 1. x > 5 x > ± 5 modo incorrecto x > 5 x > 5 x > 5-5 < x ó x > 5 modo correcto. ( x ) < 16 x < ± 16 modo incorrecto ( x ) < 16 x < 16 x < Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 1
2 < x < < x < 6 modo correcto Anexo : estudio geométrico del elipsoide Retomando, para realizar un análisis completo de una superficie tridimensional cualquiera debemos considerar lo siguiente: (1) Determinación de intersecciones con planos coordenados () Determinación de intersecciones con planos paralelos a los planos coordenados (en la región cercana al centro o vértice) (3) Identificación del tipo de superficie de sus elementos (centro o vértice, eje, valor de las s, etc.) ( ) Analicemos, a modo de ejemplo, al elipsoide cua ecuación es: ( ) x 1 z (1) Intersecciones con los planos coordenados Corte con el plano x (Plano z) ( x ) 1 ( z ) Para hallar la intersección, debemos resolver el sistema. Para esto, sencillamente se reemplaza una ecuación en la otra. En este caso se obtiene: ( 1) 0 ( z ) 1 ( z ) ( z ) = 8 Para pasar a la ecuación canónica de esta curva, debemos dividir todo por 8/. Al hacerlo se obtiene: ( ) z 3 / 8 / Esta última ecuación, corresponde a una elipse de eje paralelo al eje, que está contenida en el plano z. Corte con el plano (Plano xz) ( x ) 1 ( z ) Al reemplazar, se obtiene: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP
3 ( x ) 1 0 ( z ) ( x ) 1 ( z ) Esta es la ecuación de una elipse de eje paralelo al eje x, contenida en el plano xz. En otras palabras: la intersección es una elipse (se muestra en la siguiente figura). Vista de frente al plano xz Corte con el plano z : (Plano x) ( x ) 1 ( z ) Reemplazando, llegamos a: ( x ) (0 ) 1 = 3 Esta última expresión es un absurdo, dado que la suma de dos números positivos (en el miembro de la izquierda), nunca darán como resultado un número negativo. Esto significa que el plano x nunca corta al elipsoide. () Intersecciones con otros planos paralelos cercanos a los anteriores Con planos paralelos al plano z Estos planos, tienen ecuaciones del tipo: x ; k R. Entonces, debemos resolver el sistema: ( x ) 1 ( z ) ; k R Al reemplazar se obtiene: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 3
4 ( k ) 1 ( z ) ( z ) ( k 1) Cuando la del miembro de la derecha es un número positivo, la última expresión representa a una elipse. Es decir, la intersección entre los planos la superficie es una elipse si: ( 1) 1 k > 0 Despejemos k: ( ) 1 k > 1 que es igual a: k 1 < 3 1 ( k ) 1 < 1 que es igual a: 3 < k 1 < 3 < k < ó ( k 1) < Este resultado obtenido se interpreta como sigue: Si - < k < entonces - < x < ( 1) entonces la 1 es positiva entonces la ecuación ( k 1) ( z ) corresponde a una elipse entonces la intersección entre el elipsoide los planos del tipo x (con - < k < ), corresponde siempre a elipses En resumen: cuando - < x < se obtienen elipses como intersección Si mirás la gráfica del elipsoide, podés ver que cuando x < - cuando x >, no ha intersección entre la superficie los planos. Pero: qué ocurre cuando x = - cuando x =? Si x = - la ( 1) 1 k es igual a 0 es decir que: ( z ) La única forma de que esta última expresión (compuesta por la suma de dos términos positivos) sea nula, es que sus dos términos sean nulos. Para esto, debe ocurrir que: ; z = -. Y como x = -, en este caso, la intersección es el punto (-;0;-). 1 Si no recordás cómo trabajar con el valor absoluto, volvé al Anexo 1. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP
5 Análogamente, si x = ( 1) 1 k ( z ) La intersección es, ahora, el punto (;0;-). En resumen: Los resultados obtenidos al cortar al elipsoide con planos paralelos al plano z son elipses - < x < puntos x = - x = intersección vacía x < - x > Con planos paralelos al plano (es decir, paralelos al plano xz) Estos planos, tienen ecuaciones del tipo: ; k R. Entonces, debemos resolver el sistema: ( x ) 1 ( z ) ; k R Al reemplazar se obtiene: ( x ) k 1 ( z ) ( z ) k Cuando la del miembro de la derecha es un número positivo, la última expresión representa a una elipse: 1 k > 0 Despejemos k: 1 k k > 0 que es igual a: < 1 k < que es igual a: < k < ó k < De modo análogo a lo analizado antes, esto significa que cuando - < <, se obtienen elipses como intersección. Audándote con la gráfica del elipsoide, podrás ver que si < - ó >, no ha intersección entre el mismo los planos. Por último, analicemos los casos en que = - = Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 5
6 Si = - 1 k ( x ) 1 ( z ) Esta última expresión vale 0 si sus dos términos valen 0. Es decir, si x z = -. La intersección es, entonces, el punto (1;-;-) Si = 1 k ( x ) 1 ( z ) La intersección es el punto (1;-;) en este caso. En resumen: Los resultados obtenidos al cortar al elipsoide con planos paralelos al plano z son: elipses - < < puntos = - = intersección vacía < - > Con planos paralelos al plano z (es decir, paralelos al plano x) Estos planos, tienen ecuaciones del tipo: z ; k R. Entonces, debemos resolver el sistema: ( x ) 1 ( z ) ; k R Al reemplazar se obtiene: ( x ) 1 ( k ) ( k ) La última expresión representa a una elipse si la del miembro de la derecha es un número positivo: 1 ( k ) > 0 Despejando: 1 ( k ) > 0 que es igual a: ( k ) < 1 k < 1 que es igual a: 1 < k < 1 3 < k < 1 Esto es: cuando -3 < z < -1, se obtienen elipses como intersección. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 6
7 Cuando z < -3 ó z > -1, no ha intersección entre el mismo los planos. Por último, analicemos los casos en que z = -3 z = -1 Si z = -3 1 ( k ) Esta última expresión vale 0 si sus dos términos valen 0. Es decir, si x. La intersección es, entonces, el punto (1;0;-3). Si z = -1 1 ( k ) La intersección es el punto (1;0;-1) en este caso. En resumen: Los resultados obtenidos al cortar al elipsoide con planos paralelos al plano z son: elipses -3 < z < -1 puntos z = -3 z = -1 intersección vacía z < -3 z > -1 (3) Los elementos del elipsoide son: C(1;0;-) a = 3 b = el eje principal es paralelo al eje x (pues a > b a > c) c Con toda esta información, a es posible graficar el elipsoide. El mismo se muestra a la derecha: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 7
8 Anexo 3: hiperboloides Tomemos una hipérbola representada en un sistema de coordenadas, con su centro ubicado en el origen del sistema: qué ocurre si hacemos rotar esta curva alrededor de sus ejes de simetría? Rotación alrededor del eje Rotación alrededor del eje x La traza que va dejando la hipérbola en su movimiento, forma una superficie tridimensional. Como la hipérbola tiene dos ejes de simetría, pueden generarse entonces dos tipos diferentes de superficies. La rotación o revolución de la hipérbola alrededor del eje genera una superficie conexa, llamada hiperboloide de una hoja; mientras que la revolución alrededor del eje x (que corta dos veces a la hipérbola), da como resultado un hiperboloide de dos hojas, graficado abajo: Hiperboloide de una hoja Hiperboloide de dos hojas Una superficie conexa en 3D es toda superficie que divide al espacio en dos regiones disjuntas. Por ejemplo: una esfera, un hiperboloide de una hoja, etc. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 8
9 Anexo : Análisis del paraboloide elíptico Tomemos como ejemplo para este análisis, al paraboloide de ecuación: ( x 1) (1) Intersecciones con los planos coordenados = z Corte con el plano x (Plano z) = z Al resolver el sistema se obtiene: ( 0 1) = z = z = z Esta última ecuación, corresponde a una parábola de eje paralelo al eje z con ramas hacia arriba, contenida en el plano z. Corte con el plano (Plano xz) = z Al resolver: 0 = z ( x 1 ) ( x 1 ) = z = z La última ecuación también corresponde a una parábola de eje paralelo al eje z con ramas hacia arriba, ahora contenida en el plano xz. A continuación se muestra la intersección: Visto de frente Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP
10 Corte con el plano z (Plano x) = z Al sustituir el valor de z en la primera ecuación se obtiene: Hemos llegado a una suma de dos términos positivos. La única posibilidad de que dos números positivos sumen 0, es que ambos sean 0. Entonces, debe ocurrir que x (para que el primer término de la suma se anule) que (para que se anule el segundo término). Es decir, que hemos obtenido valores s para las tres variables: x ; ; z. Esto significa que la intersección entre el plano x la superficie es el punto (1;0;0), que coincide con el centro de la misma. () Intersecciones con planos paralelos a los planos coordenados Con planos paralelos al plano z Estos planos, tienen ecuaciones del tipo: x ; k R. Entonces, debemos resolver el sistema: = z ; k R Al reemplazar se obtiene: ( k 1) = z = z ( k 1) ( ) k 1 = z Esta última ecuación corresponde a una parábola de eje paralelo al eje z (con ramas hacia arriba siempre), independientemente del valor de la (a que al cambiar los valores de la sólo se modifica la posición del vértice de la misma). Con planos paralelos al plano xz Estos planos, tienen ecuaciones del tipo: ; k R. Entonces, debemos resolver el sistema: = z ; k R Ocurre algo similar a lo que ocurre en el caso anterior, a que al resolver el sistema se llega a: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 10
11 k = z k = z = z k Nuevamente, la última ecuación corresponde a una parábola de eje paralelo al eje z (con ramas hacia arriba siempre), independientemente del valor de la. Con planos paralelos al plano x Estos planos, tienen ecuaciones del tipo: z ; k R. Entonces, debemos resolver el sistema: = z ; k R Al reemplazar se obtiene: Esta será la ecuación de una elipse cuando k sea posible. Cuando k es 0, como a vimos, la intersección es el punto (1;0;0). Por último, cuando k es negativo la expresión es un absurdo, es decir, no ha intersección. En resumen: al cortar al paraboloide con planos horizontales, las intersecciones resultan ser elipses si z > 0 un punto si z intersección vacía si z < 0 Entonces, la superficie corresponde a un paraboloide elíptico, cuos elementos son: - el eje de la superficie es paralelo al eje z - el vértice es el punto V(1;0;0) - las s son: a = 3 ; b = ; c (3) Los elementos del paraboloide elíptico son: Centro: C(1;0;0) Valores de las s: a = 3 ; b = ; c El eje principal es paralelo al eje z porque es la variable lineal. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 11
12 Anexo 5: cálculos correspondientes a la intersección entre el paraboloide hiperbólico tomado como ejemplo el plano x En la página, se da la intersección entre la superficie en estudio el plano x: x = 16 z z 1 Al resolver, se obtiene: x 0 = 16 1 x = 16 0 x 16 = x = 16 Para sacar los cuadrados, es posible aplicar raíces cuadradas a ambos lados de la igualdad porque ambos miembros son positivos: 16 x = Dado que el valor absoluto de un número a, que se escribe a, es igual a a escribir la expresión anterior como: 3 x =, podemos Y, retomando lo visto en el Anexo 1, esto último también es igual a la siguiente expresión, que quizás te resulte más conocida: ± 3 x = La misma representa al par de rectas: x = 3 3 x = Anexo 6: soluciones de los problemas propuestos Problema1 a) La gráfica del cilindro z = x (cua ecuación canónica es: x = (z )), es la siguiente: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 1
13 Como podés ver, es un cilindro de sección parabólica, cuo eje es paralelo al eje b) Estudio del cilindro: (1) Intersecciones con los planos coordenados Corte con el plano x (Plano z) Al resolver el sistema se obtiene: z = x z = 0 z = Esta última expresión corresponde a una recta paralela al eje, contenida en el plano z. Corte con el plano (Plano xz) z = x En este caso, las intersección será la parábola de ecuación z = x, contenida en el plano xz. A continuación, se grafica la curva: Corte con el plano z (Plano x) z = x Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 13
14 Al resolver: 0 = x x = x = ± Esta última expresión corresponde a un par de rectas paralelas al eje, contenidas en el plano x. () Intersecciones con los planos paralelos a los planos coordenados Corte con planos paralelos al plano z Al resolver el sistema se obtiene: z = k z = x Para cualquier valor de k (es decir, para cualquier valor de x), esta última expresión corresponde a una recta paralela al eje, contenida en el plano z. Corte con planos paralelos al plano xz z = x En este caso, las intersecciones serán siempre parábolas, de ecuación z = x, contenidas en los distintos planos del tipo. Corte con planos paralelos al plano x z = x Al resolver: k = x x = k x = ± k son dos s reales cuando k Esto último indica que: cuando k < (z < ) la intersección es un par de rectas paralelas al eje, cada una de ellas de ecuaciones x = k x = k. cuando k = (z = ) la intersección es una recta paralela al eje, de ecuación x. Problema a) La gráfica del cilindro cua ecuación está dada por = x, es la siguiente: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 1
15 El cilindro tiene eje paralelo al eje z. Es importante recordar que, para la expresión representativa de esta superficie, x puede tomar únicamente valores maores o iguales a cero, es decir: x 0. b) Realicemos su estudio. (1) Intersecciones con los planos coordenados Corte con el plano x (Plano z) = x Al sustituir se obtiene: = 0 Esta última ecuación corresponde a una recta, que es el eje z, dado que x =. Corte con el plano x (Plano xz) = x Al resolver el sistema: 0 = x 0 = x Nuevamente, la intersección es el eje z. Corte con el plano x (Plano x) = x La intersección es la curva de ecuación = x, que se muestra a la derecha: Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 15
16 () Intersecciones con los planos paralelos a los planos coordenados Corte con planos paralelos al plano z = x Al resolver el sistema se obtiene: = k es una real cuando k 0 Esto último indica que: cuando k > 0 (x > 0) la intersección es una recta paralela al eje z. cuando k (x ) la intersección es el eje z, dado que x =. Corte con planos paralelos al plano xz = x Al resolver el sistema se obtiene: k = x k = x ( ) ( ) k = x k = x Esta última expresión, representa la ecuación de una recta paralela al eje z. Corte con planos paralelos al plano x = x La intersección es la curva de ecuación = x, como a vimos para el caso z. Problema 3 a) La gráfica del cilindro ( x 3) es: El cilindro es de sección hiperbólica, cuo eje es paralelo al eje z. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 16
17 b) Estudio del cilindro. (1) Intersecciones con los planos coordenados Corte con el plano x (Plano z) ( x 3) Al sustituir se obtiene: (0 3) 8 = 3 = ± 3 = La intersección es, entonces, un par de rectas paralelas al eje z. Corte con el plano x (Plano xz) ( x 3) Al sustituir se obtiene: 0 ( x 3) ( x 3) x 3 = ± 1 x = 3 ± 1 x = - ó x = - La intersección es, otra vez, un par de rectas paralelas al eje z. Corte con el plano x (Plano x) ( x 3) En este caso, la intersección es la hipérbola de ecuación ( x 3), de eje x, que se grafica a continuación: () Intersecciones con los planos paralelos a los planos coordenados Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 17
18 Corte con planos paralelos al plano z ( x 3) Al sustituir: ( k 3) ( k 3) 1 = ( ) ( k 3) 1 = ± ( k 3) 1) = ± ( k 3) 1 = La última expresión tiene sentido solamente si el radicando es maor o igual que cero. Es decir, cuando (k 3) 1 0, ó bien cuando (k 3) 1. Despejemos k, pero dado que el caso (k 3) a lo hemos estudiado antes, sólo usaremos la desigualdad: (k 3) > 1 k 3 > 1 k 3 > 1 Se tienen, entonces, las siguientes dos posibilidades 3 : k 3 < 1 k < k 3 > 1 k > Esto significa que cuando k es menor que cuando k es maor que, la expresión ± ( k 3) 1 = representa un par de rectas. Corte con planos paralelos al plano xz ( x 3) Al resolver, se llega a: k ( x 3) k ( x 3) k x 3 = ± 1 k x 3 = 1 ó k x = 3 1 ó k x 3 x = 3 1 k Ambas expresiones están definidas para cualquier valor de k (porque el radicando es siempre positivo), corresponden a las ecuaciones de dos rectas, paralelas al eje z. Corte con planos paralelos al plano x ( x 3) 3 Si no recordás cómo trabajar con el valor absoluto, volvé al Anexo 1. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 18
19 Para cualquier z, la intersección representa una hipérbola. Problema Realicemos el estudio del cilindro = 5. Su gráfica es: (1) Intersecciones con los planos coordenados Corte con el plano x (Plano z) = 5 Dado que x e toman un valor fijo (como indica la llave) que z es un número real cualquiera, la intersección es una recta paralela al eje z. Corte con el plano x (Plano xz) = 5 No es posible que cumpla al mismo tiempo con las dos condiciones que aparecen en la llave, por lo que no existe intersección en este caso. Corte con el plano x (Plano x) = 5 Dado que z e toman un valor fijo (como indica la llave) que x puede tomar cualquier valor real, la intersección es una recta paralela al eje x. () Intersecciones con los planos paralelos a los planos coordenados Corte con planos paralelos al plano z = 5 Para cada valor de k (es decir, para cada valor de x), la intersección es una recta paralela al eje z. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 1
20 Corte con planos paralelos al plano xz = 5 Solamente existe intersección cuando k = = 5, la misma es el plano = 5. Corte con planos paralelos al plano x = 5 Para cualquier valor de k (es decir, para cualquier valor de k), la intersección es una recta paralela al eje x. Cátedra de Matemática Nº Enrich-Creus-Carnicero FAU UNLP 0
b) En qué se diferencia la gráfica de un elipsoide que tiene un par semiejes iguales, con la de otro elipsoide cuyos semiejes son todos distintos?
 Unidad Trabajo Práctico Superficies en 3D 01 CONOCIMIENTOS PREVIOS PARA SUPERFICIES Es necesario que sepas: - operar con expresiones algebraicas - resolver sistemas de ecuaciones e interpretar sus soluciones
Unidad Trabajo Práctico Superficies en 3D 01 CONOCIMIENTOS PREVIOS PARA SUPERFICIES Es necesario que sepas: - operar con expresiones algebraicas - resolver sistemas de ecuaciones e interpretar sus soluciones
CM2 ENRICH CREUS CARNICERO Nivel 2
 CM ENRICH CREUS CARNICERO Nivel Unidad Cónicas Conocimientos previos CONOCIMIENTOS PREVIOS PARA CÓNICAS Antes de comenzar con el Trabajo Práctico, necesitás repasar algunas cuestiones como: ) graficar
CM ENRICH CREUS CARNICERO Nivel Unidad Cónicas Conocimientos previos CONOCIMIENTOS PREVIOS PARA CÓNICAS Antes de comenzar con el Trabajo Práctico, necesitás repasar algunas cuestiones como: ) graficar
CONOCIMIENTOS PREVIOS PARA SUPERFICIES EN 3D. 1. Conocimientos previos sobre puntos, rectas y planos en el espacio
 Unidad 2 Conocimientos previos Superficies en 3D 2014 CONOCIMIENTOS PREVIOS PARA SUPERFICIES EN 3D Antes de comenzar con el Trabajo Práctico 2 quizás necesites repasar, además de los conocimientos ya repasados
Unidad 2 Conocimientos previos Superficies en 3D 2014 CONOCIMIENTOS PREVIOS PARA SUPERFICIES EN 3D Antes de comenzar con el Trabajo Práctico 2 quizás necesites repasar, además de los conocimientos ya repasados
CM2 ENRICH CREUS CARNICERO Nivel 2
 CM ENRICH CREUS CARNICERO Nivel Unidad Cónicas Conocimientos previos CONOCIMIENTOS PREVIOS PARA CÓNICAS Antes de comenzar con el Trabajo Práctico N, necesitás repasar algunas cuestiones como: ) graficar
CM ENRICH CREUS CARNICERO Nivel Unidad Cónicas Conocimientos previos CONOCIMIENTOS PREVIOS PARA CÓNICAS Antes de comenzar con el Trabajo Práctico N, necesitás repasar algunas cuestiones como: ) graficar
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SUPERFICIES CUÁDRICAS
 SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Guía de estudio Nº 3: Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas
 U.C.V. Facultad de Ingeniería CÁLCULO I (5) Guía de estudio Nº : Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas.- Determine la ecuación del lugar geométrico de los puntos (, ) del plano
U.C.V. Facultad de Ingeniería CÁLCULO I (5) Guía de estudio Nº : Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas.- Determine la ecuación del lugar geométrico de los puntos (, ) del plano
Profesorado de Nivel Medio y Superior en Biología Matemática - 1º Cuatrimestre Año 2013 FUNCIÓN CUADRÁTICA
 Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Formulario: Geometría Analítica
 Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
Para ver una explicación detallada de cada gráfica, haga Click sobre el nombre.
 Para ver una explicación detallada de cada gráfica, haga Click sobre el nombre. La Parábola La Circunferencia La Elipse La Hipérbola La Parábola La parábola se define como: el lugar geométrico de los puntos
Para ver una explicación detallada de cada gráfica, haga Click sobre el nombre. La Parábola La Circunferencia La Elipse La Hipérbola La Parábola La parábola se define como: el lugar geométrico de los puntos
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R
 ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
1- Dar la ecuación ordinaria de la circunferencia de centro C( - 8; 2) y r = 5.Graficar.
 SECCIONES CONICAS CIRCUNFERENCIA 1- Dar la ecuación ordinaria de la circunferencia de centro C( - 8; 2) r = 5.Graficar. R: ( +8) 2 + ( 2) 2 = 25 2- Dar la ecuación general de la circunferencia de centro
SECCIONES CONICAS CIRCUNFERENCIA 1- Dar la ecuación ordinaria de la circunferencia de centro C( - 8; 2) r = 5.Graficar. R: ( +8) 2 + ( 2) 2 = 25 2- Dar la ecuación general de la circunferencia de centro
1. x = 2. Solución : x = 2 o x = x = 2. Solución x = 2 o x= x = 0. Solución: x = 0
 Problemas que involucran igualdades con valor absoluto. x =. Solución : x = o x = -. x =. Solución x = o x= -.. x = 0. Solución: x = 0. x =. No hay solución posible. No existen valores absolutos negativos.
Problemas que involucran igualdades con valor absoluto. x =. Solución : x = o x = -. x =. Solución x = o x= -.. x = 0. Solución: x = 0. x =. No hay solución posible. No existen valores absolutos negativos.
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
PARÁBOLA IX.
 IX. PARÁBOLA Lugar geométrico de todos los puntos tales que la distancia de éstos a un punto fijo (foco) es siempre la misma a una recta fija (directriz). p = distancia del vértice al foco o del vértice
IX. PARÁBOLA Lugar geométrico de todos los puntos tales que la distancia de éstos a un punto fijo (foco) es siempre la misma a una recta fija (directriz). p = distancia del vértice al foco o del vértice
Docente Matemáticas. Marzo 11 de 2013
 Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS
 V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS A. ANÁLISIS DE UNA ECUACIÓN En la geometría analítica hay dos problemas por resolver: 1. Dada la ecuación de una curva construir una gráfica.. Dadas algunas condiciones
V. DISCUSIÓN DE ECUACIONES ALGEBRAICAS A. ANÁLISIS DE UNA ECUACIÓN En la geometría analítica hay dos problemas por resolver: 1. Dada la ecuación de una curva construir una gráfica.. Dadas algunas condiciones
y v 0, 0, 1 y v 1, 0, 1 se tiene la ecuación
 SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
Guía de aprendizaje Nº 2
 Liceo Polivalente Juan Antonio Ríos Quinta Normal NIVEL : TERCERO MEDIO Guía de aprendizaje Nº 2 Unidad Temática: FUNCION CUADRATICA Objetivo General: Graficar y analizar las raices de la funcion cuadratica.
Liceo Polivalente Juan Antonio Ríos Quinta Normal NIVEL : TERCERO MEDIO Guía de aprendizaje Nº 2 Unidad Temática: FUNCION CUADRATICA Objetivo General: Graficar y analizar las raices de la funcion cuadratica.
GEOMETRIA ANALITICA EN EL ESPACIO
 CAPITULO VII CALCULO II GEOMETRIA ANALITICA EN EL ESPACIO Es el estudio de las formas geométricas en un sistema ordenado. Un sistema de ejes coordenados en el espacio, dividen al espacio en ocho octangulos.
CAPITULO VII CALCULO II GEOMETRIA ANALITICA EN EL ESPACIO Es el estudio de las formas geométricas en un sistema ordenado. Un sistema de ejes coordenados en el espacio, dividen al espacio en ocho octangulos.
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
Prof. Enrique Mateus Nieves. Doctorando en Educación Matemática. Cálculo multivariado REPASO DE SECCIONES CONICAS
 REPASO DE SECCIONES CONICAS SUPERFICIES CUADRICAS Y SUS TRAZAS Elipsoide x z Ecuación canónica: 1 a b c Secciones paralelas al plano x: Elipses; Secciones paralelas al plano xz: Elipses; Secciones paralelas
REPASO DE SECCIONES CONICAS SUPERFICIES CUADRICAS Y SUS TRAZAS Elipsoide x z Ecuación canónica: 1 a b c Secciones paralelas al plano x: Elipses; Secciones paralelas al plano xz: Elipses; Secciones paralelas
UNIDAD XVII LA LINEA RECTA. Modulo 4 Ecuación de la recta
 UNIDAD XVII LA LINEA RECTA Modulo 4 Ecuación de la recta OBJETIVO Encontrar y determinar la ecuación de una recta, conocidos los puntos de intersección con los ejes coordenados. 4. 1. LINEA RECTA. Lugar
UNIDAD XVII LA LINEA RECTA Modulo 4 Ecuación de la recta OBJETIVO Encontrar y determinar la ecuación de una recta, conocidos los puntos de intersección con los ejes coordenados. 4. 1. LINEA RECTA. Lugar
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA GUÍA TEÓRICO PRÁCTICA Nº8 A la función de segundo grado f() = a + b + c, siendo a, b, c lr a 0 se le denomina función cuadrática. La
C U R S O : MATEMÁTICA UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA GUÍA TEÓRICO PRÁCTICA Nº8 A la función de segundo grado f() = a + b + c, siendo a, b, c lr a 0 se le denomina función cuadrática. La
Material N 29 GUÍA TEÓRICO PRÁCTICA Nº 23
 C u r s o : Matemática Material N 9 GUÍA TEÓRICO PRÁCTICA Nº 3 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar
C u r s o : Matemática Material N 9 GUÍA TEÓRICO PRÁCTICA Nº 3 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar
FU CIÓ CUADRÁTICA. y = a.x 2 + b.x + c. Término Cuadrático Término Lineal Término Independiente. Matestay. a = 1 b = 4 c = 3. d 2.
 FU CIÓ CUADRÁTICA La función cuadrática es una función mu común en Matemática. Se trata de una función de segundo grado: la "" aparece elevada al cuadrado como máima potencia. Su representación gráfica
FU CIÓ CUADRÁTICA La función cuadrática es una función mu común en Matemática. Se trata de una función de segundo grado: la "" aparece elevada al cuadrado como máima potencia. Su representación gráfica
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
INSTITUTO UNIVERSITARIO DE CALDAS DOCENTE: ING. CRISTINA CANO. TEMA: LA PARABOLA. GRADO: FECHA: MARZO 7 DE 2016.
 Matemáticas III Unidad IV INSTITUTO UNIVERSITARIO DE CALDAS DOCENTE: ING. CRISTINA CANO. TEMA: LA PARABOLA. GRADO: 11-4. FECHA: MARZO 7 DE 2016. CARACTERIZACIÓN GEOMÉTRICA OBJETIVO Resolver problemas que
Matemáticas III Unidad IV INSTITUTO UNIVERSITARIO DE CALDAS DOCENTE: ING. CRISTINA CANO. TEMA: LA PARABOLA. GRADO: 11-4. FECHA: MARZO 7 DE 2016. CARACTERIZACIÓN GEOMÉTRICA OBJETIVO Resolver problemas que
1 + r, y = y 1 + ry Si P es el punto medio del segmento P 1 P 2, entonces x = x 1 + x 2 2
 CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
Introducción La Circunferencia Parábola Elipse Hiperbola. Conicas. Hermes Pantoja Carhuavilca
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
f(x) = a.x 2 + b.x + c
 FUNCIÓN CUADRÁTICA Diremos que una función f es una función polinómica si eisten números reales a 0, a 1, a,...a n tales que: f() = a n n + a n-1 n-1 +..... + a + a 1 + a 0 Ejemplo: f() = 5 6 + 137 4 3
FUNCIÓN CUADRÁTICA Diremos que una función f es una función polinómica si eisten números reales a 0, a 1, a,...a n tales que: f() = a n n + a n-1 n-1 +..... + a + a 1 + a 0 Ejemplo: f() = 5 6 + 137 4 3
Función lineal Ecuación de la recta
 Función lineal Ecuación de la recta Función constante Una función constante toma siempre el mismo valor. Su fórmula tiene la forma f()=c donde c es un número dado. El valor de f() en este caso no depende
Función lineal Ecuación de la recta Función constante Una función constante toma siempre el mismo valor. Su fórmula tiene la forma f()=c donde c es un número dado. El valor de f() en este caso no depende
Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro.
 Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Unidad IV. La parábola
 Unidad IV. La parábola El estudiante, resolverá problemas teóricos o prácticos relativos a la parábola, a través del análisis descriptivo, aplicación y combinación de sus propiedades, gráficas y ecuaciones,
Unidad IV. La parábola El estudiante, resolverá problemas teóricos o prácticos relativos a la parábola, a través del análisis descriptivo, aplicación y combinación de sus propiedades, gráficas y ecuaciones,
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
UNPSJB - Facultad Ciencias Naturales - Asignatura: Matemática 1 Ciclo Lectivo: 2014 CONICAS
 Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
ANALISIS MATEMATICO I (2012)
 ANALISIS MATEMATICO I (0) TRABAJO PRÁCTICO Funciones cuadráticas Ejercicio. Hacer una representación gráfica aproimada de las siguientes funciones cuadráticas:. f() =. f() = + 4 3. f() = +, Ejercicio.
ANALISIS MATEMATICO I (0) TRABAJO PRÁCTICO Funciones cuadráticas Ejercicio. Hacer una representación gráfica aproimada de las siguientes funciones cuadráticas:. f() =. f() = + 4 3. f() = +, Ejercicio.
Hipérbola, parábola y sus elementos Semana del Viernes 25 al Miércoles 30 de Abril
 UNIVERSIDAD DE CHILE Facultad de Ciencias Departamento de Matemáticas MC-140 Matemáticas I Ayudantías 06A y 06B Hipérbola, parábola y sus elementos Semana del Viernes 25 al Miércoles 0 de Abril 1. Si la
UNIVERSIDAD DE CHILE Facultad de Ciencias Departamento de Matemáticas MC-140 Matemáticas I Ayudantías 06A y 06B Hipérbola, parábola y sus elementos Semana del Viernes 25 al Miércoles 0 de Abril 1. Si la
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA II
 C u r s o : Matemática 3º Medio Material Nº MT-11 UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA II INTERSECCIÓN CON EL EJE Y La parábola asociada a la función = a + b + c siempre intersecta al eje de
C u r s o : Matemática 3º Medio Material Nº MT-11 UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA II INTERSECCIÓN CON EL EJE Y La parábola asociada a la función = a + b + c siempre intersecta al eje de
La representación gráfica de una función cuadrática es una parábola.
 Función Cuadrática A la función polinómica de segundo grado +bx+c, siendo a, b, c números reales y, se la denomina función cuadrática. Los términos de la función reciben los siguientes nombres: La representación
Función Cuadrática A la función polinómica de segundo grado +bx+c, siendo a, b, c números reales y, se la denomina función cuadrática. Los términos de la función reciben los siguientes nombres: La representación
Este trabajo debe realizarce después de haber trabajado el taller virtual
 Este trabajo debe realizarce después de haber trabajado el taller virtual qué se encuentra en la http://ceciba.escuelaing.edu.co/mre página bajo la pestaña de Talleres Virtuales.. Para las guientes funciones:
Este trabajo debe realizarce después de haber trabajado el taller virtual qué se encuentra en la http://ceciba.escuelaing.edu.co/mre página bajo la pestaña de Talleres Virtuales.. Para las guientes funciones:
LA PARÁBOLA ECUACIÓN CANÓNICA DE LA PARÁBOLA DEFINICIÓN ELEMENTOS DE LA PARÁBOLA. x 2px p y x 2px p. Geometría Analítica
 ECUACIÓN CANÓNICA DE LA PARÁBOLA DEFINICIÓN LA PARÁBOLA Parábola es el lugar geométrico de todos los puntos P del plano que equidistan de una recta fija llamada directriz (L) y de un punto fijo exterior
ECUACIÓN CANÓNICA DE LA PARÁBOLA DEFINICIÓN LA PARÁBOLA Parábola es el lugar geométrico de todos los puntos P del plano que equidistan de una recta fija llamada directriz (L) y de un punto fijo exterior
UNIDAD 13 LA CIRCUNFERENCIA Y LA PARÁBOLA
 UNIDAD 13 LA CIRCUNFERENCIA Y LA PARÁBOLA Objetivo general. Al terminar esta Unidad aplicarás las definiciones y los elementos que caracterizan a la circunferencia y a la parábola en las soluciones de
UNIDAD 13 LA CIRCUNFERENCIA Y LA PARÁBOLA Objetivo general. Al terminar esta Unidad aplicarás las definiciones y los elementos que caracterizan a la circunferencia y a la parábola en las soluciones de
INTERVALOS Y SEMIRRECTAS.
 el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
RESOLUCIÓN DE SISTEMAS DE ECUACIONES E INECUACIONES CON DOS INCÓGNITAS. Prof. Esther Morales
 1 U N E X P O UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA ANTONIO JOSÉ DE SUCRE VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICA RESOLUCIÓN DE SISTEMAS DE ECUACIONES
1 U N E X P O UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA ANTONIO JOSÉ DE SUCRE VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICA RESOLUCIÓN DE SISTEMAS DE ECUACIONES
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Guía de Funciones Cuadráticas
 Colegio Raimapu Departamento de Matemática Guía de Funciones Cuadráticas Nombre del Estudiante: ) Cuál de los siguientes gráficos representa a la función f() =? A) B) C) D) E) º Medio ) El punto que no
Colegio Raimapu Departamento de Matemática Guía de Funciones Cuadráticas Nombre del Estudiante: ) Cuál de los siguientes gráficos representa a la función f() =? A) B) C) D) E) º Medio ) El punto que no
UNIDAD DE APRENDIZAJE V
 UNIDAD DE APRENDIZAJE V Saberes procedimentales Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. Relaciona la ecuación de segundo grado en dos
UNIDAD DE APRENDIZAJE V Saberes procedimentales Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. Relaciona la ecuación de segundo grado en dos
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Respuestas ejercicios edición 2007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1
 Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Función cuadrática. Ecuación de segundo grado completa
 Función cuadrática Una función cuadrática es aquella que puede escribirse como una ecuación de la forma: f(x) = ax 2 + bx + c donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto
Función cuadrática Una función cuadrática es aquella que puede escribirse como una ecuación de la forma: f(x) = ax 2 + bx + c donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
MATEMÁTICAS III CICLO COMÚN III PARCIAL UNIDDA DIDÁCTICA #3 FUNCIÓN CUADRÁTICA RESOLUCIÓN DE PROBLEMAS APLICANDO ECUACIONES CUADRÁTICAS
 UNIDDA DIDÁCTICA #3 CONTENIDO FUNCIÓN CUADRÁTICA RESOLUCIÓN DE PROBLEMAS APLICANDO ECUACIONES CUADRÁTICAS OBJETIVOS Conocer la definición de la función cuadrática. Estudiar las propiedades de las funciones
UNIDDA DIDÁCTICA #3 CONTENIDO FUNCIÓN CUADRÁTICA RESOLUCIÓN DE PROBLEMAS APLICANDO ECUACIONES CUADRÁTICAS OBJETIVOS Conocer la definición de la función cuadrática. Estudiar las propiedades de las funciones
Cónicas y Cuádricas con Surfer
 Cónicas y Cuádricas con Surfer Daniel Alejandro Grimaldi 29/08/2016-2do Cuatrimestre de 2016 Denición: Se conoce como cuádrica a la supercie en R n que representa los ceros de un polinomio de grado 2 con
Cónicas y Cuádricas con Surfer Daniel Alejandro Grimaldi 29/08/2016-2do Cuatrimestre de 2016 Denición: Se conoce como cuádrica a la supercie en R n que representa los ceros de un polinomio de grado 2 con
Indice de contenido. Ecuaciones de los círculos / Ecuación estándar de un círculo. Problemas complementarios
 l' Indice de contenido Un sistema de coordenadas lineales / Intervalos finitos / Intervalos infinitos / Desigualdades Ejes de coordenadas / Coordenadas / Cuadrantes / Fórmula de la distancia / Fórmulas
l' Indice de contenido Un sistema de coordenadas lineales / Intervalos finitos / Intervalos infinitos / Desigualdades Ejes de coordenadas / Coordenadas / Cuadrantes / Fórmula de la distancia / Fórmulas
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Práctica complementaria resuelta: Elipse e Hipérbola (2016)
 Práctica complementaria resuelta: Elipse e Hipérbola (2016) 1. A partir de la siguiente ecuación de una elipse, ) ² + ² =1 determine las coordenadas de los focos, vértices su excentricidad. 2. Determine
Práctica complementaria resuelta: Elipse e Hipérbola (2016) 1. A partir de la siguiente ecuación de una elipse, ) ² + ² =1 determine las coordenadas de los focos, vértices su excentricidad. 2. Determine
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Aplicación: cálculo de áreas XII APLICACIÓN: CÁLCULO DE ÁREAS
 XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS 1. Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS 1 TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(x,) a las
TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS 1 TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(x,) a las
1- Dar la ecuación ordinaria de la circunferencia de centro C( - 8; 2) y r = 5. Graficar. R: (x +8) 2 + (y 2) 2 = 25
 SECCIONES CONICAS CIRCUNFERENCIA 1- Dar la ecuación ordinaria de la circunferencia de centro C( - 8; 2) r = 5. Graficar. R: ( +8) 2 + ( 2) 2 = 25 2- Dar la ecuación general de la circunferencia de centro
SECCIONES CONICAS CIRCUNFERENCIA 1- Dar la ecuación ordinaria de la circunferencia de centro C( - 8; 2) r = 5. Graficar. R: ( +8) 2 + ( 2) 2 = 25 2- Dar la ecuación general de la circunferencia de centro
Capítulo 1: Secciones Cónicas
 Capítulo : Secciones Cónicas Resumen En este apartado se trata sobre la definición, caractrización graficación de las Secciones Cónicas. Primero se definen las secciones cónicas como la curva de intersección
Capítulo : Secciones Cónicas Resumen En este apartado se trata sobre la definición, caractrización graficación de las Secciones Cónicas. Primero se definen las secciones cónicas como la curva de intersección
Clase. Función cuadrática y ecuación de segundo grado
 Clase Función cuadrática y ecuación de segundo grado Aprendizajes esperados Aplicar los conceptos matemáticos asociados al estudio de la función cuadrática. Graficar una función cuadrática, determinando
Clase Función cuadrática y ecuación de segundo grado Aprendizajes esperados Aplicar los conceptos matemáticos asociados al estudio de la función cuadrática. Graficar una función cuadrática, determinando
Funciones lineales, cuadráticas y polinómicas.
 Funciones lineales, cuadráticas El objetivo de esta ejercitación es familiarizarse con las epresiones matemáticas de funciones lineales cuadráticas, así como con sus representaciones gráficas. Matemáticamente,
Funciones lineales, cuadráticas El objetivo de esta ejercitación es familiarizarse con las epresiones matemáticas de funciones lineales cuadráticas, así como con sus representaciones gráficas. Matemáticamente,
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
GUÍA DE EJERCICIOS GEOMETRÍA ANALÍTICA (CURVAS CÓNICAS)
 U N E X P O INTRODUCCIÓN: UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA ANTONIO JOSÉ DE SUCRE VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICA GUÍA DE EJERCICIOS GEOMETRÍA
U N E X P O INTRODUCCIÓN: UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA ANTONIO JOSÉ DE SUCRE VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICA GUÍA DE EJERCICIOS GEOMETRÍA
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES. Tema 3 EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS.
 INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
ECUACIÓN GENERAL DE LA PARÁBOLA
 ECUACIÓN GENERAL DE LA PARÁBOLA Una ecuación de segundo grado en las variables que carezca del término en puede escribirse en la forma: Si A 0, C 0 D 0, la ecuación representa una parábola cuo eje es paralelo
ECUACIÓN GENERAL DE LA PARÁBOLA Una ecuación de segundo grado en las variables que carezca del término en puede escribirse en la forma: Si A 0, C 0 D 0, la ecuación representa una parábola cuo eje es paralelo
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es 1 Índice 1. Definiciones 3 2. Herramientas 5 2.1. Factorización de polinomios: Regla
de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es 1 Índice 1. Definiciones 3 2. Herramientas 5 2.1. Factorización de polinomios: Regla
(Apuntes sin revisión para orientar el aprendizaje) CÁLCULO VECTORIAL EXTREMOS DE FUNCIONES ESCALARES DE VARIABLE VECTORIAL
 (Apuntes sin revisión para orientar el aprendizaje) CÁLCULO VECTORIAL EXTREMOS DE FUNCIONES ESCALARES DE VARIABLE VECTORIAL En numerosas aplicaciones de la ingeniería se presentan problemas de optimización,
(Apuntes sin revisión para orientar el aprendizaje) CÁLCULO VECTORIAL EXTREMOS DE FUNCIONES ESCALARES DE VARIABLE VECTORIAL En numerosas aplicaciones de la ingeniería se presentan problemas de optimización,
ELIPSE. Muchos cometas tienen órbitas extremadamente excéntricas. Por ejemplo, el cometa Halley, tiene una excentricidad orbital de casi 0.97!
 ELIPSE Las órbitas de los planetas son elípticas. La excentricidad de la órbita de la Tierra es muy pequeña (menor de 0.2), de manera que la órbita es casi circular. La órbita de Plutón es la más excéntrica
ELIPSE Las órbitas de los planetas son elípticas. La excentricidad de la órbita de la Tierra es muy pequeña (menor de 0.2), de manera que la órbita es casi circular. La órbita de Plutón es la más excéntrica
Funciones algebraicas.
 UNIDAD 9: UTILICEMOS LAS FUNCIONES ALGEBRAICAS. Funciones algebraicas..1 Funciones polinomiales. Estudiaremos las funciones siguientes: constante, lineal, cuadrática y cúbica. Función constante. Las funciones
UNIDAD 9: UTILICEMOS LAS FUNCIONES ALGEBRAICAS. Funciones algebraicas..1 Funciones polinomiales. Estudiaremos las funciones siguientes: constante, lineal, cuadrática y cúbica. Función constante. Las funciones
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
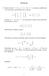 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
Departamento de Bachillerato Preparatoria UNAM Matemáticas V Plan 100 Ciclo 06 / 07 TAREA PARA EL SEGUNDO PERIODO SEMESTRAL
 Departamento de Bachillerato Preparatoria UNAM Matemáticas V Plan 100 Ciclo 06 / 07 TAREA PARA EL SEGUNDO PERIODO SEMESTRAL NOMBRE DEL ESTUDIANTE: Apellido paterno Apellido materno Nombre(s) GRUPO: No.
Departamento de Bachillerato Preparatoria UNAM Matemáticas V Plan 100 Ciclo 06 / 07 TAREA PARA EL SEGUNDO PERIODO SEMESTRAL NOMBRE DEL ESTUDIANTE: Apellido paterno Apellido materno Nombre(s) GRUPO: No.
UNIDAD 4. La Parábola
 UNIDAD 4. La Parábola Practicando con la parábola Juan Adolfo Álvarez Martínez Autor Es el lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia a una recta fija, situada
UNIDAD 4. La Parábola Practicando con la parábola Juan Adolfo Álvarez Martínez Autor Es el lugar geométrico de un punto que se mueve en un plano de tal manera que su distancia a una recta fija, situada
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos)
 CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 Función Cuadrática: Es toda función de la forma: f() = a ² + b + c con a, b, c números Reales Puede suceder que b ó c sean nulos, por ej: f() = ½ ² + 5 f() = 5 ² ¾ Pero a no puede ser = 0, de los contrario
Función Cuadrática: Es toda función de la forma: f() = a ² + b + c con a, b, c números Reales Puede suceder que b ó c sean nulos, por ej: f() = ½ ² + 5 f() = 5 ² ¾ Pero a no puede ser = 0, de los contrario
37 EJERCICIOS de FUNCIONES
 7 EJERCICIOS de FUNCIONES Concepto de función:. Dada f () =, se pide: Razonar que se trata de una función. Calcular f(4), f(), f(0), f(-9), f(/4), f() f( ). Ídem para f()=+ c) Hallar la antiimagen de,
7 EJERCICIOS de FUNCIONES Concepto de función:. Dada f () =, se pide: Razonar que se trata de una función. Calcular f(4), f(), f(0), f(-9), f(/4), f() f( ). Ídem para f()=+ c) Hallar la antiimagen de,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS LA PARABOLA
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 1º TALLER Nº 6 SEMESTRE II LA PARABOLA RESEÑA HISTÓRICA Historia de las Cónicas: El estudio de las cónicas tiene su origen en el
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 1º TALLER Nº 6 SEMESTRE II LA PARABOLA RESEÑA HISTÓRICA Historia de las Cónicas: El estudio de las cónicas tiene su origen en el
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
7. Cónicas. Propiedades métricas y ópticas
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 49 7. Cónicas. Propiedades métricas y ópticas Cónicas Círcunferencias, elipses, parábolas, e hipérbolas son llamadas secciones cónicas
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
, x es la variable independiente e y es la variable dependiente.
 INSTITUCIÓN EDUCATIVA COLEGIO ARTÍSTICO RAFAEL CONTRERAS NAVARRO OCAÑA N.S. ASIGANTURA: MATEMÁTICAS OCTAVO GRADO DOCENTE: Esp. HENRY CARRASCAL C. III PERÍODO FUNCIÓN Y ECUACIÓN CUADRÁTICA 1. DEFINICIÓN
INSTITUCIÓN EDUCATIVA COLEGIO ARTÍSTICO RAFAEL CONTRERAS NAVARRO OCAÑA N.S. ASIGANTURA: MATEMÁTICAS OCTAVO GRADO DOCENTE: Esp. HENRY CARRASCAL C. III PERÍODO FUNCIÓN Y ECUACIÓN CUADRÁTICA 1. DEFINICIÓN
Una ecuación puede tener ninguna, una o varias soluciones. Por ejemplo: 5x 9 = 1 es una ecuación con una incógnita con una solución, x = 2
 Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Secciones cónicas. Tema 02: Cónicas, cuádricas, construcción de conos y cilindros. Secciones Cónicas. Aplicaciones de las cónicas
 Secciones cónicas Tema 02: Cónicas, cuádricas, construcción de conos y cilindros Juan Ignacio Del Valle Gamboa Sede de Guanacaste Universidad de Costa Rica Ciclo I - 2014 Las secciones cónicas toman su
Secciones cónicas Tema 02: Cónicas, cuádricas, construcción de conos y cilindros Juan Ignacio Del Valle Gamboa Sede de Guanacaste Universidad de Costa Rica Ciclo I - 2014 Las secciones cónicas toman su
Matemáticas. Grado 11º. Unidad 1. Secciones cónicas
 1 Franklin Eduardo Pérez Quintero Matemáticas Grado 11º Unidad 1 Secciones cónicas 1 Franklin Eduardo Pérez Quintero LOGRO: Identificar las diferentes secciones cónicas con sus principales características
1 Franklin Eduardo Pérez Quintero Matemáticas Grado 11º Unidad 1 Secciones cónicas 1 Franklin Eduardo Pérez Quintero LOGRO: Identificar las diferentes secciones cónicas con sus principales características
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
