Tema 5: Aplicaciones del cálculo en varias variables
|
|
|
- María Concepción Franco Cruz
- hace 6 años
- Vistas:
Transcripción
1 Ingeniería Informática. Escuela Técnica Superior de Ingeniería Informática Tema 5: Aplicaciones del cálculo en varias variables 17 de diciembre de Funciones vectoriales. Curvas parametrizadas Definición 1 Una función vectorial de variable real es una aplicación f : D R R n. Esta función f viene dada por n funciones reales de variable real, f i : D R R, de modo que f(t) = (f 1 (t),..., f n (t)); escribiremos f = (f 1,..., f n ) Definición 2 Sea f = (f 1,..., f n ): D R R n, a Ac(D); decimos que el límite de f en a es v = (v 1,..., v n ) R n si lím f i(t) = v i para todo i = 1,..., n; t a y en tal caso escribimos: lím t a f(t) = v. Definición 3 Sea f = (f 1,..., f n ): D R R n : 1. Decimos que f es continua en a D si todas la funciones f i son continuas en a; es decir, si lím f(t) = f(a). t a 2. Decimos que f es derivable en a D si todas la funciones f i son derivables en a y llamamos derivada de f en a al vector: f (a) = (f 1 (a),..., f n(a)). Proposición 4 Sean f, g : R R n dos funciones vectoriales derivables, φ: R R una función real derivable y h: R n R un campo escalar; entonces: 1. f + g es derivable y (f + g) = f + g. 2. φf es derivable y (φf) = φ f + φf. 3. f g (producto escalar) es derivable y (f g) = f g + f g. 4. Para funciones sobre R 3 : f g (producto vectorial) es derivable y (f g) = f g + f g. 5. Regla de la cadena: f φ es derivable y (f φ) (t) = f (φ(t))φ (t). h f es derivable y (h f) = h (f(t)) f (t) (obsérvese que estamos usando el producto escalar) Curvas parametrizadas Ya hemos trabajado con conjunto de puntos en el plano o en el espacio que hemos denominado curvas; la gráfica de una función real de variable real es una curva y también lo son las curvas de nivel de un campo escalar en R 2. Sin embargo, no disponemos de una noción general de curva que permita considerar los casos mencionados como casos particulares, y que en consecuencia establezca una coherencia entre los distintos usos de la palabra curva. La noción general de curva es la curva parametrizada. Definición 5 Un conjunto C R n se dice que es una curva parametrizada si existe un intervalo I y una función vectorial continua f : I R n tal que C = f(i). Las ecuaciones x 1 = f 1 (t),..., x n = f n (t) t I se denominan ecuaciones paramétricas de la curva y la variable t se denomina parámetro. Debemos tener en cuenta que el concepto de curva corresponde al subconjunto de puntos y no a la función vectorial; de hecho, una curva admite muchas parametrizaciones distintas. Las gráficas de las funciones reales de variable real son efectivamente curvas parametrizadas. Si φ: I R R es una función continua, la función vectorial f(t) = (t, φ(t)), t I Curso 2002/03. Cálculo para la Computación. Tema 4. 1
2 es una parametrización del grafo de φ. El recíproco no es cierto, es decir, no todas las curvas parametrizadas en R 2 pueden describirse como el grafo de una función real de variable real; por ejemplo, la curva parametrizada f(t) = (cos t, sen t), t [0, 2π] es una circunferencia de radio 1 y centrada en el origen y no puede describirse como grafo. La situación no es tan simple para el caso de las curvas de nivel, aunque también es cierto que las curvas de nivel de campos escalares en R 2 diferenciables, también son curvas parametrizadas. Este hecho es consecuencia del teorema de la implícita que veremos más adelante, pero la justificación formal queda fuera de los objetivos de este curso; sin embargo, si describiremos algunas curvas asociadas a campos concretos. Aunque hemos exigido solamente la condición de continuidad a la parametrización, lo habitual será trabajar con curvas diferenciables. Definición 6 Una curva C R n se dice diferenciable si admite una parametrización f(t) derivable; una parametrización así se dice parametrización diferenciable. Una curva diferenciable puede tener parametrizaciones no diferenciables: ( 3 t, 3 t 2 ) es una parametrización no diferenciable de la parábola y = x 2 que sí es una curva diferenciable. La condición de continuidad asegura que la curva puede ser dibujada de un solo trazo, pero la condición de diferenciabilidad no aporta ninguna característica geométrica a la curva. Sin embargo, la noción de regularidad que damos a continuación se traduce en la ausencia de picos en la curva. Definición 7 Una curva C R n se dice regular si admite una parametrización f(t) diferenciable y tal que f (t) 0 para todo t; a una parametrización verificando las dos propiedades se le dice parametrización regular. Una curva regular puede tener parametrizaciones no regulares: (t 3, t 6 ) es una parametrización no regular (pero sí diferenciable) de la parábola y = x 2 que sí es una curva regular. La gráfica de la función y = x es una curva diferenciable, ya que la parametrizacion (x, y) = (t 3, t 3 ), t R, es una parametrización diferenciable. Sin embargo, la curva no es regular, ya que cualquier parametrización deberá tener derivada (0, 0) en el parámetro correspondiente al punto (0, 0). Definición 8 Una curva C R n diferenciable se dice regular a trozos si admite una parametrización f regular en todos los puntos excepto en un conjunto finito. Dado que una función vectorial continua, f : [a, b] R n determina completamente una curva en R n, es bastante frecuente llamar a estas funciones curvas, identificándolas con su imagen. De la misma forma, diremos que f : [a, b] R n es una curva diferenciable si es una parametrización diferenciable de su imagen; diremos que es una curva regular si es una parametrización regular de su imagen y diremos que es una curva regular a trozos si es una parametrización regular a trozos de su imagen. Definición 9 Sea (x 1 (t),..., x n (t)) una parametrización regular de la curva C; la recta X 1 = x 1 (t 0 ) + λx 1 (t 0) X 2 = x 2 (t 0 ) + λx 2 (t 0) X n = x n (t 0 ) + λx n(t 0 ) se denomina recta tangente a C en (x 1 (t 0 ),..., x n (t 0 )); es decir, el vector (x 1 (t 0),..., x n (t 0)) es tangente a la curva en dicho punto. Las nociones de curva simple, curva cerrada y curva cerrada y simple tendrán bastante importancia en los temas siguientes. Definición 10 Una curva se dice simple si admite una parametrización inyectiva. Definición 11 Una curva se dice cerrada si admite una parametrización continua definida en un intervalo cerrado, f : [a, b] R n, y tal que f(a) = f(b). Definición 12 Una curva se dice que es cerrada y simple si admite una parametrización continua definida en Curso 2002/03. Cálculo para la Computación. Tema 4. 2
3 un intervalo cerrado, f : [a, b] R n, inyectiva en [a, b) y tal que f(a) = f(b) Trayectorias en R 3 (NO) Una función f : I R R 3 puede ser entendida como la descripción del movimiento de una partícula en el espacio entendiendo que la variable de la función es el tiempo; es decir, si f(t) = (x(t), y(t), z(t)), entonces las funciones x(t), y(t) y z(t) dan las coordenadas en que se encuentra un móvil en el instante t. Si f es diferenciable, el vector f (t) = (x (t), y (t), z (t)) es el vector velocidad en el instante t. Si f es derivable, f (t) = (x (t), y (t), z (t)) es el vector aceleración. Sea f una curva en R 3 dos veces derivable; si f (t) 0, definimos el vector tangente unitario en f(t) al vector: T (t) = f (t) f (t) Llamamos vector normal unitario en f(t) al vector: N(t) = T (t) T (t) La utilidad de estos vectores está en que el vector aceleración de f(t) está en el plano formado por T (t) y N(t); las componentes del vector aceleración respecto de estos vectores unitarios (y ortogonales entre sí) son muy importantes en física ya que permiten calcular las fuerzas de inercia y centrípeta. Si f (t) = a(t) = a T (t)t (t) + a N (t)n(t), entonces: a T (t) = a(t) T (t) = f (t) f (t) f (t) 2 a N (t) = a(t) N(t) = v(t) a(t) 2 v(t) 2 El número a N (t) se denomina igualmente curvatura de f. 2. Campos vectoriales Definición 13 Un campo vectorial es una aplicación cuyo dominio está contenido en un espacio R n y su imagen lo está en otro espacio R m ; es decir, responde al esquema f : D R n R m. Un campo vectorial está determinado por m campos escalares: f = (f 1,..., f m ). Definición 14 Dado f = (f 1,..., f n ) campo vectorial y a = (a 1,... a n ) Ac(Dom(f)), se dice que el límite cuando x tiende a a es l = (l 1,..., l m ) si lím f i(x) = l i para cada i = 1,... m x a y en tal caso lo denotamos l = lím x a f(x). Decimos que f es continua en a si lím x a f(x) = f(a). Definición 15 Un campo vectorial f : D R n R m, f = (f 1,..., f n ), se dice diferenciable en a D si cada uno de los campos f i es diferenciable en a; en tal caso, llamamos matriz jacobiana de f en a a la matriz: D 1 f 1 (a) D 2 f 1 (a)... D n f 1 (a) D 1 f 2 (a) D 2 f 2 (a)... D n f 2 (a) Jf(a) = D 1 f m (a) D 2 f m (a)... D n f m (a) m n que se escribe igualmente de forma esquemática como: f 1 (a) f 2 (a) Jf(a) =. f m (a) Todas las propiedades algebraicas de la diferenciabilidad son inmediatas y su enunciado y justificación se proponen como ejercicio; enunciamos solamente la regla de la cadena, que generaliza los enunciados previos de la misma. Proposición 16 (Regla de la cadena) Si g : R n R m y f : R m R p son campos vectoriales diferenciables, entonces f g es otro campo vectorial diferenciable y J(f g)(a) = Jf(g(a)) Jg(a). En cada caso, la aplicación de la regla de la cadena da una serie de igualdades que permiten calcular las parciales de f g a partir de las parciales de las componentes de f y g. Veamos estas igualdades en un tipo Curso 2002/03. Cálculo para la Computación. Tema 4. 3
4 concreto de composición. Si g : R n R m y f : R m R, g = (g 1,..., g m ), f g es un campo escalar en R n y la regla de la cadena da las siguientes ecuaciones: (las damos con las dos notaciones introducidas) D k (f g)(a) = D 1 f(g(a))d k g 1 (a) + D 2 f(g(a))d k g 2 (a)+ + + D m f(g(a))d k g m (a) (f g) (a) x k = f (g(a)) g 1 (a) + f (g(a)) g 2 (a)+ x 1 x k x 2 x k + + f x m (g(a)) g m x k (a) 2.1. Superficies parametrizadas En la sección anterior hemos introducido el concepto de curva parametrizada en R n ; de la misma forma podemos definir una superficie parametrizada en espacio R n que generalice las nociones de superficie que hemos manejado para la gráfica de un campo escalar en R 2 o para superficie de nivel de un campo en R 3. La definición que podemos tomar como punto de partida es la siguiente. Consideremos una función vectorial f : B R 2 R n, donde B es una bola; al conjunto imagen de esta función se le denomina superficie parametrizada en R n. Las ecuaciones x 1 = f 1 (t, s),... x n = f n (t, s) se denominan ecuaciones paramétricas de la superficie y la variables t y s se denominan parámetros. Igual que para las curvas parametrizadas observamos que el concepto de superficie corresponde al subconjunto de puntos y no al campo vectorial; el campo vectorial nos da una parametrización de la superficie pero una superficie admite muchas parametrizaciones. A diferencia de lo que ocurre con las curvas, el uso de bolas en el dominio de las parametrizaciones, hace que no todas las superficies puedan ser parametrizadas con un único campo vectorial, y que en la mayoría de los casos tengamos que trabajar con uniones de parametrizaciones y con dominios más generales. De la misma forma que para curvas parametrizadas, se puede introducir los conceptos de superficies diferenciales y regulares y la noción de plano tangente. Particularizamos estas últimas definiciones para superficies en R 3. Definición 17 Sea (x(t, s), y(t, s), z(t, s)) una parametrización diferenciable de S. Decimos que es regular si para cada (t 0, s 0 ), los vectores (D 1 x(t 0, s 0 ), D 1 y(t 0, s 0 ), D 1 z(t 0, s 0 )) (D 2 x(t 0, s 0 ), D 2 y(t 0, s 0 ), D 2 z(t 0, s 0 )) son linealmente independientes. En este caso, el plano generado por esos vectores, X x(t 0, s 0 ) = λd 1 x(t 0, s 0 ) + µd 2 x(t 0, s 0 ) Y y(t 0, s 0 ) = λd 1 y(t 0, s 0 ) + µd 2 y(t 0, s 0 ) Z z(t 0, s 0 ) = λd 1 z(t 0, s 0 ) + µd 2 z(t 0, s 0 ) se denomina plano tangente a S en (x(t 0, s 0 ), y(t 0, s 0 ), z(t 0, s 0 )). El grafo de un campo escalar diferenciable, f : D R 2 R, se puede parametrizar como: (x, y, z) = (t, s, f(t, s)), (t, s) D El plano tangente a esta superficie (que es regular), es: X t 0 = λ Y s 0 = µ Z f(t 0, s 0 ) = λd 1 f(t 0, s 0 ) + µd 2 f(t 0, s 0 ) Reduciendo los parámetros, obtenemos: Z f(t 0, s 0 ) = D 1 f(t 0, s 0 )(X t 0 )+D 2 f(t 0, s 0 )(Y s 0 ) Como en el caso de las curvas, las superficies de nivel no se estudian fácilmente como superficies parametrizadas, sin embargo, las propiedades estudiadas en el tema anterior permiten deducir una expresión para el plano tangente que no requiere el uso de parametrizaciones. Concretamente, vimos que, dado que las direcciones tangentes a una superficie (respect. curva) de Curso 2002/03. Cálculo para la Computación. Tema 4. 4
5 Función Curva/Superficie Recta/Plano tangente f : R R Gráfica: curva que pasa por (a, f(a)) Y f(a) = f (a)(x a) f : R R 2 f : R R n f : R 2 R f : R 2 R 3 f : R 2 R n f : R 3 R f : R 2 R Imagen: curva que pasa por f(a) Imagen: curva que pasa por f(a) Curva de nivel que pasa por por a Imagen: superficie que pasa por f(a) Imagen: superficie que pasa por f(a) Superficie de nivel que pasa por a Gráfica: superficie que pasa por (a, f(a)) X f 1 (a) = λf 1 (a) Y f 2 (a) = λf 2 (a) X 1 f 1 (a) = λf 1 (a). X n f n (a) = λf n (a) D 1 f(a)(x a 1 ) + D 2 f(a)(y a 2 ) = 0 X f 1 (a) = λd 1 f 1 (a) + µd 2 f 1 (a) Y f 2 (a) = λd 1 f 2 (a) + µd 2 f 2 (a) Z f 3 (a) = λd 1 f 3 (a) + µd 2 f 3 (a) X 1 f 1 (a) = λd 1 f 1 (a) + µd 2 f 1 (a). X n f n (a) = λd 1 f n (a) + µd 2 f n (a) D 1 f(a)(x a 1 ) + D 2 f(a)(y a 2 ) + D 3 f(a)(z a 3 ) = 0 Z f(a) = D 1 f(a)(x a 1 ) + D 2 f(a)(y a 2 ) Figura 1: Expresiones de las rectas y planos tangentes Curso 2002/03. Cálculo para la Computación. Tema 4. 5
6 nivel corresponden a la tasa variación nula del campo, y que estas direcciones son ortogonales al vector gradiente, entonces el vector gradiente es ortogonal al plano (respect. recta) de la superficie (respect. curva) de nivel. En particular, dado un campo f : R 2 R, la recta tangente a la curva de nivel que pasa por un punto a del dominio es D 1 f(a)(x a 1 ) + D 2 f(a)(y a 2 ) = 0 De la misma forma, dado un campo f : R 3 R, el plano tangente a la superficie de nivel que pasa por un punto a del dominio es Una representación más conveniente, aunque no siempre fácil de realizar, se hace mediante las líneas de campo: una curva γ contenida en el dominio del campo f : R 2 R 2 es una línea de campo, si tiene la propiedad: f(γ(t)) = γ (t). Hallar las líneas de campo de un campo vectorial supone la resolución de un sistema de ecuaciones diferenciales cuyo estudio haremos posteriormente en el curso: x (t) = f 1 (x(t), y(t)) y (t) = f 2 (x(t), y(t)) En la figura 2, aparece la representación de un campo vectorial usando líneas de campo. D 1 f(a)(x a 1 )+D 2 f(a)(y a 2 )+D 3 f(a)(z a 3 ) = 0 Los grafos de campos escalares en R 2, pueden ser descritos como superficies de nivel, f(x, y) z = 0, y por lo tanto, podemos obtener las expresiones de sus planos tangentes de una forma alternativa: Z f(a 1, a 2 ) = D 1 f(a 1, a 2 )(X a 1 )+D 2 f(a 1, a 2 )(Y a 2 ) En la figura 1 aparece una tabla resumen con las expresiones de los planos y rectas tangentes según la expresión dada Líneas de campo Los únicos campos vectoriales para los cuales hemos introducido una representación gráfica son los campos de la forma f : R 2 R 3. En esta sección vamos a introducir una representación parecida a las curvas de nivel para los campos f : R 2 R 2 : las líneas de campo. Una primera representación de este tipo de funciones podría hacerse de la siguiente forma: en primer lugar elegimos una región del plano para la cual queremos hacer la representación; en segundo lugar cuadriculamos esta región; la representación gráfica consiste en representar sobre cada punto de corte de esta cuadrícula el vector imagen de este punto. La representación obtenida es un conjunto de vectores aplicados a una familia de puntos homogéneamente repartidos. Esta representación, por si sola, puede ser de bastante utilidad pero en muchos casos resulta poco interesante Cambios de coordenadas Una de las principales aplicaciones del cálculo en varias variables es el estudio de campos escalares y vectoriales aplicados al plano y al espacio físico; por ejemplo, para el estudio de campos de presiones, de temperaturas, electromagnéticos,... Para estudiar matemáticamente estos campos, necesitamos, en primer lugar, identificar el plano físico con el espació métrico R 2 ; la forma más frecuente de realizar esta identificación es considerando un par de ejes cartesianos en el plano físico. De esta forma, cada punto del plano queda determinado biunívocamente por un elemento de R 2, y los campos sobre el plano pueden definirse mediante funciones de R 2. La misma situación se puede describir para campos escalares en el espacio. Aparte de los ejes cartesianos, existen otros sistemas para modelar matemáticamente el plano y el espacio físico; en las secciones siguientes introducimos los más usados Coordenadas polares Un sistema de representación polar para el plano se construye considerando una semirrecta R con extremo en un punto O. Las coordenadas polares de un punto P, respecto de este sistema, es un par de números, (r, θ), en donde r > 0 es la distancia euclídea entre el punto P y el punto O y θ es el ángulo que forma el segmento OP y el eje R. La recta R se denomina eje polar, el punto Curso 2002/03. Cálculo para la Computación. Tema 4. 6
7 Figura 2: Representación del campo f(x, y) = (, x ). x 2 +y 2 x 2 +y 2 y O se denomina polo y la recta que une los puntos P y O se denomina recta radial de P. Habitualmente, los sistemas de representación cartesiano y polar se eligen coincidentes de la siguiente forma: tomamos el semieje positivo OX como eje polar y el ángulo entre este eje y las rectas radiales se mide en el sentido contrario a las agujas del reloj. En adelante indicaremos con () un par de coordenadas cartesianas y con () P un par de coordenadas polares. El cambio de coordenadas polares a cartesianas es el siguiente: (r, θ) P = (r cos θ, r sen θ) es la siguiente: (x, y) = ( x 2 + y 2, arc tg y x ) P, si x > 0 (x, y) = ( x 2 + y 2, arc tg y x ) P, si x < 0 (0, y) = (y, π / 2 ) P, si y > 0 Recuérdese que la función arcotangente se define de forma que: π / 2 < arc tg z < π / 2. La representación gráfica de la conversión es: Y y (x, y) = (r, θ) P r Estas ecuaciones tienen sentido para todo r R y todo θ R; la consideración de R como rango de θ es bastante natural por la periodicidad de las funciones sen y cos y la consideración de valores negativos para r nos lleva a la siguiente igualdad: (r, θ) = ( r, θ + π). Esta extensión, sin embargo, hace que la correspondencia entre coordenadas polares y cartesianas no sea biyectiva y Esta falta de biyección es especialmente significativa en el origen de coordenadas o polo ya que cualquier par de la forma (0, θ) representa a este punto. La trasformación inversa del cambio de coordenadas O θ Coordenadas cilíndricas Un sistema de representación cilíndrico está formado por los siguientes elementos: un punto O, una semirrecta con origen en O, R, y un plano que contiene a la semirrecta, π. Dado un punto P en el espacio, la posición de este punto respecto del sistema así definido está determinado por la terna (r, θ, z) donde: x X Curso 2002/03. Cálculo para la Computación. Tema 4. 7
8 Si consideramos la proyección del segmento OP sobre π, r es la longitud de esta proyección. θ es el ángulo que forma la proyección del segmento OP y la recta R. z es la distancia del punto P al plano π, (asignándole a uno de los lados del plano distancias negativas) Para establecer la correspondencia entre el sistema cartesiano y el cilíndrico, tomamos el siguiente sistema cilíndrico: el punto O es el origen de coordenadas, la semirrecta R es el semieje OX y el plano π es el plano XY. De esta forma tenemos la identificación que se muestra en la siguiente figura semirrecta, π. Dado un punto P en el espacio, la posición de este punto respecto del sistema así definido esta determinado por la terna (ρ, θ, φ) donde: ρ es la longitud del segmento OP. Si consideramos la proyección del segmento OP sobre π, θ es el ángulo que forma dicha proyección con R. z Z (x,y,z)=(r,θ,z) C Si consideramos la recta ortogonal a π que pasa por O, φ es el ángulo que forma el segmento OP con esta recta. X x θ En adelante indicaremos con () una terna de coordenadas cartesianas y con () C una terna de coordenadas cilíndricas: r y Y Para establecer la correspondencia entre el sistema cartesiano y el esférico, hacemos la siguiente identificación: el punto O es el origen de coordenadas, la semirrecta R es el semieje OX y el plano π es el plano XY. De esta forma tenemos la identificación que se muestra en la figura (r, θ, z) C = (r cos θ, r sen θ, z) Como para las coordenadas polares, tiene sentido considerar cualquier valor real para r y cualquier valor real para θ. La conversión inversa viene dada por: Z φ (x, y, z) = ( x 2 + y 2, arc tg y x, z) C, x > 0 z (x, y, z) = ( x 2 + y 2, arc tg y x, z) C, x < 0 (0, y, z) = (y, pi/2, z) C ρ (x,y,z)=(ρ,θ,φ) E Coordenadas esféricas x y Y Un sistema de representación esférico está formado por los siguientes elementos: un punto O, una semirrecta con origen en O, R y un plano que contiene a la X θ Curso 2002/03. Cálculo para la Computación. Tema 4. 8
9 En adelante indicaremos con () E una terna de coordenadas esféricas: (ρ, θ, φ) E = (ρ sen φ cos θ, ρ sen φ sen θ, ρ cos φ) (x, y, z) = ( x 2 + y 2 + z 2, ± arc tg y x, ± arc cos (0, y, z) = ( y 2 + z 2, ±π/2, ± arc cos z x 2 + y 2 + z 2 ) E, x 0 z y 2 + z 2 ) E donde φ [0, π], θ [0, 2π), 2.5. Paraboloide elíptico La ecuación y figura del Paraboloide elíptico son: z = x2 a 2 + y2 b 2 Z (ρ, θ, φ) E = (ρ sen φ, θ, ρ cos φ) C (r, θ, z) C = ( r 2 + z 2 r, θ, ± arc sen r 2 + z ) 2 E 2.4. Cuádricas Cualquier polinomio de dos variables de grado 2 determina una curva en el plano que se denomina cónica. De la misma forma, cualquier polinomio de tres variables de grado 2 determina una superficie en R 3 que se denomina cuádrica. En esta sección repasamos estas superficies en su posición típica; utilizando métodos de álgebra lineal, se puede identificar cualquier polinomio con una de estas superficies Elipsoide La ecuación y figura del Elipsoide son las siguientes x 2 a 2 + y2 b 2 + z2 c 2 = 1 Z Y X Una parametrización para el paraboloide elíptico es: x(r, θ) = ar cos θ y(r, θ) = br sen θ z(r, θ) = r 2 donde r [0, + ), θ [0, 2π), 2.6. Paraboloide hiperbólico X Y El Paraboloide hiperbólico se define con la ecuacion: z = y2 b 2 x2 a 2 Z Una parametrización para esta superficie es: Y x(θ, φ) = a sen φ cos θ y(θ, φ) = b sen φ sen θ z(θ, φ) = c cos φ X Curso 2002/03. Cálculo para la Computación. Tema 4. 9
10 Una parametrización para el paraboloide hiperbólico es: x(r, θ) = ar cos θ y(r, θ) = br sen θ z(r, θ) = r 2 cos 2θ donde r [0, + ), θ [0, 2π), Otro polinomio que representa igualmente un paraboloide hiperbólico es el siguiente: z = kxy Z Una importante propiedad del cono es que nos permite generar todas las curvas cónicas mediante secciones por planos; esto se puede conseguir con el cono En concreto: z 2 = λ 2 (x 2 + y 2 ) 1. Las secciones por planos paralelos al eje OZ son hipérbolas. 2. Las secciones por planos perpendiculares al eje OZ son circunferencias. 3. Las secciones por planos paralelos a la generatriz son parábolas. X Y 4. Las demás secciones son elipses. 5. Existen dos casos defectivos: las secciones por planos que contienen al eje OZ son un par de rectas y la sección por el plano XY es un punto. Esta figura se obtiene al girar π / 4 radianes la anterior. Además, esta representación permite observar una importante característica de esta superficie: es una superficie reglada, es decir, para cada punto P del paraboloide, existe una recta r que contiene a P y tal que r está contenida en el paraboloide Hiperboloide de una hoja La ecuación y figura del Hiperboloide de una hoja son las siguientes z 2 c = x2 a 2 + y2 b 2 Z 2.7. Cono La ecuación y figura del Cono son las siguientes Z X Y X Y z 2 = x2 a 2 + y2 b 2 El hiperboloide de una hoja también es una superficie reglada. Curso 2002/03. Cálculo para la Computación. Tema 4. 10
11 2.9. Hiperboloide de dos hojas La ecuación y figura del Hiperboloide de dos hojas son las siguientes z 2 c 2 1 = x2 a 2 + y2 b 2 Z permite analizar cuando es posible encontrar una función diferenciable a partir de una definición implícita. Teorema 18 Sea F : D R n R R diferenciable en el conjunto abierto D. Sea (a 1,..., a n, b) D tal que F (a 1,..., a n, b) = 0 y tal que D n+1 f(a 1,..., a n, b) 0 entonces: Y 1. existen entornos abiertos, A de a = (a 1,..., a n ) y B de b, con A B D, y un campo f : A R n R tales que X f(a) B y F (x 1,..., x n, f(x 1,..., x n )) = 0 si (x 1,..., x n ) A; es decir, F (x 1,..., x n, y) = 0 define implícitamente y en función de (x 1,..., x n ). 2. f es diferenciable y 3. Derivación implícita Para introducir el problema que queremos plantear en esta sección, comenzamos analizando un ejemplo. Consideremos el campo escalar F (x, y) = x 2 + y 2 1; la curva de nivel N 0 = {(x, y) F (x, y) = 0} es la circunferencia centrada en el origen y radio 1. Consideremos la función f(x) = 1 x 2 definida explícitamente. El grafo de la función f está contenido en la curva N 0 y, por esta razón, decimos que F (x, y) = 0 define implícitamente a la función f. Es fácil observar que una igualdad del tipo F (x, y) = 0 no define necesariamente una única función y que no siempre es posible definir una función cuyo grafo coincida con toda la curva de nivel (en el ejemplo anterior no es posible). El ejemplo anterior se puede formular de forma general como sigue: dada una ecuación de la forma F (x, y) = 0, despejar y en función de x: y = f(x). A continuación vamos a ver el resultado general que D i f(x 1,..., x n ) = f x i (x 1,..., x n ) F (x x 1,..., x n, f(x 1,..., x n )) = i F y (x 1,..., x n, f(x 1,..., x n )) Obsérvese que el resultado es local, afirmamos la existencia de una función definida en un entorno de un punto; dar una expresión explícita de esta función o encontrar el dominio más amplio dependerá de cada problema particular. Por otra parte, aunque el enunciado está enunciado para despejar la última coordenada, se pueden enunciar resultados análogos para cualquier coordenada. Utilicemos este teorema para analizar el ejemplo anterior. Partíamos del campo F (x, y) = x 2 + y 2 1: F (x, y) = (2x, 2y). El teorema 18 no puede aplicarse a los puntos (x, y) tales que F (x, y) = 0 e y = 0, es decir, a los puntos ( 1, 0) y (1, 0). Consideremos el punto (0, 1) que está en N 0 y verifica la hipótesis del teorema 18; entonces existe un entorno A = ( ε, ε) de 0 y una función f : ( ε, ε) R definida implícitamente por F (x, y) = 0. En este caso, es fácil hallar esta función: f(x) = 1 x 2 cuyo dominio de derivabilidad Curso 2002/03. Cálculo para la Computación. Tema 4. 11
12 es ( 1, 1). En el punto (0, 1) también se puede aplicar el teorema y la función definida implícitamente es g(x) = 1 x 2. Debemos tener en cuenta que el teorema no dice nada de lo que ocurre en los puntos donde la parcial respecto de y es nula; en estos puntos puede ocurrir de todo y por tanto no se puede afirmar nada en general. En el ejemplo anterior, no es posible encontrar funciones definidas implícitamente por F (x, y) = 0 en entornos de ( 1, 0) o de (1, 0). Consideremos la función G(x, y) = (x 2 + y 2 1) 2 ; G(x, y) = (4x(x 2 + y 2 1), 4y(x 2 + y 2 1)) Dado que D 2 G(0, 1) = 0, no podemos aplicar el teorema al punto (0, 1); sin embargo, la función f(x) = 1 x 2 es derivable en el intervalo ( 1, 1), está definida implícitamente por G(x, y) = 0 y pasa por el punto (0, 1). Damos a continuación el enunciado general del teorema de la función implícita para sistemas de ecuaciones. 2. f es diferenciable y f 1 f 1 x 1 x n Jf =... f m f n x 1 x n 1 F 1 F 1 F 1 F 1 y 1 y m x =. 1 x n..... F m F m F m F m y 1 y m x 1 x n Teorema 20 (de la función inversa) Sea f : D R n R n diferenciable en el conjunto abierto D; f(x 1,..., x n ). Sea a D tal que f 1 f (a) 1 (a) x 1 x n... 0 entonces: f n x 1 (a) f n x n (a) Teorema 19 (de la función implícita) Sea F : D R n R m R m diferenciable en el conjunto abierto D: F (x 1,..., x n, y 1,..., y m ). Sean a = (a 1,..., a n ) y b = (b 1,..., b m ) tales que (a 1,..., a n, b 1,..., b m ) D, F (a 1,..., a n, b 1,..., b m ) = 0 y entonces: F 1 (a, b) F 1 (a, b) y 1 y m... F m y 1 (a, b) F m y m (a, b) 0 1. existen entornos abiertos, A de a y B de b, con A B D, y un campo f : A R n R m tales que f(a) B y F (x 1,..., x n, f(x 1,..., x n )) = 0 es decir, F (x 1,..., x n, y 1,..., y m ) = 0 define implícitamente (y 1,..., y m ) en función de (x 1,..., x n ). 1. existe un entorno abierto A de a tal que f : A R n R n es inyectiva y B = f(a) es un abierto. 2. f 1 = (φ 1,..., φ n ): B R n R n es diferenciable y J(f 1 )(f(x)) = = φ 1 φ (f(x)) 1 (f(x)) y 1 y n... φ n (f(x)) φ n (f(x)) y 1 y n 1 f 1 f (x) 1 (x) x 1 x n... f n x 1 (x) J(f 1 )(f(x)) = (Jf(x)) 1 f n x n (x) 4. Derivadas de orden superior Dado un campo f : R n R diferenciable, podemos considerar el campo: f : D R n R n Curso 2002/03. Cálculo para la Computación. Tema 4. 12
13 dado por f = (D 1 f,..., D n f). La diferenciabilidad de f es equivalente a la diferenciabilidad de los campos D i f cuyo estudio incluye la existencia de derivadas parciales; en caso de existir, las derivadas parciales de los campos D i f se denominan derivadas de segundo orden o segundas derivadas de f; las notaciones para estas derivadas son: x i ( ) f x j = 2 f x i x j D i (D j f) = D ij f Por tanto, la matriz jacobiana de f es: D 11 f(a) D 21 f(a) D n1 f(a) D 12 f(a) D 22 f(a) D n2 f(a) J( f)(a) =... D 1n f(a) D 2n f(a) D nn f(a) La matriz transpuesta de la anterior se denomina matriz hessiana de f: D 11 f(a) D 12 f(a) D 1n f(a) D 21 f(a) D 22 f(a) D 2n f(a) Hf(a) =... D n1 f(a) D n2 f(a) D nn f(a) Esta matriz se corresponde con la segunda derivada de f. Teorema 21 (de Schwarz) Sea f un campo escalar tal que sus derivadas parciales de segundo orden son continuas; entonces, sus derivadas parciales mixtas son iguales: D ij = D ji para cada i, j Es decir, si las derivadas segundas de f son continuas, la matriz hessiana es simétrica. Si Hf(a) es simétrica tiene sentido definir la aplicación q a (u) = u t Hf(a)u que se denomina forma cuadrática asociada a Hf(a). Se puede observar fácilmente que las formas cuadráticas son polinomios de grado dos sin términos de grado menor. Hemos introducido en esta sección la diferencial segunda de un campo escalar; el proceso seguido puede repetirse para definir la diferencial tercera, diferencial cuarta,... ; en general, estas diferenciales se denominan diferenciales de orden superior y las derivadas parciales correspondientes derivadas parciales de orden superior. En este tema solo utilizaremos las derivadas de segundo orden, las derivadas de orden superior quedan fuera del objetivo de este curso Teorema de Taylor Igual que las funciones reales de variable real, los campos escalares varias veces diferenciables pueden ser aproximados por polinomios, de forma que el comportamiento local de la función y del polinomio es muy parecido. Aunque solo vamos a enunciar el teorema para el segundo orden, el resultado puede ser generalizado a cualquier orden. Esta restricción sin embargo, hace que sean pocas las consecuencias que podamos sacar del mismo; en la siguiente sección lo vamos a utilizar para el estudio de los extremos de campos escalares. Teorema 22 (Fórmula de Taylor de segundo orden) Sea f : D R n R un campo escalar dos veces diferenciable y con parciales de segundo orden continuas. Entonces: f(a + u) = f(a) + df a (u) q a(u) + u 2 E(a, u) donde lím u 0 E(a, u) = 0 Es decir, en un entorno lo suficientemente pequeño de a, la función f(a+u) tiene un comportamiento parecido al polinomio f(a) + df a (u) q a(u). 5. Extremos de campos escalares Definición 23 Un conjunto D R n se dice que está acotado, si existe un r > 0 tal que D B(x, r) para algún x R n. Teorema 24 Sea f un campo escalar continuo y A un subconjunto cerrado y acotado del dominio de f; entonces existen x 0, x 1 A tales que f(x 0 ) f(x) f(x 1 ) para todo x A. Es decir, todo campo escalar continuo Curso 2002/03. Cálculo para la Computación. Tema 4. 13
14 alcanza un máximo y un mínimo en cada subconjunto cerrado y acotado de su dominio. Definición 25 Un campo escalar f : D R n R tiene un máximo local (o relativo) en a D si existe un r > 0, tal que f(a) f(x) para todo x B(a, r) D Definición 26 Un campo escalar f : D R n R tiene un mínimo local (o relativo) en a D si existe un r > 0, tal que f(a) f(x) para todo x B(a, r) D Teorema 27 Sea f : D R n R un campo escalar diferenciable. Si a D es un extremo local de f, entonces df a = 0; es decir, todas las derivadas parciales de f en a son nulas. 1. Si q a (u) > 0 para todo u 0, a es un mínimo local de f. (Se dice que q a es definida positiva) 2. Si q a (u) < 0 para todo u 0, a es un máximo local de f. (Se dice que q a es definida negativa) 3. Si q a (u 1 ) > 0 y q a (u 2 ) < 0 para algún u 1, u 2 0, entonces, a es un punto silla de f. (Se dice que q a es indefinida) 4. En cualquier otro caso no podemos deducir nada. Para aplicar este teorema debemos decidir el signo de la forma cuadrática q a. Para hacerlo existen varios métodos que repasamos a continuación: En el caso n = 2, la interpretación gráfica de este resultado es la siguiente: en los extremos locales de un campo, el plano tangente a la gráfica es paralelo al plano XY. Es fácil observar que el recíproco del teorema no es cierto. Los puntos en los cuales la diferencial es nula, se denominan puntos críticos y a los puntos críticos que no son extremos locales se denominan puntos silla. Del teorema 27 se deduce el primer paso para determinar los extremos locales de un campo escalar: debemos localizar los puntos críticos y aquellos puntos en los que el campo no es diferenciable; entre estos puntos estarán todos los extremos. El siguiente paso es clasificar estos puntos, es decir, determinar cuales son máximos, cuales mínimos y cuales no son extremos. Esta clasificación se puede hacer comparando el valor de la función en el punto con los valores de la función en los puntos cercanos; aunque no siempre será sencillo, en muchas ocasiones, será la única forma de hacerlo. Para clasificar los puntos críticos, podemos utilizar el siguiente teorema, consecuencia del desarrollo de Taylor de la sección anterior, y análogo al criterio de la derivada segunda para funciones de una variable Criterio de la hessiana Teorema 28 Sea a D un punto crítico del campo f : D R n R dos veces diferenciable; sea q a la forma cuadrática asociada a f y a. Entonces: Valores propios (NO) Sean λ 1, λ 2,... λ n los valores propios de la matriz hessiana Hf(a). 1. Si λ i > 0 para todo i, la forma cuadrática es definida positiva y a es un mínimo local. 2. Si λ i < 0 para todo i, la forma cuadrática es definida negativa y a es un máximo local. 3. Si λ i > 0 y λ j < 0, la forma cuadrática es indefinida y a no es extremo. 4. En cualquier otro caso, la forma cuadrática es semidefinida (positiva o negativa) y no podemos deducir nada sobre a. Para utilizar este método, debemos conocer los valores propios de la matriz (basta conocer el signo de cada uno), es decir, las raíces del polinomio característico. El método siguiente utiliza simplemente los coeficientes de este polinomio Polinomio característico (SÍ) Proposición 29 Sea p(λ) = Hf(a) λi = c n c n 1 λ+c n 2 λ 2 + +( 1) n 1 c 1 λ n 1 +( 1) n λ n. Curso 2002/03. Cálculo para la Computación. Tema 4. 14
15 (nos referiremos brevemente a este polinomio como polinomio característico en a). 1. Si c i > 0 para todo i, entonces la forma cuadrática es definida positiva y a es un mínimo local. 2. Si el signo de c i es ( 1) i para todo i, la forma cuadrática es definida negativa y a es un máximo local. 3. Si c i > 0 hasta algún r < n y los demás son nulos, entonces la forma cuadrática es semi-definida positiva y no podemos afirmar nada sobre a. 4. Si el signo de c i es ( 1) i hasta algún r < n y los demás son nulos, la forma cuadrática es semidefinida negativa y no podemos afirmar nada sobre a. 5. En cualquier otro caso, la forma es indefinida y a no es extremo. Supongamos que la matriz hessiana de un campo f en un punto crítico a es Hf(a) = El polinomio característico de esta matriz es: p(λ) = 12λ 10λ 2 8λ 3 + λ 4 y en consecuencia, la forma cuadrática asociada es indefinida y el punto a es un punto silla. Veamos otros ejemplos de posibles polinomios característicos de matrices hessianas y las conclusiones que obtenemos: λ 4 + 2λ 3 7λ 2 20λ 12 λ 3 7λ 2 11λ 5 λ 4 λ 2 λ 4 7λ λ 2 12λ λ 4 11λ λ 2 61λ + 30 λ 5 5λ 4 8λ 3 4λ 2 Indefinida (punto silla) Definida negativa (máx.) Indefinida (punto silla) Semidefinida positiva Definida positiva (mín.) Semidefinida negativa El estudio del polinomio característico para campos sobre R 2 se reduce al siguiente resultado: Proposición 30 Sea a un punto crítico del campo f : D R 2 R dos veces diferenciable; sea Hf(a) la matriz hessiana de f en a. 1. Si Hf(a) > 0 y D 11 f(a) > 0, la forma cuadrática es definida positiva y a es un mínimo local. 2. Si Hf(a) > 0 y D 11 f(a) < 0, la forma cuadrática es definida negativa y a es un máximo local. 3. Si Hf(a) < 0, la forma cuadrática es indefinida y a no es extremo local. 4. En cualquier otro caso, la forma cuadrática es semidefinida (positiva o negativa) y no podemos deducir nada sobre a Compleción de cuadrados (NO) Mediante la técnica algebraica de completar cuadrados, se puede transformar el polinomio cuadrático q a (u) en sumas de cuadrados de polinomios de grado 1 multiplicados por un coeficiente (positivo o negativo). El número de sumandos debe ser n; si hay menos sumandos, entendemos que los que faltan están multiplicados por un coeficiente nulo. A partir de los coeficientes de estos sumandos, deducimos que: 1. Si los n coeficientes son estrictamente positivos, la forma cuadrática es definida positiva y a es un mínimo. 2. Si los n coeficientes son estrictamente negativos, la forma cuadrática es definida negativa y a es un máximo. 3. Si algún coeficiente es positivo y otro es negativo, la forma cuadrática es indefinida y a no es extremo. 4. En los demás casos, la forma es semidefinida y no podemos deducir nada sobre a. La explicación teórica del método puede resultar difícil de seguir; por ello es preferible repasarlo sobre un ejemplo: Curso 2002/03. Cálculo para la Computación. Tema 4. 15
16 Supongamos que la matriz hessiana de un campo f en un punto crítico a es Hf(a) = La forma cuadrática asociada a esta matriz es: x y q a (x, y, z, t) = (x y z t) z t = 2x 2 +2y 2 +3z 2 +t 2 +4xy+6xz+2xt+6yz+2yt+6zt El proceso empieza eligiendo una variable (por ejemplo x); a continuación multiplicamos y dividimos por el coeficiente del cuadrado de esta variable; mediante la compleción de un cuadrado conseguimos que todos los sumandos donde aparece la variable x pertenezcan a un cuadrado: 2x 2 +2y 2 +z 2 +3t 2 +4xy+6xz+2xt+6yz+2yt+6zt = = 1 2 (4x2 + 4y 2 + 2z 2 + 6t 2 + 8xy + 12xz + 4xt+ 12yz + 4yt + 12zt) = 1 2 ((2x + 2y + 3z + t)2 4y 2 9z 2 t 2 12yz 4yt 6zt + 4y 2 + 2z 2 + 6t yz + 4yt + 12zt) = 1 2 ((2x + 2y + 3z + t)2 7z 2 + 5t 2 + 6zt) Con esto, logramos eliminar la variable x (en este caso también la variable y). A partir de aquí se repite el mismo proceso con las variables restantes hasta conseguir transformar toda la expresión a la forma deseada: = 1 2 ((2x + 2y + 3z + t)2 1 7 (49z2 35t 2 42zt)) = 1 2 ((2x + 2y + 3z + t)2 1 7 ((7z 3t)2 9t 2 35t 2 )) = 1 2 ((2x + 2y + 3z + t)2 1 7 ((7z + 3t)2 44t 2 )) = 1 2 (2x + 2y + 3z + t) (7z + 3t) t2 )) Los coeficientes que hemos obtenido son 1 2, 1 14, 22 7 y 0 y en consecuencia, la forma es indefinida y el punto a no es extremo Criterio de Sylvester Por último vamos a enunciar el criterio de Sylvester que, si bien no es el que más información da, sí es el más utilizado. Este método no permite clasificar completamente la forma cuadrática y por tanto, no utiliza toda la información que da el criterio de la hessiana. Consideremos los siguientes menores de la matriz hessiana: D A 1 = D 11 f(a), A 2 = 11 f(a) D 12 f(a) D 21 f(a) D 22 f(a) D 11 f(a) D 12 f(a) D 13 f(a) A 3 = D 21 f(a) D 22 f(a) D 23 f(a) D 31 f(a) D 32 f(a) D 33 f(a)... D 11 f(a) D 12 f(a)... D 1n f(a) D 21 f(a) D 22 f(a)... D 2n f(a) A n = D n1 f(a) D n2 f(a)... D nn f(a) 1. a es mínimo de f si y solo si A 1 > 0, A 2 > 0,..., A n > a es máximo de f si y solo si A 1 > 0, A 2 > 0, A 3 > 0,..., ( 1) n A n > 0, es decir, el signo de A i es ( 1) i. 3. En los demás casos, la forma es semidefinida o indefinida y no podemos concluir nada sobre a; no obstante, podemos estudiar algunos otros casos: supongamos que no se verifican las condiciones del los dos primeros casos, entonces: a) Si A n 0, entonces a es punto de silla b) Si en la diagonal principal hay un elemento positivos y otro negativo, entonces a es punto silla (esta condición se puede aplicar siempre). Curso 2002/03. Cálculo para la Computación. Tema 4. 16
17 c) Si algún menor principal de orden 2 es negativo, entonces a es punto silla (esta condición se puede aplicar siempre). En el ejemplo del apartado anterior obtendríamos los siguientes valores: A 1 = 2 A 2 = 0 A 3 = 0 A 4 = 0 y no podríamos deducir nada con el criterio de Sylvester. Aconsejaría al alumno el uso del polinomio característico ya que: nos permite obtener la máxima información de la matriz hessiana, es sencillo de manejar y es generalizable al estudio de extremos condicionados. (El criterio de Sylvester también es generalizable, pero no extrae la máxima información de la hessiana; la compleción de cuadrados es igualmente generalizable, pero su uso es demasiado laborioso) 5.2. Método general Para terminar el estudio de los extremos locales no condicionados, sería conveniente ordenar todo lo dicho hasta ahora en un esquema. Antes de esto, vamos a ver un último resultado teórico, que permite tratar aquellos casos que no son contemplados por el criterio de la hessiana: Teorema 31 Sea f : D R n R un campo escalar, a D; para cada vector u R n unitario consideremos la función (en una variable) g u (t) = f(a + tu). Entonces: a es máximo (respectivamente mínimo) local de f si y solo si existe un número real ɛ > 0 tal que 0 es máximo (respectivamente mínimo) absoluto de todas las funciones g u sobre el intervalo ( ɛ, ɛ) La importancia de este resultado está en que reduce el estudio de extremos locales de campos escalares al estudio de extremos locales de funciones reales de variable real, (y para estas funciones podemos decidir completamente la naturaleza de un punto) y, además, se puede aplicar a puntos donde f no es diferenciable. Sin embargo, la aplicación de este teorema en la práctica no siempre es sencilla, ya que las funciones g u dependen de varios parámetros (al menos n 1 parámetros). La forma más simple de aplicar dicho teorema queda recogida en el siguiente corolario: Corolario 32 Sea f : D R n R un campo escalar, a D; para cada vector u R n unitario consideremos la función g u (t) = f(a + tu). 1. Si 0 es máximo local de una función g u y mínimo local de otra función g v, entonces a no es extremo local de f. 2. Si 0 no es ni máximo ni mínimo local de alguna función g u0, entonces, a no es ni máximo ni mínimo local de f. Resumimos en un esquema el método general que debemos seguir para determinar los extremos locales de un campo f. No debemos saltarnos ningún paso, pero en cada uno podemos concluir el estudio. 1. Determinar todos los puntos críticos y los puntos donde el campo no es diferenciable. Estos serán los candidatos a extremos locales: Si el campo es diferenciable en todo su dominio y no tiene puntos críticos, entonces no tiene extremos locales. A partir de aquí, debemos clasificar cada uno de los candidatos; por tanto, los pasos siguientes se repetirán para cada uno. 2. Si f es dos veces diferenciable en a, aplicamos el criterio de la hessiana, preferiblemente usando el polinomio característico. 3. Para cada a construimos las funciones g u (t) = f(a + tu) y estudiamos si 0 es extremo local de todas ellas; esto lo haremos, preferiblemente, estudiando el signo de la derivada de cada g u alrededor del 0; para aquellas g u que sean varias veces derivables en 0, podremos usar igualmente el criterio de las derivadas sucesivas: Si existe alguna función g u para la cual 0 no sea ni máximo ni mínimo, entonces podremos concluir Curso 2002/03. Cálculo para la Computación. Tema 4. 17
18 que a no es ni máximo ni mínimo local de f. Igualmente, si 0 es máximo local de una g u y mínimo local de g v, entonces podremos concluir que a no es ni máximo ni mínimo local de f. 4. Si llegamos hasta aquí con algún punto a de los obtenidos en el primer paso, hay bastantes posibilidades de que el punto sea máximo o mínimo, pero no podemos afirmar nada; debemos recurrir a la expresión de f y comparar f(x) con f(a) (dependiendo de la complejidad de f esto puede ser más o menos difícil). f con las condiciones o restricciones g i (x 1,..., x n ) = 0, 0 i k. Vemos abajo el grafo del campo escalar f(x, y) = x 3 +y 3. Por los métodos de la sección anterior podemos deducir que f no tiene extremos locales; es decir, la función no alcanza ni máximo ni mínimo sobre ningún conjunto abierto. Y Z Ejemplo: Determinar y clasificar los puntos críticos de f(x, y) = x 3 y 3. X D 1 f(x, y) = 3x 2 D 2 f(x, y) = 3y 2 Por tanto, el único punto crítico es (0, 0). D 11 f(x, y) = 6x D 21 f(x, y) = 0 D 22 f(x, y) = 6y Por tanto, la matriz hessiana de f en (0, 0) es y no nos permite clasificar el punto crítico. La función g (0,1) (t) = f(0, t) = t 3 tiene un punto de inflexión en 0, y por tanto, (0, 0) no es ni máximo ni mínimo de f. 6. Extremos condicionados. Multiplicadores de Lagrange Sin embargo, si restringimos f a la circunferencia S {x 2 + y 2 = 1}, observamos que sí se alcanzan máximos y mínimos. Representamos el conjunto f(s) para visualizar esta afirmación: Z En la sección anterior hemos afrontado el problema de hallar los extremos locales de un campo escalar, es decir, los extremos sobre conjuntos abiertos. Sin embargo, en muchas ocasiones nos interesará estudiar los extremos sobre conjuntos que no son abiertos; por ejemplo, estudiar los extremos de un campo sobre R 2 restringiéndonos a una circunferencia. El problema general que abordamos en esta sección es el siguiente: encontrar los extremos de la función f(x 1,..., x n ) sobre un conjunto S definido por: f (S ) S Z Y X S = {(x 1,..., x n ) g(x 1,..., x n ) = 0} donde g = (g 1,..., g k ) es un campo vectorial. Este problema se lee: encontrar los extremos del campo escalar Curso 2002/03. Cálculo para la Computación. Tema 4. 18
19 El teorema fundamental que nos permite abordar este tipo de problemas es el siguiente: Teorema 33 Sean f, g 1,..., g k : D R n R campos escalares diferenciables y con derivadas parciales continuas. Sea S un subconjunto de R n cuyos puntos verifican las condiciones: g i (x 1,..., x n ) = 0 para todo i Entonces se verifica que: si x 0 es un extremo local de f restringida a S, y { g i (x 0 )} es un sistema de vectores no nulos linealmente independientes, 1 entonces, existen números reales µ i tales que f(x 0 ) = µ 1 g 1 (x 0 ) + + µ k g k (x 0 ) A las constantes µ 1,..., µ k se las denomina multiplicadores de Lagrange asociados a x 0. Este teorema nos da el primer paso a seguir para la determinación de los extremos condicionados: Los extremos locales del campo f(x 1,... x n ) con las restricciones g 1 (x 1,..., x n ) = 0,... g k (x 1,..., x n ) = 0, se encuentran entre los puntos (x 1,..., x n ) cuyas coordenadas son solución del sistema: g 1 (x 1,..., x n ) = 0... g k (x 1,..., x n ) = 0 D 1 f(x) = µ 1 D 1 g 1 (x) + + µ k D 1 g k (x)... D n f(x) = µ 1 D n g 1 (x) + + µ k D n g k (x) Si x 1,..., x n, µ 1,..., µ k es una solución del sistema, (x 1,..., x n ) se denomina punto crítico de f con las restricciones g i, y µ 1,..., µ k son sus multiplicadores de Lagrange asociados. 1 La condición: { g i(x 0)} es un sistema de vectores no nulos linealmente independientes, exigida en el teorema, se traduce en la práctica a observar que el problema está bien planteado, es decir, que no hay condiciones superfluas, y que estas están dadas de la mejor forma posible. Igual que para los extremos no condicionados, el problema siguiente es clasificar los puntos críticos, decidiendo cuales son máximos, cuales mínimos y cuales no son extremos. Teorema 34 Sea a = (a 1,..., a n ) un punto crítico de f y (α 1,..., α k ) sus multiplicadores de Lagrange; consideremos el campo F : D R n R definido por: F (x) = f(x) α 1 g 1 (x) α k g k (x); sea q la forma cuadrática asociada a la matriz hessiana de F en a y sea T el espacio vectorial tangente a S en a (la dimensión del subespacio T es n k). 1. Si q(u) > 0 para todo u T, entonces a es punto mínimo. 2. Si q(u) < 0 para todo u T, entonces a es punto máximo. 3. Si q(u 1 ) > 0 para algún u 1 T y q(u 2 ) < 0 para algún u 2 T, entonces a no es extremo. 4. En cualquier otro caso, no podemos deducir nada. Es decir, para determinar la naturaleza de un punto crítico a tenemos que estudiar el signo de la forma cuadrática q T (restricción de la forma cuadrática q al subespacio T ). La forma más sencilla de hacer esto es utilizando el polinomio característico de la forma cuadrática q T aplicando la proposición 29, (dado que la dimensión de T es n k, el grado de este polinomio es n k). El siguiente resultado nos da una forma sencilla de obtener este polinomio característico: Proposición 35 Sea g el campo vectorial g = (g 1,..., g k ); denotemos por 0 a la matriz cuadrada de tamaño k k y cuyos elementos son todos nulos. Entonces, el polinomio característico de q T viene dado, salvo una constante, por: 0 Jg(a) P (λ) = Jg(a) t HF (a) λi Nos referiremos brevemente a este polinomio como polinomio característico en a. Curso 2002/03. Cálculo para la Computación. Tema 4. 19
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
May 4, 2012 CAPÍTULO 5: OPTIMIZACIÓN
 May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Derivadas Parciales (parte 2)
 40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
Lección 2: Funciones vectoriales: límite y. continuidad. Diferenciabilidad de campos
 Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
1. Curvas Regulares y Simples
 1. Regulares y Simples en R n. Vamos a estudiar algunas aplicaciones del calculo diferencial e integral a funciones que están definidas sobre los puntos de una curva del plano o del espacio, como por ejemplo
1. Regulares y Simples en R n. Vamos a estudiar algunas aplicaciones del calculo diferencial e integral a funciones que están definidas sobre los puntos de una curva del plano o del espacio, como por ejemplo
1 Curvas planas. Solución de los ejercicios propuestos.
 1 Curvas planas. Solución de los ejercicios propuestos. 1. Se considera el lugar geométrico de los puntos del plano tales que la suma del cuadrado de las distancias a los puntos P 1 = (, 0) y P = (, 0)
1 Curvas planas. Solución de los ejercicios propuestos. 1. Se considera el lugar geométrico de los puntos del plano tales que la suma del cuadrado de las distancias a los puntos P 1 = (, 0) y P = (, 0)
CÁLCULO DIFERENCIAL Muestras de examen
 CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
INDICE 1. Desigualdades 2. Relaciones, Funciones, Graficas 3. La Línea Recta 4. Introducción al Cálculo. Límites
 INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
Lección 4. Integrales múltiples. 4. Superficies parametrizadas.
 GRADO DE INGENIERÍA AEROESPACIAL CURSO 0 MATEMÁTICAS III DPTO DE MATEMÁTICA APLICADA II Lección 4 Integrales múltiples 4 Superficies parametrizadas Representación paramétrica de una superficie La primera
GRADO DE INGENIERÍA AEROESPACIAL CURSO 0 MATEMÁTICAS III DPTO DE MATEMÁTICA APLICADA II Lección 4 Integrales múltiples 4 Superficies parametrizadas Representación paramétrica de una superficie La primera
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
CAPÍTULO 4: DERIVADAS DE ORDEN SUPERIOR. En este capítulo D denota un subconjunto abierto de R n.
 April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
1. Hallar la ecuación del plano que pasa por el punto (3, 1, 2) y satisface la condición dada. a) paralelo al plano xy b) perpendicular al eje y
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 5 1. Hallar la ecuación del plano que
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 5 1. Hallar la ecuación del plano que
Clase 10: Extremos condicionados y multiplicadores de Lagrange
 Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Unidad V. 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales.
 Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
RESUMEN TEORIA MATEMATICAS 5
 RESUMEN TEORIA MATEMATICAS 5 LIMITES Definición. Sea :, lim,,, Significa que cuando, esta cerca de, entonces, esta cerca de L. De otra forma se dice que, pertenece a una bola centrada en, por otro lado,
RESUMEN TEORIA MATEMATICAS 5 LIMITES Definición. Sea :, lim,,, Significa que cuando, esta cerca de, entonces, esta cerca de L. De otra forma se dice que, pertenece a una bola centrada en, por otro lado,
Grado en Ingeniería de Tecnologías de Telecomunicación. Universidad de Sevilla. Matemáticas I. Departamento de Matemática Aplicada II.
 Grado en Ingeniería de Tecnologías de Telecomunicación Universidad de Sevilla Matemáticas I. Departamento de Matemática Aplicada II. Tema 1. Curvas Paramétricas. Nota Informativa: Para explicar en clase
Grado en Ingeniería de Tecnologías de Telecomunicación Universidad de Sevilla Matemáticas I. Departamento de Matemática Aplicada II. Tema 1. Curvas Paramétricas. Nota Informativa: Para explicar en clase
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
CONCEPTOS PRELIMINARES
 CONCEPTOS PRELIMINARES Matemáticas II En R un conjunto abierto es la unión de intervalos abiertos. Tanto el concepto de conjunto abierto como de intervalo abierto se generaliza en el plano y en el espacio.
CONCEPTOS PRELIMINARES Matemáticas II En R un conjunto abierto es la unión de intervalos abiertos. Tanto el concepto de conjunto abierto como de intervalo abierto se generaliza en el plano y en el espacio.
Funciones de Clase C 1
 Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
Recordemos que utilizaremos, como es habitual, la siguiente notación para algunos conjuntos de números que son básicos.
 Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 1 1. DIFERENCIABILIDAD EN VARIAS VARIABLES 1.1. DERIVADAS DIRECCIONALES Y PARCIALES Definición 1.1. Sea f : R n R, ā R n y v R n. Se define la derivada direccional de f en ā y en la dirección de v como:
1 1. DIFERENCIABILIDAD EN VARIAS VARIABLES 1.1. DERIVADAS DIRECCIONALES Y PARCIALES Definición 1.1. Sea f : R n R, ā R n y v R n. Se define la derivada direccional de f en ā y en la dirección de v como:
Funciones Inversas. Derivada de funciones inversas
 Capítulo 15 Funciones Inversas En este capítulo estudiaremos condiciones para la derivación de la inversa de una función de varias variables y, en particular, extenderemos a estas funciones la fórmula
Capítulo 15 Funciones Inversas En este capítulo estudiaremos condiciones para la derivación de la inversa de una función de varias variables y, en particular, extenderemos a estas funciones la fórmula
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
5 Continuidad y derivabilidad de funciones reales de varias variables reales.
 5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
Derivación. Aproximaciones por polinomios.
 Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Derivada de una función en un punto. Función derivada. Diferencial de una función en un punto. dy = f (x) dx. Derivada de la función inversa
 Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Prof. Enrique Mateus Nieves. Doctorando en Educación Matemática. Cálculo multivariado REPASO DE SECCIONES CONICAS
 REPASO DE SECCIONES CONICAS SUPERFICIES CUADRICAS Y SUS TRAZAS Elipsoide x z Ecuación canónica: 1 a b c Secciones paralelas al plano x: Elipses; Secciones paralelas al plano xz: Elipses; Secciones paralelas
REPASO DE SECCIONES CONICAS SUPERFICIES CUADRICAS Y SUS TRAZAS Elipsoide x z Ecuación canónica: 1 a b c Secciones paralelas al plano x: Elipses; Secciones paralelas al plano xz: Elipses; Secciones paralelas
1.1 El caso particular de las curvas planas.
 Chapter 1 Complementos de teoría de curvas 1.1 El caso particular de las curvas planas. Una curva en el espacio cuya torsión se anula está contenida en algún plano. Supongamos que ese plano es el z = 0,
Chapter 1 Complementos de teoría de curvas 1.1 El caso particular de las curvas planas. Una curva en el espacio cuya torsión se anula está contenida en algún plano. Supongamos que ese plano es el z = 0,
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
1. Lección 9 - Continuidad y Derivabilidad
 1. Lección 9 - Continuidad y Derivabilidad 1.1. Continuidad El concepto de continuación es el mismo que el visto en el primer cuatrimestre pero generalizado al caso de los campos escalares. Así, sea la
1. Lección 9 - Continuidad y Derivabilidad 1.1. Continuidad El concepto de continuación es el mismo que el visto en el primer cuatrimestre pero generalizado al caso de los campos escalares. Así, sea la
Reconocer y utilizar las propiedades sencillas de la topología métrica.
 3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
Espacios Vectoriales
 Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
Tema 2: Teorema de estructura de los grupos abelianos finitamente generados.
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Continuidad. 5.1 Continuidad en un punto
 Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
DERIVADAS PARCIALES Y APLICACIONES
 CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
Base y Dimensión de un Espacio Vectorial
 Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Función diferenciable Regla de la cadena (2 variables) Regla de la cadena (vectorial) Diferenciabilidad
 Diferenciabilidad 1 Función diferenciable 2 Regla de la cadena (2 variables) 3 Regla de la cadena (vectorial) OBJETIVO Generalizar el concepto de diferenciabilidad (conocido ya para funciones de una variable)
Diferenciabilidad 1 Función diferenciable 2 Regla de la cadena (2 variables) 3 Regla de la cadena (vectorial) OBJETIVO Generalizar el concepto de diferenciabilidad (conocido ya para funciones de una variable)
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Diferenciales de Orden Superior
 Capítulo 10 Diferenciales de Orden Superior En este capítulo extenderemos a las funciones definidas sobre espacios normados el concepto de función r-veces diferenciable y de clase C r y obtendremos las
Capítulo 10 Diferenciales de Orden Superior En este capítulo extenderemos a las funciones definidas sobre espacios normados el concepto de función r-veces diferenciable y de clase C r y obtendremos las
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2.3
 ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
Lección 4. Ecuaciones diferenciales. 1. Ecuaciones diferenciales de primer orden. Trayectorias ortogonales.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0.. Ecuaciones diferenciales de primer orden. Traectorias ortogonales. Muchas aplicaciones problemas de la ciencia, la ingeniería la economía se formulan en términos
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0.. Ecuaciones diferenciales de primer orden. Traectorias ortogonales. Muchas aplicaciones problemas de la ciencia, la ingeniería la economía se formulan en términos
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Función de dos variables
 Funciones de dos y más variables, dominio y rango, y curva de nivel Marlon Fajardo Molinares - fenix.75@hotmail.com 1. Función de dos variables 2. Funciones de varias variables 3. Método para hallar el
Funciones de dos y más variables, dominio y rango, y curva de nivel Marlon Fajardo Molinares - fenix.75@hotmail.com 1. Función de dos variables 2. Funciones de varias variables 3. Método para hallar el
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES
 SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE
 Análisis de funciones de una variable 49 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable: En la parte final hay ejercicios
Análisis de funciones de una variable 49 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable: En la parte final hay ejercicios
1 Super cies regladas
 1 Super cies regladas 1.1 De nición y ejemplos Vamos a estudiar una clase importante de super cies que son aquellas generadoas por una recta que se mueve a lo largo de una curva. Por tanto, son aquellas
1 Super cies regladas 1.1 De nición y ejemplos Vamos a estudiar una clase importante de super cies que son aquellas generadoas por una recta que se mueve a lo largo de una curva. Por tanto, son aquellas
Tema 7: Geometría Analítica. Rectas.
 Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Tema 7: Geometría Analítica. Rectas. En este tema nos centraremos en estudiar la geometría en el plano, así como los elementos que en este aparecen como son los puntos, segmentos, vectores y rectas. Estudiaremos
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
Funciones reales. Números complejos
 Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
DERIVADAS. Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto.
 DERIVADAS Tema: La derivada como pendiente de una curva Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto. La pendiente de la curva en el punto
DERIVADAS Tema: La derivada como pendiente de una curva Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto. La pendiente de la curva en el punto
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 5 - Verano 2009
 ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
Matemáticas I Grado de Administración y Dirección de Empresas Examen de Febrero Curso 2011/ ?
 Matemáticas I Grado de Administración y Dirección de Empresas Examen de Febrero Curso 011/1 1) (1 punto) Dado el subespacio vectorial,,,,,,,,,,, a) Obtener la dimensión, unas ecuaciones implícitas, unas
Matemáticas I Grado de Administración y Dirección de Empresas Examen de Febrero Curso 011/1 1) (1 punto) Dado el subespacio vectorial,,,,,,,,,,, a) Obtener la dimensión, unas ecuaciones implícitas, unas
NÚMEROS COMPLEJOS: C
 NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
Tema 2 Resolución de EcuacionesNo Lineales
 Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
Integral de superficie.
 Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una
Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Septiembre 011 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger
Selectividad Septiembre 011 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger
ELEMENTOS DE GEOMETRÍA. Eduardo P. Serrano
 ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R
 ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21
 Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
Universidad Nacional de Colombia Departamento de Matemáticas Álgebra Lineal - Grupo 1 Resumen Unidad n 3
 Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
SUPERFICIES CUÁDRICAS
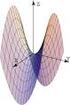 SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
SUPERFICIES CUÁDRICAS Un cuarto tipo de superficie en el espacio tridimensional son las cuádricas. Una superficie cuádrica en el espacio es una ecuación de segundo grado de la forma Ax + By + Cz + Dx +
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Superficies paramétricas
 SESIÓN 7 7.1 Introducción En este curso ya se han estudiando superficies S que corresponden a gráficos de funciones de dos variables con dos tipos de representaciones: Representación explícita de S, cuando
SESIÓN 7 7.1 Introducción En este curso ya se han estudiando superficies S que corresponden a gráficos de funciones de dos variables con dos tipos de representaciones: Representación explícita de S, cuando
Matemáticas. Si un error simple ha llevado a un problema más sencillo se disminuirá la puntuación.
 UNIVERSIDAD POLITÉCNICA DE CARTAGENA PRUEBAS DE ACCESO A LA UNIVERSIDAD DE LOS MAYORES DE 25 AÑOS CONVOCATORIA 2014 CRITERIOS DE EVALUACIÓN Matemáticas GENERALES: El examen constará de dos opciones (dos
UNIVERSIDAD POLITÉCNICA DE CARTAGENA PRUEBAS DE ACCESO A LA UNIVERSIDAD DE LOS MAYORES DE 25 AÑOS CONVOCATORIA 2014 CRITERIOS DE EVALUACIÓN Matemáticas GENERALES: El examen constará de dos opciones (dos
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
Problemas de VC para EDVC elaborados por C. Mora, Tema 4
 Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
DPTO. DE AMTEMÁTICAS I.E.S. GALLICUM CURSO 2012/13
 DESARROLLO DE LAS UNIDADES DIDÁCTICAS MATEMÁTICAS II Según REAL DECRETO 1467/2007, de 2 de noviembre, por el que se establece la estructura del bachillerato y se fijan sus enseñanzas mínimas, estas son
DESARROLLO DE LAS UNIDADES DIDÁCTICAS MATEMÁTICAS II Según REAL DECRETO 1467/2007, de 2 de noviembre, por el que se establece la estructura del bachillerato y se fijan sus enseñanzas mínimas, estas son
En este curso nos centraremos en un nuevo concepto de curva la cual estará descrita por una o mas ecuaciones denominadas ecuaciones paramétricas.
 Unidad I - Curvas en R ecuaciones paramétricas.. Ecuaciones paramétricas En cursos anteriores se ha considerado a una curva como una sucesión de pares ordenados ubicados en un plano rectangular provenientes
Unidad I - Curvas en R ecuaciones paramétricas.. Ecuaciones paramétricas En cursos anteriores se ha considerado a una curva como una sucesión de pares ordenados ubicados en un plano rectangular provenientes
Complementos de Análisis. Año 2016
 Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
Proyectos de trabajos para Matemáticas
 Proyectos de trabajos para Matemáticas 14 de julio de 2011 Resumen En cada uno de los Proyectos elegidos, los estudiantes deberán completar las etapas siguientes: Comprender el problema. Tomarse el tiempo
Proyectos de trabajos para Matemáticas 14 de julio de 2011 Resumen En cada uno de los Proyectos elegidos, los estudiantes deberán completar las etapas siguientes: Comprender el problema. Tomarse el tiempo
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS
 1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Ejercicios del Tema 2: Estructuras algebraicas básicas
 Ejercicios del Tema 2: Estructuras algebraicas básicas En los ejercicios 1, 2, 8 y 9 se utilizará que si G = {g 1,...,g n } es un conjunto finito y * una operación interna definida en G, podemos utilizar
Ejercicios del Tema 2: Estructuras algebraicas básicas En los ejercicios 1, 2, 8 y 9 se utilizará que si G = {g 1,...,g n } es un conjunto finito y * una operación interna definida en G, podemos utilizar
