Geometría 3-D. Sólidos 3-Dimensional. Slide 1 / 139. Slide 2 / 139. Slide 3 / 139. Tabla de Contenidos. Sólidos 3-Dimensional Redes
|
|
|
- Purificación Valdéz Cortés
- hace 6 años
- Vistas:
Transcripción
1 Slide 1 / 139 Geometría 3-D Tabla de Contenidos Sólidos 3-Dimensional Redes Volumen Prismas y Cilindros Pirámides, Conos y Esferas Área de la Superficie Prismas Pirámides Cilindros Esferas Más Práctica/Revisión Haga clic en el tema para ir a esa sección Slide 2 / 139 Slide 3 / 139 Sólidos 3-Dimensional Volver a la Tabla de Contenido
2 Slide 4 / 139 El siguiente enlace te llevará a un sitio con figuras y redes interactivas en 3-D. Poliedro Una figura 3-D cuyos rostros son todos polígonos Clasifica las figuras en el lado adecuado. Slide 5 / 139 Poliedro No Poliedro Sólidos 3-Dimensional Slide 6 / 139 Características y categorías de sólidos en 3-D: Prismas 1. Tiene dos bases que son polígonos congruentes y paralelas entre sí 2. Lados son rectangulares haga (paralelogramos) clic en revelar 3. Nombrado por la forma de su base Pirámides 1. Tienen una base de polígono con un vértice opuesto a este haga clic en para revelar 2. Caras son triangulares 3. Nombrado por la forma de su base
3 Sólidos 3-Dimensional Slide 7 / 139 Características y categorías de sólidos en 3-D: Cilindros 1. Tiene dos bases circulares congruentes, que son paralelas entre haga sí clic en para revelar 2. Lados son curvos Conos 1. Tiene una base circular con un vértice opuesto a este haga clic en para revelar 2. Lados son curvos Sólidos 3-Dimensional Slide 8 / 139 Palabras de Vocabulario de sólidos en 3-D: Poliedro Cara Arista Vértice (Vértices) Una figura 3-D cuyos rostros son todos polígonos (Prismas y Pirámides) Superficie plana de un Poliedro Segmento de línea formado donde dos caras se encuentran Punto en el que tres o más caras/aristas se encuentran Ordena los datos. Si fallas, la cifra será enviada de vuelta. Slide 9 / 139
4 1 Nombra la figura. Slide 10 / 139 A B C D E F Prisma Rectangular Pirámide Triangular Prisma Hexagonal Pirámide Rectangular Cilindro Cono 2 Nombra la figura Slide 11 / 139 A B C D E F Pirámide Rectangular Prisma Triangular Prisma Octogonal Pirámide Circular Cilindro Cono 3 Nombra la figura Slide 12 / 139 A B C D E F Pirámide Rectangular Pirámide Triangular Prisma Triangular Pirámide Hexagonal Cilindro Cono
5 4 Nombra la figura Slide 13 / 139 A B C D E F Prisma Rectangular Prisma Triangular Prisma Cuadrado Pirámide Rectangular Cilindro Cono 5 Nombra la figura Slide 14 / 139 A B C D E F Prisma Rectangular Pirámide Triangular Prisma Circular Pirámide Circular Cilindro Cono Para cada figura, encuentra el número de caras, vértices y aristas. Se puede encontrar una relación entre el número de caras, vértices y aristas en las figuras de 3 dimensiones? Slide 15 / 139 Nombre Caras Vértices Aristas Cubo Prisma Rectangular Prisma Triangular Pirámide Triangular Pirámide Cuadrada Pirámide Pentagonal Prisma Octagonal
6 La Fórmula de Euler Slide 16 / 139 F + V - 2 = E El número haga de aristas clic en es para 2 menos revelar que la suma de las caras y los vértices. 6 Cuántas caras tiene un prisma pentagonal? Slide 17 / Cuántas aristas tiene una pirámide rectangular? Slide 18 / 139
7 8 Cuántos vértices tiene un prisma triangular? Slide 19 / 139 Slide 20 / 139 Redes Volver a la Tabla de Contenido Redes Las redes son dibujos de dos dimensiones que representan la superficie de figuras tridimensionales. Slide 21 / 139 Hay más de una forma de dibujar una red para un cubo, sin embargo no todas las redes se pueden plegar en un cubo...
8 Redes - Patrones Planos Actividad 1 Slide 22 / 139 Corta arreglos de 6 cuadrados en papel cuadriculado. Cuántos arreglos diferentes se pueden plegar en un cubo? Sugerencia: Acabas de ver un arreglo que funciona y uno que no lo hace. vea la página siguiente para obtener respuestas... Slide 23 / 139 haga clic para mostrar los patrones del cubo plano Redes - Patrones Planos Actividad 2 Slide 24 / 139 Corta un arreglo de papel cuadriculado para crear un prisma rectangular que no es un cubo. Ahora haz otro patrón plano del mismo prisma rectangular. Trata cada patrón al plegarlo en una caja. Cuáles son las dimensiones de cada cara de tu prisma rectangular?
9 Las redes de prismas tendrán caras rectangulares y dos bases por las cuales se nombra la figura. Slide 25 / 139 Observa que los dos triángulos son opuestos el uno del otro (Bases). Slide 26 / Nombra este poliedro. Slide 27 / 139 A B C D Prisma Hexagonal Pirámide Pentagonal Prisma Pentagonal Prisma Rectangular
10 10 Nombra el poliedro. Slide 28 / 139 A B C D Prisma Hexagonal Pirámide Hexagonal Prisma Triangular Pirámide Triangular 11 Nombra la figura. Slide 29 / 139 A B C D Prisma Triangular Pirámide Triangular Prisma Rectangular Pirámide Rectanglular 12 Nombra la figura. Slide 30 / 139 A B C D Cono Circular Cono Rectangular Cilindro Pirámide Circular
11 13 Nombra la figura. Slide 31 / 139 A B C D Prisma Triangular Pirámide Triangular Prisma Pentagonal Prisma Cuadrado Slide 32 / 139 Volumen Volver a la Tabla de Contenido Volumen Slide 33 / 139 Volumen - La cantidad de espacio ocupado por una figura 3-D - El número de unidades cúbicas haga clic necesarias en para revelar para LLENAR una figura 3-D (capas) Etiqueta Unidades 3 o unidades haga clic cúbicas en para revelar
12 Actividad de Volumen Slide 34 / 139 Toma cubos de unidad y crea un prisma rectangular con dimensiones de 4 x 2 x 1. Qué sucede con el volumen si se agrega otra capa y se hace 4 x 2 x 2? Qué sucede con el volumen si se agrega otra capa y se hace 4 x 2 x 3? Nota para el profesor Slide 35 / 139 Volumen de Prismas y Cilindros Volver a la Tabla de Contenido Volumen Slide 36 / 139 Volumen de Prismas y Cilindros: Área de haga la Base clic para x Altura revelar Fórmulas del Área: Rectángulo = lw o bh Triángulo = Bh o 2 Círculo = r 2 haga clic para revelar haga clic para revelar (Bh) haga clic para revelar
13 Encuentra el volumen. Respuesta Slide 37 / m 2 m 5 m Respuesta Encuentra el volumen. 9 m Respuesta Slide 38 / m Respuesta 14 Encuentra el volumen. Respuesta Slide 39 / plg plg 1 1 plg 2 Respuesta
14 15 Encuentra el volumen de un prisma rectangular con una longitud de 2 cm, un ancho de 3,3 cm y 5,1 cm de altura. Slide 40 / 139 Respuesta 16 Cuál es una longitud, anchura y altura posible para un prisma rectangular cuyo volumen es = 18 cm 3? Slide 41 / 139 A 1 x 2 x 18 B 6 x 3 x 3 C 2 x 3 x 3 D 3 x 3 x 3 17 Encuentra el volumen. 47 pies 50 pies Respuesta Slide 42 / pies 21 pies
15 18 Un refrigerador en forma de caja mide 12 por 10 por 7 sobre el exterior. Los seis lados del refrigerador son 1 unidad de espesor. Cuál es el volumen interior del refrigerador en unidades cúbicas? Slide 43 / 139 SUGERENCIA: Es posible que desees hacer un dibujo Respuesta 19 Encuentra el volumen. Slide 44 / m 6 m Respuesta 20 Cuál vidrio circular tiene más agua? Slide 45 / 139 A B Vidrio A con un diámetro de 7,5 cm y una altura de 12 cm Vidrio B con un radio de 4 cm y una altura de 11,5 cm Respuesta
16 21 Cuál es el volumen del cilindro más grande que se puede colocar en un cubo que mide 10 pies en una arista? Slide 46 / 139 Respuesta 22 Un jardín circular tiene un diámetro de 20 pies y está rodeado por un borde de concreto que tiene una anchura de tres pies y una profundidad de 6 pulgadas. Cuál es el volumen de concreto en el camino? Usa 3,14 para π Slide 47 / 139 Respuesta Slide 48 / 139 Volumen de Pirámides, Conos y Esferas Volver a la Tabla de Contenido
17 Slide 49 / 139 Slide 50 / 139 Demostración comparando el volumen de Conos y Esferas con el volumen de Cilindros click para ir al sitio web Volumen de un Cono Slide 51 / 139 Un cono es 1/3 del volumen de un cilindro con el mismo área de base (B) Y altura (h). (Área de base x altura) 3 haga clic en para revelar 1 (Área de base x altura) 3
18 Volumen de una Esfera Slide 52 / 139 Una esfera es 2/3 del volumen de un cilindro con el mismo área de base (B) Y altura (h). V = 2/3 (Volumen del Cilindro) haga clic 2/3 en ( para V= r 2 revelar h ) o V = 4/3 r 3 Cuánto helado puede aguantar un de cono de galleta Friendly si tiene un diámetro de 6 plg y su altura es de 10 plg? Slide 53 / 139 (Sólo helado dentro del Cono. No por encima) Volumen y masa utilizada para controlar las porciones. $$$ 23 Encuentra el volumen. Slide 54 / 139 Respuesta 9 plg 4 plg
19 24 Encuentra el volumen Slide 55 / cm 5 cm Respuesta Slide 56 / 139 Si el radio de una esfera es de 5,5 cm, cuál es su volumen? V = 4/3 π r 3 V = 4/3(3,14)(5,5) 3 V = 696,6 cm 3 25 Cuál es el volumen de una esfera con un radio de 8 pies? Slide 57 / 139 Respuesta
20 26 Cuál es el volumen de una esfera con un diámetro de 4,25 plg? Slide 58 / 139 Respuesta Volumen de una Pirámide Slide 59 / 139 Una pirámide es 1/3 del volumen de un prisma con el mismo área de base (B) y altura (h). (Área de base x altura) 3 haga 1 clic en para revelar (Área de base x altura) 3 Slide 60 / 139 Las pirámides son nombradas por la forma de su base.. El volumen de una pirámide es 1/3 del volumen de un prisma con el mismo área de base (B) y altura (h). 1 V = Bh 3 1 V = Bh 3 =5 m longitud del lado = 4 m
21 27 Encuentra el volumen de una pirámide triangular con aristas de la base de 8 plg, altura de la base de 4 y una altura de pirámide de 10 plg. Slide 61 / plg Respuesta 4 plg 8 plg 28 Encuentra el volumen. Slide 62 / ,3 cm Respuesta 7 cm 8 cm Slide 63 / 139 Área de la Superficie Volver a la Tabla de Contenido
22 Slide 64 / 139 Área de la Superficie de Prismas Volver a la Tabla de Contenido Área de la Superficie Slide 65 / 139 La suma de las áreas de todas superficies exteriores de una figura 3-D. Para encontrar la superficie, debes encontrar el área de cada superficie de la figura y luego añadirlos juntos. Qué tipo de figura se representa? Cuántas superficies hay? Cómo se encuentra el área de cada superficie? 8 plg 6 plg 3 plg Área de la Superficie Slide 66 / plg 8 plg 3 plg Abajo Arriba Izquierda Derecha Frente Atrás Suma x 8 x 3 x plg 18 6 plg plg plg 3 plg 3 plg plg 2 8 plg 8 plg 8 plg
23 Disposición de los cubos de unidad Slide 67 / 139 Busque todas las maneras posibles en las cuales 24 cubos de unidad se pueden arreglar en un prisma rectangular. Dé a cada arreglo dimensiones y la superficie. También haga un dibujo. Longitud Ancho Altura Volumen Área de Superficie Dibujo Slide 68 / 139 Cuál disposición de 24 cubos tiene la menor superficie? Cuál tiene la mayor? acuerdos Disposición de los cubos de unidad Slide 69 / 139 Busque todas las maneras posibles en las cuales 64 cubos de unidad se pueden arreglar en un prisma rectangular. Dé a cada arreglo dimensiones y la superficie. También haga un dibujo. Longitud Ancho Altura Volumen Área de Superficie Dibujo
24 Slide 70 / 139 Cuál disposición de 64 cubos tiene la menor superficie? Cuál tiene la mayor? de 7 acuerdos 29 Cuál disposición de 27 cubos tiene la menor superficie? Slide 71 / 139 A 1 x 1 x 27 B 3 x 3 x 3 C 9 x 3 x 1 30 Cuál disposición de 12 cubos tiene la menor superficie? Slide 72 / 139 A 2 x 2 x 3 B 4 x 3 x 1 C 2 x 6 x 1 D 1 x 1 x 12
25 31 Cuál disposición de 25 cubos tiene la mayor superficie? Slide 73 / 139 A 1 x 1 x 25 B 1 x 5 x 5 32 Cuál disposición de 48 cubos tiene la menor superficie? Slide 74 / 139 A 4 x 12 x 1 B 2 x 2 x 12 C 1 x 1 x 48 D 3 x 8 x 2 E 1 x 2 x 24 F 4 x 3 x 4 G 1 x 8 x 6 H 4 x 2 x 6 I 3 x 16 x 1 Encuentra la superficie de una caja rectangular de zapatos que tiene una longitud de 12 pulgadas, un ancho de 6 pulgadas y una altura de 5 pulgadas. Slide 75 / plg 12 plg 6 plg Arriba/Abajo Frente/Atrás Izquierda / Derecha Área de la superficie x 6 x 5 x x 2 x 2 x plg haga clic en para revelar haga clic en para revelar haga clic en para revelar haga clic en para re
26 Nombra la figura. Encuentra la superficie de la figura. Slide 76 / m 3 m 5 m 33 Cuántas caras tiene la figura? Slide 77 / m 2 m 4 m 34 Cuántos problemas de área debes completar al encontrar la superficie? Slide 78 / m 2 m 4 m
27 35 Cuál es el área de la cara de arriba o abajo? Slide 79 / m 2 m 4 m 36 Cuál es el área de la cara izquierda o la derecha? Slide 80 / m 2 m 4 m 37 Cuál es el área de la cara de frente o atrás? Slide 81 / m 2 m 4 m
28 38 Cuál es la superficie de la figura? Slide 82 / m 2 m 4 m Encuentra el área de la superficie. Slide 83 / Dibuja y etiqueta todas las caras 2. Encuentra las dimensiones correctas para cada cara 3. Calcula el área de cada cara 4. Encuentra la suma de todas las caras 5. Etiqueta tu respuesta 5 yd ir a ver los pasos 9 yd 5 yd 4 yd 6 yd Slide 84 / yd 5 yd 5 yd 6 yd 4 yd 9 yd 5 yd 6 yd Triángulos Rectángulo Inferior 4 9 Haga x 6 clic en la x 6 caja 24 / 2 de = 12 Haga clic en 54 la revelar los x 2 caja de pasos. 24 revelar los pasos. 5 yd 6 yd 4 yd 4 yd Rectángulos de Izquierda/Derecha Área de 5 yd (Del mismo tamaño desde isósceles) Superficie 5 Haga clic en la Total Haga clic en x la 9 caja de caja de 9 yd 24 revelar los pasos. revelar los pasos. x m 2 9 yd
29 Encuentra el área de la superficie. Slide 85 / Dibuja y etiqueta todas las caras 2. Encuentra las dimensiones correctas para cada cara 3. Calcula el área de cada cara 4. Encuentra la suma de todas las caras 5. Etiqueta tu respuesta 9 cm ir a ver los pasos 9 cm 6 cm 11 cm 9 cm 9 cm 9 cm Slide 86 / cm 9 cm 6 cm 11 cm 9 cm Triángulos Rectángulos 9 (Los tres son del mismo tamaño ya que son equiláteros) X6 Haga clic en la caja de 54 / 2 = 27 9 x 2 revelar los x pasos Área de la x 3 superficie 297 Haga clic 297en la + caja 54 de revelar 351 los cmpasos. 2 9 cm 6 cm 11 cm 39 Encuentra el área de la superficie de la forma siguiente. Slide 87 / Dibuja y etiqueta todas las caras 2. Encuentra las dimensiones correctas para cada cara 3. Calcula el área de cada cara 4. Encuentra la suma de todas las caras 5. Etiqueta tu respuesta 47 pies 21 pies 50 pies 42 pies
30 Encuentra el área de la superficie. 7 cm 3 cm Slide 88 / cm 5 cm 15 cm 6 cm 7 cm 3 cm Slide 89 / cm 5 cm 15 cm Trapezoides x 4 64 / 2 = 32 x 2 64 haga clic en para revelar 6 cm Rectángulo Inferior 6 x haga clic en para revelar Área de la superficie cm 2 Rectángulo Superior 10 x haga clic en para revelar Rectángulos de lado 5 x x haga clic en para revelar haga clic en para revelar 40 Encuentra el área de la superficie de la siguiente figura. Slide 90 / cm 6 cm 9 cm 10 cm
31 41 Encuentra el área de la superficie de la siguiente figura Slide 91 / cm 2 cm 6 cm 6 cm 10 cm Slide 92 / 139 Área de la Superficie de las Pirámides Volver a la Tabla de Contenido Área de la superficie de las pirámides Slide 93 / 139 Qué es una pirámide? Poliedro con una base y caras triangulares que se encuentran en un vértice haga clic en para revelar Cómo se encuentra la superficie? Suma de las áreas de todas las superficies de la figura 3-D haga clic en para revelar
32 Encuentra el área de la superficie. Slide 94 / ,5 cm ir a ver los pasos 8 cm 8 cm Encuentra el área de la superficie. Slide 95 / ,5 cm 17,5 cm 17,5 cm 8 cm 8 cm 8 cm 8 cm Rectángulo de Abajo 8 x cm Triángulos Adelante/Atrás A = 1/2bh 2 A = 1/2(8)(17,5) 2 A = cm Triángulos Izquierda/Derecha A = 1/2bh 2 A = 1/2(8)(17,5) 2 A = 140 Área de la superficie cm 2 Encuentra el área de la superficie de una pirámide cuadrada con una arista de la base de 4 pulgadas y la altura del triángulo de 3 pulgadas. Slide 96 / plg Base 4 x 4 16 haga clic en para revelar Triángulos haga clic en para revelar Área de la superficie plg 2 haga clic en para revelar 4 plg
33 Encuentra el área de la superficie. Slide 97 / 139 Asegúrate de mirar a la base para ver si es un triángulo equilátero o triángulo isósceles (haciendo todos o dos de los triángulos laterales equivalente!). Base Triángulos (Todos iguales) A = 1/2bh A = 1/2(4)(3,5) A = 7 4 plg 3,5 plg 4 plg 6 plg 4 plg haga clic en para revelar haga clic en para revelar Área de la superficie plg 2 42 Cuál tiene un mayor área de superficie, una pirámide de base cuadrada con una arista de base de 8 plg y una altura de 4 plg o un cubo con una arista de 5 plg? Slide 98 / 139 A B Pirámide Cuadrada Cubo 43 Encuentra el área de superficie de una pirámide triangular, con aristas de la base de 8 plg, altura de la base de 4 plg y una altura inclinada de 10 plg. Slide 99 / plg 8 plg 6,9 plg 8 plg 8 plg
34 44 Encuentra el área de la superficie. Slide 100 / m 12 m 9 m 6,7 m 9 m Slide 101 / 139 Área de la Superficie de Cilindros Volver a la Tabla de Contenido Cómo se encuentra la superficie de un cilindro? Slide 102 / 139
35 Ten en cuenta la longitud del rectángulo es en realidad la circunferencia de la base circular. Slide 103 / 139 Pasos 1. Encuentra el área de las 2 bases circulares. 2. Encuentra el área de la superficie curva (en realidad, un rectángulo). 3. Añade las dos áreas. 4. Etiqueta tu respuesta. Slide 104 / 139 Radio Radio Lado curvo = circunferencia de la base circular A L T U R A A L T U R A Radio Slide 105 / 139 Radio Lado curvo = circunferencia de la base circular A L T U R A A L T U R A Área de los círculos = 2 ( r 2 ) Área de la superficie curva = Circunferencia Altura d Altura 2 r 2 + dh -O- 2 r rh
36 Encuentra la superficie de un cilindro cuya altura es de 14 pulgadas y cuya base tiene un diámetro de 16 pulgadas. Slide 106 / plg Área de los círculos = 2 ( r 2 ) = 2 ( 8 2 ) = 2 (64 ) = 128 = 401,92 plg 2 14 plg Área de la Superficie Curva = Circunferencia Altura = d Altura = (16)(14) = 224 = 703,36 plg 2 Área de Superficie = 401, ,36 = 1105,28 plg 2 45 Encuentra la superficie de un cilindro cuya altura es 8 pulgadas y cuya base tiene un diámetro de 6 pulgadas. Slide 107 / Encuentra la superficie de un cilindro cuya altura es de 14 pulgadas y cuya base tiene un diámetro de 16 pulgadas. Slide 108 / 139 S
37 47 Cuánto material se necesita para hacer una lata de jugo de cilíndrica que es de 15 cm de alto y tiene un diámetro de 10 cm? Slide 109 / Encuentra la superficie de un cilindro con una altura de 14 pulgadas y un radio de la base de 8 pulgadas. Slide 110 / Un tanque de alimentación cilíndrico en una granja tiene que ser pintado. El tanque tiene un diámetro de 7,5 pies y una altura de 11 pies Un galón de pintura cubre 325 pies cuadrados. Tienes suficiente pintura? Explica. Slide 111 / 139 Sí NO
38 Slide 112 / 139 Área de la Superficie de Esferas Volver a la Tabla de Contenido Una esfera es el conjunto de todos los puntos que están a la misma distancia del punto central. Slide 113 / 139 Como un círculo, una esfera tiene un radio y un diámetro. Verás que como un círculo, la fórmula de la superficie de una esfera también incluye pi. Radio Área de la superficie de una esfera haga clic en para revelar Si el diámetro de la Tierra es de kilometros, cuál es su superficie? Slide 114 / ,742 km Superficie = 4 r 2 Superficie = 4 (12742/2) 2 Superficie = 4 (6371) 2 Superficie = km 2
39 Intenta esto: Slide 115 / 139 Encuentra la superficie de una pelota de tenis, cuyo diámetro es 2,7 pulgadas. Superficie = 4 r 2 2,7 plg Superficie = 4 (2,7/2) 2 Superficie = 4 (1,35) 2 Superficie = 22,8906 plg 2 haga clic en para revelar 50 Encuentra la superficie de una pelota de béisbol con un diámetro 3,8 pulgadas. Slide 116 / Cuánto cuero se necesita para hacer una pelota de baloncesto con un radio de 4,7 pulgadas? Slide 117 / 139
40 52 Cuánta goma se necesita para hacer 6 pelotas de raqueta con un diámetro de 5,7 pulgadas? Slide 118 / 139 Slide 119 / 139 Más Práctica/Revisión Volver a la Tabla de Contenido 53 Encuentra el volumen. Slide 120 / mm 8 mm 15 mm
41 54 Encuentra el volumen de una pirámide rectangular con una longitud de base de 2,7 metros y una anchura de base de 1,3 metros, y una altura de la pirámide de 2,4 metros. Slide 121 / 139 SUGERENCIA: Dibujar un diagrama te ayudará 55 Encuentra el volumen de una pirámide de base cuadrada con arista de la base de 4 pulgadas y altura de la pirámide de 3 pulgadas. Slide 122 / Encuentra el volumen Slide 123 / m 9 m 12 m 6 m 9 m
42 57 Encuentra el volumen Slide 124 / pies 14 pies 58 Encuentra el volumen Slide 125 / plg 6,9 plg 59 Encuentra el volumen Slide 126 / pies 4 pies 8 pies 7 pies
43 60 Un cono de 20 cm en diámetro y 14 cm de alto se utilizó para llenar una maceta cúbica, de 25 cm por arista, con tierra. Cuántos conos-enteros de tierra se necesitan para llenar la maceta? Slide 127 / cm 14 cm 25 cm 61 Encuentra el área de la superficie del cilindro. Slide 128 / 139 Radio = 6 cm y Altura = 7 cm 62 Encuentra el área de la superficie. Slide 129 / cm 11 cm 12 cm
44 63 Encuentra el área de la superficie. Slide 130 / plg 9 plg 2 plg 7 plg 8 plg 64 Encuentra el volumen. Slide 131 / plg 9 plg 2 plg 7 plg 8 plg 65 Una caja de almacenaje rectangular es de 12 plg de ancho, 15 plg de largo y 9 plg de alto. Cuántas pulgadas cuadradas de papel de color se necesitan para cubrir la superficie de la caja? Slide 132 / 139
45 66 Encuentra el área de la superficie de una pirámide de base cuadrada con una longitud de base de 4 pulgadas y altura inclinada de 5 pulgadas. Slide 133 / 139 Slide 134 / 139 Nombra una figura 3-D que no es un poliedro. Slide 135 / 139 Define los siguientes términos: Área de la Superficie Volumen
46 Slide 136 / 139 Nombra una figura 3-D que tiene 6 caras rectangulares. 67 Encuentra el volumen. Slide 137 / m 40 m 80 m 68 Un profesor hizo dos pares de dados de espuma para uso en juegos de matemáticas. Cada cubo mide 10 plg en cada lado. Cuántas pulgadas cuadradas de tela fueron necesarias para cubrir los dos cubos? Slide 138 / 139
47 Slide 139 / 139
Slide 1 / 139. Geometría 3-D
 Slide 1 / 139 Geometría 3-D Tabla de Contenidos Sólidos 3-Dimensional Redes Volumen Prismas y Cilindros Pirámides, Conos y Esferas Área de la Superficie Prismas Pirámides Cilindros Esferas Más Práctica/Revisión
Slide 1 / 139 Geometría 3-D Tabla de Contenidos Sólidos 3-Dimensional Redes Volumen Prismas y Cilindros Pirámides, Conos y Esferas Área de la Superficie Prismas Pirámides Cilindros Esferas Más Práctica/Revisión
Untitled.notebook February 01, Geometría 3 D
 Geometría 3 D Tabla de Contenidos Sólidos 3 Dimensional Redes Volumen Prismas y Cilindros Haga clic en el tema para ir a esa sección Pirámides, Conos y Esferas Área de la Superficie Prismas Pirámides Cilindros
Geometría 3 D Tabla de Contenidos Sólidos 3 Dimensional Redes Volumen Prismas y Cilindros Haga clic en el tema para ir a esa sección Pirámides, Conos y Esferas Área de la Superficie Prismas Pirámides Cilindros
Geometría 3D: Preguntas de Capítulo
 Geometría 3D: Preguntas de Capítulo 1. Cuáles son las similitudes y diferencias entre los prismas y las pirámides? 2. Cómo se nombran los poliedros? 3. Cómo se encuentra la sección transversal de figuras
Geometría 3D: Preguntas de Capítulo 1. Cuáles son las similitudes y diferencias entre los prismas y las pirámides? 2. Cómo se nombran los poliedros? 3. Cómo se encuentra la sección transversal de figuras
Geometría en 3D: Preguntas del Capítulo
 Geometría en 3D: Preguntas del Capítulo 1. Cuáles son las similitudes y las diferencias entre prismas y pirámides? 2. Cómo se nombran los poliedros? 3. Cómo encuentras la sección transversal de una figura
Geometría en 3D: Preguntas del Capítulo 1. Cuáles son las similitudes y las diferencias entre prismas y pirámides? 2. Cómo se nombran los poliedros? 3. Cómo encuentras la sección transversal de una figura
Geometría Tridimensional. Capítulo de Preguntas. 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos?
 Geometría Tridimensional. Capítulo de Preguntas 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Geometría Tridimensional. Capítulo de Preguntas 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Examen estandarizado A
 Examen estandarizado A Elección múltiple 1. Qué figura es un poliedro? A B 7. Halla el área de la superficie de la pirámide regular. A 300 pies 2 15 pulg B 340 pies 2 C D C 400 pies 2 D 700 pies 2 10 pulg
Examen estandarizado A Elección múltiple 1. Qué figura es un poliedro? A B 7. Halla el área de la superficie de la pirámide regular. A 300 pies 2 15 pulg B 340 pies 2 C D C 400 pies 2 D 700 pies 2 10 pulg
Listo para seguir? Intervención de destrezas Cómo estimar y hallar el área
 10-1 Listo para seguir? Intervención de destrezas Cómo estimar y hallar el área El área de una figura es la cantidad de superficie que cubre. El área se mide en unidades cuadradas. Estimar el área de una
10-1 Listo para seguir? Intervención de destrezas Cómo estimar y hallar el área El área de una figura es la cantidad de superficie que cubre. El área se mide en unidades cuadradas. Estimar el área de una
Geometría 2D Parte 2: Área
 Slide 1 / 81 Geometría 2D Parte 2: Área Tabla de Contenidos Slide 2 / 81 Rectángulos Paralelogramos Triángulos Trapezoides Círculos Revisión Mixta Figuras Irregulares Regiones Sombreadas Haga clic en un
Slide 1 / 81 Geometría 2D Parte 2: Área Tabla de Contenidos Slide 2 / 81 Rectángulos Paralelogramos Triángulos Trapezoides Círculos Revisión Mixta Figuras Irregulares Regiones Sombreadas Haga clic en un
FIGURAS DEL ESPACIO. ÁREAS Y VOLÚMENES
 POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
Geometría: Preguntas del capítulo. 1. Cómo es la fórmula para el área de un paralelogramo relacionada con el área de un rectángulo?
 Geometría: Preguntas del capítulo. Cómo es la fórmula para el área de un paralelogramo relacionada con el área de un rectángulo?. Cómo es la fórmula para el área de un triángulo relacionada con el área
Geometría: Preguntas del capítulo. Cómo es la fórmula para el área de un paralelogramo relacionada con el área de un rectángulo?. Cómo es la fórmula para el área de un triángulo relacionada con el área
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS REGULARES ESFERA
 ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
5to Grado - Geometría, Medidas, y Algebra Estándar Básico 3. Evaluación.
 5to Grado - Geometría, Medidas, y Algebra Estándar Básico 3. Evaluación. 5.3.1 Identificar y clasificar triángulos de acuerdo a sus ángulos (agudo, recto, obtuso) y lados (escaleno, isósceles, equilátero).
5to Grado - Geometría, Medidas, y Algebra Estándar Básico 3. Evaluación. 5.3.1 Identificar y clasificar triángulos de acuerdo a sus ángulos (agudo, recto, obtuso) y lados (escaleno, isósceles, equilátero).
SeCrece, Inc. Matemáticas. Unidad: Geometría. Grupo: Tornasol
 SeCrece, Inc. Matemáticas Unidad: Geometría Grupo: Tornasol I. Propiedades Geométricas a. Tipos de Polígonos Nombres de Polígonos Nombre Lados Ángulos Triángulo 3 3 Cuadrilátero 4 4 Pentágono 5 5 Hexágono
SeCrece, Inc. Matemáticas Unidad: Geometría Grupo: Tornasol I. Propiedades Geométricas a. Tipos de Polígonos Nombres de Polígonos Nombre Lados Ángulos Triángulo 3 3 Cuadrilátero 4 4 Pentágono 5 5 Hexágono
TEMA 7 Las formas y las medidas que nos rodean. 2. Repaso a las figuras planas elementales
 TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
Examen A del capítulo
 Eamen A del capítulo Usar después del capítulo Indica si el sólido es un poliedro. Si es así, halla el número de caras, vértices y aristas.. 2. 3.. Determina si el poliedro es regular y/o conveo. 2. 4.
Eamen A del capítulo Usar después del capítulo Indica si el sólido es un poliedro. Si es así, halla el número de caras, vértices y aristas.. 2. 3.. Determina si el poliedro es regular y/o conveo. 2. 4.
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Primero vamos a dar algunas definiciones: Poliedros:
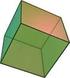 VOLUMEN Y si te dieran dos cubos similares y te preguntan cuál es el factor de escala de sus caras? Cómo encontrarías sus áreas de superficie y sus volúmenes? Después de completar éste concepto serás capaz
VOLUMEN Y si te dieran dos cubos similares y te preguntan cuál es el factor de escala de sus caras? Cómo encontrarías sus áreas de superficie y sus volúmenes? Después de completar éste concepto serás capaz
IES FONTEXERÍA MUROS. 14-II-2014 Nombre y apellidos:.
 IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
Fórmula de Superficie de Área: Si dos sólidos son similares con un factor de. escala de entonces las áreas de superficie están en una relación de.
 Materia: Matemática de Séptimo Tema: Cálculo de Volumen Y si te dieran dos cubos similares y te preguntan cuál es el factor de escala de sus caras? Cómo encontrarías sus áreas de superficie y sus volúmenes?
Materia: Matemática de Séptimo Tema: Cálculo de Volumen Y si te dieran dos cubos similares y te preguntan cuál es el factor de escala de sus caras? Cómo encontrarías sus áreas de superficie y sus volúmenes?
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
Calculando el volumen de un prisma recto triangular
 Bitácora del Estudiante Calculando el volumen de un prisma recto triangular Realiza las siguientes actividades, mientras trabajas con el tutorial. 1. Qué propiedad de una figura mides utilizando pies cúbicos
Bitácora del Estudiante Calculando el volumen de un prisma recto triangular Realiza las siguientes actividades, mientras trabajas con el tutorial. 1. Qué propiedad de una figura mides utilizando pies cúbicos
IDEAS PREVIAS. 1. Planos paralelos. 2.Planos perpendiculares
 IDEAS PREVIAS 1. Planos paralelos..planos perpendiculares .Planos oblicuos. CUERPO GEOMÉTRICO Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa
IDEAS PREVIAS 1. Planos paralelos..planos perpendiculares .Planos oblicuos. CUERPO GEOMÉTRICO Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa
Slide 1 / 174. Geometría 2D Parte 1: Relaciones Geométricas, Perímetro y Circunferencia
 Slide 1 / 174 Geometría 2D Parte 1: Relaciones Geométricas, Perímetro y Circunferencia Slide 2 / 174 Nueva Jersey, Centro de Enseñanza y Aprendizaj Matemáticas Iniciativa Progresista Este material está
Slide 1 / 174 Geometría 2D Parte 1: Relaciones Geométricas, Perímetro y Circunferencia Slide 2 / 174 Nueva Jersey, Centro de Enseñanza y Aprendizaj Matemáticas Iniciativa Progresista Este material está
Examen de Mitad de Periodo, MM-111
 Examen de Mitad de Periodo, MM-111 arlos ruz October 27, 2015 Nombre: Registro Estudiantil: Instrucciones: Resuelva cada ejercicios de forma clara honesta y ordenada mostrando todo su procedimiento de
Examen de Mitad de Periodo, MM-111 arlos ruz October 27, 2015 Nombre: Registro Estudiantil: Instrucciones: Resuelva cada ejercicios de forma clara honesta y ordenada mostrando todo su procedimiento de
CUERPOS GEOMÉTRICOS. Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas.
 CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CENTRO EDUCATIVO PAULO FREIRE TALLER
 CENTRO EDUCATIVO PAULO FREIRE TALLER 1: Una plaza circular está limitada por una circunferencia de longitud 188,4m. Determinar el diámetro y el área de la plaza. 2: Si el área de un círculo es 144 cm 2,
CENTRO EDUCATIVO PAULO FREIRE TALLER 1: Una plaza circular está limitada por una circunferencia de longitud 188,4m. Determinar el diámetro y el área de la plaza. 2: Si el área de un círculo es 144 cm 2,
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
14 CUERPOS GEOMÉTRICOS. VOLÚMENES
 EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
Geometría en 3D. Problemas del capítulo. 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos?
 Geometría en 3D. Problemas del capítulo 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Geometría en 3D. Problemas del capítulo 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones. 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides.
 Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES
 OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
POLIEDROS, PRISMAS Y PIRÁMIDES
 POLIEDROS, PRISMAS Y PIRÁMIDES 1. Completa la siguiente tabla. 2. Indica si son verdaderas o falsas (V o F) las siguientes afirmaciones. a) La suma de las caras y los vértices del cubo es 12. b) El menor
POLIEDROS, PRISMAS Y PIRÁMIDES 1. Completa la siguiente tabla. 2. Indica si son verdaderas o falsas (V o F) las siguientes afirmaciones. a) La suma de las caras y los vértices del cubo es 12. b) El menor
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA.
 GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA. Profesor: Alumno:. Curso: Sección: 1. LAS FIGURAS PLANAS 2. ÁREA DE LAS FIGURAS PLANAS 3. CUERPOS GEOMÉTRICOS . FIGURAS PLANAS 1. Los polígonos y suss elementos
GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA. Profesor: Alumno:. Curso: Sección: 1. LAS FIGURAS PLANAS 2. ÁREA DE LAS FIGURAS PLANAS 3. CUERPOS GEOMÉTRICOS . FIGURAS PLANAS 1. Los polígonos y suss elementos
Problemas geométricos
 Problemas geométricos Contenidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores y segmentos 2. Cuerpos geométricos Prismas Pirámides Troncos de
Problemas geométricos Contenidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores y segmentos 2. Cuerpos geométricos Prismas Pirámides Troncos de
Figura plana Área Ejemplo Cuadrado. Área =
 ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
OBJETIVO 1 CONOCER LOS POLIEDROS Y DIFERENCIAR LOS POLIEDROS REGULARES NOMBRE: CURSO: FECHA:
 OJETIVO 1 CONOCER LOS POLIEDROS Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro
OJETIVO 1 CONOCER LOS POLIEDROS Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Área de paralelogramos, triángulos y trapecios (páginas 314 318)
 NOMRE FECHA PERÍODO Área de paralelogramos, triángulos y trapecios (páginas 34 38) Cualquier lado de un paralelogramo o triángulo puede usarse como base. La altitud de un paralelogramo es un segmento de
NOMRE FECHA PERÍODO Área de paralelogramos, triángulos y trapecios (páginas 34 38) Cualquier lado de un paralelogramo o triángulo puede usarse como base. La altitud de un paralelogramo es un segmento de
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos
 Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS BÁSICOS. POLIEDROS REGULARES Y NO REGULARES
 ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS BÁSICOS. POLIEDROS REGULARES Y NO REGULARES 1º. Comprueba si se cumple o no la fórmula de Euler en este poliedro. 2º. Rellena la siguiente tabla: Poliedro Caras
ÁREAS Y VOLÚMENES DE CUERPOS GEOMÉTRICOS BÁSICOS. POLIEDROS REGULARES Y NO REGULARES 1º. Comprueba si se cumple o no la fórmula de Euler en este poliedro. 2º. Rellena la siguiente tabla: Poliedro Caras
Geometría en 2D: Preguntas del capítulo
 Geometría en 2D: Preguntas del capítulo 1. Cuáles son algunas de las relaciones especiales entre los ángulos? 2. Qué son perímetro y circunferencia y cómo son relevantes en la vida diaria? 3. Cómo se relaciona
Geometría en 2D: Preguntas del capítulo 1. Cuáles son algunas de las relaciones especiales entre los ángulos? 2. Qué son perímetro y circunferencia y cómo son relevantes en la vida diaria? 3. Cómo se relaciona
1. Laura y Rosa están mirando un tarro con forma de cilindro. Lo que ven está representado en la figura.
 Sector y Nivel: Matemática 4 Básico Eje: Geometría 1. Laura y Rosa están mirando un tarro con forma de cilindro. Lo que ven está representado en la figura. Desde dónde es posible que estén observando el
Sector y Nivel: Matemática 4 Básico Eje: Geometría 1. Laura y Rosa están mirando un tarro con forma de cilindro. Lo que ven está representado en la figura. Desde dónde es posible que estén observando el
Para más información vea el recuadro de Apuntes de Matemáticas de la Lección del texto Core Connections en español, Curso 3.
 CILINDROS VOLUMEN Y ÁREA SUPERFICIAL VOLUMEN DE UN CILINDRO El volumen de un cilindro es el área de su base multiplicado por su altura: V = B h Dado que la base de un cilindro es un círculo de área A =
CILINDROS VOLUMEN Y ÁREA SUPERFICIAL VOLUMEN DE UN CILINDRO El volumen de un cilindro es el área de su base multiplicado por su altura: V = B h Dado que la base de un cilindro es un círculo de área A =
UNIDAD 2: ELEMENTOS GEOMÉTRICOS
 UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
6to Grado Matemática. Slide 1 / 199. Slide 2 / 199. Slide 3 / 199. Geometría. Tabla de Contenidos
 Slide 1 / 199 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
Slide 1 / 199 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
1 Indica, en la ilustración, dos edificios que sean poliedros y tengan formas diferentes. PÁGINA 186
 PÁGINA 186 En la Casa de la Cultura se ha montado una exposición fotográfica. En ella se recogen modernos edificios en los que los poliedros y los cuerpos de revolución han sido elevados a la categoría
PÁGINA 186 En la Casa de la Cultura se ha montado una exposición fotográfica. En ella se recogen modernos edificios en los que los poliedros y los cuerpos de revolución han sido elevados a la categoría
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
FICHA TEMA 9: CUERPOS GEOMETRICOS NOMBRE Y APELLIDOS: Ejercicio nº 1.-Escribe el nombre de cada uno de los elementos de este poliedro:
 FICHA TEMA 9: CUERPOS GEOMETRICOS CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº 2.- Cuáles de las siguientes figuras
FICHA TEMA 9: CUERPOS GEOMETRICOS CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº 2.- Cuáles de las siguientes figuras
Geometría en el espacio
 Geometría en el espacio 3º E.S.O. PARTE TEÓRICA 1.- Define los siguientes conceptos: Poliedro: Vértice de un poliedro: Cara de un poliedro: Arista de un poliedro: Poliedro regular: 2.- Di cuáles son los
Geometría en el espacio 3º E.S.O. PARTE TEÓRICA 1.- Define los siguientes conceptos: Poliedro: Vértice de un poliedro: Cara de un poliedro: Arista de un poliedro: Poliedro regular: 2.- Di cuáles son los
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Click para ir al sitio web:
 Slide 1 / 199 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
Slide 1 / 199 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
POLIEDROS. ÁREAS Y VOLÚMENES.
 7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
5to Parcial de Geometría Euclidiana. 2) Sea p un polígono tal que se puede descomponer en n polígonos simples
 5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
CONOCER Y DIFERENCIAR LOS POLIEDROS REGULARES
 OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
ELEMENTOS Y CLASES DE ÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Área de paralelogramos (páginas 546 549)
 A NOMRE FECHA PERÍODO Área de paralelogramos (páginas 546 549) Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. La base es cualquiera de los lados y la altura es la distancia más corta
A NOMRE FECHA PERÍODO Área de paralelogramos (páginas 546 549) Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. La base es cualquiera de los lados y la altura es la distancia más corta
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
CUERPOS GEOMÉTRICOS. 2º E.S.O. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS
 CUERPOS GEOMÉTRICOS. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO 2º E.S.O. DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de puntos: DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de una recta:
CUERPOS GEOMÉTRICOS. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO 2º E.S.O. DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de puntos: DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de una recta:
POLÍGONOS
 POLÍGONOS 8.1.1 8.1.5 Después de estudiar los triángulos y los cuadriláteros, los alumnos ahora amplían su estudio a todos los polígonos. Un polígono es una figura bidimensional, cerrada, formada por tres
POLÍGONOS 8.1.1 8.1.5 Después de estudiar los triángulos y los cuadriláteros, los alumnos ahora amplían su estudio a todos los polígonos. Un polígono es una figura bidimensional, cerrada, formada por tres
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Enlace con el hogar no. 22 H Hoja de ejercicios
 For use after Unit Three, Session 2. NOMBRE FECHA Enlace con el hogar no. 22 H Hoja de ejercicios Rompecabezas de figuras 1 Utiliza una regla y un lapicero para dividir cada polígono de abajo en 2 figuras
For use after Unit Three, Session 2. NOMBRE FECHA Enlace con el hogar no. 22 H Hoja de ejercicios Rompecabezas de figuras 1 Utiliza una regla y un lapicero para dividir cada polígono de abajo en 2 figuras
MATEMÁTICAS BÁSICAS. Jeanneth Galeano Peñaloza. 13 de agosto de Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas
 MATEMÁTICAS BÁSICAS Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 13 de agosto de 2012 Parte I Introducción a la geometría elemental Nociones básicas
MATEMÁTICAS BÁSICAS Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 13 de agosto de 2012 Parte I Introducción a la geometría elemental Nociones básicas
Mapa conceptual. Programa Acompañamiento CUERPOS GEOMÉTRICOS. Matemática
 Programa Acompañamiento Matemática Cuadernillo de ejercitación Ejercitación Área y volumen de sólidos Mapa conceptual Tienen CUERPOS GEOMÉTRICOS Figuras geométricas que ocupan un lugar en el espacio. Se
Programa Acompañamiento Matemática Cuadernillo de ejercitación Ejercitación Área y volumen de sólidos Mapa conceptual Tienen CUERPOS GEOMÉTRICOS Figuras geométricas que ocupan un lugar en el espacio. Se
SOLIDOS LOS POLIEDROS RECTOS
 SOLIDOS Las invenciones de los objetos concretos al concepto abstracto de los griegos, sentaron las bases para la geometría Euclidea. Aquí apreciamos algunas formas que ellos derivaron y que aún hoy día
SOLIDOS Las invenciones de los objetos concretos al concepto abstracto de los griegos, sentaron las bases para la geometría Euclidea. Aquí apreciamos algunas formas que ellos derivaron y que aún hoy día
Hoja de actividad sobre las propiedades de las figuras geométricas planas
 Nombre Unidad 4.6: Diseños en nuestro mundo Hoja de actividad sobre las propiedades de las figuras geométricas planas Fecha Instrucciones: Mira cada figura con detenimiento. Nombra cada una de las figuras
Nombre Unidad 4.6: Diseños en nuestro mundo Hoja de actividad sobre las propiedades de las figuras geométricas planas Fecha Instrucciones: Mira cada figura con detenimiento. Nombra cada una de las figuras
TALLER # 5 de GEOMETRÍA EUCLIDIANA ÁREAS Y VOLÚMENES. Universidad de Antioquia. Departamento de Matemáticas. Septiembre 2008
 TALLER # 5 de GEOMETRÍA EUCLIDIANA ÁREAS Y VOLÚMENES Universidad de Antioquia Departamento de Matemáticas Septiembre 2008 1. Sea ABCD un rectángulo, E punto medio de, a) Calcular el área del rectángulo
TALLER # 5 de GEOMETRÍA EUCLIDIANA ÁREAS Y VOLÚMENES Universidad de Antioquia Departamento de Matemáticas Septiembre 2008 1. Sea ABCD un rectángulo, E punto medio de, a) Calcular el área del rectángulo
New Jersey Center for Teaching and Learning. Iniciativa de Matemática Progresiva
 Slide 1 / 232 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
Slide 1 / 232 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial de estudiantes
MATEMÁTICAS BÁSICAS. Autora: Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano
 MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad Nacional de Colombia
MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad Nacional de Colombia
Indicar y Justificar la verdad (V) o falsedad (F) de las siguientes afirmaciones:
 GEOMETRÍ DEL ESIO ompetencias: Reconoce a la recta y el plano en R. Describir las posiciones relativas entre dos planos y entre una recta y un lano. Describir el Teorema de las tres perpendiculares. Definir
GEOMETRÍ DEL ESIO ompetencias: Reconoce a la recta y el plano en R. Describir las posiciones relativas entre dos planos y entre una recta y un lano. Describir el Teorema de las tres perpendiculares. Definir
1) Si una pizza de 32cm de diámetro se corta en 8 porciones exactamente iguales, 2) Determine el área de cada una de las partes sombreadas:
 Plantear y resolver los siguientes problemas: 1) Si una pizza de 32cm de diámetro se corta en 8 porciones exactamente iguales, determinar el área de cada porción. 2) Determine el área de cada una de las
Plantear y resolver los siguientes problemas: 1) Si una pizza de 32cm de diámetro se corta en 8 porciones exactamente iguales, determinar el área de cada porción. 2) Determine el área de cada una de las
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Primer grado. Slide 2 / 232. Slide 1 / 232. Slide 3 / 232. Slide 4 / 232. Slide 6 / 232. Slide 5 / 232. Geometría. Formas 2-D
 Slide 1 / 232 Slide 2 / 232 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial
Slide 1 / 232 Slide 2 / 232 New Jersey Center for Teaching and Learning Iniciativa de Matemática Progresiva Este material está disponible gratuitamente en www.njctl.org y está pensado para el uso no comercial
Geometría 2D Parte 1: Relaciones Geométricas, Perímetro y Circunferencia
 Slide 1 / 174 Geometría 2D Parte 1: Relaciones Geométricas, Perímetro y ircunferencia Nueva Jersey, entro de Enseñanza y prendizaj Slide 2 / 174 Matemáticas Iniciativa Progresista Este material está disponible
Slide 1 / 174 Geometría 2D Parte 1: Relaciones Geométricas, Perímetro y ircunferencia Nueva Jersey, entro de Enseñanza y prendizaj Slide 2 / 174 Matemáticas Iniciativa Progresista Este material está disponible
LOS CUERPOS GEOMÉTRICOS POLIEDROS Y CUERPOS REDONDOS
 LOS CUERPOS GEOMÉTRICOS POLIEDROS Y CUERPOS REDONDOS Se llaman poliedros todos los cuerpos geométricos que tienen todas sus caras planas. Los cuerpos redondos son aquellos que tienen alguna de sus superficies
LOS CUERPOS GEOMÉTRICOS POLIEDROS Y CUERPOS REDONDOS Se llaman poliedros todos los cuerpos geométricos que tienen todas sus caras planas. Los cuerpos redondos son aquellos que tienen alguna de sus superficies
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
GEOMETRÍA DEL ESPACIO
 GEOMETRÍA DEL ESPACIO Lic. Saúl Villamizar Valencia 33 1 GEOMETRÍA DEL ESPACIO Definición: Es la parte de la geometría que estudia las propiedades de las figuras y sólidos geométricos cuyos elementos
GEOMETRÍA DEL ESPACIO Lic. Saúl Villamizar Valencia 33 1 GEOMETRÍA DEL ESPACIO Definición: Es la parte de la geometría que estudia las propiedades de las figuras y sólidos geométricos cuyos elementos
POLIEDROS E CORPOS REDONDOS
 Escribe na parte dereita o que falta. POLIEDROS E CORPOS REDONDOS 1. Os corpos redondos. A xeometría do espazo estuda os corpos que teñen tres dimensións: lonxitude, anchura e altura. Os corpos que teñen
Escribe na parte dereita o que falta. POLIEDROS E CORPOS REDONDOS 1. Os corpos redondos. A xeometría do espazo estuda os corpos que teñen tres dimensións: lonxitude, anchura e altura. Os corpos que teñen
MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) TALLER DE REPASO PARA EL BIMESTRAL 3P
 COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
PÁGINA 98. a) Tetraedro = 2 Cubo = 2 Octaedro = 2 Dodecaedro = 2 Icosaedro = 2
 PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
Una recta es una línea (de puntos) que no tiene ni principio ni final. Un segmento es la parte de una recta que se encuentra entre 2 puntos.
 RECTAS Y ÁNGULOS RECTAS Una recta es una línea (de puntos) que no tiene ni principio ni final. Un punto divide a una recta en 2 semirrectas. Un segmento es la parte de una recta que se encuentra entre
RECTAS Y ÁNGULOS RECTAS Una recta es una línea (de puntos) que no tiene ni principio ni final. Un punto divide a una recta en 2 semirrectas. Un segmento es la parte de una recta que se encuentra entre
TALLER DE SOLIDOS. Ejemplo 1: Hallar la diagonal de un cubo cuya arista mide 3 cm. Solución:
 3 TALLER DE SOLIDOS Ejemplo 1: Hallar la diagonal de un cubo cuya arista mide 3 cm. D = d a ; pero d a a a D a a ; D 3a D a 3 D 3 3 cm. Ejemplo : Hallar el área lateral de un prisma recto octagonal regular
3 TALLER DE SOLIDOS Ejemplo 1: Hallar la diagonal de un cubo cuya arista mide 3 cm. D = d a ; pero d a a a D a a ; D 3a D a 3 D 3 3 cm. Ejemplo : Hallar el área lateral de un prisma recto octagonal regular
3. Si la diferencia de volúmenes de los cilindros A) 2 3 B) En el gráfico se tiene un tronco de cilindro. A) 196p B) 200p C) 250p
 ilindro y tronco de cilindro 1. En el gráfico se muestra un cilindro recto de base circular, además, T es punto de contacto de la recta PT en la superficie cilíndrica. Si PT=15 y P=8, calcule la distancia
ilindro y tronco de cilindro 1. En el gráfico se muestra un cilindro recto de base circular, además, T es punto de contacto de la recta PT en la superficie cilíndrica. Si PT=15 y P=8, calcule la distancia
GUÍA DE APRENDIZAJE 2 BÁSICO Educación Matemática
 GUÍA DE APRENDIZAJE 2 BÁSICO Educación Matemática Nombre alumno(a) Aprendizajes Esperados Describen cuadrados, rectángulos y triángulos, considerando número de lados y de vértices, medida de sus lados
GUÍA DE APRENDIZAJE 2 BÁSICO Educación Matemática Nombre alumno(a) Aprendizajes Esperados Describen cuadrados, rectángulos y triángulos, considerando número de lados y de vértices, medida de sus lados
