Tema 3. Sólido rígido.
|
|
|
- Estefania Farías Barbero
- hace 7 años
- Vistas:
Transcripción
1 Tema 3. Sóldo rígdo. Davd Blanco Curso
2 ÍNDICE Índce 1. Sóldo rígdo. Cnemátca Condcón cnemátca de rgdez Movmento de traslacón Movmento de rotacón Momento angular y momento de una fuerza 7.1. Momento angular de una partícula Momento de una fuerza de una partícula Prncpo de conservacón del momento angular de una partícula Prncpo de conservacón del momento angular para un sstema de partículas Momento angular de un sóldo rígdo respecto de un eje de smetría 1 4. Momento de nerca. Cálculo y teoremas fundamentales Teorema de Stener Teorema de las fguras planas Ecuacón fundamental de la dnámca de rotacón 1 6. Energía del sóldo rígdo 7. Rodadura Dnámca Conservacón de la energía Davd Blanco (dblanco@ugr.es) Curso
3 1 SÓLIDO RÍGIDO. CINEMÁTICA 1. Sóldo rígdo. Cnemátca Un sóldo rígdo es un sstema de partículas en el que la dstanca entre las dstntas partículas está fja. Esto sgnfca que para dos puntos y j del sóldo, cuyas poscones venen determnadas por los vectores de poscón r y r j, se cumple que la dstanca entre estos dos puntos es constante, es decr: r j r = r j = cte (1) r r j j donde r j es el vector que va del punto al punto j, tal y como se ndca en la Fgura 1. La condcón (1) se conoce como condcón de rgdez. Esto hace que la poscón de un sóldo rígdo quede totalmente determnada con la poscón de tres puntos no alneados r 1, r y r 3. Sn embargo, la poscón de estos puntos no es ndependente entre sí, ya que la condcón de rgdez aplcada a las tres parejas de puntos mplca: Fgura 1: Dos puntos y j en un sóldo rígdo r j (x 1 x ) + (y 1 y ) + (z 1 z ) =d 1 (x 1 x 3 ) + (y 1 y 3 ) + (z 1 z 3 ) =d 13 (x x 3 ) + (y y 3 ) + (z z 3 ) =d 3 donde d 1, d 13 y d 3 son las dstancas entres los tres puntos, que son cantdades fjas. Las anterores ecuacones son un sstema de tres ecuacones con nueve ncógntas, por lo que sólo ses de las ncógntas son ndependentes, y por tanto sólo ses cantdades son necesaras para fjar completamente la poscón de un sóldo rígdo. Se dce así que el sóldo rígdo tene 6 grados de lbertad. Los grados de lbertad tambén se pueden ver de forma más ntutva observando la lbertad que encontramos al fjar los tres puntos, en orden, en el espaco. Prmero fjamos el punto 1, que se puede colocar en cualquer sto del espaco, lo que supone tres grados de lbertad. Una vez fjado el punto 1, el punto no se puede colocar en cualquer punto del espaco, ya que tene que estar a una dstanca d 1 del prmer punto. Esto supone que se puede colocar en cualquer punto de una esfera de rado d 1 y centrado en el punto 1, lo que sgnfca dos grados de lbertad más (ángulo cental y acmutal). Una vez hecho esto, se procede a colocar el punto 3, pero con los puntos 1 y fjos, el sóldo sólo puede grar en torno al eje que pasa por estos dos puntos. Esto supone que el punto 3 sólo se puede colocar sobre la únca crcunferenca que dsta d 13 del punto 1 y d 3 del punto, lo que sgnfca un grado de lbertad adconal (ángulo acmutal), con lo que suman ses grados de lbertad Condcón cnemátca de rgdez Se ha vsto que la condcón de rgdez expresa matemátcamente el hecho la dstanca entre puntos en un sóldo rígdo debe permanecer fja. Esta lmtacón tambén mpone restrccones sobre el movmento que pueden tener las dstntas partículas de un sóldo. Para poder estudar estas restrccones matemátcamente, no hay más que tomar la ecuacón de rgdez (1) y dervar Davd Blanco (dblanco@ugr.es) 3 Curso
4 1 SÓLIDO RÍGIDO. CINEMÁTICA respecto al tempo: r j r = ( r j r ) ( r j r ) = cte d ( r j r ) = d( r j r ) ( r j r ) + ( r j r ) d( r j r ) dt dt dt lo que mplca en térmnos de velocdad: = ( r j r ) d( r j r ) dt = 0 ( v j v ) ( r j r ) = 0 () La ecuacón () se conoce como Ecuacón cnemátca de rgdez, y representa la condcón geométrca que deben cumplr las poscones y velocdades de culesquera dos puntos del sóldo rígdo. Para entender mejor qué sgnfca la ecuacón () se puede utlzar el vector r j, con el que la ecuacón quedaría: v j r j = v r j es decr, la proyeccón de la velocdad de la partícula en la dreccón que une esta partícula con la partícula j tene que ser gual a la velocdad de la partícula j. j Gráfcamente se puede observar en la Fgura, en la que aparecen dos puntos y j. Esta fgura representa que s la velocdad de la partícula es v, la velocdad de la partícula j puede ser cualquera de los vectores que aparecen en el dbujo, ya que la proyeccón de estos vectores en la dreccón que une con j es gual a la Fgura : Dos puntos y j en un sóldo proyeccón de v en esa msma dreccón. rígdo y sus velocdades Otra forma de entender la condcón representada en la ecuacón () es hacendo uso del vector velocdad relatva v j = v j v, con el que la ecuacón queda: v j r j = 0 es decr, el movmento que la partícula ve de la partícula j es perpendcular a la línea que las une, lo que quere decr que n se acerca, n se aleja (lo que es lógco para un sóldo rígdo), y las partículas solo pueden tener movmentos relatvos de rotacón, una respecto de otras. 1.. Movmento de traslacón En un sóldo rígdo se pueden dstngur dos movmentos fundamentales, el de traslacón y el de rotacón y cualquer movmento se podrá expresar como una suma de estos dos movmentos. Aunque coloqualmente estos conceptos son habtuales, en esta y la sguente subseccón se estudará de forma más precsa que entenderemos por estos dos tpos de movmento. Un sóldo rígdo se dce que lleva un movmento de traslacón s el segmento defndo por dos puntos cualquera del sóldo mantene su orentacón durante el movmento, es decr: r j r = r j = cte (3) En la Fgura 3 pueden verse tres nstantes de un movmento de traslacón de un sóldo rígdo, y como el vector que une los puntos y j permanece constante a lo largo del movmento. v v j Davd Blanco (dblanco@ugr.es) 4 Curso
5 1 SÓLIDO RÍGIDO. CINEMÁTICA Para ver como son las velocdades no hay más que dervar la ecuacón (3), lo que proporcona: d( r j r ) = 0 d r j dt dt d r dt = 0 v j v = 0 v j = v El resultado fnal ndca que todos los puntos del sóldo rígdo se mueven con la msma velocdad y con la msma aceleracón (al volver a dervar se obtendría este últmo resultado). S se estudan las poscones de dos puntos en dos nstantes A y B, la ecuacón (3) quedaría: r A j r A = r B j r B lo que despejando proporcona: r B r A = r B j r A j r = r j Es decr, las varacones de poscón que expermenten cada una de las partículas del sóldo rígdo serán guales. Como el vector desplazamento no es otra cosa que la varacón de poscón en un tempo nfntesmal, la anteror gualdad mplca: d r = d r j o lo que es lo msmos, que los desplazamentos son guales para todas las partículas de un sóldo rígdo. Como la trayectora de una partícula se construye a partr de r j j r j j Fgura 3: Movmento de traslacón de un sóldo rígdo los dstntos vectores desplazamento, la trayectora de todas las partículas de un sóldo rígdo será la msma en un movmento de traslacón. Este últmo resultado queda recogdo gráfcamente en la Fgura Movmento de rotacón Se dce que un sóldo rígdo está anmado por un movmento de rotacón al rededor de un eje fjo cuando todos sus puntos descrben trayectoras crculares centradas en dcho eje y en planos perpendculares a dcho eje. En la Fgura 4 se muestran dos partículas y j del sóldo rígdo, la prmera grando descrbendo una trayectora crcular respecto al punto O y la segunda respecto al punto O. Puede verse como las trayectoras están contendas en planos paralelos y los centros de las trayectora están contendos en un eje perpendcular a todos los planos. Este eje se conoce como eje de rotacón y puede estar en el sóldo rígdo o fuera de él. En la fgura tambén se ndca como durante un determnado tempo el ángulo θ que barren las dos partículas es el msmo (s no lo fuera, las partículas se acercarían o alejarían, volando la condcón de rgdez). El espaco recorrdo por la partícula durante el tempo que ha tardado en barrer un ángulo θ es smplemente S = O θ donde O es el vector que va desde O hasta. El módulo de la velocdad de la partícula resultará de dervar el espaco recorrdo, lo que resulta: v = O dθ v = O ω dt donde ω es la dervada del ángulo barrdo por las partículas con respecto al tempo. Como el ángulo barrdo es el msmo para todas las partículas, la velocdad angular tambén será la msma para todo el sóldo rígdo. r j j Davd Blanco (dblanco@ugr.es) 5 Curso
6 1 SÓLIDO RÍGIDO. CINEMÁTICA El vector velocdad de la partícula quedará por tanto como v = O ωê t donde ê t es el vector tangente a la trayectora en el punto consderado que se estudó extensamente en el tema anteror. En la Fgura 5 aparece amplado el punto en su movmento, representando el versor tangente a la trayectora ê t, el versor normal a la trayectora ê n y un versor ê que lleva la msma dreccón del eje de rotacón, sentdo según la regla de la mano derecha, y es por tanto perpendcular a los otros dos versores. Es fácl ver que ê t = ê n ê, y s esto se substtuye en la expresón de v queda: j O O' θ θ v = O ωê n ê = ( O ê n ) (ωê) El vector O ê n no es otra cosa que el vector O, que va de hasta O. Se puede defnr el vector velocdad angular como ω = ωê, con lo que la velocdad de la partícula quedaría: Fgura 4: Movmento de rotacón pura de un sóldo rígdo v = O ω = ω O = ω O S se stúa el orgen de coordenadas en el punto O, la velocdad de la partícula se podría expresar de forma smple como v = ω r (4) sn embargo en prncpo esto no valdría para la partícula j en la Fgura 4 que gra en un plano dstnto al de la partícula. En prncpo, para la partícula j, la velocdad se expresaría según la Fgura 4 como: Sn embargo, se puede ver que v j = ω O j ω Oj = ω ( OO + O j) = ω OO + ω O j O e n e e t Fgura 5: Detalle del movmento de la partícula al rotar Pero el prmero de los últmos dos térmnos es cero, ya que es el producto vectoral de dos vectores paralelos, y el resultado es: ω Oj = ω O j Por lo tanto, s el orgen de coordenadas está stuado en el eje de rotacón la expresón (4) es válda para el vector velocdad de todos los puntos del sóldo rígdo. Todo movmento de un sóldo, por complejo que sea, se puede expresar como una traslacón más una rotacón, aunque la rotacón puede varar a largo del tempo (varacón de ω con el tempo). Las traslacones corresponden con el tpo de movmentos que hemos estudado en el tema anteror, pero las rotacones no las hemos tratado con sufcente profunddad. Por ello a contnuacón realzaremos un pequeño paréntess en el estudo y procederemos a estudar como caracterzar la rotacón prmero de masas puntuales y luego de sstemas de partículas. Davd Blanco (dblanco@ugr.es) 6 Curso
7 MOMENTO ANGULAR Y MOMENTO DE UNA FUERZA. Momento angular y momento de una fuerza En esta seccón se caracterzarán como partículas o sstemas de partículas gran respecto de puntos, y como las fuerzas pueden alterar el estado de rotacón..1. Momento angular de una partícula Una partícula se encuentra movéndose en un determnado nstante con una velocdad v y un momento lneal p, tal y como se muestra en la Fgura 6. Se trata de caracterzar como esa partícula gra en ese nstante respecto del punto O, esto se realza a través de una magntud conocda como momento angular, que es un vector y se defne como: L O O v L = O p Se puede ver como el vector es perpendcular al plano formado por la velocdad y el vector que une O y la partícula. El momento angular se mde en el SI en kgm /s. Fgura 6: Movmento angular de una partícula respecto a un punto O S la partícula lleva un movmento de rotacón pura respecto al punto O, es decr descrbe una trayectora crcular de rado a (por ejemplo) centrada en ese punto, los vectores p y O serán perpendculares y el módulo del momento angular será: L = amv = ma ω S se observa que en este caso la dreccón del vector velocdad angular concde con la del momento angular, esta últma cantdad para una partícula en un movmento de rotacón pura queda: L = amv = ma ω El momento angular jugará el msmo papel en rotacones que el momento lneal jugó en traslacones, por lo que representa el estado de rotacón de un cuerpo respecto de un punto... Momento de una fuerza de una partícula S una fuerza se aplca sobre una partícula cambará el estado de movmento de un cuerpo y pueden tambén el estado de rotacón. Sn embargo, la efectvdad con la que la fuerza cambe el estado de rotacón de un cuerpo respecto a un punto no sólo dependerá del valor de la fuerza, sno de la drecconabldad de esta fuerza respecto del punto. Esta efectvdad para cambar el estado de rotacón se mde con una magntud denomnada momento de una fuerza, que para una fuerza aplcada sobre una partícula, tal y como se muestra en la Fgura 7, se defne como: M = O F M O O F Fgura 7: Momento de una fuerza respecto de un punto O El momento de una fuerza jugará en rotacones el msmo papel que la fuerza jugó en traslacones. Davd Blanco (dblanco@ugr.es) 7 Curso
8 MOMENTO ANGULAR Y MOMENTO DE UNA FUERZA El módulo del momento de una fuerza será gual al módulo de la fuerza, por la dstanca de O al punto de aplcacón de la fuerza, por el seno del ángulo que forman la fuerza con el vector que une O con el punto de aplcacón. Así, es fácl ver que una fuerza poseerá una momento nulo respecto de un punto O cuando se aplque en este punto (la partícula se encuentre en el punto O) o cuando la fuerza lleve la msma dreccón que el vector que une el punto O con la partícula con la que está aplcada la fuerza. Aunque esta defncón pueda parecer extraña, no hay nada más que pensar en cómo hay que realzar una fuerza sobre una puerta para abrrla, y cuando la fuerza será más efectva. S la fuerza se ejerce sobre las parte cercana a las bsagras no se podrá abrr la puerta (dstanca a O es nula). Tambén, s la fuerza se ejerce en una dreccón paralela a la puerta (ángulo entre la fuerza y la línea que une el punto de aplcacón con O nulo) el momento será nulo. Por otro lado, la puerta se abrrá más fáclmente cuanto más lejos de las bsagras se aplque la fuerza y en una dreccón más perpendcular a la puerta. Por últmo recordar que en las defncones anterores es necesaro sempre determnar el punto O que se conoce como punto de reduccón de momentos. Así, el estado de rotacón de un cuerpo será sempre relatvo al punto respecto del cual se calcula el momento angular y el momento de las fuerzas..3. Prncpo de conservacón del momento angular de una partícula S en el punto O, respecto al que se quere estudar como gra una partícula, se coloca el orgen de coordenadas, la defncones de momento angular y momento de una fuerza quedan: L = r p y M = r F Esta expresón se puede dervar con respecto al tempo y s el punto O está fjo resulta: d L dt = d r p dt = d r d p p + r dt dt El prmero de los últmos dos térmnos es nulo, ya que v y p son dos vectores paralelos. En el segundo de los térmnos se puede aplcar la segunda ley de Newton y la anteror ecuacón quedaría: d L dt = r F = M (5) donde la fuerza que aparece es la resultante de las fuerzas. Esta ecuacón es la que domna la rotacón de una partícula respecto de un punto y es equvalente a la segunda ley de Newton en traslacones. Una consecuenca fácl de obtener es que en el caso de que el momento de la resultante de las fuerzas sea nulo, la dervada de L será gual a cero y por tanto el momento angular permanece constante. Este resultado se conoce como prncpo de conservacón del momento angular de una partícula. Ejemplo. Rotacón de una partícula bajo la accón de una fuerza central respecto del centro de fuerzas. S el centro de fuerzas permanece fjo y se coloca el orgen del sstema de coordenadas en este punto, la dreccón de la fuerza llevará la msma dreccón que el vector de poscón. Por lo tanto el momento de la fuerza será nulo y el momento angular se conservará. En concreto se conservará L = m r v Davd Blanco (dblanco@ugr.es) 8 Curso
9 MOMENTO ANGULAR Y MOMENTO DE UNA FUERZA Una consecuenca de este resultado se puede ver s se calcula el área que barre una partícula en su movmento nfntesmal respecto de un punto O, que en la Fgura 8 aparece sombreada. Este área es fácl de calcular y resulta: ds = 1 r d r Para calcular la varacón el área que barre por undad de tempo no hay más que dvdr ds por dt, con lo que la anteror ecuacón queda: O r r+dr dr Fgura 8: Movmento de una partícula respecto de un punto O ds dt = 1 d r r dt = 1 L r v = m Por tanto, como el momento angular permanece constante, la velocdad a la que barre áreas (velocdad areolar) permanece constante. Este resultado para el movmento de los planetas al rededor del sol lo enuncó Keppler en su segunda ley de los movmentos planetaros. Otro resultado que se puede obtener es que cómo L es constante y L = r p, entonces tanto r como p tenen que permanecer en un plano perpendcular a L durante todo el movmento, lo que mplca que el movmento será plano. Este resultado para el movmento de los planetas lo enuncó Keppler en su prmera ley del movmento planetaro. Vemos que tanto la prmera como la segunda ley de Keppler serán váldas para el movmento de cualquer partícula bajo la accón de cualquer fuerza central (no necesaramente la atraccón gravtatora)..4. Prncpo de conservacón del momento angular para un sstema de partículas Hasta ahora se ha estudado la rotacón de partículas asladas, y para obtener la relacón entre L y M se supuso que el punto respecto del cual se calculan los momentos está fjo. En este apartado se estudará el caso más general de un sstema de partículas y en el punto respecto del cual se calculan los momentos se puede mover. En este caso, el momento angular de una partícula respecto de un punto Q será el producto vectoral del vector de poscón relatvo que va del punto Q hasta el punto, r Q = r r Q, por el momento lneal que el punto Q ve que lleva la partícula, que será m ( v v Q ). Es decr, el momento angular de la partícula respecto del punto Q, L, es: L = m ( r r Q ) ( v v Q ) v Q Q x z r Q r Q O r Fgura 9: Rotacón de un sstema de partículas con respecto del punto Q El esquema de esta stuacón se presenta en Fgura 9. El momento angular total del sstema de partículas, L, será la suma de los momentos angulares de cada una de las partículas. v y F L = L Davd Blanco (dblanco@ugr.es) 9 Curso
10 MOMENTO ANGULAR Y MOMENTO DE UNA FUERZA Sobre la partícula actuará un conjunto de fuerzas, cuya resultante será F y tambén está representada en la Fgura 9. El momento de la resultante de las fuerzas que actúan sobre la partícula, respecto del punto Q, será: M = ( r r Q ) F El momento total de las fuerzas que actúan sobre el sstema de partículas respecto del punto Q será la suma de los momentos de las partículas ndvduales: M = M La pregunta nmedata será s la relacón que exstía entre L y M para una partícula aslada se cumple tambén para un sstema de partículas. Para ver s la relacón se cumple hay que empezar calculando la dervada del momento angular del sóldo rígdo con respecto al tempo: d L dt = ( d r m dt d r ) Q ( v v Q ) + dt m ( r r Q ) ( d v dt d v ) Q dt El prmer térmno de la gualdad es nulo, por lo que la anteror dervada queda: dl dt = ( d ) r m ( r r Q ) dt d r Q dt = ( r r Q ) F m ( r r Q ) d r Q dt La fuerza que actúa sobre la partícula se puede descomponer en fuerzas exterores y fuerzas nterores, estás últmas debdas a la accón del resto de partículas sobre la partícula, de forma que: F = F ext + F nt = F ext + j S esto se susttuye en la expresón de la dervada de L se tene: d L dt = ( r r Q ) F ext + F nt j ( r r Q ) F j nt j m ( r r Q ) d r Q dt El segundo térmno de la anteror gualdad es nulo para fuerzas nternas que llevan la dreccón que unen las partículas. Para poder verlo se desarrollan los sumatoros y nos fjamos en los térmnos en los que aparece la fuerza que la partícula hace sobre la j y la reaccón de está (la fuerza que la partícula j hace sobre la ): j j ( r r Q ) F nt j = + ( r r Q ) F nt j + + ( r j r Q ) F nt j +... y s se suman los térmno dos a dos, tenendo en cuenta F j = F j, el anteror térmno queda: ( r r Q ) F j nt = + ( r r j ) F j nt + = + r j F j nt +... S la fuerza F j lleva la dreccón de la línea que une las partículas y j todos los sumandos anterores son nulos. Por tanto, la dervada del momento L de un sstema de partículas queda: d L dt = ( r r Q ) F ext m ( r r Q ) d r Q dt (6) Davd Blanco (dblanco@ugr.es) 10 Curso
11 MOMENTO ANGULAR Y MOMENTO DE UNA FUERZA S el segundo térmno fuese nulo, la dervada del momento angular de un sstema de partículas quedaría: d L dt = ( r r Q ) F ext = M ext = M ext (7) donde M ext es el momento de las resultantes de las fuerzas exterores que actúan sobre la partícula, respecto del punto Q, mentras que M ext es el momento total que las fuerzas exterores genera sobre el sstema de partículas, respecto del punto Q. Por lo tanto, sólo los momentos de las fuerzas exterores nflurán en el estado de rotacón de un sstema de partículas. Para que esta últma ecuacón (7) sea válda es necesaro que el segundo térmno (6) sea nulo. Esto mplca: m ( r r Q ) d r Q dt = La anteror cantdad es nula s: El punto Q es el centro de masas. El punto Q no está acelerado. ( ( ) ( m r La aceleracón del punto Q apunta haca el centro de masa. ) ) m r Q d r Q dt = m T ( r CM r Q ) d r Q dt Resumendo, s el punto Q que se elje como punto de reduccón de momentos cumple alguna de las tres anterores condcones, el momento lneal total del sstema de partícula y el momento total generado por las fuerzas exterores cumple: d L dt = M ext (8) En la práctca el punto Q se elge o ben un punto fjo o ben un el centro de masas y en el resto del tema se supondrá que el punto elegdo cumple alguna de las tres propedades. Como consecuenca drecta de la ecuacón (8), s el momento de las fuerzas exterores es nulo, el momento angular total del sstema permanece constante. Este resultado se conoce como Prncpo de conservacón del momento angular para un sstema de partículas Ejemplo. Movmento de una puerta sobre la que choca una pelota perpendcularmente y a una determnada dstanca de las bsagras (desprecando la accón del peso), ncdendo con una velocdad v 0 y rebotando con una velocdad v f. Incalmente se supone que la puerta está en reposo y que la pelota choca con ella perpendcularmente, con una velocdad v 0 y a una dstanca de la bsagra d. La únca fuerza exteror que actúa sobre el sstema masa-pelota es la fuerza que se ejerza en la bsagra y que mpde que la puerta abandone su marco. S se elge el punto Q en la bsagra, la fuerza exteror no produce momento, por lo que el momento angular del sstema permanece constante. Justo antes del choque, a este momento angular total sólo contrbuye la pelota (que es la únca que se mueve, y cuyo momento angular es L pelota = mv 0 d, por lo que el momento angular del sstema antes del choque es L 0 = mv 0 d La dreccón es la del eje de la puerta. Después del choque todo se moverá, por lo que el momento lneal del sstema después del choque será: L f = L puerta mv f d Davd Blanco (dblanco@ugr.es) 11 Curso
12 3 MOMENTO ANGULAR DE UN SÓLIDO RÍGIDO RESPECTO DE UN EJE DE SIMETRÍA Con lo que el momento que la puerta lleva después del choque queda: L puerta = md(v 0 + v f ) En el anteror ejemplo, aunque es posble obtener el momento angular de la puerta, no lo sabemos relaconar con magntudes como la velocdad angular que llevará la puerta y que proporconan una mejor dea ntutva de como grará la puerta después del choque. Esta relacón entre el momento angular y la velocdad angular se realzará en la sguente seccón. 3. Momento angular de un sóldo rígdo respecto de un eje de smetría En este apartado se estudará la relacón entre el momento angular y la velocdad angular para un sóldo rígdo descrbendo un movmento de rotacón pura entorno a eje de smetría. S colocamos el orgen de coordenadas en un punto del eje de rotacón y suponemos que el sóldo rígdo está formado por un conjunto dscreto de partículas puntuales (s es un conjunto contnuo no hay más que transformar las sumas en ntegrales), el momento angular del sóldo rígdo quedará: L = r p = m r v = m r ( ω r ) En el últmo paso se ha tendo en cuenta la expresón de la velocdad de cualquer punto de un sóldo rígdo en funcón de ω para movmentos de rotacón pura, estudado en la prmera seccón. El trple producto vectoral entre tres vectores a, b y c cumple: a ( b c) = b( a c) c( a b) x z h O ω l Fgura 10: Poscón de una partícula de un sóldo rígdo rotando respecto de un eje r y S esto se aplca a la fórmula del momento angular queda: L = m r ω m r ( ω r ) = m r ω m r h ω (9) donde en el últmo paso se ha utlzado que ω lleva la dreccón del eje de rotacón y que la altura del punto a la que se encuentra a lo largo del eje es h (de forma que ω r = ωh ), tal y como se ndca en la Fgura 10. S el eje es un eje de smetría, es posble saber de antemano que el momento angular va a llevar al msma dreccón que la velocdad angular, dreccón que en general vene marcada por el versor ê (y que en la Fgura 10 corresponde con el eje z). Para ver esto hay que puntualzar que un eje de smetría es un eje en torno al cual la masa se dstrbuye unformemente, de forma que para cualquer partícula, con un vector de poscón r respecto un orgen stuado en un punto O del eje, exste otra partícula j de gual masa y con vector de poscón r j, de forma que su stuacón es smétrca respecto del eje de rotacón (esto sgnfca entre otras cosas que el vector r j r es perpendcular al eje). Esta stuacón se esquematza en la Fgura 11, en la que aparecen Davd Blanco (dblanco@ugr.es) 1 Curso
13 3 MOMENTO ANGULAR DE UN SÓLIDO RÍGIDO RESPECTO DE UN EJE DE SIMETRÍA las dos partículas smétrcas, con sus poscones, sus velocdades y sus momentos angulares. Al ser smétrcas respecto del eje se encuentran rotando descrbendo la msma crcunferenca y sempre en puntos opuestos de esta crcunferenca, y por tanto las velocdades llevaran la msma dreccón pero sentdos opuestos. El momento angular de la partícula, L será perpendcular a r y v, al gual que L j será perpendcular a r j y v j. Los dos momentos angulares tenen el msmo módulo y se puede ver gráfcamente que su suma (que está realzada en la fgura encma del dbujo del sóldo rígdo) lleva la msma dreccón que el eje de rotacón. Como todas las partículas se pueden agrupar de dos en dos de esta forma (al ser un eje de smetría) el momento angular del sóldo rígdo L lleva la dreccón del eje y se puede expresar como: L = Lê Por lo tanto, s el sóldo rígdo gra respecto a un eje de smetría, sabemos la dreccón y sólo nos queda saber el módulo. Para eso no hay más que utlzar que L ê = L, por lo que multplcado la ecuacón (9) se tene: ( L = m r ω ) m r h ω ê = m r ω ê m h ω r ê L L j L +L j L j Por un lado, ω lleva la msma dreccón que ê, luego ω ê = ω. Por otro lado, como ya se ha vsto, la proyeccón de r en la dreccón de ê es h, luego r ê = h ), y la anteror ecuacón queda: L = m r ω m h ω = m (r h )ω Pero como puede verse en la Fgura 10, (r h ) = l, con lo que el vector momento angular de un sóldo rígdo grando respecto de eje de smetría es L = m l ω (10) v j x j r j O r L Fgura 11: Momentos angulares de dos partículas smétrcas respecto al eje v y S se defne la magntud momento de nerca como a la cantdad escalar que relacona L con ω, es decr: I = m l (11) la ecuacón (1) queda como: L = I ω (1) que expresa el momento angular de un sóldo rígdo cuando gra respecto de un eje de smetría. El momento de nerca mde la dstrbucón de masa que hay en torno a un eje de rotacón. Es por tanto una propedad del sóldo rígdo y del eje, y se puede defnr para tantos ejes como se quera, sn necesdad de que sea de smetría. Sn embargo sólo en el caso de que el eje de smetría se cumplrá la ecuacón (1). Davd Blanco (dblanco@ugr.es) 13 Curso
14 3 MOMENTO ANGULAR DE UN SÓLIDO RÍGIDO RESPECTO DE UN EJE DE SIMETRÍA En el caso en el que el eje no sea de smetría, no se cumplrá, en general, la ecuacón (1), ya que no se cumple que en general que el momento angular tenga la msma dreccón que la velocdad angular. Sí se cumplrá la ecuacón (9), que es general. Esta ecuacón sempre se puede multplcar ambos térmnos por ê y queda: L ê = m l ω = Iω Este últmo resultado sgnfca que aunque el eje respecto al que gra un sóldo rígdo no sea de smetría, la proyeccón del momento angular en la dreccón del eje será gual al momento de nerca del sóldo rígdo respecto de ese eje por la velocdad angular. Aplcacón: Obtener la expresón del vector L para un sóldo rígdo grando respecto de un eje cualquera. Aunque el anteror resultado permte obtener la proyeccón del momento angular en la dreccón del eje en una stuacón genérca, aún queda por determnar el momento angular cuando el eje no sea un eje de smetría. Para ello se parte de la ecuacón (9), donde se tene en cuenta que h ω = r ω = x ω x +y ω y +z ω z, y se procede a calcular prmero la componente x del momento, hacendo uso de que L x = L î: L x = = m r ω î m r ω x m (x ω x + y ω y + z ω z ) r î = m (x ω x + y ω y + z ω z )x = = m (x + y + z )ω x m (x ω x + x y ω y + x z ω z ) = = m (y + z )ω x m x y ω y m x z ω z De la msma forma se puede obtener L y y L z como: L y = m x y ω x + m (x + z )ω y m y z ω z L z = m x z ω x m y z ω y + m (x + y )ω z Lo que en forma vectoral se puede escrbr como: I xx I xy I xz L = I xy I yy I yz ω I xz I yz I zz donde I xx, I yy, I zz son los momentos de nerca del sóldo rígdo respecto de los tres ejes cartesanos y I xy, I xz, I yz se conocen como productos de nerca. La matrz que aparece en la ecuacón se conoce como tensor de nerca I y utlzando este tensor el momento angular de un sóldo rígdo respecto de cualquer eje queda: L = I ω Davd Blanco (dblanco@ugr.es) 14 Curso
15 4 MOMENTO DE INERCIA. CÁLCULO Y TEOREMAS FUNDAMENTALES 4. Momento de nerca. Cálculo y teoremas fundamentales El momento de nerca mde la dstrbucón de masas que presenta un sóldo rígdo respecto de un eje. Es por tanto una propedad del sóldo rígdo y del eje que se esté consderando. La defncón para un sóldo rígdo consstente en sstema dscreto de partículas es la que aparece en la ecuacón (11). S el sóldo rígdo consste en un sstema contnuo de partículas, la sumatora se transforma en ntegrales, dvdendo el sóldo en trozos de maza dferencal dm, cada una a una dstanca del eje de gro l y sumando el cuadrado de esta dstanca por la masa dferencal dm: I = l dm Para poder realzar esta ntegral en un caso práctco, hay que expresar el dferencal de masa, utlzando la densdad, en funcón de dferencales de longtud, superfce o volumen, dependendo de s el cuerpo es longtudnal (una dmensón), superfcal (dos dmensones) o volúmco. En concreto, para cuerpos que sólo tene una dmensón, como un alambre o un anllo, el momento de nerca quedaría como: I = l ρ l dr donde ρ l es la densdad lneal de masa, defnda como el cocente entre la masa y la longtud. Ejemplo 1. Encontrar el momento de nerca de una partícula de masa m grando en torno a un eje descrbendo una crcunferenca de rado a. En la Fgura 1(a) se representa el esquema de una partícula grando respecto de un eje a una dstanca a. Según su defncón, el momento de nerca es muy fácl de calcular y sería la masa de la partícula por la dstanca de la partícula a el eje (que es a) al cuadrado, luego: I = a m a m a dm (a) Esquema de un partícula. (b) Esquema de un anllo grando. Fgura 1: Ejemplo. Encontrar el momento de nerca de un anllo de rado a y masa m respecto de un eje que pase por su centro y sea perpendcular al anllo. En la Fgura 1(b) se representa un anllo y un trozo dferencal de masa dm del anllo. En este caso el momento de nerca será la suma de la masa de cada trozo por la dstanca de cada trozo al centro del anllo al cuadrado. Como los trozos son muy pequeños, esta suma representa una ntegral. Puede verse que en este caso todos los puntos del anllo se encuentra a la msma Davd Blanco (dblanco@ugr.es) 15 Curso
16 4 MOMENTO DE INERCIA. CÁLCULO Y TEOREMAS FUNDAMENTALES dstanca del eje de rotacón, con lo que el momento de nerca quedaría: I = a dm = a dm = a m donde se ha utlzado que a es constante y que la suma de la masa de cada uno de los trozos es la masa total del anllo. Puede verse como el momento de nerca de un anllo es gual al momento de nerca de una partícula grando a la msma dstanca que el rado y con la msma masa que el anllo. Esto se debe a que el momento de nerca mde la dstrbucón de masa en funcón de la dstanca al eje, y esta dstrbucón de masa es la msma en los dos casos. Ejemplo 3. Encontrar el momento de nerca de una barra homogénea de masa m y longtud L grando respecto de un eje perpendcular que pasa por su centro. El problema se esquematza en la Fgura 13(a) Se supone que la barra es un cuerpo undmensonal con una densdad lneal de masa ρ L unforme. Se dvde en trozos dm, cada uno se encontrará a una dstanca x del centro de coordenadas, por lo que cada trozo tendrá un momento de nerca nfntesmal x dm. Al ser homogéneo, la densdad es gual a la masa de un trozo dvdda por la longtud de ese trozo, es decr, ρ L = dm dx. Por tanto, la masa dm del pequeño trozo será gual a la densdad lneal por la longtud dx del trozo (dm = ρ L dx). Tendendo esto en cuenta, el momento de nerca se puede expresar como la suma de los momentos de nerca de cada uno de los trozos: I = L L x dm = L L x ρ L dx = ρ L L L x dx = ρ L [ x 3 3 ] L L = ρ LL 3 1 Pero al ser homogéneo, la densdad lneal es gual a la masa total partdo por la longtud total, con lo que ρ L = M L y el momento de nerca queda: I = ML 1 S la barra grase respecto de un eje perpendcular pero que pase por uno de sus extremos, el momento de nerca se calcularía de la msma forma, con la únca dferenca que los lmtes de la ntegral serían desde 0 hasta L (en vez de desde L hasta L como ocurre cuando gra respecto de su centro). Es fácl comprobar que el momento de nerca de una barra grando respecto de un eje perpendcular que pase por un extremo sería: I = ML 3 Hasta aquí se han estudado cuerpos de una sola dmensón. S el sóldo es un sóldo plano, y por tanto tene dos dmensones, el momento de nerca quedaría como: I = l ρ s dr donde ρ s es la densdad superfcal de masa, defnda como el cocente entre la masa y la superfce. Ejemplo 4. Encontrar el momento de nerca de una dsco homogéneo de masa m y rado a grando respecto de un eje perpendcular que pasa por su centro. Esta stuacón se esquematza en la Fgura 13(b). Para calcular este momento de nerca se puede aprovechar que ya conocemos el momento de nerca de un anllo. El dsco se consdera que es un cuerpo de dos dmensones, de densdad superfcal constante ρ S. Un dsco se puede ver como una suma de anllos, cada uno con dstnto rado r y con un ancho dr. Cada uno de estos anllos Davd Blanco (dblanco@ugr.es) 16 Curso
17 4 MOMENTO DE INERCIA. CÁLCULO Y TEOREMAS FUNDAMENTALES z L x dm dx x ω y dr a ω r dm a b (a) Esquema de un barra grando. (b) Esquema de un dsco grando. Fgura 13: (c) Superfce de un dsco hueco. tendrán una masa dferencal dm al tener un ancho dr, y como el momento de nerca de un anllo es gual a su masa por su rado, el momento de nerca dferencal de cada anllo será di = r dm. El momento de nerca del dsco será la suma de los momentos de nerca de cada uno de los anllo: I dsco = a 0 di anllo = a 0 r dm Es necesaro calcular la masa dm de cada anllo, para ello se tene en cuenta que la superfce de una fgura tal y como aparece en Fgura 13(c) es S = πb πa. Entonces, la superfce del anllo de rado r y anchura dr será: ds = π(r + dr) πr = π(r + rdr + (dr) ) πr = π(rdr + (dr) ) Que dr sea dferencal sgnfca que es una cantdad muy pequeña, por lo que (dr) será muchísmo más pequeña y se puede desprecar frente a dr. Por tanto, el área del anllo será ds = πrdr y la masa dm del anllo será está superfce por la densdad superfcal. S esto se tene en cuenta, el momento de nerca del dsco queda: I = a 0 r dm = a 0 r ρ S ds = a 0 r ρ S πrdr = πρ S a 0 r 3 dr = πρ Sa 4 4 Como la densdad superfcal es gual a masa partdo por la superfce, es decr ρ S = m πa, el momento de nerca de un dsco grando respecto de un eje perpendcular que pase por su centro resulta: I = ma Ejemplo 5. Encontrar el momento de nerca de una plancha cuadrada unforme de masa m y lado a grando por un eje contendo en la plancha, que pasa por su centro y que es paralelo a uno de sus lados. El esquema ser representa en la Fgura 14(a), donde el eje de gro es el eje z. La plancha se dvde en pequeñas tras de masa dm, perpendculares al eje, tal y como se señala en la fgura. Estas tras se pueden consderar como barras grando respecto a un eje perpendcular que pasa por su Davd Blanco (dblanco@ugr.es) 17 Curso
18 4 MOMENTO DE INERCIA. CÁLCULO Y TEOREMAS FUNDAMENTALES z a ω dm x a a y dm (a) Esquema de una plancha grando. (b) Esquema de un clndro grando. Fgura 14: centro, luego el momento de nerca dferencal de cada una de estas tras será di = a dm 1. El momento de nerca total será la suma de estos momentos de nerca: a dm I = 1 = a 1 Pero la últma ntegral es la suma de la las masas de los dstntos trozos, y por lo tanto es gual a la masa total de la plancha. El momento de nerca de la plancha queda por tanto: I = a m 1 Este momento de nerca es gual al de una barra, lo que es de esperar porque una plancha y una barra grando respecto del eje consderado tenen la msma dstrbucón de masas respecto del eje. Ejemplo 6. Encontrar el momento de nerca de un clndro de masa m y rado a grando respecto de un eje perpendcular que pasa por su centro y concde con su eje de revolucón. En la Fgura 14(b) se esquematza la stuacón. Para calcular el momento de nerca, se dvde el clndro en pequeños clndros de masa dm y altura dferencal, de forma que cada trozo se puede consderar un dsco. El momento de nerca de cada trozo será di = a dm y el momento de nerca del clndro completo será la suma de estos momentos de nerca: a dm I = = a Al gual que en el ejemplo anteror, la últma ntegral es la masa total del clndro, con lo que el momento de nerca del clndro queda: I = a m Como cabía de esperar, el momento de nerca es gual al momento de nerca de un dsco, ya que a efectos del eje ambas fguras tenen la msma dstrbucón de masa. dm dm Davd Blanco (dblanco@ugr.es) 18 Curso
19 4 MOMENTO DE INERCIA. CÁLCULO Y TEOREMAS FUNDAMENTALES I I' z z' x O r y r CM x' r ' y' a z y a dm (a) Dos ejes paralelos, uno de ellos pasando por el centro de masas. (b) Plancha cuadrada grando respecto de un eje perpendcular Teorema de Stener Como se ha ndcado con anterordad, el momento de nerca depende del cuerpo en cuestón pero tambén del eje respecto al cual gra. Como el número de posbles ejes es nfnto, en prncpo habría que volver a calcular un nuevo momento de nerca para cada nuevo eje. Sn embargo, el Teorema de Stener permte obtener el momento de nerca de un eje que sea paralelo a un eje prncpal que pase por el centro de masa. En concreto, s el momento de nerca respecto del eje que pasa por el centro de masa es I y el momento de nerca respecto al eje paralelo al prmero es I, se cumple: I = I + md donde d es la separacón entre los dos ejes. La stuacón se esquematza en la Fgura 15(a), donde se han hecho concdr los ejes de rotacón con los ejes z y z. Esto se puede hacer sempre, ya que los ejes son paralelos. Los momentos de nerca I y I serán: I = (x + y )dm y I = (x + y )dm Los vectores de poscón r y r se relaconan según: { r = r x = x + r CM = + x CM y = y + y CM con lo que: I = (x + y )dm = ((x + x CM ) + (y + y CM ) ) dm = ( ) = x + x CM + x x CM + y + y CM + y y CM dm = = (x + y )dm + (x CM + ycm )dm + (x x CM + y y CM )dm El prmero de los sumandos del últmo térmno corresponde con I, mentras que el segundo resulta ser md. El tercer de los sumandos es nulo, ya que 1 m x dm corresponde con la componte Davd Blanco (dblanco@ugr.es) 19 Curso
20 4 MOMENTO DE INERCIA. CÁLCULO Y TEOREMAS FUNDAMENTALES x del vector de poscón del centro de masa en el sstema de coordenadas centrado en el centro de masas, por lo que dcha componente será nula. Lo msmo sucede con 1 m y dm, con lo que se demuestra el teorema. Por ejemplo, para calcular el momento de nerca de una barra grando respecto de un eje perpendcular que pasa por uno de sus extremos, se podría haber utlzado que el momento de nerca de un eje perpendcular a la barra y que pase por su centro es I = ml 1, por lo que el momento respecto del eje que pasa por su extremo será: ( ) L I = I + m = ml 1 + ml = ml 4 3 que corresponde con el momento angular que se calculó en su momento. Ejemplo 7. Encontrar el momento de nerca de una plancha cuadrada respecto de un eje perpendcular que pase por su centro La stuacón se esquematza en la Fgura 15(b). La plancha se dvde en tras estrechas, de longtud a, anchura dy y masa dm, tal y como se ndca en la fgura, que podrán consderarse como barras undmensonales. El eje de gro no pasa por el centro de las barras, sno que esta desplazado una cantdad y respecto de cada una de las barras (la dstanca y varará de unas barras a otras). El momento de nerca de las barras respecto del un eje perpendcular que pase por el centro sería di = a dm 1, lo que se puede utlzar para calcular el momento de nerca de cada una de las barras hacendo uso del teorema de Stener: di = a dm 1 + dmy El momento de nerca de la plancha total será la suma de los momentos de nerca de cada una de las planchas: a a ( ) a a ( ) I = di = a a 1 + a a ( ) y dm = a 1 + a y ρ s ds = a 1 + y ρ s ady ( a a ) a ( ) a =ρ s a dy + y 3 dy = ρ s a a3 = a4 ρ s 1 6 a a Como la densdad superfcal de masa es ρ s = m a el momento de nerca resulta: I = ma Teorema de las fguras planas En el caso de fguras planas exste un teorema que nos permte relaconar el momento de nerca respecto de un eje perpendcular a la fgura I z, con los momentos de nerca respecto de otros dos ejes que están contendos en la fgura y que son perpendculares entre sí I x y I y. En concreto el teorema nos dce que: I z = I x + I y Para demostrar el teorema, nos fjamos en la Fgura 15, donde aparece un sóldo rígdo plano, que se ha hecho concdr con el plano xy, y por tanto es perpendcular al eje z. Cuando el sóldo gra respecto del eje x, el momento de nerca respecto de este eje I x será gual a la suma de la masa de cada porcón de sóldo por la dstanca de este trozo al eje x (que corresponde con la coordenada y de cada cada trozo) al cuadrado. Por tanto: I x = y dm Davd Blanco (dblanco@ugr.es) 0 Curso
21 5 ECUACIÓN FUNDAMENTAL DE LA DINÁMICA DE ROTACIÓN De gual forma, el momento de nerca respecto del eje y será: I y = x dm Por otro lado, el momento de nerca del sóldo grando respecto del eje z, será la suma de la masa de cada trozo por la dstanca al eje z al cuadrado. Pero la dstanca de una pequeña porcón de sóldo al eje z no es otra cosa que x + y, con x e y las coordenadas del trozo. Por tanto: I y = (x + y )dm = x dm + y dm = I x + I y Lo que demuestra el teorema. Ejemplo 8. Encontrar el momento de nerca de una plancha cuadrada respecto de un eje perpendcular que pase por su centro Procedemos a repetr el ejemplo anteror que está esquematzado en la Fgura 15(b), pero hacendo uso del teorema de las fguras planas. En este caso, el momento que se quere calcular sería I z a través de los momentos I x e I y, que corresponden con los momentos de nerca de la plancha respecto de ejes que paralelos a la plancha y a uno de sus lados y que pasen por el centro. Se estudo que estos momentos de nerca eran guales a los de una barra grando por su centro, por lo que: I x = I y = ma 1 Por tanto el momento de nerca buscado será: x z Fgura 15: Fgura plana contenda en el plano xy. y I z = I x + I y = ma 1 + ma 1 = ma 6 que es el msmo resultado que obtuvmos anterormente. Ejemplo 9. Encontrar el momento de nerca de dsco de masa m y rado a grando por uno de sus dámetros. El momento de nerca respecto de un eje perpendcular que pase por su centro ya se ha estudado y resultó ser ma, que corresponderá con I z del teorema de las fguras planas. Lo que buscamos es I x e I y, que en este caso son guales debdo a la forma que posee el dsco. Por tanto I x = I y = I y el teorema de las fguras planas queda: I z = I x + I y = I I = I z = ma 5. Ecuacón fundamental de la dnámca de rotacón El movmento de cualquer sóldo rígdo se puede expresar como un movmento de traslacón de un punto, más un movmento de rotacón en torno a ese punto. Este punto puede ser cualquera, de forma que esta descomposcón de un movmento complejo en uno de traslacón y otro de rotacón no es unívoca. Para que en el movmento de rotacón se pueda descrbr de una forma senclla a través de la ecuacón (8), el punto que se elja no puede ser cualquera. Las eleccones más habtuales son o ben un punto fjo o ben el centro de masa. En el prmer caso, el movmento del sóldo es de rotacón pura en torno al punto elegdo y no hay traslacón. Davd Blanco (dblanco@ugr.es) 1 Curso
22 6 ENERGÍA DEL SÓLIDO RÍGIDO Cuando el punto elegdo es el centro de masa, el movmento de traslacón tambén se smplfca, ya que sólo hay que tener en cuenta la fuerzas exterores, de forma que: F ext = d p CM dt donde, como ya sabemos, F ext es la resultante de las fuerzas exterores aplcadas sobre el sóldo, y p CM es el producto de la masa del sstema por la velocdad del centro de masa. Ésta es déntca a la que tendría un masa puntual, de masa gual a la masa del sóldo, movéndose bajo la accón de F ext, lo que se estudó a lo largo del tema anteror. Por otro lado, s el punto elegdo como punto de reduccón de momentos es el centro de masa o un punto fjo, se puede utlzar la ecuacón (8) para descrbr el movmento de rotacón. S además, el eje respecto del que gra es un eje de smetría, el movmento de rotacón cumple: M ext = d L dt = d dt (I ω) S el eje permanece fjo, I es contante y la anteror ecuacón queda: M ext = I d ω dt = I α Cuando el eje no es un eje de smetría, se multplca la ecuacón (8) por el versor ê que marca la dreccón de la velocdad angular. Se obtene: M ext ê = d L dt ê = d ( ) L ê = d ext (Iω) = Me = I dω dt dt dt = Iα donde se ha supuesto que el eje de rotacón permanece fjo. Por lo tanto, aunque el eje no sea de smetría, s permanece fjo la rotacón en torno al eje vene descrta por la componente del momento de las fuerzas exterores en la dreccón del eje. 6. Energía del sóldo rígdo En el tema anteror se estudó que la energía mecánca de un sstema de partículas se podía expresar como: E m = E c + E p = E c + E ccm + E pext + E pnt donde E c es la energía cnétca relatva, E ccm es la energía cnétca del centro de masas, E pext es la energía potencal de las fuerzas externas conservatvas y E pnt es la energía potencal de las fuerzas nternas conservatvas. Para que la energía potencal de las fuerzas nternas conservatvas varíe, es necesaro que la dstanca entre las partículas varía, lo que no puede pasar en un sóldo rígdo. Por tanto, la energía potencal nterna no habrá que tenerla en cuenta en un sóldo rígdo. La expresón de la energía potencal de las fuerzas exterores depende de qué fuerzas sean. La fuerza exteror conservatva más habtual es la fuerza gravtatora, cerca de la superfce terrestre. En este caso, la energía potencal gravtatora del sóldo rígdo será gual a la suma de las energías potencales gravtatoras de cada una de las partículas: E p = m gh = g m h = gmh CM Es decr, es gual a la gravedad por la masa por la altura del centro de masa. Davd Blanco (dblanco@ugr.es) Curso
23 7 RODADURA La energía cnétca del centro de masa es E ccm = 1 mv CM La energía cnétca relatva tene en cuenta sólo la velocdad relatva de las partículas respecto del centro de masa, luego: E c = 1 m v 1 = m ωl = 1 ω donde l es la dstanca de cada partícula al eje de gro. Por tanto, la energía cnétca relatva queda: E c = 1 Iω Con todo esto, un sóldo rígdo movéndose bajo la únca fuerza externa conservatva de la gravedad tene una energía mecánca que resulta ser: m l 7. Rodadura E m = 1 Iω + 1 mv CM + gmh CM El movmento de rodadura es el ejemplo más común de movmento de un sóldo rígdo en el que este rota y se traslada. Es el movmento típco que realzan las ruedas o las esferas al rodar. Dentro de los movmentos de rodadura el más común es el que se conoce como rodar sn deslzar, en el cual, en el movmento sólo un punto del sóldo rígdo está en contacto con cada uno de los puntos de la superfce por la que rueda. Esto se esquematza en la Fgura 16, donde se representan dos nstantes de un sóldo desplazándose haca la derecha y rotando al msmo tempo. S el sóldo gra sn deslzar, el número de puntos que hay entre el punto A y B será gual al número de puntos en la superfce horzontal en s, que es el espaco recorrdo por el sóldo en su desplazamento. Por tanto se cumple: s = Rθ z y A R x θ B Δ s Fgura 16: Dos nstantes en el movmento de rodadura de un sóldo rígdo. θ A B Lo que se conoce como condcón de rodadura. Esta condcón es ndependente de las fuerzas que actúen sobre el sóldo y de la velocdad o la aceleracón que lleve. Es una condcón geométrca y se cumplrá sempre que el sóldo rote sn deslzar. El espaco s es el espaco que recorre el centro de masa del sóldo, por lo que, dervando la anteror ecuacón se obtene: v CM = Rω donde v es el módulo de la velocdad del centro de masa. Por su parte, ω es la velocdad a la que rota el sóldo. Davd Blanco (dblanco@ugr.es) 3 Curso
24 7 RODADURA S se vuelve a dervar se obtene una relacón entre la aceleracón del centro de masas y la aceleracón angular: a CM = Rα Una vez relaconadas las magntudes cnemátcas angulares y lneales del sóldo rígdo, pasamos a estudar como se mueven los dstntos puntos del sóldo. La velocdad de un punto será: v = v + v CM S suponemos que el sóldo se encuentra rotando con una velocdad angular ω y que el eje vertcal es el eje y y el eje horzontal el eje x, se tene, tenendo en cuenta la relacón entre las velocdades lneales y angulares, que v CM = Rωî. Por otro lado, el movmento relatvo respecto del centro de masa es un movmento de rotacón pura, por lo que se cumple v = ω r, tal y como se estudó en la prmera seccón del tema. Según lo ndcado en el dbujo ω = ωˆk y r = x î + y ĵ. Con esto, la velocdad de una partícula del sóldo será: v = rωî + ω( ˆk) (x î + y ĵ) = Rωî + ω( x ĵ + y î) = ω(r + y )î ωx ĵ Con esta expresón se puede obtener la velocdad de cualquer punto del sóldo. Por ejemplo, el punto que se encuentra más a la zquerda tendrá por coordenadas relatvas ( R, 0) y por tanto una velocdad v = Rω(î + ĵ). El punto stuado más a la derecha tene de coordenadas relatvas ( R, 0) y una velocdad v = Rω(î ĵ). Por otro lado el punto stuado más arrba tene las coordenadas relatvas (0, R) y una velocdad v = Rωî. Lo más sgnfcatvo es lo que le sucede al punto stuado en contacto con la superfce horzontal, el cual tene de coordenadas relatvas (0, R), lo que produce una velocdad v = 0, es decr, se encuentra en reposo. Como resultado de lo anteror se puede afrmar que s un sóldo gra sn deslzar, el punto en contacto se encuentra en reposo. Esto es un resultado puramente cnemátco y se cumple para cualquer fuerza o aceleracón Dnámca Es este apartado se estudan como se mueve un sóldo rígdo de masa m y rado R sometdo a fuerzas que ruede sn deslzar. En la Fgura 17 se presenta un sóldo del que se tra con una fuerza F de su punto medo. S ncalmente el sóldo estaba en reposo, al trar de él se tende a producr un desplazamento entre el punto nferor del sóldo y la superfce horzontal. A este desplazamento se opondrá una fuerza de rozamento F r. S el cuerpo gra sn deslzar, el punto en contacto estará en reposo, por lo que la fuerza de rozamento es estátca y por tanto una ncógnta del problema. Sólo se sabe que exste un límte superor a esta fuerza de rozamento estátca que es F r µ e N. Así, el equlbro de fuerzas en la dreccón horzontal producrá: F F r = ma F r R F Fgura 17: Esquema de fuerzas de un sóldo rodando. donde la masa m corresponde a la masa total del sóldo y la aceleracón a es la aceleracón del centro de masa. En esta ecuacón se desconoce tanto a como F r, por lo que no se puede resolver. Para poder hacerlo hay que recurrr a la ecuacón de rotacón, en la cual la resultante de los momentos de las fuerzas es Davd Blanco (dblanco@ugr.es) 4 Curso
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
Vectores VECTORES 1.- Magnitudes Escalares y Magnitudes Vectoriales. Las Magnitudes Escalares: Las Magnitudes Vectoriales:
 VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
VECTOES 1.- Magntudes Escalares y Magntudes Vectorales. Las Magntudes Escalares: son aquellas que quedan defndas úncamente por su valor numérco (escalar) y su undad correspondente, Eemplo de magntudes
Campo eléctrico. Líneas de campo. Teorema de Gauss. El campo de las cargas en reposo. Campo electrostático
 qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
5ª Lección: Sistema de fuerzas gravitatorias. Cálculo de centros de gravedad de figuras planas: teoremas de Guldin.
 Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Capítulo II: MECÁNICA DEL SÓLIDO RÍGIDO 5ª Leccón: Sstema de fuerzas gravtatoras. Cálculo de centros de gravedad de fguras planas: teoremas de Guldn. Sstemas de fuerzas gravtatoras La deduccón parte de
Una Reformulación de la Mecánica Clásica
 Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Una Reformulacón de la Mecánca Clásca Antono A Blatter Lcenca Creatve Commons Atrbucón 30 (2015) Buenos Ares Argentna Este trabajo presenta una reformulacón de la mecánca clásca que es nvarante bajo transformacones
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
EJERCICIOS RESUELTOS DE TRABAJO Y ENERGÍA
 JRCICIOS RSULTOS D TRABAJO Y NRGÍA. Un bloque de 40 kg que se encuentra ncalmente en reposo, se empuja con una uerza de 30 N, desplazándolo en línea recta una dstanca de 5m a lo largo de una superce horzontal
JRCICIOS RSULTOS D TRABAJO Y NRGÍA. Un bloque de 40 kg que se encuentra ncalmente en reposo, se empuja con una uerza de 30 N, desplazándolo en línea recta una dstanca de 5m a lo largo de una superce horzontal
Fugacidad. Mezcla de gases ideales
 Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
Termodnámca del equlbro Fugacdad. Mezcla de gases deales rofesor: Alí Gabrel Lara 1. Fugacdad 1.1. Fugacdad para gases Antes de abarcar el caso de mezclas de gases, debemos conocer como podemos relaconar
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Primer Semestre - Otoño 2014. Omar De la Peña-Seaman. Instituto de Física (IFUAP)
 MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
MECÁNICA CLÁSICA MAESTRÍA EN CIENCIAS (FÍSICA) Curso de Prmer Semestre - Otoño 2014 Omar De la Peña-Seaman Insttuto de Físca (IFUAP) Benemérta Unversdad Autónoma de Puebla (BUAP) 1 / Omar De la Peña-Seaman
CALCULO DE CENTROS DE MASA ! =
 CLCULO DE CENTOS DE S EXPESION GENEL: La poscón del centro de masas de un sstema de partículas vene dada por la expresón: r C.. m r m m r (1) donde es la masa total del sstema de partículas. Esta es una
CLCULO DE CENTOS DE S EXPESION GENEL: La poscón del centro de masas de un sstema de partículas vene dada por la expresón: r C.. m r m m r (1) donde es la masa total del sstema de partículas. Esta es una
Resumen de los teoremas fundamentales del análisis estructural aplicados a celosías
 Resumen de los teoremas fundamentales del análss estructural aplcados a celosías INTRODUCCIÓN Fuerzas aplcadas y deformacones de los nudos (=1,n) ESTICIDD Tensón =Ν/Α. Unforme en cada seccón de la arra.
Resumen de los teoremas fundamentales del análss estructural aplcados a celosías INTRODUCCIÓN Fuerzas aplcadas y deformacones de los nudos (=1,n) ESTICIDD Tensón =Ν/Α. Unforme en cada seccón de la arra.
Etáti Estática. 2.Centros de gravedad y 3.Momentos de inercia
 Etát Estátca.Equlbro 2.Centros de gravedad y 3.Momentos de nerca Parte de la físca que estuda el equlbro de los cuerpos Partedelafíscaqueestudalasrelaconesexstentes entre las fuerzas que actúan en un cuerpo
Etát Estátca.Equlbro 2.Centros de gravedad y 3.Momentos de nerca Parte de la físca que estuda el equlbro de los cuerpos Partedelafíscaqueestudalasrelaconesexstentes entre las fuerzas que actúan en un cuerpo
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Tema 3. Trabajo, energía y conservación de la energía
 Físca I. Curso 2010/11 Departamento de Físca Aplcada. ETSII de Béjar. Unversdad de Salamanca Profs. Alejandro Medna Domínguez y Jesús Ovejero Sánchez Tema 3. Trabajo, energía y conservacón de la energía
Físca I. Curso 2010/11 Departamento de Físca Aplcada. ETSII de Béjar. Unversdad de Salamanca Profs. Alejandro Medna Domínguez y Jesús Ovejero Sánchez Tema 3. Trabajo, energía y conservacón de la energía
ESTADÍSTICA (GRUPO 12)
 ESTADÍSTICA (GRUPO 12) CAPÍTULO II.- ANÁLISIS DE UNA CARACTERÍSTICA (DISTRIBUCIONES UNIDIMENSIONALES) TEMA 7.- MEDIDAS DE CONCENTRACIÓN. DIPLOMATURA EN CIENCIAS EMPRESARIALES UNIVERSIDAD DE SEVILLA 1.
ESTADÍSTICA (GRUPO 12) CAPÍTULO II.- ANÁLISIS DE UNA CARACTERÍSTICA (DISTRIBUCIONES UNIDIMENSIONALES) TEMA 7.- MEDIDAS DE CONCENTRACIÓN. DIPLOMATURA EN CIENCIAS EMPRESARIALES UNIVERSIDAD DE SEVILLA 1.
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
ELECTROSTÁTICA. CAMPO ELÉCTRICO EN EL VACÍO.
 ELECTROSTÁTICA. CAMPO ELÉCTRICO EN EL VACÍO..- PERSPECTIVA HISTÓRICA MATERIA { MOLÉCULAS } { ÁTOMOS}, sendo los átomos y/o moléculas estables por la nteraccón electromagnétca. Desde la perspectva electromagnétca
ELECTROSTÁTICA. CAMPO ELÉCTRICO EN EL VACÍO..- PERSPECTIVA HISTÓRICA MATERIA { MOLÉCULAS } { ÁTOMOS}, sendo los átomos y/o moléculas estables por la nteraccón electromagnétca. Desde la perspectva electromagnétca
OSCILACIONES 1.- INTRODUCCIÓN
 OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
OSCILACIONES 1.- INTRODUCCIÓN Una parte relevante de la asgnatura trata del estudo de las perturbacones, entenddas como varacones de alguna magntud mportante de un sstema respecto de su valor de equlbro.
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
6.1 EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS
 TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
TEMA NÚMEROS COMPLEJOS. EN QUÉ CONSISTEN LOS NÚMEROS COMPLEJOS DEFINICIONES Al resolver ecuacones del tpo : x + = 0 x = ± que no tene solucón en los números reales. Los números complejos nacen del deseo
i=1 Demuestre que cumple los axiomas de norma. Calcule el límite Verifiquemos cada uno de los axiomas de la definición de norma: i=1
 CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
CAPÍTULO 3 EJERCICIOS RESUELTOS: CONCEPTOS BÁSICOS DE ÁLGEBRA LINEAL Ejerccos resueltos 1 1. La norma p (tambén llamada l p ) en R n se defne como ( ) 1/p x p = x p. Demuestre que cumple los axomas de
1. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA. Definición del álgebra geométrica del espacio-tiempo
 EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
Métodos específicos de generación de diversas distribuciones discretas
 Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
Tema 3 Métodos específcos de generacón de dversas dstrbucones dscretas 3.1. Dstrbucón de Bernoull Sea X B(p). La funcón de probabldad puntual de X es: P (X = 1) = p P (X = 0) = 1 p Utlzando el método de
CÁLCULO VECTORIAL 1.- MAGNITUDES ESCALARES Y VECTORIALES. 2.- VECTORES. pág. 1
 CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
Cantidad de movimiento
 Cnétca 37 / 63 Cnétca Cantdad de momento Momento cnétco: Teorema de Koeng Energía cnétca: Teorema de Koeng Sóldo con punto fjo: Momento cnétco Sóldo con punto fjo: Energía cnétca Sóldo: Momento relato
Cnétca 37 / 63 Cnétca Cantdad de momento Momento cnétco: Teorema de Koeng Energía cnétca: Teorema de Koeng Sóldo con punto fjo: Momento cnétco Sóldo con punto fjo: Energía cnétca Sóldo: Momento relato
Física I. TRABAJO y ENERGÍA MECÁNICA. Apuntes complementarios al libro de texto. Autor : Dr. Jorge O. Ratto
 ísca I Apuntes complementaros al lbro de teto TRABAJO y ENERGÍA MECÁNICA Autor : Dr. Jorge O. Ratto Estudaremos el trabajo mecánco de la sguente manera : undmensonal constante Tpo de movmento varable bdmensonal
ísca I Apuntes complementaros al lbro de teto TRABAJO y ENERGÍA MECÁNICA Autor : Dr. Jorge O. Ratto Estudaremos el trabajo mecánco de la sguente manera : undmensonal constante Tpo de movmento varable bdmensonal
ONDAS ESFÉRICAS RADIACIÓN ACÚSTICA
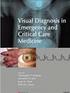 ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
Organización y resumen de datos cuantitativos
 Organzacón y resumen de datos cuanttatvos Contendos Organzacón de datos cuanttatvos: dagrama de tallos y hojas, tablas de frecuencas. Hstogramas. Polígonos. Ojvas ORGANIZACIÓN Y RESUMEN DE DATOS CUANTITATIVOS
Organzacón y resumen de datos cuanttatvos Contendos Organzacón de datos cuanttatvos: dagrama de tallos y hojas, tablas de frecuencas. Hstogramas. Polígonos. Ojvas ORGANIZACIÓN Y RESUMEN DE DATOS CUANTITATIVOS
TEMA 8: PRÉSTAMOS ÍNDICE
 TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
v i CIRCUITOS ELÉCTRICOS (apuntes para el curso de Electrónica)
 IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
Población: Es el conjunto de todos los elementos cuyo conocimiento nos interesa y serán objeto de nuestro estudio.
 Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
Resumen TEMA 5: Dinámica de percusiones
 TEM 5: Dnámca e percusones Mecánca Resumen TEM 5: Dnámca e percusones. Concepto e percusón Impulsón elemental prouca por una fuerza: F Impulsón prouca por una fuerza en un nteralo (t, t ): F Percusón es
TEM 5: Dnámca e percusones Mecánca Resumen TEM 5: Dnámca e percusones. Concepto e percusón Impulsón elemental prouca por una fuerza: F Impulsón prouca por una fuerza en un nteralo (t, t ): F Percusón es
CESMA BUSINESS SCHOOL
 CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 4 RENTAS y MÉTODOS DE AMORTIZACIÓN Javer Blbao García 1 1.- Introduccón Defncón: Conjunto de captales con vencmentos equdstantes de tempo. Para que exsta
APLICACIÓN DEL ANALISIS INDUSTRIAL EN CARTERAS COLECTIVAS DE VALORES
 APLICACIÓN DEL ANALISIS INDUSTRIAL EN CARTERAS COLECTIVAS DE VALORES Documento Preparado para la Cámara de Fondos de Inversón Versón 203 Por Rodrgo Matarrta Venegas 23 de Setembre del 204 2 Análss Industral
APLICACIÓN DEL ANALISIS INDUSTRIAL EN CARTERAS COLECTIVAS DE VALORES Documento Preparado para la Cámara de Fondos de Inversón Versón 203 Por Rodrgo Matarrta Venegas 23 de Setembre del 204 2 Análss Industral
Conservación del Momento Lineal y de la Energía
 Conservacón del Moento Lneal y de la Energía Conservacón del Moento Lneal y de la Energía Objetvos Coprobar experentalente la conservacón del oento lneal edante choques elástcos e nelástcos. Coprobar la
Conservacón del Moento Lneal y de la Energía Conservacón del Moento Lneal y de la Energía Objetvos Coprobar experentalente la conservacón del oento lneal edante choques elástcos e nelástcos. Coprobar la
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Tema 1.3_A La media y la desviación estándar
 Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
Dicha tabla adopta la forma del diagrama de árbol del dibujo. En éste, a cada uno de los sucesos A y A c se les ha asociado los sucesos B y B c.
 Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
Estadístca robablístca 6. Tablas de contngenca y dagramas de árbol. En los problemas de probabldad y en especal en los de probabldad condconada, resulta nteresante y práctco organzar la nformacón en una
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUERZAS CENTRALES. Física 2º Bachillerato
 FUERZAS CENTRALES 1. Fuerza central. Momento de una fuerza respecto de un punto. Momento de un fuerza central 3. Momento angular de una partícula 4. Relación entre momento angular y el momento de torsión
FUERZAS CENTRALES 1. Fuerza central. Momento de una fuerza respecto de un punto. Momento de un fuerza central 3. Momento angular de una partícula 4. Relación entre momento angular y el momento de torsión
Para abrirla tirando de un punto intermedio entre el eje y la manecilla habrá que realizar el mismo momentode fuerzas: Mg 50 F ʹ = 2F =
 ESTTIC La fuerza necesara para abrr una puerta trando de su maneclla es la centésma parte de su peso. S la puerta pesa 10 kg y la dstanca de la maneclla al eje de gro es 1 m, calcular la fuerza F ʹ necesara
ESTTIC La fuerza necesara para abrr una puerta trando de su maneclla es la centésma parte de su peso. S la puerta pesa 10 kg y la dstanca de la maneclla al eje de gro es 1 m, calcular la fuerza F ʹ necesara
CANTIDADES VECTORIALES: VECTORES
 INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
Pregunta Hoy está nublado, cuál es la probabilidad de que mañana continúe nublado? cuál es la probabilidad de que está nublado pasado mañana?
 Cadenas de Marov Después de mucho estudo sobre el clma, hemos vsto que s un día está soleado, en el 70% de los casos el día sguente contnua soleado y en el 30% se pone nublado. En térmnos de probabldad,
Cadenas de Marov Después de mucho estudo sobre el clma, hemos vsto que s un día está soleado, en el 70% de los casos el día sguente contnua soleado y en el 30% se pone nublado. En térmnos de probabldad,
Smoothed Particle Hydrodynamics Animación Avanzada
 Smoothed Partcle Hydrodynamcs Anmacón Avanzada Iván Alduán Íñguez 03 de Abrl de 2014 Índce Métodos sn malla Smoothed partcle hydrodynamcs Aplcacón del método en fludos Búsqueda de vecnos Métodos sn malla
Smoothed Partcle Hydrodynamcs Anmacón Avanzada Iván Alduán Íñguez 03 de Abrl de 2014 Índce Métodos sn malla Smoothed partcle hydrodynamcs Aplcacón del método en fludos Búsqueda de vecnos Métodos sn malla
APENDICE A. El Robot autónomo móvil RAM-1.
 Planfcacón de Trayectoras para Robots Móvles APENDICE A. El Robot autónomo móvl RAM-1. A.1. Introduccón. El robot autónomo móvl RAM-1 fue dseñado y desarrollado en el Departamento de Ingenería de Sstemas
Planfcacón de Trayectoras para Robots Móvles APENDICE A. El Robot autónomo móvl RAM-1. A.1. Introduccón. El robot autónomo móvl RAM-1 fue dseñado y desarrollado en el Departamento de Ingenería de Sstemas
Variable aleatoria: definiciones básicas
 Varable aleatora: defncones báscas Varable Aleatora Hasta ahora hemos dscutdo eventos elementales y sus probabldades asocadas [eventos dscretos] Consdere ahora la dea de asgnarle un valor al resultado
Varable aleatora: defncones báscas Varable Aleatora Hasta ahora hemos dscutdo eventos elementales y sus probabldades asocadas [eventos dscretos] Consdere ahora la dea de asgnarle un valor al resultado
EQUILIBRIO DE UN CUERPO RIGIDO
 Manual e Laboratoro e ísca I C - UNMSM EQUILIBRIO E UN CUERPO RIGIO EXPERIENCIA Nº 6 Cuerpo rígdo: La dstanca entre dos puntos cualesquera del cuerpo permanece nvarante en el tempo. I. OBJETIVOS - Estudar
Manual e Laboratoro e ísca I C - UNMSM EQUILIBRIO E UN CUERPO RIGIO EXPERIENCIA Nº 6 Cuerpo rígdo: La dstanca entre dos puntos cualesquera del cuerpo permanece nvarante en el tempo. I. OBJETIVOS - Estudar
Efectos fijos o aleatorios: test de especificación
 Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Cómo car?: Montero. R (2011): Efectos fjos o aleatoros: test de especfcacón. Documentos de Trabajo en Economía Aplcada. Unversdad de Granada. España Efectos fjos o aleatoros: test de especfcacón Roberto
Histogramas: Es un diagrama de barras pero los datos son siempre cuantitativos agrupados en clases o intervalos.
 ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
UNA FORMA GRÁFICA DE ENSEÑANZA: APLICACIÓN AL DUOPOLIO DE. Dpto. de Métodos Cuantitativos e Informáticos. Universidad Politécnica de Cartagena.
 UNA FORMA GRÁFICA DE ENSEÑANZA: APLICACIÓN AL DUOPOLIO DE COURNOT. Autores: García Córdoba, José Antono; josea.garca@upct.es Ruz Marín, Manuel; manuel.ruz@upct.es Sánchez García, Juan Francsco; jf.sanchez@upct.es
UNA FORMA GRÁFICA DE ENSEÑANZA: APLICACIÓN AL DUOPOLIO DE COURNOT. Autores: García Córdoba, José Antono; josea.garca@upct.es Ruz Marín, Manuel; manuel.ruz@upct.es Sánchez García, Juan Francsco; jf.sanchez@upct.es
Cálculo y EstadísTICa. Primer Semestre.
 Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado en Geomátca y Topografía Escuela Técnca Superor de Ingeneros en Topografía, Geodesa y Cartografía. Unversdad Poltécnca de Madrd
Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado en Geomátca y Topografía Escuela Técnca Superor de Ingeneros en Topografía, Geodesa y Cartografía. Unversdad Poltécnca de Madrd
Perturbación de los valores propios simples de matrices de polinomios dependientes diferenciablemente de parámetros
 Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
Perturbacón de los valores propos smples de matrces de polnomos dependentes dferencablemente de parámetros M Isabel García-Planas 1, Sona Tarragona 2 1 Dpt de Matemàtca Aplcada I, Unverstat Poltècnca de
1 Física General I Paralelos 05 y 22. Profesor RodrigoVergara R. 0501) Cuerpo Rígido y Torque. A) Noción intuitiva de torque
 050) Cuerpo Rígdo y Torque A) Nocón ntutva de torque Pense en la apertura de una puerta como la mostrada en la fgura a). Para hacerlo, la persona aplca una fuerza F a la puerta, que a su vez aplca (transmte)
050) Cuerpo Rígdo y Torque A) Nocón ntutva de torque Pense en la apertura de una puerta como la mostrada en la fgura a). Para hacerlo, la persona aplca una fuerza F a la puerta, que a su vez aplca (transmte)
Solución: Se denomina malla en un circuito eléctrico a todas las trayectorias cerradas que se pueden seguir dentro del mismo.
 1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
Colección de problemas de. Poder de Mercado y Estrategia
 de Poder de Mercado y Estratega Curso 3º - ECO- 0-03 Iñak Agurre Jaromr Kovark Marta San Martín Fundamentos del Análss Económco I Unversdad del País Vasco UPV/EHU Tema. Olgopolo y competenca monopolístca.
de Poder de Mercado y Estratega Curso 3º - ECO- 0-03 Iñak Agurre Jaromr Kovark Marta San Martín Fundamentos del Análss Económco I Unversdad del País Vasco UPV/EHU Tema. Olgopolo y competenca monopolístca.
Tema 1: Estadística Descriptiva Unidimensional Unidad 2: Medidas de Posición, Dispersión y de Forma
 Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Disipación de energía mecánica
 Laboratoro de Mecáa. Expermento 13 Versón para el alumno Dspacón de energía mecáa Objetvo general El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Objetvos partculares
Laboratoro de Mecáa. Expermento 13 Versón para el alumno Dspacón de energía mecáa Objetvo general El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Objetvos partculares
Trabajo y Energía Cinética
 Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO
 CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO 1 ÍNDICE 1. INTRODUCCIÓN 2. EL CAMPO MAGNÉTICO 3. PRODUCCIÓN DE UN CAMPO MAGNÉTICO 4. LEY DE FARADAY 5. PRODUCCIÓN DE UNA FUERZA EN UN CONDUCTOR 6. MOVIMIENTO DE
CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO 1 ÍNDICE 1. INTRODUCCIÓN 2. EL CAMPO MAGNÉTICO 3. PRODUCCIÓN DE UN CAMPO MAGNÉTICO 4. LEY DE FARADAY 5. PRODUCCIÓN DE UNA FUERZA EN UN CONDUCTOR 6. MOVIMIENTO DE
Una matriz es un conjunto de elementos de cualquier naturaleza aunque, en general, son números ordenados en filas y columnas.
 MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
MATRICES Las matrces se utlzan en el cálculo numérco, en la resolucón de sstemas de ecuacones lneales, de las ecuacones dferencales y de las dervadas parcales. Además de su utldad para el estudo de sstemas
Aplicación de la termodinámica a las reacciones químicas Andrés Cedillo Departamento de Química Universidad Autónoma Metropolitana-Iztapalapa
 Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Convertidores Digital-Analógico y Analógico-Digital
 Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
Dualidad entre procesos termodinámicos y electromecánicos
 ENERGÍA Y COENERGÍA EN IEMA ELECROMECÁNICO REALE, DEDE PROCEDIMIENO ERMODINÁMICO CLÁICO Alfredo Álvarez García Profesor de Inenería Eléctrca de la Escuela de Inenerías Industrales de adajoz. Resumen La
ENERGÍA Y COENERGÍA EN IEMA ELECROMECÁNICO REALE, DEDE PROCEDIMIENO ERMODINÁMICO CLÁICO Alfredo Álvarez García Profesor de Inenería Eléctrca de la Escuela de Inenerías Industrales de adajoz. Resumen La
9. Movimiento Circular Uniformemente Acelerado
 9. Movmento Crcular Unormemente Acelerado Ete movmento e preenta cuando un móvl con trayectora crcular aumenta o dmnuye en cada undad de tempo u velocdad angular en orma contante, por lo que u aceleracón
9. Movmento Crcular Unormemente Acelerado Ete movmento e preenta cuando un móvl con trayectora crcular aumenta o dmnuye en cada undad de tempo u velocdad angular en orma contante, por lo que u aceleracón
ANÁLISIS DE ACCESIBILIDAD E INTERACCIÓN ESPECIAL:
 Geografía y Sstemas de Informacón Geográfca (GEOSIG). Revsta dgtal del Grupo de Estudos sobre Geografía y Análss Espacal con Sstemas de Informacón Geográfca (GESIG). Programa de Estudos Geográfcos (PROEG).
Geografía y Sstemas de Informacón Geográfca (GEOSIG). Revsta dgtal del Grupo de Estudos sobre Geografía y Análss Espacal con Sstemas de Informacón Geográfca (GESIG). Programa de Estudos Geográfcos (PROEG).
Apéndice A: Metodología para la evaluación del modelo de pronóstico meteorológico
 Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Tabla de contendos Ap.A Apéndce A: Metodología
Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Apéndce A: Metodología para la evaluacón del modelo de pronóstco meteorológco Tabla de contendos Ap.A Apéndce A: Metodología
La variable compleja permite resolver problemas muy diferentes dentro de. áreas tan variadas como pueden ser hidráulica, aerodinámica, electricidad,
 17 Análss matemátco para Ingenería. M. MOLERO; A. SALVADOR; T. MENARGUEZ; L. GARMENDIA CAPÍTULO 1 Los números complejos La varable compleja permte resolver problemas muy dferentes dentro de áreas tan varadas
17 Análss matemátco para Ingenería. M. MOLERO; A. SALVADOR; T. MENARGUEZ; L. GARMENDIA CAPÍTULO 1 Los números complejos La varable compleja permte resolver problemas muy dferentes dentro de áreas tan varadas
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA
 LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
Desarrollo de sistema de control para un manipulador de seis grados de libertad
 Memora del Trabajo Fn de Máster realzado por Fdel Pérez Menéndez para la obtencón del título de Máster en Ingenería de Automatzacón e Informátca Industral Desarrollo de sstema de control para un manpulador
Memora del Trabajo Fn de Máster realzado por Fdel Pérez Menéndez para la obtencón del título de Máster en Ingenería de Automatzacón e Informátca Industral Desarrollo de sstema de control para un manpulador
Unidad I. 1. 1. Definición de reacción de combustión. 1. 2. Clasificación de combustibles
 2 Undad I.. Defncón de reaccón de combustón La reaccón de combustón se basa en la reaccón químca exotérmca de una sustanca (o una mezcla de ellas) denomnada combustble, con el oxígeno. Como consecuenca
2 Undad I.. Defncón de reaccón de combustón La reaccón de combustón se basa en la reaccón químca exotérmca de una sustanca (o una mezcla de ellas) denomnada combustble, con el oxígeno. Como consecuenca
Leyes de tensión y de corriente
 hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
www.fisicaeingenieria.es
 2.- PRIMER PRINCIPIO DE LA TERMODINÁMICA. 2.1.- Experencas de Joule. Las experencas de Joule, conssteron en colocar una determnada cantdad de agua en un calorímetro y realzar un trabajo, medante paletas
2.- PRIMER PRINCIPIO DE LA TERMODINÁMICA. 2.1.- Experencas de Joule. Las experencas de Joule, conssteron en colocar una determnada cantdad de agua en un calorímetro y realzar un trabajo, medante paletas
Análisis de error y tratamiento de datos obtenidos en el laboratorio
 Análss de error tratamento de datos obtendos en el laboratoro ITRODUCCIÓ Todas las meddas epermentales venen afectadas de una certa mprecsón nevtable debda a las mperfeccones del aparato de medda, o a
Análss de error tratamento de datos obtendos en el laboratoro ITRODUCCIÓ Todas las meddas epermentales venen afectadas de una certa mprecsón nevtable debda a las mperfeccones del aparato de medda, o a
Tema 1: Tensiones. Tema 1 : TENSIONES F 1 S. n S S O F 4 F 2. Prof.: Jaime Santo Domingo Santillana E.P.S.-Zamora (U.SAL.)
 Tema 1: Tensones Tema 1 : TENINE u F n F Prof.: Jame anto Domngo antllana E.P..-Zamora (U.AL.) - 008 1 Tema 1: Tensones 1.1.- CNCEPT DE TENIÓN Consderemos un sóldo sometdo a un sstema de fueras:, F, F
Tema 1: Tensones Tema 1 : TENINE u F n F Prof.: Jame anto Domngo antllana E.P..-Zamora (U.AL.) - 008 1 Tema 1: Tensones 1.1.- CNCEPT DE TENIÓN Consderemos un sóldo sometdo a un sstema de fueras:, F, F
Las acciones a considerar en el proyecto de una estructura o elemento estructural se pueden clasificar según los criterios siguientes:
 CAÍTULO III ACCIONES Artículo 9º Clasfcacón de las accones Las accones a consderar en el proyecto de una estructura o elemento estructural se pueden clasfcar según los crteros sguentes: - Clasfcacón por
CAÍTULO III ACCIONES Artículo 9º Clasfcacón de las accones Las accones a consderar en el proyecto de una estructura o elemento estructural se pueden clasfcar según los crteros sguentes: - Clasfcacón por
17 MOMENTOS DE INERCIA Y TEOREMA DE STEINER
 17 MOMENOS DE INERCIA Y EOREMA DE SEINER OBJEIVOS Determnacón e la constante recuperaora e un muelle espral. Comprobacón el teorema e Stener. Determnacón expermental el momento e nerca e ferentes cuerpos
17 MOMENOS DE INERCIA Y EOREMA DE SEINER OBJEIVOS Determnacón e la constante recuperaora e un muelle espral. Comprobacón el teorema e Stener. Determnacón expermental el momento e nerca e ferentes cuerpos
4 BALANZA DE MOHR: Contracción de mezcla alcohol/h2o
 4 LNZ DE OHR: Contraccón de mezcla alcohol/h2o CONTENIDOS Defncones. Contraccón de una ezcla. olumen específco deal y real. Uso de la balanza de ohr. erfcacón de Jnetllos. Propagacón de Errores. OJETIOS
4 LNZ DE OHR: Contraccón de mezcla alcohol/h2o CONTENIDOS Defncones. Contraccón de una ezcla. olumen específco deal y real. Uso de la balanza de ohr. erfcacón de Jnetllos. Propagacón de Errores. OJETIOS
El costo de oportunidad social de la divisa ÍNDICE
 El Costo de Oportundad Socal de la Dvsa El costo de oportundad socal de la dvsa ÍNDICE. INTRODUCCIÓN. EL MARCO TEÓRICO 3. CÁLCULO DEL COSTO DE OPORTUNIDAD SOCIAL DE LA DIVISA 3. Nvel agregado 3. Nvel desagregado
El Costo de Oportundad Socal de la Dvsa El costo de oportundad socal de la dvsa ÍNDICE. INTRODUCCIÓN. EL MARCO TEÓRICO 3. CÁLCULO DEL COSTO DE OPORTUNIDAD SOCIAL DE LA DIVISA 3. Nvel agregado 3. Nvel desagregado
http://www.rubenprofe.com.ar biofisica@rubenprofe.com.ar RESISTENCIAS EN PARALELO
 bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
bofsca@rubenprofe.com.ar El crcuto funcona así: ESISTENCIS EN PLELO.- Las cargas salen del extremo postvo de la fuente y recorren el conductor (línea negra) hasta llegar al punto, allí las cargas se dvden
TERMODINÁMICA AVANZADA
 ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
TÉCNICAS AUXILIARES DE LABORATORIO
 TÉCNICAS AUXILIARES DE LABORATORIO I.- ERRORES 1.- Introduccón Todas las meddas epermentales venen afectadas de una mprecsón nherente al proceso de medda. Puesto que en éste se trata, báscamente, de comparar
TÉCNICAS AUXILIARES DE LABORATORIO I.- ERRORES 1.- Introduccón Todas las meddas epermentales venen afectadas de una mprecsón nherente al proceso de medda. Puesto que en éste se trata, báscamente, de comparar
Explicación de las tecnologías - PowerShot SX500 IS y PowerShot SX160 IS
 Explcacón de las tecnologías - PowerShot SX500 IS y PowerShot SX160 IS EMBARGO: 21 de agosto de 2012, 15:00 (CEST) Objetvo angular de 24 mm, con zoom óptco 30x (PowerShot SX500 IS) Desarrollado usando
Explcacón de las tecnologías - PowerShot SX500 IS y PowerShot SX160 IS EMBARGO: 21 de agosto de 2012, 15:00 (CEST) Objetvo angular de 24 mm, con zoom óptco 30x (PowerShot SX500 IS) Desarrollado usando
REGRESION LINEAL SIMPLE
 REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una mustra de observacones formadas por pares de varables: (x 1, y 1 ) (x, y ).. (x n, y n ) A través de esta muestra, se desea estudar la relacón exstente
REGREION LINEAL IMPLE Jorge Galbat Resco e dspone de una mustra de observacones formadas por pares de varables: (x 1, y 1 ) (x, y ).. (x n, y n ) A través de esta muestra, se desea estudar la relacón exstente
Rentas financieras. Unidad 5
 Undad 5 Rentas fnanceras 5.. Concepto de renta 5.2. Clasfcacón de las rentas 5.3. Valor captal o fnancero de una renta 5.4. Renta constante, nmedata, pospagable y temporal 5.4.. Valor actual 5.4.2. Valor
Undad 5 Rentas fnanceras 5.. Concepto de renta 5.2. Clasfcacón de las rentas 5.3. Valor captal o fnancero de una renta 5.4. Renta constante, nmedata, pospagable y temporal 5.4.. Valor actual 5.4.2. Valor
De factores fijos. Mixto. Con interacción Sin interacción. No equilibrado. Jerarquizado
 Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Procesamiento Digital de Imágenes. Pablo Roncagliolo B. Nº 17
 Procesamento Dgtal de mágenes Pablo Roncaglolo B. Nº 7 Orden de las clases... CAPTURA, DGTALZACON Y ADQUSCON DE MAGENES TRATAMENTO ESPACAL DE MAGENES TRATAMENTO EN FRECUENCA DE MAGENES RESTAURACON DE MAGENES
Procesamento Dgtal de mágenes Pablo Roncaglolo B. Nº 7 Orden de las clases... CAPTURA, DGTALZACON Y ADQUSCON DE MAGENES TRATAMENTO ESPACAL DE MAGENES TRATAMENTO EN FRECUENCA DE MAGENES RESTAURACON DE MAGENES
Fisicoquímica CIBEX Guía de Trabajos Prácticos 2010. Trabajo Práctico N 7. - Medida de la Fuerza Electromotriz por el Método de Oposición-
 Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
-.GEOMETRÍA.- a) 37 cm y 45 cm. b) 16 cm y 30 cm. En estos dos, se dan la hipotenusa y un cateto, y se pide el otro cateto:
 -.GEOMETRÍA.- Ejercco nº 1.- Calcula el lado que falta en este trángulo rectángulo: Ejercco nº 2.- En los sguentes rectángulos, se dan dos catetos y se pde la hpotenusa (s su medda no es exacta, con una
-.GEOMETRÍA.- Ejercco nº 1.- Calcula el lado que falta en este trángulo rectángulo: Ejercco nº 2.- En los sguentes rectángulos, se dan dos catetos y se pde la hpotenusa (s su medda no es exacta, con una
Potenciales y campos eléctricos
 Potencales y campos eléctrcos Obetvo El obetvo de este expermento es determnar las líneas (o superfces) equpotencales es decr el lugar geométrco donde el potencal eléctrco es constante. Estos potencales
Potencales y campos eléctrcos Obetvo El obetvo de este expermento es determnar las líneas (o superfces) equpotencales es decr el lugar geométrco donde el potencal eléctrco es constante. Estos potencales
3ºESO TRANSMISIÓN DEL MOVIMIENTO: MECANISMOS. José Garrigós Dark 3ºESO
 3ºESO TRANSISIÓN DEL OVIIENTO: EANISOS José Garrgós Dark 3ºESO ÍNDIE: TRANSISIÓN DEL OVIIENTO: EANISOS 3ºESO. INTRODUIÓN. EANISOS DE TRANSISIÓN LINEAL... LA PALANA.. OENTO DE UNA FUERZA..3. LEY DE LA PALANA..4.
3ºESO TRANSISIÓN DEL OVIIENTO: EANISOS José Garrgós Dark 3ºESO ÍNDIE: TRANSISIÓN DEL OVIIENTO: EANISOS 3ºESO. INTRODUIÓN. EANISOS DE TRANSISIÓN LINEAL... LA PALANA.. OENTO DE UNA FUERZA..3. LEY DE LA PALANA..4.
CARTAS DE CONTROL. Han sido difundidas exitosamente en varios países dentro de una amplia variedad de situaciones para el control del proceso.
 CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
TERMODINÁMICA AVANZADA
 TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
TERMODINÁMICA AVANZADA Undad III: Termodnámca del Equlbro Ecuacones para el coefcente de actvdad Funcones de eceso para mezclas multcomponentes 9/7/0 Rafael Gamero Funcones de eceso en mezclas bnaras Epansón
