TITULO. Estudio analítico para hallar un modelo matemático que optimiza un perfil de ojiva balístico (región subsónica, sónica y supersónica)
|
|
|
- Ana Navarro Ortega
- hace 5 años
- Vistas:
Transcripción
1 TITULO Estuio analítico para hallar un moelo matemático que optimiza un perfil e ojiva balístico (región subsónica, sónica supersónica) Por Alfreo R Garasini RESUMEN Partieno e una función e isipación tipo Frantl, con el auilio el cálculo variacional se obtiene una epresión que aos el raio (calibre) la longitu e la ojiva, se permite eterminar la curva (perfil e ojiva) que hace mínima la resistencia el aire al avance el proectil
2 NOMENCLATURA ρ : ensia el aire C (W ) : coeficiente e arrastre : velocia en el eje : velocia en el eje s : elemento el área anular F: fuerza resistente el aire ξ : función subintegral t: variable tiempo r: raio e la ojiva h: longitu e la ojiva Página e 5
3 INTRODUCCION Hipótesis a emplear - Amitimos que la ojiva es un paraboloie e revolución - Empleamos una función e isipación tipo Frantl 3- La ensia el aire es constante 4- El coeficiente e arrastre (rag) es constante 5- La fuerza e isipación o resistencia el aire es una funcional A continuación el ibujo muestra un paraboloie elemental, esto es: Entonces la función e isipación que obra sobre la superficie elemental s, es: () F ρ C( W ) S Done: S π Por consecuencia tenemos que: F ρc( W ) π Página 3 e 5
4 O bien (3) F π ρc( w) En virtu e las hipótesis (3) (4) resulta así mismo: (4) F ρπ C( w) Como γγ t (la componente e la velocia sobre el eje γ ) la integral (4) se convierte en otra equivalente tal que: t F ρπc (5) ( w) t t Fijamos los límites e integración por ejemplo t (luego serán O t) t Ahora bien, por la estructura e la función integral, estaríamos en presencia e un problema e etremos, por lo tanto formulamos la hipótesis e que la fuerza F e la resistencia el aire es una funcional, esto significa: O δf ρπc (6) ( w) δ t t t Es ecir intentamos hallar una función que haga máima o mínima al valor F (en este caso es mínimo, pues como se avierte se cumple la conición e Legenre) Página 4 e 5
5 DESARROLLO Una vez establecios estas bases poemos aplicar las ecuaciones e Euler-Lagrange, resulta el siguiente sistema e ecuaciones iferenciales: (8) (7) t t ζ ζ ζ Sieno (9): ζ Operamos: () () t t () o a a Llevamos a ésta última a la epresión () : (3) a a t Página 5 e 5
6 Quea: t Hacemos: (el simple artificio) t Llamamos: ϕ, que resulte la ecuación iferencial orinaria: t t ϕ ϕ Eliminamos el tiempo; separamos las variables: ϕ ϕ ϕ ϕ Tenremos: b ϕ O bien: b O bien: b Página 6 e 5
7 Etraemos la raíz cuaraa: (4) b Separaremos variables e integramos nuevamente, por la naturaleza el problema los límites e integración porán ser: t t b e ahí que: (5) t b Por otra parte tenieno en cuenta la () en virtu e la (4) resulta: (6) a b O bien: ab c Evientemente: (7) ct Ahora resta por eliminar el tiempo entre las relaciones (5) (7) esto es: b c Página 7 e 5
8 Por último: bc Despejamos : bc Llamamos: (8) κ bc Obtenemos: (9) k Si aplicamos las coniciones e contorno para un proectil, el valor e la constante κ r puee ser: κ h Por lo que resulta efinitivamente: r () h Página 8 e 5
9 BREVE COMENTARIO Cabe señalar que la constante κ (relación 8) contiene la velocia c que ahora actúa como parámetro, notemos entonces que la misma figura en el enominaor, lo cual nos informa que en cuanto maor es icha velocia, menor ebe ser la orenaa, o sea: cuanto maor es la velocia, más aguzaa ebe ser la ojiva e un proectil BIBLIOGRAFIA CONSULTADA - Ecuaciones iferenciales Cálculo Variacional Autor: L Elsgoltz - Cálculo Infinitesimal (cálculo e etremales) Autor: J Re Pastor 3- Tratao e Balística Autor: Dr L Hanert 4- Tabla e Coeficientes e arrastre Autor: Pranntl Página 9 e 5
10 TABLA DE VALORES CORRESPONDIENTE AL MODELO MATEMÁTICO (FfLA) ( perfil e ojiva) X Y Página e 5
11 Página e 5
12 Página e 5
13 Página 3 e 5
14 Página 4 e 5
15 NOTA Es importante comentar que este trabajo contiene una seguna parte que se va a publicar (sin cargo también) oportunamente Este consiste en una curiosa relación matemática que puee ser e capital significación para la fabricación e municiones, pues la misma relaciona el Factor e Estabilización e un proectil con el calibre, la longitu el cuerpo la altura e la ojiva Esta epresión ha sio verificaa para 7 proectiles e istintos calibres Página 5 e 5
Parcial de Cálculo C 0
 Parcial e Cálculo C 0 0 0 Funamentos e Matemáticas Usar los polinomios e Talor para averiguar si la función g = 7 alcanza o no un etremo local en = 0 sen ln Solución: El polinomio e Talor en = 0 e un polinomio
Parcial e Cálculo C 0 0 0 Funamentos e Matemáticas Usar los polinomios e Talor para averiguar si la función g = 7 alcanza o no un etremo local en = 0 sen ln Solución: El polinomio e Talor en = 0 e un polinomio
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
Unidad 1 Ecuaciones Diferenciales de Primer Orden. 1.1 Definiciones (Ecuación Diferencial, Orden, Grado, Linealidad)
 . Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
MATEMÁTICAS II Valores extremos Curso de funciones de varias variables
 MATEMÁTICAS II Valores etremos Curso - e unciones e varias variables EJERCICIOS ) Calcular el volumen e la caja rectangular más grane situaa en el primer octante con tres e sus caras en los planos coorenaos
MATEMÁTICAS II Valores etremos Curso - e unciones e varias variables EJERCICIOS ) Calcular el volumen e la caja rectangular más grane situaa en el primer octante con tres e sus caras en los planos coorenaos
Variación de un funcional Funcional ( ) 1.6 Introducción al cálculo variacional 1.6. Introducción al cálculo variacional
 1.6. Introducción al cálculo variacional El cálculo variacional estudia los métodos, llamados variacionales, que permiten hallar los valores estacionarios de los funcionales. Puesto que un funcional representa
1.6. Introducción al cálculo variacional El cálculo variacional estudia los métodos, llamados variacionales, que permiten hallar los valores estacionarios de los funcionales. Puesto que un funcional representa
SISTEMAS DE COORDENADAS EN EL ESPACIO
 Matemática Diseño Inustrial Coorenaas en el espacio Ing. vila Ing. Moll SISTEMS DE CRDENDS EN EL ESPCI De forma similar a la vista para el plano, se pueen efinir istintos sistemas e coorenaas. CRDENDS
Matemática Diseño Inustrial Coorenaas en el espacio Ing. vila Ing. Moll SISTEMS DE CRDENDS EN EL ESPCI De forma similar a la vista para el plano, se pueen efinir istintos sistemas e coorenaas. CRDENDS
MMII_CV_c1 CÁLCULO VARIACIONAL: Introducción y modelo básico.
 MMII_CV_c CÁLCULO VARIACIONAL: Introucción moelo básico. Guión Esta es una clase e introucción al Cálculo e Variaciones (CV). Por un lao, se establece su relación con otros campos e la Optimización en
MMII_CV_c CÁLCULO VARIACIONAL: Introucción moelo básico. Guión Esta es una clase e introucción al Cálculo e Variaciones (CV). Por un lao, se establece su relación con otros campos e la Optimización en
Explicación de la velocidad de rotación en galaxias espirales Interpretación Lagragiana (Yul Goncalves,
 Explicación e la velocia e rotación en galaxias espirales Interpretación Lagragiana (Yul Goncalves, yulalebran9@gmail.com) A continuación se presenta una emostración e la velocia e rotación en galaxias
Explicación e la velocia e rotación en galaxias espirales Interpretación Lagragiana (Yul Goncalves, yulalebran9@gmail.com) A continuación se presenta una emostración e la velocia e rotación en galaxias
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-13-5-M-1--17 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: 13 TIPO DE EXAMEN: Primera Retrasaa
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-13-5-M-1--17 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: 13 TIPO DE EXAMEN: Primera Retrasaa
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
Ecuaciones Diferenciales de primer Orden
 4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
4 Ecuaciones Diferenciales e primer Oren 1.1 1.1. Introucción Las palabras ecuaciones y iferenciales nos hacen pensar en la solución e cierto tipo e ecuación que contenga erivaas. Así como al estuiar álgebra
IV.- CONDICIÓN DE CONTORNO DE CONVECCIÓN EN SÓLIDOS INFINITOS
 IV.- CONDICIÓN DE CONTONO DE CONVECCIÓN EN SÓLIDOS INFINITOS IV.1.- INTODUCCIÓN En la mayor parte e los problemas e tipo térmico que se plantean a nivel técnico intervienen variaciones e la temperatura
IV.- CONDICIÓN DE CONTONO DE CONVECCIÓN EN SÓLIDOS INFINITOS IV.1.- INTODUCCIÓN En la mayor parte e los problemas e tipo térmico que se plantean a nivel técnico intervienen variaciones e la temperatura
RESOLVIENDO PROBLEMAS DE MATEMÁTICA ( ).
 Matemática, Física, Astronomía, casanchi.com 07 RESOLVIENDO PROBLEMAS DE MATEMÁTICA RESOLUCIÓN DE LOS PROBLEMAS PROPUESTOS PROBLEMA 50 (7) Sea Γ la topología de R constituida por R, φ y todos los intervalos
Matemática, Física, Astronomía, casanchi.com 07 RESOLVIENDO PROBLEMAS DE MATEMÁTICA RESOLUCIÓN DE LOS PROBLEMAS PROPUESTOS PROBLEMA 50 (7) Sea Γ la topología de R constituida por R, φ y todos los intervalos
Principio de incertidumbre de Heisenberg
 Principio e incertiumbre e Heisenberg n un átomo e irógeno, nos se pueen meir simultáneamente la cantia e movimiento mv y la posición e su electrón. a cantia e movimiento e una partícula se enomina momento,
Principio e incertiumbre e Heisenberg n un átomo e irógeno, nos se pueen meir simultáneamente la cantia e movimiento mv y la posición e su electrón. a cantia e movimiento e una partícula se enomina momento,
Escuela Politécnica. Universidad de Alcalá
 Escuela Politécnica. Universia e Alcalá Asignatura: PROPAGACIÓN Y ONDAS Grao en Ingenieria Electrónica e Comunicaciones (G37) Grao en Ingeniería Telemática (G38) Grao en Ingeniería en Sistemas e Telecomunicación
Escuela Politécnica. Universia e Alcalá Asignatura: PROPAGACIÓN Y ONDAS Grao en Ingenieria Electrónica e Comunicaciones (G37) Grao en Ingeniería Telemática (G38) Grao en Ingeniería en Sistemas e Telecomunicación
Funciones de Bessel. Dr. Héctor René Vega-Carrillo
 Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
Funciones e Bessel Dr. Héctor René Vega-Carrillo 1 2 Ínice 1. Introucción............................. 3 2. Solución e la Ecuación iferencial e Bessel........... 5 2.1. Caso n entero............................
EXAMEN EXTRAORDINARIO DE FÍSICA I. CUESTIONES 30/01/2017
 EXAME EXTRAORDIARIO DE FÍSICA I. CUESTIOES 30/0/07.- a) Defina el momento angular e una partícula. Demostrar que si la partícula se mueve en un plano, la irección el momento angular permanece constante.
EXAME EXTRAORDIARIO DE FÍSICA I. CUESTIOES 30/0/07.- a) Defina el momento angular e una partícula. Demostrar que si la partícula se mueve en un plano, la irección el momento angular permanece constante.
LA CICLOIDE, UNA CURVA DE MUCHO EMPAQUE
 LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
LA CICLOIDE, UNA CUVA DE MUCHO EMPAQUE CALOS S CHINEA LA CICLOIDE UNA CUVA DE MUCHO EMPAQUE Una breve introucción 1 Ecuaciones paramétricas La tangente y la normal en un punto 3 Longitu e un arco 4 El
UNIDAD IV.- CÁLCULO INTEGRAL
 UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
DERIVADA. Interpretación Geométrica Encontrar la pendiente de la recta tangente a una curva en un punto dado de ella.
 DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
A y B
 TIVIDDES DE MTRIES. º HILLERTO Hallar el rango e la matriz: 7 8 7 9 8 Se observa que el menor e oren formao por la primera y tercera filas y columnas no es nulo sino igual a 8, veamos: 8 Luego rg () es
TIVIDDES DE MTRIES. º HILLERTO Hallar el rango e la matriz: 7 8 7 9 8 Se observa que el menor e oren formao por la primera y tercera filas y columnas no es nulo sino igual a 8, veamos: 8 Luego rg () es
4. Mecánica en la Medicina Derivar e Integrar
 4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
INTEGRAL INDEFINIDA. Una pregunta inicial para hacerse. Cuál es una función F(x), que al haber sido derivada se obtuvo f ( x) B?.
 es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
LAS ECUACIONES VARIACIONALES DE EULER
 LAS ECUACIONES VARIACIONALES DE EULER Los conceptos de máximo y de mínimo -de extremo o extremal, en definitivade una expresión funcional, es algo corriente en el análisis matemático, y las condiciones
LAS ECUACIONES VARIACIONALES DE EULER Los conceptos de máximo y de mínimo -de extremo o extremal, en definitivade una expresión funcional, es algo corriente en el análisis matemático, y las condiciones
La naturaleza dual de la materia. Los electrones y todas las partículas que forman parte del microcosmos tienen un comportamiento dual.
 La naturaleza ual e la materia. Los electrones y toas las partículas que forman parte el microcosmos tienen un comportamiento ual. Se comportan como onas y como corpúsculos. Orígenes: Newton consieraba
La naturaleza ual e la materia. Los electrones y toas las partículas que forman parte el microcosmos tienen un comportamiento ual. Se comportan como onas y como corpúsculos. Orígenes: Newton consieraba
Ecuación de Schrödinger
 Ecuación e Schröinger En cuanto a onas electromagnéticas, ya vimos que su comportamiento está regio por las ecuaciones e Maxwell. También hemos visto que a una partícula con masa se le puee asignar una
Ecuación e Schröinger En cuanto a onas electromagnéticas, ya vimos que su comportamiento está regio por las ecuaciones e Maxwell. También hemos visto que a una partícula con masa se le puee asignar una
DERIVADAS DERIVACIÓN DE FUNCIONES
 DERIVADAS DERIVACIÓN DE FUNCIONES Introucción: Después e haber aquirio los conocimientos e los temas anteriores e funciones límites se requiere establecer un proceimiento más eficiente que nos permita
DERIVADAS DERIVACIÓN DE FUNCIONES Introucción: Después e haber aquirio los conocimientos e los temas anteriores e funciones límites se requiere establecer un proceimiento más eficiente que nos permita
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
Ayudantía 2. Ley de Coulomb 08 de Marzo de 2018 Ayudante: Matías Henríquez - Nm 2. e = [C] (1.3)
![Ayudantía 2. Ley de Coulomb 08 de Marzo de 2018 Ayudante: Matías Henríquez - Nm 2. e = [C] (1.3) Ayudantía 2. Ley de Coulomb 08 de Marzo de 2018 Ayudante: Matías Henríquez - Nm 2. e = [C] (1.3)](/thumbs/83/88050324.jpg) Pontificia Universia Católica e Chile Faculta e Física FIS533 - Electricia y Magnetismo // -28 Profesor: Giuseppe De Nittis - gienittis@uc.cl Ayuantía 2 Ley e Coulomb 8 e Marzo e 28 Ayuante: Matías Henríquez
Pontificia Universia Católica e Chile Faculta e Física FIS533 - Electricia y Magnetismo // -28 Profesor: Giuseppe De Nittis - gienittis@uc.cl Ayuantía 2 Ley e Coulomb 8 e Marzo e 28 Ayuante: Matías Henríquez
PIEZAS SOMETIDAS A FLEXIÓN
 PIEZAS SOETIDAS A FLEXIÓN PROBLEA Nº Comprobar si un perfil IPE300 en acero S75 sería una sección aecuaa para la viga continua con os vanos e 6m cargaa vinculaa como se muestra en la figura. Suponremos
PIEZAS SOETIDAS A FLEXIÓN PROBLEA Nº Comprobar si un perfil IPE300 en acero S75 sería una sección aecuaa para la viga continua con os vanos e 6m cargaa vinculaa como se muestra en la figura. Suponremos
MATEMÁTICA DE JORGE JUAN
 LA FIGUA DE LA TIEA MATEMÁTICA DE JOGE JUAN POFESO DIEGO GACÍA CASTAÑO LA ASAMBLEA AMISTOSA LITEAIA La Figura e la Tierra E,; ED ECUADO DB SEMIEJE DE LA TIEA ; GI ; FH Ecuaciones e la elipse : cosφ; senφ
LA FIGUA DE LA TIEA MATEMÁTICA DE JOGE JUAN POFESO DIEGO GACÍA CASTAÑO LA ASAMBLEA AMISTOSA LITEAIA La Figura e la Tierra E,; ED ECUADO DB SEMIEJE DE LA TIEA ; GI ; FH Ecuaciones e la elipse : cosφ; senφ
Ejercicios N 3 (MAT 021)
 Ejercicios N 3 (MAT 021) Universidad Técnica Federico Santa María Departamento de Matemática Septiembre 2009 1 Rectas 1. En cada caso determine la ecuación de la recta L (a) L pasa por el punto P ( 1,
Ejercicios N 3 (MAT 021) Universidad Técnica Federico Santa María Departamento de Matemática Septiembre 2009 1 Rectas 1. En cada caso determine la ecuación de la recta L (a) L pasa por el punto P ( 1,
1. Grafique la familia de curvas que representa la solución general de la ecuación diferencial: y ' + y = 0
 Elaborao por: Jhonn Choquehuanca Lizarraga Ecuaciones Diferenciales e Primer oren Aplicaciones. Grafique la familia e curvas que representa la solución general e la ecuación iferencial: ' + = 0 Solución:
Elaborao por: Jhonn Choquehuanca Lizarraga Ecuaciones Diferenciales e Primer oren Aplicaciones. Grafique la familia e curvas que representa la solución general e la ecuación iferencial: ' + = 0 Solución:
(A) Primer parcial. (3) Encuentre gráfica, dominio, rango, intervalos de monotonía y paridad de la función: x 2 + x 2, x = parte entera de x.
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E3000 ) ) + + < 0. 5+4. A) Primer parcial 3) Encuentre gráfica, dominio, rango, intervalos de monotonía y paridad de la función: f) = +3, 0. 4) Determine
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E3000 ) ) + + < 0. 5+4. A) Primer parcial 3) Encuentre gráfica, dominio, rango, intervalos de monotonía y paridad de la función: f) = +3, 0. 4) Determine
PROBLEMAS DE TEOREMA DE LA DIVERGENCIA
 PROBLMA D TORMA D LA DIVRGNCIA NUNCIADO DL TORMA ea una región simple sólia cua superficie frontera tiene una orientación positiva (hacia afuera). ea un campo vectorial cuas funciones componentes tienen
PROBLMA D TORMA D LA DIVRGNCIA NUNCIADO DL TORMA ea una región simple sólia cua superficie frontera tiene una orientación positiva (hacia afuera). ea un campo vectorial cuas funciones componentes tienen
RESALTO DE ONDAS (1< Fr 1 < 1,7)
 UNIVERSIDAD DE CHIE - CI 4A HIDRÁUICA RESATO DE ONDAS (< Fr
UNIVERSIDAD DE CHIE - CI 4A HIDRÁUICA RESATO DE ONDAS (< Fr
; deben llevarse las unidades de área a m 2 y distancia a m. V = 13215V = 13, 2kV
 Física II Guía e ejercicios 5 CAPACIDAD 5. Capacia 5.. Problema 5... Enunciao Las placas e un capacitor e placas paralelas están separaas por una istancia e, 8mm y caa una tiene un área e, cm. Caa placa
Física II Guía e ejercicios 5 CAPACIDAD 5. Capacia 5.. Problema 5... Enunciao Las placas e un capacitor e placas paralelas están separaas por una istancia e, 8mm y caa una tiene un área e, cm. Caa placa
25 EJERCICIOS de RADICALES 4º ESO opc. B
 EJERCICIOS de RADICALES º ESO opc. B RECORDAR: Definición de raíz n-ésima: Consecuencia: n n x n a x x x, y también ( ) n n x n a x Equivalencia con una potencia de exponente fraccionario: Simplificación
EJERCICIOS de RADICALES º ESO opc. B RECORDAR: Definición de raíz n-ésima: Consecuencia: n n x n a x x x, y también ( ) n n x n a x Equivalencia con una potencia de exponente fraccionario: Simplificación
y C= determinar la matriz X que verifica la ecuación matricial A B X=C X+I, siendo I =
 EJERCICIOS: TEMA 1: MATRICES. 1º/ Dadas las matrices: A= 2 1 1 0 1 1 1 1, B= 2 0 3 1 y C= 2 1 0 1 determinar la matriz X que verifica la ecuación matricial A B X=C X+I, siendo I = 1 0 0 1. 2º/ Determinar
EJERCICIOS: TEMA 1: MATRICES. 1º/ Dadas las matrices: A= 2 1 1 0 1 1 1 1, B= 2 0 3 1 y C= 2 1 0 1 determinar la matriz X que verifica la ecuación matricial A B X=C X+I, siendo I = 1 0 0 1. 2º/ Determinar
Departamento de Matemáticas Página 1 PROBLEMAS DE SELECTIVIDAD. INTEGRAL INDEFINIDA. (Sugerencia: cambio de variable
 Departamento de Matemáticas Página PROBLEMAS DE SELECTIVIDAD. INTEGRAL INDEFINIDA. d 4.0.- Calcula ( ) (Sugerencia: cambio de variable t ) 4-0.- Sea f : R R la función definida por Sea f ( ) e cos ( )
Departamento de Matemáticas Página PROBLEMAS DE SELECTIVIDAD. INTEGRAL INDEFINIDA. d 4.0.- Calcula ( ) (Sugerencia: cambio de variable t ) 4-0.- Sea f : R R la función definida por Sea f ( ) e cos ( )
y = x ln x ; con los datos obtenidos representa su gráfica. f x es continua y derivable en 0, por ser producto de funciones continuas y derivables.
 Matemáticas II Curso 0/4 Opción A (ª evaluación) Ejercicio. (Puntuación máima: puntos) Estudia las características de la función = ln = ( 0, + ) ( + ) f Dom f y = ln ; con los datos obtenidos representa
Matemáticas II Curso 0/4 Opción A (ª evaluación) Ejercicio. (Puntuación máima: puntos) Estudia las características de la función = ln = ( 0, + ) ( + ) f Dom f y = ln ; con los datos obtenidos representa
Resolver ecuaciones cuadráticas. Departamento de Matemáticas Universidad de Puerto Rico - Arecibo
 Resolver ecuaciones cuadráticas Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación cuadrática tiene una forma general como sigue ax + bx
Resolver ecuaciones cuadráticas Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación cuadrática tiene una forma general como sigue ax + bx
TEMA 4 FUNCIONES ELEMENTALES
 Tema 4 Funciones elementales Matemáticas CCSSI º Bachillerato TEMA 4 FUNCIONES ELEMENTALES FUNCIÓN EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
Tema 4 Funciones elementales Matemáticas CCSSI º Bachillerato TEMA 4 FUNCIONES ELEMENTALES FUNCIÓN EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
Seminario de problemas. Curso Hoja 5. Soluciones
 Seminario e problemas. Curso 018-19. Hoja. Soluciones 49. Encuentra una expresión cerraa para la suma S m = 1 + 7 +... + 1 m+1 m 1 aplicano el cálculo e iferencias, o/y e otro moo. Solución. S n = 1 +
Seminario e problemas. Curso 018-19. Hoja. Soluciones 49. Encuentra una expresión cerraa para la suma S m = 1 + 7 +... + 1 m+1 m 1 aplicano el cálculo e iferencias, o/y e otro moo. Solución. S n = 1 +
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-103-1-M--00-017 CURSO: Matemática Básica SEMESTRE: Seguno CÓDIGO DEL CURSO: 103 TIPO DE EXAMEN: Primer eamen
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-103-1-M--00-017 CURSO: Matemática Básica SEMESTRE: Seguno CÓDIGO DEL CURSO: 103 TIPO DE EXAMEN: Primer eamen
TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES
 TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES 7 INTRODUCCIÓN El propósito e este tema es introucir a los alumnos en la terminología básica e las Ecuaciones Diferenciales eaminar brevemente como se
TEMA 1 INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES 7 INTRODUCCIÓN El propósito e este tema es introucir a los alumnos en la terminología básica e las Ecuaciones Diferenciales eaminar brevemente como se
Coordinación de Matemática I (MAT021) Taller 6
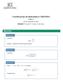 Coordinación de Matemática I MAT0 Taller 6 Primer semestre de 0 Semana 7: Lunes 07 viernes de mayo Ejercicios Ejercicio Calcular [ ] 0 + donde [ ] denota la función parte entera. Ejercicio Calcular cos
Coordinación de Matemática I MAT0 Taller 6 Primer semestre de 0 Semana 7: Lunes 07 viernes de mayo Ejercicios Ejercicio Calcular [ ] 0 + donde [ ] denota la función parte entera. Ejercicio Calcular cos
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA GUÍA TEÓRICO PRÁCTICA Nº8 A la función de segundo grado f() = a + b + c, siendo a, b, c lr a 0 se le denomina función cuadrática. La
C U R S O : MATEMÁTICA UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA GUÍA TEÓRICO PRÁCTICA Nº8 A la función de segundo grado f() = a + b + c, siendo a, b, c lr a 0 se le denomina función cuadrática. La
Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos
 página 1/12 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos Hoja 26. Problema 1 1. a) Calcula el número real m que cumple lim 0 ln(1+m ) sen(2 ) =. b) Obtener
página 1/12 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos Hoja 26. Problema 1 1. a) Calcula el número real m que cumple lim 0 ln(1+m ) sen(2 ) =. b) Obtener
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS GUÍA N 13 CÁLCULO I
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS GUÍA N CÁLCULO I Profesor: Carlos Ruz Leiva MÁXIMOS Y MÍNIMOS Criterio de la segunda derivada Supongamos que
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS GUÍA N CÁLCULO I Profesor: Carlos Ruz Leiva MÁXIMOS Y MÍNIMOS Criterio de la segunda derivada Supongamos que
Cálculo de variaciones para estudiantes de primer curso de Ingenierías: Problemas Isoperimétricos
 Cálculo de variaciones para estudiantes de primer curso de Ingenierías: Problemas Isoperimétricos Autoría: Mª José Haro Delicado Mª José Pérez Haro emática: Este documento completa otro anterior en el
Cálculo de variaciones para estudiantes de primer curso de Ingenierías: Problemas Isoperimétricos Autoría: Mª José Haro Delicado Mª José Pérez Haro emática: Este documento completa otro anterior en el
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
Capitulo IV. IV.1 Síntesis dimensional de mecanismos. Generación de funciones
 Capitulo IV IV. Síntesis imensional e mecanismos. Generación e funciones Cinemática y Dinámica e Máquinas. IV. Síntesis imensional e mecanismos. Generación e funciones Capítulo IV Síntesis imensional e
Capitulo IV IV. Síntesis imensional e mecanismos. Generación e funciones Cinemática y Dinámica e Máquinas. IV. Síntesis imensional e mecanismos. Generación e funciones Capítulo IV Síntesis imensional e
PIEZAS SOMETIDAS A FLEXIÓN
 PIEZAS SOETIDAS A FEXIÓN PROBEA 6 En la figura se representa una viga continua e os vanos e 5m y 4m respectivamente con su extremo izquiero empotrao y su extremo erecho apoyao. Tenieno en cuenta que las
PIEZAS SOETIDAS A FEXIÓN PROBEA 6 En la figura se representa una viga continua e os vanos e 5m y 4m respectivamente con su extremo izquiero empotrao y su extremo erecho apoyao. Tenieno en cuenta que las
Ordenada en el origen: Es el valor de la función cuando la variable x es 0 También llamado corte con el eje de ordenadas o corte Oy.
 Función polinómica: La función polinómica está compuesta por una serie de operaciones; sumas, restas, productos potencias. Todas ellas están perfectamente definidas en el conjunto de los números reales.
Función polinómica: La función polinómica está compuesta por una serie de operaciones; sumas, restas, productos potencias. Todas ellas están perfectamente definidas en el conjunto de los números reales.
Ejemplo de aplicación práctica de dimensionado de un bulón
 Ejemplo e aplicación práctica e imensionao e un bulón Apellios, nombre Guariola Víllora, Arianna (aguario@mes.upv.es) Departamento Centro Mecánica el Meio continuo y Teoría e Estructuras Universitat Politècnica
Ejemplo e aplicación práctica e imensionao e un bulón Apellios, nombre Guariola Víllora, Arianna (aguario@mes.upv.es) Departamento Centro Mecánica el Meio continuo y Teoría e Estructuras Universitat Politècnica
Examen Final de Precálculo (Mate 3171) Nombre 14 de diciembre de 2001
 Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
Eamen Final e Precálculo (Mate 7) Nombre e iciembre e 00 Escriba la letra que correspone a la mejor alternativa en el espacio provisto. (os puntos caa uno) ) Si la gráfica e f es la e la erecha entonces
PROPUESTA A., se pide: a) Calcula las asíntotas verticales y oblicuas de f(x). (1,25 puntos)
 PROPUEST. Dada la función f ( ), se pide: a) Calcula las asíntotas verticales y oblicuas de f(). (, puntos) b) Coordenadas de los máimos y mínimos relativos de f(). (, puntos). Calcula las siguientes integrales:
PROPUEST. Dada la función f ( ), se pide: a) Calcula las asíntotas verticales y oblicuas de f(). (, puntos) b) Coordenadas de los máimos y mínimos relativos de f(). (, puntos). Calcula las siguientes integrales:
Clase 11 Tema: Fórmula general para solucionar ecuaciones cuadráticas
 Matemáticas 9 Bimestre: III Número de clase: Clase Tema: Fórmula general para solucionar ecuaciones cuadráticas Actividad Lea la siguiente información. La deducción de una fórmula práctica nos permite
Matemáticas 9 Bimestre: III Número de clase: Clase Tema: Fórmula general para solucionar ecuaciones cuadráticas Actividad Lea la siguiente información. La deducción de una fórmula práctica nos permite
Universidad de Castilla la Mancha Septiembre Propuesta A
 A.- árbara Cánovas Conesa 67 7 Universidad de Castilla la Mancha Septiembre.7 Propuesta A www.clasesalacarta.com Septiembre 7 a) Calcula razonadamente el área de la región determinada por la curva f()
A.- árbara Cánovas Conesa 67 7 Universidad de Castilla la Mancha Septiembre.7 Propuesta A www.clasesalacarta.com Septiembre 7 a) Calcula razonadamente el área de la región determinada por la curva f()
TEMA 7: Sistemas de ecuaciones
 TEMA 7: Sistemas de ecuaciones 7.1 Ecuaciones con dos incógnitas. Soluciones Ejemplo 1. Encuentra soluciones para la siguiente ecuación de primer grado con dos incógnitas: 5 a., 0, 5 Si sustituimos en
TEMA 7: Sistemas de ecuaciones 7.1 Ecuaciones con dos incógnitas. Soluciones Ejemplo 1. Encuentra soluciones para la siguiente ecuación de primer grado con dos incógnitas: 5 a., 0, 5 Si sustituimos en
TEMA 6 PROBLEMAS DE VALOR INICIAL PROBLEMAS DE CÁLCULO NUMÉRICO (8/9) El código se lista a continuación: function [S,T]resuelve_ed(Tobs,h) T[:h:Tobs];
![TEMA 6 PROBLEMAS DE VALOR INICIAL PROBLEMAS DE CÁLCULO NUMÉRICO (8/9) El código se lista a continuación: function [S,T]resuelve_ed(Tobs,h) T[:h:Tobs]; TEMA 6 PROBLEMAS DE VALOR INICIAL PROBLEMAS DE CÁLCULO NUMÉRICO (8/9) El código se lista a continuación: function [S,T]resuelve_ed(Tobs,h) T[:h:Tobs];](/thumbs/55/35351734.jpg) TEMA 6 PROBLEMAS DE VALOR INICIAL PROBLEMAS DE CÁLCULO NUMÉRICO (8/9) TEMA 6: RESOLUCIÓN NUMÉRICA DE PROBLEMAS DE VALOR INICIAL Problema El siguiente código en MATLAB resuelve una ecuación diferencial
TEMA 6 PROBLEMAS DE VALOR INICIAL PROBLEMAS DE CÁLCULO NUMÉRICO (8/9) TEMA 6: RESOLUCIÓN NUMÉRICA DE PROBLEMAS DE VALOR INICIAL Problema El siguiente código en MATLAB resuelve una ecuación diferencial
UNIDAD 6 ORIFICIOS. VERTEDEROS Y RESALTO HIDRÁULICO
 UNIA 6 ORIFIIO. VERTEERO Y REALTO HIRÁULIO apítulo 1 EAGÚE POR ORIFIIO Y BAJO OMPUERTA EIÓN 1: EAGÚE POR ORIFIIO INTROUIÓN Estuiamos en este capítulo los esagües por orificio bajo compuerta, secciones
UNIA 6 ORIFIIO. VERTEERO Y REALTO HIRÁULIO apítulo 1 EAGÚE POR ORIFIIO Y BAJO OMPUERTA EIÓN 1: EAGÚE POR ORIFIIO INTROUIÓN Estuiamos en este capítulo los esagües por orificio bajo compuerta, secciones
Material N 29 GUÍA TEÓRICO PRÁCTICA Nº 23
 C u r s o : Matemática Material N 9 GUÍA TEÓRICO PRÁCTICA Nº 3 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar
C u r s o : Matemática Material N 9 GUÍA TEÓRICO PRÁCTICA Nº 3 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar
Para encontrar el valor de k sustituimos el valor de h en la función inicial.
 .3.4 GRÁFICAS DE FUNCIONES CUADRÁTICAS COMPLETAS. Ejemplo 1. Construir la gráfica de la siguiente función f()= -4-5, estableciendo su dominio, rango, las coordenadas de su vértice sus raíces (método de
.3.4 GRÁFICAS DE FUNCIONES CUADRÁTICAS COMPLETAS. Ejemplo 1. Construir la gráfica de la siguiente función f()= -4-5, estableciendo su dominio, rango, las coordenadas de su vértice sus raíces (método de
Derivación. (x c) que pasa por el punto fijo (c, f(c)) y el punto móvil (c + h, f(c + h)) cuando h tiende a 0.
 Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
K
 Universia e Navarra Naarroako Unibertsitatea Escuela Superior e Ingenieros Ingeniarien Goi Mailako Eskola ASIGNATURA GAIA: TECNOLOGÍAS DE FABRICACIÓN CURSO KURTSOA: 4º Tiempo: 1 hora, 30 minutos P_JUN_09
Universia e Navarra Naarroako Unibertsitatea Escuela Superior e Ingenieros Ingeniarien Goi Mailako Eskola ASIGNATURA GAIA: TECNOLOGÍAS DE FABRICACIÓN CURSO KURTSOA: 4º Tiempo: 1 hora, 30 minutos P_JUN_09
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS. S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
Problemas Tema 9 Solución a problemas de derivadas - Hoja 8 - Todos resueltos
 página 1/10 Problemas Tema 9 Solución a problemas de derivadas - Hoja 8 - Todos resueltos Hoja 8. Problema 1 a) Deriva f ()=arcosen( 1 2 ) 1 f ' ( )= 2 1 ( 1 2 ) 2 2 1 = 1 2 1 2 b) Determina el punto (,
página 1/10 Problemas Tema 9 Solución a problemas de derivadas - Hoja 8 - Todos resueltos Hoja 8. Problema 1 a) Deriva f ()=arcosen( 1 2 ) 1 f ' ( )= 2 1 ( 1 2 ) 2 2 1 = 1 2 1 2 b) Determina el punto (,
DERIVACIÓN. mtan. y x x. lim lim y ' f '( x) CAPÍTULO IV
 75 CAPÍTULO IV DERIVACIÓN. LA DERIVADA COMO PENDIENTE DE UNA CURVA La peniente e una curva en un punto ao, es iual a la peniente e la recta tanente a la curva en icho punto. Δ Q, Δ Q Q P, La peniente e
75 CAPÍTULO IV DERIVACIÓN. LA DERIVADA COMO PENDIENTE DE UNA CURVA La peniente e una curva en un punto ao, es iual a la peniente e la recta tanente a la curva en icho punto. Δ Q, Δ Q Q P, La peniente e
Cinemática y Dinámica de Fluidos: Fundamentos Básicos
 Cinemática y Dinámica e Fluios: Funamentos Básicos Santiago López Algunas Definiciones Antes e empezar con el tema central e éste capítulo, se eben introucir unos conceptos que son útiles a la hora e e
Cinemática y Dinámica e Fluios: Funamentos Básicos Santiago López Algunas Definiciones Antes e empezar con el tema central e éste capítulo, se eben introucir unos conceptos que son útiles a la hora e e
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 2013 Problemas (Dos puntos por problema).
 Eamen e Física-1, 1 Ingeniería Química Eamen final. Septiembre e 2013 Problemas Dos puntos por problema). Problema 1 Primer parcial): Un cuerpo e masa m = 0, 5kg se lanza hacia abajo meiante un muelle
Eamen e Física-1, 1 Ingeniería Química Eamen final. Septiembre e 2013 Problemas Dos puntos por problema). Problema 1 Primer parcial): Un cuerpo e masa m = 0, 5kg se lanza hacia abajo meiante un muelle
UNIDAD I CÁLCULO DIFERENCIAL
 Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Colegio Cristo Rey Matemáticas Aplicadas a las Ciencias Sociales I Temas 9 y 10. Derivadas y aplicaciones. x 3x. x x x. x 2
 Colegio Cristo Re Matemáticas Aplicadas a las Ciencias Sociales I Temas 9. Derivadas aplicaciones. Halla la derivada de estas funciones: a) f ln f ' ln ln 4 b) f f ' 4 c) f f ' ln d) f log f ' 4 4 ln e)
Colegio Cristo Re Matemáticas Aplicadas a las Ciencias Sociales I Temas 9. Derivadas aplicaciones. Halla la derivada de estas funciones: a) f ln f ' ln ln 4 b) f f ' 4 c) f f ' ln d) f log f ' 4 4 ln e)
Figura 1. Sistema de control del problema 6. = K (sin compensar) no pasa por la ubicación deseada. ( s)
 TEORÍA DEL ONTROL. SEGUNDO EXAMEN PARIAL MODELO DE SOLUIÓN. M. EN. RUBÉN VELÁZQUEZ UEVAS Problema 6. onsiere le sistema e la figura. Diseñe un compensaor e aelanto tal que los polos ominantes e lazo cerrao
TEORÍA DEL ONTROL. SEGUNDO EXAMEN PARIAL MODELO DE SOLUIÓN. M. EN. RUBÉN VELÁZQUEZ UEVAS Problema 6. onsiere le sistema e la figura. Diseñe un compensaor e aelanto tal que los polos ominantes e lazo cerrao
MÉTODO DE LOS ELEMENTOS FINITOS INTRODUCCIÓN AL CÁLCULO DE VARIACIONES
 MÉTODO DE LOS ELEMENTOS INITOS INTRODUCCIÓN AL CÁLCULO DE VARIACIONES 64.4 - método de los elementos finitos MÁXIMOS Y MÍNIMOS (I) Para la una función f(x) dada se puede hallar un extremo mediante: x df
MÉTODO DE LOS ELEMENTOS INITOS INTRODUCCIÓN AL CÁLCULO DE VARIACIONES 64.4 - método de los elementos finitos MÁXIMOS Y MÍNIMOS (I) Para la una función f(x) dada se puede hallar un extremo mediante: x df
3.1. DERIVADAS DE SEGUNDO ORDEN
 .. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
.. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
MECANISMOS DE TRANSMISIÓN Y TRANSFORMACIÓN DE MOVIMIENTOS
 MECANISMOS DE TRANSMISIÓN Y TRANSFORMACIÓN DE MOVIMIENTOS 0 . POLEAS Y CORREAS Figura : correas abiertas. La figura, muestra el caso e correas abiertas. En este caso, poemos obtener la expresión e la longitu
MECANISMOS DE TRANSMISIÓN Y TRANSFORMACIÓN DE MOVIMIENTOS 0 . POLEAS Y CORREAS Figura : correas abiertas. La figura, muestra el caso e correas abiertas. En este caso, poemos obtener la expresión e la longitu
Unidad 10 Integrales definidas. Aplicaciones
 Unidad Integrales definidas. Aplicaciones PÁGINA 5 SOLUCIONES. Las áreas quedan: A u A u A 5 u. El área del recinto viene dada por : ( ) ( ) Área d,5 u PÁGINA 9 SOLUCIONES. La solución queda: Directo:
Unidad Integrales definidas. Aplicaciones PÁGINA 5 SOLUCIONES. Las áreas quedan: A u A u A 5 u. El área del recinto viene dada por : ( ) ( ) Área d,5 u PÁGINA 9 SOLUCIONES. La solución queda: Directo:
Tema 13 La integral definida. Aplicaciones
 Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
Seminario 12: Condensadores.
 Seminario 2: Conensaores. Fabián Anrés Torres Ruiz Departamento e Física, Universia e Concepción, Chile 30 e Mayo e 2007. Problemas. (Desarrollo) Deucción el tiempo e escarga e un conensaor 2. (Problema
Seminario 2: Conensaores. Fabián Anrés Torres Ruiz Departamento e Física, Universia e Concepción, Chile 30 e Mayo e 2007. Problemas. (Desarrollo) Deucción el tiempo e escarga e un conensaor 2. (Problema
El Problema de Cauchy para EDPs de Primer Orden
 Capítulo 2 El Problema de Cauchy para EDPs de Primer Orden Este capítulo está dedicado al estudio de EDPs de primer orden, esto es, ecuaciones en las que sólo aparecen derivadas parciales de a lo sumo
Capítulo 2 El Problema de Cauchy para EDPs de Primer Orden Este capítulo está dedicado al estudio de EDPs de primer orden, esto es, ecuaciones en las que sólo aparecen derivadas parciales de a lo sumo
Ecuaciones cuadráticas Resolver ecuaciones cuadráticas fórmula cuadrática y casos especiales
 Ecuaciones cuadráticas Resolver ecuaciones cuadráticas fórmula cuadrática y casos especiales Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación
Ecuaciones cuadráticas Resolver ecuaciones cuadráticas fórmula cuadrática y casos especiales Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación
MATEMÁTICAS III. 5. Elige el Plan NME Entra al Semestre que cursas. 2. Da clic en Alumnos o Docentes.
 MATEMÁTICAS III Joven Bachiller: Como parte e las acciones e mejora para fortalecer el nivel acaémico e nuestros estuiantes, el Colegio e Bachilleres, pone a isposición, para estuiantes, irectivos, pares
MATEMÁTICAS III Joven Bachiller: Como parte e las acciones e mejora para fortalecer el nivel acaémico e nuestros estuiantes, el Colegio e Bachilleres, pone a isposición, para estuiantes, irectivos, pares
Mecanismo de reacción. Orden y Molecularidad
 Química General II puntes Cinética Mecanismos primavera 0 Mecanismo e reacción. Oren y Molecularia Mecanismo e reacción: Descripción etallaa y completa e caa una e las etapas o secuencia e reacciones que
Química General II puntes Cinética Mecanismos primavera 0 Mecanismo e reacción. Oren y Molecularia Mecanismo e reacción: Descripción etallaa y completa e caa una e las etapas o secuencia e reacciones que
UNIDAD 6 ORIFICIOS. VERTEDEROS Y RESALTO HIDRÁULICO
 UNIDAD 6 ORIFIIOS. VERTEDEROS Y RESALTO HIDRÁULIO apítulo VERTEDEROS SEIÓN 1: VERTEDEROS EN PARED DELGADA DEFINIIÓN DE VERTEDERO Y FUNIONES uano un líquio tiene su superficie lire a cota superior a la
UNIDAD 6 ORIFIIOS. VERTEDEROS Y RESALTO HIDRÁULIO apítulo VERTEDEROS SEIÓN 1: VERTEDEROS EN PARED DELGADA DEFINIIÓN DE VERTEDERO Y FUNIONES uano un líquio tiene su superficie lire a cota superior a la
ANÁLISIS DE FUNCIONES
 ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
TEORÍA DE CONTROL MODELO DE ESTADO DISCRETO
 TEORÍA DE CONTROL MODELO DE ESTADO DISCRETO Moelo e estao. De la misma forma que se planteó para sistemas continuos, existe la posibilia e moelar un sistema iscreto meiante un moelo e estaos. El sistema
TEORÍA DE CONTROL MODELO DE ESTADO DISCRETO Moelo e estao. De la misma forma que se planteó para sistemas continuos, existe la posibilia e moelar un sistema iscreto meiante un moelo e estaos. El sistema
Examen de Matemáticas II 2º de Bachillerato
 º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
APUNTES DE ECUACIONES CON UNA Y DOS INCOGNITAS Docente: Roque Julio Vargas R. Departamento de Ciencias Básicas. Unidades Tecnológicas de Santander
 APUNTES DE ECUACIONES CON UNA Y DOS INCOGNITAS Docente: Roque Julio Vargas R. Departamento de Ciencias Básicas. Unidades Tecnológicas de Santander 1 ECUACIONES DE PRIMER GRADO CON UNA Y DOS INCOGNITAS
APUNTES DE ECUACIONES CON UNA Y DOS INCOGNITAS Docente: Roque Julio Vargas R. Departamento de Ciencias Básicas. Unidades Tecnológicas de Santander 1 ECUACIONES DE PRIMER GRADO CON UNA Y DOS INCOGNITAS
Universidad Antonio Nariño Matemáticas Especiales Guía N 3: Funciones elementales complejas: exponencial, logaritmo, trigonométricas e hiperbólicas
 Universia Antonio Nariño Matemáticas Especiales Guía N 3: Funciones elementales complejas: exponencial, logaritmo, trigonométricas e hiperbólicas Grupo e Matemáticas Especiales Resumen Se presenta la efinición
Universia Antonio Nariño Matemáticas Especiales Guía N 3: Funciones elementales complejas: exponencial, logaritmo, trigonométricas e hiperbólicas Grupo e Matemáticas Especiales Resumen Se presenta la efinición
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES LA PARÁBOLA. FUNCIONES CUADRÁTICAS. FUNCIONES A TROZOS CON RECTA Y PARÁBOLAS. HIPÉRBOLAS. FUNCIONES RADICALES. FUNCIONES EXPONENCIALES. FUNCIONES LOGARITMICAS. La función =.- LA PARÁBOLA
FUNCIONES ELEMENTALES LA PARÁBOLA. FUNCIONES CUADRÁTICAS. FUNCIONES A TROZOS CON RECTA Y PARÁBOLAS. HIPÉRBOLAS. FUNCIONES RADICALES. FUNCIONES EXPONENCIALES. FUNCIONES LOGARITMICAS. La función =.- LA PARÁBOLA
APLICACIONES DE LA INTEGRAL ( ( ) ( )) A = f x g x dx EJERCICIOS: 5) Calcular el área de la región limitada por las líneas y = xln(x), y = x.
 APLICACIONES DE LA INTEGRAL Si R es la región limitada por las líneas y f() y y g(), con f() g(), entre a y b, el área de R viene dada por la integral A: b a ( ( ) ( )) A f g EJERCICIOS: ) Calcular el
APLICACIONES DE LA INTEGRAL Si R es la región limitada por las líneas y f() y y g(), con f() g(), entre a y b, el área de R viene dada por la integral A: b a ( ( ) ( )) A f g EJERCICIOS: ) Calcular el
FUNCIONES TRIGONOMÉTRICAS
 Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
