EN EL PLANO (R 2 ) EN EL ESPACIO (R 3 ) ECUACIONES CONSTRUIR CLASIFICAR ECUACIONES CONSTRUIR CLASIFICAR. Resumen de Transformaciones Geométricas
|
|
|
- María Dolores Cuenca Cano
- hace 5 años
- Vistas:
Transcripción
1 Resmen de Trnsformciones Geomérics EN EL PLNO (R ) EUIONES ONSTRUIR LSIFIR EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G..
2 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS del Plno Ecciones de los disinos Moimienos en E Se l mri: N O O, donde el rnsformdo del pno O: T(O) O O O M l mri de l rnsformción orogonl socid l moimieno, es decir: M. Idenidd.. Simerí il O α α O α α. Giro O α -α O α α 4. Trslción O O 5. Simerí desline: S d S e ot O α α O α α donde: O,O son ls coordends de T(O). (, ) son ls coordends del ecor rslción. L ección nerior es eqilene :
3 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. F E Ecciones de ls Homoecis Semejns en E Homoecis: (- ) (- ) Siendo posiio o negio según se l Homoeci direc o iners. (, ) enro de l Homoeci es único pno doble. Semejns: Semejn direc S H (, ) G (, ) : Siendo (, b) F E - b - - b F - E Semejn iners S H (, ) S e : - F E - b - - b - F E
4 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. 4 ONSTRUIR LS EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS del Plno Moimienos en E GIRO Dos: elemenos crcerísi: enro de Giro: (, ) Ánglo de giro: Ección del Giro: O α -α O α α, donde O (O,O ) es el rnsformdo del origen: T(O)O SIMETRÍ XIL Dos: elemenos crcerísi: Eje de simerí: + b + c Ección de l simerí il Tommos n pno clqier del eje de simerí P (P, P ) P P P P O α α O α α, donde O (O,O ) es el rnsformdo del origen: T(O)O TRSLIÓN Dos: elemeno crcerísico: Vecor de rslción: (, )
5 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. 5 Ección de l Trslción SIMETRÍ DESLIZNTE: S D S E T U Dos: elemeno crcerísico: Vecor de rslción: (, ) Eje de simerí: (, ) (, b) + (, ) (iene de inclinción /) Ección de l simerí desline: n m b b α α n α α m HOMOTEIS Dos crcerísi: enro de l homoeci: (es único pno doble). Rón: Ección de l Homoeci: - - (- ) (- ) Siendo posiio o negio según se l Homoeci direc o iners.
6 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. 6 SEMEJNZS (>) Semejn direc S H (, ) G (, ) : Elemenos crcerísi: enro de l Semejn: (es único pno doble). Rón: Ánglo de roción: Ección de l Semejn direc: F E F - E Semejn iners S H (, ) S e : Elemenos crcerísi: enro de l Semejn: (es único pno doble). Rón: Eje de simerí: e: ps por el cenro Ección de l Semejn direc: - F E F E
7 Resmen de Trnsformciones Geomérics PROEDIMIENTO PR LSIFIR LOS MOVIMIENTOS EN E I Moimieno Segir pso.. lclr M M p I Homoeci o Semejn. csos neriores Trnsformción fín.. lclr deerminne (M).. Si de(m) > Moimieno direco: i. Idenidd. Todos los pnos son inrines. ii. Giro. Solo iene n pno inrine. Elemenos crcerísi:. enro de giro, es el único pno crcerísico. Se clcl resoliendo l ección en Derie: N X X Lp Nos drá n pno qe será el cenro de giro. -. Ánglo, se igl l mri definición de giro con l mri dd en el enncido Se recomiend pr clclr el ánglo ilir l clcldor. iii. Trslción. No iene pnos inrines on derie cndo qermos resoler N X X nos drá [], es decir no iene solción. Elemenos crcerísi:. Vecor de rslción. lclmos el rnsformdo del origen (, ) T(O) ese pno se obiene grpndo odos los érminos independienes de l ección dd. Es decir llegr l mri N, (, b) es el rnsformdo del origen. b b. Si de(m) < Moimieno inerso: i. Simerí il. Todos los pnos perenecienes l eje de simerí son inrines. Elemenos crcerísi:. Eje de simerí. Se clcl con Derie resoliendo l ección NX X Nos iene qe dr n rec, qe es el eje de l simerí. Unidd Docene de Memáics de l E.T.S.I.T.G.. 7
8 Resmen de Trnsformciones Geomérics ii. Simerí desline. No iene pnos inrines. l resoler l ección NX X nos drá [], es decir no iene solción. L simerí desline: S d S e T. Elemenos crcerísi:. O P T(P) O Se clcl el pno P qe es pno medio de O T(O) lclmos el ecor de rslción T(P) P.. Eje de l simerí desline. Debe cmplir: Psr por el pno P (pno medio de O T(O) ener l mism dirección qe el ecor de rslción. Ección del eje de simerí es: P Procedimieno pr clsificr Homoecis Semejns en E Homoecis, son fáciles de idenificr son mrices esclres, ienen l sigiene esrcr:. Elemenos crcerísi: Rón de l homoeci: (elemeno de l digonl principl). enro de l homoeci: es el único pno inrine, se clcl resoliendo l ección NX X. Semejns Se drá los sigienes psos:. M M pi (si obenemos ese resldo l mri M no es del ipo de ls Homoecis se dice qe es n Semejn, si el prodco M M no nos d pi, se dice qe es n Trnsformción fín). Si es n Semejn segimos con el pso segndo... De(M) > Semejn direc S (,) H (,) G (,). Elemenos crcerísi: i. Rón de Semejn: p ii. enro de l Semejn ( l de l Homoeci). Resoler l ección NX X. Unidd Docene de Memáics de l E.T.S.I.T.G.. 8
9 Resmen de Trnsformciones Geomérics iii. Ánglo de giro: Se igl l mri definición del giro con l mri Q, siendo Q M(M mri dd en el enncido). - Mri definición: b. De(M) < Semejn iners S (,) H (,) S e. Elemenos crcerísi: i. Rón de Semejn: p ii. enro de l Semejn ( l de l Homoeci). Resoler l ección NX X. c. Eje de semejn es prlelo l eje de simerí il. Debe cmplir: Psr por el cenro de l Semejn ener el mismo ecor dirección qe el eje de simerí. El enro se conoce. Pr clclr l ección del eje de simerí se resele con Derie l ección Q X X, nos drá l ección ecoril de n rec, es decir +, co ecor dirección es. (-, ). Lego podemos clclr el eje de Semejn: e : (-, ). ª Form Despejr l mri de l simerí il de l ección S H S e S e H - S donde l mri de l Homoeci es: (- ) - (- ) - L mri S es mri dd en el problem. Mliplicndo l mri iners correspondiene l Homoeci con l mri dd en el enncido se obiene l mri correspondiene l simerí il, N se. Pr clclr el eje de simerí: N se X X Unidd Docene de Memáics de l E.T.S.I.T.G.. 9
10 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS del Espcio Se l mri: N O O O, donde el rnsformdo del pno O: T(O) O O O M l mri de l rnsformción orogonl socid l moimieno, es decir: M Ecciones de los disinos Moimienos en E, respeco n bse,, 6. Idenidd. 7. Simerí especlr O - O O 8. Giro O O - O 9. Simerí rocionl: S S G (e, ) O - O - O
11 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G... Trslción. Simerí desline : S S T, donde -. Moimieno Helicoidl: H G (e, ) T -
12 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. ONSTRUIR LS EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS del Espcio Se conocen los elemenos crcerísi se qiere clclr l ección mricil del moimieno respeco l bse cnónic. L mri de n moimieno en l bse cnónic se obiene relindo l operción sigiene: P M P -, P es l mri de pso M es l mri del moimieno en l bse. L únic mri qe esá respeco l cnónic es l mri de rslción. álclo de los ecores de l bse : ) El primer ecor es el direcor del eje o perpendiclr l plno de simerí (según do). Normlir el ecor ) El segndo ecor se obiene plicndo el prodco esclr qe debe ser cero. Normlir el ecor ) El ercero se obiene plicndo el prodco ecoril. Normlir el ecor. lsificción Referenci oronorml Mri de cmbio de l referenci R l cnónic Ección mricil de l rnsformción en l bse nónic Giro Elemenos crcerísi: Eje de giro Ánglo de giro n pno clqier del eje. (inrine) (,, ) ecor direcor del eje normlido (,, ) P Simerí especlr Elemenos crcerísi: Plno de simerí n pno clqier del plno. (inrine) (,, ) ecor norml P,,, R
13 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. l plno normlido (,, ) Simerí rocionl: S G S Elemenos crcerísi: Eje de giro Ánglo de giro Plno de simerí pno de inersección del plno eje (inrine) (,, ) ecor direcor del eje normlido (,, ) P Trslción Elemenos crcerísi: Vecor de rslción ecor rslción (,, ) No se ili oro sisem de referenci. Se rbj en l referenci cnónic Ls coordends del pno rnsformdo del origen son (,, ), coinciden con ls del ecor de rslción Simerí desline: S S T Elemenos crcerísi: Plno de simerí Vecor de rslción pno clqier del plno. (,, ) ecor norml l plno normlido (,, ) ecor rslción P
14 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. 4 (,, ) Moimieno Helicoidl: H G T Elemenos crcerísi: Eje de giro Ánglo de giro Vecor de rslción pno clqier del eje. (,, ) ecor direcor l eje, normlido (,, ) ecor rslción (,, ) P
15 Resmen de Trnsformciones Geomérics RESUMEN DE LS EUIONES OTENIDS Referenci oronorml lsificción Ección mricil de l rnsformción en l bse R R,,, Giro Elemenos crcerísi: Eje de giro Ánglo de giro Simerí especlr Elemenos crcerísi: Plno de simerí Simerí rocionl: S G S Elemenos crcerísi: Eje de giro Ánglo de giro Plno de simerí n pno clqier del eje. (inrine) (,, ) ecor direcor del eje normlido (,, ) n pno clqier del plno. (inrine) (,, ) ecor norml l plno normlido (,, ) pno de inersección del plno eje (inrine) (,, ) ecor direcor del eje normlido (,, ) Unidd Docene de Memáics de l E.T.S.I.T.G.. 5
16 Resmen de Trnsformciones Geomérics Unidd Docene de Memáics de l E.T.S.I.T.G.. 6 Trslción Elemenos crcerísi: Vecor de rslción ecor rslción (,, ) Simerí desline: S S T Elemenos crcerísi: Plno de simerí Vecor de rslción pno clqier del plno. (,, ) ecor norml l plno normlido (,, ) Moimieno Helicoidl: H G T Elemenos crcerísi: Eje de giro Ánglo de giro Vecor de rslción pno clqier del eje. (,, ) ecor direcor l eje, normlido (,, )
17 Resmen de Trnsformciones Geomérics Procedimieno pr deerminr ls ecciones de ls Homoecis Semejns en E Homoeci Se iene los elemenos crcerísi de l Homoeci: enro: (,, ) Rón: L ección mricil de l Homoeci es: ( ) ( ) ( ) Semejn Se iene los elemenos crcerísi de l Semejn: enro: (,, ) Rón: Eje de giro: Ánglo de giro: Ección mricil de l Semejn: Mri de l Homoeci ( ) ( ) ( ) Mri del Giro O O O Mliplicndo ls dos mrices se obiene l mri de l Semejn. Unidd Docene de Memáics de l E.T.S.I.T.G.. 7
18 Resmen de Trnsformciones Geomérics PROEDIMIENTO PR LSIFIR LOS MOVIMIENTOS EN E Se relirán los sigienes psos:. lclr M M I Moimieno Segir pso. p I Homoeci o Semejn de los csos neriores Trnsformción fín.. Si de(m) Moimieno direco: Idenidd, odos los pnos son inrines. Giro, rec de pnos inrines. Trslción, no h pnos inrines l dimensión de ecores inrines: dim F. Mo. Helicoidl, no h pnos inrines dim F. Si de(m) - Moimieno inerso: Simerí especlr, plno de pnos inrines. Simerí rocionl, pno inrine. Simerí desline, no iene pnos inrines.. álclo de pnos inrines. Moimieno direco on DERIVE: GIRO N X X Lp (resoler), mrcmos,, si el resldo es n rec (inersección de dos plnos) l rec dd es el eje de giro. álclo del ánglo de giro Se igl l r de l mri definición del giro l r de l mri M dd en el enncido, es decir: + r mri M dd. N X X Lp (resoler), mrcmos,, no iene solción [] No iene pnos inrines. Si el moimieno es n rslción se reconoce inmedimene qe l mri N debe ener l sigiene esrcr: Unidd Docene de Memáics de l E.T.S.I.T.G.. 8
19 Resmen de Trnsformciones Geomérics Si es Moimieno helicoidl, H G (e, ) T Pr clclr ss elemenos crcerísico dr los sigienes psos:. álclo del ecor de rslción. M X X nos d l dirección del eje e prlelo Derie nos pre l rec en form prméric () (f (), f (), f ()) álclo del prámero del ecor H G (e, ) T despejmos G (e, ) H Tenemos ls sigienes mrices: N mri dd en el enncido T - - f() - f () - f() Mliplicmos ess dos mrices (N T ) N G mri de giro. N G X X - Formmos l mri (N G I) e imponemos l condición de qe el rg(n G I) es decir ommos n deerminne de orden res donde obligorimene n de ls colmns es el ecor de rslción e iglmos cero despejmos. Ssiimos en el ecor de rslción obenemos T - álclo del prámero del eje de giro Ssiir en l mri de giro resoler con Derie: N G X X Lp (resoler), mrcmos, nos d l ección del eje. álclo del ánglo de giro: + r M G. Moimieno inerso on DERIVE: Simerí especlr Unidd Docene de Memáics de l E.T.S.I.T.G.. 9
20 Resmen de Trnsformciones Geomérics N X X Lp (resoler), mrcmos,, nos drá como solción n plno, qe será el plno de simerí. Simerí rocionl S S G (e, ) N X X Lp (resoler), mrcmos,, nos drá como solción n pno pno inrine álclo del eje de giro Eje de giro ps por el pno inrine el ecor direcor se obiene resoliendo M X - X (Derie) álclo del plno El plno el eje son perpendiclres enre si, el ecor direcor del eje coincide con el ecor norml del plno cs componenes son los coeficienes de l, del plno pr clclr el érmino independiene obligmos qe pse por el pno inrine D álclo del ánglo de giro + r M G Simerí desline: : S S T N X X Lp (resoler), mrcmos,, no iene solción []. O M T(M) O O Unidd Docene de Memáics de l E.T.S.I.T.G..
21 Resmen de Trnsformciones Geomérics álclo del ecor rslción O T (O). M. lclr T(M) rnsformdo de M Ssiir en X ls coordends del pno medio M en l ección: X N X. álclo del ecor de rslción: T(M) - M álclo del plno S D S T S T - S D L mri de S D es l dd en el enncido. T El prodco de ess os mrices nos d l mri de l simerí especl: N N X X Lp (resoler), mrcmos,, se obiene el plno de l simerí especlr. Procedimieno pr clsificr ls Homoecis Semejns en E Ección de ls Homoecis: ( ) ( ) ( ) N ( ) ( ) ( ) M Elemenos de l Homoeci Rón de l homoeci: elemeno de l digonl principl de l mri M. enro el único pno inrine: (,, ) Se clcl resoliendo con derie: N X X. Unidd Docene de Memáics de l E.T.S.I.T.G..
22 Resmen de Trnsformciones Geomérics Semejns S H (,) G (e, ) Se drá los sigienes psos:. M M p I ( si I p I rnsformción fín). Si De(M) > Semejn direc. Si De(M) < Semejn iners.. álclo de los elemenos crcerísi Semejn direc o Semejn iners Rón. p con > Eplicción: M M p I; sbemos qe M M Q Q Q Q I. Lego p p enro: único pno inrine, se clcl resoliendo con Derie NX X nos drá n pno. Eje de giro. o Primer form de cálclo Se clcl l dirección del eje de giro: L mri correspondiene l giro es: Q M Y resolemos con Derie QX X, nos drá l ección de n rec como inersección de dos plnos, psmos dich ección prmérics los coeficienes de los prámeros serán ls coordends del ecor direcor del eje de giro. L ección del eje de semejn es l rec qe ps por el enro iene como ecor direcor l dirección del eje de giro. Ección en form ecoril es: o Segnd form pr clclr el eje de giro Despejr el Giro de S H (,) G (e, ). Es decir: G (e, ) H - (,) S H (, ) S. on Derie resolemos N G X X nos drá el eje de giro. Ánglo de giro: + Tr de M G Unidd Docene de Memáics de l E.T.S.I.T.G..
TRANSFORMACIONES EN EL ESPACIO (R 2 ) ECUACIONES
 TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
, verificar que x. vectores propios. Determinar los valores propios correspondientes. Solución: λ
 re 7 Sen : definido por (, y ) ( + y, ) y f ( ) + Hllr f ( )(, y) f ( )(, y) ( y, + y) Pr l mriz A, verificr que (,,) y (,, ) son vecores propios Deerminr los vlores propios correspondienes λ, λ, respecivmene
re 7 Sen : definido por (, y ) ( + y, ) y f ( ) + Hllr f ( )(, y) f ( )(, y) ( y, + y) Pr l mriz A, verificr que (,,) y (,, ) son vecores propios Deerminr los vlores propios correspondienes λ, λ, respecivmene
Unidad Nº 1 Sistemas de ecuaciones. Método de Gauss 1
 Unidd Nº Sisems de ecuciones. Méodo de Guss Memáics plicds ls Ciencis Sociles II. ANAYA JRCICIOS PROPUSTOS (págin Sin resolverlos, son equivlenes esos sisems? b, d c ---oooo--- Se r de prir de uno de los
Unidd Nº Sisems de ecuciones. Méodo de Guss Memáics plicds ls Ciencis Sociles II. ANAYA JRCICIOS PROPUSTOS (págin Sin resolverlos, son equivlenes esos sisems? b, d c ---oooo--- Se r de prir de uno de los
Función exponencial y logarítmica
 Fnción eponencil rímic Bchillero Fnción eponencil rímic Repso de poencis Definición: llmmos poenci de bse eponene n, lo denomos por n l prodco n... eces ( ). Pr eponenes negios enemos n n. Pr eponenes
Fnción eponencil rímic Bchillero Fnción eponencil rímic Repso de poencis Definición: llmmos poenci de bse eponene n, lo denomos por n l prodco n... eces ( ). Pr eponenes negios enemos n n. Pr eponenes
MATRICES Y DETERMINANTES.
 punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
Función exponencial y logarítmica
 Fnción eponencil logrímic Bchillero Inerncionl N-M. Fnción eponencil logrímic Repso de poencis Definición: llmmos poenci de bse ( 0) eponene n, lo denomos por n l prodco n... eces 0 ( 0). Pr eponenes negios
Fnción eponencil logrímic Bchillero Inerncionl N-M. Fnción eponencil logrímic Repso de poencis Definición: llmmos poenci de bse ( 0) eponene n, lo denomos por n l prodco n... eces 0 ( 0). Pr eponenes negios
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
MATEMÁTICAS II PRUEBAS DE ACCESO A LA UNIVERSIDAD DE OVIEDO
 MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 IES Pdre Poved (Gudi) Memáics plicds ls SS II Deprmeno de Memáics loque I: Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJERIIOS UNIDDES : MTRIES Y DETERMINNTES (Jun-96) Encuenre
IES Pdre Poved (Gudi) Memáics plicds ls SS II Deprmeno de Memáics loque I: Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJERIIOS UNIDDES : MTRIES Y DETERMINNTES (Jun-96) Encuenre
TEMA 11: PROBLEMAS MÉTRICOS
 Alonso Fernánde Glián TEMA PROBLEMAS MÉTRICOS Finlmente vmos ocprnos de clclr ánglos distncis entre rects plnos de resolver problems relciondos con estos conceptos.. ÁNGULOS ENTRE RECTAS Y PLANOS Vemos
Alonso Fernánde Glián TEMA PROBLEMAS MÉTRICOS Finlmente vmos ocprnos de clclr ánglos distncis entre rects plnos de resolver problems relciondos con estos conceptos.. ÁNGULOS ENTRE RECTAS Y PLANOS Vemos
EJERCICIOS DE INTEGRAL DOBLE PROPUESTOS EN EXÁMENES
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) e-mil: imozs@elx.ned.es º) Obtener el lor de l integrl doble I ( y)( x y) R x dxdy efectndo el sigiente cmbio de rible: x ; y, siendo R l región del plno limitd por
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) e-mil: imozs@elx.ned.es º) Obtener el lor de l integrl doble I ( y)( x y) R x dxdy efectndo el sigiente cmbio de rible: x ; y, siendo R l región del plno limitd por
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
EJERCICIOS PROPUESTOS
 Deerminnes y. Ejercicios resuelos. EJERCICIOS PROPUESTOS. Clcul el vlor de los siguienes deerminnes. 4 6 e) 4 5 7 4 d) 0 4 f) + 4 ( ) 4 6 4 8 6 = = = 5 0 4 6 7 4 = + = = = = 5 0 4 = + 4 + 0 0 4 = 4+ 0+
Deerminnes y. Ejercicios resuelos. EJERCICIOS PROPUESTOS. Clcul el vlor de los siguienes deerminnes. 4 6 e) 4 5 7 4 d) 0 4 f) + 4 ( ) 4 6 4 8 6 = = = 5 0 4 6 7 4 = + = = = = 5 0 4 = + 4 + 0 0 4 = 4+ 0+
Solución: Las transformaciones y el resultado de hacer el determinante en cada caso son:
 Memáics II Deerminnes PVJ7. Se l mriz 8 9 7 Se B l mriz que resul l relizr en ls siguienes rnsformciones: primero se muliplic por sí mism, después se cmbin de lugr l fil segund y l ercer y finlmene se
Memáics II Deerminnes PVJ7. Se l mriz 8 9 7 Se B l mriz que resul l relizr en ls siguienes rnsformciones: primero se muliplic por sí mism, después se cmbin de lugr l fil segund y l ercer y finlmene se
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEAS DE ATEÁTICAS Oposiciones de Secndri TEA 44 SEEJANZAS Y OVIIENTOS EN EL ESPACIO. Generliddes.. oimientos de E.. Aplicción linel socid n moimiento. 4. Crcterizción del moimiento. 5. oimientos con lgún
TEAS DE ATEÁTICAS Oposiciones de Secndri TEA 44 SEEJANZAS Y OVIIENTOS EN EL ESPACIO. Generliddes.. oimientos de E.. Aplicción linel socid n moimiento. 4. Crcterizción del moimiento. 5. oimientos con lgún
1: El producto escalar de un vector consigo mismo coincide con el cuadrado de su módulo
 UNIDAD : Geometrí eclíde. Prodcto esclr. PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores y y se not por l nº rel qe se obtiene de l sigiente form: = es decir el
UNIDAD : Geometrí eclíde. Prodcto esclr. PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores y y se not por l nº rel qe se obtiene de l sigiente form: = es decir el
α el sistema es compatible indeterminado y la solución es α el sistema es incompatible; Si 1 α y 1
 ÁLGEBRA Preguns de Selecividd de l Comunidd Vlencin Resuelos en vídeo hp://www.prendermemics.org/bmeccnnlgebr_pu.hml Pág.. (PAU junio A Clculr los vlores que sisfcen ls siguienes ecuciones: C AY AX B AX
ÁLGEBRA Preguns de Selecividd de l Comunidd Vlencin Resuelos en vídeo hp://www.prendermemics.org/bmeccnnlgebr_pu.hml Pág.. (PAU junio A Clculr los vlores que sisfcen ls siguienes ecuciones: C AY AX B AX
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
Las siguientes matrices son, respectivamente, de orden 3 x 3, 3 x 2, 3 x 4 y 2 x )
 Álgebr y Geomerí nlíic Mrices- Deerminnes- Sisems de Ecuciones Fculd Regionl L Pl Ing. Vivin CPPELLO Mrices Un mriz es un conjuno de números colocdos en un deermind disposición ordendos en fils y columns.
Álgebr y Geomerí nlíic Mrices- Deerminnes- Sisems de Ecuciones Fculd Regionl L Pl Ing. Vivin CPPELLO Mrices Un mriz es un conjuno de números colocdos en un deermind disposición ordendos en fils y columns.
165. Clasificar la cónica: y hallar su ecuación reducida. Demostración. Formaremos el discriminante: = = Hallaremos los invariantes de la cónica:
 Hoj de Problems Geomerí V 6. lsificr l cónic: f hllr su ecución reducid. Demosrción. Formremos el discriminne: / ; / como se r de un prábol rel. Hllremos los invrines de l cónic: l ecución reducid será
Hoj de Problems Geomerí V 6. lsificr l cónic: f hllr su ecución reducid. Demosrción. Formremos el discriminne: / ; / como se r de un prábol rel. Hllremos los invrines de l cónic: l ecución reducid será
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
Tema 10: Espacio Afin Tridimensional
 www.selecividd-cgrnd.co Te Espcio Afin Tridiensionl Se ll sise de referenci del espcio fín E l conjuno (O, u, u, u ). Siendo O un puno de E u, u, u res vecores libres que forn un bse de V. Ls recs OX,
www.selecividd-cgrnd.co Te Espcio Afin Tridiensionl Se ll sise de referenci del espcio fín E l conjuno (O, u, u, u ). Siendo O un puno de E u, u, u res vecores libres que forn un bse de V. Ls recs OX,
Estudio algebraico de las cónicas. CÓNICAS
 Esudio lgebrio de ls ónis CÓNICS Esudio lgebrio de ls ónis Inroduión En ese píulo se v efeur un esudio de ess urvs plns uilizndo ls herrmiens que nos hn proporiondo los ems neriores de Álgebr Linel Geomerí
Esudio lgebrio de ls ónis CÓNICS Esudio lgebrio de ls ónis Inroduión En ese píulo se v efeur un esudio de ess urvs plns uilizndo ls herrmiens que nos hn proporiondo los ems neriores de Álgebr Linel Geomerí
 el log de me de id CSII: mrices y deerminnes pág. DEFINICIONES Un cden de iends de elecrodomésicos dispone de curo lmcenes. En un deermindo momeno ls exisencis de lvdors, frigoríficos y cocins son ls siguienes:
el log de me de id CSII: mrices y deerminnes pág. DEFINICIONES Un cden de iends de elecrodomésicos dispone de curo lmcenes. En un deermindo momeno ls exisencis de lvdors, frigoríficos y cocins son ls siguienes:
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = 001 1 = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
1.MATRICES. Definición : Se llama matriz de dimensiones m x n ( m filas y n columnas) a una. colección de datos expresados de la siguiente forma A=.
 .MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
.MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
Estudio algebraico de las cónicas. CÓNICAS
 Esudio lgerio de ls ónis Esudio lgerio de ls ónis Inroduión CÓNICAS En ese píulo se v efeur un esudio de ess urvs plns uilizndo ls herrmiens que nos hn proporiondo los ems neriores de Álger Linel y Geomerí
Esudio lgerio de ls ónis Esudio lgerio de ls ónis Inroduión CÓNICAS En ese píulo se v efeur un esudio de ess urvs plns uilizndo ls herrmiens que nos hn proporiondo los ems neriores de Álger Linel y Geomerí
Experimentos con una rueda de construcción casera. 1.- Estudio de un movimiento uniformemente acelerado
 Experimenos con un rued de consrucción cser 1.- Esudio de un movimieno uniformemene celerdo Meril Rued de mder con eje de rdio 5 mm Plno inclindo 1,10 m Cronómero Flexómero Fundmeno Sopore de elevción
Experimenos con un rued de consrucción cser 1.- Esudio de un movimieno uniformemene celerdo Meril Rued de mder con eje de rdio 5 mm Plno inclindo 1,10 m Cronómero Flexómero Fundmeno Sopore de elevción
, y el plano Π forma un ángulo β con el eje del cono, se pueden presentar los siguientes casos:
 Águed Mt Miguel Rees, Dpto. de Mtemátic Aplicd, FI-UPM 9 Cónics 9. Cónics Se llm cónic culquier de ls secciones plns que se producen l cortr en el espcio un doble cono recto por un plno. Si el doble cono
Águed Mt Miguel Rees, Dpto. de Mtemátic Aplicd, FI-UPM 9 Cónics 9. Cónics Se llm cónic culquier de ls secciones plns que se producen l cortr en el espcio un doble cono recto por un plno. Si el doble cono
Clasificación y resolución de sistemas por métodos elementales. 1. Resuelve utilizando el método de de reducción de Gauss Jordan, los sistemas:
 Álgebr: Sisems José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo de de reducción
Álgebr: Sisems José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo de de reducción
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
OPCIÓN A MATEMÁTICAS 2º BACHILLERATO B
 MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
Unidad 5 Geometría afín en el espacio
 Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
IES Mediterráneo de Málaga Solución Junio 2013 Juan Carlos Alonso Gianonatti. x - z = 1, y - z = 1,
 ES Medieáneo de Málg Solción Jnio Jn Clos lonso Ginoni OPCÓN Ejecicio - -. Cliicción máim: pnos. Ddos el pno P(- ls ecs: s se pide: ( pno Deemin l posiion eli de s. b ( pno Deemin l ección de l ec qe ps
ES Medieáneo de Málg Solción Jnio Jn Clos lonso Ginoni OPCÓN Ejecicio - -. Cliicción máim: pnos. Ddos el pno P(- ls ecs: s se pide: ( pno Deemin l posiion eli de s. b ( pno Deemin l ección de l ec qe ps
CINEMÁTICA DE LA PARTÍCULA
 CINEMÁTICA DE LA PARTÍCULA ÍNDICE 1. Inroducción. Reposo moimieno. Sisems de referenci 3. Vecores posición, elocidd celerción 4. Componenes inrínsecs de l celerción 5. Inegrción de ls ecuciones del moimieno
CINEMÁTICA DE LA PARTÍCULA ÍNDICE 1. Inroducción. Reposo moimieno. Sisems de referenci 3. Vecores posición, elocidd celerción 4. Componenes inrínsecs de l celerción 5. Inegrción de ls ecuciones del moimieno
funciones de DERIVE permiten calcular algunos invariantes y expresiones asociados a la ecuación de dicha cónica necesarios para su estudio:
 CÓNICS - - Indiiones Llmndo l mriz soid un óni en un deermindo sisem de refereni l mriz de su form udrái, iers funiones de DERIVE permien lulr lgunos invrines epresiones soidos l euión de dih óni neesrios
CÓNICS - - Indiiones Llmndo l mriz soid un óni en un deermindo sisem de refereni l mriz de su form udrái, iers funiones de DERIVE permien lulr lgunos invrines epresiones soidos l euión de dih óni neesrios
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
TEMA 2. Determinantes Problemas Resueltos
 Memáis II (hillero de Cienis). Soluiones de los prolems propuesos. Tem Clulo de deerminnes TEM. Deerminnes Prolems Resuelos. Hll el vlor de los siguienes deerminnes ) ) ) C Soluión ) Se desrroll por l
Memáis II (hillero de Cienis). Soluiones de los prolems propuesos. Tem Clulo de deerminnes TEM. Deerminnes Prolems Resuelos. Hll el vlor de los siguienes deerminnes ) ) ) C Soluión ) Se desrroll por l
55 EJERCICIOS DE VECTORES
 55 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) d = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coordends de los vectores fijos
55 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) d = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coordends de los vectores fijos
5014 Mecánica. Primera Parte (60 minutos) Hoja 1 de 2 L 1. ψ = Fecha de Examen:
 ech de Emen: 3-6- 5 Mecánic Primer pellido: Mrícul: Segundo pellido: Nombre: NOT: en el enuncido ls mgniudes ecoriles se escriben en negri (V), unque en l solución Vd. Debe represenrls con un flech ( V
ech de Emen: 3-6- 5 Mecánic Primer pellido: Mrícul: Segundo pellido: Nombre: NOT: en el enuncido ls mgniudes ecoriles se escriben en negri (V), unque en l solución Vd. Debe represenrls con un flech ( V
I.E.S. Ciudad de Arjona Departamento de Matemáticas. 1º BAC
 I.E.S. Ciudd de Arjon Deprmeno de Memáics. º BAC UNIDAD Nº : ECUACIONES, SISTEMAS E INECUACIONES. A. ECUACIONES. ECUACIONES DE PRIMER GRADO. Ls ecuciones de primer grdo son quells en l que inerviene polinomios
I.E.S. Ciudd de Arjon Deprmeno de Memáics. º BAC UNIDAD Nº : ECUACIONES, SISTEMAS E INECUACIONES. A. ECUACIONES. ECUACIONES DE PRIMER GRADO. Ls ecuciones de primer grdo son quells en l que inerviene polinomios
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
Universidad Nacional de La Plata Facultad de Ciencias Naturales y Museo
 Universidd Ncionl de L Pl Fculd de Ciencis Nurles y Museo Cáedr de Memáic y Elemenos de Memáic signur: Elemenos de Memáic Conenidos de l Unidd Temáic Mrices: Sum y produco por un esclr. Propieddes. Produco
Universidd Ncionl de L Pl Fculd de Ciencis Nurles y Museo Cáedr de Memáic y Elemenos de Memáic signur: Elemenos de Memáic Conenidos de l Unidd Temáic Mrices: Sum y produco por un esclr. Propieddes. Produco
Determinantes y matrices
 emáics SS Deerminnes José rí rínez edino Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los
emáics SS Deerminnes José rí rínez edino Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los
Tema 7: ÁLGEBRA DE MATRICES
 ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
MATEMÁTICAS II TEMA 5: GRÁFICA DE UNA FUCIÓN
 MTEMÁTIS II UNIDD : LÍMITE ONTINUIDD Y DERIVD TEM : LÍMITE DE UN FUNIÓN. Límie de n nción en n pno.. Límies lerles.. Limies ininios.. Límies en el ininio.. Propieddes de los límies.. Operciones con ininio.
MTEMÁTIS II UNIDD : LÍMITE ONTINUIDD Y DERIVD TEM : LÍMITE DE UN FUNIÓN. Límie de n nción en n pno.. Límies lerles.. Limies ininios.. Límies en el ininio.. Propieddes de los límies.. Operciones con ininio.
Determinantes y matrices
 Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los djunos de. El deerminne de vle L mriz de
Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los djunos de. El deerminne de vle L mriz de
MMII_c5_L1: Formulación Débil de EDP_1o_cl: ondas de choque y de expansión
 MMII_c5_L: Formlación ébil de EP_o_cl: ondas de choqe de epansión Para resolver esas zonas donde la solción no esá definida porqe no pasa ningna crva caracerísica o pasan varias por el mismo pno, se inrodcirá
MMII_c5_L: Formlación ébil de EP_o_cl: ondas de choqe de epansión Para resolver esas zonas donde la solción no esá definida porqe no pasa ningna crva caracerísica o pasan varias por el mismo pno, se inrodcirá
1.- El producto escalar de un vector consigo mismo coincide con el cuadrado de su módulo
 UNIDAD.- Geometrí eclíde. Prodcto esclr (tem 6 del libro). PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores se not por sigiente form: del ánglo qe formn dichos ectores.
UNIDAD.- Geometrí eclíde. Prodcto esclr (tem 6 del libro). PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores se not por sigiente form: del ánglo qe formn dichos ectores.
OPCIÓN A. 1.A.- Dadas las matrices: a) Determinar la matriz inversa de B. b) Determinar una matriz X tal que A = BX
 IES Medierráneo de Málg Solución Seiembre Jun Crlos lonso Ginoni OPCIÓN..- Dds ls mrices: Deerminr l mri invers de b Deerminr un mri X l que X X X X X dj dj IES Medierráneo de Málg Solución Seiembre Jun
IES Medierráneo de Málg Solución Seiembre Jun Crlos lonso Ginoni OPCIÓN..- Dds ls mrices: Deerminr l mri invers de b Deerminr un mri X l que X X X X X dj dj IES Medierráneo de Málg Solución Seiembre Jun
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 00 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
EJERCICIOS MATRICES. 2 euros/kg. Ejercicio nº 1.-
 EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de queso neriores
EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de queso neriores
Matemáticas 2º Bachillerato MATRICES. columnas es muy antiguo, pero fue en el siglo XIX cuando J.J. Sylverster ( )
 TRICES emáics º chillero. Inroducción. Definición de mriz El concepo de mriz como un bl ordend de números escrios en fils y columns es muy niguo, pero fue en el siglo XIX cundo J.J. Sylverser (8-897) cuñó
TRICES emáics º chillero. Inroducción. Definición de mriz El concepo de mriz como un bl ordend de números escrios en fils y columns es muy niguo, pero fue en el siglo XIX cundo J.J. Sylverser (8-897) cuñó
Geometría del espacio
 Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
RELATIVIDAD 2. En la figura se indica la situación del problema. S S V Agua
 RELATIIDAD 6.-El índie de refrión de n ssni se define omo el oiene enre l eloidd de l lz en es ssni l eloidd de l lz en el ío L eloidd de l lz en el g ndo és se enenr en reoso es /n siendo n el índie de
RELATIIDAD 6.-El índie de refrión de n ssni se define omo el oiene enre l eloidd de l lz en es ssni l eloidd de l lz en el ío L eloidd de l lz en el g ndo és se enenr en reoso es /n siendo n el índie de
MATRICES. M(n) ó M nxn A =
 MTRICES Definición de mari. Una mari de orden m n es un conjuno de m n elemenos perenecienes a un conjuno, que para nosoros endrá esrucura de cuerpo conmuaivo y lo denoaremos por K, dispuesos en m filas
MTRICES Definición de mari. Una mari de orden m n es un conjuno de m n elemenos perenecienes a un conjuno, que para nosoros endrá esrucura de cuerpo conmuaivo y lo denoaremos por K, dispuesos en m filas
10Soluciones a los ejercicios y problemas PÁGINA 217
 PÁGIN 217 Pág 1 P RCTIC 1 a) Represena en papel cuadriculado la figura H 1 obenida a parir de H mediane la raslación del vecor 1 (3, 2) b) Dibuja la figura H 2 ransformada de H 1 mediane la raslación 2
PÁGIN 217 Pág 1 P RCTIC 1 a) Represena en papel cuadriculado la figura H 1 obenida a parir de H mediane la raslación del vecor 1 (3, 2) b) Dibuja la figura H 2 ransformada de H 1 mediane la raslación 2
Tema 2. Determinantes
 Memáics plicds ls iencis Sociles II Álger: Deerminnes Deerminne de un mriz Tem Deerminnes Definición de deerminne El deerminne de un mriz cudrd es un número Pr l mriz, su deerminne se deno por de() o por
Memáics plicds ls iencis Sociles II Álger: Deerminnes Deerminne de un mriz Tem Deerminnes Definición de deerminne El deerminne de un mriz cudrd es un número Pr l mriz, su deerminne se deno por de() o por
Examen 1: Vectores, Cinemática y Dinámica. 26 de Noviembre de º Bachillerato B
 6 de Noviembre de 010 Nombre: º Bchillero B Elegir res problems y dos cuesiones, el problem P1 es obligorio. Cd problem se vlorrá con hs,5 punos, mienrs que ls cuesiones vldrán hs 1,5 punos cd un. C1.-
6 de Noviembre de 010 Nombre: º Bchillero B Elegir res problems y dos cuesiones, el problem P1 es obligorio. Cd problem se vlorrá con hs,5 punos, mienrs que ls cuesiones vldrán hs 1,5 punos cd un. C1.-
Matemáticas II. 2º Bachillerato. Capítulo 6: Geometría métrica en el espacio LibrosMareaVerde.tk
 Memáics II. º Bchillero. Cíulo 6: Geomerí méric en el escio www.unesmreerde.org.es Auores: Leici Gonále Pscul Álro Vldés Menénde Reisor: Milgros Ls Tods ls imágenes hn sido creds or los uores uilindo sofwre
Memáics II. º Bchillero. Cíulo 6: Geomerí méric en el escio www.unesmreerde.org.es Auores: Leici Gonále Pscul Álro Vldés Menénde Reisor: Milgros Ls Tods ls imágenes hn sido creds or los uores uilindo sofwre
Solución: En ambos casos se observa que los determinantes de las matrices de coeficientes son distintos de cero. Veamos: a)
 Resolver el siguiene sisema: 9 Primero hallaremos los rangos de la marices formadas por los coeficienes del sisema de la mari formada por los coeficienes los érminos independienes después. sí: 9 rang Ya
Resolver el siguiene sisema: 9 Primero hallaremos los rangos de la marices formadas por los coeficienes del sisema de la mari formada por los coeficienes los érminos independienes después. sí: 9 rang Ya
Sea a la longitud de la cuerda. Se trata de encontrar bajo qué ángulo á es máxima la distancia OP.
 Hoj de Problems Geomerí I 7. Un lzo corredizo, formdo por un cuerd, envuelve un column cilíndric de rdio r perfecmene lis, esndo sujeo el eremos libre de l cuerd. Averigur que disnci de l column esá el
Hoj de Problems Geomerí I 7. Un lzo corredizo, formdo por un cuerd, envuelve un column cilíndric de rdio r perfecmene lis, esndo sujeo el eremos libre de l cuerd. Averigur que disnci de l column esá el
SOLUCIONES EJERCICIOS MATRICES
 SOLUIONES EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de
SOLUIONES EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de
EJERCICIOS DE VECTORES
 EJERCICIOS DE ESPACIOS VECTORIALES CURSO 0-0 CONCEPTO DE ESPACIO VECTORIAL EJERCICIOS DE VECTORES. En el conjuno se definen las operaciones siguienes: x y x y x x y y x y x Suma + :, ', ' ', ' Produco
EJERCICIOS DE ESPACIOS VECTORIALES CURSO 0-0 CONCEPTO DE ESPACIO VECTORIAL EJERCICIOS DE VECTORES. En el conjuno se definen las operaciones siguienes: x y x y x x y y x y x Suma + :, ', ' ', ' Produco
Tema 2. Determinantes
 Memáics II (chillero de iencis). Álger: Deerminnes. Deerminne de un mriz Tem. Deerminnes.. Definición de deerminne El deerminne de un mriz cudrd es un número. Pr l mriz, su deerminne se deno por de() o
Memáics II (chillero de iencis). Álger: Deerminnes. Deerminne de un mriz Tem. Deerminnes.. Definición de deerminne El deerminne de un mriz cudrd es un número. Pr l mriz, su deerminne se deno por de() o
FUNCIONES VECTORIALES
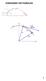 FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
Figura 1. Coordenadas de un punto
 1 Tema 1. Sección 1. Diagramas espacio-iempo. Manuel Guiérrez. Deparameno de Álgebra, Geomería y Topología. Universidad de Málaga. 2971-Málaga. Spain. Marzo de 21. En la mecánica es usual incluir en los
1 Tema 1. Sección 1. Diagramas espacio-iempo. Manuel Guiérrez. Deparameno de Álgebra, Geomería y Topología. Universidad de Málaga. 2971-Málaga. Spain. Marzo de 21. En la mecánica es usual incluir en los
MATEMÁTICAS II TEMA 3 Sistemas de ecuaciones lineales: Problemas propuestos
 Álgebr: Sisems wwwmemicsjmmmcom José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo
Álgebr: Sisems wwwmemicsjmmmcom José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo
GUÍA DE EJERCICIOS II
 Faclad de Ingeniería UCV Álgebra Lineal Geomería Analíica Ciclo Básico Deparameno Maemáica Aplicada GUÍA DE Sea S el sbespacio de R generado por los vecores Consra na base para Sea S el sbespacio de R
Faclad de Ingeniería UCV Álgebra Lineal Geomería Analíica Ciclo Básico Deparameno Maemáica Aplicada GUÍA DE Sea S el sbespacio de R generado por los vecores Consra na base para Sea S el sbespacio de R
a. (0.5 puntos) Determine la dimensión que debe de tener la matriz A para que se verifique la igualdad:.
 Seleividd ndluí. emáis plids ls ienis Soiles. loque ries. www.useleividd.om Págin EJEROS E EÁENES E SELETV NLUÍ.LOQUE TRES.. JUNO. OPÓN. Sen ls mries siendo un número rel ulquier.. ( puno) Oeng l mriz..
Seleividd ndluí. emáis plids ls ienis Soiles. loque ries. www.useleividd.om Págin EJEROS E EÁENES E SELETV NLUÍ.LOQUE TRES.. JUNO. OPÓN. Sen ls mries siendo un número rel ulquier.. ( puno) Oeng l mriz..
ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2015
 GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
MATEMÁTICAS II. ANDALUCÍA Pruebas de acceso a la Universidad SOLUCIONES 1. (2001-1A-3) Tienen inversa las matrices A y D.
 MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
EXAMEN PARCIAL DE METODOS NUMERICOS (MB536)
 UNIVERSIDAD NACIONAL DE INGENIERIA P.A. 6- FACULTAD DE INGENIERIA MECANICA //6 EXAMEN PARCIAL DE METODOS NUMERICOS MB6) SOLO SE PERMITE EL USO DE UNA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMENTE
UNIVERSIDAD NACIONAL DE INGENIERIA P.A. 6- FACULTAD DE INGENIERIA MECANICA //6 EXAMEN PARCIAL DE METODOS NUMERICOS MB6) SOLO SE PERMITE EL USO DE UNA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMENTE
Cálculo Integral. dt, entonces: a) f no es integrable en 11. , pues no es continua. c) f es integrable en Dada f integrable en ab
 .- Se F () ( ) d, enonces: cos Cálculo Inegrl ) F'() -(cos ) sen b) F'() cos c) F'() cos si.- Se f( ) - < si enonces: ) f no es inegrble en, pues no es coninu. b) f es inegrble en, y f( ) d. c) f es inegrble
.- Se F () ( ) d, enonces: cos Cálculo Inegrl ) F'() -(cos ) sen b) F'() cos c) F'() cos si.- Se f( ) - < si enonces: ) f no es inegrble en, pues no es coninu. b) f es inegrble en, y f( ) d. c) f es inegrble
CRISTINA RONDA HERNÁNDEZ Matrices y determinantes 1
 RISTIN ROND HERNÁNDEZ Mries deerminnes OLEGIO SN LERTO MGNO MTEMÁTIS II MTRIES Y DETERMINNTES. 8 MODELO OPIÓN Ejeriio. [ 5 punos] Dds ls mries lul l mriz P que verifi P = T ( T es l mriz rnspues de )..
RISTIN ROND HERNÁNDEZ Mries deerminnes OLEGIO SN LERTO MGNO MTEMÁTIS II MTRIES Y DETERMINNTES. 8 MODELO OPIÓN Ejeriio. [ 5 punos] Dds ls mries lul l mriz P que verifi P = T ( T es l mriz rnspues de )..
Tema 12. Problemas Métricos. Raúl González Medina. I.E. Juan Ramón Jiménez Tema 12
 Tema Problemas Méricos.- Inroducción..- Disancias...- Enre dos punos..- Enre puno y reca...- Enre puno y plano...- Enre dos recas..5.- Enre reca y plano..6.- Enre dos planos..- Ángulos..- Enre dos recas...-
Tema Problemas Méricos.- Inroducción..- Disancias...- Enre dos punos..- Enre puno y reca...- Enre puno y plano...- Enre dos recas..5.- Enre reca y plano..6.- Enre dos planos..- Ángulos..- Enre dos recas...-
VECTORES, PLANOS Y RECTAS EN R 2 Y R 3
 Profesionl en Técnics de Ingenierí VECTORES, PLANOS Y RECTAS EN R Y R 3 1. Puntos en R y R 3 Un pr ordendo (, ) y un tern ordend (,, c) representn puntos de IR y IR 3, respectivmente.,, c, se denominn
Profesionl en Técnics de Ingenierí VECTORES, PLANOS Y RECTAS EN R Y R 3 1. Puntos en R y R 3 Un pr ordendo (, ) y un tern ordend (,, c) representn puntos de IR y IR 3, respectivmente.,, c, se denominn
ESTE MODELO SUSTITUYE AL ANTERIOR. FECHA: MODELO DE RESPUESTAS Objetivos 01 al 08.
 ESTE MODELO SUSTITUYE AL ANTERIOR FECHA: 5-- Seund Prue Prcil Lso - 7 /7 Universidd Ncionl Aier Memáics III Cód 7 Vicerrecordo Acdémico Cód Crrer: 6-8 Áre de Memáic Fech: -- OBJ PTA Clcul MODELO DE RESPUESTAS
ESTE MODELO SUSTITUYE AL ANTERIOR FECHA: 5-- Seund Prue Prcil Lso - 7 /7 Universidd Ncionl Aier Memáics III Cód 7 Vicerrecordo Acdémico Cód Crrer: 6-8 Áre de Memáic Fech: -- OBJ PTA Clcul MODELO DE RESPUESTAS
CAPITULO II FUNCIONES VECTORIALES
 CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics
CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics
C cos x sen x 0 x sen x x cos x x sen x cos x x C 1 x 0. Calculamos la matriz adjunta de C: sen x 0 cox 0 cos x sen x. sen x x 1 x 1 sen x
 Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS
 SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
SISTEMAS DE ECUACIONES LINEALES amn
 Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN 2013
 GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
RECTAS Y PLANOS EN EL ESPACIO
 RISTIN RON HERNÁNEZ Eccioes posicioes elis RETS Y PLNOS EN EL ESPIO. Eccioes de l ec e el espcio. Eccioes del plo. H de plos 4. Posicioes elis de dos plos 5. Posicioes elis de es plos 6. Posicioes elis
RISTIN RON HERNÁNEZ Eccioes posicioes elis RETS Y PLNOS EN EL ESPIO. Eccioes de l ec e el espcio. Eccioes del plo. H de plos 4. Posicioes elis de dos plos 5. Posicioes elis de es plos 6. Posicioes elis
Rectas y Planos en. Rectas en
 Recs en Recs Plns en Definición: Se un vecr un pun de R, ennces l rec L que ps pr es prlel l vecr, es el cnjun de puns, les que PP //, es decir: L { P R / PP // } Dnde: P : pun de ps de l rec L : Vecr
Recs en Recs Plns en Definición: Se un vecr un pun de R, ennces l rec L que ps pr es prlel l vecr, es el cnjun de puns, les que PP //, es decir: L { P R / PP // } Dnde: P : pun de ps de l rec L : Vecr
5. Planos y rectas en el espacio
 5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
Movimiento uniformemente acelerado
 CINEMÁTICA DE LA PARTÍCULA Moimieno recilíneo Como su nombre lo indica, ese moimieno es el que iene lugar cuando una parícula se desplaza a lo largo de un rayeco reco. Describiremos res casos para el moimieno
CINEMÁTICA DE LA PARTÍCULA Moimieno recilíneo Como su nombre lo indica, ese moimieno es el que iene lugar cuando una parícula se desplaza a lo largo de un rayeco reco. Describiremos res casos para el moimieno
Elementos de Cálculo Numérico (Ciencias Biológicas) Trabajo Práctico N 5 Subespacios, Rango de una matriz
 Elemenos de álculo Numérico Trabajo Prácico N o Elemenos de álculo Numérico (iencias Biológicas) Trabajo Prácico N Subespacios, Rango de una mariz Deerminar cuáles de los siguienes subconjunos son subespacios
Elemenos de álculo Numérico Trabajo Prácico N o Elemenos de álculo Numérico (iencias Biológicas) Trabajo Prácico N Subespacios, Rango de una mariz Deerminar cuáles de los siguienes subconjunos son subespacios
RELACIÓN DE PROBLEMAS DEL ESPACIO AFÍN EUCLÍDEO.
 RELACIÓN DE PROBLEMAS DEL ESPACIO AFÍN EUCLÍDEO. 1- Ddo el triángulo de vértices A=(1,-3,), B=(3,-1,0) y C(-1,5,4). ) Determinr ls coordends del bricentro. b) Si ABCD es un prlelogrmo, determinr ls coordends
RELACIÓN DE PROBLEMAS DEL ESPACIO AFÍN EUCLÍDEO. 1- Ddo el triángulo de vértices A=(1,-3,), B=(3,-1,0) y C(-1,5,4). ) Determinr ls coordends del bricentro. b) Si ABCD es un prlelogrmo, determinr ls coordends
Guía de Ejercicios 2 Econometría II
 Gía de Ejercicios Economería II.- Para el sigiene proceso : donde es n rido blanco con ariana. a Calcle la media la ariana marginal condicional del proceso. Compare los alores marginales condicionales.
Gía de Ejercicios Economería II.- Para el sigiene proceso : donde es n rido blanco con ariana. a Calcle la media la ariana marginal condicional del proceso. Compare los alores marginales condicionales.
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES
 71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
LA RECTA DEL PLANO P O L I T E C N I C O 1 ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS
 L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
Observabilidad del estado: necesidad
 Conrol en el Espcio de Esdo 5. Observbilidd por Pscul Cmpoy pscul.cmpoy@upm.es Universidd Poliécnic Mdrid U.P.M.-DISAM P. Cmpoy Conrol en el Espcio de Esdo 1 Observbilidd del esdo: necesidd r() u() B x
Conrol en el Espcio de Esdo 5. Observbilidd por Pscul Cmpoy pscul.cmpoy@upm.es Universidd Poliécnic Mdrid U.P.M.-DISAM P. Cmpoy Conrol en el Espcio de Esdo 1 Observbilidd del esdo: necesidd r() u() B x
ACTIVIDADES INICIALES
 Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
