Problemas Tema 1 Enunciados de problemas de repaso de 1ºBachillerato
|
|
|
- Patricia Rico Lagos
- hace 7 años
- Vistas:
Transcripción
1 página 1/27 Problemas Tema 1 Enunciados de problemas de repaso de 1ºBachillerato Hoja 1 1. Dados tres números reales cualesquiera r 1, r 2 y r 3, hallar el numero real x que minimiza la función D( x)=(r 1 x) 2 +(r 2 x) 2 +(r 3 x) 2. x= r 1 +r 2 +r 3 3 es un mínimo absoluto de la parábola. 2. Sabiendo que x lim ( x 1 x 1 a ) es finito, calcula ln x a y el valor del límite (ln denota el logaritmo neperiano). a=1, límite = 1/2 3. Halla las dimensiones del rectángulo de área máxima inscrito en un triangulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. base = 3 metros, altura = 2 metros (máximo absoluto del área) 1 x 4. Sea la función definida por f (x)=x e para x 1, x 0. a) Calcula los límites laterales de la función en x=0. b) Estudia y determina las asíntotas de la gráfica de la función. a) 0, + b) Asíntota vertical en x=0 y asíntota oblicua y=x Sea f (x)={ sen x } +2 si x 0 x k si x=0 a) Hay algún valor de k para el cual f(x) sea continua en x=0? b) Hay algún valor de k para el cual f(x) sea derivable en x=0? c) Determinar sus asíntotas. a) k =3 b) k =3 c) Asíntota horizontal y=2
2 página 2/27 Hoja 2 1. Sea f (x)=a x 3 +b x 2 +c x+d un polinomio que cumple f (1)=0, f ' (0)=2, y tiene dos extremos relativos para x=1 y x=2. a) Determinar a,b,c y d. b) Son máximos o mínimos los extremos relativos? a) a= 1 3, b= 3 2, c=2, d = 5 6 b) x=1 es máximo, x=2 es mínimo 2. Sea la función f (x)=2 x+sen(2 x). a) Determinar si tiene asíntotas de algún tipo. b) Estudiar su monotonía y la existencia de extremos relativos. a) No tiene asíntotas. b) Creciente, sin máximos ni mínimos relativos, con puntos de inflexión en x= π 2 + k π 2, k Z 3. Se considera la función f (x)= 1 4 x 2. a) Indicar el dominio de definición de la función y hallar sus asíntotas. b) Hallar los extremos relativos de la función y sus intervalos de concavidad y convexidad. c) Dibujar la gráfica de f (x) y hallar su máximo y su mínimo absolutos en el intervalo [ 1,1]. a) Dom f =R { 2,2} b) Asíntotas verticales en x= 2 y x=2. Asíntota horizontal en y=0. No hay puntos de inflexión. La función es convexa para x < 2, cóncava para el intervalo ( 2,2), y vuelve a ser convexa para x>2. c) En el punto (0, 1 ) existe un mínimo absoluto a) Si es posible, dibujar de forma clara la gráfica de una función continua en el intervalo [0, 4] que tenga al menos un máximo relativo en el punto (2, 3) y un mínimo relativo en el punto (3, 4). b) Si la función fuera polinómica, cuál ha de ser como mínimo su grado? La función tiene, al menos, cuatro extremos, por lo que el grado del polinomio tiene que ser cinco como mínimo. De esta forma, al derivar el polinomio, tendremos al menos los cuatro extremos como solución de igualar la derivada a cero (pendiente cero).
3 página 3/27 Hoja 3 1. Expresa en función de x y simplifica. sen(2 π x) cos( x)sen( π +x )+1 2 (1+senx) cos 2 (x) sen(π x) 2. a) Determinar los extremos relativos de la función f (x)=x 2 4 x+2. Dibujar su gráfica. b) Hallar las ecuaciones de las dos rectas tangentes a la gráfica de f ( x) que pasan por el punto P (3, 5). a) Parábola con mínimo absoluto A(2, 2) b) y+ 1= 2( x 1), y 7=6( x 5) 3. Sea P (x) un polinomio de grado 4 tal que: - P (x) es una función par. - Dos de sus raíces son x=1 y x= 5. - P (0)=5. Se pide: a) Hallar sus puntos de inflexión. b) Dibujar su gráfica. a) El polinomio es P (x)=x 4 6x Puntos de inflexión en ( 1,0) y (1,0). b) Máximo (0,5), Mínimos en ( 3, 4) y ( 3, 4), cortes eje OX ( 5,0), ( 1,0), (1,0), ( 5,0) 4. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento, que dentro de 10 años la edad de la madre será la suma de las edades que los hijos tendrán en ese momento y que cuando el hijo mayor tenga la edad actual de la madre, el hijo menor tendrá 42 años. 44 años, 18 años y 16 años 5. Sea la función definida por f (x)= x ln x para x>0, x 1. a) Estudia y determina las asíntotas de la gráfica de la función. b) Calcula la ecuación de la recta tangente y de la recta normal a la gráfica de f (x ) en el punto de abscisa x=e. a) Asíntota vertical en x=1 b) Recta tangente y=e. Recta normal x=e.
4 página 4/27 Hoja 4 k 1. Sea la función definida por f (x)= (x a)(2 x 1) para x a y x 1/2. a) Halla a y k sabiendo que la gráfica de f ( x) pasa por el punto (0,2) y que la recta x=2 es una asíntota de dicha gráfica. b) Para k =4 y a=2, halla los extremos relativos de f (x) (abscisas donde se obtienen y valores que se alcanzan) y sus intervalos de crecimiento y de decrecimiento. a) a=2, k=4 b) Máximo relativo en ( 5 4, 39 2 ). Estrictamente creciente para x< 5 4 (sin incluir x= 1 2 donde hay una asíntota vertical). Estrictamente decreciente para x > 5 4 (sin incluir x=2 donde hay una asíntota vertical). 2. Un rectángulo está inscrito en un semicírculo de 5 cm de radio, de forma que uno de sus lados está contenido en el diámetro del semicírculo y el lado opuesto tiene sus vértices sobre la semicircunferencia. Calcula las dimensiones del rectángulo sabiendo que es el de mayor perímetro posible. longitud = 4 cm, altura = 1 cm 3. Considera la función f (x)=x 3 +a x 2 +b x+c. Determina a, b y c sabiendo que la recta normal a la gráfica de f (x) en el punto de abscisa x=0 es y+ x+3=0 y que el punto de inflexión tiene abscisa x=1. a= 3, b=1, c= 3 4. Sabiendo que lim x 0 b= 1, límite= 1 3 xcos(x)+b sen(x) x 3 es finito, calcula b y el valor del límite. 5. Sea f :(,1) R la función definida por f (x)={ x+2 e x si x 0 a b x si 0<x<1} a) Determina a y b sabiendo que f (x) es derivable en todo su dominio. b) Halla la ecuación de la recta tangente y de la recta normal a la gráfica de la función en el punto de abscisa x=0. a) a=2, b=1 b) Recta tangente y= x +2, recta normal y=x + 2
5 página 5/27 Hoja 5 1. Sea la función definida por g(x)= mx 3 x n (x n) 2 a) Halla m y n sabiendo que la recta y=2 x 4 es una asíntota de la gráfica de g( x). b) Determina si la gráfica de g ( x) es simétrica respecto al origen. a) m=2, n= 1 b) No es simétrica respecto al origen. 2. Sea f :R R la función definida por f (x)=x 3 +a x 2 +b x+c. Se sabe que un punto de inflexión de la gráfica tiene abscisa x=1 y que f (x) tiene un mínimo relativo en x=2 de valor 9. Calcula a, b y c. a= 3, b=0, c= 5 3. Un alambre de 10 metros de longitud se divide en dos trozos. Con uno de ellos se forma un triángulo equilátero y con el otro un cuadrado. Halla la longitud de dichos trozos para que la suma de las áreas sea mínima m, m 4. Sea f :(0,+ ) R la función definida por f (x)= 2 lnx x 2 (donde In denota el logaritmo neperiano). a) Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan). b) Estudia y determina las asíntotas de la gráfica de f. a) Estrictamente creciente en el intervalo (0, e), decreciente en ( e,+ ), máximo relativo en el punto ( e, 1 e ). b) Asíntota vertical x=0, Asíntota horizonal y=0, corte con la asíntota horizontal en (1,0). 5. Calcular la base y la altura del triángulo isósceles de perímetro 8 y área máxima. base = 8 3, atura = 4 3 3
6 página 6/27 Hoja 6 1. Se desea construir un depósito cilíndrico cerrado de área total igual a 54 m 2. Determina el radio de la base y la altura del cilindro para que éste tenga volumen máximo. r= 3 π m, h= 6 π m 2. Hallar a, b y c de modo que la función f (x)=x 3 +a x 2 +b x+c alcance en x=1 un máximo relativo de valor 2, y tenga en x=3 un punto de inflexión. a= 9, b=15, c= 5 3. Sea A(1, 1) y B( 1, 1) dos puntos del plano. a) Determinar las ecuaciones de todas las circunferencias que pasan por los puntos A y B razonando donde están situados sus centros. b) De entre las circunferencias del apartado anterior hallar el centro y el radio de la que es tangente a la recta y=x. a) x 2 + y 2 2ay+2 a 2=0, centro C (0, a) b) C (0,2), r= 2 4. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia de ecuación x 2 + y 2 4 x 2 y+1=0. La varilla se mantiene en todo momento tangente a dicha circunferencia. a) Determinar el lugar geométrico descrito por el extremo B de la varilla. b) Obtener la ecuación cartesiana de dicho lugar geométrico. a) Circunferencia concéntrica con la dada y radio CB, siendo el centro C (2,1). b) x 2 + y 2 4 x 2 y=0, C (2,1), r= 5 5. Sea f :[ 1 e,4] R la función definida por f (x)= { x ln(x)+a si 1 e x 2 bx +1 ln(2) si 2< x 4}, donde ln denota la función logaritmo neperiano. a) Calcula los valores de a y b para que f sea derivable en el intervalo ( 1 e,4). b) Para a=0 y b= 1 2 halla los extremos absolutos de f (abscisas donde se obtienen y valores que se alcanzan). a) a=0, b= 1 2 b) máximo absoluto (4, 3 ln(2)), mínimo absoluto (1,1)
7 página 7/27 Hoja 7 1. a) Hallar la ecuación del lugar geométrico de los puntos del plano tales que su distancia al punto (4,0) es el doble de su distancia a la recta x=1. b) Comprobar que el anterior lugar geométrico es una cónica. Indicar el tipo de cónica que es y hallar sus focos. a) x =1 b) Hipérbola de focos ( 4,0), (4,0) Los vértices de un triángulo son A( 2, 1), B(7,5) y C (x, y). a) Calcular el área del triángulo en función de x, y. b) Encontrar el lugar geométrico de los puntos (x, y) tales que la anterior área sea 36 u 2. a) 3 2x 3y+1 b) 2x 3 y 23= Sea la parábola x 2 =4y. Sean u y v las rectas tangentes a la parábola en los puntos P (a,0) y Q(b,0). a) Hallar las coordenadas del punto R de intersección de u y v. b) Hallar la relación entre a y b para que las rectas u y v sean perpendiculares. c) Probar que en el caso del apartado anterior, el punto R está en la directriz de la parábola. a) R(a+b, ab 2 ) b) a b= 4 c) d : y= 2, R(a+b, 2) d 4. Determinar la ecuación cartesiana de los puntos del lugar geométrico de los puntos del plano tales que la suma de los cuadrados de sus distancias a los puntos (0,0) y (1,1) es igual a 9. Si se trata de una curva cerrada, calcular el área que encierra. Circunferencia de centro ( 1 2, 1 ) y radio r=2. Área 4π u Sea la función f :(0,+ ) R definida por f (x)= 1 x +ln(x). a) Halla los extremos absolutos de f (abscisas donde se obtienen y valores que se alcanzan) en el intervalo [ 1 e, e]. b) Determina la ecuación de Ia recta tangente a la gráfica de f en el punto de abscisa x=e. a) Máximo absoluto en ( 1 e,e 1). Mínimo absoluto en (1,1) b) y=x( 1 e 2 +1 e )+ 2 e
8 página 8/27 Hoja 8 1. Sabiendo que una función tiene como derivada f ' (x)=(x 4) 2 (x 2 8 x+7). a) Hallar los intervalos de crecimiento y de decrecimiento de f (x). b) Hallar los máximos y mínimos relativos de f (x). c) Es el punto x=4 un punto de inflexión de f (x)?. Justicar razonadamente la respuesta. a) Creciente en (,1) (7,+ ). Decreciente en (1,7). b) Máximo en (1, ). Mínimo en ( 7, 5 5 ). c) Sí es un punto de inflexión: paso de cóncava hacia arriba a convexa (cóncava hacia abajo). 2 x 2 2. Sea la función definida por f (x)= (x +1)(x 2) para a) Estudia y calcula las asíntotas de la gráfica de f (x). x 1, x 2 b) Determina los intervalos de crecimiento y de decrecimiento de f (x). c) Calcula, si existe, algún punto de la gráfica de f (x) donde ésta corta a Ia asíntota horizontal. a) Asíntotas verticales x= 1, x=2. Asíntota horizontal y=2. b) Estrictamente decreciente para x < 4. Estrictamente creciente en el intervalo ( 4,0) { 1}. Estrictamente decreciente en (0,+ ) {2}. c) ( 2,2) 3. Sea la función f :[1,e] R definida por f (x)=x 2 8ln( x) donde ln denota la función logaritmo neperiano. a) Halla los intervalos de crecimiento y de decrecimiento de la función. b) Calcula los extremos absolutos y relativos de la función (abscisas donde se obtienen y valores que se alcanzan). c) Estudia los intervalos de concavidad y de convexidad. a) Estrictamente decreciente en [1, 2). Estrictamente creciente en (2, e). b) Máximo absoluto en (1,1). Mínimo absoluto en (2, 4 8 ln(2)). c) Cóncava hacia arriba en [1, e).
9 página 9/27 Hoja 9 1. Resuelve: {sen 2 x+cos 2 y= 3 4 cos 2 x sen 2 y= 1 4} x= π 6 +k π, π +k π, k Z 6 y= π 4 +k π 2, k Z 2. Resuelve: 3 {cosx cosy= 4 senx seny= 1 4 } x= π 6 +k π, y= π +k π, k Z 6 x= π +k π, y= π +k π, k Z Dadas las rectas: r : a x 2 y+7=0 x+1 s: b = y 2 Halla a y b sabiendo que las rectas son perpendiculares y que r pasa por el punto P ( 1,2). a=3, b= 3
10 página 10/27 Hoja Sea la función definida por f (x)= 3 x4 +1 x 3 para x 0. a) Estudia las asíntotas de la gráfica de la función. b) Halla los intervalos de crecimiento y de decrecimiento, y los extremos relativos (abscisas donde se obtienen y valores que se alcanzan). a) Asíntota vertical en x=0. Asíntota oblícua en y=3 x. b) Creciente en (, 1). Decreciente en ( 1,1), sin incluir x=0 donde la función no está definida. Creciente en (1,+ ). Máximo en ( 1, 4). Mínimo en (1,4). 2. Calcular los siguientes límites. a) lim x 2 + x x 2 x x b) lim x x[ arctg (e x ) π 2 ] a) 1 b) 0 3. Calcular los siguientes limites. a) lim x 0 ( 4+x 4 x ) 4x ln(cos3 x) b) lim x 0 ( ln(cos2 x) ) a) 1 8 b) 9 4
11 página 11/27 Hoja Sea la circunferencia de ecuación x 2 + y 2 2x 4y+1=0. a) Hallar su centro, su radio y dibujarla. b) Hallar el punto de la curva, de abscisa cero, más alejado del origen; hallar también la recta tangente a la curva en ese punto. c) Hallar las ecuaciones de las tangentes trazadas desde el punto P (3, 0) razonando la respuesta. a) Centro C (1,2), radio r=2. b) (0,2+ 3), y= 3 3 x+2+ 3 c) Dos rectas tangentes: x=3, y=0 2. Dada la función f (x)=x 2 exp( x 2 1) escribe la ecuación de la recta tangente a la función en el punto de abscisa x= 1. y= 4x 3 x(2x +1) 3. Dada la función f (x)= x+2 abscisa x = 2. escribe la ecuación de la recta tangente a la función en el punto de y= 31 8 x Estudia el crecimiento y curvatura de la función f (x)= x4 12 x3 9 x2 +1. Estudia sus máximos, mínimos y puntos de inflexión. decreciente en (, 2) (0, 2), creciente en ( 2, 0) ( 3,+ ). Mínimo en ( 2, 7 9 ), mínimo en (3, 17 4 ). Máximo en (0,1). Puntos de inflexión en ( 1,12, 0,03), (1,79, 1,99).
12 página 12/27 Hoja Determina los parámetros a, b, c y d para que la función f (x )=ax 3 +bx 2 +cx+d tenga un punto de inflexión en P ( 2, 6), con tangente en él paralela a la recta 8 x+ y +10=0, y tome además el valor 2 para x=0. a=1,b=6,c=4,d= 2 2. Determina los intervalos de concavidad y convexidad indicando si existen puntos de inflexión y calculándolos. f (x)={ x2 +2 si x 0 2 x+1 si x>0 } f ( x) siempre es cóncava. En x=0 hay un punto anguloso (no un punto de inflexión). 3. Un jardinero desea construir un jardín con forma de sección circular de 40 metros de perímetro. Cuál debe ser el radio para que la superficie sea máxima? 10 metros. 4. El lado de un cuadrado tiene de longitud 4 metros. Entre todos los cuadrados inscritos en el cuadrado dado, halla el de área mínima. lado 2,83 metros. Área 8m Calcula la ecuación de las asíntotas. f (x)= 1 2x2 x 2 1 x= 1, x=1, y = 2
13 página 13/27 Hoja Calcula la ecuación de las asíntotas. f (x)= 4x2 +1 2x+2 x= 1, y = 1, y=1 2. Un depósito abierto de latón con base cuadrada y capacidad para 4000 litros, qué dimensiones debe tener para que su superficie sea mínima (menor coste de fabricación)? base x=2 metros, altura y=1 metro 3. Una huerta tiene actualmente 24 árboles, que producen 600 frutos cada uno. Se estima que por cada árbol adicional, la producción de cada árbol disminuye en 15 frutos. Cuál debe ser el número total de árboles que debe tener la huerta para que la producción sea máxima? Cuál será esa producción? 32 árboles, frutos totales 4. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos para que el cono engendrado con el giro tenga volumen máximo. 3 3 dm, 6 3 dm
14 página 14/27 Hoja Calcula el límite lim x 0 ( x2 sen 2 x x 4 ) Calcula el límite lim x 0 ( cos2 x 1 x 2 ) 1 3. Calcula el límite lim x ( lnx 3 x ) 0 4. Calcula el límite lim x 0 0 ( 1 cosx ) tgx 5. Calcular la base y la altura del triángulo isósceles de perímetro 8 unidades y área máxima
15 página 15/27 Hoja Un mayorista vende billetes de avión a agencias de viajes. A una primera agencia A le vende 10 billetes nacionales, 10 billetes de países comunitarios y otros 10 billetes a países no europeos y le cobra euros. También le vende a una agencia B 10 billetes nacionales y 20 a países no europeos y le cobra Y a una agencia C le vende 10 billetes nacionales y 10 billetes comunitarios y le cobra 7000 euros. Cuál es el precio de cada billete? nacionales 300 euros, comunitarios 400 euros, no europeos 500 euros 2. El precio de un libro, una calculadora y un estuche es 57 euros. Sabiendo que el precio del libro es el doble que el de la calculadora y el estuche juntos. Es posible calcular el precio del libro? Y el de la calculadora y el estuche? 3. Entre todos los rectángulos de perímetro 12 cm, cuál tiene diagonal menor? Cuánto mide ésta? lado 3 cm, diagonal menor Se ha de construir un gran depósito cilíndrico de 81π m 3 de volumen. La superficie lateral ha de ser construida con un material que cuesta 30 el metro cuadrado y las dos bases con un material que cuesta 45 el metro cuadrado. a) Determina la relación que hay entre el radio r de las bases circulares y la altura h del cilindro, y expresa el coste C (r) del material necesario para construir este depósito en función únicamente de r. b) Qué dimensiones (radio y altura) ha de tener el depósito para que el coste de los materiales necesarios para construirlo sea el mínimo posible? Cuál será, en este caso, el coste del material? a) C (r)= 4860 π +90πr 2 b) radio 3m,altura 9m,2430 r 5. Demuestra que e x > x+1 para todo x positivo.
16 página 16/27 Hoja Se sabe que la función f (x)=x 3 +a x+b corta a su función derivada en x=1 y que, además, en dicho punto la función tiene un extremo. a) Determinar a y b. b) En x=1 hay un máximo o un mínimo? c) Existe algún otro extremo? a) a= 3, b=2 b) es un mínimo c) En x= 1 hay un máximo relativo 2. Expresa el número 60 como una suma de tres enteros positivos de forma que el mayor sea doble del menor y su producto sea máximo. Determinar el valor de dicho producto. 13, 21, 26. Producto Representa y=x 3 4 x 4. Representa y= 1 x Representa y=x 4 6 x Representa y= x Representa y= (x 2)2 x 3 8. Representa y=( x 1)e x
17 página 17/27 Hoja Representa y= 4 x x Representa y= x2 + x x 2 x 3. Representa y= 4 x x+2 4. Calcula el límite lim x (x (4 1 x ) 2) 5. Sea f (x)={ x3 +5 x 2 si 0 x<3 x x 9 si 3 x 5 2 x+16 si 5<x 10 } a) Estudia la continuidad y la derivabilidad de la función. b) Calcula los puntos de inflexión. a) continua en su dominio, derivable en (0, 3) (310). b) ( 5 3, )
18 página 18/27 Hoja Calcula el valor de a yb para que la función f (x)=a ln(x)+b x 2 +x tenga extremos en los puntos x=1, x=2. Qué tipo de extremos son? a= 2 3, b= 1 6, x=1 mínimo, x=2 máximo 2. Qué clase de triángulo determinan los puntos A( 1, 2), B(0, 5),C (3,1)? Halla la mediana del lado BA (unión del punto medio del lado con el vértice opuesto? Calcula su área. isósceles (dos lados iguales) y rectángulo en vértice C, x+7 y 10=0, área 25 2 u2. 3. Representa. y= x 2 2 x+3 4. La función y=x 3 +m x 2 +n x+ p pasa por el punto ( 1,0). Tiene un mínimo en x=1 y un punto de inflexión en x= 1. Calcula m, n, p. 3 m=1, n= 5, p=5 5. a) Dibujar la gráfica de la función g ( x)=e x x. b) Calcular el dominio de definición f (x)= 1 e x x y su comportamiento en el infinito. c) Determinar (si existen) los máximos y mínimos absolutos de f (x ) en su dominio de definición. b) R. Tiende a 0 c) máximo relativo en (0, 1)
19 página 19/27 Hoja El cajero automático de una determinada entidad bancaria solo admite billetes de 50, de 20 y de 10 euros. Los viernes depositan en el cajero 225 billetes por un importe total de 7000 euros. Averiguar el numero de billetes de cada valor depositado, sabiendo que la suma del numero de billetes de 50 y de 10 euros es el doble que el numero de billetes de 20 euros. 100 billetes de 50, 75 billetes de 20, 50 billetes de Sea la función f :R R definida por f (x)=e x (x 2 x+1). a) Calcula lim f ( x), x + lim f ( x). x b) Halla los extremos relativos de f (x) (abscisas donde se obtienen y valores que se alcanzan), determinando si son máximos o mínimos. c) Determina las abscisas de los puntos de inflexión de la gráfica. a) +, 0 b) (0,1) mínimo, ( 1, 3 ) máximo c) x= 3± 5 e 2 3. Un alambre de 100 m de longitud se divide en dos trozos. Con uno de los trozos se construye un cuadrado y con el otro un rectángulo cuya base es doble que su altura. Calcula las longitudes de cada uno de los trozos con la condición de que la suma de las áreas de estas dos figuras sea mínima. trozo para formar el cuadrado: 47,059 m. Trozo del rectángulo: 52,941 m. 4. En una piscina hay un trampolín a 8m de altura del agua. Un nadador se lanza tomando impulso y elevándose 1 m antes de empezar a caer. El nadador alcanza el agua a 8 m del borde del trampolín. a) Si tomamos como origen de coordenadas la proyección del extremo del trampolín sobre el agua y el vértice de la parábola es (a,b), cuánto vale b? b) La ecuación del movimiento es y=k( x c) Justifícala y halla k y c.
20 página 20/27 Hoja Sea la función continua f :R R definida por f (x)={ x+k si x 0 e x 2 1 x 2 si x>0} a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función en el punto de abscisa x=1. a) k =1 2. Sea la función f (x)= e x 1 x, x 1 a) Estudia las asíntotas de la gráfica de la función. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos de crecimiento y de decrecimiento de la función. a) Asíntota vertical x=1. Asíntota horizontal y=0. b) Mínimo relativo (0, 1). Estrictamente decreciente en (, 0). Estrictamente creciente en (0,+ ) {1}. 3. Queremos hacer junto a la carretera un cercado rectangular para unos caballos en una zona llana. Cada metro del lado del cercado que está junto a la carretera nos cuesta 100 euros, mientras que para el resto del cercado nos cuesta 10 euros el metro. Cuáles son las dimensiones del prado de área máxima que podemos cercar con 3000 euros? metros paralelo a la carretera, 75 metros perpendicular a la carretera. 4. Sea la función definida por f (x)=a x 3 +b x 2 +c x. Determina a,b y c sabiendo que su gráfica tiene un punto de inflexión en (1,0) y que la recta tangente en ese punto tiene por ecuación y= 3x+3. a=3,b= 9,c=6 5. Dada la función f ( x)= x3, se pide: 2 ( x 3) a) Hallar las asíntotas de su gráfica. b) Hallar la ecuación de la recta tangente a la gráfica de la función en el punto de abscisa x=2. a) asíntota vertical en x=3, asíntota oblícua y=x +6 b) y=28 x 48
21 página 21/27 Hoja Representa gráficamente f (x)={ x2 +3 si x<1 5 x 2 si x 1}. x+3 si x<1 2. Representa gráficamente f 2 (x)={ }. si x 1 x 3. Calcula las asíntotas de f (x)= x2 3 x+1 x Calcula las asíntotas de f (x)= x3 x 2 2 x. 5. Calcula el valor de k para que la función f (x)= { x 3 2 x+k si x 3 7 si x=3 } real. sea continua en toda la recta 6. Calcula las asíntotas de f (x)= x 1+2 x. 7. Calcula las asíntotas de f (x)= x3 1+ x Calcula las asíntotas de f (x)= x2 +2 x 2 2 x. 9. Calcula las asíntotas de f (x)= 2 x3 3 x 2 +7 x. 10. Calcula el límite lim x 0 4 x x 2 2 x.
22 página 22/27 Hoja Calcula los límites laterales de la siguiente función en los puntos donde se anula el denominador. f (x)= 3 x 2 x+4 2. Calcula los límites laterales de la siguiente función en los puntos donde se anula el denominador. f (x)= x 1 x 2 2 x 3. Calcula los límites laterales de la siguiente función en los puntos donde se anula el denominador. f (x)= x3 2 x 2 x 2 (3 x)2 4. Calcula las asíntotas de f (x)= 2 x Calcula las asíntotas de f (x)=x+1+ 5 x. 6. Calcula las asíntotas de f (x)= 1 e x y de g( x)=1+e x. 7. El gasto mensual en alimentación de una familia depende de su renta x, según la función 0,6 x+200 si 0 x 100 g( 1000 x x)={ }, donde los ingresos y los gastos vienen dados en euros. si x>1000 x+250 Representa la función y determina si es continua. Explica el significado del comportamiento de la función cuando la renta tiende a Calcula los siguientes límites. a) lim ( x x) b) lim (2 x x 3 ) x + x +
23 página 23/27 Hoja Representa f (x)= x2 4 para x 1. Calcula f (x 5) y f ( x+2). 2. Representa f (x)= 3 x+2. { x+1 si 3 x<0 } 3. Representa f (x)= x 2 2 x+1 si 0 x <3. 4 si x (3,7) 4. Sea f (x)=x 2 5 x+3 y g ( x)= x 2. Obtén f [ g(x)] y g [ f (x)]. 5. Sea f (x)=sen( x) y g ( x)= x Obtén f [ g(x)], g [ f (x)], f [ f ( x)] y g[ g( x)]. Hallar el valor de estas composiciones de funciones en x=0 y en x=2. 6. De un cuadrado de 4 cm de lado, se cortan en las esquinas triángulo rectángulos isósceles cuyos lados iguales miden x. Escribe el área del octógono resultante, el dominio de la función área y su recorrido. 7. Sea f (x)=x 2 +1 y g ( x)= 1 x. Obtener las siguientes composiciones: ( f g)(2), (g g )(x), (g f )( 3), ( f g)( x). 8. Calcular la función inversa de f (x)=3 x, g( x)= x+7 y h( x)=3 x Sea f (x )= 1 x. Representa f (x) 2, f (x 3), f ( x) y f (x). 10. La factura del gas de una familia, en septiembre, ha sido 24,82 euros por 12m 3. Y en octubre, 43,81 euros por 42 m 3. Escribe la función lineal que da el importe de la factura según los m 3 consumidos. Cuánto pagarán si consumen 28 m 3? 11. El precio del billete de una línea de cercanías depende linealmente de los kilómetros recorridos. Por 57 km he pagado 2,85 euros y por 168 km, 13,4 euros. Calcula el precio de un billete para una distancia de 100 km. Cuál es la función que nos indica el precio según los kilómetros recorridos?
24 página 24/27 Hoja La dosis de un medicamento es 0,25 g por cada kilo de peso del paciente, hasta un máximo de 15 g. Representa la función peso del paciente-cantidad de medicamento y halla su expresión analítica. 2. Los gastos fijos mensuales de una empresa por la fabricación de x televisores son G= x, en miles de euros, y los ingresos mensuales son I =50 x 0,02 x 2, también en miles de euros. Cuántos televisores deben fabricarse para que el beneficio (ingresos menos gastos) sea máximo? 3. Una pelota es lanzada verticalmente hacia arriba desde lo alto de un edificio. La altura que alcanza viene dada por la fórmula h=80+64 t 16 t 2 ( t en segundos y h en metros). a) Dibuja la gráfica en el intervalo [0,5]. b) Halla la altura del edificio. c) En qué instante alcanza su máxima altura? 4. El precio de venta de un artículo viene dado por la expresión p=12 0,01 x ( x = número de artículos fabricados; p = precio, en cientos de euros). a) Si se fabrican y se venden 500 artículos, cuáles serán los ingresos obtenidos? b) Representa la función Nº de artículos-ingresos. c) Cuántos artículos se deben fabricar para que los ingresos sean máximos? 5. Un fabricante vende mensualmente 100 electrodomésticos a 400 euros cada uno y sabe que por cada 10 euros de subida venderá 2 electrodomésticos menos. a) Cuáles serán los ingresos si sube los precios 50 euros? b) Escribe la función que relaciona la subida de precio con los ingresos mensuales. c) Cuál debe ser la subida para que los ingresos sean máximos? 6. El coste de producción de x unidades de un producto es igual a ( 1 4 )x2 +35 x +25 euros y el precio de venta de una unidad es 50 x 4 euros. a) Escribe la función que nos da el beneficio total si se venden las x unidades producidas. b) Halla el número de unidades que deben venderse para que el beneficio sea máximo.
25 página 25/27 Hoja Elena va a visitar a su amiga Ana y tarda 20 minutos en llegar a su casa, que está a 1 km de distancia. Está allí media hora y en el camino de vuelta emplea el mismo tiempo que en el de ida. a) Representa la función tiempo-distancia. b) Busca su expresión analítica. 2. De la función f (x)=k a x sabemos que f (0)=5 y f (3)=40. Cuanto valen k y a. 3. En el contrato de trabajo de un empleado figura que su sueldo subirá un 6% anual. a) Si empieza ganando euros anuales, cuánto ganará dentro de 10 años? b) Calcula cuánto tiempo tardará en duplicarse su sueldo. 4. Dada la función f (x)=1+ x, halla f 1 ( x). Representa las dos funciones y comprueba su simetría respecto de la bisectriz del primer cuadrante. 5. Dada la función y=a x, contesta: a) Puede ser negativa la y? Y la x? b) Para qué valores de a la función es creciente? c) Cuál es el punto por el que pasan todas las funciones del tipo y=a x? d) Para qué valores de x se verifica 0<a x <1 siendo a>1? 6. Una parábola corta al eje de abscisas en x=1 y en x=3. La ordenada del vértice es y= 4. Cuál es la ecuación de esa parábola? 7. Halla el dominio de f (x)= x+3 x 2 y g( x)= x 9 x 9. Representa f (x)= x 1 x 10. Las tarifas de una empresa de transportes son: - 40 euros por tonelada de carga si esta es menor o igual a 20 t. - Si la carga es mayor que 20 t, se restará, de los 40 euros, tantos euros como toneladas sobrepasen las 20. a) Dibuja la función ingresos de la empresa según la carga que transporte (carga máxima: 30 t). b) Obtén la expresión analítica.
26 página 26/27 Hoja a) Calcula el número real m que cumple lim x 0 ln(1+m x) sen(2 x) =3. b) Obtener el valor de a para que f (x)= { x 2 +a x+a 1 si x<2 ln(x 1) si x 2 } sea continua en x=2. c) La siguiente gráfica muestra la derivada f ' ( x) de una función f (x). Viendo la gráfica, qué podemos decir de los intervalos de crecimiento, decrecimiento y de los extremos relativos de la función original f (x)? 2. Sea la función g ( x)= x3 3 4 x2 2 x 4. Hallar los valores x de la curva en que la recta tangente 3 es paralela a la recta 0=2 x+3 y Considera la función f (x)=x 3 +a x 2 +b x+c. Determina a, b y c sabiendo que la recta normal a la gráfica de f (x) en el punto de abscisa x=0 es y+ x+3=0 y que el punto de inflexión tiene abscisa x=1. 4. Sea la función f :(0,+ ) y definida por f (x)= 1 +ln (x). a) Halla los extremos relativos de x f (x). b) Determina la ecuación explícita de la recta tangente a la función en x=e. 5. a) Sea f (x )=sen( x). Obtener la ecuación explícita de la recta tangente a la función en el punto de abscisa x= π x. b) Sabiendo que lim ( 4 x 1 x 1 a ) es finito, calcula a y el valor del límite. ln x 6. Se desea construir un contenedor con forma de paralelepípedo rectangular de 100 m 3 de volumen, de manera que el largo de su base sea 4 3 de la anchura x de su base. Los precios de m2 de pintura del suelo, del techo y de la pared lateral son, respectivamente, 225 /m 2, 300 /m 2 y 256 /m 2. Determinar razonadamente las dimensiones que minimizan el coste de pintura y dicho coste mínimo. 7. Sea f (x)=x 3 +ax 2 +bx+c un polinomio con extremo relativo en x=1, con punto de inflexión en x=3 y que pasa por el origen de coordenadas. Determinar a, b y c. 2 x 2 8. Sea la función definida por f (x)=. Estudia el dominio, los puntos de corte con los (x+1)(x 2) ejes, las asíntotas, los intervalos de crecimiento y decrecimiento, y los extremos relativos.
27 página 27/27 Hoja a) Calcula lim x 0 ( 1 cos( x) ). tg (x) b) Obtener en forma explícita la recta tangente a la función f (x)=e x ln( x)+2 x en x=1. x(2 x+1) c) Obtener en forma explícita la recta tangente a la función f (x)= x+2 en x=2. 2. a) Estudia y representa gráficamente f (x)=x 2 4 x+2. b) Sea f (x)= x ln x las asíntotas y los extremos relativos.. Estudia el dominio, 3. Sea la función f (x)=ln( x 3 4 x). a) Determina el dominio de la función. b) Halla la ecuación explícita de la recta tangente en el punto x= Sea la función f (x)=x 2 8 ln( x) definida en f :1 +. Estudia intervalos de crecimiento y decrecimiento, calcula los extremos relativos de la función y obtén el valor de la ordenada en cada extremo. 5. a) La derivada de una función es negativa para valores x <1 y positiva para valores x >1. Podemos afirmar que en x=1 tenemos un mínimo relativo? Razona tu respuesta y escribe la ecuación de una función que justifique tu respuesta. b) Calcula lim x 0 ( 1 cos( x) ). tg (x) { sen(x) } c) Sea f (x)= +2 si x 0 x. k si x=0 Calcula k para que f ( x) sea continua en x=0. 6. Estudia las asíntotas y los extremos relativos de la función f (x )= x2 +x+1 x a) Calcule a y b para que la función f (x)=x 3 +a x 2 +b x+2 pase por el punto ( 1,6) y su recta tangente en x=1 forme un ángulo de 45º con el eje OX. b) Sea la función f (x)=x 2 8 ln( x) definida en f :1 +. Obtener los puntos de inflexión y el valor de la ordenada de esos puntos. 8. Sea la función f (x)= x 2 +x+1. Qué punto de la función se encuentra a la menor distancia posible del origen (0,0)? Obtener esa distancia mínima.
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
EJERCICIOS PAU MATEMÁTICAS II ANDALUCÍA Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
. Matemáticas aplicadas CCSS. Ejercicios modelo Selectividad 2000-2011
 1. CÁLCULO DE DERIVADAS Ejercicio 1. (001) Calcule las funciones derivadas de las siguientes: Lx a) (1 punto) f ( x) = (Lx indica logaritmo neperiano de x) x 3 b) (1 punto) g( x) = (1 x ) cos x 3 1 c)
1. CÁLCULO DE DERIVADAS Ejercicio 1. (001) Calcule las funciones derivadas de las siguientes: Lx a) (1 punto) f ( x) = (Lx indica logaritmo neperiano de x) x 3 b) (1 punto) g( x) = (1 x ) cos x 3 1 c)
RELACIÓN EJERCICIOS ANÁLISIS SELECTIVIDAD MATEMÁTICAS II
 1.- Sea f : R R la función definida como f() = e X.( ). (a) [1 punto] Calcula la asíntotas de f. (b) [1 punto] Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
1.- Sea f : R R la función definida como f() = e X.( ). (a) [1 punto] Calcula la asíntotas de f. (b) [1 punto] Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
Interpretación. 1) De una función f:[0,4] R se sabe que f(1) = 3 y que la gráfica de su función derivada es la que aparece en el dibujo
![Interpretación. 1) De una función f:[0,4] R se sabe que f(1) = 3 y que la gráfica de su función derivada es la que aparece en el dibujo Interpretación. 1) De una función f:[0,4] R se sabe que f(1) = 3 y que la gráfica de su función derivada es la que aparece en el dibujo](/thumbs/83/88836487.jpg) Interpretación 1) De una función f:[0,4] R se sabe que f(1) = 3 y que la gráfica de su función derivada es la que aparece en el dibujo (a) [0'5 puntos] Halla la recta tangente a la gráfica de f en el punto
Interpretación 1) De una función f:[0,4] R se sabe que f(1) = 3 y que la gráfica de su función derivada es la que aparece en el dibujo (a) [0'5 puntos] Halla la recta tangente a la gráfica de f en el punto
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
FUNCIONES ELEMENTALES
 0 FUNCIONES ELEMENTALES Página PARA EMPEZAR, REFLEIONA RESUELVE Problema Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con
0 FUNCIONES ELEMENTALES Página PARA EMPEZAR, REFLEIONA RESUELVE Problema Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 Opción A Ejercicio 1.- Sea la función f : (0, + ) R definida por f(x) = 1 +ln(x) donde ln denota la función x logaritmo neperiano. (a) [1 75 puntos] Halla los [ extremos ] absolutos de f (abscisas donde
Opción A Ejercicio 1.- Sea la función f : (0, + ) R definida por f(x) = 1 +ln(x) donde ln denota la función x logaritmo neperiano. (a) [1 75 puntos] Halla los [ extremos ] absolutos de f (abscisas donde
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
sen sen sen a 2 a cos cos 2 a
 BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
Geometría Analítica Enero 2016
 Laboratorio #1 Distancia entre dos puntos I.- Halle el perímetro del triángulo cuyos vértices son los puntos dados 1) ( 3, 3), ( -1, -3), ( 4, 0) 2) (-2, 5), (4, 3), (7, -2) II.- Demuestre que los puntos
Laboratorio #1 Distancia entre dos puntos I.- Halle el perímetro del triángulo cuyos vértices son los puntos dados 1) ( 3, 3), ( -1, -3), ( 4, 0) 2) (-2, 5), (4, 3), (7, -2) II.- Demuestre que los puntos
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
IES Fco Ayala de Granada (Modelo 2 del 2012) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada (Modelo del 01) Soluciones Germán-Jesús Rubio Luna PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 011-01 Opción A Ejercicio 1, Opción A, Modelo de 01 Sea la
IES Fco Ayala de Granada (Modelo del 01) Soluciones Germán-Jesús Rubio Luna PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 011-01 Opción A Ejercicio 1, Opción A, Modelo de 01 Sea la
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES Página 8 PARA EMPEZAR, REFLEIONA RESUELVE Problema Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con
FUNCIONES ELEMENTALES Página 8 PARA EMPEZAR, REFLEIONA RESUELVE Problema Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
Colegio Portocarrero. Curso 2014-2015. Departamento de matemáticas. Análisis y programación lineal
 Análisis y programación lineal Problema 1: La gráfica de la función derivada de una función f es la parábola de vértice (0, 2) que corta al eje de abscisas en los puntos ( 3, 0) y (3, 0). A partir de dicha
Análisis y programación lineal Problema 1: La gráfica de la función derivada de una función f es la parábola de vértice (0, 2) que corta al eje de abscisas en los puntos ( 3, 0) y (3, 0). A partir de dicha
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 3 Especifico) Solucíon Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO PRÁCTICO DE GEOMETRÍA ANALÍTICA
 UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO PRÁCTICO DE GEOMETRÍA ANALÍTICA AÑO 014 CURSO PREPARATORIO DE INGENIERÍA CPI-014 TRASLACIÓN Y/O
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO PRÁCTICO DE GEOMETRÍA ANALÍTICA AÑO 014 CURSO PREPARATORIO DE INGENIERÍA CPI-014 TRASLACIÓN Y/O
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Enunciados) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Enunciados) Isaac Musat Hervás 28 de septiembre de 2016 2 Índice general 1. Año 2000 7 1.1. Modelo 2000 - Opción A.....................
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Enunciados) Isaac Musat Hervás 28 de septiembre de 2016 2 Índice general 1. Año 2000 7 1.1. Modelo 2000 - Opción A.....................
c) Demuestra que la función f(x) anterior y g(x) = 2x 1 se cortan al menos en un punto. (1 punto) 2
 Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
LA RECTA. Recuerda: Ejercicios de autoaprendizaje 1. Sea la gráfica siguiente:
 LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Solución:
 RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
Preparatoria Ciclo 2015-2016
 Docente: Patricia Vázquez Vázquez Página: 1 PRODUCTO CARTESIANO Resuelve los siguientes ejercicios 1.Si M={1,2,3,4},P={1,2,3,4,5,6,7,8}.Halla las parejas ordenadas que satisfagan la condición dada del
Docente: Patricia Vázquez Vázquez Página: 1 PRODUCTO CARTESIANO Resuelve los siguientes ejercicios 1.Si M={1,2,3,4},P={1,2,3,4,5,6,7,8}.Halla las parejas ordenadas que satisfagan la condición dada del
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
Más ejercicios y soluciones en fisicaymat.wordpress.com FUNCIONES
 FUNCIONES 1- a) Dibuje el recinto plano limitado por la parábola y=4x-x 2 y las tangentes a la curva en los puntos de intersección con el eje de las abscisas. b) Halle el área del recinto dibujado en a).
FUNCIONES 1- a) Dibuje el recinto plano limitado por la parábola y=4x-x 2 y las tangentes a la curva en los puntos de intersección con el eje de las abscisas. b) Halle el área del recinto dibujado en a).
Ejercicios Resueltos de Derivadas y sus aplicaciones:
 Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA 6.- FUNCIONES. LÍMITES Y CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
PROBLEMAS METRICOS. r 3
 PROBLEMAS METRICOS 1. Hallar el área del triángulo de vértices A(1,1), B(2,3) y C(5,2). 2. Halla las ecuaciones de las bisectrices determinadas por las rectas y=3x e y=1/3 x. Comprueba que ambas bisectrices
PROBLEMAS METRICOS 1. Hallar el área del triángulo de vértices A(1,1), B(2,3) y C(5,2). 2. Halla las ecuaciones de las bisectrices determinadas por las rectas y=3x e y=1/3 x. Comprueba que ambas bisectrices
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
Matemática I - Problemas de Máximos y Mínimos
 Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
f(x) = xe para x -1 y x 0, MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio 1. (Reserva 1 Septiembre 2013 Opción A) Sea f la función definida por
 MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio. (Reserva Septiembre 0 Opción A) f() = para > 0, (donde ln denota el logaritmo neperiano). ln() a) [ 5 puntos] Estudia y determina las asíntotas de la gráfica
MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio. (Reserva Septiembre 0 Opción A) f() = para > 0, (donde ln denota el logaritmo neperiano). ln() a) [ 5 puntos] Estudia y determina las asíntotas de la gráfica
9. Rectas e hipérbolas
 08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
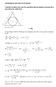 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
RELACION DE PROBLEMAS DE GEOMETRIA. Problemas propuestos para la prueba de acceso del curso 1996/97.
 RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
Figuras Planas. 100 Ejercicios para practicar con soluciones. 1 Comprueba si los siguientes ángulos son complementarios: a) 72 + 35.
 Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6 1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg) ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
1. NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de Matemáticas I)
 . NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de ). Calcula las potencias: a) -, (-), (-) -, - - (/) -, (-/), -(-/) - - (/) - 0 ( ) d) e) 0 0 + + 8 [sol] a) ; 7 ; ( 7; ; 7 d) e) 0 7 7 7. Simplifica
. NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de ). Calcula las potencias: a) -, (-), (-) -, - - (/) -, (-/), -(-/) - - (/) - 0 ( ) d) e) 0 0 + + 8 [sol] a) ; 7 ; ( 7; ; 7 d) e) 0 7 7 7. Simplifica
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO
 Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Ejercicio 2.- [2 5 puntos] Sea f : ( 2, + ) R la función
Opción A Ejercicio 1.- [2 5 puntos] Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Ejercicio 2.- [2 5 puntos] Sea f : ( 2, + ) R la función
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Cuaderno de Actividades 4º ESO
 Cuaderno de Actividades 4º ESO Relaciones funcionales. Estudio gráfico y algebraico de funciones 1. Interpretación de gráficas 1. Un médico dispone de 1hora diaria para consulta. El tiempo que podría,
Cuaderno de Actividades 4º ESO Relaciones funcionales. Estudio gráfico y algebraico de funciones 1. Interpretación de gráficas 1. Un médico dispone de 1hora diaria para consulta. El tiempo que podría,
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 Selectividad CCNN 0. [ANDA] [JUN-A] Sea la función f: definida por f(x) = e x (x - ). a) Calcula la asíntotas de f. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan)
Selectividad CCNN 0. [ANDA] [JUN-A] Sea la función f: definida por f(x) = e x (x - ). a) Calcula la asíntotas de f. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan)
EJERCICIOS PAU MAT II CC SOC. ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com.
 FUNCIONES 1- a) Dada la función:, Definida para 0, 0, encontrar el punto (x,y) que maximiza f sujeto a la restricción x+y=36. b) Calcular: Aragón 2014 Opción A Junio 2- Dada la función: Calcular: a) Dominio
FUNCIONES 1- a) Dada la función:, Definida para 0, 0, encontrar el punto (x,y) que maximiza f sujeto a la restricción x+y=36. b) Calcular: Aragón 2014 Opción A Junio 2- Dada la función: Calcular: a) Dominio
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
Hoja de problemas nº 7. Introducción a la Geometría
 Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
(1-mx)(2x+3) x 2 +4 = 6. x > -1
 . [04] [EXT-A] Sea la función f(x) = e x +ax+b a) Calcular a y b para que f(x) tenga un extremo en el punto (,). b) Calcular los extremos de la función f(x) cuando a = 0 y b = 0.. [04] [EXT-B] En la figura
. [04] [EXT-A] Sea la función f(x) = e x +ax+b a) Calcular a y b para que f(x) tenga un extremo en el punto (,). b) Calcular los extremos de la función f(x) cuando a = 0 y b = 0.. [04] [EXT-B] En la figura
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD
 DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
IES Fco Ayala de Granada Junio de 2011 (Específico 2 Modelo 1) Soluciones Germán-Jesús Rubio Luna
 PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
APLICACIONES DE LAS DERIVADAS
 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
TEMA 2: DERIVADA DE UNA FUNCIÓN
 TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA. 3. Determinar analíticamente cuando dos rectas son paralelas o perpendiculares.
 ESTUDIO ANALÍTICO DE LA LÍNEA RECTA Y APLICACIONES SEMESTRE II VERSIÓN 03 FECHA: Septiembre 29 de 2011 MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA LOGROS: 1. Hallar la dirección, la
ESTUDIO ANALÍTICO DE LA LÍNEA RECTA Y APLICACIONES SEMESTRE II VERSIÓN 03 FECHA: Septiembre 29 de 2011 MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA LOGROS: 1. Hallar la dirección, la
FUNCIONES TRIGONOMÉTRICAS, EXPONENCIALES Y LOGARÍTMICAS
 UNIDAD 5 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES Y LOGARÍTMICAS Página. La distancia al suelo de una barquilla de la noria varía conforme ésta gira. Representamos gráficamente la función que da la altura
UNIDAD 5 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES Y LOGARÍTMICAS Página. La distancia al suelo de una barquilla de la noria varía conforme ésta gira. Representamos gráficamente la función que da la altura
1. Halla la derivada de la función f(x)= en el punto x=3, aplicando la definición de derivada. Solc:
 ANÁLISIS 1. Halla la derivada de la función f(x)= en el punto x=3, aplicando la definición de derivada. Solc: 2. Comprueba que la siguiente función es continua y derivable y halla f (0),f (3) y f (1).
ANÁLISIS 1. Halla la derivada de la función f(x)= en el punto x=3, aplicando la definición de derivada. Solc: 2. Comprueba que la siguiente función es continua y derivable y halla f (0),f (3) y f (1).
1.- Efectúa las siguientes operaciones con cantidades expresadas en notación científica. Expresa el resultado también en notación científica:
 Pàgina 1 de 6 Alumnes suspesos: fer tot el treball obligatòriament. Altres alumnes: Es recomana que realitzeu aquells apartats on heu tingut més dificultats durant el curs. 1.- Efectúa las siguientes operaciones
Pàgina 1 de 6 Alumnes suspesos: fer tot el treball obligatòriament. Altres alumnes: Es recomana que realitzeu aquells apartats on heu tingut més dificultats durant el curs. 1.- Efectúa las siguientes operaciones
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
PROBLEMAS RESUELTOS GEOMETRÍA
 PROBLEMAS RESUELTOS GEOMETRÍA ) Uno de los vértices de un paralelogramo ABCD es el punto A(, ) y dos de los lados están sobre las rectas r : 3x -y- =, s : 6x -7y- =. Calcula los demás vértices. Como el
PROBLEMAS RESUELTOS GEOMETRÍA ) Uno de los vértices de un paralelogramo ABCD es el punto A(, ) y dos de los lados están sobre las rectas r : 3x -y- =, s : 6x -7y- =. Calcula los demás vértices. Como el
a) A la mitad del número le sumo 3 y el resultado es 8 ( ) 9 b) En la ecuación 3x = 54 Qué valor puede tomar x? ( ) Rombo
 Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
TEMA 8 GEOMETRÍA ANALÍTICA
 Tema 8 Geometría Analítica Matemáticas 4º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Halla el punto medio del segmento de extremos P, y Q4,. Las coordenadas del punto medio,
Tema 8 Geometría Analítica Matemáticas 4º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Halla el punto medio del segmento de extremos P, y Q4,. Las coordenadas del punto medio,
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Tipos de funciones. Clasificación de funciones. Funciones algebraicas
 Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Colegio Portocarrero. Curso Departamento de matemáticas. Análisis. (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas)
 Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Problemas Tema 3 Enunciados de problemas de Derivabilidad
 página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
Representación gráfica de funciones. De la fórmula a la tabla. Resolución de problemas
 REPRESENTACIÓN DE PUNTOS EN EL PLANO RELACIÓN ENTRE DOS MAGNITUDES Ejes de coordenadas y coordenadas de puntos FUNCIÓN Tipos: - Lineal. - Afín. - Constante. - De proporcionalidad inversa. - Cuadrática.
REPRESENTACIÓN DE PUNTOS EN EL PLANO RELACIÓN ENTRE DOS MAGNITUDES Ejes de coordenadas y coordenadas de puntos FUNCIÓN Tipos: - Lineal. - Afín. - Constante. - De proporcionalidad inversa. - Cuadrática.
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. e) f) es divisible por 6. a) b) c) d) e) f)
 1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
f (x) = 3(1 + x2 cos x)(x sin x 1) 2 x ( x + 7x) 2/3 cos 4 (tan x) ) 1/5 f (x) = 3x4 + 6x 3 9x 2 + 3x + 3 x(x 3 + 3x 1)
 1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
TRANSFORMACIONES DEL PLANO
 PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
Departamento de matemáticas
 Análisis con solución (Límites, derivadas y aplicaciones) Problema 1: Determina los valores de a y b para los cuales Problema 2: Calcula Problema 3: Una persona camina a la velocidad constante de 3 m/s
Análisis con solución (Límites, derivadas y aplicaciones) Problema 1: Determina los valores de a y b para los cuales Problema 2: Calcula Problema 3: Una persona camina a la velocidad constante de 3 m/s
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/78/78369935.jpg) cos(3) - e + a 1. [ANDA] [EXT-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte. 2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso
cos(3) - e + a 1. [ANDA] [EXT-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte. 2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso
Página 267 EJERCICIOS Y PROBLEMAS PROPUESTOS. Dominio de definición PARA PRACTICAR UNIDAD. 1 Halla el dominio de definición de estas funciones:
 0 Página 7 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Dominio de definición Halla el dominio de definición de estas funciones: y = y = c) y = + ( ) d) y = e) y = f) y = + + 5 + Á {, 0} Á {} c) Á {
0 Página 7 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Dominio de definición Halla el dominio de definición de estas funciones: y = y = c) y = + ( ) d) y = e) y = f) y = + + 5 + Á {, 0} Á {} c) Á {
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones.
 Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
3. [2014] [JUN-A] Considere la función: f(x) = x2 +3
![3. [2014] [JUN-A] Considere la función: f(x) = x2 +3 3. [2014] [JUN-A] Considere la función: f(x) = x2 +3](/thumbs/80/80888765.jpg) x [04] [EXT-A] Considere la función: f(x) = x-6 a) Determine el dominio y las asíntotas, si existen, de esa función b) Determine los intervalos de crecimiento y decrecimiento y los máximos y mínimos relativos,
x [04] [EXT-A] Considere la función: f(x) = x-6 a) Determine el dominio y las asíntotas, si existen, de esa función b) Determine los intervalos de crecimiento y decrecimiento y los máximos y mínimos relativos,
EJERCICIOS DE CONTINUIDAD Y APLICACIONES DE LA DERIVADA
 EJERCICIOS DE CONTINUIDAD Y APLICACIONES DE LA DERIVADA 1º) Estudia la continuidad de la siguiente función: x+3 si x < 2 fx = x +1 si x 2 La función está definida para todos los reales: D(f)=R Tanto a
EJERCICIOS DE CONTINUIDAD Y APLICACIONES DE LA DERIVADA 1º) Estudia la continuidad de la siguiente función: x+3 si x < 2 fx = x +1 si x 2 La función está definida para todos los reales: D(f)=R Tanto a
PENDIENTES 2º ESO. Tercer examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del tercer examen de recuperación de MATEMÁTICAS DE 2º ESO Curso 2013-2014
 014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
EJERCICIOS Nº 10: GEOMETRIA ANALITICA. se extiende hacia cada extremo en una longitud igual a su longitud original. Halle las coordenadas de
 EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días
![5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días 5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días](/thumbs/40/21102307.jpg) . [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
. [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
Matemáticas 4 Enero 2016
 Laboratorio #1 Vectores I.- Calcule el producto escalar de los dos vectores y el coseno del ángulo entre ellos. 1) u = 3i + 2j 4k; v = i + 5j 3k 2) u = i + 2j 3k; v = 1i 2j + 3k 3) u = 1 2 i + 1 3 j +
Laboratorio #1 Vectores I.- Calcule el producto escalar de los dos vectores y el coseno del ángulo entre ellos. 1) u = 3i + 2j 4k; v = i + 5j 3k 2) u = i + 2j 3k; v = 1i 2j + 3k 3) u = 1 2 i + 1 3 j +
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES. 2.- La suma de dos números es 15 y su producto es 26. Cuáles son dichos números?
 RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
FUNCIONES. 7.(99).- Hallar la longitud de los lados del triángulo isósceles de área máxima cuyo perímetro sea 60 m.
 Enunciados de problemas de selectividad. Matemáticas II. Funciones FUNCIONES.(97).- Hay alguna función f() que no tenga límite cuando y que, sin embargo, [f()] sí tenga límite cuando?. Si la respuesta
Enunciados de problemas de selectividad. Matemáticas II. Funciones FUNCIONES.(97).- Hay alguna función f() que no tenga límite cuando y que, sin embargo, [f()] sí tenga límite cuando?. Si la respuesta
1. [2014] [EXT] Sean las funciones f(x) = eax +b
![1. [2014] [EXT] Sean las funciones f(x) = eax +b 1. [2014] [EXT] Sean las funciones f(x) = eax +b](/thumbs/60/44820262.jpg) 1. [01] [ET] Sean las funciones f(x) = eax +b y g(x) = + 3x+. a) Determine el dominio y el recorrido de la función g. b) Calcule para qué valores de a y b las gráficas de las dos funciones son tangentes
1. [01] [ET] Sean las funciones f(x) = eax +b y g(x) = + 3x+. a) Determine el dominio y el recorrido de la función g. b) Calcule para qué valores de a y b las gráficas de las dos funciones son tangentes
