EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
|
|
|
- María del Pilar Saavedra Vázquez
- hace 7 años
- Vistas:
Transcripción
1 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica de la derivada, vimos que el signo de esta determinaba el crecimiento o decrecimiento de la función. Proposición Sea I un intervalo y f ( ) una función derivable en I, entonces se verifica: Si f ( ) > 0 I f ( ) es creciente en I Si f ( ) < 0 I f ( ) es decreciente en I PUNTOS CRÍTICOS En el estudio del crecimiento y decrecimiento de una función, los puntos en los que la derivada se anula desempeñan un papel fundamental. Estos puntos de derivada nula, junto a aquellos del domino en los que la función no es derivable, reciben el nombre de puntos críticos de la función. En la figura aparece la gráfica de una función derivable en R y con tres puntos críticos: =, = 0 y = 4. En =, la función pasa de ser creciente a decreciente y en él alcanza el máimo valor de sus proimidades. En matemáticas se dice que en =, la función alcanza un máimo relativo. En = 0 la función pasa de ser decreciente a creciente y en él alcanza el mínimo valor de sus proimidades. Diremos que en = 0 la función alcanza un mínimo relativo. En 4 f ' 4 = 0, pero la función es creciente tanto a la izquierda de = 4 como a su = es ( ) derecha. En 4 = no hay etremos relativos, es un punto de infleión, que estudiaremos con mas detalle en el tema siguiente
2 Etremos y optimización de funciones EXTREMOS ABSOLUTOS f ( γ ) f ( α ) f ( b ) f ( β ) f ( a ) a α β γ b En la figura aparece la gráfica de f ( ), función continua en el intervalo [ a, b ]. El teorema de Weierstrass asegura que la función alcanza un máimo y un mínimo absoluto en este intervalo. En este apartado vamos a estudiar la forma de localizar estos etremos absolutos. Los etremos absolutos pueden alcanzarse en los límites del intervalo, es decir, en = a, = b, o en el interior del intervalo, es decir, en el abierto ( a, b ). Si se alcanza en el interior del intervalo, además de etremo absoluto también será relativo, y en consecuencia un punto crítico. Según el razonamiento anterior, para localizar los etremos absolutos: Encontramos los puntos críticos. En el ejemplo son tres: γ, en el que la función no es derivable, y α y β en los que la derivada se anula. Calculamos los valores de la función en los puntos críticos y en los etremos del dominio, y comparamos los valores obtenidos. En el ejemplo: f a < f β < f b < f α < f γ La función alcanza un mínimo absoluto en = a ( ) ( ) ( ) ( ) ( ) y un máimo absoluto en = γ. Ejercicio resuelto Estudia los intervalos de crecimiento y decrecimiento, máimos y mínimo relativos y absolutos de: 1, R Solución f = + ( ) La función es continua por ser suma de funciones continuas, luego en el cerrado [ 1, ] alcanza un máimo y un mínimo absolutos si 0 ( ) f = + = + si 0 < 1 + si < 0 La función es derivable en R { 0 }, siendo ( ) f = si 0 < Los puntos críticos son = 0, porque en el la función no es derivable, y aquellos en los que ( ) 0. f = Podemos comprobar que la derivada, teniendo en cuenta su dominio, solo se anula para = 1, por lo que los etremos relativos únicamente se pueden alcanzan en 1 o en 0. Si estudiamos el signo de f (), obtenemos: - -
3 Etremos y optimización de funciones Si observamos el crecimiento y decrecimiento de la función, podemos afirmar que: en = 0 se alcanza un máimo relativo y en = 1 un mínimo relativo. Para estudiar los etremos absolutos, se compara los relativos con el valor que toma la función en 1,. los etremos del intervalo [ ] 1 5 f = 4 f (0) = f (1) = 1 5 f = 4 La función alcanza un máimo absoluto en = 0, que vale, y un mínimo absoluto en = 1, que vale 1 Ejercicio resuelto e 1 si 0 Se considera la función f ( ) = + si > 0 preguntas. a) Es continua la función en el punto = 0. b) Es derivable en = 0. c) Alcanza algún etremo?. Contestar razonadamente las siguientes Solución f (0) = 0 a) lím f ( ) = lím e 1 = 0 lím ( ) = (0 lím ( ) = 0 ) 0 0 f f f 0 0 lím f ( ) = lím + = b) La función es derivable en { } c) f ( ) R 0, siendo ( ) ( ) lím f = lím e = 1 lím f = lím + 1 = ( ) ( ) e f ( ) = + 1 si < 0 si > 0 f ( ) es continua en 0. La función no es derivable en = 0. no se anula, pues e 0 y > 0. El único punto crítico de la función es 0, { 0} = el estudio del signo de f '( ) en R nos permite asegurar que en = 0 se alcanza un mínimo relativo. Como además es lím f ( ) lím f ( ) = =, la función no está acotada superiormente, el mínimo relativo es también un mínimo absoluto, siendo este el único etremo de la función. sig ( f '( )) = 0 - -
4 Etremos y optimización de funciones Ejercicio resuelto Estudia los intervalos de monotonía y los etremos de e > 0 e. ln f ( ) =. Como aplicación, prueba que si Solución En primer lugar estudiamos el domino: = ( 0, ) domino. f ln ) = ( f ( ) D y la función es continua y derivable en su f 1 ln =. > 0 D f sig ( f ( ) ) = sig ( 1 ln ) 1 ln = 0 ln = 1 = e e 0 e Según esto, la función alcanza un máimo absoluto en = e. Por definición de máimo absoluto: lne ln f ( e) f ( ) Df > 0 lne eln > 0 e e e > 0 lne e ln > 0 OPTIMIZACIÓN DE FUNCIONES En este apartado vamos a resolver problemas en los que una magnitud depende de una variable y se trata de averiguar para qué valor de la variable, el de la magnitud estudiada es el óptimo. Se tratará, por ejemplo, de conseguir que utilizando una cantidad de material determinado, el volumen del recipiente obtenido sea máimo; que el tiempo invertido en hacer un recorrido sea mínimo, etc. Ejercicio resuelto P 4 Km A 10 Km B Un hombre se encuentra en un punto P del mar con una barca, y desea trasladarse hasta un punto B de una costa rectilínea. Con la barca es capaz de navegar a una velocidad de 4 Km/h, mientras que por tierra puede avanzar a 0 Km/h. En qué punto de la costa le conviene desembarcar para que el tiempo invertido en el recorrido sea mínimo? - 4 -
5 Etremos y optimización de funciones Solución. El tiempo invertido en hacer el recorrido, que es la magnitud a optimizar, depende de la distancia, que determina el punto de desembarco A. El tiempo total es la suma del tiempo que está en el agua y del que está en tierra, que en cada caso es el espacio en ese medio, dividido por la velocidad correspondiente t( ) = Es evidente que el valor mínimo del tiempo corresponde a algún valor de tal que El problema planteado se reduce a encontrar el mínimo absoluto de la función: t [ 0,10] R t( ) = t( ) = + ( ) = t t ( ) = 0 = 5 = = 16 + = = = El mínimo absoluto se alcanza en el punto crítico o en algún etremo del dominio: t ( 0) 1.5 horas, t ( 10).69 horas, t + = = = 1, 48 horas, = 10 Conviene desembarcar en el punto A para el cual es = Km. Ejercicio resuelto A un espejo rectangular de 0 cm. de largo y 0 de ancho se le ha roto en una esquina un trozo de forma triangular, de modo que la longitud ha disminuido 5 cm. y la anchura en cm. Con la parte restante se quiere hacer un nuevo espejo con bordes paralelos a los primeros y con la mayor superficie posible. Encuentra las dimensiones del nuevo espejo. Solución 0 Si hacemos un dibujo, enseguida nos damos cuenta que poner la magnitud a optimizar, la superficie, en función de dos variables es muy sencillo. Si designamos por e y las dimensiones del nuevo espejo es: S(, y) = y. 5 5 y 5 y En bachillerato solo estudiamos las funciones que dependen de una S, y está fuera de los variable, por lo que optimizar la función ( ) objetivos de este curso. Sin embargo, son frecuentes las situaciones en las que, como en esta, es sencillo plantear el problema utilizando dos variables. En esos casos habrá que, analizando el enunciado, encontrar una relación entre ellas para despejar una en función de la otra. Si observas la figura, hay varios triángulos semejantes en los que aparecen nuestras variables e y. Aplicando a dos de ellos el teorema - 5 -
6 Etremos y optimización de funciones de Tales tenemos que ( ) 5 y = y = 0 Llevando la relación entre e y a la función (, ). S y obtenemos la superficie en función de una única variable: S(, y) = y 5( 5 ) ( 5 ) S ( ) = = y = Por otra parte, es evidente que los valores lógicos de nuestra variable están comprendidos entre y 0 cm. Se trata de encontrar el máimo absoluto de S ( ) = con [ 17, 0] S ( ) = S ( ) La función tiene un punto crítico en = 5. Comparamos los valores que alcanza la función en el punto crítico y en los etremos del dominio: S (17) = 510 cm, S (0) = 500 cm y S cm = 15 El espejo de superficie máima que podemos conseguir es el que tiene por dimensiones: = = 18.5 cm. e y = 9.17 cm
7 Etremos y optimización de funciones EJERCICIOS Y PROBLEMAS 1. Estudia el dominio, crecimiento, máimos y mínimos relativos de las siguientes funciones: a) d) f ( ) = b) f ( ) = e c) f ( ) = ln e sen f ( ) = ln e) f ( ) = f) f ( ) = e cos ( ). Si f ( ) es una función definida en (,π ) 0 tal que crecimiento y decrecimiento y los etremos relativos de f ( ). cos f ( ) =, obtén los intervalos de. Si la curva (I) es la gráfica de la función f ( ), cuál o cuáles de las otras tres pueden ser la gráfica de f ( )? Razona la respuesta (I) (II) (III) (IV) - 7 -
8 Etremos y optimización de funciones 4. Si la gráfica I corresponde a la curva y = f ( ), cuál o cuáles de la otras tres puede corresponder a y = f ( )? ( I ) ( II ) ( III ) ( IV ) Puede haber dos funciones distintas con la misma función derivada?, en qué se diferencian dos funciones que tienen la misma derivada? 5. Sean f ( ) y g( ) dos funciones tales que f '( ) = g '( ). Podemos asegurar que f ( ) = g( )? Qué se puede afirmar de las funciones f ( ) y g( )? 6. Indicar cuál o cuales de las siguientes afirmaciones son ciertas. Justifica la respuesta: a) Si f () alcanza un máimo o un mínimo relativo en = a y f es derivable en a, entonces f ( a) = 0 b) Si f ( a) = 0, entonces f alcanza un máimo o un mínimo relativo en = a. c) Si f () alcanza un máimo o un mínimo relativo en = a, entonces f ( a) = 0 7. Halla b y c para que la curva y + b + c = tenga un mínimo relativo en el punto (,4) Halla a, b y c para que la función f ( ) = a + b + c tenga un mínimo relativo en el punto 6, 1 y se anule en = 8. ( ) - 8 -
9 Etremos y optimización de funciones 9. Halla a y b para que la función f ( ) = a ln + b + tenga etremos relativos en 1 = 1y en =. De qué tipo son esos etremos? 10. Halla el valor de k para que la función trata de un máimo o un mínimo? e f ( ) = tenga un etremo único. En ese caso, se + k 11. Halla los máimos y mínimos absolutos de las siguientes funciones: f ( ) ( 1) ( 1) con,1 f = con 1,1 a) = + [ ] b) ( ) [ ] = d) f ( ) = ( 4 ) con [ 1, ] c) f ( ) 4 + con [, 4 ] 1. Halla los máimos y mínimos de la función ( ) f = e 1 1. Halla los puntos de la curva y = 1+ en los que la recta tangente tiene pendiente máima y el valor de esa pendiente. 14. Encuentra dos números cuya suma sea 4 y que el producto del cubo de uno por el cuadrado del otro sea máimo. 15. Hallar las dimensiones de un campo rectangular de. 600 m de superficie para poder cercarlo con una valla de longitud mínima. 16. Entre todos los triángulos rectángulos de hipotenusa 10 cm., cuál es el de área máima? 17. Entre los rectángulos de 4m de perímetro, determina el de diagonal mínima. 18. De una lámina rectangular de cartón, cuyas dimensiones son 6 dm. y 8 dm. respectivamente, se cortan cuadrados iguales para construir una caja sin tapa. Qué dimensiones deben tener estos cuadrados para que el volumen sea máimo? 19. Se quiere cercar una zona rectangular de una finca. Uno de los lados de la parte cercada da a un camino, por lo que en ese lado se pondrá una valla de calidad superior al resto, que quedara en el interior de la finca. Si la valla que está al lado del camino cuesta 6 /m y la de los otros lados 1 /m. Hallar el área máima que podemos cercar con Encuentra las dimensiones del rectángulo de área máima que puede inscribirse en una circunferencia de 5 cm. de radio. 1. Halla las dimensiones del rectángulo de mayor área que se puede inscribir en un triángulo isósceles que tiene por base 10 cm. y 15 cm. de altura.. La resistencia de una viga de sección rectangular es proporcional a la anchura y al cuadrado de la altura. Halla las dimensiones de la viga de máima resistencia que se puede obtener de un madero de 60 cm. de diámetro.. Halla la base y la altura del triángulo isósceles de área máima que podemos inscribir en una circunferencia de 1 cm. de radio
10 Etremos y optimización de funciones 4. Con una cuerda hacemos un recinto con la forma indicada en la figura. Si la longitud de la cuerda es 50 cm., cuánto debe medir "" para que el área del recinto encerrado sea máimo? 5. Queremos construir una caja abierta de base cuadrada y 108 litros de capacidad. Hallar las dimensiones para que el material utilizado, y en consecuencia el coste, sea mínimo. 6. En un triángulo isósceles de 1 cm. de base y 5 cm. de altura, determinar un punto sobre esta tal que la suma de sus distancias a los tres vértices sea mínima. 7. Cuál es el punto de la curva 4y 0, 4? = más próimo a ( ) 8. Halla los vértices de un rectángulo que se debe inscribir en la elipse área sea máima. y + = 1, para que su Un jardinero ha de construir un parterre en forma de sector circular con un perímetro de 0 m. Cuál será el radio que da el parterre de área máima? 0. Se desea hacer un cono, recortando su superficie de una chapa circular de radio conocido R. Halla el ángulo del sector circular que hay que cortar para que el volumen del cono se máimo. 1. Las manecillas de un reloj miden 6 y 8 cm. Uniendo sus etremos se forma un triángulo. Hallar el instante entre las 1 horas y las 1 y media en el que el área del triángulo es máima.. Halla el punto del suelo desde el cual se ve un segmento vertical de m de longitud, y cuyo etremo inferior dista 1 m. del suelo, bajo un ángulo máimo. CUESTIONES PROPUESTAS EN SELECTIVIDAD 1. Se sabe que y = f () e y = g() son dos curvas crecientes en = a. Analícese si la curva y = f ( ) g( ) ha de ser, entonces, creciente en = a. Si la respuesta es afirmativa, justifíquese, en caso contrario, encuéntrese un contraejemplo.. Dada la función f ( ) ln ( 4 5) = +, se pide: a) Determinar el dominio de la función y las asíntotas verticales de su gráfica. b) Estudiar los intervalos de crecimiento y decrecimiento de f ( ). + 6 < 0 1 =, se pide: a) Estudiar su continuidad b) Estudiar la eistencia de asíntotas de su gráfica y, en su caso, calcularlas. c) Hallar los etremos relativos y esbozo de la función. Dada la función f ( )
11 Etremos y optimización de funciones 4. Dada la función f ( ) = + sen, se pide: a) Determinar si tiene asíntotas de algún tipo. b) Estudiar su monotonía y etremos relativos. 5. Sabiendo que una función ( ) f tiene como derivada f ( ) = ( 4) ( 8 + 7) a) Hallar los intervalos de crecimiento y decrecimiento. b) Hallar máimos y mínimo relativos de la función c) Es el punto = 4 un punto de infleión? Razonar la respuesta. 6. a) Si es posible, dibujar de forma clara la gráfica de una función continua en el intervalo [ 0,4] que tenga al menos un máimo relativo en el punto (,) y un mínimo relativo en el punto (,4) b) Si la función fuera polinómica, cuál ha de ser como mínimo su grado? 7. La gráfica de la figura corresponde a la primera derivada de una función f ( ). Qué puede decirse de los posibles máimos y mínimos relativos de f (). Razonar la respuesta.. 8. Sea la función f ( ) = a + b + c + d un polinomio que cumple: f ( 1) = 0, f ( 0) = y tiene dos etremos relativos para = 1 y = a) Determinar a, b, c y d. b) Son máimos o mínimos los etremos relativos? 9. Dado el polinomio P ( ) = + a + b + c, obtener a, b y c para que se verifiquen las siguientes condiciones: El polinomio P ( ) tenga etremos relativos en los puntos de abscisas = 1 y = 1. La recta de ecuación y = + sea tangente a la gráfica de P ( ) en el punto 0, P ( 0) Dada la función f ( ) = 1 + sen, se pide: a) Encontrar los puntos críticos en el intervalo ( π, π ). b) Calcular etremos relativos y/o absolutos de la función ( ) ( ) f en el intervalo [ π, π ]. π c) Encontrar la ecuación de la recta tangente a la gráfica de la función f ( ) en = Halla los máimos y mínimos de la función ( ) f = e 1. Dados tres números reales r 1, r y r, hallar el número que minimiza la epresión: ( r ) + ( r ) + ( r ) D( ) = 1 1. Dos vías férreas se cortan perpendicularmente. Por cada línea avanza una locomotora (de longitud despreciable) dirigiéndose ambas al punto de corte; sus velocidades con 60 y 10 Km/h y han salido simultáneamente de estaciones situadas, respectivamente, a 40 y 0 Km del punto de corte
12 Etremos y optimización de funciones a) Halla la distancia a la que se encuentran las locomotoras, en función del tiempo transcurrido desde que inician su recorrido. b) Hallar el valor mínimo de esa distancia. 14. Dos avionetas se encuentran situadas a las nueve de la mañana a una distancia de 54 km, en las posiciones indicadas en la figura. La avioneta A se mueve hacia el sur a una velocidad de 70 km/h, mientras la avioneta B se dirige hacia el oeste a 00 km/h. a) Escribir las funciones que indican las posiciones de A y B en cada instante, así como la distancia entre ambas. b) A qué hora será mínima esa distancia? A A ( t ) 54 Km B ( t ) B 15. Se considera una caja sin tapa. Sabiendo que el fondo es un cuadrado y conociendo que el área total es de 1 cm, hallar sus dimensiones para que tenga la mayor capacidad posible. 16. Se desea construir una caja cerrada de base cuadrada, cuya capacidad sea de las dimensiones de la caja, para que la superficie eterior sea mínima. 8 dm. Averiguar 17. Queremos diseñar un envase cuya forma sea un prisma regular de base cuadrada y volumen 80 cm. Para la tapa y la superficie lateral usaremos un determinado material; pero para la base debemos emplear un material un 50% más caro. Hallar las dimensiones de este envase para que su precio sea mínimo. 18. Se considera un triángulo isósceles cuya base, el lado desigual, mide 10 cm y cuya altura mide 6 cm. En él se inscribe un rectángulo, cuya base está situada sobre la base del triángulo. a) Epresa el área A de dicho rectángulo en función de la longitud de su base. b) Escribe el dominio de la función A() y dibuja su gráfica. c) Hallar el valor máimo de dicha función. 19. Se considera un círculo de radio r. a) Probar que el rectángulo de área máima inscrito en el círculo dado es un cuadrado. b) Considerando el círculo inscrito en dicho cuadrado, calcular el cociente entre las áreas de los dos círculos. 0. Calcular la base y la altura del triángulo isósceles de perímetro 8 dm y área máima. 1. Dada la función f ( ) 1 = se pide: ( ) a) Hallar la ecuación de la recta tangente en el punto, ( ) a f a para a > 0. b) Hallar los puntos de corte de la recta hallada en el apartado anterior con los dos ejes de coordenadas. c) Hallar el valor de a > 0 que hace que la distancia entre los dos puntos hallados en b) sea mínima
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
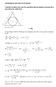 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6 1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg) ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
sen sen sen a 2 a cos cos 2 a
 BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES. 2.- La suma de dos números es 15 y su producto es 26. Cuáles son dichos números?
 RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
APLICACIONES DE LAS DERIVADAS
 0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
a) A la mitad del número le sumo 3 y el resultado es 8 ( ) 9 b) En la ecuación 3x = 54 Qué valor puede tomar x? ( ) Rombo
 Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
EJERCICIOS PAU MATEMÁTICAS II ANDALUCÍA Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
Selectividad hasta el año incluido = 0. Página 1 de 13 ANÁLISIS
 ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
1 Calcula en la siguiente figura el elemento que falta: 2 Calcula en la siguiente figura el elemento que falta:
 1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
APLICACIONES DE LAS DERIVADAS
 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
TEMA 10 FUNCIÓN DERIVADA. REPRESETACIÓN y aplicaciones.
 A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
FUNCIONES. 7.(99).- Hallar la longitud de los lados del triángulo isósceles de área máxima cuyo perímetro sea 60 m.
 Enunciados de problemas de selectividad. Matemáticas II. Funciones FUNCIONES.(97).- Hay alguna función f() que no tenga límite cuando y que, sin embargo, [f()] sí tenga límite cuando?. Si la respuesta
Enunciados de problemas de selectividad. Matemáticas II. Funciones FUNCIONES.(97).- Hay alguna función f() que no tenga límite cuando y que, sin embargo, [f()] sí tenga límite cuando?. Si la respuesta
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Aplicaciones de la derivada.
 Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar.
 C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
FIGURAS PLANAS: RECTÁNGULOS. R1.
 NÚMEROS. N1. Encuentra dos números positivos cuya suma sea 120, tales que el producto de uno de ellos por el cuadrado del otro sea máximo. N2. Expresa el número 90 como suma de tres enteros positivos de
NÚMEROS. N1. Encuentra dos números positivos cuya suma sea 120, tales que el producto de uno de ellos por el cuadrado del otro sea máximo. N2. Expresa el número 90 como suma de tres enteros positivos de
f (x) (1+[f (x)] 2 ) 3 2 κ(x) =
![f (x) (1+[f (x)] 2 ) 3 2 κ(x) = f (x) (1+[f (x)] 2 ) 3 2 κ(x) =](/thumbs/40/20918876.jpg) MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
PENDIENTES 2º ESO. Tercer examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del tercer examen de recuperación de MATEMÁTICAS DE 2º ESO Curso 2013-2014
 014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
Trigonometría y problemas métricos
 Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
EJERCICIOS. ÁREAS Y VOLÚMENES.
 EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
Unidad 2: Resolución de triángulos
 Ejercicio 1 Unidad : Resolución de triángulos En las siguientes figuras, calcula las medidas de los segmentos desconocidos indicados por letras (ambos triángulos son rectángulos en A): cm 16'5 7'5 cm a
Ejercicio 1 Unidad : Resolución de triángulos En las siguientes figuras, calcula las medidas de los segmentos desconocidos indicados por letras (ambos triángulos son rectángulos en A): cm 16'5 7'5 cm a
x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1
![x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1 x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1](/thumbs/80/80474947.jpg) Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones:
 APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
6. Optimización de funciones de una variable.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. 6. Optimización de funciones de una variable. En esta sección estudiaremos cómo calcular los extremos absolutos (si estos existen) de una función suficientemente
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. 6. Optimización de funciones de una variable. En esta sección estudiaremos cómo calcular los extremos absolutos (si estos existen) de una función suficientemente
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO
 Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
Colegio LOPE DE VEGA Luis de Medina, 12 28805 Alcalá de Henares DIBUJO TÉCNICO II EJERCICIOS DE APOYO 1º.- Deducir razonadamente el valor del ángulo α marcado en la figura sabiendo que esta representa
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
Figuras Planas. 100 Ejercicios para practicar con soluciones. 1 Comprueba si los siguientes ángulos son complementarios: a) 72 + 35.
 Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Las superficies serán: Tapa y superficie lateral S 1 = ( x 2 +4xy ) cm 2 Superficie de la base: S 2 = x 2 cm 2
 MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
FUNCIONES RACIONALES. HIPÉRBOLAS
 www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
Tema: Aplicaciones de derivadas. Sean x e y las dimensiones del rectángulo. Área del rectángulo: A = x y. 36 x. Luego, el área es A(x) =
 JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
EJERCICIOS RESUELTOS. x )
 BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
8. y = Solución: x 4. 9. y = 3 5x. Solución: y' = 5 3 5x L 3. 10. y = Solución: 4 4 (5x) 3. 11. y = Solución: (x 2 + 1) 2. 12.
 7 Cálculo de derivadas. Reglas de derivación. Tabla de derivadas Aplica la teoría Deriva en función de :. y = 8. y = 5 3 5 4. y = ( ) 5 0( ) 4 9. y = 3 5 5 3 5 L 3 3. y = 7 + 3 4. y = e e 5. y = 7 7 +
7 Cálculo de derivadas. Reglas de derivación. Tabla de derivadas Aplica la teoría Deriva en función de :. y = 8. y = 5 3 5 4. y = ( ) 5 0( ) 4 9. y = 3 5 5 3 5 L 3 3. y = 7 + 3 4. y = e e 5. y = 7 7 +
1.- 3.- Las áreas de dos polígonos semejantes son 121 cm 2 y 324 cm 2. Si el perímetro del primero es 44 cm, cuál es el perímetro del segundo?
 olegio-laret 1.- 10m 7m 30m SMINRIO MTMÁTIS l dibujo presenta un método aproximado para medir la anchura de un río sin necesidad más que de tomar medidas en una orilla. Situándonos en el punto hemos realizado
olegio-laret 1.- 10m 7m 30m SMINRIO MTMÁTIS l dibujo presenta un método aproximado para medir la anchura de un río sin necesidad más que de tomar medidas en una orilla. Situándonos en el punto hemos realizado
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =
![x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) = x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =](/thumbs/76/74425342.jpg) Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA 6.- FUNCIONES. LÍMITES Y CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
LA RECTA. Ax By C 0. y y m x x. y mx b. Geometría Analítica 2 ECUACIÓN GENERAL. Teorema: ECUACIÓN PUNTO - PENDIENTE .
 LA RECTA En geometría definimos a la recta como la sucesión infinita de puntos uno a continuación de otro en la misma dirección. En el plano cartesiano, la recta es el lugar geométrico de todos los puntos
LA RECTA En geometría definimos a la recta como la sucesión infinita de puntos uno a continuación de otro en la misma dirección. En el plano cartesiano, la recta es el lugar geométrico de todos los puntos
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
EXAMEN GEOMETRÍA. 5. Halla el perímetro y el área de un triángulo isósceles cuyos lados miden 5, 5 y 8 cms., respectivamente.
 1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
Nombre: EJERCICIO 1 (1): Dado un rectángulo cuyos lados miden 4 cm y 3 cm, qué medidas tendrá una ampliación suya si la razón de semejanza es 2,5?
 Matemáticas 3ºESO D Examen: 1º 30. 04.14 EJERCICIO 1 (1): Dado un rectángulo cuyos lados miden 4 cm y 3 cm, qué medidas tendrá una ampliación suya si la razón de semejanza es 2,5? EJERCICIO 2: (2) Dado
Matemáticas 3ºESO D Examen: 1º 30. 04.14 EJERCICIO 1 (1): Dado un rectángulo cuyos lados miden 4 cm y 3 cm, qué medidas tendrá una ampliación suya si la razón de semejanza es 2,5? EJERCICIO 2: (2) Dado
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS
 SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
ANÁLISIS (Selectividad)
 ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
tiene un máximo relativo en x = asíntota horizontal la recta y = 3. Razonar si para a = 2 y b = 3 la función f(x) tiene algún mínimo relativo.
 Selectividad CCNN 006. [ANDA] [SEP-A] Sea f: la función definida por f() = -. a) Estudia la derivabilidad de f. b) Determina los intervalos de crecimiento y decrecimiento de f. c) Calcula los etremos relativos
Selectividad CCNN 006. [ANDA] [SEP-A] Sea f: la función definida por f() = -. a) Estudia la derivabilidad de f. b) Determina los intervalos de crecimiento y decrecimiento de f. c) Calcula los etremos relativos
5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días
![5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días 5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días](/thumbs/40/21102307.jpg) . [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
. [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
TRANSFORMACIONES DEL PLANO
 PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
1 Indica cuál es el valor de los ángulo Â, Bˆ. en las siguientes figuras: a) b) 2 Calcula los ángulos dados por letras:
 1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
1. f(x) = x+5 ; f (2) 2. f(x) x 2-3x+2 ; f (1) 3. f(x) = sen 2x ; f (0) 4. f(x) = x+1 x-2 ; f (1)
 Derivadas. Dada la siguiente función, calcular, por la definición, la derivada que se indica:. f() = +5 ; f (). f() -+ ; f (). f() = sen ; f (0) 4. f() = + - ; f () 5. f() =,
Derivadas. Dada la siguiente función, calcular, por la definición, la derivada que se indica:. f() = +5 ; f (). f() -+ ; f (). f() = sen ; f (0) 4. f() = + - ; f () 5. f() =,
Efa Moratalaz PCPI - Matemáticas GEOMETRÍA PLANA
 GEOMETRÍA PLANA Geometría Plana Ficha 1 (Ejercicios Cuadrado) Área de un cuadrado: Perímetro de un cuadrado: 1) Halla el perímetro y el área de un cuadrado de 3 m de lado. 2) Halla el perímetro y el área
GEOMETRÍA PLANA Geometría Plana Ficha 1 (Ejercicios Cuadrado) Área de un cuadrado: Perímetro de un cuadrado: 1) Halla el perímetro y el área de un cuadrado de 3 m de lado. 2) Halla el perímetro y el área
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Integral definida. 1. Integral definida. Piensa y calcula. Aplica la teoría. 3. Siendo x el valor absoluto o módulo de x, calcula la. 2.
 Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
UNIDAD X - GEOMETRIA. Ejercitación
 UNIDAD X - GEOMETRIA Programa Analítico Segmentos. Operaciones con segmentos. Ángulos. Clasificación de los ángulos: Complementarios, suplementarios, adyacentes, alternos-internos, opuestos por el vértice.
UNIDAD X - GEOMETRIA Programa Analítico Segmentos. Operaciones con segmentos. Ángulos. Clasificación de los ángulos: Complementarios, suplementarios, adyacentes, alternos-internos, opuestos por el vértice.
Hoja de problemas nº 7. Introducción a la Geometría
 Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. e) f) es divisible por 6. a) b) c) d) e) f)
 1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
Unidad didáctica 3. Cálculo de superficies y volúmenes
 Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
Unidad didáctica. Cálculo de superficies y volúmenes.1 Cálculo de superficies. En el presente apartado se estudiarán las superficies, perímetros y relaciones geométricas más importantes de las principales
SOLUCIONES MINIMOS 2º ESO TEMA 7 TEOREMA DE PITÁGORAS.SEMEJANZA
 SOLUCIONES MINIMOS º ESO TEMA 7 TEOREMA DE PITÁGORAS.SEMEJANZA Ejercicio nº 1.- Los lados de un triángulo miden, respectivamente, 9 cm, 1 cm y 15 cm. Averigua si el triángulo es rectángulo. Según el teorema
SOLUCIONES MINIMOS º ESO TEMA 7 TEOREMA DE PITÁGORAS.SEMEJANZA Ejercicio nº 1.- Los lados de un triángulo miden, respectivamente, 9 cm, 1 cm y 15 cm. Averigua si el triángulo es rectángulo. Según el teorema
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción B Junio, Ejercicio, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción B Junio, Ejercicio, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva,
Polígonos y circunferencia
 826464 _ 055-070.qxd 12/2/07 09:22 Página 55 Polígonos y circunferencia INTRODUCCIÓN RESUMEN DE LA UNIDAD Nos introducimos en el estudio de los polígonos, recordando contenidos trabajados por los alumnos
826464 _ 055-070.qxd 12/2/07 09:22 Página 55 Polígonos y circunferencia INTRODUCCIÓN RESUMEN DE LA UNIDAD Nos introducimos en el estudio de los polígonos, recordando contenidos trabajados por los alumnos
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD
 DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
TEMA 10. CÁLCULO DIFERENCIAL
 TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
 Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón: 2 ) Calcula el perímetro y el área de esta figura: 3 ) Calcula el perímetro y el área de
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón: 2 ) Calcula el perímetro y el área de esta figura: 3 ) Calcula el perímetro y el área de
La circunferencia y el círculo
 La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto).
 1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
MATEMÁTICAS 1º BAC Aplicaciones de las derivadas
 . Queremos construir una caja abierta, de base cuadrada y volumen 56 litros. Halla las dimenones para que la superficie, y por tanto el coste, sea mínimo.. Entre todos los rectángulos de área 6 halla el
. Queremos construir una caja abierta, de base cuadrada y volumen 56 litros. Halla las dimenones para que la superficie, y por tanto el coste, sea mínimo.. Entre todos los rectángulos de área 6 halla el
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2009 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
ANÁLISIS. d) No, se podrían haber considerado infinitas funciones diferenciadas en una constante.
 Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
RELACION DE PROBLEMAS DE GEOMETRIA. Problemas propuestos para la prueba de acceso del curso 1996/97.
 RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
x 2-4 intervalos de crecimiento y decrecimiento, sus máximos y mínimos, sus intervalos de concavidad y convexidad y sus puntos de inflexión.
 . [ANDA] [JUN-A] De la función f: definida por f() = a 3 +b +c+d se sabe que tiene un máimo en = -, que su gráfica corta al eje O en el punto de abscisa = y tiene un punto de infleión en el punto de abscisa
. [ANDA] [JUN-A] De la función f: definida por f() = a 3 +b +c+d se sabe que tiene un máimo en = -, que su gráfica corta al eje O en el punto de abscisa = y tiene un punto de infleión en el punto de abscisa
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
TEMA 2: DERIVADA DE UNA FUNCIÓN
 TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
