EJERCICIOS RESUELTOS. x )
|
|
|
- María Teresa Vargas Hernández
- hace 7 años
- Vistas:
Transcripción
1 BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos la primera derivada: sen cos sen f'() = = ( 4 cos ) ( 4 cos ) Como 4 cos 0 para todo número real, el dominio de f'() es R, por lo tanto también eiste en ]0, π[. Estudiamos ahora el signo de f'(), que es el de sen π π sen = 0 = 0, =, = π, 4 = y 5 = π en [ 0, π] consecuentemente: Signo de f '() 0 π/ π π/ π 4 cos en ]0, π[. π π y f() es creciente en y decreciente en π π,, 0, π π. π, π π Del estudio de la monotonía de f() (signo de f'()) se deduce que tiene máimo relativo en = y = y míni- mo relativo en = π. Los dos máimos tienen el mismo valor que es 4 y el valor del mínimo es. Representa gráficamente la función y =. ntes de representarla haremos el estudio de la función que comprende los siguientes puntos:. Dominio. Para que la función eista se necesita que 0 y 0. Por tanto: D(f) = ], ] [, [. síntotas. a) Horizontales: por la izquierda: lim = y = es asíntota horizontal por la izquierda por la derecha: lim = y = es asíntota horizontal por la derecha. b) Verticales. No tiene porque la función no tiende a infinito para valores finitos de. c) Oblicuas. No tiene por tener asíntota horizontal por la izquierda y por la derecha. Tema 8. plicaciones de la derivada 77
2 BXX5744_08 /6/09 09:59 Página 78 EJERCICIOS RESUELTOS. Puntos de corte con los ejes. a) Con OX = (, 0) = 0 = 0 = (, 0) b) Con OY no puede tener pues 0 D(f ). 4. Simetrías. ( ) Como f( ) = = = f(), la función es impar y la curva es simétrica respecto del origen de coordenadas. 5. Crecimiento, decrecimiento, máimos y mínimos. Estudiamos el signo de la primera derivada. y ( ) ' = = = y 0, luego no hay ni máimo ni mínimos Signo de y' ] [ Es creciente en todo su dominio. 6. Concavidad, conveidad y puntos de infleión. Estudiamos el signo de la segunda derivada ( y '' = = ) = = ( ) 4( ) 4( ) ( ) y'' = 0 = 0 = ±, ninguno de los dos valores pertenece al dominio de la función. Por tanto: Signo de y'' ] [ Es cóncava en ], [. Es convea en ], [. No tiene puntos de infleión. 7. Tabla de sistematización. f() 0 0 f' Su gráfica es: Y f'' f O X 78
3 BXX5744_08 /6/09 09:59 Página 79 Representa gráficamente la función y =, llamada «Tridente de Newton». Esta función también se puede epresar como y =, epresiones que utilizaremos indistintamente para su estudio.. Dominio. D(f )= R {0}. síntotas. a) Horizontales no tiene pues lim = lim = b) Verticales. Sólo puede ser la recta = 0. Veamos los límites laterales y lim lim = = ; luego = 0 es una asíntota vertical. 0 0 c) Oblicuas por la izquierda: lim = no tiene; por la derecha: lim = no tiene. Puntos de corte con los ejes a) Con OX = 0 = 0 = = (, 0) b) Con OY no puede tener pues 0 D(f) 4. Simetrías Como f( ) = ( ) = f() y f(), la curva no tiene simetrías. 5. Crecimiento, decrecimiento, máimos y mínimos. Estudiamos el signo de la primera derivada. ; y' = 0 = y' = = = = Signo de y' 0 Por tanto es: decreciente en ], 0[ 0, ; creciente en, ; tiene un mínimo en, 4 (0,8,,9) no tiene máimo. Tema 8. plicaciones de la derivada 79
4 BXX5744_08 /6/09 09:59 Página 80 EJERCICIOS RESUELTOS 6. Concavidad, conveidad y puntos de infleión. Estudiamos el signo de la segunda derivada. ( ) y '' = = y'' = 0 = = Signe de y" 0 Y Del signo de y'' se deduce que es cóncava en ], [ ]0, [ convea en ], 0[ tiene un punto de infleión en (, 0). 7. Tabla de sistematización Su gráfica es: 0 f() 0 f' 0 O X f'' 0 f 4 las h. de la noche, un barco está a 75 km al este de otro B. El barco navega hacia el oeste a 0 km/h y el B navega hacia el sur a 5 km/h. Si mantienen esos rumbos, cuál será la mínima distancia entre ellos? y a qué hora se producirá? Sean 0 y B 0 las posiciones de los barcos y B a las h. y y B sus posiciones después de navegar t horas. Se tiene así la siguiente figura: B t 0 5t d O N E S B La distancia entre los barcos después de t horas de navegación es: dt () = ( 75 0t) ( 5t) = t 65t 80
5 BXX5744_08 /6/09 09:59 Página 8 la distancia d será mínima cuando también lo sea D = d por lo que calcularemos el valor de t para cuando D sea mínima. D(t) = t 65t D'(t) = t D'(t) = 0 50t = 000 t =,4 h ó h 4 min Veamos si D es mínimo para este valor de t D'' = 50 > 0 sí es mínimo. Por tanto se encuentran más próimos a las h. 4 min. y la distancia entre ellos es: dt () = , 4 65(, 4) = 05 = 45 km 5 Un espejo plano tenía forma de un cuadrado de 80 cm de lado y se ha roto por una esquina según una recta. Uno de los trozos tiene forma de triángulo rectángulo de catetos 40 y cm. Hallar las dimensiones del espejo rectangular de área máima que se puede recortar del otro trozo, de modo que los bordes del nuevo espejo sean paralelos a los del primitivo. Con los datos del problema, podemos construir las figuras siguientes. y 80 y 40 D 80 y B E F C Si e y son las dimensiones pedidas, la función área que hay que hacer máima es: S = y Por la semejanza de los triángulos DB y EC sabemos: B C = es decir: = DB EC 80 y despejando y: y = Sustituyendo en S tenemos: S = =. 5 5 Esta función nos permite obtener el área buscada en función de una sola variable. Para obtener el máimo de dicha función derivamos: S' = ; S' = = 8 = 70 5 como S'' = 8/5 < 0; para = 70 hay un máimo. Obteniendo para este valor de el correspondiente valor de y, las dimensiones pedidas son: = 70; y = 56. Tema 8. plicaciones de la derivada 8
6 BXX5744_08 /6/09 09:59 Página 8 EJERCICIOS RESUELTOS 6 Calcular los posibles máimos y mínimos de las funciones siguientes en los intervalos que se indican: a) f() = ( ) ( ) en [, ] b) g() = 8 en [, ] a) Obtendremos una epresión más simple de f si operamos: f() = ( )( ) = 4 Derivando: f'() = 4 4 = 4( ) f'() = 0 si = 0 pues 0 para todo. Como f''() = 4 entonces f''(0) = 4 > 0, luego en = 0 hay un mínimo relativo en (0, ) y dicho punto pertenece al intervalo [, ]. demás en dicho intervalo sólo hay un punto que anule a la primera derivada, luego deducimos que los posibles valores máimos y mínimos absolutos los alcanzará la función en los etremos del intervalo. sí pues: f( ) = y también es f() = pues la función es par, luego f alcanza el máimo absoluto en los puntos (, ) y (, ). b) Como g() = 8, derivando: g'() = 8 g'() = 0 8 = 0 = y = 4 La derivada segunda es: g''() = 6 y verifica 4 g''() = 0 > 0 y g'' = 0 < 0 luego hay un mínimo relativo en P(, ) y un máimo relativo en Q y ambos etremos tiene la abscisa en el intervalo [, ]. El máimo absoluto lo puede obtener la función en el etremo inferior del intervalo, pero en él es 0 g( ) = 5 < y por tanto el máimo relativo obtenido es también máimo absoluto en el intervalo [, ]. 7 7 Obtén el valor de las constantes a, b y c para que la gráfica de la curva f() = a b c pase por el punto (, ) y sea tangente a la recta g() = en el punto (0, 0). Por pasar por el punto (, ): f() = a b c = Por pasar por el punto (0, 0): f(0) = 0 c = 0 Por ser tangente a la recta g() = en el (0, 0): f '(0) = b = Se deduce que a = y por tanto la curva es f() = 8
7 BXX5744_08 /6/09 09:59 Página 8 8 Las gráficas siguientes representan las funciones f 'y g', derivadas respectivamente de sendas funciones f y g. Y Y f g' O X O X Esboza, razonadamente, una posible gráfica de las funciones f y g. Como f' < 0 si ], [ y f' > 0 en ], [, entonces f es decreciente en ], [ y creciente en ], [. l ser f'( ) = 0 entonces f tiene un mínimo en =. Una posible gráfica es: Y f O X La función g' es positiva en los intervalos ], [ y ], [, por tanto g será creciente en dichos intervalos. sí mismo g' es negativa en ], [ por tango g será decreciente en dicho intervalo. Como g'( ) = 0 y en dicho punto g pasa de ser creciente a decreciente se deduce que en = hay un máimo relativo. l igual, en = se verifica que g'() = 0 y la función g pasa de ser decreciente a creciente, luego en = la función g tien un mínimo relativo. Una posible gráfica de g es: Y O X 9 Estudia los intervalos de crecimiento y decrecimiento así como los etremos relativos de la función f() = El dominio de la función es D(f) = R {}. Tema 8. plicaciones de la derivada 8
8 BXX5744_08 /6/09 09:59 Página 84 EJERCICIOS RESUELTOS f'() = ( ) = ( ) ( ) f'() = 0 = 0 = 0, =. Los puntos críticos de f son los de abscisa = 0 y =. El signo de f' queda determinado por el signo de puesto que ( ) es siempre positivo en el dominio de f. Signo f ' 0 f es creciente en ], 0[ ], [; f es decreciente en ]0, [ ], [ f tiene en = 0 un máimo relativo y en = un mínimo relativo. Estos puntos etremos son M(0, 0) y m(, 4). Y 4 O X 0 Halla el valor de «a» para que la recta tangente a la gráfica de la función f() = a a en el punto de abscisa forme un ángulo de 45 con el eje OX. Se resuelve aplicando la interpretación geométrica de la derivada de una función en un punto. En realidad se trata de ver qué valor debe tomar a para que la derivada de la función valga cuando = f'()= ( a) ( a) 6a = ( a) ( a) Eigiendo la condición mencionada: 6a = ( a) 6a = 0 a 4a = 0 a = ó a =. ( a) 84
9 BXX5744_08 /6/09 09:59 Página 85 Halla a, b y c para que la función f() = a b c pase por el punto P(, ) y tenga un mínimo en m(, 4). Si pasa por P(, ) entonces = a b c. Si tiene un mínimo en m(, 4) entonces en primer lugar se deduce que f'() = 0, es decir: f'() = a b f'() = 4a b = 0 Pero además el punto mínimo m(, 4) también pertenece a la gráfica, luego se cumple que f() = 4 es decir: 4a b c = 4 a b c = Estas condiciones han generado el sistema de ecuaciones: 4a b = 0 4a b c = 4 Cuyas soluciones son: a =, b = 8, c = 4, y por tanto la función buscada es: f() = 8 4. Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de paralelepípedo rectangular sabiendo que su volumen debe ser de 9 m, su altura m y que el coste de construcción por m es de 0 euros para la base, 6 euros para la tapadera y 4 para cada pared lateral. Si e y son las dimensiones de la base del contenedor, V = y = y = 9. y y La función a minimizar será el coste de construcción. C(, y) = 0 y 6 y 4 4 y = 66y 48 48y 9 Como y = 9 entonces y = y sustituyendo en la función obtenemos una epresión del coste en función de una sola variable: 4 C() = Derivando: C'() = C'() = 0 48 = = = Como C''() =, entonces C''() > 0 luego la función coste es mínima si =. Las dimensiones óptimas de la base son: = e y =. Tema 8. plicaciones de la derivada 85
10 BXX5744_08 /6/09 09:59 Página 86 FORMULRIO Monotonía Si f'( 0 ) > 0 f() es creciente en 0 Si f'( 0 ) < 0 f() es decreciente en 0 Etremos relativos Criterio de la primera derivada Si f'( 0 ) > 0 y f'( 0 ) < 0 entonces hay un máimo en 0. Si f'( 0 ) < 0 y f'( 0 ) > 0 entonces hay un mínimo en 0. Si f'( 0 ) y f'( 0 ) tienen igual signo entonces hay una infleión en 0. Criterio de la segunda derivada Sea f una función tal que admita segunda derivada en ]a, b[ y sea 0 un punto del intervalo tal que f'( 0 ) = 0. Entonces: Si f''( 0 ) < 0 f() tiene un máimo relativo en 0. Si f''( 0 ) > 0 f() tiene un mínimo relativo en 0. Si f''( 0 ) = 0 f() puede tener un máimo o un mínimo o un punto de infleión en 0. Concavidad y conveidad Si f''( 0 ) > 0 f() es cóncava en 0 Si f''( 0 ) < 0 f() es convea en 0 Si f''( 0 ) = 0 y f''() tiene distinto signo a ambos lados de 0 f() tiene un punto de infleión en ( 0, f( 0 )) Si una función f tiene en 0 un punto de infleión y además es f'( 0 ) = 0, entonces es un punto de infleión de tangente horizontal Criterio de la tercera derivada Si f es una función que admite tercera derivada en un punto 0, entonces: Si f''( 0 ) = 0 y f'''( 0 ) 0 la función tiene un punto de infleión en 0 86
11 BXX5744_08 /6/09 09:59 Página 87 EJERCICIOS FINLES 0 4 Hallar los intervalos de crecimiento y decrecimiento y los etremos de la función: f ( ) = 6 8 Demostrar que la función f() = 5 9 no tiene etremos. Halla los etremos relativos de las funciones: a) f() = ( ) b) g() = Halla los etremos relativos de las funciones: a) h() = ln ( ) b) j() = ln Calcular los intervalos de concavidad, conveidad y puntos de infleión de: a) f() = 4 6 b) g() = ( ) 0 b) En qué momentos el rendimiento es nulo. c) Cuándo se obtiene el mayor rendimiento y cuál es? El beneficio diario obtenido por una empresa, en función del número de unidades producidas, viene dado por la función f() = 4. Dibuja la gráfica de dicha función para 0 8, deduciendo su forma del estudio del signo de f'(), y deduce de la gráfica para qué valores de, con 0 8, se obtienen los beneficios máimos y mínimos. a) Calcula la derivada de la función f() = y justifica si esa función es creciente o decreciente en el intervalo [, 7]. b) Representa la gráfica de y = Obtén el área de un rectángulo inscrito en una circunferencia de radio en función de la base del rectángulo. Representa la función área obtenida, deduciendo de la derivada dónde es creciente o decreciente, así como cuál es el rectángulo de área máima inscrito en dicha circunferencia. Hallar las funciones polinómicas f() = a b c d, cuya segunda derivada sea. Cuál o cuáles de ellas tienen un mínimo relativo en el punto (4, /)? Determina una función polinómica de segundo grado tal que su gráfica corte al eje OX en = y que tenga un mínimo relativo en el punto (, 6). La función f() = a b c pasa por (, 0) y tiene un máimo en (0, 4). Halla: a) La función. b) El punto de infleión. 4 5 l vender un producto a un precio entre 40 y 65 euros, el beneficio es y = euros. Obtener, razonadamente, el precio que maimiza y. Representa gráficamente la función y = ( ) ( ), indicando máimos y mínimos, crecimiento y decrecimiento, concavidad y conveidad. Durante los treinta días consecutivos de un mes las acciones de una determinada compañía han tenido unas cotizaciones dadas por la función f() = 0, 8 00, donde es el número de días transcurridos. Halla los días en que las respectivas acciones estuvieron en baja (bajando de precio) y los que estuvieron en alza. Qué día del mes alcanzaron el valor máimo? Y el valor mínimo? Hallar a, b, c y d en la función y = a b c d sabiendo que su tangente en el punto (, ) es la recta y = y que tiene un etremo en el punto (0, ). 9 Supongamos que el rendimiento r en % de un alumno en un eamen de una hora viene dado por r = 00t ( t), donde 0 t es el tiempo en horas. Se pide: a) En qué momentos aumenta o disminuye el rendimiento? 6 El área ocupada por una infección cutánea se desarrolla a partir del instante t = 0 según la función t f(t) = 0 t a) Calcular la superficie ocupada por la infección al principio. Tema 8. plicaciones de la derivada 87
12 BXX5744_08 /6/09 09:59 Página 88 EJERCICIOS FINLES b) Hallar el instante en que es máima el área infectada y calcular dicha área. c) Estudiar qué ocurre con el transcurso del tiempo. Se estabiliza o desparece la infección? Del al 45. Representar gráficamente las funciones: a) f() = b) f() = Dada la función f() = 5, se pide: Máimos y mínimos. Intervalos de crecimiento y decrecimiento. Intervalos de concavidad y conveidad. Se ha comprobado empíricamente que las ganancias que proporciona cierto juego dependen del tiempo que se esté jugando a través de la epresión: G ( ) = (donde representa el tiempo de juego epresado en minutos). Se pide: a) Cuanto más tiempo se permanezca jugando es mayor la ganancia que se obtiene? Justificar la respuesta. b) Determinar el tiempo de juego que proporciona la mayor ganancia. c) Puede ocurrir que si se sobrepasa cierto tiempo, el juego dé pérdidas (ganancias negativas)? Por qué? k Se define la función f() =. Se pide: a) Determina k, de modo que dicha función tenga un máimo para =. b) Dibujar una gráfica razonable de la función f() para el valor de k obtenido en el apartado anterior. Estudiar el crecimiento y decrecimiento y los máimo y mínimos de la función f() = Demostrar que la función f ( ) = ln es creciente en todo su dominio de definición a) f() = b) f() = 4 a) f() = b) f() = 5 a) f() = b) f() = a) f() = ( ) ( ) b) f() = a) f() = e b) f() = a) f() = b) f() = 6 a) f() = b) f() = a) f() = b) f() = e / a) f() = b) f() = ( )( ) e a) f() = b) f() = e 6 5 a) f() = b) f() = ( ) 8 6 ( ) Calcular los valores de a, b y c sabiendo que la función f() = a b c pasa por los puntos (, 0) y (0, ) y presenta un máimo en = f() = ( )( ) Cuál es el número que sumado con su recíproco da una suma máima relativa? 88
13 BXX5744_08 /6/09 09:59 Página Una bala disparada verticalmente hacia arriba alcanza, al cabo de t segundos, la altura h = 500t 5t metros. Cuál será la altura máima que puede alcanzar? Inscribir en una circunferencia de radio 0 m un triángulo rectángulo de perímetro máimo. Hallar el área del triángulo rectángulo máimo que tenga 0 m de hipotenusa. De todos los triángulos isósceles inscritos en una circunferencia de radio 5 m, cuál es el de área máima? De todos los rectángulos de 64 cm de perímetro, determina el de área máima Un depósito cuadrado de forma de paralelepípedo rectangular de base cuadrada tiene de volumen 5 m. Calcular las dimensiones de sus aristas para que la cantidad de material empleado sea mínima. Un triángulo isósceles que tiene 0 cm de perímetro gira alrededor de su altura engendrando un cono. Hallar las longitudes de los lados del triángulo para que el volumen engendrado sea máimo. De la siguiente figura, formada por un rectángulo y un semicírculo, se sabe que su perímetro es 50 m. Se pide determinar: 5 De todos los rectángulos de 6 cm de superficie, determina el de perímetro mínimo. 5 De todos los rectángulos de 6 cm de superficie, determina el de diagonal mínima. y Determinar la diagonal mínima de todos los rectángulos de 8 m de perímetro. La suma de la base y de la altura de un triángulo es 0 cm. Qué longitud debe tener la base para que el área del triángulo sea máima? Hallar la base de un triángulo isósceles de perímetro 0 m y área máima. De qué clase de triángulo se trata? Inscribir un rectángulo en un triángulo isósceles de modo que tenga un lado sobre la base del triángulo y los otros dos vértices sobre cada uno de los lados iguales, y que el área del rectángulo sea máima. Las dimensiones del triángulo son: base = cm, altura = 0 cm. Se desea comprar un terreno rectangular de 400 m de superficie. Cuáles serán las dimensiones más convenientes para que la construcción de la cerca resulte lo más económica posible? Calcular las dimensiones que debe tener un estanque de forma de paralelepípedo rectangular de base cuadrada de modo que su volumen sea máimo. Entre las cinco caras del estanque tienen 9 m de área a) El área en función de. b) para que su área sea máima. De todos los cilindros que tienen m de superficie total, cuál es el de volumen máimo? El coste de un marco para una ventana se estima en 5 euros por cada metro de altura y 80 euros por cada metro de anchura. La ventana tendrá un metro cuadrado de superficie. Qué dimensiones debe tener el marco para que resulte lo más económico posible? De una lámina de cartón de 40 cm de ancho por 60 de largo se debe cortar de cada ángulo un cuadrado igual, de modo que con el cartón resultante, doblándolo convenientemente, se pueda construir una caja sin tapa. veriguar la longitud del lado del cuadrado para que la capacidad de la caja sea máima. Una hoja de papel debe contener 88 cm de teto impreso. Los márgenes superior e inferior deben tener cm cada uno, y los laterales, cm. Se piden las dimensiones de la hoja para las que el gasto de papel sea mínimo. Tema 8. plicaciones de la derivada 89
14 BXX5744_08 /6/09 09:59 Página 90 EJERCICIOS FINLES Hallar el número positivo que sumando con 5 veces su recíproco de un valor mínimo. De todos los pares e y de números reales positivos cuya suma sea 0, determina razonadamente el par (, y) cuyo producto y es máimo. La siguiente figura indica la posición de tres ciudades, B y C. La distancia entre y C es de 4 km y entre B y C es de 8 km. Se desea hacer un tendido eléctrico entre las ciudades y B. El tendido que sigue la carretera (CD) cuesta unidad monetaria el kilómetro y el tendido que atraviesa el campo (D) cuesta unidades monetarias el kilómetro. Justificar que el costo del tendido es (8 ), y hallar a qué punto (D) de la carretera hay que dirigirse para que el costo del tendido sea mínimo. 8 C D B Qué dimensiones debe tener una caja de 6 dm de volumen, base rectangular y 4 dm de altura para que su superficie total (con tapa) sea mínima? De entre todos los cuadrados inscritos en un cuadrado de lado 0 cm hallar las dimensiones del que tiene área mínima. Hallar las dimensiones de un bote cilíndrico de 0 litros, si el gasto de la chapa ha de ser mínimo. Descomponer 8 como suma de dos números positivos, de manera que el producto de uno de ellos por el cuadrado del otro sea máimo. Un terreno rectangular se va a vallar y dividir en tres rectángulos iguales mediante dos vallas divisorias paralelas a los lados más pequeños del rectángulo. Si únicamente se dispone de m de valla qué dimensiones del terreno maimizan el área vallada? Con un alambre de 4 metros se quiere construir el borde de un rectángulo de área máima. Qué dimensiones hay que dar al rectángulo? dosada a un muro se quiere construir una parcela rectangular para lo que se dispone de 00 m de alambrada. Se pide hallar: a) El área de la parcela en función del lado perpendicular al muro. b) Las dimensiones de la parcela de área máima. Se corta una cuerda de 00 m en dos partes para construir un cuadrado y un rectángulo de base el doble que altura. a) Obtener la suma de las áreas del cuadrado y del rectángulo en función de la base del rectángulo. b) Halla razonadamente las dimensiones del cuadrado y del rectángulo para que la suma de sus áreas sea mínima El consumo de un coche depende de la velocidad en km/h según la función e, fv ( ) = 00ν litros/km ν Cuál es la velocidad más económica? Cuántos litros por cada 00 km se gastarán a esta velocidad? Nota: e,78. El índice de inflación de cierto país fue variando, durante el año 008, según la epresión t 8t it () = 5 0 donde t es el tiempo en meses desde principios del año. Se pide: a) Durante qué meses el índice de inflación fue creciendo? b) partir de qué mes se supera la inflación inicial del mes de enero? El propietario de un inmueble tiene alquilados los 40 pisos del mismo a 600. al mes cada uno. Por cada 60 euros de aumento en el precio del alquiler pierde un inquilino, que se traslada a otro piso más económico. Cuál es el alquiler que más beneficio produce al propietario? 90
15 BXX5744_08 /6/09 0:00 Página 9 UTOEVLUCIÓN La función f() = es creciente en: ], [ ]0, [ B ], 0[ C [, 0] D nada de lo anterior La función f() = 4 tiene un máimo en: = B = 0 C = D nada de lo anterior La función f() = 6 tiene un mínimo en: (4, ) B no tiene C (0, 0) D nada de lo anterior 4 La función f() = es convea en: R { } B ], [ C ], [ D nada de lo anterior 5 Los puntos de infleión de la función f() = ln son: no tiene B (, 0) C (0, ) D nada de lo anterior 6 Si una función es par entonces es simétrica respecto de: el eje OX B el eje OY C el origen de coordenadas D nada de lo anterior 7 Las asíntotas de la función f() = son: no tiene B = y = C y = 0 D nada de lo anterior 8 Dos números positivos cuyo producto es 6 y la suma de uno de ellos con el cuadrado del otro es mínima, son: 4 y 4 B 6 y C 8 y D nada de lo anterior 9 La ecuación de la recta que pasa por el punto P(, ) y determina con los ejes coordenados un triángulo de área mínima, no nula, es: y = 4 6 B y = 4 C y = D nada de lo anterior 0 De todas las pendientes de las rectas tangentes a la gráfica de la función y = 6 4 la máima es: B C D nada de lo anterior Tema 8. plicaciones de la derivada 9
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
REPRESENTACIÓN GRÁFICA DE FUNCIONES
 REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
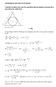 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
APLICACIONES DE LAS DERIVADAS
 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
TEMA 8 : APLICACIÓN DE LAS DERIVADAS
 TEMA 8 : APLICACIÓN DE LAS DERIVADAS 1. MONOTONÍA Una función es creciente en un punto 0 cuando para puntos próimos a 0 se cumple que al aumentar también aumenta f() y al disminuir también disminuye f().
TEMA 8 : APLICACIÓN DE LAS DERIVADAS 1. MONOTONÍA Una función es creciente en un punto 0 cuando para puntos próimos a 0 se cumple que al aumentar también aumenta f() y al disminuir también disminuye f().
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días
![5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días 5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días](/thumbs/40/21102307.jpg) . [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
. [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
 Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Propiedades de las funciones derivables. Representación gráfica de funciones. Determinar los puntos de inflexión. (Junio 1997)
 Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
EJERCICIOS PAU MATEMÁTICAS II ANDALUCÍA Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
Tema: Aplicaciones de derivadas. Sean x e y las dimensiones del rectángulo. Área del rectángulo: A = x y. 36 x. Luego, el área es A(x) =
 JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA 6.- FUNCIONES. LÍMITES Y CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
sen sen sen a 2 a cos cos 2 a
 BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
Las superficies serán: Tapa y superficie lateral S 1 = ( x 2 +4xy ) cm 2 Superficie de la base: S 2 = x 2 cm 2
 MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción B Junio, Ejercicio, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción B Junio, Ejercicio, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva,
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL
 EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
FUNCIONES RACIONALES. HIPÉRBOLAS
 www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
Máximo o mínimo de una función. Solución: El mínimo de una función se da en los puntos que anulan su derivada y tiene derivada segunda positiva.
 Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
APLICACIONES DE LAS DERIVADAS
 0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
DERIVADAS EN LA EBAU DE MURCIA. 2x 2 2x 1. 2x + 2x + 1 (2x + 1) 2x + 1. g'(x) = 2xe + x 2xe g'(x) = 2xe (1 + x )
 DERIVADAS EN LA EBAU DE MURCIA a + b 1. (Septiembre 017) Dada la función f() =, donde a y b son números reales, halla el + 1 valor de a y b para que se cumpla que f(0) = 1 y f (0) = 1. b = 1 y a = 1..
DERIVADAS EN LA EBAU DE MURCIA a + b 1. (Septiembre 017) Dada la función f() =, donde a y b son números reales, halla el + 1 valor de a y b para que se cumpla que f(0) = 1 y f (0) = 1. b = 1 y a = 1..
I E S CARDENAL CISNEROS -- DEPARTAMENTO DE MATEMÁTICAS APLICACIÓN DE LAS DERIVADAS
 I E S CARDENAL CISNEROS -- DEPARTAMENTO DE MATEMÁTICAS APLICACIÓN DE LAS DERIVADAS Dada la función f() = + 1 + 4. Calcular la tangente a la gráfica de la función en el punto =. La fórmula de la recta tangente
I E S CARDENAL CISNEROS -- DEPARTAMENTO DE MATEMÁTICAS APLICACIÓN DE LAS DERIVADAS Dada la función f() = + 1 + 4. Calcular la tangente a la gráfica de la función en el punto =. La fórmula de la recta tangente
Teoría Tema 9 Representación gráfica de funciones
 página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
1. f(x) = x+5 ; f (2) 2. f(x) x 2-3x+2 ; f (1) 3. f(x) = sen 2x ; f (0) 4. f(x) = x+1 x-2 ; f (1)
 Derivadas. Dada la siguiente función, calcular, por la definición, la derivada que se indica:. f() = +5 ; f (). f() -+ ; f (). f() = sen ; f (0) 4. f() = + - ; f () 5. f() =,
Derivadas. Dada la siguiente función, calcular, por la definición, la derivada que se indica:. f() = +5 ; f (). f() -+ ; f (). f() = sen ; f (0) 4. f() = + - ; f () 5. f() =,
APLICACIONES DE LA DERIVADA CCSS
 APLICACIONES DE LA DERIVADA CCSS Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en
APLICACIONES DE LA DERIVADA CCSS Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en
RELACIÓN EJERCICIOS ANÁLISIS SELECTIVIDAD MATEMÁTICAS II
 1.- Sea f : R R la función definida como f() = e X.( ). (a) [1 punto] Calcula la asíntotas de f. (b) [1 punto] Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
1.- Sea f : R R la función definida como f() = e X.( ). (a) [1 punto] Calcula la asíntotas de f. (b) [1 punto] Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
TEMA 10 FUNCIÓN DERIVADA. REPRESETACIÓN y aplicaciones.
 A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
f(x) = xe para x -1 y x 0, MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio 1. (Reserva 1 Septiembre 2013 Opción A) Sea f la función definida por
 MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio. (Reserva Septiembre 0 Opción A) f() = para > 0, (donde ln denota el logaritmo neperiano). ln() a) [ 5 puntos] Estudia y determina las asíntotas de la gráfica
MATEMÁTICAS II PROBLEMAS DE FUNCIONES. Ejercicio. (Reserva Septiembre 0 Opción A) f() = para > 0, (donde ln denota el logaritmo neperiano). ln() a) [ 5 puntos] Estudia y determina las asíntotas de la gráfica
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos
 64 TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión. Dada la función
64 TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión. Dada la función
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. e) f) es divisible por 6. a) b) c) d) e) f)
 1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA
 CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1
![x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1 x 2-4x+3 si -1 < x < 0 x 2 +a 2. [ANDA] [JUN-B] Se sabe que la función f:(-1,+ ), definida por f(x) = es continua en (-1,+ ). x+1](/thumbs/80/80474947.jpg) Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
Selectividad CCNN 004. [ANDA] [JUN-A] Considerar la función f: definida por f() = (+)(-)(-). (a) Hallar las ecuaciones de las rectas tangente y normal a la gráfica de f en el punto de abscisa =. (b) Determinar
ANÁLISIS. d) No, se podrían haber considerado infinitas funciones diferenciadas en una constante.
 Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 04 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 04 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar.
 C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
Hacia la universidad Análisis matemático
 Hacia la universidad Análisis matemático OPCIÓN A. a) Deriva las funciones f( ) = 8, g ( ) =, h ( ) = e. f( ) si 0 b) Indica si la función m ( ) = es continua en =. g ( ) si < c) Escribe la ecuación de
Hacia la universidad Análisis matemático OPCIÓN A. a) Deriva las funciones f( ) = 8, g ( ) =, h ( ) = e. f( ) si 0 b) Indica si la función m ( ) = es continua en =. g ( ) si < c) Escribe la ecuación de
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6 1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg) ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
Aplicaciones de la derivada.
 Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
6 si x -4 (x+2) 2 si -4 < x -1 4 si x > x+1 si 0 x 1 x si 1 < x < 3 6-x si 3 x 4
 . Calcula la derivada de las siguientes funciones:. y = 2-2 +2 2. y = 2-2 2 +2. y = 2 -ln +e 4. y = 2 e 2 5. y = e 6. y = 2 ln 2 7. y = 2-8. y = e. y = 2 + 4. y = ln 2-5. y = 2 2 2 6. y = 2-9. y = e 2
. Calcula la derivada de las siguientes funciones:. y = 2-2 +2 2. y = 2-2 2 +2. y = 2 -ln +e 4. y = 2 e 2 5. y = e 6. y = 2 ln 2 7. y = 2-8. y = e. y = 2 + 4. y = ln 2-5. y = 2 2 2 6. y = 2-9. y = e 2
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2017 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 017 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 017 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
x 2-4 intervalos de crecimiento y decrecimiento, sus máximos y mínimos, sus intervalos de concavidad y convexidad y sus puntos de inflexión.
 . [ANDA] [JUN-A] De la función f: definida por f() = a 3 +b +c+d se sabe que tiene un máimo en = -, que su gráfica corta al eje O en el punto de abscisa = y tiene un punto de infleión en el punto de abscisa
. [ANDA] [JUN-A] De la función f: definida por f() = a 3 +b +c+d se sabe que tiene un máimo en = -, que su gráfica corta al eje O en el punto de abscisa = y tiene un punto de infleión en el punto de abscisa
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
 1 de 7 Manizales, 08 de Octubre de 010 1.- La temperatura T, en grados centígrados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la epresión: T t t t con
1 de 7 Manizales, 08 de Octubre de 010 1.- La temperatura T, en grados centígrados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la epresión: T t t t con
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS
 REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
PAU: Aplicaciones de la derivada MATEMÁTICAS II 1. 2cos. x 0 x 0
 PAU: Aplicaciones de la derivada MATEMÁTICAS II JULIO 0 ESPECÍFICA. Calcule a para que las siguientes funciones: sen a cos f( ) g() tengan el mismo límite en el punto 0. Calculamos cada límite: sen a 0
PAU: Aplicaciones de la derivada MATEMÁTICAS II JULIO 0 ESPECÍFICA. Calcule a para que las siguientes funciones: sen a cos f( ) g() tengan el mismo límite en el punto 0. Calculamos cada límite: sen a 0
LA RECTA. Recuerda: Ejercicios de autoaprendizaje 1. Sea la gráfica siguiente:
 LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE
 DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Matemáticas II TEMA 9 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Propuestos
 Matemáticas II TEMA 9 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Propuestos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión
Matemáticas II TEMA 9 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Propuestos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 29-OCTUBRE-1996. (1) 2x 3 > 4.
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 9-OCTUBRE-199 1) 3 > 4. +1 ) Sea la función 3 si 1 a + b si 1 . Encontrar los valores de a, b, c para que la función
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 9-OCTUBRE-199 1) 3 > 4. +1 ) Sea la función 3 si 1 a + b si 1 . Encontrar los valores de a, b, c para que la función
Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos
 página 1/12 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos Hoja 26. Problema 1 1. a) Calcula el número real m que cumple lim 0 ln(1+m ) sen(2 ) =. b) Obtener
página 1/12 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos Hoja 26. Problema 1 1. a) Calcula el número real m que cumple lim 0 ln(1+m ) sen(2 ) =. b) Obtener
Ejercicios Resueltos de Derivadas y sus aplicaciones:
 Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
Ejercicios Resueltos de Derivadas y sus aplicaciones: 1.- Sea la curva paramétrica definida por, con. a) Halle. b) Para qué valor(es) de, la curva tiene recta tangente vertical? 2.- Halle para : a) b)
PROBLEMAS DE RECTA TANGENTE. 6 en el punto de abscisa 2. Halla la ecuación de la recta tangente a. ( en el punto de abscisa. x 3x
 PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
Construye la gráfica de las funciones propuestas a continuación, y estudia el signo de las mismas: (h)
 Construye la gráfica de las funciones propuestas a continuación, y estudia el signo de las mismas: (a) y 6 ; (b) y ( )( ) + ; (c) (e) y + 6 ; + 4; (d) y ( ) 9 + 5 5; (f) 4 y y 9 ; ; (h) y ( + ) ; 4 (g)
Construye la gráfica de las funciones propuestas a continuación, y estudia el signo de las mismas: (a) y 6 ; (b) y ( )( ) + ; (c) (e) y + 6 ; + 4; (d) y ( ) 9 + 5 5; (f) 4 y y 9 ; ; (h) y ( + ) ; 4 (g)
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN
 BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN Crecimiento y decrecimiento. Extremos absolutos y relativos. Concavidad y convexidad. Asíntotas.
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE. ESTUDIO DE LA GRÁFICA DE UNA FUNCIÓN Crecimiento y decrecimiento. Extremos absolutos y relativos. Concavidad y convexidad. Asíntotas.
x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =
![x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) = x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =](/thumbs/76/74425342.jpg) Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
1 (a) Cortes con los ejes. (b) Intervalos de crecimiento y decrecimiento. (c) Máximos y mínimos, si los hay.
 http://www.jezasoft.co.cc 1 de 7 TALLER 0 DE APLICACIONES DE Manizales, 05 de Septiembre de 010 1. La temperatura T, en grados centígrados, que adquiere una pieza sometida a un proceso viene dada en función
http://www.jezasoft.co.cc 1 de 7 TALLER 0 DE APLICACIONES DE Manizales, 05 de Septiembre de 010 1. La temperatura T, en grados centígrados, que adquiere una pieza sometida a un proceso viene dada en función
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES. 2.- La suma de dos números es 15 y su producto es 26. Cuáles son dichos números?
 RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO
 EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Matemática I - Problemas de Máximos y Mínimos
 Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
, hallar su dominio, los puntos de corte con los ejes y la pendiente de la recta x 2-4 tangente a la gráfica de la función en x = 1.
 . [04] [ET-A] El beneficio semanal (en miles de euros) que obtiene una fábrica por la producción de aceite viene dado por la función B(x) = -x +6x-8, donde x representa los hectolitros de aceite producidos
. [04] [ET-A] El beneficio semanal (en miles de euros) que obtiene una fábrica por la producción de aceite viene dado por la función B(x) = -x +6x-8, donde x representa los hectolitros de aceite producidos
TEMA 10. CÁLCULO DIFERENCIAL
 TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
tiene un máximo relativo en x = asíntota horizontal la recta y = 3. Razonar si para a = 2 y b = 3 la función f(x) tiene algún mínimo relativo.
 Selectividad CCNN 006. [ANDA] [SEP-A] Sea f: la función definida por f() = -. a) Estudia la derivabilidad de f. b) Determina los intervalos de crecimiento y decrecimiento de f. c) Calcula los etremos relativos
Selectividad CCNN 006. [ANDA] [SEP-A] Sea f: la función definida por f() = -. a) Estudia la derivabilidad de f. b) Determina los intervalos de crecimiento y decrecimiento de f. c) Calcula los etremos relativos
derivable en x = 0. b) Para los valores encontrados, calcula la ecuación de la recta tangente a la gráfica de f(x) en el punto de abscisa x = 0.
 . [04] [EXT-A] a) Calcula los intervalos de concavidad y conveidad de la función f() = - +. Estudia si tiene puntos de infleión. b) En qué puntos de la gráfica de f() la recta tengente es paralela a la
. [04] [EXT-A] a) Calcula los intervalos de concavidad y conveidad de la función f() = - +. Estudia si tiene puntos de infleión. b) En qué puntos de la gráfica de f() la recta tengente es paralela a la
9. Rectas e hipérbolas
 08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
