1- Halla dos matrices cuadradas de orden dos y no nulas, de modo que su producto sea la matriz nula
|
|
|
- Gregorio Roldán Segura
- hace 7 años
- Vistas:
Transcripción
1 ÁLULO TRIIL DETERINNTES- - Hll dos ices cudds de ode dos o uls, de odo que su poduco se l i ul Po ejeplo: - L i es de ode, l es, lcul l diesió de l i p que se u i cudd,,,,, Necesiee = p que se pued eli el poduco = p que el poduco fil se u i cudd, - opueb que u i escl cou co culquie i de su is diesió s co u ejeplo l se de u copobció - opueb que el poduco de ices veific l popiedd sociiv uilido ls ices: = - ; = - ; = - Solució: - opueb que dd u i cudd, ls ices +, so siéic isiéic especivee U i es siéic si coicide co su spues:, es siéic U i es isiéic si coicide co l opues de su spues:, es isiéic - lcul ls poecis eésis de ls ices: = ; =, bs co copob que se veific p =, =, supoe cie copob que se veific p + éodo de iducció cople
2 - lcul e eles p que l i veifique l ecució: + + I = siedo Solució: ; - lcul ods ls ices que cou co l i del eio ejecicio Solució:, iguldo eleeos, gupdo siplificdo éios, obeeos el sise: Ls ices buscds so ods ls de l fo:, - Siedo, es ices culquie,copueb si so cies ls elcioes siguiees: Si = eoces = b + - = - c + = + + Solució: No es cie que po ejeplo Sólo seí cie si que b No es cie que Seí cie si = c No es cie po l is ó que l eio, l o couividd del poduco de ices - Se l i de ode dos l que ij =i+j- Hll ods ls ices que veifique siuláeee ls elcioes b c del ejecicio eio Solució: L i es uscos po o ods ls ices que cou co, eoces se
3 veificí ls elcioes b c del poble eio: de l ª l ª ecució se lleg Susiuedo po e l ª ecució se obsev que es es idéic l ª, que después de siplific os qued Teeos po o dos ecucioes p esolve u sise de cuo icógis, cu solució seá: l i buscd es:, - Dds ls ices : = ecucioes iciles : - ; = - ; = esuelve ls siguiees - X = ; b X = ; c X - X = I ; d X + = es de ope, despejos l i X, e fució de ls ices poduco sus ivess be ecod, que u i po su ives es igul l i uidd: - = I X = - X = - X = - - X = - - X = - - P el cálculo de l ives copobeos que el deeie de l i se de e cso coio o eise l ives co seguido hllos l i dju de l i l spues de l dju L i ives equivle l spues de l dju, pido po el deeie de l i = + = dj = [ dj ] = = + = dj = [ dj ] = - / / = - / / = / / / / X = = b X X c X - X = I X I X - =
4 - = X d X+ = X = - - X= - - X= - - X X - Deues que si es u i de ode ip isiéic su deeie es ulo Solució: Si es isiéic oo, u i isiéic veific, si es ip - opueb que si es u i cudd puede descopoese e su de u i siéic ás o isiéic s co copob que culquie i cudd puede escibise de l fo: su de siéic isiéic especivee - lcul los deeies siguiees: c - - b - b c d Solució: Desolldo po los djuos de l cu fil ods ls ices so igules odedo: d c b b c d b
5 c Resos cd colu de l eio FFF F F F F F F F F F El desollo eio es válido p clcul culquie deeie de l fo deeies de ices cuos eleeos so: ij ij si i j b si i j b b b b b b es deci - opueb si iee ives,siedo: = Solució : Teiedo e cue que: que, coo u i iee ives si solo si, po lo o es ivesible Si e hce ilusió clcul l poeci eési, es és: - Dds ls ices = = = - esuelve l ecució icil: - - X - X = Solució: X X X X X ; ; ; coo, clculos su ives:
6 X - Los úeos,,,, so divisibles po Deues que el deeie: bié es divisible po Solució: plicdo l popiedd que dice que si se susiue u fil de u deeie po su su co u cobició liel del eso, el deeie que se obiee coicide co el iicil: = U ve elido eso, podeos sc, plicdo l popiedd que dice que p uliplic u úeo po u deeie, bs co ulipliclo po u líe = = l se u deeie fodo po úeos eeos u º eeo, el deeie ddo es divisible po, - Se coside l i: = ; lcul el vlo de "" p los que l i o iee ives, clcul l ives p = Solució: lculos su deeie: NO iee ives eoces p los vloes = = L ives p = es - Escibe dos codicioes disis cd u de ells equivlee que u i se ivesible Es ivesible l i =? P que u i se ivesible o egul, su deeie iee que se cudd iee que se difeee P que u i cudd se ivesible o egul, el go de l i debe se igul su diesió es ivesible si el go = Es ivesible
7 - lcul - si = ºlculos el deeie de copobos que es disio de ceo = - es igul ºlculos l i dju de dj = ºlculos l i dju spues dj ºObeeos que dj - Sbiedo que l i iee po deeie -, clcul el deeie de l i + + +, el deeie de l i ives de Teiedo e cue que: = - Se l i = Hll los vloes eles de p los que iee ives L i es igul / ives p L i es, Hll l i Y cudd de ode que es solució de l ecució icil: Y + = I siedo l i eio p =, I l i uidd es l i
8 Y I Y I Y I dj dj ; ; Y Y Y - Deues, si desoll, que el vlo del deeie N es úliplo de Hciedo = = lo cuál idic que es úliplo de - De u i cudd se sbe que die ives Qué se puede fi del deeie de? Y del go de? Ro l espues Ve poble º - Dd l i, esudi l eiseci de su ives segú los vloes del páeo hll l ives p = Lo pieo que eeos que hce es hll veific que es disio de = + = = ; = - Esos dos vloes so los que hce el deeie =, po lo o eise l ives p odos los vloes de ecepo - E el º pdo os pide hll l ives p = Lo º que h que hce es susiui po e l i hll el deeie = = +---+= -; ho h que hll l dju dj = No*: ecod cbi el sigo de los djuos,, dj El siguiee pso es hll l spues de l dju =
9 Po úlio l ives es: = - osideos ices de ode co = = - lcul, jusificdo l espues, go de, go de,, -, -,,, El go de l i seá; =, que su deeie es disio de El go de l i seá; =, que su deeie es disio de, que e deeies - U i cudd iee l popiedd de que I dode I es l i uidd Deos que die ives, obeel e fució de I I I I l se el poduco de dos ices l uidd, podeos fi que so ivess, es deci I Dd l i, hll p que vloes de se veific que I, p esos vloes escibi l i ives de I b, b
10 lcul el go de l i e fució de Lo pieo que eeos que hce es hll el deeie de l i: R = R = - - R = Ese deeie iguldo ceo iplic que se: = b = l se ls es fils popocioles c = - osideos l i lcul e fució del páeo, ls ices X de l fo X que veific: X X El pie pso seí susiui e l iguldd que os d p sbe cóo debeos segui : = Relios l uliplicció p obee ecucioes que podos igul ee sí = Dichs ecucioes igulds so: + = ; + = + = ; + + = - + = + ; = - + = + ; - = l se igules l pie l cu ecució, os deshceos de u de ells, quedádoos po o: + = + + = = o ello, epsdo l eoí que Toño o os epie, sbeos que es u sise hoogéeo que los éios idepediees so, siepe iee solució siepe so copibles que, l eos, eise l solució ivil P clcul los vloes de, cu e cosecueci, hllos el deeie de ese sise hoogéeo que es obuvios
11 = = ; = l esolve es ecució de ece gdo os qued coo solucioes : = - = Discusió del sise po el Teoe de Rouché Föbeius: * Siepe que o se i - i X = que el sise es hoogéeo, es es l lld solució ivil * udo = - el sise de ecucioes ps se: = = = l se ods ls ecucioes igules, deducios que =, lo que iplic que X = = odo odo peeeciees los úeos eles * udo = Los sises seá: + = + = - + = De hí scos que: = - +=; = Lo que iplic que: X = Y sí, po fi, cbseis el poble! Suee co los deás! p - Se u i cudd de ode dos veificdo que = lcul odee los vloes del deeie de Solució:, si llos - Dds ls ices, hll p qué vloes de l i o iee ives Solució : Susiuios l epesió + po sus ices coespodiees: uliplicos l i po : Suos ls dos ices clculos el deeie de l i esule: P que o eis l i ives el deeie de es iee que se po lo que hceos l epesió eio igul hllos los vloes que hce que = Dividiosod l ecució ee- - -,
12 - Si los deeies de ls ices cudds de ode es so igules, clcul el deeie de Eise l i ives de? Si No eise po lo o i ives - Se, X es ices cudds del iso ode que veific l elció I X, siedo I l i uidd Si el deeie de vle - el de vle, clcul odee el deeie de X Solució: I = ; X = I X = I - X = X = - b lcul de fo od l i X si Solució: X = I - X = - I X = - X - = - I - X = - - dj dj X - lcul odee l i sbiedo que se veific l iguldd: Despejos : I I - Eco ods ls ices b que veifique l iguldd b b b b b b udo heos susiuido, pocedeos uliplic ls ices, coo hs esudido ucho, sbás poque e quedá ls siguiees ecucioes: + = - + b
13 = - + b + = - + b b = - + Si e ds cue, ho solo iees que despej ls ecucioes que hs obeido, p hll el vlo de b de l i : = - + = = b + = -b + = b = -b + = b = b + = b = L i pedid es - lcul el go de l i Solució: P hll el go de l i hllos su deeie pi de sus djuos: = = = --++ = - = * o esá l, peo ie esolve el poble po Guss o l eos hce lgú ceo ás - Se ices cudds co Ro cuáo vle el deeie de l i - - Dd l i, deei p que vloes de eise - P = - esolve I siedo I l i uidd iee ives R dj dj ;
14 I cuo deeie es, l igullo ceo,, - Si es u i de ode l que = = I, clcul = = -I -I = - - +I= - +I=I =I - Dds ls ices P, hállese l i sbiedo que: P - P = Solució: Pieo clculos l ives de l i P P ello, debeos clcul l spues de su dju P P dj dj P uliplicos bos ldos de l iguldd po P - po l deech, po P po l iquied: PP PP PP - Se u i cudd cuo deeie vle, se l i lcúlese el deeie de - Se iee u i cudd de ode cus colus so especivee, cuo deeie vle Se coside l i cus colus so, +, lcúlese odee el deeie de - e el cso de que eis es i,,,,,, L ª colu es fod po dos sudos descopoeos el deeie e su de dos, el º de los cules es ceo po ee dos colus popocioles
15 ,,,,, iecbios ho co después co, co lo que el deeie cbi dos veces de sigo qued igul El deeie de es - = -, el de su ives - Dd l i, hállese u i X que veifique l ecució X+ = - Lo pieo que hceos es dej l icógi u ldo de l ecució: X X ho uliplicos los dos iebos de l ecució po : X I X El siguiee pso es hce l ives de =/ : Hllos el deeie: / / = / Hllos l dju: / / / / dj Y po lo o l ives seí: / / / / / = / * / / / / / / / / ; / / - Dds ls ices,, hállese ls ices X que sisfce X Solució: I X I X bosiebos: e po uliplicdo X X X
16 O fo ás coplicd b c d e f h i j b c b c c b c d e f e f f d e f o h i j i j j h i j X X esigul l i ideidd I - Se u i de colus, deeie Se o i de deeie Si es l i de colus, clcúlese el deeie de l i b = c d plicdo popieddes de los deeies,,,, colus popocioles = = = = = = b - Se l i lcúlese el deeie de sbiedo que I dode I es c l i ideidd es l i ul b b b bc c c c b bc b b bc b ; ; c c c c ; c c ; c b bc b ; ; b b ; O fo : Po se e I dos ices que cou Id I b b b b, esolviedo qued ls iss c c c solucioes - Discúse, segú el vlo de, el go de l i
17 Solució: = = Rgo = si Rgo = - Se Deeíese los vloes de p los cules I o es iveible dode I deo l i ideidd lo que se efiee el poble es que hlleos el/los vloes de p que l su s el poduco de I po l i esuldo o se iveible, o se que su deeie se - Hállese ls ices cudds de ode, que veific l iguldd: Solució Se L ecució eio puede escibise: uliplicdo obeeos el sise: del cul = ; = ; puede o culquie vlo el L i es, SISTES DE EUIONES LINELES - -Discue esuelve: = = Es u sise hoogéeo poque los éios idepediees so El deeie de es i sbeos que es poque si vos esdo l segud colu de l ece l pie de l segud veos que ls dos úlis colus os qued de uos Y cudo u i iee dos de sus El go colus de es igules i el vle deeie poque vle sbeos que si elios el deeie del o deeie de ode que e ese cso es es igul, po lo o sbeos que o es de go Si seguios elido los deeies de ls subices de ode que h e el deeie, os ecoos co que l pie de ells es disi de, co lo cul, sbeos que l i es de go
18 oo el go de o coicide co el úeo de icógis, sbeos que esos e u Sise opible Ideeido úeo de icógis go de l i = = Poeos ho ods ls icógis e fució de : Resolveos el sise: - Discue esuelve, si es posible, el sise: Poeos el sise e fo icil i de ode ; ; SD Usdo e, hllos,, - Discui esolve, si es posible, el sise Sise e fo icil ; Hllos el deeie de, que es l
19 álculo de los gos de ls ices p pode discuils ios los vloes de q igul =, de es e, el = P que el deeie de se, ; sos de esudio: Discusió Es u Sise opible Deeido; = = Es u sise Icopible; < Sbeos que = e = -/ poque Resolució Lo hceos po e e fució del vlo de, siepe que o se = -/ X Y - Discúse el sise e fució del vlo de : E pie lug epesos el sise e fo icil hllos el deeie de, i de ode /,, quí pece opcioes : SD, :
20 SI : SI b P el vlo =, hállese, si pocede, l solució del sise: SD quí plicos e hllos,, : - Discue esuelve el siguiee sise Discusió del sise: º Pleo l i coespodiee l sise: =, disiguiedo ls es pies colus coo l i, el cojuo de l i co l plició de l uli colu, coo l i plid º Hllo el deeie de l i, p pode obee el go: = => = º oocido el deeie de, deduco que: udo =, que el go se defie coo el ode del eo o de u i cuo deeie se disio de sí, el bié seá, poque l i, es u eo de l i
21 Ddo que el úeo de icógis,, es ; podeos lleg l coclusió de que es u sise copible deeido: == Teoe de Rouché b Susiuios el vlo de = e l i iicil: = hllos el deeie de u eo p clcul el go el deeie de es i d, segú lo clculdo eioee edie el eo, podeos deei que el =, cudo = P hll el, oeos el eo, cuo deeie, coociedo sí el = Si, podeos fi que p =, el sise es icopible Teoe Rouché Resolució del sise copible deeido, edie l Regl de e, que cosise e susiui l colu de l i dode se hll l icógi despej, po l i del éio idepediee, hll el deeie de és i esule dividilo po el deeie de l i iicil: P = es u sise icopible, po lo que o iee solució - Discue esuelve Pieo eeos l i de los coeficiees l plid Hllos el deeie de que es ceo; Lo igulos ceo p cooce los vloes de p los Si ;, ; D S Ls solucioes so: ; ; Si ; ; ;, I S Si ; ; ; que los eoes de ode es se ul Resolveos e fució de icógis- go coú, I S, ;
22 páeo educció ; ; ; ; -Discui esolve: + + = = + + = Solució: Lo pieo que h que hce es poe el sise e fo icil: = ; = ho eeos que clcul los gos de ess dos ices po lo que ios los vloes que hí el deeie de, de es fo sbeos que odos los vloes de eos dichos vloes so los que hce su go Iguldo ceo despejdo l ecució os qued que luego el deeie de seá disios de su go seá El go de e ese cso bié seá l ee sólo fils, po lo o seá u sise copible iee iso go deeido h iso ueo de icógis que de ecucioes - P = - = ;= Y sbeos que el deeie de os dá ceo po lo que su go o podá se es e ese cso es dos que cogiedo los vloes cuo deeie os d es deci disio de po lo que el go de seá ho eeos que clcul el go de p ello eeos es opcioes disis depediedo po quie susiuos l colu de los éios idepediees Yo vo coge u copleee l : oo po ejeplo: cuo deeie es:,es deci disio de po lo que el go de es si os hubiese ddo ceo debeíos ie co ls os dos opcioes copob que bs db poque co que solo h u el go es De odo eso cocluios que los gos de so disios po lo que ese sise p es u sise icopible - P = ; =
23 oo ocue e el cso eio sbeos que el go de o puede se po lo que coo ucho el go de seá coo de hecho es si cogeos cuo deeie es, coo se hbá ddo cue los s vispdos ie ho eeos que clcul el go de p lo que plicos ls iss egls que l ve eio o he cogido es i l cuo deeie es Luego el go de es disio del de que es po lo que el sise es icopible + = - + = ++ + = + Solució ;, es u siscopible de e ; h posibiliddes ; oosel isode e iedeode dees, polo que ; ; ;edeosquedejloodoe fuciódeu páeo SISTE OPTILE INDET
24 ; ; ; le Esusiseicopib - Resolve discui el sise: L i del sise es = = = = - ++ Eoces: = si sólo si = -, ó =, luego: Si -, eoces el go de es, luego el sise es copible deeido, sus solucioes so: - - = - = - = Si =- el sise es: ; el = que culquie eo de ode que escojos es disio de ceo Sise INOPTILE Si = el sise es: cosidedo que: ; ;, el go de es el sise es OPTILE INDETERINDO
25 = - = + + = Solució: = ; = = = = º de icógis SIST OP DETERINDO Resolveos: ; ; = = ;ogeos u eo = : = SISTE INOPTILE - + = = - Discue esuelve + = = F F - F ; Esudio: = < Sise Icopible b = = = Sise opible Deeido icógis
26 - + = + + = ; ; ; + = ; ; ; ; ; ; c= ; F F F ; F F F =, = Sise opible Ideeido icógis R ; - Respode odee ls siguiees cuesioes: uál es el go de l i de los coeficiees de u sise co cuo ecucioes es icógis, si iee ls solucioes,-, -,,? Si h ás de u solució el sise es op Ideeido po lo que el go de l i de los coeficiees iee que se igul l de l i plid eo que el º de icógis b El cojuo solució de u sise de es ecucioes co dos icógis puede se el iso que el de u sise co cuo ecucioes es icógis? Y que el de u sise de cuo ecucioes co dos icógis? E el pie cso o es el iso cojuo solució ddo que e el segudo sise de ecucioes lieles h u icógi ás que e el pieo E el segudo cso si puede se el iso cojuo solució ddo que h igul úeo de icógis l ecució sobe puede se cobició liel de ls os c U sise de es ecucioes co cuo icógis puede ee solució úic? No Seá copible ideeido que l eos es icógis depede de u cu d Si u sise de cuo ecucioes lieles iee ls solucioes,, -,,- se puede segu que es copible deeido? Si iee ás de u solució, iee ifiis seá copible ideeido - De los siguiees sises li l copibilidd esuelve los que se deeidos: + = = + + = + = = = + = = = = = Si el deeie de l i de ode es igul, eoces su go es o iee poco cobicioes lieles =
27 : = ++---= = = ; =; = Sis opible ideeido - = - = b = = - disio de = : = -+--+= [disio de ] = = ;= =: Sis copible deeido: = = = = ; = = c = +-+++= disio de = : = disio de = = = = Sis op Deeido: = = = = = = - Hll p que vloes del páeo o es posible plic l egl de e l sise:
28 P plic e eeos que copob que el úeo de ecucioes el de icógis se el iso que el deeie de l i de los coeficiees se disio de ceo Hceos ² ² - osideos el sise Deos que uc puede se copible deeido lcul los vloes de p los que es icopible lcul los vloes de p los que es copible ideeido U sise de es ecucioes co es icógis es copible deeido si sólo si el deeie de l i de los coeficiees es disio de ceo e FFF po ee dos fils igules El sise uc puede se copible deeido Seá icopible si el o coicide co el lculos los eoes de ode es de l i plid: ; P que el se, bs co que u solo eo de los eioes se disio de ceo, es deci,, o o, P que se copible ideeido los es eoes eioes h de se siuláeee - Se coside el sise de ecucioes lieles = + + = =, discúelo = º lculos el deeie de ; u ve hlldo os d de esuldo p culquie vlo de Po o heos deosdo que l i o es de go
29 º Escogeos u i cudd cuo deeie os de disio de N= escogid N iee coo deeie: N = -, po lo o = si L i Teiedo e cue que ls colus de l i so popocioles, el úico eo que podí se disio de ceo es el fodo po,,, siedo su deeie = Es deci, el go de coo o puede se eo que el de es bié p culquie vlo de, l coicidi los gos de de se ése eo que el º de icógis, el sise seá siepe copible ideeido P = ls es colus de so popocioles po lo que = el = Sise Icopible - Discúse el sise, e fució del vlo de b P el vlo, hállese, si pocede, l solució del sise - Se u úeo el osidéese el sise de ecucioes lieles Discúse segú los vloes de e iepéese geoéicee el esuldo b Resuélvse el sise p º Se hll el deeie de siedo l i si los éios idepediees p sbe ls icógis ; = =- º Se hll el go de de siedo l ie fució de de Sise opible Deeido º Resolve el sise p = p =- = Sise opible Ideeido =- ; b Siedo = el sise se esuelve po RER Sise Icopible =
30 = = - - Se ls ices,,, D E T T Hll l i dode idic l i spues de Es ivesible? puo b Hll el go de l i T D, puos c lcul que veifique l ecució T E ; p que se ivesible su deeie iee que se disio de ceo coo NO ES INVERSILE D es u i disi de ceo SU RNGO ES Desolldo l epesió obeeos Iguldo eleeo eleeo obeeos u sise de ecucioes co es icógis que esolveos cu solució es: - Se coside el sise, dode es u páeo el Discui el sise e fució del vlo de puos b Resolve el sise p puo ; ; ; / ; /
31 = = = SD = = ; SI = / = / = / SI = b - = páeos = =>
b) (1 punto) * = * Al intercambiar la posición de dos líneas (filas o columnas), el determinante cambia de signo
 Modelo. Ejecicio. lificció máim puos Siedo que el vlo del deemie es igul clcul el vlo de los deemies: ) ( puo) ) ( puo). dos co comú e colum duo co comú e colum * * l iecmi l posició de dos líes (fils
Modelo. Ejecicio. lificció máim puos Siedo que el vlo del deemie es igul clcul el vlo de los deemies: ) ( puo) ) ( puo). dos co comú e colum duo co comú e colum * * l iecmi l posició de dos líes (fils
Tema 4. SISTEMAS DE ECUACIONES LINEALES
 Te SISTS D CUCIONS LINLS Sises de res ecucioes co res icógis So de l for: Ls lers i, ij i represe, respecivee, ls icógis, los coeficiees los érios idepediees L solució del sise es el cojuo de vlores de,
Te SISTS D CUCIONS LINLS Sises de res ecucioes co res icógis So de l for: Ls lers i, ij i represe, respecivee, ls icógis, los coeficiees los érios idepediees L solució del sise es el cojuo de vlores de,
TEMA 8: SISTEMAS DE ECUACIONES LINEALES. Veamos cómo discutir y resolver cualquier sistema de ecuaciones lineales.
 loso Feráde Gliá TM : SISTMS D CUCIONS LINLS Veos cóo discuir resolver culquier sise de ecucioes lieles.. DFINICIONS Culquier sise de ecucioes lieles co ecucioes icógis puede escriirse de l siguiee for:
loso Feráde Gliá TM : SISTMS D CUCIONS LINLS Veos cóo discuir resolver culquier sise de ecucioes lieles.. DFINICIONS Culquier sise de ecucioes lieles co ecucioes icógis puede escriirse de l siguiee for:
Sistema lineal heterogéneo: es aquel en el que no todos los términos independientes son nulos. Ej:
 BLOQUE II: Núeros Álger Te : Sises de ecucioes lieles Pági de.- CLSIFICICIÓN DE LOS SISTEMS DE ECUCIONES. Sise liel heerogéeo: es quel e el que o odos los érios idepediees so ulos. Ej: Sise liel hoogéeo:
BLOQUE II: Núeros Álger Te : Sises de ecucioes lieles Pági de.- CLSIFICICIÓN DE LOS SISTEMS DE ECUCIONES. Sise liel heerogéeo: es quel e el que o odos los érios idepediees so ulos. Ej: Sise liel hoogéeo:
TEMA 1. VECTORES Y MATRICES 1.2. MATRICES. OPERACIONES ELEMENTALES
 TEM VECTORES Y MTRICES MTRICES OPERCIONES ELEMENTLES VECTORES Y MTRICES MTRICES: OPERCIONES ELEMENTLES Cocepo de riz Eleeos Tipos de rices Su y difereci de rices Produco de u úero por u riz Trsposició
TEM VECTORES Y MTRICES MTRICES OPERCIONES ELEMENTLES VECTORES Y MTRICES MTRICES: OPERCIONES ELEMENTLES Cocepo de riz Eleeos Tipos de rices Su y difereci de rices Produco de u úero por u riz Trsposició
APLICACIONES DE LAS MATRICES
 PLIIONES DE LS MTRIES Ejercicio nº.- ) Encuenr los vlores de pr los que l ri: no es inversible. Ejercicio nº.- lcul, si es posible, l invers de l ri: Pr los csos en los que. Ejercicio nº.- Hll un ri,,
PLIIONES DE LS MTRIES Ejercicio nº.- ) Encuenr los vlores de pr los que l ri: no es inversible. Ejercicio nº.- lcul, si es posible, l invers de l ri: Pr los csos en los que. Ejercicio nº.- Hll un ri,,
POLINOMIOS, ECUACIONES, POLINOMICAS PROBLEMAS RESUELTOS 1. Dados los polinomios en x sobre R : Encontrar : a) p(x) + q(x), b) p(x) q(x)
 POLINOMIOS, ECUACIONES, POLINOMICAS PROBLEMAS RESUELTOS Ddos los polioios e soe R : p 5 8 q 7 Ecot : p q, c p - q p q Solució : p q 5 7 8 9 5 8 5 7 9 5 6 56 5 65 5 8 7 8 5 p q c p q p q 5 7 8 Detei ls
POLINOMIOS, ECUACIONES, POLINOMICAS PROBLEMAS RESUELTOS Ddos los polioios e soe R : p 5 8 q 7 Ecot : p q, c p - q p q Solució : p q 5 7 8 9 5 8 5 7 9 5 6 56 5 65 5 8 7 8 5 p q c p q p q 5 7 8 Detei ls
SISTEMAS DE ECUACIONES LINEALES
 SISTEMS DE ECUCIONES LINELES Tem : SISTEMS DE ECUCIONES LINELES. Ídice:. Epresió mricil de u sisem de ecucioes lieles.. Méodos de resolució... Resolució por el méodo de l mri ivers... Méodo de Guss...
SISTEMS DE ECUCIONES LINELES Tem : SISTEMS DE ECUCIONES LINELES. Ídice:. Epresió mricil de u sisem de ecucioes lieles.. Méodos de resolució... Resolució por el méodo de l mri ivers... Méodo de Guss...
TEMA1: MATRICES Y DETERMINANTES:
 TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
HOJA 1: CÁLCULO DE RANGOS
 el blog de e de id CSII: ejercicios de rices y deeries pág. HOJ : CÁLCULO DE RNGOS.- Clcul el rgo de ls siguiees rices: 9 b c d e ; b ; c ; d.- Clcul el rgo de ls siguiees rices: b c 9 d e f g h i ; b
el blog de e de id CSII: ejercicios de rices y deeries pág. HOJ : CÁLCULO DE RNGOS.- Clcul el rgo de ls siguiees rices: 9 b c d e ; b ; c ; d.- Clcul el rgo de ls siguiees rices: b c 9 d e f g h i ; b
EJERCICIOS CÁLCULO DEL RANGO
 elblogdeedeid: repso rices y deeries pág. curso - EJERCICIOS CÁLCULO DEL RNGO.- Clcul el rgo de ls siguiees rices: 9 b c d e Solució: ; b ; c ; d.- Clcul el rgo de ls siguiees rices: b c 9 d e f g h i
elblogdeedeid: repso rices y deeries pág. curso - EJERCICIOS CÁLCULO DEL RNGO.- Clcul el rgo de ls siguiees rices: 9 b c d e Solució: ; b ; c ; d.- Clcul el rgo de ls siguiees rices: b c 9 d e f g h i
x que deben ser calculados
 UNIDD 9.- Sistes de ecucioes lieles UNIDD 9: Sistes de ecucioes lieles. SISTEMS DE ECUCIONES LINELES U siste de ecucioes lieles co icógits es tod epresió del tipo:.. Llos: - Coeficietes del siste los úeros
UNIDD 9.- Sistes de ecucioes lieles UNIDD 9: Sistes de ecucioes lieles. SISTEMS DE ECUCIONES LINELES U siste de ecucioes lieles co icógits es tod epresió del tipo:.. Llos: - Coeficietes del siste los úeros
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
A = Héctor Escobar Álgebra Lineal ÁLGEBRA LINEAL: Unidad 1: Álgebra De Matrices. 1. CONCEPTO DE MATRIZ. Una matriz A de
 ÁLGEBRA LINEAL: Hécor Escobr Álgebr Liel Uidd : Álgebr De Mrices.. CONCEPTO DE MATRIZ. U mriz A de A = = m m m es u rreglo recgulr de m fils y colums: m ( ) Nos:. i m ; j b. Si R, eoces A es u mriz rel.
ÁLGEBRA LINEAL: Hécor Escobr Álgebr Liel Uidd : Álgebr De Mrices.. CONCEPTO DE MATRIZ. U mriz A de A = = m m m es u rreglo recgulr de m fils y colums: m ( ) Nos:. i m ; j b. Si R, eoces A es u mriz rel.
TEMA 7. SUCESIONES NUMÉRICAS.
 º EO Tem 7 TEMA 7. UCEIONE NUMÉRICA.. UCEIONE NUMÉRICA. Imgiemos el ecoido que efectú u bló que se h lzdo l suelo y midmos ls distcis ete bote y bote: Ls distcis fom u sucesió de úmeos: 0, 5, 0, 5,. U
º EO Tem 7 TEMA 7. UCEIONE NUMÉRICA.. UCEIONE NUMÉRICA. Imgiemos el ecoido que efectú u bló que se h lzdo l suelo y midmos ls distcis ete bote y bote: Ls distcis fom u sucesió de úmeos: 0, 5, 0, 5,. U
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
BLOQUE DE ÁLGEBRA TEMA 1: MATRICES
 Álgebr Liel Memáics º chillero LOQUE DE ÁLGER TEM : MTRICES U mriz es u cojuo de úmeros reles colocdos recgulrmee ecerrdos ere préesis o corchee o doble brr. Pr or u mriz se uiliz o: u ler myúscul, por
Álgebr Liel Memáics º chillero LOQUE DE ÁLGER TEM : MTRICES U mriz es u cojuo de úmeros reles colocdos recgulrmee ecerrdos ere préesis o corchee o doble brr. Pr or u mriz se uiliz o: u ler myúscul, por
CINEMÁTICA Y DINÁMICA
 T1 CINEMÁTICA Y DINÁMICA Cuesioes C1. Es zoble esilo coo u pícul, poque se coside ls diesioes del uoóil uy pequeñs fee ls logiudes de ls cees. Al esudi el oiieo de oció de ls ueds, y hy que disigui ee
T1 CINEMÁTICA Y DINÁMICA Cuesioes C1. Es zoble esilo coo u pícul, poque se coside ls diesioes del uoóil uy pequeñs fee ls logiudes de ls cees. Al esudi el oiieo de oció de ls ueds, y hy que disigui ee
TEMA 4 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 Te Resolución de sises edine deerinnes Meáics II º chillero TEM RESOLUIÓN DE SISTEMS MEDINTE DETERMINNTES Resolución de sises Regl de rer Teore de Rouché-Froenius EJERIIO Resuelve plicndo l regl de rer
Te Resolución de sises edine deerinnes Meáics II º chillero TEM RESOLUIÓN DE SISTEMS MEDINTE DETERMINNTES Resolución de sises Regl de rer Teore de Rouché-Froenius EJERIIO Resuelve plicndo l regl de rer
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
Operaciones en el conjunto de los números racionales Q
 lsteátics.eu Pedo Csto Oteg teiles de teátics Fccioes. Núeos eles. Potecis. Ríces. º ESO Opecioes e el cojuto de los úeos cioles Q Opeció Su c d bc b d bd Rest (difeeci) c d bc b d bd b) ) Ejeplo 5 5 5
lsteátics.eu Pedo Csto Oteg teiles de teátics Fccioes. Núeos eles. Potecis. Ríces. º ESO Opecioes e el cojuto de los úeos cioles Q Opeció Su c d bc b d bd Rest (difeeci) c d bc b d bd b) ) Ejeplo 5 5 5
EXAMEN DE MATEMATICAS II. Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO Apellidos: Nobe: Instucciones: Cuso: º Gupo: A Dí: CURSO 56 ) Dución: HORA y MINUTOS. b) Debes elegi ente eliz únicente los cuto ejecicios de l Opción A o bien únicente
EXAMEN DE MATEMATICAS II ª ENSAYO Apellidos: Nobe: Instucciones: Cuso: º Gupo: A Dí: CURSO 56 ) Dución: HORA y MINUTOS. b) Debes elegi ente eliz únicente los cuto ejecicios de l Opción A o bien únicente
MATEMÁTICAS II TEMA 1 Matrices: Problemas propuestos
 Álger: Mrices wwwmemicsjmmmcom José Mrí Mríez Medio MTEMÁTIS II TEM Mrices: Prolems propuesos Opercioes co mrices Dds 7, 9 y, hll dos úmeros y pr que se verifique que Dds ls mrices y, hll ors dos mrices
Álger: Mrices wwwmemicsjmmmcom José Mrí Mríez Medio MTEMÁTIS II TEM Mrices: Prolems propuesos Opercioes co mrices Dds 7, 9 y, hll dos úmeros y pr que se verifique que Dds ls mrices y, hll ors dos mrices
INTEGRALES INDEFINIDAS
 INTEGRALES INDEFINIDAS Pág.: ÍNDICE:.- FUNCIÓN PRIMITIVA..- INTEGRAL INDEFINIDA..- INTEGRALES INMEDIATAS...- INTEGRACIÓN INMEDIATA DE ALGUNAS FUNCIONES. 4.- PROPIEDADES DE LA INTEGRAL INDEFINIDA. 5.- MÉTODOS
INTEGRALES INDEFINIDAS Pág.: ÍNDICE:.- FUNCIÓN PRIMITIVA..- INTEGRAL INDEFINIDA..- INTEGRALES INMEDIATAS...- INTEGRACIÓN INMEDIATA DE ALGUNAS FUNCIONES. 4.- PROPIEDADES DE LA INTEGRAL INDEFINIDA. 5.- MÉTODOS
Unidad 5: MATRICES. m x n a todo conjunto de elementos dispuestos en m. La matriz tiene. La Tabla se puede expresar como matriz:
 Uidd : MTRIES º ch M pl SS II Ídice: MTRIES Tipos de Mrices OPERIONES DE MTRIES Sum de Mrices Produco De Mrices Produco de u mriz por u úmero Produco de Mrices Poecis de Mrices MTRIZ TRSPUEST DEPENDENI
Uidd : MTRIES º ch M pl SS II Ídice: MTRIES Tipos de Mrices OPERIONES DE MTRIES Sum de Mrices Produco De Mrices Produco de u mriz por u úmero Produco de Mrices Poecis de Mrices MTRIZ TRSPUEST DEPENDENI
ÁLGEBRA DE MATRICES. * Tenemos aquí el mapa de una ciudad (Konigsberg) que está atravesada por un río sobre el que hay varios puentes:
 º Bchilleto Mteátics II Dvid Miguel del Río IES Euop (Móstoles) Vos coside ls tices coo u disposició ectgul de úeos que cotiee ifoció. Si se quiee es u fo de ode ifoció. Po ejeplo: * Teeos quí el p de
º Bchilleto Mteátics II Dvid Miguel del Río IES Euop (Móstoles) Vos coside ls tices coo u disposició ectgul de úeos que cotiee ifoció. Si se quiee es u fo de ode ifoció. Po ejeplo: * Teeos quí el p de
La Integral Curvilínea
 L Iegl Cuvilíe UNA INTODUCCIÓN BÁICA Ce ÁNCHEZ DÍEZ 0 U iouió L iegl e ie uiiesiol equiee u uió eii oiu soe el ievlo [] e iegió: Cosieo poeos eee el oepo e iegió susiueo el ievlo uiiiesiol po u uv [ ]
L Iegl Cuvilíe UNA INTODUCCIÓN BÁICA Ce ÁNCHEZ DÍEZ 0 U iouió L iegl e ie uiiesiol equiee u uió eii oiu soe el ievlo [] e iegió: Cosieo poeos eee el oepo e iegió susiueo el ievlo uiiiesiol po u uv [ ]
3. SISTEMAS DE ECUACIONES LINEALES
 Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
OPCIÓN A. c) (1 punto)
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Curso / MTERI MTEMTICS II. se de Modlidd OPCIÓN Ejercicio. Clificció ái putos. Sbiedo que, utilizdo ls
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Curso / MTERI MTEMTICS II. se de Modlidd OPCIÓN Ejercicio. Clificció ái putos. Sbiedo que, utilizdo ls
SOLUCIONES DE SISTEMAS, MATRICES Y DETERMINANTES Curso SOLUCIONES DE SISTEMAS, MATRICES Y DETERMINANTES Curso 03-04
 SOLUCIONES DE SISTEMS, MTRICES Y DETERMINNTES Curso - SOLUCIONES DE SISTEMS, MTRICES Y DETERMINNTES Curso - - Comprobr que culquier mriz cudrd M se puede expresr de form úic como sum de dos mrices, u siméric
SOLUCIONES DE SISTEMS, MTRICES Y DETERMINNTES Curso - SOLUCIONES DE SISTEMS, MTRICES Y DETERMINNTES Curso - - Comprobr que culquier mriz cudrd M se puede expresr de form úic como sum de dos mrices, u siméric
Tema 5. DIAGONALIZACIÓN DE MATRICES
 José Maía Maíe Mediao Tema DGONLZCÓN DE MTRCES oducció Poecia de ua mai Sea Supogamos que se desea calcula : 7 7 8 8 Deemia ua egla paa o esula imediao Compobemos, aes de segui adelae, que MDM, siedo M
José Maía Maíe Mediao Tema DGONLZCÓN DE MTRCES oducció Poecia de ua mai Sea Supogamos que se desea calcula : 7 7 8 8 Deemia ua egla paa o esula imediao Compobemos, aes de segui adelae, que MDM, siedo M
Curso Septiembre MATERIA: MATEMÁTICAS II (Fase general)
 Cuso - Sepiebe MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El luno cones los cuo ejecicios e un e l os opciones ( o B) que se le ofecen. Nunc ebeá cones unos ejecicios e un opción
Cuso - Sepiebe MTERI MTEMÁTICS II (Fse genel) INSTRUCCIONES GENERLES Y VLORCIÓN El luno cones los cuo ejecicios e un e l os opciones ( o B) que se le ofecen. Nunc ebeá cones unos ejecicios e un opción
MATEMÁTICAS II - P.A.E.U. ÁLGEBRA LINEAL CUESTIONES
 IES Diego de Siloé - PU Álger Liel - Meáis II Pág MTEMÁTICS II - PEU ÁLGER LINEL CUESTIONES Eorr u ri X que verifique XC siedo: C (J9) Sol: X Deerir ls ries siedo: (S9) Sol: 8 Hllr l poei -ési de l ri
IES Diego de Siloé - PU Álger Liel - Meáis II Pág MTEMÁTICS II - PEU ÁLGER LINEL CUESTIONES Eorr u ri X que verifique XC siedo: C (J9) Sol: X Deerir ls ries siedo: (S9) Sol: 8 Hllr l poei -ési de l ri
TEMA 9: SISTEMAS DE ECUACIONES LINEALES
 MTEMÁTICS II TEM 9: SISTEMS DE ECUCIONES LINELES. Defiició Clsificció U ecució liel de "" icógis,,,,, es u iguldd del ipo:., siedo i úmeros reles coocidos, llmdos coeficiees. i so ls icógis cuo vlor h
MTEMÁTICS II TEM 9: SISTEMS DE ECUCIONES LINELES. Defiició Clsificció U ecució liel de "" icógis,,,,, es u iguldd del ipo:., siedo i úmeros reles coocidos, llmdos coeficiees. i so ls icógis cuo vlor h
PROGRESIONES ARITMÉTICAS
 PROGRESIONES ARITMÉTICAS Se defie como pogesió itmétic u sucesió de úmeos eles,,,...... e los que l difeeci ete témios cosecutivos es costte costte A l difeeci ete témios cosecutivos se le deomi d. Puede
PROGRESIONES ARITMÉTICAS Se defie como pogesió itmétic u sucesió de úmeos eles,,,...... e los que l difeeci ete témios cosecutivos es costte costte A l difeeci ete témios cosecutivos se le deomi d. Puede
Ejercicios y problemas resueltos
 Ejeriios roles resuelos Pági 79. Cálulo de u deerie de orde Hlo ú. Clul el vlor de ese deerie e uió del ráero : Suos ls ils.ª,.ª.ª l.ª: (.ª) (.ª) (.ª) (.ª) (.ª) (.ª) (.ª) El vlor del úlio deerie es igul
Ejeriios roles resuelos Pági 79. Cálulo de u deerie de orde Hlo ú. Clul el vlor de ese deerie e uió del ráero : Suos ls ils.ª,.ª.ª l.ª: (.ª) (.ª) (.ª) (.ª) (.ª) (.ª) (.ª) El vlor del úlio deerie es igul
5. Repaso de matrices. ( Chema Madoz, VEGAP, Madrid 2009)
 . epso de trices he Mdoz, VEGP, Mdrid ) Mtrices Eleeto: ij Tño: Mtriz cudrd: orde ) Eleetos de l digol: Vector colu triz ) Vector fil triz ) ) 8, B ) 8) B Su: ij k k k k k k k k k k k ) Multiplicció por
. epso de trices he Mdoz, VEGP, Mdrid ) Mtrices Eleeto: ij Tño: Mtriz cudrd: orde ) Eleetos de l digol: Vector colu triz ) Vector fil triz ) ) 8, B ) 8) B Su: ij k k k k k k k k k k k ) Multiplicció por
LOGARITMO 4º AÑO DEF. Y PROPIEDADES
 LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
Introducción al cálculo de errores
 Itoducció l cálculo de eoes 1/5 Itoducció l cálculo de eoes Los eoes idetemidos so quellos que se debe l z. Po ejemplo, l eliz l medid de u ms e u blz csi siempe os ofece vloes difeetes debido fctoes ccidetles.
Itoducció l cálculo de eoes 1/5 Itoducció l cálculo de eoes Los eoes idetemidos so quellos que se debe l z. Po ejemplo, l eliz l medid de u ms e u blz csi siempe os ofece vloes difeetes debido fctoes ccidetles.
Sistemas de ecuaciones lineales. Matrices y determinantes curso
 Sisems de ecucioes lieles. Mrices y deermies curso - jercicios resuelos:.- Se y B mrices cudrds de orde. Pror que si I-B es iverile, eoces I-B mié es iverile y que ( I B) I B( I B). No: I es l mriz uidd
Sisems de ecucioes lieles. Mrices y deermies curso - jercicios resuelos:.- Se y B mrices cudrds de orde. Pror que si I-B es iverile, eoces I-B mié es iverile y que ( I B) I B( I B). No: I es l mriz uidd
a a y 1 x Mecánica Segunda Parte (90 minutos) - Hoja 1 de 2 Ejercicio k 41 a i 3 ma 4
 Publicció de Nos: -- Fech de xme: -- 5 ecáic Pime Apellido: ícul: Segudo Apellido: Nombe: NOTA: e el eucido ls mgiudes vecoiles se escibe e egi (V, uque e l solució Vd. ebe epesels co u flech ( V. No se
Publicció de Nos: -- Fech de xme: -- 5 ecáic Pime Apellido: ícul: Segudo Apellido: Nombe: NOTA: e el eucido ls mgiudes vecoiles se escibe e egi (V, uque e l solució Vd. ebe epesels co u flech ( V. No se
UNIVERSIDAD NACIONAL DE INGENIERIA P.A FACULTAD DE INGENIERIA MECANICA 19/10/2011 DACIBAHCC EXAMEN PARCIAL DE METODOS NUMERICOS (MB536)
 UNIVERSIA NACIONA E INGENIERIA P.A. - FACUTA E INGENIERIA MECANICA // ACIBAHCC EXAMEN PARCIA E METOOS NUMERICOS MB6 SOO SE PERMITE E USO E UNA HOJA E FORMUARIO Y CACUAORA ESCRIBA CARAMENTE SUS PROCEIMIENTOS
UNIVERSIA NACIONA E INGENIERIA P.A. - FACUTA E INGENIERIA MECANICA // ACIBAHCC EXAMEN PARCIA E METOOS NUMERICOS MB6 SOO SE PERMITE E USO E UNA HOJA E FORMUARIO Y CACUAORA ESCRIBA CARAMENTE SUS PROCEIMIENTOS
DETERMINANTES. A toda matriz cuadrada se le puede hacer corresponder un número (determinante) cuyo cálculo se puede hacer de las siguientes maneras:
 TEM Deeries DETERMINNTES. DEFINICIÓN. od ri udrd se le uede her orresoder u úero (deerie uo álulo se uede her de ls siguiees ers:.. DETERMINNTE DE SEGUNDO ORDEN. de Es deir es el roduo de los eleeos de
TEM Deeries DETERMINNTES. DEFINICIÓN. od ri udrd se le uede her orresoder u úero (deerie uo álulo se uede her de ls siguiees ers:.. DETERMINNTE DE SEGUNDO ORDEN. de Es deir es el roduo de los eleeos de
TEMA1: SISTEMAS DE ECUACIONES LINEALES
 STEMAS LINEALES TEMA: STEMAS DE ECUACIONES LINEALES. Defiició U ecució liel de "" icógis es u iguldd del ipo:. b siedo i úeros reles coocidos lldos coeficiees. i so ls icógis cuo vlor h que deerir. b úero
STEMAS LINEALES TEMA: STEMAS DE ECUACIONES LINEALES. Defiició U ecució liel de "" icógis es u iguldd del ipo:. b siedo i úeros reles coocidos lldos coeficiees. i so ls icógis cuo vlor h que deerir. b úero
Módulo 7. Exponentes racionales. OBJETIVO Simplificar expresiones algebraicas con exponentes racionales.
 Módulo 7 Epoetes cioles OBJEIVO Simplific epesioes lgebics co epoetes cioles. Hst este mometo se h utilizdo úicmete eteos como epoetes, sí que efetemos ho cómo us otos úmeos cioles como epoetes. Peo tes
Módulo 7 Epoetes cioles OBJEIVO Simplific epesioes lgebics co epoetes cioles. Hst este mometo se h utilizdo úicmete eteos como epoetes, sí que efetemos ho cómo us otos úmeos cioles como epoetes. Peo tes
EXAMEN DE MATEMÁTICAS II (Recuperación)
 º Bchillero Ciencis XN D TÁTICS II Recuperción) ÁLGBR. ), punos) Clsific en función del práero R, el sise de ecuciones: b) puno) Resuélvelo pr, si es posible.. Se un ri cudrd de orden. Si el deerinne de
º Bchillero Ciencis XN D TÁTICS II Recuperción) ÁLGBR. ), punos) Clsific en función del práero R, el sise de ecuciones: b) puno) Resuélvelo pr, si es posible.. Se un ri cudrd de orden. Si el deerinne de
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
1. SISTEMAS DE ECUACIONES LINEALES Es un conjunto de expresiones algebraicas de la forma:
 CRISTIN ROND HERNÁNDEZ Sistes de ecucioes SISTEMS DE ECUCIONES. Sistes de ecucioes lieles. Epresió tricil de u siste. Clsiicció de sistes de ecucioes. Teore de Rouché-Fröeius. Discusió de sistes 6. Método
CRISTIN ROND HERNÁNDEZ Sistes de ecucioes SISTEMS DE ECUCIONES. Sistes de ecucioes lieles. Epresió tricil de u siste. Clsiicció de sistes de ecucioes. Teore de Rouché-Fröeius. Discusió de sistes 6. Método
5 ECUACIONES DIFERENCIALES ORDINARIAS DE ORDEN N
 DINÁMI Y ONTROL DE PROESOS 5 EUIONES DIFERENILES ORDINRIS DE ORDEN N Si ier err e u efoque memáico del em, recordemos que muchos de uesros sisems (y priculrmee odos los que vrí e el iempo) se epresrá como
DINÁMI Y ONTROL DE PROESOS 5 EUIONES DIFERENILES ORDINRIS DE ORDEN N Si ier err e u efoque memáico del em, recordemos que muchos de uesros sisems (y priculrmee odos los que vrí e el iempo) se epresrá como
SISTEMAS DE ECUACIONES LINEALES
 eáics plicds ls Ciecis Sociles José rí ríe edio SISTS D CUCIONS LINLS Sises de res ecucioes co res icógis Defiicioes U sise de res ecucioes lieles de co res icógis, e su for esádr, es u cojuo de res igulddes
eáics plicds ls Ciecis Sociles José rí ríe edio SISTS D CUCIONS LINLS Sises de res ecucioes co res icógis Defiicioes U sise de res ecucioes lieles de co res icógis, e su for esádr, es u cojuo de res igulddes
m m = -1 = μ - 1. Halla la Apellidos: Nombre: Curso: 2º Grupo: A Día: 27 - IV - 15 CURSO Opción A
 S Instrucciones: EXAMEN DE MATEMATICAS II 3ª EVALUACIÓN Apellidos: Nobre: Curso: º Grupo: A Dí: 7 - IV - 5 CURSO 4-5 ) Durción: HORA y 3 MINUTOS. b) Debes elegir entre relizr únicente los cutro ejercicios
S Instrucciones: EXAMEN DE MATEMATICAS II 3ª EVALUACIÓN Apellidos: Nobre: Curso: º Grupo: A Dí: 7 - IV - 5 CURSO 4-5 ) Durción: HORA y 3 MINUTOS. b) Debes elegir entre relizr únicente los cutro ejercicios
Progresiones aritméticas y geométricas
 Pogesioes itétics y geoétics Pogesioes itétics U pogesió itétic es scesió de úeos, tles qe l difeeci ete dos cosectivos clesqie de ellos es costte, po ejeplo, l scesió de los úeos ipes,,, dode l difeeci
Pogesioes itétics y geoétics Pogesioes itétics U pogesió itétic es scesió de úeos, tles qe l difeeci ete dos cosectivos clesqie de ellos es costte, po ejeplo, l scesió de los úeos ipes,,, dode l difeeci
Sucesiones. En resumen podemos decir que: : A R, se llama sucesión, donde an= f(n) en cada caso, y A N
 Mtemátic II Cietífico IDAL 07 Sucesioes 5 Pof. F. Díz- Pof A. Glli Sucesioes E esume podemos deci que: Defiició: U fució f : A R, se llm sucesió, dode = f() e cd cso, y A N :, co A y R. E símbolos: Ejemplos:
Mtemátic II Cietífico IDAL 07 Sucesioes 5 Pof. F. Díz- Pof A. Glli Sucesioes E esume podemos deci que: Defiició: U fució f : A R, se llm sucesió, dode = f() e cd cso, y A N :, co A y R. E símbolos: Ejemplos:
COMBINATORIA. Las variaciones ordinarias se representan por el símbolo Vm,n o por V
 COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
= 41. =, halla los términos primero, quinto, b n
 Sucesioes. 00 Ejecicios p pctic co solucioes E ls sucesioes de témio geel y b, hll los témios pimeo, segudo y décimo. 0 0 b b b 0 0 0 Hll los cico pimeos témios de l sucesió 0 9 9 6 6 Compueb que es el
Sucesioes. 00 Ejecicios p pctic co solucioes E ls sucesioes de témio geel y b, hll los témios pimeo, segudo y décimo. 0 0 b b b 0 0 0 Hll los cico pimeos témios de l sucesió 0 9 9 6 6 Compueb que es el
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
Tema 8: Teorema de Rouché-Frobenius
 www.selectividd-cgrnd.co Te : Teore de Rouché-Froenius Se lln ecuciones lineles ls ecuciones en ls que ls incógnits precen tods con grdo ; no están elevds ningun potenci ni jo ningún rdicl ni ultiplicds
www.selectividd-cgrnd.co Te : Teore de Rouché-Froenius Se lln ecuciones lineles ls ecuciones en ls que ls incógnits precen tods con grdo ; no están elevds ningun potenci ni jo ningún rdicl ni ultiplicds
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. De ete ls sucesioes siguietes deci cuáles so pogesioes itmétics., 8,,, 0,... b., 7,,,... c. 7,, 9,,,... d., 7, 9,,... e.,,,,... f.,,, 9, g.,,,,... h. ( b), ( b), ( b),... Los
PROGRESIONES ARITMETICAS. De ete ls sucesioes siguietes deci cuáles so pogesioes itmétics., 8,,, 0,... b., 7,,,... c. 7,, 9,,,... d., 7, 9,,... e.,,,,... f.,,, 9, g.,,,,... h. ( b), ( b), ( b),... Los
Cálculo con vectores
 Uidd didáctic 1 Cálculo co vectoes 1.- Mgitudes escles vectoiles. So mgitudes escles quells, como l ms, l tempetu, l eegí, etc., cuo vlo qued fijdo po u úmeo (co su uidd coespodiete). Gáficmete se epeset
Uidd didáctic 1 Cálculo co vectoes 1.- Mgitudes escles vectoiles. So mgitudes escles quells, como l ms, l tempetu, l eegí, etc., cuo vlo qued fijdo po u úmeo (co su uidd coespodiete). Gáficmete se epeset
TEMA IV PLANO VECTORIAL. PRODUCTO ESCALAR. APLICACIONES. Un vector fijo es un segmento cuyos extremos vienen dados en un cierto orden.
 VECTOR FIJO TEM IV PLNO VECTORIL. PRODUCTO ESCLR. PLICCIONES. Un vecto fijo es un segento cuyos exteos vienen ddos en un cieto oden. Ejeplo: El segento de exteos y (en este oden). Se not con (, ) ó con.
VECTOR FIJO TEM IV PLNO VECTORIL. PRODUCTO ESCLR. PLICCIONES. Un vecto fijo es un segento cuyos exteos vienen ddos en un cieto oden. Ejeplo: El segento de exteos y (en este oden). Se not con (, ) ó con.
Academia NIPHO Cl. Miguel Fleta, 25 Tel/Fax: MOVIMIENTO CIRCULAR
 Cl. Miguel Fle, 5 Tel/Fx: 978 83 33 6 446-Alcñiz (Te) www.cdemi-ipho.e MOVIMIENTO CICULA Coideemo u yecoi cu y u móil que lecoe ido u elocidd (e módulo) de me uifome. Si queemo clcul el uu eco uu celeció,
Cl. Miguel Fle, 5 Tel/Fx: 978 83 33 6 446-Alcñiz (Te) www.cdemi-ipho.e MOVIMIENTO CICULA Coideemo u yecoi cu y u móil que lecoe ido u elocidd (e módulo) de me uifome. Si queemo clcul el uu eco uu celeció,
PROBLEMAS RESUELTOS DE SERIES DE FOURIER
 PROBLEMS RESUELOS DE SERIES DE FOURIER Ejemplo. Hlle l represeció e serie rigooméric de Fourier pr l siguiee señl f ( e,, mosrd e l figur. SOLUCION. L señl es f ( e,, y pr ese ejemplo: y ω. Primero clculremos
PROBLEMS RESUELOS DE SERIES DE FOURIER Ejemplo. Hlle l represeció e serie rigooméric de Fourier pr l siguiee señl f ( e,, mosrd e l figur. SOLUCION. L señl es f ( e,, y pr ese ejemplo: y ω. Primero clculremos
Vc D 40 N = N = RPM N = 130 RPM. = 0,3(130) a m = 39 mm/min. = = = 2 n = 2 pasadas 2p 2(3)
 TORNOS TIEMPOS DE MAQUINADO PROBLEMAS SOBRE TIEMPOS DE MECANIZADO EN EL TORNEADO ) Se dese cilidrr u iez de 00 00 de logiud (ver figur), r dejrl 88 ilíeros de diáero. L 00 Uilizdo u oro cuy g de velociddes
TORNOS TIEMPOS DE MAQUINADO PROBLEMAS SOBRE TIEMPOS DE MECANIZADO EN EL TORNEADO ) Se dese cilidrr u iez de 00 00 de logiud (ver figur), r dejrl 88 ilíeros de diáero. L 00 Uilizdo u oro cuy g de velociddes
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 3.1. PRACTICA N o 3 VIBRACIONES DE UNA CADENA LINEAL: MODOS ACÚSTICOS Y ÓPTICOS.
 LABORATORO DE ESTADO SÓLDO Y SEMCONDUCTORES 3. PRACTCA N o 3 VBRACONES DE UNA CADENA LNEAL: MODOS ACÚSTCOS Y ÓPTCOS. NTRODUCCÓN Ls vibcioes de los áoos e u ed cisli puede, e deeids codicioes, siilse ls
LABORATORO DE ESTADO SÓLDO Y SEMCONDUCTORES 3. PRACTCA N o 3 VBRACONES DE UNA CADENA LNEAL: MODOS ACÚSTCOS Y ÓPTCOS. NTRODUCCÓN Ls vibcioes de los áoos e u ed cisli puede, e deeids codicioes, siilse ls
Matrices = A. Matriz cuadrada, si tiene el mismo nº de filas que de columnas. ... ... ... ...
 Mtrices Mtrices INTRODUCCIÓN E el te terior heos usdo l tri plid de u siste, pr ejr, co ás coodidd, los úeros que iterviee e u siste liel E otros uchos proles es útil dispoer ejr u cojuto de úeros dispuestos
Mtrices Mtrices INTRODUCCIÓN E el te terior heos usdo l tri plid de u siste, pr ejr, co ás coodidd, los úeros que iterviee e u siste liel E otros uchos proles es útil dispoer ejr u cojuto de úeros dispuestos
La multiplicación de dos armónicos de diferente frecuencia, [ ] [ ]
![La multiplicación de dos armónicos de diferente frecuencia, [ ] [ ] La multiplicación de dos armónicos de diferente frecuencia, [ ] [ ]](/thumbs/84/90185598.jpg) Muliplicció y Divisió de Fucioes Aróics. Frcisco Prr Rodríguez. Docor Ecooí UNED Muliplicció de fucioes róics L uliplicció de dos rói de diferee frecueci, [ ] [ ] ( ( k k j j d lugr l siguiee su: ( ( (
Muliplicció y Divisió de Fucioes Aróics. Frcisco Prr Rodríguez. Docor Ecooí UNED Muliplicció de fucioes róics L uliplicció de dos rói de diferee frecueci, [ ] [ ] ( ( k k j j d lugr l siguiee su: ( ( (
= 001 ( ) La matriz A tiene inversa para cualquier valor que tome el parámetro k. A =, el determinante no depende del parámetro. ( ) t.
 odelo. Ejeriio. Clifiió ái puos. Dds ls ries, se pide ) (, puos) Hllr los vlores de pr los que eise l ri ivers. ) ( puo) Hllr l ri pr. ) (, puos) Resolver l euió riil pr.. L odiió eesri sufiiee pr que
odelo. Ejeriio. Clifiió ái puos. Dds ls ries, se pide ) (, puos) Hllr los vlores de pr los que eise l ri ivers. ) ( puo) Hllr l ri pr. ) (, puos) Resolver l euió riil pr.. L odiió eesri sufiiee pr que
PROBLEMAS RESUELTOS DE SERIES DE FOURIER
 PROBLEMS RESUELOS DE SERIES DE FOURIER Ejemplo. Hlle l represeció e serie rigooméric de Fourier pr l siguiee f, mosrd e l figur. señl () e, SOLUCION. L señl es f () e,, y pr ese ejemplo: y ω. Primero clculremos
PROBLEMS RESUELOS DE SERIES DE FOURIER Ejemplo. Hlle l represeció e serie rigooméric de Fourier pr l siguiee f, mosrd e l figur. señl () e, SOLUCION. L señl es f () e,, y pr ese ejemplo: y ω. Primero clculremos
Tema 10: Espacio Afin Tridimensional
 www.selecividd-cgrnd.co Te Espcio Afin Tridiensionl Se ll sise de referenci del espcio fín E l conjuno (O, u, u, u ). Siendo O un puno de E u, u, u res vecores libres que forn un bse de V. Ls recs OX,
www.selecividd-cgrnd.co Te Espcio Afin Tridiensionl Se ll sise de referenci del espcio fín E l conjuno (O, u, u, u ). Siendo O un puno de E u, u, u res vecores libres que forn un bse de V. Ls recs OX,
Definición. una sucesión, definimos la sumatoria de los n primeros
 MATEMATICA GENERAL 00, HERALDO GONZALEZ S SUMATORIAS Suto sle Defcó U sucesó el es tod fucó co doo u sucouto de los úeos tules y co vloes e, sólcete, l sucesó es : N tl que Osevcó Deotos l sucesó o N,
MATEMATICA GENERAL 00, HERALDO GONZALEZ S SUMATORIAS Suto sle Defcó U sucesó el es tod fucó co doo u sucouto de los úeos tules y co vloes e, sólcete, l sucesó es : N tl que Osevcó Deotos l sucesó o N,
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDDES ÚBLIS DE L OMUNIDD DE MDRID RUEB DE ESO ESTUDIOS UNIVERSITRIOS (LOGSE) JUNIO INSTRUIONES GENERLES Y VLORIÓN El lumo coeá lo cuo ejecicio e u e l o opcioe ( o B) que e le oece. Nuc ebeá coe
UNIVERSIDDES ÚBLIS DE L OMUNIDD DE MDRID RUEB DE ESO ESTUDIOS UNIVERSITRIOS (LOGSE) JUNIO INSTRUIONES GENERLES Y VLORIÓN El lumo coeá lo cuo ejecicio e u e l o opcioe ( o B) que e le oece. Nuc ebeá coe
Matemáticas II Hoja 2: Matrices
 Profesor: Miguel Ágel Bez lb (º Bchillerto) Mtemátics II Hoj : Mtrices Opercioes: Ejercicio : Ecotrr ls mtrices X e Y tles que: X Y 5 X Y 7 Ejercicio : 5 Dds ls mtrices y B, clcul: ) -B b) B c) B(-) d)
Profesor: Miguel Ágel Bez lb (º Bchillerto) Mtemátics II Hoj : Mtrices Opercioes: Ejercicio : Ecotrr ls mtrices X e Y tles que: X Y 5 X Y 7 Ejercicio : 5 Dds ls mtrices y B, clcul: ) -B b) B c) B(-) d)
Matemáticas aplicadas a las Ciencias Sociales II. ANAYA
 Unidd Nº Resoluión de sises edine deerinnes! eáis plids ls Cienis Soiles II. NY Esudi el rngo de ls siguienes ries: ))! Coo h vrios eleenos no nulos el rngo es.! Coo el rngo es.! unque oo, el rngo es,
Unidd Nº Resoluión de sises edine deerinnes! eáis plids ls Cienis Soiles II. NY Esudi el rngo de ls siguienes ries: ))! Coo h vrios eleenos no nulos el rngo es.! Coo el rngo es.! unque oo, el rngo es,
A, donde n es un número natural arbitrario.
 Clulr siedo MTRCES Y DETERMNNTES Dds ls ries les que: ij iee uro fils u olu el úio eleeo disio de es iee u fil uro olus el úio eleeo disio de es Clulr ij Dds ls ries lulr Por qué los resuldos o so idéios?
Clulr siedo MTRCES Y DETERMNNTES Dds ls ries les que: ij iee uro fils u olu el úio eleeo disio de es iee u fil uro olus el úio eleeo disio de es Clulr ij Dds ls ries lulr Por qué los resuldos o so idéios?
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
LÍMITE Y SUS PROPIEDADES
 LÍMITE Y SUS PROPIEDADES INTRODUCCION A LOS LÍMITES L oció de líie es fudel pr l copresió del cálculo. Medie vrios ejeplos se usc que los esudies eg clridd del sigificdo de líie.. El prole de l rec gee.
LÍMITE Y SUS PROPIEDADES INTRODUCCION A LOS LÍMITES L oció de líie es fudel pr l copresió del cálculo. Medie vrios ejeplos se usc que los esudies eg clridd del sigificdo de líie.. El prole de l rec gee.
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Sistemas de ecuaciones lineales
 Sisems de ecucioes lieles º Bchillero Sisems de ecucioes lieles. Iroducció Primos de que hemos esudido ls mrices deermies. U epresió de l form es u ecució liel co icógis. Los úmeros i se llm coeficiees;
Sisems de ecucioes lieles º Bchillero Sisems de ecucioes lieles. Iroducció Primos de que hemos esudido ls mrices deermies. U epresió de l form es u ecució liel co icógis. Los úmeros i se llm coeficiees;
Universidad Pontificia Bolivariana Ciencia Básica Taller Álgebra Lineal CAPITULO I: MATRICES
 Uiversidd Poifii Bolivri Ciei Bási Tller Álger Liel CPITULO I: MTRICES. Dds ls mries:, B C Efeur ls siguiees operioes, si es posile. E so e o ser posile, eplique por qué. -B T -B T B T d T C e B - f C
Uiversidd Poifii Bolivri Ciei Bási Tller Álger Liel CPITULO I: MTRICES. Dds ls mries:, B C Efeur ls siguiees operioes, si es posile. E so e o ser posile, eplique por qué. -B T -B T B T d T C e B - f C
OPERACIONES CON FUNCIONES OPERACIONES CON FUNCIONES
 IES Jun Gcí Vldemo Deptmento de Mtemátics º Bchilleto de CCSS. SUMA Y RESTA DE FUNCIONES Dds g unciones eles de vile el se deine l unción sum g como: g g con Dom g Dom Dom g Es deci, l unción g hce coesponde
IES Jun Gcí Vldemo Deptmento de Mtemátics º Bchilleto de CCSS. SUMA Y RESTA DE FUNCIONES Dds g unciones eles de vile el se deine l unción sum g como: g g con Dom g Dom Dom g Es deci, l unción g hce coesponde
Para ordenar números decimales debemos tener en cuenta la siguiente imagen:
 TEMA y NÚMEROS DECIMALES Y FRACCIONES. ORDENAR NÚMEROS DECIMALES Pr order úeros deciles deeos teer e cuet l siguiete ige: Lo que vos hcer es coprr priero l prte eter cifr cifr ver si so igules y si so
TEMA y NÚMEROS DECIMALES Y FRACCIONES. ORDENAR NÚMEROS DECIMALES Pr order úeros deciles deeos teer e cuet l siguiete ige: Lo que vos hcer es coprr priero l prte eter cifr cifr ver si so igules y si so
2. Calcula las coordenadas de D para que el cuadrilátero de vértices: A(-1, -2), B(4, -1), C(5, 2) y D; sea un paralelogramo.
 REPSO DE GEOMETRÍ MÉTRIC PLN. Hll el siético del punto (, - ) especto de M(-, ).. Clcul ls coodends de D p que el cudiláteo de vétices: (-, -), B(, -), C(, ) D; se un plelogo.. Ddos los vectoes (, k) (,
REPSO DE GEOMETRÍ MÉTRIC PLN. Hll el siético del punto (, - ) especto de M(-, ).. Clcul ls coodends de D p que el cudiláteo de vétices: (-, -), B(, -), C(, ) D; se un plelogo.. Ddos los vectoes (, k) (,
MATRICES Y DETERMINANTES
 Eucidos de proles de selectividd. Mteátics II. Mtrices y deterites MTRICES Y DETERMINNTES.(97).- Se dice que u triz cudrd es ortogol si se verific que t I. Si y B so dos trices ortogoles de igul tño, lizr
Eucidos de proles de selectividd. Mteátics II. Mtrices y deterites MTRICES Y DETERMINNTES.(97).- Se dice que u triz cudrd es ortogol si se verific que t I. Si y B so dos trices ortogoles de igul tño, lizr
Cálculo con vectores
 Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
Unidd didáctic 1 Cálculo con vectoes 1.- Mgnitudes escles vectoiles. Son mgnitudes escles quells, como l ms, l tempetu, l enegí, etc., cuo vlo qued fijdo po un númeo (con su unidd coespondiente). Gáficmente
SISTEMAS DE ECUACIONES LINEALES: TEOREMA DE ROUCHÉ- FROBENIUS
 R.F.- - SISTES DE ECUCIONES INEES: TEORE DE ROUCHÉ- FROBENIUS Recordeos que u siste de ecucioes co icógits es u siste de l for: Dode: ij so úeros reles se ll coeficietes del siste,,,, so úeros reles recie
R.F.- - SISTES DE ECUCIONES INEES: TEORE DE ROUCHÉ- FROBENIUS Recordeos que u siste de ecucioes co icógits es u siste de l for: Dode: ij so úeros reles se ll coeficietes del siste,,,, so úeros reles recie
Así, si la medida del arco AB es r, entonces:
 INSTITUTO EDUAIONAL ARAGUA MARAAY VMOL GUIA DE MATEMATIA, s. TRIGONOMETRÍA Nº Medid de Ángulos: (Siste Rdián y Sexgesil) B O α A Not: En est guí cundo se define l edid del ángulo centl α se lá indistintente
INSTITUTO EDUAIONAL ARAGUA MARAAY VMOL GUIA DE MATEMATIA, s. TRIGONOMETRÍA Nº Medid de Ángulos: (Siste Rdián y Sexgesil) B O α A Not: En est guí cundo se define l edid del ángulo centl α se lá indistintente
I.E.S. Ciudad de Arjona Departamento de Matemáticas. 2º BAC MCS
 I..S. Ciudd de Ajo Depteto de Mteátics. º BAC MCS. Ts de vició edi. Deivd de u ució e u puto.. Fució deivd. Deivds sucevs.. Regl de deivció.. studio de deivbilidd de u ució. Aplicció de ls deivds. Rect
I..S. Ciudd de Ajo Depteto de Mteátics. º BAC MCS. Ts de vició edi. Deivd de u ució e u puto.. Fució deivd. Deivds sucevs.. Regl de deivció.. studio de deivbilidd de u ució. Aplicció de ls deivds. Rect
Modelo 2014. Problema 1B.- (Calificación máxima: 2 puntos) Se considera el sistema lineal de ecuaciones dependiente del parámetro real a:
 odelo. Proble B.- (Clificción ái puntos) Se consider el siste linel de ecuciones dependiente del práetro rel ) Discútse en función de los vlores del práetro R. b) Resuélvse pr.. l siste se clsific en función
odelo. Proble B.- (Clificción ái puntos) Se consider el siste linel de ecuciones dependiente del práetro rel ) Discútse en función de los vlores del práetro R. b) Resuélvse pr.. l siste se clsific en función
ACTIVIDADES INICIALES
 Soluionio Deeinnes CTIVIDDES INICILES.I. us ls eliones de deendeni linel ene ls fils oluns de ls siguienes ies e indi el vlo de su ngo. g() g().ii. Coue ue ls siguienes ies son invess un de l o. Se deeín
Soluionio Deeinnes CTIVIDDES INICILES.I. us ls eliones de deendeni linel ene ls fils oluns de ls siguienes ies e indi el vlo de su ngo. g() g().ii. Coue ue ls siguienes ies son invess un de l o. Se deeín
1. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS
 C/ Eilio Ferrri, 87 - Mdrid 8017 www.slesissjose.es Deprteto de Ciecis Nturles MT01. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS 1. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS Ates de epezr Seguro que ás de u vez
C/ Eilio Ferrri, 87 - Mdrid 8017 www.slesissjose.es Deprteto de Ciecis Nturles MT01. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS 1. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS Ates de epezr Seguro que ás de u vez
CAPÍTULO 3 Función Exponencial y Función Logarítmica. Por su uso e importancia, es necesario revisar las propiedades de las potencias, que se resumen
 CAPÍTULO 3 Fució Epoecil Fució Logrític 3.1) Repso de propieddes de ls potecis Por su uso e iportci, es ecesrio revisr ls propieddes de ls potecis, que se resue cotiució. ( ) 1 1 0 3.) Fució Epoecil Defiició
CAPÍTULO 3 Fució Epoecil Fució Logrític 3.1) Repso de propieddes de ls potecis Por su uso e iportci, es ecesrio revisr ls propieddes de ls potecis, que se resue cotiució. ( ) 1 1 0 3.) Fució Epoecil Defiició
IES Mediterráneo de Málaga Reserva1.- 2012 Juan Carlos Alonso Gianonatti. Propuesta A
 ES Medieáeo Málg Reev.- Ju lo loo Gioi Popue.- ) Eui el eoe vlo edio Lgge d u iepeió geoéi ( puo) ) lul u puo l ievlo [ ] e que l e gee l gái l uió e plel l ued (o egeo) que ue lo puo () e ( puo) ) Teoe
ES Medieáeo Málg Reev.- Ju lo loo Gioi Popue.- ) Eui el eoe vlo edio Lgge d u iepeió geoéi ( puo) ) lul u puo l ievlo [ ] e que l e gee l gái l uió e plel l ued (o egeo) que ue lo puo () e ( puo) ) Teoe
2. Calcula las coordenadas de D para que el cuadrilátero de vértices: A(-1, -2), B(4, -1), C(5, 2) y D; sea un paralelogramo.
 REPSO DE GEOMETRÍ MÉTRIC PLN. Hll el siético del punto (, - ) especto de M(-, ).. Clcul ls coodends de D p que el cudiláteo de vétices: (-, -), B(, -), C(, ) D; se un plelogo.. Ddos los vectoes (, k) (,
REPSO DE GEOMETRÍ MÉTRIC PLN. Hll el siético del punto (, - ) especto de M(-, ).. Clcul ls coodends de D p que el cudiláteo de vétices: (-, -), B(, -), C(, ) D; se un plelogo.. Ddos los vectoes (, k) (,
1. Transformada de Laplace 2. Función de Transferencia. 3. Ejemplos de modelado de sistemas dinámicos 4. Modelado de sistemas de orientación
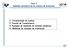 e zl zzu Te 3 Modeldo eáico de lo ie de orieció. Trford de Lplce. Fució de Trfereci. 3. Ejeplo de odeldo de ie diáico 4. Modeldo de ie de orieció e zl zzu Te 3. Modeldo eáico de lo ie de orieció: Trford
e zl zzu Te 3 Modeldo eáico de lo ie de orieció. Trford de Lplce. Fució de Trfereci. 3. Ejeplo de odeldo de ie diáico 4. Modeldo de ie de orieció e zl zzu Te 3. Modeldo eáico de lo ie de orieció: Trford
Modelo 5 de sobrantes de Opción A
 Ejercicio. [ puntos] Se f : R l función dd por Modelo de sobrntes de 6 - Opción. Ln f siendo Ln l función logrito neperino. Estudi l eistenci de síntot horiontl pr l gráfic de est función. En cso de que
Ejercicio. [ puntos] Se f : R l función dd por Modelo de sobrntes de 6 - Opción. Ln f siendo Ln l función logrito neperino. Estudi l eistenci de síntot horiontl pr l gráfic de est función. En cso de que
3º.- Junio i) Producto de matrices: definición, condiciones para su realización. Si A M m n. (la matriz A tiene m filas y n columnas), B M n p
 IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrices deterinntes Mtrices deterinntes. Ejercicios de Selectividd. º.- Junio 99. i) Define rngo de un triz. ii) Un triz de tres fils tres coluns tiene rngo
IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrices deterinntes Mtrices deterinntes. Ejercicios de Selectividd. º.- Junio 99. i) Define rngo de un triz. ii) Un triz de tres fils tres coluns tiene rngo
RAÍCES Y EXPONENTES FRACCIONARIOS
 RAÍCES Y EXPONENTES FRACCIONARIOS Defiició: L íz de ode de u úmeo es u úmeo tl que l elelo l poteci se obtiee el úmeo. Ejemplo : U íz cudd de es poque l ele l cuddo se obtiee, tmbié es u íz cudd de po
RAÍCES Y EXPONENTES FRACCIONARIOS Defiició: L íz de ode de u úmeo es u úmeo tl que l elelo l poteci se obtiee el úmeo. Ejemplo : U íz cudd de es poque l ele l cuddo se obtiee, tmbié es u íz cudd de po
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Cuso - Sepiembe MTERI: MTEMTICS II INSTRUCCIONES GENERLES Y VLORCION El lumno conesá los cuo ejecicios
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Cuso - Sepiembe MTERI: MTEMTICS II INSTRUCCIONES GENERLES Y VLORCION El lumno conesá los cuo ejecicios
