TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
|
|
|
- Miguel Ángel Murillo Cordero
- hace 7 años
- Vistas:
Transcripción
1 TEMAS DE MATEMÁTICAS Oposicioes de Secudri TEMA 0 RIMITIVA DE UNA FUNCIÓN. CÁLCULO DE ALGUNAS RIMITIVAS. ALICACIONES DE LA INTEGRAL AL CÁLCULO DE MAGNITUDES GEOMÉTRICAS.. Iroducció.. Cocepo de rimiiv.. Iegrles Imedis... Lis de Iegrles Imedis... Desrrollo de ls Iegrles Imedis. 4. Iegrció de Fucioes Rcioles. 4.. Cso : Grdo>GrdoQ 4.. Cso : GrdoGrdoQ 4.. Cso : Grdo<GrdoQ 4... Ríces Reles Simples Ríces Reles Múliples Ríces Complejs Simples Ríces Complejs Múliples. 5. Méodo de Hermie. 6. Iegrció por res. 6.. Iegrció por Reducció. 7. Cmio de Vrile. 7.. Susiució e fucioes epoeciles, logrímics e iverss de rigoomérics circulres e hiperólics. 7.. Susiució e iegrles de fucioes rigoomérics circulres. 7.. Susiució e iegrles de fucioes hiperólics. 8. Fórmuls Recurrees. 9. Iegrció de Fucioes Irrcioles. 9.. Iegrció por susiució e fucioes irrcioles. 9.. Méodos especiles de iegrció de fucioes irrcioles. 0. Iegrles Biomis.. Apliccioes... Áres de Figurs pls... Volúmees de Cuerpos de Revolució... Áre de u superficie de Revolució. Biliogrfí Recomedd. /7
2 . INTRODUCCIÓN. A lo lrgo del siglo XVIII se cosideró l iegrció como el proceso corrio l diferecició. El sigificdo geomérico de l iegrl idefiid es u fmili de curvs, ods ells oeids por desplzmieo vericl de u culquier. E ese em vmos rr de oeer primiivs de fucioes. r ello esudiremos diferees méodos. Hemos de eer e cue que l derivd de u fució elemel es siempre u fució elemel, e cmio l primiiv de u fució elemel puede o epresrse medie u úmero fiio de fucioes elemeles.. CONCETO DE RIMITIVA. DEF Dd f:[,] R, u primiiv de f es u fució F:[,] R, derivle e[,] y l que F f, Como od fució derivle e u iervlo es coiu e dicho iervlo, eoces od fució F primiiv de f es coiu e el mismo iervlo. NOTACION: Represeremos como primiiv u culquier de f y se lee iegrl idefiid de f. f d RO Se f:[,] R y F, F dos primiivs de f. Eoces F -F ce dem Defiimos l fució F 0 F -F [,]. Es clro que F 0 es u fució coiu y derivle, siedo Se 0, F 0F -F f-f 0 Ddo culquier oro puo ierior [,] se verific ls hipóesis del eorem del vlor medio del cálculo diferecil pr F 0 e [ 0,] ó [, 0 ] siedo ξ 0, / F 0 -F 0 F 0ξ - 0 Como F 0ξ 0 F 0 F 0 0 or o F 0 ce y F -F ce /7
3 Dds dos primiivs de f, como se difereci e u cose, pr poder idicrls ods, escriiremos f d F C RO Se f:[,] R u fució coiu. Eoces iee primiiv e [,]. dem L demosrció es imedi si más que eer e cue que es u primiiv de f. F f d. INTEGRALES INMEDIATAS... Lis de Iegrles Imedis. Epresmos coiució u lis de iegrles imedis. Es lis l oeemos si más que recordr ls derivds de ls fucioes de uso más geerlizdo. Si leemos ls igulddes de derech izquierd, l lis os puede servir como u lis de derivds, eiedo e cue el cocepo de iegrl idefiid. Tipo oecil. d C d p C p p d c C c p Tipo Epoecil. f f f ' e d e C c Tipo Logrímico. d L C d L C d L C d Tipo Trigoomérics circulres e hiperólics. /7
4 Cosd Se C Sed Cos C d Tg C Cos d Cog C Se g d l cos C co gd l se C cos d Cosec C se se d sec C cos cosh d seh C seh d cosh d C d gh C cosh d co gh C seh gh d l cosh C co ghd l seh C e Tipo iverss de Trigoomérics circulres e hiperólics. d rcse C d rg seh C l ± d rg cosh C l ± d rcg C d C rg gh l C d rcse C C C.. Desrrollo de ls iegrles imedis. Iegrles imedis de ipo poecil. 4/7
5 Siempre que jo el sigo iegrl prezc u fució elevd u cose, si lo que l muliplic es l meos e su pre vrile l derivd de l fució, podremos jusr co coses y será u iegrl imedi de ipo poecil. Iegrles imedis de ipo Epoecil. Siempre que jo el sigo iegrl prezc u cose elevd u fució, si lo que l muliplic es, l meos e su pre vrile, l derivd de l fució, podremos jusr co coses, y será u iegrl imedi de ipo epoecil. c Iegrles Imedis de ipo Logrímico. Siempre que jo el sigo iegrl prezc u cociee, si el umerdor es l meos e su pre vrile l derivd del deomidor, se podrá jusr co coses, y será u iegrl imedi de ipo Logrímico. d Iegrles Imedis de ipo Arco o Argumeo. Siempre que jo el sigo iegrl prezc u epresió de lguo de esos res ipos d d d c c podremos resolver l iegrl plicdo u méodo que desrrollremos e curo psos. ASO : Muliplicmos umerdor y deomidor por l riz cudrd de curo veces el vlor soluo del coeficiee umérico del érmio e 4 ASO : Se epres el érmio ierior l riz oeido e el pso erior e l form ± m ± ± p ideificdo coeficiees co es epresió. ASO : Se divide umerdor y deomidor por l riz cudrd de p. ASO 4: Se jus medie coses el resuldo oeido lgu de ls iegrles imedis del prdo e del puo.. OBS Ess iegrles o ls podremos resolver dero del cuerpo de los úmeros reles cudo los res o los dos coeficiees uméricos del poliomio se egivos. O mié porque después de plicr el pso oegmos egivos los dos érmios jo el sigo iegrl. De form muy similr l erior, si eemos u iegrl que se semej uo de esos res ipos 5/7
6 d d d c c su resolució es siguedo oro méodo de curo psos, muy precido l erior. ASO : Se muliplic umerdor y deomidor por curo veces el vlor soluo del coeficiee umérico del érmio e 4. ASO : Se epres el érmio del deomidor e l form ± m ± ± p ideificdo coeficiees co es epresió. ASO : Se divide umerdor y deomidor por p. ASO 4: Se jus por coses el resuldo oeido lgu de ls iegrles imedis del ipo e del puo.. 4. INTEGRACIÓN DE FUNCIONES RACIONALES. Es l iegrció de l form d, siedo y Q poliomios de Q coeficiees reles y epoees urles. OBS Cudo os ecoremos co ese ipo de iegrles, es de d coviee relizr l comproció de que o se r de u iegrl imedi de ipo Logrímico. 4.. CASO : grdo > grdo Q. E es siució, lo primero que hemos de relizr es l divisió de por Q queddo Q CR siedo C el cociee de l divisió y R el reso grdo R< grdo Q. Eoces l iegrl os qued como Q R Q d d C d L iegrl C d es de ipo poecil, y por o imedi. R L iegrl d puede o eisir si R 0, siedo l divisió ec. Si Q o es sí, oeemos u iegrl dode grdo R< grdoq que esudiremos más dele. 6/7
7 4.. CASO : grdo grdoq. El proceso pr resolver ese cso es el mismo que el erior. L úic difereci es que CK cose. Eoces l primer iegrl es mié es imedi, siedo Todo lo demás es álogo. 4.. CASO : grdo > grdo Q. Kd K C E ese cso y o podemos relizr l divisiló de por Q. El proceso que deemos seguir serí, e primer lugr, oeer ls rices de Q, y se del ipo que se. Hemos de recordr que culquier poliomio co coeficiees reles y epoees urles puede eer Ríces Reles Simples Ríces Reles Múliples Ríces Complejs Simples 4 Ríces Complejs Múliples Esudiremos cd uo de ess curo siucioes de form idepediee Rices Reles Simples. E ese prdo vmos supoer que l igulr Q cero oeemos sólo rices reles simples. Vmos supoer que Q , siedo 0 el coefiee umérico del érmio de myor grdo de Q. El moivo de elegir Q de grdo y o de grdo es pr o complicr l escriur co sumorios y producos. El méodo de resolució pr el cso de u poliomio de grdo superior es el mismo, pero más edioso. r eplicr ese méodo vmos supoer que 0, y que si o lo fuer, l cose / 0 se podrí scr fuer de l iegrl: d d Q d 0 0 Los psos seguir so los siguiees: so: Descompoer e frccioes simples. L descomposició es úic, Q siedo ls frccioes de l descomposició el umerdor u coeficiee ideermido y el deomidor uo de los fcores de Q. 7/7
8 8/7 C B A Q co A,B y C coses. so: Se epres mos érmios co u comú deomidor, que siempre será Q. C B A Q so: Al eer mos miemros el mismo deomidor, igulmos los umerdores. A- - B- - C- - so4: Se clcul los coeficiees A, B y C hcemos, verificádose A - - A hcemos B - - B hcemos C - - C so 5: U vez oeidos los coeficiees, procedemos l iegrció. K C B A Cd Bd Ad d Q l l l 4... Ríces Reles Complejs. Vmos supoer que l igulr Q cero oeemos rices reles múliples. r simplificr l descripció del méodo, pero cosiderádolo e od su geerlidd, omremos Q siedo u ríz simple, u ríz múliple co ídice de muliplicidd y 0 el coeficiee umérico del érmio de myor grdo de Q.
9 9/7 Aálogmee l cso erior, vmos supoer que 0 Los psos seguir so los mismos que e el cso erior: so: Descompoer Q e frccioes simples. Ls ríces reles simples se descompoe de l mism form. r ls ríces reles múliples, el umerdor siempre es u coeficiee ideermido y el deomidor es el fcor múliple co epoee vrido de su muliplicidd e cd frcció. D C B A Q co A, B,C y D coses. so: Se epres mos érmios co u comú deomidor, que siempre será Q. D C B A Q so: Igulmos los umerdores: D C B A so4: L ideificció de coeficiees se puede relizr e ese cso de ls siguiees forms: Susiuyedo por los vlores de ls ríces oedremos os coeficiees ideermidos como ríces disis hy. A A D D El reso de coeficiees los podemos oeer ddo vlores pequeños disios de ls ríces y. Tos vlores como coeficiees quede por clculr. E uesro cso, dos D C B A
10 A B C D Como A y D so coocidos, llegmos u sisem de dos ecucioes co dos icógis, que u vez resuelo os drá B y C. Si relizmos ls opercioes que idic el segudo miemro e igulmos los coeficiees de mos miemros del mismo grdo, oeemos u sisem de s ecucioes como icógis. so5: U vez oeidos los coeficiees procedemos l iegrció: Ad Bd Cd Dd d Q C D A l B l K Ls dos primers iegrles so imedis de ipo logrímico y ls dos úlims so imedis de ipo poecil: 4... Ríces Complejs Simples. Descriiremos el méodo de resolució supoiedo que el poliomio Q es de grdo 5, co ríces rel simple, rel múliple de orde y i, -i ríces complejs simples. Escogemos sí Q por ser el supueso más compleo de los que cosiuye ese cso. Q i--i Los dos úlimos fcores se puede escriir como queddo eoces -i--i- Q De form álog los dos csos eriores, supodremos que 0. Los psos seguir e ese méodo so los mismos que hemos viso e los dos prdos eriores. E l descomposició de e frccioes simples, ls frccioes que Q correspode ls ríces reles simples so de l mism form que e puo 4...; ls frccioes correspodiees ls ríces reles múliples so de l form que e el puo 4...; y ls frccioes correspodiees ls ríces imgiris simples so: el umerdor u poliomio e de primer grdo compleo de coeficiees ideermidos, y el deomidor l epresió -. 0/7
11 /7 Aes de proseguir co l eplicció de ese méodo, vos relizr u iciso, pr eplicr como se iegr ess frccioes uevs que hemos oeido. d N d M d N M '' ' d M d M d M d M l ' M d M d N M '' Es u iegrl del ipo rcogee que se resuelve como sigue: N M d N M rcg co lo cul l iegrl clculr qued como K M N M d N M l rcg Co eso ermimos el iciso y proseguimos co el méodo. so: N M C B A Q co A, B, C, M y N coses. so: Reducimos comú deomidor. Omiimos l fórmul por o ser de ierés. so: Igulmos los umerdores. N M C B A so4: E ese cso podemos relizr l ideificció de coeficiees de l mism form que e 4...
12 so5: C M d Al Bl l Q Ríces Complejs Múliples. M N rcg K Veremos ese cso e el supueso priculr de que le poliomio Q se de oveo grdo, siedo sus ríces ríz rel simple ríz rel múliple de orde. i y -i ríces complejs simples cdi y c-di ríces complejs múliples de orde. Eoces Q c d siedo 0 el coeficiee pricipl de Q, que supodremos, si pérdid de geerlidd que es 0. A Q B C M N S T U V c d c d Hs el pso 4 se reliz de l mism form que e 4.. y 4... Al llegr l pso 5, u vez oeidos los coeficiees ideermidos, procedemos l iegrció de cd u de ls frccioes, siedo y coocido el resuldo meos de l úlim.remiimos l lecor l hoj de prolems pr coocer su resolució. No resolveremos e el em l iegrl de l úlim frcció por o eederos iecesrimee, y que vmos ver u méodo lerivo pr resolver ls iegrles de cociees de poliomios co deomidor co ríces complejs múliples, llmdo Méodo de Hermie. 5. MÉTODO DE HERMITE. r eplicr ese méodo, primos de u cociee de poliomios dode ls Q ríces de Q puede ser o reles como complejs y simples o múliples. or o, esmos e l mism siució que e el puo 4..4 De uevo supodremos que Q es u poliomio de oveo grdo cuy descomposició es /7
13 Q c d siedo 0 el coeficiee pricipl de Q, que supodremos, si pérdid de geerlidd que es 0. so: - Ls ríces reles simples se descompoe como hemos viso e el puo 4, co u coeficiee ideermido como umerdor y el fcor que coiee l ríz como deomidor. - Ls ríces reles múliples se descompoe como si fuer simples, si eer e cue su ídice de muliplicidd. - Ls ríces complejs simples se descompoe como hemos viso e el puo Ls ríces complejs múliples se descompoe como si fuer simples, si eer e cue su ídice de muliplicidd. - Además, hy u érmio más que psmos descriir: L derivd de u cociee dode el deomidor es el produco de los fcores múliples co epoees igul sus ídices de muliplicidd respecivos meos uo. El umerdor será u poliomio compleo de grdo iferior e u uidd del grdo del poliomio del deomidor. OBS Se suele uilizr lers miúsculs pr epresr los coeficiees ideermidos del érmio crcerísico de Hermie. A B M N Q S T c d m p c d siedo A, B, M, N, S, T, m, y p coses deermir. so: Se deriv le úlimo érmio co respeco. A B M N Q zm c S T c d d m p c c d d d d c so: so4: Se epres mos miemros co u comú deomidor que será siempre Q. Se igul los umerdores /7
14 A M N c m m p c c c m p c d d B S T d d c c d d so5: Cálculo de los coeficiees ideermidos, que se hrá de l mism form que e 4.., 4.. ó so6: Iegrció de cd u de ls frccioes oeids. E uesro ejemplo, ls iegrles primer y segud so imedis de ipo Logrímico. L ercer y cur ls hemos resuelo e el puo 4... y l úlim es imedi eiedo e cue ls propieddes de l iegrl. M d Al B l l Q S l Sc T c m p c d rcg K d d c M N rcg d OBS E el méodo de Hermie, si se relizó correcmee, o prece uc iegrles imedis de ipo poecil. 6. INTEGRACIÓN OR ARTES. Si u ý v so fucioes de, por ejemplo uf y vg, plicdo l fórmul de l diferecil de u produco de fucioes duv udv vdu y si de es epresió despejmos udv udv duv - vdu Iegrdo mos miemros de l iguldd udv d uv vdu que se puede escriir como udv uv vdu que es l llmd fórmul de iegrció por pres. Si hor eemos e cue que 4/7
15 u f du f d v g dv g d y los susiuimos e l fórmul de iegrció por pres, oeemos vdu f g' d f g g f ' d Es uev form de epresr l fórmul de iegrció por pres os epres mejor ése méodo de iegrció, el cul cosise e coverir u iegrl e u pre y iegrd más u uev iegrl. Se r de descompoer l iegrl origil como produco de dos fucioes, escogiedo éss de l mer que l plicr l fórmul l uev iegrl resule más secill que l iicil. Vmos ver coiució us recomedcioes que os puede servir pr descompoer l iegrl e dos pres. rimos del supueso de que culquier fució se puede epresr como produco de ors dos, uque u de ells se u cose. Adjumos u l, e l que llmremos y Q los dos fcores e los que dividimos l fució iegrr. Q u dv L uidd o culquier cose Qd Fució ivers de Trigoomeric circulr o hiperólic o fució logrímic Fució ivers de Trigoomeric circulr o hiperólic o fució logrímic oliomio e o fució rciol e Fució Epoecil ormlmee de iegrció imedi 6.. Iegrció por Reducció. oliimio e o fució rciol e Qd Fució Trigooméric circulr o hiperólic direc, o fució epoecil ormlmee de iegrció imedi Fució Trigooméric circulr o hiperólic direc. o Q Qd Qd o d L iegrció por reducció l plicremos iegrles co fucioes de epoees hiulmee eeros pero elevdos. Se r de oeer u pre iegrd y or si iegrr l que, l plicr l fórmul de iegrció por pres, se oeg u uev iegrl co l fució co el epoee dismiuido. El méodo es muy similr e odos los csos. rimero plicmos l iegrció por pres, oeiedo u pre y iegrd y u iegrl e l que se dee, u oeer l iegrl iicil reducid de epoee, o descompoerl e sum de iegrles, siedo 5/7
16 u de ells l iegrl iicil reducid de epoee y l or l propi iegrl iicil. E ese segudo cso llegmos u iegrl recurree y rremos como l. U ejemplo de fórmul de reducció: se m m m m m m d se cos se d 7. CAMBIO DE VARIABLE. Ese méodo mié se cooce como iegrció por susiució. Ae iegrles cuy resolució o podemos relizr como imedi, i rciol, i por pres o de culquier or form que veremos después se recurre ese méodo. Cosise e ecorr u fució g l cul, l susiuirl jo el sigo iegrl, coviere l iegrl e or más secill co l uev vrile. L susiució g dee cumplir Ser derivle y co derivd o ul. d g d Admiir fució ivers. g h Eoces f d f g g' d F C F h C Sólo os qued por compror, pr ver que es correco, que l derivd de Fh es f: df h d df d df d F ' d d g' f g g' g' f g f El méodo de susiució es uo de los más mplios por l gr vriedd de susiucioes que se puede dr. ero hemos de plicr cd cso el cmio decudo, y que si o, el cmio os puede llevr iegrles de myor dificuld. El los suprdos siguiees idicremos ls susiucioes pr ipos cocreos. L epresió R idicrá fució rciol de los elemeos ere préesis elemeos relciodos ere sí por ls opercioes rcioles de sum, res, produco y cociee. 7.. Susiució e fucioes epoeciles, logrímics e iverss de rigoomérics circulres e hiperólics. 6/7
17 Tipo de Iegrl Susiució Cálculo de elemeos pr l susiució. R d l d d R, d l l R e d R, e d e e l d d R, l d l l e de d R, rcg d rcg g d d cos R, rcse d rcse se d-se d R, rccos d rccos cos d-se d R, rg gh d d rggh gh d cosh R, rg seh d rgseh seh d cosh d R, rg cosh d rgcosh cosh d seh d 7.. Susiució e iegrles de fucioes rigoomérics circulres. Susiució Si Rse, cos es impr e se, hremos: cos Si Rse, cos es impr e cos, hremos: se Si Rse, cos es pr e se y cos, hremos: g Si Rse, cos o cumple co igu de ls crcerísics eriores, hremos: g Cálculo de elemeos pr l susioció cos d se d d d d g d se d d se cos se cos cos 7. Susiucio e iegrles de fucioes hiperolics. Susiució Cálculo de elemeos pr l susioció Si Rseh, cosh es d impr e seh, hremos: d seh cosh 7/7
18 Si Rseh, cosh es impr e cosh, hremos: d d cosh seh Si Rseh, cosh es pr e seh y cosh, hremos: gh Si Rseh, cosh o cumple co igu de ls crcerísics eriores, hremos: gh d d d d seh cosh seh cosh 8. FÓRMULAS RECURRENTES. Dd u iegrl l cul o podemos plicr el méodo de susiució, y el méodo de iegrció por pres os dé u iegrl similr iegrl prid, podemos plicr l resolució por recurreci. e d Llmremos l iegrl clculr I e d u dv e d du e v e e I L ecució recurree es: I e I Se m Im se, cos d m m u se d du m se cos d dv se cos d cos v 8/7
19 se cos m cos m m m m se cos d Im, Luego l ecució es: I se m m m, se cos I m, 9. INTEGRACIÓN DE FUNCIONES IRRACIONALES. 9.. Iegrció por susiució e fucioes irrcioles. E l l siguiee prece ls susiucioes más impores pr l resolució de ese ipo de iegrles. Dremos el ipo de iegrl l que se plic, l susiució que se reliz y el cálculo de quellos elemeos ecesrios pr compler l susiució. Tipo de Iegrl Susiució m p q s R,,, K, d M c d c d c d c d siedo M el m.c.m. de los deomidores Cálculo de los elemeos pr l susiució M d f fució rciol e d f ' d M c Tipo de Iegrl Susiució m p q s R,,, K, d M siedo M el m.c.m. de los es similr l cso erior, co c0 y d deomidores Cálculo de los elemeos pr l susiució M f fució rciol e d f ' d Tipo de Iegrl Susiució m p q s R,,, K, d M siedo M el m.c.m. de los es similr l cso erior, co 0 y deomidores Cálculo de los elemeos pr l susiució M d M d 9.. Méodos especiles de iegrció de fucioes irrcioles. Iegrles de l form c d co grdo 9/7
20 Vemos los psos seguir e l resolució: so : Descompoemos l frcció como sigue: U primer érmio que es l derivd idicd co respeco del produco de u poliomio que llmremos Q, compleo e co coeficiees ideermidos y de grdo meor e u uidd l grdo de, muliplicdo por l ríz cudrd del deomidor. A eso sumremos u segudo érmio que será u frcció formd por u coeficiee ideermido, λ, como umerdor, y l ríz como deomidor. No demosrremos que l descomposició es úic. d λ Q c c d c so : so : Se deriv l epresió que hy idicd. Q Q c λ ' c c c Reducimos mos miemros comú deomidor. Q Q' c λ c c c c so 4: Igulmos los umerdores de mos miemros y procedemos l ideificció de coeficiees. Q' c Q λ so 5: Iegrmos e mos miemros de l epresió oeid e el so º. El primer érmio qued iegrdo co sólo elimir l idicció de derivd, y el segudo érmio es u iegrl que y resolvimos e u prdo erior. d c Q c λ d c 0/7
21 Iegrles de l form d p c Ese ipo de iegrl es muy específico, y medie l siguiee susiució que recomedmos se reduce iegrles y viss. Susiució: Elemeos ecesrios pr compler l susiució: d d c Cso Geerl. Susiució e fucioes irrcioles. A coiució epoemos u l co susiucioes esádr pr resolver iegrles del ipo R, c d Ess susiucioes se puede plicr los dos csos eriores, pero o es cosejle. Tipo de Iegrl Susiució R, c d Si >0 c ± Cálculo de los elemeos pr l susiució c f fució rciol e m d f ' d c ± f Tipo de Iegrl Susiució R, c d Si c>0 c ± c Cálculo de los elemeos pr l susiució ± c f fució rciol e d f ' d c ± c f Tipo de Iegrl Susiució R, c d c Siedo u de ls dos ríces que se oiee l resolver l ecució y l or β. /7
22 Cálculo de los elemeos pr l susiució β f fució rciol e d f ' d c f Si e l iegrl erior eemos que 0 podemos plicr ors susiucioes más fáciles que ls esádr, usdo fucioes rigoomérics circulres. Tipo de Iegrl Susiució Cálculo de elemeos pr l susiució. R, c d R, c d R, c d 0. INTEGRALES BINÓMIAS. c se c sec c g c c cos c d cosdi rcse c c c g c se d di cos rcse c c c sec c d di cos rcg c Ls iegrles que llmremos Biomis so de l form: m p d y ls susiucioes que hy que relizr so ls que prece e l l siguiee: /7
23 Tipo de Iegrl m p d Susiució Si p es u úmero eero m Si es u úmero eero deomidor de l frcció p m Si p es u úmero eero el deomidor de l frcció p s siedo s el s siedo s. ALICACIONES... Áres de Figurs ls. Áre de l figur limid por l curv y f ere, y el eje OX >. odemos disiguir dos csos segú l gráfic y f core l eje OX e lgú puo del iervlo [, ] o o. Si o cor l eje e [,] S f d Supogmos hor que f cor OX e, [,] S f d f d f d Áre de l figur limid por l curv y f y el eje OX..i Eise dos puos de core. Supogmos que se y /7
24 S f d.ii Eise más de dos puos de core. Supogmos que se res:, y S f d f d c Áre de l figur limid ere ls curvs y f, y g, y co f y g posiivs o egivs e [,]. S f g d d Áre de l figur limid ere ls curvs y f, y g, y f > 0 y g < 0 e [,]. S f g d 4/7
25 e Áre de l figur limid ere ls curvs y f, y g, y f y g posiivs o egivs ms co u puo de core. Se solució f g S f g d f g d f Áre limid ere ls curvs y f e y g Se resuelve l ecució pr f g pr hllr los puos de core. Supogmos que sólo sle dos, y que f > g [,]. S f g d Si eisiese más de dos puos de core, plicremos l fórmul pr cd dos puos cosecuivos... Volúmees de cuerpos de Revolució. Volume del cuerpo egedrdo por l revolució de l curv y f lrededor del eje OX ere y. V π f d Volume del cuerpo egedrdo por l revolució de l curv y f lrededor del eje OY ere y. 5/7
26 V π f d c Volume del cuerpo egedrdo por l revolució de u figur limid por ls curvs y f e y g f > g ere y l girr lrededor del eje OX V π f g d d Volume del cuerpo egedrdo por l revolució de u figur limid por ls curvs y f e y g f > g ere y l girr lrededor del eje OY. V π f g d.. Are de u superficie de revolució. Are de l superficie geerd por el giro lrededor del eje OX de l rco de l curv y f ere y. V π f f ' d 6/7
27 Biliogrfí Recomedd. Aálisis Memáico I. Au. J.A. Ferádez Viñ. Ed. Tecos Leccioes de Cálculo Ifiiesiml I. Au. R. Moli Legz, M. Frco. Ed. Uiversidd de Murci. ricipios de Aálisis Memáico. Au. W. Rudi. Ed. McGrw-Hill Curso de Aálisis Memáico I. Au. E.L. Lu. Ed. Edus, 99. Clculus. Au. M. Spivk. Ed. Reveré. Aálisis Memáico. Au. M. de Guzmá, B. Ruio. Ed. irámide. Clculus. Au. Aposol. Ed. Reveré 7/7
TEMA 1. VECTORES Y MATRICES 1.2. MATRICES. OPERACIONES ELEMENTALES
 TEM VECTORES Y MTRICES MTRICES OPERCIONES ELEMENTLES VECTORES Y MTRICES MTRICES: OPERCIONES ELEMENTLES Cocepo de riz Eleeos Tipos de rices Su y difereci de rices Produco de u úero por u riz Trsposició
TEM VECTORES Y MTRICES MTRICES OPERCIONES ELEMENTLES VECTORES Y MTRICES MTRICES: OPERCIONES ELEMENTLES Cocepo de riz Eleeos Tipos de rices Su y difereci de rices Produco de u úero por u riz Trsposició
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
BLOQUE DE ÁLGEBRA TEMA 1: MATRICES
 Álgebr Liel Memáics º chillero LOQUE DE ÁLGER TEM : MTRICES U mriz es u cojuo de úmeros reles colocdos recgulrmee ecerrdos ere préesis o corchee o doble brr. Pr or u mriz se uiliz o: u ler myúscul, por
Álgebr Liel Memáics º chillero LOQUE DE ÁLGER TEM : MTRICES U mriz es u cojuo de úmeros reles colocdos recgulrmee ecerrdos ere préesis o corchee o doble brr. Pr or u mriz se uiliz o: u ler myúscul, por
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 Jun nonio González o Proesor de emáics del Colegio Jun XIII Zidín de Grnd ITEGRCIÓ ITEGRES IDEFIIDS ÉTODOS DE ITEGRCIÓ PRIITIV DE U FUCIÓ ITEGR IDEFIID Sen y F dos unciones reles deinids en un mismo dominio
Jun nonio González o Proesor de emáics del Colegio Jun XIII Zidín de Grnd ITEGRCIÓ ITEGRES IDEFIIDS ÉTODOS DE ITEGRCIÓ PRIITIV DE U FUCIÓ ITEGR IDEFIID Sen y F dos unciones reles deinids en un mismo dominio
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Tema 4. SISTEMAS DE ECUACIONES LINEALES
 Te SISTS D CUCIONS LINLS Sises de res ecucioes co res icógis So de l for: Ls lers i, ij i represe, respecivee, ls icógis, los coeficiees los érios idepediees L solució del sise es el cojuo de vlores de,
Te SISTS D CUCIONS LINLS Sises de res ecucioes co res icógis So de l for: Ls lers i, ij i represe, respecivee, ls icógis, los coeficiees los érios idepediees L solució del sise es el cojuo de vlores de,
Universidad Abierta Interamericana. Facultad de Tecnología Informática
 Uiversidd Abier Iermeric Fculd de Tecologí Iformáic Crrer: Liceciur e Memáic U speco de l Diámic de Poblcioes: Relció Depreddor-Pres por Prici Móic Grcí Direcor de Tesis: Dr Mrí Lore Bergmii Tesis presed
Uiversidd Abier Iermeric Fculd de Tecologí Iformáic Crrer: Liceciur e Memáic U speco de l Diámic de Poblcioes: Relció Depreddor-Pres por Prici Móic Grcí Direcor de Tesis: Dr Mrí Lore Bergmii Tesis presed
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
Unidad 7: Sucesiones. Solución a los ejercicios
 Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES
 CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
Matemáticas Aplicadas a la Ciencias Sociales II SISTEMAS DE ECUACIONES. , a toda ecuación que pueda escribirse de la forma: ...
 Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
MATRICES Y DETERMINANTES.
 punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
TEMA1: MATRICES Y DETERMINANTES:
 TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
CAPÍTULO 2: POTENCIAS Y RAÍCES 1. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES
 CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
ANALISIS MATEMATICO I Ciclo Lectivo Guía de Estudio y Práctica 07 DIFERENCIALES. Ing. Jorge J. L. Ferrante
 ANALISIS MATEMATICO I Ciclo Lecivo 9 Guí de Esudio Prácic 7 DIFERENCIALES Ig. Jorge J. L. Ferre I CONSOLIDACIÓN DE CONCEPTOS Correspode señlr que l oció que se uiliz e es pre de l sigur es l mism que e
ANALISIS MATEMATICO I Ciclo Lecivo 9 Guí de Esudio Prácic 7 DIFERENCIALES Ig. Jorge J. L. Ferre I CONSOLIDACIÓN DE CONCEPTOS Correspode señlr que l oció que se uiliz e es pre de l sigur es l mism que e
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Tema 2. Operaciones con Números Reales
 Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
SISTEMAS DE ECUACIONES LINEALES
 SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
85.- Sea B j (t) la función polinómica: n j. Demostrar que: iii) Solución: Consideremos la identidad: (t+x) n =
 Hoa Problemas Aálisis II /9 85.- Sea la fució oliómica: N R Demosrar que: i ii iii iv Solució: Cosideremos la ideidad: R N. Derivado e ambos miembros reseco de mulilicado desués or se obiee: - Derivado
Hoa Problemas Aálisis II /9 85.- Sea la fució oliómica: N R Demosrar que: i ii iii iv Solució: Cosideremos la ideidad: R N. Derivado e ambos miembros reseco de mulilicado desués or se obiee: - Derivado
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Resumen: Límites de funciones. Asíntotas
 Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Se llama logaritmo en base a de P, y se escribe log a P, al exponente al que hay que elevar la base a para obtener P.
 Log P X Se llm ritmo en bse de P, y se escribe P, l eponente l que hy que elevr l bse pr obtener P. Log P P Ejemplo: 8 8 L l it b d 8 Leemos, ritmo en bse de 8 es porque elevdo es 8. Anámente podemos decir:
Log P X Se llm ritmo en bse de P, y se escribe P, l eponente l que hy que elevr l bse pr obtener P. Log P P Ejemplo: 8 8 L l it b d 8 Leemos, ritmo en bse de 8 es porque elevdo es 8. Anámente podemos decir:
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
Cap 3 La Integral Definida MOISES VILLENA MUÑOZ
 Cp L Iegrl ed. EINICIÓN. TEOREMA E INTEGRABILIA. TEOREMA UNAMENTAL EL CÁLCULO. PROPIEAES E LA INTEGRAL EINIA.. PROPIEA E LINEALIA.. PROPIEA E AITIVIA.. PROPIEA E COMPARACIÓN.. PROPIEA E ACOTAMIENTO.. PROPIEA
Cp L Iegrl ed. EINICIÓN. TEOREMA E INTEGRABILIA. TEOREMA UNAMENTAL EL CÁLCULO. PROPIEAES E LA INTEGRAL EINIA.. PROPIEA E LINEALIA.. PROPIEA E AITIVIA.. PROPIEA E COMPARACIÓN.. PROPIEA E ACOTAMIENTO.. PROPIEA
MATEMÁTICAS: 4ºB ESO Capítulo 3: Expresiones algebraicas. Polinomios. www.apuntesmareaverde.org.es
 MATEMÁTICAS: ºB ESO Cítulo : Eresioes lgebrics. Poliomios. commos.wikimedi Eresioes lgebrics. Poliomios. ºB ESO Ídice. INTRODUCCIÓN. EXPRESIONES ALGEBRAICAS.. INTRODUCCIÓN.. EXPRESIONES ALGEBRAICAS. POLINOMIOS.
MATEMÁTICAS: ºB ESO Cítulo : Eresioes lgebrics. Poliomios. commos.wikimedi Eresioes lgebrics. Poliomios. ºB ESO Ídice. INTRODUCCIÓN. EXPRESIONES ALGEBRAICAS.. INTRODUCCIÓN.. EXPRESIONES ALGEBRAICAS. POLINOMIOS.
A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS PROPIEDADES.
 CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
CAPÍTULO 3. PROCEDIMIENTOS DE INTEGRACIÓN 3.1. Integración por cambio de variable 3.2. Integración por partes 3.2.1. Producto de un polinomio por una
 CAPÍTULO. PROCEDIMIENTOS DE INTEGRACIÓN.. Integrción por cmbio de vrible.. Integrción por prtes... Producto de un polinomio por un eponencil... Producto de un polinomio por un seno o un coseno... Producto
CAPÍTULO. PROCEDIMIENTOS DE INTEGRACIÓN.. Integrción por cmbio de vrible.. Integrción por prtes... Producto de un polinomio por un eponencil... Producto de un polinomio por un seno o un coseno... Producto
1. Cálculo de primitivas. 2. Reglas de cálculo de primitivas. (I Integrales inmediatas)
 Tem : L integrl definid. Cálculo de primitivs. Aplicciones.. Cálculo de primitivs. Definición. Dds f, F : D R R, decimos que F es un primitiv de l función f si: F ( f(, D. Está clro que si F es un primitiv
Tem : L integrl definid. Cálculo de primitivs. Aplicciones.. Cálculo de primitivs. Definición. Dds f, F : D R R, decimos que F es un primitiv de l función f si: F ( f(, D. Está clro que si F es un primitiv
16/11/2015. Tema 1: Números reales REALES. Racionales (Q) Irracionales (I) Naturales (N) REALES (I) (Q) (Z) (N)
 rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.
![LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b. LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.](/thumbs/52/29237757.jpg) Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática.
 Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
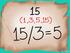 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
FASE COGNITIVA. LOS NUMEROS REALES Los números reales se conforman por los decimales finitos, decimales infinitos periódicos e infinitos no periódicos
 Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Enteros (Z) Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto de cero
 www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
EL TEOREMA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE. Alberto E. J. Manacorda*
 EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
Estructuras Discretas. Unidad 3 Teoría de números
 Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
COMBINATORIA. Las variaciones ordinarias se representan por el símbolo Vm,n o por V
 COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
Toda expresión que conste de una expresión algebraica en su denominador y en el numerador.
 TEMA : Epresiones Rcionles Contenio TEMA H: Epresiones Rcionles... Introucción epresiones rcionles... PRÁCTICA: Inic los vlores que no formn prte el conjunto solución... Simplificr Epresiones Rcionles...
TEMA : Epresiones Rcionles Contenio TEMA H: Epresiones Rcionles... Introucción epresiones rcionles... PRÁCTICA: Inic los vlores que no formn prte el conjunto solución... Simplificr Epresiones Rcionles...
Aplicaciones de la integral
 5 Mtemátics I : Cálculo integrl en I Tem 4 Aplicciones de l integrl 4. Áres de superficies plns 4.. Funciones dds de form explícit A l vist del estudio de l integrl definid relizdo en el Tem 3, prece rzonle
5 Mtemátics I : Cálculo integrl en I Tem 4 Aplicciones de l integrl 4. Áres de superficies plns 4.. Funciones dds de form explícit A l vist del estudio de l integrl definid relizdo en el Tem 3, prece rzonle
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
i 1,2,..., m (filas) j 1,2,..., n (columnas) t
 MTRICES Y DETERMINNTES Cocepos básicos Deermiaes Mariz iversa CONCEPTOS BÁSICOS MTRIZ de m filas y columas: a11 a12 a1 a21 a22 a 2 am1 am2 am i1,2,..., m (filas) Se represea por a j 1,2,..., (columas)
MTRICES Y DETERMINNTES Cocepos básicos Deermiaes Mariz iversa CONCEPTOS BÁSICOS MTRIZ de m filas y columas: a11 a12 a1 a21 a22 a 2 am1 am2 am i1,2,..., m (filas) Se represea por a j 1,2,..., (columas)
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
LOGARITMO 4º AÑO DEF. Y PROPIEDADES
 LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
ANÁLISIS MATEMÁTICOS
 ANÁLISIS MATEMÁTICOS TEMA. FUNCION REAL DE VARIABLE REAL..... Itroducció..... Domiio..... Limites...6.4. Cotiuidd...9 TEMA : DERIVADAS..... Itroducció..... Sigos de l derivd..... Formuls priciples de derivds....4.
ANÁLISIS MATEMÁTICOS TEMA. FUNCION REAL DE VARIABLE REAL..... Itroducció..... Domiio..... Limites...6.4. Cotiuidd...9 TEMA : DERIVADAS..... Itroducció..... Sigos de l derivd..... Formuls priciples de derivds....4.
Ejercicios: 1. Coloca donde corresponda los siguientes números: N Z Q FRACCIONARIOS I
 TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES
 LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES L integrl definid Se y f un función definid en el intervlo,, se llm integrl definid de f en n el intervlo, y se denot por fd lim fc i i i. n i y se llmn límites
LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES L integrl definid Se y f un función definid en el intervlo,, se llm integrl definid de f en n el intervlo, y se denot por fd lim fc i i i. n i y se llmn límites
[FACTORIZACION DE POLINOMIOS]
![[FACTORIZACION DE POLINOMIOS] [FACTORIZACION DE POLINOMIOS]](/thumbs/40/21635409.jpg) 009 CETis 6 Ing. Gerrdo Srmiento Díz de León [FACTORIZACION DE POLINOMIOS] Documento que enseñ como fctorizr polinomios Pr fctorizr polinomios hy vrios métodos: FACTORIZACIÓN DE POLINOMIOS. Scr fctor común:
009 CETis 6 Ing. Gerrdo Srmiento Díz de León [FACTORIZACION DE POLINOMIOS] Documento que enseñ como fctorizr polinomios Pr fctorizr polinomios hy vrios métodos: FACTORIZACIÓN DE POLINOMIOS. Scr fctor común:
Planificación contra stock. Presentación. Introducción
 Plaificació cora sock 09.0.07 Preseació Fabricar cora sock? No iee que ser cero el iveario? Se vio e el capíulo de iroducció. Plaificar cora sock Ciclo de pedido y fabricació idepediees. Demada aual coocida.
Plaificació cora sock 09.0.07 Preseació Fabricar cora sock? No iee que ser cero el iveario? Se vio e el capíulo de iroducció. Plaificar cora sock Ciclo de pedido y fabricació idepediees. Demada aual coocida.
Potencias, Raíces y logaritmos
 Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
TRANSFORMADA z Y DE FOURIER
 Uiversidad de Medoa Dr Ig Jesús Rubé Aor Mooya Aálisis de Señales OBJEIVOS: RANSFORMADA Y DE FOURIER - Expoer los cocepos de fucioes discreas e cuao a la visió del proceso de raamieo de señales que pare
Uiversidad de Medoa Dr Ig Jesús Rubé Aor Mooya Aálisis de Señales OBJEIVOS: RANSFORMADA Y DE FOURIER - Expoer los cocepos de fucioes discreas e cuao a la visió del proceso de raamieo de señales que pare
GESTIÓN FINANCIERA. 1. Por qué se caracteriza una operación financiera? (1,5 puntos)
 Escuel Técic Superior de Iformátic Covoctori de Juio - Primer Sem Mteril Auxilir: Clculdor ficier GESTIÓN FINANCIERA 27 de Myo de 2-8, hors Durció: 2 hors. Por qué se crcteriz u operció ficier? (, putos)
Escuel Técic Superior de Iformátic Covoctori de Juio - Primer Sem Mteril Auxilir: Clculdor ficier GESTIÓN FINANCIERA 27 de Myo de 2-8, hors Durció: 2 hors. Por qué se crcteriz u operció ficier? (, putos)
INTEGRACIÓN. CÁLCULO DE
 Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
Cpítulo INTEGRACIÓN. CÁLCULO DE ÁREAS.. Introducción Si el problem del cálculo de l rect tngente llevó los mtemáticos del siglo XVII l desrrollo de ls técnics de l derivción, otro problem, el del cálculo
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
ESTADÍSTICA II SOLUCIÓN-PRÁCTICA 7: SERIES DE TIEMPO EJERCICIO 1 (NOVALES 2.1)
 ESTADÍSTICA II SOLUCIÓN-PRÁCTICA 7: SERIES DE TIEMPO EJERCICIO (NOVALES.) Cosideremos P P e g. Dado que dicha fució es coiua y que exise y so coiuas las derivadas de odos los órdees, podemos aplicar Taylor
ESTADÍSTICA II SOLUCIÓN-PRÁCTICA 7: SERIES DE TIEMPO EJERCICIO (NOVALES.) Cosideremos P P e g. Dado que dicha fució es coiua y que exise y so coiuas las derivadas de odos los órdees, podemos aplicar Taylor
8 - Ecuación de Dirichlet.
 Ecuciones Diferenciles de Orden Superior Prte V III Integrl de Dirichle t Ing. Rmón scl Prof esor Titulr de nálisi s de Señles Sistems Teorí de los Circuit os I I en l UTN, Fcultd Regionl vellned uenos
Ecuciones Diferenciles de Orden Superior Prte V III Integrl de Dirichle t Ing. Rmón scl Prof esor Titulr de nálisi s de Señles Sistems Teorí de los Circuit os I I en l UTN, Fcultd Regionl vellned uenos
ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS
 ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS Métodos Numéricos /Aálisis Numérico/ Cálculo Numérico Objetivo: Resolució de sistems de ecucioes lieles homogées por métodos proimdos. SISTEMAS DE ECUACIONES
ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS Métodos Numéricos /Aálisis Numérico/ Cálculo Numérico Objetivo: Resolució de sistems de ecucioes lieles homogées por métodos proimdos. SISTEMAS DE ECUACIONES
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
