TEMA 2. Métodos iterativos de resolución de Sistemas de Ecuaciones Lineales
|
|
|
- Esteban Maestre Ríos
- hace 5 años
- Vistas:
Transcripción
1 TEMA : Métodos tertvos de resolucón TEMA. Métodos tertvos de resolucón de Sstems de Ecucones Lneles. Métodos tertvos: ntroduccón Aplcr un método tertvo pr l resolucón de un sstem S A b, consste en trnsformrlo en lo que se denomn un sstem de punto fjo, que se equvlente l ddo y cuy solucón se prom pso pso. Pr obtener el sstem de punto fjo equvlente l ddo se elge un mtrz M que se fácl de nvertr y se escrbe l mtrz A como: A M + (A M Entonces el sstem A b se trnsform en: (M + (A M b M (M A + b S desgnmos N M-A, qued M N + b (*. L promcón -ésm de l solucón,, se obtene, en l tercón, prtr de l promcón nteror (- : Es decr: M N (- + b B (- + c Sendo B M - N M - (M-A y c M - b. Cundo este proceso es convergente el límte de ls promcones cundo es l solucón del sstem de punto fjo plntedo y, en consecuenc, del sstem S ncl. Los métodos tertvos son más decudos que los métodos drectos pr grndes sstems A b con mtrz de los coefcentes dspers y que en los métodos drectos los elementos de l mtrz A se vn modfcndo y elementos que ern nulos dejn de serlo lo lrgo del proceso de resolucón, mentrs que en los métodos tertvos sólo se hce uso de l mtrz orgnl A. El error de redondeo no tene tnt mportnc quí como en los métodos drectos. L solucón obtend es promd y hy que estblecer un crtero de prd, dependendo de l precsón requerd, del tpo: ( ε En cd tercón, el sstem (* es fácl de resolver s M es dgonl o trngulr, o en generl fáclmente nversble. Est cuestón es fundmentl en l práctc pues, unque no hy que clculr M -, sí es precso resolver sstems lneles en los que M es l mtrz de los coefcentes. Ls tres opcones pr M que presentn mejores resultdos son: M D, donde D es l mtrz dgonl cuy dgonl es l de A (Método de Jcob Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II
2 TEMA : Métodos tertvos de resolucón M L+D, donde L+D es l prte trngulr nferor de A (Método de Guss-Sedel M L+D/ω, donde ω es un número elegdo pr pondercón (Método de Sobrerreljcón El Método de Guss-Sedel es un cso prtculr del de Sobrerreljcón cundo se tom ω. El método de Sobrerreljcón con 0 < ω <, se utlz pr obtener l convergenc cundo Guss-Sedel no converge. Se tom < ω < pr celerr l convergenc cundo Guss-Sedel converge. S w < 0 ó w >, el método de Sobrerreljcón dverge. Observcones: L precsón de l solucón obtend por un método tertvo dependerá del número de tercones y de l convergenc del método. Todos los métodos tertvos requeren un estmcón ncl que desgnmos por (0 pr comenzr l tercón. (0 puede ser culquer vector (n-úpl rbtrro pero s se dspone de un buen estmcón ncl el proceso de convergenc se celer. En cso de no dsponer de un buen estmcón ncl se puede tomr (0 como el vector 0.. Convergenc de los métodos tertvos Como se h ndcdo nterormente los métodos tertvos solo se pueden plcr quellos sstems de ecucones lneles cuys propeddes grntcen l convergenc, lo que no sempre es posble...defncón Se dce que un sucesón de vectores { } converge respecto de cert norm y se escrbe lm, (o ben, s cundo: lm 0, (o ben, 0 s s respecto de l norm, s y solo s, lo hce componente componente, es decr,,,, n n cundo. Ls epresones escrts son ndependentes de l norm elegd... Teorem de crcterzcón de l convergenc Son equvlentes:. El método tertvo converge. ρ B <, pr B M - N M - (M-A.. 3. B <, pr l menos lgun norm mtrcl subordnd. Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II
3 TEMA : Métodos tertvos de resolucón Not: El coste operconl de cd pso en los métodos tertvos es del orden de n opercones. Recordemos (tem que l resolucón por métodos drectos conllev un número de opercones del orden de n 3 por lo que los métodos tertvos resultn rentbles s l solucón puede hllrse en bstnte menos de n psos. 3. Método de Jcob Ddo un sstem S A b, el método de Jcob consste en terr el sstem de punto fjo D (D A + b, es decr, D (D A (- + b donde D es l mtrz dgonl cuyos elementos son los de l dgonl de A. Observemos que equvle despejr ls ncógnts de los elementos de l dgonl en S. ( b 3 3 n n nn b ( b 33 n n nn b S n + n + + nnn b n n n n n ( b nn n El método de Jcob se plc sguendo l sguente secuenc de psos: Prmer pso: se susttuye en el segundo membro ls ncógnts por l estmcón ncl,,,,, n n Los vlores obtendos en el prmer membro consttuyen l prmer promcón ( ( (,, 3,,n Segundo pso: se susttuye en el segundo membro ls ncógnts por l promcón obtend en el pso nteror,,,,, 3 3 n n Los vlores obtendos en el prmer membro consttuyen l segund promcón ( En generl: ( (,, 3,,n y sí sucesvmente. nn Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 3
4 TEMA : Métodos tertvos de resolucón ( b 33 nn n ( b 33 nn ( bn n n nn n nn Cuándo prmos?: Crtero de convergenc (crtero de prd Se utlz como crtero un cot de l dferenc en norm entre dos promcones (terdos consecutvs. ( Tol < (tolernc O ben ( < Tol Como norm hbtul se us l norm del supremo (, es decr má ( ( n Ejercco: Pr el sstem lnel Se pde clculr ls dos prmers tercones pr el método de Jcob, tomndo como estmcón ncl (0 (,, (Usr 3 cfrs decmles pr redondeo en ls opercones 4. Método de Guss-Sedel Ddo S A b, el método de Guss-Sedel consste en terr el sstem de punto fjo (L+D (L+D A + b, Obsérvese que A-(L+D es l mtrz trngulr superor cuyos elementos no nulos son los que están por encm de l dgonl superor, es decr, Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 4
5 TEMA : Métodos tertvos de resolucón 0 n 0 0 n A-(L+D U Luego, l ecucón nteror qued de l form (L+D -U + b, y ls sucesvs tercones se obtenen mednte (L+D U (- + b ( b 3 3 n n nn b ( b 33 nn nn b S n + n + + nnn b n n ( b n n n nn n L secuenc de psos es semejnte l segud en el método de Jcob con l dferenc de que los vlores obtendos pr j, j,,, se utlzn pr promr +. Prmer pso: se susttuye en l prmer ecucón del segundo membro ls ncógnts en negro por l estmcón ncl,,, pr obtener, 3 3 n n nn A contnucón, se susttuye en l segund ecucón pr obtener,,, n n Segudmente sustturímos en l tercer ecucón,, ,,n n pr obtener 3 y sí sucesvmente hst obtener ( (,, 3,,n Segundo pso: se procede ecucón por ecucón del sstem de mner nálog l prmer pso pr obtener ( (,, 3,,n y sí sucesvmente. En generl: ( ( ( ( b 33 nn n ( ( ( b 33 nn ( bn n n nn n nn Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 5
6 TEMA : Métodos tertvos de resolucón Se utlz el msmo crtero de convergenc (o de prd que en el método de Jcob. 4.. Teorem S A es un mtrz estrctmente dgonlmente domnnte, entonces pr culquer estmcón ncl (0, ls tercones de Jcob y de Guss-Sedel convergen l solucón del sstem ncl S A b. S A es un mtrz smétrc defnd postv, Guss-Sedel converge sempre l solucón del sstem ncl S A b. 5. Método de Sobrerreljcón S pr un sstem determndo, S A b, el método de Guss-Sedel converge, entonces h de verfcrse, en generl, que cd promcón de cd ncógnt estrá más cerc de l solucón que ( pr cd n. El método de sobrerreljcón se bs en l de de que el proceso de convergenc puede ( celerrse ponderndo l dferenc entre los vlores y pr cd n, es decr, ( + ω d pr cd n, donde d ˆ (denotndo por ( sobrerreljcón y por Susttuyendo y operndo, qued: ( + ω d l promcón obtend por el método de ˆ l que se obtendrí plcndo Guss-Sedel ( ( + ω ( ˆ ω + ωˆ pr cd n ( El proceso consste, en consecuenc, en hllr cd tercón de Guss-Sedel y ponderrl con el ω elegdo. L secuenc de psos es l sguente: Prmer pso: prtendo de l estmcón ncl (0 se obtene l prmer tercón de Guss-Sedel como se h eplcdo nterormente y se l desgn ( 3 n ˆ ˆ, ˆ, ˆ,,ˆ ( A contnucón, se hll l prmer tercón de sobrerreljcón según l fórmul de dcho método ω + ω ˆ ω ω ( ω + ω ˆ ( (0 ( ( (0 ( ˆ + ( (0 ( n n Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 6
7 TEMA : Métodos tertvos de resolucón Segundo pso: con est promcón obtend ( (,, 3,,n segund tercón con Guss-Sedel y l denotmos ˆ ( ( ˆ, ˆ ˆ ˆ, 3,,n se clcul l y se plc l fórmul de sobrerreljcón pr obtener l segund tercón ( (,, 3,,n ω + ω ˆ ω + ω ˆ ( ω + ω ˆ ( ( ( ( ( ( ( ( ( n n y sí sucesvmente. Es decr, en generl: ω + ω ˆ ω + ω ˆ ( ω + ω ˆ ( ( ( n n ( Y desrrollándol completmente: ( ( ( ( b 33 nn ( ( ω + ω ( ( ( ( ˆ b 33 nn ( ω + ω ( b ˆ ˆ ( n n n nn ˆ n n ( ω n + ω nn L ecucón mtrcl del método se obtene prtr de l ecucón de sobrerreljcón ( ( ( ˆ ω + ω L solucón Operndo: ˆ de Guss-Sedel se obtene l despejr (L+D U (- + b en l ecucón L + D U (- + b D - L U (- + b ( D - (- L U (- + b ( ( ( ω ω D ( L U b + + Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 7
8 TEMA : Métodos tertvos de resolucón ( D ( ( + + ( D ω ω DD ( L U b D ( ω ω ω ( ( + ( D L U b D ω ω ω ( L+ D U + b El crtero de convergenc (o de prd es el msmo que en los métodos nterores. 5.. Teorem S A es un mtrz smétrc defnd postv y 0 < ω <, entonces pr culquer estmcón ncl (0, ls tercones obtends con el método de sobrerreljcón convergen l únc solucón del sstem ncl S A b. 5.. Estmcón del error Prtendo del sstem A b, se construye el sstem de punto fjo M N+b. Despejndo M - N + M - b y desgnndo por B M - N qued B + M - b y en cd tercón B (- + M - b con n. Restndo membro membro: ( ( B Y, nálogmente, ( + ( B( Aplcndo que en generl b + b, se verfc: ( ( + ( ( + ( ( ( + ( ( + B( B ( ( ( + ( B Clculndo est últm epresón: ( 0 ( + B C B C B B B Susttuyendo rrb, se tene: 0 0 B B B B Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 8
9 TEMA : Métodos tertvos de resolucón Sempre que B > 0, es decr, B <. B 0 ( B Undd Docente de Mtemátcs de l ETSITGC Asgntur: Cálculo II 9
TEMA 2. Métodos iterativos de resolución de Sistemas de Ecuaciones Lineales
 TEMA : Métodos tertvos de resolucó TEMA. Métodos tertvos de resolucó de Sstems de Ecucoes Leles. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A = b, cosste e trsformrlo e
TEMA : Métodos tertvos de resolucó TEMA. Métodos tertvos de resolucó de Sstems de Ecucoes Leles. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A = b, cosste e trsformrlo e
Sistemas de ecuaciones lineales
 Tem : Sstems de ecucones lneles A Condconmento del prolem. Cá álculo umérco Tem : Resolucón de sstems lneles B Métodos terdos: Jco, Guss-Sedel Reljcón C Métodos drectos: Fctorzcón LU Fctorzcón QR D Sstems
Tem : Sstems de ecucones lneles A Condconmento del prolem. Cá álculo umérco Tem : Resolucón de sstems lneles B Métodos terdos: Jco, Guss-Sedel Reljcón C Métodos drectos: Fctorzcón LU Fctorzcón QR D Sstems
SISTEMAS DE ECUACIONES LINEALES
 Sstems de Ecucones Lneles www.tgors.es SISTEMS DE ECUCIONES LINELES Estudr un Sstem de Ecucones Lneles S.E.L.) es responder ls pregunts: tene solucón?. s es sí,, cuánts tene cuáles son?. l vst de ests
Sstems de Ecucones Lneles www.tgors.es SISTEMS DE ECUCIONES LINELES Estudr un Sstem de Ecucones Lneles S.E.L.) es responder ls pregunts: tene solucón?. s es sí,, cuánts tene cuáles son?. l vst de ests
SISTEMAS DE ECUACIONES LINEALES. TEMA 3. Métodos iterativos para Sistemas de Ecuaciones Lineales
 TEMA3: Métodos tertvos pr Sstems de Ecucoes Leles TEMA 3. Métodos tertvos pr Sstems de Ecucoes Leles 3. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A=b, cosste e trsformrlo
TEMA3: Métodos tertvos pr Sstems de Ecucoes Leles TEMA 3. Métodos tertvos pr Sstems de Ecucoes Leles 3. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A=b, cosste e trsformrlo
TEMA 4: RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES Y NO LINEALES. MÉTODOS ITERATIVOS.
 Tem 4: esolucón de sstems de ecucones lneles y no lneles. étodos tertvos. TEA 4: ESLUCIÓ DE SISTEAS DE ECUACIES LIEALES Y LIEALES. ÉTDS ITEATIVS. 4..- AS VECTIALES Y ATICIALES Tnto en el estudo del condconmento
Tem 4: esolucón de sstems de ecucones lneles y no lneles. étodos tertvos. TEA 4: ESLUCIÓ DE SISTEAS DE ECUACIES LIEALES Y LIEALES. ÉTDS ITEATIVS. 4..- AS VECTIALES Y ATICIALES Tnto en el estudo del condconmento
Números Reales y Complejos
 Apéndce C Números Reles y Complejos C.. Los números reles Suponemos conocdo el conjunto de los números reles. Vmos defnr y estudr en lgunos conceptos como relcones de orden, ntervlos, cots y vlor bsoluto.
Apéndce C Números Reles y Complejos C.. Los números reles Suponemos conocdo el conjunto de los números reles. Vmos defnr y estudr en lgunos conceptos como relcones de orden, ntervlos, cots y vlor bsoluto.
Calcular el equivalente Thevenin y Norton entre los puntos a y b en el circuito de la figura
 Ejemplos de cálculo de crcutos equlentes. Aplccón de los teorems de Theenn y Norton Clculr el equlente Theenn y Norton entre los puntos y en el crcuto de l fgur Ω 4Ω 3 6Ω L Ω 5Ω V L Pr clculr el equlente
Ejemplos de cálculo de crcutos equlentes. Aplccón de los teorems de Theenn y Norton Clculr el equlente Theenn y Norton entre los puntos y en el crcuto de l fgur Ω 4Ω 3 6Ω L Ω 5Ω V L Pr clculr el equlente
FUNDAMENTOS DE INGENIERÍA ELÉCTRICA. José Francisco Gómez González Benjamín González Díaz María de la Peña Fabiani Bendicho Ernesto Pereda de Pablo
 FUNDAMENTOS DE NGENEÍA EÉCTCA José Frncsco Gómez González Benjmín González Díz Mrí de l Peñ Fn Bendcho Ernesto Pered de Plo Tem 1: Generlddes y CC en régmen estconro PUNTOS OBJETO DE ESTUDO 3 Generlddes
FUNDAMENTOS DE NGENEÍA EÉCTCA José Frncsco Gómez González Benjmín González Díz Mrí de l Peñ Fn Bendcho Ernesto Pered de Plo Tem 1: Generlddes y CC en régmen estconro PUNTOS OBJETO DE ESTUDO 3 Generlddes
Práctica 2: Codificación Aritmética.
 TRANMÓN DE DATO 006/07 Práctc : Codfccón Artmétc. Apelldos, nombre Apelldos, nombre Grupo Puesto Fech 0 Octubre/ Novembre 006 El objetvo de est práctc es ntroducr l lumno en los fundmentos de ls codfccón
TRANMÓN DE DATO 006/07 Práctc : Codfccón Artmétc. Apelldos, nombre Apelldos, nombre Grupo Puesto Fech 0 Octubre/ Novembre 006 El objetvo de est práctc es ntroducr l lumno en los fundmentos de ls codfccón
EJERCICIOS NÚMEROS COMPLEJOS. 3+4i 20º
 EJERCICIOS NÚMEROS COMPLEJOS Represent gráfcmente pr: --- -- - -- - - / - Hll ls rones trgonométrcs del ángulo AOB sendo que A es el fjo del complejo ε B el fjo del complejo σ O ˆ â B - ε ; ˆ rg sen ˆ
EJERCICIOS NÚMEROS COMPLEJOS Represent gráfcmente pr: --- -- - -- - - / - Hll ls rones trgonométrcs del ángulo AOB sendo que A es el fjo del complejo ε B el fjo del complejo σ O ˆ â B - ε ; ˆ rg sen ˆ
FUNDAMENTOS TICOS TEMA 5: CÁLCULO INTEGRAL DE FUNCIONES DE UNA Y DOS VARIABLES
 FUNDAMENTOS MATEMÁTICOS TICOS TEMA 5: CÁLCULO INTEGRAL DE FUNCIONES DE UNA Y DOS VARIABLES CÁLCULO INTEGRAL DE FUNCIONES DE UNA VARIABLE Integrl defnd Dd un funcón f, exste otr F tl que F = f? Integrcón
FUNDAMENTOS MATEMÁTICOS TICOS TEMA 5: CÁLCULO INTEGRAL DE FUNCIONES DE UNA Y DOS VARIABLES CÁLCULO INTEGRAL DE FUNCIONES DE UNA VARIABLE Integrl defnd Dd un funcón f, exste otr F tl que F = f? Integrcón
INTEGRACION DE ECUACIONES DIFERENCIALES
 INTEGRACION DE ECUACIONES DIFERENCIALES Métodos que no comenzn por s msmos Métodos Numércos G. Pce Edtorl EUDENE -997. Métodos Numércos pr Ingeneros.- Cpr Cnle. Ed. McGrw Hll Intermercn.007. Análss Numérco.-
INTEGRACION DE ECUACIONES DIFERENCIALES Métodos que no comenzn por s msmos Métodos Numércos G. Pce Edtorl EUDENE -997. Métodos Numércos pr Ingeneros.- Cpr Cnle. Ed. McGrw Hll Intermercn.007. Análss Numérco.-
José Francisco Gómez González Benjamín González Díaz María de la Peña Fabiani Bendicho Ernesto Pereda de Pablo
 José Frncsco Gómez González Benjmín González Díz Mrí de l Peñ Fn Bendcho Ernesto Pered de Plo PUNTOS OBJETO DE ESTUDO Generlddes Análss de crcutos por el método mtrcl. Teorems de crcutos: Superposcón
José Frncsco Gómez González Benjmín González Díz Mrí de l Peñ Fn Bendcho Ernesto Pered de Plo PUNTOS OBJETO DE ESTUDO Generlddes Análss de crcutos por el método mtrcl. Teorems de crcutos: Superposcón
Dado el sistema de ecuaciones lineales de la forma
 Aálss del Error e Solucó de Sstems de Ecucoes Leles Ddo el sstem de ecucoes leles de l form R A b, dode A ; b R E reldd teemos: A δa δ b δb A Aδ δa δa δ A δb S desprecmosδa δ : δ A - δb δa Métodos Numércos
Aálss del Error e Solucó de Sstems de Ecucoes Leles Ddo el sstem de ecucoes leles de l form R A b, dode A ; b R E reldd teemos: A δa δ b δb A Aδ δa δa δ A δb S desprecmosδa δ : δ A - δb δa Métodos Numércos
i = -1 / i = 1 se pueden calcular las raíces de índice par con cantidad subradical negativa, las que no tienen solución en IR. Ejemplos: d) 81 e) 121
 Los números gnros: Clse-15 En hy stucones que no tenen solucón; por ejemplo no exste nngún número cuyo cudrdo se gul -1. Pr dr solucón est stucón recurrremos l conjunto de los números mgnros, donde se
Los números gnros: Clse-15 En hy stucones que no tenen solucón; por ejemplo no exste nngún número cuyo cudrdo se gul -1. Pr dr solucón est stucón recurrremos l conjunto de los números mgnros, donde se
8. 3 2a = 0 a = 3 / 2 3b 4 = 0 b = 4 / 3. Página a) (2, 4) b) (4, 1) c) ( 3, 4) d) (5, 0)
 TEMA. NÚMEROS COMPLEJOS SOLUCIONES DE LAS ACTIVIDADES Págs. 9 55 Págn 9. S x es un número dferente de 0, x > 0. S x 0, x 0. Por lo tnto, no exste nngún número rel cuyo cudrdo se.. Debe ser menor que 0.
TEMA. NÚMEROS COMPLEJOS SOLUCIONES DE LAS ACTIVIDADES Págs. 9 55 Págn 9. S x es un número dferente de 0, x > 0. S x 0, x 0. Por lo tnto, no exste nngún número rel cuyo cudrdo se.. Debe ser menor que 0.
INDICE. Operaciones básicas. Matrices. Matriz cuadrada. Traza de una matriz. Suma y resta de matrices. Producto de matrices.
 Fculltd de Cencs Agrrs - MATERIIALL PPREPPARADO PPOR LL cc Mss Scc Abbbb tttt Noorr IInngg Aggrr.. Mss Scc.. Boocc Teerreess IInngg Zoooott.. FFeerrnnáánnddeezz Edduurrddoo IInngg.. Aggrr.. Mss Scc.. PPeerreerr
Fculltd de Cencs Agrrs - MATERIIALL PPREPPARADO PPOR LL cc Mss Scc Abbbb tttt Noorr IInngg Aggrr.. Mss Scc.. Boocc Teerreess IInngg Zoooott.. FFeerrnnáánnddeezz Edduurrddoo IInngg.. Aggrr.. Mss Scc.. PPeerreerr
MATEMÁTICA 4º. Prof. Sandra Corti
 L rdccón de se negtv e índce pr no tene solucón en el conjunto de los números reles ( 4; 25, 16, etc.), y que no exste nngún número rel que elevdo un potenc pr dé por resultdo un número negtvo. Se defne
L rdccón de se negtv e índce pr no tene solucón en el conjunto de los números reles ( 4; 25, 16, etc.), y que no exste nngún número rel que elevdo un potenc pr dé por resultdo un número negtvo. Se defne
RAÍCES COMPLEJAS DE LAS FUNCIONES CUADRÁTICAS: INTERPRETACIÓN GRÁFICA
 RAÍCES COMPLEJAS DE LAS FUNCIONES CUADRÁTICAS: INTERPRETACIÓN GRÁFICA Hydeé Blnco Insttuto Superor del Profesordo "Dr. Joquín V. González" Buenos Ares (Argentn) RESUMEN En este rtículo se present un form
RAÍCES COMPLEJAS DE LAS FUNCIONES CUADRÁTICAS: INTERPRETACIÓN GRÁFICA Hydeé Blnco Insttuto Superor del Profesordo "Dr. Joquín V. González" Buenos Ares (Argentn) RESUMEN En este rtículo se present un form
Examen de Física-1, 1 Ingeniería Química Enero de 2011 Cuestiones (Un punto por cuestión).
 Exmen de Físc-1, 1 Ingenerí Químc Enero de 211 Cuestones (Un punto por cuestón). Cuestón 1: Supong que conocemos l poscón ncl x y l velocdd ncl v de un oscldor rmónco cuy frecuenc ngulr es tmén conocd;
Exmen de Físc-1, 1 Ingenerí Químc Enero de 211 Cuestones (Un punto por cuestón). Cuestón 1: Supong que conocemos l poscón ncl x y l velocdd ncl v de un oscldor rmónco cuy frecuenc ngulr es tmén conocd;
MALLAS EN CIRCUTOS CC
 LECCIÓN Nº 03 MALLAS EN CICUTOS CC 1. EDES ELECTICAS Cundo los elementos áscos de un crcuto se conectn pr formr un crcuto, l nterconexón resultnte se descre en térmnos de nodos, cmnos, rms, lzos y mlls.
LECCIÓN Nº 03 MALLAS EN CICUTOS CC 1. EDES ELECTICAS Cundo los elementos áscos de un crcuto se conectn pr formr un crcuto, l nterconexón resultnte se descre en térmnos de nodos, cmnos, rms, lzos y mlls.
Resolución de sistemas de congruencias
 Resolucó de sstems de cogruecs E este prtdo veremos cómo utlzr l rtmétc modulr pr resolver u problem muy tguo, coocdo como problem cho de los restos, que reformulremos hor utlzdo el leguje modero de ls
Resolucó de sstems de cogruecs E este prtdo veremos cómo utlzr l rtmétc modulr pr resolver u problem muy tguo, coocdo como problem cho de los restos, que reformulremos hor utlzdo el leguje modero de ls
En general puede representarse por : Clase 6 3
 Encontrar raíces de uncones es uno de los problemas más comunes en ngenería Los métodos numércos para encontrar raíces de uncones son utlzados cuando las técncas analítcas no pueden ser aplcadas. Esto
Encontrar raíces de uncones es uno de los problemas más comunes en ngenería Los métodos numércos para encontrar raíces de uncones son utlzados cuando las técncas analítcas no pueden ser aplcadas. Esto
EJERCICIOS REPASO II
 EJERCICIOS REPASO II Profesor: Jun Antono González Díz Deprtmento Métodos Cuntttvos Unversdd Pblo de Olvde EJERCICIO 4: El S. Sous h percbdo un herenc vlord en 90.000. L entdd que geston el cobro de l
EJERCICIOS REPASO II Profesor: Jun Antono González Díz Deprtmento Métodos Cuntttvos Unversdd Pblo de Olvde EJERCICIO 4: El S. Sous h percbdo un herenc vlord en 90.000. L entdd que geston el cobro de l
LONGITUD DE ARCO. Una aproximación es una línea recta desde el punto x=a hasta el punto x=b, como se indica en la figura:
 LONGITUD DE ARCO Clculr l longtud de rco o de un curv dd por un funcón f en un ntervlo x, tene muchs plccones en ls cencs. Es necesro que hgmos un reve estudo del cálculo de ells. Un proxmcón es un líne
LONGITUD DE ARCO Clculr l longtud de rco o de un curv dd por un funcón f en un ntervlo x, tene muchs plccones en ls cencs. Es necesro que hgmos un reve estudo del cálculo de ells. Un proxmcón es un líne
Interpolación Polinómica
 .- Dd l tbl de vlores: Interpolcón Polnómc - y 7 9 ) Encontrr el splne cúbco nturl que nterpol estos dtos, mponendo ls condcones requerds y resolvendo el sstem. b) Msm cuestón resolvendo prevmente el sstem
.- Dd l tbl de vlores: Interpolcón Polnómc - y 7 9 ) Encontrr el splne cúbco nturl que nterpol estos dtos, mponendo ls condcones requerds y resolvendo el sstem. b) Msm cuestón resolvendo prevmente el sstem
Tema 10: Variables aleatorias
 Análss de Dtos I Esquem del Tem Tem : Vrbles letors. VARIABLES ALEATORIAS DISCRETAS FUNCIÓN DE PROBABILIDAD, f(x ) FUNCIÓN DE DISTRIBUCIÓN, F(x ) CARACTERÍSTICAS DE LAS VARIABLES DISCRETAS UNA VARIABLE:
Análss de Dtos I Esquem del Tem Tem : Vrbles letors. VARIABLES ALEATORIAS DISCRETAS FUNCIÓN DE PROBABILIDAD, f(x ) FUNCIÓN DE DISTRIBUCIÓN, F(x ) CARACTERÍSTICAS DE LAS VARIABLES DISCRETAS UNA VARIABLE:
TEMA: EXPRESIONES ALGEBRAICAS
 TEMA: EXPRESIONES ALGEBRAICAS CONCEPTO Son quells epresones en ls que ls opercones que se usn son sólo ls de dcón, sustrccón, multplccón, dvsón, potenccón, rdccón entre sus vrbles en un número lmtdo de
TEMA: EXPRESIONES ALGEBRAICAS CONCEPTO Son quells epresones en ls que ls opercones que se usn son sólo ls de dcón, sustrccón, multplccón, dvsón, potenccón, rdccón entre sus vrbles en un número lmtdo de
ALGEBRA VECTORIAL. cúbico Caudal de volumen Metro cúbico por segundo. m 3 /s CAP Magnitudes físicas. Pág. 1
 FISI I P 1 LGER VETORIL 11 Mgntudes físcs Ls mgntudes físcs, son ls propeddes que le crctern los cuerpos o los fenómenos nturles que se pueden medr, E: L longtud, l ms, l velocdd, l tempertur, etc Mentrs
FISI I P 1 LGER VETORIL 11 Mgntudes físcs Ls mgntudes físcs, son ls propeddes que le crctern los cuerpos o los fenómenos nturles que se pueden medr, E: L longtud, l ms, l velocdd, l tempertur, etc Mentrs
TEORÍA DE RENTAS DISCRETAS 1 Rentas Constantes (teoría)
 TEORÍA DE RENTAS DISCRETAS 1 Rents Constntes (teorí) Profesor: Jun Antono González Díz Deprtmento Métodos Cuntttvos Unversdd Pblo de Olvde www.clsesunverstrs.com Concepto y clsfccón En generl, un rent
TEORÍA DE RENTAS DISCRETAS 1 Rents Constntes (teorí) Profesor: Jun Antono González Díz Deprtmento Métodos Cuntttvos Unversdd Pblo de Olvde www.clsesunverstrs.com Concepto y clsfccón En generl, un rent
Programación y Métodos Numéricos: Integración Numérica- Fórmulas de de tipo interpolatorio
 Progrmcón y Métodos Numércos: Integrcón Numérc- Fórmuls de de tpo nterpoltoro Prof. Crlos Conde LázroL Prof. Arturo Hdlgo LópezL Prof. Alfredo LópezL Mrzo, 27 Deprtmento de Mtemátc Aplcd y Métodos Informátcos
Progrmcón y Métodos Numércos: Integrcón Numérc- Fórmuls de de tpo nterpoltoro Prof. Crlos Conde LázroL Prof. Arturo Hdlgo LópezL Prof. Alfredo LópezL Mrzo, 27 Deprtmento de Mtemátc Aplcd y Métodos Informátcos
(Apuntes sin revisión para orientar el aprendizaje) CÁLCULO INTEGRAL LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA
 (Aputes s revsó pr oretr el predzje) CÁLCULO INTEGRAL LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA Sumtor Pr represetr e form revd determdo tpo de sums, se utlz como símolo l letr greg sgm. Ejemplos.
(Aputes s revsó pr oretr el predzje) CÁLCULO INTEGRAL LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA Sumtor Pr represetr e form revd determdo tpo de sums, se utlz como símolo l letr greg sgm. Ejemplos.
, , ia Prestación real del acreedor Contraprestación real para el acreedor 0, ,6701
 Determnr los tntos efectvos e un préstmo smple e 0.000 euros, mortzr los ños con un tpo e nterés nul el %, s en l opercón ncen ls sguentes crcterístcs comercles: Gstos crgo el euor en el orgen y l fnl
Determnr los tntos efectvos e un préstmo smple e 0.000 euros, mortzr los ños con un tpo e nterés nul el %, s en l opercón ncen ls sguentes crcterístcs comercles: Gstos crgo el euor en el orgen y l fnl
PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 28 FISICA TOMO 2. Tercera y quinta edición. Raymond A. Serway
 PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3
PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3
Métodos computacionales Solución de sistemas de ecuaciones
 Métodos computconles Solucón de sstems de ecucones Método de Guss Sedel Introduccón Breve repso de métodos drectos Método de Guss Sedel Comprcón de Guss Sedel con Jcob Convergenc del método Conclusones
Métodos computconles Solucón de sstems de ecucones Método de Guss Sedel Introduccón Breve repso de métodos drectos Método de Guss Sedel Comprcón de Guss Sedel con Jcob Convergenc del método Conclusones
2º DE BACHILLERATO MATRICES Y DETERMINANTES Soluciones -1- DETERMINANTES MATRIZ INVERSA. Anulamos. pivotando
 º DE HLLERTO MTRES Y DETERMNNTES Soluones -- DETERMNNTES MTRZ NVERS. lulr el vlor del determnnte. Hllr, en funón de, el vlor del determnnte: en Sndo on votndo nulmos en Sndo ( ( en Sndo ( ( (. Enontrr
º DE HLLERTO MTRES Y DETERMNNTES Soluones -- DETERMNNTES MTRZ NVERS. lulr el vlor del determnnte. Hllr, en funón de, el vlor del determnnte: en Sndo on votndo nulmos en Sndo ( ( en Sndo ( ( (. Enontrr
Ecuaciones de 1 er y 2º grado
 Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
6. INTERPOLACIÓN POLINOMIAL: SPLINES
 6. INTERPOLACIÓN POLINOMIAL: SPLINES Jorge Edurdo Ortz Trvño jeortzt@unl.edu.o http:/www.doentes.unl.edu.o/jeortzt/ Coeentes de un polnomo de nterpolón Un método dreto pr lulr los oeentes de un polnomo
6. INTERPOLACIÓN POLINOMIAL: SPLINES Jorge Edurdo Ortz Trvño jeortzt@unl.edu.o http:/www.doentes.unl.edu.o/jeortzt/ Coeentes de un polnomo de nterpolón Un método dreto pr lulr los oeentes de un polnomo
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO FÍSICA C Tercera evaluación SOLUCIÓN
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 0-03 FÍSICA C Tercer evlucón SOLUCIÓN Pregunt (5 puntos) Un eser conductor con rdo nteror de 7 cm y rdo exteror de 8 cm
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 0-03 FÍSICA C Tercer evlucón SOLUCIÓN Pregunt (5 puntos) Un eser conductor con rdo nteror de 7 cm y rdo exteror de 8 cm
Resolución de sistemas lineales por métodos directos
 Resolucón de sstemas lneales por métodos drectos Descomposcón LU S la matr del sstema Ax = b se expresa como producto de una matr trangular nferor, L, de una superor, U, la resolucón del msmo se reduce
Resolucón de sstemas lneales por métodos drectos Descomposcón LU S la matr del sstema Ax = b se expresa como producto de una matr trangular nferor, L, de una superor, U, la resolucón del msmo se reduce
10 1 deca da 10 2 hecto h 10 3 kilo k 10 6 Mega M 10 9 Giga G Tera T Peta P Exa E Zetta Z Yotta Y
 Un mgntud es culquer cos que puede ser medd medr no es más que comprr un mgntud con otr de l msm espece que se tom como referenc. Ls mgntudes se epresn con un número uns unddes. En lguns ocsones el número
Un mgntud es culquer cos que puede ser medd medr no es más que comprr un mgntud con otr de l msm espece que se tom como referenc. Ls mgntudes se epresn con un número uns unddes. En lguns ocsones el número
Aprendizaje en redes neuronales. Inteligencia Artificial Josué Jesús Pedroza Almaguer Profr. Alfonso Garcés Báez BUAP-FCC, Verano 2003
 Aprendze en redes neuronles. Intelgenc Artfcl Josué Jesús Pedroz Almguer Profr. Alfonso Grcés Báez BUAP-FCC, Verno 2003 Introduccón Como funcon el cerebro Ls neurons Axones Snpss Potencl de ccón, exctdores,
Aprendze en redes neuronles. Intelgenc Artfcl Josué Jesús Pedroz Almguer Profr. Alfonso Grcés Báez BUAP-FCC, Verno 2003 Introduccón Como funcon el cerebro Ls neurons Axones Snpss Potencl de ccón, exctdores,
LA RIOJA / JUNIO 01. LOGSE / FÍSICA / EXAMEN COMPLETO
 LA RIOJA / JUNIO 1. LOGS / FÍSICA / XAMN COMPLTO l luno elegá un de ls opcones de pobles y cuto de ls cnco cuestones popuests. Cd poble puntú sobe tes puntos y cd cuestón sobe uno. Opcón de pobles 1 A.
LA RIOJA / JUNIO 1. LOGS / FÍSICA / XAMN COMPLTO l luno elegá un de ls opcones de pobles y cuto de ls cnco cuestones popuests. Cd poble puntú sobe tes puntos y cd cuestón sobe uno. Opcón de pobles 1 A.
Matemáticas Avanzadas para Ingeniería Convergencia de Series de Potencias
 Mateátcas Avanzadas para Ingenería Convergenca de Seres de Potencas. Para la sere de potencas + ( + 2 + z) ( + ) = converge sólo para su centro z o = 2 + 3 y rado R = 4 Tenendo la varable z, teneos una
Mateátcas Avanzadas para Ingenería Convergenca de Seres de Potencas. Para la sere de potencas + ( + 2 + z) ( + ) = converge sólo para su centro z o = 2 + 3 y rado R = 4 Tenendo la varable z, teneos una
Te c n o l o g í a d e l o s S e r v i c i o s A u x i l i a r e s - A p u n t e s d e C l a s e - 1
 ENTALPA NORMAL DE FORMACÓN : f L entlpí norml de formcón de un compuesto es el clor que se extre durnte su reccón de formcón sempre que se mnteng constnte l presón durnte todo el proceso y ls temperturs
ENTALPA NORMAL DE FORMACÓN : f L entlpí norml de formcón de un compuesto es el clor que se extre durnte su reccón de formcón sempre que se mnteng constnte l presón durnte todo el proceso y ls temperturs
I Resolución de sistemas de ecuaciones lineales
 ESCUELA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA FUNDAMENTOS MATEMÁTICOS I Resolución de sistems de ecuciones lineles Objetivo: El lumno deberá tener
ESCUELA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA FUNDAMENTOS MATEMÁTICOS I Resolución de sistems de ecuciones lineles Objetivo: El lumno deberá tener
PRÉSTAMOS HIPOTECARIOS J 12 = 4,5 % (NOMINAL) T.A.E. 4,6386 %
 Escuel Técnc Superor de Informátc Convoctor de Juno - Prmer Semn Mterl Auxlr: Clculdor fnncer GESTIÓN FINANCIERA 5 de Myo de 7-8,3 hors Durcón: hors. Ley de descuento compuesto: expresón mtemátc, vlor
Escuel Técnc Superor de Informátc Convoctor de Juno - Prmer Semn Mterl Auxlr: Clculdor fnncer GESTIÓN FINANCIERA 5 de Myo de 7-8,3 hors Durcón: hors. Ley de descuento compuesto: expresón mtemátc, vlor
OCW-V.Muto Técnicas iterativas para resolver sistemas lineales Cap. XVII CAPITULO XVII. TECNICAS ITERATIVAS PARA RESOLVER SISTEMAS LINEALES
 CAPITULO XVII. TECNICAS ITERATIVAS PARA RESOLVER SISTEMAS LINEALES. INTRODUCCION Y METODO Una técnca teratva para resolver un sstema lneal A x = b de n n empeza con una aproxmacón ncal x (0) a la solucón
CAPITULO XVII. TECNICAS ITERATIVAS PARA RESOLVER SISTEMAS LINEALES. INTRODUCCION Y METODO Una técnca teratva para resolver un sstema lneal A x = b de n n empeza con una aproxmacón ncal x (0) a la solucón
TRABAJO 1: Variables Estadísticas Unidimensionales (Tema 1).
 TRABAJO 1: Varables Estadístcas Undmensonales (Tema 1). Técncas Cuanttatvas I. Curso 2016/2017. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: En los enuncados de los ejerccos que sguen aparecen
TRABAJO 1: Varables Estadístcas Undmensonales (Tema 1). Técncas Cuanttatvas I. Curso 2016/2017. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: En los enuncados de los ejerccos que sguen aparecen
Lenguaje humano. Representación de la información. Utiliza un conjunto de símbolos alfanuméricos. Puede representar Información
 Leguje humo Represetcó de l formcó Utlz u cojuto de símbolos lfumércos Crcteres lfbétcos:, B, C,.Z,, b, c,...z Símbolos umércos 9 sgos de putucó... Puede represetr Iformcó umérc lfumérc Leguje del ordedor
Leguje humo Represetcó de l formcó Utlz u cojuto de símbolos lfumércos Crcteres lfbétcos:, B, C,.Z,, b, c,...z Símbolos umércos 9 sgos de putucó... Puede represetr Iformcó umérc lfumérc Leguje del ordedor
Ondas y Rotaciones. Dinámica de las Rotaciones V
 Hoj de Trjo Onds Rotcones Dnámc de ls Rotcones V Jme Felcno Hernández Unversdd Autónom etropoltn - ztplp éco, D. F. de gosto de 0 A. ACTVDAD NDVDUAL. En est Hoj de trjo veremos otro conjunto de prolems
Hoj de Trjo Onds Rotcones Dnámc de ls Rotcones V Jme Felcno Hernández Unversdd Autónom etropoltn - ztplp éco, D. F. de gosto de 0 A. ACTVDAD NDVDUAL. En est Hoj de trjo veremos otro conjunto de prolems
MICROSOFT EXCEL EN LA SOLUCIÓN DE PROBLEMAS DE ÁLGEBRA LINEAL
 Revst Pedgogí Unverstr Vol. 8 o. MICROSOFT EXCEL E LA SOLUCIÓ DE PROBLEMAS DE ÁLGEBRA LIEAL Lc. Mrels Rsú López Proesor Asstente Dpto Mtemátcs Comptcón ISMM mrs@smm.ed.c RESUME El objetvo del presente
Revst Pedgogí Unverstr Vol. 8 o. MICROSOFT EXCEL E LA SOLUCIÓ DE PROBLEMAS DE ÁLGEBRA LIEAL Lc. Mrels Rsú López Proesor Asstente Dpto Mtemátcs Comptcón ISMM mrs@smm.ed.c RESUME El objetvo del presente
ENUNCIADOS DE LOS EJERCICIOS PROPUESTOS EN 2011 EN MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES. 3 y
 ENUNCADOS DE LOS EJERCCOS PROPUESTOS EN 011 EN MATEMÁTCAS APLCADAS A LAS CENCAS SOCALES. EJERCCO 1 a (5 puntos Raconalce las epresones y. 7 b (5 puntos Halle el conjunto de solucones de la necuacón EJERCCO
ENUNCADOS DE LOS EJERCCOS PROPUESTOS EN 011 EN MATEMÁTCAS APLCADAS A LAS CENCAS SOCALES. EJERCCO 1 a (5 puntos Raconalce las epresones y. 7 b (5 puntos Halle el conjunto de solucones de la necuacón EJERCCO
Uno de los problemas que dio origen al concepto de integral definida fue de origen geométrico:
 Mtemátc II 7 Modulo 5 Integrcón. L ntegrl defnd Uno de los prolems que do orgen l concepto de ntegrl defnd fue de orgen geométrco: Hllr el áre de un regón pln lmtd por l gráfc de un funcón f() postv y
Mtemátc II 7 Modulo 5 Integrcón. L ntegrl defnd Uno de los prolems que do orgen l concepto de ntegrl defnd fue de orgen geométrco: Hllr el áre de un regón pln lmtd por l gráfc de un funcón f() postv y
Análisis Poblacional de Mulliken y Löwdin
 nálss Poblconl de Mullken y Löwdn Densdd de Mtrz de crg (defncón): consderemos el cso de cp cerrd entonces sbemos que l probbldd de encontrr un electrón en l poscón r en el entorno dr que est en un orbtl
nálss Poblconl de Mullken y Löwdn Densdd de Mtrz de crg (defncón): consderemos el cso de cp cerrd entonces sbemos que l probbldd de encontrr un electrón en l poscón r en el entorno dr que est en un orbtl
Métodos Matemá5cos en la Ingeniería Tema 1. Ecuaciones no lineales
 Métodos Matemá5cos en la Ingenería Tema. Ecuacones no lneales Jesús Fernández Fernández Carmen María Sordo García DEPARTAMENTO DE MATEMÁTICA APLICADA Y CIENCIAS DE LA COMPUTACIÓN UNIVERSIDAD DE CANTABRIA
Métodos Matemá5cos en la Ingenería Tema. Ecuacones no lneales Jesús Fernández Fernández Carmen María Sordo García DEPARTAMENTO DE MATEMÁTICA APLICADA Y CIENCIAS DE LA COMPUTACIÓN UNIVERSIDAD DE CANTABRIA
(4 3 i)(4 3 i)
 E.T.S.I. Industrales y Telecomuncacón Curso 00-0 Grados E.T.S.I. Industrales y Telecomuncacón Asgnatura: Cálculo I Ejerccos resueltos Calcular el valor de a y b para que b a 4 sea real y de módulo undad
E.T.S.I. Industrales y Telecomuncacón Curso 00-0 Grados E.T.S.I. Industrales y Telecomuncacón Asgnatura: Cálculo I Ejerccos resueltos Calcular el valor de a y b para que b a 4 sea real y de módulo undad
C Capacitores e inductores. Circuitos de Primer Orden
 C Cpctores e nductores. Crcutos de Prmer Orden C El crcuto que se muestr en l fgur c h llegdo ls condcones de estdo estle ( l corrente en el cpctor es cero ) con el nterruptor en l poscón. S el nterruptor
C Cpctores e nductores. Crcutos de Prmer Orden C El crcuto que se muestr en l fgur c h llegdo ls condcones de estdo estle ( l corrente en el cpctor es cero ) con el nterruptor en l poscón. S el nterruptor
Práctica 4ª: RESOLUCIÓN DE SISTEMAS LINEALES. METODOS ITERATIVOS.
 practca4srnb Apelldos Nombre: Práctca 4ª: RESOLUCIÓN DE SISTEMAS LINEALES METODOS ITERATIVOS Normas vectorales normas matrcales Número de condcón de una matr Cuando se construe una sucesón de vectores
practca4srnb Apelldos Nombre: Práctca 4ª: RESOLUCIÓN DE SISTEMAS LINEALES METODOS ITERATIVOS Normas vectorales normas matrcales Número de condcón de una matr Cuando se construe una sucesón de vectores
Universidad Técnica Federico Santa María
 Unversdd Técnc Federco Snt Mrí Vrles Aletors Cpítulo 5: Vrles Aletors Dstrucones stdístc Computconl II Semestre Profesor : Héctor Allende Págn : www.nc.nf.utfsm.cl/~hllende e-ml : hllende @nf.utfsm.cl
Unversdd Técnc Federco Snt Mrí Vrles Aletors Cpítulo 5: Vrles Aletors Dstrucones stdístc Computconl II Semestre Profesor : Héctor Allende Págn : www.nc.nf.utfsm.cl/~hllende e-ml : hllende @nf.utfsm.cl
UNIVERSIDAD DIEGO PORTALES Instituto de Ciencias Básicas. Álgebra Lineal. Isabel Arratia Zárate
 UNIVERSIDD DIEGO PORTLES Insttuto de Cencs Báscs Álgebr Lnel Isbel rrt Zárte Mtrces y Sstems de ecucones lneles [Versón prelmnr] Un mtrz con componentes en un cuerpo es un rreglo en fls y columns de elementos
UNIVERSIDD DIEGO PORTLES Insttuto de Cencs Báscs Álgebr Lnel Isbel rrt Zárte Mtrces y Sstems de ecucones lneles [Versón prelmnr] Un mtrz con componentes en un cuerpo es un rreglo en fls y columns de elementos
RESISTENCIAS EN SERIE Y LEY DE LAS MALLAS V 1 V 2 V 3 A B C
 RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
Matemáticas II. Segundo Curso, Grado en Ingeniería Electrónica Industrial y Automática Grado en Ingeniería Eléctrica. 17 de febrero de
 Matemátcas II Segundo Curso, Grado en Ingenería Electrónca Industral y Automátca Grado en Ingenería Eléctrca 7 de febrero de 0. Conteste las sguentes cuestones: Ã! 0 (a) (0.5 ptos.) Escrba en forma bnómca
Matemátcas II Segundo Curso, Grado en Ingenería Electrónca Industral y Automátca Grado en Ingenería Eléctrca 7 de febrero de 0. Conteste las sguentes cuestones: Ã! 0 (a) (0.5 ptos.) Escrba en forma bnómca
Problemas de Optimización. Conceptos básicos de optimización. Indice. Un problema de optimización NLP. Equivalencias. Contornos / Curvas de nivel
 Conceptos báscos de optmzacón Problemas de Optmzacón Prof. Cesar de Prada Dpt. Ingenería de Sstemas y Automátca UVA prada@autom.uva.es mn J() h() = g() Problema general NPL Para encontrar una solucón al
Conceptos báscos de optmzacón Problemas de Optmzacón Prof. Cesar de Prada Dpt. Ingenería de Sstemas y Automátca UVA prada@autom.uva.es mn J() h() = g() Problema general NPL Para encontrar una solucón al
Métodos Numéricos. Resolución de sistemas de ecuaciones
 Al flzr est udd el prtcpte estrá e cpcdd de resolver u sstem de ecucoes leles o o leles de ecucoes co cógts por los métodos drectos e tertvos. Itroduccó Prolem clásco del álger lel: se quere solucor u
Al flzr est udd el prtcpte estrá e cpcdd de resolver u sstem de ecucoes leles o o leles de ecucoes co cógts por los métodos drectos e tertvos. Itroduccó Prolem clásco del álger lel: se quere solucor u
APLICACIONES DE LOS SISTEMAS LINEALES 1. MODELACION DE POLINOMIOS CONOCIENDO UN NUMERO DETERMINADO DE PUNTOS DEL PLANO.
 APLICACIONES DE LOS SISTEMAS LINEALES 1. MODELACION DE POLINOMIOS CONOCIENDO UN NUMERO DETERMINADO DE PUNTOS DEL PLANO. Dado un numero n de puntos del plano ( a, b ) es posble encontrar una funcón polnómca
APLICACIONES DE LOS SISTEMAS LINEALES 1. MODELACION DE POLINOMIOS CONOCIENDO UN NUMERO DETERMINADO DE PUNTOS DEL PLANO. Dado un numero n de puntos del plano ( a, b ) es posble encontrar una funcón polnómca
Problemas de Dinámica del Sólido Rígido
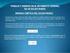 E.T.S... T Deprtento de ísc e ngenerí ucler robles de Dnác del Sóldo ígdo 1 étodo de ls celercones étodo de los oentos 3 étodo de l energí ro. J. rtín 3 1 étodo de ls celercones 1.1 Un plc rectngulr unore
E.T.S... T Deprtento de ísc e ngenerí ucler robles de Dnác del Sóldo ígdo 1 étodo de ls celercones étodo de los oentos 3 étodo de l energí ro. J. rtín 3 1 étodo de ls celercones 1.1 Un plc rectngulr unore
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL.
 VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL. Concepto de varable aleatora. Se llama varable aleatora a toda aplcacón que asoca a cada elemento del espaco muestral de un expermento, un número real.
VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL. Concepto de varable aleatora. Se llama varable aleatora a toda aplcacón que asoca a cada elemento del espaco muestral de un expermento, un número real.
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
1. Definición. Formas de definir una sucesión.
 . Definición. Forms de definir un sucesión. Un sucesión es un plicción que nos relcion los números nturles con un conjunto, de form que orden los elementos de tl conjunto. Ejemplos:. : selección espñol
. Definición. Forms de definir un sucesión. Un sucesión es un plicción que nos relcion los números nturles con un conjunto, de form que orden los elementos de tl conjunto. Ejemplos:. : selección espñol
METODOS NUMERICOS CATEDRA 0 6. Ingeniería Civil ING.CRISTIANCASTROP. Facultad de Ingeniería de Minas, Geología y Civil
 ING.CRISTIANCASTROP. CATEDRA 0 6 Facultad de Ingenería de Mnas, Geología Cvl Departamento académco de ngenería de mnas cvl METODOS NUMERICOS Ingenería Cvl ING.CRISTIANCASTROP. Captulo VI Sstema de Ecuacones
ING.CRISTIANCASTROP. CATEDRA 0 6 Facultad de Ingenería de Mnas, Geología Cvl Departamento académco de ngenería de mnas cvl METODOS NUMERICOS Ingenería Cvl ING.CRISTIANCASTROP. Captulo VI Sstema de Ecuacones
Variables Aleatorias
 Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Máximos y mínimos de una función real de dos variables reales
 Mámos mínmos de una uncón real Dencón Sea D una regón del plano Sea :D R Se dce que alcanza su valor mámo absoluto M en un punto P =, ) D cuando M =, ),),) D Se dce que tene un mámo relatvo en un punto
Mámos mínmos de una uncón real Dencón Sea D una regón del plano Sea :D R Se dce que alcanza su valor mámo absoluto M en un punto P =, ) D cuando M =, ),),) D Se dce que tene un mámo relatvo en un punto
5 Métodos iterativos para la resolución de ecuaciones algebraicas lineales Método de Gauss-Jacobi Método de Gauss-Seidel...
 CONTENIDO 5 Métodos teratvos para la resolucón de ecuacones algebracas lneales 95 5.1 Método de Gauss-Jacob................................ 95 5.2 Método de Gauss-Sedel................................
CONTENIDO 5 Métodos teratvos para la resolucón de ecuacones algebracas lneales 95 5.1 Método de Gauss-Jacob................................ 95 5.2 Método de Gauss-Sedel................................
Minimizando el error cuadrático medio se calculan los coeficientes a k : [ ] a, queda [ ] [ ] = [ ] [ ]
![Minimizando el error cuadrático medio se calculan los coeficientes a k : [ ] a, queda [ ] [ ] = [ ] [ ] Minimizando el error cuadrático medio se calculan los coeficientes a k : [ ] a, queda [ ] [ ] = [ ] [ ]](/thumbs/87/96074214.jpg) TCNOLOGÍ DL HBL. CUSO 9/ TM : PDICCIÓN LINL. Los vlores de se uede romr or u combcó lel de ls últms muestrs. co.. Método de l utocorrelcó. rror e Mmzdo el error cudrátco medo se clcul los coefcetes : e
TCNOLOGÍ DL HBL. CUSO 9/ TM : PDICCIÓN LINL. Los vlores de se uede romr or u combcó lel de ls últms muestrs. co.. Método de l utocorrelcó. rror e Mmzdo el error cudrátco medo se clcul los coefcetes : e
POLINOMIOS ORTOGONALES Apuntes y Ejercicios RESUMEN DE CONTENIDOS POLINOMIOS ORTOGONALES. Se define, en primer lugar, el operador proyección mediante
 Uversdd de Stgo de Chle Fcultd de Cecs Deprtmeto de Mtemátcs y Cecs de l Computcó Aputes y Ejerccos RESUMEN DE CONTENIDOS. Recordr: Proceso de ortogolzcó de Grm-Schmdt: Se defe, e prmer lugr, el operdor
Uversdd de Stgo de Chle Fcultd de Cecs Deprtmeto de Mtemátcs y Cecs de l Computcó Aputes y Ejerccos RESUMEN DE CONTENIDOS. Recordr: Proceso de ortogolzcó de Grm-Schmdt: Se defe, e prmer lugr, el operdor
Ejercicios T2- ANÁLISIS DE DATOS UNIDIMENSIONALES
 Ejerccos T- NÁLII DE DTO UNIDIMENIONLE.- El número de clentes qe cden n estblecmento en cert hor hn sdo lo lrgo del últmo mes h sdo:,,,,7,,,,,,6,,6,,8,,,,,6,,8,,9,,,, Representr l tbl de frecencs, el dgrm
Ejerccos T- NÁLII DE DTO UNIDIMENIONLE.- El número de clentes qe cden n estblecmento en cert hor hn sdo lo lrgo del últmo mes h sdo:,,,,7,,,,,,6,,6,,8,,,,,6,,8,,9,,,, Representr l tbl de frecencs, el dgrm
Variables Aleatorias
 Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Varables Aleatoras VARIABLES ALEATORIAS. Varable aleatora. Tpos.... Dstrbucón de probabldad asocada a una varable aleatora dscreta... 4. Funcón de dstrbucón. Propedades... 5 4. Funcón de densdad... 7 5.
Determinantes y la Regla de Cramer
 Determinntes y l Regl de Crmer Mtriz Invers Not: un mtriz cudrd que no tiene invers se llm mtriz singulr. Ejemplo: Hllr l invers de A. A 4 Si l plicr el método de Guss se obtiene ceros en los elementos
Determinntes y l Regl de Crmer Mtriz Invers Not: un mtriz cudrd que no tiene invers se llm mtriz singulr. Ejemplo: Hllr l invers de A. A 4 Si l plicr el método de Guss se obtiene ceros en los elementos
VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL.
 VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL. Concepto de varable aleatora. Se llama varable aleatora a toda aplcacón que asoca a cada elemento del espaco muestral de un epermento, un número real.
VARIABLE ALEATORIA DISCRETA. DISTRIBUCIÓN BINOMIAL. Concepto de varable aleatora. Se llama varable aleatora a toda aplcacón que asoca a cada elemento del espaco muestral de un epermento, un número real.
En este capítulo se describe el problema de máxima cobertura sin capacidad (MCLP) y con
 CAPITULO 3 Descrcón del roblem En este cítulo se descrbe el roblem de mám cobertur sn ccdd (MCLP) con ccdd (CMCLP). Posterormente se resentn los modelos de rogrmcón mtemátc r mbos. 3.1 Descrcón del MCLP
CAPITULO 3 Descrcón del roblem En este cítulo se descrbe el roblem de mám cobertur sn ccdd (MCLP) con ccdd (CMCLP). Posterormente se resentn los modelos de rogrmcón mtemátc r mbos. 3.1 Descrcón del MCLP
MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA
 MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA Dr. José A. Peñlbert Unversdd de Puerto Rco en Croln Deprtmento de Cencs Nturles Introduccón Hn surgdo un sere de teorís sobre el funconnmento
MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA Dr. José A. Peñlbert Unversdd de Puerto Rco en Croln Deprtmento de Cencs Nturles Introduccón Hn surgdo un sere de teorís sobre el funconnmento
ESTIMACIÓN DE DEMANDA DE TRANSITO EN CARRETERAS COMBINANDO ESTUDIOS ORIGEN-DESTINO CON AFOROS
 ISS 088797 ESIMACIÓ DE DEMADA DE RASIO E CARREERAS COMBIADO ESUDIOS ORIGEDESIO CO AFOROS Roberto de l LLt Gómez Publccón écnc o. 5 Snfndl, Qro, 99 SECREARIA DE COMUICACIOES Y RASPORES ISIUO MEXICAO DEL
ISS 088797 ESIMACIÓ DE DEMADA DE RASIO E CARREERAS COMBIADO ESUDIOS ORIGEDESIO CO AFOROS Roberto de l LLt Gómez Publccón écnc o. 5 Snfndl, Qro, 99 SECREARIA DE COMUICACIOES Y RASPORES ISIUO MEXICAO DEL
El estudio de los determinantes será el hilo conductor de la unidad, los alumnos aprenderán a trabajar con ellos y comprobarán
 DETERMINANTES El estudo de los deternntes será el lo conductor de l undd, los lunos prenderán trbjr con ellos y coprobrán su plccón en l resolucón de probles y en prtculr en l resolucón de sstes de ecucones
DETERMINANTES El estudo de los deternntes será el lo conductor de l undd, los lunos prenderán trbjr con ellos y coprobrán su plccón en l resolucón de probles y en prtculr en l resolucón de sstes de ecucones
DESARROLLO DE UN SOFTWARE EN
 DESARROO DE UN SOFTWARE EN EEMENTOS FINITOS COMPATIBE CON GID PARA RESOUCIÓN DE PROBEMAS EÁSTICO INEAES. Verónc Gllego Otlvro Coordndor Sntgo Corre Grupo de Bongenerí EAFIT //9 Contendo INTRODUCCIÓN...
DESARROO DE UN SOFTWARE EN EEMENTOS FINITOS COMPATIBE CON GID PARA RESOUCIÓN DE PROBEMAS EÁSTICO INEAES. Verónc Gllego Otlvro Coordndor Sntgo Corre Grupo de Bongenerí EAFIT //9 Contendo INTRODUCCIÓN...
Factorizar un polinomio consiste en convertir un polinomio en un producto de expresiones algebraicas.
 Fctorizr un polinomio consiste en convertir un polinomio en un producto de epresiones lgebrics. Cso 1. Monomio como fctor común. Un polinomio tiene fctor común sí y sólo sí todos los términos del polinomio
Fctorizr un polinomio consiste en convertir un polinomio en un producto de epresiones lgebrics. Cso 1. Monomio como fctor común. Un polinomio tiene fctor común sí y sólo sí todos los términos del polinomio
a (3, 1, 1), b(1, 7, 2), c (2, 1, 4) = 18,5 u 3
 8 Clcul el volumen del prlelepípedo determindo por u(,, ), v (,, ) y w = u v. Justific por qué el resultdo es u v. w = u Ò v = (,, ) (,, ) = (, 6, 5) [u, v, w] = 6 5 u v = 9 + 6 + 5 = 7 = 7 Volumen = 7
8 Clcul el volumen del prlelepípedo determindo por u(,, ), v (,, ) y w = u v. Justific por qué el resultdo es u v. w = u Ò v = (,, ) (,, ) = (, 6, 5) [u, v, w] = 6 5 u v = 9 + 6 + 5 = 7 = 7 Volumen = 7
4. Movimiento Relativo: Sistemas de Coordenadas en Rotación (SCR)
 DINMIC PR INGENIERI: NOTS DE CLSE 4. Momento Relto: Sstems e Coorens en Rotcón (SCR) Ultm resón 31052005 En este ocumento se presentn l euccón e l ecucón generl el momento relto. L plccón e est ecucón
DINMIC PR INGENIERI: NOTS DE CLSE 4. Momento Relto: Sstems e Coorens en Rotcón (SCR) Ultm resón 31052005 En este ocumento se presentn l euccón e l ecucón generl el momento relto. L plccón e est ecucón
Tema9. Sucesiones. Tema 9. Sucesiones.
 Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
Tem 9. Sucesiones.. Definición. Forms de definir un sucesión.. Progresión ritmétic... Definición.. Sum progresión ritmétic. Progresión geométric... Definición.. Sum finit de progresión geométric... Sum
Geometría convexa y politopos, día 1
 Geometría convexa y poltopos, día 1 Alexey Beshenov (cadadr@gmal.com) 8 de agosto de 2016 Los objetos geométrcos que nos nteresan en esta hstora son subconjuntos de R n. Voy a denotar los puntos de R n
Geometría convexa y poltopos, día 1 Alexey Beshenov (cadadr@gmal.com) 8 de agosto de 2016 Los objetos geométrcos que nos nteresan en esta hstora son subconjuntos de R n. Voy a denotar los puntos de R n
es toda la línea determinada por estos dos puntos, mientras que el conjunto de todas las combinaciones convexas es el segmento de línea que une a
 5 dsttos Cosecuetemete el cojuto de tods ls combcoes fes de dos putos R es tod l líe determd por estos dos putos metrs que el cojuto de tods ls combcoes coves es el segmeto de líe que ue y. Obvmete cd
5 dsttos Cosecuetemete el cojuto de tods ls combcoes fes de dos putos R es tod l líe determd por estos dos putos metrs que el cojuto de tods ls combcoes coves es el segmeto de líe que ue y. Obvmete cd
Procesamiento de Imágenes Satelitales. Clase Teórico
 Proesmento de Imágenes Steltles Clse Teóro ro-prát Nro. Georreferenón L georreferenón de mágenes steltles es el proeso mednte el ul se dot de vldez rtográf un mgen dgtl orrgendo geométrmente l posón de
Proesmento de Imágenes Steltles Clse Teóro ro-prát Nro. Georreferenón L georreferenón de mágenes steltles es el proeso mednte el ul se dot de vldez rtográf un mgen dgtl orrgendo geométrmente l posón de
ANÁLISIS EXPERIMENTAL DE ESTRUCTURAS RESPUESTA SÍSMICA DE UNA ESTRUCTURA MÉTODO MODAL ESPECTRAL
 ANÁISIS EXPERIMENTA DE ESTRUCTURAS RESPUESTA SÍSMICA DE UNA ESTRUCTURA MÉTODO MODA ESPECTRA CONCEPTOS ACCIÓN SÍSMICA r ESPECTRO DE RESPUESTA PROCEDIMIENTO DETERMINISTA O ESTOCÁSTICO. MODEO DINÁMICO - MASAS
ANÁISIS EXPERIMENTA DE ESTRUCTURAS RESPUESTA SÍSMICA DE UNA ESTRUCTURA MÉTODO MODA ESPECTRA CONCEPTOS ACCIÓN SÍSMICA r ESPECTRO DE RESPUESTA PROCEDIMIENTO DETERMINISTA O ESTOCÁSTICO. MODEO DINÁMICO - MASAS
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
2. EL TENSOR DE TENSIONES. Supongamos un cuerpo sometido a fuerzas externas en equilibrio y un punto P en su interior.
 . EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
. EL TENSOR DE TENSIONES Como se explcó prevamente, el estado tensonal en un punto nteror de un cuerpo queda defndo por 9 componentes, correspondentes a componentes por cada una de las tensones nternas
