Hidrodinámica. Elaborado por: Ing. Enriqueta Del Ángel Hernández. Noviembre, 2014
|
|
|
- Isabel Dolores Valdéz Lucero
- hace 6 años
- Vistas:
Transcripción
1 Hidrodinámica Elaborado por: Ing. Enriqueta Del Ángel Hernández Noviembre, 01
2 HIDRODINÁMICA Etudia el comportamiento del movimiento de lo fluido; en í la hidrodinámica e fundamenta principalmente en lo fluido incompreible e decir lo líquido; para ello conidera la velocidad, preión, flujo y gato. Se aplica en el dieño y contrucción de prea, canale, acueducto, caco de barco, avione, hélice, turbina, freno, amortiguadore, colectore pluviale entre otra aplicacione. El etudio de lo líquido en movimiento conidera que: Son completamente incomprenible. Ideale, eto e que carecen de vicoidad. El flujo e etacionario o etable, porque e conidera que la velocidad de cada partícula de líquido que paa por el mimo punto e igual. CONCEPTOS IMPORTANTES. GASTO (G): E la relación entre el volumen del líquido que fluye por un conducto y el tiempo que tarda en fluir. Gato = Volumen tiempo G = v t Fórmula 1 u unidade on: m3 en el SI (Sitema Internacional de Unidade) Exite otra forma de calcular el gato o caudal cuando e conoce la velocidad del líquido y el área de la ección tranveral de la tubería por la cual circula; de tal forma que: Gato = (Area de la ección tranveral de la tubería)( velocidad del líquido) G = A v Fórmula
3 EJEMPLOS DE GASTO. Ejemplo 1.- Calcular el gato de agua por una tubería i en 30 minuto fluyeron 100 litro. SOLUCIÓN: Para calcular el gato e importante exprear y utituir lo 30 minuto en egundo aí como lo 100 litro en metro cúbico. 30 min min ( ) ( ) = = min 1 min 100 litro 1 m 3 litro m3 ( ) ( ) = (100 ) = 1. m litro litro Sutituyendo en la fórmula 1. G = v t ; G = 1. m = x 10 m3 Significa que en un egundo fluyen 6.66 x 10 - m 3 / ; expreando lo m 3 en litro para que quede mejor comprendido el reultado on: 0.66 litro cada egundo (no llega a un litro por egundo). Ejemplo. Calcular el gato de agua a travé de una tubería con un diámetro de 5 cm i la velocidad con la cual fluye e de.8 m/. SOLUCIÓN. Como e conoce la velocidad con la cual fluye el agua y el diámetro de la tubería e aplica la fórmula, ólo que ante e tiene que calcular el área de la ección tranveral de la tubería. Recordando A = 1.96 x 10 3 m π φ ; utituyendo valore e tiene: A = π (0.05 m) =
4 Sutituyendo en la fórmula. G = A v; Se tiene: G = (1. 96 x 10 3 m ) (.8 m ) = 9. 0 x 10 3 m3 El gato de agua e de 9.0 X 10-3 m 3 /, explicado de manera má entendible on 9. litro cada egundo. Ejemplo 3.- Qué diámetro debe tener una tubería para que el gato ea de 10 litro/ a una velocidad de 5m/? SOLUCIÓN: Se utiliza la fórmula ; G = A v; de donde e depeja A : A = G v A = π φ π φ = G v Poteriormente e utituye A por la fórmula para calcular área, e depeja φ φ = G πv ; φ = G π v Sutituyendo valore en la expreión anterior: m3 (0. 01 φ = ) π( 5 m ) = m La tubería debe tener un diámetro de 0.05 m o ea de 5 cm.
5 FLUJO (F). Cantidad de maa de líquido que fluye a travé de una tubería en un egundo; matemáticamente: maa Flujo = tiempo F = m Fórmula 3 t u unidade on Kg Exite otra fórmula para calcular flujo i e relaciona con la denidad, de tal forma que: Flujo = Gato por denidad F = Gρ Fórmula EJEMPLOS DE FLUJO. Ejemplo.- Calcular el flujo de agua a travé de una tubería i el gato e de litro cada egundo. Recuerde que la denidad del agua e de 1000 Kg/m 3. Solución: De acuerdo a que ólo e conoce el gato e puede utilizar la fórmula ; ante de utituir en eta fórmula el gato e debe exprear en m 3 /. ( litro 1 m 3 ) ( 1000 litro ) = litro m litro = x 10 3 m3 Sutituyendo: F = ( x 10 F = Gρ = 3 m3 Kg Kg ) (1000 m3) = Significa que cada egundo fluyen kg de agua.
6 ECUACIÓN DE CONTINUIDAD. En la figura anterior la tubería preenta una reducción de u ección tranveral del punto A1 al punto A; in embargo la cantidad de líquido que paa por ambo punto e la mima; por lo cual el gato en el punto A1 e el mimo que en punto A; expreado matemáticamente: G 1 = G A 1 v 1 = A v llamada ECUACIÓN DE CONTINUIDAD Fórmula 5 Lo anterior e coniderando que lo líquido on incompreible de tal forma que la velocidad del líquido que fluye por la ección tranveral mayor tiene una menor velocidad y al paar por la ección tranveral de menor tamaño el líquido incrementa u velocidad, compenando aí el gato. A MAYOR SECCIÓN, MENOR VELOCIDAD A MENOR SECCIÓN, MAYOR VELOCIDAD
7 EJEMPLOS DE LA APLICACIÓN DE LA ECUACIÓN DE CONTINUIDAD. 1.- Por una tubería con un diámetro de cm circula agua a una velocidad de 3m/, i la tubería preenta una reducción de u ección tranveral encontrándoe que u diámetro en eta parte e de.5 cm; Cuál e la velocidad del agua a travé de eta última ección? Solución: Dato: Diámetro 1 = φ 1 = cm o 0.0 m Diámetro = φ =.5 cm o 0.05 m Velocidad 1 = v1 = 3 m/ Se deconoce la v. Utilizando la Ecuación de Continuidad; A 1 v 1 = A v ; e depeja v; quedando como: v = A 1v 1 A expreión 1 Coniderando que el área de la ección tranveral e: A = πφ que para cada área e tiene: A 1 = π(φ 1) y A = π(φ ) Ahora utituyendo en la expreión 1, e tiene: de tal forma v = ( π(φ 1 ) ) (v 1 ) π(φ ) expreión
8 Dividiendo y cancelando π de la expreión, e obtiene: Sutituyendo valore en la expreión 3; v = (φ 1 ) (v 1 ) (φ ) expreión 3 v = (0. 0 m) ( 3 m ) (0. 05 m) v = (1. 6 x 10 3 m ) ( 3 m ) 6. 5 x 10 m = m La velocidad del agua en la ección etrecha de la tubería e de 7.68 m/. TEOREMA DE BERNOULLI. En un líquido ideal cuyo flujo e etacionario, la uma de la energía cinética, potencial y de preión que tiene el líquido en un punto, e igual a la uma de eta energía en otro punto cualquiera ECUACIÓN DEL TEOREMA DE BERNOULLI (v 1 ) + gh 1 + P 1 ρ 1 = (v ) + gh + P ρ
9 TEOREMA DE TORRICELLI Una de la aplicacione del Teorema de Bernoulli e el Teorema de Torricelli que enuncia: La velocidad con la que ale un líquido por el orificio de un recipiente e igual a la que adquiriría un cuerpo que e dejara caer libremente dede la uperficie libre del líquido hata el nivel del orificio El Teorema anterior fue etablecido por Evangelita Torricelli y fundamentado en la iguiente ecuación: v = gh Aimimo, dentro de la aplicacione también e encuentran: Tubo de Pitot y Tubo de Venturi. TUBO DE PITOT. E utilizado para medir la velocidad de la corriente de agua de un río. v = gh
10 TUBO DE VENTURI. Se emplea para medir la velocidad de un líquido que circula a preión dentro de una tubería. La iguiente ecuación obtenida a partir del Teorema De Bernoulli permite calcular la velocidad. ρ (P A P B ) v A = ( A A) A 1 B v A =Velocidad del líquido a travé de la tubería en m. P A =Preión del líquido en la parte ancha del tubo en N m. P B =Preión del liquido en la parte má etrecha del tubo en N m ρ=denidad del líquido en Kg m 3 A A =Área de la ección tranveral de la parte má ancha de la tubería en m. A B =Área de la ección tanveral de la parte má etrecha de la tubería en m.
11 EJEMPLOS. 1.- El tubo cerca del extremo inferior de un tanque de almacenamiento de agua tiene una pequeña fuga y de ella ale una corriente de agua. La uperficie del agua en el tanque e localiza a 15 m encima del punto de la fuga. a) Qué velocidad tiene la corriente del agua que ale del agujero? b) Si el agujero tiene un área de 60 miléimo de cm ; Cuánta agua fluirá en un egundo? SOLUCIÓN: a) Para calcular la velocidad del agua que ale del agujero e utiliza: v = gh De acuerdo a lo dato proporcionado en el ejemplo la altura e de 15 m; aimimo ya e conoce el valor de la aceleración de la gravedad que e g = 9.81m/, utituyendo en la fórmula: v = gh v = ( m ) ( 15m) = 9. 3 m v = m velocidad con la cual ale el agua por el agujero. b) Para calcular cuánta agua fluirá en un egundo, e debe calcular entonce el volumen de agua; por lo tanto primero e calcula el gato ya que e conoce área del agujero ademá de la velocidad con la cual fluye el agua. Para calcular gato e utiliza: G = Av Ante de utituir en la fórmula e deben convertir lo cm a m cm 1 m ( ) ( 1 1 x 10 cm ) = cm m 1 x 10 cm = 6 x 10 6 m Sutituyendo en G = Av G = (6 x 10 6 m ) (17.15 m De donde: G = Gato en m 3 / V = volumen en m 3. t = Tiempo en. Se depeja V; quedando: m3 ) = 1.09 x 10 ; ete e el gato. Poteriormente de la fórmula V = G t G = V t V = ( 1.09 x 10 m 3 ) (1 ) = 1.09 x 10 m 3 volumen de agua que fluye en un egundo.
12 .- Por una tubería de 5.08 cm de diámetro circula agua a una velocidad de 1.6 m/. Calcular la velocidad del agua, al paar por el etrechamiento de la tubería donde el diámetro e de cm. Solución: DATOS: Diámetro 1 = φ 1 = 5.08 cm o m Diámetro = φ = cm o 0.0 m Velocidad 1 = v 1 = 1.6 m/ Se deconoce la v =? De acuerdo a lo dato e utiliza la ecuación de continuidad. Utilizando la Ecuación de Continuidad; A 1 v 1 = A v ; e depeja v ; quedando como: v = A 1v 1 A expreión 1 Coniderando que el área de la ección tranveral e: A = πφ cada área e tiene: A 1 = π(φ 1) Ahora utituyendo en la expreión 1, e tiene: v = y ( π(φ 1) ) (v 1 ) π(φ ) A = π(φ ) expreión Dividiendo y cancelando π de la expreión, e obtiene: de tal forma que para Sutituyendo valore en la expreión 3; v = v = (φ 1 ) (v 1 ) (φ ) expreión 3 ( m) 1. 6 m ( v ) = (0. 0 m) (3. 36 x 10 3 m 1. 6 m ) ( ) 1. 6 x 10 3 m = m La velocidad del agua en la ección etrecha de la tubería e de 3.36 m/.
13 3.- En la parte má ancha de un tubo de Venturi exite un diámetro de cm y una preión de.9 x 10 N/ m, en la parte má etrecha el diámetro e de 8 cm y la preión de 1.5 x 10 N/m. Cuál e la velocidad del agua que fluye por la tubería? Solución: Para calcular la velocidad e utiliza: De acuerdo a lo dato e conoce: PA =.9 x 10 N/m. PB = 1.5 x 10 N/m. φ A = cm = m φ B = 8 cm = 0.08m Denidad del agua = ρ agua = 1000 Kg m Ante de utituir e calculan la área: ρ (P A P B ) v A = ( A A) A 1 B A A = π(φ 1) y A B = π(φ ) A A = π(φ 1) π ( m ) = = m A B = π(φ ) π ( m ) = = 5. 0 x 10 3 m Sutituyendo valore en la fórmula: ρ (P A P B ) v A = ( A A A ) 1 B v A = 1000 kg (.9 x 10 N m 1.5 x 10 N m ) m m ( 5.0 x 10 3 ) 1 m
14 v A = 1000 kg (.9 x 10 N m 1.5 x 10 N m ) m m ( 5.0 x 10 3 ) 1 m N v A = 1000 kg (1 000 m ) m 3 (3.98) 1 m v A = (8 ) m v A = (8 ) v A = m velocidad del agua a travé de la tubería..- Por un tubo de 10 x 10-6 m de ección tranveral paa agua y en 1 min e recogen 80 X 10-6 m 3 de dicho líquido. Con qué velocidad etá fluyendo el agua? DATOS: La ección tranveral = A = 10 x 10-6 m Tiempo = t = 1 min = 70 egundo. Volumen = 80 X 10-6 m 3 INCÓGNITA: Se deea aber la velocidad con la cual fluye el agua = v =? SOLUCIÓN: Para calcular la velocidad e puede utilizar la fórmula: Gato = área de la ección tranveral x velocidad G = Av depejando v: v = G A expreión 1.
15 Ya e conoce área de la ección tranveral, ólo e neceita conocer cuál e el valor del gato, para ello e utiliza la fórmula: G = V expreión t De donde e conoce el volumen que e de 80 X 10-6 m 3 y tiempo de 10 egundo, ólo e utituye en la fórmula de la expreión. G = 80 x 10 6 m 3 m3 7 = 1.11 x Una vez que e conoce el gato e utituye en la expreión 1 para calcular la velocidad con la cual fluye el agua por la tubería. v = G A v = x m x 10 6 m = m 3 m v = m 5.- Calcular el diámetro de una tubería, para que el gato ea de 0.0 m 3 / a una velocidad de 1.5 m/ DATOS: G = 0.0 m 3 / v = 1.5 m/ INCÓGNITA: Diámetro de la tubería = φ =? SOLUCIÓN: La fórmula que implica gato, velocidad y diámetro (debido al área de ección tranveral) e: G = Av De la fórmula anterior e depeja A: A = G expreión 1 v Recordando que la fórmula para calcular área cuando e conoce el diámetro e: A = π(φ) Se utituye A en la expreión 1 quedando. π(φ) = G v expreión
16 De la expreión e depeja φ (φ) = G φ = G vπ vπ expreión 3 m3 (0. 0 φ = ) (1. 5 m ) π = m m φ = m o ea φ = 13 cm e el diámetro de la tubería. FUENTES DE INFORMACIÓN. Bueche, J.F. (1993). Fíica general México, D.F Octava edición. Mc. Graw Hill. Pérez, M. H. (006). Fíica General Tercera edición. Publicacione Culturale. México, D.F
17 Colaborador: Ing. Enriqueta del Angel Hernández Nombre de la aignatura: Tema Selecto de Fíica Programa educativo: Bachillerato virtual
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 1: MECÁNICA DE SÓLIDOS Y FLUIDOS
 Facultad de Ciencia Curo 00-0 SOLUCIONES PROBLEMAS FÍSICA. TEMA : MECÁNICA DE SÓLIDOS Y FLUIDOS. Una gota eférica de mercurio de radio,0 mm e diide en do gota iguale. Calcula a) el radio de la gota reultante
Facultad de Ciencia Curo 00-0 SOLUCIONES PROBLEMAS FÍSICA. TEMA : MECÁNICA DE SÓLIDOS Y FLUIDOS. Una gota eférica de mercurio de radio,0 mm e diide en do gota iguale. Calcula a) el radio de la gota reultante
HIDRODINÁMICA. Profesor: Robinson Pino H.
 HIDRODINÁMICA Profesor: Robinson Pino H. 1 CARACTERÍSTICAS DEL MOVIMIENTO DE LOS FLUIDOS Flujo laminar: Ocurre cuando las moléculas de un fluido en movimiento siguen trayectorias paralelas. Flujo turbulento:
HIDRODINÁMICA Profesor: Robinson Pino H. 1 CARACTERÍSTICAS DEL MOVIMIENTO DE LOS FLUIDOS Flujo laminar: Ocurre cuando las moléculas de un fluido en movimiento siguen trayectorias paralelas. Flujo turbulento:
! y teniendo en cuenta que el movimiento se reduce a una dimensión
 Examen de Fíica-1, 1 Ingeniería Química Examen final Septiembre de 2011 Problema (Do punto por problema) Problema 1 (Primer parcial): Una lancha de maa m navega en un lago con velocidad En el intante t
Examen de Fíica-1, 1 Ingeniería Química Examen final Septiembre de 2011 Problema (Do punto por problema) Problema 1 (Primer parcial): Una lancha de maa m navega en un lago con velocidad En el intante t
P t. Primer Semestre 2010 PAUTA AYUDANTÍA 7 DINÁMICA DE FLUIDOS. Loa fluidos se pueden clasificar de las siguientes maneras:
 Unieridad Técnica Federico Santa María Introducción a la Mecánica de Fluido y Calor Prier Seetre 00 Profeor: Rodrigo Suárez yudante: Macarena Molina PUT YUDNTÍ 7 DINÁMIC DE FLUIDOS Loa fluido e pueden
Unieridad Técnica Federico Santa María Introducción a la Mecánica de Fluido y Calor Prier Seetre 00 Profeor: Rodrigo Suárez yudante: Macarena Molina PUT YUDNTÍ 7 DINÁMIC DE FLUIDOS Loa fluido e pueden
UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 38 PRINCIPIO DE PASCAL. OBJETIVOS DEL APRENDIZAJE:
 UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 38 PRINCIPIO DE PASCAL. OBJETIVOS DEL APRENDIZAJE: ESTUDIAR LAS APLICACIONES DEL PRINCIPIO DE PASCAL. OBSERVAR LA
UNIVERSIDAD POLITÉCNICA DE EL SALVADOR ESCUELA DE FORMACIÓN BÁSICA. FÍSICA II PRÁCTICA 38 PRINCIPIO DE PASCAL. OBJETIVOS DEL APRENDIZAJE: ESTUDIAR LAS APLICACIONES DEL PRINCIPIO DE PASCAL. OBSERVAR LA
HIDRÁULICA Ingeniería en Acuicultura.
 HIDRÁULICA Ingeniería en Acuicultura. Omar Jiménez Henríquez Departamento de Física, Universidad de Antofagasta, Antofagasta, Chile, I semestre 2011. Omar Jiménez. Universidad de Antofagasta. Chile Hidráulica
HIDRÁULICA Ingeniería en Acuicultura. Omar Jiménez Henríquez Departamento de Física, Universidad de Antofagasta, Antofagasta, Chile, I semestre 2011. Omar Jiménez. Universidad de Antofagasta. Chile Hidráulica
1. Tipos de flujo. 2. Caudal. 3. Conservación de la energía en fluidos. 4. Roce en fluidos
 1. Tipos de flujo. Caudal 3. Conservación de la energía en fluidos 4. Roce en fluidos Tipos de flujos Existen diversos tipos de flujos en donde se distinguen: Flujo laminar: Ocurre cuando las moléculas
1. Tipos de flujo. Caudal 3. Conservación de la energía en fluidos 4. Roce en fluidos Tipos de flujos Existen diversos tipos de flujos en donde se distinguen: Flujo laminar: Ocurre cuando las moléculas
Guía de estudio 3. Ecuación de Bernoulli (sin interacciones). Programa de Ing. Pesquera. Unefm
 PARTE I: ECUACIÓN DE BERNOULLI (SIN INTERACCIONES ENERGÉTICAS) OBJETIVOS Los objetivos de estas clases son: CONSIDERACIONES TEÓRICAS DE LA ECUACIÓN DE BERNOULLI La ecuación de Bernoulli es la siguiente:
PARTE I: ECUACIÓN DE BERNOULLI (SIN INTERACCIONES ENERGÉTICAS) OBJETIVOS Los objetivos de estas clases son: CONSIDERACIONES TEÓRICAS DE LA ECUACIÓN DE BERNOULLI La ecuación de Bernoulli es la siguiente:
ADMINISTRACION DE EMPRESA OPERACIONES INDUSTRIALES Instructor: Ing. Luis Gomez Quispe SEMESTREIII
 ADMINISTRACION DE EMPRESA OPERACIONES INDUSTRIALES Instructor: Ing. Luis Gomez Quispe SEMESTREIII - 017 SEMANA 11 : FLUJO DE LOS FLUIDOS LIQUIDOS Inst. Ing. Luis Gomez Quispe 1 OBJETIVO GENERAL Al término
ADMINISTRACION DE EMPRESA OPERACIONES INDUSTRIALES Instructor: Ing. Luis Gomez Quispe SEMESTREIII - 017 SEMANA 11 : FLUJO DE LOS FLUIDOS LIQUIDOS Inst. Ing. Luis Gomez Quispe 1 OBJETIVO GENERAL Al término
Instituto de Física Facultad de Ingeniería Universidad de la República
 Intituto de Fíica Facultad de Ingeniería Univeridad de la República do. PARCIAL - Fíica General 9 de noviembre de 007 VERSIÓN El momento de inercia de una efera maciza de maa M y radio R repecto de un
Intituto de Fíica Facultad de Ingeniería Univeridad de la República do. PARCIAL - Fíica General 9 de noviembre de 007 VERSIÓN El momento de inercia de una efera maciza de maa M y radio R repecto de un
Prácticas de Laboratorio de Hidráulica
 Universidad Politécnica de Madrid E.T.S. Ingenieros de Caminos, Canales y Puertos Prácticas de Laboratorio de Hidráulica Jaime García Palacios Francisco V. Laguna Peñuelas 2010 Índice general 3. Venturi
Universidad Politécnica de Madrid E.T.S. Ingenieros de Caminos, Canales y Puertos Prácticas de Laboratorio de Hidráulica Jaime García Palacios Francisco V. Laguna Peñuelas 2010 Índice general 3. Venturi
1. 2º EXAMEN. 2. Investigación 11. Fluidos. Contenido:
 SESIÓN 21 17 OCTUBRE 1. 2º EXAMEN 2. Investigación 11. Fluidos. Contenido: Estados de la materia. Características moleculares de sólidos, líquidos y gases. Fluido. Concepto de fluido incompresible. Densidad
SESIÓN 21 17 OCTUBRE 1. 2º EXAMEN 2. Investigación 11. Fluidos. Contenido: Estados de la materia. Características moleculares de sólidos, líquidos y gases. Fluido. Concepto de fluido incompresible. Densidad
Número Reynolds. Laboratorio de Operaciones Unitarias Equipo 4 Primavera México D.F., 12 de marzo de 2008
 Número Reynold Laboratorio de Operacione Unitaria Equipo 4 Primavera 2008 México D.F., 12 de marzo de 2008 Alumno: Arlette Mayela Canut Noval arlettecanut@hotmail.com Francico Joé Guerra Millán fjguerra@prodigy.net.mx
Número Reynold Laboratorio de Operacione Unitaria Equipo 4 Primavera 2008 México D.F., 12 de marzo de 2008 Alumno: Arlette Mayela Canut Noval arlettecanut@hotmail.com Francico Joé Guerra Millán fjguerra@prodigy.net.mx
Mecánica II GONZALO GUTÍERREZ FRANCISCA GUZMÁN GIANINA MENESES. Universidad de Chile, Facultad de Ciencias, Departamento de Física, Santiago, Chile
 Mecánica II GONZALO GUTÍERREZ FRANCISCA GUZMÁN GIANINA MENESES Universidad de Chile, Facultad de Ciencias, Departamento de Física, Santiago, Chile Guía 4: Mecánica de fluidos Martes 25 de Septiembre, 2007
Mecánica II GONZALO GUTÍERREZ FRANCISCA GUZMÁN GIANINA MENESES Universidad de Chile, Facultad de Ciencias, Departamento de Física, Santiago, Chile Guía 4: Mecánica de fluidos Martes 25 de Septiembre, 2007
HIDRODINAMICA Fluidos en movimiento
 HIDRODINAMICA Fluidos en movimiento Principio de la conservación de la masa y de continuidad. Ecuación de Bernoulli. 3/0/0 Yovany Londoño Flujo de fluidos Un fluido ideal es o o Incompresible si su densidad
HIDRODINAMICA Fluidos en movimiento Principio de la conservación de la masa y de continuidad. Ecuación de Bernoulli. 3/0/0 Yovany Londoño Flujo de fluidos Un fluido ideal es o o Incompresible si su densidad
PROBLEMAS DINÁMICA DE FLUIDOS
 PROBLEMA DINÁMICA DE FLUIDO PROBLEMA En una tubería horizontal hay dos secciones diferentes, cuyos radios son cm y 8 cm respectivamente. En cada sección hay un tubo vertical abierto a la atmósfera, y entre
PROBLEMA DINÁMICA DE FLUIDO PROBLEMA En una tubería horizontal hay dos secciones diferentes, cuyos radios son cm y 8 cm respectivamente. En cada sección hay un tubo vertical abierto a la atmósfera, y entre
MECANICA DE LOS FLUIDOS
 MECANICA DE LOS FLUIDOS 7 FUNDAMENTOS DEL FLUJO DE FLUIDOS Ing. Alejandro Mayori Flujo de Fluidos o Hidrodinámica es el estudio de los Fluidos en Movimiento Principios Fundamentales: 1. Conservación de
MECANICA DE LOS FLUIDOS 7 FUNDAMENTOS DEL FLUJO DE FLUIDOS Ing. Alejandro Mayori Flujo de Fluidos o Hidrodinámica es el estudio de los Fluidos en Movimiento Principios Fundamentales: 1. Conservación de
COLEGIO DE BACHILLERES DEL ESTADO DE QUERÉTARO Plantel No. 7 El Marqués GUIA DE REGULARIZACIÓN DE FÍSICA II UNIDAD 1
 UNIDAD 1 I. INTRODUCCIÓN 1. Investiga y resume los siguientes conceptos: a. HIDRODINÁMICA: b. HIDROSTÁTICA: c. HIDRÁULICA 2. Investiga y resume en qué consiste cada una de las características de los fluidos
UNIDAD 1 I. INTRODUCCIÓN 1. Investiga y resume los siguientes conceptos: a. HIDRODINÁMICA: b. HIDROSTÁTICA: c. HIDRÁULICA 2. Investiga y resume en qué consiste cada una de las características de los fluidos
m s EJEMPLO 14.7 Se bombea aceite con densidad ρ aceite
 EJEMPLO 4.7 Se bobea aceite con denidad aceite 850 kg/ a traé de un tubo cilíndrico de diáetro d8 c a razón de 9.5 litro/. a Calcule la raidez del aceite y la razón de flujo de aa. b Si el diáetro del
EJEMPLO 4.7 Se bobea aceite con denidad aceite 850 kg/ a traé de un tubo cilíndrico de diáetro d8 c a razón de 9.5 litro/. a Calcule la raidez del aceite y la razón de flujo de aa. b Si el diáetro del
Práctica 1: Dobladora de tubos
 Práctica : Dobladora de tubo Una máquina dobladora de tubo utiliza un cilindro hidráulico para doblar tubo de acero de groor coniderable. La fuerza necearia para doblar lo tubo e de 0.000 N en lo 00 mm
Práctica : Dobladora de tubo Una máquina dobladora de tubo utiliza un cilindro hidráulico para doblar tubo de acero de groor coniderable. La fuerza necearia para doblar lo tubo e de 0.000 N en lo 00 mm
DINAMICA DE FLUIDOS O HIDRODINAMICA.
 DINAMICA DE FLUIDOS O HIDRODINAMICA. Es la rama de la mecánica de fluidos que se ocupa de las leyes de los fluidos en movimientos; estas leyes son enormemente complejas, y aunque la hidrodinámica tiene
DINAMICA DE FLUIDOS O HIDRODINAMICA. Es la rama de la mecánica de fluidos que se ocupa de las leyes de los fluidos en movimientos; estas leyes son enormemente complejas, y aunque la hidrodinámica tiene
TUTORIAL BÁSICO DE MECÁNICA FLUIDOS
 TUTORIAL BÁSICO DE MECÁNICA FLUIDOS El tutorial es básico pues como habréis visto en muchos de ellos es haceros entender no sólo la aplicación práctica de cada teoría sino su propia existencia y justificación.
TUTORIAL BÁSICO DE MECÁNICA FLUIDOS El tutorial es básico pues como habréis visto en muchos de ellos es haceros entender no sólo la aplicación práctica de cada teoría sino su propia existencia y justificación.
CINEMÁTICA II. ) cuerpos de diferentes masas desde la misma altura, llegarán al suelo con la misma velocidad y en el mismo instante de tiempo.
 C U R S O: FÍSICA MENCIÓN MATERIAL: FM-3 CINEMÁTICA II CAIDA LIBRE En cinemática, la caída libre e un movimiento dónde olamente influye la gravedad. En ete movimiento e deprecia el rozamiento del cuerpo
C U R S O: FÍSICA MENCIÓN MATERIAL: FM-3 CINEMÁTICA II CAIDA LIBRE En cinemática, la caída libre e un movimiento dónde olamente influye la gravedad. En ete movimiento e deprecia el rozamiento del cuerpo
( s) ( ) CAPITULO II 2.1 INTRODUCCIÓN. 1 ss. θ θ K = θ θ. θ θ 0, ) 2-1. Fig.2.1: Diagrama de bloques de. : Amplificador + motor T
 -1 CAPITULO II.1 INTRODUCCIÓN Fig..1: Diagrama de bloque de donde: A J : Momento de inercia B : Coeficiente de roce T() Torque : Amplificador + motor T J B W G FTLC 1 J ( + ) θ θ o i B J. ( ) ( ) + + Donde
-1 CAPITULO II.1 INTRODUCCIÓN Fig..1: Diagrama de bloque de donde: A J : Momento de inercia B : Coeficiente de roce T() Torque : Amplificador + motor T J B W G FTLC 1 J ( + ) θ θ o i B J. ( ) ( ) + + Donde
Física General II. Guía N 2: Hidrodinámica y Viscosidad
 Física General II Guía N 2: Hidrodinámica y Viscosidad Problema 1: Ley de Torricelli. La figura muestra un líquido que está siendo descargado de un tanque a través de un orificio que se encuentra a una
Física General II Guía N 2: Hidrodinámica y Viscosidad Problema 1: Ley de Torricelli. La figura muestra un líquido que está siendo descargado de un tanque a través de un orificio que se encuentra a una
Fracción de petróleo Tubería Q min = m / C. = 2m
 Ejercicio para fluido incopreible: Un edidor de orificio e intala en una conducción con el fin de edir la velocidad de flujo de una fracción de petróleo de.6 API que e introduce en una unidad de craking.
Ejercicio para fluido incopreible: Un edidor de orificio e intala en una conducción con el fin de edir la velocidad de flujo de una fracción de petróleo de.6 API que e introduce en una unidad de craking.
FUNDACIÓN EDUCACIONAL DE CHUQUICAMATA COLEGIO CHUQUICAMATA
 FUNDACIÓN EDUCACIONAL DE CHUQUICAMATA COLEGIO CHUQUICAMATA INSTRUMENTO : GUIA DE APRENDIZAJE N 1 NIVEL (O CURSO) : CUARTO AÑO MEDIO PLAN : COMÚN UNIDAD (O EJE) : FUERZA Y MOVIMIENTO CONTENIDO(S) : ECUACIÓN
FUNDACIÓN EDUCACIONAL DE CHUQUICAMATA COLEGIO CHUQUICAMATA INSTRUMENTO : GUIA DE APRENDIZAJE N 1 NIVEL (O CURSO) : CUARTO AÑO MEDIO PLAN : COMÚN UNIDAD (O EJE) : FUERZA Y MOVIMIENTO CONTENIDO(S) : ECUACIÓN
Dinámica de Fluidos. Mecánica y Fluidos VERANO
 Dinámica de Fluidos Mecánica y Fluidos VERANO 1 Temas Tipos de Movimiento Ecuación de Continuidad Ecuación de Bernouilli Circulación de Fluidos Viscosos 2 TIPOS DE MOVIMIENTO Régimen Laminar: El flujo
Dinámica de Fluidos Mecánica y Fluidos VERANO 1 Temas Tipos de Movimiento Ecuación de Continuidad Ecuación de Bernouilli Circulación de Fluidos Viscosos 2 TIPOS DE MOVIMIENTO Régimen Laminar: El flujo
Solución: a) A dicha distancia la fuerza centrífuga iguala a la fuerza de rozamiento, por lo que se cumple: ω r= m mg 0, 4 9,8.
 C.- Una plataforma gira alrededor de un eje vertical a razón de una vuelta por egundo. Colocamo obre ella un cuerpo cuyo coeficiente etático de rozamiento e 0,4. a) Calcular la ditancia máxima al eje de
C.- Una plataforma gira alrededor de un eje vertical a razón de una vuelta por egundo. Colocamo obre ella un cuerpo cuyo coeficiente etático de rozamiento e 0,4. a) Calcular la ditancia máxima al eje de
ACTIVIDADES RESUELTAS T 3 MCU Ley de Gravitación Universal. Actividad 1.- Define movimiento circular uniforme, radio vector y desplazamiento angular.
 ACTIVIDADES RESUELTAS T 3 MCU Ley de Gravitación Univeral Actividad 1.- Define movimiento circular uniforme, radio vector y deplazamiento angular. Movimiento circular uniforme (MCU) e el movimiento de
ACTIVIDADES RESUELTAS T 3 MCU Ley de Gravitación Univeral Actividad 1.- Define movimiento circular uniforme, radio vector y deplazamiento angular. Movimiento circular uniforme (MCU) e el movimiento de
SOLUCIONES DE LOS EJERCICIOS DE LA OLIMPIADA DEL FASE LOCAL
 SOLUCIONES DE LOS EJERCICIOS DE LA OLIMIADA DEL 1. FASE LOCAL ución ejercicio nº 1 Una plataforma circular, colocada horizontalmente, gira con una frecuencia de vuelta por egundo alrededor de un eje vertical
SOLUCIONES DE LOS EJERCICIOS DE LA OLIMIADA DEL 1. FASE LOCAL ución ejercicio nº 1 Una plataforma circular, colocada horizontalmente, gira con una frecuencia de vuelta por egundo alrededor de un eje vertical
Universidad de Antioquia, Depto. de Matematicas
 minuto. Si la cantidad máxima de sal en el tanque se obtiene a los 0 minutos. Cual era la cantidad de sal inicial en el tanque? (ta.: 375 libras) Ejercicio 10. Un tanque contiene 00 litros de una solución
minuto. Si la cantidad máxima de sal en el tanque se obtiene a los 0 minutos. Cual era la cantidad de sal inicial en el tanque? (ta.: 375 libras) Ejercicio 10. Un tanque contiene 00 litros de una solución
COLEGIO LA PROVIDENCIA
 COLEGIO LA PROVIDENCIA Hna de la Providencia y de la Inmaculada Concepción 2013 ALLER MOVIMIENO CIRCULAR UNIFORME DOCENE: Edier Saavedra Urrego Grado: décimo fecha: 16/04/2013 Realice un reumen de la lectura
COLEGIO LA PROVIDENCIA Hna de la Providencia y de la Inmaculada Concepción 2013 ALLER MOVIMIENO CIRCULAR UNIFORME DOCENE: Edier Saavedra Urrego Grado: décimo fecha: 16/04/2013 Realice un reumen de la lectura
Solución de Examen Final Física I
 Solución de Examen Final Física I Temario A Departamento de Física Escuela de Ciencias Facultad de Ingeniería Universidad de San Carlos de Guatemala 28 de mayo de 2013 Un disco estacionario se encuentra
Solución de Examen Final Física I Temario A Departamento de Física Escuela de Ciencias Facultad de Ingeniería Universidad de San Carlos de Guatemala 28 de mayo de 2013 Un disco estacionario se encuentra
Fluidos. Repaso. Problemas.
 Fluidos. Repaso. Problemas. Resumen: Fluidos. 1. La presión en un fluido es la fuerza por unidad de área que un fluido ejerce sobre un superficie. Se mide: 1 pascal = 1 newton /metro 2 2. La presión en
Fluidos. Repaso. Problemas. Resumen: Fluidos. 1. La presión en un fluido es la fuerza por unidad de área que un fluido ejerce sobre un superficie. Se mide: 1 pascal = 1 newton /metro 2 2. La presión en
GUIA PARA EXAMEN DE EXTRAORDINARIO DE FISICA I
 I. Cinemática: MRU, MRUA, MCU, MCUA Teoría: 1. Parte de la mecánica que etudia lo diferente tipo de movimiento de lo cuerpo in atender la caua que lo producen: Cinemática. Cuando etudiamo el movimiento
I. Cinemática: MRU, MRUA, MCU, MCUA Teoría: 1. Parte de la mecánica que etudia lo diferente tipo de movimiento de lo cuerpo in atender la caua que lo producen: Cinemática. Cuando etudiamo el movimiento
Física para Ciencias: Principio de Arquímedes, Ecuaciones de Continuidad y Bernoulli.
 Física para Ciencias: Principio de Arquímedes, Ecuaciones de Continuidad y Bernoulli. Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Presión de un fluido Presión depende de la profundidad P = ρ
Física para Ciencias: Principio de Arquímedes, Ecuaciones de Continuidad y Bernoulli. Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Presión de un fluido Presión depende de la profundidad P = ρ
PROBLEMA Nº1. Z 3 =80 Z 2 =20 Z 1 =40 O 2
 PROLEM Nº1. El mecanimo de la figura e compone de un diferencial que tranmite el movimiento a un tren de engranaje epicicloidal mediante un tornillo in fin. El brazo de ete tren de engranaje e el elabón
PROLEM Nº1. El mecanimo de la figura e compone de un diferencial que tranmite el movimiento a un tren de engranaje epicicloidal mediante un tornillo in fin. El brazo de ete tren de engranaje e el elabón
Respecto del eje de giro de la rueda, cuál de las siguientes cantidades permanece constante mientras esta desciende por el plano inclinado?
 CIENCIAS (BIOLOGÍA, FÍSICA, QUÍMICA) MÓDULO 3 Eje temático: Mecánica - Fluido 1. Una rueda deciende rodando por un plano inclinado que forma un ángulo α con la horizontal del modo que e ilutra en la figura
CIENCIAS (BIOLOGÍA, FÍSICA, QUÍMICA) MÓDULO 3 Eje temático: Mecánica - Fluido 1. Una rueda deciende rodando por un plano inclinado que forma un ángulo α con la horizontal del modo que e ilutra en la figura
Aforo en Canales MEJORAMIENTO DEL SISTEMA DE RIEGO DE RÍO TORO
 Aforo en Canales MEJORAMIENTO DEL SISTEMA DE RIEGO DE RÍO TORO Medición del caudal del Agua de riego Porque medir? (Aforo) Para un máximo aprovechamiento, buen manejo y administración equitativa del recurso
Aforo en Canales MEJORAMIENTO DEL SISTEMA DE RIEGO DE RÍO TORO Medición del caudal del Agua de riego Porque medir? (Aforo) Para un máximo aprovechamiento, buen manejo y administración equitativa del recurso
EJERCICIOS DE FÍSICA II Profesor: José Fernando Pinto Parra
 Ejercicios de Dinámica de los Fluidos: REPÚBLICA BOLIVARIANA DE VENEZUELA EJERCICIOS DE FÍSICA II Profesor: José Fernando Pinto Parra. Entre dos líneas de corriente bidimensionales de un escurrimiento
Ejercicios de Dinámica de los Fluidos: REPÚBLICA BOLIVARIANA DE VENEZUELA EJERCICIOS DE FÍSICA II Profesor: José Fernando Pinto Parra. Entre dos líneas de corriente bidimensionales de un escurrimiento
Se comprime aire, inicialmente a 17ºC, en un proceso isentrópico a través de una razón de
 Ejemplo 6-9 Se comprime aire, inicialmente a 7ºC, en un proceo ientrópico a travé de una razón de preión de 8:. Encuentre la temperatura final uponiendo calore epecífico contante y calore epecífico variable,
Ejemplo 6-9 Se comprime aire, inicialmente a 7ºC, en un proceo ientrópico a travé de una razón de preión de 8:. Encuentre la temperatura final uponiendo calore epecífico contante y calore epecífico variable,
CATEDRA DE FISICA I HIDROSTÁTICA E HIDRODINÁMICA - PROBLEMAS RESUELTOS
 CATEDRA DE FISICA I Ing. Civil, Ing. Electromecánica, Ing. Eléctrica, Ing. Mecánica IDROSTÁTICA E IDRODINÁMICA - PROBLEMAS RESUELTOS PROBLEMA Nº 2: Tres líquidos inmiscibles se vierten en un recipiente
CATEDRA DE FISICA I Ing. Civil, Ing. Electromecánica, Ing. Eléctrica, Ing. Mecánica IDROSTÁTICA E IDRODINÁMICA - PROBLEMAS RESUELTOS PROBLEMA Nº 2: Tres líquidos inmiscibles se vierten en un recipiente
El hecho de llevar un 90% de aceite parafínico y un 10% de aromático ( I.V.
 LUBRICACIÓN 175 8.1.- Un aceite etá formado or un 90% de hidrocarburo arafínico y el 10% de un hidrocarburo aromático. Se le añaden aditivo que mejoran u índice de vicoidad (I.V.) en un 0% Calcular el
LUBRICACIÓN 175 8.1.- Un aceite etá formado or un 90% de hidrocarburo arafínico y el 10% de un hidrocarburo aromático. Se le añaden aditivo que mejoran u índice de vicoidad (I.V.) en un 0% Calcular el
Guía de Ejercicios Resueltos Física General Hidrodinámica
 Refuerzo: Fíica General Eteban A. Rodríguez M. Guía de Ejercicio Reuelto Fíica General Hidrodináica Lo ejercicio explicado en ete docuento on bae para la prueba, la ayoría de ello on copiado dede el libro.
Refuerzo: Fíica General Eteban A. Rodríguez M. Guía de Ejercicio Reuelto Fíica General Hidrodináica Lo ejercicio explicado en ete docuento on bae para la prueba, la ayoría de ello on copiado dede el libro.
CENTRO DE BACHILLERATO TECNOLOGICO agropecuario No. 2. Hidrodinámica. Cd. Delicias, Chih
 CENTRO DE BACHILLERATO TECNOLOGICO agropecuario No. Hidrodinámica. Cd. Delicias, Chih. 015. Situación problema para el estudio de la hidrodinámica. Definición de conceptos Gasto o Caudal. Ecuación de continuidad
CENTRO DE BACHILLERATO TECNOLOGICO agropecuario No. Hidrodinámica. Cd. Delicias, Chih. 015. Situación problema para el estudio de la hidrodinámica. Definición de conceptos Gasto o Caudal. Ecuación de continuidad
Describe, en función de la diferencia de fase, qué ocurre cuando se superponen dos ondas progresivas armónicas de la misma amplitud y frecuencia.
 El alumno realizará una opción de cada uno de lo bloque. La puntuación máxima de cada problema e de punto, y la de cada cuetión de 1,5 punto. BLOQUE I-PROBLEMAS Se determina, experimentalmente, la aceleración
El alumno realizará una opción de cada uno de lo bloque. La puntuación máxima de cada problema e de punto, y la de cada cuetión de 1,5 punto. BLOQUE I-PROBLEMAS Se determina, experimentalmente, la aceleración
Hidrodinámica. Conceptos
 Conceptos Hidrostática tica Caudal Es la cantidad de líquido que pasa en un cierto tiempo. Concretamente, el caudal sería el volumen de líquido que circula dividido el tiempo: Sus unidades son volumen
Conceptos Hidrostática tica Caudal Es la cantidad de líquido que pasa en un cierto tiempo. Concretamente, el caudal sería el volumen de líquido que circula dividido el tiempo: Sus unidades son volumen
Tema V: BALANCES DE MATERIA
 Tema V: BLNCES DE MTERI Eta obra etá bajo una licencia Reconocimiento No comercial Compartir bajo la mima licencia 3.0 Internacional de Creative Common. Para ver una copia de eta licencia, viite http://creativecommon.org/licene/by
Tema V: BLNCES DE MTERI Eta obra etá bajo una licencia Reconocimiento No comercial Compartir bajo la mima licencia 3.0 Internacional de Creative Common. Para ver una copia de eta licencia, viite http://creativecommon.org/licene/by
Mecánica de Fluidos. Docente: Ing. Alba V. Díaz Corrales
 Mecánica de Fluidos Docente: Ing. Alba V. Díaz Corrales Mecánica de Fluidos Contenido Fluidos incompresibles Ecuación de continuidad Ecuación de Bernoulli y aplicaciones Líneas de cargas piezométricas
Mecánica de Fluidos Docente: Ing. Alba V. Díaz Corrales Mecánica de Fluidos Contenido Fluidos incompresibles Ecuación de continuidad Ecuación de Bernoulli y aplicaciones Líneas de cargas piezométricas
La solución del problema requiere de una primera hipótesis:
 RIOS 9 Cuarto Simpoio Regional obre Hidráulica de Río. Salta, Argentina, 9. CALCULO HIDRAULICO EN RIOS Y DISEÑO DE CANALES ESTABLES SIN USAR ECUACIONES TRADICIONALES Eduardo E. Martínez Pérez Profeor agregado
RIOS 9 Cuarto Simpoio Regional obre Hidráulica de Río. Salta, Argentina, 9. CALCULO HIDRAULICO EN RIOS Y DISEÑO DE CANALES ESTABLES SIN USAR ECUACIONES TRADICIONALES Eduardo E. Martínez Pérez Profeor agregado
PRÁCTICA N 5: DEMOSTRACIÓN DEL TEOREMA DE BERNOULLI
 PRÁCTICA N 5: DEMOSTRACIÓN DEL TEOREMA DE BERNOULLI INTRODUCCIÓN La dinámica de fluidos analiza los gases y líquidos en movimiento. Además, es una de las ramas más complejas de la mecánica. La conservación
PRÁCTICA N 5: DEMOSTRACIÓN DEL TEOREMA DE BERNOULLI INTRODUCCIÓN La dinámica de fluidos analiza los gases y líquidos en movimiento. Además, es una de las ramas más complejas de la mecánica. La conservación
respecto del eje de las x: 30º 45º a) 6.00 unidades y 90º b) 2.16 unidades y 80º x c) 2.65 unidades y 70º d) 2.37 unidades y 52º C r
 Guía de Fíica I. Vectore. 1. Conidere lo vectore A ByC r r r,. Su valore y aboluto, en unidade arbitraria, on de 3, 2 y 1 repectivamente. Entonce el vector reultante r r r r D = A + B + C erá de valor
Guía de Fíica I. Vectore. 1. Conidere lo vectore A ByC r r r,. Su valore y aboluto, en unidade arbitraria, on de 3, 2 y 1 repectivamente. Entonce el vector reultante r r r r D = A + B + C erá de valor
LABORATORIO #6 DEMOSTRACIÓN DEL TOREMA DE BERNOULLI LUIS CARLOS DE LA CRUZ TORRES GILDARDO DIAZ CARLOS ROJAS PRESENTADO EN LA CÁTEDRA:
 LABORATORIO #6 DEMOSTRACIÓN DEL TOREMA DE BERNOULLI LUIS CARLOS DE LA CRUZ TORRES GILDARDO DIAZ CARLOS ROJAS PRESENTADO EN LA CÁTEDRA: LABORATORIO DE MECÁNICA DE FLUIDOS PRESENTADO A: ING. VLADIMIR QUIROZ
LABORATORIO #6 DEMOSTRACIÓN DEL TOREMA DE BERNOULLI LUIS CARLOS DE LA CRUZ TORRES GILDARDO DIAZ CARLOS ROJAS PRESENTADO EN LA CÁTEDRA: LABORATORIO DE MECÁNICA DE FLUIDOS PRESENTADO A: ING. VLADIMIR QUIROZ
SISTEMAS ABIERTOS BALANCE DE MASA ELABORÓ MSc. EFRÉN GIRALDO TORO.
 1 SISTEMAS ABIERTOS BALANCE DE MASA ELABORÓ MSc. EFRÉN GIRALDO TORO. REVISÓ PhD. CARLOS A. ACEVEDO. PRESENTACIÓN HECHA EXCLUIVAMENTE CON EL FIN DE FACILITAR EL ESTUDIO. MEDELLÍN 2016 2 Contenido Sistemas
1 SISTEMAS ABIERTOS BALANCE DE MASA ELABORÓ MSc. EFRÉN GIRALDO TORO. REVISÓ PhD. CARLOS A. ACEVEDO. PRESENTACIÓN HECHA EXCLUIVAMENTE CON EL FIN DE FACILITAR EL ESTUDIO. MEDELLÍN 2016 2 Contenido Sistemas
2. Arreglo experimental
 Efecto fotoeléctrico Diego Hofman y Alejandro E. García Roelli Departamento de Fíica, Laboratorio 5,Facultad de Ciencia Exacta y Naturale, Univeridad de Bueno Aire A lo largo de ete trabajo e etudió el
Efecto fotoeléctrico Diego Hofman y Alejandro E. García Roelli Departamento de Fíica, Laboratorio 5,Facultad de Ciencia Exacta y Naturale, Univeridad de Bueno Aire A lo largo de ete trabajo e etudió el
Diapositiva 1. Tema 9: Convección forzada CONVECCIÓN FORZADA. JM.Corberán, R. Royo (upv) 1
 iapoitiva 1 CONVECCIÓN FORZAA JM.Corberán, R. Royo (upv 1 iapoitiva 2 ÍNICE Flujo externo Flujo interno incompreible placa compreible tubo único circulare normal a tubo hace no circulare laminar turbulento
iapoitiva 1 CONVECCIÓN FORZAA JM.Corberán, R. Royo (upv 1 iapoitiva 2 ÍNICE Flujo externo Flujo interno incompreible placa compreible tubo único circulare normal a tubo hace no circulare laminar turbulento
PRACTICA Nº 2. PESO ESPECÍFICO RELATIVO DE LOS SÓLIDOS, Gs.
 PRACTICA Nº 2 PESO ESPECÍFICO RELATIVO DE LOS SÓLIDOS, G. OBJETIVO: Determinar por medio de enayo de laboratorio, el peo epecífico relativo de lo ólido para uelo grueo (grava) y uelo arenoo y fino. PESO
PRACTICA Nº 2 PESO ESPECÍFICO RELATIVO DE LOS SÓLIDOS, G. OBJETIVO: Determinar por medio de enayo de laboratorio, el peo epecífico relativo de lo ólido para uelo grueo (grava) y uelo arenoo y fino. PESO
Capítulo 8. Flujo de fluidos a régimen transitorio.
 Capítulo 8 Flujo de fluidos a régimen transitorio. Flujo de fluidos a régimen transitorio. En flujo de fluidos se puede encontrar el régimen transitorio fenómeno de la descarga de tanques. cuando se presenta
Capítulo 8 Flujo de fluidos a régimen transitorio. Flujo de fluidos a régimen transitorio. En flujo de fluidos se puede encontrar el régimen transitorio fenómeno de la descarga de tanques. cuando se presenta
Mecánica de Fluidos. Docente: Ing. Alba V. Díaz Corrales
 Mecánica de Fluidos Docente: Ing. Alba V. Díaz Corrales Mecánica de Fluidos Contenido Fluidos incompresibles Ecuación de continuidad Ecuación de Bernoulli y aplicaciones Líneas de cargas piezométricas
Mecánica de Fluidos Docente: Ing. Alba V. Díaz Corrales Mecánica de Fluidos Contenido Fluidos incompresibles Ecuación de continuidad Ecuación de Bernoulli y aplicaciones Líneas de cargas piezométricas
Escuela de Ingenieros School of Engineering
 Ecuela de Ingeniero Aignatura / Gaia ERMODINÁMICA 2º EORÍA 1 (10 punto) Curo / Kurtoa IEMPO: 45 minuto. Lea la 10 cuetione y ecriba dentro de la cailla a la derecha de cada cuetión V i conidera que la
Ecuela de Ingeniero Aignatura / Gaia ERMODINÁMICA 2º EORÍA 1 (10 punto) Curo / Kurtoa IEMPO: 45 minuto. Lea la 10 cuetione y ecriba dentro de la cailla a la derecha de cada cuetión V i conidera que la
Lugar Geométrico de las Raíces
 Lugar Geométrico de la Raíce N de práctica: 9 Tema Correpondiente: Lugar geométrico de la raíce Nombre completo del alumno Firma N de brigada: Fecha de elaboración: Grupo: Elaborado por: Reviado por: Autorizado
Lugar Geométrico de la Raíce N de práctica: 9 Tema Correpondiente: Lugar geométrico de la raíce Nombre completo del alumno Firma N de brigada: Fecha de elaboración: Grupo: Elaborado por: Reviado por: Autorizado
Hidráulica. Temario: Tuberías Hidrostática Hidrodinámica. Energía. Perdidas de Carga Software para diseño Información en la Web
 Temario: Tuberías Hidrostática Hidrodinámica Hidráulica Flujo laminar intermedio turbulento Energía Bernoulli Torricelli Ec. Gral del gasto Perdidas de Carga Software para diseño Información en la Web
Temario: Tuberías Hidrostática Hidrodinámica Hidráulica Flujo laminar intermedio turbulento Energía Bernoulli Torricelli Ec. Gral del gasto Perdidas de Carga Software para diseño Información en la Web
Estructura de Materia 1 Verano Práctica 2 Leyes de conservación
 Estructura de Materia 1 Verano 2017 Práctica 2 Leyes de conservación Problema 1. Un líquido incompresible de densidad ρ 0 fluye de manera estacionaria por el interior de un conducto de longitud finita
Estructura de Materia 1 Verano 2017 Práctica 2 Leyes de conservación Problema 1. Un líquido incompresible de densidad ρ 0 fluye de manera estacionaria por el interior de un conducto de longitud finita
Guía de Trabajo. Presión, Arquímedes, Bernoulli. Resolver de manera clara y ordenada cada uno de los ejercicios en hojas blancas tamaño carta.
 Guía de Trabajo Presión, Arquímedes, Bernoulli Resolver de manera clara y ordenada cada uno de los ejercicios en hojas blancas tamaño carta. 1._Una rana en una vaina hemisferica descubre que flota sin
Guía de Trabajo Presión, Arquímedes, Bernoulli Resolver de manera clara y ordenada cada uno de los ejercicios en hojas blancas tamaño carta. 1._Una rana en una vaina hemisferica descubre que flota sin
INGENIERIA CIVIL ASIGNATURA: HIDRÁULICA GENERAL GUÍA DE PRÁCTICA DE LABORATORIO Nº 1 AÑO 2010
 AÑO 010 OBJETIVOS DE LA PRÁCTICA DE LABORATORIO 1. Visualización de escurrimientos en tuberías en general.. Aplicación del Teorema de Bernoulli a través de la medición de sus variables. 3. Medición de
AÑO 010 OBJETIVOS DE LA PRÁCTICA DE LABORATORIO 1. Visualización de escurrimientos en tuberías en general.. Aplicación del Teorema de Bernoulli a través de la medición de sus variables. 3. Medición de
Guía 9: Fluidos. Hidrostática
 Guía 9: Fluidos Hidrostática Unidades de presión: [P] = [F]/[S] : [MKS] Pascal (Pa), 1Pa =1N/m 2 ; [CGS] bar, 1bar = 10 6 dyn/ cm 2 =10 5 Pa (Atmosfera:at) 1at =760 mmhg=760 Torr= 1,033 kg/ m 2 = 1,01325
Guía 9: Fluidos Hidrostática Unidades de presión: [P] = [F]/[S] : [MKS] Pascal (Pa), 1Pa =1N/m 2 ; [CGS] bar, 1bar = 10 6 dyn/ cm 2 =10 5 Pa (Atmosfera:at) 1at =760 mmhg=760 Torr= 1,033 kg/ m 2 = 1,01325
ENERGÍA (I) CONCEPTOS FUNDAMENTALES
 NRGÍA (I) CONCPTOS UNDAMNTALS IS La Magdalena. Avilé. Aturia La energía e una magnitud de difícil definición, pero de gran utilidad. Para er exacto, podríamo decir que má que de energía (en entido general),
NRGÍA (I) CONCPTOS UNDAMNTALS IS La Magdalena. Avilé. Aturia La energía e una magnitud de difícil definición, pero de gran utilidad. Para er exacto, podríamo decir que má que de energía (en entido general),
GUIA DE PROBLEMAS N 5
 GUIA DE PROBLEMAS N 5 PROBLEMA N 1 Se produce un vacío parcial en una caja estanca, que tiene una tapa cuya área es 7,5 10-3 m 2. Si se requiere una fuerza de 480N para desprender la tapa de la caja y
GUIA DE PROBLEMAS N 5 PROBLEMA N 1 Se produce un vacío parcial en una caja estanca, que tiene una tapa cuya área es 7,5 10-3 m 2. Si se requiere una fuerza de 480N para desprender la tapa de la caja y
1. Cómo sabemos que un cuerpo se está moviendo?
 EL MOVIMIENTO. CONCEPTOS INICIALES I.E.S. La Magdalena. Avilé. Aturia A la hora de etudiar el movimiento de un cuerpo el primer problema con que no encontramo etá en determinar, preciamente, i e etá moviendo
EL MOVIMIENTO. CONCEPTOS INICIALES I.E.S. La Magdalena. Avilé. Aturia A la hora de etudiar el movimiento de un cuerpo el primer problema con que no encontramo etá en determinar, preciamente, i e etá moviendo
1.- Qué valor ha de tener el parámetro m para que el vector A=3i+mj forme un ángulo de 60 con el eje OX? existe más de un valor?
 Nombre: Curo: FYQ 4º ESO Examen II Fecha: 5 de Diciembre de 06 ª Evaluación Opción A.- Qué valor ha de tener el parámetro m para que el vector A=3i+mj forme un ángulo de 60 con el eje OX? exite má de un
Nombre: Curo: FYQ 4º ESO Examen II Fecha: 5 de Diciembre de 06 ª Evaluación Opción A.- Qué valor ha de tener el parámetro m para que el vector A=3i+mj forme un ángulo de 60 con el eje OX? exite má de un
MECANICA DE FLUIDOS. Qué estudia la hidráulica?. Líquidos. Fuidos
 1 GUIA FISICA GRADO ONCE: MECANICA DE FLUIDOS AUTOR Lic. Fíica, ERICSON SMITH CASTILLO MECANICA DE FLUIDOS La leye de Newton que etudiao para lo ólido on aplicable a lo fluido, pero ante debeo conocer
1 GUIA FISICA GRADO ONCE: MECANICA DE FLUIDOS AUTOR Lic. Fíica, ERICSON SMITH CASTILLO MECANICA DE FLUIDOS La leye de Newton que etudiao para lo ólido on aplicable a lo fluido, pero ante debeo conocer
ANÁLISIS DEL LUGAR GEOMÉTRICO DE LAS RAÍCES
 CAPITULO 3 ANÁLISIS DEL LUGAR GEOMÉTRICO DE LAS RAÍCES 3. INTRODUCCIÓN La etabilidad relativa y la repueta tranitoria de un itema de control en lazo cerrado etán directamente relacionada con la localización
CAPITULO 3 ANÁLISIS DEL LUGAR GEOMÉTRICO DE LAS RAÍCES 3. INTRODUCCIÓN La etabilidad relativa y la repueta tranitoria de un itema de control en lazo cerrado etán directamente relacionada con la localización
Gasto a través de un tubo
 Gasto a través de un tubo Laboratorio de Mecánica y fluidos Objetivos Medir el gasto de un líquido que fluye a través de un tubo. Observar y medir las presiones a lo largo de un tubo por el cual se mueve
Gasto a través de un tubo Laboratorio de Mecánica y fluidos Objetivos Medir el gasto de un líquido que fluye a través de un tubo. Observar y medir las presiones a lo largo de un tubo por el cual se mueve
TEMA I DIAGRAMAS DE BLOQUES, FLUJOGRAMAS Y SUS OPERACIONES. Universidad de Oriente Núcleo de Anzoátegui Escuela de Ingeniería y Ciencias Aplicadas
 Título Univeridad de Oriente Núcleo de nzoátegui Ecuela de Ingeniería y Ciencia plicada Dpto de Computación y Sitema TEM I DIRMS DE OQUES, FUJORMS Y SUS OPERCIONES Ec. De Ing. Y C. plicada Tema I: Diag
Título Univeridad de Oriente Núcleo de nzoátegui Ecuela de Ingeniería y Ciencia plicada Dpto de Computación y Sitema TEM I DIRMS DE OQUES, FUJORMS Y SUS OPERCIONES Ec. De Ing. Y C. plicada Tema I: Diag
3.11 Intervalos de confianza basados en una población con distribución normal pero con muestras pequeñas
 3. Intervalo de confianza baado en una población con ditribución normal pero con muetra pequeña Cuando n < 30 no e poible uar el teorema central del límite habría que hacer una upoición epecífica acerca
3. Intervalo de confianza baado en una población con ditribución normal pero con muetra pequeña Cuando n < 30 no e poible uar el teorema central del límite habría que hacer una upoición epecífica acerca
Estática y Dinámica de Fluidos
 Estática y Dinámica de Fluidos 1. Hidrostática. Principio de Pascal. Principio de Arquímedes. Conceptos básicos de hidrodinámica: Una importante propiedad de una sustancia es la densidad, que la definiremos
Estática y Dinámica de Fluidos 1. Hidrostática. Principio de Pascal. Principio de Arquímedes. Conceptos básicos de hidrodinámica: Una importante propiedad de una sustancia es la densidad, que la definiremos
Tema 1. Los circuitos neumáticos y oleohidáulicos (problemas)
 Tema 1. Los circuitos neumáticos y oleohidáulicos (problemas) Víctor M. Acosta Guerrero Profesor de Tecnología Tema 1. Los circuitos neumáticos y oleohidráulicos. 1. ENERGÍA NEUMÁTICA: Las principales
Tema 1. Los circuitos neumáticos y oleohidáulicos (problemas) Víctor M. Acosta Guerrero Profesor de Tecnología Tema 1. Los circuitos neumáticos y oleohidráulicos. 1. ENERGÍA NEUMÁTICA: Las principales
Física II. 1 Fluidos. 2 Movimiento Armónico. 3 Ondas Mecánicas. 4 Superposición de Ondas. 5 Sonido. 6 Calor. 7 Propiedades Térmicas de la Materia
 Fluidos Física II Moimiento Armónico 3 Ondas Mecánicas 4 Suerosición de Ondas 5 Sonido 6 Calor 7 Proiedades Térmicas de la Materia 8 Primera Ley de la Termodinámica Fluidos Presión Un fluido en reoso esta
Fluidos Física II Moimiento Armónico 3 Ondas Mecánicas 4 Suerosición de Ondas 5 Sonido 6 Calor 7 Proiedades Térmicas de la Materia 8 Primera Ley de la Termodinámica Fluidos Presión Un fluido en reoso esta
s 4 1,65 8 f 4 = +20 cm = 50,8 cm 1,65 1,00 1,00 8 f = 20 cm = 30,8 cm 1,65 1,00
 TEMA 0: ÓPTICA GEOMÉTRICA NOMBRE DEL ALUMNO: CURSO: ºBach GRUPO: ACTIVIDADES PARES DE LAS PAGINAS 320-322 2. Qué ignificado tiene la aproximación de rao paraxiale? Conite en uponer que lo rao inciden obre
TEMA 0: ÓPTICA GEOMÉTRICA NOMBRE DEL ALUMNO: CURSO: ºBach GRUPO: ACTIVIDADES PARES DE LAS PAGINAS 320-322 2. Qué ignificado tiene la aproximación de rao paraxiale? Conite en uponer que lo rao inciden obre
Para conocer el caudal que circula por el punto 2, es necesario determinar la velocidad a la que se mueve el fluido. Para ello aplicamos Bernoulli.
 Edificio Minas, Pº Alfonso XIII, 8 3003 Cartagena (SPAIN) Tel. 968-3573 Fax. 968-3573 TEMA. DINÁMICA Problemas Tema. Cuál será el caudal que circula por una tubería de 0,505 m de diámetro y es detectado
Edificio Minas, Pº Alfonso XIII, 8 3003 Cartagena (SPAIN) Tel. 968-3573 Fax. 968-3573 TEMA. DINÁMICA Problemas Tema. Cuál será el caudal que circula por una tubería de 0,505 m de diámetro y es detectado
Flujo estacionario laminar
 HIDRODINÁMICA Hidrodinámica Es una disciplina parte de la física cuyo objetivo es explicar el comportamiento de los fluidos en movimiento, para lo cual se hace necesario definir algunos conceptos importantes:
HIDRODINÁMICA Hidrodinámica Es una disciplina parte de la física cuyo objetivo es explicar el comportamiento de los fluidos en movimiento, para lo cual se hace necesario definir algunos conceptos importantes:
Comportamiento del nivel de líquido en un sistema de dos tanques en serie
 Comportamiento del nivel de líquido en un itema de do tanque en erie Marcela Echavarria R., Gloria Lucía Orozco C., Alan Didier Pérez Á. Abtract Se deea conocer el comportamiento del nivel de un itema
Comportamiento del nivel de líquido en un itema de do tanque en erie Marcela Echavarria R., Gloria Lucía Orozco C., Alan Didier Pérez Á. Abtract Se deea conocer el comportamiento del nivel de un itema
FÍSICA 2-1 er control de la 2ª evaluación Propiedades de las Ondas. 27 de Enero de 2010
 FÍSICA - er control de la ª evaluación Propiedade de la Onda. 7 de Enero de 00 CUESTIONES ( punto):.- Define qué e una onda etacionaria y cómo e produce. Cuál e la diferencia má detacada entre la onda
FÍSICA - er control de la ª evaluación Propiedade de la Onda. 7 de Enero de 00 CUESTIONES ( punto):.- Define qué e una onda etacionaria y cómo e produce. Cuál e la diferencia má detacada entre la onda
UNIDAD IV. Ecuaciones diferenciales Lineales
 UNIDAD IV Ecuaciones diferenciales Lineales 24 UNIDAD 4 0, ECUACIONES DIFERENCIALES LINEALES Se llama ecuación lineal de primer orden a la que es lineal con respecto a la función incógnita y su derivada.
UNIDAD IV Ecuaciones diferenciales Lineales 24 UNIDAD 4 0, ECUACIONES DIFERENCIALES LINEALES Se llama ecuación lineal de primer orden a la que es lineal con respecto a la función incógnita y su derivada.
OPERACIONES UNITARIAS
 OPERACIONES UNITARIAS UNIDAD I: MECÁNICA DE FLUIDOS INTRODUCCIÓN (CLASE TEÓRICA) DOCENTE: ING. PABLO GANDARILLA CLAURE pgandarilla@hotmail.com p.gandarilla@gmail.com Santa Cruz, noviembre de 2009 SUMARIO
OPERACIONES UNITARIAS UNIDAD I: MECÁNICA DE FLUIDOS INTRODUCCIÓN (CLASE TEÓRICA) DOCENTE: ING. PABLO GANDARILLA CLAURE pgandarilla@hotmail.com p.gandarilla@gmail.com Santa Cruz, noviembre de 2009 SUMARIO
1 PRACTICA # 1 PROPIEDADES FISICAS DE LOS FLUIDOS
 1 PRACTICA # 1 PROPIEDADE FIICA DE LO FLUIDO 1.1 DENIDAD Es una propiedad intensiva que se define como la masa (m) por unidad de volumen (V), y es denotada con la letra "ρ", donde: masa de la sustancia
1 PRACTICA # 1 PROPIEDADE FIICA DE LO FLUIDO 1.1 DENIDAD Es una propiedad intensiva que se define como la masa (m) por unidad de volumen (V), y es denotada con la letra "ρ", donde: masa de la sustancia
PRÁCTICA 3F. CALIBRACIÓN DE MEDIDORES DE FLUJO VOLUMÉTRICO. unidad de tiempo, pasa a través de determinada sección transversal.
 PRÁCTICA 3F. CALIBRACIÓN DE MEDIDORES DE FLUJO VOLUMÉTRICO A.- Objetivo Calibrar los siguientes medidores de flujo volumétrico: placa orificio, tobera y venturi, mediante el cálculo de los coeficientes
PRÁCTICA 3F. CALIBRACIÓN DE MEDIDORES DE FLUJO VOLUMÉTRICO A.- Objetivo Calibrar los siguientes medidores de flujo volumétrico: placa orificio, tobera y venturi, mediante el cálculo de los coeficientes
U.L.A. FACULTAD DE INGENIERIA. Mérida, 02/10/2008 ESCUELA DE MECANICA. MECANICA DE FLUIDOS. Sección 01 y 02. TERCER EXAMEN PARCIAL
 U.L.A. FACULTAD DE INGENIERIA. Mérida, 02/10/2008 ESCUELA DE MECANICA. MECANICA DE FLUIDOS. Sección 01 y 02. TERCER EXAMEN PARCIAL Problema 1 Para construir una bomba grande que debe suministrar 2 m 3
U.L.A. FACULTAD DE INGENIERIA. Mérida, 02/10/2008 ESCUELA DE MECANICA. MECANICA DE FLUIDOS. Sección 01 y 02. TERCER EXAMEN PARCIAL Problema 1 Para construir una bomba grande que debe suministrar 2 m 3
2. Ecuación de Bernoulli
 Descargar versión para imprimir. Ecuación de Bernoulli Repaso: trabajo de una fuerza, energía potencial gravitatoria, y energía cinética 1. Trabajo de una fuerza. Uno de los efectos producido por las fuerzas
Descargar versión para imprimir. Ecuación de Bernoulli Repaso: trabajo de una fuerza, energía potencial gravitatoria, y energía cinética 1. Trabajo de una fuerza. Uno de los efectos producido por las fuerzas
Etapa 1 Ecuación de Bernoulli
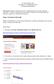 Dr. Omar Olmos López Actividad de Aprendizaje Activo Ecuación de Bernoulli Instrucciones: Sigue las instrucciones que a continuación se te dan y para cada etapa documenta y analiza la situación que se
Dr. Omar Olmos López Actividad de Aprendizaje Activo Ecuación de Bernoulli Instrucciones: Sigue las instrucciones que a continuación se te dan y para cada etapa documenta y analiza la situación que se
Física de fluidos. Densidad. kg/m. kg/m = S. kg/m. Principio de Arquímedes
 Física de fluidos Densidad ρ V dv 3 σ S ds L dl λ Principio de Arquímedes Principio de Arquímedes: todo cuerpo sumergido en un fluido eperimenta un empuje vertical y hacia arriba igual al peso de fluido
Física de fluidos Densidad ρ V dv 3 σ S ds L dl λ Principio de Arquímedes Principio de Arquímedes: todo cuerpo sumergido en un fluido eperimenta un empuje vertical y hacia arriba igual al peso de fluido
Tema VI: Balances de energía. Ingeniería Química. Grado en Ciencia y Tecnología Alimentos. Tema 6: Balances de energía
 Tema VI: Balance de energía Eta obra etá bajo una licencia Reconocimiento No comercial Compartir bajo la mima licencia 3.0 Internacional de Creative Common. Para ver una copia de eta licencia, viite http://creativecommon.org/licene/by
Tema VI: Balance de energía Eta obra etá bajo una licencia Reconocimiento No comercial Compartir bajo la mima licencia 3.0 Internacional de Creative Common. Para ver una copia de eta licencia, viite http://creativecommon.org/licene/by
El objetivo de nuestro trabajo es construir una clepsidra. Para ello se tuvo que:
 XXII CONGRESO DE INVESTIGACIÓN CUAM, MOR COLEGIO ALEMÁN ALEXANDER VON HUMBOLDT A.C. Clepsidra Sebastián Sánchez Alcalá, Luis Alberto Pacheco Pimentel, Santiago Hernández Haller Asesor: Carlos Prieto de
XXII CONGRESO DE INVESTIGACIÓN CUAM, MOR COLEGIO ALEMÁN ALEXANDER VON HUMBOLDT A.C. Clepsidra Sebastián Sánchez Alcalá, Luis Alberto Pacheco Pimentel, Santiago Hernández Haller Asesor: Carlos Prieto de
CHOQUES, EXPLOSIONES Y DEFORMACIONES EN SÓLIDOS
 CHOQUES, EXPLOSIONES Y DEFORMACIONES EN SÓLIDOS En tipo de problema, y de forma general, aplicaremo la conervación del momento angular repecto al eje fijo i lo hay (la reacción del eje, por muy grande
CHOQUES, EXPLOSIONES Y DEFORMACIONES EN SÓLIDOS En tipo de problema, y de forma general, aplicaremo la conervación del momento angular repecto al eje fijo i lo hay (la reacción del eje, por muy grande
es el que corresponde a una velocidad de oscilación positiva, calculamos dicha velocidad y aplicamos de nuevo las condiciones iniciales:
 CURSO BACH Pregunta 8 PAU Una onda armónica tranveral e propaga por un medio elático a lo largo del eje X (entido poitivo), produciendo un deplazamiento en la partícula del medio a lo largo del eje Y.
CURSO BACH Pregunta 8 PAU Una onda armónica tranveral e propaga por un medio elático a lo largo del eje X (entido poitivo), produciendo un deplazamiento en la partícula del medio a lo largo del eje Y.
Anexo 1.1 Modelación Matemática de
 ELC-3303 Teoría de Control Anexo. Modelación Matemática de Sitema Fíico Prof. Francico M. Gonzalez-Longatt fglongatt@ieee.org http://www.giaelec.org/fglongatt/tic.html Modelación de Sitema Fíico Francico
ELC-3303 Teoría de Control Anexo. Modelación Matemática de Sitema Fíico Prof. Francico M. Gonzalez-Longatt fglongatt@ieee.org http://www.giaelec.org/fglongatt/tic.html Modelación de Sitema Fíico Francico
Bases Físicas del Medio Ambiente. Dinámica de Fluidos
 Bases Físicas del Medio Ambiente Dinámica de Fluidos Programa IV. DINÁMICA DE FLUIDOS. (3h) Introducción. Fluidos ideales. Flujo estacionario. Ecuación de continuidad. Ecuación de Bernouilli. Aplicaciones
Bases Físicas del Medio Ambiente Dinámica de Fluidos Programa IV. DINÁMICA DE FLUIDOS. (3h) Introducción. Fluidos ideales. Flujo estacionario. Ecuación de continuidad. Ecuación de Bernouilli. Aplicaciones
LENTE CONVERGENTE 2: Imágenes en una lente convergente
 LENTE CONVERGENTE : Imágene en una lente convergente Fundamento En una lente convergente delgada e conidera el eje principal como la recta perpendicular a la lente y que paa por u centro. El corte de eta
LENTE CONVERGENTE : Imágene en una lente convergente Fundamento En una lente convergente delgada e conidera el eje principal como la recta perpendicular a la lente y que paa por u centro. El corte de eta
