Comisión de Pedagogía - Diego Chamorro Espacios Funcionales y Aplicaciones (Nivel 3).
|
|
|
- Francisco Acosta Agüero
- hace 5 años
- Vistas:
Transcripción
1 AMARUN Comisión de Pedagogía - Diego Chamorro Esacios Funcionales y Alicaciones (Nivel 3). Lección n : Esacios de Lebesgue, esacios de Lorentz, Funciones Maximales UCE, verano 23 Introducción Como vamos a ver en este curso, los esacios de Lebesgue constituyen la herramienta de base ara la construcción de muchos otros esacios funcionales y uede considerárselos como una materia rima necesaria ara la correcta comrensión de estos esacios de funciones. En este sentido, muchísimas de las roiedades de los esacios de Lebesgue se transmitirán a los diferentes esacios que serán construidos con ellos y es or esta razón que es necesario tener en mente las rinciales roiedades y características de los esacios de Lebesgue. Sin embargo, en muchas situaciones rácticas, los esacios de Lebesgue no son suficientes y es necesario medir el tamaño de las funciones de forma más recisa. Para ello vamos a estudiar los esacios Lorentz débiles, que son una generalización de los esacios de Lebesgue, y que tienen varias alicaciones interesantes, esecialmente or las imortantes relaciones que existen entre estos esacios y las funciones maximales lo cual nos ermitirá deducir algunos resultados muy imortantes.. Esacios de Lebesgue En todo esta lección trabajaremos rincialmente sobre el esacio euclídeo R n, con n, dotado de su estructura de gruo usual y de la norna canónica x = (x 2 + +x2 n )/2. Consideraremos además el esacio medido (R n,bor(r n ),dx) en donde Bor(R n ) es la σ-álgebra de los borelianos de R n y dx es la medida de Lebesgue. De ser necesario consideraremos también esacios medidos más generales (, Bor(), µ). Definición (Esacios de Lebesgue) Definimos sobre el esacio medido (R n,bor(r n ),dx) los esacios de Lebesgue L (R n ), con < +, como el conjunto de funciones f : R n K con K = R o C, cuyo módulo a la otencia es integrable. Este esacio admite la siguiente norma: ( ) / f L = f(x) dx. R n Si = +, definimos el esacio L (R n ) como el conjunto de funciones esencialmente acotadas, normado or la funcional f L = su x R n ess f(x). Proosición (Estructura) Los esacios de Lebesgue L (R n ) son: ) esacios de Banach si +. 2) esacios searables si < + (atención: el esacio L (R n ) no es searable) Observación Si < <, los esacios de Lebesgue L no son esacios localmente convexos y no ueden ser normados, lo que hace su utilización oco interesante en las alicaciones.
2 Proosición 2 (Resultados de Densidad) ) El conjunto de funciones simles integrables es denso en L (R n ) si < +. 2) El esacio de funciones continuas a soorte comacto es denso en L (R n ) si < +. Proosición 3 (Dualidad y Reflexibilidad) ) Si <,q < + son tales que + q =, entonces el esacio dual del esacio de Lebesgue L (R n ) es el esacio de Lebesgue L q (R n ). Es decir que (L ) = L q. En articular, es osible calcular la norma L or dualidad: f L = su f(x)g(x)dx R n g L q= Además estos esacios son reflexivos y se tiene (L ) = L. 2) Si =, el esacio dual del esacio de Lebesgue L (R n ) es el esacio de Lebesgue L (R n ). Pero este esacio no es reflexivo. Proosición 4 (Teoremas Clásicos) ) Teorema de Convergencia Monótona de Beo Levi: sea (f k ) k N una sucesión creciente de funciones medibles definidas sobre R n a valores en R + y sea f tal que lím f k(x) = f(x) en casi todas k + artes. Entonces f(x)dx = lím f k (x)dx R n k + R n 2) Lema de Fatou: sea (f k ) k N una sucesión de funciones medibles definidas sobre R n a valores en R +. Entonces límínf f k(x)dx límínf f k (x)dx R n k + k + R n 3) Teorema de Convergencia Dominada de Lebesgue: sea (f k ) k N una sucesión de funciones medibles definidas sobre R n a valores en R. Si lím f k(x) = f(x) en casi todas artes y si existe una k + función integrable g : R n R tal que f(x) g(x) en casi todas artes, entonces la función f es integrable y se tiene lím f k (x)dx = f(x)dx k + R n R n 4) Teorema de Fubini-Tonelli: sean (, Bor(), µ) y (, Bor(), ν) dos esacios medidos. Si f : R + es una función Bor() Bor()-medible, entonces las alicaciones x f(x,y)dν(y) y y f(x, y)dµ(x) son Bor()- y Bor()- medibles resectivamente y se tiene f(x,y)dµ ν(x,y) = ( ) f(x, y)dµ(x) dν(y) = ( ) f(x, y)dν(y) dµ(x) 2
3 Proosición 5 (Desigualdades imortantes) ) Desigualdad de Hölder: si f L (R n ) y g L q (R n ) con,q + y tales que + q =, entonces se tiene la desigualdad: R n f(x)g(x) dx f L g L q 2) Desigualdad de Minkowski continua: sean (, Bor(), µ) y (, Bor(), ν) dos esacios medidos. Si f : K es una función Bor() Bor()-medible y si < + entonces ( ( / f(x,y) dν(y)) dµ(x)) ( f(x,y) dµ(x)) / dν(y) 3) Desigualdad de Interolación: si f L (R n ) L (R n ) con < +, entonces ara todo θ [,] se tiene que f L (R n ) con = θ + θ. Además se tiene la desigualdad f L f θ L f θ L 4) Desigualdad de Jensen: sea (,Bor(),µ) un esacio medido tal que µ() =. Si ϕ : I R R es una función convexa y si f L () es una función tal que f(x) I ara µ-casi todo x, entonces se tiene la desigualdad: ( ) ϕ f(x)dµ(x) ϕ ( f ) (x)dµ(x) 5) Desigualdad de Tchebychev: sea (,Bor(),µ) un esacio medido y sea f : K una función tal que f L () con < +. Entonces, ara todo α > se tiene la desigualdad µ ( {x : f(x) > α} ) / α f L Observación 2 Estos resultados se mantienen si se consideran los esacios de sucesiones l (N) con +, caracterizados or la funcional a l = ( n N ) / a n si < + y a l = su a n si = +. n N Definición 2 (Esacios de Lebesgue locales) Definimos sobre el esacio medido (R n,bor(r n ),dx) los esacios de Lebesgue locales L loc (Rn ), con < +, como el conjunto de funciones f : R n K con K = R o C, cuyo módulo a la otencia es integrable sobre todo comacto K: { ( } / L loc (Rn ) = f : R n K : f L (K) = f(x) dx) < +, K R n comacto K Proosición 6 (Estructura) Sea (K n ) n N una sucesión exhaustiva de comactos de R n (es decir que R n = n N K n). Los esacios de Lebesgue locales L loc (Rn ) son esacios de Fréchet ara la familia de seminormas L (K n). Proosición 7 (Inclusiones) Para todo + se tienen las inclusiones L (R n ) L loc (Rn ). 3
4 2. Esacios de Lorentz Son una generalización de los esacios de Lebesgue: miden el tamaño de las funciones. Muy útiles cuando se trabaja con oeradores, es decir en todo el análisis. Muchas veces sólo se disonen de estimaciones en donde intervienen los esacios de Lorentz no se uede asar a estimaciones más fuertes en donde intervienen esacios de Lebesgue. 2.. Función de distribución Definición 3 Sea (,Bor(),µ) un esacio medido, sea f : K una función medible y sea α [,+ [ un real. Definimos sobre [,+ [ la función de distribución asociada a la función f or d f (α) = { f(x) >α} (x)dµ(x) = µ({x : f(x) > α}). Proosición 8 Sea (,Bor(),µ) un esacio medido y sean f,g : K dos funciones medibles. Entonces, ara todo α,β tenemos: () d f es decreciente y continua a la derecha sobre [,+ [, (2) si g(x) f(x) µ-c.t.. entonces d g (α) d f (α), ara todo α, (3) ara toda constante λ K, se tiene d λf (α) = d f (α/ λ ), ara todo α, (4) d f+g (α+β) d f (α)+d g (β), (5) d fg (αβ) d f (α)+d g (β). Proosición 9 Sea (,Bor(),µ) un esacio medido, sea f : K una función medible y sea < + un arámetro real. Se tiene entonces la identidad f L = + α d f (α)dα. Prueba. + α d f (α)dα = + α ( ) { f >α} (x)dµ(x) dα. Alicamos el teorema de Fubini en la última integral ara obtener + f(x) = α { f >α} (x)dα dµ(x) = α dα dµ(x) = f dµ(x) = f L Esacios de Lorentz L, También llamados esacios de Lebesgue débiles o esacios de Marcinkiewicz. Definición 4 Sea (,Bor(),µ) un esacio medido y sea f : K una función medible. ) Sea < + un número real, diremos que f ertenece al esacio L, () si la cantidad { } } f L, = su α d / f (α) = ínf {d f (α) C α> C> α, α > es finita. 2) El esacio L, () es or definición el esacio L (). 4
5 Proosición Sea < + y sea (,Bor(),µ) un esacio medido. Entonces tenemos la inclusión: L () L, (). f L, f L. Esta inclusión es estricta. Prueba. Sea α > un número real, entonces f L = f(x) dµ(x) = { f >α} Es decir, ara todo α >, f L αd / f (α). { f >α} f(x) dµ(x) α f(x) dµ(x)+ f(x) dµ(x) { f α} { f >α} dµ(x) = α d f (α). La inclusión es estricta: Sea la función f : x x n/ definida sobre = R n. Se tiene f / L (R n ). Pero f L, es igual a la raiz -ésima de la medida de la bola unidad de R n, en efecto, un cambio de variable ermite ver que d / f (α) = α B(,) /. Luego se tiene f L, = B(,) /. Primera utilidad de los esacios de Lorentz: = Permiten mejorar el resultado de interolación entre los esacios de Lebesgue. Sabíamos que se tiene la estimación f L r f /r < r < +. Con los esacios de Lorentz tenemos algo mejor: f /r L L ara toda función f L () L (), con Proosición Sean < q + y sea f L, () L q, (), entonces f L r () ara todo < r < q: f L r C(,q,r) f θ L, f θ L q, con θ = r q r q si q < + y θ = /r si q = +. Prueba. Sea q < +. Sabemos que Fijemos T = ( f q ) L q, q f L, ara escribir + f r L r = r α r d f (α)dα r r T α r f L, dα+r ( f ) L d f (α) mín, α, f q L q, α q + + T ( f α r mín r r f L T r + r, q r f q L T r q = q, L, α, f q L q, α q ) dα α r q f q L dα () q, ( r r + r ) ( f q r L ) q ( f q r q, L ) r q, q Sea q = +. Como d f (α) = si α > f L entonces basta utilizar la estimación d f (α) α f L ara, la arte α f L en la integral () ara obtener f r L r r r f L f r, L 5
6 Teorema (Caracterización) Sean < < + y sea f : R n R una función medible. Entonces f L, (R n ) si y solo si ( A > ) ( f,f : R n R) t.q. f(x) = f (x)+f (x) con f L C A θ y f L C A θ con A >, = θ + θ, < < y < θ <. Además se tiene f L, = ínf {C > : f = f +f con f L CA θ, f L CA θ} Prueba. (= ) Seaf L, (R n ).Definimosf = f {x R n : f(x) >B} yf = f {x R n : f(x) B} conunciertob >.Mostremos que f L y que f L : Para f : f dx = R n f dx = { f(x) >B} (2 j+ B) d f (2 j B) j= j= f dx (2 j+ B) dx j= {2 j B< f(x) <2 j+ B} j= {2 j B< f(x) <2 j+ B} (2 j+ B) (2 j B) f L, = B C f L, la suma anterior converge ues < y or lo tanto f L. Para f : R n f dx = f { f(x) B} j= dx = f dx j= {2 j B< f(x) <2 j+ B} (2 j+ B) d f (2 j B) la suma anterior converge ues < y or lo tanto f L. Reescribimos estas estimaciones de la siguiente forma: j= f L CB / f / L, = C f L, f L CB / f / L, = C f L, j= (2 j+ B) dx {2 j B< f(x) <2 j+ B} (2 j+ B) (2 j B) f L, = B C f L, ( B f L, ( B ( / (/ / ) B basta entonces escribir A = f L, ) y C = C f L,. f L, ) / ) / ( =) Tenemos la estimación { f(x) > α} { f (x) > α/2} + { f (x) > α/2}. Alicando la desigualdad de Tchebychev y las hiótesis obtenemos { f(x) > α} C f ( C α L α ) [ +C f L A (θ ) α ( C α C A(θ ) α ) +A θ + C Aθ α ( C α ) ] Para terminar basta escojer A tal que la cantidad entre corchete anterior siemre sea igual a : tenemos entonces que f L,. 6
7 3. Teoremas de interolación de Marcinkiewicz y de Riesz-Thorin es un tio de resultado esencial en el análisis. estos teoremas son la fuente de muchas alicaciones muy útiles. son el unto de artida de la teoría de interolación entre esacios de Banach. Definición 5 Sea (,Bor(),µ) un esacio medido. Definimos L ()+L () como el esacio de todas las funciones f tales que f = f +f en donde f L () y f L (). Proosición 2 Sea (,Bor(),µ) un esacio medido. Si < se tiene L () L () + L () ara todo tal que < <. Prueba. Sea f una función de L () y sea γ una constante ositiva fijada. Escribimos f(x) si f(x) > γ f(x) si f(x) γ f (x) = f (x) = si f(x) γ si f(x) > γ de manera que f = f +f. Puesto que se tiene f (x) dµ(x) = De forma similar tenemos f (x) dµ(x) = f (x) f (x) dµ(x) γ f (x) f (x) dµ(x) γ f(x) dµ(x) f(x) dµ(x), luego f L () y f L (). 3.. Interolación de Marcinkiewicz Un oerador sublineal verifica T(αf +βg) αt(f)+βt(g). Teorema 2 Sean (,Bor(),µ) y (,Bor(),ν) dos esacios medidos. Sea < +. Sea T un oerador sublineal definido en el esacio L () + L () y que toma valores en el esacio de funciones medibles definidas sobre. Suongamos que existen dos constantes ositivas A y A tales que: T(f) L, () A f L (), ara toda función f L (), (2) T(f) L, () A f L (), ara toda función f L (). (3) Entonces, ara todo < < y ara todo f L (), tenemos la estimación: T(f) L () A f L (), (4) en donde ( A = 2 + ) / / / A / A / / / /. (5) Demostración. 7
8 Suongamos que < + y fijemos una función f L () y un arámetro α >. Utilizamos la descomosición anterior de la función f escribiendo f = f α +fα en donde f α (x) = { f(x) si f(x) > δα si f(x) δα f α (x) = { f(x) si f(x) δα si f(x) > δα. Aqui δ es un arámetro ositivo cuyo valor será determinado osteriormente. Obsérvese que f α ertenece al esacio L () y que f α ertenece al esacio L (). Utilizemos la hiótesis de sublinealidad ara obtener T(f) = T(f α +fα ) T(fα ) + T(fα ), lo que imlica las inclusiones {x : T(f)(x) > α} {x : T(f α) > α/2} {x : T(fα ) > α/2}, de donde se tiene, al nivel de las funciones de distribución Esta estimación anterior, junto con a las hiótesis (2) y (3), nos da d T(f) (α) A (α/2) { f >δα} d T(f) (α) d T(f α )(α/2)+d T(f α )(α/2). (6) f(x) dµ(x)+ A (α/2) f(x) dµ(x) { f δα} Ahora vamos a contruir la norma L de T(f) utilizando la roosición 9, en efecto: T(f) L = + α d T(f) (α)dα (2A ) +(2A ) + Alicamos el teorema de Fubini ara obtener T(f) L (2A ) f(x) es decir T(f) L (2A ) f /δ α + { f δα} α { f >δα} f(x) dµ(x)dα. α dαdµ(x)+(2a ) f(x) f(x) f(x) δ dµ(x)+(2a ) f(x) dµ(x)dα + f /δ α dαdµ(x), f(x) f(x) δ dµ(x). De donde se obtiene T(f) L [ (2A ) δ +(2A ) δ ] f L. Faltaahorafijarunvalordeδ araterminarlarueba;araelloessuficenteescribirδ = (2A ) (2A ). El lector verificará sin roblema que se tiene la estimación deseada. Caso cuando = +. Escribamos otra vez f = f α +fα con f α (x) = { f(x) si f(x) > γα si f(x) γα f α (x) = { f(x) si f(x) γα si f(x) > γα. Tenemos las estimaciones siguientes T(f α ) L A f α L A γα = α/2 8
9 siemre y cuando fijemos γ = 2A. Se deduce de esto que el conjunto {x : T(f α ) > α/2} es de medida cero; or lo tanto d T(f) (α) d T(f α )(α/2). Se construye otra vez la norma L de T(f) utilizando la roosición 9: Alicando el teorema de Fubini se tiene Es decir de donde concluimos que lo que termina la rueba. T(f) L + (2A ) f(x) (2A ) T(f) L 2 A α d T(f α )(α/2)dα. 2A f α dαdµ(x). f(x) f(x) (2A ) dµ(x). A f L 3.2. Alicación: Funciones Maximales Funciones de gran imortancia en el análisis armónico: una herramienta indisensable Ejemlo de oeradores que no son acotados en L en L : ilustración de la necesidad de los esacios de Lorentz Definición 6 Sea f : R n R una función localmente integrable. Definimos el romedio de f sobre la bola B = B(x,r) como m B (f)(x) = f(y)dy B(x, r) B(x,r) Definición 7 (función maximal centrada) Sea f : R n R una función medible. La función maximal centrada de Hardy-Littlewood es: M(f)(x) = su m B ( f )(x) = su r> r> v n r n f(x y) dy { y <r} Definición 8 (función maximal no centrada) Sea f : R n R una función medible. La función maximal no centrada de Hardy-Littlewood es: M(f)(x) = su m B(y,δ) ( f )(x) δ>; x y <δ Teorema 3 (Control sobre funciones maximales) Sea ϕ una función continua y decreciente definida sobre [,+ [. Si Φ(x) = ϕ( x ) es una función integrable sobre R n entonces, ara toda función f localmente integrable sobre R n, se tiene la estimación ( ) su f Φε (x) Φ L M(f)(x) ε> en donde hemos notado Φ ε (x) = ε n Φ(ε x). Observación 3 M(f) nunca está en L (R n ) si f. Se tiene M(f) M(f). 9
10 Teorema 4 Las funciones maximales M y M son oeradores acotados: de L (R n ) en L, (R n ) de L (R n ) en L (R n ) de L (R n ) en L (R n ) ara todo < < + Demostración. de L (R n ) en L, (R n ): Dado que M(f) M(f), se tiene la inclusión de conjuntos {x R n : M(f)(x) > α} {x R n : M(f)(x) > α}. Como M(f) es el suremo de funciones continuas, se tiene que M(f) es semi-continua inferiormente y el conjunto E α = {x R n : M(f)(x) > α} es abierto. Sea K un comacto de E α, entonces ara todo x K existe una bola B x tal que: B x f(y) dy > α B x Por comacidad de K existe un recubrimiento finito {B x,,...,b x,k } de K. Lema (Teorema de recubrimiento) Sea {B,...,B k } una familia finita de bolas abiertas de R n. Existe entonces una subcolección finita {B j,,...,b j,l } formada or bolas disjuntas tales que l k B j,i 3 n B i i= i= Alicamos este lema a la familia de bolas {B x,,...,b x,k } ara obtener K k l B x,i 3 n B x,ji 3n α i= i= l i= B x,ji f(y) dy 3n α R n f(y) dy Tomando el suremo de todos los comactos contenidos en E α obtenemos α E α 3 n f L de donde se deduce M(f) L, M(f) L, 3 n f L. de L (R n ) en L (R n ): Se tiene inmediatamente M(f) L M(f) L f L. de L (R n ) en L (R n ) ara todo < < + : Aquí se alica el teorema de interolación de Marcinkiewicz!
11 3.3. Interolación de Riesz-Thorin Teorema 5 Sean (,Bor(),µ) y (,Bor(),ν) dos esacios medidos. Sea T un oerador lineal definido sobre el conjunto de todas las funciones simles f :. Sean,,q,q +. Si se tiene T(f) L q () M f L (), T(f) L q () M f L (), ara toda función simle f sobre, entonces, ara todo < θ < se tiene T(f) L q () M θ M θ f L () ara todas las funciones simles de en donde = θ + θ y q = θ simles, T osee una única extensión acotada de L () en L q (). q + θ q. Por densidad de las funciones Demostración. Sea f = m a k e iα k Ak k= una función simle sobre en donde a k >, α k R y A k son subconjuntos disjuntos de de medida finita. Por dualidad, necesitamos controlar la cantidad T(f) L q () = su T(f)(x)g(x)dν(x) en donde el suremo toma en cuenta todas las funciones simles g L q () tales que g L q (). Escribimos entonces n g = b j e iβ j Bj j= en donde β j >, β j R y B j son subconjuntos disjuntos de de medida finita. Definimos ahora las cantidades Para z {z C : Re(z) } definimos F(z) = en donde Por linealidad se tiene P(z) = ( z)+ z y Q(z) = q q ( z)+ q q z. F(z) = f z = m m k= n k= j= T(f z )(x)g z (x)dν(x) a P(z) k e iα k Ak y g z = a P(z) k b Q(z) j notar que F es analítica en z uesto que a k,b j >. e iα k e iβ j n j= b Q(z) j e iβ j Bj. T( Ak )(x) Bj (x)dν(x) Sea ahora z tal que Re(z) =. Dado que los conjuntos A k son disjuntos y que a P(z) k = a / k f z L = f L. Simétricamente como se tiene b Q(z) j = b q /q j, odemos escribir g z q L q Si z es tal que Re(z) =, or las mismas razones tenemos f z L = f L y g z q L q Utilizando la desigualdad de Hölder y la hiótesis tenemos cuando Re(z) = : F(z) T(f z ) L q g z L q M f z L g z L q = M f / L g q /q L q = g q L q. = g q L q. tenemos
12 Cuando Re(z) = se tiene: Necesitaremos el lema siguiente: F(z) M f / L g q /q L q. Lema 2 (de las tres líneas de Hadamard) Sea F una función analítica sobre la banda abierta que es continua y acotada sobre B y tal que F(z) B cuando Re(z) = F(z) B cuando Re(z) = B = {z C : < Re(z) < } con < B,B < +. Entonces se tiene F(z) B θ B θ si Re(z) = θ, con θ. Suoniendo este lema odemos escribir directamente, cuando Re(z) = θ: F(z) M θ M θ f L g L q Para terminar notamos que P(θ) = Q(θ) = y entonces F(θ) = T(f)gdν. Podemos concluir tomando el suremo sobre todas las funciones simles g definidas sobre a valores en L q de norma g L q () Alicación: Desigualdad de oung Teorema 6 Sea,q,r + tal que + q = + r. Entonces, ara todo f L (R n ) y todo g L r (R n ) se tiene f g L q f L g L r. Sea g L r y definamos T(f) = f g. = Nótese que T : L L r con norma mayorada or g L r: T(f) L r = f g L r f L g L r (desigualdad de Minkowski continua) = que T : L r L con norma mayorada or g L r: f(y)g(x y)dy f L r g L r = T(f) L f L r g L r R n Entonces una alicación directa del teorema de Riesz-Thorin nos da que T envía L en L q con norma mayorada or g θ L r g θ L = g r L r con / = θ +θ/r y /q = ( θ)/r +θ/ ; es decir: f g L q f L g L r. 2
1. Espacio de funciones esencialmente acotadas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 6: Esacios de Lebesgue EPN, verano 2009 Todos los resultados anteriores ermiten el estudio de esacios
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 6: Esacios de Lebesgue EPN, verano 2009 Todos los resultados anteriores ermiten el estudio de esacios
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS. Conjunto de estabilidad y aproximación de Yosida para un sistema hiperbólico
 UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P DE MATEMÁTICA PURA Conjunto de estabilidad y aroximación de Yosida ara un sistema hierbólico Caítulo I. Preliminares TRABAJO
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P DE MATEMÁTICA PURA Conjunto de estabilidad y aroximación de Yosida ara un sistema hierbólico Caítulo I. Preliminares TRABAJO
1. Funciones medibles
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 4: Construcción de la integral de Lebesgue EPN, verano 2009 1. Funciones medibles Un concepto de medibilidad
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 4: Construcción de la integral de Lebesgue EPN, verano 2009 1. Funciones medibles Un concepto de medibilidad
La desigualdad de Minkowski de tipo débil y aplicaciones. Consuelo Ramírez Torreblanca
 La desigualdad de Minkowski de tio débil y alicaciones Consuelo Ramírez Torreblanca 2 Sean (X, M, µ), (Y, N, ν) dos esacios de medida. Sea T un oerador que transforma funciones M-medibles en funciones
La desigualdad de Minkowski de tio débil y alicaciones Consuelo Ramírez Torreblanca 2 Sean (X, M, µ), (Y, N, ν) dos esacios de medida. Sea T un oerador que transforma funciones M-medibles en funciones
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 3: Lema de Baire y Teorema clásicos del Análisis Funcional EPN, verano 2012 Definición 1 (Espacio de
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 3: Lema de Baire y Teorema clásicos del Análisis Funcional EPN, verano 2012 Definición 1 (Espacio de
1. Convergencia monótona
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 5: Teoremas clásicos EPN, verano 29 Todo el poder de la integral de Lebesgue está condensado en estos
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 5: Teoremas clásicos EPN, verano 29 Todo el poder de la integral de Lebesgue está condensado en estos
1. Unicidad de Medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
Parte 4: Teoremas de convergencia.
 Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Ejercicios de Análisis Funcional
 Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3). Lección n : La ecuación de ondas como punto de partida UCE, otoño 04 Introducción El objetivo
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Un (corto) panorama de Análisis Armónico (Nivel 3). Lección n : La ecuación de ondas como punto de partida UCE, otoño 04 Introducción El objetivo
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 2012
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
1. Propiedades básicas de las medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
Teoremas de Tonelli y Fubini
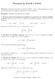 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
1. Teoría de Littlewood-Paley
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis armónico y espacios funcionales (Nivel 3). Lección n 2: Teoría y Descomposiciones de Littlewood-Paley. EPN, verano 2010 1. Teoría de
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis armónico y espacios funcionales (Nivel 3). Lección n 2: Teoría y Descomposiciones de Littlewood-Paley. EPN, verano 2010 1. Teoría de
Introducción a la Teoría Analítica de Números
 Introducción a la Teoría Analítica de Números Pablo De Náoli clase 11 1. Introducción Recordamos que Z n = unidades del anillo Z n = {a Z n : (a, n) = 1} es un gruo abeliano [=conmutativo] (con la oeración
Introducción a la Teoría Analítica de Números Pablo De Náoli clase 11 1. Introducción Recordamos que Z n = unidades del anillo Z n = {a Z n : (a, n) = 1} es un gruo abeliano [=conmutativo] (con la oeración
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Teorema de Hahn-Banach
 Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
El Teorema de Fubini-Tonelli
 Capítulo 23 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 23 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
5.- discontinuidad se dice esencial Ejemplo: f(x) = x - 2 es continua en a = 2 punto de acumulación de Dom(f) = lr. De Equivalentemente.
 x a 5.- discontinuidad se dice esencial Continuidad Sí lim de f(x) funciones no existe en una ó variable no es finito real la x a Ejemlo: f(x) x - es continua en a unto de acumulación de Dom(f) lr (i)
x a 5.- discontinuidad se dice esencial Continuidad Sí lim de f(x) funciones no existe en una ó variable no es finito real la x a Ejemlo: f(x) x - es continua en a unto de acumulación de Dom(f) lr (i)
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 2: Teorema de Hahn-Banach EPN, verano 2012
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 2: Teorema de Hahn-Banach EPN, verano 2012 1. Forma analítica Empecemos directamente con la primera
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 2: Teorema de Hahn-Banach EPN, verano 2012 1. Forma analítica Empecemos directamente con la primera
El Teorema de Fubini-Tonelli
 Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Teoría de Calderón-Zygmund con medidas generales
 Teoría de Calderón-Zygmund con medidas generales José Manuel Conde Alonso Seminario de Doctorandos UCM Consejo Superior de Investigaciones Científicas - Universidad Autónoma de Madrid 15 de octubre de
Teoría de Calderón-Zygmund con medidas generales José Manuel Conde Alonso Seminario de Doctorandos UCM Consejo Superior de Investigaciones Científicas - Universidad Autónoma de Madrid 15 de octubre de
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Sobre los Operadores de Multiplicación y Composición en espacios Weak L p. Fabio Andrés Vallejo Narvaez
 Sobre los Oeradores de Multilicación y Comosición en esacios Weak L Fabio Andrés Vallejo Narvaez Universidad Nacional de Colombia Deartamento de Matemáticas Bogotá Colombia 22 Sobre los Oeradores de Multilicación
Sobre los Oeradores de Multilicación y Comosición en esacios Weak L Fabio Andrés Vallejo Narvaez Universidad Nacional de Colombia Deartamento de Matemáticas Bogotá Colombia 22 Sobre los Oeradores de Multilicación
Cambio de Variables en la Integral Múltiple
 Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
1. Espacios de Hilbert
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 6: Espacios de Hilbert, Espacios de Sobolev UPS, julio 015 Índice 1. Espacios de Hilbert
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 6: Espacios de Hilbert, Espacios de Sobolev UPS, julio 015 Índice 1. Espacios de Hilbert
II Encuentro Internacional de Matemáticas, Estadística y Educación Matemática 2013
 II Encuentro Internacional de Matemáticas, Estadística y Educación Matemática 013 LA GEOMETRIA DE LOS ESPACIOS L. Erika Eliana Toloza Gordillo* y Richard De La Cruz Guerrero ** *Universidad Pedagógica
II Encuentro Internacional de Matemáticas, Estadística y Educación Matemática 013 LA GEOMETRIA DE LOS ESPACIOS L. Erika Eliana Toloza Gordillo* y Richard De La Cruz Guerrero ** *Universidad Pedagógica
1 Espacios de Banach:
 Ecuaciones Diferenciales - 2 cuatrimestre 2003 Resultados preliminares parte II Espacios de Banach: Sea X un IR-espacio vectorial. Definición. Una función : X [0, + ) se dice una norma si. x + y x + y
Ecuaciones Diferenciales - 2 cuatrimestre 2003 Resultados preliminares parte II Espacios de Banach: Sea X un IR-espacio vectorial. Definición. Una función : X [0, + ) se dice una norma si. x + y x + y
El Teorema de Stone-Weierstrass
 Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 2: Soluciones clásicas de las ecuaciones de Navier-Stokes USFQ, noviembre 215 Índice
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Ecuaciones en Derivadas Parciales (Nivel 3). Lección n 2: Soluciones clásicas de las ecuaciones de Navier-Stokes USFQ, noviembre 215 Índice
Reciprocidad Cuadrática
 Caítulo 4 Recirocidad Cuadrática En este caítulo estudiamos una serie de resultados dirigidos a demostrar la Ley de Rerocidad Cuadrática, la cual fue robada or Gauss en su libro Disquisitiones Arithmeticae
Caítulo 4 Recirocidad Cuadrática En este caítulo estudiamos una serie de resultados dirigidos a demostrar la Ley de Rerocidad Cuadrática, la cual fue robada or Gauss en su libro Disquisitiones Arithmeticae
IRREDUCIBILIDAD EN K[X 1,..., X n ]
![IRREDUCIBILIDAD EN K[X 1,..., X n ] IRREDUCIBILIDAD EN K[X 1,..., X n ]](/thumbs/58/41991469.jpg) IRREDUCIBILIDAD EN K[X 1,..., X n ] SAURON Índice General 1. DFU y anillos de olinomios 1 2. Irreducibilidad de olinomios sobre un DFU 3 3. Algunos ejemlos 5 Referencias 6 1. DFU y anillos de olinomios
IRREDUCIBILIDAD EN K[X 1,..., X n ] SAURON Índice General 1. DFU y anillos de olinomios 1 2. Irreducibilidad de olinomios sobre un DFU 3 3. Algunos ejemlos 5 Referencias 6 1. DFU y anillos de olinomios
Espacios compactos. 7.1 Espacios compactos
 58 Capítulo 7 Espacios compactos 7.1 Espacios compactos Definición 7.1.1 (Recubrimiento). Sea X un conjunto y sea S X. Un recubrimiento de S es una familia A = {A i } i I de subconjuntos de X tales que
58 Capítulo 7 Espacios compactos 7.1 Espacios compactos Definición 7.1.1 (Recubrimiento). Sea X un conjunto y sea S X. Un recubrimiento de S es una familia A = {A i } i I de subconjuntos de X tales que
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
Elementos Básicos de Análisis Funcional en. Dr. Oldemar Rodríguez Rojas
 Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Una introducción a la teoría de pesos A p
 Una introducción a la teoría de pesos A p Martha Guzmán Partida UNISON Martha Guzmán Partida (UNISON) Una introducción a la teoría de pesos A p / 44 Sesión 2. Sea f 2 L loc (Rn ). La función maximal de
Una introducción a la teoría de pesos A p Martha Guzmán Partida UNISON Martha Guzmán Partida (UNISON) Una introducción a la teoría de pesos A p / 44 Sesión 2. Sea f 2 L loc (Rn ). La función maximal de
Apuntes sobre la integral de Lebesgue
 Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
Análisis de Fourier. Resumen de los apuntes de D. Antonio Cañada Villar. Sergio Cruz Blázquez. Curso 2015/2016
 Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
INTRODUCCIÓN A LOS ESPACIOS DE FUNCIONES. Problemas
 Problemas Curso 2013-2014 Problemas 1. Sea E un espacio normado. Si a, b son elementos de E, probar: (a) 1 2 (a + b) 2 1 2 a 2 + 1 2 b 2. (b) a max{ a + b, a b }. 2. Demostrar que en un espacio normado,
Problemas Curso 2013-2014 Problemas 1. Sea E un espacio normado. Si a, b son elementos de E, probar: (a) 1 2 (a + b) 2 1 2 a 2 + 1 2 b 2. (b) a max{ a + b, a b }. 2. Demostrar que en un espacio normado,
Aplicaciones de desigualdades con pesos a ecuaciones diferenciales
 I UNIVERSIDAD NACIONAL DE LA PLATA Facultad de Ciencias Exactas Deartamento de Matemática Alicaciones de desigualdades con esos a ecuaciones diferenciales Trabajo de Tesis Doctoral MARIA EUGENIA CEJAS
I UNIVERSIDAD NACIONAL DE LA PLATA Facultad de Ciencias Exactas Deartamento de Matemática Alicaciones de desigualdades con esos a ecuaciones diferenciales Trabajo de Tesis Doctoral MARIA EUGENIA CEJAS
Notas de clase sobre la Transformada de Fourier
 Notas de clase sobre la Transformada de Fourier Pablo L. De Nápoli 3 de noviembre de 205. La definición de la transformada de Fourier Definición. Si f L ( ) definimos su transformada de fourier por f(ξ)
Notas de clase sobre la Transformada de Fourier Pablo L. De Nápoli 3 de noviembre de 205. La definición de la transformada de Fourier Definición. Si f L ( ) definimos su transformada de fourier por f(ξ)
Cubierta de Vitali y el Teorema de Diferenciación de Lebesgue
 Cubierta de Vitali y el Teorema de Diferenciación de Lebesgue Isaac Meza López Club de Análisis ITAM Abstract En esta sesión se discutió sobre el Teorema de la Cubierta de Vitali y su aplicación en el
Cubierta de Vitali y el Teorema de Diferenciación de Lebesgue Isaac Meza López Club de Análisis ITAM Abstract En esta sesión se discutió sobre el Teorema de la Cubierta de Vitali y su aplicación en el
Tema 10: Teorema de Hahn-Banach. 14 y 17 de junio de 2010
 Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Espacios de funciones: Una introducción a los Espacios de Sobolev
 UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO Decanato de Ciencias y Tecnología Licenciatura en Ciencias Matemáticas Esacios de funciones: Una introducción a los Esacios de Sobolev Trabajo Esecial de Grado
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO Decanato de Ciencias y Tecnología Licenciatura en Ciencias Matemáticas Esacios de funciones: Una introducción a los Esacios de Sobolev Trabajo Esecial de Grado
Cambio de Variables en la Integral Múltiple
 Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
El Teorema de Baire y sus consecuencias en espacios de Banach
 Trabajo Final de Grado Grado en Matemáticas Facultad de Matemáticas Universidad de Barcelona El Teorema de Baire y sus consecuencias en espacios de Banach Autor: Sergi Arias Garcia Tutora: María Jesús
Trabajo Final de Grado Grado en Matemáticas Facultad de Matemáticas Universidad de Barcelona El Teorema de Baire y sus consecuencias en espacios de Banach Autor: Sergi Arias Garcia Tutora: María Jesús
Cambio de variables en la integral múltiple.
 Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
 Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
1. MEDIDA E INTEGRACIÓN.
 1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
XAX > i 0. i 4 2i. 2 i i 8
 Álgebra Lineal Caítulo. Tóicos Eseciales y Alicaciones.. Matrices y formas ositivas En esta sección estudiamos matrices ositivas, formas sesquilineales ositivas, y formas cuadráticas ositivas. a. Matrices
Álgebra Lineal Caítulo. Tóicos Eseciales y Alicaciones.. Matrices y formas ositivas En esta sección estudiamos matrices ositivas, formas sesquilineales ositivas, y formas cuadráticas ositivas. a. Matrices
Normas Equivalentes. Espacios Normados de Dimensión Finita
 Capítulo 2 Normas Equivalentes. Espacios Normados de Dimensión Finita Dos son los resultados más importantes que, sobre la equivalencia de normas, veremos en este capítulo. El primero de ellos establece
Capítulo 2 Normas Equivalentes. Espacios Normados de Dimensión Finita Dos son los resultados más importantes que, sobre la equivalencia de normas, veremos en este capítulo. El primero de ellos establece
Medida y Probabilidad
 Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
Ejercicios Variable Real
 UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
 UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P DE MATEMÁTICAS Decaimiento exponencial para la ecuación de onda con amortiguamiento localmente distribuido - caso globalmente
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P DE MATEMÁTICAS Decaimiento exponencial para la ecuación de onda con amortiguamiento localmente distribuido - caso globalmente
Funciones integrables en R n
 Capítulo 1 Funciones integrables en R n Sean un subconjunto acotado de R n, y f : R una función acotada. Sea R = [a 1, b 1 ]... [a n, b n ] un rectángulo que contenga a. Siempre puede suponerse que f está
Capítulo 1 Funciones integrables en R n Sean un subconjunto acotado de R n, y f : R una función acotada. Sea R = [a 1, b 1 ]... [a n, b n ] un rectángulo que contenga a. Siempre puede suponerse que f está
2. CONSTRUCCIÓN DE MEDIDAS.
 2. CONSTRUCCIÓN DE MEDIDAS. 1. MEDIDAS EXTERIORES. (2,1,1) Definición. Una medida exterior es una aplicación µ : P(X) [0, + ] que cumple: (a) µ ( ) = 0. (b) Monotonía: Si A B, entonces µ (A) µ (B). (c)
2. CONSTRUCCIÓN DE MEDIDAS. 1. MEDIDAS EXTERIORES. (2,1,1) Definición. Una medida exterior es una aplicación µ : P(X) [0, + ] que cumple: (a) µ ( ) = 0. (b) Monotonía: Si A B, entonces µ (A) µ (B). (c)
Algunos conceptos básicos del Análisis Funcional Memoria
 Algunos conceptos básicos del Análisis Funcional Memoria Mar Jiménez Sevilla Universidad Complutense de Madrid Facultad de Ciencias Matemáticas Departamento de Análisis Matemático Índice general Capítulo
Algunos conceptos básicos del Análisis Funcional Memoria Mar Jiménez Sevilla Universidad Complutense de Madrid Facultad de Ciencias Matemáticas Departamento de Análisis Matemático Índice general Capítulo
La siguiente definición es muy intuitiva. Se dice que una sucesión {x n } es:
 Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Sucesiones monótonas Monotonía. Tema 6
 Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Tema 6 Sucesiones monótonas Vamos a discutir ahora una importante propiedad de ciertas sucesiones de números reales: la monotonía. Como primer resultado básico, probaremos que toda sucesión monótona y
Espacios métricos completos
 5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
Principio de acotación uniforme
 Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
SERIES DE FOURIER RESPECTO DE SISTEMAS ORTOGONALES: ESTUDIO DE LA CONVERGENCIA EN ESPACIOS DE LEBESGUE Y DE LORENTZ
 SERIES DE FOURIER RESPECTO DE SISTEMAS ORTOGONALES: ESTUDIO DE LA CONVERGENCIA EN ESPACIOS DE LEBESGUE Y DE LORENTZ or Mario Pérez Riera Memoria resentada ara otar al grado de Doctor en Ciencias Matemáticas.
SERIES DE FOURIER RESPECTO DE SISTEMAS ORTOGONALES: ESTUDIO DE LA CONVERGENCIA EN ESPACIOS DE LEBESGUE Y DE LORENTZ or Mario Pérez Riera Memoria resentada ara otar al grado de Doctor en Ciencias Matemáticas.
Clase 3: Teorema de Fundamental de la Aritmética
 Clase 3: Teorema de Fundamental de la Aritmética Dr. Daniel A. Jaume, * 12 de agosto de 2011 1. Primos Definición 1.1 Un entero ositivo se dice que es un número rimo si tiene exactamente 2 divisores ositivos
Clase 3: Teorema de Fundamental de la Aritmética Dr. Daniel A. Jaume, * 12 de agosto de 2011 1. Primos Definición 1.1 Un entero ositivo se dice que es un número rimo si tiene exactamente 2 divisores ositivos
Ejercicios de Análisis Funcional. Curso
 Ejercicios de Análisis Funcional Curso 2010-2011 1 1 Preliminares de espacios normados Problema 1.1. Demostrar que para 1 < p < la norma. p en R 2 verifica la siguiente propiedad: Si x, y R 2 con x y y
Ejercicios de Análisis Funcional Curso 2010-2011 1 1 Preliminares de espacios normados Problema 1.1. Demostrar que para 1 < p < la norma. p en R 2 verifica la siguiente propiedad: Si x, y R 2 con x y y
Análisis Matemático Ingenierías en Informática Soluciones del examen de febrero de 2009
 Análisis Matemático Ingenierías en Informática Soluciones del examen de febrero de 9. a) Prueba, usando el teorema de Bolzano, que la función f.x/ D e x Cx x se anula en al menos tres untos del intervalo
Análisis Matemático Ingenierías en Informática Soluciones del examen de febrero de 9. a) Prueba, usando el teorema de Bolzano, que la función f.x/ D e x Cx x se anula en al menos tres untos del intervalo
Teoría de la Integración
 Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
1. Funciones Medibles
 1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
Medidas. Problemas para examen. Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez.
 Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Ejercicios de teoría de la medida
 Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Espacios de Banach. Problemas para examen
 Espacios de Banach Problemas para examen Se marcan con azul algunos ejercicios que no vimos bien en clase. La lista todavía no es completa; se pueden agregar algunos teoremas y ejercicios que vimos bien
Espacios de Banach Problemas para examen Se marcan con azul algunos ejercicios que no vimos bien en clase. La lista todavía no es completa; se pueden agregar algunos teoremas y ejercicios que vimos bien
La Propiedad de Radon-Nikodým y el Teorema de Representación de Riesz
 Capítulo 3 La Propiedad de Radon-Nikodým y el Teorema de Representación de Riesz n este capítulo definiremos la Propiedad de Radon-Nikodým en un espacio de Banach X y estableceremos su equivalencia con
Capítulo 3 La Propiedad de Radon-Nikodým y el Teorema de Representación de Riesz n este capítulo definiremos la Propiedad de Radon-Nikodým en un espacio de Banach X y estableceremos su equivalencia con
CAPITULO 4. ECUACIONES DIFERENCIALES DE PRIMER ORDEN Introducción
 CAPITULO 4. ECUACIONES DIFERENCIALES DE PRIMER ORDEN 4.. Introducción Se denomina ecuación diferencial ordinaria a toda ecuación en la que aarecen una o varias derivadas de una función. Cuando las derivada
CAPITULO 4. ECUACIONES DIFERENCIALES DE PRIMER ORDEN 4.. Introducción Se denomina ecuación diferencial ordinaria a toda ecuación en la que aarecen una o varias derivadas de una función. Cuando las derivada
Notas de Análisis Funcional
 Notas de Análisis Funcional Ventura Echandía Liendo. Carlos E. Finol Caracas, Octubre 2002. 2 Contenido 1 Nociones de espacios normados 7 1.1 Espacios métricos y espacios vectoriales............. 7 1.1.1
Notas de Análisis Funcional Ventura Echandía Liendo. Carlos E. Finol Caracas, Octubre 2002. 2 Contenido 1 Nociones de espacios normados 7 1.1 Espacios métricos y espacios vectoriales............. 7 1.1.1
Capítulo La integral de Riemann
 Capítulo 5 Integración 1. La integral de iemann Empecemos por recordar la integral de iemann de una función acotada f : [a, b]. Una partición P de [a, b] es un subconjunto finito P [a, b] tal que a, b
Capítulo 5 Integración 1. La integral de iemann Empecemos por recordar la integral de iemann de una función acotada f : [a, b]. Una partición P de [a, b] es un subconjunto finito P [a, b] tal que a, b
Derivadas en variedades
 Derivadas en variedades Luis Guijarro UAM 19 de mayo de 2010 Luis Guijarro ( UAM) Derivadas en variedades 19 de mayo de 2010 1 / 68 Curvas suaves en una variedad Definición Una curva suave en una variedad
Derivadas en variedades Luis Guijarro UAM 19 de mayo de 2010 Luis Guijarro ( UAM) Derivadas en variedades 19 de mayo de 2010 1 / 68 Curvas suaves en una variedad Definición Una curva suave en una variedad
TEOREMA DE HAHN-BANACH.
 TEOREMA DE HAHN-BANACH. Sea E un e.v y M un s.v. de E. Toda aplicación lineal T 0 : M F de M en otro e.v. F se extiende a una aplicación lineal T : E F. Por ejemplo, basta considerar un suplementario algebraico
TEOREMA DE HAHN-BANACH. Sea E un e.v y M un s.v. de E. Toda aplicación lineal T 0 : M F de M en otro e.v. F se extiende a una aplicación lineal T : E F. Por ejemplo, basta considerar un suplementario algebraico
RESUMEN ELEMENTOS DE GEOMETRÍA DIFERENCIAL Y TOPOLOGÍA CURSO
 RESUMEN ELEMENTOS DE GEOMETRÍA DIFERENCIAL Y TOPOLOGÍA CURSO 2008-09 En este resumen no se puede escribir o añadir nada, ni por delante, ni por detrás. En todo caso, sólo se permite subrayar lo que se
RESUMEN ELEMENTOS DE GEOMETRÍA DIFERENCIAL Y TOPOLOGÍA CURSO 2008-09 En este resumen no se puede escribir o añadir nada, ni por delante, ni por detrás. En todo caso, sólo se permite subrayar lo que se
Métodos matemáticos: Análisis funcional
 Métodos matemáticos: Análisis funcional Conceptos y resultados fundamentales Curso 2011/2012 Aquí encontrarás los Teoremas hay que saber para el primer parcial ( 1) así como las definiciones, problemas
Métodos matemáticos: Análisis funcional Conceptos y resultados fundamentales Curso 2011/2012 Aquí encontrarás los Teoremas hay que saber para el primer parcial ( 1) así como las definiciones, problemas
3. INTEGRACION. La (µ)-integral de una función simple no negativa es, por definición:
 3. INTEGRACION La (µ)-integral de una función simple no negativa es, por definición: En este caso se sigue la convención de que si µ(y E i ) = pero como a i = 0 entonces a i µ(y E i ) = 0. Evidentemente,
3. INTEGRACION La (µ)-integral de una función simple no negativa es, por definición: En este caso se sigue la convención de que si µ(y E i ) = pero como a i = 0 entonces a i µ(y E i ) = 0. Evidentemente,
Parte II. Cálculo Diferencial para Funciones de Varias Variables Reales
 Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
10. Series de potencias
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
Ejercicios Análisis II
 Ejercicios Análisis II Ejercicios resueltos del libro Real and Complex Analysis de Walter Rudin Mauricio Bravo Vera mauro.bravo@gmail.com Segundo semestre 2010 Índice general 1. Integración Abstracta
Ejercicios Análisis II Ejercicios resueltos del libro Real and Complex Analysis de Walter Rudin Mauricio Bravo Vera mauro.bravo@gmail.com Segundo semestre 2010 Índice general 1. Integración Abstracta
INTERPOLACIÓN DE OPERADORES. EN ESPACIOS L p. Guillermo Javier Flores Directora: Dra. Elida Ferreyra
 UNIVERSIDAD NACIONAL DE CÓRDOBA, FACULTAD DE MATEMÁTICA, ASTRONOMÍA Y FÍSICA Trabajo especial de licenciatura INTERPOLACIÓN DE OPERADORES EN ESPACIOS L p Guillermo Javier Flores Directora: Dra. Elida Ferreyra
UNIVERSIDAD NACIONAL DE CÓRDOBA, FACULTAD DE MATEMÁTICA, ASTRONOMÍA Y FÍSICA Trabajo especial de licenciatura INTERPOLACIÓN DE OPERADORES EN ESPACIOS L p Guillermo Javier Flores Directora: Dra. Elida Ferreyra
Desigualdades con pesos para la función maximal de Hardy-Littlewood
 UNIVERSIDAD DE SONORA División de Ciencias Exactas y Naturales Departamento de Matemáticas Desigualdades con pesos para la función maximal de Hardy-Littlewood TESIS que para obtener el grado académico
UNIVERSIDAD DE SONORA División de Ciencias Exactas y Naturales Departamento de Matemáticas Desigualdades con pesos para la función maximal de Hardy-Littlewood TESIS que para obtener el grado académico
Funciones de Clase C 1
 Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
sup si A no es acotado.
 Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS. Fracciones continuas, ecuación de Pell y unidades en el anillo de enteros de los cuerpos cuadráticos
 UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS MATEMÁTICAS EAP DE MATEMÁTICA PURA Fracciones continuas, ecuación de Pell y unidades en el anillo de enteros de los cueros cuadráticos Caítulo
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS FACULTAD DE CIENCIAS MATEMÁTICAS EAP DE MATEMÁTICA PURA Fracciones continuas, ecuación de Pell y unidades en el anillo de enteros de los cueros cuadráticos Caítulo
EL SÍMBOLO DE LEGENDRE Y LA LEY DE RECIPROCIDAD CUADRÁTICA. Proposiciones Previas. Dos hechos que se deben tener presentes:
 EL SÍMBOLO DE LEGENDRE Y LA LEY DE RECIPROCIDAD CUADRÁTICA Sea un rimo imar y a Z. El Símbolo de Legendre ( a ) se define de la siguiente manera: ( a 0, if divide a a ) := 1, si existe x Z tal que x 2
EL SÍMBOLO DE LEGENDRE Y LA LEY DE RECIPROCIDAD CUADRÁTICA Sea un rimo imar y a Z. El Símbolo de Legendre ( a ) se define de la siguiente manera: ( a 0, if divide a a ) := 1, si existe x Z tal que x 2
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Relación de ejercicios. Topología en R N
 Relación de ejercicios. Topología en R N Abraham Rueda Zoca Ejercicio. Sea N un número natural. Demostrar que dados x, y R N se cumple que x y x y. Indicación: Utilizar la desigualdad triangular. Ejercicio
Relación de ejercicios. Topología en R N Abraham Rueda Zoca Ejercicio. Sea N un número natural. Demostrar que dados x, y R N se cumple que x y x y. Indicación: Utilizar la desigualdad triangular. Ejercicio
El teorema de Lebesgue
 Capítulo 3 El teorema de Lebesgue En este capítulo estudiaremos un teorema que nos dice exactamente qué funciones son integrables y cuán grande puede ser la frontera de un conjunto para que éste tenga
Capítulo 3 El teorema de Lebesgue En este capítulo estudiaremos un teorema que nos dice exactamente qué funciones son integrables y cuán grande puede ser la frontera de un conjunto para que éste tenga
TEMA VI: ESPACIOS DE HILBERT
 TEMA VI: ESPACIOS DE HILBERT. Espacios con producto escalar Definición: Sea L un espacio vectorial sobre el cuerpo K (R ó C). Por un producto escalar (o interno) sobre L entedemos una aplicación :
TEMA VI: ESPACIOS DE HILBERT. Espacios con producto escalar Definición: Sea L un espacio vectorial sobre el cuerpo K (R ó C). Por un producto escalar (o interno) sobre L entedemos una aplicación :
Extensión de medidas
 Extensión de medidas Problemas para examen Semianillos de conjuntos 1. Escriba la definición de semianillo de conjuntos. 2. Convenio: el conjunto vacío pertenece a cualquier semianillo. En los siguientes
Extensión de medidas Problemas para examen Semianillos de conjuntos 1. Escriba la definición de semianillo de conjuntos. 2. Convenio: el conjunto vacío pertenece a cualquier semianillo. En los siguientes
2.3. Aplicaciones del teorema de Baire a espacios de Banach
 40 CAPÍTULO. COMPLETITUD Y CATEGORÍAS.3. Aplicaciones del teorema de Baire a espacios de Banach En esta sección, veremos algunas aplicaciones del teorema de Baire a espacios vectoriales normados. En particular,
40 CAPÍTULO. COMPLETITUD Y CATEGORÍAS.3. Aplicaciones del teorema de Baire a espacios de Banach En esta sección, veremos algunas aplicaciones del teorema de Baire a espacios vectoriales normados. En particular,
Convergencia Sucesiones convergentes
 Lección 6 Convergencia Vamos a estudiar la noción de convergencia de sucesiones en un espacio métrico arbitrario, generalizando la que conocemos en R. La definimos de forma que quede claro que se trata
Lección 6 Convergencia Vamos a estudiar la noción de convergencia de sucesiones en un espacio métrico arbitrario, generalizando la que conocemos en R. La definimos de forma que quede claro que se trata
La propiedad de compacidad
 En un artículo anterior hemos obtenido dos importantes resultados relacionados con la continuidad de una función en un intervalo: el teorema de los ceros de Bolzano y el teorema del valor intermedio. De
En un artículo anterior hemos obtenido dos importantes resultados relacionados con la continuidad de una función en un intervalo: el teorema de los ceros de Bolzano y el teorema del valor intermedio. De
ANALISIS MATEMATICO V
 ASIGNATURA: ANALISIS MATEMATICO V Curso 2015/2016 (Código:01085121) AVISO IMPORTANTE En el Consejo de Gobierno del 30 de junio de 2015 se aprobó, por unanimidad, que la convocatoria de exámenes extraordinarios
ASIGNATURA: ANALISIS MATEMATICO V Curso 2015/2016 (Código:01085121) AVISO IMPORTANTE En el Consejo de Gobierno del 30 de junio de 2015 se aprobó, por unanimidad, que la convocatoria de exámenes extraordinarios

 Espacios L p con 0
Espacios L p con 0