Aproximación por rectángulos del área de f(x) = x 3 en [0, 2]
|
|
|
- Clara Peralta Luna
- hace 6 años
- Vistas:
Transcripción
1 Cpítulo 5 Integrión 5.. Introduión Hst hor hemos borddo tems reliondos básimente on el Análisis y el Cálulo iferenil (espeilmente en espios de Bnh), y que en prinipio relionábmos on el so prtiulr en que el espio fuer R, o lgún subonjunto de él, tnto pr el álulo de límites, omo derivds, óptimos de funiones, noiones de ontinuidd, etéter. Lo que introduiremos en este pítulo orresponde un extensión de lo que onoemos hst hor por Integrión, y que fue borddo en el urso previo. Pr dr un orret noión de ómo se integr en e.v.n. ms generles, uyo estudio se insert en un teorí generl de ls Mtemátis denomind Teorí de l Medid, debemos omenzr por trtr el so de R n, reordndo lguns noiones vists pr el so pr n y generlizndo n 2 y n 3 en funión de ls pliiones físis y geométris de l ingenierí, y sí definir inequívomente el onepto de integrl múltiple. Volveremos revisr oneptos omo Prtiiones, Sums de Riemnn, ondiiones de Riemnn-integrbilidd y Prmetrizión on tl de mplir nuestro estudio relizdo pr Cálulo de un Vrible. A ontinuión, dremos un onjunto de ejemplos y rgumentos que permitn no sólo lulr integrles sino que demás entregr ls herrmients pr juzgr l pertineni del onepto Conepto de Áre d un funión positiv f, un pregunt muy nturl es si existe un expresión pr el áre bjo su grfo. Pr responder est interrognte, podemos intentr proximr un vlor rel que represente dih áre, y un de ls forms de herlo es onsiderr dos proximiones: un inferior, que sume áres de retángulos insritos en l urv de f; l segund, un superior, que sume áres de retángulos irunsritos en l urv de f, omo indi l figur. Aproximión por retángulos del áre de f(x) x 3 en [, 2] Pr lulr ests ntiddes de form onsistente, debemos estbleer regls que se pliquen onjuntos generles. Luego, el álulo de áres será un pliión prtiulr de est teorí. 2
2 5.2. CONCEPTO E ÁREA CAPÍTULO 5. INTEGRACIÓN Se prte por sumir tres hipótesis (que hrán l suerte de xioms). enotremos por R un región del plno, y será A(R) un número rel que determin el áre que enierr dih región. iho esto, ( R R 2 ) A(R) R R 2 A(R R 2 ) A(R ) + A(R 2 ) Si R es un retángulo, es deir, R [, b] [, d], entones A(R) (b ) (d ) Proposiión R R 2 A(R ) A(R 2 ) em.: Podemos esribir R 2 omo R 2 R (R 2 \ R ) que result ser un unión disjunt. Luego, por el segundo postuldo, A(R 2 ) A(R (R 2 \ R )) A(R ) + A(R 2 \ R ), donde A(R 2 \ R ) A(R ) Si onsidermos el onjunto { (x, y) R 2 x [, b], y f(x) }, ls hipótesis nteriores pueden plirse en él. Pr esto, un ondiión que impondremos en f es que esté bien definid en [, b], es deir, que no se hg infinit. Si esto se umple, diremos que f es otd. Notemos demás que no pediremos que f se ontinu en [, b]. Finlmente, dd un funión f, lo que lulremos será extmente el áre bjo su urv si demás f. Cómo podemos relizr, formlmente, un proedimiento omo el desrito en l imgen nterior? Es deir, pree orreto tomr retángulos que hgn lo que menionmos, pero es perentorio sber ómo se definen mtemátimente y si so es posible que umpln su misión. Neesitmos dos oss pr definir d retángulo: un bse y un ltur. remos definiiones de ésts en funión de [, b] y f. efiniión : Se define un prtiión de un intervlo I [, b] omo P (I) {x i I x < x <... < x n < x n b} Notemos que, omo resultdo de l prtiión, neesrimente se tiene que el intervlo originl se divide en subintervlos I i [x i, x i ] uy unión es el mismo intervlo, esto es I n [x i, x i ] i n i I i enotmos por P I l onjunto de tods ls prtiiones sobre el intervlo I. Ejemplo: Si tenemos el intervlo I [, ], podemos definir en él ls siguientes prtiiones:. P {, } (prtiión trivil) 2. P 2 {, 2, } 3. P 3 {, 7, 3, π 4, } 4. P 4 { i n} n i efiniión 2: Se define l norm de un prtiión P (I) omo l myor distni entre puntos veinos ontenidos en ell, esto es: P (I) máx i n {x i x i }
3 5.2. CONCEPTO E ÁREA CAPÍTULO 5. INTEGRACIÓN Ejemplo: Considerndo nuevmente I [, ]:. P 2. P P 3 π P 4 n Observión: Si l prtiión es uniforme (todos los puntos están equiespidos), se tiene que P (I) (x i x i ) i,...,n b n Otrs epiones equivlentes son prtiión regulr, equidistnte o equiprtiión. En el ejemplo nterior, P, P 2 y P 4 son uniformes. Normlmente usremos este último tipo de prtiiones, pr lulr de form simple los primeros resultdos. Finlmente, notemos que, dd un prtiión finit ulquier, podemos onstruir otr prtiión que inluy los puntos de l primer más (resp. menos) lgunos otros. Esto define l noión de prtiión más fin (resp. menos fin). efiniión 3 iremos que un prtiión Q es más fin que P si P Q. Tmbién diremos que Q es un refinmiento de P, o que P Q. Observión: es un relión de orden pril pr P I. Es fáil drse uent de que, en [, b], P {, +b 2, b} y Q {, +b 3, b} no son omprbles. L form más intuitiv de proximr el áre enerrd entre un intervlo y su imgen, es trvés de ls llmds Sums de Riemnn, en que se tom el intervlo de interés, se prtiion (idelmente en prtes igules), y l longitud de d subintervlo definido por l prtiión se interpret omo l bse de un retángulo; por último, ls Sums de Riemnn proximn inferior y superiormente el áre busd tomndo omo lturs el ínfimo y el supremo de l funión en d subintervlo, respetivmente, y lulndo l sum del áre de todos los retángulos sí definidos. Formlmente: efiniión 4: Sen f : R R un funión, I [, b] un intervlo tl que I dom(f), y P un prtiión de diho intervlo. efinimos ls ntiddes: x i x i x i m i (f) M i (f) ínf f(x) x [x i,x i] sup f(x) x [x i,x i] Entones, se definen l sum inferior y l sum superior de f on respeto l prtiión P omo s(f, P ) S(f, P ) n m i (f) x i i n M i (f) x i Ls sums inferior y superior suelen onoerse tmbién omo proximión por defeto y proximión por exeso, respetivmente. Es lro que x i P, por lo que l ide de tomr un prtiión equittiv (que podemos llmr, simplemente, equiprtiión) es que ( i {,..., n}) x i P b n i y que, demás, ( i {,..., n}) x i + i b n.
4 5.2. CONCEPTO E ÁREA CAPÍTULO 5. INTEGRACIÓN Ejemplo: Sen I [, ] y su prtiión P P 4 dd en el ejemplo nterior, y f(x) e x. Tenemos: x i i n i n m i (f) M i (f) n ínf x [x ex e xi e i n i,x i] sup e x e xi e i n x [x i,x i] Luego, s(f, P 4 ) S(f, P 4 ) n i n i e i n e i n n e n(e n ) n e n (e ) n(e n ) Un propiedd muy nturl es que, independientemente de l prtiión esogid, se tiene donde m ínf f(x) y M sup f(x). x [,b] x [,b] m(b ) s(f, P ) S(f, P ) M(b ) Otr propiedd importnte es que, pr ulquier prtiión P, si P Q, entones s(f, P ) s(f, Q) S(f, P ) S(f, Q) ) b) Refinmiento de un sum inferior () y superior (b) Lo nterior puede demostrrse sin myor difiultd, por lo que qued omo ejeriio. Sin embrgo, es más interesnte lo siguiente: Proposiión 2: Se f : I R R un funión, on I [, b]. Se tiene que ( P, Q P I ) s(f, P ) S(f, Q) em.: No import ómo sen P y Q, sbemos que P Q debe ser más fin que mbs. Por ls propieddes menionds nteriormente, se tiene s(f, P ) s(f, P Q) S(f, P Q) S(f, Q)
5 5.2. CONCEPTO E ÁREA CAPÍTULO 5. INTEGRACIÓN Es nturl preguntrse de qué sirve est proposiión, y en qué medid es más importnte que ls dos propieddes nteriores. L verdd es que este resultdo es vitl, y que nos die que si tommos ulquier suesión de prtiiones (P n ) n N tl que P n P n+ (d prtiión en l suesión es estritmente más fin que su predeesor), entones tod suesión de sums inferiores s(f, P n ) es reiente y otd superiormente, y tod suesión de sums superiores S(f, P n ) es dereiente y otd inferiormente, luego ests dos ntiddes deben onverger un número rel (no neesrimente onvergen l mismo). L úni sutilez que hy que uidr insistentemente, es que f se otd en [, b]. iho esto, sbemos que existen el supremo de ls sums inferiores y el ínfimo de ls sums superiores, que podemos denotr b b f sup s(f, P ) P P I f ínf S(f, P ) P P I Observión: Siempre se umple que b f b efiniión 5: iremos que f, otd en el intervlo I [, b], es Riemnn-integrble en I si f. A prtir de esto, si f es Riemnn-integrble en I, podemos definir unívomente l integrl definid omo I f b b f b f sup P P I s(f, P ) ínf P P I S(f, P ) Est últim expresión es onoid omo notión de Leibnitz. f b f(x)dx Observión: Por l observión nterior, pr que f se Riemnn-integrble bst que se umpl Además, si f es Riemnn-integrble, f es el únio número que stisfe I ( P P I ) s(f, P ) f S(f, P ) Finlmente, si l prtiión es equittiv, es equivlente onsiderr el supremo y el ínfimo de un sum omo el límite undo n (el tmño de l prtiión) tiende infinito. Es deir, si sólo onsidermos PI R P I el onjunto de prtiiones equidistntes, tenemos que sup s(f, P ) lím s(f, P ) P PI R n ínf P P R I S(f, P ) lím n S(f, P ) I b f b f. Ejemplo: Notemos que en el ejemplo nterior, sup P P R I ínf P P R I s(f, P ) lím s(f, P e 4) lím n n n(e n ) e S(f, P ) lím S(f, P e n (e ) 4) lím n n n(e n ) e
6 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN Ambos resultdos oiniden, por lo tnto f(x) e x es integrble en [, ], y podemos deir sin equivornos que e x dx e. Pr onluir est seión, dremos el resultdo lve pr segurr que el áre bjo un urv existe y tiene un vlor determindo (sin neesidd de proximrl itertivmente). Proposiión 3 (Condiión de Riemnn): Un funión f otd sobre un intervlo I [, b] es Riemnn-integrble en I si, y sólo si, ( ε > ) ( P P I ) S(f, P ) s(f, P ) < ε em.: ) Como f es integrble, existe f, y podemos esoger dos prtiiones, P y Q, tles que I f s(f, P ) ε S(f, Q) f ε 2 2 I Tomndo K P Q, que es más fin que mbs prtiiones originles, lo nterior qued f s(f, K) ε S(f, K) f ε 2 2 y sumndo mbos resultdos, ) Sbemos que pr ulquier prtiión P I S(f, K) s(f, K) ε s(f, P ) I f I I f S(f, P ) I Neesitmos que I f f, es deir, I I f f ε. Pr ver que esto es ierto, bst usr l desiguldd I nterior; omo f stisfe l ondiión de Riemnn, Luego tenemos que ( P ε P I ) S(f, P ε ) s(f, P ε ) ε f f S(f, P ε ) s(f, P ε ) ε I I Ejemplo: Se define l funión de irihlet omo si x Q (x) si x / Q Es lro que (x) no es Riemnn-integrble en ningún intervlo [, b], y l prueb está en que l sum inferior siempre es, mientrs que l superior es b, pr ulquier prtiión Generlizión de integrl: volumen e hipervolumen Trbjremos dos situiones en prieni distints: el so en que tengmos un mpo eslr f uyo dominio esté en R 2, y el so en que el mpo eslr teng dominio en R n. Como veremos, el segundo so generlizrá l primero y ulquier otro. Además, lo visto previmente servirá pr onstruir ls misms ides, hiendo del problem de dimensionlidd un mer sutilez.
7 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN f : R 2 R Ls funiones que responden est estrutur tomn omo rgumento puntos en el plno rel, que luego trnsformn en otro número rel. En onreto, ls funiones de este tipo pueden visulizrse omo mntos en el espio tridimensionl, por lo que uno podrí estr summente interesdo en lulr el áre de dihos mntos, o bien el volumen ontenido entre un región del plno y l imgen de dih región ví l funión. Clulremos primero el volumen bjo un mnto (nos referiremos mnto omo el símil bidimensionl de urv), puesto que se dpt l mism noión que usmos l definir ls sums de Riemnn. En est osión, reemplzremos el onepto de intervlo por el de retángulo. efiniión 6: Se define un retángulo en el plno omo el onjunto [, b] [, d] { (x, y) R 2 x b, y d } Observión: Si los intervlos fuern biertos por izquierd y dereh, hblrímos de un retángulo bierto. Estmos interesdos en funiones que estén bien definids en un determindo retángulo, es deir, que sen otds. Nuevmente, neesitmos nuestr list de xioms pr poder onstruir un teorí onsistente on lo que hremos, lgo similr lo que hiimos en l primer prte de este pítulo. enotemos por R un región en el espio, y digmos que V (R) es un número rel que represent el volumen que ontiene. ( R R 3 ) V (R) R R 2 V (R R 2 ) V (R ) + V (R 2 ) Si R es un prism, es deir, R [, b] [, d] [e, f], entones V (R) (b ) (d ) (f e) Proposiión 4: R R 2 V (R ) V (R 2 ) em.: Qued omo ejeriio. efiniión 7: Se define un prtiión del retángulo R [, b] [, d] omo P (R) {(x i, y j ) R x < x <... < x n < x n b, y < y <... < y m < y m d} Posible prtiión de un retángulo [, b] [, d] Notemos que, omo resultdo de l prtiión, neesrimente se tiene que el retángulo originl se divide en subretángulos uy unión es el mismo retángulo, esto es ( n ) m R [x i, x i ] [y j, y j ] i j
8 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN Además, d subretángulo puede notrse omo R ij [x i, x i ] [y j, y j ], de form que R i,j R ij. enotmos por P R l onjunto de tods ls prtiiones sobre el retángulo R. efiniión 8: d un prtiión P, deimos que un prtiión Q es más fin que P si P Q. efiniión 9: Se f : R R 2 R, R [, b] [, d], P un prtiión sobre diho retángulo y R ij d subretángulo resultnte de est prtiión. Siguiendo el mismo proedimiento de l seión nterior, es onveniente definir ls ntiddes A(R ij ) (x i x i ) (y j y j ) m ij (f) M ij (f) ínf f(x, y) (x,y) R ij sup f(x, y) (x,y) R ij e est form, definimos ls sums inferior y superior de f on respeto P omo s(f, P ) S(f, P ) n i j n i j m m ij (f) A(R ij ) m M ij (f) A(R ij ) Elementos de l sum superior de un funión eslr de dos vribles Podemos menionr vris propieddes, bsds en los mismos rgumentos expuestos nteriormente. Así, es lro que, pr ulquier prtiión, en un retángulo R [, b] [, d] donde m ínf f(x, y) y M sup f(x, y). (x,y) R (x,y) R Además, si tenemos dos prtiiones P y Q tles que P Q m(b )(d ) s(f, P ) S(f, P ) M(b )(d ) s(f, P ) s(f, Q) e esto se desprende l importnte propiedd S(f, P ) S(f, Q) ( P, Q P R ) s(f, P ) S(f, Q)
9 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN Luego, se definen ls ntiddes (ls ules existen por el rgumento esgrimido on nterioridd) R f f R b d b d f sup P P R s(f, P ) f ínf P P R S(f, P ) efiniión : iremos que f, definid en el retángulo R [, b] [, d], es Riemnn-integrble en R si R f f R L proposiión 3, llmd Condiión de Riemnn, sigue siendo válid. Si f es Riemnn-integrble, definimos sin mbigüedd l integrl sobre el retángulo R omo ulquier de ls ntiddes nteriores (omo oiniden, d igul uál se esrib), y se denot de mner equivlente b d f da R f da donde da es llmdo diferenil de áre, que represent ls vribles on respeto ls que integrmos. En el so usul, da dxdy o bien da dydx (prenderemos qué importni tiene el orden), pero tmbién veremos que, dependiendo de l funión, podrí ser más onveniente representrl on oordends polres, en uyo so hbrá que onsiderr otro diferenil de áre que se deúe tl modelo. Tmbién es importnte destr que el nombre se relion on áre en el sentido de que l región sobre l que se integr es pln, por lo que evo l ide de superfiie. Similrmente, si integrármos sobre un región tridimensionl, hblrímos de diferenil de volumen. Sin embrgo, prtir de utro dimensiones, estos nombres no hen refereni lgo onoido, por lo que hbrá que bstrerse de ls noiones físis y ostumbrrse trbjr on ls definiiones y propieddes de este objeto f : R n R Al terminr est seión mnejremos los elementos básios pr definir bien un integrl pr ulquier vlor de n, unque los sos más usules son n, 2 y 3. efiniremos un pr de oneptos nuevos, que no se trtrán on estrito rigor, sino más bien nos drán ides prehensibles y fáiles de entender de lo que está ourriendo. efiniión : Se define un retángulo n-dimensionl, o simplemente retángulo, l onjunto R [, b ] [ 2, b 2 ] [ n, b n ] { (x, x 2,, x n ) R n ( i,, n) i x i b i } Si los intervlos son biertos, hblmos de un retángulo bierto. Queremos generlizr l noión de áre y ún más de volumen, lgo que podemos llmr hipervolumen. Sin embrgo, el nombre en sí no port informión relevnte, pues pli pr ulquier vlor de n 4. En lugr de lulr ests mgnitudes, distinguiendo nombres por dimensión, simplemente definiremos l llmd medid de Lebesgue de un región R (que denotmos λ(r)) omo un generlizión de longitud, áre, volumen, et. efiniión 2: Pr un número finito n N, y pr un retángulo ulquier, definimos su medid de Lebesgue omo λ(r) n (b i i ) i
10 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN Además, onsiderremos l medid de Lebesgue de un onjunto numerble omo nul. Esto se dpt l ide de que l integrl sobre un ntidd finit de puntos es simplemente nul, extendiendo l finitud numerbilidd. Luego, ls propieddes inherentes de est definiión generlizn ls que y vimos, est vez pr R R n : λ(r) R R 2 λ(r R 2 ) λ(r ) + λ(r 2 ) L propiedd reltiv l medid de Lebesgue de un retángulo viene dd por l definiión mism. Además, de lo nterior se desprende el resultdo (uy demostrión qued omo ejeriio) Proposiión 5: R R 2 λ(r ) λ(r 2 ) efiniión 3: Se define un prtiión del retángulo R [, b ] [ n, b n ] omo P P P 2 P n donde P i es un prtiión del intervlo [ i, b i ]. L notión puede tornrse omplid l hor de representr l prtiión por ompleto, pero vle l pen reordr que P i { i x (i) < x (i) <... < x (i) m i b i }, y que esto define n prtiiones (pues i,... n), determindos d uno por m i puntos (pues d intervlo lo podemos dividir en distints ntiddes de prtes). A su vez, l unión de estos subintervlos gener el intervlo originl, por lo que m [ ] R x () j, m 2 [ ] m x() j x (2) j, n [ ] x(2) j x (n) j, x(n) j j j j Qued omo ejeriio personl onvenerse de que podemos representr d subretángulo omo [ ] [ ] [ ] R jj 2...j n x () j, x() j x (2) j, 2 x(2) j 2... x (n) j, n x(n) j n j i,..., m i enotmos por P R l onjunto de tods ls prtiiones sobre R. Observión: Es importnte notr que m m 2 j j 2... m n j n λ(r jj 2...j n ) j...j n λ(r jj 2...j n ) λ(r) efiniión 4: Sen P, Q P R. iremos que Q es más fin que P si ( i {,..., n}) P i Q i efiniión 5: Sen f : R n R un funión otd sobre el retángulo R, P P R y R j...j n resultnte de est prtiión. Consideremos ls ntiddes λ(r j...j n ) n i ( ) x (i) j x (i) j m j...j n (f) ínf { f(x,... x n ) (x,... x n ) R j...j n } un subretángulo M j...j n (f) sup { f(x,... x n ) (x,... x n ) R j...j n } Luego, se definen ls sums inferior y superior de f en R on respeto P omo s(f, P ) m m 2 j j 2... m n j n m jj 2...j n (f) λ(r jj 2...j n ) j...j n m jj 2...j n (f) λ(r jj 2...j n )
11 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN S(f, P ) m m 2 j j 2... m n j n M jj 2...j n (f) λ(r jj 2...j n ) j...j n M jj 2...j n (f) λ(r jj 2...j n ) Qued omo ejeriio plnter un generlizión (donde orrespond) de ls propieddes y proposiión vists ntes. Pr terminr, denotmos... f sup s(f, P ) R P P R 2... R R n... f ínf S(f, P ) R P P R 2... R R n efiniión 6: iremos que f es Riemnn integrble si ls ntiddes nteriores son igules, en uyo so, ulquier de ess dos expresiones equivle... fdr fdr R R 2... R n R Notemos que usmos R y dr, básimente porque represent de form ompt tods ls vribles que modeln el retángulo sobre el que integrmos. Pr finlizr l introduión, dremos el resultdo que nos permitirá desrrollr más teorí sin estnrnos en l dud sobr l integrbilidd de ierts funiones. Proposiión 6: Un funión f : R R n R ontinu en R un retángulo, es integrble sobre R. em.: Primero notemos (puede, omo ejeriio, probr l siguiente firmión) que, omo f es ontinu sobre un ompto, lnz máximo y mínimo en él, los lnz en d subretángulo, y demás es uniformemente ontinu en dih región. Por lo tnto, ddo un ε > rbitrrio, existe un δ > tl que ( x, x 2 R) x x 2 δ f(x ) f(x 2 ) ε λ(r) Consideremos un prtiión P P R tl que P i δ, i,..., n. Como f lnz mínimos y máximos en d subretángulo, podemos segurr que ( x j R j...j n ) f(x j ) ínf{f(x) x R j...j n } Luego, ( x j R j...j n ) f(x j ) sup{f(x) x R j...j n } S(f, P ) s(f, P ) j...j n [M j...j n m j...j n ] λ(r j...j n ) j...j n [ f(x j) f(x j) ] λ(r j...j n ) Es lro que x j x j λ(r j...j n ) δ, pues d intervlo que ompone l retángulo tiene lrgo menor que δ. Finlmente, tenímos que l funión es uniformemente ontinu, umpliéndose l proposiión por lo que x j x j δ f(x j ) f(x j) ε λ(r)
12 5.3. GENERALIZACIÓN E INTEGRAL: VOLUMEN E HIPERVOLUMEN CAPÍTULO 5. INTEGRACIÓN S(f, P ) s(f, P ) [ f(x j) f(x j) ] λ(r j...j n ) j...j n ε λ(r j...j λ(r) n ) j...j n ε Proposiión 7: Si f : A R n [, b] R es integrble en el retángulo A y h : [, b] R es ontinu en [, b], entones h f : A R es integrble en A. esde hor, trbjremos on funiones que umpln l hipótesis de ser integrbles. Sin embrgo, es buen ejeriio orroborrlo ntes de iniir ulquier inursión. En este ontexto, sbemos que l integrl (sí hemos llmdo l límite de ls sums de Riemnn) existe, y que es un operdor que trnsform funiones en vlores reles. e momento no hemos meniondo ómo lulr l integrl de un funión de vris vribles (que tmbién podemos llmr integrl múltiple), pero de l definión y propieddes que dimos de ls sums, se desprende lo siguiente. Teorem : Sen A R n un retángulo y f, g : A R funiones integrbles en A.. f + g tmbién es integrble, y (f + g) f + g 2. Pr α R, αf tmbién es integrble, y (αf) α 3. Si f, entones 4. Si f g, entones A A f f 5. f tmbién es integrble, y A g A A f A f 6. mx{f, g} y min{f, g} tmbién son integrbles 7. f 2 tmbién es integrble 8. El produto f g tmbién es integrble Teorem 2: Sen R 2 un retángulo y f : R un funión integrble en.. Áre() dxdy 2. ( m, M R) ( (x, y) ) m f(x, y) M m Áre() f f + f 2 4. f ontinu en ( (x, y ) ) f f(x, y ) Áre() em.: Qued omo ejeriio. A A A A f f M Áre() Observión: L propiedd 4 del Teorem 2, es preismente el Teorem del Vlor Medio pr integrles.
13 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN 5.4. Cálulo de integrles dobles Integrles sobre retángulos En est seión prenderemos lulr, undo existn, ls integrles sobre regiones n-dimensionles, unque por simpliidd de notión nos restringiremos l so n 2; no es difíil extender los resultdos que veremos dimensiones myores. Además, undo hblemos de integrles pr funiones de un vrible, nos referiremos ls integrles definids vists en el urso de Cálulo iferenil e Integrl. Lo primero que hy que dejr lro, es que el orden en que se pongn los difereniles es relevnte, l punto que hy que signrles el orden estbleido por los signos integrles. Cundo hgmos es distinión, estremos hblndo de integrles iterds (un integrl múltiple en que se disting un signo integrl de otro). Así, si queremos lulr l integrl undo x [, b] e y [, d], podemos herlo sí: o sí: b d d b fdydx fdxdy pero no en distinto orden; en otrs plbrs, los difereniles se ubin en el orden inverso de los signos integrles según orrespond el intervlo l ul pertenez d vrible. Un form lr de verlo, es usndo préntesis: ( b ) d ( d ) b fdy dx fdx dy Supongmos que tenemos un funión f, integrble en un retángulo A [, b] [, d], y queremos lulr l integrl sobre diho retángulo. Hy dos posibiliddes: Cso : Queremos lulr Cso 2: Queremos lulr d b b d f(x, y)dxdy. efiniendo Ψ(y) d b b f(x, y)dxdy f(x, y)dydx. efiniendo Φ(x) b d d f(x, y)dydx f(x, y)dx, tenemos d Ψ(y)dy f(x, y)dy, tenemos b Φ(x)dx Qué podemos deir de ests dos integrles? Import el orden en que integremos? Teorem 2 (Teorem de Fubini): Sen R [, b] [, d] un retángulo y f : R R un funión Riemnn-integrble en dih región. Se tiene que ( x [, b]) Φ(x) d f(x, y)dy < R fdr d b f(x, y)dxdy Lo mismo suede si reemplzmos Φ(x) por Ψ(y) omo lo definimos on nterioridd. b d f(x, y)dydx
14 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN El teorem de Fubini nos die que el volumen de un funión integrble no depende de ómo se brre el retángulo. em.: Se Φ : [, b] R l funión definid por Neesitmos que Φ se integrble en [, b] y que b d Φ(x) d f(x, y)dydx f(x, y)dy b Φ(x)dx Sen P x P [,b] un prtiión que defin los subintervlos G i [x i, x i ], on i {,..., n}, y P y P [,d] otr prtiión que defin los subintervlos H j [y j, y j ], on j {,..., m}. Luego, tenemos pr el retángulo R [, b] [, d] l prtiión P P R, que define los subretángulos R ij G i H j. Tenemos entones que s(f, P ) n m m ij (f) A(R ij ) m ij (f) y j x i i,j i j Además, pr d x G i y pr d j {,..., m} se tiene que m ij (f) m j (f x ), pues el primer término es el ínfimo sobre todo el subretángulo, mientrs que el segundo es el ínfimo l fijr un oordend x G i. Sumndo sobre j, se tiene que m m d m ij (f) y j m j (f x ) y j f x (y)dy Φ(x) j Como ests desigulddes vlen pr todo x G i, tommos ínfimo en x, lo que d m m ij (f) y j m i (Φ) j j pr d i {,..., n}. Sumndo sobre i, obtenemos s(f, P ) s(φ, P x ) S(Φ, P x ) S(f, P ) Como esto vle pr ulquier prtiión de P de R (por ende, pr ulquier prtiión P x de [, b] y P y de [, d]) y f es integrble, se dedue de ests desigulddes que Φ es integrble sobre [, b], y ( b ) d b f f(x, y)dy dx Φ(x)dx L demostrión es nálog si estbleemos l existeni de Ψ(y) R b f(x, y)dx, on lo que obtendrímos l integrl en el orden inverso. Como todo en Cálulo, se tiene que f es integrble en el retángulo, o que l integrl doble de f existe, sólo si mbos resultdos oiniden, pero por hipótesis f es Riemnn-integrble, por lo que onluimos que ésto último tmbién se stisfe.
15 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Ejemplos: Vemos distintos sos en que podemos o no plir el teorem de Fubini. Clulr x 2 + y 2 da, donde R [, ] [, 2] R R x 2 + y 2 da ( x 2 + y 2 dxdy ) x 2 + y 2 dx dy ( x 2 dx + ( x y 2 x ) dy 3 + y2 dy 2 3 y + y3 2 3 dy 3 (2 ) + (8 3 3 ) ) y 2 dx dy 8 3 Qued omo ejeriio demostrr que ls ondiiones pr usr el teorem de Fubini se umplen, y verifir que mbs integrles oiniden. Se f : [, ] [, ] R tl que f(x, y) x os(y). Tenemos que f(x, y)dxdy f(x, y)dydx x2 2 lím x 2 2 x os(y)dxdy os(y)dy os(y)dy dy t x os(y)dydx t x os(y)dydx t x lím sin(y) t dx lím t sin(t) lím t sin(t)
16 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN L últim iguldd se tiene por tener el produto entre un límite otdo y un término nulo. Por lo tnto, mbs integrles dobles existen y son igules. Sin embrgo, un de ls integrles no: Φ(x) x os(y)dy x lím t sin(t) Clrmente, Φ está bien definid únimente pr x. Por lo que el reíproo del teorem no es ierto (que l existeni de l integrl doble implique que d integrl simple exist). Se f : [, ] [, ] R un funión otd, definid por { 2x, y / Q f(x, y), y Q Vemos que Ψ(y) Sin embrgo, Φ(x) f(x, y)dx 2xdx, por lo que f(x, y)dxdy dy f(x, y)dy no existe, pues on respeto y se nos present el problem reliondo l funión de irihlet. e ese modo, no podemos lulr f(x, y)dydx Conluimos que f no stisfe el teorem de Fubini (que ls integrles iterds oinidn) y, por ontrrreípro, f no puede ser integrble. Sin embrgo, hgmos un pequeño ejeriio prte. efinimos ls funiones Φ inf (x) Ψ inf (y) f(x, y)dy Φ sup (x) f(x, y)dy Ψ sup (y) f(x, y)dy 2x f(x, y)dy Luego, tenemos que tods ells son ontinus, y por lo tnto integrbles. Pero no sólo eso; l integrl de Φ inf y Φ sup sobre [, ] es, l igul que l integrl de Ψ inf y Ψ sup sobre [, ]. Es eso oinideni? Corolrio (Teorem de Fubini generlizdo): Sen A [, b] [, d] y f : A R un funión otd e integrble en A. Pr d x [, b], se g x : [, d] R l funión definid por g x (y) f(x, y). Consideremos ls funiones L(x) d g x (y)dy U(x) d g x (y)dy Sbemos por un observión que ests ntiddes siempre existen. Entones, ls funiones L(x) y U(x) son integrbles en [, b], y b b L(x)dx f(x, y)dxdy U(x)dx A Esto es nálogo definiendo en [, d], y de form similr, L(y) y U(y). L demostrión se bs en l mism que dimos pr el teorem de Fubini. Ejeriio: Verifir el resultdo nterior pr l funión f : [, ] [, ] R dd por (x, y) / Q 2 {(, )} {(, )} f(x, y) n + q x m n, y p q, on (m, n) y (p, q) primos reltivos
17 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Corolrio 2 (Funiones seprbles): Se f un funión integrble sobre un retángulo R [, b] [, d] y tl que ( x, y R) f(x, y) g(x)h(y) (en ese so, deimos que f es un funión seprble). Entones b ( d ) ( b ) d f(x, y)dydx g(x)dx h(y)dy Ls funiones seprbles son muy fáiles de mnejr l hor de integrr, pues he intuitiv l form que dquiere su gráfi, permitiéndonos lulr áres y volúmenes sin relizr álulos omplidos, más ún undo f(x, y) es en relidd un funión de un sol vrible (pues se puede notr f(x, y) g(x) h(y), por ejemplo). Sin profundizr muho, ls seiones trnsversles en los ejes muestrn el omportmiento de d prte de l funión omo urvs de nivel, omo vemos en los siguientes ejemplos. Ejemplo: Se f : R 2 R definid por f(x, y) e x sin(y). Y vemos que f(x, y) g(x) h(y), on g(x) e x y h(y) sin(y). No lulremos integrles, pero veremos qué nos referímos on lo simple que es visulizr ls urvs de nivel de f en los plnos XZ y Y Z. Ejemplo: Se f : [, ] [, R] R, definid omo f(x, y) 2 x 2 on R >. Queremos lulr l integrl doble de f en su dominio (es deir, el volumen ontenido entre el plno y l gráfi de f). Se puede lulr sin myor difiultr usndo ténis de integrión y prendids, pero tmbién podemos notr que f(x, y) g(x) h(y), on g(x) 2 x 2 y h(y). Es deir, onforme se vnz en el eje Y, ls urvs de nivel de f en el plno XZ no vrín. e heho, ésts desriben un semiírulo de rdio.
18 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Luego, omo Ψ(y) x2 dx es el áre del semiírulo, l integrr Ψ(y) sobre [, R] obtendremos el volumen de medio ilindro de lrgo R y rdio. Finlmente, el resultdo es π2 R. 2 Como onseueni del teorem de Fubini, dds ls ondiiones neesris, podemos integrr sin preouprnos por el orden en que lo hgmos (respetndo l orrespondeni intervlo-diferenil). Además, se evideni que no tiene sentido el álulo de primitivs o integrles indefinids undo se trt de integrles múltiples, y que todo se redue un problem numério. No está de más dvertir, no obstnte, que el proedimiento usul de álulo es desde dentro hi fuer, es deir, se resuelve l integrl uyo diferenil esté en primer lugr de l mism form en que lulmos un integrl ordinri, y se sigue en ese orden, hst llegr l último diferenil. Hemos diho que el álulo de integrles dobles tiene relión on el álulo del volumen omprendido entre el grfo de un funión y el plno XY, otdo por el retángulo R. En ese sentido, el enunido del ejemplo nterior pudo ser Clulr el volumen ontenido bjo el grfo de f(x, y) x 2 + y 2 en el retángulo R [, ] [, 2], y hbrí sido ompletmente equivlente lo resuelto, on l úni slvedd que, eventulmente, f puede ser negtiv, en uyo so pr obtener volumen l integrl lulr no es sobre f, sino sobre f Integrles sobre onjuntos más generles Todo lo que hemos heho hst hor, es lulr integrles sobre retángulos, y deberímos ser pes de integrr sobre uniones, interseiones y ombiniones de ésts operiones plids retángulos. Sin embrgo, no hemos todo el tem de integrr sobre triángulos, írulos y otros onjuntos muho más omplejos. ebemos definir formlmente un funión uyo vlor depende del onjunto l que pertenee el rgumento. efiniión 7: Se A R 2 un onjunto otdo. Se define l funión inditriz o indidor on respeto A omo si (x, y) A χ A (x, y) si (x, y) / A efiniión 8: Se f : A R 2 R un funión otd. Se define l integrl de f sobre A omo f(x, y)dxdy f(x, y) χ A (x, y)dxdy A donde R es ulquier retángulo que ontiene A. Vemos que est definiión está bien estbleid: Sen R, R 2 R 2 tles que A R y A R 2 (R y R 2 no neesrimente son igules). Entones se tiene que R (R \ A) A y R 2 (R 2 \ A) A. Luego f χ A f χ A + f χ A R R \A A f χ A A f χ A f χ A + f χ A R 2 R 2\A A f χ A A Esto se tiene porque χ A (R \ A) χ A (R 2 \ A) {}. Por lo tnto, l integrl está bien definid, pues no depende del retángulo que esojmos, siempre que éste onteng A. Más generlmente, se tiene que está bien definid si esogemos R ulquier región (no neesrimente retngulr) que onteng A, y l demostrión es ompletmente idénti l nterior. R
19 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Observión: Como se ps de un onjunto ulquier un retángulo que lo ontiene, ls propieddes omo l linelidd se onservn. Podemos horrr notión definiendo f f χ A ; hor busremos ondiiones pr que f se integrble en el sentido ddo nteriormente. Usulmente, f es ontinu, pero por lo generl f no. Esto nos oblig onsiderr otrs propieddes más generles que l ontinuidd, unque sumiremos que l menos f l stisfe. efiniión 9: Se die que un onjunto A R n tiene ontenido ero si ( ε > ) ( U,..., U m retángulos errdos) A m i U i m λ(u i ) < ε donde λ(u i ) denot l medid de Lebesgue del retángulo U i (volumen n-dimensionl). Tmbién diremos que un onjunto que tiene ontenido ero, es un onjunto de medid de Jordn nul. Proposiión 8: Se tiene. Si A es un onjunto de medid nul y B A, entones B tmbién es de medid nul. 2. Si A y B son onjuntos de medid nul, entones A B tmbién es de medid nul. 3. enotndo A A A 2... A n, si pr lgún i {,..., n} A i es numerble, A tiene es de medid nul en R n. Ejemplo: Mostrremos tres sos en que quermos ver si lgún onjunto es o no de medid nul. Es importnte notr que, dependiendo de l dimensión del espio, esto equivle mostrr si el onjunto tiene longitud, áre, volumen, et. emostremos que el onjunto S { (x, y) R 2 x + y } es de medid nul en R 2. Pr esto, podemos reubrir S on retángulos (udrdos) uyos áres disminuyen itertivmente, omo ilustr l figur. i Así, S se puede enerrr en 4n udrdos errdos, d uno de áre n. Luego, el áre totl del reubrimiento es 4 2 n, el ul se puede her rbitrrimente pequeño. En resumen, tenemos que S es subonjunto de l unión finit de retángulos errdos y que l sum de sus medids de Lebesgue (en este so, áre) es tn hi omo quermos. Luego, S es de medid nul. emostrr que, si < b, entones [, b] R no tiene ontenido ero en R. Lo que hremos será mostrr por induión que, prtir de un reubrimiento finito de errdos de [, b], digmos m U,..., U m tles que [, b] U i, se tiene neesrimente que i m λ(u i ) b i
20 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Es evidente que pr m se umple, pues U [, d] neesrimente debe ser tl que y d b, por lo que λ(u ) d b. Supongmos que est propiedd se umple pr un reubrimiento de m intervlos errdos, {U,..., U m }, y onsideremos hor el onjunto {U,..., U m, U m+ }. Es lro que este onjunto es un reubrimiento finito de [, b], pues m+ i ( m ) U i U i U m+ [, b] U m+ [, b] i Supongmos, sin pérdid de generlidd, que U. Como U [α, β], entones α β. Ahor, si b β, se tiene que [, b] U, y l demostrión termin. Si b > β, entones {U 2,... U m+ } reubre [β, b], y por hipótesis indutiv, Así, tenemos que m+ i m+ i2 λ(u i ) b β λ(u i ) (β α) + (b β) b α b Se f : [, b] R un funión ontinu. emostrremos que su gráfio, el onjunto G { (x, f(x)) R } 2 x [, b], tiene ontenido ero en R 2. Se ε >. Como f es ontinu en el ompto [, b], es uniformemente ontinu en diho intervlo. Luego, existe δ > tl que f(x) f(y) < ε b pr todo x, y [, b] tles que x y < δ. Se P {x, x,..., x n, x n b} un prtiión de [, b] tl que P máx i n {x i x i } < δ Sen M i y m i el máximo y el mínimo de f en [x i, x i ], y sen i, i tles que f( i) M i y f( i ) m i. Como tenemos que ( i {,..., n}) i i x i x i < δ M i m i f( i ) f( i) < ε b Finlmente, los n retángulos errdos U i [x i, x i ] [m i, M i ] reubren G, y demás n λ(u i ) i n (x i x i )(M i m i ) i n ε < (x i x i ) b i ε n (x i x i ) b i ε efiniión 2: iremos que un onjunto A R n es medible en el sentido de Jordn, Jordn-medible o simplmente medible si su fronter, A, tiene ontenido ero. Ejemplo: El onjunto M R {(x, y) [, ] [, ] x, y R} es medible en R 2, mientrs que M Q {(x, y) [, ] [, ] x, y Q} no lo es.
21 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN A ontinuión, enunimos el teorem que nos permitirá trbjr on integrles sobre onjuntos más generles. Teorem 3 (Teorem de Lebesgue): Se f : A R n R un funión otd y ontinu, on A un onjunto otdo. Entones l funión f : R A R, on f f χ A, es Riemnn-integrble si y sólo si A es Jordn-medible. En prtiulr, si n 2, el áre de A está bien definid y se lul omo Áre(A) χ A dxdy Lo que propone este teorem, es que el áre de un región puede lulrse sobre otr región que l onteng, medinte un funión que disrimin puntos dentro y fuer de l región de interés. L demostrión se drá en un péndie, puesto que requiere iert espeilizión sobre lgunos oneptos que no se bord por su difiultd y po relevni pr el resto del urso. L myorí de los ejemplos que onsiderremos en este urso orresponden regiones Jordn-medibles, o uniones e interseiones finits de regiones de este tipo Integrles dobles sobre onjuntos generles Hemos visto que l integrl sobre un retángulo (de ulquier dimensión) medinte integrión reiterd y hiendo uso del teorem de Fubini. Ahor enfrentmos el problem de lulr integrles dobles sobre onjuntos medibles rbitrrios Vmos empezr onsiderndo dos tipos de estos onjuntos pr los que l integrl doble puede lulrse por integrión reiterd de un mner similr l que hemos empledo en el so de retángulos. efiniión 2: Un onjunto A R 2 se die de tipo I o x-proyetble si es de l form A { (x, y) R 2 x b, f (x) y f 2 (x) } donde f, f 2 : [, b] R. Ls integrles sobre este tipo de onjuntos se luln omo ( b ) f2(x) f(x, y)dxdy f(x, y)dy dx A I f (x) Ejemplo: Clulr l integrl de f(x, y) x + y 2 sobre A { (x, y) R 2 x, y x }. A x + y 2 dxdy ( x (xy + y3 3 x 2 + x3 3 dx ( ) x x ) x + y 2 dy dx ) x dx A omo región tipo I efiniión 22: Un onjunto A R 2 se die de tipo II o y-proyetble si es de l form A { (x, y) R 2 y d, g (y) x g 2 (y) } donde g, g 2 : [, d] R. Ls integrles sobre este tipo de onjuntos se luln omo ( d ) g2(y) f(x, y)dxdy f(x, y)dx dy A g (y)
22 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Ejemplo: Clulr l integrl de f(x, y) xe y5 sobre A { (x, y) R 2 y, x y 2 }. A xe y5 dxdy ( y 2 ( x 2 2 ey y ey dy ) ( 5 ey e xe y5 dx ) 5 y 2 ) dy dy A omo región tipo II Observión: El tipo del onjunto qued determindo por l form de desribirlo; en este sentido, ddo un onjunto en el plno rel, tenemos que busr un form de prmetrizrlo. L justifiión de esto l dmos ontinuión. Además, puede hber onjuntos que sen simultánemente de tipo I y de tipo II, en uyo so se die que son de tipo III y se puede plir ulquier de los dos álulos nteriores. En generl, unque un onjunto se de tipo III, l prmetrizión de tipo I no oinide on l de tipo II, lo ul verifiremos más delnte. Justifiremos lo nterior. Se R l región de tipo I dd por R { (x, y) R 2 x b, ϕ (x) y ϕ 2 (x) }. Si ínf (x)} x b d sup x b {ϕ 2 (x)} entones R [, b] [, d]. Luego f(x, y)dxdy R [,b] [,d] f(x, y)dxdy donde f f χ R. Como trbjmos on f ontinu tenemos que, pr d x [, b], l funión Ψ(y) f(x, y) es integrble sobre [, d], y por definiión de f sigue que d f(x, y)dy ϕ2(x) ϕ (x) f(x, y)dy Luego, por teorem de Fubini, R f(x, y)dxdy Pr regiones de tipo II se sigue un rzonmiento nálogo. b ( ) ϕ2(x) f(x, y)dy dx Ahor veremos ómo enontrr l prmetrizión neesri en un so simple, que result ser un onjunto de tipo III. Así, veremos el proeso generl pr enontrr los límites de l integrl doble y verifiremos que los límites enontrdos pr el tipo I no neesrimente oiniden on los enontrods pr el tipo II. Ejemplo: Se f : A R 2 R un funión ontinu, on A desrit omo en ls figurs siguientes. Queremos enontrr un form de desribir A explíitmente.. ϕ (x)
23 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN En este so, l form más senill de desribir l región, es por medio de funiones de x, undo x [, 2]. Es fáil ver que y está otdo inferiormente por f (x) y superiormente por f 2 (x) 3 2x + 3. Así, A es de tipo I, y { A (x, y) R } 2 3 x 2, y 2 x + 3 Además, podemos onsiderr desribir A por medio de funiones de y, undo y [, 3]. Por despeje de l vrible x en l funión f 2 (en f no se puede), tenemos que x está otdo inferiormente por g (y) y superiormente por g 2 (y) 2 3y + 2. Así, A es de tipo II, y A {(x, y) R 2 y 3, x 23 } y + 2 Por lo tnto, A es de tipo III, pues se puede desribir de mbs forms, pero vemos que ésts son distints. 2. Primero desribiremos est región omo un onjunto de tipo II. Es fáil ver que ls rets involurds tienen euión L : y 3x + 3 y L 2 : y 3 2x + 3, prtir de lo que podemos despejr x en funión de y. Así, undo y [, 3], x está otd inferiormente por g (y) 3 y + y superiormente por g 2(y) 2 3y + 2. Luego, A {(x, y) R 2 y 3, 3 } y + x 23 y + 2 Además, podemos desribir A omo onjunto de tipo I, pero est vez se omplirá un poo, pues y en funión de x es distinto en los intervlos [, ] y [, 2]. Por ls propieddes de l integrl, podemos seprr A en dos regiones, A y A 2. Luego sólo tendrímos que sumr ls integrles sobre dihs regiones.
24 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Cundo x [, ], A está otdo inferiormente por f (x) 3x + 3 y superiormente por f 2 (x) 3 2x + 3. Cundo x [, 2], A 2 está otdo inferiormente por f (x) y superiormente por f 2 (x) 3 2x + 3. Así, { A (x, y) R 2 } 3 x, 3x + 3 y { A (x, y) R 2 } 3 x 2, y A A A 2 Como vemos, est vez A tmbién es de tipo III. Tmbién es lro que l representión omo región tipo I difiere muho de l de tipo II, unque desribn l mism región. Ejeriio: esribir omo región tipo I o II, o omo unión o interseión de ells, l región nulr R { (x, y) R 2 x 2 + y 2 4 } Tmbién se nos puede presentr el problem inverso: determinr l región de integrión (por ejemplo, en un gráfio) prtir de los límites de l integrl. Esto en sí no es un problem, unque podrí ser útil (undo se posible) mbir el orden de ls integrles, es deir, psr de un onjunto tipo I un de tipo II, o viesvers. Ejemplo: Los siguientes ejemplos mostrrán ómo mbir el orden de integrión, y l utilidd de ello. ( e ) ln(y) Consideremos l integrl iterd f(x, y)dx dy. Es lro que l región se ve gráfimente omo en l figur, ddo que y e y x ln(y) Pr invertir el orden de integrión, simplemente debemos ver qué funiones otn l vrible y undo x [, ]. Result fáil onluir que l región está otd inferiormente por f (x) e x y superiormente por f 2 (x) e. Así, ( e ) ln(y) ( e ) f(x, y)dx dy f(x, y)dy dx e x Clulr r os(y) sin(x) + sin 2 (x)dxdy. Podrímos lulr diretmente est integrl, pero en generl serí un tre summente omplid. Pr evitrlo, veremos si integrndo en orden inverso se simplifi el problem. Tenemos que y x r os(y)
25 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Cundo y [, ], dds ls ots de x sbemos que x [, π 2 ]. Además, en ese intervlo, y está otdo inferiormente por f (x) y superiormente por f 2 (x) os(x). Así r os(y) sin(x) + sin 2 (x)dxdy π/2 os(x) π/2 π/2 2 sin(x) + sin 2 (x)dydx sin(x) + sin 2 (x)y os(x) dx sin(x) + sin 2 (x) os(x)dx u + sin2 (x) du 2 sin(x) os(x)dx udu u3/2 ( 2 ) 2 3 Clulr 2 / 2 y/2 os(πx 2 )dxdy. Nuevmente, lulr diretmente est integrl puede resultr muy omplido; tl vez imposible. Notemos hor que l región dd por y 2 y x 2 2 puede ser desrit tmbién omo x 2 y 2x
26 5.4. CÁLCULO E INTEGRALES OBLES CAPÍTULO 5. INTEGRACIÓN Así, 2 / 2 y/2 os(πx 2 )dxdy π / 2 2x / 2 / 2 π/2 π sin(u) π/2 π os(πx 2 )dydx os(πx 2 )y 2x dx os(πx 2 )2xdx os(u)du u πx 2 ; du 2πxdx Ejemplo: Veremos ómo lulr un integrl sobre un región desrit omo unión de dos regiones distints. Pr ello, onsideremos l funión f : R 2 R dd por f(x, y) x 2 + y 2 y l región S que pree en l figur Es fáil drse uent de que S es de tipo I, pues onoemos l euión de los írulos que l delimitn. Además, pr desribirl, es neesrio dividirl en dos regiones omo en l figur siguiente Sigue que S S 2 {(x, y) R 2 x [, ], x2 y 4 x 2 } { (x, y) R } 2 x (, 2], y 4 x 2 Luego, l integrl de f sobre S es l sum de l integrl de f sobre S on l integrl sobre S 2, pues S S S 2. Así, f(x, y)dydx S f(x, y)dydx + S f(x, y)dydx S 2 4 x 2 x 2 x 2 + y 2 dydx x 2 x 2 + y 2 dydx
27 5.5. CAMBIO E VARIABLES CAPÍTULO 5. INTEGRACIÓN Qued omo ejeriio verifir que el resultdo es 5π/8. El que hymos omitido el desrrollo de est integrl, es básimente puesto que es engorroso y requerirí vris línes. Por ello, surge l pregunt de si so hy un form más diret de evlur l integrl. L respuest es que, dds ierts ondiiones, sí existe un mner de ortr el proeso de álulo. e esto se trt l siguiente seión Cmbio de vribles Teorem 4: Se f : R R un funión integrble y g : R R un funión diferenible. Se tiene entones que b f(g(x))g (x)dx g(b) g() f(u)du Este teorem nos entreg omo herrmient los llmdos mbios de vrible, bstnte útiles si dentro de un integrl enontrmos el produto entre un funión (en este so g) on su derivd (quí g ). Como vimos en los dos últimos ejemplos nteriores, el álulo de un integrl puede simplifirse si relizmos un mbio de vrible onveniente. Podremos her lgo preido en un integrl múliple? L respuest es sí, y de form muy similr l que usmos en integrles simples. El teorem que presentremos ontinuión permite que, prtir de un funión, enontremos un trnsformión de ls vribles que hg más ómodo el álulo, lo que rre omo onseueni que l región sobre l que se integr tmbién se trnsforme. Teorem 5 (Cmbio de vribles): Sen f : R n R un funión ontinu en l región y T : R n R n un funión biyetiv y ontinu en, tl que T ( u) ( x) (x ( u),..., x n ( u)). Luego,... f( x)dx... dx n... f(x ( u),..., x n ( u)) det [J T ( u)] du... du n donde J T es el jobino de l funión T. En prtiulr, si n 2, tenemos que f : R 2 R es ontinu en, T : R 2 R 2 es biyetiv y ontinu en tl que T (u, v) (x, y) (x(u, v), y(u, v)) y f(x, y)dxdy f(x(u, v), y(u, v)) det [J T (u, v)] dudv [ x ] x f(x(u, v), y(u, v)) det u v y dudv u y v L demostrión de este teorem us rgumentos que espn l lne del urso, por lo que eptremos este resultdo generl sin demostrrlo. Sin embrgo, podemos her un sketh of proof pr el mbio de vribles oordends polres. Éste es muy onveniente undo podemos provehr propieddes trigonométris prtir de l funión que queremos integrr. Está ddo por l biyeión x r os(θ) y r sin(θ) donde r [, ) y θ [, 2π). L trnsformión invers está dd, omo se puede omprobr, por r x 2 + y 2 ( y θ rtn x)
28 5.5. CAMBIO E VARIABLES CAPÍTULO 5. INTEGRACIÓN El mbio de vribles oordends polres trnsform seiones irulres en retángulos. ejndo de ldo tod formlidd, podemos lulr de qué form vrín ls vribles rdil y ngulr en l medid en que vrín x e y por medio del operdor grdiente, y lulndo después l norm de este vetor. Tenemos ( r x x r, x2 + y 2 y y r x2 + y 2 x, r ) x y 2 + y 2 r θ x y, x2 + y 2 θ y x x2 + y 2 ( θ x, θ y ) y2 + x 2 x 2 + y 2 Luego, el diferenil de áre neesrimente inluye r en su expresión, es deir, dxdy rdrdθ. Y vemos que, en efeto, el teorem rroj el mismo resultdo: [ x ] [ ] x detj T (r, θ) det r θ y os(θ) r sin(θ) det r os 2 (θ) + r sin 2 (θ) r sin(θ) r os(θ) r y θ Es neesrio her hinpié en que el teorem de mbio de vribles nos revel que el objeto que llmmos diferenil no está multiplindo en form lgun l funión, sino que desribe l medid en que fet l funión d pso infinitesiml que relizmos, los ules debemos onsiderr si queremos lulr un integrl (vist omo un sum infinit de l funión sobre pequeñs vriiones en su dominio). Así, en oordends rtesins el objeto diferenil de áre da dxdy se identifi en oordends polres on el diferenil da rdrdθ, y esto es independiente de qué funión quermos integrr. Est independeni se present en ulquier mbio de vribles que reliemos. Ejemplo: Clulemos l integrl de f(x, y) x 2 y 2 sobre { (x, y) R 2 x 2 + y 2 4 }. Primero, notemos que est región es irulr. Luego, bjo el mbio de vrible (x, y) (r os(θ), r sin(θ)), obtenemos que f(r, θ) r 2 os(2θ) y T () { (r, θ) R + [, 2π) r 2 }, que es un región retngulr.
29 5.5. CAMBIO E VARIABLES CAPÍTULO 5. INTEGRACIÓN Luego x 2 y 2 dxdy 2π 2 2π 2 2π 2 2π 2π r 2 os(2θ) J T (r, θ) drdθ r 2 os(2θ) rdrdθ r 3 os(2θ)drdθ r os(2θ)dθ 4 os(2θ)dθ 4 sin(2θ) 2 2π Clulemos l integrl de f(x, y) x 2 + y 2 sobre l región S desrit en el ejemplo de l seión nterior. Tenemos que en oordends polres f(r, θ) r 2 y { S (r, θ) [, ) [, 2π) r [, 2], θ π } 2 Luego S f(x, y)dxdy S f(r, θ) rdrdθ π/2 2 π/2 2 π/2 π/2 5 4 θ π/2 5 8 π r 2 rdrdθ r 3 drdθ r dθ 5 4 dθ Clulemos I e x2 dx.
30 5.5. CAMBIO E VARIABLES CAPÍTULO 5. INTEGRACIÓN Como e x2 dx I 2 Por lo tnto, I π. Clulemos 2 x 3 x π e y2 dy, ( ) ( ) e x2 dx e y2 dy 2π 2π 2π 2π e x2 y 2 dxdy e r2 rdrdθ e u dθ e u dudθ dθ (x, y) (r os(θ), r sin(θ)); dxdy rdrdθ u r 2 ; du 2rdr xdydx usndo vribles polres. Primero, hy que trnsformr l región de integrión. Es fáil notr que se trt de un triángulo, por lo que l trnsformión viene dd por y x, x 2 r sin(θ) r os(θ), r os(θ) 2 sin(θ) os(θ), r os(θ) 2 θ π/4, r 2 2 y x 3, x 2 r sin(θ) 3r os(θ), r os(θ) 2 sin(θ) 3 os(θ), r os(θ) 2 θ π/3, r 4 x 2, 2 y 2 3 r os(θ) 2, 2 r sin(θ) 2 3 r 2 se(θ), 2 2 tn(θ) 2 3 r 2 se(θ), π/4 θ π/3
31 5.6. APLICACIONES E LA INTEGRAL OBLE CAPÍTULO 5. INTEGRACIÓN Luego 2 x 3 x xdydx π/3 2 se(θ) π/4 π/3 2 se(θ) π/4 π/3 π/4 π/3 π/4 π/3 π/4 os(θ) r tn(θ) π/3 8 3 r os(θ)rdrdθ r 2 os(θ)drdθ 2 se(θ) dθ os(θ) se 3 (θ)dθ se 2 (θ)dθ π/4 ( 3 ) Por supuesto, éste no es el únio mbio de vribles posible. Existe infinidd de ellos, que se deún en iert form l problem que se nos plnte. Ejemplo: Si S es l región del primer udrnte limitd por ls urvs xy, xy 2, y x, y 4x, probr que S f(xy)dxdy ln(2) 2 f(v)dv L fronter de l región S sugiere relizr el mbio u y/x, v xy. Hiendo esto, obtenemos un región S limitd por v 2, u 4. Además, despejndo x e y en funión de u y v, tenemos que x v/u e y uv, por lo que [ x ] [ ] x detj T (u, v) det u v y det 2 u 3/2 v /2 2 u /2 v /2 2 u /2 v /2 2 u/2 v /2 2u u y v e est mner, l integrl dd se puede esribir omo S f(xy)dxdy 2 4 f(v) 2u dudv f(v) ln(u) 4 dv ln(2) f(v)dv 5.6. Apliiones de l integrl doble En est seión presentremos ls pliiones más reurrentes de l integrl doble, que enontrremos útiles en geometrí y en físi lási, unque de esto se puede extender su uso áres más generles, omo Eletromgnetismo o Meáni de Medios Continuos.. Áre de regiones: Si S R 2, su áre es A(S) dxdy S 2. Mss y entro de grvedd: Si S R 2 represent un superfiie pln on densidd puntul ρ(x, y) pr d (x, y) S, entones l ms de S viene dd por m(s) ρ(x, y)dxdy S
32 5.7. CÁLCULO E INTEGRALES TRIPLES CAPÍTULO 5. INTEGRACIÓN y el su entro de grvedd (x g, y g ) estrí ddo por x g xρ(x, y)dxdy y g m(s) m(s) 3. Volumen: Se R 3 un región xy-proyetble, definid por Entones su volumen está ddo por S S yρ(x, y)dxdy { (x, y, z) R 3 (x, y) S R 2, f(x, y z g(x, y)) } V () S [g(x, y) f(x, y)] dxdy L pliión es nálog pr regiones xz-proyetbles e yz-proyetbles. 4. Áre de mntos: Se Ω R 3 l superfiie xy-proyetble definid por Entones el áre de su mnto viene ddo por Ω { (x, y, z) R 3 (x, y) S R 2, z f(x, y) } A(Ω) S + ( ) 2 f + x ( ) 2 f y L pliión es nálog pr regiones xz-proyetbles e yz-proyetbles Cálulo de integrles triples Como ests integrles se plin regiones tridimensionles (desrits por tres vribles), tods ls definiiones dds l prinipio del pítulo se plin l so prtiulr en que n 3. Esto inluye l medid de Lebesgue de un región retngulr (que se trdue en volumen de prlelepípedos), prtiiones, sums de Riemnn, ondiión de integrbilidd, etéter. Aquí repsremos lgunos resultdos en que l tridimensionlidd se determinnte. Teorem 6 (Teorem de Fubini): Se R [, b] [, d] [e, f] y h : R R un funión otd e integrble sobre R. Supongmos que, pr todo x [, b], está bien definid l funión J(x) h(x, y, z)dydz R donde R [, d] [e, f]. Entones tmbién existe l integrl de J(x) sobre [, b], y se umple b b ( ) h(x, y, z)dxdydz J(x)dx h(x, y, z)dydz dx R R Observión: Tl omo en el so de integrles dobles, podemos definir de form similr ls funiones K(y) y L(z) en los intervlos [, d] y [e, f], respetivmente. Además, plindo el teorem de Fubini pr integrles dobles, podemos mbir el orden de ls integrles que definen d un de ests funiones, por lo que, en relidd, podemos intermbir nuestro ntojo el orden de integrión sobre regiones retngulres. En totl, hy 6 forms distints de lulr l mism integrl triple (debido que, pr n signos integrles, hy n! permutiones). Como en tod funión, teniendo ls ondiiones de integrbilidd sufiientes (omo ontinuidd) podemos evitr lulr un integrl triple omo el límite de ls sums de Riemnn orrespondientes simplemente plindo un versión tridimensionl de los teorems de Fubini, de Lebesgue, de Cmbio de Vribles, et. Supongmos que queremos integrr un funión F : R 3 R sobre un región otd por un superfiie errd φ(x, y, z), es deir, otd inferiormente por un superfiie z f (x, y), superiormente por un superfiie
33 5.7. CÁLCULO E INTEGRALES TRIPLES CAPÍTULO 5. INTEGRACIÓN z 2 f 2 (x, y) y lterlmente por un ilindro C prlelo l eje OZ. enotemos por R l proyeión vertil de sobre el plno XY, que está enerrdo en l proyeión de C sobre el plno XY. Así, podemos definir omo { (x, y, z) R 3 (x, y) R, f (x, y) z f 2 (x, y) } Podemos sumir el so en que f y f 2 son funiones ontinus en R. Luego, l integrl de F se lul omo ( ) f2(x,y) F (x, y, z)dv F (x, y, z)dz da R Los límites de integrión pr z indin que, pr (x, y) perteneiente R, l oordend z se extiende desde l superfiie inferior z f (x, y) hst l superior z f 2 (x, y), donde los vlores de z se deduen de l euión φ(x, y, z). Luego, el ilindro C puede tener sus tps de forms irregulres, no neesrimente plns. Un vez se lul l integrl dentro del préntesis, obtendremos un funión G(x, y), l ul integrremos sobre l región R. Pr esto, pliremos lo prendido en l seión de integrles dobles, on lo que obtendremos un expresión del tipo f (x,y) F (x, y, z)dv ( ) f2(x,y) F (x, y, z)dz dydx R f (x,y) G(x, y)dydx R 2 y2(x) f2(x,y) y (x) f (x,y) F (x, y, z)dzdydx o bien F (x, y, z)dv ( ) f2(x,y) F (x, y, z)dz dxdy R f (x,y) G(x, y)dxdy R b2 x2(y) f2(x,y) b x (y) f (x,y) F (x, y, z)dzdxdy Luego, el ilindro tmpoo debe tener neesrimente un mnto regulr. En prtiulr, si éste se redue ero, tendremos que f (x, y) f 2 (x, y) y no existe dependeni de z, lo ul define l fronter de R. iho de otr form, podemos desribir un región errd intersetndo un superfiie f (x, y) on otr f 2 (x, y), y onsiderndo los puntos omprendidos entre ells. Todos estos resultdos no son solmente plibles z; omo lo hímos on integrles dobles, podemos intermbir los roles entre ls vribles de l funión. Si podemos prmetrizr l región de integrión prtir de l vrible z, diremos que l región es xy-proyetble. Si, en mbio, podemos prmetrizrl prtir de y, diremos que es xz-proyetble, y es yz-proyetble si se puede prmetrizr prtir de x. L figur ilustr un región que es proyetble en los tres plnos, por lo que es posible prmetrizrl prtir de ulquier de ls tres vribles rtesins.
34 5.7. CÁLCULO E INTEGRALES TRIPLES CAPÍTULO 5. INTEGRACIÓN Ejemplo: d l integrl x y f(x, y, z)dzdydx, enontrr l región de integrión R. En este so, qued lro que R { (x, y, z) R 3 z y, y x, x } (bst ver l orrespondeni entre signo integrl y diferenil). Luego, y está otdo por ls funiones ϕ (x) y ϕ 2 (x) x; en el plno xy se gener un triángulo. Además, z está otdo por ls funiones ψ (y) y ψ 2 (y) y; en el plno yz tmbién se gener un triángulo. Finlmente, omo y x, tenemos que z x, por lo que en el plno xz tendremos otro triángulo. Luego, l extender estos triángulos en ls oordends z, x e y, respetivmente, tendremos que l interseión nos d l región R que busmos, y que es extmente l región de l figur nterior. Qued omo ejeriio expresr l integrl nterior en tods sus 6 forms posibles. Enontrr los límites de integrión pr f(x, y, z)dv, donde R es l región que enierrn el prboloide de euión y x 2 + z 2 y el plno y 4. L región se ve gráfimente sí R Luego, no es difíil drse uent de que, en el plno xy, se form un región otd inferiormente por un prábol y superiormente por l ret y 4. Est región se desribe tomndo 2 x 2, x 2 y 4. Finlmente, de l euión de l prábol, podemos despejr z en funión de x e y, de form que x 2 y z x 2 y. Así, R qued ompletmente desrit y l integrl se esribe 2 4 x 2 y f(x, y, z)dv 2 x 2 x 2 y
1.1 Integral doble de una función acotada en un rectángulo.
 Tem Integrl doble Tods ls definiiones y resultdos que preen en este Tem son un so prtiulr de ls definiiones y resultdos más generles del Tem siguiente. in embrgo, el so de l integrl doble permite un mejor
Tem Integrl doble Tods ls definiiones y resultdos que preen en este Tem son un so prtiulr de ls definiiones y resultdos más generles del Tem siguiente. in embrgo, el so de l integrl doble permite un mejor
Integrales dobles y triples
 Integrles dobles y triples 1 Integrles dobles Integrles triples 3 Cmbios de vrible R: retángulo R = [, b [, d f : R R: mpo eslr e dos vribles. Si f es ontinu en R f x : [, d R y f y : [, b R son funiones
Integrles dobles y triples 1 Integrles dobles Integrles triples 3 Cmbios de vrible R: retángulo R = [, b [, d f : R R: mpo eslr e dos vribles. Si f es ontinu en R f x : [, d R y f y : [, b R son funiones
f(t)dt para todo x [a, b].
![f(t)dt para todo x [a, b]. f(t)dt para todo x [a, b].](/thumbs/63/48527259.jpg) ANÁLISIS MATEMÁTICO BÁSICO. EL TEOREMA FUNDAMENTAL DEL CÁLCULO. L integrl lnz todo su poder undo se li on l derivd. Esto ourre en el Teorem Fundmentl del Cálulo. Funiones definids trvés de l integrl. Dd
ANÁLISIS MATEMÁTICO BÁSICO. EL TEOREMA FUNDAMENTAL DEL CÁLCULO. L integrl lnz todo su poder undo se li on l derivd. Esto ourre en el Teorem Fundmentl del Cálulo. Funiones definids trvés de l integrl. Dd
Integrales Dobles e Integrales Triples
 Tem 6 Integrles Dobles e Integrles Triples 6.1 Introduión Comenzremos este tem on un repso de l Integrión de funiones de un vrible rel, pr introduir posteriormente ls integrles dobles y triples. 6.2 epso
Tem 6 Integrles Dobles e Integrles Triples 6.1 Introduión Comenzremos este tem on un repso de l Integrión de funiones de un vrible rel, pr introduir posteriormente ls integrles dobles y triples. 6.2 epso
El teorema de Fubini. f(x, y)dy es integrable en [a, b], y. o, con una notación más práctica, f = f(x, y)dx ) dy. Análogamente, si se supone que b
![El teorema de Fubini. f(x, y)dy es integrable en [a, b], y. o, con una notación más práctica, f = f(x, y)dx ) dy. Análogamente, si se supone que b El teorema de Fubini. f(x, y)dy es integrable en [a, b], y. o, con una notación más práctica, f = f(x, y)dx ) dy. Análogamente, si se supone que b](/thumbs/40/20974900.jpg) Cpítulo 5 El teorem de Fubini Hst hor hemos rterizdo ls funiones que son integrbles y hemos estudido ls propieddes básis de l integrl, pero en relidd no sbemos ómo lulr ls integrles inluso de ls funiones
Cpítulo 5 El teorem de Fubini Hst hor hemos rterizdo ls funiones que son integrbles y hemos estudido ls propieddes básis de l integrl, pero en relidd no sbemos ómo lulr ls integrles inluso de ls funiones
a vectores a y b se muestra en la figura del lado derecho.
 Produto ruz o produto vetoril Otr form nturl de definir un produto entre vetores es trvés del áre del prlelogrmo determindo por dihos vetores. El prlelogrmo definido por los h vetores y se muestr en l
Produto ruz o produto vetoril Otr form nturl de definir un produto entre vetores es trvés del áre del prlelogrmo determindo por dihos vetores. El prlelogrmo definido por los h vetores y se muestr en l
FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL
 FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL El prolem de l práol horizontl Qué relión h entre ls propieddes nlítis de l funión udráti ls propieddes geométris de l práol horizontl? Como
FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL El prolem de l práol horizontl Qué relión h entre ls propieddes nlítis de l funión udráti ls propieddes geométris de l práol horizontl? Como
7 Integral triple de Riemann
 Miguel eyes, pto. de Mtemátic Aplicd, FI-UPM 1 7 Integrl triple de iemnn 7.1 efinición Llmremos rectángulo cerrdo de 3 (prlelepípedo) l producto de tres intervlos cerrdos y cotdos de, es decir = [, b]
Miguel eyes, pto. de Mtemátic Aplicd, FI-UPM 1 7 Integrl triple de iemnn 7.1 efinición Llmremos rectángulo cerrdo de 3 (prlelepípedo) l producto de tres intervlos cerrdos y cotdos de, es decir = [, b]
ANALISIS MATEMATICO II INTEGRAL DEFINIDA - 2 PARTE
 ANALISIS MATEMATICO II INTEGRAL DEFINIDA - 2 PARTE Mrí Susn Montelr Fultd de Cienis Exts, Ingenierí y Agrimensur - UNR EXTENSIÓN DEL SÍMBOLO INTEGRAL < b f(x) dx = g(x) dx b = b f(x) dx = 0 PROPIEDADES
ANALISIS MATEMATICO II INTEGRAL DEFINIDA - 2 PARTE Mrí Susn Montelr Fultd de Cienis Exts, Ingenierí y Agrimensur - UNR EXTENSIÓN DEL SÍMBOLO INTEGRAL < b f(x) dx = g(x) dx b = b f(x) dx = 0 PROPIEDADES
Tema 4.1: Integral curvilínea. Caracterización de la existencia de primitiva
 Tem 4.1: Integrl urvilíne. Crterizión de l existeni de primitiv Fultd de Cienis Experimentles, Curso 2008-09 E. de Amo En este tem se front el problem que en Vrible Rel se onoe omo Teorem Fundmentl del
Tem 4.1: Integrl urvilíne. Crterizión de l existeni de primitiv Fultd de Cienis Experimentles, Curso 2008-09 E. de Amo En este tem se front el problem que en Vrible Rel se onoe omo Teorem Fundmentl del
2. Integrales iteradas dobles.
 2 Integrles prmétris e integrles dobles y triples. Eleonor Ctsigers. 9 Julio 26. 2. Integrles iterds dobles. 2.. Integrles iterds en dominios simples respeto de x. Se omo en l subseión.2, el retángulo
2 Integrles prmétris e integrles dobles y triples. Eleonor Ctsigers. 9 Julio 26. 2. Integrles iterds dobles. 2.. Integrles iterds en dominios simples respeto de x. Se omo en l subseión.2, el retángulo
CÁLCULO INTEGRAL. Víctor Manuel Sánchez de los Reyes. Departamento de Análisis Matemático Universidad Complutense de Madrid
 CÁLCULO INTEGRL Vítor Mnuel Sánhez de los Reyes Deprtmento de nálisis Mtemátio Universidd Complutense de Mdrid Índie 1. Integrión 5 1.1. Funiones integrbles.............................. 5 1.2. El teorem
CÁLCULO INTEGRL Vítor Mnuel Sánhez de los Reyes Deprtmento de nálisis Mtemátio Universidd Complutense de Mdrid Índie 1. Integrión 5 1.1. Funiones integrbles.............................. 5 1.2. El teorem
5.2 Integral Definida
 80 CÁLCULO / CIENCIAS AMBIENTALES / TEMA 5 5.2 Integrl Definid Definición de Integrl Definid El concepto de integrl definid se construye prtir de l ide de psr l límite un sum cundo el número de sumndos
80 CÁLCULO / CIENCIAS AMBIENTALES / TEMA 5 5.2 Integrl Definid Definición de Integrl Definid El concepto de integrl definid se construye prtir de l ide de psr l límite un sum cundo el número de sumndos
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS.. INTEGRAL DEFINIDA Se y = f(x) definid pr todo x [, b]. Consideremos un prtiión P del intervlo [, b] P {x 0 = < x < x 2 < < x n = b} Sen P = máx{x i x i }, s n = n m
. INTEGRALES DEFINIDAS E IMPROPIAS.. INTEGRAL DEFINIDA Se y = f(x) definid pr todo x [, b]. Consideremos un prtiión P del intervlo [, b] P {x 0 = < x < x 2 < < x n = b} Sen P = máx{x i x i }, s n = n m
Departamento: Física Aplicada III
 Fund mentos Físi os de l Ingenierí. (Ind ustri les) Prlelogrmo insrito en trpezoide Ddo un trpezoide (udrilátero irregulr que no tiene ningún ldo prlelo otro), demuestre, usndo el álger vetoril, que los
Fund mentos Físi os de l Ingenierí. (Ind ustri les) Prlelogrmo insrito en trpezoide Ddo un trpezoide (udrilátero irregulr que no tiene ningún ldo prlelo otro), demuestre, usndo el álger vetoril, que los
Notas de Análisis I. Gabriel Larotonda. Parte 7: Integrales múltiples
 Nots de Análisis I Gbriel Lrotond 1. Integrles en el plno Prte 7: Integrles múltiples Comenemos por definir integrles pr funiones on dominio en lgún subonjunto 2. Nos vmos enontrr on difiultdes propis
Nots de Análisis I Gbriel Lrotond 1. Integrles en el plno Prte 7: Integrles múltiples Comenemos por definir integrles pr funiones on dominio en lgún subonjunto 2. Nos vmos enontrr on difiultdes propis
INTEGRALES IMPROPIAS
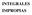 INTEGRALES IMPROPIAS INDICE.- Integrles impropis de primer espeie....- Integrles impropis de segund espeie.- Integrles impropis del tipo C... 8 4.- Criterios de omprión 8.- Biliogrfi 0 DEFINICION DE INTEGRALES
INTEGRALES IMPROPIAS INDICE.- Integrles impropis de primer espeie....- Integrles impropis de segund espeie.- Integrles impropis del tipo C... 8 4.- Criterios de omprión 8.- Biliogrfi 0 DEFINICION DE INTEGRALES
22. Trigonometría, parte II
 22. Trigonometrí, prte II Mtemátis II, 202-II 22. Trigonometrí, prte II Extensión del dominio Se P un punto sore l irunfereni x 2 + 2 =. Est irunfereni tiene rdio entro el origen O(0, 0). Denotmos por
22. Trigonometrí, prte II Mtemátis II, 202-II 22. Trigonometrí, prte II Extensión del dominio Se P un punto sore l irunfereni x 2 + 2 =. Est irunfereni tiene rdio entro el origen O(0, 0). Denotmos por
Coordinación de Matemática II (MAT022)
 oordinión de Mtemáti II (MT22) Primer semestre de 23 Semn 8: Lunes 6 de Myo Viernes de Myo ÁLULO ontenidos lse : Integrles Impropis de primer espeie. L integrl p. riterios de onvergeni. lse 2: Integrles
oordinión de Mtemáti II (MT22) Primer semestre de 23 Semn 8: Lunes 6 de Myo Viernes de Myo ÁLULO ontenidos lse : Integrles Impropis de primer espeie. L integrl p. riterios de onvergeni. lse 2: Integrles
Integral Definida. Tema 6. 6.1 Introducción. 6.2 Definición de Integral Definida
 Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Lección 5. INTEGRALES MÚLTIPLES
 Mtemátis III (GITI, 2016 2017) Leión 5. INTEGRALES MÚLTIPLES 1. INTEGRALES OBLES Ls integrles dobles y triples integrles de funiones de dos o tres vribles son un generlizión nturl de ls integrles de funiones
Mtemátis III (GITI, 2016 2017) Leión 5. INTEGRALES MÚLTIPLES 1. INTEGRALES OBLES Ls integrles dobles y triples integrles de funiones de dos o tres vribles son un generlizión nturl de ls integrles de funiones
7.1. Definición de la Integral de Riemann
 Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
UNIDAD VI LA ELIPSE 6.1. ECUACIÓN EN FORMA COMÚN O CANÓNICA DE LA ELIPSE
 UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
β (t) = (1) 2 + ( t 1 t 2 dt = + 1 dt = 1 t 2 + t 1 f(β(ϕ(t))) β (ϕ(t)) ϕ (t)dt = }{{}
 Vmos lulr ls siguientes integrles de tryetori ) Se α(t) = (os(t), sin(t)) on t [, π ] y f(x, y) = x + y Sol. Tenemos que f(α(t)) = os(t) + sin(t) por otro ldo α (t) = ( sin(t), os(t) α (t) = ( os(t)) +
Vmos lulr ls siguientes integrles de tryetori ) Se α(t) = (os(t), sin(t)) on t [, π ] y f(x, y) = x + y Sol. Tenemos que f(α(t)) = os(t) + sin(t) por otro ldo α (t) = ( sin(t), os(t) α (t) = ( os(t)) +
Determinantes Bachillerato 2º. Determinantes. Los determinantes históricamente son anteriores a las matrices, pero por el auge de éstos han quedado
 Determinntes hillerto º Determinntes Introduión: Los determinntes histórimente son nteriores ls mtries, pero por el uge de éstos hn queddo relegdos un º plno. El uso de los determinntes nos permitirá:
Determinntes hillerto º Determinntes Introduión: Los determinntes histórimente son nteriores ls mtries, pero por el uge de éstos hn queddo relegdos un º plno. El uso de los determinntes nos permitirá:
Si este proceso de subdivisión se repitiese muchas veces, se obtendrían dos sucesiones, s i y S
 Integrles LA INTEGRAL DEFINIDA Integrl definid: áre jo un urv L integrl definid permite lulr el áre del reinto limitdo, en su prte superior por l gráfi de un funión f (, ontinu y no negtiv, en su prte
Integrles LA INTEGRAL DEFINIDA Integrl definid: áre jo un urv L integrl definid permite lulr el áre del reinto limitdo, en su prte superior por l gráfi de un funión f (, ontinu y no negtiv, en su prte
5. RECTA Y PLANO EN EL ESPACIO
 Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
Propuesta sobre la enseñanza de los números racionales Geovany Sanabria Brenes
 Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
Integración de funciones de una variable real
 Cpítulo 5 Integrción de funciones de un vrible rel 5.1. Introducción Los inicios del Cálculo Integrl se remontn Arquímedes, mtemático, físico e ingeniero griego del S.III A.C., quién clculó el áre de numeross
Cpítulo 5 Integrción de funciones de un vrible rel 5.1. Introducción Los inicios del Cálculo Integrl se remontn Arquímedes, mtemático, físico e ingeniero griego del S.III A.C., quién clculó el áre de numeross
1.-Algunas desigualdades básicas.
 Preprión Olimpid Mtemáti Espñol. Curso 05-6. Desigulddes (y polinomios, y funiones). 3 de Noviemre de 05. Fernndo Myorl..-Alguns desigulddes ásis. ) 0 pr ulquier R. L iguldd sólo se umple pr = 0. ) (Desiguldd
Preprión Olimpid Mtemáti Espñol. Curso 05-6. Desigulddes (y polinomios, y funiones). 3 de Noviemre de 05. Fernndo Myorl..-Alguns desigulddes ásis. ) 0 pr ulquier R. L iguldd sólo se umple pr = 0. ) (Desiguldd
Anexo 3: Demostraciones
 170 Mtemátics I : Cálculo integrl en IR Anexo 3: Demostrciones Integrl de Riemnn Demostrción de: Propieddes 264 de l págin 142 Propieddes 264.- Se f: [, b] IR un función cotd. ) Pr tod P P[, b], se verific
170 Mtemátics I : Cálculo integrl en IR Anexo 3: Demostrciones Integrl de Riemnn Demostrción de: Propieddes 264 de l págin 142 Propieddes 264.- Se f: [, b] IR un función cotd. ) Pr tod P P[, b], se verific
1 - Resolver los siguientes determinantes usando propiedades 1/10
 - Resolver los siguientes determinntes usndo propieddes ) ) / ) d) e) f) / / g) / / / / / / / / / / / / / h) / / / / / / / / / / / / / / / i) / / / / j) / / 8 / k) h k w k w h w h k h k w - Hllr los vlores
- Resolver los siguientes determinntes usndo propieddes ) ) / ) d) e) f) / / g) / / / / / / / / / / / / / h) / / / / / / / / / / / / / / / i) / / / / j) / / 8 / k) h k w k w h w h k h k w - Hllr los vlores
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE ZARAGOZA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
1. Definición de Semejanza. Escalas
 Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Fundamentos Matemáticos de la Ingeniería. Tema 9: Cálculo integral de funciones de varias variables Curso
 Fundmentos Mtemáticos de l Ingenierí. (Tem 9) Hoj Escuel Técnic Superior de Ingenierí Civil e Industril (Esp. en Hidrologí) Fundmentos Mtemáticos de l Ingenierí. Tem 9: Cálculo integrl de funciones de
Fundmentos Mtemáticos de l Ingenierí. (Tem 9) Hoj Escuel Técnic Superior de Ingenierí Civil e Industril (Esp. en Hidrologí) Fundmentos Mtemáticos de l Ingenierí. Tem 9: Cálculo integrl de funciones de
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Funciones continuas. Mariano Suárez-Alvarez. 4 de junio, Índice
 Funciones continus Mrino Suárez-Alvrez 4 de junio, 2013 Índice 1. Funciones continus................... 1 2. Alguns propieddes básics............ 3 3. Los teorems de Weierstrss y Bolzno... 6 4. Funciones
Funciones continus Mrino Suárez-Alvrez 4 de junio, 2013 Índice 1. Funciones continus................... 1 2. Alguns propieddes básics............ 3 3. Los teorems de Weierstrss y Bolzno... 6 4. Funciones
5.4. Longitud de un Arco de Curva (Rectificación)
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 7-2 SEMANA 1: APLICACIONES DE LA INTEGRAL 5.4. Longitud de un Arco de Curv (Rectificción)
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 7-2 SEMANA 1: APLICACIONES DE LA INTEGRAL 5.4. Longitud de un Arco de Curv (Rectificción)
Cuestionario Respuestas
 Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
Cuestionrio Respuests Copright 2014, MtemtiTu Derehos reservdos 1) Un ineuión o desiguldd on un vrile (inógnit) es un enunido en que se presentn dos epresiones, l menos un on l vrile entre ells uno de
TEMA 2 INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS
 Frnisnos T.O.R. Cód. 867 TEMA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS. INTEGRAL DEFINIDA El álulo de l integrl definid, que se denot por: f ( d, onsiste en lulr l integrl de l funión f( en el intervlo [, ].
Frnisnos T.O.R. Cód. 867 TEMA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS. INTEGRAL DEFINIDA El álulo de l integrl definid, que se denot por: f ( d, onsiste en lulr l integrl de l funión f( en el intervlo [, ].
TEMA 7: DETERMINANTES
 lonso Fernández Glián TEM : DETERMINNTES El determinnte de un mtriz udrd es ierto número que se lul prtir de ell y que ontiene informión signifitiv sore l mtriz.. DETERMINNTES DE ORDEN Y El álulo de determinntes
lonso Fernández Glián TEM : DETERMINNTES El determinnte de un mtriz udrd es ierto número que se lul prtir de ell y que ontiene informión signifitiv sore l mtriz.. DETERMINNTES DE ORDEN Y El álulo de determinntes
Sistemas de Ecuaciones lineales Discusión con parámetros. Discutir el siguiente sistema de ecuaciones lineales según el valor del parámetro a:
 ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
ALGEBRA Sistems de Euiones lineles Disusión on prámetros Disutir el siguiente sistem de euiones lineles según el vlor del prámetro : + ( + ) = + = + = Interpretión: Del enunido se dedue que se trt de un
Primitivas e Integrales
 Cpítulo 25 Primitivs e Integrles En este cpítulo vmos trbjr con funciones de un vrible. En él estbleceremos un cso prticulr del Teorem Fundmentl del Cálculo Integrl (ver [3] pr el cso generl), con el que
Cpítulo 25 Primitivs e Integrles En este cpítulo vmos trbjr con funciones de un vrible. En él estbleceremos un cso prticulr del Teorem Fundmentl del Cálculo Integrl (ver [3] pr el cso generl), con el que
DETERMINANTES SELECTIVIDAD ZARAGOZA
 DETERMINANTES SELECTIVIDAD ZARAGOZA. (S-97)Hllr el rngo de l mtriz B 0 0 según se el vlor del prámetro [,5 puntos] Puesto que el menor 0 0 rgb 0 () 0 ( ) 0 ) Pr 0 r(b) ) Pr 0 0 - B 0-0 0 - r(b) 0-0 - 0-0
DETERMINANTES SELECTIVIDAD ZARAGOZA. (S-97)Hllr el rngo de l mtriz B 0 0 según se el vlor del prámetro [,5 puntos] Puesto que el menor 0 0 rgb 0 () 0 ( ) 0 ) Pr 0 r(b) ) Pr 0 0 - B 0-0 0 - r(b) 0-0 - 0-0
TRIGONOMETRÍA. 1. ÁNGULOS 1.1. Ángulo en el plano Criterios de orientación de ángulo Sistema de medida de ángulos. Sistema sexagesimal
 . ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
. ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
5. Aplicación de la Integral de Riemann
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 8-2 Ingenierí Mtemátic Universidd de Chile SEMANA 9: APLICACIONES DE LA INTEGRAL 5. Aplicción
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencil e Integrl 8-2 Ingenierí Mtemátic Universidd de Chile SEMANA 9: APLICACIONES DE LA INTEGRAL 5. Aplicción
Integral de una función real. Tema 08: Integrales Múltiples. Integral definida. Aproximación de una integral simple
 Integrl de un función rel Tem 08: Integrles Múltiples Jun Igncio Del Vlle Gmbo Sede de Guncste Universidd de Cost ic Ciclo I - 2014 Ls integrles definids clculn el áre bjo un curv y = f (x) pr un región
Integrl de un función rel Tem 08: Integrles Múltiples Jun Igncio Del Vlle Gmbo Sede de Guncste Universidd de Cost ic Ciclo I - 2014 Ls integrles definids clculn el áre bjo un curv y = f (x) pr un región
Colegio Nuestra Señora de Loreto TRIGONOMETRÍA 4º E.S.O.
 TRIGONOMETRÍ 4º E.S.O. Frniso Suárez Bluen TRIGONOMETRÍ PREVIOS. Teorem de Tles (Semejnz) Si ortmos dos rets por un serie de rets prlels, los segmentos determindos en un de ells son proporionles los segmentos
TRIGONOMETRÍ 4º E.S.O. Frniso Suárez Bluen TRIGONOMETRÍ PREVIOS. Teorem de Tles (Semejnz) Si ortmos dos rets por un serie de rets prlels, los segmentos determindos en un de ells son proporionles los segmentos
α A TRIGONOMETRÍA PLANA
 TRIGONOMETRÍ PLN El origen de l plr trigonometrí puede enontrrse en el griego, trígono triángulo y metrí medid. L trigonometrí justmente trt de eso, l mediión y resoluión de situiones donde se preten triángulos.
TRIGONOMETRÍ PLN El origen de l plr trigonometrí puede enontrrse en el griego, trígono triángulo y metrí medid. L trigonometrí justmente trt de eso, l mediión y resoluión de situiones donde se preten triángulos.
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
1.- MEDIDA DE ÁNGULOS. - El sistema sexagesimal que usa como unidad de medida el grado. Un grado es la 90-ava parte del ángulo recto.
 º Bhillerto Mtemátis I Dpto de Mtemátis- I.E.S. Montes Orientles (Iznlloz)-Curso 0/0 TEMAS 4 y 5.- RESOLUCIÓN DE TRIÁNGULOS. FUNCIONES FÓRMULAS TRIGONOMÉTRICAS Pr medir ángulos se suelen usr dos sistems
º Bhillerto Mtemátis I Dpto de Mtemátis- I.E.S. Montes Orientles (Iznlloz)-Curso 0/0 TEMAS 4 y 5.- RESOLUCIÓN DE TRIÁNGULOS. FUNCIONES FÓRMULAS TRIGONOMÉTRICAS Pr medir ángulos se suelen usr dos sistems
La Integral Definida
 Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.
![LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b. LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.](/thumbs/52/29237757.jpg) Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
Teóricas de Análisis Matemático (28) - Práctica 10 - Área entre curvas. y = f (x) f (x)dx A =
 Teórics de nálisis Mtemático 28) - Práctic 0 - Áre entre curvs Práctic 0 - Prte Áre entre curvs Un de ls plicciones del cálculo de integrles definids es el cálculo de áres de regiones cotds del plno delimitds
Teórics de nálisis Mtemático 28) - Práctic 0 - Áre entre curvs Práctic 0 - Prte Áre entre curvs Un de ls plicciones del cálculo de integrles definids es el cálculo de áres de regiones cotds del plno delimitds
1.4. Sucesión de funciones continuas ( )
 1.4. Sucesión de funciones continus (18.04.2017) Se {f n } un sucesión de funciones f n, definids en I. Si {f n } converge uniformemente f en I y ls f n son continus en I, entonces f es continu en I. D:
1.4. Sucesión de funciones continus (18.04.2017) Se {f n } un sucesión de funciones f n, definids en I. Si {f n } converge uniformemente f en I y ls f n son continus en I, entonces f es continu en I. D:
Números Irracionales
 Números Irrionles Los griegos ern onoedores de los números nturles: 0, 1,,,, 5, Estos números son los que se utilizn pr numerr o ontr, pero no nos sirven si queremos expresr ntiddes no exts, omo "l mitd
Números Irrionles Los griegos ern onoedores de los números nturles: 0, 1,,,, 5, Estos números son los que se utilizn pr numerr o ontr, pero no nos sirven si queremos expresr ntiddes no exts, omo "l mitd
En donde x representa la incógnita, y a, b y c son constantes.
 FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
7.1. Definición de integral impropia y primeras propiedades
 Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Profesora Jessica Mora Bolaños Décimo año // Liceo San Nicolás de Tolentino Pág. 1 Función
 Déimo ño // Lieo Sn Niolás de Tolentino Pág. 1 Funión Ddos dos onjuntos no víos y, se denomin funión de en, l relión o orrespondeni de d elemento del onjunto on un ÚNICO elemento del onjunto. lgunos spetos
Déimo ño // Lieo Sn Niolás de Tolentino Pág. 1 Funión Ddos dos onjuntos no víos y, se denomin funión de en, l relión o orrespondeni de d elemento del onjunto on un ÚNICO elemento del onjunto. lgunos spetos
TRIGONOMETRÍA (4º OP. A)
 SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
La Integral de Riemann
 Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función potencil Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función
Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función potencil Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función
Matemáticas Empresariales I. Integral Definida
 Mtemátics Empresriles I Lección 8 Integrl Definid Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 31 Construcción de l integrl definid Se f un función definid
Mtemátics Empresriles I Lección 8 Integrl Definid Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 31 Construcción de l integrl definid Se f un función definid
1. INTEGRAL DEFINIDA DE UNA FUNCIÓN CONTÍNUA Y POSITIVA EN UN INTERVALO.
 TEMA 9 Integrl Definid. INTEGRAL DEFINIDA DE UNA FUNCIÓN CONTÍNUA Y POSITIVA EN UN INTERVALO. y = f() Un trpeio urvilíneo (o mitilíneo) T es un figur pln omo l que pree en l figur: T O Está limitd por:
TEMA 9 Integrl Definid. INTEGRAL DEFINIDA DE UNA FUNCIÓN CONTÍNUA Y POSITIVA EN UN INTERVALO. y = f() Un trpeio urvilíneo (o mitilíneo) T es un figur pln omo l que pree en l figur: T O Está limitd por:
TEMA 5: INTEGRACIÓN. f(x) dx.
 TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE-
 Resumen teorí Prof Alón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- 1 Números enteros Un número rel se die entero si es ero o es un número nturl o es el opuesto de un número nturl Si indimos on N l subonjunto
Resumen teorí Prof Alón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- 1 Números enteros Un número rel se die entero si es ero o es un número nturl o es el opuesto de un número nturl Si indimos on N l subonjunto
4.6. Teorema Fundamental del Cálculo
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 07-2 SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl del Cálculo Proposición 4.5. Se un
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 07-2 SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl del Cálculo Proposición 4.5. Se un
MATEMÁTICA MÓDULO 3 Eje temático: Geometría
 MATEMÁTICA MÓDULO 3 Eje temátio: Geometrí 1. SEGMENTOS PROPORCIONALES EN EL TRIÁNGULO RECTÁNGULO En el ABC retángulo en C de l figur: Se pueden estbleer ls siguientes semejnzs: 1) De est semejnz, se obtienen
MATEMÁTICA MÓDULO 3 Eje temátio: Geometrí 1. SEGMENTOS PROPORCIONALES EN EL TRIÁNGULO RECTÁNGULO En el ABC retángulo en C de l figur: Se pueden estbleer ls siguientes semejnzs: 1) De est semejnz, se obtienen
11La demostración La demostración en matemáticas (geometría)
 L demostrión en mtemátis (geometrí) ág. 1 Tl vez los lumnos y lumns hyn demostrdo, en lgun osión, lgun fórmul o lgun propiedd mtemáti, o hyn ontempldo su demostrión. omo semos, pr ellos, el proeso no es
L demostrión en mtemátis (geometrí) ág. 1 Tl vez los lumnos y lumns hyn demostrdo, en lgun osión, lgun fórmul o lgun propiedd mtemáti, o hyn ontempldo su demostrión. omo semos, pr ellos, el proeso no es
Unidad didáctica 4. Trigonometría plana
 Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
6.1 Sumas de Riemann e integral definida
 Tem 6 Integrción Definid 6.1 Sums de Riemnn e integrl definid Supongmos que estmos interesdos en clculr el áre que se encuentr bjo un curv y = f(x) en un intervlo [, b] (pr simplificr, consideremos el
Tem 6 Integrción Definid 6.1 Sums de Riemnn e integrl definid Supongmos que estmos interesdos en clculr el áre que se encuentr bjo un curv y = f(x) en un intervlo [, b] (pr simplificr, consideremos el
SEMANA 8: INTEGRAL DE RIEMANN
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Ingenierí Mtemátic Universidd de Chile SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Ingenierí Mtemátic Universidd de Chile SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl
La integral de Riemann
 L integrl de Riemnn 1 Vmos dr un definición precis de l integrl de un función definid en un intervlo. Este tiene que ser un intervlo cerrdo y cotdo, es decir [,] con < R, y l definición que dremos de integrl
L integrl de Riemnn 1 Vmos dr un definición precis de l integrl de un función definid en un intervlo. Este tiene que ser un intervlo cerrdo y cotdo, es decir [,] con < R, y l definición que dremos de integrl
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
7 Semejanza. y trigonometría. 1. Teorema de Thales
 7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
Funciones de variable compleja
 Funciones de vrible complej Integrles impropis. Mrí Eugeni Torres Universidd Ncionl de Entre Ríos Fcultd de Ingenierí Funciones de Vrible Complej (Bioingenierí, Pln 28) Myo 29 Integrles impropis Alcnce
Funciones de vrible complej Integrles impropis. Mrí Eugeni Torres Universidd Ncionl de Entre Ríos Fcultd de Ingenierí Funciones de Vrible Complej (Bioingenierí, Pln 28) Myo 29 Integrles impropis Alcnce
Notas de Integral de Riemann-Stieltjes
 Nots de Integrl de Riemnn-Stieltjes 1. Definición y propieddes Dds funciones g, F : [, b] R que cumpln ciertos requisitos, definiremos l expresión g(x)df(x) de tl mner que cundo consideremos el cso prticulr
Nots de Integrl de Riemnn-Stieltjes 1. Definición y propieddes Dds funciones g, F : [, b] R que cumpln ciertos requisitos, definiremos l expresión g(x)df(x) de tl mner que cundo consideremos el cso prticulr
Integrales impropias
 Integrles impropis Ejeriios resueltos CRESLINE, S.L. Integrles impropis Ejeriio : Estudir l onvergeni de l impropi os x y en so de onvergeni, lulr su vlor. Soluión: Pr b>, se tiene b os x= [sin x]b = sin
Integrles impropis Ejeriios resueltos CRESLINE, S.L. Integrles impropis Ejeriio : Estudir l onvergeni de l impropi os x y en so de onvergeni, lulr su vlor. Soluión: Pr b>, se tiene b os x= [sin x]b = sin
Teorema de Green. 6.1 Introducción
 SESIÓN 6 6.1 Introducción En est sesión se revis el primero de los 3 teorem clves del cálculo vectoril: el. Este teorem estblece que un integrl doble sobre un región del plno es igul un integrl de líne
SESIÓN 6 6.1 Introducción En est sesión se revis el primero de los 3 teorem clves del cálculo vectoril: el. Este teorem estblece que un integrl doble sobre un región del plno es igul un integrl de líne
TEMA 4. Cálculo integral
 TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
Visualización de triángulos. Curso de Matemáticas para Física. Trigonometría. Trigonometría. Física I, Internet A b.
 Visulizión de triángulos Curso de Mtemátis pr Físi Curso de Mtemátis pr Físi Físi I, vi@ Internet 2004 B A C Físi I, vi@ Internet 2004 Visulizión de triángulos Fijémonos en un triángulo ulquier. Curso
Visulizión de triángulos Curso de Mtemátis pr Físi Curso de Mtemátis pr Físi Físi I, vi@ Internet 2004 B A C Físi I, vi@ Internet 2004 Visulizión de triángulos Fijémonos en un triángulo ulquier. Curso
Cálculo integral de funciones de una variable
 Lino Alvrez - Aure Mrtínez CÁLCULO II Cálculo integrl de funciones de un vrible 1 L integrl de Riemnn Se f : [, b] R R un función cotd en [, b]. Definición 1.- Un prtición P = {t 0, t 1,..., t n } del
Lino Alvrez - Aure Mrtínez CÁLCULO II Cálculo integrl de funciones de un vrible 1 L integrl de Riemnn Se f : [, b] R R un función cotd en [, b]. Definición 1.- Un prtición P = {t 0, t 1,..., t n } del
5. Integral y Aplicaciones
 Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
ECUACIONES DE PRIMER Y SEGUNDO GRADO
 UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
x x = 0 es una ecuación compatible determinada por que sólo se
 Euiones Denominmos euión l iguldd que se stisfe pr uno o más vlores de l(s) vrile(s), o inógnit(s), que interviene en ell. Ejemplos: + 5 + 5 + 6 0 + 0 Denominmos euión lgeri tod euión del tipo: n n n +
Euiones Denominmos euión l iguldd que se stisfe pr uno o más vlores de l(s) vrile(s), o inógnit(s), que interviene en ell. Ejemplos: + 5 + 5 + 6 0 + 0 Denominmos euión lgeri tod euión del tipo: n n n +
Clase del Miércoles 13 de Junio de 2012: Ecuaciones Integrales.
 Clse del Miércoles 3 de Junio de 22: Ecuciones Integrles. Introducción En est clse estudiremos ls ecuciones integrles de Fredholm y de Volterr. -+ - Empezremos por considerr l ecución de Fredholm de segund
Clse del Miércoles 3 de Junio de 22: Ecuciones Integrles. Introducción En est clse estudiremos ls ecuciones integrles de Fredholm y de Volterr. -+ - Empezremos por considerr l ecución de Fredholm de segund
Integración de funciones reales de una variable real. 24 de octubre de 2014
 Cálculo Integrción de funciones reles de un vrible rel 24 de octubre de 2014 c Dpto. de Mtemátics UDC Integrción de funciones reles de un vrible rel L integrl indefinid. Cálculo de primitivs L integrl
Cálculo Integrción de funciones reles de un vrible rel 24 de octubre de 2014 c Dpto. de Mtemátics UDC Integrción de funciones reles de un vrible rel L integrl indefinid. Cálculo de primitivs L integrl
Herramientas digitales de auto-aprendizaje para Matemáticas
 Mtemático Tem: L integrl Integrl Herrmients digitles de uto-prendizje pr Mtemátics, Grupo de Innovción Didáctic Deprtmento de Mtemátics Universidd de Extremdur Mtemático Tem: L integrl Integrl Mtemático
Mtemático Tem: L integrl Integrl Herrmients digitles de uto-prendizje pr Mtemátics, Grupo de Innovción Didáctic Deprtmento de Mtemátics Universidd de Extremdur Mtemático Tem: L integrl Integrl Mtemático
(Ésta es una versión preliminar de la teoría del tema.)
 Estudio de funciones periódics Ést es un versión preliminr de l teorí del tem. Un función fx se dice que es periódic de periodo cundo fx = fx +, x. Si se conoce fx en el intervlo [, ] su ciclo, se l conoce
Estudio de funciones periódics Ést es un versión preliminr de l teorí del tem. Un función fx se dice que es periódic de periodo cundo fx = fx +, x. Si se conoce fx en el intervlo [, ] su ciclo, se l conoce
TRANSFORMACIONES LINEALES
 . 7 Cpítulo 5 RANSFORMACIONES LINEALES Mrtínez Hétor Jiro Snri An Mrí Semestre,.7 5.. Introduión Reordemos que un funión : A B es un regl de soiión entre los elementos de A y los elementos de B, tl que
. 7 Cpítulo 5 RANSFORMACIONES LINEALES Mrtínez Hétor Jiro Snri An Mrí Semestre,.7 5.. Introduión Reordemos que un funión : A B es un regl de soiión entre los elementos de A y los elementos de B, tl que
Integración. du sinh udu = cosh u + c, cosh udu = sinh u + c, cosh 2 = tanh u + c, = f(u)du = F (u) + c = F (ϕ(x)) + c.
 Integrión Integrles indefinids Definiión. Diremos que F :, b) R es un primitiv de f :, b) R undo F ) f),, b). Usremos el símbolo F ) f) pr denotr que F ) es un primitiv de f). Observión. Tods ls primitivs
Integrión Integrles indefinids Definiión. Diremos que F :, b) R es un primitiv de f :, b) R undo F ) f),, b). Usremos el símbolo F ) f) pr denotr que F ) es un primitiv de f). Observión. Tods ls primitivs
CALCULO DE CENTROS DE MASA: PLACAS
 CALCULO DE CENTROS DE MASA: PLACAS Clulr l posiión el entro e mss e l siguiente pl suponieno que su ms está uniformemente istribui por to ell: b b( 1 k 3 ) Soluión: I.T.I. 1,, I.T.T. 1, En primer lugr,
CALCULO DE CENTROS DE MASA: PLACAS Clulr l posiión el entro e mss e l siguiente pl suponieno que su ms está uniformemente istribui por to ell: b b( 1 k 3 ) Soluión: I.T.I. 1,, I.T.T. 1, En primer lugr,
LA INTEGRAL DE RIEMANN
 LA INTEGRAL DE RIEMANN En este tem se introduce el Cálculo Integrl que demás de permitir clculr longitudes, áres y volúmenes, tiene multiples plicciones en l Ciencis, Ingenierí, etc... En primer lugr,
LA INTEGRAL DE RIEMANN En este tem se introduce el Cálculo Integrl que demás de permitir clculr longitudes, áres y volúmenes, tiene multiples plicciones en l Ciencis, Ingenierí, etc... En primer lugr,
Teoremas de convergencia
 Cpítulo 3 Teorems de convergenci L necesidd de considerr límites de sucesiones o series de funciones es básic en el estudio del nálisis. Por tnto, es nturl preguntrse bjo qué condiciones se tiene que un
Cpítulo 3 Teorems de convergenci L necesidd de considerr límites de sucesiones o series de funciones es básic en el estudio del nálisis. Por tnto, es nturl preguntrse bjo qué condiciones se tiene que un
determinante haciendo todos los productos, Tema 8. Determinantes.
 Tem. Determinntes.. Definiión de determinntes.. Propieddes de los determinntes.. Cálulo de determinntes de orden myor que (No entr en seletividd).. Rngo de un mtriz.. Mtriz invers... Definiión del determinnte
Tem. Determinntes.. Definiión de determinntes.. Propieddes de los determinntes.. Cálulo de determinntes de orden myor que (No entr en seletividd).. Rngo de un mtriz.. Mtriz invers... Definiión del determinnte
Una condición necesaria y suficiente para que el triangulo PBP sea equilátero es que el ángulo HBP sea 30º. b que es la relación buscada.
 Hoj de Prolems Geometrí III 49. Dd l elipse, si tommos el etremo B de ordend positiv del eje menor omo entro, se desrie un irunfereni de rdio igul diho eje menor, ortr l elipse en dos punto P P. Determinr
Hoj de Prolems Geometrí III 49. Dd l elipse, si tommos el etremo B de ordend positiv del eje menor omo entro, se desrie un irunfereni de rdio igul diho eje menor, ortr l elipse en dos punto P P. Determinr
Funciones de una variable real II Integrales impropias
 Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
f(x) dx = F (x) + C, siendo F (x) una antiderivada de f(x), es decir, siendo F (x) tal que F (x) = f(x)
 Cálculo de primitivs: f(x) dx = F (x) + C, siendo F (x) un ntiderivd de f(x), es decir, siendo F (x) tl que F (x) = f(x) L constnte C se denomin constnte de integrción; es un constnte rbitrri porque se
Cálculo de primitivs: f(x) dx = F (x) + C, siendo F (x) un ntiderivd de f(x), es decir, siendo F (x) tl que F (x) = f(x) L constnte C se denomin constnte de integrción; es un constnte rbitrri porque se
X. LA ELIPSE DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO. La recta que pasa por el punto medio del segmento el, se llama EJE MENOR de la elipse.
 X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
