TEMA N 1.- MODELOS EN INVESTIGACIÓN OPERATIVA
|
|
|
- Marcos Torregrosa Montes
- hace 7 años
- Vistas:
Transcripción
1 UNIVERSIDAD DE ORIENTE NÚCLEO DE ANZOÁTEGUI EXTENSIÓN REGIÓN CENTRO-SUR ANACO, ESTADO ANZOÁTEGUI 1.1 Modelo de transporte Asignatura: Investigación Operativa I Docente: Ing. Jesús Alonso Campos TEMA N 1.- MODELOS EN INVESTIGACIÓN OPERATIVA El problema de transporte es un tipo especial de programación lineal que, aun cuando se puede resolver por el método símplex, sus propiedades especiales ofrecen un procedimiento de solución más sencillo. Las técnicas de transporte tratan de encontrar los caminos para trasladar mercancía desde varías plantas (orígenes) a diferentes centros de almacenamiento (destinos), de tal manera que se minimice el costo de transporte. Para que los problemas puedan resolverse por el método de transporte, se deben cumplir los siguientes requisitos: a. La función objetivo y las restricciones deben ser lineales. b. Las mercancías (o recursos) a distribuir deben ser uniformes y no se pueden cambiar entre sí. c. Los coeficientes de las variables en las restricciones deben ser cero o uno. d. La suma de la capacidad de todos los orígenes debe ser igual que la capacidad de los destinos, es decir, la demanda total debe ser igual a la oferta total Método simplex para el modelo de transporte Se tiene m centros de oferta (orígenes) y n centros de demanda (destinos), a i es el número de unidades disponibles en cada centro de oferta i, y b j es el número requerido de
2 : unidades de mercancía en el centro de demanda j. Si se considera C ij como el costo unitario de transporte en la ruta del centro de oferta i al centro de demanda j, el objetivo entonces es determinar el número de unidades de mercancía que debe transportarse desde las fuentes i a los destinos j, de tal forma que se minimice el costo total de transporte. Si X ij es la cantidad transportada del centro de oferta i al centro de demanda j, entonces el modelo será: Min Z = C 11 X 11 + C 12 X C 1n X 1n + C 21 X 21 + C m1 X n1 + + C mn X mn Sujeto a: Capacidad disponible (oferta) X 11 + X X 1n a 1 X 21 + X X 2n a 2 : : : : X m1 + X m2 + + X mn a m Demanda X 11 + X X m1 b 1 X 12 + X X m2 b 2 : : : : X 1n + X 2n + + X mn b n X ij 0 i = 1, 2, 3,,n j = 1, 2, 3, m X ij : Número de unidades transportadas de origen i al destino j. C ij : Costo de transportar una unidad desde el origen i hasta el destino j. a i : Capacidad de la planta i. b j : Número de unidades requeridas por el almacén j Modelo tabular del problema de transporte n Oferta X 11 X 12 X 13 : X 1n a 1 X 21 X 22 X 23 : X 2n a 2 X 31 X 32 X 33 : X 3n a 3 : : : : : : X m1 X m2 X m3 : X mn a m Demanda b 1 b 2 b 3 b n Condiciones para resolver el modelo de transporte 1. ΣOferta = ΣDemanda 2. ΣOferta ΣDemanda: cuando esto sucede, pueden presentarse dos casos:
3 a. Cuando la oferta es mayor que la demanda (ΣOferta > ΣDemanda) En este caso, se adiciona una demanda ficticia, se le agrega esa demanda ficticia al modelo tabular, cuya demanda ficticia va a ser igual a ΣOferta - ΣDemanda y los coeficientes de los costos serán cero para cada una de las casillas. b. Cuando la oferta es menor que la demanda (ΣOferta < ΣDemanda) En este caso, se adiciona una oferta ficticia, se le agrega esa oferta ficticia al modelo tabular, cuya oferta ficticia va a ser igual a ΣDemanda - ΣOferta y los coeficientes de los costos serán cero para cada una de las casillas Métodos para la solución del problema de transporte Método de la esquina noroeste: consiste en embarcar la cantidad máxima a través de la esquina noroeste de la matriz; se analizan entonces los máximos embarques a través de las celdas restantes, moviéndose hacia la derecha y hacia abajo en la matriz, hasta que se cubran todos los renglones y columnas. Este método tiene la desventaja que la solución puede resultar bastante costosa, pues no se presta atención a los valores de los costos Método del costo mínimo: este método trata de asignar tanto como sea posible al centro de distribución que tenga el costo unitario de transporte más bajo. En el caso de que existan dos o más iguales, la elección es arbitraria. Al completarse la demanda, esta se va ajustando a las cantidades que están disponibles, a la par que se disminuye la oferta; así quedarán eliminados del problema las columnas o renglones saturados y se continúa el procedimiento de escoge el costo más pequeño, dentro del área no saturada. Si se satura el renglón y la columna simultáneamente, hay que eliminarlos los dos Método de aproximaciones de Vogel: se inicia calculando la diferencia entre el costo más bajo y el costo inmediato superior en cada renglón o columna (costos de oportunidad). El renglón o columna con la diferencia de costo más elevada (penalizaciones) se selecciona entonces para el embarque. Se embarca tanto como sea posible a través de la celda de costo mínimo en el renglón o columna seleccionados. Entonces el renglón o columna que se llena, deja de considerarse y se repite el método. Debido a la eliminación del renglón o columna, al menos una de las diferencias de renglón y columna debe calcularse nuevamente en cada paso. Si se agota la oferta y la demanda simultáneamente, se elimina uno sólo a la vez y al otro se le coloca cero. 1.2 Modelo de asignación Es una forma de programación lineal que busca asignar trabajos o trabajadores a máquinas, nuevos productos a planes de producción, etc. Los métodos de asignación como los de transporte se basan en tablas y el problema puede solucionarse con una serie de operaciones repetitivas (sumar o restar) para maximizar o minimizar). El método de asignación requiere que a cada trabajador se le asigne un y sólo un trabajo, planteando una matriz cuadrada, donde el número de renglones o filas es igual al número de columnas. El proceso de solución no es factible si se asigna un trabajador a dos o más actividades. Si el número de filas no es igual al número de columnas, se adicionan variables ficticias para obtener una tabla balanceada.
4 1.2.1 Aplicación del método húngaro para la solución del modelo de asignación La estructura especial del modelo de asignación hace posible crear un método de solución bastante eficiente llamado método húngaro, el cual se describe a continuación: a. Para encontrar los costos de oportunidad para cada columna se resta el costo mínimo de cada una, de los demás costos de la misma columna. b. Se resta el costo mínimo de cada renglón a los costos de la columna correspondiente. También se puede cambiar el orden, primero renglones y luego columnas. c. Trazar una línea recta en cada columna o renglón que tenga valor cero. Se debe trazar el mínimo de líneas rectas para cubrir todos los valores cero de renglón y columna. Si el mínimo de líneas rectas es igual al número de columnas o renglones, la solución es óptima. d. Asignar cada renglón y columna donde haya sólo un valor cero. e. Si se necesitan menos de m líneas, encuentre el menor elemento no cero, llámelo k, en la matriz de costos reducidos, que no está cubierto por las líneas dibujadas, ahora reste k, de cada elemento no cubierto de la matriz de costos reducidos y sume k a cada elemento de la matriz de costos reducidos cubierto por dos líneas, regrese al paso 3 (trazar las líneas). 1.3 Modelo de transbordo El modelo de transbordo consiste en enviar bienes (cantidades) desde un punto i a únicamente destinos finales j. El envío no se produce entre orígenes o entre destinos, tampoco entre destinos a orígenes. El modelo de trasbordo nos demuestra que resulta mas económico (minimizar costos) enviar a través de nodos intermedios o transitorios antes de llegar al punto de destino final Clases de nodos a. Nodos de oferta pura: Solo actúan como origen o envían. b. Nodos de demanda pura: Solo actúan como destino o reciben. c. Nodos de transbordo: Actúan como origen y destino a la vez, o reciben y envían. Nota importante: en el modelo de transbordo, la cantidad de flujo saliente debe ser exactamente igual a la cantidad de flujo entrante (equilibrar oferta y demanda).
5 1.4 Ejercicios para resolver en clase: Modelo de transporte 1. Una empresa producirá tres productos nuevos. En este momento, cinco de sus plantas tienen exceso de capacidad de producción. El costo unitario respectivo de fabricación del primer producto será de $31, $29, $32, $28 y $29, en las plantas 1, 2, 3, 4 y 5. El costo unitario de fabricación del segundo producto será de $45, $41, $46, $42 y $43 en las plantas respectivas 1, 2, 3, 4 y 5; y para el tercer producto será de $38, $35 y $40 en las plantas respectivas 1, 2 y 3, pero las plantas 4 y 5 no pueden fabricar este producto. Los pronósticos de ventas indican que la producción diaria debe ser 600, 1000 y 800 unidades de los productos 1, 2 y 3, respectivamente. Las plantas 1, 2, 3, 4 y 5 tienen capacidades para producir 400, 600, 400, 600 y 1000 unidades diarias, sin importar el producto o combinación de productos. Suponga que cualquier planta que tiene capacidad y posibilidad de fabricarlos podrá producir cualquier combinación de productos en cualquier cantidad. La gerencia desea asignar los nuevos productos a las plantas con el mínimo costo total de fabricación. a. Formule este problema como un problema de transporte construyendo la tabla de parámetros adecuada. b. Obtenga una solución óptima para este problema, empleando los métodos vistos en clase. 2. Una empresa produce motores eléctricos pequeños para cuatro fabricantes de instrumentos, en cada una de sus tres plantas. Los costos de producción por unidad varían según las ubicaciones debido a diferencias en el equipo de producción y en el rendimiento de los obreros. Los costos de producción por unidad y la capacidad mensual de producción se indican en la siguiente tabla: Planta Costo de producción Capacidad mensual de por unidad producción (unidades) A $ B $ C $ Los pedidos de clientes que deben producirse el siguiente mes se muestran en la tabla que se muestra a continuación: Cliente Demanda (unidades) El costo de abastecimiento de estos clientes varía de una planta a otra. El costo de transporte por unidad aparece en la tabla adjunta:
6 Hacia Desde A $3 $2 $5 $7 B $6 $4 $8 $3 C $9 $1 $5 $4 La gerencia de la empresa debe decidir cuantas unidades se debe producir en cada planta y qué porción de la demanda de cada cliente se surtirá desde cada una de ellas. Se desea minimizar el costo total de producir y transportar los motores para los clientes. a. Formule este problema como un problema de transporte construyendo la tabla de parámetros adecuada. b. Obtenga una solución óptima para este problema, empleando los métodos vistos en clase. 3. Suponga que Inglaterra, Francia y España producen todo el trigo, cebada y avena en el mundo. La demanda mundial de trigo requiere 125 millones de acres (tierra) a la producción de este cereal. De igual manera, se necesitan 60 millones de acres para cebada y 75 millones de acres para avena. La cantidad total de tierra disponible en Inglaterra, Francia, y España es 70, 110 y 80 millones de acres. El número de horas de mano de obra necesarias para producir un acre de trigo en los respectivos países es 18, 13 y 16 horas. La producción de un acre de cebada requiere 15, 12 y 12 horas de mano de obra y la producción de un acre de avena requiere 12, 10 y 16 horas de mano de obra en Inglaterra, Francia y España. El costo de mano de obra por hora en cada país es de $9.00, $7.20 y $9.90 para la producción de trigo, $8.10, $9.00 y $8.40 para la de cebada y $6.90, $7.50 y $6.30 para la avena. El problema es asignar de la tierra en cada país de manera que se cumpla con los requerimientos de alimentación en el mundo y se minimice el costo total de mano de obra. a. Formule este problema como un problema de transporte, construyendo la tabla de parámetros adecuada. b. Obtenga una solución óptima para este problema, empleando cualquiera de los métodos vistos en clase. Modelo de asignación 1. Una empresa adquirió cuatro máquinas nuevas de diferentes tipos. Existen cinco sitios disponibles dentro del taller en donde se podría instalar una máquina. Algunos de ellos son más adecuados que otros para ciertas máquinas en particular por su cercanía a los centros de trabajo que tendrían un flujo intenso de trabajo hacia y desde estas máquinas. Cabe destacar que no habrá flujo de trabajos entre las nuevas máquinas. Por lo tanto, el objetivo es asignar las nuevas máquinas a los lugares disponibles de manera que se minimice el costo total del manejo de materiales, partiendo de la tabla que se muestra a continuación, la cual recoge los costos estimados por unidad de tiempo del manejo de materiales en cuestión, con cada una de las máquinas en los sitios respectivos.
7 Máquinas Localidades Aplique el método húngaro para asignar de forma óptima las máquinas a las respectivas localidades. 2. Considere el problema de asignar cuatro operadores a cuatro máquinas. En la tabla que se muestra seguidamente se dan los costos de asignación en unidades monetarias: Máquinas Localidades El operador 1 no puede ser asignado a la máquina 3. Asimismo, el operador 3 no puede ser asignado a la máquina 4. Obtenga la solución óptima empleando el método húngaro. 3. Se usarán cuatro barcos cargueros para transportar bienes de un puerto a otros cuatro puertos (numerados 1, 2, 3 y 4). Se puede usar cualquier barco para hacer cualquiera de los cuatro viajes. Sin embargo, dadas algunas diferencias entre los barcos y las cargas, el costo total de carga, transporte y descarga de bienes para las distintas combinaciones de barcos y puertos varía mucho. Estos costos se muestran en la siguiente tabla: Barco Puerto $500 $400 $600 $700 2 $600 $600 $700 $500 3 $700 $500 $700 $600 4 $500 $400 $600 $600 El objetivo es asignar los barcos a los puertos en una correspondencia uno a uno de manera que se minimice el costo total de los cuatro envíos. Por lo tanto, formule este problema como un problema de asignación y obtenga la solución óptima. Modelo de transbordo La siguiente red representa las rutas de transporte desde los nodos 1 y 2 a los nodos 5, 6 y 7, pasando por los nodos 3 y 4. Los costos unitarios de transporte se muestran sobre los arcos respectivos:
8 a. Escriba el modelo de programación lineal asociado. b. Escriba el modelo de transbordo asociado, especificando el tamaño del amortiguamiento y las cantidades de oferta y demanda. c. Obtenga una solución óptima para la red, mediante la aplicación del método de aproximaciones de Vogel. d. Replantee la red con los resultados obtenidos y determine cuál es la ruta más óptima. e. Convierta el modelo de transbordo de la parte b en un modelo regular de transporte, exactamente con dos fuentes y tres destinos. f. Demuestre cómo la solución de la parte e proporciona una solución factible a la red original.
Práctica Método Dual simplex y Método de transporte
 Práctica Método Dual simplex y Método de transporte a) Resolver con el método Dual Simplex: 1. Maximizar Z= 2000X1 + 1000X2 3X1 + X2 >= 40 2X1 + 2X2 >= 60 X1 + X2 >= 0 2. Maximizar Z= 5X1 + 6X2 X1 + 9X2
Práctica Método Dual simplex y Método de transporte a) Resolver con el método Dual Simplex: 1. Maximizar Z= 2000X1 + 1000X2 3X1 + X2 >= 40 2X1 + 2X2 >= 60 X1 + X2 >= 0 2. Maximizar Z= 5X1 + 6X2 X1 + 9X2
Modelos de Transporte: Problemas de Asignación. M. En C. Eduardo Bustos Farías
 Modelos de Transporte: Problemas de asignación M. En C. Eduardo Bustos Farías as Problemas de Asignación Problemas de Asignación: Son problemas balanceados de transporte en los cuales todas las ofertas
Modelos de Transporte: Problemas de asignación M. En C. Eduardo Bustos Farías as Problemas de Asignación Problemas de Asignación: Son problemas balanceados de transporte en los cuales todas las ofertas
MODELOS DE PROGRAMACION LINEAL VARIABLES Xij
 MODELOS DE PROGRAMACION LINEAL VARIABLES Xij 1. Construcción de modelos de programación lineal con variables Xij. 2. Aplicaciones en finanzas, marketing, producción. 3. Modelos de transporte y transbordo.
MODELOS DE PROGRAMACION LINEAL VARIABLES Xij 1. Construcción de modelos de programación lineal con variables Xij. 2. Aplicaciones en finanzas, marketing, producción. 3. Modelos de transporte y transbordo.
UNIDAD DOS MODELOS DE TRANSPORTE
 Ing. César Urquizú UNIDAD DOS MODELOS DE TRANSPORTE Ing. César Urquizú Modelos de Transporte Método de la Esquina Noroeste Método del Costo Mínimo o Menor Método de Aproximación de Vogel (MAV) Método del
Ing. César Urquizú UNIDAD DOS MODELOS DE TRANSPORTE Ing. César Urquizú Modelos de Transporte Método de la Esquina Noroeste Método del Costo Mínimo o Menor Método de Aproximación de Vogel (MAV) Método del
TRANSPORTE Y TRANSBORDO
 TRANSPORTE Y TRANSBORDO En ésta semana estudiaremos un modelo particular de problema de programación lineal, uno en el cual su resolución a través del método simplex es dispendioso, pero que debido a sus
TRANSPORTE Y TRANSBORDO En ésta semana estudiaremos un modelo particular de problema de programación lineal, uno en el cual su resolución a través del método simplex es dispendioso, pero que debido a sus
X m,j. X m,n C m,n C m,j. X m, C m,1. X i,n. C i,n MODELO DE TRANSPORTE. Matemáticamente:
 MODELO DE TRANSPORTE El modelo de transporte se define como una técnica que determina un programa de transporte de productos o mercancías desde unas fuentes hasta los diferentes destinos al menor costo
MODELO DE TRANSPORTE El modelo de transporte se define como una técnica que determina un programa de transporte de productos o mercancías desde unas fuentes hasta los diferentes destinos al menor costo
1. Considerar el problema de transporte definido por (Origen) a= (6, 7, 8), (Destino) b= (6, 9, 4, 2) y
 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono 2532-2668/Telefax 2532-2684 INVESTIGACIÓN DE OPERACIONES I TAREA Problemas de Transporte, transbordo y asignación Prof. :
UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono 2532-2668/Telefax 2532-2684 INVESTIGACIÓN DE OPERACIONES I TAREA Problemas de Transporte, transbordo y asignación Prof. :
Modelos de Transporte: Problemas de asignación. M. En C. Eduardo Bustos Farías
 Modelos de Transporte: Problemas de asignación M. En C. Eduardo Bustos Farías as Problemas de Asignación 2 Problemas de Asignación: Son problemas balanceados de transporte en los cuales todas las ofertas
Modelos de Transporte: Problemas de asignación M. En C. Eduardo Bustos Farías as Problemas de Asignación 2 Problemas de Asignación: Son problemas balanceados de transporte en los cuales todas las ofertas
PROGRAMACION DE REDES. MODELOS DE TRANSPORTE
 PROGRAMACION DE REDES. MODELOS DE TRANSPORTE El modelo de transporte o modelo de distribución es un ejemplo de un problema de optimización de redes. Se aplican para resolver ciertos tipos de problemas
PROGRAMACION DE REDES. MODELOS DE TRANSPORTE El modelo de transporte o modelo de distribución es un ejemplo de un problema de optimización de redes. Se aplican para resolver ciertos tipos de problemas
El Problema de Transporte
 El Problema de Transporte INVESTIGACIÓN DE OPERACIONES I Maestro Ing. Julio Rito Vargas Avilés Julio 202 Problema de Transporte Es un caso especial de problema de programación lineal (PPL), para el cual
El Problema de Transporte INVESTIGACIÓN DE OPERACIONES I Maestro Ing. Julio Rito Vargas Avilés Julio 202 Problema de Transporte Es un caso especial de problema de programación lineal (PPL), para el cual
Investigación de Operaciones I. Problemas de Asignación
 Investigación de Operaciones I Problemas de Asignación MSc. Ing. Julio Rito Vargas II cuatrimestre Introducción Los problemas de asignación incluyen aplicaciones tales como asignar personas a tareas. Aunque
Investigación de Operaciones I Problemas de Asignación MSc. Ing. Julio Rito Vargas II cuatrimestre Introducción Los problemas de asignación incluyen aplicaciones tales como asignar personas a tareas. Aunque
PROBLEMA DE FLUJO DE COSTO MINIMO.
 PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
UNIDAD DOS MODELO DE ASIGNACIÓN
 Ing. César Urquizú UNIDAD DOS MODELO DE ASIGNACIÓN Ing. César Urquizú Modelos de Transporte Método de la Esquina Noroeste Método del Costo Mínimo o Menor Método de Aproximación de Vogel (MAV) Método del
Ing. César Urquizú UNIDAD DOS MODELO DE ASIGNACIÓN Ing. César Urquizú Modelos de Transporte Método de la Esquina Noroeste Método del Costo Mínimo o Menor Método de Aproximación de Vogel (MAV) Método del
Problema 1. Oferta /15/ /20/0 5 40/30/0. Demanda 45/30/10/0 20/0 30/0 30/
 Problema 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35, 50 y 40 millones de [kwh] respectivamente.
Problema 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35, 50 y 40 millones de [kwh] respectivamente.
El Problema de Transporte
 El Problema de Transporte INVESTIGACIÓN DE OPERACIONES I Maestro Ing. Julio Rito Vargas Avilés Octubre 2008 Problema de Transporte Es un caso especial de problema de programación lineal (PPL), para el
El Problema de Transporte INVESTIGACIÓN DE OPERACIONES I Maestro Ing. Julio Rito Vargas Avilés Octubre 2008 Problema de Transporte Es un caso especial de problema de programación lineal (PPL), para el
Modelos de Transporte: método de la esquina noroeste. M. En C. Eduardo Bustos Farías
 Modelos de Transporte: método de la esquina noroeste M. En C. Eduardo Bustos Farías as Problemas de transporte Surge cuando se necesita un modelo costo-efectividad que permita transportar ciertos bienes
Modelos de Transporte: método de la esquina noroeste M. En C. Eduardo Bustos Farías as Problemas de transporte Surge cuando se necesita un modelo costo-efectividad que permita transportar ciertos bienes
Programación Lineal Modelo de transporte Asignación
 Programación Lineal Modelo de transporte Asignación Curso: Investigación de Operaciones Ing. Javier Villatoro MODELO DE ASIGNACIÓN Modelo de Asignación Consiste en asignar al mínimo costo los requerimientos
Programación Lineal Modelo de transporte Asignación Curso: Investigación de Operaciones Ing. Javier Villatoro MODELO DE ASIGNACIÓN Modelo de Asignación Consiste en asignar al mínimo costo los requerimientos
- Contenido UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-NORTE SEDE ESTELI. Carrera: Ingeniería de Sistemas
 UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-NORTE SEDE ESTELI Carrera: Ingeniería de Sistemas Nombre de la asignatura: Investigación de Operaciones I Año académico: Tercer año Semestre: Sexto - Contenido I-
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-NORTE SEDE ESTELI Carrera: Ingeniería de Sistemas Nombre de la asignatura: Investigación de Operaciones I Año académico: Tercer año Semestre: Sexto - Contenido I-
El Problema del Transporte M.C. Ing. Julio Rito Vargas Avilés.
 Universidad Nacional de Ingeniería Sede: UNI-Norte II Semestre 2008 Investigación de Operaciones I El Problema del Transporte M.C. Ing. Julio Rito Vargas Avilés. martes, 21 de octubre de 2008 El Problema
Universidad Nacional de Ingeniería Sede: UNI-Norte II Semestre 2008 Investigación de Operaciones I El Problema del Transporte M.C. Ing. Julio Rito Vargas Avilés. martes, 21 de octubre de 2008 El Problema
Dirección de Operaciones
 Dirección de Operaciones 1 Sesión No. 9 Nombre: Problemas de transporte y asignación. Primera parte. Objetivo Al finalizar la sesión, el alumno será capaz de Contextualización Cuál es el valor de estudiar
Dirección de Operaciones 1 Sesión No. 9 Nombre: Problemas de transporte y asignación. Primera parte. Objetivo Al finalizar la sesión, el alumno será capaz de Contextualización Cuál es el valor de estudiar
Unidad 6 Método de transporte
 Unidad 6 Método de transporte Como ya se vio en la unidad 3, los problemas de transporte son problemas de programación lineal (pl), pero con una estructura muy particular de la matriz de los coeficientes
Unidad 6 Método de transporte Como ya se vio en la unidad 3, los problemas de transporte son problemas de programación lineal (pl), pero con una estructura muy particular de la matriz de los coeficientes
PROBLEMA DE FLUJO DE COSTO MINIMO.
 PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
Fundamentos de Investigación de Operaciones Certamen # 2
 Certamen # 2 Profesores: María Cristina Riff & Esteban Sáez 6 de junio de 2003 1. Una pequeña empresa constructora debe construir 3 casas en los próximos 5 meses. Una vez que alguna de las casas está terminada,
Certamen # 2 Profesores: María Cristina Riff & Esteban Sáez 6 de junio de 2003 1. Una pequeña empresa constructora debe construir 3 casas en los próximos 5 meses. Una vez que alguna de las casas está terminada,
Modelos de Transporte: método de la esquina noroeste. M. En C. Eduardo Bustos Farías
 Modelos de Transporte: método de la esquina noroeste M. En C. Eduardo Bustos Farías as LA REGLA DE LA ESQUINA NOROESTE 2 Esta regla nos permite encontrar una solución n factible básica b inicial (SFBI),
Modelos de Transporte: método de la esquina noroeste M. En C. Eduardo Bustos Farías as LA REGLA DE LA ESQUINA NOROESTE 2 Esta regla nos permite encontrar una solución n factible básica b inicial (SFBI),
UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono /Telefax
 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono 2532-2668/Telefax 2532-2684 INVESTIGACIÓN DE OPERACIONES EJERCICIOS PARA RESOLVER Problemas de Transporte y Transborde Profesor:
UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono 2532-2668/Telefax 2532-2684 INVESTIGACIÓN DE OPERACIONES EJERCICIOS PARA RESOLVER Problemas de Transporte y Transborde Profesor:
Tema 7: Problemas clásicos de Programación Lineal
 Tema 7: Problemas clásicos de Programación Lineal 1.- Características generales de un problema de transporte y asignación Surgen con frecuencia en diferentes contextos de la vida real. Requieren un número
Tema 7: Problemas clásicos de Programación Lineal 1.- Características generales de un problema de transporte y asignación Surgen con frecuencia en diferentes contextos de la vida real. Requieren un número
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
SOLUCION DE MODELOS DE PROGRAMACION LINEAL EN UNA HOJA DE CALCULO. PROBLEMAS DE TRANSPORTE Y ASIGNACION.
 UNIVERSIDAD NACIONAL DE LA PLATA FACULTAD DE INGENIERÍA DEPARTAMENTO DE INGENIERÍA DE LA PRODUCCIÓN INGENIERÍA INDUSTRIAL SOLUCION DE MODELOS DE PROGRAMACION LINEAL EN UNA HOJA DE CALCULO. PROBLEMAS DE
UNIVERSIDAD NACIONAL DE LA PLATA FACULTAD DE INGENIERÍA DEPARTAMENTO DE INGENIERÍA DE LA PRODUCCIÓN INGENIERÍA INDUSTRIAL SOLUCION DE MODELOS DE PROGRAMACION LINEAL EN UNA HOJA DE CALCULO. PROBLEMAS DE
INVESTIGACIÓN OPERATIVA
 FACULTAD DE INGENIERÍA Y ARQUITECTURA ESCUELA PROFESIONAL DE INGENIERÍA DE SISTEMAS INVESTIGACIÓN OPERATIVA Mg Jessica Pérez Rivera PROBLEMAS DE TRANSPORTE Y ASIGNACIÓN Las aplicaciones de la programación
FACULTAD DE INGENIERÍA Y ARQUITECTURA ESCUELA PROFESIONAL DE INGENIERÍA DE SISTEMAS INVESTIGACIÓN OPERATIVA Mg Jessica Pérez Rivera PROBLEMAS DE TRANSPORTE Y ASIGNACIÓN Las aplicaciones de la programación
EL PROBLEMA DE TRANSPORTE
 1 EL PROBLEMA DE TRANSPORTE La TÉCNICA DE TRANSPORTE se puede aplicar a todo problema físico compatible con el siguiente esquema: FUENTES DESTINOS TRANSPORTE DE UNIDADES Donde transporte de unidades puede
1 EL PROBLEMA DE TRANSPORTE La TÉCNICA DE TRANSPORTE se puede aplicar a todo problema físico compatible con el siguiente esquema: FUENTES DESTINOS TRANSPORTE DE UNIDADES Donde transporte de unidades puede
Universidad Autónoma de Guadalajara 3.1 Modelo de Transporte. Nomenclatura
 UNIDAD III. ANÁLISIS DE REDES OBJETIVO DE APRENDIZAJE: El alumno identificará y analizará problemas de optimización de funciones y recursos para mejorar la operación de una organización. Modelos de transporte
UNIDAD III. ANÁLISIS DE REDES OBJETIVO DE APRENDIZAJE: El alumno identificará y analizará problemas de optimización de funciones y recursos para mejorar la operación de una organización. Modelos de transporte
Optimización y Programación Lineal
 Optimización y Programación Lineal El Problema del Transporte Departamento de Matemáticas ITESM El Problema del Transporte TC3001 - p. 1/25 Veamos ahora el problema del transporte, cuál es su formulación
Optimización y Programación Lineal El Problema del Transporte Departamento de Matemáticas ITESM El Problema del Transporte TC3001 - p. 1/25 Veamos ahora el problema del transporte, cuál es su formulación
Contenido: Solución algebraica a los problemas de programación lineal con el método simplex.
 Tema II: Programación Lineal Contenido: Solución algebraica a los problemas de programación lineal con el método simplex. Introducción El método simplex resuelve cualquier problema de PL con un conjunto
Tema II: Programación Lineal Contenido: Solución algebraica a los problemas de programación lineal con el método simplex. Introducción El método simplex resuelve cualquier problema de PL con un conjunto
Planteamiento de problemas de programación lineal
 Planteamiento de problemas de programación lineal M. En C. Eduardo Bustos Farías 1 Ejemplo. Protac Programación de máquinas M. En C. Eduardo Bustos Farías 2 M. En C. Eduardo Bustos Farías 3 M. En C. Eduardo
Planteamiento de problemas de programación lineal M. En C. Eduardo Bustos Farías 1 Ejemplo. Protac Programación de máquinas M. En C. Eduardo Bustos Farías 2 M. En C. Eduardo Bustos Farías 3 M. En C. Eduardo
EJERCICIOS DE PROGRAMACIÓN LINEAL
 EJERCICIOS DE PROGRAMACIÓN LINEAL 1 Un fabricante desea encontrar la producción semanal óptima de los artículos A, B y C para maximizar sus beneficios. Las ganancias por unidad de estos artículos son:
EJERCICIOS DE PROGRAMACIÓN LINEAL 1 Un fabricante desea encontrar la producción semanal óptima de los artículos A, B y C para maximizar sus beneficios. Las ganancias por unidad de estos artículos son:
Práctico N 5 Parte a: Programación lineal
 U.N.C.P.B.A FACULTAD DE INGENIERÍA PROCESOS QUÍMICOS II Práctico N 5 Parte a: Programación lineal Planteo n 1: Supóngase que una compañía fabrica 2 conjuntos xx e yy. Cada unidad de los respectivos productos
U.N.C.P.B.A FACULTAD DE INGENIERÍA PROCESOS QUÍMICOS II Práctico N 5 Parte a: Programación lineal Planteo n 1: Supóngase que una compañía fabrica 2 conjuntos xx e yy. Cada unidad de los respectivos productos
IN34A - Optimización
 IN34A - Optimización Modelos de Programación Lineal Leonardo López H. lelopez@ing.uchile.cl Primavera 2008 1 / 24 Contenidos Programación Lineal Continua Problema de Transporte Problema de Localización
IN34A - Optimización Modelos de Programación Lineal Leonardo López H. lelopez@ing.uchile.cl Primavera 2008 1 / 24 Contenidos Programación Lineal Continua Problema de Transporte Problema de Localización
Examen de Investigación Operativa (Plan 96) Febrero de er Parcial
 Examen de Investigación Operativa (Plan 96) Febrero de 2010 1 er Parcial Solución del Ejercicio 1. Definimos las variables de decisión ½ 1, si se coloca una cámara en el punto de localización i x i = 0,
Examen de Investigación Operativa (Plan 96) Febrero de 2010 1 er Parcial Solución del Ejercicio 1. Definimos las variables de decisión ½ 1, si se coloca una cámara en el punto de localización i x i = 0,
II. INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES
 II. INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El estudiante, conocerá los fundamentos en que se basan las herramientas de la investigación de operaciones para la toma de decisiones.
II. INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El estudiante, conocerá los fundamentos en que se basan las herramientas de la investigación de operaciones para la toma de decisiones.
El Problema del Transporte
 ASIGNATURA PROGRAMACIÓN LINEAL El Problema del Transporte Maestro Ing. Julio Rito Vargas Avilés Octubre 2014 1 Problema de Transporte Es un caso especial de problema de programación lineal (PPL), para
ASIGNATURA PROGRAMACIÓN LINEAL El Problema del Transporte Maestro Ing. Julio Rito Vargas Avilés Octubre 2014 1 Problema de Transporte Es un caso especial de problema de programación lineal (PPL), para
1 $10 $0 $20 $11 15 2 $12 $7 $9 $20 25 3 $0 $14 $16 $18 10 Total demanda
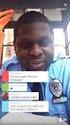 UNIDAD V. ALGORITMOS ESPECIALES 5.4. Métodos de aproximación para obtener una solución básica inicial Para resolver problemas de transporte se debe crear una solución básica inicial, la obtención de esta
UNIDAD V. ALGORITMOS ESPECIALES 5.4. Métodos de aproximación para obtener una solución básica inicial Para resolver problemas de transporte se debe crear una solución básica inicial, la obtención de esta
PROBLEMA 1. Considere el siguiente problema de programación lineal:
 PROBLEMA 1 Considere el siguiente problema de programación lineal: Sean h1 y h2 las variables de holgura correspondientes a la primera y segunda restricción, respectivamente, de manera que al aplicar el
PROBLEMA 1 Considere el siguiente problema de programación lineal: Sean h1 y h2 las variables de holgura correspondientes a la primera y segunda restricción, respectivamente, de manera que al aplicar el
Fundamentos de Investigación de Operaciones Modelos de Grafos
 Fundamentos de Investigación de Operaciones de junio de 00 Muchos problemas de optimización puedes ser analizados y resueltos a través de representaciones gráficas. Tal es el caso de los problemas de planificación
Fundamentos de Investigación de Operaciones de junio de 00 Muchos problemas de optimización puedes ser analizados y resueltos a través de representaciones gráficas. Tal es el caso de los problemas de planificación
Problemas de Transbordo
 Universidad Nacional de Ingeniería UNI-Norte Problemas de Transbordo III Unidad Temática MSc. Ing. Julio Rito Vargas II semestre 2008 El problema de transbordo Un problema de transporte permite sólo envíos
Universidad Nacional de Ingeniería UNI-Norte Problemas de Transbordo III Unidad Temática MSc. Ing. Julio Rito Vargas II semestre 2008 El problema de transbordo Un problema de transporte permite sólo envíos
Métodos de distribución
 Métodos de distribución Ejercicios: 1)Que es una red de distribución. Describa sus componentes. 2)Enuncie las condiciones que debe satisfacer una solución inicial factible básica. 3)Detalle el procedimiento
Métodos de distribución Ejercicios: 1)Que es una red de distribución. Describa sus componentes. 2)Enuncie las condiciones que debe satisfacer una solución inicial factible básica. 3)Detalle el procedimiento
Problemas de transporte, asignación y trasbordo
 Problemas de transporte, asignación y trasbordo 1. Plantear un problema de transporte Tiene como objetivo encontrar el mejor plan de distribución, generalmente minimizando el coste. Un problema está equilibrado
Problemas de transporte, asignación y trasbordo 1. Plantear un problema de transporte Tiene como objetivo encontrar el mejor plan de distribución, generalmente minimizando el coste. Un problema está equilibrado
La solución inicial puede ser óptima o no, la forma de saberlo es realizando la prueba de optimalidad que consiste en los siguientes pasos:
 Solución óptima a los problemas de transporte La solución inicial puede ser óptima o no, la forma de saberlo es realizando la prueba de optimalidad que consiste en los siguientes pasos: a) Calcular los
Solución óptima a los problemas de transporte La solución inicial puede ser óptima o no, la forma de saberlo es realizando la prueba de optimalidad que consiste en los siguientes pasos: a) Calcular los
Universidad Nacional de Ingeniería
 Universidad Nacional de Ingeniería Recinto Universitario Augusto Cesar Sandino Uni - RUACS Trabajo de Investigación de Operaciones Orientado Por: Ing. Mario Pastrana Moreno Carrera: Ingeniería de Sistemas
Universidad Nacional de Ingeniería Recinto Universitario Augusto Cesar Sandino Uni - RUACS Trabajo de Investigación de Operaciones Orientado Por: Ing. Mario Pastrana Moreno Carrera: Ingeniería de Sistemas
Trabajo Práctico Nº 8: Programación Lineal
 Trabajo Práctico Nº 8: Programación Lineal 1. Utilice el método gráfico para resolver los siguientes problemas: a. Maximizar Z = x1 + x2 x 1 + 5x 2 = 0 b. Maximizar
Trabajo Práctico Nº 8: Programación Lineal 1. Utilice el método gráfico para resolver los siguientes problemas: a. Maximizar Z = x1 + x2 x 1 + 5x 2 = 0 b. Maximizar
FUNDACION UNIVERSITARIA LOS LIBERTADORES DEPARTAMENTO DE CIENCIAS GUÍA INVESTIGACIÓN DE OPERACIONES
 FUNDACION UNIVERSITARIA LOS LIBERTADORES DEPARTAMENTO DE CIENCIAS GUÍA INVESTIGACIÓN DE OPERACIONES AUTOR: Arturo Yesid Córdoba Berrio Ing. Industrial Administrador de Empresas Especialización en Transporte
FUNDACION UNIVERSITARIA LOS LIBERTADORES DEPARTAMENTO DE CIENCIAS GUÍA INVESTIGACIÓN DE OPERACIONES AUTOR: Arturo Yesid Córdoba Berrio Ing. Industrial Administrador de Empresas Especialización en Transporte
Optimización y Programación Lineal
 Optimización y Programación Lineal Método Simplex: Minimización 3 de enero de Método Simplex: Minimización () Optimización y Programación Lineal 3 de enero de / 4 Minimización Minimización En la definición
Optimización y Programación Lineal Método Simplex: Minimización 3 de enero de Método Simplex: Minimización () Optimización y Programación Lineal 3 de enero de / 4 Minimización Minimización En la definición
UNIDAD III. INVESTIGACIÓN DE OPERACIONES
 UNIDAD III. INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El alumno resolverá problemas utilizando la programación lineal y de proyectos para sugerir cursos de acción de mejora en las empresas turísticas
UNIDAD III. INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El alumno resolverá problemas utilizando la programación lineal y de proyectos para sugerir cursos de acción de mejora en las empresas turísticas
1. Considerar el problema de transporte definido por (Origen) a= (6, 7, 8), (Destino) b= (6, 9, 4, 2) y 4 1 5 6 C = 2 8 9 3.
 UNIVERSIDAD DE MANAGUA CURSO: PROGRAMACIÓN LINEAL TAREA # 2 Problemas de Transporte, transbordo y asignación Prof. : MSc. Julio Rito Vargas Avilés III C 2015 1. Considerar el problema de transporte definido
UNIVERSIDAD DE MANAGUA CURSO: PROGRAMACIÓN LINEAL TAREA # 2 Problemas de Transporte, transbordo y asignación Prof. : MSc. Julio Rito Vargas Avilés III C 2015 1. Considerar el problema de transporte definido
UNIDAD II. PROGRAMACIÓN LINEAL
 UNIDAD II. PROGRAMACIÓN LINEAL OBJETIVO DE APRENDIZAJE: El alumno identificará y analizará problemas de optimización de funciones y recursos para mejorar la operación de una organización. Introducción
UNIDAD II. PROGRAMACIÓN LINEAL OBJETIVO DE APRENDIZAJE: El alumno identificará y analizará problemas de optimización de funciones y recursos para mejorar la operación de una organización. Introducción
Investigación de Operaciones
 En el Cuadro de Transporte, las variables básicas corresponden a asignaciones, por lo que habrá (m+n) asignaciones. En algunos problemas de transporte, se presentan situaciones en las que se requerirán
En el Cuadro de Transporte, las variables básicas corresponden a asignaciones, por lo que habrá (m+n) asignaciones. En algunos problemas de transporte, se presentan situaciones en las que se requerirán
INVESTIGACION DE OPERACIONES (HAMDY A. TAHA) PROBLEMAS DE PLANTEAMIENTO DEL CAPITULO II
 INVESTIGACION DE OPERACIONES (HAMDY A. TAHA) PROBLEMAS DE PLANTEAMIENTO DEL CAPITULO II (TAHA) 2.2-1 Se procesan tres productos a través de tres opciones diferentes. Los tiempos en minutos requeridos por
INVESTIGACION DE OPERACIONES (HAMDY A. TAHA) PROBLEMAS DE PLANTEAMIENTO DEL CAPITULO II (TAHA) 2.2-1 Se procesan tres productos a través de tres opciones diferentes. Los tiempos en minutos requeridos por
Ejercicios Propuestos
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA ÁREA DE TECNOLOGÍA DEPARTAMENTO DE GERENCIA INVESTIGACIÓN DE OPERACIONES PROFESOR: Dr. JUAN LUGO MARÍN Tema No. 1 Modelación Matemática. Programación
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA ÁREA DE TECNOLOGÍA DEPARTAMENTO DE GERENCIA INVESTIGACIÓN DE OPERACIONES PROFESOR: Dr. JUAN LUGO MARÍN Tema No. 1 Modelación Matemática. Programación
Producto Maquina A Maquina B Acabado Muñecas 2 hr 1 hr 1 hr Soldados 1 hr 1 hr 3 hr
 Nombre: UNIVERSIDAD NACIONAL AUTONOMA DE HONDURAS METODOS CUANTITATIVOS II EXAMEN PARCIAL I /3/7 Sección # Cuenta: Catedrático: Desarrolle en forma clara y ordenada lo que a continuación se le pide:.-
Nombre: UNIVERSIDAD NACIONAL AUTONOMA DE HONDURAS METODOS CUANTITATIVOS II EXAMEN PARCIAL I /3/7 Sección # Cuenta: Catedrático: Desarrolle en forma clara y ordenada lo que a continuación se le pide:.-
UNIDAD 5. Problema de Transporte
 UNIDAD 5 Problema de Transporte En matemáticas y economía, un problema de transporte es un caso particular de problema de programación lineal en el cual se debe minimizar el coste del abastecimiento a
UNIDAD 5 Problema de Transporte En matemáticas y economía, un problema de transporte es un caso particular de problema de programación lineal en el cual se debe minimizar el coste del abastecimiento a
UNIVERSIDAD DE MANAGUA Asignatura: Investigación de Operaciones I. Prof.: MSc. Ing. Julio Rito Vargas Avilés junio 2012
 UNIVERSIDAD DE MANAGUA Asignatura: Investigación de Operaciones I Prof.: MSc. Ing. Julio Rito Vargas Avilés junio 2012 Problemas de PL con varias variables Análisis de Sensibilidad Problema 1: Ken & Larry
UNIVERSIDAD DE MANAGUA Asignatura: Investigación de Operaciones I Prof.: MSc. Ing. Julio Rito Vargas Avilés junio 2012 Problemas de PL con varias variables Análisis de Sensibilidad Problema 1: Ken & Larry
Unidad 5 Modelo de transporte
 Unidad 5 Modelo de transporte Objetivos: Al nalizar la unidad, el alumno: Construirá el modelo de transporte asociado a un problema. Resolverá problemas de transporte con los métodos de la esquina noroeste,
Unidad 5 Modelo de transporte Objetivos: Al nalizar la unidad, el alumno: Construirá el modelo de transporte asociado a un problema. Resolverá problemas de transporte con los métodos de la esquina noroeste,
Modelos de Redes: Problema del flujo máximom. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Problema del flujo máimom M. En C. Eduardo Bustos Farías as Problema del flujo máimom Problema del flujo máimom Este modelo se utiliza para reducir los embotellamientos entre ciertos
Modelos de Redes: Problema del flujo máimom M. En C. Eduardo Bustos Farías as Problema del flujo máimom Problema del flujo máimom Este modelo se utiliza para reducir los embotellamientos entre ciertos
Tema No. 6 Transporte y Asignación. Introducción
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA ÁREA DE TECNOLOGÍA DEPARTAMENTO DE GERENCIA INVESTIGACIÓN DE OPERACIONES PROFESOR: Dr. JUAN LUGO MARÍN Tema No. 6 Transporte y Asignación Introducción
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA ÁREA DE TECNOLOGÍA DEPARTAMENTO DE GERENCIA INVESTIGACIÓN DE OPERACIONES PROFESOR: Dr. JUAN LUGO MARÍN Tema No. 6 Transporte y Asignación Introducción
Capítulo Cuatro PLANEACIÓN AGREGADA DE LA PRODUCCIÓN
 Capítulo Cuatro 1 PLANEACIÓN AGREGADA DE LA PRODUCCIÓN 2 La esencia de la gestión de la producción es la habilidad para gestionar la demanda R. B. Chase y F. R. Jacobs 3 4 5 Antecedentes 6 La planeación
Capítulo Cuatro 1 PLANEACIÓN AGREGADA DE LA PRODUCCIÓN 2 La esencia de la gestión de la producción es la habilidad para gestionar la demanda R. B. Chase y F. R. Jacobs 3 4 5 Antecedentes 6 La planeación
PROBLEMAS DE PROGRAMACIÓN ENTERA I
 Problemas de Programación Entera I 1 PROBLEMAS DE PROGRAMACIÓN ENTERA I 1. Un departamento ha dispuesto 2 millones de pesetas de su presupuesto general para la compra de material informático, con el que
Problemas de Programación Entera I 1 PROBLEMAS DE PROGRAMACIÓN ENTERA I 1. Un departamento ha dispuesto 2 millones de pesetas de su presupuesto general para la compra de material informático, con el que
METODO DE LA ESQUINA NOR-OESTE,
 METODO DE LA ESQUINA NOR-OESTE, MODELO DE TRANSPORTE LAURA SANDOVAL TORRES DANIELA RAMIREZ NOREÑA INTRODUCCIÓN Método capaz de solucionar problemas de TRANSORTE O DISTRIBUCIÓN mediante una solución básica
METODO DE LA ESQUINA NOR-OESTE, MODELO DE TRANSPORTE LAURA SANDOVAL TORRES DANIELA RAMIREZ NOREÑA INTRODUCCIÓN Método capaz de solucionar problemas de TRANSORTE O DISTRIBUCIÓN mediante una solución básica
Tema 1 Introducción. José R. Berrendero. Departamento de Matemáticas Universidad Autónoma de Madrid
 Tema 1 Introducción José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Información de contacto José Ramón Berrendero Díaz Correo electrónico: joser.berrendero@uam.es Teléfono:
Tema 1 Introducción José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Información de contacto José Ramón Berrendero Díaz Correo electrónico: joser.berrendero@uam.es Teléfono:
Control 2 IN mayo 2009
 Profs: Auxs: Daniel Espinoza Gonzalo Romero Víctor Bucarey Nelson Devia Jocelyn González Daniel Lillo Fernando Solari Control 2 IN3701 28 mayo 2009 Pregunta 1 La empresa de pigmentos LILLO & Co. debe decidir
Profs: Auxs: Daniel Espinoza Gonzalo Romero Víctor Bucarey Nelson Devia Jocelyn González Daniel Lillo Fernando Solari Control 2 IN3701 28 mayo 2009 Pregunta 1 La empresa de pigmentos LILLO & Co. debe decidir
INVESTIGACION DE OPERACIONES:
 METODO SIMPLEX El algoritmo símplex fue descubierto por el matemático norteamericano George Bernard Dantzig en 1947, es una técnica para dar soluciones numéricas a problema de programación lineal Un problema
METODO SIMPLEX El algoritmo símplex fue descubierto por el matemático norteamericano George Bernard Dantzig en 1947, es una técnica para dar soluciones numéricas a problema de programación lineal Un problema
Programación de producción.
 Programación de producción. 1. Sensibilización 2. Conceptos 3. Taller práctico AGENDA PRESENTACIÓN DE LA DOCENTE LUZ ADRIANA GALEANO JARAMILLO (lucilugaleano@hotmail.com) COLEGIO TERESIANO (1994) INGENIERA
Programación de producción. 1. Sensibilización 2. Conceptos 3. Taller práctico AGENDA PRESENTACIÓN DE LA DOCENTE LUZ ADRIANA GALEANO JARAMILLO (lucilugaleano@hotmail.com) COLEGIO TERESIANO (1994) INGENIERA
Programación Lineal. María Muñoz Guillermo Matemáticas I U.P.C.T. M. Muñoz (U.P.C.T.) Programación Lineal Matemáticas I 1 / 13
 Programación Lineal María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Programación Lineal Matemáticas I 1 / 13 Qué es la Programación Lineal? Introducción La Programación
Programación Lineal María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Programación Lineal Matemáticas I 1 / 13 Qué es la Programación Lineal? Introducción La Programación
Formulación del Modelo de Transporte.
 Formulación del Modelo de Transporte La programación lineal es un campo tan amplio que se extiende a subclases de problemas para los cuales existen métodos de solución especiales Una de estas subclases
Formulación del Modelo de Transporte La programación lineal es un campo tan amplio que se extiende a subclases de problemas para los cuales existen métodos de solución especiales Una de estas subclases
Curso: Teoría, Algoritmos y Aplicaciones de Gestión Logística. Modelos de Ubicación de Instalaciones
 Curso: Teoría, Algoritmos y Aplicaciones de Gestión Logística. Modelos de Ubicación de Instalaciones Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad
Curso: Teoría, Algoritmos y Aplicaciones de Gestión Logística. Modelos de Ubicación de Instalaciones Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad
Programación Lineal. El método simplex
 Programación Lineal El método simplex El método simplex es una herramienta algebraica que permite localizar de manera eficiente el óptimo entre los puntos extremos de una solución a un problema de programación
Programación Lineal El método simplex El método simplex es una herramienta algebraica que permite localizar de manera eficiente el óptimo entre los puntos extremos de una solución a un problema de programación
Práctica N 6 Modelos de Programación Lineal Entera
 Práctica N 6 Modelos de Programación Lineal Entera 6.1 Una empresa textil fabrica 3 tipos de ropa: camisas, pantalones y shorts. Las máquinas necesarias para la confección deben ser alquiladas a los siguientes
Práctica N 6 Modelos de Programación Lineal Entera 6.1 Una empresa textil fabrica 3 tipos de ropa: camisas, pantalones y shorts. Las máquinas necesarias para la confección deben ser alquiladas a los siguientes
MODELOS DE TRANSPORTE
 Universidad Mariano Gálvez de Guatemala Centro Universitario de Escuintla Facultad de Ciencias de la Administración Maestría en Dirección y Gestión del Recurso Humano Curso Modelos para la toma de decisiones
Universidad Mariano Gálvez de Guatemala Centro Universitario de Escuintla Facultad de Ciencias de la Administración Maestría en Dirección y Gestión del Recurso Humano Curso Modelos para la toma de decisiones
UNIVERSIDAD DE MANAGUA Al más alto nivel
 UNIVERSIDAD DE MANAGUA Al más alto nivel Investigación de Operaciones Encuentro #3 Tema: Optimización de Redes: El problema del árbol de expansión mínima y el problema de costo mínimo Prof.: MSc. Julio
UNIVERSIDAD DE MANAGUA Al más alto nivel Investigación de Operaciones Encuentro #3 Tema: Optimización de Redes: El problema del árbol de expansión mínima y el problema de costo mínimo Prof.: MSc. Julio
OPTIMIZACION DETERMINISTICA
 OPTIMIZACION DETERMINISTICA 1 PROBLEMA GENERAL Además de analizar los flujos de caja de las las alternativas de inversión, también se debe analizar la forma como se asignan recursos limitados entre actividades
OPTIMIZACION DETERMINISTICA 1 PROBLEMA GENERAL Además de analizar los flujos de caja de las las alternativas de inversión, también se debe analizar la forma como se asignan recursos limitados entre actividades
Figura 1: Esquema de las tablas simplex de inicio y general.
 RELACIONES PRIMAL-DUAL Los cambios que se hacen en el modelo original de programación lineal afectan a los elementos de la tabla óptima actual el que se tenga en el momento, que a su vez puede afectar
RELACIONES PRIMAL-DUAL Los cambios que se hacen en el modelo original de programación lineal afectan a los elementos de la tabla óptima actual el que se tenga en el momento, que a su vez puede afectar
HERRAMIENTAS DE PLANIFICACIÓN
 ADMINISTRACIÓN GENERAL I HERRAMIENTAS DE PLANIFICACIÓN Dr. Alfredo Rébori Se han desarrollado distintas técnicas para ayudar a los gerentes en uno de los aspectos más desafiantes de la planificación estratégica:
ADMINISTRACIÓN GENERAL I HERRAMIENTAS DE PLANIFICACIÓN Dr. Alfredo Rébori Se han desarrollado distintas técnicas para ayudar a los gerentes en uno de los aspectos más desafiantes de la planificación estratégica:
815 6 10 9 35/15/0 9 20 12 13 7 50/20/0 1410 9 16 5 40/30/0 45/30/10/0 20/0 30/0 30/0 125 \125. Costo total: 15(8)+20(9)+10(14)+20(6)+30(16) 1250
 Problema 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35, 50 y 40 millones de [kwh] respectivamente.
Problema 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35, 50 y 40 millones de [kwh] respectivamente.
x 1 : número de viviendas tipo I por construir x 2 : número de viviendas tipo II por construir
 Una empresa desarrolladora iniciará un proyecto urbano en un terreno de hectáreas. En él se construirán dos tipos distintos de casas: las viviendas tipo I que ocupan una superficie de 70 m y tendrán un
Una empresa desarrolladora iniciará un proyecto urbano en un terreno de hectáreas. En él se construirán dos tipos distintos de casas: las viviendas tipo I que ocupan una superficie de 70 m y tendrán un
FORMULACIÓN DE MODELOS DE PROGRAMACIÓN ENTERA PROBLEMAS DE REDES
 19 de Marzo de 2015 FORMULACIÓN DE MODELOS DE PROGRAMACIÓN ENTERA PROBLEMAS DE REDES Postgrado de Investigación de Operaciones Facultad de Ingeniería Universidad Central de Venezuela Programación Entera
19 de Marzo de 2015 FORMULACIÓN DE MODELOS DE PROGRAMACIÓN ENTERA PROBLEMAS DE REDES Postgrado de Investigación de Operaciones Facultad de Ingeniería Universidad Central de Venezuela Programación Entera
CAPÍTULO 11 INVESTIGACIÓN OPERATIVA CON R 3.- LOS PROBLEMAS DE TRANSPORTE Y DE ASIGNACIÓN
 CAPÍTULO 11 INVESTIGACIÓN OPERATIVA CON R 1.- PROGRAMACIÓN LINEAL 2.- PROGRAMACIÓN LINEAL ENTERA 3.- LOS PROBLEMAS DE TRANSPORTE Y DE ASIGNACIÓN 4.- OTRAS OPCIONES PARA RESOLVER PROBLEMAS DE PROGRAMACIÓN
CAPÍTULO 11 INVESTIGACIÓN OPERATIVA CON R 1.- PROGRAMACIÓN LINEAL 2.- PROGRAMACIÓN LINEAL ENTERA 3.- LOS PROBLEMAS DE TRANSPORTE Y DE ASIGNACIÓN 4.- OTRAS OPCIONES PARA RESOLVER PROBLEMAS DE PROGRAMACIÓN
Enero Febrero Marzo Abril. D: uds D: uds D: uds D: uds
 PROBLEMA Una empresa dedicada a la fabricación de diferentes artículos, ante la inminente llegada de la estación invernal se plantea establecer su política de fabricación almacenae de estufas de gas para
PROBLEMA Una empresa dedicada a la fabricación de diferentes artículos, ante la inminente llegada de la estación invernal se plantea establecer su política de fabricación almacenae de estufas de gas para
EL MÉTODO SIMPLEX ALGEBRAICO. M. En C. Eduardo Bustos Farías
 EL MÉTODO SIMPLEX ALGEBRAICO M. En C. Eduardo Bustos Farías Modelos sin solución Degeneración. óptima Soluciones múltiples o alternativas () No acotado: Ocurre cuando el objetivo puede crecer infinitamente
EL MÉTODO SIMPLEX ALGEBRAICO M. En C. Eduardo Bustos Farías Modelos sin solución Degeneración. óptima Soluciones múltiples o alternativas () No acotado: Ocurre cuando el objetivo puede crecer infinitamente
Lo que se hace entonces es introducir variables artificiales ADAPTACIÓN A OTRAS FORMAS DEL MODELO.
 Clase # 8 Hasta el momento sólo se han estudiado problemas en la forma estándar ADAPTACIÓN A OTRAS FORMAS DEL MODELO. Maximizar Z. Restricciones de la forma. Todas las variables no negativas. b i 0 para
Clase # 8 Hasta el momento sólo se han estudiado problemas en la forma estándar ADAPTACIÓN A OTRAS FORMAS DEL MODELO. Maximizar Z. Restricciones de la forma. Todas las variables no negativas. b i 0 para
AlumnosA N AlumnosB AlumnosC
 Ejercicios de matrices como expresiones de tablas y grafos: Ejemplo. Sean los grafos siguientes: a) Escriba la matriz de adyacencia asociada a los grafos y de la figura anterior. b) Si las matrices y D
Ejercicios de matrices como expresiones de tablas y grafos: Ejemplo. Sean los grafos siguientes: a) Escriba la matriz de adyacencia asociada a los grafos y de la figura anterior. b) Si las matrices y D
UNIVERSIDAD DE MANAGUA
 UNIVERSIDAD DE MANAGUA Sistemático de Programación Lineal Problemas de Programación Lineal: Solución Gráfica, Analítica, Sensibilidad y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés IIIC- 2016
UNIVERSIDAD DE MANAGUA Sistemático de Programación Lineal Problemas de Programación Lineal: Solución Gráfica, Analítica, Sensibilidad y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés IIIC- 2016
Fundamentos de Investigación de Operaciones El Problema de Transporte
 Fundamentos de Investigación de Operaciones El Problema de Transporte Septiembre 2002 El Problema de Transporte corresponde a un tipo particular de un problema de programación lineal. Si bien este tipo
Fundamentos de Investigación de Operaciones El Problema de Transporte Septiembre 2002 El Problema de Transporte corresponde a un tipo particular de un problema de programación lineal. Si bien este tipo
PROBLEMAS RESUELTOS DE ASIGNACIÓN POR EL MÉTODO HUNGARO INVESTIGACIÓN DE OPERACIONES I
 PROBLEMAS RESUELTOS DE ASIGNACIÓN POR EL MÉTODO HUNGARO INVESTIGACIÓN DE OPERACIONES I Prof.: MSc. Julio Rito Vargas Avilés. Método Húngaro: Los problemas de asignación incluyen aplicaciones tales como
PROBLEMAS RESUELTOS DE ASIGNACIÓN POR EL MÉTODO HUNGARO INVESTIGACIÓN DE OPERACIONES I Prof.: MSc. Julio Rito Vargas Avilés. Método Húngaro: Los problemas de asignación incluyen aplicaciones tales como
Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas.
 1.- CONCEPTO DE MATRIZ. TIPOS DE MATRICES Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas. 1 3 4 Por ejemplo, A = es una matriz de 2 filas y 3 columnas 0 5
1.- CONCEPTO DE MATRIZ. TIPOS DE MATRICES Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas. 1 3 4 Por ejemplo, A = es una matriz de 2 filas y 3 columnas 0 5
Ejemplo: ubicación de estación de bomberos
 15.053 Jueves, 11 de abril Más aplicaciones de la programación entera. Técnicas de plano de corte para obtener mejores cotas. Ejemplo: ubicación de estación de bomberos Considere la ubicación de estaciones
15.053 Jueves, 11 de abril Más aplicaciones de la programación entera. Técnicas de plano de corte para obtener mejores cotas. Ejemplo: ubicación de estación de bomberos Considere la ubicación de estaciones
Para que un problema pueda ser solucionado por el método de transporte, este debe reunir tres condiciones:
 MÉTODO DE TRANSPORTE Es un método de programación lineal para la asignación de artículos de un conjunto de origines a un conjunto de destinos de tal manera que se optimice la función objetivo. Esta técnica
MÉTODO DE TRANSPORTE Es un método de programación lineal para la asignación de artículos de un conjunto de origines a un conjunto de destinos de tal manera que se optimice la función objetivo. Esta técnica
PROBLEMA DE FLUJO DE COSTO MINIMO.
 EL PROBLEMA DE TRANSPORTE PROBLEMA DE FLUJO DE COSTO MINIMO. 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
EL PROBLEMA DE TRANSPORTE PROBLEMA DE FLUJO DE COSTO MINIMO. 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
CAPITULO III. Determinación de Rutas de Entregas
 CAPITULO III Determinación de Rutas de Entregas Un importante aspecto en la logística de la cadena de abastecimiento (supply chain), es el movimiento eficiente de sus productos desde un lugar a otro. El
CAPITULO III Determinación de Rutas de Entregas Un importante aspecto en la logística de la cadena de abastecimiento (supply chain), es el movimiento eficiente de sus productos desde un lugar a otro. El
A 2 E 4 I. Las cámaras situadas en puntos capaces de vigilar 2, 3 y 4 zonas cuestan 5, 7 y 8 unidades monetarias,
 Programación Lineal Entera / Investigación Operativa 1 MODELIZACIÓN Y RESOLUCIÓN CON SOLVER. Hoja 3 Para los siguientes problemas, se pide: 1. Plantear el correspondiente modelo de Programación Lineal
Programación Lineal Entera / Investigación Operativa 1 MODELIZACIÓN Y RESOLUCIÓN CON SOLVER. Hoja 3 Para los siguientes problemas, se pide: 1. Plantear el correspondiente modelo de Programación Lineal
 3.1 Por inspección del tablero óptimo genere las respuestas a los numerales dados. X 1 = Cantidad de tarjetas de invitación a producir semanalmente en Kimberly Colpapel y X 2 = Cantidad de tarjetas de
3.1 Por inspección del tablero óptimo genere las respuestas a los numerales dados. X 1 = Cantidad de tarjetas de invitación a producir semanalmente en Kimberly Colpapel y X 2 = Cantidad de tarjetas de
Carrera: AGM Participantes Representante de las academias de Ingeniería Agronomía de los Institutos Tecnológicos. Academias
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Investigación de Operaciones Ingeniería en Agronomía AGM 0622 3 2 8 2. HISTORIA
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Investigación de Operaciones Ingeniería en Agronomía AGM 0622 3 2 8 2. HISTORIA
