UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
|
|
|
- Virginia Molina Salas
- hace 8 años
- Vistas:
Transcripción
1 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES Y CRITERIOS GENERALES DE CALIFICACIÓN Estructur de l prueb: l prueb se compone de dos opciones "A" y "B" cd un de ls cules const de cinco cuestiones que su vez pueden comprender vrios prtdos. Puntución: Cd cuestión se clificrá con un puntución máxim de 2 puntos. Los prtdos de cd cuestión se punturán con el vlor que se indic en los enuncidos. Puntución globl máxim 0 puntos. Instrucciones: Sólo se podrá contestr un de ls dos opciones, desrrollndo íntegrmente su contenido. TIEMPO: Un hor y treint minutos OPCIÓN A Cuestión nº (2 puntos) En el digrm Fe-C simplificdo de l figur djunt, determine: ) Porcentje máximo de solubilidd de C en Feγ (ustenit) y tempertur l que existe es máxim solubilidd. (0,5 puntos) b) Temperturs de solidificción del hierro puro y de l ledeburit (eutéctico). (0,5 puntos) c) Porcentje de fses (ferrit-cementit) que componen el eutectoide (perlit). Indique l tempertur l que se form el eutectoide. (0,5 puntos) d) Porcentje de constituyentes (ferrit-perlit) de un cero con el 0,5 % de C tempertur mbiente. (0,5 puntos) 500 º C Líquido 600 º C Austenit 00 º C 900 º C Ferrit 700 º C Fe 2 4,5 7 % en peso de crbono Fe 3 C (Cementit) Cuestión n 2 (2 puntos) ) Explique cómo trnscurre el ciclo de funcionmiento de un motor de explosión de dos tiempos. (,5 puntos) b) Indique l menos dos ventjs de este tipo de motores. (0,5 puntos)
2 Cuestión nº3 (2 puntos) En el sistem relimentdo mostrdo se cumple que el vlor de l slid es 2 (Z = 2); en est condición rellene un tbl como l mostrd con los vlores de l señl en los puntos indicdos. (2 puntos) A B - P =2 P 2 = Z C P 3 = P 4 =4 Punto A B C (entrd) Vlor Cuestión nº 4 (2 puntos) ) Clcule el trbjo desrrolldo por un cilindro neumático cuyo émbolo posee un diámetro de 20 mm y un crrer de 00 mm, limentdo con un presión de 58,8 N/cm 2. Supong que desrroll l fuerz máxim pr l que está diseñdo. ( punto) b) Dibuje un cilindro de doble efecto e indique sobre el dibujo l menos cutro de ls prtes más importntes. ( punto) Cuestión nº 5 (2 puntos) ) Represente sobre un mp de Krnugh l función lógic, z(,b,c,d), que reliz el circuito mostrdo en l figur ( punto). b) Simplifique dich función por el método de Krnugh. ( punto) b 0 I S S 0 c d S S 0 b I z 0 I S S 0
3 OPCIÓN B Cuestión nº (2 puntos) ) Describ brevemente en qué consiste el trtmiento térmico del temple del cero indicndo ls propieddes que se consiguen. ( punto) b) Describ brevemente como se reliz el ensyo Jominy de templbilidd. ( punto) Cuestión n 2 (2 puntos) El frigorífico de un resturnte tiene dos comprtimentos isldos, con dos máquins independientes: un pr refrigerción 4 C y otr pr congelción 25 C. Sbiendo que mbs máquins funcionn de cuerdo l Ciclo de Crnot, y que l tempertur medi del locl donde se encuentr el frigorífico se mntiene en 25 C, clcule: ) L eficienci de l máquin utilizd pr refrigerción. ( punto) b) L eficienci de l máquin utilizd pr congelción. ( punto) Cuestión nº3 (2 puntos) Ddo el digrm de bloques de l figur: ) Obteng l función de trnsferenci Y = f(). ( punto) b) Obteng l función de trnsferenci Z = f(). ( punto) P P 2 Y P 4 Z P 3 P 5 _ Cuestión nº 4 (2 puntos) ) En un recipiente de 40 L se introduce ire un presión de N/m 2. Clcule l presión si el volumen se reduce l mitd, permneciendo constnte l tempertur. ( punto) b) Antes de ser utilizdo el ire en los circuitos neumáticos es sometido unos trtmientos. Indique con sus símbolos respectivos estos trtmientos poniendo el nombre cd uno. ( punto) Cuestión nº 5 (2 puntos) ) Represente en complemento 2 y usndo 8 bits el número 26. (0,5 puntos) b) Represente en complemento 2 y usndo 8 bits el número 5. (0,5 puntos) c) Obteng el vlor deciml de sbiendo que está representdo en complemento 2 usndo 8 bits. (0,5 puntos) d) Obteng el vlor deciml de sbiendo que está representdo en complemento 2 usndo 8 bits. (0,5 puntos)
4 TECNOLOGÍA INDUSTRIAL II CRITERIOS ESPECÍFICOS DE CORRECCIÓN Y CALIFICACIÓN Los profesores encrgdos de l corrección de ls cuestiones dispondrán, un vez relizds ls pruebs, de un solución de ls misms, pr que les sirv de guí en el desrrollo de su trbjo. En quells cuestiones en ls que los resultdos de un prtdo intervengn en los cálculos de los siguientes, los correctores deberán vlorr como válidos estos últimos prtdos si su plntemiento fuese correcto y tn solo se tiene como error el derivdo del cálculo inicil. OPCIÓN A Cuestión nº : 2 PUNTOS reprtidos de l siguiente form: Aprtdo : 0,5 puntos. Aprtdo b: 0,5 puntos. Aprtdo : 0,5 puntos. Aprtdo b: 0,5 puntos. Cuestión nº 2: 2 PUNTOS reprtidos de l siguiente form: Aprtdo :,5 puntos. Aprtdo b: 0,5 puntos. Cuestión nº 3: 2 PUNTOS (0,5 puntos por cd vlor). Cuestión nº 4: 2 PUNTOS reprtidos de l siguiente form: Aprtdo : punto. Aprtdo b: punto (0,25 puntos por cd prte del cilindro). Cuestión nº 5: 2 PUNTOS reprtidos de l siguiente form: Aprtdo : punto. Aprtdo b: punto. Puntución totl 0 puntos OPCIÓN B Cuestión nº : 2 PUNTOS reprtidos de l siguiente form: Aprtdo : punto. Aprtdo b: punto. Cuestión nº 2: 2 PUNTOS reprtidos de l siguiente form: Aprtdo : punto. Aprtdo b: punto. Cuestión nº 3: 2 PUNTOS reprtidos de l siguiente form: Aprtdo : punto. Aprtdo b: punto. Cuestión nº 4: 2 PUNTOS reprtidos de l siguiente form: Aprtdo : punto. Aprtdo b: punto (0,25 puntos por cd componente). Cuestión nº 5: 2 PUNTOS reprtidos de l siguiente form: Aprtdo : 0,5 puntos. Aprtdo b: 0,5 puntos. Aprtdo c: 0,5 puntos. Aprtdo d: 0,5 puntos. Puntución totl 0 puntos
5 TECNOLOGÍA INDUSTRIAL II SOLUCIONES OPCIÓN A Cuestión nº (2 puntos) En el digrm Fe-C simplificdo de l figur djunt, determine: ) Porcentje máximo de solubilidd de C en Feγ (ustenit) y tempertur l que existe es máxim solubilidd. (0,5 puntos) b) Temperturs de solidificción del hierro puro y de l ledeburit (eutéctico). (0,5 puntos) c) Porcentje de fses (ferrit-cementit) que componen el eutectoide (perlit). Indique l tempertur l que se form el eutectoide. (0,5 puntos) d) Porcentje de constituyentes (ferrit-perlit) de un cero con el 0,5 % de C tempertur mbiente. (0,5 puntos) 500 º C Líquido 600 º C Austenit 00 º C 900 º C Ferrit 700 º C Fe 2 4,5 7 % en peso de crbono Fe 3 C (Cementit) ) 2% de C 00 ºC. b) El hierro puro solidific 500 ºC; l ledeburit 00 ºC. c) /7 = 4,3 % de cementit; 6/7 = 85,7% de ferrit. Se form 700 ºC prtir de l ustenit. d) 50 % de ferrit; 50 % de perlit. Cuestión n 2 (2 puntos) ) Explique cómo trnscurre el ciclo de funcionmiento de un motor de explosión de dos tiempos. (,5 puntos) b) Indique l menos dos ventjs de este tipo de motores. (0,5 puntos) ) ª etp: Expnsión-Escpe (0,75 puntos): Con l combustión de l mezcl se ejerce un presión sobre el pistón, que desciende rrstrndo el cigüeñl. Se descubre l lumbrer de escpe, sliendo l exterior los gses de combustión, y l brirse l lumbrer de trnsferenci entr l cilindro l mezcl procedente del cárter, deslojndo el resto de los gses de combustión. El pistón, que hor se encuentr en el Punto Muerto Inferior (PMI) está preprdo pr comenzr un nuevo ciclo. 2ª etp: Admisión-Compresión (0,75 puntos): El pistón, impulsdo por el cigüeñl, sciende desde el PMI hst el Punto Muerto Superior (PMS) comprimiendo l mezcl que está en el cilindro. A l vez, con l lumbrer de escpe cerrd, se descubre
6 l lumbrer de dmisión pr que entre l cárter un nuev cntidd de mezcl. Cundo el pistón lcnz el PMS l chisp ocsion l combustión de l mezcl presente en el cilindro. b) Indicr l menos dos de ls siguientes ventjs (0,5 puntos): sencillez de construcción, no existen válvuls (originn problems de desgste), myor potenci (se gener trbjo útil en cd vuelt de cigüeñl), mejor funcionmiento del sistem de trnsmisión. Cuestión nº3 (2 puntos) En el sistem relimentdo mostrdo se cumple que el vlor de l slid es 2 (Z = 2); en est condición rellene un tbl como l mostrd con los vlores de l señl en los puntos indicdos. (2 puntos) A B - P =2 P 2 = Z C P 3 = P 4 =4 Punto A B C (entrd) Vlor Punto Vlor A (A = B / 2) B 2 (B = Z) C 8 (C = 4 Z) (entrd) 7 (8 - = ) Cuestión nº 4 (2 puntos) ) Clcule el trbjo desrrolldo por un cilindro neumático cuyo émbolo posee un diámetro de 20 mm y un crrer de 00 mm, limentdo con un presión de 58,8 N/cm 2. Supong que desrroll l fuerz máxim pr l que está diseñdo. ( punto) b) Dibuje un cilindro de doble efecto e indique sobre el dibujo l menos cutro de ls prtes más importntes. ( punto) SOLUCIÓN ) Volumen desplzdo: V = (π D 2 / 4) x = (π/4) ( ) 2 m 2 ( ) m = π 0-5 m 3 Trbjo relizdo W = p V = ( ) N/m 2 π 0-5 m 3 = 8,47 Julios b). Cmis 2. Pistón 3. Vástgo 4. Entrd/slid de ire 5. Entrd/slid de ire
7 Cuestión nº 5 (2 puntos) ) Represente sobre un mp de Krnugh l función lógic, z(,b,c,d), que reliz el circuito mostrdo en b 0 I S S 0 c d S S 0 b I z 0 I S S 0 l figur ( punto). b) Simplifique dich función por el método de Krnugh. ( punto) ) Representmos sobre Krnugh: b cd
8 b) Simplificndo, obtenemos: f(,b,c,d) = c b d c
9 OPCIÓN B Cuestión nº (2 puntos) ) Describ brevemente en qué consiste el trtmiento térmico del temple del cero indicndo ls propieddes que se consiguen. ( punto) b) Describ brevemente como se reliz el ensyo Jominy de templbilidd. ( punto) ) El temple consiste en clentr el cero hst l tempertur de ustenizción pr relizr después un enfrimiento rápido del mismo y convertirlo sí en cero mrtensítico. Se umentn l durez y l resistenci, unque disminuyen l plsticidd y tencidd. b) Se templ un probet scd del horno con un chorro de gu sobre uno de sus extremos y después se mide l durez en distintos puntos diferentes distncis, trzndo su curv de templbilidd de l durez en función de l distnci l extremo. Cuestión n 2 (2 puntos) El frigorífico de un resturnte tiene dos comprtimentos isldos, con dos máquins independientes: un pr refrigerción 4 C y otr pr congelción 25 C. Sbiendo que mbs máquins funcionn de cuerdo l Ciclo de Crnot, y que l tempertur medi del locl donde se encuentr el frigorífico se mntiene en 25 C, clcule: ) L eficienci de l máquin utilizd pr refrigerción. ( punto) b) L eficienci de l máquin utilizd pr congelción. ( punto) Q = clor portdo l foco cliente por unidd de tiempo Q 2 = clor elimindo del foco frío por unidd de tiempo W = trbjo relizdo sobre el sistem por unidd de tiempo Q = Q 2 W ) T = (25) (273) = 298 K T 2 = (4) (273) = 277 K ef mf = Q 2 / W = Q 2 / (Q Q 2 ) = T 2 / (T T 2 ) = (277) / ( ) = 3,2 b) T = (25) (273) = 298 K T 2 = (-25) (273) = 248 K ef mf = Q 2 / W = Q 2 / (Q Q 2 ) = T 2 / (T T 2 ) = (248) / ( ) = 5,0 Cuestión nº3 (2 puntos) Ddo el digrm de bloques de l figur: ) Obteng l función de trnsferenci Y = f(). ( punto) b) Obteng l función de trnsferenci Z = f(). ( punto) P P 2 Y P 4 Z Y ) = P.P2 P 3 P 5 _ Z b) = [ P. P2 P P5 P3. P5 ]. P4 ;
10 Cuestión nº 4 (2 puntos) ) En un recipiente de 40 L se introduce ire un presión de N/m 2. Clcule l presión si el volumen se reduce l mitd, permneciendo constnte l tempertur. ( punto) b) Antes de ser utilizdo el ire en los circuitos neumáticos es sometido unos trtmientos. Indique con sus símbolos respectivos estos trtmientos poniendo el nombre cd uno. ( punto) SOLUCIÒN: ) p V = p 2 V 2 ; p = N/m 2 ; V = 0,040 m 3 ; V 2 = 0,020 m 3 p 2 = p V / V 2 = N/m 2 (0,0409) m 3 / (0,020) m 3 = N/m 2 b) Cuestión nº 5 (2 puntos) ) Represente en complemento 2 y usndo 8 bits el número 26 (0,5 puntos). b) Represente en complemento 2 y usndo 8 bits el número 5 (0,5 puntos). c) Obteng el vlor deciml de sbiendo que está representdo en complemento 2 usndo 8 bits (0,5 puntos). d) Obteng el vlor deciml de sbiendo que está representdo en complemento 2 usndo 8 bits (0,5 puntos). SOLUCIÒN: ) (26) 0 = (00000) 2 (-26) 0 = C2(00000) = (000) C2 b) (5) 0 = (000) 2 (5) 0 = (000) C2 c) (00000) C2 es negtivo, C2(00000) = (000) y (000) 2 = (0) 0 (00000) C2 = (-0) 0 d) (000000) C2 es positivo y (000000) 2 = (8) 0 (000000) C2 = (8) 0
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 Tempertur (ºC) UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Modelo Tecnologí Industril II. 21-211 Opción A Cuestión nº1 (2 puntos)
Tempertur (ºC) UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Modelo Tecnologí Industril II. 21-211 Opción A Cuestión nº1 (2 puntos)
ELIJA UNA DE LAS DOS OPCIONES A o B Y DESARROLLE CUATRO CUESTIONES DE LAS CINCO PROPUESTAS.
 UNIVERSIDAD DE ZARAGOZA PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. - JUNIO DE 2005 Ejercicio de: TECNOLOGÍA INDUSTRIAL Tiempo disponible: 1 h. 30 m. Se valorará el uso de vocabulario y la notación científica.
UNIVERSIDAD DE ZARAGOZA PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E. - JUNIO DE 2005 Ejercicio de: TECNOLOGÍA INDUSTRIAL Tiempo disponible: 1 h. 30 m. Se valorará el uso de vocabulario y la notación científica.
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012
 UNIVERSIDADES ÚBLICAS DE LA COMUNIDAD DE MADRID RUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 20-202 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES ÚBLICAS DE LA COMUNIDAD DE MADRID RUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 20-202 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
Tiempo: La duración máxima de la prueba es de 90 minutos. Opción A
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2008-2009 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN Estructura de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2008-2009 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN Estructura de
MECANICA DE FLUIDOS Y MAQUINAS FLUIDODINAMICAS. Guía Trabajos Prácticos N 4 Ecuación de Bernoulli. Mediciones manométricas
 MECNIC DE FLUIDOS Y MQUINS FLUIDODINMICS Guí Trbjos Prácticos N 4 Ecución de Bernoulli. Mediciones mnométrics. L presión mnométric en es -0, Kg/cm. Determinr el peso específico reltivo del líquido mnométrico.
MECNIC DE FLUIDOS Y MQUINS FLUIDODINMICS Guí Trbjos Prácticos N 4 Ecución de Bernoulli. Mediciones mnométrics. L presión mnométric en es -0, Kg/cm. Determinr el peso específico reltivo del líquido mnométrico.
FÍSICA FARMACIA. Examen Final Ordinario
 FÍSICA FARMACIA. Exmen Finl Ordinrio. -- Apellidos y nombre PROBLEMA (Experimentl,.5 p) En el lbortorio de Físic se quiere verificr si el y y proceso de vcido de un buret en función del tiempo se just
FÍSICA FARMACIA. Exmen Finl Ordinrio. -- Apellidos y nombre PROBLEMA (Experimentl,.5 p) En el lbortorio de Físic se quiere verificr si el y y proceso de vcido de un buret en función del tiempo se just
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 007-008 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES GENERALES Y VALORACIÓN Estructura
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 007-008 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES GENERALES Y VALORACIÓN Estructura
UNIVERSIDAD COMPLUTENSE DE MADRID INSTRUCCIONES GENERALES Y VALORACIÓN
 TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN La duración máxima de la prueba es de 90 minutos. INSTRUCCIONES: La prueba se compone de dos opciones "A" y "B" cada una de las cuales consta de cinco cuestiones,
TIEMPO: INSTRUCCIONES GENERALES Y VALORACIÓN La duración máxima de la prueba es de 90 minutos. INSTRUCCIONES: La prueba se compone de dos opciones "A" y "B" cada una de las cuales consta de cinco cuestiones,
UNIVERSIDAD COMPLUTENSE DE MADRID
 INSTRUCCIONES GENERALES Y VALORACIÓN TIEMPO: ESTRUCTURA DE LA PRUEBA E INSTRUCCIONES: PUNTUACIÓN: La duración máxima de la prueba es de 90 minutos. La prueba se compone de dos opciones "A" y "B" cada una
INSTRUCCIONES GENERALES Y VALORACIÓN TIEMPO: ESTRUCTURA DE LA PRUEBA E INSTRUCCIONES: PUNTUACIÓN: La duración máxima de la prueba es de 90 minutos. La prueba se compone de dos opciones "A" y "B" cada una
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2005-2006 MATERIA: TECNOLOGÍAINDUSTRIAL II 6 INSTRUCCIONES GENERALES Y VALORACIÓN Estructura de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2005-2006 MATERIA: TECNOLOGÍAINDUSTRIAL II 6 INSTRUCCIONES GENERALES Y VALORACIÓN Estructura de
I.3.1.3 Hidroformilación bifásica de 1-octeno con sistemas de Rh/fosfina perfluorada P(C 6 H 4 -p-och 2 C 7 F 15 ) 3
 I.3 Discusión de resultdos I.3.1.3 Hidroformilción ifásic de 1-octeno con sistems de Rh/fosfin perfluord P(C 6 H 4 -p-och 2 C 7 F 15 ) 3 Como y se h comentdo en l introducción l ctálisis ifásic en sistems
I.3 Discusión de resultdos I.3.1.3 Hidroformilción ifásic de 1-octeno con sistems de Rh/fosfin perfluord P(C 6 H 4 -p-och 2 C 7 F 15 ) 3 Como y se h comentdo en l introducción l ctálisis ifásic en sistems
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID MATERIA: TECNOLOGÍA INDUSTRIAL II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: TECNOLOGÍA INDUSTRIAL II MODELO INSTRUCCIONES Y CRITERIOS GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2007-2008 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN Estructura de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 2007-2008 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN Estructura de
Qué es la aceleración? Es una magnitud vectorial que nos permite determinar la rapidez con la que un móvil cambia de velocidad. www.fisicaa.
 Qué es el movimiento rectilíneo uniformemente vrido? Es un movimiento mecánico que experiment un móvil donde l tryectori es rectilíne y l celerción es constnte. Qué es l celerción? Es un mgnitud vectoril
Qué es el movimiento rectilíneo uniformemente vrido? Es un movimiento mecánico que experiment un móvil donde l tryectori es rectilíne y l celerción es constnte. Qué es l celerción? Es un mgnitud vectoril
INGENIERIA DE EJECUCION EN CLIMATIZACION 15082-15202
 UNIVERSIDAD DE SANTIAGO DE CHILE FACULTAD DE INGENIERÍA Deprtmento de Ingenierí Mecánic CAV/mm. INGENIERIA DE EJECUCION EN CLIMATIZACION 15082-15202 ASIGNATURA MECANICA DE FLUIDOS NIVEL 04 EXPERIENCIA
UNIVERSIDAD DE SANTIAGO DE CHILE FACULTAD DE INGENIERÍA Deprtmento de Ingenierí Mecánic CAV/mm. INGENIERIA DE EJECUCION EN CLIMATIZACION 15082-15202 ASIGNATURA MECANICA DE FLUIDOS NIVEL 04 EXPERIENCIA
PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 28 FISICA TOMO 2. Tercera y quinta edición. Raymond A. Serway
 PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3
PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3
FUNDICIONES. 2 a 4,5 % C 0,5 a 3,5 % Si 0,4 a 2 % Mn 0,01 a 0,2 % S 0,04 a 0,8 % P
 FUNDICIONES FUNDICIONES Las fundiciones de hierro son aleaciones de hierro carbono del 2 al 5%, cantidades de silicio del 0.5 al 4%, del manganeso hasta 2%, bajo azufre y bajo fósforo. Se caracterizan
FUNDICIONES FUNDICIONES Las fundiciones de hierro son aleaciones de hierro carbono del 2 al 5%, cantidades de silicio del 0.5 al 4%, del manganeso hasta 2%, bajo azufre y bajo fósforo. Se caracterizan
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
PROBLEMAS DE MÁQUINAS TÉRMICAS, REFRIGERADORES y
 PROBLEMAS DE DE MÁUINAS ÉRMICAS, REFRIGERADORES y BOMBAS BOMBAS DE DE CALOR CALOR Equipo docente Antonio J. Brero / Alfonso Cler / Mrino Hernández Dpto. Físic Aplicd. E..S. Agrónomos (Alcete) Plo Muñiz
PROBLEMAS DE DE MÁUINAS ÉRMICAS, REFRIGERADORES y BOMBAS BOMBAS DE DE CALOR CALOR Equipo docente Antonio J. Brero / Alfonso Cler / Mrino Hernández Dpto. Físic Aplicd. E..S. Agrónomos (Alcete) Plo Muñiz
CONTROL DE PROCESOS FACET UNT TEMA 1 Nota Auxiliar B ÁLGEBRA DE BLOQUES
 Digrms en Bloques Un sistem de control puede constr de ciert cntidd de componentes. Pr mostrr ls funciones que reliz cd componente se costumr usr representciones esquemátics denominds Digrm en Bloques.
Digrms en Bloques Un sistem de control puede constr de ciert cntidd de componentes. Pr mostrr ls funciones que reliz cd componente se costumr usr representciones esquemátics denominds Digrm en Bloques.
Cuál es su valor de CRF? Es normal? Qué enfermedad le sugiere esta valor de CRF?
 1 Bloque 1 Problem 1. Un niño es conectdo, después de un espirción norml, un bols conteniendo 2 litros de 8% He, 92% O 2. Respir de l bols hst que l mezcl es complet, y en ese momento l concentrción de
1 Bloque 1 Problem 1. Un niño es conectdo, después de un espirción norml, un bols conteniendo 2 litros de 8% He, 92% O 2. Respir de l bols hst que l mezcl es complet, y en ese momento l concentrción de
1. Cuales son los números naturales?
 Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
PROBLEMAS TEMA 2. FASES y TRANSFORMACIONES DE FASE. DIAGRAMAS DE EQUILIBRIO
 PROBLEMAS TEMA 2. FASES y TRANSFORMACIONES DE FASE. DIAGRAMAS DE EQUILIBRIO 1. Se adjunta el peso atómico y el radio atómico de tres hipotéticos metales. Determinar para cada una de ellas si su estructura
PROBLEMAS TEMA 2. FASES y TRANSFORMACIONES DE FASE. DIAGRAMAS DE EQUILIBRIO 1. Se adjunta el peso atómico y el radio atómico de tres hipotéticos metales. Determinar para cada una de ellas si su estructura
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Mezclas de gases ideales y aplicaciones psicrométricas.
 Mezcls de gses ideles y plicciones psicrométrics. Aplicciones de Mezcls de Gses Ideles Dos plicciones de prticulr importnci: 1. Sistems que involucrn recciones químics, en prticulr, l combustión. Pr ests
Mezcls de gses ideles y plicciones psicrométrics. Aplicciones de Mezcls de Gses Ideles Dos plicciones de prticulr importnci: 1. Sistems que involucrn recciones químics, en prticulr, l combustión. Pr ests
Tecnología Industrial II
 Tecnología Industrial II Exámenes de Selectividad I.E.S. El Palmeral Prof. Cristóbal García Ruiz BACHILLERATO b) El alumno elegirá una sola de las dos opciones, sin mezclarlas, indicando la opción elegida.
Tecnología Industrial II Exámenes de Selectividad I.E.S. El Palmeral Prof. Cristóbal García Ruiz BACHILLERATO b) El alumno elegirá una sola de las dos opciones, sin mezclarlas, indicando la opción elegida.
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
CARTUCHOS PARA MOTORES Y TURBINAS DE GAS
 CARTUCHOS PARA MOTORES Y TURBINAS DE GAS CARTUCHOS TG CARTUCHOS TG INFORMACIÓN GENERAL Los filtros Crtuchos TG hn sido diseñdos pr trbjr en condiciones de trbjo extrems en l spirción de ls Turbins de Gs,
CARTUCHOS PARA MOTORES Y TURBINAS DE GAS CARTUCHOS TG CARTUCHOS TG INFORMACIÓN GENERAL Los filtros Crtuchos TG hn sido diseñdos pr trbjr en condiciones de trbjo extrems en l spirción de ls Turbins de Gs,
ÁREA DE INGENIERÍA QUÍMICA Prof. Isidoro García García. Operaciones Básicas de Transferencia de Materia. Tema 6
 ÁRE DE INGENIERÍ QUÍIC Prof. Isidoro Grcí Grcí Operciones Básics de Trnsferenci de teri Tem 6 Operciones Básics de Trnsferenci de teri INTRODUCCIÓN Como se sbe, ls operciones en columns de relleno son
ÁRE DE INGENIERÍ QUÍIC Prof. Isidoro Grcí Grcí Operciones Básics de Trnsferenci de teri Tem 6 Operciones Básics de Trnsferenci de teri INTRODUCCIÓN Como se sbe, ls operciones en columns de relleno son
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
PRUEBA DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR SEPTIEMBRE 2013 PARTE ESPECÍFICA OPCIÓN B TECNOLOGÍA Materia: DIBUJO TÉCNICO SOLUCIÓN
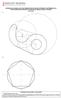 1. PRUEBA DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR SEPTIEMBRE 2013 PARTE ESPECÍFICA OPCIÓN B TECNOLOGÍA Materia: DIBUJO TÉCNICO SOLUCIÓN 2. PRUEBA DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR
1. PRUEBA DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR SEPTIEMBRE 2013 PARTE ESPECÍFICA OPCIÓN B TECNOLOGÍA Materia: DIBUJO TÉCNICO SOLUCIÓN 2. PRUEBA DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR
PREGUNTAS PRUEBAS PAU MATERIALES
 PREGUNTAS PRUEBAS PAU MATERIALES JUNIO 2010 FE Opción A Defina brevemente las siguientes propiedades que presentan los compuestos metálicos: a) Elasticidad (0,5 puntos) b) Tenacidad (0,5 puntos) c) Maleabilidad
PREGUNTAS PRUEBAS PAU MATERIALES JUNIO 2010 FE Opción A Defina brevemente las siguientes propiedades que presentan los compuestos metálicos: a) Elasticidad (0,5 puntos) b) Tenacidad (0,5 puntos) c) Maleabilidad
La Geometría de las Normas del Espacio de las Funciones Continuas
 Divulgciones Mtemátics Vol. 11 No. 1(2003), pp. 71 82 L Geometrí de ls Norms del Espcio de ls Funciones Continus The Geometry of the Norms of the Spce of Continuous Functions Arístides Arellán (ristide@ciens.ul.ve)
Divulgciones Mtemátics Vol. 11 No. 1(2003), pp. 71 82 L Geometrí de ls Norms del Espcio de ls Funciones Continus The Geometry of the Norms of the Spce of Continuous Functions Arístides Arellán (ristide@ciens.ul.ve)
Resolución de circuitos complejos de corriente continua: Leyes de Kirchhoff.
 Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
DETERMINACIÓN DEL COEFICIENTE ADIABÁTICO DEL AIRE
 Lbortorio de Físic Generl rimer Curso (Termodinánic) DETERMINACIÓN DEL COEFICIENTE ADIABÁTICO DEL AIRE Fech: 07/0/05. Objetivo de l práctic Medir el coeficiente dibático del ire relizndo un expnsión rápid..
Lbortorio de Físic Generl rimer Curso (Termodinánic) DETERMINACIÓN DEL COEFICIENTE ADIABÁTICO DEL AIRE Fech: 07/0/05. Objetivo de l práctic Medir el coeficiente dibático del ire relizndo un expnsión rápid..
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
TRABAJO PRACTICO No 7. MEDICION de DISTORSION EN AMPLIFICADORES DE AUDIO
 TRBJO PRCTICO No 7 MEDICION de DISTORSION EN MPLIFICDORES DE UDIO INTRODUCCION TEORIC: L distorsión es un efecto por el cul un señl pur (de un únic frecuenci) se modific preciendo componentes de frecuencis
TRBJO PRCTICO No 7 MEDICION de DISTORSION EN MPLIFICDORES DE UDIO INTRODUCCION TEORIC: L distorsión es un efecto por el cul un señl pur (de un únic frecuenci) se modific preciendo componentes de frecuencis
CONSIDERACIONES SOBRE LAS COMPUERTAS
 Abril de 006 CONSDERACONES SOBRE LAS COMPUERTAS Cátedr de Mecánic de los Fluidos Escuel de ngenierí Mecánic Autores: ngeniero Edgr Blbstro ngeniero Gstón Bourges e-mil: gbourges@fcei.unr.edu.r 1 Abril
Abril de 006 CONSDERACONES SOBRE LAS COMPUERTAS Cátedr de Mecánic de los Fluidos Escuel de ngenierí Mecánic Autores: ngeniero Edgr Blbstro ngeniero Gstón Bourges e-mil: gbourges@fcei.unr.edu.r 1 Abril
XII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN FLUJO EN CONDUCTOS
 XII.- TANSMISIÓN DE CALO PO CONVECCIÓN FLUJO EN CONDUCTOS XII.1.- FLUJO ISOTÉMICO EN CONDUCTOS CICULAES; ECUACIÓN DE POISEUI- LLE En un flujo lminr l corriente es reltivmente lent y no es perturbd por
XII.- TANSMISIÓN DE CALO PO CONVECCIÓN FLUJO EN CONDUCTOS XII.1.- FLUJO ISOTÉMICO EN CONDUCTOS CICULAES; ECUACIÓN DE POISEUI- LLE En un flujo lminr l corriente es reltivmente lent y no es perturbd por
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2013-2014 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES
 TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
PRÁCTICA 5. Corrección del factor de potencia
 PRÁTIA 5 orrección del fctor de potenci Objetivo: Determinr el fctor de potenci de un crg monofásic y de un crg trifásic Efectur l corrección del fctor de potenci de un crg monofásic y de un crg trifásic.
PRÁTIA 5 orrección del fctor de potenci Objetivo: Determinr el fctor de potenci de un crg monofásic y de un crg trifásic Efectur l corrección del fctor de potenci de un crg monofásic y de un crg trifásic.
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) (Curso 2003-2004) MATERIA: TECNOLOGÍA INDUSTRIAL II Junio Septiembre R1 R2 INSTRUCCIONES GENERALES Y
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) (Curso 2003-2004) MATERIA: TECNOLOGÍA INDUSTRIAL II Junio Septiembre R1 R2 INSTRUCCIONES GENERALES Y
MÁQUINAS TÉRMICAS, REFRIGERADORES y BOMBAS DE CALOR
 MÁUINAS ÉRMICAS, REFRIGERADORES y BOMBAS DE CALOR Equipo docente Antonio J. Brero / Alfonso Cler / Mrino Hernández Dpto. Físic Aplicd. E..S. Agrónomos (Alcete) Plo Muñiz / José A. de oro Dpto. Físic Aplicd.
MÁUINAS ÉRMICAS, REFRIGERADORES y BOMBAS DE CALOR Equipo docente Antonio J. Brero / Alfonso Cler / Mrino Hernández Dpto. Físic Aplicd. E..S. Agrónomos (Alcete) Plo Muñiz / José A. de oro Dpto. Físic Aplicd.
METODOLOGÍA PARA LOS PROYECTOS DE SUSTITUCIÓN DE COMBUSTIBLES FÓSILES POR ENERGÍA SOLAR EN UNA INSTALACIÓN DE RIEGO AISLADA NUEVA O YA EXISTENTE
 METODOLOGÍA PARA LOS PROYECTOS DE SUSTITUCIÓN DE COMBUSTIBLES FÓSILES POR ENERGÍA SOLAR EN UNA INSTALACIÓN DE RIEGO AISLADA NUEVA O YA EXISTENTE Sector: Agricultur. Est metodologí plicrá los proyectos
METODOLOGÍA PARA LOS PROYECTOS DE SUSTITUCIÓN DE COMBUSTIBLES FÓSILES POR ENERGÍA SOLAR EN UNA INSTALACIÓN DE RIEGO AISLADA NUEVA O YA EXISTENTE Sector: Agricultur. Est metodologí plicrá los proyectos
Psicrometría. nrt. nrt. p p p. nrt. a a. v v
 Estudio de sistems consistentes en ire seco y gu. Aire húmedo: mezcl de ire seco y or de gu. El ire seco se trt como si fuer un comonente uro. L mezcl globl y sus comonentes se comortn como un gs idel
Estudio de sistems consistentes en ire seco y gu. Aire húmedo: mezcl de ire seco y or de gu. El ire seco se trt como si fuer un comonente uro. L mezcl globl y sus comonentes se comortn como un gs idel
GUÍA V : MÁQUINAS DE CORRIENTE CONTINUA
 Sistems Electromecánicos, Guí : Máquins de Corriente Continu GUÍA : MÁQUNAS DE COENTE CONTNUA. L crcterístic de mgnetizción de un generdor de corriente continu operndo un velocidd de 500 [rpm] es: [A]
Sistems Electromecánicos, Guí : Máquins de Corriente Continu GUÍA : MÁQUNAS DE COENTE CONTNUA. L crcterístic de mgnetizción de un generdor de corriente continu operndo un velocidd de 500 [rpm] es: [A]
Unidad6 ENDURECIMIENTO POR ALEACION. ALEACIONES CON SOLUBILIDAD PARCIAL EN ESTADO SOLIDO
 Unidad6 ENDURECIMIENTO POR ALEACION. ALEACIONES CON SOLUBILIDAD PARCIAL EN ESTADO SOLIDO 1 PRESENTACION En esta Unidad se analiza la casuística que aparece cuando en el estado sólido existen componentes
Unidad6 ENDURECIMIENTO POR ALEACION. ALEACIONES CON SOLUBILIDAD PARCIAL EN ESTADO SOLIDO 1 PRESENTACION En esta Unidad se analiza la casuística que aparece cuando en el estado sólido existen componentes
Matemáticas Unidad: Las Fracciones
 Mtemátics Unidd: Ls Frcciones Ejercicio nº 1.- Escribe, en cd cso, l frcción del todo que corresponde l prte indicd: De un docen de huevos se hn roto. Qué frcción se h roto? b En un urbnizción se hn construido
Mtemátics Unidd: Ls Frcciones Ejercicio nº 1.- Escribe, en cd cso, l frcción del todo que corresponde l prte indicd: De un docen de huevos se hn roto. Qué frcción se h roto? b En un urbnizción se hn construido
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
.0. Problems de plicciones de máximos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores extremos en los llmdos: problems de plicciones o problems
Primer octante Segundo octante Tercer octante Cuarto octante P ( X, Y, Z ) P (-X, Y, Z ) P (-X,-Y, Z ) P ( X,-Y, Z )
 Cpítulo III. Álgebr vectoril Objetivo: El lumno plicrá el álgebr vectoril en l resolución de problems geométricos. Contenido: 3.1 Sistem crtesino en tres dimensiones. Simetrí de puntos. 3. Cntiddes esclres
Cpítulo III. Álgebr vectoril Objetivo: El lumno plicrá el álgebr vectoril en l resolución de problems geométricos. Contenido: 3.1 Sistem crtesino en tres dimensiones. Simetrí de puntos. 3. Cntiddes esclres
Si la base de una potencia es positiva y el exponente es negativo de qué signo es el resultado. Pon un ejemplo. Expresa como potencia única de 10:
 Potencis Potenci Qué es un potenci? Relizr el siguiente cálculo : 7 Utilizndo solmente tres doses escribe tods ls epresiones numérics que se pueden formr con ellos. No vle usr otros signos. Cuál es el
Potencis Potenci Qué es un potenci? Relizr el siguiente cálculo : 7 Utilizndo solmente tres doses escribe tods ls epresiones numérics que se pueden formr con ellos. No vle usr otros signos. Cuál es el
INFORME DE LA PRÁCTICA nº 2: LA RUEDA DE MAXWELL. Fernando Hueso González. Carlos Huertas Barra. (1º Fís.), L1, 21-XI-07 - 0 -
 INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID MATERIA: TECNOLOGÍA INDUSTRIAL II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2015-2016 MATERIA: TECNOLOGÍA INDUSTRIAL II INSTRUCCIONES GENERALES Y VALORACIÓN
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
7Soluciones a los ejercicios y problemas PÁGINA 161
 7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
103.- Cuándo un contrato de arrendamiento puede considerarse de tipo financiero?
 103.- Cuándo un contrto pue consirrse tipo finnciero? Autor: Gregorio Lbtut Serer. Universidd Vlenci. Según el PGC Pymes, y el nuevo PGC, un contrto se clificrá como finnciero, cundo ls condiciones económics
103.- Cuándo un contrto pue consirrse tipo finnciero? Autor: Gregorio Lbtut Serer. Universidd Vlenci. Según el PGC Pymes, y el nuevo PGC, un contrto se clificrá como finnciero, cundo ls condiciones económics
MATRICES DE NÚMEROS REALES
 MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
MTRICES. MTURITS Luis Gil Guerr.- DEFINICIÓN MTRICES DE NÚMEROS RELES Llmmos mtriz de números reles de orden m x n un conjunto ordendo de m. n números reles dispuestos en m fils y en n columns i m i m
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: TECNOLOGÍA INDUSTRIAL II Examen para coincidencias INSTRUCCIONES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2012-2013 MATERIA: TECNOLOGÍA INDUSTRIAL II Examen para coincidencias INSTRUCCIONES
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
UNIVERSIDAD NACIONAL DE SAN LUIS FACULTAD DE INGENIERIA Y CIENCIAS AGROPECUARIAS
 V=17V ri=0, UNIVERSIDD NCIONL DE SN LUIS FCULTD DE INGENIERI Y CIENCIS GROPECURIS FÍSIC II TRBJO PRÁCTICO Nº 7: CIRCUITOS DE CORRIENTE CONTINU Ing. Electromecánic-Industril-Quimic-limentos-Electrónic-Mectrónic
V=17V ri=0, UNIVERSIDD NCIONL DE SN LUIS FCULTD DE INGENIERI Y CIENCIS GROPECURIS FÍSIC II TRBJO PRÁCTICO Nº 7: CIRCUITOS DE CORRIENTE CONTINU Ing. Electromecánic-Industril-Quimic-limentos-Electrónic-Mectrónic
TEMA VI: ACIDOS Y BASES
 www.selectividd-cgrnd.com TEMA VI: ACIDOS Y BASES 1.- El ácido clorocético (ClCH COOH) en concentrción 0,01M y 5 C se encuentr disocido en 1%. Clculr: ) L constnte de disocición de dicho ácido. b) El ph
www.selectividd-cgrnd.com TEMA VI: ACIDOS Y BASES 1.- El ácido clorocético (ClCH COOH) en concentrción 0,01M y 5 C se encuentr disocido en 1%. Clculr: ) L constnte de disocición de dicho ácido. b) El ph
Pruebas t para una y dos muestras independientes
 Densidd Densidd AGRO 55 LAB 9 Pruebs t pr un y dos muestrs independientes 1. Clcule ls siguientes probbiliddes usndo l tbl t e InfoStt. Incluy un digrm en cd cso.. P(T>1.356) si gl=1 b. P(T
Densidd Densidd AGRO 55 LAB 9 Pruebs t pr un y dos muestrs independientes 1. Clcule ls siguientes probbiliddes usndo l tbl t e InfoStt. Incluy un digrm en cd cso.. P(T>1.356) si gl=1 b. P(T
CAPÍTULO. Aplicaciones
 CAPÍTULO 3 Aplicciones 3.5 Trbjo de un fuerz 1 Se dice que un fuerz reliz un trbjo cundo cmbi el estdo de reposo o estdo de movimiento de un cuerpo. En este sentido, el trbjo que reliz un fuerz pr llevr
CAPÍTULO 3 Aplicciones 3.5 Trbjo de un fuerz 1 Se dice que un fuerz reliz un trbjo cundo cmbi el estdo de reposo o estdo de movimiento de un cuerpo. En este sentido, el trbjo que reliz un fuerz pr llevr
Desarrollos para planteamientos de ecuaciones de primer grado
 1) Hllr un número tl que su triple menos 5 se igul su doble más 2. 5= 2 + 2 2= 2+ 5 = 7 2) El triple de un número es igul l quíntuplo del mismo menos 20. Cuál es este número? = 5 20 20 = 5 20 = 2 = 10
1) Hllr un número tl que su triple menos 5 se igul su doble más 2. 5= 2 + 2 2= 2+ 5 = 7 2) El triple de un número es igul l quíntuplo del mismo menos 20. Cuál es este número? = 5 20 20 = 5 20 = 2 = 10
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
Ejercicios Contabilidad Tema 4 EMPRESA CRECESA
 EMPRESA CRECESA Ejercicios Contbilidd Tem 4 CRECESA es un empres dedicd l comercilizción de plnts de interior. Se h constituido principios de 20XX y su Blnce finles de ese ño (expresdo en uniddes monetris)
EMPRESA CRECESA Ejercicios Contbilidd Tem 4 CRECESA es un empres dedicd l comercilizción de plnts de interior. Se h constituido principios de 20XX y su Blnce finles de ese ño (expresdo en uniddes monetris)
DESIGUALDADES < d < En el campo de los números reales tenemos una. Un momento de reflexión muestra que una
 DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
MOVIMIENTO DE RODADURA
 E.T.S.. Agrónomos. U.P.. OVENTO DE ODADUA Cuerpos rodntes. Considermos el moimiento de cuerpos que, debido su geometrí, tienen l cpcidd de rodr: eser, ro, disco, supericie eséric, cilindro poydo sobre
E.T.S.. Agrónomos. U.P.. OVENTO DE ODADUA Cuerpos rodntes. Considermos el moimiento de cuerpos que, debido su geometrí, tienen l cpcidd de rodr: eser, ro, disco, supericie eséric, cilindro poydo sobre
Serie 240 Válvulas de accionamiento neumático Tipo y Tipo Válvula de paso recto Tipo 3241
 Serie 240 Válvuls de ccionmiento neumático Tipo 3241-1 y Tipo 3241-7 Válvul de pso recto Tipo 3241 Aplicción Válvul de control pr procesos industriles Diámetro nominl DN 15 DN 300 Presión nominl PN 10
Serie 240 Válvuls de ccionmiento neumático Tipo 3241-1 y Tipo 3241-7 Válvul de pso recto Tipo 3241 Aplicción Válvul de control pr procesos industriles Diámetro nominl DN 15 DN 300 Presión nominl PN 10
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
PLACAS ACANALADAS DE CAUCHO PARA ASIENTO DE RIEL 1 ESPECIFICACIONES A CONSULTAR. Recepción por atributos.
 CONTROL DE CLIDD NORMS Y ESPECIFICCIONES PLCS CNLDS DE CUCHO PR SIENTO DE RIEL Febrero de 1983 1 ESPECIFICCIONES CONSULTR NORM IRM 15/73 IRM 18/60 IRM 21 322/69 IRM 113 027/71 F 124/70 F 125/70 F 126/70
CONTROL DE CLIDD NORMS Y ESPECIFICCIONES PLCS CNLDS DE CUCHO PR SIENTO DE RIEL Febrero de 1983 1 ESPECIFICCIONES CONSULTR NORM IRM 15/73 IRM 18/60 IRM 21 322/69 IRM 113 027/71 F 124/70 F 125/70 F 126/70
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
Tema 4. Integración de Funciones de Variable Compleja
 Tem 4. Integrción de Funciones de Vrible omplej Prof. Willim L ruz Bstids 7 de octubre de 22 Tem 4 Integrción de Funciones de Vrible omplej 4. Integrl definid Se F (t) un función de vrible rel con vlores
Tem 4. Integrción de Funciones de Vrible omplej Prof. Willim L ruz Bstids 7 de octubre de 22 Tem 4 Integrción de Funciones de Vrible omplej 4. Integrl definid Se F (t) un función de vrible rel con vlores
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) (Curso 2003-2004) MATERIA: TECNOLOGÍA INDUSTRIAL II Junio Septiembre R1 R2 INSTRUCCIONES GENERALES Y
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) (Curso 2003-2004) MATERIA: TECNOLOGÍA INDUSTRIAL II Junio Septiembre R1 R2 INSTRUCCIONES GENERALES Y
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Señaléticas Diseño gráfico de señales
 Señlétics Diseño gráfico de señles El cálculo de perímetros y áres de figurs plns es de grn utilidd en l vid práctic, pues l geometrí se encuentr presente en tods prtes. En un min subterráne, ls señles
Señlétics Diseño gráfico de señles El cálculo de perímetros y áres de figurs plns es de grn utilidd en l vid práctic, pues l geometrí se encuentr presente en tods prtes. En un min subterráne, ls señles
CALOR Y TEMPERATURA. b) T real = 47.76 C c) T = -400 C
 CALOR Y TEMPERATURA 1.- En un lugr en que l presión tmosféric es 760 mm de mercurio, introducimos un termómetro centígrdo en hielo fundente y luego en vpor de gu hirviendo. El termómetro, ml grdudo, mrc
CALOR Y TEMPERATURA 1.- En un lugr en que l presión tmosféric es 760 mm de mercurio, introducimos un termómetro centígrdo en hielo fundente y luego en vpor de gu hirviendo. El termómetro, ml grdudo, mrc
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B TECNOLOGÍA. Instrucciones:
 PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B TECNOLOGÍA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: Lee atentamente
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B TECNOLOGÍA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: Lee atentamente
PM/31000 Cilindros elásticos compactos Simple efecto - Ø 2 3/4... 12 pulgadas
 PM/ Cilindros elásticos compactos Simple efecto - Ø 2 /... 2 pulgadas ESTÁNDR MODELOS Ø Nominal Lóbulos (pulgadas) Carrera máxima (mm) Sin rozamiento en la maniobra Libre de mantenimiento o lubricación
PM/ Cilindros elásticos compactos Simple efecto - Ø 2 /... 2 pulgadas ESTÁNDR MODELOS Ø Nominal Lóbulos (pulgadas) Carrera máxima (mm) Sin rozamiento en la maniobra Libre de mantenimiento o lubricación
Protección de forjados de hormigón con Igniplaster. Resistencia al fuego 60, 90, 120 y 180 minutos.
 Protección de forjdos de hormigón con Igniplster. Resistenci l fuego 60, 90, 0 y 80 minutos. Ensyo: LICOF - 56/0 0.06 Dtos técnicos: Forjdo de hormigón. Armdur de cero. Igniplster plicdo por proyección
Protección de forjdos de hormigón con Igniplster. Resistenci l fuego 60, 90, 0 y 80 minutos. Ensyo: LICOF - 56/0 0.06 Dtos técnicos: Forjdo de hormigón. Armdur de cero. Igniplster plicdo por proyección
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD OPCIÓN A
 1.- El bismuto tiene una temperatura de fusión de 271 ºC y el cadmio de 320 ºC, siendo totalmente insolubles en estado sólido. Forman una eutéctica a 144 ºC, que contiene 60 % de Bi. Se pide: a) Dibuje
1.- El bismuto tiene una temperatura de fusión de 271 ºC y el cadmio de 320 ºC, siendo totalmente insolubles en estado sólido. Forman una eutéctica a 144 ºC, que contiene 60 % de Bi. Se pide: a) Dibuje
Física y Química 1º Bach.
 Físic Químic º Bch. I.E.S. Elviñ Problems Recuperción del tercer trimestre 8/06/0 Nombre: Tipo A Tipo B. Un muchcho intent hcer psr un pelot sobre un muro situdo 4,0 m de distnci lnzándol con un velocidd
Físic Químic º Bch. I.E.S. Elviñ Problems Recuperción del tercer trimestre 8/06/0 Nombre: Tipo A Tipo B. Un muchcho intent hcer psr un pelot sobre un muro situdo 4,0 m de distnci lnzándol con un velocidd
COMPRESORES FRIGORIFICOS
 Moelo M M7 M Moelo M4 M6 MOSKAR S.A.I.C. Sntner 66 (1439) Cp. Fe. Repúlic Argentin Tel.: 463816/161/83/3743 4611683 49174 Fx: 46371 Moelo M M7 M Moelo M4 M6 Crcterístics Generles. Por su iseño y construcción,
Moelo M M7 M Moelo M4 M6 MOSKAR S.A.I.C. Sntner 66 (1439) Cp. Fe. Repúlic Argentin Tel.: 463816/161/83/3743 4611683 49174 Fx: 46371 Moelo M M7 M Moelo M4 M6 Crcterístics Generles. Por su iseño y construcción,
TECNA COOLBREEZE. Los nuevos Enfriadores Evaporativos Inteligentes, con control automático de todas las funciones
 TECNA COOLBREEZE Los nuevos Enfridores Evportivos Inteligentes, con control utomático de tods ls funciones Control electrónico de l velocidd REVERSIBLES. Pueden extrer el ire vicido. Limpiez utomátic de
TECNA COOLBREEZE Los nuevos Enfridores Evportivos Inteligentes, con control utomático de tods ls funciones Control electrónico de l velocidd REVERSIBLES. Pueden extrer el ire vicido. Limpiez utomátic de
CAMPOS ELECTROMAGNÉTICOS ESTÁTICOS
 CAMPOS ELECTROMAGNÉTICOS ESTÁTICOS PROBLEMAS PROPUESTOS 1: Se hce girr un superficie pln con un áre de 3,2 cm 2 en un cmpo eléctrico uniforme cuy mgnitud es de 6,2 10 5 N/C. ( ) Determine el flujo eléctrico
CAMPOS ELECTROMAGNÉTICOS ESTÁTICOS PROBLEMAS PROPUESTOS 1: Se hce girr un superficie pln con un áre de 3,2 cm 2 en un cmpo eléctrico uniforme cuy mgnitud es de 6,2 10 5 N/C. ( ) Determine el flujo eléctrico
El Dipolo Plegado. Laboratorio de Electrónica de Comunicaciones Dpto. de Señales y Comunicaciones, U.L.P.G.C
 El Dipolo Plegdo Lbortorio de Electrónic de Comunicciones Dpto. de Señles y Comunicciones, U.L.P.G.C 1 Introducción Un nten muy utilizd en l práctic como receptor es el dipolo plegdo. Este tipo de dipolo
El Dipolo Plegdo Lbortorio de Electrónic de Comunicciones Dpto. de Señles y Comunicciones, U.L.P.G.C 1 Introducción Un nten muy utilizd en l práctic como receptor es el dipolo plegdo. Este tipo de dipolo
Definición genérica de motor: Aparato que transforma en trabajo mecánico cualquier otra forma de energía.
 Definición genérica de motor: Aparato que transforma en trabajo mecánico cualquier otra forma de energía. Nociones sobre el motor: Para empezar, definamos lo que la mayoría de la gente entiende por automóvil.
Definición genérica de motor: Aparato que transforma en trabajo mecánico cualquier otra forma de energía. Nociones sobre el motor: Para empezar, definamos lo que la mayoría de la gente entiende por automóvil.
EJERCICIO PARTE ESPECÍFICA OPCIÓN B DIBUJO TÉCNICO Duración: 1h 15
 Personas Adultas PARTE ESPECÍFICA: DIBUJO TÉCNICO OPCIÓN B DATOS DEL ASPIRANTE CALIFICACIÓN Apellidos:. Nombre:.... EJERCICIO PARTE ESPECÍFICA OPCIÓN B DIBUJO TÉCNICO Duración: 1h 15 EJERCICIO 1. CIRCUNFERENCIAS
Personas Adultas PARTE ESPECÍFICA: DIBUJO TÉCNICO OPCIÓN B DATOS DEL ASPIRANTE CALIFICACIÓN Apellidos:. Nombre:.... EJERCICIO PARTE ESPECÍFICA OPCIÓN B DIBUJO TÉCNICO Duración: 1h 15 EJERCICIO 1. CIRCUNFERENCIAS
SECCIÓN 3 DESCRIPCIÓN DE LOS NÚMEROS REALES
 SEMANA I I I Números Positivos y Negtivos Representción gráfic: SECCIÓN DESCRIPCIÓN DE LOS NÚMEROS REALES -5-4 - - - 0 4 5 Sentido izquierdo Sentido derecho El cero represent l usenci de l cntidd, y es
SEMANA I I I Números Positivos y Negtivos Representción gráfic: SECCIÓN DESCRIPCIÓN DE LOS NÚMEROS REALES -5-4 - - - 0 4 5 Sentido izquierdo Sentido derecho El cero represent l usenci de l cntidd, y es
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERIA MECANICA Y ELECTRICA INGENIERIA EN COMUNICACIONES Y ELECTRÓNICA ACADEMIA DE COMPUTACIÓN
 I. P. N. ESIME Unidad Culhuacan INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERIA MECANICA Y ELECTRICA UNIDAD CULHUACAN INGENIERIA EN COMUNICACIONES Y ELECTRÓNICA ACADEMIA DE COMPUTACIÓN LABORATORIO
I. P. N. ESIME Unidad Culhuacan INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE INGENIERIA MECANICA Y ELECTRICA UNIDAD CULHUACAN INGENIERIA EN COMUNICACIONES Y ELECTRÓNICA ACADEMIA DE COMPUTACIÓN LABORATORIO
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO
 PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
PROBLEMAS RESUELTOS SUMA DE VECTORES METODO GEOMÉTRICO 1. Los vectores mostrdos en l figur tienen l mism mgnitud (10 uniddes) El vector (+c) + (d+) - c, es de mgnitud: c ) 0 ) 0 c) 10 d) 0 e) 10 d Este
Para cuantificar el flujo neto de calor entre dos cuerpos negros, se puede realizar usando la siguiente expresión:
 Flujo de clor neto entre cuerpos negros. Pr cuntificr el flujo neto de clor entre dos cuerpos negros, se puede relizr usndo l siguiente expresión: ( Figur.7 Flujo de clor neto entre cuerpos negros Flujo
Flujo de clor neto entre cuerpos negros. Pr cuntificr el flujo neto de clor entre dos cuerpos negros, se puede relizr usndo l siguiente expresión: ( Figur.7 Flujo de clor neto entre cuerpos negros Flujo
