ÁREAS. 3. Área de una región triangular en función de: 1. Del inradio. 1. Fórmula básica. 2. Fórmula trigonométrica DEFINICIÓN
|
|
|
- María Soledad Márquez Prado
- hace 7 años
- Vistas:
Transcripción
1 ÁS FINIIÓN Áe es e númeo que expes mei e un egión. egión egión uniti 3. Áe e un egión tingu en funión e: 1. e inio omo: p = p. 1u : uni e áe. e ex io Áe e un egión tingu 1. Fómu ási > 9 (p ) (p ) (p ) 3. e iunio. Fómu tigonométi 4. Teoem e Heón omo : p = 5. Segmentos eteminos en ipotenus: m. n m n
2 4. Áe e un equiáteo n funión e o: 3. Peogmo P = omo = Áe e egiones ungues 1. Fómu ási 5. etánguo. 6. uo. Tpeio m n funión e o Τ T = m. n funión e igon 7. uiáteo insito so ptiu n T = n. // 1
3 omo : p = Áe e egiones iues íuo = 8. uiáteo iunsito: oon iu = ( - ) omo : p = p. 9. uiáteo iéntio T. e Piot : + = + Seto iu omo : p = Tpeio iu 1. uiáteo ex insito Segmento iu omo : es ex io ( ) - O O Not: Teoem e Steine: = -
4 = 4 POLMS POPUSTOS 1. H e áe e un uo insito en un íuo e io ) 8m ) 14m ) 16m ) 1m e) N... áe e un íuo es m. uá es e áe e tinguo equiáteo insito en iunfeeni? ) ) ) ) e) N.. 3. u ongitu e un iunfeeni insito en un tiánguo e 3 m e peímeto y uy áe es e 3 m. ) L = ) L = 4 ) L = 8 ) L = 6 e) L = 1 4. uá es e áe e un tiánguo en m, si sus os mien 13 ; y 1m? ) 1m ) 14m ) 16m ) 13m e) N.. 5. Los os e un tinguo mien 1;1 y 14 m. uánto mie e io e íuo insito? ) ) ) ) e) 6. H e áe e íuo. ) (4-1 = 4 ) (4-16 ) (1-4 ) (3 4 e) ( H e áe e egión some. 8 4 ) 1 ) 6 ) 8 ) 1 e) N.. 8. u e áe e egión some. ) 4 6 ) 3 ) 48 ) 3 e) 1 9. H e 8áe e tpeio. ) T = ) T = 1 ) T = 5 ) T = e) T = 6 1. n un tpeio, ( //; > ). Ls áes e os tiánguos O y O son e 5m y 1 m. H e áe e tpeio ( es e punto e ote e s igones). ) 71m ) 36m ) 71,6m ) 36,6m e) 7,6m 3
5 PISM H s Un poieo imito po poígonos igues y peos mos ses y po peogmos mos s. se ists tu: istni ente sus ses Poígonos F G Peepípeo eto: s ists tees son pepeniues s ses, Peepípeo oiuo: ists no pepeniues s ses Peepípeo etánguo: sus s son etánguos. uo o exeo egu: sus s son uos. o = o = o V = 3 o 6 PISM TO PLLPÍO TÁNGULO ist pepeniues s ses s etngues = V =.. PISM OLIUO ist no pepeniues se s omoies PLLPÍPOS s e pism uys ses son peogmos igon: (ee uni os véties opuestos) Áe tot: es sum e tos s s Áe te: es sum e s s tees Supefiies y voúmenes e pisms 1. Áe te ( L ) L = (ist te). (peímeto e se). Áe tot ( T ) T = L + (Áe e se) 3. Voumen (V) ILINO V = (Áe e se). 4
6 g: genetíz : tu Áe te L =. Áe tot T = (+) PIÁMI s egión e espio imit po un supefiie pimi e y un pno que ot tos sus ists. Voumen V =. V ONO VOLUIÓN g V g Áe Lte L = g Áe tot T = g + T = (g + ) Voumen V =. Áe te ( L ) L = (peímeto e se) SF Áe tot ( T ) T = L + Áe e se Áe e supefiie esféi 4 Voumen ( V ) V = (tu) Voumen V = NOT Los iámetos e os piámies semejntes son ente sí omo os uos e sus eementos omóogos 5
7 POLMS POPUSTOS 1. H e áe tot e un peepípeo etngu e 13 m e igon, sieno s imensiones e se 4m y 3m. ) 14m ) 19m ) 136m ) 15m e)18m. Si s ists e un uo se umentn espetivmente en, 4 y 6m, e voumen e peepípeo otenio exee en 568 m 3 voumen e uo o. H igon e uo. ) 5 ) 4 ) 5 ),5 e) N.. 3. L ist e un pism exgon egu mie 1m y ist e se,mie 5m. Que inemento eiiá su ist te e moo que sus áes tees se ifeenien en 4 m? ) 8m ) 6m ) 4m )6m e) m 4. voumen engeno po un tiánguo equiáteo e o X metos que gi eeo e su tu es igu : ) V= x 3 7. áe tot e un teteo es 36. H tu e un se sus s. ) ) 3 ) 5 ) 4 e) 6 8. Ls áes e s ses e un tono e ono son 3 m y 18 m espetivmente y tu es e 6m. uá es su voumen en m 3? ) 14m 3 ) 15m 3 )148m 3 ) 14m 3 e) 96m 9. L ongitu e un iunfeeni máxim e un esfe mie 6,8 m. u e áe e supefiie esféi. ) 1 ) ) 3 ) 4 e) 5 1. áe tot e un pism exgon es e tipe e su áe te. H e voumen e pism, si e o e se mie m. ) 8m 3 ) 7m 3 ) 1m 3 ) 9m 3 e) 9m 3 ) V= x ) V= 1 x 3 ) V= 4 x 3 e) N.. 5. Se tiene un piámie egu e se u e o. H su voumen si te est etemin po un tinguo equiáteo. ) ) ) ) e) 6. Si s figus son un semiesfe y un ono eto, eión e sus voúmenes ) 1 ) 3 ) 3 ) 1 e) N.. 6
Área de figuras planas
 4º ESO Mtemátics Acdémics Unidd 0. Áes y voúmenes Áe de figus pns Tendemos en cuent que, en cd cso, memos A áe o supeficie de cd un de s figus pns. Poígonos Cuddo Rectánguo Romo A = do A = se = tu Romoide
4º ESO Mtemátics Acdémics Unidd 0. Áes y voúmenes Áe de figus pns Tendemos en cuent que, en cd cso, memos A áe o supeficie de cd un de s figus pns. Poígonos Cuddo Rectánguo Romo A = do A = se = tu Romoide
CALCULAR ÁREAS DE POLÍGONOS Y FIGURAS CIRCULARES
 REPSO Y POYO OBJETIVO 1 6 CLCULR ÁRES DE POLÍONOS Y FIURS CIRCULRES Nome: Cuso: Fec: ÁRE DE POLÍONOS Áe de tiánguo Áe de cuddo Áe de ectánguo se? tu? = = =? =? Áe de peogmo Áe de tpecio Áe de omo B D d
REPSO Y POYO OBJETIVO 1 6 CLCULR ÁRES DE POLÍONOS Y FIURS CIRCULRES Nome: Cuso: Fec: ÁRE DE POLÍONOS Áe de tiánguo Áe de cuddo Áe de ectánguo se? tu? = = =? =? Áe de peogmo Áe de tpecio Áe de omo B D d
LUGARES GEOMÉTRICOS Y ÁNGULOS
 REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nome: Cuso: Fec: Se m ug geomético conjunto de todos os puntos que cumpen un detemind popiedd geométic. EJEMPLO Cuá es e ug geomético de os puntos
REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nome: Cuso: Fec: Se m ug geomético conjunto de todos os puntos que cumpen un detemind popiedd geométic. EJEMPLO Cuá es e ug geomético de os puntos
CALCULAR ÁREAS DE POLÍGONOS Y FIGURAS CIRCULARES
 REPSO Y POYO OBJETIVO 6 CLCULR ÁRES DE POLÍONOS Y FIURS CIRCULRES Nome: Cuso: Fec: ÁRE DE POLÍONOS Áe de tiánguo Áe de cuddo Áe de ectánguo se? tu? = = =? =? Áe de peogmo Áe de tpecio Áe de omo B D d B
REPSO Y POYO OBJETIVO 6 CLCULR ÁRES DE POLÍONOS Y FIURS CIRCULRES Nome: Cuso: Fec: ÁRE DE POLÍONOS Áe de tiánguo Áe de cuddo Áe de ectánguo se? tu? = = =? =? Áe de peogmo Áe de tpecio Áe de omo B D d B
Siempre verifica que a 2 = b 2 + c 2 (Th. Pitágoras)
 Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
10. Teoremas de Thales y Pitágoras
 140 SOLUCIONRIO 10. Teoems de Tles y itágos 5. Dibuj un eágono y todos sus ángulos. Cuánto sumn ente todos ellos? 1. LUGRES GEOMÉTRICOS Y ÁNGULOS IENS Y CLCUL Cuánto mide d uno de los ino ángulos entles
140 SOLUCIONRIO 10. Teoems de Tles y itágos 5. Dibuj un eágono y todos sus ángulos. Cuánto sumn ente todos ellos? 1. LUGRES GEOMÉTRICOS Y ÁNGULOS IENS Y CLCUL Cuánto mide d uno de los ino ángulos entles
( x ) ( x 2 4 ) = x 2
 9. Teoems de Tles y itágos 5. Dibuj un eágono y todos sus ángulos. Cuánto sumn ente todos ellos? 1. Luges geométios y ángulos IENS Y CLCUL Cuánto mide d uno de los ino ángulos entles de un pentágono egul?
9. Teoems de Tles y itágos 5. Dibuj un eágono y todos sus ángulos. Cuánto sumn ente todos ellos? 1. Luges geométios y ángulos IENS Y CLCUL Cuánto mide d uno de los ino ángulos entles de un pentágono egul?
FIGURAS EN EL PLANO Y EN EL ESPACIO
 Consejeí de Educción, Cultu y Depotes CENTRO DE EDUCACIÓN DE PERSONAS ADULTAS. Simienz C/ Fncisco Gcí Pvón, 16 Tomelloso 1700 (C. Rel) Teléfono Fx: 96 51 9 9 Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS
Consejeí de Educción, Cultu y Depotes CENTRO DE EDUCACIÓN DE PERSONAS ADULTAS. Simienz C/ Fncisco Gcí Pvón, 16 Tomelloso 1700 (C. Rel) Teléfono Fx: 96 51 9 9 Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS
Colegio Villa María la Planicie ÁREA DE MATEMÁTICA
 oleio Vill Mí l Plnicie ÁRE DE MEMÁI MERI N 10 Pofeso: S. los lmeid ellido Quinto de Secundi oodindo de áe: S. Gby Sáncez Fec: ctube de 2016 1. U ó HEXEDR REGUR SÓIDS GEMÉRIS Áe del cubo: = 6 2 Volumen
oleio Vill Mí l Plnicie ÁRE DE MEMÁI MERI N 10 Pofeso: S. los lmeid ellido Quinto de Secundi oodindo de áe: S. Gby Sáncez Fec: ctube de 2016 1. U ó HEXEDR REGUR SÓIDS GEMÉRIS Áe del cubo: = 6 2 Volumen
2πR π =
 PÁGIN 11 Pág. 1 oodends geogáfi cs 19 os ciuddes tienen l mism longitud, 15 E, y sus ltitudes son 7 5' N y 5' S. uál es l distnci ente ells? R b 7 5' b 5' Tenemos que ll l longitud del co coespondiente
PÁGIN 11 Pág. 1 oodends geogáfi cs 19 os ciuddes tienen l mism longitud, 15 E, y sus ltitudes son 7 5' N y 5' S. uál es l distnci ente ells? R b 7 5' b 5' Tenemos que ll l longitud del co coespondiente
( ) 2 ( ) ( ) ( ) ( ) RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN SEMANA 11 ÁREAS I RPTA.: D = = RPTA.: D = AE AE = 12. 5a = 6 5.
 SEMN ÁRES I. En un tiánguo ectánguo ecto en, e ánguo mide 75 y distnci de hipotenus mide 6 cm. cue e áe de egión. ) 00 cm ) 36 cm ) 84 cm D) 44cm E) 7cm Popiedd (75º; 75º) H 4 4 4 6 ( ) 44 cm RPT.: D.
SEMN ÁRES I. En un tiánguo ectánguo ecto en, e ánguo mide 75 y distnci de hipotenus mide 6 cm. cue e áe de egión. ) 00 cm ) 36 cm ) 84 cm D) 44cm E) 7cm Popiedd (75º; 75º) H 4 4 4 6 ( ) 44 cm RPT.: D.
SISTEMA SEXAGESIMAL. Unidad: El grado sexagesimal (º). 1 º = ángulo completo 360. ángulo completo = º = 400 g = 2π rad
 TRIGNMETRÍ. ÁNGULS igen: Positivos: tido ntihoio. Negtivos: tido hoio. + MEDID DE ÁNGULS Sistem segesiml Sistem entesiml Rdines SISTEM SEXGESIML. Unidd: El gdo segesiml (º. ángulo ompleto 60º º ángulo
TRIGNMETRÍ. ÁNGULS igen: Positivos: tido ntihoio. Negtivos: tido hoio. + MEDID DE ÁNGULS Sistem segesiml Sistem entesiml Rdines SISTEM SEXGESIML. Unidd: El gdo segesiml (º. ángulo ompleto 60º º ángulo
GEOMETRÍA 3º E.S.O. FIGURAS SEMEJANTES SEMEJANZA DE TRIÁNGULOS SEMEJANZA DE TRIÁNGULOS
 GEOMETRÍ DEL PLNO 3º E.S.O. FIGURS SEMEJNTES Dos figus son semejntes cundo sólo difieen en tmño. Los segmentos coespondientes son popocionles. d longitud de un de ells se otiene multiplicndo l longitud
GEOMETRÍ DEL PLNO 3º E.S.O. FIGURS SEMEJNTES Dos figus son semejntes cundo sólo difieen en tmño. Los segmentos coespondientes son popocionles. d longitud de un de ells se otiene multiplicndo l longitud
3.3.6 Perímetro en la circunferencia y área en el círculo.
 3.3.6 Peímeto en a cicunfeencia y áea en e cícuo. Peímeto de a cicunfeencia. Es a ongitud (L de a cicunfeencia, se cacua con as siguientes fómuas. d adio diámeto L = d Peo d =, entonces L = Ecuación paa
3.3.6 Peímeto en a cicunfeencia y áea en e cícuo. Peímeto de a cicunfeencia. Es a ongitud (L de a cicunfeencia, se cacua con as siguientes fómuas. d adio diámeto L = d Peo d =, entonces L = Ecuación paa
BORSÍ TÈCNIC/A AUXILIAR D'INFERMERIA LLISTAT PROVISIONAL
 OÍ ÈI/ UII 'II I OIIO ÈI UII 'II 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 otal 48,8000
OÍ ÈI/ UII 'II I OIIO ÈI UII 'II 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 otal 48,8000
Escaleno: TEOREMAS FUNDAMENTALES O PROPIEDADES DE LOS TRIÁNGULOS
 TRIÁNGULO: Supefiie pln limitd po tes segmentos o ldos que se otn dos dos en tes véties. NOENLTUR: Los véties se nomn on lets minúsuls y los ldos on lets myúsuls emplendo l mism let que el vétie opuesto.
TRIÁNGULO: Supefiie pln limitd po tes segmentos o ldos que se otn dos dos en tes véties. NOENLTUR: Los véties se nomn on lets minúsuls y los ldos on lets myúsuls emplendo l mism let que el vétie opuesto.
Geometría. Ángulos. Complementarios y suplementarios. Clasificación de los ángulos. Lados paralelos. Lados perpendiculares
 Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. Jesús Grcí de Jón de Fuente IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios
Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. Jesús Grcí de Jón de Fuente IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios
Lados Vértice complementarios CONVEXO CÓNCAVO suplementarios
 Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios CÓNCAVO CONVEXO Dos ánguos
Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios CÓNCAVO CONVEXO Dos ánguos
Tema 13: INTEGRALES DEFINIDAS
 Tem : INTEGRALES DEFINIDAS REFLEXIONA Ls gnnis de l ompñí RAMSES S.L. dunte los meses de un ño, en deens de miles de euos, se dn en l siguiente gái: 5 ENE FEB MAR ABR MAY JUN JUL AGO SEP OCT NOV DIC Si
Tem : INTEGRALES DEFINIDAS REFLEXIONA Ls gnnis de l ompñí RAMSES S.L. dunte los meses de un ño, en deens de miles de euos, se dn en l siguiente gái: 5 ENE FEB MAR ABR MAY JUN JUL AGO SEP OCT NOV DIC Si
UNIVERSIDAD NACIONAL DE FRONTERA CEPREUNF CICLO REGULAR
 UNIVERSIDD NIONL DE FRONTER EPREUNF ILO REGULR 0708 URSO: MTEMÁTI SEMN 0 TEM: TRIÀNGULOS R.T. NGULOS GUDOS R.T. ULQUIER MGNITUD TEM: PRODUTOS NOTLES DIVISIÓN LGERI OIENTES NOTLES TRINGULOS DEFINIIÓN: Tiángulo
UNIVERSIDD NIONL DE FRONTER EPREUNF ILO REGULR 0708 URSO: MTEMÁTI SEMN 0 TEM: TRIÀNGULOS R.T. NGULOS GUDOS R.T. ULQUIER MGNITUD TEM: PRODUTOS NOTLES DIVISIÓN LGERI OIENTES NOTLES TRINGULOS DEFINIIÓN: Tiángulo
TRIGONOMETRÍA. rad equivalen a 180º Observación: Generalmente no se utiliza «rad», cuando se da la medida de un ángulo en sistema absoluto.
 TRIGONOMETRÍA INTRODUCCIÓN En un sentido ásio, se puede fim que l Tigonometí es el estudio de ls eliones numéis ente los ángulos ldos del tiángulo. Peo su desollo l h llevdo tene un ojetivo más mplio,
TRIGONOMETRÍA INTRODUCCIÓN En un sentido ásio, se puede fim que l Tigonometí es el estudio de ls eliones numéis ente los ángulos ldos del tiángulo. Peo su desollo l h llevdo tene un ojetivo más mplio,
CAMPOS ELECTROMAGNÉTICOS Tema 2.1 Electrostática
 TS. Ingenieí e Teleomniión Dto. Teoí e l Señl y Comniiones CMPOS LCTROMGNÉTICOS Tem. letostáti P.- n los véties e n tiánglo eqiláteo e los s están sits tes ts ositivs igles e vlo q. Cál es l fez qe tú
TS. Ingenieí e Teleomniión Dto. Teoí e l Señl y Comniiones CMPOS LCTROMGNÉTICOS Tem. letostáti P.- n los véties e n tiánglo eqiláteo e los s están sits tes ts ositivs igles e vlo q. Cál es l fez qe tú
GEOMETRÍA ANALÍTICA - SECCIONES CÓNICAS
 GEOMETRÍA ANALÍTICA SECCIONES CÓNICAS PARÁBOLA ELIPSE p + oe + M(0, ) p F(0, p) V P (, p) P(, ) V(, 0) F(, 0) F(, 0) V(, M(0, ) HIPÉRBOLA oe + W(0, ) F(, 0) F(, 0) V(, 0) V(, 0) W(0, ) fe mejo e FORMULAS
GEOMETRÍA ANALÍTICA SECCIONES CÓNICAS PARÁBOLA ELIPSE p + oe + M(0, ) p F(0, p) V P (, p) P(, ) V(, 0) F(, 0) F(, 0) V(, M(0, ) HIPÉRBOLA oe + W(0, ) F(, 0) F(, 0) V(, 0) V(, 0) W(0, ) fe mejo e FORMULAS
RAZONAMIENTO CUANTITATIVO
 Guí Emen psiométio e ingeso ls univesies RZONMIENTO UNTITTIVO En est áe se nlizn ls pies e utilizión e númeos téminos mtemátios p esolve polems untittivos, l pi e nliz tos pesentos jo ivess foms tles omo
Guí Emen psiométio e ingeso ls univesies RZONMIENTO UNTITTIVO En est áe se nlizn ls pies e utilizión e númeos téminos mtemátios p esolve polems untittivos, l pi e nliz tos pesentos jo ivess foms tles omo
12 Cuerpos. en el espacio. 1. Elementos básicos en el espacio. Dibuja a mano alzada un punto, una recta, un romboide y un cubo.
 12 uepos en el espcio 1. Elementos básicos en el espcio ibuj mno lzd un punto, un ect, un omboide y un cubo. P I E N S A Y A L U L A Rect Punto Romboide ubo né clculist 489,6 : 7,5 = 65,28; R = 0 1 2 Escibe
12 uepos en el espcio 1. Elementos básicos en el espcio ibuj mno lzd un punto, un ect, un omboide y un cubo. P I E N S A Y A L U L A Rect Punto Romboide ubo né clculist 489,6 : 7,5 = 65,28; R = 0 1 2 Escibe
ANÁLISIS DE LA COMPACIDAD DE FORMAS POLIÉDRICAS OBTENIDAS POR TRUNCAMIENTO DE OTRAS QUE POSEAN ESFERA INSCRITA
 XI CONGRESO INTERNACIONAL E INGENIERÍA GRÁFICA ANÁLISIS E LA COMACIA E FORMAS OLIÉRICAS OBTENIAS OR TRUNCAMIENTO E OTRAS QUE OSEAN ESFERA INSCRITA SUÁREZ GONZÁLEZ, Jesús; ÁLAREZ GÓMEZ, José Manuel; EGA
XI CONGRESO INTERNACIONAL E INGENIERÍA GRÁFICA ANÁLISIS E LA COMACIA E FORMAS OLIÉRICAS OBTENIAS OR TRUNCAMIENTO E OTRAS QUE OSEAN ESFERA INSCRITA SUÁREZ GONZÁLEZ, Jesús; ÁLAREZ GÓMEZ, José Manuel; EGA
Perímetros. Cuadrado: EL PERÍMETRO: a a P = a + a + a + a P = 4a
 Perímetros EL PEÍMETO: udrdo: P El perímetro de ls figurs puede medirse usndo uniddes de medid de longitud. Por lo tnto se puede medir en centímetros, decímetros, metros. Ejemplo: El perímetro del triángulo
Perímetros EL PEÍMETO: udrdo: P El perímetro de ls figurs puede medirse usndo uniddes de medid de longitud. Por lo tnto se puede medir en centímetros, decímetros, metros. Ejemplo: El perímetro del triángulo
APUNTES DE CRISTALOGRAFÍA: RETÍCULO RECÍPROCO Màrius Vendrell RETÍCULO RECÍPROCO
 RETÍCULO RECÍPROCO A pti el etíulo efinio nteiomente, en el que omo nuo oespone un motivo o llmemos etíulo ieto, es posible efini oto etíulo (que llmemos eípoo) en el ul los tes vetoes funmentles son:
RETÍCULO RECÍPROCO A pti el etíulo efinio nteiomente, en el que omo nuo oespone un motivo o llmemos etíulo ieto, es posible efini oto etíulo (que llmemos eípoo) en el ul los tes vetoes funmentles son:
VOLÚMENES Y ÁREAS DE LOS PRINCIPALES POLIEDROS
 Macosap Matemática lgea 0 OÚMENES Y ÁES DE OS PINCIPES POIEDOS olumen y Áea e un Otoeo Consieemos el siguiente otoeo: a Diagonal Caa volumen ista a ista: ínea fomaa po la unión e os caas Caa: Caa uno e
Macosap Matemática lgea 0 OÚMENES Y ÁES DE OS PINCIPES POIEDOS olumen y Áea e un Otoeo Consieemos el siguiente otoeo: a Diagonal Caa volumen ista a ista: ínea fomaa po la unión e os caas Caa: Caa uno e
( ) ( ) ( ) RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN SEMANA 2 LONGITUD DE ARCO RPTA.: D RPTA.: C
 EMN ONGITU E O 3. i: l + l 6. Hlle el áe del sect cicul EOF.. lcule l lngitud de un c en un sect cicul cuy ángul centl mide º y su di mide 00 cm. ) m ) m ) m ) ) ) 3 E ) 0 m E) 0 m º i: º d ; 00 cm m 0
EMN ONGITU E O 3. i: l + l 6. Hlle el áe del sect cicul EOF.. lcule l lngitud de un c en un sect cicul cuy ángul centl mide º y su di mide 00 cm. ) m ) m ) m ) ) ) 3 E ) 0 m E) 0 m º i: º d ; 00 cm m 0
2.7 Cilindros, conos, esferas y pirámides
 UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
Razón Trigonométrica (R.T) Propiedades Fundamentales. 54 Trigonometría Und. 2 R.T. de Ángulos Agudos A.
 Luego estbleemos que:.o = Longitud del teto opuesto. RAZÓN TRIGONOMÉTRIA NOTAIÓN EFINIIÓN RAZÓN.A = Longitud del teto dyente. H = Longitud de l hipotenus. En físi es de gn impotni l pliión de los vetoes
Luego estbleemos que:.o = Longitud del teto opuesto. RAZÓN TRIGONOMÉTRIA NOTAIÓN EFINIIÓN RAZÓN.A = Longitud del teto dyente. H = Longitud de l hipotenus. En físi es de gn impotni l pliión de los vetoes
2. TRANSFORMACIONES GEOMÉTRICAS
 IUJO TÉNIO HILLRTO Lámins esuelts del TM. TRNSFORMIONS GOMÉTRIS eptmento de tes Plástis y iujo Tz un plel s que diste 5 mm de l et dd. dos los segmentos y, hll su poduto (x). d = = d = 1 m = 1d = d x =
IUJO TÉNIO HILLRTO Lámins esuelts del TM. TRNSFORMIONS GOMÉTRIS eptmento de tes Plástis y iujo Tz un plel s que diste 5 mm de l et dd. dos los segmentos y, hll su poduto (x). d = = d = 1 m = 1d = d x =
Óvalo dados los dos ejes: óvalo óptimo
 l óvlo es un urv err y pln que está ompuest por utro, o más, ros e irunferéni simétrios entre sí. Suele venir efinio por os ejes que mrn sus imensiones y sirven e ejes e simetrí e los ros. Se emple freuentemente
l óvlo es un urv err y pln que está ompuest por utro, o más, ros e irunferéni simétrios entre sí. Suele venir efinio por os ejes que mrn sus imensiones y sirven e ejes e simetrí e los ros. Se emple freuentemente
TRIGONOMETRÍA (Resumen) Definiciones generales (válidas para cualquier ángulo de cualquier cuadrante) y r. cosec. sec. cotg x +
 TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto opuesto Razones de
TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto opuesto Razones de
RELACIONES METRICAS. Proyección de un segmento AB sobre una recta L
 ELIONE METI ELIONE MÉTI P el estudio de ls eliones métis ente los elementos de los tiángulos, es indispensle se el onepto de poyeión. Poyeión de un punto: L poyeión de un punto P soe un et L, es el pie
ELIONE METI ELIONE MÉTI P el estudio de ls eliones métis ente los elementos de los tiángulos, es indispensle se el onepto de poyeión. Poyeión de un punto: L poyeión de un punto P soe un et L, es el pie
ACTIVIDADES DE REPASO - 3ª EVALUACIÓN
 Coeio o e Dios oi Mteátics - º ESO CIIDDES DE REPSO - ª EUCIÓN ECUCIONES DE º GRDO Resueve s siuientes ecuciones: c Resueve s siuientes ecuciones: c Resueve s siuientes ecuciones: c Resueve s siuientes
Coeio o e Dios oi Mteátics - º ESO CIIDDES DE REPSO - ª EUCIÓN ECUCIONES DE º GRDO Resueve s siuientes ecuciones: c Resueve s siuientes ecuciones: c Resueve s siuientes ecuciones: c Resueve s siuientes
Integrales dobles. divide al rectángulo I ab, cd. , j 1, 2,, m. n m ij i i 1 j j 1
 ntegrles oles NTEGRALES OBLES e l mism mner que el onepto e integrl efini pr funiones e un vrile sirve pr resolver e un moo generl, el prolem e l eterminión e áres e figurs plns, el onepto e integrl ole
ntegrles oles NTEGRALES OBLES e l mism mner que el onepto e integrl efini pr funiones e un vrile sirve pr resolver e un moo generl, el prolem e l eterminión e áres e figurs plns, el onepto e integrl ole
α = β Geometría Compendio Blademir González Parián
 = Geoetí opeio ei Goáe iá GÍ IÍ ÍU I GU: IIIÓ, IIIÓ Y I. eetos e Geoetí IIIÓ IIIÓ I igu geoéti s stió que se tiee e fo e u ojeto e o ieistete. uto íe óio o. uto. o. spio 4. íe 5. íe et 6. o 7. eiet 8.
= Geoetí opeio ei Goáe iá GÍ IÍ ÍU I GU: IIIÓ, IIIÓ Y I. eetos e Geoetí IIIÓ IIIÓ I igu geoéti s stió que se tiee e fo e u ojeto e o ieistete. uto íe óio o. uto. o. spio 4. íe 5. íe et 6. o 7. eiet 8.
TRIGONOMETRÍA 1 (Resumen) cotg. Definiciones generales (válidas para cualquier ángulo de cualquier cuadrante) y r. cosec. sec.
 Tignometía Resumen TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto
Tignometía Resumen TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto
COTOS REGIONALES Y ZONAS DE CAZA CONTROLADA
 OO IO O OO 2013 esto cazadores istado de dmitidos por úmero de orteo úm ol. 5 11 12 13 14 15 17 18 19 20 21 22 25 26 27 28 29 31 32 34 35 37 38 41 42 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 60 61
OO IO O OO 2013 esto cazadores istado de dmitidos por úmero de orteo úm ol. 5 11 12 13 14 15 17 18 19 20 21 22 25 26 27 28 29 31 32 34 35 37 38 41 42 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 60 61
COMPRENDER EL TEOREMA DE PITÁGORAS
 OBJETIVO 1 COMPRENDER EL TEOREMA DE PITÁGORAS NOMBRE: CURSO: ECHA: TRIÁNGULO RECTÁNGULO Un triánguo rectánguo tiene un ánguo recto (90 ). Los os que formn e ánguo recto se enominn ctetos, b y c. E o myor
OBJETIVO 1 COMPRENDER EL TEOREMA DE PITÁGORAS NOMBRE: CURSO: ECHA: TRIÁNGULO RECTÁNGULO Un triánguo rectánguo tiene un ánguo recto (90 ). Los os que formn e ánguo recto se enominn ctetos, b y c. E o myor
2πε. V b a. b a. dr r 850V E 3
 3.6 El tuo e un conto Geige tiene un cilino metálico lgo y hueco e cm e iámeto. too lo lgo el eje el tuo hy un lme e.7 mm e iámeto. uno el tuo está funcionno, se plic un voltje e 85 V ente los conuctoes.
3.6 El tuo e un conto Geige tiene un cilino metálico lgo y hueco e cm e iámeto. too lo lgo el eje el tuo hy un lme e.7 mm e iámeto. uno el tuo está funcionno, se plic un voltje e 85 V ente los conuctoes.
LUGARES GEOMÉTRICOS Y ÁNGULOS
 REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nombe: Cuso: Fec: Se llm lug geomético l conjunto de todos los puntos que cumplen un detemind popiedd geométic. EJEMPLO Cuál es el lug geomético
REPASO Y APOYO OBJETIVO 1 LUGARES GEOMÉTRICOS Y ÁNGULOS Nombe: Cuso: Fec: Se llm lug geomético l conjunto de todos los puntos que cumplen un detemind popiedd geométic. EJEMPLO Cuál es el lug geomético
Apéndice D. Estimación de los efectos capacitivos e inductivos entre el inyector y el detector
 Apénice D D-1 Apénice D. Estimación e os efectos capacitivos e inuctivos ente e inyecto y e etecto E acopamiento capacitivo e inuctivo ente e sistema inyecto y e etecto puee povoca eoes en a tensión etectaa.
Apénice D D-1 Apénice D. Estimación e os efectos capacitivos e inuctivos ente e inyecto y e etecto E acopamiento capacitivo e inuctivo ente e sistema inyecto y e etecto puee povoca eoes en a tensión etectaa.
4 Dibuja dos rectas perpendiculares al segmento AB por sus
 1 Hll l meditiz del egmento. 2 Tz l et pependiul l et po el punto. m 3 Tz l pependiul l et dede el punto. uál e l ditni del punto l et? 4 ibuj do et pependiule l egmento po u extemo. pli do método ditinto.
1 Hll l meditiz del egmento. 2 Tz l et pependiul l et po el punto. m 3 Tz l pependiul l et dede el punto. uál e l ditni del punto l et? 4 ibuj do et pependiule l egmento po u extemo. pli do método ditinto.
1. SUPERFICIE PRISMÁTICA Y PRISMA
 1. SUPERFICIE PRISMÁTICA Y PRISMA. SUPERFICIE PIRAMIDAL Y PIRÁMIDE. CUERPOS REDONDOS. 4. SÓLIDOS DE REVOLUCIÓN Objetivos: Detemin áes de supeficies. Detemin volúmenes de sólidos. 1 1. SUPERFICIE PRISMÁTICA
1. SUPERFICIE PRISMÁTICA Y PRISMA. SUPERFICIE PIRAMIDAL Y PIRÁMIDE. CUERPOS REDONDOS. 4. SÓLIDOS DE REVOLUCIÓN Objetivos: Detemin áes de supeficies. Detemin volúmenes de sólidos. 1 1. SUPERFICIE PRISMÁTICA
Multiplicando miembro a miembro las siguientes desigualdades
 Miguel mengul ov L deiguldd de Eule pti de ot deiguldde ente elemento de un tiángulo. Ete tíulo e ontinuión del pulido en el númeo 5 (eneo-feeo 003). En et egund pte e etleen ei deiguldde geométi do tigonométi,
Miguel mengul ov L deiguldd de Eule pti de ot deiguldde ente elemento de un tiángulo. Ete tíulo e ontinuión del pulido en el númeo 5 (eneo-feeo 003). En et egund pte e etleen ei deiguldde geométi do tigonométi,
, donde a y b son números cualesquiera.
 Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Esto es sólo una muestras de los ejercicios, repasa también los de la libreta y los del libro.
 MATEMÁTICAS º ESO Esto es sólo un muestrs e los ejeriios, reps tmién los e l liret los el liro. Deprtmento e Mtemátis Coleio Sgro Corzón e Jesús ontever. eliz ests operiones: - 8 - -. Efetú: - - - - -
MATEMÁTICAS º ESO Esto es sólo un muestrs e los ejeriios, reps tmién los e l liret los el liro. Deprtmento e Mtemátis Coleio Sgro Corzón e Jesús ontever. eliz ests operiones: - 8 - -. Efetú: - - - - -
UNIDAD 7 Problemas métricos
 Pág. 1 e x = 11 + 4l x = 11 9l 1 1 : y = + l : y = l z = 7 + l z = 7 7l a) Halla las istancias ente los puntos e cote e 1 y con π: x y + z 4 = 0. b) Halla el ángulo e 1 con. c) Halla el ángulo e 1 con
Pág. 1 e x = 11 + 4l x = 11 9l 1 1 : y = + l : y = l z = 7 + l z = 7 7l a) Halla las istancias ente los puntos e cote e 1 y con π: x y + z 4 = 0. b) Halla el ángulo e 1 con. c) Halla el ángulo e 1 con
Ejercicios TIPO de estequiometría Factores Conversión 4º ESO diciembre
 Ejeriios TIPO e estequiometrí Ftores Conversión 4º ESO iiemre 011 1 1. Cálulos ms ms. Cálulos ms volumen. Cálulos volumen volumen 4. Cálulos on retivos impuros 5. Cálulos on renimiento istinto el 100 %
Ejeriios TIPO e estequiometrí Ftores Conversión 4º ESO iiemre 011 1 1. Cálulos ms ms. Cálulos ms volumen. Cálulos volumen volumen 4. Cálulos on retivos impuros 5. Cálulos on renimiento istinto el 100 %
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/74/71224437.jpg) IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
IES P Pov (Gui Mtmátis II UNIDD : INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los vlos,,
INTRODUCCIÓN AL CÁLCULO VECTORIAL
 INTRODUCCIÓN L CÁLCULO VECTORIL 1.- MGNITUDES ESCLRES Y VECTORILES. Mgnitudes esles: son ls que quedn pefetmente definids po el vlo de l medid. Mgnitudes vetoiles: son ls que p definils pefetmente es peiso
INTRODUCCIÓN L CÁLCULO VECTORIL 1.- MGNITUDES ESCLRES Y VECTORILES. Mgnitudes esles: son ls que quedn pefetmente definids po el vlo de l medid. Mgnitudes vetoiles: son ls que p definils pefetmente es peiso
Con la medida del radio r dibujar una circunferencia y dibujar sus diámetros vertical y horizontal que pase por el centro. o
 * constucciones de cuadiáteos (pobemas de cuadiáteos 5.3- CUADRADO *conocido e ado. Se toma a medida de ado con e compás y a dibujamos sobe una ecta cuaquiea Con a medida de ado se dibuja un aco desde
* constucciones de cuadiáteos (pobemas de cuadiáteos 5.3- CUADRADO *conocido e ado. Se toma a medida de ado con e compás y a dibujamos sobe una ecta cuaquiea Con a medida de ado se dibuja un aco desde
a la componente imaginaria de z. Dos números complejos son iguales cuando tienen la misma parte real y la misma parte imaginaria.
 Númeos Complejos Un Defnón Llmemos númeo omplejo un númeo z que se ese e l fom, one y son númeos eles, e vef:. Al númeo se lo enomn pte el e z y l númeo, pte mgn e z. pte } pte } mgn Se esgn on Re ( z)
Númeos Complejos Un Defnón Llmemos númeo omplejo un númeo z que se ese e l fom, one y son númeos eles, e vef:. Al númeo se lo enomn pte el e z y l númeo, pte mgn e z. pte } pte } mgn Se esgn on Re ( z)
MATRICES: un apunte teórico-práctico
 MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
Arista Los polígonos que limitan al poliedro se llaman caras. Tetraedro Cubo Octaedro Dodecaedro Icosaedro
 OBJETIVO 1 CLASIICAR POLIEDROS NOMBRE: CURSO: ECHA: POLIEDROS Un poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Aista Los polígonos que limitan al poliedo se llaman caas. Caa
OBJETIVO 1 CLASIICAR POLIEDROS NOMBRE: CURSO: ECHA: POLIEDROS Un poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Aista Los polígonos que limitan al poliedo se llaman caas. Caa
CURVAS TÉCNICAS Óvalo, ovoide, espiral y voluta. Trazado como aplicación de tangencias TEMA9. Objetivos y orientaciones metodológicas. 1.
 URS ÉNIS Óvlo, ovoide, espil y volut. zdo omo pliión de tngenis jetivos y oientiones metodológis E9 IUJ GEÉRI Se tt de un unidd temáti ot y senill. El lumno pendeá, l menos, un poedimiento de onstuión
URS ÉNIS Óvlo, ovoide, espil y volut. zdo omo pliión de tngenis jetivos y oientiones metodológis E9 IUJ GEÉRI Se tt de un unidd temáti ot y senill. El lumno pendeá, l menos, un poedimiento de onstuión
α A TRIGONOMETRÍA PLANA
 TRIGONOMETRÍ PLN El origen de l plr trigonometrí puede enontrrse en el griego, trígono triángulo y metrí medid. L trigonometrí justmente trt de eso, l mediión y resoluión de situiones donde se preten triángulos.
TRIGONOMETRÍ PLN El origen de l plr trigonometrí puede enontrrse en el griego, trígono triángulo y metrí medid. L trigonometrí justmente trt de eso, l mediión y resoluión de situiones donde se preten triángulos.
1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }
![1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x } 1. ÁREA BAJO UNA CURVA. INTEGRAL DEFINIDA. PROPIEDADES. Sea f continua en [ ] = K con. : Conjunto finito de puntos P { x x,, x, x }](/thumbs/64/51459891.jpg) IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
IES P Pov (Gui Mtmátis II UNIDD INTEGRL DEFINID.. ÁRE BJO UN CURV. INTEGRL DEFINID. PROPIEDDES., o (,. S otiu [ (Positiv [ Ptiió [, : Cojuto iito putos P {,,, } < < < K < K o, Diámto l ptiió P : Myo los
ELECTRICIDAD Y MAGNETISMO. Electromagnetismo
 ELECTCDAD Y MAGNETSMO. Eectomgnetimo ) Ccu fue eectomoti inducid en un epi po un p de io peo de gn ongitud, po o que cicu un coiente igu peo con entido contio. b ) En un emiepcio > exite un cmpo mgnético,
ELECTCDAD Y MAGNETSMO. Eectomgnetimo ) Ccu fue eectomoti inducid en un epi po un p de io peo de gn ongitud, po o que cicu un coiente igu peo con entido contio. b ) En un emiepcio > exite un cmpo mgnético,
7 Semejanza. y trigonometría. 1. Teorema de Thales
 7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
OBJETIVOS MÍNIMOS Y TRABAJO DE VERANO MATEMÁTICAS 2013
 MATEMÁTICAS 0 OBJETIVOS MÍNIMOS REQUERIDOS - Operiones omins on números enteros. - Potenis ríes urs. - Operiones on friones. - Operiones on números eimles. - Euiones e primer seguno gro. - Usr e form eu
MATEMÁTICAS 0 OBJETIVOS MÍNIMOS REQUERIDOS - Operiones omins on números enteros. - Potenis ríes urs. - Operiones on friones. - Operiones on números eimles. - Euiones e primer seguno gro. - Usr e form eu
Razones y Proporciones
 Rzones y Proporiones 01. L rzón geométri e os números es 1/ y su rzón ritméti es 7. Hllr el myor. ) 117 ) 11 ) 119 ) 118 e) 110 0. L rzón geométri entre l sum e números y su ifereni es :. Hllr l rzón geométri
Rzones y Proporiones 01. L rzón geométri e os números es 1/ y su rzón ritméti es 7. Hllr el myor. ) 117 ) 11 ) 119 ) 118 e) 110 0. L rzón geométri entre l sum e números y su ifereni es :. Hllr l rzón geométri
PÁGINAS DE REFERENCIA
 PÁGINAS DE REFERENIA ÁLGEBRA OPERAIONES ARITMÉTIAS EXPONENTES Y RADIALES m s m m m m m m s m (s ) m GEOMETRÍA FÓRMULAS GEOMÉTRIAS Fómls p áe A, ifeei volme V: Tiáglo ílo Seto il A h Esfe ilio oo 3 3 h
PÁGINAS DE REFERENIA ÁLGEBRA OPERAIONES ARITMÉTIAS EXPONENTES Y RADIALES m s m m m m m m s m (s ) m GEOMETRÍA FÓRMULAS GEOMÉTRIAS Fómls p áe A, ifeei volme V: Tiáglo ílo Seto il A h Esfe ilio oo 3 3 h
ESQUEMA. Las unidades de la velocidad de reacción son M/s o mol / l s. podemos definir las siguientes velocidades de reacción:
 TEMA 6. CINÉTICA QUÍMICA. I. VELOCIDAD DE UNA REACCIÓN. Después e estui l temoinámic e un ección, los intecmbios e enegí que conlle, pece que tiene sentio estui con qué eloci se pouce un ección. L eloci
TEMA 6. CINÉTICA QUÍMICA. I. VELOCIDAD DE UNA REACCIÓN. Después e estui l temoinámic e un ección, los intecmbios e enegí que conlle, pece que tiene sentio estui con qué eloci se pouce un ección. L eloci
Son Co Razones Seno y Coseno Tangente y Cotangente Secante y Cosecante RAZONES TRIGONOMETRICAS DE UN ÁNGULO AGUDO. 3. Triángulos Notables
 Elusivo Universidd grri Elusivo Universidd grri on o zones eno oseno Tngente otngente ente osente ZONE TIGONOMETI DE UN ÁNGUO GUDO opuesto en hipotenus s hipotenus opuesto dente os hipotenus e hipotenus
Elusivo Universidd grri Elusivo Universidd grri on o zones eno oseno Tngente otngente ente osente ZONE TIGONOMETI DE UN ÁNGUO GUDO opuesto en hipotenus s hipotenus opuesto dente os hipotenus e hipotenus
NOCIONES DE TRIGONOMETRÍA
 Ejeiios de Tigonometí http://pi-tgos.esp.st NOCIONES DE TRIGONOMETRÍA L Tigonometí tiene po ojeto l esoluión de tiángulos, es dei, onoe los vloes de sus tes ldos de sus tes ángulos. P esolve un tiángulo
Ejeiios de Tigonometí http://pi-tgos.esp.st NOCIONES DE TRIGONOMETRÍA L Tigonometí tiene po ojeto l esoluión de tiángulos, es dei, onoe los vloes de sus tes ldos de sus tes ángulos. P esolve un tiángulo
OBJETIVO 1 DETERMINAR LAS RECTAS Y PUNTOS NOTABLES EN TRIÁNGULOS
 OJETIVO 1 DETERMINR LS RETS Y PUNTOS NOTLES EN TRIÁNULOS NOMRE: URSO: EH: RETS Y PUNTOS NOTLES DE UN TRIÁNULO Ls medins de un triánguo son s rects que unen cd uno de os vértices de triánguo con e punto
OJETIVO 1 DETERMINR LS RETS Y PUNTOS NOTLES EN TRIÁNULOS NOMRE: URSO: EH: RETS Y PUNTOS NOTLES DE UN TRIÁNULO Ls medins de un triánguo son s rects que unen cd uno de os vértices de triánguo con e punto
ÁNGULOS Nombre Grupo N.L. fecha Curso: Matemáticas 2 Apartado: 1.4, 1.5 y 1.6 Eje temático: FE y M
 urso: Mtemátis 2 prto: 1.4, 1.5 y 1.6 Eje temátio: FE y M onsign: resuelvn l siguiente situión: El í e yer, enrgué e tre trzr lgunos ángulos. Hoy por l mñn, Luis mneió on fiebre y envió el trbjo on su
urso: Mtemátis 2 prto: 1.4, 1.5 y 1.6 Eje temátio: FE y M onsign: resuelvn l siguiente situión: El í e yer, enrgué e tre trzr lgunos ángulos. Hoy por l mñn, Luis mneió on fiebre y envió el trbjo on su
NUEVA YORK, M ARTES 10 DE JU L IO DE 1934 SEIS SACERD OTES DE TRES RELIGIONES EN CONFERENCIA P A R A PU RIFICAR EL TE A T R O
 25 - W YK 6-2 á Ñ Y K ; w í«ú /! ó «/ «ú ú # ó ó íó - X 9 ó á í «! - «ó 2 á íó é x» ó ú í é " í í ; x á ; íí x! é W é \ ó í ó > ó é ó á ó x ó x í ó -» ó í x K \ ú > «ó x ó w é # W YW é é -2 í _ á ««- á
25 - W YK 6-2 á Ñ Y K ; w í«ú /! ó «/ «ú ú # ó ó íó - X 9 ó á í «! - «ó 2 á íó é x» ó ú í é " í í ; x á ; íí x! é W é \ ó í ó > ó é ó á ó x ó x í ó -» ó í x K \ ú > «ó x ó w é # W YW é é -2 í _ á ««- á
: TEORÍA DE CAMPOS ELECTROMAGNÉTICOS PROBLEMAS RESUELTOS DE INDUCTANCIA MUTUA Y AUTOINDUCTANCIA
 UNVERSDAD NACONAL DEL CALLAO FACULTAD DE NGENERÍA ELÉCTRCA Y ELECTRÓNCA ESCUELA PROFESONAL DE NGENERÍA ELÉCTRCA CURSO : TEORÍA DE CAMPOS ELECTROMAGNÉTCOS PROFESOR : ng. JORGE MONTAÑO PSFL PROLEMAS RESUELTOS
UNVERSDAD NACONAL DEL CALLAO FACULTAD DE NGENERÍA ELÉCTRCA Y ELECTRÓNCA ESCUELA PROFESONAL DE NGENERÍA ELÉCTRCA CURSO : TEORÍA DE CAMPOS ELECTROMAGNÉTCOS PROFESOR : ng. JORGE MONTAÑO PSFL PROLEMAS RESUELTOS
Representar las dos proyecciones y la tercera proyección de los puntos dados a continuación:
 Reeent l o oyeione y l tee oyeión e lo unto o ontinuión: to. lej. ot A + 0 B + = + C + < + D 0 + E - > + F - = + G - > + H - 0 I - > - J - = - K - < - L 0 - M + < - N + = - + > - Lo igno =,> y < e efieen
Reeent l o oyeione y l tee oyeión e lo unto o ontinuión: to. lej. ot A + 0 B + = + C + < + D 0 + E - > + F - = + G - > + H - 0 I - > - J - = - K - < - L 0 - M + < - N + = - + > - Lo igno =,> y < e efieen
perspectiva cónica & proyección de sombras
 expresión grái rojs mioletti primer ño este ossier es sólo un poyo el ontenio pso en lses, pensno en reorzr oneptos que pueen ser un tnto omplejos e explir... y más, e entener. l prouni on l que se ps
expresión grái rojs mioletti primer ño este ossier es sólo un poyo el ontenio pso en lses, pensno en reorzr oneptos que pueen ser un tnto omplejos e explir... y más, e entener. l prouni on l que se ps
DEFINICIÓN DE CIRCUNFERENCIA. Es el conjunto de puntos de un plano que equidistan (están a la misma distancia) de otro punto llamado centro.
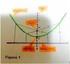 CIRCUNFERENCI. DEFINICIÓN DE CIRCUNFERENCI. Es e cnjunt de punts de un pan que equidistan (están a a misma distancia de t punt amad cent. ELEMENTOS DE UN CIRCUNFERENCI. Cicunfeencia. Es e cnjunt de punts
CIRCUNFERENCI. DEFINICIÓN DE CIRCUNFERENCI. Es e cnjunt de punts de un pan que equidistan (están a a misma distancia de t punt amad cent. ELEMENTOS DE UN CIRCUNFERENCI. Cicunfeencia. Es e cnjunt de punts
GUÍA NÚMERO 16 CUADRILATEROS:
 Sint Gspr ollege MISIONEROS E L PREIOS SNGRE Formno Persons Íntegrs eprtmento e Mtemátic RESUMEN PSU MTEMTI GUÍ NÚMERO 16 URILTEROS: Los ángulos interiores sumn 360º Los ángulos exteriores sumn 360º lsificción
Sint Gspr ollege MISIONEROS E L PREIOS SNGRE Formno Persons Íntegrs eprtmento e Mtemátic RESUMEN PSU MTEMTI GUÍ NÚMERO 16 URILTEROS: Los ángulos interiores sumn 360º Los ángulos exteriores sumn 360º lsificción
CAPÍTULO 24: RESOLUCIÓN DE TRIÁNGULOS ESFÉRICOS (I)
 ÍTUL 24: RESLUIÓ DE TRIÁGULS ESFÉRIS (I) Dnte Gueeo-hnduví iu, 2015 FULTD DE IGEIERÍ Áe Detmentl de Ingenieí Industil y de Sistems ÍTUL 24: RESLUIÓ DE TRIÁGULS ESFÉRIS (I) Est o está jo un lieni etive
ÍTUL 24: RESLUIÓ DE TRIÁGULS ESFÉRIS (I) Dnte Gueeo-hnduví iu, 2015 FULTD DE IGEIERÍ Áe Detmentl de Ingenieí Industil y de Sistems ÍTUL 24: RESLUIÓ DE TRIÁGULS ESFÉRIS (I) Est o está jo un lieni etive
RESOLUCIÓN RESOLUCIÓN SEMANA 6 CIRCUNFERENCIA RPTA.: C. 2r 2k = 2R 5k r 2 = R 5 RPTA.: A
 SEMN 6 IRUNFERENI. En un tiángulo ectángulo cuyos ángulos gudos miden 7 y 5. lcule l elción ente ls medids indio y el cicundio. ) /5 ) /5 )/0 D) /5 E) /7 Indio R = icundio Dto: + b + c = 4. R =.. : Teoem
SEMN 6 IRUNFERENI. En un tiángulo ectángulo cuyos ángulos gudos miden 7 y 5. lcule l elción ente ls medids indio y el cicundio. ) /5 ) /5 )/0 D) /5 E) /7 Indio R = icundio Dto: + b + c = 4. R =.. : Teoem
TRANSFORMACIONES GEOMÉTRICAS: Inversión.
 PRFESR: FRNCISC MNUEL GLÁN SN JSÉ. TRNSFRMCINES GEMÉTRICS: Invesión. INVERSIÓN siguientes leyes: La invesión es una tansfomaión que se ige po las M' ' 1. Dos puntos invesos y están alineados on un punto
PRFESR: FRNCISC MNUEL GLÁN SN JSÉ. TRNSFRMCINES GEMÉTRICS: Invesión. INVERSIÓN siguientes leyes: La invesión es una tansfomaión que se ige po las M' ' 1. Dos puntos invesos y están alineados on un punto
ANGULO TRIGONOMETRICO SISTEMA DE MEDICION ANGULAR
 1. NGUO TIGONOMÉTIO. Es una fiura enea por la rotación de un rayo, alrededor de un punto fijo llamado vértice, desde una posición inicial hasta una posición final..i.: ado inicial.f.: ado Final NGUO TIGONOMETIO
1. NGUO TIGONOMÉTIO. Es una fiura enea por la rotación de un rayo, alrededor de un punto fijo llamado vértice, desde una posición inicial hasta una posición final..i.: ado inicial.f.: ado Final NGUO TIGONOMETIO
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
Recuerda lo fundamental
 13 Áes y peímetos Recued o fundment Nome y peidos:... Cuso:... Fech:... ÁREA Y PERÍMETRO DE FIGURAS PLANAS CUADRADO RECTÁNGULO PARALELOGRAMO c ROMBO TRIÁNGULO TRAPECIO ' D d ' POLÍGONO REGULAR CÍRCULO
13 Áes y peímetos Recued o fundment Nome y peidos:... Cuso:... Fech:... ÁREA Y PERÍMETRO DE FIGURAS PLANAS CUADRADO RECTÁNGULO PARALELOGRAMO c ROMBO TRIÁNGULO TRAPECIO ' D d ' POLÍGONO REGULAR CÍRCULO
Semejanza. 2. Relación entre perímetros, áreas y volúmenes de figuras semejantes 51
 Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
x y z 3 x y z x y z x y z 5 0 3
 leto Enteo onde Mite González Jueo MTEMÁTIS II Deteminntes. Soluiones z. Siendo que, lul n desoll el vlo de los guientes deteminntes: z z z z z z z z z z z z en en z z z z z z + Segundo método evit ls
leto Enteo onde Mite González Jueo MTEMÁTIS II Deteminntes. Soluiones z. Siendo que, lul n desoll el vlo de los guientes deteminntes: z z z z z z z z z z z z en en z z z z z z + Segundo método evit ls
PROBLEMAS DE CINEMÁTICA
 E.T.S. INGENIEROS GÓNOOS NDENTOS ÍSIOS DE INGENIERÍ PROES DE INEÁTI Equo oente: ntono J. beo no Henánez Puhe fono e emonte 1 INEÁTI Pobem 1 (1) Dee o to e un toe uy tu e h 1 m e nz h b un e fomno un ánuo
E.T.S. INGENIEROS GÓNOOS NDENTOS ÍSIOS DE INGENIERÍ PROES DE INEÁTI Equo oente: ntono J. beo no Henánez Puhe fono e emonte 1 INEÁTI Pobem 1 (1) Dee o to e un toe uy tu e h 1 m e nz h b un e fomno un ánuo
Trazados fundamentales en el plano
 ontenio 1. Elemento Xxxxxx geométio funmentle 2. oiione e et en el plno 3. Ángulo 4. L iunfeeni 5. El íulo uni 3 6. Luge geométio en el plno Tzo funmentle en el plno Eulie, mtemátio giego que vivió en
ontenio 1. Elemento Xxxxxx geométio funmentle 2. oiione e et en el plno 3. Ángulo 4. L iunfeeni 5. El íulo uni 3 6. Luge geométio en el plno Tzo funmentle en el plno Eulie, mtemátio giego que vivió en
Departamento de Matemáticas
 Deprtmento e Mtemátis PROBLEMAS DE TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS. 1º Un señl e rreter ini que l peniente e ese trmo es el 1%, lo que quiere eir que por metros que reorre en horizontl siene 1
Deprtmento e Mtemátis PROBLEMAS DE TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS. 1º Un señl e rreter ini que l peniente e ese trmo es el 1%, lo que quiere eir que por metros que reorre en horizontl siene 1
1 i. Hojas de Problemas Álgebra IX
 Hojs e Polems Álge IX 7 Se A l ml e uoes :R * R es o log, " N R *{ R:>} Estu su eee lel e el R-eso etol AlR *,R Hll l mesó y u se el sueso que ege Soluó: Es log log log S m, y m so lelmete eeetes: α β
Hojs e Polems Álge IX 7 Se A l ml e uoes :R * R es o log, " N R *{ R:>} Estu su eee lel e el R-eso etol AlR *,R Hll l mesó y u se el sueso que ege Soluó: Es log log log S m, y m so lelmete eeetes: α β
GEOMETRÍA. punto, la recta y el plano.
 MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
TEMA 10: INTEGRALES DOBLES Y TRIPLES.
 ESCUELA TÉCNICA SUPERIOR E INGENIERÍA EPARTAMENTO E MATEMÁTICA APLICAA TITULACIONES Ingenieí Industil GITIGITI+AE Ingenieí de Telecomunicción GITTGITT+AE CÁLCULO Cuso 5-6 TEMA : INTEGRALES OBLES Y TRIPLES.
ESCUELA TÉCNICA SUPERIOR E INGENIERÍA EPARTAMENTO E MATEMÁTICA APLICAA TITULACIONES Ingenieí Industil GITIGITI+AE Ingenieí de Telecomunicción GITTGITT+AE CÁLCULO Cuso 5-6 TEMA : INTEGRALES OBLES Y TRIPLES.
UNIDAD TEMÁTICA: Cambios de Planos de Proyección. DIBUJO GEOMÉTRICO. DEPARTAMENTO DE DIBUJO. SISTEMA DIÉDRICO. MÉTODO DIRECTO. HOJA DE EJERCICIOS: 7.
 DIBUJO GEOMÉTRICO. Cmios e Plnos e Poyeión. 7.1 Resolve los mios e Plnos e Poyeión popuestos en so p ls ets s. 1 2 1 1 3 4 1 1 5 6 1 1 Ejeiios elizos y pouios po Alfeo Aguil Gutiéez. DIBUJO GEOMÉTRICO.
DIBUJO GEOMÉTRICO. Cmios e Plnos e Poyeión. 7.1 Resolve los mios e Plnos e Poyeión popuestos en so p ls ets s. 1 2 1 1 3 4 1 1 5 6 1 1 Ejeiios elizos y pouios po Alfeo Aguil Gutiéez. DIBUJO GEOMÉTRICO.
A B. Teniendo en cuenta que el lado de un pentágono regular es la sección aurea de su diagonal, se tiene la siguiente construcción:
 1. Dibuja el pentágono egula de diagonal 120 mm. D E O G AF/2 A B F Pate pimea: Dibujo del pentágono. Teniendo en cuenta que el lado de un pentágono egula es la sección auea de su diagonal, se tiene la
1. Dibuja el pentágono egula de diagonal 120 mm. D E O G AF/2 A B F Pate pimea: Dibujo del pentágono. Teniendo en cuenta que el lado de un pentágono egula es la sección auea de su diagonal, se tiene la
Unidad 1 Matrices PÁGINA 7 SOLUCIONES. 1. La resolución de los sistemas puede expresarse de la forma siguiente:
 Uni Mtries PÁGINA 7 SOLUCIONES. L resoluión e los sistems puee expresrse e l form siguiente: L segun mtriz proporion l soluión x 5,y 6. L últim mtriz proporion l soluión x, y, z 4. . Vemos que P P. Pr
Uni Mtries PÁGINA 7 SOLUCIONES. L resoluión e los sistems puee expresrse e l form siguiente: L segun mtriz proporion l soluión x 5,y 6. L últim mtriz proporion l soluión x, y, z 4. . Vemos que P P. Pr
Propiedad elipse: la normal en un punto de la elipse es la bisectriz de los segmentos que pasan por los focos
 Óits elíptis Euiones elipse: y / x /,,,, ε (exentiidd / Popiedd elipse: l noml en un punto de l elipse es l isetiz de los segmentos que psn po los foos Euión dinámi: El ento de fuezs está en un foo Fuez
Óits elíptis Euiones elipse: y / x /,,,, ε (exentiidd / Popiedd elipse: l noml en un punto de l elipse es l isetiz de los segmentos que psn po los foos Euión dinámi: El ento de fuezs está en un foo Fuez
2014 Rececho Regional. Listado de Admitidos por Apellidos. Apellidos
 2014 ececho egional istado de dmitidos por pellidos úm ol. úm orteo I pellidos ombre 72 412 2172 447 444 83 201 207 413 186 187 414 415 161 195 2148 416 417 254 418 55 419 394 420 2150 264 421 2138 422
2014 ececho egional istado de dmitidos por pellidos úm ol. úm orteo I pellidos ombre 72 412 2172 447 444 83 201 207 413 186 187 414 415 161 195 2148 416 417 254 418 55 419 394 420 2150 264 421 2138 422
