APLICACIÓN DERIVADAS
|
|
|
- Eva María José Herrera Henríquez
- hace 6 años
- Vistas:
Transcripción
1 APLICACIÓN DERIVADAS 1 RELACIÓN ENTRE LA MONOTONÍA DE UNA FUNCIÓN Y SU DERIVADA Si f ( 0 ) > 0 f es creciente en 0. Si f ( 0 ) < 0 f es decreciente en 0. EJERCICIOS: 1º.- Dada la función y = , averigua: a) Dónde crece. b) Dónde decrece. Selectividad nº 16, 40 a) 2 RELACIÓN ENTRE CURVATURA Y SEGUNDA DERIVADA Si f ( 0 ) > 0 f es cóncava en 0 (la curva queda por arriba de la tangente) Si f ( 0 ) < 0 f es cónvea en EJERCICIO: Dada la función y = , averigua: a) Dónde es cóncava. b) Dónde es convea. 3 EXTREMOS ABSOLUTOS Y RELATIVOS Una función f presenta un máimo absoluto (mínimo absoluto) en 0 A si f( 0 )f() A [f( 0 )f() A] Una función f presenta un máimo relativo (mínimo relativo) en 0 A cuando E( 0 ) tal que f( 0 )f() E( 0 ) ( f( 0 )f() E( 0 ) ) (AD) (AD) 4 ESTUDIO DE LOS EXTREMOS EN UNA FUNCIÓN Como se observa en la figura, una función definida en el intervalo [a,b] y continua en él, puede presentar etremos en: Derivables Los Puntos Interiores No Derivables (absolutos o relativos) Los Etremos del Intervalo (Absolutos) pág. 95
2 a o b 4.1 EXTREMOS EN PUNTOS DERIVABLES Llamamos puntos singulares a las raíces de la ecuación f ()=0. En ellos la recta tangente es horizontal Si una función alcanza un Máimo en un punto c(a,b) en el que es derivable: f '( c) 0 Condición Necesaria f ''( c) 0, C. S. La condición suficiente puede sustituirse por el estudio de la monotonía a izq y dcha de los valores que anulan la primera derivada Si una función alcanza un mínimo en un punto c(a,b) en el que es derivable: f '( c) 0 Condición Necesaria f ''( c) 0, C. S. La condición suficiente puede sustituirse por el estudio de la monotonía a izq y dcha de los valores que anulan la primera derivada EJERCICIO: Halla todos los puntos singulares (abscisa y ordenada) de la función y = Averigua de qué tipo es cada uno de ellos. b) Ídem para y = y = EXTREMOS ABSOLUTOS Para calcular los etremos absolutos de una función en un intervalo [a,b]: 1º.- Se hallan los etremos relativos en (a,b), según se eplica en la pregunta anterior 2º.- se calcula f(a) y f(b) 3º.- se comparan los valores de f(a) y f(b) con los valores máimos o mínimos de la función en (a,b). El mayor de ellos será el máimo absoluto y el menor el mínimo absoluto. EJERCICIOS: pág. 96
3 1.- Determinar el valor máimo y mínimo absoluto de la función f()= en el intervalo [0,3]. Selectividad nº 31 a, b, nº 33, nº 34 a), 48, 50a 5 ESTUDIO DE LOS PUNTOS DE INFLEXIÓN EN UNA FUNCIÓN Son aquellos que separan arcos de curva cóncavos y conveos, es decir, en ellos cambia la curvatura de la función. En ellos la tangente atraviesa la curva. Si una función presenta un punto de infleión en 0, en el que es dos veces derivable: 0 Condición Necesaria : f (c) 0 Condición Suficiente : Se estudia la curvaturaa ambos lados del punto;sicambia en chay infleión EJERCICIOS: 1.- Determinar los puntos de infleión de la función: y = Sea f () = a 3 + b 2 + c + d un polinomio que cumple f (1) = 0, f ' (0) = 2 y tiene dos etremos relativos para = 1 y = 2. a) Halla a, b, c y d. b) Son máimos o mínimos los etremos relativos? 3.- La función f () = 3 + a 2 + b + c verifica que f (1) = 1, f ' (1) = 0 y que f no tiene etremo relativo en = 1. Calcula a, b y c. 4.- Halla los coeficientes a, b, c, d de la función f() = a 3 +b 2 +c+d. sabiendo que la ecuación de la tangente a la curva en el punto de infleión (1,0) es y= - 3+3, y que la función tiene un etremo relativo en = 0 Selectividad nº: 22, 26 a), 36, 41 a) b), 43a) b) 6 PROBLEMAS DE OPTIMIZACIÓN En estos problemas se trata de conseguir un volumen, unos beneficios, una población máimos; o unos costes, un área mínimos. En ellos nos interesan los etremos absolutos, por lo que siempre habrá que calcular el valor de la función en los etremos del intervalo. EJERCICIO: 1º.- De todos los triángulos rectángulos cuyos catetos suman 10 cm, halla las dimensiones de aquel cuya área es máima. pág. 97
4 2º.- Entre todos los rectángulos de perímetro 12 m, cuál es el que tiene la diagonal menor? 3º.- Determina las dimensiones que debe tener un recipiente cilíndrico de volumen igual a 6,28 litros para que pueda construirse con la menor cantidad posible de hojalata. 4º.- Entre todos los triángulos isósceles de perímetro 30 cm, cuál es el de área máima? 5º.- Se quiere construir un recipiente cónico de generatriz 10 cm y de capacidad máima. Cuál debe ser el radio de la base? 6º.- Se desea construir una caja cerrada de base cuadrada cuya capacidad sea 8 dm3. Averigua las dimensiones de la caja para que su superficie eterior sea mínima. 7º.- En un triángulo isósceles de base 12 cm (el lado desigual) y altura 10 cm, se inscribe un rectángulo de forma que uno de sus lados esté sobre la base del triángulo y dos de sus vértices sobre los lados iguales: a) Epresa el área, A, del rectángulo en función de la longitud de su base,, y di cuál es el dominio de la función. b) Halla el valor máimo de esa función. 8º.- Halla la base y la altura de una cartulina rectangular de perímetro 60 cm que, al dar la vuelta completa alrededor de un lado vertical, genere un cilindro de volumen máimo. 9º.- Queremos hacer un envase con forma de prisma regular de base cuadrada y capacidad 80 cm3. Para la tapa y la superficie lateral usamos un determinado material, pero para la base debemos emplear un material un 50% más caro. Halla las dimensiones de este envase para que su precio sea el menor posible. 10º.- Con una lámina cuadrada de 10 dm de lado se quiere construir una caja sin tapa. Para ello, se recortan unos cuadrados de los vértices. Calcula el lado del cuadrado recortado para que el volumen de la caja sea máimo. Si la altura de la caja no puede pasar de 2 dm, cuál es la medida del lado del cuadrado que debemos recortar? 11º.- El valor, en millones de euros, de una empresa en función del tiempo t viene dado por f (t) = 9 - (t - 2) 2, 0 t 4,5. Deduce en que valor de t alcanzo su máimo valor y en que valor de t alcanzo su valor mínimo. 12º.- Dos postes de 12 y 18 m de altura distan entre sí 30 m. Se desea tender un cable que una un punto del suelo entre los dos postes con los etremos de estos. pág. 98
5 Dónde hay que situar el punto del suelo para que la longitud total del cable sea mínima? Selectividad Todos ecepto los 4 primeros. Empezar por el final (no olvidar 43c) 7 REPRESENTACIÓN GRÁFICA DE FUNCIONES A pesar de que, para representar una función, siempre haremos el mínimo número de cálculos, suele ser imprescindible: 1. Dominio y continuidad 2. Asíntotas y Ramas Infinitas 3. Monotonía y Etremos 4. Curvatura y puntos de infleión En el supuesto de que estos cálculos no aporten los datos suficientes para la representación, se podrá completar con: puntos de corte con los ejes, simetrías, tabla de valores REPASO DE ASÍNTOTAS Y RAMAS INFINITAS Asíntota horizontal: Si lim f ( ) l (no infinito) entonces la asíntota horizontal por la derecha es la recta de ecuación: y= l Si lim f ( ) l (no infinito) entonces la asíntota horizontal por la izquierda es la recta de ecuación: y= l Asíntota Vertical: Si lim f ( ), a, hay asíntota vertical; es la recta de ecuación = a. a Para saber la posición de la curva respecto a la asíntota es preciso calcular los límites laterales. Asíntota Oblicua: Si: f ( ) lim f ( ), lim m 0 y lim Entonces la recta y= m+n es una asíntota oblicua por la derecha. Para calcularla por la izquierda, se efectúan los mismos cálculos con. P( ) En el caso de funciones racionales y la localización de la asíntota Q( ) oblicua es mucho más sencilla: Si grado de P() grado de Q() = 1 hay asíntota oblicua. Su ecuación es y= m+n, siendo m+n el cociente de dividir P() entre Q() Ramas Parabólicas f ( ) m n siendo m, n pág. 99
6 lim f ( ) Si y no hay asíntota oblicua, entonces puede haber rama parabólica. Análogamente se procede para P( ) En el caso de funciones racionales y si grado de P() grado de Q( ) Q() > 1 hay rama parabólica EJERCICIOS: Selectividad: 35 a), 37 a) 43 a), 49 Representa las funciones 1 : 1.- y = y ln y 5.- y y e 1 Recuerda las funciones elementales ln, e, sen, cos y sus transformadas obtenidas sumando o restando k, a la función y a la pág. 100
7 EJERCICIOS SELECTIVIDAD TEMA 7 Aplicación de derivadas 1.-Un hilo de alambre de longitud dada se corta en dos trozos, formando con uno de ellos una circunferencia y con el otro un cuadrado. Demuestra que la suma de las áreas es mínimo cuando el lado del cuadrado es doble que el radio del círculo. (1994) 2.- Un camión está a 975 Km al este de un automóvil y está viajando hacia el oeste a una velocidad constante de 60 Km/h. Mientras tanto, el automóvil está yendo al norte a una velocidad constante de 90 Km/h. En qué momento estarán el camión y el automóvil más próimos el uno del otro? (1994) 3.- En un instante t = 0 el móvil A está situado en (100,0) y el móvil B se halla en el punto (0,5). Ambos comienzan un movimiento uniforme con velocidades v A = - 3i y v B = 2i-j. Determinar el instante y las posiciones para las que la distancia entre ambos móviles sea mínima. (1995) 4.- Una partícula recorre la curva y = de manera que en el tiempo t segundos ocupa la posición = t e y = - t 2 +10t 25. Al llegar al instante t = 5 segundos se escapa por la tangente a la curva recorriendo diez unidades de longitud en cada segundo en la dirección positiva del eje OX, es decir hacia la derecha. Calcular la posición de la partícula en el instante 15 segundos. (1995) 5.- Se divide un alambre de longitud 100m en dos trozos. Con uno de ellos se forma un triángulo equilátero y con el segundo un cuadrado. Determina las longitudes de esos trozos para que la suma de las áreas del triángulo y del cuadrado sea máima. (1995) 6.- Representar la función f() tal que: f() = +6 si [ - 6,- 3] f() = 3 si ( - 3, 3) f() = 6 - si [ 3,6] Halla el conjunto de puntos donde está definida la derivada y representa la función f (). ( A Junio 1996) 7.- Halla la base y la altura y de una cartulina rectangular de perímetro 60 cm que al dar la vuelta completa alrededor de un lado vertical genere un cilindro de volumen máimo. (B Junio 1996) 8.- Un punto material recorre la parábola y 2 = 8 9. Determinar razonadamente en que posición la distancia del punto al origen (0,0) es mínima. (A Septiembre1996) 9.- Un hilo elástico tiene un etremo fijo en el punto O = (0,0) y el otro etremo P recorre la curva ( 3) 2 + (y 4) 2 = 4 Determinar las coordenadas de P cuando sea máima la longitud OP, interpretando geométricamente el resultado obtenido. (B Junio 1997) pág. 101
8 10.- Descomponer un segmento del longitud 20 metros en cuatro partes para obtener el paralelogramo de la mayor área posible. (A Septiembre1997) 11.- Un punto material recorre la parábola y = 2 7. Determinar razonadamente la posición o posiciones en que la distancia del punto al origen (0,0) es mínima. (B Junio.1998) 12.- Un hilo de 100 metros se divide en dos trozos de longitudes e y; con el primero se forma un cuadrado y con el segundo un círculo. Razonadamente: a) Halla e y para que la suma de las áreas del cuadrado y del círculo sea máima. b) Halla e y para que la suma de las áreas del cuadrado y del círculo sea mínima. (B Septiembre.1998) 13.- Con un hilo de 60 cm formamos un rectángulo que al girar alrededor de uno de sus lados engendra un cilindro de área total (área lateral + área de las bases) máima. (B Junio 1999) 14.- El punto P(,y) recorre la elipse de ecuación 2 y 2 1. Deduce las posiciones 25 9 del punto P para las que su distancia al punto (0,0) es máima, y también las posiciones de P para las que su distancia es mínima. (A Septiembre.1999) 15.- El punto P(,y) recorre la curva y = 2. Utilizando razonadamente el cálculo de derivadas, calcula la posición del punto P para la cual su distancia al punto (0, -4) es mínima. (A Junio.2000) 16.- A través de la utilización razonada de la relación de la derivada de una función con su crecimiento o decrecimiento, obtén en que puntos del intervalo [ - 2,2] son crecientes o decrecientes las funciones: a) f()= 2 b) g()= 3 7 (2000) 17.- Se divide un hilo de 100 metros en dos trozos de longitudes e y. Con el trozo de longitud se forma un cuadrado y con el de longitud y se forma un rectángulo, el lado mayor del cual mide el doble que el lado menor. Encuentra e y para que la suma de las áreas del cuadrado y del rectángulo sea máima. Idem para que sea mínima. (A.Septiembre.2000) 18.- Se divide un alambre de 100 m de longitud en dos segmentos de longitudes y 100. Con el de longitud se forma un triángulo equilátero y con el otro segmento se forma un cuadrado. Sea f() la suma de las áreas del triángulo y del cuadrado. a) Determina el dominio de la función f; es decir, los valores que puede tomar b) Con el estudio de la derivada de f obtén cuando f es creciente y cuando es decreciente. c) Indica razonadamente para que valor de se obtiene que la suma de las áreas del triángulo y del cuadrado es mínima. (A Junio.2001) pág. 102
9 4 si Sea la función definida por f () Justifica si f es 7 si 3 7 derivable o no en = 3. Que significado geométrico tiene el resultado obtenido? (B Junio.2001) 20.- Descomponer un segmento de longitud 200 m en cuatro partes, de manea que esas partes sean los lados de un rectángulo cuya área sea máima dentro de la familia de rectángulos de perímetro 200 m. (B Septiembre.2001) 21.- Considerad las funciones definidas para 0, f () arcsen y g() arccos. Calculad f () y g () epresadlas del modo más 2 1 simplificado posible. Comparad los resultados y deducid justificadamente la diferencia entre f() y g() (B Junio 2002) 22.-Sea f()= 3 + a 2 + b + c. Hallad a, b, c sabiendo que f alcanza un máimo en = - 4 y un mínimo en = 0 y que f(1) =1 (A Septiembre. 2002) Sea T un triángulo de perímetro 60 cm. Uno de los lados del triángulo T mide cm y los otros dos lados tienen la misma longitud. a) Deducir razonadamente las epresiones de las funciones A y f tales que: A() = Área del triángulo. f() = {A()} 2 Indicar además entre qué valores puede variar. c) Obtener, razonadamente, el valor de para el que f() alcanza el valor máimo. ( B Junio.2003) 24.- En una gran pradera se tiene que vallar una zona de 400 m 2, que debe tener forma de rectángulo. Cada metro de valla cuesta 100 euros. Si es la medida en metros de uno de sus lados, se pide: a) Obtener razonadamente la función de f tal que f() sea el coste de la valla, indicando entre qué valores puede variar. b) Deducir razonadamente el valor de para el que la función f() alcanza el valor mínimo. (A Septiembre 2003) Encontrar razonadamente el punto de la curva y= en que la recta tangente a 2 1 la curva tiene pendiente máima y calcular el valor de esa pendiente. (Junio ,3 puntos) 26.- Sea f()= 2 +m (donde m es un parámetro real) y f () la función derivada de f(). Se pide: a) Hallar el valor del parámetro m para que f() tenga un mínimo relativo en =-3/4 1,5 puntos 2 b) Para el valor de m calculado en a), determinar el área de la región comprendida entre la curva y=f() y la recta de ecuación y = f () 1,8 puntos ( septiembre 2004.) 2 Este apartado se hará en el tema de Áreas pág. 103
10 ln a 27.- Hallar las constantes reales a y b para que f()= b sen función continua para todo valor de. (3,3 puntos. Junio 2005) si si si sea una 28.- En el plano se tiene la curva y = Encontrar razonadamente las ecuaciones de las rectas que pasan por el punto (2, 3) y son tangentes a dicha curva. (Septiembre ,3 puntos) a) El perímetro de un sector circular de radio R es 4 m. Cuántos radianes α debe medir su ángulo central para que su área sea máima? (1,8 puntos). (Nota: Perímetro = 2R +R α ; Área = ½ α R 2 ) b) El, área de otro sector circular es de 1m 2. Para qué radio es mínimo su perímetro? (1,5 puntos. Septiembre 2005) Dada la función y= Ln en el intervalo [1,e], siendo e= 2, : a) Razonar que eiste un punto P de la gráfica y= Ln en el que la recta tangente a ella es paralela a la recta que pasa por los puntos A=(1,0) y B(e,1) (1 p) b) Obtener el punto P considerado en a) (1,8 p) c) Calcular la pendiente de la recta tangente a y= Ln en P (0,5 p) Junio a) Dibujar razonadamente la gráfica de la función g()= 2 4, cuando 1 4 (1,1 p) b) Obtener razonadamente los valores máimo y mínimo absolutos de la función f ( ) 2 4 en el intervalo [-1,4] (1,1 p) c) 3 Calcular el área del recinto limitado por la curva de ecuación y= f() y las rectas = -1 e y= 0 (1,1 p) Junio El coste de un marco de una ventana rectangular es de 12,5 por metro lineal de los lados verticales y 8 por metro lineal de los lados horizontales. a) Calcular razonadamente las dimensiones que debe tener el marco de una ventana de 1 m 2 de superficie para que resulte lo más económico posible (2,3 p) b) Calcular, además el coste de ese marco más económico posible considerado en a) (1 p) Junio a) Obtener la derivada de la función f() a b sen (0,5 puntos). Calcular a y b si O (0, 0) es un punto de la curva y a b sen, cuya recta tangente en O(0, 0) es el eje OX (1,8 puntos). 3 Este apartado se hará en el tema de Áreas pág. 104
11 2 b) Justificar que la función g() sen se anula en dos puntos del intervalo 0, (0,5 puntos). c) Calcular esos dos puntos (0,5 puntos). Septiembre Dadas las funciones f () y g() 3, se pide: a) Calcular el máimo absoluto de la función f () en el intervalo 3, 0(1 p). b) Calcular el punto de corte de la curva y f () y la recta y g() (1 punto). c) Obtener el área del recinto limitado por la curva y f () y las rectas y g(), 3 y 0 (1,3 puntos). Septiembre Se consideran las funciones reales f() = y g() = Se pide: f () a) Determinar las ecuaciones de las asíntotas a la gráfica de la función (1,6 g() puntos). f () b) Calcular la función H() = d que cumple H(1)=1. (1,7 puntos) g() Junio Se considera la función real f () 3 a 2 b c, donde a, b y c son parámetros reales. a) Averiguar los valores de a y b para los que las rectas tangentes a la gráfica de f() en los puntos de abscisas = 2 y = 4 son paralelas al eje OX. (2 puntos). b) Con los valores de a y b hallados anteriormente, obtener el valor de c para el que se cumple que el punto de infleión de la gráfica de f() está en el eje OX. (1,3 puntos). Junio Dadas las funciones reales f ()= y g() = Se pide: f() a) Determinar las ecuaciones de las asíntotas a la gráfica de la función (1,6 P. g() f() b) Calcular la función H() d que cumple H(0) = 0. (1,7 puntos). Sept 07 g() Sea la función con dominio los números reales no nulos f() a) Calcular la ecuación de la recta tangente y de la recta normal a la gráfica de f() en el punto de abscisa = 2. (1.8 puntos). b) Determinar los puntos M y N de la gráfica de f() para los que las rectas tangentes a la gráfica en M y N se cortan en el punto (4, - 8 ). (1.5 puntos). Sept Se considera la función real f() = 2 4. Obtener, eplicando el proceso de cálculo: a) La gráfica de la curva y = f(). (0,7 puntos). b) Los valores de para los que está definida la función real g() = Ln f(). (1,3 p) pág. 105
12 c) Los intervalos de crecimiento y decrecimiento de la función g(), razonando si tiene, o no, máimo absoluto. (1,3 Puntos) Junio Junio 2009 a) Determinar, razonadamente, el dominio y los intervalos de crecimiento y 1 decrecimiento de la función f() =. (1 punto) b) Obtener razonadamente los valores de A y B tales que = 3 3 A B (1 punto) 3 3 c) Calcular razonadamente el área de la superficie S limitada por la curva 1 y =, el eje OX y las rectas de ecuaciones = - 2 y = (1,3 puntos) 41.- Dada la función f() = e e, se pide calcular razonadamente: a) La función f()+f( - ). (1,1 puntos) a b) La integral f ()d, donde a es un número real positivo. (1,1 puntos) a c) El punto de infleión de f(). (1,1 puntos) Junio Se consideran las funciones reales f() = y g() = ( 2)( 2 +9). Se pide obtener razonadamente: a) Las ecuaciones de las asíntotas a la gráfica de la función (1,6 puntos) b) La función que cumple. (1,7 puntos) Sep Dada la función real, se pide calcular razonadamente: a) Las derivadas primera y segunda de la función f(). (0,8 puntos) b) Los puntos de infleión de la curva y = f(). (1 punto) c) La pendiente máima de las rectas tangentes a la curva y = f(). (1,5 p) Sep Se quiere construir un estadio cerrado de m 2 de superficie. El estadio está formado por un rectángulo de base y dos semicírculos eteriores de diámetro, de manera, que cada lado horizontal del rectángulo es diámetro de uno de los semicírculos. El precio de 1 m 2 de valla para los lados verticales del rectángulo es de 1 y el precio de 1 m 2 de valla para las semicircunferencias es de 2. Se pide obtener razonadamente: a) La longitud del perímetro del campo en función de. (3 puntos) b) El coste f() de la valla en función de. (3 puntos) c) El valor de para que el coste de la valla sea mínimo. (4 puntos) Junio 2010 pág. 106
13 45.- Dada la función polinómica f()= 4 2, se pide obtener razonadamente: a) La gráfica de la curva y = 4 2. (2 puntos) b) El punto P de esa curva cuya tangente es perpendicular a la recta de ecuación +y=0. (3 puntos) c) Las rectas que pasan por el punto (- 2, 1) y son tangentes a la curva y = 4 2, obteniendo los puntos de tangencia. (5 puntos) Junio Dos elementos de un escudo son una circunferencia y un triángulo. La circunferencia tiene centro en (0,0) y radio 5. Uno de los vértices del triángulo es el punto A=(-5,0). Los otros dos vértices del triángulo son los puntos de la circunferencia B=(, y) y C=(, - y). Se pide obtener razonadamente: a) El área del triángulo en función de. (3 puntos) b) Los vértices B y C para los que es máima el área del triángulo. (5 puntos) c) El valor máimo del área del triángulo. (2 puntos) Septiembre Se desea construir un campo rectangular con vértices A, B, C y D de manera que: Los vértices A y B sean puntos del arco de la parábola y = 4-2, - 2 2, y el segmento A y B es horizontal. Los vértices C y D sean puntos del arco de la parábola y = 2-16, - 4 4, y el segmento C y D es también horizontal. Los puntos A y C tienen la misma abscisa, cuyo valor es el número real positivo. Los puntos B y D tienen la misma abscisa, cuyo valor es el número real positivo -. Se pide obtener razonadamente: a) La epresión S() del área del campo rectangular en función del número real positivo..(4 puntos) b) El número real positivo para el que el área S() es máima..(4 puntos) c) El valor del área máima. (2 puntos) Junio Un coche recorre un arco de parábola Γ de ecuación 2y=36 2, variando la de -6 a 6. Se representa por f() a la distancia del punto (0,9) al punto (,y) del arco Γ donde está situado el coche. Se pide obtener razonadamente: a) La epresión de f(). (2 puntos) b) Los puntos del arco Γ donde la distancia f() tiene mínimos relativos. (2 p) c) Los valores máimo y mínimo de la distancia f(). (2 puntos) d) El área de la superficie limitada por el arco de parábola Γ y el segmento rectilíneo que une los puntos (-6,0) y (6,0). (4 puntos) Sep Dada la función f definida por: Obtener razonadamente: a) El dominio y recorrido de la función f. (2 puntos) b) Los valores de donde la función f alcanza el máimo y el mínimo relativo. (2 puntos) pág. 107
14 c) Los intervalos de crecimiento y decrecimiento de dicha función f. (2 puntos) d) Los valores de donde la función tiene puntos de infleión. (2 puntos) e) La gráfica de la curva, eplicando con detalle la obtención de la asíntota horizontal. (2 puntos). Sep Con el símbolo ln se representa el logaritmo de un número positivo cuando la base del logaritmo es el número e. Sea la función f, que para un número positivo está definida por la igualdad 4 Obtener razonadamente: a) El valor de donde la función f alcanza el mínimo relativo. (4puntos). b) La ecuación de la recta tangente a la curva y = 4ln en el punto (1, 0). (3 puntos) c) El área limitada entre las rectas y= 0, =e y =e2 y la curva y = 4ln (3 puntos) Junio Para diseñar un escudo se dibuja un triángulo T de vértices A=(0, 12), B=(-, 2 ) y C=(, 2 ), siendo 2 <12. Obtener razonadamente: a) El área del triángulo T en función de la abscisa del vértice C. (2 puntos) b) Las coordenadas de los vértices B y C para que el área del triángulo T sea máima. (3 puntos) Para completar el escudo se añade al triángulo T de área máima la superficie S limitada entre la recta y = 4 y el arco de parábola y = 2, cuando Obtener razonadamente: c) El área de la superficie S. (3 puntos). d) El área total del escudo (2 puntos). Junio 2012 pág. 108
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
APLICACIONES DE LAS DERIVADAS
 UNIDAD APLICACIONES DE LAS DERIVADAS Página 98 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f
UNIDAD APLICACIONES DE LAS DERIVADAS Página 98 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f
12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación media (T.V.M.) de una unción, y = () en un intervalo
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad
 PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
APLICACIONES DE LA DERIVADA
 7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES
 UNIDAD 6 DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES Página 5 Problema y f () 5 5 9 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(). f'() 0; f'(9) ; f'() Di otros tres puntos en
UNIDAD 6 DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES Página 5 Problema y f () 5 5 9 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(). f'() 0; f'(9) ; f'() Di otros tres puntos en
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL. PRIMERA EVALUACIÓN. ANÁLISIS
 Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
dada por c(x) = donde x indica el tamaño de los pedidos para renovar existencias
 FUNCIONES +, si
FUNCIONES +, si
b) Cuántas asíntotas oblicuas y cuántas asíntotas verticales puede tener una función racional cualquiera?. Razónalo. dx x 2 1 x 1 si x >1 x 1 x < 0
 ANÁLISIS. (Junio 994) a) Encontrar las asíntotas de la curva f () = 2 3 2 4 b) Cuántas asíntotas oblicuas y cuántas asíntotas verticales puede tener una función racional cualquiera?. Razónalo. 2. (Junio
ANÁLISIS. (Junio 994) a) Encontrar las asíntotas de la curva f () = 2 3 2 4 b) Cuántas asíntotas oblicuas y cuántas asíntotas verticales puede tener una función racional cualquiera?. Razónalo. 2. (Junio
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
Colegio Portocarrero. Curso Departamento de matemáticas. Análisis. (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas)
 Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
1. Estudia la derivabilidad de la función )En qué punto del intervalo (0,ð) la recta tangente a y=tg(x) tiene pendiente 2?.
 ejerciciosyeamenes.com EXAMEN DERIVADAS. Estudia la derivabilidad de la función si f ()= si > 3. )En qué punto del intervalo (0,ð) la recta tangente a y=tg() tiene pendiente?. 4. Ecuación de la recta tangente
ejerciciosyeamenes.com EXAMEN DERIVADAS. Estudia la derivabilidad de la función si f ()= si > 3. )En qué punto del intervalo (0,ð) la recta tangente a y=tg() tiene pendiente?. 4. Ecuación de la recta tangente
REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN.. Se pide: x
 1 REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN IBJ05 1. Se considera la función f ( ). Se pide: a) Encontrar los intervalos donde esta función es creciente y donde es decreciente. ( puntos) b) Calcular las asíntotas.
1 REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN IBJ05 1. Se considera la función f ( ). Se pide: a) Encontrar los intervalos donde esta función es creciente y donde es decreciente. ( puntos) b) Calcular las asíntotas.
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Ejercicios de Análisis propuestos en Selectividad
 Ejercicios de Análisis propuestos en Selectividad.- Dada la parábola y 4, se considera el triángulo rectángulo T( r ) formado por los ejes coordenados y la tangente a la parábola en el punto de abscisa
Ejercicios de Análisis propuestos en Selectividad.- Dada la parábola y 4, se considera el triángulo rectángulo T( r ) formado por los ejes coordenados y la tangente a la parábola en el punto de abscisa
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 12.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bac TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación
TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bac TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Deinición Se llama tasa de variación
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Demuestra que el punto de tangencia, T, es el lugar de la recta r desde el que se ve el segmento AB con ángulo máximo.
 Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 7 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura.
Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 7 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura.
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 Selectividad CCNN 0. [ANDA] [JUN-A] Sea la función f: definida por f(x) = e x (x - ). a) Calcula la asíntotas de f. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan)
Selectividad CCNN 0. [ANDA] [JUN-A] Sea la función f: definida por f(x) = e x (x - ). a) Calcula la asíntotas de f. b) Halla los extremos relativos (abscisas donde se obtienen y valores que se alcanzan)
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Ejercicio 1 Relacione convenientemente cada una de las siguientes expresiones: (considere x > 0 ) P Q a b. ax + bxh + h. x bxh
 Módulo 1 DERIVADAS 1.1 Reglas de diferenciación Reconocimiento de saberes Ejercicio 1 Relacione convenientemente cada una de las siguientes epresiones: (considere > 0 ) ln ( e ) ln ln ( e ) ln e ln + ln
Módulo 1 DERIVADAS 1.1 Reglas de diferenciación Reconocimiento de saberes Ejercicio 1 Relacione convenientemente cada una de las siguientes epresiones: (considere > 0 ) ln ( e ) ln ln ( e ) ln e ln + ln
Problemas de selectividad. Análisis
 Departamento de Matemáticas Página 1 Problemas de selectividad. Anális 14.01.- De entre todos los triángulos rectángulos de área 8 cm, determina las dimenones del que tiene la hipotenusa de menor longitud.
Departamento de Matemáticas Página 1 Problemas de selectividad. Anális 14.01.- De entre todos los triángulos rectángulos de área 8 cm, determina las dimenones del que tiene la hipotenusa de menor longitud.
Funciones 1. D = Dom ( f ) = x R / f(x) R. Recuerda como determinabas los dominios de algunas funciones: x x
 Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
7 Aplicaciones de las derivadas
 Solucionario 7 Aplicaciones de las derivadas ACTIVIDADES INICIALES 7.I. Calcula el volumen del cilindro que está inscrito en el cono de la figura: cm 8 cm Aplicando el Teorema de Pitágoras, se calcula
Solucionario 7 Aplicaciones de las derivadas ACTIVIDADES INICIALES 7.I. Calcula el volumen del cilindro que está inscrito en el cono de la figura: cm 8 cm Aplicando el Teorema de Pitágoras, se calcula
La variable independiente x es aquella cuyo valor se fija previamente. La variable dependiente y es aquella cuyo valor se deduce a partir de x.
 Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Tema Derivadas. Aplicaciones Matemáticas I º Bacillerato TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN EN UN INTERVALO EJERCICIO : Halla la tasa de variación
Aplicaciones de la integral definida al cálculo de áreas
 Aplicaciones de la integral definida al cálculo de áreas 1º) Interpreta geométricamente el área que define la integral y obtenla. Geométricamente, la integral representa el área de la región del plano
Aplicaciones de la integral definida al cálculo de áreas 1º) Interpreta geométricamente el área que define la integral y obtenla. Geométricamente, la integral representa el área de la región del plano
UNIDAD 2: ELEMENTOS GEOMÉTRICOS
 UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
DERIVADAS. * Definición de derivada. Se llama derivada de la función f en el punto x=a al siguiente límite, si es que existe: lim
 DERIVADAS. CONTENIDOS. Recta tangente a una curva en un punto. Idea intuitiva del concepto de derivada de una función en un punto. Función derivada. sucesivas. Reglas de derivación Aplicación de la derivada
DERIVADAS. CONTENIDOS. Recta tangente a una curva en un punto. Idea intuitiva del concepto de derivada de una función en un punto. Función derivada. sucesivas. Reglas de derivación Aplicación de la derivada
1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Solución:
 RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
TEMA 7: CÓNICAS CIRCUNFERENCIA. A partir de esta ecuación podemos hallar el centro y el radio sin más que deshacer los cambios:
 TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
11 Aplicaciones. de las derivadas. 1. Máximos, mínimos y monotonía. Piensa y calcula. Aplica la teoría
 Aplicaciones de las derivadas. Máimos, mínimos y monotonía Piensa y calcula Dada la gráfica de la función f representada en el margen, halla los máimos y los mínimos relativos y los intervalos de crecimiento
Aplicaciones de las derivadas. Máimos, mínimos y monotonía Piensa y calcula Dada la gráfica de la función f representada en el margen, halla los máimos y los mínimos relativos y los intervalos de crecimiento
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
Funciones reales. Números complejos
 Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
f: D IR IR x f(x) v. indep. v. dependiente, imagen de x mediante f, y = f(x). A x se le llama antiimagen de y por f, y se denota por x = f -1 (y).
 TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
La concentración de ozono contaminante, en microgramos por metro cúbico, en una
 ANÁLISIS MATEMÁTICO. PAU CASTILLA Y LEÓN A) EJERCICIOS DE APLICACIÓN A LAS CCSS La concentración de ozono contaminante, en microgramos por metro cúbico, en una ciudad viene dada por la función C ( ) 90
ANÁLISIS MATEMÁTICO. PAU CASTILLA Y LEÓN A) EJERCICIOS DE APLICACIÓN A LAS CCSS La concentración de ozono contaminante, en microgramos por metro cúbico, en una ciudad viene dada por la función C ( ) 90
IES Fco Ayala de Granada Septiembre de 2011 (Septiembre Modelo 2) Solución Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
APLICACIONES DEL CÁLCULO DIFERENCIAL-II
 APLICACIONES DEL CÁLCULO DIFERENCIAL-II. Estudia si crecen o decrecen las siguientes funciones en los puntos indicados: π a) f() cos en 0 b) f() ln ( arc tg ) en 0 π c) f() arc sen en 0 d) f() ln en 0
APLICACIONES DEL CÁLCULO DIFERENCIAL-II. Estudia si crecen o decrecen las siguientes funciones en los puntos indicados: π a) f() cos en 0 b) f() ln ( arc tg ) en 0 π c) f() arc sen en 0 d) f() ln en 0
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES.
 APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INTEGRAL DEFINIDA. APLICACIONES
 COLEGIO SAN ALBERTO MAGNO MATEMÁTICAS II INTEGRAL DEFINIDA. APLICACIONES. 008 MODELO OPCIÓN A. Ejercicio. [ 5 puntos] Dadas las funciones f : [0,+ ) R y g : [0, + ) R definidas por y calcula el área del
COLEGIO SAN ALBERTO MAGNO MATEMÁTICAS II INTEGRAL DEFINIDA. APLICACIONES. 008 MODELO OPCIÓN A. Ejercicio. [ 5 puntos] Dadas las funciones f : [0,+ ) R y g : [0, + ) R definidas por y calcula el área del
EJERCICIOS Y PROBLEMAS PROPUESTOS (ANÁLISIS) x +
 EJERCICIOS Y PROBLEMAS PROPUESTOS (ANÁLISIS).- La temperatura T, en grados centígrados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la epresión: Tt t
EJERCICIOS Y PROBLEMAS PROPUESTOS (ANÁLISIS).- La temperatura T, en grados centígrados, que adquiere una pieza sometida a un proceso viene dada en función del tiempo t, en horas, por la epresión: Tt t
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
ACTIVIDADES PROPUESTAS
 GEOMETRÍA DINÁMICA ACTIVIDADES PROPUESTAS 1. Dibujar un pentágono y trazar sus diagonales. 2. A partir de una circunferencia c y de un punto exterior A, trazar la circunferencia que tiene centro en el
GEOMETRÍA DINÁMICA ACTIVIDADES PROPUESTAS 1. Dibujar un pentágono y trazar sus diagonales. 2. A partir de una circunferencia c y de un punto exterior A, trazar la circunferencia que tiene centro en el
Aplicaciones de la derivada 7
 Aplicaciones de la derivada 7 ACTIVIDADES 1. Página 160 a) La pendiente de la recta tangente es 12. b) La pendiente de la recta tangente es 3. 2. Página 160 a) La pendiente de la recta tangente es. b)
Aplicaciones de la derivada 7 ACTIVIDADES 1. Página 160 a) La pendiente de la recta tangente es 12. b) La pendiente de la recta tangente es 3. 2. Página 160 a) La pendiente de la recta tangente es. b)
Completa esta parábola y señala sus elementos y sus propiedades. 1 X. El dominio de la función es todos los números reales:.
 Representa la función que relaciona el área de un triángulo rectángulo isósceles la longitud del cateto. a) Cuál es la variable dependiente? b) la variable independiente? = a) La variable independiente
Representa la función que relaciona el área de un triángulo rectángulo isósceles la longitud del cateto. a) Cuál es la variable dependiente? b) la variable independiente? = a) La variable independiente
Cálculo de derivadas
 0 Cálculo de derivadas. La derivada Piensa y calcula La gráfica f() representa el espacio que recorre un coche en función del tiempo. Calcula mentalmente: a) la pendiente de la recta secante, r, que pasa
0 Cálculo de derivadas. La derivada Piensa y calcula La gráfica f() representa el espacio que recorre un coche en función del tiempo. Calcula mentalmente: a) la pendiente de la recta secante, r, que pasa
2. Obtener la longitud de la base de un triángulo isósceles cuyos lados iguales miden 17 cm y su altura 8 cm.
 ACTIVIDAD DE APOYO GEOMETRIA GRADO 11 1. Calcular el valor de la altura del triángulo equilátero y de la diagonal del cuadrado (resultado con dos decimales, bien aproimados): h 6 cm (Sol: 3,46 cm) (Sol:
ACTIVIDAD DE APOYO GEOMETRIA GRADO 11 1. Calcular el valor de la altura del triángulo equilátero y de la diagonal del cuadrado (resultado con dos decimales, bien aproimados): h 6 cm (Sol: 3,46 cm) (Sol:
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
; f(x) = 3 x 5 2) Halla los límites laterales de las siguientes funciones en los valores de x que se indican: -5x + 4); f(x) = 2 ; f(x) =
 º BT Mat II CNS PROBLEMAS ANALISIS 1) Halla los dominios de las siguientes funciones: f() = 9 ; f () = Ln ( -5 + ); f() = ; f() = Problemas Análisis Pág 1 + + ; f() = 5 ) Halla los límites laterales de
º BT Mat II CNS PROBLEMAS ANALISIS 1) Halla los dominios de las siguientes funciones: f() = 9 ; f () = Ln ( -5 + ); f() = ; f() = Problemas Análisis Pág 1 + + ; f() = 5 ) Halla los límites laterales de
Aplicación: cálculo de áreas XII APLICACIÓN: CÁLCULO DE ÁREAS
 XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
XII APLICACIÓN: CÁLCULO DE ÁREAS El estudiante, hasta este momento de sus estudios, está familiarizado con el cálculo de áreas de figuras geométricas regulares a través del uso de fórmulas, como el cuadrado,
EJERCICIOS MÓDULO 6. 1) Graficar aproximadamente cada ángulo dado en un sistema de ejes cartesianos:
 Seminario Universitario Matemática EJERCICIOS MÓDULO 1) Graficar aproximadamente cada ángulo dado en un sistema de ejes cartesianos: a) 5 b ) 170 c ) 0 d ) 75 e) 10 f ) 50 g ) 0 h ) 87 i ) 08 j ) 700 k
Seminario Universitario Matemática EJERCICIOS MÓDULO 1) Graficar aproximadamente cada ángulo dado en un sistema de ejes cartesianos: a) 5 b ) 170 c ) 0 d ) 75 e) 10 f ) 50 g ) 0 h ) 87 i ) 08 j ) 700 k
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
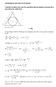 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
Ejercicios para aprender a derivar
 Ejercicios para aprender a derivar Derivación de polinomios y series de potencias Reglas de derivación: f ( ) k f '( ) 0 f ( ) a f '( ) a n n f ( ) a f '( ) an f ( ) u( ) + v( ) f '( ) u' + v' Ejemplos:
Ejercicios para aprender a derivar Derivación de polinomios y series de potencias Reglas de derivación: f ( ) k f '( ) 0 f ( ) a f '( ) a n n f ( ) a f '( ) an f ( ) u( ) + v( ) f '( ) u' + v' Ejemplos:
NIVEL : 1er. AÑO PROF. L. ALTIMIRAS R. CARRERA : GEOGRAFÍA AYUD. C. ESCOBEDO C. AÑO : 2009 GEOMETRÍA ANALÍTICA
 UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
a) La ecuación del plano que pasa por el punto ( 1, 1, 0 ). (3 puntos) b) La ecuación del plano que es paralelo a la recta r.
 PROBLEMAS DE SELECTIVIDAD. BLOQUE GEOMETRÍA 1. En el espacio se dan las rectas Obtener a) El valor de para el que las rectas r y s están contenidas en un plano. (4 puntos) b) La ecuación del plano que
PROBLEMAS DE SELECTIVIDAD. BLOQUE GEOMETRÍA 1. En el espacio se dan las rectas Obtener a) El valor de para el que las rectas r y s están contenidas en un plano. (4 puntos) b) La ecuación del plano que
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
95 EJERCICIOS de RECTAS
 9 EJERCICIOS de RECTAS Forma paramétrica: 1. Dado el punto A(,3) y el vector director ur = (1, ), se pide: a) Hallar las ecuaciones paramétricas de la recta r que determinan. b) Obtener otros tres puntos
9 EJERCICIOS de RECTAS Forma paramétrica: 1. Dado el punto A(,3) y el vector director ur = (1, ), se pide: a) Hallar las ecuaciones paramétricas de la recta r que determinan. b) Obtener otros tres puntos
1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones:
 F. EJERCICIOS PROPUESTOS. 1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones: (a) f(x) =x 3 /3+3x 2 /2 10x. Resp.: Crece en (, 5) y en (2, ); decrece en ( 5, 2). (b) f(x) =x 3
F. EJERCICIOS PROPUESTOS. 1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones: (a) f(x) =x 3 /3+3x 2 /2 10x. Resp.: Crece en (, 5) y en (2, ); decrece en ( 5, 2). (b) f(x) =x 3
FIGURAS PLANAS. Es una figura plana delimitada por una línea poligonal cerrada.
 1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
La circunferencia y el círculo
 La circunferencia y el círculo 1.- LA CIRCUNFERENCIA Es una línea curva, cerrada y plana en la que todos sus puntos están a la misma distancia de un punto interior llamado centro. 2.- ELEMENTOS DE LA CIRCUNFERENCIA:
La circunferencia y el círculo 1.- LA CIRCUNFERENCIA Es una línea curva, cerrada y plana en la que todos sus puntos están a la misma distancia de un punto interior llamado centro. 2.- ELEMENTOS DE LA CIRCUNFERENCIA:
Problemas de limites, continuidad y derivabilidad. Calcula los siguientes límites de funciones racionales, irracionales y exponenciales
 Problemas de limites, continuidad y derivabilidad Calcula los siguientes límites de funciones racionales, irracionales y eponenciales - ) = [ = = = = = = = . ) = [0. ] = = = = = = = = = 0 = [ = p=
Problemas de limites, continuidad y derivabilidad Calcula los siguientes límites de funciones racionales, irracionales y eponenciales - ) = [ = = = = = = = . ) = [0. ] = = = = = = = = = 0 = [ = p=
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
5.5 LÍNEAS TRIGONOMÉTRICAS
 5.5 LÍNES TRIGONOMÉTRIS Sea (O, ) una circunferencia con centro en el origen de coordenadas O(0, 0) radio la unidad. Si se construe un ángulo con vértice en el origen sentido positivo podemos obtener las
5.5 LÍNES TRIGONOMÉTRIS Sea (O, ) una circunferencia con centro en el origen de coordenadas O(0, 0) radio la unidad. Si se construe un ángulo con vértice en el origen sentido positivo podemos obtener las
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Ángulos 1º = 60' = 3600'' 1' = 60''
 Ángulos Definición de ángulo Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. Medida de ángulos Para
Ángulos Definición de ángulo Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. Medida de ángulos Para
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA 1. MONOTONÍA (CRECIMIENTO O DECRECIMIENTO) Si una función es derivable en un punto = a, podemos determinar su crecimiento o decrecimiento en ese punto a partir del signo de
APLICACIONES DE LA DERIVADA 1. MONOTONÍA (CRECIMIENTO O DECRECIMIENTO) Si una función es derivable en un punto = a, podemos determinar su crecimiento o decrecimiento en ese punto a partir del signo de
TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7.1 CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO
 TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
TEMA 7 DERIVADAS Y APLICACIONES MATEMÁTICAS CCSSI º Bac TEMA 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES 7. CRECIMIENTO DE UNA FUNCIÓN EN UN INTERVALO TASA DE VARIACIÓN MEDIA Definición : Se llama
«La derivada de una función en un punto representa geométricamente la pendiente de la recta tangente a la función en dicho punto»
 TEMA 10 DERIVADA DE UNA FUNCIÓN EN UN PUNTO f (a): Consideremos una función f(x) y un punto P de su gráfica (ver figura), de abscisa x=a. Supongamos que damos a la variable independiente x un pequeño incremento
TEMA 10 DERIVADA DE UNA FUNCIÓN EN UN PUNTO f (a): Consideremos una función f(x) y un punto P de su gráfica (ver figura), de abscisa x=a. Supongamos que damos a la variable independiente x un pequeño incremento
AYUDAS SOBRE LA LINEA RECTA
 AYUDAS SOBRE LA LINEA RECTA AYUDA : Grafiquemos la función Solución: Se debe escoger algunos números que representan a la variable x, para obtener el valor de la variable y respectivamente así: El proceso:
AYUDAS SOBRE LA LINEA RECTA AYUDA : Grafiquemos la función Solución: Se debe escoger algunos números que representan a la variable x, para obtener el valor de la variable y respectivamente así: El proceso:
( ), está dada por: g ( x) = log 2 ( x),x > 0. # % 3x log 2 ( 5), x 1 & + -, . log 2. log 2 ( x 3
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN 05 S SEGUNDA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y EDUCACIÓN
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS CURSO DE NIVELACIÓN 05 S SEGUNDA EVALUACIÓN DE MATEMÁTICAS PARA INGENIERÍAS Y EDUCACIÓN
EJERCICIOS PROPUESTOS
 EJERCICIOS PROPUESTOS ) Se dan los siguientes puntos por sus coordenadas: A(3, 0), B(, 0), C(0, ) y sea P un punto variable sobre el eje. i) Hallar la ecuación de la recta (AC) y de la recta (r) perpendicular
EJERCICIOS PROPUESTOS ) Se dan los siguientes puntos por sus coordenadas: A(3, 0), B(, 0), C(0, ) y sea P un punto variable sobre el eje. i) Hallar la ecuación de la recta (AC) y de la recta (r) perpendicular
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
= 1. x = 3: Lím = Asíntota vertical en x = 3: = 0 ; No se anula nunca. Punto de corte con OY es (0, 3) 3 x
 Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
Modelo 4. Problema A.- (Calificación máima: puntos) 4 si Se considera la función real de variable real f ( ) si > a) Determínense las asíntotas de la función y los puntos de corte con los ejes. a. Asíntotas
1 Ángulos en las figuras planas
 Unidad 11. Elementos de geometría plana 1 Ángulos en las figuras planas Página 139 1. Cinco de los ángulos de un heágono irregular miden 147, 101, 93, 1 y 134. Halla la medida del seto ángulo. Los seis
Unidad 11. Elementos de geometría plana 1 Ángulos en las figuras planas Página 139 1. Cinco de los ángulos de un heágono irregular miden 147, 101, 93, 1 y 134. Halla la medida del seto ángulo. Los seis
UNIDAD 2: DERIVADAS Y APLICACIONES
 UNIDAD : DERIVADAS Y APLICACIONES UNIDAD : DERIVADAS Y APLICACIONES ÍNDICE DE LA UNIDAD - INTRODUCCIÓN 6 - DERIVADA DE UNA FUNCIÓN EN UN PUNTO 7 - INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA 8 4- CONTINUIDAD
UNIDAD : DERIVADAS Y APLICACIONES UNIDAD : DERIVADAS Y APLICACIONES ÍNDICE DE LA UNIDAD - INTRODUCCIÓN 6 - DERIVADA DE UNA FUNCIÓN EN UN PUNTO 7 - INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA 8 4- CONTINUIDAD
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
Aplicaciones de la derivada Ecuación de la recta tangente
 Aplicaciones de la derivada Ecuación de la recta tangente La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto. La recta tangente a una curva en un punto
Aplicaciones de la derivada Ecuación de la recta tangente La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto. La recta tangente a una curva en un punto
