5 Teorías de Escala. Igualdad de Rushbrooke: α + 2β + γ = 2. Igualdad de Fisher: Igualdad de Josephson (hiperescala):
|
|
|
- Ernesto Juan Manuel Belmonte Montes
- hace 6 años
- Vistas:
Transcripción
1 5 Teorías de Escala Hemos visto que los fenómenos críticos presentan una serie de características notables: i) divergencias en forma de leyes de potencia caracterizadas por exponentes críticos; ii) universalidad, esto es, los exponentes no dependen de los detalles microscópicos del sistema y solo dependen de algunas propiedades globales: dimensión espacial, dimensión del parámetro de orden (simetrías del Hamiltoniano) e interacciones de corto alcance iii) los exponentes críticos no son independientes entre sí, sinó que satisfacen un conjunto de relaciones conocidas como leyes de escala, a saber: Igualdad de Rushbrooke: α + 2β + γ = 2 Igualdad de Griffiths: α + β(1 + δ) = 2 Igualdad de Fisher: Igualdad de Josephson (hiperescala): (2 η)ν = γ d ν = 2 α Este último hecho es no trivial. Dado que todas las funciones respuesta, excepto la función de correlación, se obtienen de derivar la energía libre, e incluso la función de correlación se encuentra relacionada con la susceptibilidad a través del Teorema de Fluctuación-Disipación, las relaciones anteriores nos dicen que la energía libre tiene que presentar una forma bastante particular en el entorno de la región crítica. Mas aún, el hecho de que exista universalidad nos dice que tiene que existir un mecanismo microscópico general asociado con los fenómenos críticos que da lugar a esa forma particular de la energía libre. En esta sección vamos a analizar un conjunto hipótesis, las cuales explican de manera fenomenológica las leyes de escala. Estas suelen denominarse Teorías ó Hipótesis de Escala. La idea básica por detras de la Teorías de Escala esta relacionada con la divergencia de la longitud de correlación en el punto crítico. Se asume entonces que esta es la única escala espacial relevante del problema, esto es, que las propiedades que determinan la forma de las funciones termodinámicas ocurren en una escala espacial de dimensión lineal del orden de ξ. Ante esta suposición, un cambio en los parámetros 177
2 termodinámicos (por ej., la temperatura o el campo externo) en las cercanías del punto crítico equivaldrá a un cambio de escala. En otras palabras, cuando ξ 1, podemos esperar que los detalles a pequeñas escalas (esto es, para escalas lineales ξ) se tornen irrelevantes. Un cambio en los parámetros termodinámicos que me acerque al punto crítico va a aumentar ξ; si asumimos que los detalles de pequeñas escalas son irrelevantes, al aumentar ξ esperamos ver mas o menos lo mismo, pero en una escala distinta (como si hiciéramos un zoom). Así, esperamos que la energía libre no cambie su forma funcional y solo cambie su escala. Que significa esto? Supongamos que a una temperatura fija T T c graficamos por ejemplo m vs B. Si cambiamos levemente la temperatura obtenemos una nueva curva diferente m vs B. Si ahora elejimos adecuadamente las escalas del nuevo gráfico esperamos que ambas curvas coincidan. Una propiedad de este tipo se conoce como ley de estados correspondientes y de hecho se observa experimentalmente. Que tipo de funciones presentan esta invariancia de ante cambios de escala? Precisamente las leyes de potencia satisfacen esta propiedad. Que significa esto? Supongamos que tenemos el gráfico de una función exponencial del tipo f(r) = e r/r 0 que puede representar, por ejemplo, una función de correlación lejos del punto crítico. Esta función tiene una escala característica dada por r 0, el valor para el cual f(r) decae a 1/e de su valor en r = 0. Supongamos además que r está medida en [cm]. Si ahora hacemos un cambio de escala en las longitudes, expresando las distancias en [m], los valores de r se contraen en un factor 100, en particular, r 0. Si uno conoce de antemano el valor de r 0 puede identificar en que unidades están medidas las longitudes en el gŕafico, solo mirando en que valor de r f(r) decae a 1/e en la escala dada. Supongamos ahora que la función de correlación que nos dan es una ley de potencia del tipo g(r) = A/r α. Si ahora cambiamos la escala de longitud de r [cm] a r [m], con lo cual r = r/100 tenemos que g(r) = A 100 α r Si además cambiamos simultanemente la escala de las ordenadas en el grágico, de manera que representamos 178
3 g (r ) = 100 α g(r) = A r el gráfico g(r) vs r será idéntico al gráfico g(r ) vs r. Si nadie se molesta en especificar las unidades en que están mediadas las cantidades del gráfico somos incapaces de deducirlas con el solo dato del gráfico! Esto es porque las leyes de potencia no definen ninguna escala característica. Dedimos que son invariantes por escala. Las leyes de potencia pertenecen a una clase mas general de funciones invariantes por escala, las cuales analizaremos a continuación Funciones homogeneas generalizadas Se define una función homogenea de una variable a una función f(x) con la siguiente propiedad: f(λx) = g(λ)f(x) λ real (188) la cual nos dá la forma mas general de una función de una variable que es invariante por escala. De la Ec.(188) de donde f(λµx) = g(λµ)f(x) = g(λ)f(µx) g(λµ) = g(λ)g(µ) Puede demostrarse que una función continua con la propiedad anterior necesariamente tiene la forma g(λ) = λ p. Veamos la demostración para el caso en que g(λ) es diferenciable. µ g(λµ) = λg (λµ) = g(λ)g (µ) Tomando µ = 1 y definiendo p g (µ = 1) tenemos g (λ) g(λ) = d dλ ln g(λ) = p λ 179
4 de donde g(λ) = Aλ p. Derivando esta última expresión y evaluando en λ = 1 tenemos g (1) = pa de donde A = 1. De esta manera, una función homogenea satisface f(λx) = λ p f(x) Dado que esta ecuación se satisface para λ arbitrario, en particular podemos tomar λ = 1/x. Si llamamos B = f(1) tenemos finalmente que f(x) = Bx p Las únicas funciones homogeneas de una variable son las leyes de potencia. En forma análoga se define una función homogenea de varias variables como aquella que satisface: f(λx 1, λx 2,..., λx n ) = g(λ)f(x 1, x 2,..., x n ) λ real Utilizando el mismo tipo de argumentos que en el caso anterior se demuestra que g(λ) = λ p. Se dice en este caso que f es homogenea de grado p. La interpretación geométrica de esta propiedad es la misma que antes. Si cambiamos la escala de todas las variables independientes en un mismo factor x i λx i la función f resulta la misma que antes, pero re-escalada por un factor λ p. Un ejemplo conocido es la entropía (o la energía) en termodinámica, la cual es una función homogenea de primer grado de los parámetros extensivos del sistema. Finalmente se define una función homogenea generalizada como aquella que satisface f(λ a 1 x 1, λ a 2 x 2,..., λ a n x n ) = λf(x 1, x 2,..., x n ) λ real (189) donde a i son números reales. Una función de este tipo presenta invariancia de escala ante cambios de escala heterogeneos en las variables independientes. ejemplo el caso de dos variables independientes: Tomemos por f(λ a x, λ b y) = λf(x, y) Dado que esta ecuación se satisface para λ arbitrario, en particular podemos tomar λ b y = 1, esto es, λ = y 1/b, de donde 180
5 Definiendo F (z) f(z, 1) tenemos que ( ) x f y a/b, 1 = y 1/b f(x, y) f(x, y) = y 1/b F ( ) x y a/b Se demuestra facilmente que la recíproca también es cierta, esto es si, f(x, y) = y p F (x/y q ) es facil demostrar que f satisface la propiedad (189) con a = q/p y b = 1/p. Las siguientes propiedades también son simples de demostrar: 1. f(0, 0) = 0 ó f(0, 0) =. 2. Las derivadas f x y f y son también funciones homogeneas generalizadas. 3. La transformada de Legendre g(x, u) definida como g(x, u) = f(x, y(x, u)) y(x, u)u donde u(x, y) = f y es también una función homogenea generalizada Hipótesis de escala de Widom (1965) (homogeneidad de la energía libre) Consideremos por simplicidad un sistema que presenta un punto crítico descripto por un parámetro de orden escalar, tal como un ferromagneto. La energía libre es función de la temperatura y el campo externo f = f(t, B). Sea t = (T T c )/T c la temperatura reducida y asumimos que el punto crítico ocurre en B = 0. La hipótesis de Widom es la siguente: 181
6 1. En las proximidades del punto crítico f puede expresarse como f(t, B) = f r (T, B) + f s (t, B) donde la parte regular f r es una función analítica de sus parámetros, la cual puede asumirse aproximadamente constante en la región crítica. 2. La parte singular f s es una función homegenea generalizada: f s (λ at t, λ a B B) = λf s (t, B) (190) Dado que estamos interesados en la derivadas de f y f r se asume constante en el entorno del punto crítico, vamos a considerar solo f s. Analicemos primero las consecuencias derivadas para la parte singular de la magnetización: Derivando la Ec.(190) de donde m(t, B) = f s (t, B) B λ a f B s(λ at t, λ a BB) (λ a = λ f s(t, B) B B) B λ a B m(λ a t t, λ a B B) = λm(t, B) (191) Elijiendo λ = λ at tenemos a campo nulo m(λ t, 0) = λ 1 a B a t m(t, 0) de donde, o bien m 0 ó m(t, 0) es una ley de potencia. Dado que m(t, 0) tiene que anularse para t > 0 tenemos que 0 para t > 0 m(t, 0) = ( t) 1 a B a t m( 1, 0) para t < 0 182
7 donde para t < 0 hemos tomado λ t = 1. Así, el exponente crítico de la magnetización resulta Consideremos ahora el caso t = 0. Tomando λ = λ a B β = 1 a B a t (192) en la Ec.(191) obtenemos m(0, λ B) = λ 1 a B a B m(0, B) de donde m(0, B) resulta una ley de potencia 1 a B a m(0, B) B B = B 1/δ Consideremos ahora la susceptibilidad Derivando la relación (191) obtenemos δ = a B 1 a B (193) χ = m B λ 2a B χ(λ at t, λ a B B) = λχ(t, B) (194) Siguiendo el mismo procedimiento que antes obtenemos (t) 2a B 1 a t χ(1, 0) para t > 0 χ(t, 0) = ( t) 2a B 1 a t χ( 1, 0) para t < 0 de donde γ = γ = 2a B 1 a t (195) Combinando las Ecs.(192), (193) y (195) obtenemos la ley de escala γ = β(δ 1) (196) 183
8 que es conocida como relación de Windom. Analicemos ahora la parte singular del calor específico Derivando la Ec.(190) obtenemos C = T c 2 f s t 2 y siguiendo los mismos pasos que antes tenemos que C(t, 0) de donde λ 2a t C(λ a t t, λ a B B) = λc(t, B) (197) (t) 2a t 1 a t para t > 0 ( t) 2a t 1 a t para t < 0 α = α = 2a t 1 a t = 2 1 a t (198) Combinando las Ecs.(192), (193) y (198) obtenemos la relación de Griffiths α + β(δ + 1) = 2 y reemplazando la relación de Widom (196) en la anterior obtenemos la relación de Rushbroke α + 2β + γ = 2 Vemos de esta manera que la hipótesis de escala de Widom explica de manera completa todas las leyes de escala. Mas aún, la hipótesis de homogeneidad nos brinda algunas predicciones nuevas. Tomando λ a t t = ±c (c > 0) en la Ec.(191) para B 0 obtenemos ( ) ( ) m(t, B) = t 1 a B a B B t F ± t a = t β F ± B/a t t donde βδ = a B a t 184
9 Las funciones F ± (z) son proporcionales a las curvas de magnetización en función del campo externo para dos temperaturas de referencia T = T c (1 ± c). Estas se conocen como funciones de escala y dependen del sistema particular (no son universales). No obstante, si escribimos la ecuación anterior como ( ) m(t, B) B t β = F ± t esto nos dice que, cualquiera sea el material, si medimos las curvas de magnetización vs campo para diferentes temperaturas y las representamos en un gráfico m/ t β vs B/ t, todas las curvas tienen que coincidir en una misma F ± (z), dependiendo de que la temperatura sea mayor o menor que T c respectivamente. A este tipo de comportamiento (leyes de estados correspondientes) se lo denomina también colapso de las curvas ( data collapse ) y se verifica experimentalmente. Debemos recalcar que la hipótesis fenomenológica de escala constituye una conjetura plausible, la cual no ha sido demostrada rigurósamente. No obstante, dada la amplia confirmación experimental (y numérica) de la misma, se la acepta como válida en general Bloques de Kadanoff (homogeneidad en las correlaciones) Existe un argumento heurístico propuesto por Kadanoff para justificar la hipótesis de homogeneidad. A pesar de basado en una serie de conjeturas (algunas de las cuales incluso son incorrectas) posee bastante interés por los siguientes motivos: 1. Las suposiciones introducidas para justificar la homogeneidad son a nivel microscópico. 2. El argumento fué el primer paso que condujo a las ideas de Grupo de Renormalización, Teoría estadística que explica de manera completa la universalidad del comportamiento crítico. 3. Permite deducir a la vez la homogeneidad de la energía libre y de las funciones de correlación. 185
10 S i ba I S I a ba Figura 40: Ejemplo de bloques de Kadanoff en la red cuadrada para un factor de escala b = 2. El argumento trabaja específicamente sobre el modelo de Ising: βh = K N S i S j + h S i S i = ±1 <i,,j> i=1 con K βj y h βb. Vamos a suponer por simplicidad que el modelo está definido en una red hipercúbica d-dimensional. Vamos dividir el sistema en bloques hipercúbicos de dimensión lineal ba, donde a es el parámetro de red original y b > 1 es un factor de escala (ver Fig.40). De esta manera tenemos b d spines (sitios) en cada bloque y N b = N/b d bloques en total. El conjunto de los N b bloques, denominados bloques de Kadanoff, conforman a su vez una red hipercúbica de parámetro de red ba, cuyos sitios vamos a denotar con letras mayusculas (ver Fig.40). El spin total en el bloque I es S I = S i = b d, b d + 1,..., 0, 1,..., b d 1, b d i I Esta construcción constituye una transformación de escala espacial (un zoom) a nivel microscópico. La idea básica del argumento de Kadanoff es que, si el sistema presenta 186
11 invariancia de escala suficientemente cerca del punto crítico, entonces el sistema de bloques tiene que verse aproximadamente igual al sistema de spines. Esto es, suficientemente cerca del punto crítico, ξ ba tendremos regiones de dimensión lineal ξ donde los spines va a apuntar mayoritariamente en la misma dirección; estas regiones van a contener un número grande de bloques de Kadanoff y por lo tanto podemos esperar que los spines dentro de un bloque apunten en su mayoría en la misma dirección. Dicho de otra manera, si pintamos los spines S i = +1 de negro y los S j = 1 de blanco, visto de lejos esperamos ver casi exclusivamente bloques totalmente blancos ó totalmente negros (a lo sumo gris oscuro o blanco sucio ). Así, de todos los valores posibles que puede asumir S I, esperamos que los valores ±bd tengan una probabilidad mucho mayor que los restantes. Introducimos entonces las nuevas variables de spin de bloque S I = zs I, donde S I = ±1 y z < b d ; z evidentemente depende del factor de escala y vamos a asumir la forma z = b y, con y < d. Si el sistema de bloques se comporta aproximadamente igual al sistema de sitios, la termodinámica de ambos debe ser la misma, esto es, la forma funcional de la energía libre debe ser idéntica en ambos casos. Una forma de obtener esto (no es la única) es que la energía libre del sistema de bloques se derive de un Hamiltoniano de bloques con la misma forma funcional que el Hamiltoniano de sitios, esto es, βĥ({s I}) = ˆK N b S I S J + ĥ <I,Jj> S I I=1 Para considerar los bloques como sitios hemos hecho un cambio de escala espacial, es decir, estamos midiendo ahora las longitudes en unidades de ba. Bajo este cambio de escala la longitud de correlación va a disminuir ξ ξ/b, lo cual implica un cambio en los parámetros intensivos t y h; de ahi que Ĥ tiene que tener parámetros diferentes ˆK y ĥ. Dado que los Hamiltonianos de bloque y de sitios tienen la misma forma, la energía libre por bloque obtenida usando Ĥ, f b(ˆt, ĥ) tendrá la misma forma funcional que la energía libre por sitio f s (t, h), esto es, f b (x, y) = f s (x, y) = f(x, y). Pero dado que estamos describiendo el mismo sistema (solo hemos hecho un cambio de escala), la energía libre total tiene que ser la misma en ambos casos 187
12 N f(ˆt, ĥ) = Nf(t, h) bd f(ˆt, ĥ) = bd f(t, h) (199) El último paso en el argumento es discernir como dependen ˆt y ĥ de (t, h). Como primero vamos a asumir que ˆt no depende de h; esto es válido solo para sistemas con la simetría de inversión discreta del Hamiltoniano. Además, sabemos que t = 0 ˆt = 0, ya que siendo ambos sistemas idénticos tienen el mismo punto crítico. Fuera del punto crítico, la transformación de escala nos aleja del mismo, ya que la longitud de correlación disminuye ξ ξ/b y por lo tanto ˆt > t y este alejamiento aumenta con el factor de escala b. La relación mas simple que satisface estos requerimientos es ˆt = g(b)t, con g(b) > 1. Supongamos ahora que hacemos dos transformaciones de escala sucesivas, una con un factor b 1 y la otra con b 2. El resultado final tiene que ser equivalente a una única transformación con un factor b = b 1 b 2 y por lo tanto g(b 1 b 2 ) = g(b 1 )g(b 2 ). Por los resultados de la sección anterior tenemos que g(b) = b x, con x > 0. Finalmente, el término de interacción con el campo externo es N N b N b h S i = h S i = h S N b i h z S I i=1 I=1 i I I=1 I=1 de donde ĥ = z h = by h. Reemplazando en la Ec.(199) obtenemos f(b x t, b y h) = b d f(t, h) (200) El factor de escala en la ecuación anterior es un número entero, por la forma en que construimos la transformación de escala. Sin embargo, suficientemente cerca del punto crítico, donde ξ 1, podemos generalizar la idea anterior para factores de escala arbitrarios y por lo tanto la Ec(200) resulta equivalente a la hipótesis de homogeneidad (190) con x = da t y = da B 188
13 Una consecuencia nueva de esta derivación surge de la restricción y < d, la cual implica a B < 1; esto último se corrobora experimentalmente. Notemos que, dado que el Hamiltoniano de bloques tiene la misma dependencia funcional en los parámetros termodinámicos que el de sitios, todos los promedios estadísticos van a compartir esta propiedad. Esto es válido en particular para la longitud de correlación ξ(t, h), la cual satisface por lo tanto que ξ(ˆt, ĥ) = ξ(bx t, b y h) = ξ(t, h)/b En particular a campo nulo tenemos que bξ(b x t) = ξ(t); tomando b x t = 1 obtenemos ξ t 1/x de donde ν = 1 x = 1 da t Reemplazando en la Ec.(198) obtenemos entonces la ley de hiperescala 2 α = νd Finalmente vamos a considerar la función correlación conectada. Consideremos por simplicidad el caso h = 0. C(r ij, t) = S i S j S i S j donde r ij r i r j es la distancia entre los spines i y j, medida en unidades del parámetro de red a. Definimos de igual manera la función de correlación entre spines de bloque C(r IJ, ˆt) = S I S J S I S J donde hemos asumido la misma forma funcional y donde r IJ r I r J es la distancia entre los centros de los bloques I y J, medida en unidades de ba. En la expresión anterior los promedios se toman utilizando la distribución de probabilidad de Boltzmann asociada con el Hamiltoniano de bloques. Es razonable suponer que el resultado no va a cambiar si tomamos los promedios utilizando la distribución de probabilidad asociada con el Hamiltoniano de sitios. Tenemos entonces 189
14 C(r IJ, ˆt) = 1 [ S z 2 I S J S I S ] J = 1 b 2y = 1 b 2y b d b d i I j J b d b d i I j J [ S i S j S i S j ] C(r ij, t) Para bloques distantes r IJ ba, la distancia entre spines pertenecientes a diferentes bloques puede asumirse aproximadamente constante r ij r = br IJ. Así, obtenemos la relación de homogeneidad Tomando b = r C(r/b, tb x ) = b 2(d y) C(r, t) (201) En el punto crítico t = 0 de donde 2 η = d(2a B 1). C(r, t) = r 2(y d) F c (tr x ) = r 2d(a B 1) F c (tr dat ) (202) C(r) finalmente la ley de escala de Fisher 1 r 2d(1 a B) 1 r d 2+η Recordando que 2a B 1 = γa t = γ/νd obtenemos (2 η)ν = γ La Ec.(202) puede entonces ser escrita como C(r, t) = 1 r d 2+η F c(tr 1/ν ) = 1 ( r d 2+η F c (t ν r) 1/ν) = 1 g(r/ξ) rd 2+η En general se observa que g(x) e x. Por otra parte, tomando tb x = 1 en la Ec.(201) obtenemos C(r, t) = t 2(d y)/x ˆFc (rt 1/x ) 190
15 Si de alguna manera podemos obtener el comportamiento asintótico de la función de correlación, la expresión anterior puede utilizarse para corroborar las hipótesis de escala, utilizando los valores de x, y calculados a partir de las leyes de escala. Por ejemplo, para el modelo de Ising en d = 2, usando los exponentes críticos de la solución de Onsager y tomando ν = 1 tenemos que x = 1 e y = 15/8, lo que nos da C(r, t) t 1/4 ˆFc (rt) Esta forma asintótica fué corroborada rigurósamente por Wu en Finalmente pueden repetirse todos los pasos anteriores a campo no nulo, de donde se obtiene la forma de escala C(r, t, h) = t ν(d 2+η) F ( r t ν, h ) t Notemos que las hipótesis de escala no dan cuenta para nada de la universalidad de los exponentes críticos. Si bien el argumento fue planteado específicamente para el modelo de Ising, es claro que es posible generalizarlo a otros modelos. No obstante, este tiene algunos puntos incorrectos. Repasemos la suposiciones mas importantes utilizadas en la derivación del argumento. Estas son dos: i) El Hamiltoniano de bloques tiene la misma forma que el Hamiltoniano de sitios; ii) las relaciones ĥ = by h y ˆt = b x t. Mientras que el segundo punto es correcto, el punto debil del argumento es el primero. Esta suposición es básicamente incorrecta. Como veremos en la sección siguiente, no es necesario mantener la invariancia de forma del Hamiltoniano para obtener la homogeneidad de las funciones termodinámicas y de hecho levantar esta restricción fué la idea clave que permitió explicar la universalidad. 191
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
May 4, 2012 CAPÍTULO 5: OPTIMIZACIÓN
 May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Universidad Nacional de Colombia Departamento de Matemáticas Álgebra Lineal - Grupo 1 Resumen Unidad n 3
 Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Tema 2 TRANSICIONES DE FASE Y FENÓMENOS CRÍTICOS Transiciones de fase de primer orden. Transiciones de fase de orden superior y fenómenos críticos.
 ema RANSICIONES DE FASE Y FENÓMENOS CRÍICOS ransiciones de fase de primer orden. ransiciones de fase de orden superior y fenómenos críticos. eoría de Landau y parámetro de orden. Exponentes críticos y
ema RANSICIONES DE FASE Y FENÓMENOS CRÍICOS ransiciones de fase de primer orden. ransiciones de fase de orden superior y fenómenos críticos. eoría de Landau y parámetro de orden. Exponentes críticos y
Problemas de VC para EDVC elaborados por C. Mora, Tema 4
 Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Modelos Estocásticos I Tercer Examen Parcial Respuestas
 Modelos Estocásticos I Tercer Examen Parcial Respuestas. a Cuál es la diferencia entre un estado recurrente positivo y uno recurrente nulo? Cómo se define el período de un estado? Demuestre que si el estado
Modelos Estocásticos I Tercer Examen Parcial Respuestas. a Cuál es la diferencia entre un estado recurrente positivo y uno recurrente nulo? Cómo se define el período de un estado? Demuestre que si el estado
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Funciones convexas Definición de función convexa. Tema 10
 Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Semana03[1/17] Funciones. 16 de marzo de Funciones
![Semana03[1/17] Funciones. 16 de marzo de Funciones Semana03[1/17] Funciones. 16 de marzo de Funciones](/thumbs/48/24900626.jpg) Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Espacios Vectoriales Asturias: Red de Universidades Virtuales Iberoamericanas 1
 Espacios Vectoriales 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Espacios Vectoriales... 4 1.1 Definición de espacio vectorial... 4 1.2 Definición de subespacio vectorial...
Espacios Vectoriales 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Espacios Vectoriales... 4 1.1 Definición de espacio vectorial... 4 1.2 Definición de subespacio vectorial...
Base y Dimensión de un Espacio Vectorial
 Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
CONCEPTOS BASICOS DE LA TRANSFORMADA DE LAPLACE LA TRANSFORMADA DE LAPLACE
 LA TRANSFORMADA DE LAPLACE Por cálculo integral sabemos que cuando vamos a determinar una integral impropia de la forma,su desarrollo se obtiene realizando un cambio de variable en el límite superior de
LA TRANSFORMADA DE LAPLACE Por cálculo integral sabemos que cuando vamos a determinar una integral impropia de la forma,su desarrollo se obtiene realizando un cambio de variable en el límite superior de
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
6.4 Método de solución de las ecuaciones diferenciales parciales (directos, equiparables con las ordinarias, separación de variables)
 6.4 Método de solución de las ecuaciones diferenciales parciales(directos, equiparables con las ordinarias, separación de variables) 439 6.4 Método de solución de las ecuaciones diferenciales parciales
6.4 Método de solución de las ecuaciones diferenciales parciales(directos, equiparables con las ordinarias, separación de variables) 439 6.4 Método de solución de las ecuaciones diferenciales parciales
Funciones de Clase C 1
 Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Distribuciones de probabilidad bidimensionales o conjuntas
 Distribuciones de probabilidad bidimensionales o conjuntas Si disponemos de dos variables aleatorias podemos definir distribuciones bidimensionales de forma semejante al caso unidimensional. Para el caso
Distribuciones de probabilidad bidimensionales o conjuntas Si disponemos de dos variables aleatorias podemos definir distribuciones bidimensionales de forma semejante al caso unidimensional. Para el caso
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
ELEMENTOS DE GEOMETRÍA. Eduardo P. Serrano
 ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Clase 10: Extremos condicionados y multiplicadores de Lagrange
 Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Diferenciales de Orden Superior
 Capítulo 10 Diferenciales de Orden Superior En este capítulo extenderemos a las funciones definidas sobre espacios normados el concepto de función r-veces diferenciable y de clase C r y obtendremos las
Capítulo 10 Diferenciales de Orden Superior En este capítulo extenderemos a las funciones definidas sobre espacios normados el concepto de función r-veces diferenciable y de clase C r y obtendremos las
Modelización por medio de sistemas
 SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
4.2. Funciones inyectivas, sobreyectivas y biyectivas
 4.. Funciones inyectivas, sobreyectivas y biyectivas En esta sección estudiaremos tres conceptos básicos sobre funciones. 4... Funciones inyectivas Definición 4.. Sea f una función de en. Diremos que f
4.. Funciones inyectivas, sobreyectivas y biyectivas En esta sección estudiaremos tres conceptos básicos sobre funciones. 4... Funciones inyectivas Definición 4.. Sea f una función de en. Diremos que f
. Universidad Tecnológica Nacional - Facultad Regional Rosario. Álgebra y Geometría Analítica EL PLANO
 . Universidad Tecnológica Nacional - Facultad Regional Rosario Álgebra y Geometría Analítica EL PLANO Autores: Lic. Martha Fascella Ing. Ricardo F. Sagristá 0 Contenido EL PLANO... 3.- Definición del plano
. Universidad Tecnológica Nacional - Facultad Regional Rosario Álgebra y Geometría Analítica EL PLANO Autores: Lic. Martha Fascella Ing. Ricardo F. Sagristá 0 Contenido EL PLANO... 3.- Definición del plano
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
1 Ecuaciones diferenciales
 1 Ecuaciones diferenciales La solución a una ecuación algebraica es un número, o un conjunto de números que satisfacen la ecuación. Por ejemplo las soluciónes de x 2 4x + 3 = 0 son x 0 = 1 y x 1 = 3. Las
1 Ecuaciones diferenciales La solución a una ecuación algebraica es un número, o un conjunto de números que satisfacen la ecuación. Por ejemplo las soluciónes de x 2 4x + 3 = 0 son x 0 = 1 y x 1 = 3. Las
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Universidad Nacional de Colombia Departamento de Matemáticas Álgebra Lineal - Grupo 5 Resumen Unidad n 3
 Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 5 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 5 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
4. Complementos sobre Problemas de Contorno para S.D.O. Lineales. 4. Complementos sobre Problemas de Contorno
 para S.D.O. Lineales 4.1. Problemas de contorno para s.d.o. lineales. Teorema de alternativa 4.1. Problemas de contorno. Teorema de alternativa Fijemos A C 0 ([α, β]; L(R N )) y b C 0 ([α, β]; R N ), dos
para S.D.O. Lineales 4.1. Problemas de contorno para s.d.o. lineales. Teorema de alternativa 4.1. Problemas de contorno. Teorema de alternativa Fijemos A C 0 ([α, β]; L(R N )) y b C 0 ([α, β]; R N ), dos
SESIÓN 11 DERIVACIÓN DE FUNCIONES TRIGONOMETRICAS INVERSAS
 SESIÓN 11 DERIVACIÓN DE FUNCIONES TRIGONOMETRICAS INVERSAS I. CONTENIDOS: 1. Función inversa, conceptos y definiciones 2. Derivación de funciones trigonométricas inversas 3. Ejercicios resueltos 4. Estrategias
SESIÓN 11 DERIVACIÓN DE FUNCIONES TRIGONOMETRICAS INVERSAS I. CONTENIDOS: 1. Función inversa, conceptos y definiciones 2. Derivación de funciones trigonométricas inversas 3. Ejercicios resueltos 4. Estrategias
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Algunas Distribuciones Continuas de Probabilidad. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Funciones homogéneas. Funciones
 Lección 4 Funciones homogéneas Funciones implícitas 41 Funciones homogéneas Una clase de funciones especialmente importantes en economía es la de las funciones homogéneas Si consideramos, por ejemplo,
Lección 4 Funciones homogéneas Funciones implícitas 41 Funciones homogéneas Una clase de funciones especialmente importantes en economía es la de las funciones homogéneas Si consideramos, por ejemplo,
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
MATEMÁTICA D y D 1 Módulo I: Análisis de Variable Compleja
 Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple
 Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
NÚMEROS COMPLEJOS: C
 NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
2.2 Rectas en el plano
 2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
La función, definida para toda, es periódica si existe un número positivo tal que
 Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
CAPÍTULO 4: DERIVADAS DE ORDEN SUPERIOR. En este capítulo D denota un subconjunto abierto de R n.
 April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Problema 1. Calcula las derivadas parciales de las siguientes funciones: (d) f(x, y) = arctan x + y. (e) f(x, y) = cos(3x) sin(3y),
 Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Ecuaciones diferenciales homogéneas y no homogéneas lineales a coeficientes constantes. Búsqueda de la solución particular.
 Ecuaciones diferenciales homogéneas y no homogéneas lineales a coeficientes constantes. Búsqueda de la solución particular. 1. Definiciones previas 1.1. Wronskiano Diremos que el Wronskiano de un conjunto
Ecuaciones diferenciales homogéneas y no homogéneas lineales a coeficientes constantes. Búsqueda de la solución particular. 1. Definiciones previas 1.1. Wronskiano Diremos que el Wronskiano de un conjunto
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Enteros
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Z = N {0} N Enteros Las operaciones + y. son cerradas en Z, es decir la suma de dos números enteros es un número entero y el producto
Operador Diferencial y Ecuaciones Diferenciales
 Operador Diferencial y Ecuaciones Diferenciales. Operador Diferencial Un operador es un objeto matemático que convierte una función en otra, por ejemplo, el operador derivada convierte una función en una
Operador Diferencial y Ecuaciones Diferenciales. Operador Diferencial Un operador es un objeto matemático que convierte una función en otra, por ejemplo, el operador derivada convierte una función en una
Descomposición en forma canónica de Jordan (Segunda versión)
 Descomposición en forma canónica de Jordan (Segunda versión) Francisco J. Bravo S. 1 de septiembre de 211 En esta guía se presentan los resultados necesarios para poder construir la forma de Jordan sin
Descomposición en forma canónica de Jordan (Segunda versión) Francisco J. Bravo S. 1 de septiembre de 211 En esta guía se presentan los resultados necesarios para poder construir la forma de Jordan sin
Funciones Inversas. Derivada de funciones inversas
 Capítulo 15 Funciones Inversas En este capítulo estudiaremos condiciones para la derivación de la inversa de una función de varias variables y, en particular, extenderemos a estas funciones la fórmula
Capítulo 15 Funciones Inversas En este capítulo estudiaremos condiciones para la derivación de la inversa de una función de varias variables y, en particular, extenderemos a estas funciones la fórmula
Tema 2 Resolución de EcuacionesNo Lineales
 Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
TEMA 8.- NORMAS DE MATRICES Y
 Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
Álgebra II: Tema 8. TEMA 8.- NORMAS DE MATRICES Y NúMERO DE CONDICIóN Índice. Introducción 2. Norma vectorial y norma matricial. 2 2.. Norma matricial inducida por normas vectoriales......... 4 2.2. Algunos
DERIVADAS PARCIALES Y APLICACIONES
 CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
Anillo de polinomios con coeficientes en un cuerpo
 Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
Capítulo 2 Anillo de polinomios con coeficientes en un cuerpo En el conjunto Z se ha visto cómo la relación ser congruente módulo m para un entero m > 1, es compatible con las operaciones suma y producto.
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
Grupos libres. Presentaciones.
 S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
S _ Tema 12.- Grupos libres. Presentaciones. 12.1 Grupos libres. En el grupo Z de los enteros vimos una propiedad (cf. ejemplos.5), que lo caracteriza como grupo libre. Lo enunciamos al modo de una Propiedad
Complementos de Análisis. Año 2016
 Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Matrices y determinantes. Sistemas de ecuaciones lineales
 Tema 0 Matrices y determinantes Sistemas de ecuaciones lineales 01 Introducción Definición 011 Se llama matriz a un conjunto ordenado de números, dispuestos en filas y columnas, formando un rectángulo
Tema 0 Matrices y determinantes Sistemas de ecuaciones lineales 01 Introducción Definición 011 Se llama matriz a un conjunto ordenado de números, dispuestos en filas y columnas, formando un rectángulo
Aplicaciones de los S.E.D.O.
 Tema 7 Aplicaciones de los S.E.D.O. 7. Introducción Nota: APUNTES INCOMPLETOS Estudiaremos en este Tema algunos modelos de interés en las Ciencias Naturales que utilizan para su modelización sistemas de
Tema 7 Aplicaciones de los S.E.D.O. 7. Introducción Nota: APUNTES INCOMPLETOS Estudiaremos en este Tema algunos modelos de interés en las Ciencias Naturales que utilizan para su modelización sistemas de
Variables aleatorias
 Distribuciones continuas Se dice que una variable aleatoria X tiene una distribución continua, o que X es una variable continua, si existe una función no negativa f, definida sobre los números reales,
Distribuciones continuas Se dice que una variable aleatoria X tiene una distribución continua, o que X es una variable continua, si existe una función no negativa f, definida sobre los números reales,
Tema 5: Sistemas de ecuaciones lineales.
 TEORÍA DE ÁLGEBRA: Tema 5 DIPLOMATURA DE ESTADÍSTICA 1 Tema 5: Sistemas de ecuaciones lineales 1 Definiciones generales Definición 11 Una ecuación lineal con n incognitas es una expresión del tipo a 1
TEORÍA DE ÁLGEBRA: Tema 5 DIPLOMATURA DE ESTADÍSTICA 1 Tema 5: Sistemas de ecuaciones lineales 1 Definiciones generales Definición 11 Una ecuación lineal con n incognitas es una expresión del tipo a 1
Límites y continuidad. Cálculo 1
 Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
MA1001: Introducción al Cálculo
 Semestre otoño 2008 Que estudia el cálculo? Estudia funcionesfunciones realesreales de variable real.variable real. Debemos comenzar por estudiar la base de todo, es decir los números reales Que son los
Semestre otoño 2008 Que estudia el cálculo? Estudia funcionesfunciones realesreales de variable real.variable real. Debemos comenzar por estudiar la base de todo, es decir los números reales Que son los
Tensores cartesianos.
 Tensores cartesianos. Transformación de coordenadas. Consideremos dos sistemas de coordenadas cartesianas ortogonales en el plano, identificados como σ y σ. Supongamos que ambos tienen un origen común,
Tensores cartesianos. Transformación de coordenadas. Consideremos dos sistemas de coordenadas cartesianas ortogonales en el plano, identificados como σ y σ. Supongamos que ambos tienen un origen común,
La reordenación aleatoria de un conjunto finito
 La reordenación aleatoria de un conjunto finito Pérez Cadenas J. I. 0.06.2003 Resumen Al desordenar y, a continuación, reordenar aleatoriamente un conjunto finito es posible que algunos de sus elementos
La reordenación aleatoria de un conjunto finito Pérez Cadenas J. I. 0.06.2003 Resumen Al desordenar y, a continuación, reordenar aleatoriamente un conjunto finito es posible que algunos de sus elementos
1. Convergencia en medida
 FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
La cuerda vibrante. inicialmente se encuentra sobre el eje de abscisas x la posición de un punto de la cuerda viene descrita por su posición vertical
 la cuerda es extensible La cuerda vibrante inicialmente se encuentra sobre el eje de abscisas x la posición de un punto de la cuerda viene descrita por su posición vertical y(x, t) la posición depende
la cuerda es extensible La cuerda vibrante inicialmente se encuentra sobre el eje de abscisas x la posición de un punto de la cuerda viene descrita por su posición vertical y(x, t) la posición depende
En la notación C(3) se indica el valor de la cuenta para 3 kilowatts-hora: C(3) = 60 (3) = 1.253
 Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
Eje temático: Álgebra y funciones Contenidos: Operatoria con expresiones algebraicas Nivel: 2 Medio Funciones 1. Funciones En la vida diaria encontramos situaciones en las que aparecen valores que varían
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
es el lugar geométrico de los puntos p tales que p 0 p n o p 0 p o. p x ; y ; z perteneciente a y un vector no
 El Plano y la Recta en el Espacio Matemática 4º Año Cód. 145-15 P r o f. M a r í a d e l L u j á n M a r t í n e z P r o f. J u a n C a r l o s B u e P r o f. M i r t a R o s i t o P r o f. V e r ó n i
El Plano y la Recta en el Espacio Matemática 4º Año Cód. 145-15 P r o f. M a r í a d e l L u j á n M a r t í n e z P r o f. J u a n C a r l o s B u e P r o f. M i r t a R o s i t o P r o f. V e r ó n i
Tema 9: Contraste de hipótesis.
 Estadística 84 Tema 9: Contraste de hipótesis. 9.1 Introducción. El objetivo de este tema es proporcionar métodos que permiten decidir si una hipótesis estadística debe o no ser rechazada, en base a los
Estadística 84 Tema 9: Contraste de hipótesis. 9.1 Introducción. El objetivo de este tema es proporcionar métodos que permiten decidir si una hipótesis estadística debe o no ser rechazada, en base a los
«La derivada de una función en un punto representa geométricamente la pendiente de la recta tangente a la función en dicho punto»
 TEMA 10 DERIVADA DE UNA FUNCIÓN EN UN PUNTO f (a): Consideremos una función f(x) y un punto P de su gráfica (ver figura), de abscisa x=a. Supongamos que damos a la variable independiente x un pequeño incremento
TEMA 10 DERIVADA DE UNA FUNCIÓN EN UN PUNTO f (a): Consideremos una función f(x) y un punto P de su gráfica (ver figura), de abscisa x=a. Supongamos que damos a la variable independiente x un pequeño incremento
Teorema Central del Límite (1)
 Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Prácticas para Resolver PROBLEMAS MATEMÁTICOS
 Prácticas para Resolver PROBLEMAS MATEMÁTICOS 1 Prólogo El presente manual está dirigido a los estudiantes de las facultades de físico matemáticas de las Escuelas Normales Superiores que estudian la especialidad
Prácticas para Resolver PROBLEMAS MATEMÁTICOS 1 Prólogo El presente manual está dirigido a los estudiantes de las facultades de físico matemáticas de las Escuelas Normales Superiores que estudian la especialidad
Tema 4: Cinética química
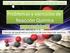 Tema 4: Cinética química Velocidad de reacción. Velocidad media e instantánea. Ecuación de velocidad. Obtención de la ecuación de velocidad: método de las concentraciones iniciales. Ecuaciones de velocidad
Tema 4: Cinética química Velocidad de reacción. Velocidad media e instantánea. Ecuación de velocidad. Obtención de la ecuación de velocidad: método de las concentraciones iniciales. Ecuaciones de velocidad
3. ANÁLISIS DE DATOS DE PRECIPITACIÓN.
 3. ANÁLISIS DE DATOS DE PRECIPITACIÓN. Teniendo en cuenta que la mayoría de procesos estadísticos se comportan de forma totalmente aleatoria, es decir, un evento dado no está influenciado por los demás,
3. ANÁLISIS DE DATOS DE PRECIPITACIÓN. Teniendo en cuenta que la mayoría de procesos estadísticos se comportan de forma totalmente aleatoria, es decir, un evento dado no está influenciado por los demás,
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Lección 2: Funciones vectoriales: límite y. continuidad. Diferenciabilidad de campos
 Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Capitulo IV - Inecuaciones
 Capitulo IV - Inecuaciones Definición: Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que sólo se verifica para determinados valores de la incógnita o
Capitulo IV - Inecuaciones Definición: Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que sólo se verifica para determinados valores de la incógnita o
Sistemas de ecuaciones lineales dependientes de un parámetro
 Vamos a hacer uso del Teorema de Rouché-Frobenius para resolver sistemas de ecuaciones lineales de primer grado. En particular, dedicaremos este artículo a resolver sistemas de ecuaciones lineales que
Vamos a hacer uso del Teorema de Rouché-Frobenius para resolver sistemas de ecuaciones lineales de primer grado. En particular, dedicaremos este artículo a resolver sistemas de ecuaciones lineales que
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS
 1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
SESIÓN 6 INTERPRETACION GEOMETRICA DE LA DERIVADA, REGLA GENERAL PARA DERIVACIÓN, REGLAS PARA DERIVAR FUNCIONES ALGEBRAICAS.
 SESIÓN 6 INTERPRETACION GEOMETRICA DE LA DERIVADA, REGLA GENERAL PARA DERIVACIÓN, REGLAS PARA DERIVAR FUNCIONES ALGEBRAICAS. I. CONTENIDOS: 1. Interpretación geométrica de la derivada 2. Regla general
SESIÓN 6 INTERPRETACION GEOMETRICA DE LA DERIVADA, REGLA GENERAL PARA DERIVACIÓN, REGLAS PARA DERIVAR FUNCIONES ALGEBRAICAS. I. CONTENIDOS: 1. Interpretación geométrica de la derivada 2. Regla general
Inducción Matemática Conjuntos Funciones. Matemática Discreta. Agustín G. Bonifacio UNSL. Repaso de Inducción, Conjuntos y Funciones
 UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
Tema 2: Teorema de estructura de los grupos abelianos finitamente generados.
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 215/216 Tema 2: Teorema de estructura de los grupos abelianos finitamente generados. 1.1. Grupo abeliano libre. Bases. Definición 1.1. El grupo Z n con
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
1. Producto escalar. Propiedades Norma de un vector. Espacio normado. 1.2.Ortogonalidad. Ángulos. 1.4.Producto escalar en V 3.
 . Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
. Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
Derivadas Parciales (parte 2)
 40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis Facultad de Ciencias Sociales, UdelaR Índice 1. Introducción: hipótesis estadística, tipos de hipótesis, prueba de hipótesis 2.
Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis Facultad de Ciencias Sociales, UdelaR Índice 1. Introducción: hipótesis estadística, tipos de hipótesis, prueba de hipótesis 2.
Contenido. 4. Dinámica Lagrangiana y Hamiltoniana. 1 / Omar De la Peña-Seaman IFUAP Métodos Matemáticos Propedéutico Física 1/38 38
 Contenido 4. Dinámica Lagrangiana y Hamiltoniana 1 / Omar De la Peña-Seaman IFUAP Métodos Matemáticos Propedéutico Física 1/38 38 Contenido: Tema 04 4. Dinámica Lagrangiana y Hamiltoniana 4.1 Coordenadas
Contenido 4. Dinámica Lagrangiana y Hamiltoniana 1 / Omar De la Peña-Seaman IFUAP Métodos Matemáticos Propedéutico Física 1/38 38 Contenido: Tema 04 4. Dinámica Lagrangiana y Hamiltoniana 4.1 Coordenadas
2.1. Estructura algebraica de espacio vectorial
 Tema 2 Espacios vectoriales de dimensión finita 21 Estructura algebraica de espacio vectorial Los vectores libres en el plano son el sustento geométrico del concepto de espacio vectorial Se trata de segmentos
Tema 2 Espacios vectoriales de dimensión finita 21 Estructura algebraica de espacio vectorial Los vectores libres en el plano son el sustento geométrico del concepto de espacio vectorial Se trata de segmentos
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
3.3. Número de condición de una matriz.
 96 33 Número de condición de una matriz Consideremos el sistema Ax = b, de solución u Queremos controlar qué cambios se producen en la solución cuando hacemos pequeños cambios en las componentes de b o
96 33 Número de condición de una matriz Consideremos el sistema Ax = b, de solución u Queremos controlar qué cambios se producen en la solución cuando hacemos pequeños cambios en las componentes de b o
