Primer Examen Parcial
|
|
|
- Luis Soto Miranda
- hace 6 años
- Vistas:
Transcripción
1 Primer Parcial. -. R- -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Primer Examen Parcial. --. Ejercicio. (a) Sea Q : R R la forma cuadrática definida mediante Q(x, y, z) = x + y + αz xy 6yz + xz (α R). (a) Reduce Q a suma de cuadrados (dando las relaciones entre las variables iniciales y las finales) y estudiala en función de α. (a) Tomando α =, determina (si es posible) dos puntos (x, y, z) R tales que Q(x, y, z) = 4. (a) Completando cuadrados tenemos, Por tanto, Q(x, y, z) = [x + x( y + z) + y + αz 6yz = [x + ( y + z) ( y + z) + y + αz 6yz = [x y + z y z + yz + y + αz 6yz = [x y + z + y + (α )z 4yz = [x y + z + (y z) z + (α )z = [x y + z + (y z) + (α )z = x + y + (α )z siendo x = x y + z, y = y z, z = z. Si α > ( α > ) la forma cuadrática es definida positiva (los tres coeficientes son positivos); Q(x, y, z) >, (x, y, z) (,, ). Si α = ( α = ) la forma cuadrática es semi-definida positiva (hay dos coeficientes positivos y uno nulo); Q(x, y, z), (x, y, z) R y (x, y, z ) (,, ) tal que Q(x, y, z ) =.
2 R- Primer Parcial. -. Si α < ( α < ) la forma cuadrática es indefinida (hay dos coeficientes positivos y uno negativo); (x, y, z ) tal que Q(x, y, z ) > y (x, y, z ) tal que Q(x, y, z ) <. (a) Para α = la forma cuadrática es indefinida, es decir, existen puntos para los que toma valores negativos y otros para los que alcanza valores positivos. Para obtener puntos (x, y, z) para los que Q(x, y, z) = 4 bastará obtener las coordenadas (x, y, z ) y puesto que tenemos la expresión en suma de cuadrados esto es inmediato. Por ejemplo, Q(x =, y =, z = ±) = 4. Las coordenadas (x, y, z) las obtenemos de resolver los sistemas correspondientes (x =, y =, z = ), x = x y + z = y = y z = z = z = ± = x = y = z = ± z = ± = (x =, y =, z = ). Ejercicio. (b) Calcula la ecuación reducida y (dando sus elementos característicos) representa gráficamente la cuádrica de ecuación 4x + 4y z 6x 8y + 6 =. De qué tipo de cuádrica se trata? Es una superficie de revolución? Completando cuadrados tenemos 4x + 4y z 6x 8y + 6 = 4(x ) 6 + 4(y ) 4 z + 6 = (x ) + (y ) z 4 =. Por tanto, la ecuación representa a un Z hiperboloide de una hoja con centro (de { simetría) en el punto (,, ) y x = eje la recta y =. La superficie dada es una superficie de revolución puesto que al cortar con planos paralelos al plano OXY (perpendiculares al eje del hiperboloide) z = k se obtienen circunferencias (x ) + (y ) = + k 4. X Y (,, ) { x = y =
3 Ejercicio. R- Ejercicio. (c) Calcula A n siendo A = Siendo I la matriz identidad de orden 4, podemos expresar la matriz A mediante A = I + y, puesto que la matriz I conmuta con cualquier otra matriz (4 4), podemos aplicar la fórmula del binomio de Newton a la potencia (I + B) n siendo B = y obtenemos A n = ( (I + ) B) n = ( n n = (I) n B + + m ) ( n (I) n m B m + + n ) (I) n n B n. Puesto que B =, tenemos que B k = para k =,,... y, por tanto, para n se verifica n n n A n = (I + B) n = n I + n n B + = n n n n. n
4 R-4 Primer Parcial. -. Ejercicio. Considera la matriz A A = Sin hacer intercambios de filas, reduce A a forma escalonada por filas y de lo que obtengas deduce: (a) La factorización A = LU. (b) La dimensión y una base de Col (A). (c) La dimensión y una base de Nul (A). Hacemos la reducción por filas almacenando en las posiciones por debajo de la diagonal los coeficientes utilizados para hacer los ceros,. A F F F + F F 4 F F + F F 4 F -. (a) Por tanto: A = LU siendo L =, U = -. (b) Puesto que las posiciones pivote obtenidas en la forma escalonada (por filas) están en las columnas,, y 5, las correspondientes columnas de A son linealmente independientes y generan todo el espacio columna de A (puesto que la columna 4 de la forma escalonada es combinación lineal de las tres anteriores, lo mismo sucede para las correspondientes columnas de A). Por tanto, las columnas,, y 5 de A forman una base de Col (A) y la dimensión de Col (A) es 4 (el rango de A es 4). Una base de Col (A) es v =, v = 4, v =, v 5 =. (c) La dimensión de Nul (A) = {x R 5 : Ax = } es (el número de variables libres): dim [Nul (A) = n dim [Col (A) = 5 4 =.
5 Ejercicio. R-5 Resolviendo el sistema Ax = (equivalentemente el sistema Ux = ) obtenemos - x x x x 4 x 5 Por tanto, Nul (A) = Gen {u}, F F F F 4 F + F 4 {u} es una base de Nul (A) y la dimensión de Nul (A) es. = α α α α - = αu α R, siendo u =.
6 R-6 Primer Parcial. -. Ejercicio. (a) Da la interpretación geométrica y expresa en forma compleja y en forma matricial el resultado de las siguientes transformaciones en el plano (en el orden dado) Giro de centro el origen y ángulo ϕ = π. Simetría respecto al eje OY. Homotecia de centro el origen y razón ρ =. Traslación de vector (, ). Giro de centro el origen y ángulo ϕ = π : z C z = e π i z C. Simetría respecto al eje OY : z C z = z C. z z z π/ z z Homotecia de centro el origen y razón ρ = : z C z = z C. Traslación de vector (, ): z C z 4 = z + i C. z z z 4 z (, ) Por tanto, el resultado de las transformaciones dadas sobre un punto z es, en forma compleja, [ z C w = z 4 = e π i z + i = e π i z + i C. Para obtener la expresión vectorial basta con obtener las partes real e imaginaria de w = u+iv en función de las partes real e imaginaria de z = x + iy. w = u + iv = [ cos( π ) + i sen( π ) (x iy) + i = = = [ i (x iy) + i [ x y i x i y + i.
7 Ejercicio. R-7 Por lo tanto, u = [ x y + [ v = x y [ u v = [ [ x y + [. Obteniendo paso a paso la expresión matricial tendríamos [ [ [ u [ x = v y + [. Ejercicio. (b) Calcula { la ecuación de la superficie de revolución que se obtiene al girar la recta x = d alrededor del eje OZ. y + z = Z Al girar un punto (, y, z) del plano OY Z alrededor del eje OZ se obtienen los puntos de coordenadas (X, Y, Z) dados mediante (x =, y, z) θ (X, Y, Z) X = y sen θ Y = y cosθ θ π Z = z O Y siendo θ el ángulo que forman los vectores (, y, ) y (X, Y, ). X Por tanto, X + Y = y y si el punto (, y, z) está en la recta dada obtenemos La superficie de revolución que se obtiene = X + Y = y = ( z) = ( Z). es un cono circular recto con vértice en el punto (,, ) y eje OZ y tiene por ecuación X + Y = ( Z).
8 R-8 Primer Parcial. -. Ejercicio. (c) Determina cual de los siguientes enunciados, referidos a una matriz real A m n, no es equivalente a los restantes y da condiciones equivalentes a dicho enunciado A El sistema homogéneo Ax = tiene solución única. B Los vectores columna de la matriz A son linealmente independientes. C Para cada b R m, el sistema de ecuaciones Ax = b es compatible. D Para cada b R m, el sistema de ecuaciones Ax = b es o bien un sistema compatible determinando o bien un sistema incompatible. Qué relación debe existir entre m y n para que el sistema homogéneo Ax = pueda tener solución única? (Justifica la respuesta) Los enunciados A, B y D son todos equivalentes entre sí (si un sistema homogéneo es compatible determinado, un sistema completo con la misma matriz de los coeficientes de las incógnitas puede ser o bien compatible determinado o bien incompatible) y equivalentes a que Nul (A) = {} (y esto es lo mismo que decir que no hay variables libres o que rango(a) = n o que el número de pivotes coincide con el número de columnas). Desde el punto de vista de la transformación lineal definida por la matriz A, x R n y = Ax R m (si la matriz A es real), estos enunciados son equivalentes a decir que ésta transformación lineal es inyectiva (su núcleo es el subespacio nulo). El enunciado C es equivalente a que todo vector de R m se pueda expresar como combinación lineal de las columnas de A y, por tanto es equivalente a decir que Col (A) = R m o, lo que es lo mismo, que el rango de A es m (o que el número de pivotes coincide con el número de filas). Desde el punto de vista de la transformación lineal definida por la matriz A, x R n y = Ax R m (si la matriz A es real), el enunciado C es equivalente a decir que ésta transformación lineal es sobreyectiva (su espacio imagen es el total R m ). Si un sistema homogéneo Ax = tiene solución única es porque el rango es igual al número de columnas (el número de pivotes coincide con el número de columnas) y por tanto el número de filas tiene que ser mayor o igual (puesto que en cada fila de A hay a lo sumo un pivote), es decir tiene que ser m n.
9 Ejercicio 4. R-9 Ejercicio 4. Considera los subespacios vectoriales E y F de R 4 definidos mediante E = Gen u =, u =, u = 5 4, F (a) Determina E F y E + F en forma implícita y en forma paramétrica. (b) Calcula una base de E, una base de F y una base de E + F. x +x +x +x 4 =, x +x x x 4 =, x +x +4x +4x 4 =, x +x +5x +5x 4 =. (c) Calcula las coordenadas de w respecto de la base de E + F obtenida en b) y expresa w = [,,, 4 T como suma w = u + v con u E y v F. Puesto que tenemos que obtener E F y E + F, conviene tener ambos subespacios en forma implícita y en forma paramétrica. El subespacio vectorial E viene definido en forma paramétrica (el subespacio vectorial E está formado por todas las combinaciones lineales de los vectores u, u y u ). Obtengamos unas ecuaciones implícitas que le definan. Puesto que E := { x R 4 : existen α, α, α, α 4 tales que x = α u + α u + α u } dicho subespacio está formado por los vectores x R 4 tales que el sistema [A x es un sistema compatible donde A es la matriz cuyas columnas son los vectores u, u y u. Reduciendo el sistema a forma escalonada tenemos: 5 x x 4 x x 4 F F F + F F 4 F 5 x - 9 x x 9 x + x x 4 x F + F F 4 + F 5 x - 9 x x x + x + x 5 x x + x 4. Por tanto E = {x R 4 : x + x + x = } y, teniendo en cuenta los pivotes que hemos obtenido, los vectores {u, u, u } son linealmente independientes (y forman una base de E) y dim (E) =. El subespacio vectorial F viene definido en forma implícita (como conjunto-solución de un sistema homogéneo). Resolvamos el sistema homogéneo que determina al subespacio para obtener unas ecuaciones paramétricas (y una base y la dimensión de dicho
10 R- Primer Parcial. -. subespacio). Expresamos el sistema en forma matricial y reducimos a forma escalonada: F F F F F 4 F Por tanto operaciones fila = F = Gen x x x x 4 v = = α F F + β, v =. siendo {v, v } una base de F y, por tanto, dim (F) =. Notemos además que las ecuaciones asociadas a la forma escalonada obtenida son unas ecuaciones implícitas que definen F (y son el menor número de ecuaciones implícitas que pueden definir F) { x +x F =, x +x 4 =. (a) Puesto que tenemos unas ecuaciones implícitas de E y de F, tenemos unas ecuaciones implícitas de E F y, resolviendo el sistema, tendremos unas ecuaciones paramétricas, x +x +x = E F x +x = - - x +x 4 = - x x x x 4 = α α α α = αw siendo w = Por tanto E F = Gen {w }, una base de E F es {w } y dim (E F) =. Teniendo en cuenta las dimensiones de E, F y E F, podemos obtener la dimensión de E + F, dim (E + F) = dim (E) + dim (F) dim (E F) = + = 4 y, puesto que E + F R 4, tenemos que E + F = R 4 y, por ejemplo, la base canónica de R 4 es una base de E +F. Así tenemos la descripción paramétrica de E +F asociada.
11 Ejercicio 4. R- a dicha base x = α, x = α, x = α, x 4 = α 4 (α, α, α, α 4 arbitrarios). Dados 4 vectores linealmente independientes de R 4, una combinación lineal genérica de éstos nos dará una descripción paramétrica de E + F. Puesto que todos los vectores de R 4 están en E + F, no hace ninguna ecuación implícita para caracterizar los vectores que están en E + F (o si se quiere la ecuación x + x + x + x 4 = ). (b) Antes hemos calculado una base de E y una base de F así como una base de E + F (teniendo en cuenta quién es el subespacio E + F). Puesto que en el apartado (c) se pide expresar un vector de E + F como suma de un vector de E y uno de F, conviene tener una base de E + F formada por vectores de E y por vectores de F. Para esto consideremos una base de E y una base de F y del conjunto formado por todos esos vectores extraeremos una base de E + F, 5 4 F F F + F F 4 F F F 4 F + F F 4 + F Teniendo esto en cuenta se obtiene que los cuatro primeros vectores-columna {u, u, u, v } de la matriz considerada son linealmente independientes y el quinto v es combinación lineal de los anteriores. Por tanto {u, u, u, v } es una base del subespacio (E + F) generado por los 5 vectores columna de la matriz original. (c) Las coordenadas del vector w = [,,, 4 T respecto de la base B = {u, u, u, v } son los los coeficientes [α, α, α, α 4 T para los cuales se cumple la igualdad w = α u + α u + α u + α 4 v, es decir, vendrán dadas por la solución del sistema de ecuaciones 5 4 α α α α 4 = w = 4,
12 R- Primer Parcial F F F + F F 4 F F + F 4 F F 4 F + F 4 Por tanto w = u + u v y basta tomar u = u + u = F F E y v = v = para obtener una descomposición como la pedida. F + F F 4 F F + F α α α α 4 F =.
13 Segundo Parcial. -. R- -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Segundo Examen Parcial Ejercicio. Consideremos la matriz A y el vector w dados por A = 7 6 (a) [ puntos Estudia si A es diagonalizable., w = (b) [ puntos Estudia si w es un autovector o un autovector generalizado de A (o ninguna de las dos cosas). (c) [ puntos Calcula A 5 w. (d) [ puntos Es diagonalizable A T A mediante una matriz de paso ortogonal? Justifica la respuesta.. (a) Estudia si A es diagonalizable. En primer lugar, calculamos los autovalores de A obteniendo y resolviendo la ecuación característica p(λ) = det (A λi) =, p(λ) = det (A λi) = = ( λ) λ λ λ λ 7 6 λ λ λ + ( ) = 7 6 λ λ desarrollando por los elementos de la primera columna + = = ( λ)( λ) (λ 6 7λ) = λ 4 λ λ + 7λ + 6 =. = Buscando soluciones entre los divisores de 6 (el término independiente de la ecuación polinómica obtenida): ±, ±, ±, ±6, tenemos que p() = 8, p( ) =
14 R-4 Segundo Parcial. -. y por tanto, ya tenemos una solución, λ =, de la ecuación característica y dividiendo p(λ) por λ + tenemos que y por tanto, p(λ) = (λ + ) ( λ 4λ + λ + 6 ). El cociente obtenido, λ 4λ + λ + 6, también se anula para λ = y volviendo a dividir por λ + tenemos la ecuación cuyas soluciones son p(λ) = (λ + ) ( λ 5λ + 6 ) = λ = (doble), λ = (simple), λ = (simple). El que la matriz A sea o no diagonalizable dependerá exclusivamente de que la multiplicidad geométrica de su único autovalor múltiple λ = coincida o no con su multiplicidad algebraica. Estudiemos, por tanto, la multiplicidad geométrica de λ =, es decir, la dimensión del espacio propio asociado Nul (A λ I) = Nul (A + I). (A + I) x = operaciones fila Puesto que tenemos posiciones pivote, el rango de la matriz A+I es y la multiplicidad geométrica de λ será mg(λ ) = 4 = < ma(λ ) =. Por tanto la matriz A, NO es diagonalizable. (b) Estudia si w es un autovector o un autovector generalizado de A (o ninguna de las dos cosas). Haciendolo en el orden en el que está enunciado: Para comprobar si w es un autovector de A bastará comprobar si Aw es o no un múltiplo de w, Aw = 7 6 = Por tanto, w no es un autovector de A. λ λ C. Comprobemos si w es o no un autovector generalizado de A. Si lo es, estará asociado al único autovalor múltiple λ =. Tenemos que comprobar si se verifica la.
15 Ejercicio. R-5 igualdad (A + I) w =. Puesto que ya hemos calculado Aw, (A + I) w = Aw + w = + = (A + I) w = (A + I) =. Por tanto, w es un autovector generalizado de A. (c) Calcula A 5 w. Puesto que (A + I) w =, se verifica que (A + I) k w = para k y, aplicando la fórmula del binomio de Newton, tenemos A 5 w = (A + I I) 5 w = = [ ( 5 ( I) 5 + ) ( 5 ( I) 49 (A + I) + = w 5(A + I)w = ) ( I) 48 (A + I) + w 5 = (d) Es diagonalizable A T A mediante una matriz de paso ortogonal? Justifica la respuesta. Por el Teorema espectral para matrices (reales) simétricas, una matriz (real) es simétrica si y sólo si es diagonalizable ortogonalmente, es decir, si y sólo si es diagonalizable con una matriz de paso ortogonal. Teniendo esto en cuenta, lo único que tenemos que comprobar es si la matriz A T A es simétrica. Y lo es puesto que ( A T A ) T = A T ( A T) T = A T A..
16 R-6 Segundo Parcial. -. Ejercicio. (a) [4 puntos Consideremos una matriz A real m n, el subespacio S = Col (A) y un vector b R m. Demuestra que los sistemas de ecuaciones Ax = proy S (b) y A T Ax = A T b son compatibles y tienen los mismos conjuntos de soluciones. Qué tiene que verificar la matriz A para que los sistemas anteriores tengan solución única? (b) [4 puntos Consideremos los vectores y el subespacio vectorial dados por α α v =, v = α, u = ; S x + x + αx =. Determina α sabiendo que proy S (v ) = proy S (v ) = u. (un dibujo puede ayudar) (c) [ puntos Sea A una matriz cuadrada de orden 5 cuyo rango es. Qué sucede al aplicar el método de Gram-Schmidt a los vectores columna de A? Cuántas veces? Por qué? (a) Teoría (Soluciones en mínimos cuadrados y ecuaciones normales de Gauss). (a.) El sistema Ax = proy S (b) es compatible. Puesto que proy S (b) S = Col (A), tenemos que proy S (b) se puede expresar como combinación lineal de las columnas de A, los pesos (coeficientes) de cada una de las posibles formas de expresar proy S (b) como combinación lineal de las columnas de A darán lugar a un vector solución x de Ax = proy S (b). A = A... A j... A n = x A + + x j A j + + x n A n = A Col (A) = {Ax : x R n } = {y R m : Ax = y es un SC}. (a.) Toda solución de Ax = proy S (b) es solución de A T Ax = A T b. Si x R n verifica Ax = proy S (b), entonces, multiplicando a la izquierda por A T tenemos que A T Ax = A T proy S (b). Por otra parte, A T b = A T (b proy S (b) + proy S (b)) = A T (b proy S (b)) + A T proy S (b) y, puesto que b proy S (b) = proy S (b) S = [Col (A) = Nul (A T ) = A T (b proy S (b)) = obtenemos que A T b = A T proy S (b) y por tanto x verifica A T Ax = A T b. x x. x n,
17 Ejercicio. R-7 (a.) Toda solución de A T Ax = A T b es solución de Ax = proy S (b). Si un vector x R n verifica A T Ax = A T b tenemos A T Ax = A T b A T (b Ax) = b Ax Nul (A T ) = Col (A). Por tanto, } Ax S = Col (A) b Ax S = Ax es la proyección ortogonal de b sobre S Ax = proy S (b). Los apartados (a.) y (a.) nos dicen que los dos sistemas citados (que no son equivalentes en el sentido de que se pueda pasar de uno a otro mediante operaciones elementales fila) tienen los mismos conjuntos de soluciones. Junto con el apartado (a.) nos dicen que los sistemas considerados son siempre compatibles. Notemos que el sistema Ax = proy S (b) es un sistema de m ecuaciones con n incógnitas mientras el sistema A T Ax = A T b es un sistema de n ecuaciones con n incógnitas. (a.4) Qué tiene que verificar la matriz A para que los sistemas anteriores tengan solución única? Si tenemos un sistema de ecuaciones Ax = y que es compatible, puesto que [ solución general de Ax = y = [ solución particular de Ax = y + [ solución general de Ax = se verifica que Ax = y es un sistema compatible determinado lo es el sistema homogéneo asociado Ax =. Por tanto, los sistemas considerados tendrán solución única si y sólo si el sistema homogéneo Ax = tiene solución única. Esto es equivalente a que los vectores columna de A sean linealmente independientes, o lo que también es equivalente, el rango de A es igual a n (número de columnas=número de pivotes). (b) Se trata de determinar el valor de α conociendo dos condiciones sobre los vectores y el subespacio dados, que proy S (v ) = proy S (v ) y que estás proyecciones son iguales al vector u. La condición proy S (v ) = proy S (v ) es equivalente a decir que el vector v v está en S con lo cual proy S (v ) = proy S (v ) v v = v v es múltiplo de α α 6 α S = Gen v v = α α 6 para algún c R. Resolviendo el sistema de ecuaciones que se obtiene α = c { α = α = c. c = 6 = cα α = c Hemos obtenido un único valor posible de α utilizando sólo una de las dos condiciones dadas, ahora hay que comprobar que efectivamente para dicho valor de α se verifican las α
18 R-8 Segundo Parcial. -. dos condiciones. Para obtener los vectores proyección sobre S lo más cómodo es trabajar con S que tiene dimensión. S x + x x = S = Gen proy S (v ) = = proy S (v ) = v Por tanto proy S (v ) = u y también proy S (v ) = u. Observaciones. = = u. () Algunos alumnos han resuelto el ejercicio de la siguiente forma: Puesto que la proyección ortogonal de v sobre S es u, la proyección ortogonal de v sobre el subespacio R = Gen {u} generado por u también es u y, por tanto, tenemos u = proy S (v ) = proy R (v ) = v u u u = α + α + u α + α + = α +α =. Análogamente, para v tenemos u = proy S (v ) = proy R (v ) = v u u u = α α + u α α + = α = 4. El valor buscado de α (o posibles valores a priori) debe verificar las dos ecuaciones α + α = α = 4 Resolviendo obtenemos que el único valor posible es α =. Sin embargo, el argumento anterior no es completo puesto que }. proy S (v ) = u = = proy R (v ) = u (R = Gen {u}) y habría que comprobar que efectivamente el valor de α verifica las condiciones deseadas (No se ha penalizado la no comprobación de dichas condiciones a posteriori). () Si tenemos una base {w, w,...} de un subespacio vectorial S y un vector v, el vector dado por la fórmula v w w w + v w w w + es el vector proyección ortogonal de v sobre S cuando la base es una base ortogonal de S. Si la base de S dada no es ortogonal, la expresión anterior da lugar a un vector de S que no es la proyección ortogonal de v sobre S.
19 Ejercicio. R-9 (c) Sea A una matriz cuadrada de orden 5 cuyo rango es. Qué sucede al aplicar el método de Gram-Schmidt a los vectores columna de A? Cuántas veces? Por qué? Puesto que el rango de A es, la dimensión del espacio Col (A) es y por tanto, si consideramos los vectores columna de A en el orden en el que aparecen en la matriz, hay 5 = 4 vectores que se pueden expresar como combinación lineal de los anteriores (en el caso del primer vector columna, puede suceder que sea nulo). Al aplicar el método de Gram-Schmidt a los vectores columna de A, cada vez que lleguemos a un vector que es combinación lineal de los anteriores, obtendremos el vector nulo puesto que un paso típico del método de Gram-Schmidt consiste en obtener la proyección ortogonal del vector v k+ sobre el ortogonal del subespacio generado por los vectores anteriores, v k+ = v k+ proy Sk (v k+ ) S k = Gen {v,...,v k } con lo cual, si v k+ es combinación lineal de los anteriores tenemos que proy Sk (v k+ ) = v k+ y por tanto v k+ =. Resumiendo, al aplicar el método de Gram-Schmidt a los vectores columna de la matriz A: Qué sucede? Que en algunos pasos de dicho método se obtiene el vector nulo puesto que los vectores originales no son linealmente independientes. Cuántas veces? Cuatro. Cada vez que llegamos a un vector que es combinación lineal de los anteriores. Por qué? Porque un paso típico del método de Gram-Schmidt...
20 R- Segundo Parcial. -. Ejercicio. (a) [ puntos Sea A una matriz cuadrada diagonalizable cuyos únicos autovalores son λ = y λ = (con sus correspondientes multiplicidades). Demuestra que A = A. (b) [4 puntos Sean S y S los subespacios vectoriales de R 4 definidos mediante S x + x + x + x 4 =, S x + x x x 4 =. Determina el vector v R 4 sabiendo que sus proyecciones ortogonales sobre S y S son respectivamente 7 u = proy S (v) = 5 5, u = proy S (v) = 7. (c) [4 puntos Siendo S y S los subespacios vectoriales dados en el apartado anterior, calcula la matriz de la proyección ortogonal sobre el subespacio S = S S. (a) Puesto que A es diagonalizable, puede obtenerse una matriz P no-singular para la que se verifica que P AP = D es una matriz diagonal. La matriz P está formada, por columnas, por autovectores de A que son linealmente independientes (que formarán una base de R n o de C n ). Los elementos diagonales de la matriz D son los autovalores de A (en el orden correspondiente a los autovectores dados en P). Puesto que los autovalores λ de A son cero o uno, en cualquier caso tenemos que λ = λ y por tanto D = D. Así, tenemos A = PDP = P P = = A = PDP PDP = PD P = PDP = A. (b) Es inmediato comprobar que u S y que u S. Entonces tenemos, u = proy S (v) v u S = Gen = v = u + α
21 Ejercicio. R- para algún α R. De forma análoga u = proy S (v) v u S = Gen v = u + β para algún β R. Por tanto, v = α = β Y basta con resolver el sistema de ecuaciones lineales en α y β que se obtiene: α β = 4 α β = 4 α + β = α + β = Por tanto, existen dos números reales α y β tales que v = = 7 7 { α =, β =. = Observación. El vector v se puede obtener de otras muchas formas (no muy distintas), por ejemplo utilizando que ) proy S (v) = proy S (u + proy S (v) = (c) Matriz de la proyección ortogonal sobre el subespacio S = S S S = S S { x + x + x + x 4 = x + x x x 4 = S = Nul S = Col = Gen w = Puesto que {w, w } es una base ortogonal de S, tenemos que { } { w w, w = w w, } w [, w =.
22 R- Segundo Parcial. -. es una base ortonormal de S y, por tanto, la matriz de la proyección ortogonal sobre S es T [ P S = = 4 = = Teniendo en cuenta que. proy S (w) + proy S (w) = w, w R 4, para las correspondientes matrices de proyección se verifica que P S + P S = I y, por tanto, la matriz de la proyección ortogonal sobre S es P S = I P S = = Observaciones: () No conlleva ninguna dificultad adicional el calcular directamente la matriz P S sin pasar por la matriz de la proyección ortogonal sobre S, siempre y cuando no se aplique de manera incorrecta la fórmula P S = UU T siendo U una matriz cuyos vectores-columna... () Puesto que se trataba de calcular la matriz de la proyección ortogonal sobre un subespacio vectorial de R 4 (lo que quiere decir que al multiplicar un vector de R 4 por dicha matriz el resultado es el vector, de R 4, que se obtiene como proyección ortogonal del vector dado sobre el subespacio considerado), dicha matriz tiene que ser una matriz 4 4..
23 Examen de Junio (Segundo Parcial). -. R- -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Examen Final de Junio (Segundo Parcial) Ejercicio. Considera la matriz A dada por A = (.) [4 puntos Determina, si es posible, una base de R formada por autovectores y autovectores generalizados de A. (.) [4 puntos Calcula A n para n =,,.... (.) [ puntos Calcula los autovalores y autovectores de A + I y determina los vectores b R para los que el sistema de ecuaciones es compatible.. (A + I)x = b (.) Determina, si es posible, una base de R formada por autovectores y autovectores generalizados de A. Calculemos los autovalores de A: Ecuación característica 5 λ p(λ) = det(a λi) = 8 λ 4 λ = λ ( 5 λ) 4 8λ = = λ 5λ 8λ 4 =. Puesto que p( ) = =, p(λ) es divisible por λ + y tenemos y, por tanto, p(λ) = (λ + ) [ λ 4λ 4 = (λ + )(λ + ). Los autovalores de A son, por lo tanto, λ = (simple) λ = (doble). Autovectores asociados a λ = :
24 R-4 Examen de Junio (Segundo Parcial). -. (A + I)x = Nul (A + I) = Gen Autovectores asociados a λ = : (A + I)x = 8 4 Puesto que x x x = x = x 4 Nul (A + I) = Gen v = x x x -4 - = x 4 = Gen v = 4. mg(λ ) = dim (A λ I) = < ma(λ ) = 4 4. la matriz A NO es diagonalizable, y no puede obtenerse una base de R formada exclusivamente por autovectores. Necesitamos recurrir al cálculo de autovectores generalizados (asociados al único autovalor múltiple). [ Autovectores generalizados asociados a λ = : Nul (A + I) k, (A + I) x = 8 4 x x x = Nul [(A + I) = Gen x x x = x, x Para obtener una base de R formada por autovectores y autovectores generalizados de A basta tener una base de Nul (A + I) y una base de Nul [(A + I). Puesto que Nul [(A + I) Nul [ (A + I)
25 Ejercicio. R-5 podemos tomar como base de Nul [(A + I) una que este formada por un autovector y un autovector generalizado, por ejemplo v =,w =. Por tanto, {v, v, w} es una base de R formada por autovectores y autovectores generalizados de A. (.) Calcula A n para n =,,.... Para obtener la matriz A n bastará obtener el resultado del producto A n P siendo P una matriz no-singular, y de ahí despejar A n multiplicando por P a la derecha. Equivalentemente, basta obtener el producto de A n por cada uno de los vectores de una base de R (para los que sea cómodo calcular A n v) y a partir de esos resultados despejar A n. Una base de R apropiada para este problema sería una base formada por autovectores (si la hubiera, que en nuestro caso no la hay, puesto que A no es diagonalizable) puesto que para un autovector v de A asociado a un autovalor λ se verifica que A n v = λ n v. Ya que no podemos tener una base de R formada exclusivamente por autovectores, recurrimos a los autovectores generalizados. En el apartado anterior hemos obtenido una base de R {v, v, w} formada por autovectores y autovectores generalizados. Para los autovectores tenemos: A n v = λ n v = ( ) n v A n v = λ n v = ( ) n v y puesto que para el autovector generalizado w se verifica (A + I) w =, aplicando la fórmula del binomio de Newton tenemos A n w = (A + I I) n w = = [ ( n ( I) n + ) ( I) n (A + I) + w = = ( ) n w + n( ) n (A + I)w + ( n = ( ) n w + n( ) n (A + I)w + + = = ( ) n w + n( ) n (A + I)w = = ( ) n + n( ) n 6 4 = ( ) n ) ( ) n (A + I) w + = + n + n n.
26 R-6 Examen de Junio (Segundo Parcial). -. Expresando las anteriores igualdades vectoriales en forma matricial tenemos ( ) n ( ) n ( + n)( ) n A n v v w = ( ) n 4 ( ) n ( + n)( ) n = ( ) n+ 4 ( ) n n( ) n y despejando A n A n = ( ) n = ( ) n = ( )n = ( ) n n ( + n) n 4 n ( + n) n 4 n+ n n+ n ( + n) n 4 n ( + n) n 4 n+ n n+ n ( + n) n 4 n ( + n) n 4 n+ n n+ v v w = = + n n+ (n ) n+ (n ) n 8 + (n ) n+ 8 (n 5) n+ 8 (n 8) n 8 (n ) n+ 8 + (n ) n+ 8 + (n ) n+ Observación. De las expresiones consideradas podemos obtener una factorización de A n : A n v = λ n v. A n v = λ n v A n w = λ n w + nλ n (A + I)w = λ n w + nλ n v λ n = A n v v w = v v w λ n nλ n λ n λ n A n = v v w λ n nλ n v v w λ n (.) Calcula los autovalores y autovectores de A + I y determina los vectores b R para los que el sistema de ecuaciones (A + I)x = b es compatible. Un vector u R, u es un autovector de A + I asociado a un cierto autovalor µ si, y sólo si, se verifica que (A+I)u = µu. Equivalentemente, Au = (µ )u. Es decir, un vector u R, u es un autovector de A + I asociado a un cierto autovalor µ si, y sólo si, λ = µ es un autovalor de A y u es un autovector de A asociado a λ = µ. Por tanto:.
27 Ejercicio. R-7 λ = autovalor de A µ = λ + = autovalor de A + I λ = autovalor de A µ = λ + = autovalor de A + I En lo que se refiere a los autovectores correspondientes tenemos: } λ =, Nul (A λ µ = I) = Nul (A + I µ I) = Nul (A + I) = Gen {v }, λ =, µ = } Nul (A λ I) = Nul (A + I µ I) = Nul (A + I) = Gen {v }. Por último, el conjunto { b R : (A + I)x = b es un sistema compatible } no es otra cosa que el espacio columna de A+I. Con las operaciones que hemos hecho a la hora de calcular los autovectores de A asociados a λ =, se obtiene que dicho espacio columna coincide con el subespacio generado por las dos primeras columnas de A + I, es decir Gen 8 4,. Este subespacio vectorial lo podríamos pasar a forma implícita, sin más que imponer la condición de compatibilidad del sistema b 8 b 4 b y se obtiene la ecuación 4b b b =.
28 R-8 Examen de Junio (Segundo Parcial). -. Ejercicio. (.) [ puntos Enuncia las propiedades más importante de los autovalores y autovectores de una matriz simétrica real y el Teorema espectral (para matrices reales simétricas). (.) [5 puntos Determina una matriz real simétrica A sabiendo que sus autovalores son λ = (simple) y λ = (doble) y que los vectores v =, v = son autovectores de A asociados respectivamente a λ y λ. (.) [ puntos Siendo A la matriz obtenida en el apartado anterior, calcula la matriz de la proyección ortogonal sobre el espacio nulo de A y sobre el espacio columna de A. (.) Si A es una matriz real simétrica se verifica: (a) Todos sus autovalores son reales. (b) Si u y v son dos autovectores (reales) de A correspondientes a autovalores distintos λ µ, entonces u y v son ortogonales, u v =. Teorema espectral para matrices reales simétricas : Siendo A una matriz real se verifica que (c) A es simétrica A es diagonalizable mediante una matriz de paso ortogonal. (.) Puesto que A es una matriz simétrica real, es diagonalizable ortogonalmente, es decir, podemos obtener una matriz ortogonal Q que verifica que λ Q T AQ = D = λ λ = Los vectores columna de Q son autovectores de A que forman una base ortonormal de R. El primer vector columna q de Q será un autovector unitario de A asociado a λ =, con lo cual podemos tomar q = v v = 6 El segundo y tercer vector columna q y q de Q serán dos autovectores de A asociados a λ = ortogonales y unitarios, con lo cual podemos tomar q = v v = 5...
29 Ejercicio. R-9 Por tanto, A será de la forma 5 A = QDQ T 6 = Observaciones: = = = = () A pesar de haberlo considerado, el vector v no ha sido necesario en la obtención de la matriz A puesto que λ =. De hecho, las restantes condiciones son suficientes para determinar A. Puesto que la dimensión de Nul (A λ I) = Nul (A) tiene que ser (A es diagonalizable) y todo vector de Nul (A λ I) = Nul (A) tiene que ser ortogonal a todo vector de Nul (A λ I) = Nul (A + I) (A es simétrica), necesariamente tiene que cumplirse Nul (A λ I) = Nul (A λ I) = [Gen {v } = Nul [ v T = x + x x = () Una buena opción para determinar A es considerar una descomposición espectral de A. Siendo {q, q, q } una base ortonormal de R formada por autovectores de A asociados respectivamente a λ =, λ y λ = λ, se verifica que A = λ q q T + λ q q T + λ q q T = ( )q q T + q q T + q q T = = tomando el vector q = v v dado antes = 6 6 [ =... () Un buen ejercicio (en el que habrá que obtener una base de Nul (A λ I)) es sustituir en el enunciado λ = por un valor λ y obtener la correspondiente matriz A. (.) Siendo A la matriz obtenida en el apartado anterior, calcula la matriz de la proyección ortogonal sobre el espacio nulo de A y sobre el espacio columna de A. Puesto que S = Col (A) = Gen v =,
30 R- Examen de Junio (Segundo Parcial). -. la matriz de la proyección ortogonal sobre Col (A) es P S = [ = Puesto que Nul (A) = [ Col (A T ) = [Col (A), la matriz de la proyección ortogonal sobre Nul (A) es P S = I P S = Observación. Para tener una interpretación geométrica de los ingredientes que aparecen en el ejercicio, notemos que si tenemos una base {u, u, u } de R, de forma que {u } genera S = Nul (A + I) = Col (A) y {u, u } generan su ortogonal, S = Nul (A), entonces cualquier vector v R se puede escribir como combinación lineal. con lo cual v = c v + c v + c v Av = c Av + c Av + c Av = c ( )v + v + v = c v. Por tanto al multiplicar la matriz A por un vector v S = Av = v, un vector v S = Av =. Tiene alguna relación la matriz A con proyecciones ortogonales y simetrías y los subespacios S (recta) y S (plano)?
31 Ejercicio. R- Ejercicio. (.) [4 puntos Halla la ecuación reducida, dando los cambios de variables adecuados, y representa la cónica de ecuación x + 4xy + 4y 5x + 5y =. (.) [4 puntos Sea S el subespacio de R 4 definido por S x +x +x +4x 4 =. Calcula los vectores de R 4 cuya proyección ortogonal sobre S es el vector u = [ T y cuya distancia a S es 5. (.) [ puntos Determina los valores de α para los que el sistema de ecuaciones x α y = α z tiene infinitas soluciones en el sentido de los mínimos cuadrados y calcula dichas soluciones. (.) Diagonalizamos ortogonalmente la matriz simétrica asociada a la parte cuadrática de la ecuación x + 4xy + 4y = [ x y [ [ [ x A = p(λ) = λ(λ 5). 4 y 4 Por tanto la ecuación dada es la de una cónica de tipo parabólico (parábola o par de rectas). Autovectores asociados al autovalor λ = 5: [ [ [ 4 x (A 5I)x = y [ = x [ v = Autovectores asociados al autovalor λ = : serán los vectores (no nulos) ortogonales a v (A es una matriz simétrica real). Tomamos [ v =. de forma que el sentido de giro de v a v es positivo. Por tanto, puesto que v = v = 5, la matriz Q = [ = 5 [ diagonaliza ortogonalmente a la matriz A: [ 5 AQ = Q, Q = Q T.
32 R- Examen de Junio (Segundo Parcial). -. Haciendo el cambio de variables [ [ x x x = 5 (x y ), = Q y y y = 5 (x + y ), y [ [ x x = x 5 (x + y), y = Q T y y = 5 ( x + y), y sustituyendo en la ecuación de la cónica, tenemos [ [ x x y Q T AQ + [ 5 5 [ x Q = 5x 5 5 (x y ) (x + y ) = 5x + 5y = y = x. Por tanto, la cónica dada es una parábola que tiene como vértice el punto y como ejes V = (x =, y = ) = (x =, y = ) Eje principal (de simetría): OY x = x = 5 (x + y) = x + y =, Eje secundario: OX y = y = 5 ( x + y) = y = x. Los cortes de la parábola con los ejes coordenados (originales) son Corte con OX: y = x x = (, ) 5x = = x = 5 ( 5, ) Corte con OY : x = 4y + y = (, ) 5y = = y = 5 (, 5 ) 4 4 Por tanto, la representación gráfica en los ejes originales es y Y x + 4xy + 4y 5x + 5y = Y X X ( 5, ) y 4 (, 5 4 ) x
33 Ejercicio. R- (.) Dado un vector v R 4, el vector proyección ortogonal de v sobre S es el único vector u de S para el cual v se puede expresar como para algún vector w S. Es decir, v = u + w proy S (v) = u v u S = Gen w = 4. Por tanto { v R 4 : proy S (v) = u } = { v R 4 : v = u + tw, t R }. Es decir, dicho conjunto no es otra cosa que la recta (en R 4 ) que pasa por u y tiene como vector dirección w. Puesto que dist (v, S) = v proy S (v), para determinar los vectores cuya proyección ortogonal sobre S es u y distan 5 de S basta determinar los valores de t R tales que v u = u + tw u = tw = t w = t = 5. Por tanto, los vectores pedidos en el enunciado son + 5 t = ± 5 = v = u+ 5 w = , v = u 5 w = (.) Un sistema de ecuaciones Ax = b, (A m n, b R m ) tiene infinitas soluciones en mínimos cuadrados si, y sólo si, el sistema de ecuaciones (compatible) Ax = proy S (b), S = Col (A), tiene infinitas soluciones y esto es equivalente a que el sistema homogéneo asociado Ax = tenga infinitas soluciones: Es decir, el sistema homogéneo es compatible indeterminado o, equivalentemente, los vectores-columna de A son linealmente dependientes. De forma esquemática: los siguientes enuciados son equivalentes: el sistema Ax = b tiene infinitas soluciones en mínimos cuadrados, el sistema Ax = tiene infinitas soluciones, las columnas de A son linealmente dependientes, el rango de A es menor que n. Calculemos los valores de α para los que los vectores columna de A son linealmente dependientes, α - α + - α +. α α α.
34 R-4 Examen de Junio (Segundo Parcial). -. Los vectores columna de A son linealmente dependientes si, y sólo si, en la forma escalonada se obtienen menos de pivotes, es decir si, y sólo si se verifica α + = y α = α =. Tenemos que calcular las infinitas soluciones en mínimos cuadrados del sistema que se obtiene para α = : x x =. x Mediante las ecuaciones normales de Gauss, por ejemplo, tenemos A T Ax = A T b, = 4 7 x y z = z En términos geométricos, el conjunto de soluciones en mínimos cuadrados es la recta de R que pasa por el punto ( 4,, ) y tiene como vector dirección (,, ). 7 7
35 Examen de Junio (Primer Parcial). -. R-5 -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Examen Final de Junio (Primer Parcial) Ejercicio 4. Sean E y F los subespacios vectoriales definidos por E = Col 4, x + x x x 4 =, F x + x x =, x + x 5x x 4 =. (4.) [ puntos Determina las ecuaciones implícitas de E y una base de F. (4.) [ puntos Calcula una base de E F y amplíala hasta una base de F. (4.) [ punto Calcula la dimensión de E + F. (4.4) [ puntos Demuestra que si {v, v,...,v r } es un conjunto de vectores de R n linealmente independientes y P es una matriz n n no-singular, entonces los vectores son linealmente independientes. Pv, Pv,...,Pv r (4.) Ecuaciones implícitas de E: - x x x 4 x 4 - x x + x x + x x 4 + x - x x + x x x x x 4 + x + x E { x + x x =, x + x + x 4 =, la dimensión de E es dim (E) = y una base de E es...
36 R-6 Examen de Junio (Primer Parcial). -. Una base de F: Resolvemos el sistema homogéneo que define F, F = Por tanto, { F x x x x 4 = x + x 4 x + x + x 4 =, x + x + x 4 =, y la dimensión de F es dim (F) =.. una base de F es u =, u = (4.) Calcula una base de E F y amplíala hasta una base de F. El subespacio vectorial E F viene dado en forma implícita mediante { x +x x = x +x +x 4 = E F { x +x +x 4 = x +x +x 4 = una base de E F es w = - - x x x x 4 = x 4. Para ampliar una base de E F F hasta una base de F, puesto que dim (E F) = y dim (F) = (y E F F), basta tomar un vector (no nulo) de E F (por ejemplo {w }) y un vector de F que sea linealmente independiente con el anterior, por ejemplo u. Así tenemos {w } base de E F, {w, u } base de F.
37 Ejercicio 4. R-7 (4.) Calcula la dimensión de E + F. Puesto que, como ya hemos calculado, tenemos que dim (E) = dim (F) =, dim (E F) = dim (E + F) = dim (E) + dim (F) dim (E F) = + =. (4.4) Demuestra que si {v, v,...,v r } es un conjunto de vectores de R n linealmente independientes y P es una matriz n n no-singular, entonces los vectores Pv, Pv,..., Pv r son linealmente independientes. Si tenemos una combinación lineal de los vectores Pv, Pv,..., Pv r igual al vector nulo c Pv + c Pv + + c r Pv r =, multiplicando (a la izquierda) por P obtenemos P (c Pv + c Pv + + c r Pv r ) = c P Pv + c P Pv + + c r P Pv r = = c v + c v + + c r v r =. Puesto que estamos considerando vectores v,...,v r linealmente independientes, la igualdad anterior sólo puede verificarse para c = c = =. Por tanto son linealmente independientes. {Pv, Pv,...,Pv r }
38 R-8 Examen de Junio (Primer Parcial). -. Ejercicio 5. (5.) [ puntos Reduce y clasifica, en función de a R, la forma cuadrática ϕ : R R definida por ϕ(x, x, x ) = x + ax + x 4x x + x x 8x x. (5.) [ puntos Determina el punto del plano que se obtiene a partir de z = +i al hacer un giro de ángulo θ = π/6 radianes alrededor de z = + i. (5.) [ puntos (5..) Calcula la parte imaginaria del coeficiente del término de grado de ( ) z + e i π 4. (5..) Resuelve (calcula todas las soluciones complejas de) la ecuación (z + + i) 4 = 4. (5.4) [ puntos Calcula la ecuación reducida y (dando sus elementos característicos) representa gráficamente la cuádrica de ecuación 4x y 4z + 8x + 4y 8z = 8. De qué tipo de cuádrica se trata? Es una superficie de revolución? (5.) Vamos a reducir a suma de cuadrados completando cuadrados. Comenzamos completando cuadrados en x, [ ϕ(x, x, x ) = x + x ( x + x ) + ax + x + 8x completando x = = cuadrados en x = = [x + ( x + x ) ( x + x ) + ax + x 8x x = [ siendo = y y = x x + x 4x x + 4x x + ax + x 8x x = [ = y + (a 4)x + x 4x x = = y + (x x ) x + (a 4)x = [ = y + y + (a 6)x. completando = cuadrados en x siendo y = x x Por lo tanto, la forma cuadrática es, según los valores de a R: a < 6 a = 6 a > 6 Indefinida Semidefinida Positiva Definida Positiva =
39 Ejercicio 5. R-9 (5.) Denotando por z al punto (del plano complejo) que se obtiene al hacer el giro indicado se verifica z z = e i π 6 (z z ) y por tanto, z = z + e i π 6 (z z ) = ( + i) + ( + i = + i + + i + i = + ( + ) ( + i) = + ) i. (5.) (5..) El término de grado del desarrollo de ( z + e i π 4 ) es ( ) (e ) i π 7 4 z = 9 8 7π ei 4 z = e i π 4 z y la parte imaginaria del coeficiente de z es Im ( ) ( e i π 4 = sen π ) = 6. 4 (5..) Un número complejo z es solución de la ecuación considerada si, y sólo si, w = z + + i es una raíz cuarta de 4. Basta por tanto obtener las cuatro raíces cuartas de 4 y a partir de ellas los valores de z: w = 4 4 = w = e i π 4 = + i = 4 w 4e iπ = e i( π 4 +π 4 ) = + i = w = e i( π 4 +π 4 ) = i w = e i( π 4 +π 4 ) = i z = z = z = w i = = z = i z = i. (5.4) Completando cuadrados (mediante expresiones del tipo x + a, y + b, z + c) tenemos 4x y 4z + 8x + 4y 8z = 4 (x + ) 4 (y ) (z + ) + 4 y, por tanto, la ecuación dada es equivalente a la ecuación (x + ) (y ) 4 (z + ) = (x ) (y ) (z ) = siendo 4 x = x +, y = y, z = z +. En resumen, la cuádrica es un hiperboloide elíptico (o de hojas) con centro (x =, y =, z = ) (x =, y =, z = )
40 R-4 Examen de Junio (Primer Parcial). -. y eje el eje X es decir la recta { y = z = { y =, z =. Z La superficie no es de revolución puesto que al cortar con planos Z x = cte x = k, perpendiculares al eje, no se obtinen circunferencias sino elipses (con semiejes distintos) (y ) + (z + ) = (k + ) 4 X (,, ) Y Y o un único punto o nada. X
41 Examen de Septiembre -. R-4 -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Examen Final de Septiembre Ejercicio. Considera la matriz A = 4 4 α 4 para α R. (.) [ puntos Calcular, cuando exista, la factorización A = LU. Para α =, determinar una base y unas ecuaciones implícitas de Col (U). (.) [5 puntos Para α =, calcular A n u siendo u =. (.) [ puntos Definir el concepto de matriz de Markov. Probar que λ = siempre es autovalor de una matriz de Markov. (.) Utilizando transformaciones elementales, analizamos la factorización LU. 4 4 A = 4 α 4 F F α ; (hay que exigir α ) F α F ) 4 α α = 4 α α+4 α = U Por tanto, existe factorización LU si y sólo si α. En dicho caso, dicha factorización es 4 L =, U = α. α+4 α α Obviamente, para α =, un sistema generador de Col (U) (no de Col (A)) es 4 {v =,v =,v = }. Como los tres vectores anteriores están en forma escalonada, se deduce que una base de Col (U) es {v, v }. Además, mirando la forma de v y v, se tiene que {e, e } también es una base de Col (U). Por tanto, Col (U) viene dado por la ecuación implícita x =.
42 R-4 Examen de Septiembre -. (.) Para calcular A n u, expresamos u como combinación lineal de autovectores de A, u = αv + βv + (con lo cual será A n u = λ n v + λ n v + ) o, si esto no es posible, como combinación lineal de autovectores y autovectores generalizados para después obtener A n v para cada uno de los autovectores y autovectores generalizados que intervienen en dicha combinación lineal. Primero calculamos los autovalores de A. La ecuación característica es p(λ) = det (A λi) = det 4 λ 4 λ 4 λ = = (4 + λ)( λ)( + λ) 8 + 4(4 + λ) ( + λ) = (4 + λ)(4 λ ) λ 4 λ = 6 4λ + 4λ λ 8λ 6 = (λ + 4λ + 4λ) = λ(λ + ) = y sus soluciones son los autovalores λ = (simple), λ = (doble). Pasamos al cálculo de los autovectores. λ = Aprovechamos los cálculos del apartado (.) Av = F + F operaciones fila = v = = Nul (A) = Gen v =. x x x 4 = x
43 Ejercicio. R-4 λ = (A + I)v = F, ( ) = v = x x F,( ) = x F,( ) Nul (A + I) = Gen v =. Por tanto, el subespacio propio asociado a λ = tiene dimensión uno y, puesto que λ = es un autovalor doble, la matriz A no es diagonalizable (con lo cual hay vectores en R que no pueden expresarse como combinación lineal de autovectores de A). Qué sucede para el vector u dado?, puede expresarse como combinación lineal de v y v?: [ αv + βv = u α = β / / / [ sistema incompatible Por tanto, u no puede expresarse como combinación lineal de autovectores y necesitamos recurrir al cálculo de autovectores generalizados (asociados a λ =, único autovalor múltiple de A). La dimensión del subespacio Nul [ (A λ I) = Nul [ (A + I) tiene que ser dos y, por tanto, el rango de (A λ I) tiene que ser uno (A + I) w = w = = w = x + x x x = x + x = Nul [ (A + I) = Gen v =,w =. Por tanto, ya tenemos una base de R, {v, v, w}, formada por autovectores y autovectores generalizados de A y ahora calculamos las coordenadas de u en dicha base: u = αv + βv + γw.
44 R-44 Examen de Septiembre -. F F F F F F α + β = F F β + γ = γ = Es decir, u = αv + βv + γw = v w y, por tanto A n u = αa n v + βa n v + γa n w = puesto que Av = λ v Av = λ v γ = β = ( + γ) = α = β = = αλ n v + βλ n v + γa n w = A n w. Sólo nos queda calcular A n w. Teniendo en cuenta que w es un autovector generalizado de A, ((A + I) w =, obtenemos (para n ) aplicando la fórmula del A n w = ( I + A + I) n w = binomio de Newton con sumandos A + I, I = = = n k= [ ( n k ) ( I) n k (A + I) k w = puesto que (A + I) k w = para k puesto que (A + I)w = v = ( n ) ( n ( I) n w + = ( ) n w + n( ) n v = = ( ) n [ w + nv = ( ) n + n n. ) ( I) n (A + I)w =. Por tanto, A n u = A n w = ( ) n n n para n, Au =. (.) Una matriz de Markov o estocástica es toda matriz cuadrada real tal que sus elementos son no negativos y los elementos de cada una de sus columnas suman uno. Sea A = [a i,j una matriz de Markov de orden n y consideremos el vector e R n dado por e =..
45 Ejercicio. R-45 Entonces, A T e = n k=. n k= a,k a n,k =. = e. Por tanto, λ = es autovalor de A T y, como el conjunto de los autovalores de A y A T coinciden, se tiene que λ = también es autovalor de A. Observaciones.- () La única propiedad que se utiliza de las matrices de Markov para deducir que λ = es uno de sus autovalores es que la suma de los elementos de cada columna es. No se utiliza ni que la matriz sea real ni que sus elementos sean no negativos. () A partir del polinomio característico de una matriz de Markov A también se puede obtener que uno de los autovalores es λ =. Para una matriz en la que la suma de los elementos de cada columna sea tenemos el polinomio característico det(a λi) = = a λ a a nn a a λ a n..... =. a n a n a nn λ λ a a nn λ a λ a n..... =. λ a n a nn λ sumando todas las columnas a la primera restando F F. F n F = = λ a a nn b λ b n b λ b n =..... = ( λ) b n b nn λ b n b nn λ Es decir, para un cierto polinomio q(λ), la ecuación característica es de la forma y por tanto una de sus soluciones es λ =. det(a λi) = ( λ)q(λ) =
46 R-46 Examen de Septiembre -. Ejercicio. Sea A una matriz 4 tal que Nul (A) = Gen 5, Col (A) = Gen v =, v =. (.) [4 puntos Calcula la proyección ortogonal del vector v = [ T R 4 sobre el subespacio Col (A). (.) [ puntos Amplía {v, v } a una base de R 4 y calcula las coordenadas de v respecto a dicha base. (.) [4 puntos Determina la matriz A sabiendo que es de la forma A =. (.) Proyectamos sobre Col (A) y luego usamos que P Col (A) + P Col(A) = I. Para ello, obtenemos una base ortonormal del subespacio Col (A), aplicando el método de Gram-Schmidt a la base que nos da el enunciado: u = v =, u = v v v v = v v =. Cada uno de los vectores obtenidos tiene norma. Dividiendo cada vector por su norma y colocándolo por columnas en una matriz U (4 ) obtenemos la matriz, UU t, de la proyección ortogonal sobre Col (A). La proyección del vector v sobre el subespacio Col (A) es ( I UU t ) v = Otros caminos para resolver este apartado son: = Calcular una base de Col (A) sabiendo que las componentes de los vectores de una base de Col (A) son los coeficientes de unas ecuaciones implícitas de Col (A): { x x Col (A) + x =, x x + x 4 =. O bien, resolver antes el apartado (.), pues de las columnas de la matriz A se obtiene fácilmente una base de Col (A). 4.
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
ÁLGEBRA LINEAL. EXAMEN FINAL 18 de Enero de b) (0, 5 puntos) Estudia si la siguiente afirmación es verdadera o falsa, justificando
 ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
f(x, y, z, t) = (x + y t, x + 2y z 3t, 3x + 5y 2z 7t).
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Aplicaciones Lineales. Diagonalización de matrices.
 Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Departamento de Matemática Aplicada II. Universidad de Sevilla. Solución de la Primera Prueba Alternativa ( )
 MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2
![a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2 a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2](/thumbs/65/53464617.jpg) 68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Ejercicios resueltos del capítulo 4
 Ejercicios resueltos del capítulo 4 Ejercicios impares resueltos..a Calcular los autovalores y subespacios invariantes asociados a la matriz: A = Calculamos el polinomio característico y resolvemos: λ
Ejercicios resueltos del capítulo 4 Ejercicios impares resueltos..a Calcular los autovalores y subespacios invariantes asociados a la matriz: A = Calculamos el polinomio característico y resolvemos: λ
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
6.8. Descomposición mediante valores singulares. v 2 =
 68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
Diagonalización. Tema Valores y vectores propios Planteamiento del problema Valores y vectores propios
 61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
Diagonalización de matrices
 7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
7 Diagonalización de matrices 7.1. Matrices diagonalizables Existen diversos procesos en los que el estado en cada uno de sus pasos se puede representar por un determinado vector y en los que, además,
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
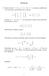 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
VECTORES EN EL ESPACIO
 UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero
 Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Geometría afín y proyectiva, 2016 SEMANA 4
 Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Capítulo 1: Diagonalización de matrices
 Capítulo : Diagonalización de matrices Matrices y determinantes Definición Una matriz es un arreglo rectangular de números reales a a a m a A a a m a n a n a nm La matriz es de orden n m si consta de n
Capítulo : Diagonalización de matrices Matrices y determinantes Definición Una matriz es un arreglo rectangular de números reales a a a m a A a a m a n a n a nm La matriz es de orden n m si consta de n
Tema 4.- Espacios vectoriales. Transformaciones lineales.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I - Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4- Espacios vectoriales Transformaciones lineales
Ingenierías: Aeroespacial, Civil y Química Matemáticas I - Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4- Espacios vectoriales Transformaciones lineales
SISTEMAS DE ECUACIONES. Un sistema de m ecuaciones lineales con n incógnitas, x 1, x 2,, x n es un conjunto de m igualdades de la forma:
 TEMA Sistemas de ecuaciones SISTEMAS DE ECUACIONES. DEFINICIÓN SISTEMAS DE ECUACIONES Un sistema de m ecuaciones lineales con n incógnitas,,,, n es un conjunto de m igualdades de la forma: a a an n b a
TEMA Sistemas de ecuaciones SISTEMAS DE ECUACIONES. DEFINICIÓN SISTEMAS DE ECUACIONES Un sistema de m ecuaciones lineales con n incógnitas,,,, n es un conjunto de m igualdades de la forma: a a an n b a
Matrices, determinantes y sistemas de ecuaciones lineales
 Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Espacios Vectoriales. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21
 Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Tema 1. 1 Álgebra lineal. Aurea Grané Departamento de Estadística Universidad Carlos III de Madrid. 1.1 Vectores de R n. 1. Vectores. 2.
 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Tema 1 Álgebra lineal 1. Vectores 2. Matrices 1 Álgebra lineal Aurea Grané
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Aquella que tiene nulos los elementos nos situados en la diagonal principal. Los elementos situados por encima de la diagonal principal son nulos.
 Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Sesión 18: Diagonalización (I) Método práctico para diagonalizar una matriz cuadrada A M nxn K
 Sesión 8: Diagonalización (I) Método práctico para diagonalizar una matriz cuadrada A M nxn K ) Calculamos los valores propios de A y sus multiplicidades algebraicas con: d A λ = det A λi nxn = Si d A
Sesión 8: Diagonalización (I) Método práctico para diagonalizar una matriz cuadrada A M nxn K ) Calculamos los valores propios de A y sus multiplicidades algebraicas con: d A λ = det A λi nxn = Si d A
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos.
 Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
Teoría Tema 9 Ecuaciones del plano
 página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial, Especialidad de Electricidad
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial, Especialidad de Electricidad Fundamentos Matemáticos de la Ingeniería Diciembre de 5. Primera parte Tiempo: horas. Se recuerda
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial, Especialidad de Electricidad Fundamentos Matemáticos de la Ingeniería Diciembre de 5. Primera parte Tiempo: horas. Se recuerda
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
Examen de Selectividad Matemáticas JUNIO Andalucía OPCIÓN A
 Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 9: Diagonalización de matrices
 Capítulo 9: Diagonalización de matrices 1. Lección 33. Transformaciones lineales Del mismo modo que el estudio de las funciones usuales es importante para analizar las relaciones y la evolución de magnitudes
Capítulo 9: Diagonalización de matrices 1. Lección 33. Transformaciones lineales Del mismo modo que el estudio de las funciones usuales es importante para analizar las relaciones y la evolución de magnitudes
UTN FRBA Final de Álgebra y Geometría Analítica 21/05/2013. Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:...
 UTN FRBA Final de Álgebra y Geometría Analítica 1/05/01 Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:... La condición para aprobar esta evaluación es tener bien resueltos como mínimo tres ejercicios.
UTN FRBA Final de Álgebra y Geometría Analítica 1/05/01 Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:... La condición para aprobar esta evaluación es tener bien resueltos como mínimo tres ejercicios.
PROPUESTA A. b) Para el valor de a obtenido, calcula los puntos de inflexión de la función f(x). (1 25 puntos)
 PROPUESTA A 1A. a) Determina el valor del parámetro a R, para que la función f(x) = (x a) e x tenga un mínimo relativo en x = 0. Razona, de hecho, es un mínimo absoluto. (1 25 puntos) b) Para el valor
PROPUESTA A 1A. a) Determina el valor del parámetro a R, para que la función f(x) = (x a) e x tenga un mínimo relativo en x = 0. Razona, de hecho, es un mínimo absoluto. (1 25 puntos) b) Para el valor
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
TEMA 6. Ángulos, distancias, simetrías Problemas Resueltos
 Matemáticas II (Bachillerato de Ciencias) Soluciones de los problemas propuestos Tema 6 88 Ángulos entre rectas y planos TEMA 6 Ángulos, distancias, simetrías Problemas Resueltos Dadas las rectas r y s
Matemáticas II (Bachillerato de Ciencias) Soluciones de los problemas propuestos Tema 6 88 Ángulos entre rectas y planos TEMA 6 Ángulos, distancias, simetrías Problemas Resueltos Dadas las rectas r y s
1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS
 1 1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS Sea f : V V un endomorfismo de V, f End(V, con V un K-espacio vectorial de dimensión n, y sean B = {e 1,..., e n } B = {e 1,..., e n} bases de V. La matriz de f
1 1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS Sea f : V V un endomorfismo de V, f End(V, con V un K-espacio vectorial de dimensión n, y sean B = {e 1,..., e n } B = {e 1,..., e n} bases de V. La matriz de f
A d) Estudiar la diagonalización del endomorfismo T. Es posible encontrar una base de vectores propios de R 2 [x]? Razonar la respuesta.
![A d) Estudiar la diagonalización del endomorfismo T. Es posible encontrar una base de vectores propios de R 2 [x]? Razonar la respuesta. A d) Estudiar la diagonalización del endomorfismo T. Es posible encontrar una base de vectores propios de R 2 [x]? Razonar la respuesta.](/thumbs/65/53726322.jpg) Universidad de Oviedo Ejercicio.5 puntos Se consideran las aplicaciones lineales T : R [x] R y T : R R [x] de las que se conoce la matriz A asociada a T en las bases canónicas de R [x] y R y la matriz
Universidad de Oviedo Ejercicio.5 puntos Se consideran las aplicaciones lineales T : R [x] R y T : R R [x] de las que se conoce la matriz A asociada a T en las bases canónicas de R [x] y R y la matriz
UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA
 AL GEBRA III UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA ALGEBRA III DEFINICION : Sea L : V V un operador lineal sobre el espacio vectorial
AL GEBRA III UNIVERSIDAD DE CONCEPCION FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS DEPARTAMENTO DE INGENIERIA MATEMATICA ALGEBRA III DEFINICION : Sea L : V V un operador lineal sobre el espacio vectorial
Clase 7 Herramientas de Álgebra Lineal
 Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
Descomposición en valores singulares Notas para los cursos 21 y 22 (J.L. Mancilla Aguilar)
 Valores Singulares Descomposición en valores singulares Notas para los cursos y (JL Mancilla Aguilar) Tanto los valores singulares como la descomposición en valores singulares de una matriz son conceptos
Valores Singulares Descomposición en valores singulares Notas para los cursos y (JL Mancilla Aguilar) Tanto los valores singulares como la descomposición en valores singulares de una matriz son conceptos
5.1.- Autovalores y autovectores. Definición y propiedades. La ecuación característica. El teorema de Cayley-Hamilton.
 MATEMÁTICAS I (Curso 2-22) Primer Curso del Grado en Ingeniería Electrónica, Robótica y Mecatrónica, Ingeniería de la Energía e Ingeniería de Organización Industrial Departamento de Matemática Aplicada
MATEMÁTICAS I (Curso 2-22) Primer Curso del Grado en Ingeniería Electrónica, Robótica y Mecatrónica, Ingeniería de la Energía e Ingeniería de Organización Industrial Departamento de Matemática Aplicada
Tema 5.- Autovalores y autovectores.
 Ingenierías: Aeroespacial, Civil y Química. Matemáticas I. -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 5.- Autovalores y autovectores. 5..- Autovalores
Ingenierías: Aeroespacial, Civil y Química. Matemáticas I. -. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 5.- Autovalores y autovectores. 5..- Autovalores
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
Tema 3: Sistemas de ecuaciones lineales
 Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
Ejercicios Resueltos de A lgebra Lineal
 Ejercicios Resueltos de A lgebra Lineal Nu meros Complejos Sean z = i y w = eiπ/4 (a) Representa gra ficamente en un mismo sistema de coordenadas los nu meros complejos z z w w (Recuerda: Un solo par de
Ejercicios Resueltos de A lgebra Lineal Nu meros Complejos Sean z = i y w = eiπ/4 (a) Representa gra ficamente en un mismo sistema de coordenadas los nu meros complejos z z w w (Recuerda: Un solo par de
6.14 Descomposición ortogonal y proyección ortogonal
 CAPÍTULO. ESPACIO EUCLÍDEO CANÓNICO IR N 282.14 Descomposición ortogonal y proyección ortogonal El resultado W W = IR n, significa que cada y IR n se puede escribir de forma única como suma de un vector
CAPÍTULO. ESPACIO EUCLÍDEO CANÓNICO IR N 282.14 Descomposición ortogonal y proyección ortogonal El resultado W W = IR n, significa que cada y IR n se puede escribir de forma única como suma de un vector
PROPUESTA A. 3A. a) Despeja X en la ecuación matricial X A B = 2X donde A, B y X son matrices cuadradas
 PROPUESTA A 1A a) Calcula el valor de a R, a > 0, para que la función sea continua en x = 0. b) Calcula el límite 2A. Calcula las siguientes integrales (1 25 puntos por cada integral) Observación: El cambio
PROPUESTA A 1A a) Calcula el valor de a R, a > 0, para que la función sea continua en x = 0. b) Calcula el límite 2A. Calcula las siguientes integrales (1 25 puntos por cada integral) Observación: El cambio
Una ecuación puede tener ninguna, una o varias soluciones. Por ejemplo: 5x 9 = 1 es una ecuación con una incógnita con una solución, x = 2
 Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Podemos definir a las ecuaciones como una igualdad entre expresiones algebraicas (encadenamiento de números y letras ligados por operaciones matemáticas diversas),en la que intervienen una o más letras,
Base y Dimensión de un Espacio Vectorial
 Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Base y Dimensión de un Espacio Vectorial 201 6Asturias: Red de Universidades Virtuales Iberoamericanas 1 Índice 1 Qué es un sistema generador?... 4 2 Base de un espacio vectorial... 4 3 Dimensión de un
Resuelve. Unidad 4. Vectores en el espacio. BACHILLERATO Matemáticas II. Diagonal de un ortoedro y volumen de un paralelepípedo.
 Resuelve Página Diagonal de un ortoedro y volumen de un paralelepípedo. Expresa la diagonal de un ortoedro en función de sus dimensiones, a, b y c. c b a c c b b a Diagonal = a + b + c. Calcula el volumen
Resuelve Página Diagonal de un ortoedro y volumen de un paralelepípedo. Expresa la diagonal de un ortoedro en función de sus dimensiones, a, b y c. c b a c c b b a Diagonal = a + b + c. Calcula el volumen
ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3
 ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3 Matrices y determinantes (Curso 2011 2012) 2. Sea A una matriz diagonal n n y supongamos que todos los elementos de su diagonal son distintos entre sí.
ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3 Matrices y determinantes (Curso 2011 2012) 2. Sea A una matriz diagonal n n y supongamos que todos los elementos de su diagonal son distintos entre sí.
ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3
 ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3 Matrices y determinantes (Curso 010 011). Sea A una matriz diagonal n n y supongamos que todos los elementos de su diagonal son distintos entre sí. Demostrar
ÁLGEBRA LINEAL I Algunas soluciones a la Práctica 3 Matrices y determinantes (Curso 010 011). Sea A una matriz diagonal n n y supongamos que todos los elementos de su diagonal son distintos entre sí. Demostrar
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 8: Vectores
 Capítulo 8: Vectores 1. Lección 30. Operaciones con vectores 1.1. Vectores El concepto de vector aparece en Física para describir magnitudes, tales como la fuerza que actúa sobre un punto, en las que no
Capítulo 8: Vectores 1. Lección 30. Operaciones con vectores 1.1. Vectores El concepto de vector aparece en Física para describir magnitudes, tales como la fuerza que actúa sobre un punto, en las que no
Superficies cuádricas
 Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Conjuntos y matrices. Sistemas de ecuaciones lineales
 1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas resueltos del libro de texto. Tema 8. Geometría Analítica.
 Problemas resueltos del libro de texto Tema 8 Geometría Analítica Combinación lineal de vectores 9- Es evidente que sí es combinación lineal de estos dos vectores, ya que -4 y permiten escribir z como
Problemas resueltos del libro de texto Tema 8 Geometría Analítica Combinación lineal de vectores 9- Es evidente que sí es combinación lineal de estos dos vectores, ya que -4 y permiten escribir z como
7 Aplicaciones ortogonales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 7 Aplicaciones ortogonales 7.1 Aplicación ortogonal Se llama aplicación ortogonal a un endomorfismo f : V V sobre un espacio vectorial
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 7 Aplicaciones ortogonales 7.1 Aplicación ortogonal Se llama aplicación ortogonal a un endomorfismo f : V V sobre un espacio vectorial
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Grado en Edificación MATERIAL DOCENTE: PRESENTACIÓN DEL TEMA III. Ana Isabel Garralda Guillem y Manuel Ruiz Galán
 MATEMÁTICAS TICAS I Grado en Edificación MATERIAL DOCENTE: PRESENTACIÓN DEL TEMA III Ana Isabel Garralda Guillem y Manuel Ruiz Galán Tema. Diagonalización de matrices.1. Diagonalización de matrices por
MATEMÁTICAS TICAS I Grado en Edificación MATERIAL DOCENTE: PRESENTACIÓN DEL TEMA III Ana Isabel Garralda Guillem y Manuel Ruiz Galán Tema. Diagonalización de matrices.1. Diagonalización de matrices por
Matrices y sistemas de ecuaciones lineales. Autovalores y autovectores.
 Tema 5 Matrices y sistemas de ecuaciones lineales Autovalores y autovectores 5 Introducción Una matriz es una disposición ordenada de elementos de la forma: a a a m a a a m a n a n a nm Sus filas son las
Tema 5 Matrices y sistemas de ecuaciones lineales Autovalores y autovectores 5 Introducción Una matriz es una disposición ordenada de elementos de la forma: a a a m a a a m a n a n a nm Sus filas son las
APÉNDICE A. Algebra matricial
 APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
Tema 1: Espacios vectoriales
 PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina
PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS
 RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
Tema 6.- Autovalores y autovectores.
 Ingeniería Civil. Matemáticas I. -3. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 6.- Autovalores autovectores. 6..- Autovalores autovectores. Definición
Ingeniería Civil. Matemáticas I. -3. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 6.- Autovalores autovectores. 6..- Autovalores autovectores. Definición
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Ba s e, d i M e n s i ó n y Mat r i z
 Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
A1.- Determina a y b sabiendo que el sistema de ecuaciones. x + 3y +z = 1 -x + y +2z = -1 ax + by + z = 4 tiene, al menos, dos soluciones distintas.
 A1.- Determina a y b sabiendo que el sistema de ecuaciones x + 3y +z = 1 -x + y +z = -1 ax + by + z = 4 tiene, al menos, dos soluciones distintas. Para que el sistema tenga, al menos, dos soluciones distintas
A1.- Determina a y b sabiendo que el sistema de ecuaciones x + 3y +z = 1 -x + y +z = -1 ax + by + z = 4 tiene, al menos, dos soluciones distintas. Para que el sistema tenga, al menos, dos soluciones distintas
IES Fco Ayala de Granada Sobrantes de 2011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Sobrantes de 011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 4 del 011 [ 5 puntos] Queremos hacer junto a la carretera un cercado rectangular
IES Fco Ayala de Granada Sobrantes de 011 (Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 4 del 011 [ 5 puntos] Queremos hacer junto a la carretera un cercado rectangular
UNIVERSIDAD SIMON BOLIVAR MA1116 abril-julio de 2009 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 I / Ejercicios sugeridos para : los temas de las clases del 2 y 23 de abril de 29. Tema : Matrices. Operaciones con matrices. Ejemplos. Operaciones elementales
UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 I / Ejercicios sugeridos para : los temas de las clases del 2 y 23 de abril de 29. Tema : Matrices. Operaciones con matrices. Ejemplos. Operaciones elementales
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
Matrices y Sistemas de Ecuaciones lineales
 Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Algunos Tipos de matrices. Matrices. Algunos Tipos de matrices. Algunos Tipos de matrices
 Matrices Una matriz de orden m n es un conjunto ordenado de m n números reales dispuestos en m filas y n columnas de la forma: A = a 11 a 12 a 1j a 1n a 21 a 22 a 2j a 2n a i1 a i2 a ij a in a m1 a m2
Matrices Una matriz de orden m n es un conjunto ordenado de m n números reales dispuestos en m filas y n columnas de la forma: A = a 11 a 12 a 1j a 1n a 21 a 22 a 2j a 2n a i1 a i2 a ij a in a m1 a m2
Unidad 5: Geometría analítica del plano.
 Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales 1. Estudiar el sistema de ecuaciones según los valores del parámetro a. ax + y + z = a x y + z = a 1 x + (a 1)y + az = a + 3 Resolverlo (si es posible) para a = 1. (Junio
Sistemas de ecuaciones lineales 1. Estudiar el sistema de ecuaciones según los valores del parámetro a. ax + y + z = a x y + z = a 1 x + (a 1)y + az = a + 3 Resolverlo (si es posible) para a = 1. (Junio
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
CAPÍTULO 5: AUTOVALORES Y AUTOVECTORES, FORMA CANÓNICA DE JORDAN
 CAPÍTULO 5: AUTOVALORES Y AUTOVECTORES, FORMA CANÓNICA DE JORDAN 5.1- Definición: matrices semejantes. Se dice que dos matrices A y B son semejantes si existe una matriz regular P tal que se verifica B
CAPÍTULO 5: AUTOVALORES Y AUTOVECTORES, FORMA CANÓNICA DE JORDAN 5.1- Definición: matrices semejantes. Se dice que dos matrices A y B son semejantes si existe una matriz regular P tal que se verifica B
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
