Potencias y radicales
|
|
|
- Sebastián Flores Peña
- hace 7 años
- Vistas:
Transcripción
1 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 00 Simplific y clcul. z z... z x x... x () 0 veces 0 veces z 0 x 0 00 Escribe el inverso de los siguientes números como potenci de exponente entero Expres ests frcciones como potencis de exponentes enteros. Indic cuánto vle () n pr los vlores positivos y negtivos de n. Pr ello, comienz dndo vlores pequeños y obtén un regl generl. Independientemente de si n es positivo o negtivo, () n si n es pr si n es impr Aplic ls propieddes de ls potencis, y expres el resultdo como potenci de exponente positivo. 8 8 (8 ) e) 8 f) ( ) Indic qué propiedd hs utilizdo en cd cso ( 8() ) ( ) e) 0 ( ) ( ) f) 0
2 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Clcul. (x y ) : (x y ) (x y ) : (x y ) ( ) x y x y xy x y () x y 00 Simplific y expres el resultdo como potenci. 9 8 () () ( ) () Expres en notción científic g) 0,0089 0,000 h) i) diezmilésim billón j) centésims e) Medi decen k) 9 milésims f) l) trillones 9, 0 g) 8,9 0, 0 h), 0,89 0 i) 0 0 j) 0 e) 0 0 k) 9 0 f) l) Estos números no están correctmente escritos en notción científic. Corrígelos. 0, 0, 0 0, 0
3 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 00 Clcul., ( 0 ) (, 0 ), , 0 0, Reliz ls siguientes operciones, y expres el resultdo en notción científic. 9, 0 +, 0 e) (, 0 ) (8 0 ), f) ( 0 ) : ( 0 8 ) 0 0 g) ( 0 ) : (, 0 ) (9 0 ) (8, 0 ) h) ( 0 ) ( 0 ) : (8 0 ) 9, 0 e), 0 8,88 0 f) 0,99 0 g) 0, 0 h) Un microorgnismo mide, micrs. Sbiendo que micr es l millonésim prte de metro, expres, en metros y en notción científic, l longitud de millones de microorgnismos dispuestos en fil. ( 0 ) (, 0 ), 0 metros 0 Reliz, utilizndo l clculdor y tmbién sin ell, est sum: 9, , Qué diferencis observs entre ls dos forms de relizr l sum? En el cso de que l clculdor solo dmit dos cifrs en el exponente, no será cpz de hcerlo e indicrá un error. Si se reliz mnulmente, el resultdo es, Trnsform ls potencis en ríces..09 () () Clcul el vlor numérico, si existe, de los siguientes rdicles y No existe
4 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Hll, con l clculdor, el vlor numérico de ests expresiones. + ( ) +,989,989,89,88 No existe 0 Pon dos ejemplos de rdicles cuys ríces sen y. Existe un rdicl con ríces y? Ejemplos: 9 y 8 No es posible que un rdicl teng como ríces y, y que en el cso de tener dos ríces, ests deben ser opuests. 08 Expres ls siguientes potencis como rdicles y hll su vlor numérico. e) ( ) ( ) f) ( ), no existe.,990 e),88,80 f) ( ),99 09 D dos rdicles equivlentes cd uno y 8 y 0 y 0 00 Rzon si son equivlentes estos rdicles. 0 y y 0 y y 0 Equivlentes No equivlentes 0 No equivlentes Equivlentes 0 Expres en form de potenci. x xy x x x x ( xy ) x ( 8x)
5 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 0 Compr los siguientes rdicles., y < < 0 Simplific estos rdicles. b b b 0 Introduce fctores dentro del rdicl Simplific, si es posible Oper y simplific
6 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Clcul. ( ) 9 ( ) ( ) Hz est operción. 9 ( ) ( ) Trnsform ests frcciones en otrs equivlentes sin rdicles en el denomindor. e) f) e) f) 00 Rcionliz.
7 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 0 Resuelve y rcionliz ( ) Clcul el conjugdo de estos números, y efectú el producto de cd número por su conjugdo. + Conjugdo ( ) ( ) + Conjugdo + + Conjugdo Conjugdo + ( ) ( + ) 0 Rcionliz ls siguientes expresiones. + ( + ) ( ) ( + ) ( + ) ( ) ( + ) ( ) ( )
8 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Efectú ests operciones y rcionliz el resultdo, si fuer preciso ( + ) ( + ) ( ) ( + ) Clcul el inverso de estos números ( + ) ( ) ( 00 + ) ( 00 ) ACTIVIDADES 0 Clcul ls siguientes potencis. 0 e) () g) () i) () 8 f) () h) () g) 8 8 ( ) e) h). 0 ( ) f) i) ( ) 0 Hll el inverso de estos números. e) f) e) f) 8
9 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 08 Expres ests frcciones como potencis de números enteros, emplendo exponentes negtivos, si es preciso. e) f) 9 e) f) 09 Simplific, expresndo como únic potenci. () : () : () () : () () : + () () () () () 8 () 0 00 Oper y expres el resultdo en form de un sol potenci. 0 0 : : : Efectú ls operciones. : e) : ( ) () ( ) f) [() ] ( ) : ( ) g) [( 8 ) ] ( ) ( ) h) ( ) : ( ) : 8 e) : [() ] () 8 f) () : ( ) () g) [( ) ] () () h) ( ) : [() ] 9
10 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: HAZLO ASÍ CÓMO SE RESUELVEN OPERACIONES CON POTENCIAS FACTORIZANDO LAS BASES? Resuelve est operción con potencis, simplificndo todo lo que pueds. PRIMERO. Se descomponen ls bses de ls potencis en fctores primos. SEGUNDO. Se plic es descomposición l operción. ( ) ( ) ( ) ( ) TERCERO. Se resuelve l operción. + + ( ) ( ) 0 Oper y simplific el resultdo. (0 : 0 ) (9 0 : 9 ) e) ( : ) ( ) (0 0 0 ) f) (0 : 0 ) ( ) (0 ) 0 ( ) e) ( : ) ( ) (9 ) 9 f) ( ) 0 Clcul y simplific el resultdo. : : : [( ) ] :[( ) ] ( ) ( 8 8 ) ( ) 8 [() : ] ( : ) () [() : ] : [ : () ] () 0 Efectú y simplific. 0 : 8 9 : : 8 9 : 8 : : 0
11 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles Simplific. 8 ( ) ( 8) 9 9 ( ) () 8 Reliz ests operciones con potencis, efectundo primero ls operciones dentro del corchete. Comprueb que si lo hces l revés, el resultdo no vrí. [ ()] e) [0 : ()] [() 8] f) [9 : () ] [ : () ] g) [ 0 ] [(0) : ()] h) [ ] e) [ 00] [ 80] [ ] f) [ ] [ ] g) [ 0] [ 0] h) [ 9 ] 0 Oper y expres el resultdo en form de potenci de exponente entero. e) 8 : : : f) 9 : : + + ( )8 [ ] ( ) 8 e) 8 [ () ] 0 f) [ ] 9
12 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: HAZLO ASÍ CÓMO SE EFECTÚAN OPERACIONES COMBINADAS CON POTENCIAS? Efectú est operción. 8 PRIMERO. Se relizn ls operciones que están dentro de los préntesis. 8 8 SEGUNDO. Se clculn ls potencis TERCERO. Se efectún ls operciones, respetndo l jerrquí Reliz ls siguientes operciones. + + : 0 : + : : 0 9 9
13 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 0 0 Indic qué igulddes son verdders, y escribe el resultdo correcto en ls flss. b c b c Fls b 8 c 8 Fls + Fls Verdder Escribe en notción científic los siguientes números, e indic su orden de mgnitud e) , f) 0, g) , h).000, 0 0 Orden de mgnitud: 0, 0 Orden de mgnitud:,9 0 Orden de mgnitud: Orden de mgnitud: 0 e), Orden de mgnitud: 9 f) 9, 0 Orden de mgnitud: g),9 0 8 Orden de mgnitud: 8 h), 0 Orden de mgnitud: 0 Desrroll estos números escritos en notción científic.,8 0 8 e), 0 8 8, 0 f), 0,9 0 g),8 0,9 0 9 h), e) 0, , f) 0, , g) h) 0,
14 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Indic cuáles de los siguientes números están escritos en notción científic. 0 e), 0 0, 0 f) 0, g) 0, ,0000 h) 8, 0 Solo está escrito en notción científic el número del prtdo e), 0. 0 Efectú ls operciones., 0 +, 0 8, 0 + 9, 0, 0 +,8 0, 0 +, 0 +, 0 e), 0 +,9 0 +,8 0,89 0,09 0,0 0 e),980 0, Clcul. 9, 0, 0 8, 0, 0,9 0, 0, 0 +, 0,9 0 e) ,8 0, 0 8,0 0 e),99 0, Hz ls operciones., 0, 0 8, 0 :, 0 8,9 0, 0 9, 0 :, 0,8 0, 0,08 0 0, Simplific., 0, 0 8 9, 0, 0,8 0, 0 8, 9 0, , 0 8
15 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 09 Clcul, si es posible, el vlor numérico de los siguientes rdicles g) e) h) f) i) ± 0 g) ± e) No es posible h) ± f) i) Indic en estos rdicles cuáles son el índice y el rdicndo. Después, expréslos como potenci de exponente frccionrio. 9 e) f) Índice:, rdicndo: Índice:, rdicndo: Índice: 9, rdicndo: Índice:, rdicndo: e) Índice:, rdicndo: f) Índice:, rdicndo: ( ) 9 ( ) 0 Trnsform los rdicles en potencis y ls potencis en rdicles. g) e) 0 h) f) i) g) e) 0 h) f) i) 0 De estos rdicles, cuáles son equivlentes? ,,,,,,, y 0 Son equivlentes:
16 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Extre fctores de los siguientes rdicles. b 0 bc e) f) b 8 b b bc b e) b f) b 0 HAZLO ASÍ CÓMO SE EXTRAEN FACTORES DE UN RADICAL DESCOMPONIENDO EL RADICANDO EN FACTORES PRIMOS? Simplific el rdicl PRIMERO. Se fctoriz el rdicndo SEGUNDO. Se expres el rdicl como potenci de exponente frccionrio ( ) TERCERO. Si lgun de ls frcciones de los exponentes es impropi, se pone como l sum de un número entero y un frcción. CUARTO. Se expres como producto de potencis y se vuelve trnsformr en rdicl Extre fctores de ls ríces g) 8 e) h) 0 f) i) g) 0 e) h) f) i)
17 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 0 Simplific estos rdicles. g) e) 8 h) 8 f) i) 8 g) e) h) f) i) 0 Introduce fctores en el rdicl. g) 0 e) h) f) i) 8 0 g). 80 e) h) 8. f) i) 8 08 Introduce fctores en el rdicl, si es posible. b cb e) 8 c 8 + f) b b e) b c No es posible f) 8b 09 Efectú ls siguientes operciones
18 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Reliz ests operciones Oper y simplific. e) : g) : 8 f) : h) : e) g) 8 f) 0 h) 0 Clcul. ( ) + ( ) e) ( ) f) ( ) 8 ( ) ( 9 ) ( 8 ) + + e) + f) 0 Oper y simplific. ( ) ( ) + ( ) ( + ) ( + ) ( ) ( ) ( + ) 8
19 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 0 Clcul y simplific. ( ) + ( + ) ( + ) ( ) ( ) ( + ) ( ) + ( + + ) ( ) ( 9 + ) ( + ) ( + + ) 0 Hz ls operciones y simplific. ( ) ( ) ( + ) ( + ) ( ) ( + ) ( ) ( ) Clcul. b b b : b b b + + b b b b b 9 9 b : b b 0 0 b b b b 9
20 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Efectú y simplific. ( ) ( ) + ( + ) ( + ) ( ) ( + ) ( ) + ( ) ( + ) ( + ) ( + ) + + ( ) (9 ) + ( 80) ( 0 + ) ( ) ( ) Efectú y expres el resultdo como potenci. ( ) 8 8 ( ) Escribe los siguientes rdicles como potencis de exponente frccionrio. g) e) h) f) i) 0
21 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 080 Expres medinte un solo rdicl. e) f) 0 0 e) 8 f) 08 Rzon si son verdders o flss ests igulddes. n m n m b b e) + b + b n m n+ m b b f) n n n + b + b g) b b 8 b b n m n m b ( h) n m nm m b mn n nm b m b n nm b Fls nm n+ m n m nm m b mn n b m b n b Fls Fls, excepto cundo n. Y se comprueb probndo con culquier vlor de, b y n. n m n b n b m n m m b Fls, excepto si n m. e) Fls, y que si elevmos l cudrdo los términos: ( ) b b b b ( b ) f) b b b Verdder 8 g) b b b b Fls b + c b + c h) b + c b + c b + c Fls, excepto pr. 08 Rcionliz los denomindores y simplific.
22 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Rcionliz los denomindores y simplific. + ( ) ( ) ( ) + + ( ) 08 Rcionliz los denomindores y simplific. + e) f) + 8 ( ) 0 e) f) ( + ) ( ) ( + ) ( ) ( + ) ( + ) ( ) ( + ) + ( + ) ( ) ( + ) + ( ) ( + ) ( ) + 8 ( 0 + ) ( ) ( + )
23 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 08 Rcionliz ( ) + + ( ) ( + ) ( ) ( + ) ( ) HAZLO ASÍ CÓMO SE RESUELVEN OPERACIONES DE FRACCIONES CON DENOMINADORES EN FORMA DE RADICAL? Resuelve: 0 PRIMERO. Se rcionlizn ls frcciones SEGUNDO. Se resuelve l operción
24 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Rcionliz y oper Rcionliz y efectú ls operciones ( + ) ( ) ( + ) ( ) ( + ) ( ) ( 8 + ) 9 ( 8 ) ( 8 + ) + ( + ) ( ) ( + ) Rcionliz y oper
25 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles 090 HAZLO ASÍ ( ) n CÓMO SE RACIONALIZAN FRACCIONES CON DENOMINADORES DEL TIPO b + c? Rcionliz: ( ) n n PRIMERO. Se multiplic por. ( ) ( ) ( ) SEGUNDO. Se multiplic por el conjugdo del denomindor resultnte. ( + ) ( ) ( + ) ( + ) ( + ) 09 Rcionliz ls siguientes expresiones. ( + ) ( ) + + ( ) + ( ) ( ) ( ) + + ( ) + + ( ) 0 ( ) ( ) ( ) ( ) + 09 Escribe en notción científic. Distnci Tierr-Lun: km. Distnci Tierr-Neptuno: km. Diámetro de un electrón: 0, m. Superficie de l Tierr: km. e) Longitud de un virus (gripe): 0, m. f) Rdio del protón: 0, m. g) Peso de un estfilococo: 0, g. h) Un ño luz: km. i) Distnci del universo observble:.000 millones de ños luz.
26 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: 9 9 9,8 0 km, 0 8 km g) 0 g, km e), 0 9 m h) 9, 0 km 0 0 m f) 0 m i), 0 0 ños luz 09 Ls uniddes de medid con ls que medimos l cntidd de informción son: Byte bits Kilobyte 0 bytes Megbyte 0 Kilobytes Gigbyte 0 Megbytes Expres, en form de potenci y en notción científic, ests cntiddes de informción en bits y bytes. Un disco duro de 0 Gb. Un disquete de, Mb. Un trjet de memori de Mb. Un CD-Rom de 0 Mb. 0 Gb 0 0 bytes, bytes, bits Mb 0 bytes, bytes, bits, Mb, 0 bytes, bytes,099 0 bits 0 Mb 0 0 bytes,8 bytes 0 8,9 0 9 bits 09 L ms de Plutón es, 0 9 veces l ms del Sol, y est, su vez, es, 0 veces l ms de l Tierr. Si l ms de l Tierr es 0 kg, hll l ms de Plutón y del Sol. Ms del Sol: 0, 0,98 0 kg Ms de Plutón:,98 0, 0 9,08 0 kg 09 Se h observdo que l poblción de cierts bcteris se duplic cd hor. Si el número inicil es de 8 0 bcteris: Cuánts bcteris hbrá ls hors? Y ls hors? Cuánts hors tendrán que psr pr que sen,0 0 bcteris? 8 0, 0 bcteris 8 0, 0 bcteris,0 0 : 8 0 8, por lo que n 8 n. Tendrán que psr hors.
27 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles Cuánto mide l rist de un cubo cuyo volumen es m? Expres el resultdo en form de rdicles. Arist m Arist m Cuánto mide el áre de l cr de un cubo cuyo volumen es 9 cm? Expres el resultdo como rdicl y como potenci. Arist 9 m Arist 9 m Áre de l cr m m Si el volumen de un cubo es 0 cm, hll el vlor de l sum de sus rists. Arist 0 cm Arist 0 cm Sumderists Con los dtos de l ctividd nterior, clcul l superficie lterl del cubo. Arist 0 cm Arist 0 cm Áre de l cr 0 cm Áre lterl 0 0 cm Generliz los resultdos de ls ctividdes nteriores, dndo el vlor de l rist y l superficie lterl de un cubo en función de su volumen. Arist Volumen Arist Volumen Áre de l cr Áre lterl 0 Volumen Volumen Expres en notción científic cm 0 0, , , ,0 0 0, , Reflexion y responde. En qué csos ocurre que <? Y en qué csos ocurre que >? <, cundo 0 < <. >, cundo >.
28 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Rcionliz ( + ) ( + ) ( ) ( + + ) Explic cómo se rcionlizn ls frcciones del tipo n n. b n n Volvemos rcionlizr hst que eliminmos totlmente ls ríces del denomindor n n b b n n n ( + b ) b n n n n ( ) + n n n ( ) + b b n ( ) n ( ) ( ) n n n n n + b + b + b n b b n n n n ( + ) ( + b b ) ( + b ) b ( ) n n b EN LA VIDA COTIDIANA 0 Un equipo de ingenieros eronáuticos v presentr un proyecto pr l construcción de un nuevo vión. Por ello quieren construir un mquet. Sin embrgo, se hn encontrdo con un problem. Te hs fijdo en est piez? Es un rectángulo de cm de lrgo, pero su ncho Sí, es cierto; debe medir cm. 8
29 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Potencis y rdicles Pr no cometer errores en l construcción, se plnten cómo trzr un segmento que mid exctmente cm. Así, el equipo h resuelto el problem pr poder relizr l mquet. Podemos trzr un triángulo rectángulo cuyos ctetos midn cm y cm, y utilizr el teorem de Pitágors. Otr de ls piezs v ser un rectángulo que mid + cm de lrgo y cm de ncho. Cómo conseguirán dibujrlo con precisión? Un vez conocido el segmento de cm, trzmos el segmento de cm medinte un triángulo rectángulo, de ctetos cm y cm, y se hce lo mismo con el segmento de cm con un triángulo de ctetos cm y cm. Teniendo el segmento de cm, le ñdimos cm prolongndo l rect, con lo que result un segmento de + cm. Trzmos l meditriz del segmento y conseguimos un segmento + de cm. Pr el otro ldo del rectángulo, trzmos primero un segmento de cm, medinte un triángulo rectángulo de ctetos cm, y proyectmos cutro veces el segmento utilizndo un compás, por lo que conseguimos un segmento de cm. 0 Pr motivr los lumnos de un centro escolr sobre el excesivo consumo que se hce del gu, los profesores hn orgnizdo un visit l emblse de su región. Pr que os hgáis un ide precis de l cpcidd del emblse, imgind que es l mism que l de un cubo de 0 metros de rist El doble del lrgo de un cmpo de fútbol! EMBALSE EL COLIBRÍ 9
30 C/ Frncisco Grcí Pvón, Tomelloso 00 (C. Rel) Teléfono Fx: Los lumnos mirn sorprendidos el pnel con los dtos del emblse. Nos está diciendo l verdd? No estoy seguro. Informción sobre el emblse CAPACIDAD 9, hm Justific si el guí h hecho bien los cálculos. Al finl de l visit, el profesor decide entregrles este folleto. El gsto de gu l ño de un fmili es de unos..000 litros. Cuántos metros medirá el ldo de un cubo con est cpcidd? Si el cubo tiene 0 m de rist, su cpcidd es de 0 m m 9, hm. Por tnto, el guí no h relizdo bien el cálculo de l rist litros..000 dm. m L rist del cubo mide., m. 0
Potencias y radicales
 Potencis y rdicles POTENCIAS DE EXPONENTE ENTERO NOTACIÓN CIENTÍFICA RADICALES EQUIVALENTES SEMEJANTES OPERACIONES CON RADICALES SUMA Y RESTA PRODUCTO Y COCIENTE POTENCIA Y RAÍZ RACIONALIZACIÓN DENOMINADOR
Potencis y rdicles POTENCIAS DE EXPONENTE ENTERO NOTACIÓN CIENTÍFICA RADICALES EQUIVALENTES SEMEJANTES OPERACIONES CON RADICALES SUMA Y RESTA PRODUCTO Y COCIENTE POTENCIA Y RAÍZ RACIONALIZACIÓN DENOMINADOR
Colegio La Inmaculada Misioneras Seculares de Jesús Obrero. TEMA 2: actividades
 º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
º E.S.O. TEMA : ctividdes. Sc del rdicndo l myor cntidd posible de fctores: 0 0 0 800.. Epres como rdicl:. Simplific los siguientes rdicles: 8. Ps estos números de notción científic form ordinri:, 0 =,
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
2 Números reales: la recta real
 Unidd. Números reles ls Enseñnzs Aplicds Números reles: l rect rel Págin. ) Justific que el punto representdo es. 0 Represent 7 (7 ) y 0 (0 + ). ) Aplicndo Pitágors: x x + x + x x 0 7 7 0 0 7 0 0 7. Qué
Unidd. Números reles ls Enseñnzs Aplicds Números reles: l rect rel Págin. ) Justific que el punto representdo es. 0 Represent 7 (7 ) y 0 (0 + ). ) Aplicndo Pitágors: x x + x + x x 0 7 7 0 0 7 0 0 7. Qué
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Si la base de una potencia es positiva y el exponente es negativo de qué signo es el resultado. Pon un ejemplo. Expresa como potencia única de 10:
 Potencis Potenci Qué es un potenci? Relizr el siguiente cálculo : 7 Utilizndo solmente tres doses escribe tods ls epresiones numérics que se pueden formr con ellos. No vle usr otros signos. Cuál es el
Potencis Potenci Qué es un potenci? Relizr el siguiente cálculo : 7 Utilizndo solmente tres doses escribe tods ls epresiones numérics que se pueden formr con ellos. No vle usr otros signos. Cuál es el
Tema 1: Números reales.
 Tem : Números reles. Ejercicio. Representr los siguientes conjuntos numéricos: ) Números myores que. b) x / x c) x / x x d) Números menores que excluyendo el 0. e) / x x / x x / x ) (, ) b) [,) 0 c) [,]
Tem : Números reles. Ejercicio. Representr los siguientes conjuntos numéricos: ) Números myores que. b) x / x c) x / x x d) Números menores que excluyendo el 0. e) / x x / x x / x ) (, ) b) [,) 0 c) [,]
Números racionales son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresar en forma de fracción.
 MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
MATEMÁTICAS ºACT TEMA. EL NÚMERO REAL. NÚMEROS RACIONALES. Números rcionles son los que se pueden poner como cociente de dos números enteros. Es decir, se pueden expresr en form de frcción. Los números
NÚMEROS REALES 1º Bachillerato CC. SS.
 Números Reles NÚMEROS REALES 1º Bchillerto CC. SS. Reles R Irrcionles I Enteros Rcionles Z Q Nturles Nturles N 1,,,... EnterosZ, 1, 0, 1,... Rcionles Q 7,, 6'... 5 N Irrcionles I π,, 7'114... Números Reles
Números Reles NÚMEROS REALES 1º Bchillerto CC. SS. Reles R Irrcionles I Enteros Rcionles Z Q Nturles Nturles N 1,,,... EnterosZ, 1, 0, 1,... Rcionles Q 7,, 6'... 5 N Irrcionles I π,, 7'114... Números Reles
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
1. Utilizando las propiedades de las potencias simplifica las siguientes expresiones: c) 2. d) 0,001 e) 0, f) 0,
 TEMA POTENCIAS, RADICALES A) POTENCIAS Y NOTACIÓN CIENTÍFICA.. Utilizndo ls propieddes de ls potencis simplific ls siguientes expresiones: ) ) ) ) c) 0 e) f) g) h) 0) ) ) ). Expres con un potenci de se
TEMA POTENCIAS, RADICALES A) POTENCIAS Y NOTACIÓN CIENTÍFICA.. Utilizndo ls propieddes de ls potencis simplific ls siguientes expresiones: ) ) ) ) c) 0 e) f) g) h) 0) ) ) ). Expres con un potenci de se
Números reales. 1. Números y expresiones decimales. página El conjunto de los números reales página La recta real. Intervalos página 9
 Números reles E S Q U E M A D E L A U N I D A D.. Los números rcionles págin.. Los números irrcionles págin. Números y expresiones decimles págin. El conjunto de los números reles págin 8 4.. Orden y desiguldd
Números reles E S Q U E M A D E L A U N I D A D.. Los números rcionles págin.. Los números irrcionles págin. Números y expresiones decimles págin. El conjunto de los números reles págin 8 4.. Orden y desiguldd
ACTIVIDADES VERANO 4º ESO opción A a b) 3 2 x. 121x 169y. 8 y. a Expresa en forma de potencia: a) Expresa en forma de radical:
 ACTIVIDADES VERANO º ESO opción A 01 NOMBRE: Grupo: 1.- Expres en form de potenci: ) 1 x c) b b.- Expres en form de rdicl: ) = =.- Reduce común índice: ) x,, 8.- Clcul ls siguientes ríces: 1 ) 81 0, 000081.-
ACTIVIDADES VERANO º ESO opción A 01 NOMBRE: Grupo: 1.- Expres en form de potenci: ) 1 x c) b b.- Expres en form de rdicl: ) = =.- Reduce común índice: ) x,, 8.- Clcul ls siguientes ríces: 1 ) 81 0, 000081.-
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
Ejercicios. Números enteros, fraccionarios e irracionales.
 CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
CEPA Enrique Tierno Glván. Ámbito Científico-Tecnológico. Nivel Ejercicios. Números enteros frccionrios e irrcionles. Números enteros. Represent en l rect rel los siguientes números enteros - 0 - -. Qué
1Soluciones a los ejercicios y problemas
 Soluciones los ejercicios y problems ) 8 : 8 ) 8 8 : ) 8 8 : Pág PÁGINA 8 Clcul y comprueb con l clculdor ) ) : : ) ) ) 8 [ 0 )] ) ) : ) [ 0 ] : : 0 88 8 ) ) ) 8 [ ) 0) : ) ] : ) 8 8 Reduce un frcción
Soluciones los ejercicios y problems ) 8 : 8 ) 8 8 : ) 8 8 : Pág PÁGINA 8 Clcul y comprueb con l clculdor ) ) : : ) ) ) 8 [ 0 )] ) ) : ) [ 0 ] : : 0 88 8 ) ) ) 8 [ ) 0) : ) ] : ) 8 8 Reduce un frcción
el blog de mate de aida.: ECUACIONES 4º ESO pág. 1 ECUACIONES
 el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
LITERATURA Y MATEMÁTICAS. El código Da Vinci
 Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
Números reles SOLUCIONARIO Números reles LITERATURA Y MATEMÁTICAS El código D Vinci El profesor Lngdon se sintió un vez más en Hrvrd, de nuevo en su clse de «Simbolismo en el Arte», escribiendo su número
TEMA 1. LOS NÚMEROS REALES
 TEMA. LOS NÚMEROS REALES. Operciones con números nturles. Los números nturles son los que se utilizn pr contr 0,,,,,, Con los números nturles podemos relizr diferentes operciones, como - Sum + = 8 - Rest
TEMA. LOS NÚMEROS REALES. Operciones con números nturles. Los números nturles son los que se utilizn pr contr 0,,,,,, Con los números nturles podemos relizr diferentes operciones, como - Sum + = 8 - Rest
1 Agrupa aquellos monomios de los que siguen que sean semejantes, y halla su suma: , cuando:
 Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Departamento de Matemática
 Deprtmento de Mtemátic Trjo Práctico N : Tercer Año Números Reles Ddos los siguientes números clsificrlos en nturles, enteros, rcionles, irrcionles, reles o no reles. 9 7 ;, ; - ; e- ; + ; - ; ; 0,7 ;
Deprtmento de Mtemátic Trjo Práctico N : Tercer Año Números Reles Ddos los siguientes números clsificrlos en nturles, enteros, rcionles, irrcionles, reles o no reles. 9 7 ;, ; - ; e- ; + ; - ; ; 0,7 ;
PENDIENTE MATEMÁTICAS DE 2º ESO CUADERNILLO I
 PENDIENTE MATEMÁTICAS DE º ESO CUADERNILLO I Fech de entreg de enero Fech del primer emen de enero NOMBRE CURSO Bloques temáticos Criterios de evlución Ejercicios.- Números enteros. I, II Del l.- Sistem
PENDIENTE MATEMÁTICAS DE º ESO CUADERNILLO I Fech de entreg de enero Fech del primer emen de enero NOMBRE CURSO Bloques temáticos Criterios de evlución Ejercicios.- Números enteros. I, II Del l.- Sistem
TEMA 3: ECUACIONES ECUACIONES DE 2º GRADO Las ecuaciones de 2º grado son de la forma ax 2 +bx+c=0 y su solución es:
 TEMA : ECUACIONES ECUACIONES DE º GRADO Ls ecuciones de º grdo son de l form +b+c=0 y su solución es: b b 4c Cundo b=o o c=0 son incomplets y se resuelven de l siguiente form. Cso b=0, por ejemplo: 6 7=0
TEMA : ECUACIONES ECUACIONES DE º GRADO Ls ecuciones de º grdo son de l form +b+c=0 y su solución es: b b 4c Cundo b=o o c=0 son incomplets y se resuelven de l siguiente form. Cso b=0, por ejemplo: 6 7=0
SOLUCIONES DE LAS ACTIVIDADES Págs. 4 a 21
 TEMA. NÚMEROS REALES SOLUCIONES DE LAS ACTIVIDADES Págs. Págin. Actividd personl, por ejemplo:,...,...,...,9...,8.... ) No, pues un deciml puede tener un número limitdo de cifrs o ser periódico. Por ejemplo,,
TEMA. NÚMEROS REALES SOLUCIONES DE LAS ACTIVIDADES Págs. Págin. Actividd personl, por ejemplo:,...,...,...,9...,8.... ) No, pues un deciml puede tener un número limitdo de cifrs o ser periódico. Por ejemplo,,
Potencias y radicales
 Potencis y rdicles. Rdicles Definición Llmmos ríz n-ésim de un número ddo l número que elevdo n nos d. por ser n n Un rdicl es equivlente un potenci de eponente frccionrio en l que el denomindor de l frcción
Potencis y rdicles. Rdicles Definición Llmmos ríz n-ésim de un número ddo l número que elevdo n nos d. por ser n n Un rdicl es equivlente un potenci de eponente frccionrio en l que el denomindor de l frcción
T1 Números. 2. Escribe en forma de inecuaciones o sistemas de inecuaciones e intervalos los números que verifican las desigualdades:
 T Números. Escribe en form de intervlos los números que verificn ests desigulddes y represéntlos: ) x < o x 6 x > y x < 6 x - y x > x < o x -. Escribe en form de inecuciones o sistems de inecuciones e
T Números. Escribe en form de intervlos los números que verificn ests desigulddes y represéntlos: ) x < o x 6 x > y x < 6 x - y x > x < o x -. Escribe en form de inecuciones o sistems de inecuciones e
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS ACADÉMICAS 4º E.S.O.
 4º E.S.O. UNIDAD 1: LOS NÚMEROS REALES Ejercicio nº 1.- ) Escribe en form de intervlo, di su nombre y represent en cd cso:.1) { R / x 4}.) { R / < x } x (0.5 puntos) x (0.5 puntos) b) Escribe en form de
4º E.S.O. UNIDAD 1: LOS NÚMEROS REALES Ejercicio nº 1.- ) Escribe en form de intervlo, di su nombre y represent en cd cso:.1) { R / x 4}.) { R / < x } x (0.5 puntos) x (0.5 puntos) b) Escribe en form de
IES Capellanía 4º ESOB Departamento de Matemáticas. Alumno: Ejercicios Temas 1 y 2: Números Reales. Potencias y Radicales
 IES Cpellní º ESOB Deprtmento de Mtemátics Alumno: Efectú el cociente Ejercicios Tems y : Números Reles Potencis y Rdicles,,0, 0, psndo frcciones genertrices Represent en l rect rel, utilizndo el teorem
IES Cpellní º ESOB Deprtmento de Mtemátics Alumno: Efectú el cociente Ejercicios Tems y : Números Reles Potencis y Rdicles,,0, 0, psndo frcciones genertrices Represent en l rect rel, utilizndo el teorem
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
Multiplicar por la potencia de 10 adecuada para convertirlo en entero. Despejar N 119. Simplificar la fracción, si es posible N = 50
 .0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS.
.0 INTRODUCCIÓN º.0. ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 8... ENTEROS (Z) - ENTEROS NEGATIVOS -; ; 8... Decimles exctos :0,; ;... FRACCIONARIOS.
EXPONENTES Y RADICALES
 . UNIDAD EXPONENTES Y RADICALES Objetivo generl. Al terinr est Unidd resolverás ejercicios probles en los que pliques ls lees de los eponentes de los rdicles. Objetivos específicos:. Recordrás l notción
. UNIDAD EXPONENTES Y RADICALES Objetivo generl. Al terinr est Unidd resolverás ejercicios probles en los que pliques ls lees de los eponentes de los rdicles. Objetivos específicos:. Recordrás l notción
( ) ( ) ( ) ( ) 4. Aplique las propiedades de la potenciación y la radicación para simplificar las siguientes expresiones.
 DEPARTAMENTO DE MATEMÁTICAS ÁREA DE MATEMÁTICAS TEMA: PERÍODO: ORIENTADOR: ESTUDIANTE: E-MAIL: FECHA: TEORÍA DE LOS EXPONENTES, LOS RADICALES Y LOS LOGARITMOS PRIMERO UNIDAD TEORÍA DE LOS EXPONENTES, LOS
DEPARTAMENTO DE MATEMÁTICAS ÁREA DE MATEMÁTICAS TEMA: PERÍODO: ORIENTADOR: ESTUDIANTE: E-MAIL: FECHA: TEORÍA DE LOS EXPONENTES, LOS RADICALES Y LOS LOGARITMOS PRIMERO UNIDAD TEORÍA DE LOS EXPONENTES, LOS
Operaciones. a a a a Ejercicios y Problemas de Matemáticas de 1º a 3º de ESO. 3.
 74 Ejercicios y Problems de Mtemátics de 1º 3º de ESO 3. Tercero de ESO 3.1. Números, medids y operciones 3.1.1. Operciones 1. Reduce ls expresiones siguientes un sol potenci: ) 3 6 - -1 5-3 -3 3-3 3 3
74 Ejercicios y Problems de Mtemátics de 1º 3º de ESO 3. Tercero de ESO 3.1. Números, medids y operciones 3.1.1. Operciones 1. Reduce ls expresiones siguientes un sol potenci: ) 3 6 - -1 5-3 -3 3-3 3 3
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA
 EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
EJERCICIOS DE LA ASIGNATURA DE ALGEBRA 1 INTRODUCCION Estimdo estudinte, el prendizje de est rm de l mtemátic, requiere que se dominen completmente los siguientes conocimientos y procedimientos prendidos
TEMA 1: NÚMEROS REALES. 2. Indica el menor conjunto numérico al que pertenecen los siguientes números:
 I.E.S. Tierr de Ciudd Rodrigo Deprtmento de Mtemátics Conjuntos numéricos. Relción entre ellos.. Complet: TEMA : NÚMEROS REALES Números reles. Indic el menor conjunto numérico l que pertenecen los siguientes
I.E.S. Tierr de Ciudd Rodrigo Deprtmento de Mtemátics Conjuntos numéricos. Relción entre ellos.. Complet: TEMA : NÚMEROS REALES Números reles. Indic el menor conjunto numérico l que pertenecen los siguientes
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
P I E N S A Y C A L C U L A
 Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
Áres y volúmenes. Uniddes de volumen P I E N S Y C C U L Clcul mentlmente el volumen de ls siguientes figurs teniendo en cuent que cd cubo es un unidd. ) b) c) d) e) ) 7 u b) 4 u c) 8 u d) 6 u e) 8 u Crné
UNIDAD: ÁLGEBRA Y FUNCIONES RAÍCES FUNCIÓN RAÍZ CUADRADA
 C u r s o : Mtemátic Mteril N 7 UNIDAD: ÁLGEBRA Y FUNCIONES RAÍCES FUNCIÓN RAÍZ CUADRADA GUÍA TEÓRICO PRÁCTICA Nº DEFINICIÓN : Si n es un entero pr positivo es un rel no negtivo, entonces n es el único
C u r s o : Mtemátic Mteril N 7 UNIDAD: ÁLGEBRA Y FUNCIONES RAÍCES FUNCIÓN RAÍZ CUADRADA GUÍA TEÓRICO PRÁCTICA Nº DEFINICIÓN : Si n es un entero pr positivo es un rel no negtivo, entonces n es el único
RESUMEN 01 NÚMEROS. Nombre : Curso. Profesor :
 RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
RESUMEN 01 NÚMEROS Nomre : Curso : Profesor : PÁGINA 1 Números Los elementos del conjunto N = {1, 2, 3, 4, 5, } se denominn Números Nturles. Los Números Crdinles corresponden l unión del conjunto de los
Colegio Diocesano Sagrado Corazón de Jesús EJERCICIOS MATEMÁTICAS 3º ESO VERANO 2015
 Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
OPERACIONES CON RADICALES
 OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
EJERCICIOS DE RAÍCES
 EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
EJERCICIOS DE RAÍCES º ESO RECORDAR: Definición de ríz n-ésim: n x x Equivlenci con un potenci de exponente frccionrio: n m x Simplificción de rdicles/índice común: Propieddes de ls ríces: x m/n n n b
a n =b Si a es múltiplo de b, entonces b es divisor de a. Números primos: son números cuyos únicos divisores son ellos mismos y el 1.
 1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
1) NÚMEROS NATURALES Son números que sirven pr contr. Descomposición polinómic de un número. Ej : 1.34.567 1: Uniddes de millón : Centens de millr 3: Decens de millr 4: Uniddes de millr 5: Centens 6: Decens
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
NÚMEROS REALES, R. Es el conjunto de números que se obtiene al unir el conjunto de los números racionales con el conjunto de los números irracionales.
 NÚMEROS REALES, R CPR. JORGE JUAN Xuvi-Nrón Es el conjunto de números que se obtiene l unir el conjunto de los números rcionles con el conjunto de los números irrcionles. R= QI Los números reles poseen
NÚMEROS REALES, R CPR. JORGE JUAN Xuvi-Nrón Es el conjunto de números que se obtiene l unir el conjunto de los números rcionles con el conjunto de los números irrcionles. R= QI Los números reles poseen
Unidad I: Números Reales. 1) Expresar como fracción y luego resolver: b) 5,08. a) 4,1 0, 21 1,2 0,6 0,7 0,3 1 0,027 0,3 0,05 2,3 1, 2 3, 4
 MATEMATICA II Trbjo Práctico Unidd I: Números Reles ) Epresr como frcción y luego resolver: ) 4, 0,, 0,6 c) 0,07 0, 0,05 b) 0, 0, 0,4 0,5 d) 0,7 0,,, e), 4 f ),7,7 0,7 0,8 5, 4 ) Resolver ls siguientes
MATEMATICA II Trbjo Práctico Unidd I: Números Reles ) Epresr como frcción y luego resolver: ) 4, 0,, 0,6 c) 0,07 0, 0,05 b) 0, 0, 0,4 0,5 d) 0,7 0,,, e), 4 f ),7,7 0,7 0,8 5, 4 ) Resolver ls siguientes
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
MATEMATICAS 3º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION
 MATEMATICAS º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION FRACCIONES Ejercicio 1: resuelve l siguiente operción psndo cd número deciml frcción previmente: ' '1'6 '1 0'15 Ejercicio : simplific ls
MATEMATICAS º ESO EJERCICIOS DE RECUPERACION DE LA 1ª EVALUACION FRACCIONES Ejercicio 1: resuelve l siguiente operción psndo cd número deciml frcción previmente: ' '1'6 '1 0'15 Ejercicio : simplific ls
Ejercicios de números reales
 Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
Ejercicios de números reles Clsific los siguientes números como nturles, enteros, rcionles o reles:, Ejercicio nº.- Consider los siguientes números: 1,000000... 1,,1... Clsifíclos según sen nturles, enteros,
1. Números reales. Resuelve BACHILLERATO. Página 29
 . Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin 9 A l F B d C. Demuestr que los triángulos ABF y EBD son semejntes (es decir, demuestr que sus ángulos
. Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin 9 A l F B d C. Demuestr que los triángulos ABF y EBD son semejntes (es decir, demuestr que sus ángulos
La raíz cuadrada de un número es otro nº que al elevarlo al cuadrado nos da el radicando La raíz cuadrado de 9 es 3. Pues 3 2 es
 Curso 1/1 Mtemátics L ríz es l oerción contrri l otenci. c c L ríz cudrd de un número es otro nº que l elevrlo l cudrdo nos d el rdicndo. 9 L ríz cudrdo de 9 es. Pues es 9 9 L ríz cudrd de culquier nº
Curso 1/1 Mtemátics L ríz es l oerción contrri l otenci. c c L ríz cudrd de un número es otro nº que l elevrlo l cudrdo nos d el rdicndo. 9 L ríz cudrdo de 9 es. Pues es 9 9 L ríz cudrd de culquier nº
Manual de teoría: Álgebra Matemática Bachillerato
 Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Identificación de propiedades de triángulos
 Grdo 10 Mtemtics - Unidd 2 L trigonometrí, un estudio de l medid del ángulo trvés de ls funciones Tem Identificción de propieddes de triángulos Nombre: Curso: Ls ctividdes propuests continución se centrn
Grdo 10 Mtemtics - Unidd 2 L trigonometrí, un estudio de l medid del ángulo trvés de ls funciones Tem Identificción de propieddes de triángulos Nombre: Curso: Ls ctividdes propuests continución se centrn
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
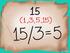 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
1 Halla las razones trigonométricas del ángulo a en cada uno de estos triángulos: a) b) c)
 Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
Pág. 1 Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m 25 m 11,6 cm 8 m 32 m 60 m 2 Midiendo los ldos, hll ls rzones trigonométrics
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Myo de 2015 Operciones Básics con Frcciones Número
1. Números reales. Resuelve BACHILLERATO. Página 25
 . Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin A l F B d C. Demuestr que los triángulos ABF EBD son semejntes (es decir, demuestr que sus ángulos
. Números reles Unidd. Números reles Mtemátics plicds Mtemátics ls I Ciencis Sociles I Resuelve Págin A l F B d C. Demuestr que los triángulos ABF EBD son semejntes (es decir, demuestr que sus ángulos
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
I.E.S. El Burgo de Las Rozas
 I.E.S. El Burgo de Ls Rozs NÚMEROS ENTEROS Y FRACCIONES. Clcul ) [ ( ) ] ( ) [ + (+)]( ) + ( )( ) c) ( ) ( ) ( ) d) [ ( + ( + ( ))) + ] e) ( ) ( ) ( ) f) ( + ) [ + ( ) ( ) + ] g) [ ( 0) ] h) ( + ) [ (
I.E.S. El Burgo de Ls Rozs NÚMEROS ENTEROS Y FRACCIONES. Clcul ) [ ( ) ] ( ) [ + (+)]( ) + ( )( ) c) ( ) ( ) ( ) d) [ ( + ( + ( ))) + ] e) ( ) ( ) ( ) f) ( + ) [ + ( ) ( ) + ] g) [ ( 0) ] h) ( + ) [ (
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN:
 TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
TEMA LOS NÚMEROS REALES. LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los números rcionles: Se crcterizn porque pueden epresrse: En form de frcción, es decir, como cociente de dos números enteros: Q,
NÚMEROS REALES 1. RECTA NUMÉRICA REAL. Indicadores 2. RELACIÓN DE ORDEN. Contenido. Números Reales
 Indicdores NÚMEROS REALES Identific ls propieddes de los números reles, determinndo el vlor de verdd de proposiciones. Clcul el vlor de epresiones lgebrics usndo ls propieddes del vlor bsoluto. Evlú y
Indicdores NÚMEROS REALES Identific ls propieddes de los números reles, determinndo el vlor de verdd de proposiciones. Clcul el vlor de epresiones lgebrics usndo ls propieddes del vlor bsoluto. Evlú y
Se desea calcular la longitud de un lado de una pista de baile de forma cuadrada, cuya área es 16 u 2. Sustituyendo el valor del área
 Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
Núeros irrcionles Algun vez hs utilizdo núeros irrcionles? Se dese clculr l longitud de un ldo de un pist de bile de for cudrd, cuy áre es 6 u A = 6 u x x Definios los eleentos: x = ldo del cudrdo A =
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
Tema: Polinomios y fracciones algebraicas
 Polinomios frcciones lgerics Ejercicios resueltos en los videos: www.josejime.com/videosdemtemtics Ejercicios pr cs resueltos en http://cursosieslsuncion.edu.gv.es/moodle Tem: Polinomios frcciones lgerics.
Polinomios frcciones lgerics Ejercicios resueltos en los videos: www.josejime.com/videosdemtemtics Ejercicios pr cs resueltos en http://cursosieslsuncion.edu.gv.es/moodle Tem: Polinomios frcciones lgerics.
Propiedades de la Potencia. Observación: La potencia no es distributiva con respecto a la suma ni a la resta.
 Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
Propieddes de l Potenci Distributiv con respecto l producto ( = b Distributiv con respecto l división b b Producto de potencis de igul bse n = n + División de potencis de igul bse n n Potenci de potenci
Concepto clave. La derivada de una función se define principalmente de dos maneras: 1. Como el límite del cociente de Fermat ( )( )
 Concepto clve L derivd de un función se define principlmente de dos mners: 1. Como el límite del cociente de Fermt f ( ) lím x f ( x) f ( ) x. Como el límite del cociente de incrementos f ( x) lím x 0
Concepto clve L derivd de un función se define principlmente de dos mners: 1. Como el límite del cociente de Fermt f ( ) lím x f ( x) f ( ) x. Como el límite del cociente de incrementos f ( x) lím x 0
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
Cálculo del valor decimal de una fracción Para obtener el valor de una fracción se divide el numerador entre el denominador. 2 5
 LECCIÓN : FRACCIONES.- QUÉ ES UNA FRACCIÓN? UNA FRACCIÓN ES...... L epresión un prte un cntidd enter. Términos un frcción: DENOMINADOR: Es el número que se coloc bjo l r frcción e indic el número totl
LECCIÓN : FRACCIONES.- QUÉ ES UNA FRACCIÓN? UNA FRACCIÓN ES...... L epresión un prte un cntidd enter. Términos un frcción: DENOMINADOR: Es el número que se coloc bjo l r frcción e indic el número totl
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Multiplicar y dividir radicales
 Multiplicr y dividir rdicles 1 Repso Simplificr: 000 4 0 18 1000 4 4 4 10 4 0 0 ( ( ) 0 8) 0 0 0 8 Multiplicción de rdicles Si y son números reles, n n n n n Podemos decir que cundo multiplicmos rdicles
Multiplicr y dividir rdicles 1 Repso Simplificr: 000 4 0 18 1000 4 4 4 10 4 0 0 ( ( ) 0 8) 0 0 0 8 Multiplicción de rdicles Si y son números reles, n n n n n Podemos decir que cundo multiplicmos rdicles
