6 Sistemas Autoorganizados
|
|
|
- Guillermo de la Cruz Fuentes
- hace 5 años
- Vistas:
Transcripción
1 6 Sstemas Autooganzados 6.. Intoduccón Las edes de neuonas atfcales con aendzae no suevsado se han alcado con éxto a oblemas de econocmento de atones y deteccón de señales. Estas edes constuyen clases o categoías a at de los datos de entada utlzando coelacones o meddas de smltud y tatan de dentfca atcones ótmas en el conunto de datos de entada. En una ed neuonal comettva las undades de salda comten ente sí aa actvase; sólo se actva la de mayo otencal snátco. La dea del aendzae comettvo está ya tazada en los meos tabaos de von de Malsbug (973) sobe la autooganzacón de las células nevosas de la coteza ceebal. En 975, Fukushma ouso el cognton que es una ed comettva multcaa y autooganzada. Wllsha y von de Malsbug (976) tabaaon sobe la fomacón de las conexones neuonales medante autooganzacón y Gossbeg (97, 976) sobe la clasfcacón adatatva de atones. Rumelhat y Zse (985) esecfcaon los tes elementos báscos de una egla de aendzae comettva: Un conunto de neuonas (undades de oceso) que se actvan o no en esuesta a un conunto de atones de entada (estímulos) y que dfeen en los valoes de un conunto de esos snátcos esecífco de cada neuona. Un límte muesto sobe la fueza de cada neuona. Un mecansmo que emte comet a las neuonas aa esonde a un subconunto de entadas de tal manea que una y sólo una neuona o guo se actva. En una ed neuonal comettva smle las neuonas ndvduales aenden a esecalzase sobe conuntos de atones smlaes y, o lo tanto, llegan a se detectoas de caacteístcas de los atones de entada. El algotmo de aendzae comettvo smle se uede contemla como un método aoxmado aa la econstuccón de vectoes de eesentacón, tambén llamados de eoduccón, ototos o códgos, de manea no suevsada. Ahalt, Kshnamuthy and Chen (990) han llevado a cabo la alcacón de las edes neuonales comettvas a la cuantfcacón vectoal (VQ) y han desaollado un nuevo algotmo no suevsado aa el dseño de la tablas de códgos (vectoes de
2 eesentacón o ototos) que conducen a esultados ótmos o cas ótmos. Además, las exeencas comutaconales muestan un conunto de ventaas de dcho algotmo fente al algotmo tadconal LBG (Lnde et al., 980) aa el dseño de cuantfcadoes vectoales. Ya, Zege y Gesho (99) han demostado oedades de la convegenca de la ed autooganzada de Kohonen alcada al dseño de cuantfcadoes vectoales y oonen condcones sobe los aámetos de aendzae. Pal, Bezdek y Tsao (993) han ouesto una genealzacón de la técnca de aendzae de cuantfcacón vectoal (LVQ) aa la fomacón de guos que evta la necesdad de defn un esquema de vecndad y donde los centodes fnales no aece que sean sensbles a los valoes ncales. Xu, Kzyzak y Oa (993) han desaollado un nuevo algotmo, llamado aendzae comettvo con vales enalzados, donde aa cada entada no sólo se modfca la undad de oceso ganadoa aa adatala al atón de entada sno que tambén sus vales se modfcan seaándolas del atón de entada (desaenden) con una tasa de aendzae meno. Ueda y Nakano (994) han esentado un nuevo algotmo de aendzae comettvo con un mecansmo de seleccón basado en el nco de equdstosón aa dseña cuantfcadoes vectoales ótmos; el mecansmo de seleccón le emte al sstema escaa de los mínmos locales. Mao y Jan (996) han ouesto una ed neuonal autooganzada aa aguacones heelsodales que alcan a oblemas de segmentacón de textuas. Po ota ate, el análss de guos clásco (cluste analyss) tata de foma automátcamente guos o categoías (clustes) a at de un conunto de datos de manea que a cada dato o entada le asgna una únca etqueta o guo. La aguacón va a suone una atcón de los datos en categoías o clases con caacteístcas smlaes y se lleva a cabo asgnando datos o atones con atbutos smlaes a la msma clase. Cuando se elge el cteo de mínmos cuadados (mínma dstosón o nco de los M meoes centodes) la fomacón de guos basada en atcones se uede ealza o el algotmo clásco de las K-MEDIAS ouesto o McQueen (967). Uchyama y Abb (994) han demostado la elacón que hay ente la fomacón de guos (clusteng) basada en atcones y la cuantfcacón vectoal; así, el oblema de la fomacón de guos basada en el nco de mínmos cuadados es el msmo que el oblema de la seleccón ótma de los vectoes de eesentacón (tambén llamados de eoduccón o ototos). Además, esentan un algotmo de aendzae comettvo que genea undades donde la densdad de vectoes de entada es más alta y muestan su efcenca como una heamenta aa la fomacón de guos en el esaco de colo que emte la segmentacón de mágenes de colo basada en el cteo de mínmos cuadados. 6.. Redes Neuonales Comettvas no suevsadas Una undad de oceso bnaa (neuonal atfcal) es un dsostvo smle de cálculo que solo uede esenta dos estados, actvo (encenddo) e nactvo (aagado). El estado que esenta deende de las señales que le lleguen de los sensoes de entada o de otas undades de oceso. Cada undad de oceso bnaa,, va a tene asocado un vecto de esos snátcos (,,, N ), con el que va a ondea los valoes que le lleguen de los sensoes de entada.
3 Comenzaemos defnendo lo que se entende o el otencal snátco de una undad de oceso. S a la undad de oceso le llegan N señales, dadas o el vecto (x,x,,x N ), y el vecto de esos snátcos de dcha undad es (,,, N ),entonces el otencal snátco vene dado o la exesón: donde θ = ( N ). h =... x + x + + N x N θ () Defncón Una ed comettva está consttuda o N sensoes de entada, M undades de oceso (neuonas atfcales), y conexones ente cada senso y cada undad de oceso, de manea que la conexón ente el senso y la undad de oceso tene asocado un valo. Paa cada entada ecogda o los sensoes solamente una undad de oceso se actva, aquella que tene el mayo otencal snátco, que se le consdea como la undad ganadoa. Fgua. Aqutectua de la ed. Po lo tanto, s eesentamos el estado de la undad de oceso o la vaable bnaa y, que toma el valo cuando dcha undad está actvada y ceo en caso contao, la dnámca de la comutacón de la ed vene dada o la exesón: { h, h,..., h } s h = max M k y =, =,,,M () 0 en oto caso Cada entada a la ed, es un vecto (x,x,,x N ) R N, que vene ecogdo o los sensoes de entada, y aa el cual se actva una sola undad de oceso, emanecendo las estantes desactvadas. Así, odemos dec que la ed neuonal comettva es una funcón de R N en el conunto {,,,M}, que alca un unto (x,x,,x N ) R N en el valo {,,,M}, cuando sea la undad ganadoa. Dcha funcón oduce una atcón del esaco de los datos (atones) de entada en M egones dsuntas. Dcho de ota foma, la ed comettva agua el conunto de datos de entada en M guos o clases. Cómo se detemnan los esos snátcos? Medante un oceso de aendzae no suevsado. Se etende que se actve aquella undad de oceso cuyo vecto de esos
4 snátcos sea el más aecdo al vecto de entada. De manea que los esos snátcos de cada undad de oceso sean la meo eesentacón del conunto de atones que hacen que esa undad de oceso sea ganadoa. Paa ello sólo tenemos que demosta que la undad ganadoa es aquella cuyo vecto de esos snátcos es el que más se aece al vecto de entada. El aecdo ente el vecto de entada x=(x,x,,x N ) y el vecto de esos snátcos de la undad de oceso, =(,,, N ), vendá dado o la dstanca euclídea ente dchos vectoes, es dec, d ( x, ) = x = ( x ) ( x N N ) A contnuacón vamos a demosta que la undad ganadoa es aquella cuyo vecto de esos snátcos es el que más se aece al vecto de entada. Teoema S es la undad de oceso ganadoa cuando se ntoduce el atón de entada, x=(x,x,,x N ), entonces d( x, ) d( x, k ), k =,,..., M Demostacón: En efecto, ( d( x, )) = x = ( x )'( x ) = x' x ' x + ' = x ' x h x ' x h = d( x, ) k ( ) k Vamos a detemna los esos snátcos de la ed utlzando un conunto de atones de entenamento, que eesentaemos o =(x (, x (,,x N (), k=,,,, y sguendo una egla de aendzae, es dec, una ecuacón matemátca que me esecfque cómo se actualzan los esos snátcos cada vez que ntoduzco, como entada, un atón de entenamento. Los atones de entenamento están aguados en M clases, C,C,,C M, desuntas ente sí, de manea que cada atón de entenamento etenece a una sola clase. Las clases no son conocdas eo tenen que esta fomadas o los atones más cecanos (óxmos) ente s, es dec, más smlaes. El obetvo de la ed comettva con aendzae no suevsado (uesto que no conocemos las clases) es descub o sí msma los guos o clases que foman los atones de entenamento. Paa ello, vamos a eleg un cteo o nco. Dcho cteo va a se el cteo de mínmos cuadados. Según este cteo se tata de enconta M vectoes de esos snátcos,,, M, tales que la funcón suma de eoes cuadátcos sea mínma, es dec, se tata de mnmza la exesón: donde Ε = M = = a x ( ) (3) a s ) C = 0 en oto caso
5 la funcón a ( me ndca s el atón de entada es, o no, de la clase C, eo dcha funcón no es conocda. Vamos a detemna los vectoes de esos snátcos sguendo un oceso teatvo que mnmce la funcón de eo cuadátco en cada aso, es dec, el nuevo vecto detemnado o dcho oceso dsmnuya el eo cuadátco E. A dcho oceso lo llamaemos egla de aendzae. La egla de aendzae uede se de dos fomas, según que actualcemos los esos snátcos cada vez que ntoducmos un atón de entada a la ed, en cuyo caso demos que el aendzae es ndvdualzado o en línea, o actualza los esos snátcos desués de ntoduc todos los atones de entada, en cuyo caso demos que el aendzae es o lotes. Suongamos meo que el aendzae es en línea. Sea el atón que ntoducmos en la ed en la teacón k. Se tata de modfca los vectoes de esos snátcos de modo que se mnmce la exesón del eo que deende de dcho atón: E a x = M = S en la teacón k los vectoes de esos snátcos son (, (,, M ( entonces vamos a detemna los nuevos vectoes en la teacón k+ sguente el método del descenso del gadente que vene dado o la exesón: E ( k + ) = λ donde λ es el aámeto que egula la longtud del aso en la deccón ouesta al gadente. Tenendo en cuenta que E = a k ( ) (4) y que el atón solo uede etenece a una de las M clases, vamos a estma los valoes desconocdos a k,,a k,,a Mk. que son todos nulos menos uno, medante la exesón s <, aˆ = (5) 0 en oto caso A la undad de oceso que le coesonde â =, es dec, aquella cuyo vecto de esos snátcos está más ceca del atón de entada, demos que es la undad ganadoa, y seá la únca que modfque su vecto de esos snátcos, las demás no lo modfcan, como se desende de la exesón (4). Po lo tanto la egla de aendzae es la sguente: donde ( k + ) = + (6)
6 η ( ( k + ) = 0 s s = (7) y es la undad ganadoa, es dec, la de mayo otencal snátco (según el teoema ) Note que η=λ. Al aámeto η lo llamaemos tasa de aendzae, ues confome mayo sea más se modfcan los esos snátcos. Paa entende meo dcha egla de aendzae vamos a ealza la sguente nteetacón geométca. S es la undad ganadoa entonces es dec, ( k + ) = + η ( ) ( k + ) = ( η ) + η( Po lo tanto, el nuevo vecto de esos snátcos (k+) es una combnacón lneal de los vectoes ( y. Quee dec que el vecto de esos snátcos se modfca acecándose al atón de entada, como se muesta en la fgua. Confome mayo es el valo del aámeto de aendzae más se aceca. ( (k+) Fgua. El nuevo vecto de esos snátcos. En cada teacón se ntoduce un atón de entada selecconado aleatoamente. El oceso contnua hasta ealza un númeo total de T teacones, es dec, desués de que cada atón se haya ntoducdo en la ed un númeo detemnado de veces (o eemlo 0 veces). Los valoes ncales de los vectoes de esos snátcos ueden se M atones de entada selecconados aleatoamente. El aámeto de aendzae debe de dsmnuyendo a lo lago de oceso de aendzae hasta alcanza el valo ceo aa el cual la ed dea de aende. Incalmente se uede eleg un valo η o (0,). El valo de dcho aámeto en la teacón k uede ven dado o la exesón:
7 k η = η 0 ( ), k =,,... (8) T que suone un dececmento lneal con esecto al númeo de teacón. El aámeto T es el númeo total de teacones del algotmo hasta conclu el oceso de aendzae. ALGORITMO DE APRENDIZAJE COMPETITIVO INDIVIDUALIZADO Paso 0 Eleg como vectoes de esos snátcos ncales M atones de entenamento y one k=. Paso Eleg aleatoamente un atón de entenamento. Paso Calcula los otencales snátcos h (,h (,,h M (. Paso 3 Detemna la neuona ganadoa, es dec, la de mayo otencal snátco h = máx h M { } Paso 4 Actualza como sgue: [ ( )] ( k + ) = + ( η ) k Paso 5 Calcula la nueva tasa de aendzae según la exesón k η =η 0 ( ) T Paso 6 S k=t aa. Hemos encontado los vectoes snátcos. En oto caso one k=k+ e al aso. Note que la condcón de aada se uede establece fando el númeo total de teacones T o establecendo un valo sufcentemente equeño de la tasa de aendzae. S actualzamos los vectoes de esos snátcos desués de ntoduc los atones de entada, entonces tendemos que mnmza en cada teacón la exesón: Ε = M = = a x ( ) (9) Paa ello utlzamos tambén el método del descenso del gadente. En este caso, E = a ( ) ) = y la egla de aendzae es la sguente:
8 donde ( k + ) = + ( k + ) = η a ( ) ) (0) = y los coefcentes de etenenca de atones a clases, a se estman según la exesón (5). Puede obsevase que cuando = = aˆ ) = aˆ es dec, cuando el vecto de esos snátcos de la undad de oceso es el atón omedo de todos los atones de entada asgnados a dcha undad (aquellos que la hacen ganadoa o su oxmdad con su vecto snátco) entonces (k+)=0, y así no modfca sus esos, ues ha encontado el valo buscado. ALGORITMO DE APRENDIZAJE COMPETITIVO POR LOTES Paso 0 Eleg como vectoes de esos snátcos ncales M atones de entenamento. Paso Calcula los otencales snátcos h (,h (,,h M ( aa cada atón de entada, k=,,,. Paso 3 Detemna la neuona ganadoa, es dec, la de mayo otencal snátco, h = máx{ h } M aa cada atón de entada, k=,,,. Pone ˆ a = 0 s es la undad ganadoa aa ) en oto caso Paso 4 (Regla de aendzae) Actualza cada como sgue: ( k + ) = + η = aˆ [ ) ]
9 Paso 5 Calcula la nueva tasa de aendzae según la exesón k η =η 0 ( ) T Paso 6 S k=t aa. Hemos encontado los vectoes snátcos. En oto caso one k=k+ e al aso. Note que la condcón de aada se uede establece fando el númeo total de teacones T o establecendo un valo sufcentemente equeño de la tasa de aendzae. La eleccón del cteo de mínma suma de eoes cuadátcos (9) es aoada cuando los guos foman nubes comactas que están ben seaadas unas de otas. Sn embago, no es aoada cuando hay una gan dfeenca ente el tamaño de los guos, es dec, ente el númeo de elementos que foman cada guo. En la fgua obsevamos que la aguacón (a), que coesonde a un mayo valo del eo cuadátco total, es la natual, mentas que la (b), que tene un meno eo cuadátco total, no lo es. Fgua. (a) Aguacón natual con valo de E gande. (b) Aguacón con valo de E equeño. Esta stuacón se esenta tambén con la esenca de atones atícos que oducen aguacones que no son adecuadas. Un cteo altenatvo es mnmza el eo cuadátco medo de eesentacón dento de cada guo, es dec, mnmza la funcón: Ε = M n = = a x ( ) sendo n en númeo de atones del guo, es dec, de aendzae o lotes vene dada o la exesón: n = a. En este caso, la egla = ( k + ) = η aˆ ( ) ) () nˆ = es dec,
10 ( k + ) = + η aˆ nˆ = = (-η) + η( nˆ [ ) ] = aˆ ) Obsévese que el nuevo valo del eso snátco es una combnacón lneal de su valo actual con el atón omedo de los atones asgnados a la clase. Asmsmo, la egla de aendzae en línea vene dada o la sguente exesón: η ( k + = nˆ ( ) 0 s s = () sendo la undad ganadoa en esta teacón. Asmsmo, tenendo en cuenta que ( k + ) = + η ( ) nˆ = ( η ) + η( nˆ nˆ vemos que tambén el nuevo valo del vecto snátco es una combnacón lneal de su valo actual con el atón de entada, ondeado de foma nvesa con el tamaño de la clase a la que etenece, como aece lógco. Es dec, se modfca menos el vecto snátco cuantos más atones tenga la clase a la que ha sdo asgnado el atón de entada Redes autooganzadas: La ed de Kohonen En el aendzae comettvo no hemos tendo en cuenta aa nada la oscón físca de las undades de oceso. Sn embago, no ocue así en el ceebo humano, donde neuonas óxmas físcamente esentan caacteístcas y comotamento smlaes. Así, el desaollo de estos modelos está motvado o la manea que tene de oganzase el ceebo. Las dfeentes áeas de la coteza ceebal están caactezadas o la delgadez de sus caas y o el to de neuonas que hay dento de ellas; así tenemos las áeas vsual, audtva, motoa, etc. Cada entada sensoal es alcada al áea coesondente de la coteza ceebal de una manea odenada. Po lo tanto, la localzacón esacal de una neuona dento de un maa toogáfco va a coesonde a un domno o caacteístca atcula de los datos de entada. Así, las undades de oceso se van a coloca sobe una cuadícula o ella ectangula dento de la cual cada undad de oceso va a tene un conunto de undades vecnas, de manea que los esos snátcos de las undades vecnas debeán se aecdos. Esta dea está nsada en los estudos oneos que hzo von de Malsbug (973) ndcando que un modelo del coteza vsual uede no esta comletamente edetemnado genétcamente sno que un oceso de autooganzacón o aendzae uede se esonsable de la odenacón local de las neuonas. Kohonen (98) esentó un modelo sencllo aa la fomacón autooganzada de maas de caacteístcas de los datos de entada del que nos ocuaemos en este caítulo.
11 El oósto de las edes autooganzadas es descub atones sgnfcatvos o caacteístcas en los datos de entada sn ayuda de un ofeso, es dec, medante aendzae no suevsado. Consdeemos M M undades de oceso colocadas sobe una ella ectangula (fgua 3) de manea que el vecto =(, ) nos da oscón de la undad de oceso. Paa establece la nocón de oxmdad ente las undades de oceso defnemos una funcón dstanca, d(, ) =, que nos da la dstanca que hay ente la undad y la undad. Podemos utlza la dstanca euclídea, la dstanca ectangula, d o cualque ota funcón dstanca. d (, ) = ( ) + ( ), (, ) = + A contnuacón defnmos una funcón de vecndad (o funcón de ventana) que tomaá valoes mayoes confome más óxmas estén las dos undades de oceso, es dec, es cualque funcón dececente de la dstanca ente las msmas. Un eemlo de funcón de vecndad es la sguente: Λ (, ) = e, Tambén se uede defn la funcón de vecndad medante una lantlla o ventana, como o eemlo: que nos dce que vale cuando concde con ; vale 0.5 cuando es la undad vecna que está encma, debao, a la deecha o a la zqueda de, y vale ceo aa el esto de los casos. La taea que etendemos ealza es la sguente: Dado un conunto de atones del esaco de entadas, vamos a constu una alcacón ente dcho esaco y el esaco de colocacón de las undades de oceso de manea que cada atón de entada se asgna a una undad de oceso (la undad ganadoa) de foma que atones de entada vecnos según la toología defnda en el esaco de entadas se coesondan con undades de oceso vecnas según la toología defnda ente las undades de oceso. Paa ello seguemos una la egla de aendzae smla a la egla comettva donde habá una undad ganadoa eo ahoa se modfcan tambén los vectoes snátcos de las undades de oceso vecnas, aunque en meno medda, según su oxmdad a la undad ganadoa, acecándose al atón de entada. Ello gaantza que las undades de oceso vecnas tengan sus vectoes snátcos aecdos, es dec, se eseve la toología del esaco de entada. Po eemlo, s se tata de agua fonemas, las señales de sondo coesondentes a la onuncacón del fonema be seá asgnaán a una undad de oceso leana de la undad de oceso coesondente al fonema tu eo vecna de la undad coesondente al fonema ve.
12 Neuonas Sensoes Fgua 3. Rella de colocacón de las undades de oceso. Po lo tanto, s es el vecto de esos snátcos de la undad de oceso coesondente a la conexón ente el senso de entada y dcha undad, la actualzacón del msmo se ealza según la sguente egla de aendzae: (, )( ( )) ( k + ) = + η Λ k, =,,,M M (3) sendo la undad de oceso ganadoa que, de manea smla a la egla del aendzae comettvo, es la de mayo otencal snátco. La nteetacón de esta egla de aendzae es la sguente: Paa cada atón de entada se austa el vecto de esos snátcos de la undad ganadoa de manea que sea más aecdo a dcho atón, es dec, se aceca al msmo; tambén se austan los vectoes snátcos de las undades vecnas, eo en meno medda, deendendo de su oxmdad.
13 Alcacón : Cómo se uede esolve el oblema del vaante con una Red autooganzada de Kohonen? Tenendo en cuenta que la solucón del oblema del vaante es un ecodo (uta) que asa o cada una de las N cudades sólo una vez y egesa a la cudad de atda, vamos a utlza una ed autooganzada con un númeo mayo de undades de oceso (o eemlo, 3N) que cudades a vsta. Las undades de oceso van a esta colocadas sobe una ccunfeenca e gualmente esacadas, de manea que la ccunfeenca nos detemnaá la uta a segu y los esos snátcos de cetas undades de oceso van a llega a se las coodenadas de los ueblos que eesentan. Vamos a toma como funcón de vecndad: Fgua 4. Toología de la ed autooganzada. s θ θ = 0 π / s θ θ = Λ( θ, ) = 3N θ, =,,...,3N 4π /4 s θ θ = 3N 0 en oto caso sendo la neuona ganadoa y θ el ángulo, en adanes, que detemna la oscón de la neuona atfcal con esecto al ogen y el ee de abscsas. Con esta funcón la undad ganadoa comate la mtad de sus ganancas con cuato neuonas vecnas. Así, conseguemos que los vectoes snátcos de neuonas vecnas sean tambén óxmos. Po lo tanto, la dnámca de comutacón es la sguente: Se detemna la undad ganadoa,, es dec, la de mayo otencal snátco: h h sendo = N N x = = y se sgue la sguente egla de aendzae: h /
14 = η Λ( θ, θ )( x ), =,,...,N tomando como conunto de atones de entenamento el conunto de N untos: {(x, y ), =,,...,N} que coesonden a las coodenadas de la cudades. Los vectoes snátcos seán ataídos o los untos donde están stuadas las cudades y cuando se establce la ed los esos snátcos seán las coodenadas de las cudades y la uta vene detemnada o la secuenca de cudades sobe la ccunfeenca. Fgua 5. Evolucón de los esos snátcos. En la fgua 5 esentamos la tayectoa de los esos snátcos y el esultado obtendo cuando el númeo de cudades es gual a 5 y el númeo de undades de oceso es gual a 45. Alcacón : Se dsone de 3 untos (x, y ), =,,...,3, que confguan el contono dfuso de un vaso sanguíneo en una mamogafía (ve la fgua 6). Se tata dseña una ed neuonal que constuya el contono olgonal de 30 vétces que meo se austa al contono del vaso sanguíneo. Fgua 6. Vaso cala en una mamogafía. Se uede utlza una ed autooganzada de Kohonen con tantas neuonas atfcales como vétces tenga el contono olgonal. Como no conocemos la oscón n la oentacón del vaso sanguíneo, la neuonas atfcales estaán colocadas sobe una ccunfeenca e gualmente esacadas (fgua 7). Vamos a toma como funcón de vecndad:
15 Λ θ, θ ) = / 0 s ( θ θ = 0 π s θ θ = 0 en oto caso, =,,...,N sendo la neuona ganadoa y θ el ángulo, en adanes, que detemna la oscón de la neuona atfcal con esecto al ogen y el ee de abscsas. Con esta funcón la undad ganadoa comate la mtad de sus ganancas con dos neuonas vecnas. Así, conseguemos que los vectoes snátcos de neuonas vecnas sean tambén óxmos. neuona θ Fgua 7. Toología de la Red autooganzada. Po lo tanto, la dnámca de comutacón es la sguente: Se detemna la undad ganadoa,, es dec, la de mayo otencal snátco: h h sendo h = N N x = = y se sgue la sguente egla de aendzae: / = η Λ( θ, θ )( x ), =,,...,N tomando como conunto de atones de entenamento el conunto de 3 untos: {(x, y ), =,,...,3} que coesonden a las oscones de los íxeles del contono en la magen de ees. Los vectoes snátcos seán ataídos o los untos que confguan el contono del vaso sanguíneo y nos daán los vétces del contono olgonal (fgua 8).
16 Fgua 8. Auste al contono de vaso sanguíneo de una mamogafía. 6.4 Redes Neuonales Comettvas Suevsadas Como vmos con anteodad, una ed comettva está consttuda o N sensoes de entada, M undades de oceso (neuonas atfcales), y conexones ente cada senso y cada undad de oceso, de manea que la conexón ente el senso y la undad de oceso tene asocado un valo. Paa cada entada ecogda o los sensoes se actva solamente una undad de oceso, aquella que tene el mayo otencal snátco. Po lo tanto, la dnámca de la comutacón de la ed vene dada o la exesón: s h = max{ h, h,..., hm } k y =, =,,,M (4) 0 en oto caso donde el otencal snátco de la undad de oceso vene dado o la exesón con θ = ( N ). x + x + + N x N θ (5) h =... Paa una entada x=(x,x,,x N ) R N se actva la undad de oceso cuyo vecto de esos snátcos =(,,, N ) está más óxmo a x. Así, se uede dec que la ed neuonal comettva es una funcón de R N en el conunto {,,,M}, que alca un unto (x,x,,x N ) R N en el valo {,,,M}, cuando sea la undad ganadoa. Dcha funcón oduce una atcón del esaco de los datos (atones) de entada en M egones dsuntas. Dcho de ota foma, la ed comettva agua el conunto de datos de entada en M guos o clases. Cómo se detemnan los esos snátcos? En este caso dsonemos de un conunto de atones de entenamento etquetados, {(x, z ), =,,,}, es dec, odemos sabe s la undad que se actva coesonde, o no, a la clase a la que etenece el atón
17 de entada. Paa ncooa dcha nfomacón al oceso de aendzae nos basamos en la dea de aceca el vecto snátco al atón de entada seme y cuando la undad ganadoa sea la de la clase coecta (como en el aendzae no suevsado), y en caso contao, cuando la asgnacón sea ncoecta, aleamos el vecto snátco de la undad ganadoa del vecto de entada x. Po lo tanto, en el oceso de aendzae el vecto snátco de la undad ganadoa es ataído o atón de entada s la clasfcacón es coecta, y eeldo s la clasfcacón es ncoecta. Concetamente, cuando el atón de entada x es de la clase s, y la undad ganadoa es la, entonces la egla de aendzae suevsado es la sguente: donde ( k + ) = + (6) η ( ) ( k + ) = η ( () ( k + ) = 0, s = s s s (7) Al aámeto η lo llamaemos tasa de aendzae, ues confome mayo sea más se modfcan los esos snátcos. Sn embago, la evolucón de dcho aámeto duante el oceso de entenamento de la ed no va a se seme dececente como en el caso del aendzae no suevsado. Paa meoa la velocdad de convegenca cada undad de oceso tene su oa tasa de aendzae y evolucona según la sguente egla ouesta o Kohonen (990): η s = s + η η = (8) η s s η Así, se dsmnuye la tasa de aendzae cuando la clasfcacón ha sdo coecta y se aumenta en caso contao. Po lo tanto, vamos a tene una ed neuonal con K m undades de oceso (K o cada clase), las K meas son de la mea clase, y así sucesvamente. El vecto snátco de la undad de oceso vene dado o un ototo de la clase coesondente. Los vectoes snátcos (ototos) se van modfcando según la anteo egla de aendzae y así se obtene el sguente algotmo: Algotmo de aendzae comettvo suevsado Paso : Eleg K ototos ncales aa cada clase (se uede utlza aa ello la ed comettva no suevsada o el algotmo de las K-medas) que consttuán los vectoes snátcos de las undades de oceso.
18 Paso (k-ésma teacón): Seleccona aleatoamente (con eemlazamento)un atón del conunto de entenamento,. Paso 3: Detemna la undad ganadoa medante la exesón h = max h Paso 4 (Fase de aendzae): =,..., M S es la undad ganadoa y coesonde a la msma clase que la entada entonces se modfca el vecto snátco de la msma según la exesón: { } ( k + ) = + η ( ) Las demás undades de oceso no modfcan sus esos. En oto caso se modfca el vecto snátco de la undad ganadoa según la exesón: ( k + ) = η ( ) Las demás undades de oceso no modfcan sus esos. Paso 5: Reet el aso modfcando la tasa de aendzae de la undad ganadoa según la exesón (5). El algotmo fue ouesto o Kohonen (989) y se suele llama Aendzae de la Cuantfcacón Vectoal (Leanng Vecto Quantzaton) o algotmo LVQ. Paa entende meo dcha egla de aendzae vamos a ealza la sguente nteetacón geométca. S es la undad ganadoa y el atón de entada es de la msma clases entonces ( k + ) = + η ( ) = ( η ) + η( Es dec, el nuevo vecto de esos snátcos (k+) es una combnacón lneal de los vectoes ( y. Quee dec que el vecto de esos snátcos se modfca acecándose al atón de entada, como se muesta en la fgua 9. Confome mayo es el valo del aámeto de aendzae más se aceca. En oto caso, entonces ( k + ) = η ( ) = ( +η( ) η(
19 ( (k+) Fgua 9. El nuevo vecto de esos snátcos en caso de ataccón. Es dec, el nuevo vecto snátco se eta del atón de entada en la deccón ouesta, como se muesta en la fgua 0. (k+) ( Fgua 0. El nuevo vecto de esos snátcos en caso de eulsón. La utlzacón de la egla (8) aa modfca la tasa de aendzae uede conduc a valoes altos de la msma, uesto que s una undad de oceso ganadoa se equvoca vaas veces consecutvas en la asgnacón de la clase, entonces s vale 0.00, va asando a los valoes 0., 0.5, 0.43, 0.67, 0.00, 0.50, 0.333, 0.50,,. Po ello, es meo utlza la sguente egla: η s = s + η η = (9) η k ( ) mn, η (0) s s η
RESPUESTAS al examen de MODELOS COMPUTACIONALES 19/VI/2007 E. T. S. de Ingeniería Informática Universidad de Málaga
 REPUETA al examen de MODELO COMPUTACIOALE 9/VI/007 E. T.. de Ingeneía Infomátca Unvesdad de Málaga Cuestones: 5.- Las calfcacones de las asgnatuas son 0 (susenso), (aobado), (notable), 3 (sobesalente)
REPUETA al examen de MODELO COMPUTACIOALE 9/VI/007 E. T.. de Ingeneía Infomátca Unvesdad de Málaga Cuestones: 5.- Las calfcacones de las asgnatuas son 0 (susenso), (aobado), (notable), 3 (sobesalente)
6 Sistemas Autoorganizativos
 6 Sstemas Autooganzatvos 6.1 Intoduccón Las edes de neuonas atfcales con apendzae no supevsado se han aplcado con éxto a poblemas de econocmento de patones y deteccón de señales. Estas edes constuyen clases
6 Sstemas Autooganzatvos 6.1 Intoduccón Las edes de neuonas atfcales con apendzae no supevsado se han aplcado con éxto a poblemas de econocmento de patones y deteccón de señales. Estas edes constuyen clases
La Carga Eléctrica Puntual, es una partícula cuya masa se supone está concentrada en un punto, y en el mismo se concentra su carga eléctrica.
 LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
Profesor Francisco R. Villatoro 15 de Noviembre de 1999 SOLUCIONES. Soluciones de los ejercicios de la tercera relación de problemas.
 Tecea elacón de poblemas Técncas Numécas Pofeso Fancsco R. Vllatoo 5 de Novembe de 999 SOLUCIONES Solucones de los ejeccos de la tecea elacón de poblemas.. Se defne la taza de la matz cuadada A como la
Tecea elacón de poblemas Técncas Numécas Pofeso Fancsco R. Vllatoo 5 de Novembe de 999 SOLUCIONES Solucones de los ejeccos de la tecea elacón de poblemas.. Se defne la taza de la matz cuadada A como la
Una Variante del Teorema de la Amistad. Sampertegui M. 1. (Recibido: 18/04/ Aceptado: 01/07/2016) A Variant of The Theorem of Friendship
 PESQUIMAT, Revsta de la F.C.M. de la Unvesdad Naconal Mayo de San Mac Vol. XIX N ı 2,. 4-25, Julo Dcembe 206 Una Vaante del Teoema de la Amstad Montoo E. Huamán C. Castllo E. Melgaeo G. Amas E. Sametegu
PESQUIMAT, Revsta de la F.C.M. de la Unvesdad Naconal Mayo de San Mac Vol. XIX N ı 2,. 4-25, Julo Dcembe 206 Una Vaante del Teoema de la Amstad Montoo E. Huamán C. Castllo E. Melgaeo G. Amas E. Sametegu
APÉNDICE 1 1. Sistemas de coordenadas
 APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
MOVIMIENTO DE UNA PARTICULA EN EL CAMPO GRAVITACIONAL REAL
 MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
I ESCUELA DE EMPRESARIALES DIPLOMATURA DE EMPRESARIALES ESTADÍSTICA
 Depatamento de Economía Aplcada I EUELA DE EMPREARIALE DIPLOMATURA DE EMPREARIALE ETADÍTIA Ejeccos Resueltos REGREIÓ O LIEAL Y REGREIÓ LIEAL MÚLTIPLE uso 006-00 Escuela de Empesaales Depatamento de Economía
Depatamento de Economía Aplcada I EUELA DE EMPREARIALE DIPLOMATURA DE EMPREARIALE ETADÍTIA Ejeccos Resueltos REGREIÓ O LIEAL Y REGREIÓ LIEAL MÚLTIPLE uso 006-00 Escuela de Empesaales Depatamento de Economía
Reflexión y Refracción
 eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
Coordenadas Generales.
 oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
OBJETIVO. La guía debe ser resuelta de manera grupal o individual y tendrá un valor según lo pactado.
 1 DEPARTAMENTO DE CIENCIAS BÁSICAS CALCULO VECTORIAL Y MULTIVARIADO TALLER 1 CAMPOS VECTORIALES CAMPOS CONSERVATIVOS ROTACIONAL Y DIVERGENCIA BIBLIOGRAÍA SUGERIDA CALCULO JAMES STEWART CALCULO THOMAS INNEY
1 DEPARTAMENTO DE CIENCIAS BÁSICAS CALCULO VECTORIAL Y MULTIVARIADO TALLER 1 CAMPOS VECTORIALES CAMPOS CONSERVATIVOS ROTACIONAL Y DIVERGENCIA BIBLIOGRAÍA SUGERIDA CALCULO JAMES STEWART CALCULO THOMAS INNEY
Ondas. Conceptos básicos
 Ondas. Conceptos báscos IES La Magdalena. Avlés. Astuas Una onda es una petubacón que se popaga. Con la palaba petubacón se quee ndca cualque tpo de alteacón del medo: una ondulacón en una cueda, una sobepesón
Ondas. Conceptos báscos IES La Magdalena. Avlés. Astuas Una onda es una petubacón que se popaga. Con la palaba petubacón se quee ndca cualque tpo de alteacón del medo: una ondulacón en una cueda, una sobepesón
Optica I. seni nsenr seni nsenr nsen(90 i) ncos i seni tg i n 1,5 i 56,30º cosi. nseni sen90 1 seni 0,66 i 41,30º.
 01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
Momento cuadrupolar eléctrico
 Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
v 2 10 AIRE f Un rayo de luz monocromática incide sobre una cara lateral de un prisma de vidrio con índice de
 01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
Tema 7. Regresión Lineal
 Análss de Datos I Esquema del Tema 7 Tema 7. Regesón Lneal 1. INTRODUCCIÓN. IDENTIFICACIÓN DEL MODELO 3. VALORACIÓN DEL MODELO Coefcente de detemnacón Descomposcón de la vaanza del cteo. APLICACIÓN DEL
Análss de Datos I Esquema del Tema 7 Tema 7. Regesón Lneal 1. INTRODUCCIÓN. IDENTIFICACIÓN DEL MODELO 3. VALORACIÓN DEL MODELO Coefcente de detemnacón Descomposcón de la vaanza del cteo. APLICACIÓN DEL
TEMA 3.1 Mecánica del sólido deformable: Análisis de tensiones
 TEMA. Mecánca del sóldo defomable: Análss de tensones Físca Mecánca de las Constuccones ... Intoduccón MECÁNICA DEL MEDIO CONTINUO OBJETIVO: - estudo del compotamento de los medos defomables - establece
TEMA. Mecánca del sóldo defomable: Análss de tensones Físca Mecánca de las Constuccones ... Intoduccón MECÁNICA DEL MEDIO CONTINUO OBJETIVO: - estudo del compotamento de los medos defomables - establece
CAPÍTULO V SISTEMAS DE PARTÍCULAS
 CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA
 PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
Bibliografía. Bibliografía. Fundamentos Físicos de la Ingeniería. Tema 3 Mc Graw Hill. - Tipler. "Física". Cap. 23. Reverté.
 Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Electricidad y Magnetismo Curso 2010/2011
 lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
DISEÑO Y MODIFICACION DE MOLDE INVERSO PARA PROTESIS MEDIANTE HERRAMIENTAS COMPUTACIONALES
 ONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA DISEÑO Y MODIFICACION DE MOLDE INVERSO ARA ROTESIS MEDIANTE HERRAMIENTAS COMUTACIONALES MARÍA CONSUELO DÍAZ WICHMANN Tess aa ota al gado de
ONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA DISEÑO Y MODIFICACION DE MOLDE INVERSO ARA ROTESIS MEDIANTE HERRAMIENTAS COMUTACIONALES MARÍA CONSUELO DÍAZ WICHMANN Tess aa ota al gado de
PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medida del índice de refracción de una lámina de vidrio
 Coodnacón EVAU. Páctcas cuso 2017-18 P2 Objetvo: Detemna el índce de efaccón de un vdo. Fundamento: PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medda del índce de efaccón de una lámna de vdo La ley de la efaccón,
Coodnacón EVAU. Páctcas cuso 2017-18 P2 Objetvo: Detemna el índce de efaccón de un vdo. Fundamento: PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medda del índce de efaccón de una lámna de vdo La ley de la efaccón,
Análisis de Correspondencias Simples ACS. Prof: Salvador Carrasco Arroyo
 Análss de Coespondencas Smples ACS Po: Salvado Caasco Aoyo Mateas Toncales Estadístca I Estadístca II Tema : Análss de Datos Multvaantes Tema : Análss de la Vaanza Tema 3: Técncas de Análss Multvaantes
Análss de Coespondencas Smples ACS Po: Salvado Caasco Aoyo Mateas Toncales Estadístca I Estadístca II Tema : Análss de Datos Multvaantes Tema : Análss de la Vaanza Tema 3: Técncas de Análss Multvaantes
seni nsenr seni nsenr nsen(90 i) ncos i r
 0. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal del
0. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal del
PROBLEMA Flujo uniforme con superficie libre, a lo largo de un plano inclinado.
 1 IQ36A FENOMENOS DE TRANSPORTE, SEMESTRE 08-1 GUIA CAPITULO 6. Cap. 6.: Ecuacón de Nave-Stokes. PROBLEMA 6.-1.- Flujo unfome con supefce lbe, a lo lago de un plano nclnado. Analza el flujo gavtaconal
1 IQ36A FENOMENOS DE TRANSPORTE, SEMESTRE 08-1 GUIA CAPITULO 6. Cap. 6.: Ecuacón de Nave-Stokes. PROBLEMA 6.-1.- Flujo unfome con supefce lbe, a lo lago de un plano nclnado. Analza el flujo gavtaconal
CAPÍTULO 3. Modelos DEA en presencia de entradas y salidas enteras.
 Modelos DEA en pesenca de entadas saldas enteas. CAPÍTULO 3. Modelos DEA en pesenca de entadas saldas enteas.. Intoduccón. En este capítulo del poecto se desaollaán un conunto de modelos DEA cuas entadas
Modelos DEA en pesenca de entadas saldas enteas. CAPÍTULO 3. Modelos DEA en pesenca de entadas saldas enteas.. Intoduccón. En este capítulo del poecto se desaollaán un conunto de modelos DEA cuas entadas
EMPAQUETAMIENTO DE CUERPOS CIRCULARES
 UNIVERSIDAD AUTONOMA DE NUEVO LEON Facultad de Ingeneía Mecánca Eléctca Pogama de Posgado en Ingeneía de Sstemas X VERANO DE INVESTIGACION CIENTIFICA EMPAQUETAMIENTO DE CUERPOS CIRCULARES CHRISTIAN GREGORIO
UNIVERSIDAD AUTONOMA DE NUEVO LEON Facultad de Ingeneía Mecánca Eléctca Pogama de Posgado en Ingeneía de Sstemas X VERANO DE INVESTIGACION CIENTIFICA EMPAQUETAMIENTO DE CUERPOS CIRCULARES CHRISTIAN GREGORIO
DISEÑO DE RUTAS. Presentación. B. Adenso Díaz Universidad de Oviedo. 1. El problema del viajante (TSP)
 Dseño del sstema de utfcacón. Unvesdad de Ovedo. Adenso Díaz http://dv.ms/tssjph DISEÑO DE RUTAS B. Adenso Díaz Unvesdad de Ovedo Dseño del sstema de utfcacón. Unvesdad de Ovedo. Adenso Díaz Pesentacón.
Dseño del sstema de utfcacón. Unvesdad de Ovedo. Adenso Díaz http://dv.ms/tssjph DISEÑO DE RUTAS B. Adenso Díaz Unvesdad de Ovedo Dseño del sstema de utfcacón. Unvesdad de Ovedo. Adenso Díaz Pesentacón.
Campo producido por un sistema de cargas puntuales
 lectcdad Magnetsmo / lectostátca Defncón os conductoes en electostátca. Campo de una caga puntual. Aplcacones de la e de Gauss Integales de supeposcón. Potencal electostátco. Defncón e Intepetacón. cuacones
lectcdad Magnetsmo / lectostátca Defncón os conductoes en electostátca. Campo de una caga puntual. Aplcacones de la e de Gauss Integales de supeposcón. Potencal electostátco. Defncón e Intepetacón. cuacones
TEMA 2. CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS
 TEMA. CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS El capítulo tata de obtene una see de caacteístcas o meddas sobe una vaable aleatoa X que está especfcada a tavés de su funcón de pobabldad y que nos esuman
TEMA. CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS El capítulo tata de obtene una see de caacteístcas o meddas sobe una vaable aleatoa X que está especfcada a tavés de su funcón de pobabldad y que nos esuman
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO.
 Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
CONTENIDO SISTEMA DE PARTÍCULAS. Definición y cálculo del centro de masas. Movimiento del centro de masas. Fuerzas internas y fuerzas externas
 COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
Corrección topográfica de la imagen para mejorar las clasificaciones en zonas montañosas. Por Carmen Recondo. Modelos y métodos.
 Po Camen Recondo Coeccón toogáfca de la magen aa mejoa la clafcacone en zona montañoa. Modelo método. Jonada de Coeccón Toogáfca de mágene de Satélte Camu de Mee. Unvedad de Ovedo. 7 de dcembe de 009.
Po Camen Recondo Coeccón toogáfca de la magen aa mejoa la clafcacone en zona montañoa. Modelo método. Jonada de Coeccón Toogáfca de mágene de Satélte Camu de Mee. Unvedad de Ovedo. 7 de dcembe de 009.
ANEXO 4.1: Centro de masa y de gravedad
 Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
POLARIZACIÓN DEL CAMPO ELECTROMAGNÉTICO
 POLARIZACIÓN DL CAMPO LCTROMAGNÉTICO CARLOS S CHINA POLARIZACIÓN DL CAMPO LCTROMAGNÉTICO Vemos a connuacón cómo el camo elécco y ambén el camo magnéco se olazan elícamene, a a de la exesón maemáca de las
POLARIZACIÓN DL CAMPO LCTROMAGNÉTICO CARLOS S CHINA POLARIZACIÓN DL CAMPO LCTROMAGNÉTICO Vemos a connuacón cómo el camo elécco y ambén el camo magnéco se olazan elícamene, a a de la exesón maemáca de las
Sistemas Lineales de Masas-Resortes 2D
 Sstemas neales de Masas-Resortes D José Cortés Pareo. Novembre 7 Un Sstema neal de Masas-Resortes está consttudo por una sucesón de puntos (de ahí lo de lneal undos cada uno con el sguente por un resorte
Sstemas neales de Masas-Resortes D José Cortés Pareo. Novembre 7 Un Sstema neal de Masas-Resortes está consttudo por una sucesón de puntos (de ahí lo de lneal undos cada uno con el sguente por un resorte
FI1002 Sistemas Newtonianos Judit Lisoni Sección 6
 F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
Para caracterizar completamente una magnitud vectorial, como son la velocidad, aceleración, fuerza, etc, es preciso indicar tres cosas:
 VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
Estructura de la materia 3 Serie 2 Modelo de Thomas-Fermi y Sistemas Atómicos Cátedra: Jorge Miraglia. Segundo cuatrimestre de 2013
 Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
r V CINEMÁTICA DEL SÓLIDO RÍGIDO
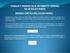 1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
du du du du A du ( u + u) du du du 1. Vector función de un escalar Un vector A es función del escalar u si lo es alguna de sus componentes:
 A UNTE DE: CA M ECA LARE Y ECTRIALE. ecto funcón de un escala Un vecto A es funcón del escala u s lo es alguna de sus componentes: A( A ( + A (j + A (k () Al da valoes a u vamos obtenendo una see de vectoes
A UNTE DE: CA M ECA LARE Y ECTRIALE. ecto funcón de un escala Un vecto A es funcón del escala u s lo es alguna de sus componentes: A( A ( + A (j + A (k () Al da valoes a u vamos obtenendo una see de vectoes
Capítulo 4 CORRIENTE ELÉCTRICA
 Capítulo 4 CORRIENTE ELÉCTRICA 4. Coente eléctca y movmento de cagas. (5.) 4. Resstenca y Ley de Ohm. (5.) 4. La enegía en los ccutos eléctcos. (5.) 4.4 Combnacones de esstencas. (5.4) BIBLIOGRAFÍA. Conduccón
Capítulo 4 CORRIENTE ELÉCTRICA 4. Coente eléctca y movmento de cagas. (5.) 4. Resstenca y Ley de Ohm. (5.) 4. La enegía en los ccutos eléctcos. (5.) 4.4 Combnacones de esstencas. (5.4) BIBLIOGRAFÍA. Conduccón
Solucionario de las actividades propuestas en el libro del alumno
 Soluconao de las actvdades popuestas en el lbo del alumno 7.. LEY DE COULOMB Págna 47. La dstanca que sepaa ente sí los dos potones de un núcleo de helo es del oden de fm (0 5 m). a) Calcula el módulo
Soluconao de las actvdades popuestas en el lbo del alumno 7.. LEY DE COULOMB Págna 47. La dstanca que sepaa ente sí los dos potones de un núcleo de helo es del oden de fm (0 5 m). a) Calcula el módulo
TEMA 0: FÍSICA DE 2º DE BACHILLERATO. CONTENIDOS PREVIOS DE MATEMÁTICAS.
 TEMA 0: FÍSICA DE º DE BACHILLERATO. CONTENIDOS PREVIOS DE MATEMÁTICAS.. TRIGONOMETRÍA.. Raones tgonométcas de n ánglo agdo.. Raones tgonométcas de n ánglo calqea.. Relacones ente las aones tgonométcas.4.
TEMA 0: FÍSICA DE º DE BACHILLERATO. CONTENIDOS PREVIOS DE MATEMÁTICAS.. TRIGONOMETRÍA.. Raones tgonométcas de n ánglo agdo.. Raones tgonométcas de n ánglo calqea.. Relacones ente las aones tgonométcas.4.
Elementos de Aritmética de Computadoras Parte I
 Elementos de Atmétca de Computadoas Pate I M. Vázquez, E. Todoovch, M. Tosn Aqutectua I - Cuso 3 UNICEN Cómputo Atmétco Las peguntas de fondo cuando se aboda el tema de la atmétca de computadoas son: Cómo
Elementos de Atmétca de Computadoas Pate I M. Vázquez, E. Todoovch, M. Tosn Aqutectua I - Cuso 3 UNICEN Cómputo Atmétco Las peguntas de fondo cuando se aboda el tema de la atmétca de computadoas son: Cómo
VECTORES. En este apartado vamos a trabajar exclusivamente con los vectores en el espacio a los que vamos a llamar F 3.
 Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
3.DINÁMICA DE LOS SISTEMAS DE PUNTOS
 3.DINÁMICA DE OS SISTEMAS DE PUNTOS 3.1. Cento de masas. Detemnacón 3.. Movmento del cento de masas. 3.3. Cantdad de movmento. Consevacón de la cantdad de movmento 3.4. Sstema de efeenca del cento de masas
3.DINÁMICA DE OS SISTEMAS DE PUNTOS 3.1. Cento de masas. Detemnacón 3.. Movmento del cento de masas. 3.3. Cantdad de movmento. Consevacón de la cantdad de movmento 3.4. Sstema de efeenca del cento de masas
Electromagnetismo: Electrostática
 lectomagnetsmo: lectostátca 1.1 Intoduccón La electcdad está pesente en nuestas vdas cotdanas. asta pensa en desaollos tecnológcos como la ed de alumbado eléctco o los electodoméstcos, o en fenómenos meteoológcos
lectomagnetsmo: lectostátca 1.1 Intoduccón La electcdad está pesente en nuestas vdas cotdanas. asta pensa en desaollos tecnológcos como la ed de alumbado eléctco o los electodoméstcos, o en fenómenos meteoológcos
Destilación Multicomponente
 Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
ELIMINATORIA, 14 de abril de 2007 PROBLEMAS
 ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
T E M A 7: CONTROLADORES P.I.D.
 E M A 7: CONOLAOES.I...- ISEÑO E SISEMAS E CONOL: En esta tema vamos a combna las caacteístcas de la esuesta temoal y la técnca del luga de la aíces. Lo que etendemos es consegu que el sstema, medante
E M A 7: CONOLAOES.I...- ISEÑO E SISEMAS E CONOL: En esta tema vamos a combna las caacteístcas de la esuesta temoal y la técnca del luga de la aíces. Lo que etendemos es consegu que el sstema, medante
Estadística aplicada a las ciencias sociales. Examen Febrero de 2008 primera semana
 Estadístca alcada a las cencas socales. Examen Febrero de 008 rmera semana Ejercco. - En la sguente tabla, se reresentan los datos de las edades de los trabajadores de una gran emresa. Gruos de edad Nº
Estadístca alcada a las cencas socales. Examen Febrero de 008 rmera semana Ejercco. - En la sguente tabla, se reresentan los datos de las edades de los trabajadores de una gran emresa. Gruos de edad Nº
clasificación digital
 clasfcacón dgtal leccón 3 sumao Intoduccón. Conceptos estadístcos. Fase de entenamento. Fase de clasfcacón. Contol de caldad. La es un poceso de genealzacón temátca que, medante categozacón, convete la
clasfcacón dgtal leccón 3 sumao Intoduccón. Conceptos estadístcos. Fase de entenamento. Fase de clasfcacón. Contol de caldad. La es un poceso de genealzacón temátca que, medante categozacón, convete la
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls. Examen Final
 OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Examen Fnal Pregunta ( punto) Responda brevemente a las sguentes preguntas: a) Cuál es el obetvo en el aprendzae del Perceptron
OPENCOURSEWARE REDES DE NEURONAS ARTIFICIALES Inés M. Galván José M. Valls Examen Fnal Pregunta ( punto) Responda brevemente a las sguentes preguntas: a) Cuál es el obetvo en el aprendzae del Perceptron
r r r dt dt dt El primer sumando es cero porque es el producto vectorial de dos vectores en la misma r r r r r r dt
 MOMENTO ANGULAR O MOMENTO CINÉTICO Se defne momento angula (l ) de una patícula, especto de un punto O, como el poducto vectoal de su vecto de poscón (especto de O) po su momento lneal: l p mv Recodando
MOMENTO ANGULAR O MOMENTO CINÉTICO Se defne momento angula (l ) de una patícula, especto de un punto O, como el poducto vectoal de su vecto de poscón (especto de O) po su momento lneal: l p mv Recodando
LOS SIMBOLOS DE CHRISTOFFEL
 CRLOS S. CHINE LOS SIMBOLOS DE CHRISTOFFEL Lo íbolo ue etudao auí fueon ntoducdo en la ateátca, a fnale del lo XIX, o el aleán Elwn Buno Ctoffel (89 900, ue fue, unto con Benad Reann, el eo en etablece
CRLOS S. CHINE LOS SIMBOLOS DE CHRISTOFFEL Lo íbolo ue etudao auí fueon ntoducdo en la ateátca, a fnale del lo XIX, o el aleán Elwn Buno Ctoffel (89 900, ue fue, unto con Benad Reann, el eo en etablece
Problemas tema 3: Campo eléctrico. Problemas de Campo Eléctrico. Boletín 3 Tema 3. Fátima Masot Conde. Ing. Industrial 2007/08
 /7 Poblemas e Campo léctco Boletín ema Fátma Masot Cone Ing. Inustal 7/8 Poblema Dos patículas cagaas con cagas guales opuestas están sepaaas po una stanca. Sobe la ecta ue las une se coloca una nueva
/7 Poblemas e Campo léctco Boletín ema Fátma Masot Cone Ing. Inustal 7/8 Poblema Dos patículas cagaas con cagas guales opuestas están sepaaas po una stanca. Sobe la ecta ue las une se coloca una nueva
Unidad didáctica 9 La luz y sus propiedades
 Undad ddáctca 9 La luz y sus popedades Solucones undad 9: La luz y sus popedades 2º Bachlleato 200 SOLUCIONES UNIDAD 9. LA LUZ Y SUS PROPIEDADES CUESTIONES INICIALES. )Qué dfeencas hay ente las ondas lumnosas
Undad ddáctca 9 La luz y sus popedades Solucones undad 9: La luz y sus popedades 2º Bachlleato 200 SOLUCIONES UNIDAD 9. LA LUZ Y SUS PROPIEDADES CUESTIONES INICIALES. )Qué dfeencas hay ente las ondas lumnosas
ANEXO A: Método de Interpolación de Cokriging Colocado
 ANEXO A: Método de Interpolacón de Corgng Colocado A. Conceptos Báscos de Geoestadístca Multvarada La estmacón conunta de varables aleatoras regonalzadas, más comúnmente conocda como Corgng (Krgng Conunto),
ANEXO A: Método de Interpolacón de Corgng Colocado A. Conceptos Báscos de Geoestadístca Multvarada La estmacón conunta de varables aleatoras regonalzadas, más comúnmente conocda como Corgng (Krgng Conunto),
dq de x r CAMPO DE UN ANILLO CON CARGA UNIFORME r α P de y de x
 y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
9. Análisis de correspondencias
 9. Análss de oespondenas OBETIVO: Poedmento gáfo paa epesenta asoaones en una tabla de feuenas o onteos. Paa la despón del método nos onentaemos en una tabla de feuenas de dos vaables ategóas o tabla de
9. Análss de oespondenas OBETIVO: Poedmento gáfo paa epesenta asoaones en una tabla de feuenas o onteos. Paa la despón del método nos onentaemos en una tabla de feuenas de dos vaables ategóas o tabla de
el conjunto de puntos del espacio que notaremos por A, B, Dados dos puntos A, B de E
 IES Pade Poeda (Gadx) Matemátcas II UNIDAD 8: VECTORES EN EL ESPACIO.. VECTORES FIJOS EN EL ESPACIO. Sea E el connto de pntos del espaco qe notaemos po A B C K Dados dos pntos A B de E se llama ecto fo
IES Pade Poeda (Gadx) Matemátcas II UNIDAD 8: VECTORES EN EL ESPACIO.. VECTORES FIJOS EN EL ESPACIO. Sea E el connto de pntos del espaco qe notaemos po A B C K Dados dos pntos A B de E se llama ecto fo
TRABAJO Y ENERGIA. 5.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE.
 TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
3.2. MOVIMIENTO DEL CENTRO DE MASAS
 .. MOVIMIENTO DEL CENTRO DE MASAS... S dos cuepos de masas guales se mueven en una tayectoa ectlínea peo en sentdos opuestos con velocdades de gual módulo v, la velocdad del cento de masas del sstema tendá
.. MOVIMIENTO DEL CENTRO DE MASAS... S dos cuepos de masas guales se mueven en una tayectoa ectlínea peo en sentdos opuestos con velocdades de gual módulo v, la velocdad del cento de masas del sstema tendá
Potencial eléctrico. Física II Grado en Ingeniería de Organización Industrial Primer Curso. Departamento de Física Aplicada III Universidad de Sevilla
 Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
UNIDAD 3: CONFIGURACIONES COMPUESTAS
 4/5/009 Undad 3 lectónca UNA 3: ONFGUAONS OMPUSTAS OJTO PATULA l alumn estudaá ls dfeentes tps de cnfguacnes y su análss 3. nexnes en cascada, cascde y alngtn 3. Pa etalmentad 3.3 cut MOS, de fuente de
4/5/009 Undad 3 lectónca UNA 3: ONFGUAONS OMPUSTAS OJTO PATULA l alumn estudaá ls dfeentes tps de cnfguacnes y su análss 3. nexnes en cascada, cascde y alngtn 3. Pa etalmentad 3.3 cut MOS, de fuente de
INTRODUCCIÓN A LA ESTADÍSTICA. CURSO FEBRERO. Código de carrera 43. Código de asignatura 203. n i l
 TUTORÍA DE ITRODUCCIÓ A LA ESTADÍSTICA. º CURSO ECOOMÍA e-mal: mozas@elx.uned.es www.telefonca.net/web/mm ITRODUCCIÓ A LA ESTADÍSTICA. CURSO.000-.00. FEBRERO. Códgo de caea 43. Códgo de asgnatua 03. Peguntas
TUTORÍA DE ITRODUCCIÓ A LA ESTADÍSTICA. º CURSO ECOOMÍA e-mal: mozas@elx.uned.es www.telefonca.net/web/mm ITRODUCCIÓ A LA ESTADÍSTICA. CURSO.000-.00. FEBRERO. Códgo de caea 43. Códgo de asgnatua 03. Peguntas
VISIÓN POR COMPUTADOR
 Escuela Poltécnca Superor de Elche VISIÓN POR COMPUTADOR Grado en Electrónca y Automátca Industral PRÁCTICAS TITERE Práctca 4: Segmentacón, Localzacón y Reconocmento de Obetos Departamento de Ingenería
Escuela Poltécnca Superor de Elche VISIÓN POR COMPUTADOR Grado en Electrónca y Automátca Industral PRÁCTICAS TITERE Práctca 4: Segmentacón, Localzacón y Reconocmento de Obetos Departamento de Ingenería
Tema 4: Intersecciones. Perpendicularidad y mínimas distancias. Paralelismo.
 Tema 4: nteeccone. ependculadad y mínma dtanca. aalelmo. nteeccone. Una nteeccón e el luga geométco de lo punto que petenecen a la vez a todo lo elemento que ntevenen (fgua ). La nteeccón de do plano e
Tema 4: nteeccone. ependculadad y mínma dtanca. aalelmo. nteeccone. Una nteeccón e el luga geométco de lo punto que petenecen a la vez a todo lo elemento que ntevenen (fgua ). La nteeccón de do plano e
Física y Mecánica de las Construcciones ETS Arquitectura/ Curso
 Físca Mecánca de las Constuccones ETS Aqutectua/ Cuso 8-9. MECÁNICA DEL MEDIO CONTINÚO Nuesto objetvo seá estuda el compotamento de los sóldos defomables paa pode establece los cteos que nos pemtan detemnan
Físca Mecánca de las Constuccones ETS Aqutectua/ Cuso 8-9. MECÁNICA DEL MEDIO CONTINÚO Nuesto objetvo seá estuda el compotamento de los sóldos defomables paa pode establece los cteos que nos pemtan detemnan
Junio 2010 OPCIÓN A. A vemos que se diferencian en el cuadrado de la matriz unitaria. Dado que en este caso. por ser la matriz nula.
 Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
( v) Temario. Teorema de la energía a cinética. Objetivos. Leyes Fundamentales de la Mecánica de Fluidos (Tercera Parte) ( )
 Leyes Funamentales e la Mecánca e Fluos (ecea Pate Joseh Foue Sa Canot (1768-1830 (1796-183 emao eoema e la Enegía Cnétca Ecuacón e Conseacón e la Enegía: Foma Integal Foma Local Enegía Potencal Funcón
Leyes Funamentales e la Mecánca e Fluos (ecea Pate Joseh Foue Sa Canot (1768-1830 (1796-183 emao eoema e la Enegía Cnétca Ecuacón e Conseacón e la Enegía: Foma Integal Foma Local Enegía Potencal Funcón
RECOMENDACIÓN UIT-R M.1641
 ec. UIT- M.64 ECOMENDACIÓN UIT- M.64 Metodología de evaluacón de la ntefeenca cocanal paa detemna la dstanca de sepaacón ente un sstema que utlza estacones stuadas en platafomas a gan alttud y un sstema
ec. UIT- M.64 ECOMENDACIÓN UIT- M.64 Metodología de evaluacón de la ntefeenca cocanal paa detemna la dstanca de sepaacón ente un sstema que utlza estacones stuadas en platafomas a gan alttud y un sstema
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
3 - VARIABLES ALEATORIAS
 arte Varables aleatoras rof. María B. ntarell - VARIABLES ALEATORIAS.- Generaldades En muchas stuacones epermentales se quere asgnar un número real a cada uno de los elementos del espaco muestral. Al descrbr
arte Varables aleatoras rof. María B. ntarell - VARIABLES ALEATORIAS.- Generaldades En muchas stuacones epermentales se quere asgnar un número real a cada uno de los elementos del espaco muestral. Al descrbr
CAPÍTULO 11: ÁREAS Y VOLÚMENES (I)
 CAPÍTULO 11: ÁREA Y VOLÚMENE (I) Dante Gueeo-Canduví Piua, 015 FACULTAD DE INGENIERÍA Áea Deatamental de Ingenieía Industial y de istemas CAPÍTULO 11: ÁREA Y VOLÚMENE (I) Esta oba está bajo una licencia
CAPÍTULO 11: ÁREA Y VOLÚMENE (I) Dante Gueeo-Canduví Piua, 015 FACULTAD DE INGENIERÍA Áea Deatamental de Ingenieía Industial y de istemas CAPÍTULO 11: ÁREA Y VOLÚMENE (I) Esta oba está bajo una licencia
ISBN: Wenceslao Segura González
 Wenceslao Segua González TEORÍA DE CAMPO RELATIVISTA Wenceslao Segua González WENCESLAO SEGURA GONZÁLEZ WT Edcones TEORÍA DE CAMPO RELATIVISTA Esta oba se edta bajo una lcenca Ceatve Commons (Atbucón-
Wenceslao Segua González TEORÍA DE CAMPO RELATIVISTA Wenceslao Segua González WENCESLAO SEGURA GONZÁLEZ WT Edcones TEORÍA DE CAMPO RELATIVISTA Esta oba se edta bajo una lcenca Ceatve Commons (Atbucón-
Tema 6 Interacción electrostática
 Tema 6 Inteaccón electostátca 6.. Fueza eléctca. 6.. Campo eléctco. 6.3. Enegía potencal eléctca. 6.4. Potencal eléctco. Relacón ente el potencal y el campo. 6.5. Efecto de los campos eléctcos en mateales.
Tema 6 Inteaccón electostátca 6.. Fueza eléctca. 6.. Campo eléctco. 6.3. Enegía potencal eléctca. 6.4. Potencal eléctco. Relacón ente el potencal y el campo. 6.5. Efecto de los campos eléctcos en mateales.
Cálculo Diferencial e Integral - Plano cartesiano. Funciones. Farith J. Briceño N.
 Cálculo Difeencial e Integal - Plano catesiano. Funciones. Fait J. Biceño N. Objetivos a cubi Código : MAT-CDI. Plano catesiano. Distancia ente dos untos. Punto medio de un segmento. De nición de luga
Cálculo Difeencial e Integal - Plano catesiano. Funciones. Fait J. Biceño N. Objetivos a cubi Código : MAT-CDI. Plano catesiano. Distancia ente dos untos. Punto medio de un segmento. De nición de luga
CASTILLA Y LEÓN / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS II / EXAMEN COMPLETO PRUEBA A
 CASTILLA Y LEÓN / SEPTIEMBRE. LOGSE / MATEMÁTICAS II / EXAMEN CRITERIOS GENERALES DE EVALUACIÓN DE LA PRUEBA: Se obsevaán fundamentalmente los siguientes aspectos: coecta utilización de los conceptos,
CASTILLA Y LEÓN / SEPTIEMBRE. LOGSE / MATEMÁTICAS II / EXAMEN CRITERIOS GENERALES DE EVALUACIÓN DE LA PRUEBA: Se obsevaán fundamentalmente los siguientes aspectos: coecta utilización de los conceptos,
Leyes de Kepler. Antes de demostrar las tres leyes de Kepler, haré un análisis matemático de lo que es una elipse.
 Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
SOLUCIÓN DE LA PRUEBA DE ACCESO
 ísca 1 ísca SOLUCÓN DE LA PRUEBA DE ACCESO AUTOR: Tomás Caballeo Rodíguez Opcón A a) Ley de gavtacón unvesal de Newton: dos masas cualesquea se ataen con una fueza que es dectamente popoconal al poducto
ísca 1 ísca SOLUCÓN DE LA PRUEBA DE ACCESO AUTOR: Tomás Caballeo Rodíguez Opcón A a) Ley de gavtacón unvesal de Newton: dos masas cualesquea se ataen con una fueza que es dectamente popoconal al poducto
0.2.4 Producto de un escalar por un vector. Vector unitario. 0.3 Vectores en el sistema de coordenadas cartesianas.
 VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
Cinemática del Brazo articulado PUMA
 Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
Cnemátca del Brazo artculado PUMA José Cortés Parejo. Enero 8. Estructura del brazo robótco El robot PUMA de la sere es un brazo artculado con artculacones rotatoras que le proporconan grados de lbertad
HTML GUIA 3 PÁRRAFOS, ALINEACION Y LISTAS EN HTML
 HTML GUIA 3 PÁRRAFOS, ALINEACION Y LISTAS EN HTML La mayo pate del contendo de las págnas HTML habtuales está fomado po texto, llegando a se más del 90% del códgo de la págna. Po este motvo, es muy mpotante
HTML GUIA 3 PÁRRAFOS, ALINEACION Y LISTAS EN HTML La mayo pate del contendo de las págnas HTML habtuales está fomado po texto, llegando a se más del 90% del códgo de la págna. Po este motvo, es muy mpotante
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Examen de Física I. 1.- Explique como se puede reducir el siguiente sistema de vectores deslizantes
 Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
Licenciatura en Administración y Dirección de Empresas INTRODUCCIÓN A LA ESTADÍSTICA EMPRESARIAL
 INTRODUCCIÓN A LA ESTADÍSTICA EMPRESARIAL Relacón de Ejerccos nº 2 ( tema 5) Curso 2002/2003 1) Las cento trenta agencas de una entdad bancara presentaban, en el ejercco 2002, los sguentes datos correspondentes
INTRODUCCIÓN A LA ESTADÍSTICA EMPRESARIAL Relacón de Ejerccos nº 2 ( tema 5) Curso 2002/2003 1) Las cento trenta agencas de una entdad bancara presentaban, en el ejercco 2002, los sguentes datos correspondentes
CAPÍTULO III TRABAJO Y ENERGÍA
 TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA
 LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
Gráficos de flujo de señal
 Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente en el análss y dseño de sstemas de control. Otro procedmento alternatvo
Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente en el análss y dseño de sstemas de control. Otro procedmento alternatvo
Formulación Espacial de la Función de Green para el Análisis de Circuitos de Radiofrecuencia en Cavidades de Geometría Arbitraria
 ESCUEL TÉCNIC SUPERIOR DE INGENIERÍ DE TELECOMUNICCIÓN UNIVERSIDD POLITÉCNIC DE CRTGEN Poyecto Fn de Caea Fomulacón Espacal de la Funcón de Geen paa el nálss de Ccutos de Radofecuenca en Cavdades de Geometía
ESCUEL TÉCNIC SUPERIOR DE INGENIERÍ DE TELECOMUNICCIÓN UNIVERSIDD POLITÉCNIC DE CRTGEN Poyecto Fn de Caea Fomulacón Espacal de la Funcón de Geen paa el nálss de Ccutos de Radofecuenca en Cavdades de Geometía
Operadores por Regiones
 Operadores por Regones Fltros por Regones Los fltros por regones ntentan determnar el cambo de valor de un píxel consderando los valores de sus vecnos I[-1,-1] I[-1] I[+1,-1] I[-1, I[ I[+1, I[-1,+1] I[+1]
Operadores por Regones Fltros por Regones Los fltros por regones ntentan determnar el cambo de valor de un píxel consderando los valores de sus vecnos I[-1,-1] I[-1] I[+1,-1] I[-1, I[ I[+1, I[-1,+1] I[+1]
CAPÍTULO 4 MARCO TEÓRICO
 CAPÍTULO 4 MARCO TEÓRICO Cabe menconar que durante el proceso de medcón, la precsón y la exacttud de cualquer magntud físca está lmtada. Esta lmtacón se debe a que las medcones físcas sempre contenen errores.
CAPÍTULO 4 MARCO TEÓRICO Cabe menconar que durante el proceso de medcón, la precsón y la exacttud de cualquer magntud físca está lmtada. Esta lmtacón se debe a que las medcones físcas sempre contenen errores.
