3.DINÁMICA DE LOS SISTEMAS DE PUNTOS
|
|
|
- Marcos Quiroga Castilla
- hace 7 años
- Vistas:
Transcripción
1 3.DINÁMICA DE OS SISTEMAS DE PUNTOS 3.1. Cento de masas. Detemnacón 3.. Movmento del cento de masas Cantdad de movmento. Consevacón de la cantdad de movmento 3.4. Sstema de efeenca del cento de masas 3.. Choque 3.6. Consevacón del momento angula.
2 3.1. DETERMINACIÓN DE CENTRO DE MASAS * El cento de masas de un cuepo o de un sstema de puntos mateales, es el punto de aplcacón de la esultante de todas las fuezas exteoes que actúan sobe el sstema. Suele dentfcase genealmente con el cento de gavedad del cuepo, peo esto sólo ocue cuando: a) E CUERPO ES UN SÓIDO HOMOGÉNEO b) AS FUERZAS EXTERIORES SON PRODUCIDAS POR E CAMPO GRAVITATORIO c) E CUERPO NO ES EXCESIVAMENTE EXTENSO d) SIEMPRE COINCIDE CON E CENTRO DE GRAVEDAD e) OS PUNTOS MATERIAES TIENEN TODOS A MISMA MASA El cento de masas de un sstema de puntos mateales es el punto donde se debe aplca la esultante de todas las fuezas exteoes que actúan sobe el sstema. S las fuezas exteoes que actúan sobe los puntos son úncamente debdas al campo gavtatoo, y el cuepo no es excesvamente extenso de foma que se puedan consdea como fuezas paalelas actuando sobe todos los puntos del sstema, o del cuepo, y dgdas haca el cento de la Tea, en éste caso concdá con el cento de gavedad. En defntva concdán cuando las fueza exteoes sean las debdas a un campo gavtatoo unfome, lo cual exge que el cuepo no sea extenso. as opcones coectas son b y c a masa de la Tea es 81 veces mayo que la de la una y la dstanca ente sus centos es sesenta ados teestes (6 R). El cento de masas del sstema Tea-una ocupa una poscón que está: a) POR ENCIMA DE A SUPERFICIE TERRESTRE b) POR DEAJO DE A SUPERFICIE TERRESTRE c) A A MITAD DE A DISTANCIA ENTRE AMOS CUER- POS CEESTES d) INDETERMINADA, YA QUE DEPENDE DE AS FASES DE A UNA Imagnemos una ecta que une los centos de la Tea y la una y stuemos el ogen en el cento de la Tea; la poscón del cento de masas es: x x, de lo que x M T. + M.6R M.6R M + M 81M + M, 73 T el valo numéco anteo ndca que el cento de masas dsta del cento de la Tea una dstanca que es nfeo al ado teeste, po lo que la solucón coecta de la pueba es la opcón b. R
3 El cento de masas de un sstema fomado po cnco masas puntuales guales colocadas en la foma que ndca la fgua, está en la bsectz del ángulo y a una dstanca del vétce de: a) b) 3 c) 6 d) 8 os vectoes de poscón de las cnco masas son,,, j, j y el vecto cento de masas es:, de lo que m. + m. + m. + m. j + m. j 3 3 j + m a dstanca al ogen de coodenadas es el módulo del vecto de poscón d m En los vétces de un cuadado de lado a se stúan cuato masas tal como ndca la fgua. S en el medo de la ecta que une las masas de 1 kg se stúa una masa de M klos, esulta que el cento de masas del sstema fomado está en el cento de dcho cuadado, po tanto el valo de M es: a) 1 b) c) 3 d) 4 e) El cento de masas está en el punto de coodenadas (a/, a/) y el a aj coespondente vecto de poscón es: + y aplcando la fómula a j 1. a + 1. a + M. a +. aj + 1. aj + M., a aj + M + 6 a (. a + Ma) + (3a + M. ) j, de donde a/ (a+ma)/(m+6); M kg M + 6 a cuestón se puede esolve ápdamente s obsevamos que las dos masas de kg equvalen a una de cuato en el punto de coodenadas (, a/) y que las otas tes masas (1+1+M) tenen su cento de masas en el punto (a, a/) y paa que el conjunto de las cnco masas esté en el cento M debe se kg ya que M. a solucón coecta seá la b.
4 3.1.. Cuato masas puntuales de 1,, 3 y 4 kg espectvamente están stuadas sobe una ccunfeenca de ado undad tal como ndca la fgua. Se añade una qunta masa M, en un luga de la ccunfeenca de modo que el cento de masas de todo el sstema se encuente en el punto O. El valo de la masa añadda M, expesada en klogamos, es: a) / b) 3/ c) 6 d) 8//3 y las coodenadas del luga que ocupa M son: a) 1, ) b), c), d), Desgnamos con M la masa añadda, sendo sus coodenadas de poscón (x, y). Tenendo pesente que el ado de la ccunfeenca es 1, se cumple que x +y 1. El cento de masas del sstema está en O, po tanto a + M. x +. j 4. j + M. y j ( + Mx) + ( + M y) j, ; M + 1 M + 1 M + ; x y + Mx + My 1 x y xy, como x + y 1. Se deduce que, susttuyendo el valo de x + M M kg as solucones coectas seán la a en la pmea, y la c, en la segunda El luga geométco del cento de masas de todos los sstemas fomados po dos puntos mateales de masas m y m stuados espectvamente sobe los ejes X e Y y a gual dstanca del ogen, debeá se: a) A RECTA ISECTRIZ b) A RECTA DE ECUACIÓN yx c) UNA RECTA DE ECUACIÓN yx/3 d) UNA RECTA DE ECUACIÓN y3x/ e) NADA DE O DICHO Aplcando la defncón de vecto de poscón del cento de masas: y consdeando la masa m, con vecto de poscón 1 a, mentas que el de la masa m, es a j, el vecto de poscón del cento de masas del sstema seá: m. a + m. aj a aj +. m + m 3 3 y sus componentes seán : xa/3, ya/3. Elmnado a ente ambas, tendemos que : yx Esta ecuacón seá el luga geométco del cento de masas del sstema, paa cualque valo de a, lo que coesponde a la popuesta b.
5 Dos puntos mateales A y de masas guales están stuados en el plano XY. A vene detemnado po un vecto de poscón cuyo módulo vale y foma un ángulo de 3 gados con el eje X, mentas que se puede enconta en cualque punto del eje Y. Po ello dás que el luga geométco de las poscones del cento de masas del sstema debeá se: a) UNA RECTA QUE PASA POR E PUNTO, CON PENDIENTE /3 b) UNA RECTA PARAEA A EJE Y c) UNA CIRCUNFERENCIA d) UNA PARÁOA e) NADA DE O DICHO Consdeamos los vectoes de poscón de A, v cos3 + sen3 j 3 + j y y j A Aplcando las popedades del cento de masas del sstema, su vecto de poscón: v m 3 v + ( m + m y ) 3 v 1 y + + m En consecuenca, el c.d.m.del sstema, estaá en una ecta que cota al eje X, en el punto 3,paalela al eje Y, y cuya coodenada y seá (,+,y ), tal como ndca la solucón b, excluyéndose todas las demás popuestas. v j En los vétces A, y C del cubo de lado 1m de la fgua, se encuentan tes masas guales, m. Po lo tanto el cento de masas de la fgua debeá esta en: a) E CENTRO DE A DIAGONA DE A CARA SUPERIOR b) E CENTRO DE CUAQUIER DIAGONA DE CUO c) E CENTRO DE A DIAGONA DE A ASE DE CUO d) UNA PERPENDICUAR A CENTRO DE A ASE DE CUO e) E PUNTO (1/3, 1/3, 1/3) Obsevando el esquema de la fgua, las poscones de las masas stuadas en los vétces A,, y C, seán espectvamente: A(1,, ), (,,1) y C (,1,).Po lo tanto el vecto de poscón del cento de masas del sstema m A + m + m C, seá : m. + m. j + m. k j k + + 3m Sólo seá coecta la solucón e, puesto que el cento de la dagonal de la caa supeo del cubo (popuesta a),seía el cento del cuadado, que tendía po coodenadas (1/, 1/, 1),mentas que el de la caa opuesta( dagonal de la base del cubo y popuesta c),seía el punto (1/, 1/,). El cento de cualque dagonal del cubo (popuesta b) coespondeía a un punto de coodenada z1/,y po lo tanto no puede coesponde al dado, mentas que cualque punto de la pependcula a la base del cubo tendía las msmas coodenadas x e y,esto es (1/,1/).
6 En los vétces A, y C del cubo de lado 1m de la fgua, se encuentan tes masas, m, m y 3m, espectvamente. Po lo tanto el cento de masas de la fgua debeá tene como vecto de poscón : 3 4 j k j k 4 j 3k a) + + b) + + c) d) UN VECTOR CUYAS COMPONENTES X,Y,Z SEAN UNA PROGRESIÓN ARITMÉTICA CUYO PRIMER TÉRMINO SEA 3/6, Y RAZÓN 1/6 e) NADA DE O DICHO Obsevando el esquema dado, los vectoes de poscón de las masas stuadas en v v v A, y C seán espectvamente A + k, j + k y C + j. Po lo tanto el vecto de poscón del cento de masas del sstema, m A + m + m C, seá : m.( + k ) + m.( j + k ) + 3m.( + j) j k + + m, que concde 6m 3 6 úncamente con la popuesta b. a pogesón atmétca mplcaía un punto con coodenadas: (3/6,4/6, /6),y pecsamente este oden no se sgue en el c.d.m. de la fgua(4/6,/6,3/6) S tomas un alambe de 7 cm y lo doblas en ángulo ecto de foma que uno de los lados sea de 3cm, dás que el cento de masas de la fgua fomada se encuenta en: a) A ISECTRIZ DE ÁNGUO RECTO b) E VÉRTICE DE ÁNGUO RECTO c) E PUNTO MEDIO DE A RECTA QUE UNE OS DOS EXTREMOS d) A RECTA QUE UNE OS PUNTOS MEDIOS DE OS DOS ADOS, A 14,3 cm DE DE 3 cm. En el esquema de la fgua se obseva que al doblase en ángulo ecto, podemos toma dos pocones de alambe A (la pequeña de 3cm) y (la gande de 4cm), y detemna el cento de masas del sstema fomado po A y, en el sstema de efeenca X/Y, dado. a masa de cada pocón seá la densdad lneal de masa, λ po la longtud coespondente, supuesto que sea homogéneo. Así: v v En A : 1 j, m A 3 λ y En :, m 4 λ A 4λ. + 3λ.1 j 8 4 j Po lo que + 7λ 7 7 El punto que detemna el c.d.m., P (8/7, 4/7), no va a encontase en la bsectz del ángulo ecto, cuya ecuacón xy, no contene a P. No puede esta en el vétce del ángulo ecto (,) n en el punto medo de la v v ecta que une los dos extemos ( + 1 j ), que tampoco contene a P. a dstanca ente P y el punto (,1), seá 8 4 d , 3 cm 7 7 a únca popuesta coecta seá la d.
7 En la fgua se encuenta una vesón smplfcada de la molécula de agua. a longtud del enlace O-H es,984 nm y el ángulo de enlace H-O-H 14,4E. El cento de masas de esta molécula especto a los ejes dbujados están en el eje Y sendo el valo de dcha coodenada expesada en nm: a) -6,3 1-3 b) -4,3 1-3 c) -3, d) -, as coodenadas de poscón de los tes átomos que foman la molécula de agua son: Oxígeno (, ) Hdógeno (3º cuadante): -,984sen(14, 4/), -,984cos(14,4/) Hdógeno (4º cuadante): +,984sen(14,4/), -,984cos(14,4/) a coodenada Y es: Y (m O +m H (-,984cos(14,4/)+ m H (-,984cos(14,4/))/(m O +m H ) a masa del átomo de oxígeno es apoxmadamente 16 veces mayo que la del átomo de hdógeno, po lo que susttuyendo en la fómula anteo esulta: Y (m O +m H (-,984cos(14,4/)+m H (-,984cos(14,4/))/(m O +m H ) m H (-,984cos(14,4/))/18m H -6,3 1-3 nm.es coecta la popuesta a Una baa clíndca de longtud tene una densdad que no es constante a lo lago de ella, sno que cece lnealmente desde un valo ρ en un extemo A hasta en el extemo. El cento de masas de dcha baa está a una dstanca de A gual a: a) / b) 3/7 c) 3/8 d) /8 e) /9 Puesto que la densdad de la baa aumenta lnealmente de un extemo a oto (en A, ρ y en, ρ), la vaacón de la densdad po undad de longtud es ρ /, po consguente la densdad en un luga que dste x del extemo A vale, la densdad en A más la vaacón coespondente, esto es, ρ +( ρ /)x. S consdeamos un tocto de baa que tenga po espeso dx, y dste x, del extemo A de la baa, tendá un volumen Sdx, sendo S la seccón nomal de la baa. a masa de ese tocto de baa es gual a su volumen po su densdad: dm Sdx( ρ + ρ /x) a coodenada x consdeada a lo lago de la baa es: ρ xdm S ρ + x xdx A x, po lo que A x ρ dm S ρ + x dx A A ρ 3 Sρ xdx + S x dx ρ + ρ 3 x, ρ 9 S x dx + S dx + ρ ρ ρ tal como se ndca en e.
8 Se sueldan, una a contnuacón de ota, dos vallas homogéneas A y de la msma longtud peo hechas de dos mateales dfeentes, sendo la densdad de A doble que la de. El cento de masas del conjunto se encuenta a una dstanca del extemo de A gual a: a) / b) 3/7 c) 3/8 d) /6 e) /9 El cento de masas de una baa homogénea se encuenta en el punto medo de la msma. S tomamos como ogen de dstancas el extemo lbe de la baa A, el cento de masas se encuenta a una dstanca /. Como la baa está conectada a contnuacón de la A y tene la msma longtud su cento de masas se encuenta a una dstanca 3/ del extemo lbe de la baa A. Podemos escb paa la poscón del cento de masas del conjunto de las dos baas: x (m A /+m 3/)/(m A +m ) Como la densdad de la baa A es doble que la de, se deduce que la masa de la baa A es doble de la de. Susttuyendo en la ecuacón anteo: x (m /+m 3/)/(m +m ) (+3/)/3 /6. a espuesta coecta es la d Con un alambe fno de seccón constante se moldea una semccunfeenca de ado R. El cento de masas se encuenta en el eje de smetía a una dstanca del cento de la ccunfeenca a la que petenece la fgua gual a: a) R/ b) R/p c) R/p d) R/ Desgnemos con λ la densdad lneal del alambe fno. Consdeemos sobe el msmo un aco nfntesmal que está sustentado po un ángulo d β. a masa de ese tocto nfntesmal es dm densdad longtud, y la longtud está elaconada con el ángulo medante la expesón aco ángulo ado, po tanto: dm λ R d β a poscón del cento de masas sobe el eje Y es: y ydm Peo, sen by/r, despejando yrsenb, sendo y la odenada de dm, fnalmente, ydm λ. Rsenβ. R dβ y R dm R. λdβ a espuesta válda es la b. [ cos β ] R [ β ] dm
9 Calcula el cento de masas de una valla de longtud, no homogénea, cuya densdad lneal vaía con la longtud según la elacón (4-x/) kg/m, sendo x la dstanca desde el extemo más denso a cualque punto de la valla. a densdad lneal mínma de esta valla es de kg/m. El c.d.m. de la valla se encuenta a una dstanca del extemo de mayo densdad lneal. gual a: a),m b) 4,4m c) 6,6m d) 8,8m e) NINGUNO DE OS VAORES DADOS a densdad máxma de la valla se obtene hacendo x, y vale 4 kg/m. a densdad mínma de dcha valla se obtene cuando x 4 1m S tomamos un sstema de efeenca centado en el extemo de la baa de mayo densdad, tal como se muesta en el dbujo, en estas condcones el c.d.m. de la baa, tendá una coodenada 1 x 3 x dm x 4 dx x x 1 1 x x dm 4 dx 4 x 1 la popuesta coecta seá la b , 4 1 m Con un alambe de seccón unfome se moldea una fgua fomada po dos semccunfeencas de ados R y R 1 sendo R 1 R, especto de los ejes dbujados en la fgua dada, la coodenada X del cento de masas es: a) R/ b) R c) R d) 3R e) 4R y la coodenada Y es: a) -R/ b) -R/ c) -R/ d) -3R/ Paa la semccunfeenca de ado R la abscsa de su cento de masas está en la poscón R y paa la de ado R 1 está en la poscón R+R 1 4R S desgnamos con λ a la densdad del alambe, se deduce que las masas son: m 1 Rλ paa la fgua meno y m R 1 λ Rλ paa la mayo. m1r + m 4R R λ + 8 R λ x 3R m + m 3 Rλ 1 Paa calcula la odenada del cento de masas debemos ecoda tal como se hzo en el ejecco que su valo es Rado/. Paa la ccunfeenca meno vale R/ y paa la mayo -R 1 / -4R/ R 4R R 4R m1 m Rλ Rλ R y m + m 3Rλ 1 solucones coectas son la d en la pmea, y la c, en la segunda.
10 * Como ees muy afconado a la físca, has convetdo tu habtacón en una espece de laboatoo de mecánca, con constuccones y dsposcones de objetos en aos equlbos. Paa ematalo decdes hace una mayúscula ecotándola de una catulna, de foma que su pate vetcal sea 4 veces el ancho b, mentas que la base hozontal sólo lo sea 3, y después clavala po su cento de masas, con una chncheta en el maco de madea. Sn embago esta opeacón te va a esulta extemadamente dfícl poque: a) E EQUIIRIO ES INDIFERENTE SI SE CAVA EN CUAQUIER PUNTO DE A PARTE VERTICA b) QUEDARÍA EN EQUIIRIO EN E CENTRO DE A ASE HORIZONTA c) E CENTRO DE MASAS DE A FIGURA NO ESTÁ DENTRO DE EA d) EN UN SISTEMA DE REFERENCIA CENTRADO EN E VÉRTICE INFERIOR IZQUIERDA DE A, E CENTRO DE MASAS TENDRÍA UNA POSICIÓN DADA POR E VECTOR: b +1,b j Paa que el equlbo sea estable es necesao que el cento de gavedad de la fgua, esté po debajo del punto donde se clave la chncheta. Inestable s lo está po encma, e ndfeente s concde con el c.d.g., po lo tanto es necesao detemna dcho punto. Paa ello: a) Fjamos la, en un sstema de efeenca, centado en el vétce de la leta, como ndca la fgua b) Patmos la leta en dos fagmentos A, vetcal y hozontal de foma que la detemnacón de sus c.d.m. sea lo más senclla posble. Consdeando que m supefce po densdad supefcal de masa, detemnaemos tambén las masas de A y. b En A : A b j +, m 4b σ A bj En : b +, m b σ c) Detemnamos el cento de masa del sstema fomado po las masas de A y, conocendo éstas y sus espectvos vectoes de poscón, dado que: Así: b b v 4b σ. + bj + b σ. b + j v b + 1,bj 6b σ as coodenadas del c.d.m. o del c.d.g son: P(b, 1,b) Este luga coesponde a un punto del bode de la en la pate vetcal, po lo cual seá muy dfícl engancha po dcho punto la leta, po lo tanto las solucones a y b, no son coectas, puesto que mplcaía clava la chncheta, po fuea o po debajo de la poscón del c.d.g. S lo son la c, pues P no está dento de la, y la d.
11 De una plancha de catón peda ecotas un cuadado de lado a y un tángulo sósceles de lados guales, y cuya base se adapta al cuadado. a elacón que debeá exst ente y a paa que el cento de masas del sstema esté stuado en el punto medo de la unón de ambas fguas, tal como ndca el esquema debeá se : a) 1 b) 1, c)1,8 d) e)ninguno DE OS VAORES DADOS Como son fguas geométcas planas y homogéneas, un cuadado C y un tángulo T, detemnaemos fundamentalmente el c.d.m. del sstema, que al elmnase la densdad, cumple la condcón:: v SC. C + ST. T (I) ( S supefce) S total Tomamos el sstema de efeenca, de foma que smplfque al máxmo los cálculos de detemnacón del c.d.m. Paa ello, su ogen O, seá el punto medo del lado que une el cuadado con el tángulo sósceles, tal como muesta el dbujo. De esa foma, po las condcones del enuncado, el c.d.m. de la fgua seá O (,) Así paa el cuadado C : c.d.m (, a/). S C a². paa el tángulo T: c.d.m (,-h/3) S T ah/ a altua h del tángulo, se detemnaá a pat del teoema de Ptágoas: h a a 4 4 Aplcando la ecuacón (I). a a. + a. a 4 4 a. 4 6 Supefce total Smplfcando, y sepaando vaables: a²/ (4²-a²)/4, concde con la popuesta c. 13 a 1, 8a que 4, tendemos: S a la plancha cuadada anteo, le ecotas un tángulo sósceles cuya base es un lado a y el vétce un punto P tal que sea el cento de masas de la nueva fgua, la supefce de ésta seá: a) E DOE DE A PARTE EXTRAÍDA b) MENOS DE DOE DE A PARTE EXTRAÍDA c) MÁS DE DOE DE A PARTE EXTRAÍDA d) IGUA A A DE A PARTE EXTRAÍDA e) NINGUNO DE OS VAORES DADOS Esta cuestón la planteaemos como la anteo, con la dfeenca que al se extaída la masa del tángulo sósceles, ésta se consdeaá negatva. Paa smplfca el cálculo, stuaemos el sstema de efeenca de foma que po azones de smetía el c.d.m de la fgua tenga como abscsa, tal como se obseva en la fgua, denomnado h la altua del tángulo. De esta foma el punto P, seá el (,h). Así paa el cuadado C: c.d.m. (,a/); S C a². Paa el tángulo T: c.d.m.(,h/3); S T ah/ S y S aplcamos la fómula y tendemos: S h [a².a/ + (-ah/).h/3]/(a²-ah/). Smplfcando y esolvendo: h²-6ah+3a². S nvaldamos la solucón en la que h>a, tendemos que h,634a. Po lo tanto la supefce extaída (tángulo) seá: a.,634a/,317a², mentas que la de la nueva fgua: a²-,317a²,683a², que es más del doble de la extaída, lo que hace válda sólo la popuesta b.
La Carga Eléctrica Puntual, es una partícula cuya masa se supone está concentrada en un punto, y en el mismo se concentra su carga eléctrica.
 LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
Optica I. seni nsenr seni nsenr nsen(90 i) ncos i seni tg i n 1,5 i 56,30º cosi. nseni sen90 1 seni 0,66 i 41,30º.
 01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
Bibliografía. Bibliografía. Fundamentos Físicos de la Ingeniería. Tema 3 Mc Graw Hill. - Tipler. "Física". Cap. 23. Reverté.
 Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
CAPÍTULO V SISTEMAS DE PARTÍCULAS
 CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
MOVIMIENTO DE UNA PARTICULA EN EL CAMPO GRAVITACIONAL REAL
 MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
r V CINEMÁTICA DEL SÓLIDO RÍGIDO
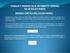 1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
Solucionario de las actividades propuestas en el libro del alumno
 Soluconao de las actvdades popuestas en el lbo del alumno 7.. LEY DE COULOMB Págna 47. La dstanca que sepaa ente sí los dos potones de un núcleo de helo es del oden de fm (0 5 m). a) Calcula el módulo
Soluconao de las actvdades popuestas en el lbo del alumno 7.. LEY DE COULOMB Págna 47. La dstanca que sepaa ente sí los dos potones de un núcleo de helo es del oden de fm (0 5 m). a) Calcula el módulo
CONTENIDO SISTEMA DE PARTÍCULAS. Definición y cálculo del centro de masas. Movimiento del centro de masas. Fuerzas internas y fuerzas externas
 COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
Ondas. Conceptos básicos
 Ondas. Conceptos báscos IES La Magdalena. Avlés. Astuas Una onda es una petubacón que se popaga. Con la palaba petubacón se quee ndca cualque tpo de alteacón del medo: una ondulacón en una cueda, una sobepesón
Ondas. Conceptos báscos IES La Magdalena. Avlés. Astuas Una onda es una petubacón que se popaga. Con la palaba petubacón se quee ndca cualque tpo de alteacón del medo: una ondulacón en una cueda, una sobepesón
dq de x r CAMPO DE UN ANILLO CON CARGA UNIFORME r α P de y de x
 y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
seni nsenr seni nsenr nsen(90 i) ncos i r
 0. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal del
0. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal del
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA
 PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
r r r dt dt dt El primer sumando es cero porque es el producto vectorial de dos vectores en la misma r r r r r r dt
 MOMENTO ANGULAR O MOMENTO CINÉTICO Se defne momento angula (l ) de una patícula, especto de un punto O, como el poducto vectoal de su vecto de poscón (especto de O) po su momento lneal: l p mv Recodando
MOMENTO ANGULAR O MOMENTO CINÉTICO Se defne momento angula (l ) de una patícula, especto de un punto O, como el poducto vectoal de su vecto de poscón (especto de O) po su momento lneal: l p mv Recodando
2 pr = (B.5) Fig. B.2 Tensión longitudinal en un cilindro
 ANXO B- Tensones en un clndo debdas a pesón hdáulca ANXO B Tensones en un clndo debdas a la pesón hdáulca. B.1 Tensones en un anllo ccula y en un clndo de paed guesa S se somete un anllo ccula delgado
ANXO B- Tensones en un clndo debdas a pesón hdáulca ANXO B Tensones en un clndo debdas a la pesón hdáulca. B.1 Tensones en un anllo ccula y en un clndo de paed guesa S se somete un anllo ccula delgado
Matemáticas 4º ESO Fernando Barroso Lorenzo GEOMETRÍA ANALÍTICA. r r
 Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
ANEXO 4.1: Centro de masa y de gravedad
 Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
Sistemas de partículas
 Ssteas de patículas Hasta aquí heos aplcado las leyes de ewton tatando a los objetos coo s fuean patículas puntuales que tenen asa peo no taaño, aunque uchas de las aplcacones se extendían a objetos coo
Ssteas de patículas Hasta aquí heos aplcado las leyes de ewton tatando a los objetos coo s fuean patículas puntuales que tenen asa peo no taaño, aunque uchas de las aplcacones se extendían a objetos coo
TRABAJO Y ENERGIA. 5.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE.
 TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
Reflexión y Refracción
 eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
8. EL CAMPO GRAVITATORIO.
 ísca. 8. El campo avtatoo. 1 Ley e la avtacón unvesal. 8. EL CMPO GVIOIO. Ley e la avtacón unvesal e Newton. Daas os patículas e masas m y m, sepaaas una stanca, la e masa m atae a la e masa m con una
ísca. 8. El campo avtatoo. 1 Ley e la avtacón unvesal. 8. EL CMPO GVIOIO. Ley e la avtacón unvesal e Newton. Daas os patículas e masas m y m, sepaaas una stanca, la e masa m atae a la e masa m con una
Tema 7. Regresión Lineal
 Análss de Datos I Esquema del Tema 7 Tema 7. Regesón Lneal 1. INTRODUCCIÓN. IDENTIFICACIÓN DEL MODELO 3. VALORACIÓN DEL MODELO Coefcente de detemnacón Descomposcón de la vaanza del cteo. APLICACIÓN DEL
Análss de Datos I Esquema del Tema 7 Tema 7. Regesón Lneal 1. INTRODUCCIÓN. IDENTIFICACIÓN DEL MODELO 3. VALORACIÓN DEL MODELO Coefcente de detemnacón Descomposcón de la vaanza del cteo. APLICACIÓN DEL
Problemas de la Unidad 1
 Poblemas de la Unidad.- Dado el vecto a = i + 5 j - k, calcula: a) Sus componentes catesianas, b) Módulo de las componentes catesianas, c) Módulo del vecto a, d) Los cosenos diectoes, e) Ángulo que foma
Poblemas de la Unidad.- Dado el vecto a = i + 5 j - k, calcula: a) Sus componentes catesianas, b) Módulo de las componentes catesianas, c) Módulo del vecto a, d) Los cosenos diectoes, e) Ángulo que foma
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO.
 Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
RELACION DE ORDEN: PRINCIPALES TEOREMAS
 RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
Coordenadas Generales.
 oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
APÉNDICE 1 1. Sistemas de coordenadas
 APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
GEOMETRÍA. 1. Sin resolver el sistema, determina si la recta 2x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia
 Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Potencial eléctrico. Física II Grado en Ingeniería de Organización Industrial Primer Curso. Departamento de Física Aplicada III Universidad de Sevilla
 Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
I ESCUELA DE EMPRESARIALES DIPLOMATURA DE EMPRESARIALES ESTADÍSTICA
 Depatamento de Economía Aplcada I EUELA DE EMPREARIALE DIPLOMATURA DE EMPREARIALE ETADÍTIA Ejeccos Resueltos REGREIÓ O LIEAL Y REGREIÓ LIEAL MÚLTIPLE uso 006-00 Escuela de Empesaales Depatamento de Economía
Depatamento de Economía Aplcada I EUELA DE EMPREARIALE DIPLOMATURA DE EMPREARIALE ETADÍTIA Ejeccos Resueltos REGREIÓ O LIEAL Y REGREIÓ LIEAL MÚLTIPLE uso 006-00 Escuela de Empesaales Depatamento de Economía
Momento cuadrupolar eléctrico
 Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
el conjunto de puntos del espacio que notaremos por A, B, Dados dos puntos A, B de E
 IES Pade Poeda (Gadx) Matemátcas II UNIDAD 8: VECTORES EN EL ESPACIO.. VECTORES FIJOS EN EL ESPACIO. Sea E el connto de pntos del espaco qe notaemos po A B C K Dados dos pntos A B de E se llama ecto fo
IES Pade Poeda (Gadx) Matemátcas II UNIDAD 8: VECTORES EN EL ESPACIO.. VECTORES FIJOS EN EL ESPACIO. Sea E el connto de pntos del espaco qe notaemos po A B C K Dados dos pntos A B de E se llama ecto fo
Tema 4: Intersecciones. Perpendicularidad y mínimas distancias. Paralelismo.
 Tema 4: nteeccone. ependculadad y mínma dtanca. aalelmo. nteeccone. Una nteeccón e el luga geométco de lo punto que petenecen a la vez a todo lo elemento que ntevenen (fgua ). La nteeccón de do plano e
Tema 4: nteeccone. ependculadad y mínma dtanca. aalelmo. nteeccone. Una nteeccón e el luga geométco de lo punto que petenecen a la vez a todo lo elemento que ntevenen (fgua ). La nteeccón de do plano e
W = dw = F.dr. , el trabajo total es la suma de todos los trabajos elementales realizados a lo largo del recorrido determinado por r i
 Físca paa encas e Ingeneía 131 131 Tabajo mecánco Supongamos que una patícula se mueve bajo la accón de una ueza F a lo lago de una tayectoa abtaa, como ndca la gua [13-1] Po dencón: F Se denomna tabajo
Físca paa encas e Ingeneía 131 131 Tabajo mecánco Supongamos que una patícula se mueve bajo la accón de una ueza F a lo lago de una tayectoa abtaa, como ndca la gua [13-1] Po dencón: F Se denomna tabajo
v L G M m =m v2 r D M S r D
 Poblemas de Campo Gavitatoio 1 Calcula la velocidad media de la iea en su óbita alededo del ol y la de la luna en su óbita alededo de la iea, sabiendo que el adio medio de la óbita luna es 400 veces meno
Poblemas de Campo Gavitatoio 1 Calcula la velocidad media de la iea en su óbita alededo del ol y la de la luna en su óbita alededo de la iea, sabiendo que el adio medio de la óbita luna es 400 veces meno
Electromagnetismo: Electrostática
 lectomagnetsmo: lectostátca 1.1 Intoduccón La electcdad está pesente en nuestas vdas cotdanas. asta pensa en desaollos tecnológcos como la ed de alumbado eléctco o los electodoméstcos, o en fenómenos meteoológcos
lectomagnetsmo: lectostátca 1.1 Intoduccón La electcdad está pesente en nuestas vdas cotdanas. asta pensa en desaollos tecnológcos como la ed de alumbado eléctco o los electodoméstcos, o en fenómenos meteoológcos
TEMA 2. MOVIMIENTO EN UNA DIMENSION.
 Tema. Movmento en una dmensón. TEMA. MOVIMIENTO EN UNA DIMENSION. La cnemátca es la ama de la mecánca que estuda la geometía del movmento. Usa las magntudes undamentales longtud, en oma de camno ecodo,
Tema. Movmento en una dmensón. TEMA. MOVIMIENTO EN UNA DIMENSION. La cnemátca es la ama de la mecánca que estuda la geometía del movmento. Usa las magntudes undamentales longtud, en oma de camno ecodo,
CUERPOS REDONDOS. LA ESFERA TERRESTRE
 IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
Junio 2010 OPCIÓN A. A vemos que se diferencian en el cuadrado de la matriz unitaria. Dado que en este caso. por ser la matriz nula.
 Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Tema 7 Geometría en el espacio Matemáticas II 2º Bachillerato 1
 Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
du du du du A du ( u + u) du du du 1. Vector función de un escalar Un vector A es función del escalar u si lo es alguna de sus componentes:
 A UNTE DE: CA M ECA LARE Y ECTRIALE. ecto funcón de un escala Un vecto A es funcón del escala u s lo es alguna de sus componentes: A( A ( + A (j + A (k () Al da valoes a u vamos obtenendo una see de vectoes
A UNTE DE: CA M ECA LARE Y ECTRIALE. ecto funcón de un escala Un vecto A es funcón del escala u s lo es alguna de sus componentes: A( A ( + A (j + A (k () Al da valoes a u vamos obtenendo una see de vectoes
PROYECTO DE TEORIA DE MECANISMOS. Análisis cinemático y dinámico de un mecanismo plano articulado con un grado de libertad.
 Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
Nombre: Mecansmo: PROYECTO DE TEORIA DE MECANISMOS. Análss cnemátco y dnámco de un mecansmo plano artculado con un grado de lbertad. 10. Análss dnámco del mecansmo medante el método de las tensones en
FÍSICA I TEMA 0: INTRODUCCIÓN
 FÍSICA I TEMA 0: INTRODUCCIÓN 1. Expesa en los sistemas cegesimal, intenacional y técnico el peso y la masa de un cuepo de 80 Kg. de masa. CEGESIMAL Centímeto, gamo y segundo. 80 Kg 80 Kg * 1000 g /Kg
FÍSICA I TEMA 0: INTRODUCCIÓN 1. Expesa en los sistemas cegesimal, intenacional y técnico el peso y la masa de un cuepo de 80 Kg. de masa. CEGESIMAL Centímeto, gamo y segundo. 80 Kg 80 Kg * 1000 g /Kg
FUERZA MAGNÉTICA SOBRE UN CONDUCTOR QUE TRANSPORTA CORRIENTE
 UERZA MAGNÉTCA SORE UN CONDUCTOR QUE TRANSPORTA CORRENTE J v d +q J Podemos calcula la fueza magnética sobe un conducto potado de coiente a pati de la fueza qv x sobe una sola caga en movimiento. La velocidad
UERZA MAGNÉTCA SORE UN CONDUCTOR QUE TRANSPORTA CORRENTE J v d +q J Podemos calcula la fueza magnética sobe un conducto potado de coiente a pati de la fueza qv x sobe una sola caga en movimiento. La velocidad
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
6: PROBLEMAS METRICOS
 Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Situaciones 1: Dada una carga eléctrica puntual, determine el campo eléctrico en algún punto dado. r u r. r 2. Esmelkys Bonilla
 Situaciones 1: Dada una caga eléctica puntual, detemine el campo eléctico en algún punto dado. E = k q 2 u 1.- Una caga puntual positiva, situada en el punto P, cea un campo eléctico E v en el punto, epesentado
Situaciones 1: Dada una caga eléctica puntual, detemine el campo eléctico en algún punto dado. E = k q 2 u 1.- Una caga puntual positiva, situada en el punto P, cea un campo eléctico E v en el punto, epesentado
Estructura de la materia 3 Serie 2 Modelo de Thomas-Fermi y Sistemas Atómicos Cátedra: Jorge Miraglia. Segundo cuatrimestre de 2013
 Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
L r p. Teniendo en cuenta que p es el momento lineal (masa por el vector velocidad) la expresión anterior nos queda: L r mv m r v. d L dr dv dt dt dt
 EOEA DE CONSEVACIÓN DE OENO ANGUA: El momento angula se define como: p CASE 4.- EYES DE CONSEVACIÓN eniendo en cuenta que p es el momento lineal (masa po el vecto velocidad) la expesión anteio nos queda:
EOEA DE CONSEVACIÓN DE OENO ANGUA: El momento angula se define como: p CASE 4.- EYES DE CONSEVACIÓN eniendo en cuenta que p es el momento lineal (masa po el vecto velocidad) la expesión anteio nos queda:
CAPÍTULO III TRABAJO Y ENERGÍA
 TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
CAMPO ELÉCTRICO { } ( ) ( ) ( ) ( ) { } 2 { } ( ) ( ) ( ) ( ) ( ) ( ) C
 MPO LÉTRIO Septembe 0. Pegunta B.- Dos esfeas peueñas tenen caga postva. uano se encuentan sepaaas una stanca e cm, exste una fueza epulsva ente ellas e 0,0. alcule la caga e caa esfea y el campo eléctco
MPO LÉTRIO Septembe 0. Pegunta B.- Dos esfeas peueñas tenen caga postva. uano se encuentan sepaaas una stanca e cm, exste una fueza epulsva ente ellas e 0,0. alcule la caga e caa esfea y el campo eléctco
INTRODUCCIÓN A LA ESTADÍSTICA. CURSO FEBRERO. Código de carrera 43. Código de asignatura 203. n i l
 TUTORÍA DE ITRODUCCIÓ A LA ESTADÍSTICA. º CURSO ECOOMÍA e-mal: mozas@elx.uned.es www.telefonca.net/web/mm ITRODUCCIÓ A LA ESTADÍSTICA. CURSO.000-.00. FEBRERO. Códgo de caea 43. Códgo de asgnatua 03. Peguntas
TUTORÍA DE ITRODUCCIÓ A LA ESTADÍSTICA. º CURSO ECOOMÍA e-mal: mozas@elx.uned.es www.telefonca.net/web/mm ITRODUCCIÓ A LA ESTADÍSTICA. CURSO.000-.00. FEBRERO. Códgo de caea 43. Códgo de asgnatua 03. Peguntas
r i r ri r r r = ω v = ω
 MOVIMIENTO de un cuepo TRANSLACIÓN + ROTACIÓN + DEFORMACIÓN 3.11 Gados de lbetad y cnemátca del sóldo ígdo El sóldo ígdo es un modelo de los objetos que pemte descb su foma, tamaño, y otacón. Un cuepo
MOVIMIENTO de un cuepo TRANSLACIÓN + ROTACIÓN + DEFORMACIÓN 3.11 Gados de lbetad y cnemátca del sóldo ígdo El sóldo ígdo es un modelo de los objetos que pemte descb su foma, tamaño, y otacón. Un cuepo
Al estar la fuerza dirigida hacia arriba y la intensidad del campo eléctrica hacia abajo, la carga de la esfera es negativa:
 PROLMS CMPO LÉCTRICO. FÍSIC CHILLRTO. Pofeso: Féli Muñoz Jiménez Poblema 1 Detemina la caga de una peueña esfea cagada de 1, mg ue se encuenta en euilibio en un campo eléctico unifome de 000 N /C diigido
PROLMS CMPO LÉCTRICO. FÍSIC CHILLRTO. Pofeso: Féli Muñoz Jiménez Poblema 1 Detemina la caga de una peueña esfea cagada de 1, mg ue se encuenta en euilibio en un campo eléctico unifome de 000 N /C diigido
 .-. La dencón de choque ontal totalente nelástco es aquel en el que los cuepos que colsonan se acoplan y se ueven con la velocdad del cento de asas..- D. La tecea ley de Newton dce que las uezas ejecdas
.-. La dencón de choque ontal totalente nelástco es aquel en el que los cuepos que colsonan se acoplan y se ueven con la velocdad del cento de asas..- D. La tecea ley de Newton dce que las uezas ejecdas
Examen de Física I. 1.- Explique como se puede reducir el siguiente sistema de vectores deslizantes
 Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA
 LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
IES Menéndez Tolosa Física y Química - 1º Bach Campo eléctrico I. 1 Qué afirma el principio de conservación de la carga eléctrica?
 IS Menéndez Tolosa ísica y Química - º Bach ampo eléctico I Qué afima el pincipio de consevación de la caga eléctica? l pincipio indica ue la suma algebaica total de las cagas elécticas pemanece constante.
IS Menéndez Tolosa ísica y Química - º Bach ampo eléctico I Qué afima el pincipio de consevación de la caga eléctica? l pincipio indica ue la suma algebaica total de las cagas elécticas pemanece constante.
RR 1 Para interpretar los fenómenos de reflexión y refracción de la luz, debemos considerar que la luz se propaga en forma de rayos.
 3. Refaccón de la Luz. Psmas. 3.. Intoduccón. S un ayo de luz que se popaga a tavés de un medo homogéneo ncde sobe la supefce de un segundo medo homogéneo, pate de la luz es eflejada y pate enta como ayo
3. Refaccón de la Luz. Psmas. 3.. Intoduccón. S un ayo de luz que se popaga a tavés de un medo homogéneo ncde sobe la supefce de un segundo medo homogéneo, pate de la luz es eflejada y pate enta como ayo
CÁLCULO VECTORIAL. Operaciones con vectores libres. , siendo las componentes de ( )
 CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
Columna armada del Grupo II (con forros intermedios) sometida a compresión axil y a compresión y tracción axil. Aplicación Capítulos A, B, C, D y E.
 73 EJEMPLO N 13 Columna amada del Gupo II (con foos intemedios) sometida a compesión ail a compesión tacción ail. Aplicación Capítulos A, B, C, D E. Enunciado Dimensiona los codones supeioes e infeioes
73 EJEMPLO N 13 Columna amada del Gupo II (con foos intemedios) sometida a compesión ail a compesión tacción ail. Aplicación Capítulos A, B, C, D E. Enunciado Dimensiona los codones supeioes e infeioes
EJERCICIOS DE GEOMETRÍA ANALITICA DEL ESPACIO
 EJERCICIOS DE GEOMETRÍA ANALITICA DEL ESPACIO Detemina la posición elativa de las siguientes paejas de planos a) 8 ' 4 6 6 b) 6 7 ' 4 c) ' 6 7 d) 4 7 Dado el plano que contenga al punto A(-,, 4), detemina
EJERCICIOS DE GEOMETRÍA ANALITICA DEL ESPACIO Detemina la posición elativa de las siguientes paejas de planos a) 8 ' 4 6 6 b) 6 7 ' 4 c) ' 6 7 d) 4 7 Dado el plano que contenga al punto A(-,, 4), detemina
COLEGIO ESTRADA DE MARIA AUXILIADORA CIENCIA, TRABAJO Y VALORES: MI PROYECTO DE VIDA NIVELACION DE MATEMATICAS GRADO DECIMO (10 )
 COLEGIO ESTRADA DE MARIA AUILIADORA CIENCIA, TRABAJO VALORES: MI PROECTO DE VIDA NIVELACION DE MATEMATICAS GRADO DECIMO (0 ) Fecha: Nombe del estudiante: N O T A La nivelación es en foma de talle donde
COLEGIO ESTRADA DE MARIA AUILIADORA CIENCIA, TRABAJO VALORES: MI PROECTO DE VIDA NIVELACION DE MATEMATICAS GRADO DECIMO (0 ) Fecha: Nombe del estudiante: N O T A La nivelación es en foma de talle donde
Tema 6 Puntos, rectas y planos en el espacio
 Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
IV. Geometría plana. v v2 2. u v = u v cos α
 Talle de Matemáticas 16 IV. Geometía plana IR 2 = {(x, y)/x, y IR} puede identificase con el espacio de vectoes libes del plano utilizando la base canónica: v =(v 1,v 2 )=v 1 (1, 0) + v 2 (0, 1) = v 1
Talle de Matemáticas 16 IV. Geometía plana IR 2 = {(x, y)/x, y IR} puede identificase con el espacio de vectoes libes del plano utilizando la base canónica: v =(v 1,v 2 )=v 1 (1, 0) + v 2 (0, 1) = v 1
Solución al examen de Física
 Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
OBJETIVO. La guía debe ser resuelta de manera grupal o individual y tendrá un valor según lo pactado.
 1 DEPARTAMENTO DE CIENCIAS BÁSICAS CALCULO VECTORIAL Y MULTIVARIADO TALLER 1 CAMPOS VECTORIALES CAMPOS CONSERVATIVOS ROTACIONAL Y DIVERGENCIA BIBLIOGRAÍA SUGERIDA CALCULO JAMES STEWART CALCULO THOMAS INNEY
1 DEPARTAMENTO DE CIENCIAS BÁSICAS CALCULO VECTORIAL Y MULTIVARIADO TALLER 1 CAMPOS VECTORIALES CAMPOS CONSERVATIVOS ROTACIONAL Y DIVERGENCIA BIBLIOGRAÍA SUGERIDA CALCULO JAMES STEWART CALCULO THOMAS INNEY
INSTITUTO DE FÍSICA MECÁNICA NEWTONIANA
 INSTITUT DE FÍSIC ECÁNIC NEWTNIN Cuso 009 Páctico V Sistemas de Patículas y Sistemas ígidos Pate : Sistemas de patículas Ejecicio N o 1 Halla geométicamente, es deci, aplicando popiedades de simetía o
INSTITUT DE FÍSIC ECÁNIC NEWTNIN Cuso 009 Páctico V Sistemas de Patículas y Sistemas ígidos Pate : Sistemas de patículas Ejecicio N o 1 Halla geométicamente, es deci, aplicando popiedades de simetía o
RECTAS EN EL PLANO. r datos, podemos dar la ecuación de dicha recta de varias P o Ecuación vectorial
 RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
. Desarrollando esta ecuación vectorial, obtenemos: a = 3. : a = 2, b =, c = 0, y para w : a = 0, b =, c = -2.
 1 Sean los vectoes: v 1 ( 1, 1, 1) v (,, ) y v (, 1, ) Compueba que foman una base de V. Halla las coodenadas especto de dicha base de los vectoes u ( 1,, ) y w ( 1,, 1). Paa ve si son linealmente independientes
1 Sean los vectoes: v 1 ( 1, 1, 1) v (,, ) y v (, 1, ) Compueba que foman una base de V. Halla las coodenadas especto de dicha base de los vectoes u ( 1,, ) y w ( 1,, 1). Paa ve si son linealmente independientes
CAMPO ELÉCTRICO El signo negativo nos indica que el trabajo se esta realizando en contra el campo por medio de una fuerza exterior.
 MPO LÉTRIO Moelo 08. Pegunta.- onséese una caga puntual n stuaa en el cento e una esfea e ao R 0 cm. Detemne: a) l fluo el campo eléctco a tavés e la supefce e la esfea. b) l tabao ue es necesao ealza
MPO LÉTRIO Moelo 08. Pegunta.- onséese una caga puntual n stuaa en el cento e una esfea e ao R 0 cm. Detemne: a) l fluo el campo eléctco a tavés e la supefce e la esfea. b) l tabao ue es necesao ealza
RECOMENDACIÓN UIT-R M.1641
 ec. UIT- M.64 ECOMENDACIÓN UIT- M.64 Metodología de evaluacón de la ntefeenca cocanal paa detemna la dstanca de sepaacón ente un sstema que utlza estacones stuadas en platafomas a gan alttud y un sstema
ec. UIT- M.64 ECOMENDACIÓN UIT- M.64 Metodología de evaluacón de la ntefeenca cocanal paa detemna la dstanca de sepaacón ente un sstema que utlza estacones stuadas en platafomas a gan alttud y un sstema
Derivando dos veces respecto del tiempo obtenemos la aceleración del cuerpo:
 MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
MMENT ANGULAR: El vecto de posición de un cuepo de 6 kg de masa está dado po = ( 3t 2 6t) i ˆ 4t 3 ˆ j ( en m y t en s). Halla la fueza que actúa sobe la patícula, el momento de fuezas especto del oigen,
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Lección 4: Dinámica de los sistemas de partículas y del sólido rígido
 Leccón 4: Dnámca de ls sstemas de patículas y del sóld ígd.-intduccón..- Mvment del cent de masa de un sstema de patículas. 3.- Mment angula de un sstema de patículas. 4.- Mment angula de un sóld ígd.
Leccón 4: Dnámca de ls sstemas de patículas y del sóld ígd.-intduccón..- Mvment del cent de masa de un sstema de patículas. 3.- Mment angula de un sstema de patículas. 4.- Mment angula de un sóld ígd.
TEMA 6: RENTAS VARIABLES. (1+i) A n-1
 TEMA 6: RENTAS VARIABLES. RENTAS VARIABLES EN GENERAL Son auellas entas en las ue los témnos no son constantes, su valo actual y fnal se calculan a pat del pncpo de euvalenca fnancea, actualzando (valo
TEMA 6: RENTAS VARIABLES. RENTAS VARIABLES EN GENERAL Son auellas entas en las ue los témnos no son constantes, su valo actual y fnal se calculan a pat del pncpo de euvalenca fnancea, actualzando (valo
GEOMETRÍA ANALÍTICA EN EL ESPACIO
 GEOMETRÍ NLÍTI EN EL ESPIO PROUTO ESLR a b a1 b1 + a b + a b (uando sepamos las coodenadas de a y b). a b a b cosx (uando queamos halla el ángulo que foman a y b). uando los vectoes son pependiculaes su
GEOMETRÍ NLÍTI EN EL ESPIO PROUTO ESLR a b a1 b1 + a b + a b (uando sepamos las coodenadas de a y b). a b a b cosx (uando queamos halla el ángulo que foman a y b). uando los vectoes son pependiculaes su
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
PROBLEMA EXAMEN B2. CURSO MODELO A
 OEM EMEN. USO 007-008. MODEO Un clndo hueco y homoéneo, de ado nteo y ado exteo, ueda sn deslza a lo lao de un plano nclnado un ánulo sobe la hozontal. Suponendo que ncalmente se encontaba en eposo, se
OEM EMEN. USO 007-008. MODEO Un clndo hueco y homoéneo, de ado nteo y ado exteo, ueda sn deslza a lo lao de un plano nclnado un ánulo sobe la hozontal. Suponendo que ncalmente se encontaba en eposo, se
Campo eléctrico. 3 m. respectivamente. Calcular el campo eléctrico en el punto A (4,3). Resp.:
 Campo eléctico 1. Calcula el valo de la fueza de epulsión ente dos cagas Q 1 = 200 µc y Q 2 = 300 µc cuando se hallan sepaadas po una distancia de a) 1 m. b) 2 m. c) 3 m. Resp.: a) 540 N, b) 135 N, c )
Campo eléctico 1. Calcula el valo de la fueza de epulsión ente dos cagas Q 1 = 200 µc y Q 2 = 300 µc cuando se hallan sepaadas po una distancia de a) 1 m. b) 2 m. c) 3 m. Resp.: a) 540 N, b) 135 N, c )
Para caracterizar completamente una magnitud vectorial, como son la velocidad, aceleración, fuerza, etc, es preciso indicar tres cosas:
 VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
TEMA 1 CAMPO ELÉCTRICO
 TMA CAMP LÉCTIC. Natualea eléctca de la matea Desde la antgüedad se conoce la estenca de una nteaccón ente los objetos mateales ue no se pone de manfesto en todo momento, como ocue con el peso. ólo se
TMA CAMP LÉCTIC. Natualea eléctca de la matea Desde la antgüedad se conoce la estenca de una nteaccón ente los objetos mateales ue no se pone de manfesto en todo momento, como ocue con el peso. ólo se
CAMPOS ELECTROMAGNÉTICOS Tema 3 Ecuaciones de Maxwell
 CAMPOS ELECTROMAGNÉTICOS Tema Ecuaciones de Mawell P.- En una egión totalmente vacía ha un campo eléctico E = kt uˆ oto magnético con B B =. La magnitud k es constante. Calcula B. = B = ε µ + k k ' P.-
CAMPOS ELECTROMAGNÉTICOS Tema Ecuaciones de Mawell P.- En una egión totalmente vacía ha un campo eléctico E = kt uˆ oto magnético con B B =. La magnitud k es constante. Calcula B. = B = ε µ + k k ' P.-
a) Estudiar su posición relativa en el espacio. b) Calcular las distancias entre ellas. c) Trazar una recta que corte perpendicularmente a ambas.
 º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
XIII.- TEOREMA DEL IMPULSO
 XIII.- TEOREMA DEL IMPULSO http://libos.edsauce.net/ XIII.1.- REACCIÓN DE UN FLUIDO EN MOVIMIENTO SOBRE UN CANAL GUÍA El cálculo de la fueza ejecida po un fluido en movimiento sobe el canal que foman los
XIII.- TEOREMA DEL IMPULSO http://libos.edsauce.net/ XIII.1.- REACCIÓN DE UN FLUIDO EN MOVIMIENTO SOBRE UN CANAL GUÍA El cálculo de la fueza ejecida po un fluido en movimiento sobe el canal que foman los
CAPÍTULO 15: TRIÁNGULOS RECTÁNGULOS
 PÍTULO 15: TRIÁNGULOS RETÁNGULOS Dante Gueeo-handuví Piua, 2015 FULTD DE INGENIERÍ Áea Depatamental de Ingenieía Industial y de Sistemas PÍTULO 15: TRIÁNGULOS RETÁNGULOS Esta oba está bajo una licencia
PÍTULO 15: TRIÁNGULOS RETÁNGULOS Dante Gueeo-handuví Piua, 2015 FULTD DE INGENIERÍ Áea Depatamental de Ingenieía Industial y de Sistemas PÍTULO 15: TRIÁNGULOS RETÁNGULOS Esta oba está bajo una licencia
Lección 2. El campo de las cargas en reposo: campo electrostático.
 Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
Departamento de Física y Química. I. E. S. Atenea (S. S. Reyes, Madrid) Examen de Selectividad de Física. Junio Soluciones
 Examen de Selectividad de Física. Junio 2008. Soluciones imea pate Cuestión.- Un cuepo de masa m está suspendido de un muelle de constante elástica k. Se tia veticalmente del cuepo desplazando éste una
Examen de Selectividad de Física. Junio 2008. Soluciones imea pate Cuestión.- Un cuepo de masa m está suspendido de un muelle de constante elástica k. Se tia veticalmente del cuepo desplazando éste una
Física 2º Bacharelato
 Física º Bachaelato Gavitación 19/01/10 DEPARAMENO DE FÍSICA E QUÍMICA Nombe: 1. Calcula la pimea velocidad obital cósmica, es deci la velocidad que tendía un satélite de óbita asante.. La masa de la Luna
Física º Bachaelato Gavitación 19/01/10 DEPARAMENO DE FÍSICA E QUÍMICA Nombe: 1. Calcula la pimea velocidad obital cósmica, es deci la velocidad que tendía un satélite de óbita asante.. La masa de la Luna
Ejemplos 2. Cinemática de los Cuerpos Rígidos
 Ejemplos. Cinemática de los Cuepos Rígidos.1. Rotación alededo de un eje fijo.1.** El bloque ectangula ota alededo de la ecta definida po los puntos O con una velocidad angula de 6,76ad/s. Si la otación,
Ejemplos. Cinemática de los Cuepos Rígidos.1. Rotación alededo de un eje fijo.1.** El bloque ectangula ota alededo de la ecta definida po los puntos O con una velocidad angula de 6,76ad/s. Si la otación,
U.D. 3. I NTERACCIÓN GRAVITATORIA
 U.D. 3. I NERACCIÓN GRAVIAORIA RESUMEN Ley de gavitación univesal: odos los cuepos se ataen con una fueza diectamente popocional al poducto de sus masas e invesamente popocional al cuadado de la distancia
U.D. 3. I NERACCIÓN GRAVIAORIA RESUMEN Ley de gavitación univesal: odos los cuepos se ataen con una fueza diectamente popocional al poducto de sus masas e invesamente popocional al cuadado de la distancia
CAPITULO 8. DINAMICA DE ROTACIÓN.
 CAPITULO 8. DINAMICA DE ROTACIÓN. Cuando un objeto eal ga alededo de algún eje, su movmento no se puede analza como s fuea una patícula, poque en cualque nstante, dfeentes pates del cuepo tenen velocdades
CAPITULO 8. DINAMICA DE ROTACIÓN. Cuando un objeto eal ga alededo de algún eje, su movmento no se puede analza como s fuea una patícula, poque en cualque nstante, dfeentes pates del cuepo tenen velocdades
Destilación Multicomponente
 Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
TANGENCIAS (Julio Catalán)
 NGENIS (Julio atalán) Los poblemas de tangencia que pueden pesentase son innumeables y van desde los muy sencillos a los más complejos, ecuiéndose paa su solución a pocedimientos muy distintos: desde los
NGENIS (Julio atalán) Los poblemas de tangencia que pueden pesentase son innumeables y van desde los muy sencillos a los más complejos, ecuiéndose paa su solución a pocedimientos muy distintos: desde los
Segunda ley de Newton
 Segunda ley de Newton Fundamento La segunda ley de la mecánica de Newton se expesa matemáticamente. F = ext m a El sumatoio se efiee a las fuezas exteioes. En la páctica, dento de las fuezas exteioes que
Segunda ley de Newton Fundamento La segunda ley de la mecánica de Newton se expesa matemáticamente. F = ext m a El sumatoio se efiee a las fuezas exteioes. En la páctica, dento de las fuezas exteioes que
TEMA 3.2 Mecánica del medio continuo: Análisis de deformaciones
 TEMA. Mecánca del medo contno: Análss de defomacones Físca Mecánca de las Constccones ... Intodccón ESTUDIO DE LOS SÓLIDOS DEFORMABLES: efectos de las feas aplcadas MÉTODO DE TRABAJO: las TENSIONES INTERIORES
TEMA. Mecánca del medo contno: Análss de defomacones Físca Mecánca de las Constccones ... Intodccón ESTUDIO DE LOS SÓLIDOS DEFORMABLES: efectos de las feas aplcadas MÉTODO DE TRABAJO: las TENSIONES INTERIORES
CANARIAS / SEPTIEMBRE 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 CANAIAS / SEPTIEMBE 0. LOGSE / FÍSICA / EXAMEN COMPLETO De las dos opciones popuestas, sólo hay que desaolla una opción completa. Cada poblema coecto vale po tes puntos. Cada cuestión coecta vale po un
CANAIAS / SEPTIEMBE 0. LOGSE / FÍSICA / EXAMEN COMPLETO De las dos opciones popuestas, sólo hay que desaolla una opción completa. Cada poblema coecto vale po tes puntos. Cada cuestión coecta vale po un
1 Halla la mediatriz del segmento AB. 2 Traza la recta perpendicular a la recta r por el punto A.
 1 Halla la mediatiz del segmento. 2 Taza la ecta pependicula a la ecta po el punto. 3 Taza la pependicula a la ecta desde el punto. uál es la distancia del punto a la ecta? 4 Dibuja dos ectas pependiculaes
1 Halla la mediatiz del segmento. 2 Taza la ecta pependicula a la ecta po el punto. 3 Taza la pependicula a la ecta desde el punto. uál es la distancia del punto a la ecta? 4 Dibuja dos ectas pependiculaes
