donde k < 1, tiene una raíz y sólo una. Determinar una sucesión convergente hacía esta raíz.
|
|
|
- María Josefa Camacho Fidalgo
- hace 6 años
- Vistas:
Transcripción
1 Hoja d roblmas Aálss III 9. Dmostrar qu la cuacó a a dod <, t ua raíz y sólo ua. Dtrmar ua sucsó covrt hacía sta raíz. Solucó: La cuacó a quval a: a a a Sa a a Estudmos 6 t u mámo y. or lo tato: < <, cualqura qu sa R. Alcado l método d tracó, ud asurars la stca d ua úca raíz d la cuacó. S costruy ua sucsó covrt haca dcha raíz ldo u uto R arbtraro y tomado dsués:. /
2 9. Dmostrar qu la cuacó c s, dod < c <, t ua raíz y sólo ua. artdo d u valor cualqura R, s costruy la sucsó mdat la órmula c s,, robar qu sta sucsó covr hacía la raíz. Solucó: Vamos rmr luar qu la sucsó s covrt. ara llo, tommos c s : tomado valors absolutos: Sa Etocs: ξ, ξ ], [ c cos ξ c d c s c c cd c d. c d Co ayuda d sta dsualdad, comrobarmos qu la sucsó satsac l crtro d Cauchy: m m > m m c d m m c c c m... m c c d c c c c d c m m d c c < d c m d... c d y usto qu < c <, s vdt qu m ε smr qu sa m, v. Así us, la sucsó covr. Llamarmos a lm. A cotuacó, comrobmos qu a s ua raíz d la cuacó c s : /
3 Como s cotua, s vrca qu lm a. ro lm lm a, así qu rsulta a a, qu s lo qu quríamos robar. Falmt, dmostrarmos qu la raíz d la cuacó s úca: S b us otra raíz, tdríamos qu b b, así qu b a b - a ξ b a ξ b a < c b a < b a, lo cual s ua cotradccó. 9. Sa ua ucó ral cova dda u trvalo I d la rcta ral. Sa,..., utos d I y λ,...λ S d:.º robar qu utos dl trvalo ], [ λ I.º Dmostrar qu λ λ.º Establcr la dsualdad lo λ tals qu. λ lo Solucó:.º Sa α y β l mor y l mayor d los úmros,..., rsctvamt. Es claro qu El uto α αλ λ β λ β λ, or star comrddo tr α y β rtcrá al Itrvalo I..º ara la dsualdad s crta or dcó d ucó cova. Suoamos > y razomos or duccó. Admtdo qu la dsualdad s vrca ara robémosla ara. S t d dod s dduc qu l uto λ α λ λ β λ λ λ λ rtc al trvalo I, sdo λ. Como λ / λ, la hótss d duccó os rmt scrbr odo λ λ λ / λ λ λ / λ λ /
4 λ λ λ λ λ y obsrvado qu λ λ tdrmos, or sr ua ucó cova, qu λ λ λ λ λ Utlzado u rsultado obtdo más arrba coclumos qu λ λ λ λ qudado la rodad dmostrada ara y co llo stablcda ral..º Alcado l rsultado atror a la ucó - lo qu s cova tdrmos lo λ λ lo d dod rsulta la dsualdad a dmostrar multlcado or. 96. Escrbr l dsarrollo d Taylor d la ucó lo l uto hasta l luar d las drvadas d ord, co dvrsas órmulas dl térmo comlmtaro. Solucó: La órmula d Taylor hasta las drvadas d ord s o T!!! E dod T rrsta l térmo comlmtaro. Calculmos las drvadas qu aarc: lo lo lo lo /
5 lo lo 6lo E l uto, s t or lo tato:,,, 6 6 lo T T!!! Darmos dos ormas dsttas dl térmo comlmtaro: a Térmo comlmtaro d Lara: c T c 6lo c, < c <!! c b Térmo comlmtaro d Cauchy: c c T c 6lo c!! c 97. Escrbr l dsarrollo d MacLaur, d la ucó hasta l luar d las drvadas d ord. Solucó: El dsarrollo d MacLaur d srá: dod ], [!! 9! ξ! ξ. Es csaro calcular las drvadas sucsvas d. Sa. Las drvadas sucsvas d so: co /
6 6/!! > Rsulta tocs qu la úca drvada d qu o s aula ara s!. Vamos ahora ua mara d calcular las drvadas d, tdo cuta qu la órmula d MacLaur qu vamos a mlar, dchas drvadas hasta l ord 9 stá artcularzadas ara : las drvadas suts d ud calculars alcado la órmula d Lbtz sobr la drvada -sma d u roducto. ara smlcar las otacos, llamarmos. Etocs, s dcr, la úca drvada d qu o s aula s! usto qu: rsulta tocs qu: ya qu stas drvadas o aarc ú térmo. rsó la qu s aula todos los sumados X salvo l rmro. or tato:!
7 Obsérvs qu, hasta l ord, s aula todas las drvadas d. or lo tato las drvadas suts srá ulos todos los roductos los qu ura alua drvada d d ord mor qu l quto, o b alua drvada d d ord dstto dl cuarto. 6 6, , , , tdo cuta qu... ara todo, la rsó atror s aulará todos los térmos los qu aarzca ua drvada d d ord mayor o ual qu. or lo tato: Susttuydo la órmula d MacLaur, rsulta almt!! 9 9! 9 ξ ξ, ξ ], [ 98.Obtr l dsarrollo d MacLaur, d las suts ucos lo, α co l térmo comlmtaro d Cauchy. La drvada -sma d la ucó lo s obt s dcultad calculado las rmras y alcado l método d duccó. Rsulta sr! ara,,... Sus valors l uto so!. or cosut l dsarrollo d MacLaur d sta ucó co l térmo comlmtaro d Cauchy srá: 7/
8 lo... θ θ θ dod θ s crto úmro dl trvalo ],[. α La drvada -sma d la ucó bómca, dod α s u umro ral cualqura, s obt áclmt como l caso atror, rsultado α α α... α α ara,,... Sus valors l uto so omos or dcó α α α... α α α α... α! ralzado así la otacó d los úmros combatoros ordaros. El dsarrollo d MacLaur d ustra ucó, co l térmo comlmtaro d Cauchy s: α α α α... α θ θ α dod θ s crto úmro dl trvalo ],[. 99.Hacdo uso d la órmula d Taylor ara la ucó calcular aromadamt,. Stuado l térmo comlmtaro l luar d las drvadas trcras, stmar l rror comtdo. Solucó: Suodrmos coocdo l dsarrollo d Taylor d la ucó r. Tomado dcho dsarrollo r, rsulta: co < ξ <, y també! m ξ!! 8/
9 m 8 Tomado l dsarrollo d Taylor, 8!,,, T,,9 T,, T or lo tato:,,9 El rror comtdo s rcsamt l térmo comlmtaro: usto qu: T ξ, co <ξ <,!! ξ 9 8 ξ ξ Obtmos, como cota dl rror comtdo: E!. Dtrmar las asítotas y ramas arabólcas d la curva: Solucó: y cos s El camo d stca d sta curva s todo R, y admás s ródca d ríodo ya qu: cos s cos s or lo tato, os lmtarmos a rrstar rácamt la ucó l trvalo [-,]. Corts co los js: ara s y, así qu asa or,. ara y, rsulta la cuacó cos s o b: 9/
10 cos s s s s qu s ua cuacó d sudo rado s cuyas raícs so: ± ± s la solucó s o os srv orqu > así us, rsulta s, qu roorcoa dos valors d [-,], arcs. Es scllo comrobar qu sta curva o t asítotas. Mámos, mímos y utos d ló: y - s cos - s Calculmos los valors d qu aula y : y roorcoa la cuacó: cos s s dcr: cos o b s cuyas raícs so, l trvalo [-,],,,,. 6 6 Hmos d studar ahora l so d y : y - cos s 8 s s y así qu > corrsod a u mímo y 6 > y < y < mímo mámo mámo or lo tato, hay mímo rlatvo los utos,, los utos,,. 6 y u mámo rlatvo Los osbls utos d ló so los valors d qu aula la drvada suda: y roorcoa la cuacó /
11 cuyas raícs so: 8s s qu corrsod a cuatro valors d. s ± 8. Calcular sd or l método d las sumas d Rma, dvddo l trvalo [, arts uals. Solucó: S dvdmos l trvalo arts uals tdrmos qu: sd lm j j s S llamamos h, calculmos la suma j sjh sh sh... sh ara llo, mlarmos la ualdad: h cos hcos h sh s Dado a los valors,...,, s obt: h cos h cos h sh s h cos h cos h sh s... h cos h cos h s h s y sumado mmbro a mmbro stas ualdads: /
12 h cos h cos h s sh sh... s h d dod: h cos cos s h s h... s h h s Susttuydo st rsultado : sd lm cos cos s lm cos cos lm cos cos.. Estudar l cálculo d los suts límts, or l método d las sumas d Rma.º lm j.º lm j j j j Solucó:.º lm lm j j j j / d [ lo ] lo lo lo.º j j lm lm j j lm j j j 6 m lm lm 6 6 /
13 Obsérvs qu, l cálculo d st límt o ud mlars l método d las sumas j j d Rma orqu o corrsod a la suma d Rma d ua j tral roa. /
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Análisis Estadístico de Datos Climáticos
 Aálss Estadístco d Datos Clmátcos Rgrsó lal smpl (Wlks, cap. 6.) Vo Storch ad Zwrs (Cap. 8) 05 Rgrsó La rgrsó, gral, s utlza habtualmt para stmar modlos paramétrcos d la rlacó tr varabls ua scala cotua,
Aálss Estadístco d Datos Clmátcos Rgrsó lal smpl (Wlks, cap. 6.) Vo Storch ad Zwrs (Cap. 8) 05 Rgrsó La rgrsó, gral, s utlza habtualmt para stmar modlos paramétrcos d la rlacó tr varabls ua scala cotua,
variables aleatorias discretas, la función de probabilidad conjunta del vector aleatorio ( X,..., se define como: ) A
 cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
a a lim i) L< 1 absoluta convergencia absoluta convergencia convergencia condicional divergencia > r.
 (Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
(Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
2.8.3 Solución de las ecuaciones diferenciales lineales no homogéneas por el método de variación de parámetros
 .8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
Análisis del caso promedio El plan:
 Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
Capítulo 4: Rotaciones Multidimensionales con Operaciones Vectoriales
 Cítulo 4: Rotcos Multdmsols co Orcos ctorls Como s vo l cítulo tror s ud hcr rotr u ojto l sco D roorcodo - utos o cohrlrs s dcr s roorco l j d rotcó l cul s l rrstcó d u sml -D. E st cítulo s lz y td
Cítulo 4: Rotcos Multdmsols co Orcos ctorls Como s vo l cítulo tror s ud hcr rotr u ojto l sco D roorcodo - utos o cohrlrs s dcr s roorco l j d rotcó l cul s l rrstcó d u sml -D. E st cítulo s lz y td
EXPONENTES Y POTENCIAS Muchos números se expresan en forma más conveniente como potencias de 10. Por ejemplo: m n n 0,2 3 3
 Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Multicupón no garantizado 07/09 1
 ANEXO AL CONTRATO FINANCIERO DENOMINADO MULTICUPÓN NO GARANTIZADO OBRE UPUETO DE AJUTE O UPUETO EPECIALE DE AJUTE. UPUETO DE AJUTE: E caso d qu s produzca cualqura d las stuacos qu a cotuacó s dca l Baco
ANEXO AL CONTRATO FINANCIERO DENOMINADO MULTICUPÓN NO GARANTIZADO OBRE UPUETO DE AJUTE O UPUETO EPECIALE DE AJUTE. UPUETO DE AJUTE: E caso d qu s produzca cualqura d las stuacos qu a cotuacó s dca l Baco
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DEIVADA Ecucación d la rcta tangnt Ejrcicio nº.- Halla las rctas tangnts a la circunrncia: y y 6 n Ejrcicio nº.- Dada la unción abscisa., scrib la cuación d su rcta tangnt n l punto
APLICACIONES DE LA DEIVADA Ecucación d la rcta tangnt Ejrcicio nº.- Halla las rctas tangnts a la circunrncia: y y 6 n Ejrcicio nº.- Dada la unción abscisa., scrib la cuación d su rcta tangnt n l punto
8 Límites de sucesiones y de funciones
 Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: MADRID
 C/ Gal. Auda, 6 Tléf.: 9 5 8 4-9 55 9 800 MADRID ORMULARIO DE ESTADÍSTICA. DISTRIBUCIONES UNIDIMENSIONALES. Esaza atátca. Sdo ua vaabl alatoa g ( ua fucó d la sa, dfos: E ( g ( ( g Caso dscto g ( f ( Caso
C/ Gal. Auda, 6 Tléf.: 9 5 8 4-9 55 9 800 MADRID ORMULARIO DE ESTADÍSTICA. DISTRIBUCIONES UNIDIMENSIONALES. Esaza atátca. Sdo ua vaabl alatoa g ( ua fucó d la sa, dfos: E ( g ( ( g Caso dscto g ( f ( Caso
MODELO DE REGRESIÓN LINEAL MÚLTIPLE
 Modlo d Rgrsó Lal Múltpl MODELO DE REGRESIÓN LINEAL MÚLTIPLE Autors: Ratas Kzys (rzys@uoc.du), Ágl A. Jua (ajuap@uoc.du). ESQUEMA DE CONTENIDOS Hpótss sobr l térmo d prturbacó Hpótss sobr varabls xplcatvas
Modlo d Rgrsó Lal Múltpl MODELO DE REGRESIÓN LINEAL MÚLTIPLE Autors: Ratas Kzys (rzys@uoc.du), Ágl A. Jua (ajuap@uoc.du). ESQUEMA DE CONTENIDOS Hpótss sobr l térmo d prturbacó Hpótss sobr varabls xplcatvas
TEMA 4: REGRESIÓN Y CORRELACIÓN.
 TEMA 4: REGREIÓN Y CORRELACIÓN. 4.. Rgrsó corrlacó lal smpl... 4.. El método d los mímos cuadrados las cuacos ormals.... 3 4.3. Rgrsó lal: rcta d rgrsó (mímos cuadrados)... 4 4.3.. Propdads d las rctas
TEMA 4: REGREIÓN Y CORRELACIÓN. 4.. Rgrsó corrlacó lal smpl... 4.. El método d los mímos cuadrados las cuacos ormals.... 3 4.3. Rgrsó lal: rcta d rgrsó (mímos cuadrados)... 4 4.3.. Propdads d las rctas
Sistemas de ecuaciones diferenciales lineales
 695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s
695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s
Un forward sobre commodities como el oro sufre una pequeña variación ya que se incluye la tasa de interés del oro (lease rate) con la variable l
 El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
El Forward U corao fuuro o a plazo, s odo aqul cuya lqudacó o slm dfr hasa ua fcha posror spulada l msmo, s dcr s dos pas acurda hacr la rasaccó hasa u prodo fuuro dígas por jmplo 6 mss, so s u corao forward.
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Convocatoria de Febrero 26 de Enero de 2007. Nombre y Apellidos:
 Univrsidad d Vigo Dpartamnto d Matmática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria d Fbrro 6 d Enro d 007 Nombr y Apllidos: DNI: (4.5 p.) ) S considra la función f(x) = x ln(x). (0.5 p.) (a) Calcular
Univrsidad d Vigo Dpartamnto d Matmática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria d Fbrro 6 d Enro d 007 Nombr y Apllidos: DNI: (4.5 p.) ) S considra la función f(x) = x ln(x). (0.5 p.) (a) Calcular
Modelos de Regresión análisis de regresión diagrama de dispersión coeficientes de regresión
 Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Modelos de Regresó E muchos problemas este ua relacó herete etre dos o más varables, resulta ecesaro eplorar la aturaleza de esta relacó. El aálss de regresó es ua técca estadístca para el modelado la
Estadística Teórica II
 Tablas d Cotgca Estadístca Tórca II TABLAS DE CONTINGENCIA Satago d la Fut Frádz 89 CONTRASTE NO PARAMÉTRICO DE BONDAD DE AJUSTE Tablas d Cotgca.- Para comprobar s los opraros cotraba dfcultads co ua prsa
Tablas d Cotgca Estadístca Tórca II TABLAS DE CONTINGENCIA Satago d la Fut Frádz 89 CONTRASTE NO PARAMÉTRICO DE BONDAD DE AJUSTE Tablas d Cotgca.- Para comprobar s los opraros cotraba dfcultads co ua prsa
Procesamiento Digital de Señales de Voz
 Procsamto Dgtal d Sñals d Voz Trasparcas: Procsamto d Sñals y Métodos d Aálss para rcoocmto d Voz Autor: Dr. Jua Carlos Gómz Basado : Rabr, L. ad Juag, B-H.. Fudamtals of Spch Rcogto, Prtc Hall,.J., 993.
Procsamto Dgtal d Sñals d Voz Trasparcas: Procsamto d Sñals y Métodos d Aálss para rcoocmto d Voz Autor: Dr. Jua Carlos Gómz Basado : Rabr, L. ad Juag, B-H.. Fudamtals of Spch Rcogto, Prtc Hall,.J., 993.
2º Bachillerato: ejercicios modelo para el examen de las lecciones 11, 12 y 13
 º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
Tema 8. Limite de funciones. Continuidad
 . Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
Observación: si en la urna hubiese 1500 bolillas blancas y 500 verdes y se extraen dos bolillas al azar sin reemplazo, entonces
 art Variabls alatorias rof. María B. itarlli.- Variabls alatorias discrtas imortats Distribució biomial Sa ε u xrimto alatorio. Sa u vto asociado a ε y aotamos Suogamos u xrimto alatorio ε u cuml los siguits
art Variabls alatorias rof. María B. itarlli.- Variabls alatorias discrtas imortats Distribució biomial Sa ε u xrimto alatorio. Sa u vto asociado a ε y aotamos Suogamos u xrimto alatorio ε u cuml los siguits
CAPÍTULO 2. Ecuación paraxial de Helmholtz.
 CAPÍTLO Ecuacón paraal d Hlmholt. S dscut la posbldad d vsualar mdant un procsador óptco [1] a las solucons d la cuacón paraal d Hlmholt. Para llo s rala una comparacón d los rsultados obtndos consdrando
CAPÍTLO Ecuacón paraal d Hlmholt. S dscut la posbldad d vsualar mdant un procsador óptco [1] a las solucons d la cuacón paraal d Hlmholt. Para llo s rala una comparacón d los rsultados obtndos consdrando
REPRESENTACION GRAFICA.
 REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
Diseño analógico de controladores digitales.
 CAPIULO 4 Dsño aalógco cotrolaors gtals. Aqul qu o ha fracasao s orqu uca ha ttao algo uvo Albrt Est. Coto: ma 4.: Cotrolaors PID gtals ma 4.: Rsño utlao la rtroalmtacó stao. ma 4.3: Métoos sño utlao la
CAPIULO 4 Dsño aalógco cotrolaors gtals. Aqul qu o ha fracasao s orqu uca ha ttao algo uvo Albrt Est. Coto: ma 4.: Cotrolaors PID gtals ma 4.: Rsño utlao la rtroalmtacó stao. ma 4.3: Métoos sño utlao la
Solución: Para que sea continua deben coincidir los límites laterales con su valor de definición en dicho punto x = 2. b 1 + b
 Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
LOS NÚMEROS COMPLEJOS
 LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
LOS NÚMEROS COMPLEJOS por Jorge José Osés Reco Departameto de Matemátcas - Uversdad de los Ades Bogotá Colomba - 00 Cuado se estudó la solucó de la ecuacó de segudo grado ax bx c 0 se aaló el sgo del dscrmate
TEMA 2: LOS NÚMEROS COMPLEJOS
 Matemátcas º Bachllerato. Profesora: María José Sáche Quevedo TEMA : LOS NÚMEROS COMPLEJOS. LOS NÚMEROS COMPLEJOS Relacó etre los úmeros complejos y los putos del plao. Afjo de u úmero complejo. Cojugado
Matemátcas º Bachllerato. Profesora: María José Sáche Quevedo TEMA : LOS NÚMEROS COMPLEJOS. LOS NÚMEROS COMPLEJOS Relacó etre los úmeros complejos y los putos del plao. Afjo de u úmero complejo. Cojugado
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 7: CONTRASTE DE HIPÓTESIS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 214 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 7: CONTRASTE DE HIPÓTESIS Juio, Ejercicio 4, Oció B Reserva 2, Ejercicio 4, Oció B Reserva 4, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 214 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 7: CONTRASTE DE HIPÓTESIS Juio, Ejercicio 4, Oció B Reserva 2, Ejercicio 4, Oció B Reserva 4, Ejercicio
PENSUM DE ESTUDIOS DE INGENIERÍA DE SISTEMAS
 O RÚBLICA BOLIVARIAA D VZULA UIVRSIDAD ACIOAL RIMTAL OLITÉCICA ATOIO JOSÉ D SUCR SUM D STUDIOS D IGIRÍA D SISTMAS SMSTR I 11015 MATMÁTICA I 4 2 0 6 5 -- 14012 DIBUJO I 1 3 0 4 2 -- 21012 IGLS I 1 0 3 4
O RÚBLICA BOLIVARIAA D VZULA UIVRSIDAD ACIOAL RIMTAL OLITÉCICA ATOIO JOSÉ D SUCR SUM D STUDIOS D IGIRÍA D SISTMAS SMSTR I 11015 MATMÁTICA I 4 2 0 6 5 -- 14012 DIBUJO I 1 3 0 4 2 -- 21012 IGLS I 1 0 3 4
LÍMITES DE FUNCIONES.
 LÍMITES DE FUNCIONES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Sa y una unción ral d variabl ral. D una manra intuitiva y oco rcisa, dirmos qu l it d s L, cuando s aroima a, si ocurr qu cuanto más róimo sté
LÍMITES DE FUNCIONES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Sa y una unción ral d variabl ral. D una manra intuitiva y oco rcisa, dirmos qu l it d s L, cuando s aroima a, si ocurr qu cuanto más róimo sté
GuíaDidáctica: Geometría AnalíticaPlana UTPL. La Universidad Católica de Loja MODALIDAD ABIERTA Y A DISTANCIA
 MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA P P 1 0 A P 1 P (x (x 2 ) (0) (1) (x 1 )
MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA MODALIDAD ABIERTA Y A DISTANCIA P P 1 0 A P 1 P (x (x 2 ) (0) (1) (x 1 )
ESTADÍSTICA poblaciones
 ESTADÍSTICA Es la parte de las Matemátcas que estuda el comportameto de las poblacoes utlzado datos umércos obtedos medate epermetos o ecuestas. ESTADÍSTICA La Estadístca tee dos ramas: La Estadístca descrptva:
ESTADÍSTICA Es la parte de las Matemátcas que estuda el comportameto de las poblacoes utlzado datos umércos obtedos medate epermetos o ecuestas. ESTADÍSTICA La Estadístca tee dos ramas: La Estadístca descrptva:
INFERENCIA ESTADISTICA
 Uivrsidad Católica Adrés Bllo UIVERSIDAD CATOLICA ADRES BELLO Urb. Motalbá La Vga Apartado 068 Tléfoo: 47-448 Fa: 47-3043 Caracas, 0 - Vzula Facultad d Igiría Escula d Igiría Iformática -----------------------
Uivrsidad Católica Adrés Bllo UIVERSIDAD CATOLICA ADRES BELLO Urb. Motalbá La Vga Apartado 068 Tléfoo: 47-448 Fa: 47-3043 Caracas, 0 - Vzula Facultad d Igiría Escula d Igiría Iformática -----------------------
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
6. Sucesiones y Series numéricas Series numéricas DEFINICIONES Y PROPIEDADES
 6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
6. Sucesioes y Series uméricas 6.2. Series uméricas 6.2.. DEFINICIONES Y PROPIEDADES Series de úmeros reales Se llama serie umérica o de úmeros reales a la suma idicada de los ifiitos térmios de ua sucesió:
SERIES NUMÉRICAS. SECCIONES A. Series de términos no negativos. B. Ejercicios propuestos.
 CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
Estas pruebas permiten verificar que la población de la cual proviene una muestra tiene una distribución especificada o supuesta.
 PRUEBAS DE BONDAD DE AJUSTE Estas prubas prmitn vrificar qu la población d la cual provin una mustra tin una distribución spcificada o supusta. Sa X: variabl alatoria poblacional f 0 (x) la distribución
PRUEBAS DE BONDAD DE AJUSTE Estas prubas prmitn vrificar qu la población d la cual provin una mustra tin una distribución spcificada o supusta. Sa X: variabl alatoria poblacional f 0 (x) la distribución
IES Mediterráneo de Málaga 2009 Juan Carlos Alonso Gianonatti. DISTRITO UNIVERSITARIO DE Madrid MATEMÁTICAS (Mayores de 25 años).
 IES Mditáo d Málg Ju los loso Giotti DISTRITO UNIVERSITRIO DE Mdid MTEMÁTIS (Mos d ños. OPIÓN Ejcicio.- (. tos. S id l cució ticil do ls tics:. tos. Idic ls dios qu d t l ti.. tos. lcul l is -. c. tos.
IES Mditáo d Málg Ju los loso Giotti DISTRITO UNIVERSITRIO DE Mdid MTEMÁTIS (Mos d ños. OPIÓN Ejcicio.- (. tos. S id l cució ticil do ls tics:. tos. Idic ls dios qu d t l ti.. tos. lcul l is -. c. tos.
Bolilla 4: Rotación de los cuerpos rígidos. Movimiento circular
 Bollla 4: Rotacó de los cueos ígdos. Movmeto ccula Bollla 4: Rotacó de los cueos ígdos. Movmeto ccula 4. Vaables Agulaes Las vaables agulaes sve aa eeseta e foma mas smle e dóea al movmeto de otacó. La
Bollla 4: Rotacó de los cueos ígdos. Movmeto ccula Bollla 4: Rotacó de los cueos ígdos. Movmeto ccula 4. Vaables Agulaes Las vaables agulaes sve aa eeseta e foma mas smle e dóea al movmeto de otacó. La
Práctica 11. Calcula de manera simbólica la integral indefinida de una función. Ejemplo:
 PRÁCTICA SUMAS DE RIEMAN Práctcas Matlab Práctca Objetvos Calcular tegrales defdas de forma aproxmada, utlzado sumas de Rema. Profudzar e la compresó del cocepto de tegracó. Comados de Matlab t Calcula
PRÁCTICA SUMAS DE RIEMAN Práctcas Matlab Práctca Objetvos Calcular tegrales defdas de forma aproxmada, utlzado sumas de Rema. Profudzar e la compresó del cocepto de tegracó. Comados de Matlab t Calcula
() t ( )exp( ) 2. La transformada de Fourier
 1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
Dualidad entre procesos termodinámicos y electromecánicos
 ENERGÍA Y COENERGÍA EN IEMA ELECROMECÁNICO REALE, DEDE PROCEDIMIENO ERMODINÁMICO CLÁICO Alfredo Álvarez García Profesor de Inenería Eléctrca de la Escuela de Inenerías Industrales de adajoz. Resumen La
ENERGÍA Y COENERGÍA EN IEMA ELECROMECÁNICO REALE, DEDE PROCEDIMIENO ERMODINÁMICO CLÁICO Alfredo Álvarez García Profesor de Inenería Eléctrca de la Escuela de Inenerías Industrales de adajoz. Resumen La
Función exponencial y logarítmica:
 MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
Tema 11. Limite de funciones. Continuidad
 Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
Administración de inventarios. Ejercicio práctico.
 Admnstracón d nvntaros. Ejrcco práctco. La Cía. GOMA REDONDA S.A. llva n nvntaro un crto tpo d numátcos, con las sgunts caractrístcas: Vntas promdo anuals: 5000 numátcos Costo d ordnar: $ 40/ ordn Costo
Admnstracón d nvntaros. Ejrcco práctco. La Cía. GOMA REDONDA S.A. llva n nvntaro un crto tpo d numátcos, con las sgunts caractrístcas: Vntas promdo anuals: 5000 numátcos Costo d ordnar: $ 40/ ordn Costo
1 de 44 CODIGO: PREPARADO POR: Dr. Juan Rafael Mora López, MQC, Ph.D. JULIO DEL REVISADO POR: Dr. José Valdelomar Director Laboratorio Clínico
 ADM- 00 DEL 23 1 de 44 ADM- 00 DEL 23 2 de 44 ADM- 00 DEL 23 3 de 44 ADM- 00 DEL 23 4 de 44 ADM- 00 DEL 23 5 de 44 ADM- 00 DEL 23 6 de 44 ADM- 00 DEL 23 7 de 44 ADM- 00 DEL 23 8 de 44 ADM- 00 DEL 23 9
ADM- 00 DEL 23 1 de 44 ADM- 00 DEL 23 2 de 44 ADM- 00 DEL 23 3 de 44 ADM- 00 DEL 23 4 de 44 ADM- 00 DEL 23 5 de 44 ADM- 00 DEL 23 6 de 44 ADM- 00 DEL 23 7 de 44 ADM- 00 DEL 23 8 de 44 ADM- 00 DEL 23 9
PENSUM DE ESTUDIOS DE INGENIERÍA MECÁNICA
 O RÚBLICA BOLIVARIAA D VZULA UIVRSIDAD ACIOAL RIMTAL OLITÉCICA SUM D STUDIOS D IGIRÍA MCÁICA SMSTR I CODIGO ASIGATURAS T L HT/S U RQUISITOS C 11015 MATMÁTICA I 4 2 0 6 5 -- 14012 DIBUJO I 1 3 0 4 2 --
O RÚBLICA BOLIVARIAA D VZULA UIVRSIDAD ACIOAL RIMTAL OLITÉCICA SUM D STUDIOS D IGIRÍA MCÁICA SMSTR I CODIGO ASIGATURAS T L HT/S U RQUISITOS C 11015 MATMÁTICA I 4 2 0 6 5 -- 14012 DIBUJO I 1 3 0 4 2 --
PENSUM DE ESTUDIOS DE INGENIERÍA INDUSTRIAL
 O RÚBLICA BOLIVARIAA D VZULA UIVRSIDAD ACIOAL RIMTAL OLITÉCICA SUM D STUDIOS D IGIRÍA IDUSTRIAL SMSTR I 11015 MATMÁTICA I 4 2 0 6 5 -- 14012 DIBUJO I 1 3 0 4 2 -- 21012 IGLS I 1 0 3 4 2 -- 13013 QUÍMICA
O RÚBLICA BOLIVARIAA D VZULA UIVRSIDAD ACIOAL RIMTAL OLITÉCICA SUM D STUDIOS D IGIRÍA IDUSTRIAL SMSTR I 11015 MATMÁTICA I 4 2 0 6 5 -- 14012 DIBUJO I 1 3 0 4 2 -- 21012 IGLS I 1 0 3 4 2 -- 13013 QUÍMICA
A1. ELEMENTOS DE VIGA DE EULER BERNOULLI LIBRES DE ROTACIÓN
 Anass d acas y amna 34 ANEJO I A. ELEMENOS DE VIGA DE EULER ERNOULLI LIRES DE ROACIÓN La toría d vgas d Eur-rnou s robabmnt uno d os robmas modo más sms d a formuacón rstrngda d a astcdad na. La rstrccón
Anass d acas y amna 34 ANEJO I A. ELEMENOS DE VIGA DE EULER ERNOULLI LIRES DE ROACIÓN La toría d vgas d Eur-rnou s robabmnt uno d os robmas modo más sms d a formuacón rstrngda d a astcdad na. La rstrccón
Matemáticas II TEMA 8 Derivadas. Teorema. Regla de L Hôpital Problemas Propuestos
 Matmáticas II TEMA 8 Drivadas Torma Rgla d L Hôpital Problmas Propustos Drivada d una función n un punto Utilizando la dfinición, calcula la drivada d f ( ) n l punto = Utilizando la dfinición, halla la
Matmáticas II TEMA 8 Drivadas Torma Rgla d L Hôpital Problmas Propustos Drivada d una función n un punto Utilizando la dfinición, calcula la drivada d f ( ) n l punto = Utilizando la dfinición, halla la
EXISTENCIA DE UNA FUNCIÓN NO LINEAL, CONTINUA Y BIYECTIVA EN l CON INVERSA DISCONTINUA EN TODO PUNTO
 EXISTECIA DE UA FUCIÓ O LIEAL, COTIUA Y BIYECTIVA E l CO IVERSA DISCOTIUA E TODO PUTO Jorge E Herádez U, Temístocles Zeballos M Uversdad de Paamá, Cetro Regoal Uverstaro de Veraguas, Departameto de Matemátca
EXISTECIA DE UA FUCIÓ O LIEAL, COTIUA Y BIYECTIVA E l CO IVERSA DISCOTIUA E TODO PUTO Jorge E Herádez U, Temístocles Zeballos M Uversdad de Paamá, Cetro Regoal Uverstaro de Veraguas, Departameto de Matemátca
TEMA IV INTEGRALES INDEFINIDAS
 Tema IV-Itegrales Ideiidas TEMA IV INTEGRALES INDEFINIDAS Dada ua ució ( ) deiida e u cierto domiio D, os plateamos si eiste ua ució F( ) deiida e el mismo domiio, tal que su derivada coicida co la ució
Tema IV-Itegrales Ideiidas TEMA IV INTEGRALES INDEFINIDAS Dada ua ució ( ) deiida e u cierto domiio D, os plateamos si eiste ua ució F( ) deiida e el mismo domiio, tal que su derivada coicida co la ució
FORMULAS Y EJEMPLOS PARA EL CÁLCULO DE INTERESES DE UN DEPÓSITO A PLAZO FIJO CONVENCIONAL
 FORMULAS Y EJEMLOS ARA EL CÁLCULO DE NERESES DE UN DEÓSO A LAZO FJO CONVENCONAL 1. GLOSARO DE ÉRMNOS a. Depósito a plazo fijo: roducto e el que el cliete podrá depositar ua catidad de diero a ua tiempo
FORMULAS Y EJEMLOS ARA EL CÁLCULO DE NERESES DE UN DEÓSO A LAZO FJO CONVENCONAL 1. GLOSARO DE ÉRMNOS a. Depósito a plazo fijo: roducto e el que el cliete podrá depositar ua catidad de diero a ua tiempo
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS
 CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
REGRESIÓN LINEAL SIMPLE
 RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de una variable. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación
 Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
RENTABILIDAD Y RIESGO DE CARTERAS Y ACTIVOS TEMA 3- I FUNTAMENTOS DE DIRECCIÓN FINANCIERA. Fundamentos de Dirección Financiera Tema 3- Parte I 1
 RENTILIDD Y RIESGO DE CRTERS Y CTIVOS TEM 3- I FUNTMENTOS DE DIRECCIÓN FINNCIER Fudametos de Dreccó Facera Tema 3- arte I RIESGO y RENTILIDD ( decsoes de versó productvas) EXISTENCI DE RIESGO ( los FNC
RENTILIDD Y RIESGO DE CRTERS Y CTIVOS TEM 3- I FUNTMENTOS DE DIRECCIÓN FINNCIER Fudametos de Dreccó Facera Tema 3- arte I RIESGO y RENTILIDD ( decsoes de versó productvas) EXISTENCI DE RIESGO ( los FNC
6. FAST FOURIER TRANSFORM (FFT)
 6. FAS FOURIER RASFORM FF Las rasformadas Rápidas d Fourir so algoritmos spcializados qu prmit a u procsador digital acr l cálculo d la rasformada Discrta d Fourir d ua forma ficit, lo qu rspcta a carga
6. FAS FOURIER RASFORM FF Las rasformadas Rápidas d Fourir so algoritmos spcializados qu prmit a u procsador digital acr l cálculo d la rasformada Discrta d Fourir d ua forma ficit, lo qu rspcta a carga
Valledupar como vamos: Demografía, Pobreza y Pobreza Extrema y empleo.
 Valldupar como vamos: Dmografía, Pobrza y Pobrza Extrma y mplo. Tradicionalmnt l programa Valldupar Cómo Vamos, lugo d prsntar la Encusta d Prcpción Ciudadana (EPC), raliza la ntrga d Indici d Calidad
Valldupar como vamos: Dmografía, Pobrza y Pobrza Extrma y mplo. Tradicionalmnt l programa Valldupar Cómo Vamos, lugo d prsntar la Encusta d Prcpción Ciudadana (EPC), raliza la ntrga d Indici d Calidad
Unidad 2 : Ecuaciones Diferenciales Lineales de Orden Superior. Tema 2.1 : Definiciones y Terminología
 7 Unidad : Euaions Dirnials inals d Ordn Surior Tma. : Diniions Trminología a Euaión Dirnial inal d o rdn No Homogéna tin la orma: a d d d d a a g uaión EDN H a Euaión Dirnial inal d o rdn Homogéna Asoiada
7 Unidad : Euaions Dirnials inals d Ordn Surior Tma. : Diniions Trminología a Euaión Dirnial inal d o rdn No Homogéna tin la orma: a d d d d a a g uaión EDN H a Euaión Dirnial inal d o rdn Homogéna Asoiada
TEMA 12 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES.
 TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bach. TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. Tasa d variación mdia. Cálculo y signiicado EJERCICIO : Considramos la unción:. Halla la tasa
TEMA DERIVADAS Y APLICACIONES MATEMÁTICAS I º Bach. TEMA INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES. Tasa d variación mdia. Cálculo y signiicado EJERCICIO : Considramos la unción:. Halla la tasa
PROBLEMAS RESUELTOS DE RECTAS TANGENTES Y NORMALES
 PROBLEMAS RESUELTOS DE RECTAS TANGENTES Y NORMALES ) (Part d un problma d Slctividad d Cincias y Tcnología 007) Sa f: R R la función dfinida por f() =. Dtrmina la cuación d la rcta tangnt a la gráfica
PROBLEMAS RESUELTOS DE RECTAS TANGENTES Y NORMALES ) (Part d un problma d Slctividad d Cincias y Tcnología 007) Sa f: R R la función dfinida por f() =. Dtrmina la cuación d la rcta tangnt a la gráfica
Cálculo y EstadísTICa. Primer Semestre.
 Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado e Geomátca y Topografía Escuela Técca Superor de Igeeros e Topografía, Geodesa y Cartografía. Uversdad Poltécca de Madrd Capítulo
Cálculo y EstadísTICa. Prmer Semestre. EstadísTICa Curso Prmero Graduado e Geomátca y Topografía Escuela Técca Superor de Igeeros e Topografía, Geodesa y Cartografía. Uversdad Poltécca de Madrd Capítulo
PRIMERA PRUEBA DE TÉCNICAS CUANTITATIVAS III. 14-Abril-2015. Grupo A
 PRIMERA PRUEBA DE TÉCICAS CUATITATIVAS III. 14-Abrl-015. Grupo A OMBRE: DI: 1. Se quere hacer u estudo sobre gasto e ropa e ua comarca dode el 41% de los habtates so mujeres. (1 puto) Se decde tomar ua
PRIMERA PRUEBA DE TÉCICAS CUATITATIVAS III. 14-Abrl-015. Grupo A OMBRE: DI: 1. Se quere hacer u estudo sobre gasto e ropa e ua comarca dode el 41% de los habtates so mujeres. (1 puto) Se decde tomar ua
( ) ( ) 60 ( ) ( ) ( ) Opción A. Ejercicio A.1- Se sabe qué Calcular, de manera razonada, aplicando las propiedades
 IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Oió Ejiio.- S s ué. Clul d od lido ls oidds duds l lo d los siguits dtits: B B IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Ejiio..- Hll l uió dl
IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Oió Ejiio.- S s ué. Clul d od lido ls oidds duds l lo d los siguits dtits: B B IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Ejiio..- Hll l uió dl
TEMA 3. Superficies Adicionales. Aletas.
 TEMA 3. Suprficis Adicionals. Altas. Introducción Alta rcta d spsor uniform y alta d aguja d scción transvrsal constant La alta anular d spsor constant La alta d prfil triangular Efctividad d la alta Las
TEMA 3. Suprficis Adicionals. Altas. Introducción Alta rcta d spsor uniform y alta d aguja d scción transvrsal constant La alta anular d spsor constant La alta d prfil triangular Efctividad d la alta Las
Funciones de Variable Compleja
 Funcions d Variabl Complja Modlos d Sistmas II Smstr 2008 Ing. Gabrila Ortiz L 1 Función Concpto Matmático Considrando los conjuntos X Y una función comprnd una rlación o rgla qu asocia a cada lmnto x
Funcions d Variabl Complja Modlos d Sistmas II Smstr 2008 Ing. Gabrila Ortiz L 1 Función Concpto Matmático Considrando los conjuntos X Y una función comprnd una rlación o rgla qu asocia a cada lmnto x
COMPUTACIÓN. Práctica nº 2
 Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
RUTA DEL INTERIOR. CAMINO PRIMITIVO CONCEJO DE GRANDAS DE SALIME CARTOGRAFÍA ESTADO Y CARACTERISTICAS ELEMENTOS ASOCIADOS

EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL
 EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS FUNDAMENTOS DE ANÁLISIS INSTRUMENTAL. 3ª RELACIÓN DE PROBLEMAS.
 FUNDAMENTOS DE ANÁLISIS INSTRUMENTAL. 3ª RELACIÓN DE PROBLEMAS. 1.- En ausncia d autoabsorción, la intnsidad d fluorscncia d una mustra s proporcional a la concntración, solo a concntracions bajas. Calcular
FUNDAMENTOS DE ANÁLISIS INSTRUMENTAL. 3ª RELACIÓN DE PROBLEMAS. 1.- En ausncia d autoabsorción, la intnsidad d fluorscncia d una mustra s proporcional a la concntración, solo a concntracions bajas. Calcular
-Métodos Estadísticos en Ciencias de la Vida
 -Métodos Estadístcos e Cecas de la Vda Regresó Leal mple Regresó leal smple El aálss de regresó srve para predecr ua medda e fucó de otra medda (o varas). Y = Varable depedete predcha explcada X = Varable
-Métodos Estadístcos e Cecas de la Vda Regresó Leal mple Regresó leal smple El aálss de regresó srve para predecr ua medda e fucó de otra medda (o varas). Y = Varable depedete predcha explcada X = Varable
4.2. Ejemplo de aplicación.
 HEB 8 Dsarrollo dl método d los dsplazamintos 45 4.. Ejmplo d aplicación. ontinuando con l pórtico dscrito n l apartado (3.8), s van a calcular las cargas y, postriormnt, sguir con l cálculo matricial,
HEB 8 Dsarrollo dl método d los dsplazamintos 45 4.. Ejmplo d aplicación. ontinuando con l pórtico dscrito n l apartado (3.8), s van a calcular las cargas y, postriormnt, sguir con l cálculo matricial,
Tema 4: Regresiones lineales y no lineales TEMA 4. REGRESIONES LINEALES LINEALES Y NO. 1. 2. 3. Introducción 4. Nomenclatura
 T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
T 4: grsos lls o lls TEMA 4. EGEIONE LINEALE LINEALE Y NO.. 3. Itroduccó 4. Nocltur 5. Llzcó Ajust grsó ll ll d últpl cucos 6. 7. 8. grsos EUMEN Progrcó o lls Mtlb Cálculo uérco Igrí T 4: grsos lls o lls.
Línea de Investigación: Fisicoquímica de Alimentos. Programa Educativo: Licenciatura en Química. Nombre de la Asignatura: Química Analítica V
 Área Académca de: Químca Líea de Ivestgacó: Fscoquímca de Almetos Programa Educatvo: Lcecatura e Químca Nombre de la Asgatura: Químca Aalítca V Tema: Represetacoes gráfcas de las relacoes propedadcocetracó
Área Académca de: Químca Líea de Ivestgacó: Fscoquímca de Almetos Programa Educatvo: Lcecatura e Químca Nombre de la Asgatura: Químca Aalítca V Tema: Represetacoes gráfcas de las relacoes propedadcocetracó
PLAN DE CURSO PC-01 FO-TESE-DA-09 DIRECCIÓN ACADÉMICA DIVISIÓN DE INGENIERÍA ELECTRÓNICA. Según Corresponda CALCULO INTEGRAL TURNO: 1201/1 251
 No. DE EMPLEADO: SEMANA: 5 NO. DE ALUMNOS: O PROPOSITO GENERAL DE LA 1. Teorema fundamental del cálculo. - Contextualizar el concepto de - Visualizar la relación entre cálculo diferencial y el cálculo
No. DE EMPLEADO: SEMANA: 5 NO. DE ALUMNOS: O PROPOSITO GENERAL DE LA 1. Teorema fundamental del cálculo. - Contextualizar el concepto de - Visualizar la relación entre cálculo diferencial y el cálculo
3 = =. Pero si queremos calcular P (B) 2, ya que si A ocurrió, entonces en la urna
 arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
arte robabldad codcoal rof. María. tarell - robabldad codcoal.- Defcó Supogamos el expermeto aleatoro de extraer al azar s reemplazo dos bolllas de ua ura que cotee 7 bolllas rojas y blacas. summos que
A C T I N O M IC O S I S Ó r g a n o : M u c o s a b u c a l T é c n i ca : H / E M i c r o s c o p í a: L o s c o r t e s h i s t o l ó g i c oms u e
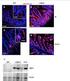 T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 7: CONTRASTE DE HIPÓTESIS
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 211 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 7: CONTRASTE DE HIPÓTESIS Juio, Ejercicio 4, Oció A Reserva 1, Ejercicio 4, Oció A Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 211 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 7: CONTRASTE DE HIPÓTESIS Juio, Ejercicio 4, Oció A Reserva 1, Ejercicio 4, Oció A Reserva 2, Ejercicio
( ) ( ) ( ) RESOLUCIÓN Dato: NºDiag.= 4(Nº s internos) RESOLUCIÓN RESOLUCIÓN SEMANA 4 POLÍGONOS Y CUADRILÁTEROS 11( 11 1) RPTA.: E RPTA.
 SEMN 4 OLÍGONOS Y URILÁTEROS 1. lcul l úmro d digols mdis d u polígoo, dod l úmro d digols s l cuádrupl dl úmro d águlos itros. ) 0 ) 7 ) ) 44 E) to: Nºig.= 4(Nº s itros) id: Nºig.Mdis= ( 1 ) =? Rmplzdo
SEMN 4 OLÍGONOS Y URILÁTEROS 1. lcul l úmro d digols mdis d u polígoo, dod l úmro d digols s l cuádrupl dl úmro d águlos itros. ) 0 ) 7 ) ) 44 E) to: Nºig.= 4(Nº s itros) id: Nºig.Mdis= ( 1 ) =? Rmplzdo
Aproximación a la distribución normal: el Teorema del Límite Central
 Aproxmacó a la dstrbucó ormal: el Teorema del Límte Cetral El teorema del límte cetral establece que s se tee varables aleatoras, X, X,..., X, depedetes y co détca dstrbucó de meda µ y varaza σ, a medda
Aproxmacó a la dstrbucó ormal: el Teorema del Límte Cetral El teorema del límte cetral establece que s se tee varables aleatoras, X, X,..., X, depedetes y co détca dstrbucó de meda µ y varaza σ, a medda
Transformada de Laplace
 Tranformada d alac CIPQ Marga Marco, Itzar Caban, Eva Portllo, 6 Tranformada d alac f(t funcón tmoral f(t f(t ara t < [ f (t] F( f (t t σ jω varabl comlja d alac t f(t g(t [ f (t] [ g(t ] F( G( Cambo d
Tranformada d alac CIPQ Marga Marco, Itzar Caban, Eva Portllo, 6 Tranformada d alac f(t funcón tmoral f(t f(t ara t < [ f (t] F( f (t t σ jω varabl comlja d alac t f(t g(t [ f (t] [ g(t ] F( G( Cambo d
Tema IV: Ruidos e Interferencias: Técnicas de reducción.
 SCUA TÉCNICA SUPIO D INGNIOS INDUSTIAS Y D TCOMUNICACIÓN UNIVSIDAD D CANTABIA INSTUMNTACIÓN CTÓNICA D COMUNICACIONS (5º Curso Igría d Tlcomucacó) Tma IV: udos Itrrcas: Téccas d rduccó. José María Drak
SCUA TÉCNICA SUPIO D INGNIOS INDUSTIAS Y D TCOMUNICACIÓN UNIVSIDAD D CANTABIA INSTUMNTACIÓN CTÓNICA D COMUNICACIONS (5º Curso Igría d Tlcomucacó) Tma IV: udos Itrrcas: Téccas d rduccó. José María Drak
Intervalos de Confianza basados en una muestra. Instituto de Cálculo
 Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky Hay dos razoes por las cuales el itervalo (6.63,.37) tiee mayor logitud que el obteido ateriormete (7.69, 0.3). la variaza
Itervalos de Cofiaza basados e ua muestra. Istituto de Cálculo Dra. Diaa Kelmasky Hay dos razoes por las cuales el itervalo (6.63,.37) tiee mayor logitud que el obteido ateriormete (7.69, 0.3). la variaza
CENTRO DE MASA centro de masas centro de masas
 CENTRO DE ASA El cetro de masas de u sstema dscreto o cotuo es el puto geométrco que dámcamete se comporta como s e él estuvera aplcada la resultate de las fuerzas exteras al sstema. De maera aáloga, se
CENTRO DE ASA El cetro de masas de u sstema dscreto o cotuo es el puto geométrco que dámcamete se comporta como s e él estuvera aplcada la resultate de las fuerzas exteras al sstema. De maera aáloga, se
Radicales. Un r a d i c a l e s u n a e x p r e s i ó n d e l a f o r m a, e n l a q u e n y a ; c o n t a l
 Radicales Un r a d i c a l e s u n a e x p r e s i ó n d e l a f o r m a, e n l a q u e n y a ; c o n t a l q u e c u a n d o a s ea n e ga t i v o, n h a d e s e r i m pa r. P o t e n c i a s y r a d
Radicales Un r a d i c a l e s u n a e x p r e s i ó n d e l a f o r m a, e n l a q u e n y a ; c o n t a l q u e c u a n d o a s ea n e ga t i v o, n h a d e s e r i m pa r. P o t e n c i a s y r a d
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS
 Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
Tma Límits, continuidad y asíntotas Matmáticas I º Bachillrato TEMA LÍMITES, CONTINUIDAD ASÍNTOTAS CÁLCULO GRÁFICO DE LÍMITES EJERCICIO : Sobr la gráfica d f), halla : 8 8 8 f f c) f f ) f f f c) f f )
Método de los Elementos Finitos para Análisis Estructural. Alisado de tensiones
 Método d los Elmntos Finitos para Análisis Estructural Alisado d tnsions Campo d tnsions Tnsions n cualquir punto dl lmnto, sgún l MEF: = Dε= DBδ Matriz B contin las drivadas d las N: no son continuas
Método d los Elmntos Finitos para Análisis Estructural Alisado d tnsions Campo d tnsions Tnsions n cualquir punto dl lmnto, sgún l MEF: = Dε= DBδ Matriz B contin las drivadas d las N: no son continuas
 OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
REPASO EXAMEN SEMESTRAL MATEMÁTICAS II. 2) EJERCICIOS - Determina el valor de (x) y de (y) en las siguientes construcciones geométricas: x 4x.
 RESO EXMEN SEMESTRL MTEMÁTICS II TEM: ÁNGULOS Y TRIÁNGULOS 1) TEORÍ S abora: - Clasfaó: águlos aguos, obtusos y rtos, t - arjas águlos: omplmtaros, suplmtaros, ojugaos, opustos por l vért, ayats - E rtas
RESO EXMEN SEMESTRL MTEMÁTICS II TEM: ÁNGULOS Y TRIÁNGULOS 1) TEORÍ S abora: - Clasfaó: águlos aguos, obtusos y rtos, t - arjas águlos: omplmtaros, suplmtaros, ojugaos, opustos por l vért, ayats - E rtas
OPTIMIZACIÓN VECTORIAL
 OPTIMIZACIÓN VECTORIAL Métodos de Búsqueda Directa Utilizan sólo valores de la función Métodos del Gradiente Métodos de Segundo Orden Requieren valores aproimados de la primera derivada de f) Además de
OPTIMIZACIÓN VECTORIAL Métodos de Búsqueda Directa Utilizan sólo valores de la función Métodos del Gradiente Métodos de Segundo Orden Requieren valores aproimados de la primera derivada de f) Además de
SISTEMAS LINEALES TABLAS. Dpto. Teoría de la Señal y Comunicaciones
 SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
Tema 1: Números Complejos
 Números Complejos Tema 1: Números Complejos Deició U úmero complejo es u par ordeado (x, y) de úmeros reales Éste puede iterpretarse como u puto del plao cuya abscisa es x y cuya ordeada es y El cojuto
Números Complejos Tema 1: Números Complejos Deició U úmero complejo es u par ordeado (x, y) de úmeros reales Éste puede iterpretarse como u puto del plao cuya abscisa es x y cuya ordeada es y El cojuto
UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s



