Criterio no asintótico para el diseño de sistemas Bonus-Malus mediante GPBM
|
|
|
- Catalina Piñeiro Nieto
- hace 7 años
- Vistas:
Transcripción
1 Cteo no asntótco paa el dseño de ssteas Bonus-Malus edante GPBM Resuen Mª Pla Gacía Pneda Antono Heas Matínez Avda El Feol nº 9, 3º, Madd Tfno: E-al: MGARCIAPI@NEXO.ES El dseño de ssteas Bonus-Malus habtualente está basado en la dstbucón estaconaa de la pobabldad. Se supone que una pólza ha alcanzado el estado estaconao (n 0 ) cuando la pobabldad de que dcha pólza petenezca a la clase C es constante paa todo n ayo o gual que n 0. Esta dstbucón estaconaa de pobabldad es senclla de calcula. Su cálculo está basado en la Teoía de Cadenas de Makov y equee que el sstea cupla cetas condcones (sea Cadena de Makov educble y todos sus estados sean ecuentes en tepo espeado fnto). Podía ocu que estas condcones no se cuplan y en este caso no se podía utlza la dstbucón estaconaa. Po ota pate, los cteos basados en la dstbucón estaconaa no tenen en cuenta a las pólzas nuevas en la epesa n a las que llevan poco tepo. Po estos otvos, se popone un nuevo cteo que tenga en cuenta la edad de las pólzas de la catea. Palabas clave Bonus-Malus, Pogaacón po Metas. Ssteas Bonus-Malus Una copañía de seguos utlza un sstea Bonus-Malus cuando se cuplen las sguentes condcones: Exste un núeo fnto de clases C...C tales que cada pólza peanece en una clase duante un peodo de seguo (habtualente un año). La pa paa cada pólza depende úncaente de la clase en la que está. La clase a la que petenece la pólza duante un peodo dado está detenado po la clase en el peodo pecedente y el núeo de snestos declaados en ese peodo, lo que se conoce coo Condcón de Makov. Cada sstea Bonus-Malus está detenado po tes eleentos: La clase ncal, que es la que se asgna a las nuevas pólzas. La escala de pas π = ( π,..., π ) donde π es la pa paa la clase C.
2 Las eglas de tanscón, es dec, las eglas que establecen las condcones bajo las cuales una pólza que está en la clase C pasa a la clase C j en el sguente peodo. Estas eglas de tanscón venen dadas en una atz T de densón x donde sus eleentos T j cuplen las sguentes condcones: Son conjuntos de núeos enteos tales que una pólza pasa de la clase C a la clase C j s declaa snestos. T = { 0,, 2,... } y Tj Tj ' = cuando j j'. j= j Se supone que las caacteístcas de esgo de cada pólza están esudas en el valo de un ceto paáeto λ, dchos valoes paa todas las pólzas de la catea se supone que son una vaable aleatoa Λ, y que los núeos de snestos de la pólza, duante los dfeentes años de vgenca de ésta, son vaables aleatoas condconalente ndependentes y e déntcaente dstbudas paa cada valo del paáeto de esgo de la pólza. Se supone tabén que las cuantías de la snestaldad ndvdual son ndependentes de del núeo de snestos y del paáeto de esgo, y utuaente ndependentes e déntcaente dstbudas. Este paáeto de esgo, λ, se dentfca con la fecuenca eda de snestos, que se supone estaconaa en el tepo. Escala de Bayes Toando la eda de la snestaldad coo undad onetaa, el objetvo del dseño de un sstea Bonus-Malus consste en calcula una pa pua paa cada aseguado tan póxa coo sea posble al vedadeo valo (desconocdo) de su paáeto. La etodología ás habtual, en la lteatua actuaal, paa dseña ssteas Bonus- Malus es la constuccón de la escala de Bayes. Esta escala se obtene nzando la espeanza del cuadado del eo de tafcacón, defndo coo la espeanza del cuadado de la dfeenca ente la vedadea pa pua y la pa ealente pagada paa una pólza nfntaente veja elegda al aza. La pobabldad de tanscón condconada de una clase C a C j en un peodo, paa un valo de Λ= λ dado, vene dada po p ( λ) p ( λ) t p λ es la pobabldad condconada a T j y 0 en caso contao. = donde ( ) j j = 0 Λ= λ de declaa snestos y t toa los valoes s Estos valoes se ecogen en una atz P ( λ ) de densón x, llaada atz de tanscón. Estas defncones nos peten consdea un sstea Bonus-Malus coo una cadena de Makov y, tenendo en cuenta las popedades de las cadenas de Makov, es posble deosta que exste una dstbucón de pobabldad estaconaa (condconada) ( p ( λ),..., p ( λ )) donde p ( λ ) está defnda coo el valo del líte, cuando el núeo de peodos, de la pobabldad condconada de que una pólza petenezca a la clase C, dado Λ= λ. j 2
3 Esta dstbucón de pobabldad estaconaa concde con el autovecto po la zqueda asocado con el autovalo de la coespondente atz de tanscón, cuyas coponentes sean postvas y suen la undad. Metodología GPBM paa el dseño de ssteas Bonus-Malus Esta etodología está basada en Pogaacón po Metas. Coo paa la obtencón de la escala de Bayes, el cálculo de la escala de pas de un sstea Bonus-Malus se puede consdea coo un poblea de teoía de la decsón en el cual las posbles decsones son la escala de pas ( ),..., π π, los estados aleatoos de la natualeza son los valoes de Λ, y la pédda asocada a cada posble decsón ( π,..., π ) y a cada π λ λ. valo de Λ es el valo absoluto del eo de tafcacón p ( ). Esta expesón es, en geneal, bastante dfícl de esolve. No obstante, s suponeos que el paáeto Λ tene una dstbucón dsceta, es dec, toa los valoes ( λ,..., λ ) con pobabldades ( q,..., q ) espectvaente, entonces es equvalente a La decsón ópta seá la escala ( π,..., π ) que nce πp( λ) λ du( λ) nza p ( ) lneal j= π λ λq, lo que es tabén equvalente al sguente pogaa j n ( + ) j= x y q j j j ( ) ( ) π. p λ π. p λ + x+ y = λ... π. p( λ) π. p ( λ) + x + y = λ π 0 =... xj, yj 0 j =... donde los valoes óptos de las vaables x j e y j epesentan los eoes de tafcacón negatvo y postvo, espectvaente, paa una pólza de paáeto λ j. En los pogaas geneales de pogaacón po etas el decso ntenta enconta los valoes de las vaables de decsón tales que cetas funcones objetvo toen valoes tan póxos coo sea posble a un conjunto de etas pevas. En este caso, dchas etas son los valoes λ,..., λ, posbles valoes del paáeto Λ e ntentaos enconta los valoes de las vaables de decsón π,..., π tales que se apoxen, paa cada pólza de paáeto λ j, el valo de la eda de las pas pagadas po ese aseguado π p( λj) y su fecuenca de snestos eal λ j. 3
4 0 0 El gado de desequlbo fnanceo vene dado po ( ) xj yj. qj donde x 0, y 0 j j son las vaables de desvacón óptas solucón del pogaa lneal. Luego es posble ncopoa la popedad de equlbo fnanceo al sstea Bonus-Malus spleente 0 0 añadendo al pogaa lneal la estccón ( ) j= j= xj yj. qj = 0. Asso, es posble ncopoa otas necesdades de ecado sepe y cuando se puedan expesa coo estcccones lneales, coo po ejeplo: π π d + π π + π π π... π n d D π π D Objecones del uso de la dstbucón estaconaa Los étodos paa el dseño de ssteas Bonus-Malus expuestos hasta ahoa están basados en la eleccón de una pólza nfntaente veja elegda al aza, es dec, en la dstbucón estaconaa de pobabldad, se puede objeta que en la ealdad el núeo de vgenca de las pólzas es fnto. Aunque se puede consdea que a pat de un ceto núeo de peodos n 0 la pólza está sufcenteente póxa al estado estaconao, tabén habá en la copañía aseguadoa otas pólzas que no cuplan esta condcón. S la ayoía de las pólzas están lejos del estado estaconao, paece azonable odfca el cteo paa así tene en cuenta el eo de tafcacón tabén paa las nuevas pólzas y las que lleven un tepo odeado de peanenca en la epesa. Nuevo étodo no asntótco Tabén es posble aplca esta etodología sn utlza la dstbucón estaconaa. Consdeeos los vectoes de pobabldad condconados a Λ= λ, paa cada año n de la vda de la pólza. S n=, es dec, el pe año el vecto de pobabldades de petenece a cada una de las clases vene dado po p () ( λ ) = ( 0,...,,...0), donde todas las cooodenadas son nulas salvo la k-ésa que es la undad, ya que la pólza estaá en C k que es la clase de entada. ( 2 S n=2, el vecto de pobabldad condconada se obtene ) () p ( λ) = p ( λ). P sendo P la atz de pobabldades de un paso coespondente a la cadena de Makov. ( Así sucesvaente n ) ( ( ) ) () p λ p n ( λ). P... p ( λ). P n = = =. S n, p ( λ ) es el autovecto asocado al autovalo undad cuyas coponentes son no negatvas y suan la undad. 4
5 Consdeaos tabén la vaable aleatoa, N a, núeo de años de antgüedad de la w = P N = n. pólza y toaos coo valoes de los pesos ( ) En este caso, la escala de pas ópta se podía calcula esolvendo el sguente pogaa lneal: n ( xj + yj). qj j= sujeto a ( n ) π wp n ( λj) + xj + yj = λj n= j =,..., π 0 =,..., xj, yj 0 j =,..., Aunque podía paece que este pogaa lneal tene nfntos suandos en las peas estcccones, el núeo de suando se educe a un núeo fnto ya que P N = n = 0 paa algún núeo de años de antgüedad de la pólza n 0 ; y po lo tanto ( ) a n= 0 se podía susttu po n0 n= n a quedando así un núeo fnto de suandos. Ejeplo utlzando la dstbucón estaconaa Se quee dseña un sstea Bonus-Malus que tenga 3 clases con eglas de tanscón dadas po la atz {, 2,...} {} 0 {, 2,...} {} 0 {, 2,...} {} 0 { 2, 3,...} {} { } 0 { 2, 3,...} {} { 0} { 3, 4,...} {} 2 {} { 0} T = { 3, 4,...} {} 2 {} { 0} { 4, 5,...} {} 3 {} 2 {} { 0} { 4, 5,...} {} 3 {} 2 {} { 0} { 5, 6,...} {} 4 {} 3 {} 2 {} { 0} { 5, 6,...} {} 4 {} 3 {} 2 {} { 0} { 6, 7,...} {} 5 {} 4 {} 3 {} 2 {} { 0} { 6, 7,...} {} 5 {} 4 {} 3 {} 2 {} { 0} cuya clase de entada sea C 0, que los aseguados nuevos en la copañía paguen la eda de la snestaldad total y que la pa ente dos clases consecutvas vaíe al enos el % de la popocón ente dchas pas. Se sabe que la snestaldad se 5
6 ajusta a una vaable aleatoa dsceta Λ cuya dstbucón de pobabldad vene dada po la sguente tabla: λ j P(Λ=λ j )=q j y que la dstbucón de la snestaldad ndvdual se copota coo una Posson de paáeto λ. Calculaos E(Λ)=0.52 y esa seá la pa que deben paga los aseguados nuevos en la epesa toando coo undad onetaa el coste edo de un snesto. El poblea lneal que debeos de esolve seá, po tanto, 3 ( + ) n x y. q sujeto a 3 p( λj) π + xj yj = λj j =,...,20 π π2, π2 π3,..., π2 π3 π 0, xj 0, yj 0, 3 ( x y). q = 0 =,...,3 j =,...,20 π 5π3 π.0π+ =,...,3 π0 = 0.52 Resolvendo el pogaa con Maple V se obtene coo solucón ópta la escala de pas j π j
7 Ejeplo utlzando la dstbucón no estaconaa Se desea dseña una sstea Bonus-Malus con las sas caacteístcas que en el ejeplo anteo y que adeás tenga en cuenta el tepo de peanenca de las pólzas en la epesa. Se supone que la dstbucón de la vaable aleatoa N a (núeo de años que lleva la pólza en la epesa) se dstbuye de odo unfoe duante los vente peos años. En este caso el valo de los pesos wn = n=,...,20 y 0 en oto caso. 20 Debeos calcula el vecto de pobabldades de la nueva dstbucón no estaconaa (véase pogaa ds-no-est ) y basándonos en esta dstbucón de pobabldades, plantea el sguente pogaa lneal 3 ( + ) n x y. q sujeto a 3 20 ( n ) n ( λj) π j j λj n= w. p + x y = j =,...,20 π π2, π2 π3,..., π2 π3 π 0, xj 0, yj 0, 3 ( x y). q = 0 =,...,3 j =,...,20 π 5π3 π.0π+ =,...,3 π0 = 0.52 Resolvendo el pogaa con Maple V se obtene coo solucón ópta la escala de pas j π j Que coo podeos copoba esultan bastante paecdas a las que se obtenen toando la dstbucón estaconaa. 7
8 Bblogafía Atículo Nobeg, R. (976). A Cedblty Theoy fo Autooble Bonus Systes. Scandnavan Actuaal Jounal, pp Atículo Boga, O., Hoe, J. y Nobeg, R. (98). A Non Asyptotc Cteon fo the Evaluaton of Autooble Bonus Systes. Scandnavan Actuaal Jounal, pp Tess Gacía P. (200). Dseño de Ssteas de Tafcacón Bonus-Malus edante la etodología de Pogaacón po Metas. Facultad de CC EE. UCM. Madd 8
ANEXO 4.1: Centro de masa y de gravedad
 Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
Profesor Francisco R. Villatoro 15 de Noviembre de 1999 SOLUCIONES. Soluciones de los ejercicios de la tercera relación de problemas.
 Tecea elacón de poblemas Técncas Numécas Pofeso Fancsco R. Vllatoo 5 de Novembe de 999 SOLUCIONES Solucones de los ejeccos de la tecea elacón de poblemas.. Se defne la taza de la matz cuadada A como la
Tecea elacón de poblemas Técncas Numécas Pofeso Fancsco R. Vllatoo 5 de Novembe de 999 SOLUCIONES Solucones de los ejeccos de la tecea elacón de poblemas.. Se defne la taza de la matz cuadada A como la
Examen de Física I. 1.- Explique como se puede reducir el siguiente sistema de vectores deslizantes
 Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
El Modelo Quark (III) Teoría de Grupos
 El Modelo Quak (III) Teoía de Gupos Rubén Sánchez-Raíez Según el teoea de Noethe, cada setía de la natualeza está asocada a una cantdad consevada y vcevesa. Una opeacón de setía es aquella que dea el sstea
El Modelo Quak (III) Teoía de Gupos Rubén Sánchez-Raíez Según el teoea de Noethe, cada setía de la natualeza está asocada a una cantdad consevada y vcevesa. Una opeacón de setía es aquella que dea el sstea
APÉNDICE B LOS ERRORES DE MUESTREO
 APÉNDICE B OS ERRORES DE MUESTREO OS ERRORES DE MUESTREO APÉNDICE B Po tatase de una encuesta po uesteo, los esultados de la ENDES 05 que se ncluyen en el pesente noe son estacones que están aectadas
APÉNDICE B OS ERRORES DE MUESTREO OS ERRORES DE MUESTREO APÉNDICE B Po tatase de una encuesta po uesteo, los esultados de la ENDES 05 que se ncluyen en el pesente noe son estacones que están aectadas
APÉNDICE 1 1. Sistemas de coordenadas
 APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
TEMA 2. CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS
 TEMA. CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS El capítulo tata de obtene una see de caacteístcas o meddas sobe una vaable aleatoa X que está especfcada a tavés de su funcón de pobabldad y que nos esuman
TEMA. CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS El capítulo tata de obtene una see de caacteístcas o meddas sobe una vaable aleatoa X que está especfcada a tavés de su funcón de pobabldad y que nos esuman
Coordenadas Generales.
 oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
Campo producido por un sistema de cargas puntuales
 lectcdad Magnetsmo / lectostátca Defncón os conductoes en electostátca. Campo de una caga puntual. Aplcacones de la e de Gauss Integales de supeposcón. Potencal electostátco. Defncón e Intepetacón. cuacones
lectcdad Magnetsmo / lectostátca Defncón os conductoes en electostátca. Campo de una caga puntual. Aplcacones de la e de Gauss Integales de supeposcón. Potencal electostátco. Defncón e Intepetacón. cuacones
COMPETENCIA ESPACIAL POR CUOTAS DE MERCADO: EL PROBLEMA DEL LÍDER-SEGUIDOR MEDIANTE PROGRAMACIÓN LINEAL
 Revsta Electónca de Councacones y Tabaos de ASEPUMA. Rect@ Voluen 2. Págnas 68 a 84. COMPETENCIA ESPACIAL POR CUOTAS DE MERCADO: EL PROBLEMA DEL LÍDER-SEGUIDOR MEDIANTE PROGRAMACIÓN LINEAL CLARA M. CAMPOS
Revsta Electónca de Councacones y Tabaos de ASEPUMA. Rect@ Voluen 2. Págnas 68 a 84. COMPETENCIA ESPACIAL POR CUOTAS DE MERCADO: EL PROBLEMA DEL LÍDER-SEGUIDOR MEDIANTE PROGRAMACIÓN LINEAL CLARA M. CAMPOS
Tema 2. DINÁMICA DE SISTEMAS DE PARTÍCULAS
 Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
Tema 7. Regresión Lineal
 Análss de Datos I Esquema del Tema 7 Tema 7. Regesón Lneal 1. INTRODUCCIÓN. IDENTIFICACIÓN DEL MODELO 3. VALORACIÓN DEL MODELO Coefcente de detemnacón Descomposcón de la vaanza del cteo. APLICACIÓN DEL
Análss de Datos I Esquema del Tema 7 Tema 7. Regesón Lneal 1. INTRODUCCIÓN. IDENTIFICACIÓN DEL MODELO 3. VALORACIÓN DEL MODELO Coefcente de detemnacón Descomposcón de la vaanza del cteo. APLICACIÓN DEL
DISEÑO DE SISTEMAS BONUS-MALUS EN EL CASO TRANSITORIO
 DISEÑO DE SISTAS BONUS-MALUS EN EL CASO TRANSITORIO Atoo Heas Matíez, José A. Gl Faa y José L. Vla Zaó Resume.- A la hoa de dseña u sstema bous-malus o paece adecuado cosdea sólo sus caacteístcas ua vez
DISEÑO DE SISTAS BONUS-MALUS EN EL CASO TRANSITORIO Atoo Heas Matíez, José A. Gl Faa y José L. Vla Zaó Resume.- A la hoa de dseña u sstema bous-malus o paece adecuado cosdea sólo sus caacteístcas ua vez
Cantidad de Momento, Conservación, Choques, Centro de Masa
 Cantdad de Moento, Conseracón, Choques, Centro de Masa Moentu líneal Las fuerzas aplcadas en una dreccón que no pasa por el centro de graedad de un objeto producen un gro en éste objeto. Para edr la agntud
Cantdad de Moento, Conseracón, Choques, Centro de Masa Moentu líneal Las fuerzas aplcadas en una dreccón que no pasa por el centro de graedad de un objeto producen un gro en éste objeto. Para edr la agntud
I ESCUELA DE EMPRESARIALES DIPLOMATURA DE EMPRESARIALES ESTADÍSTICA
 Depatamento de Economía Aplcada I EUELA DE EMPREARIALE DIPLOMATURA DE EMPREARIALE ETADÍTIA Ejeccos Resueltos REGREIÓ O LIEAL Y REGREIÓ LIEAL MÚLTIPLE uso 006-00 Escuela de Empesaales Depatamento de Economía
Depatamento de Economía Aplcada I EUELA DE EMPREARIALE DIPLOMATURA DE EMPREARIALE ETADÍTIA Ejeccos Resueltos REGREIÓ O LIEAL Y REGREIÓ LIEAL MÚLTIPLE uso 006-00 Escuela de Empesaales Depatamento de Economía
RELACIÓN DE PROBLEMAS DE CLASE DE MODELADO DE DECISIÓN MULTICRITERIO PROBLEMA 1: FÁBRICA DE COMPONENTES ELECTRÓNICOS (FACTORY OF
 RELACIÓN DE PROBLEMAS DE CLASE DE MODELADO DE DECISIÓN MULTICRITERIO PROBLEMA 1: FÁBRICA DE COMPONENTES ELECTRÓNICOS (FACTOR OF ELECTRONIC PARTS) Una empresa fabrca tres tpos de componentes electróncos,
RELACIÓN DE PROBLEMAS DE CLASE DE MODELADO DE DECISIÓN MULTICRITERIO PROBLEMA 1: FÁBRICA DE COMPONENTES ELECTRÓNICOS (FACTOR OF ELECTRONIC PARTS) Una empresa fabrca tres tpos de componentes electróncos,
5. DIAGONALIZACIÓN DE MATRICES
 Dagonalzacón Herraentas nforátcas para el ngenero en el estudo del algebra lneal 5. DIAGONALIZACIÓN DE MATRICES 5.1. INTRODUCCIÓN 5.2. VALORES Y VECTORES PROPIOS 5.3. MATRICES DIAGONALIZABLES 5.4. DIAGONALIZACIÓN
Dagonalzacón Herraentas nforátcas para el ngenero en el estudo del algebra lneal 5. DIAGONALIZACIÓN DE MATRICES 5.1. INTRODUCCIÓN 5.2. VALORES Y VECTORES PROPIOS 5.3. MATRICES DIAGONALIZABLES 5.4. DIAGONALIZACIÓN
LECTURA 02: DISTRIBUCIONES DE FRECUENCIAS (PARTE I) DISTRIBUCIONES DE FRECUENCIAS EN PUNTOS AISLADOS
 Unversdad Católca Los Ángeles de Cbote LECTURA 0: DISTRIBUCIONES DE FRECUENCIAS (PARTE I) DISTRIBUCIONES DE FRECUENCIAS EN PUNTOS AISLADOS TEMA : DISTRIBUCION DE FRECUENCIAS: DEFINICIÓN Y CLASIFICACIÓN
Unversdad Católca Los Ángeles de Cbote LECTURA 0: DISTRIBUCIONES DE FRECUENCIAS (PARTE I) DISTRIBUCIONES DE FRECUENCIAS EN PUNTOS AISLADOS TEMA : DISTRIBUCION DE FRECUENCIAS: DEFINICIÓN Y CLASIFICACIÓN
La Carga Eléctrica Puntual, es una partícula cuya masa se supone está concentrada en un punto, y en el mismo se concentra su carga eléctrica.
 LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
Destilación Multicomponente
 Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
El modelo de Hicks-Hansen (IS LM).
 El odelo de Hcks-Hansen (IS M). Hstoa del Modelo IS M En una Confeenca con teas de econoía, ealzada en Oxfod en septee de 1936, sugó el odelo IS M. Roy Haod, John R. Hcks, y Jaes Meade pesentaon docuentos
El odelo de Hcks-Hansen (IS M). Hstoa del Modelo IS M En una Confeenca con teas de econoía, ealzada en Oxfod en septee de 1936, sugó el odelo IS M. Roy Haod, John R. Hcks, y Jaes Meade pesentaon docuentos
Una Variante del Teorema de la Amistad. Sampertegui M. 1. (Recibido: 18/04/ Aceptado: 01/07/2016) A Variant of The Theorem of Friendship
 PESQUIMAT, Revsta de la F.C.M. de la Unvesdad Naconal Mayo de San Mac Vol. XIX N ı 2,. 4-25, Julo Dcembe 206 Una Vaante del Teoema de la Amstad Montoo E. Huamán C. Castllo E. Melgaeo G. Amas E. Sametegu
PESQUIMAT, Revsta de la F.C.M. de la Unvesdad Naconal Mayo de San Mac Vol. XIX N ı 2,. 4-25, Julo Dcembe 206 Una Vaante del Teoema de la Amstad Montoo E. Huamán C. Castllo E. Melgaeo G. Amas E. Sametegu
Estructura de la materia 3 Serie 2 Modelo de Thomas-Fermi y Sistemas Atómicos Cátedra: Jorge Miraglia. Segundo cuatrimestre de 2013
 Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
EJERCICIO RESUELTO DE RIESGO MORAL
 Pontfca Unversdad Católca del Perú Prograa de Maestría en Econoía Curso Mcroeconoía Avanzada Profesora Clauda Barrga Ch. Asstente Sandro A. Huaaní. EJERCICIO RESUELTO DE RIESGO MORAL Aplcacón al ercado
Pontfca Unversdad Católca del Perú Prograa de Maestría en Econoía Curso Mcroeconoía Avanzada Profesora Clauda Barrga Ch. Asstente Sandro A. Huaaní. EJERCICIO RESUELTO DE RIESGO MORAL Aplcacón al ercado
Bibliografía. Bibliografía. Fundamentos Físicos de la Ingeniería. Tema 3 Mc Graw Hill. - Tipler. "Física". Cap. 23. Reverté.
 Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
MOVIMIENTO DE UNA PARTICULA EN EL CAMPO GRAVITACIONAL REAL
 MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
Comportamiento elástico de los materiales. A r. B r. A, B son constantes de proporcionalidad para atracción y repulsión.
 Pogaa de Doctoado en Ingeneía eonáutca apítulo I. opotaento elástco de los ateales ases tócas del opotaento Elástco Enegía Fuea de Enlace opotaento elástco de los ateales La Enegía Potencal de un pa de
Pogaa de Doctoado en Ingeneía eonáutca apítulo I. opotaento elástco de los ateales ases tócas del opotaento Elástco Enegía Fuea de Enlace opotaento elástco de los ateales La Enegía Potencal de un pa de
Métodos Prácticos para obtener la Prima del Reaseguro de Stop Loss en el Seguro de Vida
 Métodos áctcos paa obtene la ma del Reaseguo de top Loss en el eguo de Vda Rcado Nava Ramíez y Tapen nha Julo 999 ee Documentos de Tabajo Documento de Tabajo No. 74 Índce Reseña apítulo I Qué es el Reaseguo?
Métodos áctcos paa obtene la ma del Reaseguo de top Loss en el eguo de Vda Rcado Nava Ramíez y Tapen nha Julo 999 ee Documentos de Tabajo Documento de Tabajo No. 74 Índce Reseña apítulo I Qué es el Reaseguo?
El Modelo IS LM: un enfoque Conceptual, Geométrico y Algebraico.
 El Modelo IS LM: un enfoque Conceptual, Geoétco Algeaco. 1.- Intoduccón El Modelo IS LM es una epesentacón splfcada del funconaento de una econoía e ntenta explca la nteelacón ente las pncpales vaales
El Modelo IS LM: un enfoque Conceptual, Geoétco Algeaco. 1.- Intoduccón El Modelo IS LM es una epesentacón splfcada del funconaento de una econoía e ntenta explca la nteelacón ente las pncpales vaales
E.T.S. Ingenieros de Caminos, Canales y Puertos
 E.T.S. Ingeneos de anos, anales y Puetos Unvesdad de Ganada TEE PÁTI TEOÍ E ESTUTUS IL PELLIOS: FIM: NOME: NI: Ipescndble entega el anuscto ognal gapado a este enuncado (no olvde ellena los datos pesonales
E.T.S. Ingeneos de anos, anales y Puetos Unvesdad de Ganada TEE PÁTI TEOÍ E ESTUTUS IL PELLIOS: FIM: NOME: NI: Ipescndble entega el anuscto ognal gapado a este enuncado (no olvde ellena los datos pesonales
Capítulo 5: Variables Aleatorias Distribuciones Estadística Computacional I Semestre Variables Aleatorias
 Unvedad Técnca Fedeco Santa Maía Depatamento de Infomátca ILI-80 Capítulo 5: Vaable Aleatoa Dtbucone Etadítca Computaconal I Semete 006 Pofeo : Pofeo : Hécto Allende Calo Valle Funcón que agna a cada punto
Unvedad Técnca Fedeco Santa Maía Depatamento de Infomátca ILI-80 Capítulo 5: Vaable Aleatoa Dtbucone Etadítca Computaconal I Semete 006 Pofeo : Pofeo : Hécto Allende Calo Valle Funcón que agna a cada punto
Planeación y Control de Proyectos con Diferentes Tipos de Precedencias Utilizando Simulación Estocástica
 Infoacón Tecnológca Planeacón Vol. 2(4), y 25-33 Contol (200) de Poyectos con Dfeentes Tpos de Pecedencas do:0.62/nf.tecnol.4338t.09 Planeacón y Contol de Poyectos con Dfeentes Tpos de Pecedencas Utlzando
Infoacón Tecnológca Planeacón Vol. 2(4), y 25-33 Contol (200) de Poyectos con Dfeentes Tpos de Pecedencas do:0.62/nf.tecnol.4338t.09 Planeacón y Contol de Poyectos con Dfeentes Tpos de Pecedencas Utlzando
r R r M SISTEMA DE PARTÍCULAS CINEMATICA DEL SISTEMA DE PARTICULAS:
 FíscaGuay SISTEA DE PARTÍCULAS CINEATICA DEL SISTEA DE PARTICULAS: Un sstea de patículas es un conjunto de patículas con alguna elacón ente ellas, peo cada una de ellas poseen un ecto de poscón, una elocdad,
FíscaGuay SISTEA DE PARTÍCULAS CINEATICA DEL SISTEA DE PARTICULAS: Un sstea de patículas es un conjunto de patículas con alguna elacón ente ellas, peo cada una de ellas poseen un ecto de poscón, una elocdad,
Momento cuadrupolar eléctrico
 Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
TEMA 6 VALORACIÓN FINANCIERA DE RENTAS (III)
 Facultad de.ee. Dpto. de Ecooía Facea I Dapostva Mateátca Facea TEMA 6 VALORAIÓN FINANIERA DE RENTAS III. Faccoaeto atétco y faceo de ua eta 2. Retas faccoadas 3. Retas cotuas Facultad de.ee. Dpto. de
Facultad de.ee. Dpto. de Ecooía Facea I Dapostva Mateátca Facea TEMA 6 VALORAIÓN FINANIERA DE RENTAS III. Faccoaeto atétco y faceo de ua eta 2. Retas faccoadas 3. Retas cotuas Facultad de.ee. Dpto. de
SOLUCIONARIO GUÍA ESTÁNDAR ANUAL Dinámica II: ley de gravitación y fuerza de roce
 SOLUCIONARIO GUÍA ESTÁNDAR ANUAL Dináica II: ley de gavitación y ueza de SGUICES017CB3-A16V1 Solucionaio guía Dináica II: ley de gavitación y ueza de Íte Altenativa Habilidad 1 C Copensión E Reconociiento
SOLUCIONARIO GUÍA ESTÁNDAR ANUAL Dináica II: ley de gavitación y ueza de SGUICES017CB3-A16V1 Solucionaio guía Dináica II: ley de gavitación y ueza de Íte Altenativa Habilidad 1 C Copensión E Reconociiento
CAPÍTULO 3 - POTENCIA ALTERNA
 CAPÍTULO 3 - POTENCA ALTERNA 3-- POTENCA ACTVA (t) Dadas v(t) e (t) la potenca nstantánea en un crcuto genérco es: p(t) = v(t). (t) v(t) Crcuto La potenca p puede ser postva o negatva según el nstante
CAPÍTULO 3 - POTENCA ALTERNA 3-- POTENCA ACTVA (t) Dadas v(t) e (t) la potenca nstantánea en un crcuto genérco es: p(t) = v(t). (t) v(t) Crcuto La potenca p puede ser postva o negatva según el nstante
Ondas. Conceptos básicos
 Ondas. Conceptos báscos IES La Magdalena. Avlés. Astuas Una onda es una petubacón que se popaga. Con la palaba petubacón se quee ndca cualque tpo de alteacón del medo: una ondulacón en una cueda, una sobepesón
Ondas. Conceptos báscos IES La Magdalena. Avlés. Astuas Una onda es una petubacón que se popaga. Con la palaba petubacón se quee ndca cualque tpo de alteacón del medo: una ondulacón en una cueda, una sobepesón
TEMA 3. VARIABLE ALEATORIA
 TEMA 3. VARIABLE ALEATORIA 3.. Introduccón. 3... Dstrbucón de Probabldad de una varable aleatora 3... Funcón de Dstrbucón de una varable aleatora 3.. Varable aleatora dscreta 3... Funcón masa de probabldad
TEMA 3. VARIABLE ALEATORIA 3.. Introduccón. 3... Dstrbucón de Probabldad de una varable aleatora 3... Funcón de Dstrbucón de una varable aleatora 3.. Varable aleatora dscreta 3... Funcón masa de probabldad
Análisis de Correspondencias Simples ACS. Prof: Salvador Carrasco Arroyo
 Análss de Coespondencas Smples ACS Po: Salvado Caasco Aoyo Mateas Toncales Estadístca I Estadístca II Tema : Análss de Datos Multvaantes Tema : Análss de la Vaanza Tema 3: Técncas de Análss Multvaantes
Análss de Coespondencas Smples ACS Po: Salvado Caasco Aoyo Mateas Toncales Estadístca I Estadístca II Tema : Análss de Datos Multvaantes Tema : Análss de la Vaanza Tema 3: Técncas de Análss Multvaantes
3.5 OPERADORES DIFERENCIALES EN COORDENADAS CURVILÍNEAS ORTOGONALES.
 .5 OPERADORES DIFERENCIALES EN COORDENADAS CURVILÍNEAS ORTOGONALES..5. Opeado en coodenadas cuvíneas. Opeado naba en coodenadas catesanas: j + + x y z La foa de este opeado en coodenadas cuvíneas (no necesaaente
.5 OPERADORES DIFERENCIALES EN COORDENADAS CURVILÍNEAS ORTOGONALES..5. Opeado en coodenadas cuvíneas. Opeado naba en coodenadas catesanas: j + + x y z La foa de este opeado en coodenadas cuvíneas (no necesaaente
3. VARIABLES ALEATORIAS.
 3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
dq de x r CAMPO DE UN ANILLO CON CARGA UNIFORME r α P de y de x
 y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Ximénez & San Martín, 2004)
 FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Xménez & San Martín, 004) Capítulo. Nocones báscas de álgebra de matrces Fe de erratas.. Cálculo de la transpuesta de una matrz
FE DE ERRATAS Y AÑADIDOS AL LIBRO FUNDAMENTOS DE LAS TÉCNICAS MULTIVARIANTES (Xménez & San Martín, 004) Capítulo. Nocones báscas de álgebra de matrces Fe de erratas.. Cálculo de la transpuesta de una matrz
INTRODUCCIÓN A LA ESTADÍSTICA. CURSO FEBRERO. Código de carrera 43. Código de asignatura 203. n i l
 TUTORÍA DE ITRODUCCIÓ A LA ESTADÍSTICA. º CURSO ECOOMÍA e-mal: mozas@elx.uned.es www.telefonca.net/web/mm ITRODUCCIÓ A LA ESTADÍSTICA. CURSO.000-.00. FEBRERO. Códgo de caea 43. Códgo de asgnatua 03. Peguntas
TUTORÍA DE ITRODUCCIÓ A LA ESTADÍSTICA. º CURSO ECOOMÍA e-mal: mozas@elx.uned.es www.telefonca.net/web/mm ITRODUCCIÓ A LA ESTADÍSTICA. CURSO.000-.00. FEBRERO. Códgo de caea 43. Códgo de asgnatua 03. Peguntas
CAPÍTULO III TRABAJO Y ENERGÍA
 TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
Apéndice A. Principio de Mínima Acción y Energía Mecánica total.
 Apéndce A Prncpo de Mína Accón y Energía Mecánca total. E l prncpo de ína accón es equvalente a decr que la tayectora que sgue una partícula en el espaco de conguracón es aquella para la cual la dferenca
Apéndce A Prncpo de Mína Accón y Energía Mecánca total. E l prncpo de ína accón es equvalente a decr que la tayectora que sgue una partícula en el espaco de conguracón es aquella para la cual la dferenca
LECCIÓN Nº 06 TRANSISTORES DE EFECTO CAMPO
 UNIESIA JOSE CAOS MAIATEGUI ECCIÓN Nº 6 TANSISTOES E EFECTO CAMPO. ESTABIIA E POAIZACION FET os tansstoes de efecto de capo o FET (Feld Electc Tanssto) son patculaente nteesantes en ccutos nteados y pueden
UNIESIA JOSE CAOS MAIATEGUI ECCIÓN Nº 6 TANSISTOES E EFECTO CAMPO. ESTABIIA E POAIZACION FET os tansstoes de efecto de capo o FET (Feld Electc Tanssto) son patculaente nteesantes en ccutos nteados y pueden
Diagramas de Heissler para la solución de problemas de conducción transitoria.
 Dagraas de Hessler para la solucón de probleas de conduccón transtora. Cuando el núero de Bot odfcado, descrto en la seccón anteror supera el valor de 0,1, la resstenca nterna ya no es desprecable, de
Dagraas de Hessler para la solucón de probleas de conduccón transtora. Cuando el núero de Bot odfcado, descrto en la seccón anteror supera el valor de 0,1, la resstenca nterna ya no es desprecable, de
Potencial eléctrico. Física II Grado en Ingeniería de Organización Industrial Primer Curso. Departamento de Física Aplicada III Universidad de Sevilla
 Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
Se le define como toda situación física producidapor una masa men el espacio que lo rodeay que es perceptible debido a la fuerza que ejerce sobre una
 Cpo vtconl Se le defne coo tod stucón físc poducdpo un s en el espco que lo ode que es peceptble debdo l fuez que ejece sobe un s colocd en dco espco. Dd un s en el espco un s en dfeentes poscones lededo
Cpo vtconl Se le defne coo tod stucón físc poducdpo un s en el espco que lo ode que es peceptble debdo l fuez que ejece sobe un s colocd en dco espco. Dd un s en el espco un s en dfeentes poscones lededo
Apuntes de Evaluación de Proyectos X. Indicadores para Evaluación de Proyectos Riesgosos
 Apuntes de Evaluacón de Poyectos X. Indcadoes paa Evaluacón de Poyectos Resgosos. CONSIDERACIÓN DEL RIESGO EN LA EVALUACIÓN DE PROYECTOS DE INVERSIÓN - INTRODUCCIÓN Demos que un poyecto es esgoso cuando
Apuntes de Evaluacón de Poyectos X. Indcadoes paa Evaluacón de Poyectos Resgosos. CONSIDERACIÓN DEL RIESGO EN LA EVALUACIÓN DE PROYECTOS DE INVERSIÓN - INTRODUCCIÓN Demos que un poyecto es esgoso cuando
II. Electrostática tica en el vacío
 II. Electostátca tca en el vacío 8. Dpolo eléctco Gabel Cano Gómez, G 29/ Dpto. Físca F Aplcada III (U. Sevlla) Campos Electomagnétcos tcos Ingeneo de Telecomuncacón II. Electostátca tca en el vacío Gabel
II. Electostátca tca en el vacío 8. Dpolo eléctco Gabel Cano Gómez, G 29/ Dpto. Físca F Aplcada III (U. Sevlla) Campos Electomagnétcos tcos Ingeneo de Telecomuncacón II. Electostátca tca en el vacío Gabel
TEMA 6: RENTAS VARIABLES. (1+i) A n-1
 TEMA 6: RENTAS VARIABLES. RENTAS VARIABLES EN GENERAL Son auellas entas en las ue los témnos no son constantes, su valo actual y fnal se calculan a pat del pncpo de euvalenca fnancea, actualzando (valo
TEMA 6: RENTAS VARIABLES. RENTAS VARIABLES EN GENERAL Son auellas entas en las ue los témnos no son constantes, su valo actual y fnal se calculan a pat del pncpo de euvalenca fnancea, actualzando (valo
Optica I. seni nsenr seni nsenr nsen(90 i) ncos i seni tg i n 1,5 i 56,30º cosi. nseni sen90 1 seni 0,66 i 41,30º.
 01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
Electricidad y Magnetismo Curso 2010/2011
 lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medida del índice de refracción de una lámina de vidrio
 Coodnacón EVAU. Páctcas cuso 2017-18 P2 Objetvo: Detemna el índce de efaccón de un vdo. Fundamento: PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medda del índce de efaccón de una lámna de vdo La ley de la efaccón,
Coodnacón EVAU. Páctcas cuso 2017-18 P2 Objetvo: Detemna el índce de efaccón de un vdo. Fundamento: PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medda del índce de efaccón de una lámna de vdo La ley de la efaccón,
EL EQUILIBRIO DEL MERCADO TEMA 4 FUNDAMENTOS DE DIRECCIÓN FINANCIERA. Fundamentos de Dirección Financiera Tema 4
 EL EQUILIRIO DEL ERCADO TEA 4 FUNDAENTOS DE DIRECCIÓN FINANCIERA 1 OJETIVO DEL TEA. usca una medda apopada del esgo y su valoacón (conoce la estuctua de los pecos de los actvos en elacón a su esgo) usca
EL EQUILIRIO DEL ERCADO TEA 4 FUNDAENTOS DE DIRECCIÓN FINANCIERA 1 OJETIVO DEL TEA. usca una medda apopada del esgo y su valoacón (conoce la estuctua de los pecos de los actvos en elacón a su esgo) usca
EXÁMENES DE CURSOS ANTERIORES
 EXÁMENES DE CURSOS NTERIORES CURSO 8 LOQUE. GEOMETRÍ EXMEN. Geoetía afín euclídea en el epacio tidienional. RECUPERIÓN EXMEN. Geoetía afín euclídea en el epacio tidienional. º CT. MTEMÁTICS II. LOQUE.
EXÁMENES DE CURSOS NTERIORES CURSO 8 LOQUE. GEOMETRÍ EXMEN. Geoetía afín euclídea en el epacio tidienional. RECUPERIÓN EXMEN. Geoetía afín euclídea en el epacio tidienional. º CT. MTEMÁTICS II. LOQUE.
Sistemas de partículas
 Ssteas de patículas Hasta aquí heos aplcado las leyes de ewton tatando a los objetos coo s fuean patículas puntuales que tenen asa peo no taaño, aunque uchas de las aplcacones se extendían a objetos coo
Ssteas de patículas Hasta aquí heos aplcado las leyes de ewton tatando a los objetos coo s fuean patículas puntuales que tenen asa peo no taaño, aunque uchas de las aplcacones se extendían a objetos coo
Elementos de Aritmética de Computadoras Parte I
 Elementos de Atmétca de Computadoas Pate I M. Vázquez, E. Todoovch, M. Tosn Aqutectua I - Cuso 3 UNICEN Cómputo Atmétco Las peguntas de fondo cuando se aboda el tema de la atmétca de computadoas son: Cómo
Elementos de Atmétca de Computadoas Pate I M. Vázquez, E. Todoovch, M. Tosn Aqutectua I - Cuso 3 UNICEN Cómputo Atmétco Las peguntas de fondo cuando se aboda el tema de la atmétca de computadoas son: Cómo
PROBLEMA Flujo uniforme con superficie libre, a lo largo de un plano inclinado.
 1 IQ36A FENOMENOS DE TRANSPORTE, SEMESTRE 08-1 GUIA CAPITULO 6. Cap. 6.: Ecuacón de Nave-Stokes. PROBLEMA 6.-1.- Flujo unfome con supefce lbe, a lo lago de un plano nclnado. Analza el flujo gavtaconal
1 IQ36A FENOMENOS DE TRANSPORTE, SEMESTRE 08-1 GUIA CAPITULO 6. Cap. 6.: Ecuacón de Nave-Stokes. PROBLEMA 6.-1.- Flujo unfome con supefce lbe, a lo lago de un plano nclnado. Analza el flujo gavtaconal
CAPÍTULO 2 - CORRIENTES ALTERNAS
 APÍTUO - OIENTES ATENAS -- FOMAS DE ONDA aos a ltar el estudo de foras de onda peródca, es decr donde f(t) f (t + nt), sendo n un núero entero y T el período.- T T T -- AO MEDIO El valor edo de una funcón
APÍTUO - OIENTES ATENAS -- FOMAS DE ONDA aos a ltar el estudo de foras de onda peródca, es decr donde f(t) f (t + nt), sendo n un núero entero y T el período.- T T T -- AO MEDIO El valor edo de una funcón
3 - VARIABLES ALEATORIAS
 arte Varables aleatoras rof. María B. ntarell - VARIABLES ALEATORIAS.- Generaldades En muchas stuacones epermentales se quere asgnar un número real a cada uno de los elementos del espaco muestral. Al descrbr
arte Varables aleatoras rof. María B. ntarell - VARIABLES ALEATORIAS.- Generaldades En muchas stuacones epermentales se quere asgnar un número real a cada uno de los elementos del espaco muestral. Al descrbr
6. CAPM: Capital Asset Pricing Model IN56A
 6. CA: Captal Asset cng odel IN56A Otoño 009 Gonzalo atuana F. Recuedo cap. anteo Fontea de Invesón (Ecente) 5% 4% ed pestado Retono Espeado 3% % % 0% 9% esta 8% 7% 6% 0% 5% 0% 5% 0% 5% 30% 35% 40% 45%
6. CA: Captal Asset cng odel IN56A Otoño 009 Gonzalo atuana F. Recuedo cap. anteo Fontea de Invesón (Ecente) 5% 4% ed pestado Retono Espeado 3% % % 0% 9% esta 8% 7% 6% 0% 5% 0% 5% 0% 5% 30% 35% 40% 45%
CAPÍTULO V SISTEMAS DE PARTÍCULAS
 CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
SISTEMA DE PEARSON GENERALIZADO MEDIANTE SPLINES
 SISTEMA DE PEARSON GENERALIZADO MEDIANTE SPLINES Fedeco Palacos González - fpalaco@ug.es Rafael Heeías Pleguezuelo - hee@ug.es José Calleón Céspedes - calleon@ug.es Unvesdad de Ganada Resevados todos los
SISTEMA DE PEARSON GENERALIZADO MEDIANTE SPLINES Fedeco Palacos González - fpalaco@ug.es Rafael Heeías Pleguezuelo - hee@ug.es José Calleón Céspedes - calleon@ug.es Unvesdad de Ganada Resevados todos los
LOS SIMBOLOS DE CHRISTOFFEL
 CRLOS S. CHINE LOS SIMBOLOS DE CHRISTOFFEL Lo íbolo ue etudao auí fueon ntoducdo en la ateátca, a fnale del lo XIX, o el aleán Elwn Buno Ctoffel (89 900, ue fue, unto con Benad Reann, el eo en etablece
CRLOS S. CHINE LOS SIMBOLOS DE CHRISTOFFEL Lo íbolo ue etudao auí fueon ntoducdo en la ateátca, a fnale del lo XIX, o el aleán Elwn Buno Ctoffel (89 900, ue fue, unto con Benad Reann, el eo en etablece
MEDIDAS DE FORMA: ASIMETRÍA Y CURTOSIS. MOMENTOS
 Julo Olva Coteo Estadístca TEMA 6 MEDIDA DE FORMA: AIMETRÍA Y CURTOI. MOMETO. Moetos de ua dstbucó Los oetos de ua dstbucó so eddas obtedas a pat de todos sus datos y de sus fecuecas absolutas. Estas eddas
Julo Olva Coteo Estadístca TEMA 6 MEDIDA DE FORMA: AIMETRÍA Y CURTOI. MOMETO. Moetos de ua dstbucó Los oetos de ua dstbucó so eddas obtedas a pat de todos sus datos y de sus fecuecas absolutas. Estas eddas
SOLUCIÓN DE LA PRUEBA DE ACCESO
 ísca 1 ísca SOLUCÓN DE LA PRUEBA DE ACCESO AUTOR: Tomás Caballeo Rodíguez Opcón A a) Ley de gavtacón unvesal de Newton: dos masas cualesquea se ataen con una fueza que es dectamente popoconal al poducto
ísca 1 ísca SOLUCÓN DE LA PRUEBA DE ACCESO AUTOR: Tomás Caballeo Rodíguez Opcón A a) Ley de gavtacón unvesal de Newton: dos masas cualesquea se ataen con una fueza que es dectamente popoconal al poducto
TRABAJO Y ENERGIA. 5.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE.
 TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
OPTIMIZACIÓN CON RESTRICCIONES DE IGUALDAD
 OPIMIZACIÓN CON RESRICCIONES DE IGUALDAD Localzacón de óptos de funcones sujetas a restrccones en fora de gualdad écnca de los ultplcadores de Lagrange Forulacón estándar del problea f =,,..., Se consderarán
OPIMIZACIÓN CON RESRICCIONES DE IGUALDAD Localzacón de óptos de funcones sujetas a restrccones en fora de gualdad écnca de los ultplcadores de Lagrange Forulacón estándar del problea f =,,..., Se consderarán
[1] [1 ] Esta condición evita que haya rotación del sistema Composición de fuerzas paralelas.
![[1] [1 ] Esta condición evita que haya rotación del sistema Composición de fuerzas paralelas. [1] [1 ] Esta condición evita que haya rotación del sistema Composición de fuerzas paralelas.](/thumbs/68/58837177.jpg) Tea 4 Ssteas de partículas 4.. Estátca y equlbro. 4... Condcones de equlbro. Las condcones de equlbro conssten en que para que un sstea esté en equlbro, la fuerza total externa aplcada debe ser nula: F
Tea 4 Ssteas de partículas 4.. Estátca y equlbro. 4... Condcones de equlbro. Las condcones de equlbro conssten en que para que un sstea esté en equlbro, la fuerza total externa aplcada debe ser nula: F
Tema 2. Oligopolio. Introducción El modelo de Cournot Duopolio Equilibrio Colusión:
 Tea. Olgopolo Tea. Olgopolo Introduccón.. El odelo de Cournot.... Duopolo.... Equlbro.... Colusón:... Colusón a corto plazo.... Establdad de los acuerdos y juegos repetdos.... Olgopolo (n epresas)....
Tea. Olgopolo Tea. Olgopolo Introduccón.. El odelo de Cournot.... Duopolo.... Equlbro.... Colusón:... Colusón a corto plazo.... Establdad de los acuerdos y juegos repetdos.... Olgopolo (n epresas)....
Programación y Métodos Numéricos Interpolación polinómica de de Hermite: PLANTEAMIENTO Y CASO DE PRIMER ORDEN
 Prograacón y Métodos Nuércos Interpolacón polnóca de de Herte: PLANTEAMIENTO Y CASO DE PRIMER ORDEN Alfredo López L Bento Carlos Conde LázaroL Arturo Hdalgo LópezL Marzo, 7 Departaento de Mateátca Aplcada
Prograacón y Métodos Nuércos Interpolacón polnóca de de Herte: PLANTEAMIENTO Y CASO DE PRIMER ORDEN Alfredo López L Bento Carlos Conde LázaroL Arturo Hdalgo LópezL Marzo, 7 Departaento de Mateátca Aplcada
FI1002 Sistemas Newtonianos Judit Lisoni Sección 6
 F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
LABORATORIO DE FÍSICA
 LABORATORIO DE FÍSICA Ley de Faaday-Lenz. 6.04 1-Suponga que el plano de u hoja contene un ao conducto. Exte una fe () ucda en el ao paa lo guente cao?. Jutfque u epueta. a- El polo Note de un án en baa
LABORATORIO DE FÍSICA Ley de Faaday-Lenz. 6.04 1-Suponga que el plano de u hoja contene un ao conducto. Exte una fe () ucda en el ao paa lo guente cao?. Jutfque u epueta. a- El polo Note de un án en baa
LA RIOJA / JUNIO 01. LOGSE / FÍSICA / EXAMEN COMPLETO
 LA RIOJA / JUNIO 1. LOGS / FÍSICA / XAMN COMPLTO l luno elegá un de ls opcones de pobles y cuto de ls cnco cuestones popuests. Cd poble puntú sobe tes puntos y cd cuestón sobe uno. Opcón de pobles 1 A.
LA RIOJA / JUNIO 1. LOGS / FÍSICA / XAMN COMPLTO l luno elegá un de ls opcones de pobles y cuto de ls cnco cuestones popuests. Cd poble puntú sobe tes puntos y cd cuestón sobe uno. Opcón de pobles 1 A.
CONTENIDO SISTEMA DE PARTÍCULAS. Definición y cálculo del centro de masas. Movimiento del centro de masas. Fuerzas internas y fuerzas externas
 COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
Ecuaciones de Lagrange. Ecuaciones de Lagrange: Cálculo de variaciones
 Unvesa Són Bolíva. ees e ewon. Cneáca. Dnáca Ss. e paículas Cuepo ígo Defncones a le a le enso e neca a le unplana 3 a le Ecs. e agange Ecuacones e agange as ecuacones e agange peen la foulacón e las lees
Unvesa Són Bolíva. ees e ewon. Cneáca. Dnáca Ss. e paículas Cuepo ígo Defncones a le a le enso e neca a le unplana 3 a le Ecs. e agange Ecuacones e agange as ecuacones e agange peen la foulacón e las lees
TEMA 4. SISTEMAS DE PARTÍCULAS
 EMA 4. SISEMAS DE PARÍCULAS. Cento de asas y coodenadas elatvas. Fuezas ntenas y enas.. Consevacón del oento lneal total de un sstea. Ssteas de asa vaable y ejeplos. 3. Consevacón del oento angula de un
EMA 4. SISEMAS DE PARÍCULAS. Cento de asas y coodenadas elatvas. Fuezas ntenas y enas.. Consevacón del oento lneal total de un sstea. Ssteas de asa vaable y ejeplos. 3. Consevacón del oento angula de un
sea un nº real. Hallar su cociente. Solución. Se multiplica numerador y denominador por el conjugado del denominador.
 . Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
. Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
Redes abiertas. Pág. 345 (Sotelo)
 Redes abertas. Pág. 45 (Sotelo) ecos que una red de tuberías es aberta cuando los tubos que la coponen se racan, sn ntersectarse después para orar crcutos. Los extreos nales de las racacones pueden ternar
Redes abertas. Pág. 45 (Sotelo) ecos que una red de tuberías es aberta cuando los tubos que la coponen se racan, sn ntersectarse después para orar crcutos. Los extreos nales de las racacones pueden ternar
GEOMETRÍA ANALÍTICA PLANA
 GEOMETRÍ NLÍTIC PLN / Ecuaciones de la ecta Un punto y un vecto Dos puntos Un punto y la pendiente,,,,,, Coodenadas del vecto diecto ECUCION VECTORIL (x, y) (p, p ) + τ (v, v ) ECUCION PRMETRIC x p + τ
GEOMETRÍ NLÍTIC PLN / Ecuaciones de la ecta Un punto y un vecto Dos puntos Un punto y la pendiente,,,,,, Coodenadas del vecto diecto ECUCION VECTORIL (x, y) (p, p ) + τ (v, v ) ECUCION PRMETRIC x p + τ
SELECTIVIDAD SEPTIEMBRE 2004 MATEMÁTICAS II
 Depatament de Matemàtiques Ieslaasuncionog/matematicas SELECTIVIDAD SEPTIEMBRE MATEMÁTICAS II EJERCICIO A PROBLEMA Obtene todos los valoes eales x, y, z, t paa los que se veifica AX XA, siendo X y A z
Depatament de Matemàtiques Ieslaasuncionog/matematicas SELECTIVIDAD SEPTIEMBRE MATEMÁTICAS II EJERCICIO A PROBLEMA Obtene todos los valoes eales x, y, z, t paa los que se veifica AX XA, siendo X y A z
sea un nº real. Hallar su cociente. Solución. Se multiplica numerador y denominador por el conjugado del denominador.
 . Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
. Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador, de esta
Gráficos de flujo de señal
 Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente en el análss y dseño de sstemas de control. Otro procedmento alternatvo
Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente en el análss y dseño de sstemas de control. Otro procedmento alternatvo
+ y 1 ; U 2 (x 2,y 2 ) = ax 2 (x 2) 2 2
 13. Consdere un mercado en el que hay dos consumdores con las sguentes funcones de utldad: U 1 (x 1,y 1 = 4x 1 (x 1 + y 1 ; U (x,y = ax (x + y con 4 > a >0 donde x, =1,, es la cantdad del ben x consumda
13. Consdere un mercado en el que hay dos consumdores con las sguentes funcones de utldad: U 1 (x 1,y 1 = 4x 1 (x 1 + y 1 ; U (x,y = ax (x + y con 4 > a >0 donde x, =1,, es la cantdad del ben x consumda
Introducción al Método de los Elementos Finitos
 S 4 v v 5 Introduccón al Método de los Elementos Fntos Parte 4 Estmacón de error en problemas elíptcos Alberto Cardona, Víctor Facnott Cmec-Intec (UNL/Concet), Santa Fe, Argentna Estmacón de error en problemas
S 4 v v 5 Introduccón al Método de los Elementos Fntos Parte 4 Estmacón de error en problemas elíptcos Alberto Cardona, Víctor Facnott Cmec-Intec (UNL/Concet), Santa Fe, Argentna Estmacón de error en problemas
Solución. Se multiplica numerador y denominador por el conjugado del denominador.
 . Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Solucón. Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador,
. Hallar "a" para que el complejo : a a) sea real puro b) sea magnaro puro Solucón. Lo prmero de todo es hacer la dvsón en forma bnómca, multplcando numerador y denomnador por el conjugado del denomnador,
* Introducción * Principio de mínima energía * Transformaciones de Legendre * Funciones (o potenciales) termodinámicas. Principios de mínimo.
 5. otencales emonámcos * Intouccón * ncpo e mínma enegía * ansomacones e Legene * Funcones (o potencales) temonámcas. ncpos e mínmo. * Enegía lbe (potencal) e Helmholtz lt * Entalpía. * Enegía lbe e Gbbs.
5. otencales emonámcos * Intouccón * ncpo e mínma enegía * ansomacones e Legene * Funcones (o potencales) temonámcas. ncpos e mínmo. * Enegía lbe (potencal) e Helmholtz lt * Entalpía. * Enegía lbe e Gbbs.
CUESTIÓN 2 ,R ~ β B =
 Fundamentos de Diección Financiea (4º EO) onvocatoia: Septiembe 006 UESTIÓN Dado que la catea A tiene más iesgo que la catea ( A = 0,1 > = 0,08) y su coelación con el mecado es meno (ρ A = 0,5 < ρ = 0,75),
Fundamentos de Diección Financiea (4º EO) onvocatoia: Septiembe 006 UESTIÓN Dado que la catea A tiene más iesgo que la catea ( A = 0,1 > = 0,08) y su coelación con el mecado es meno (ρ A = 0,5 < ρ = 0,75),
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA
 PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
r V CINEMÁTICA DEL SÓLIDO RÍGIDO
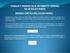 1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
A. De la Ficha nº13, recordamos las nociones de asociación o correlación y las distintas formas en que una relación puede ser analizada.
 CEFICIENTE DE CRRELACIÓN LINEAL DE PEARN A. De la Fcha nº13, ecodamos las nocones de asocacón o coelacón y las dstntas fomas en que una elacón puede se analzada. guendo la tadcón pncpal de la estadístca,
CEFICIENTE DE CRRELACIÓN LINEAL DE PEARN A. De la Fcha nº13, ecodamos las nocones de asocacón o coelacón y las dstntas fomas en que una elacón puede se analzada. guendo la tadcón pncpal de la estadístca,
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
TEMA 3.1 Mecánica del sólido deformable: Análisis de tensiones
 TEMA. Mecánca del sóldo defomable: Análss de tensones Físca Mecánca de las Constuccones ... Intoduccón MECÁNICA DEL MEDIO CONTINUO OBJETIVO: - estudo del compotamento de los medos defomables - establece
TEMA. Mecánca del sóldo defomable: Análss de tensones Físca Mecánca de las Constuccones ... Intoduccón MECÁNICA DEL MEDIO CONTINUO OBJETIVO: - estudo del compotamento de los medos defomables - establece
el conjunto de puntos del espacio que notaremos por A, B, Dados dos puntos A, B de E
 IES Pade Poeda (Gadx) Matemátcas II UNIDAD 8: VECTORES EN EL ESPACIO.. VECTORES FIJOS EN EL ESPACIO. Sea E el connto de pntos del espaco qe notaemos po A B C K Dados dos pntos A B de E se llama ecto fo
IES Pade Poeda (Gadx) Matemátcas II UNIDAD 8: VECTORES EN EL ESPACIO.. VECTORES FIJOS EN EL ESPACIO. Sea E el connto de pntos del espaco qe notaemos po A B C K Dados dos pntos A B de E se llama ecto fo
