IDENTIFICACIÓN DE UN SISTEMA DE TEMPERATURA EN LAZO ABIERTO USANDO PROGRAMACIÓN GENÉTICA
|
|
|
- Sebastián Herrera Calderón
- hace 5 años
- Vistas:
Transcripción
1 IDETIFICACIÓ DE U SISTEMA DE TEMPERATURA E LAZO ABIERTO USADO PROGRAMACIÓ GEÉTICA Crlos F. Regifo, Juli P. Certuhe y Wiler Auñ B. 3 Uiversidd del Cu, Colomi. e-mil: fere@uiu.edu.o Uiversidd del Quidío. e-mil: juli_p@hotmil.om 3 Uiversidd. e-mil: RESUME Este doumeto muestr los resultdos de l pliió de u téi evolutiv ooid omo progrmió geéti, e l idetifiió de u sistem de tempertur. Este efoue us soluior el prolem ue represet l seleió de l estrutur ue será prmetrizd, udo se he el modelmieto de sistems prtir de dtos experimetles, propoiedo estruturs didts ue será modifids e el proeso evolutivo, efetudo l fse de prmetrizió del modelo de mer utomáti, mietrs se seleio l estrutur. Est implemetió oij el so de idetifiió más seillo, es deir, sistems lieles lizdo u ojuto de dtos tomdos o el sistem operdo e lzo ierto. L pliió del prdigm evolutivo, se he segú ls regls origiles defiids por Koz e uto l represetió de los idividuos, uue se he uso de lgus herrmiets propis de otros prdigms, tles omo GAP, elitismo y mutió.. ITRODUCCIÓ El tem de l idetifiió es u áre ojeto de ivestigioes permetes, trtdo ltertivs pr su implemetió, omo lgoritmos pr el juste de prámetros; uevs téis, omo ls redes euroles rtifiiles[] [3] o l trsformd wvelet[4]; segú lo reuier l gm de prolems ue se presete y ls rterístis de los sistems ue se lie, lieles, o lieles, et. El ojeto de este trjo es oteer el modelo de u sistem de tempertur por medio de l progrmió geéti, propoiedo u form de seleior l estrutur ue presetrá el modelo idetifido, detro de l fmili de ls estruturs ARMAX, ue mejor desri el ojuto de dtos. El prolem de l seleió de l estrutur, h sido orddo por lguos utores desde diferetes putos de vist, tl es el so de l idetifiió e suespios[5] e dode el úio prámetro ue se dee seleior es el orde del modelo; o l idetifiió sd e el ooimieto previo de lguos prámetros del sistem omo l ostte de tiempo o l freuei de resoi, trtd e [6]. Ls pliioes de ls téis evolutivs e el áre del otrol so freuetes, e [7] se he u resume de ls pliioes más omues juto o u iliogrfí e el áre.. COCEPTOS BÁSICOS SOBRE IDETIFICACIÓ L idetifiió de sistems osiste e el álisis de u ojuto de pres de dtos de etrd-slid del sistem ue se esté lizdo, otdo de mer úi o l iformió oteid e éstos pr oteer u modelo lo más exto posile del sistem. Deido est rterísti, se ostumr utilizr omo seuei de etrd u señl
2 seudoletori iri, ri e ompoetes de freuei, pr sí expoer l myorí de ls uliddes del sistem... Represetió de los modelos E geerl, u sistem diámio puede ser represetdo omo l sum de u prte determiísti y u estoásti, l primer desriiedo el modelo mtemátio de l plt y l segud u represetió del ruido ue fet los dtos durte el proeso de l tom de los mismos, sí[8]: e H u G y dode, G represet l fuió de trsferei del sistem e fuió del operdor de desplzmieto, es deir, y y ; u l señl sumiistrd l etrd del sistem, y e u señl ruido lo ue está siedo fetd por el sistem liel H. E relidd el sistem H o existe e form físi, sólo es l mer de represetr el ruido imerso e los dtos... Idetifiió prmétri L idetifiió prmétri se s e l represetió del modelo utilizdo prámetros. U form omú de est represetió, l ul será utilizd e est pliió, está dd e térmios de poliomios[8], [9], sí: e D C u F B y A dode, f f f F d d d D C B A K K K K K Los oefiietes de estos poliomios form el llmdo vetor de prámetros, y su estimió ostituye l prmetrizió del modelo. Aetudo l depedei del vetor de prámetros por prte del modelo, l E. se reesrie omo:,,, e H u G y θ θ θ dode, [ ] T f d f f d d L L L L L θ es el vetor de prámetros ue se dee estimr pr el modelo..3. Mediió de l lidd de u modelo Pr medir l lidd de u modelo existe dos efoues priiples, los métodos de vrile istrumetl[9] y los sdos e el error de prediió. E estos últimos l lidd de u modelo se mide e térmios de su pidd preditiv. El so geerl de u ídie de desempeño sdo e métodos de prediió del error, es u fuió de l diferei etre l slid medid y l predih, sí:, ˆ, θ θ ε y y p Es posile filtrr el error de prediió por medio de u filtro liel L, es deir:
3 ε pf, θ L ε p, θ 7 o el ojetivo de relzr o dismiuir lgus ompoetes de freuei. E diió se defie u fuió de vlor rel por lo geerl positiv F omo u ormlizió del error de prediió, y se tom el promedio de estos vlores, sí: J θ F ε pf, θ 8 Y se us el modelo, tl ue: θˆ rg mi θ 9 es deir, el modelo uyo vetor de prámetros miimie el ídie J θ. Como u so prtiulr de l E. 8, e est pliió se defie el filtro L y l fuió F x, oteiedo etoes: J θ ε p, θ 0 Auue el efoue del error de prediió represet u mer seill pr medir l lidd de los modelos, o grtiz l oteió de modelos de jo orde [9], [0], [5]. 3. IDETIFICACIÓ DE SISTEMAS VIA PROGRAMACIÓ GEÉTICA L progrmió geéti[] GP de sus sigls e igles, es u método de úsued sdo e l imitió del proeso de evoluió turl, uyo ojetivo es geerr estruturs o seueis de llmds fuioes ue l ser evluds miimie o mximie lgú riterio. 3.. Represetió de los modelos Segú l defiiió origil del prdigm propuesto por Koz, l represetió de los idividuos se he por medio de ároles prse trees[], [], es deir, estruturs jeráruis. L iformió oteid detro de los ároles depede por ompleto de l pliió omo se verá más delte Represetió usdo l estrutur ARMAX L idetifiió de sistems permite ostruir modelos mtemátios o se e dtos experimetles: Z { u, y, Lu y } dode, u y y represet l etrd y slid de mer respetiv e el istte, del sistem ue se está idetifido. L turlez disret de l iformió, ls señles sólo so ooids e los isttes de muestreo sugiere l utilizió de modelos tmié de tiempo disreto. E est pliió se utilizrá l siguiete estrutur pr represetr los sistems: y y L y u L u e e L e dode, y es l slid del sistem, u l etrd del mismo y e es u ruido iherete todo sistem de mediió. L E. orrespode l estrutur ARMAX y es o freuei utilizd e este tipo de pliioes[3] [5], pues se sume ue o su modelo de ruido u filtro IIR es posile desriir u gr tidd de modelos. θ J 3
4 Etoes, o el efoue utilizdo e este trjo, se esoge l fmili de estruturs ARMAX etre ls demás estruturs omo puto de prtid; uál de ells represet mejor el ojuto de dtos, será defiido por el lgoritmo evolutivo hiedo prues de diferetes órdees y sus prmetrizioes, durte el trsurso de l evoluió. De uerdo o ls ides teriores, l represetió pr l pliió de l GP será ároles, uys rms y odos otiee frgmetos de euioes e difereis del tipo de l E., orgizdos e los siguietes ojutos: Cojuto de Fuioes: Cotiee los odos iteros de los ároles, es deir, ls operioes ue será sometidos los termiles. Está defiido omo: F {,, } dode es el operdor ue desplz hi l dereh u señl isttes de muestreo x x. Cojuto de Termiles: Cotiee los rgumetos ue reie ls fuioes defiids detro del ojuto F. Está defiido omo: F { αy, βu, γe, R} dode α, β y γ so osttes diiods los regresores y, u y e. R es ooid omo ostte letori efímer[6], y e este so sólo fet l operió de multipliió. L difereiió de estos dos tipos de osttes, oedee l heho ue udo se utiliz l GP e este tipo de prolems, uo de los priiples ioveietes está e l geerió de u mplio espetro de osttes de u espio limitdo de úsued. Segú l defiiió de l GP, ls osttes so geerds de mer letori, est rterísti puede trduir e u j lidd de ls osttes, es deir, l geerió por ompleto letori de ls osttes ue ompñ los térmios de regresió es isufiiete[7], [8], y pr ello se defie dos tipos de osttes detro de dos rgos: [-5 5] pr R y [ ] pr α, β y γ, de tl mer ue l operió multipliió ls itegre y mejore los rgos de úsued del lgoritmo, lro está, estos rgos sólo h sido prodos e est implemetió. E diió, se geer u uevo ojuto C ue otiee l uió etre los ojutos T y F, esto o el ojetivo de extrer u fuió o u termil de mer letori de diho ojuto, udo se está formdo los idividuos. Co estos ojutos, se puede firmr ue se umple los priipios de sufiiei y lusur defiidos e l form origil de l progrmió geéti[0], [], [6]. 3.. Fuió de juste E l seió.3, se mostró l form omo so o freuei lifidos los modelos segú ls téis lásis de idetifiió. L pliió del prdigm evolutivo, he impertiv l eesidd de l utilizió de meismos de evluió ue o sólo usue miimizr l disti etre l slid medid y l slid predih, sio, ue grtie l oteió de modelos o po omplejidd, es deir, oteer soluioes prsimoioss[9]. Pr esto, se ostumr utilizr dos riterios: El Criterio de Iformió de Aie AIC. Defiido e su form origil omo[0]: AIC θ l f θ 3 Priipio de Desripió por Logitud Míim MDL, Defiido segú l implemetió de STROGAOFF omo[8], [], []: 4
5 Tree _ Codig _ Legth 0.5 log 4 Exeptio _ Codig _ Legth 0.5 log S Otro efoue pr el MDL puede ser osultdo e [3] [5]. E est pliió estos dos riterios so implemetdos omo: 5 AIC θ l ε p l 0 6 MDL θ l ε p l l 0 dode, es el úmero de pres de etrd slid, y idi l omplejidd del modelo, luld omo: LA LB LC 7 dode, LA, LB y LC so ls logitudes de los vetores A, B y C de mer respetiv. Otr rzó por l ul se us soluioes simples, es l eorme rg omputiol ue puede represetr los idividuos detro de u polió e determido mometo, pues o uos utos miles de idividuos e l polió, si o se otrol l omplejidd de éstos, se puede torr imejle el progrm pr los sistems de ómputo oveioles. ote de l E. 5 ue el AIC, puede sigr el mismo vlor modelos de diferete fmili de estruturs, pues diho riterio se vle sólo de los errores de prediió y el orde del modelo, si disrimir ul de ells perteee. Por est rzó y otrs expuests tes se h tomdo omo estrutur geerl e est pliió los modelos ARMAX Modifiioes ls estruturs Cudo el lgoritmo empiez su úsued, geer u polió del tmño desedo de estruturs jeráruis ároles. Es de esperrse ue por el ráter letorio o ue es oformdo este grupo de modelos, su lidd se muy pore; pr ello los lgoritmos evolutivos propoe l pliió de mios e los idividuos sdos e ls regls de l evoluió y l seleió turl, itroduiedo los llmdos operdores geétios el letor puede dirigirse [6] o [7] pr profudizr este tópio. Auí los perdores plidos so: Reproduió: Cosiste e seleior segú su medid de juste u grupo de idividuos, uyo tmño es determido por l proilidd de reproduió Pr, pr ser opidos si modifiió lgu e l siguiete geerió. Crue: Cosiste e seleior dos idividuos segú su ptitud, luego se proede seleior de form letori u puto detro de l estrutur de d uo de ellos, prtir de ese puto es itermid l iformió etre los dos ároles. L tidd de idividuos sometidos est operió está determid por l proilidd de rue P. Mutió: Cosiste e seleior u tidd de idividuos ditd por l proilidd de mutió Pm pr ser modifid su estrutur si iterió o otros idividuos. Por ejemplo, si utiliz mutió por otrió shri muttio se seleio u puto itero del árol y prtir de llí es orrd l iformió ue teg. E l defiiió origil de Koz, este operdor o se tom e uet. 4. PRUEBAS Y RESULTADOS El módulo didátio PT36, es u proeso de tempertur e el ul es iyetdo ire trvés de u tuo o u elemeto leftor detro. Ls prues y resultdos mostrdos 5
6 otiuió so hehos sore est plt. E uto l hrdwre utilizdo ls prues fuero hehs e u omputdor o u proesdor Itel Petium 4 u freuei de 600 MHz, 5 MB de memori priipl y sore el sistem opertivo Liux. 4.. El ojuto de dtos Z El ojuto de dtos de etrd, fue u seuei seudoletori de dtos irios sore u ivel de 4.9V o u mplitud de.5v, es deir, se euetr etre 3.4V y 6.4V. Est ompuesto por 000 dtos, de los ules los primeros 500 fuero utilizdos pr el proeso de idetifiió y los resttes pr el proeso de vlidió. 4.. Proeso de idetifiió E u omiezo, se hizo l implemetió tl omo fue defiido el prdigm de l progrmió geéti[], es deir, si utilizr el modelo elitist, si mutió y e dode l polió tul es reemplzd por ompleto por sus desedietes, o se, si itermio geeriol geertio GAP[6], [8], [9]. Los prámetros de otrol utilizdos pr her l idetifiió del módulo jo ests odiioes, se euetr resumidos e l tl. E l tl se resume los resultdos de 5 orrids del lgoritmo o estos prámetros, pr los tres ídies ue se está miimizdo. Prámetro Vlor o poretje % Vriles 50 % Completos 50 Profudidd Iiil 5 Tmño Polió 500 % Reproduió 0 % Crue 90 % Mutió 0 úmero de Geerioes 750 Tl. Prámetros de otrol pr l idetifiió del sistem utilizdo GP ói. Corrid J θ AICθ MDLθ Tl. Medids de ptitud files pr io orrids del lgoritmo utilizdo GP ói Vlidió de los modelos L vlidió del modelo idetifido, es u proeso dode se liz los residuos produto de l idetifiió, es deir, ls difereis existetes etre l slid medid y l slid predih ε p, θ. Auí se lul l fuió de utoorrelió de los ε p, θ y l orrelió ruzd etre los residuos y l etrd[8] [0]. E ls figurs 3, se muestr ls vlidioes orrespodietes los sistems o los tres meores ídies de desempeño etre los mostrdos e l tl. Se puede evideir de ls tres vlidioes, ue l señl de exitió y los residuos o so por ompleto idepedietes, heho ue revel ue existe errores e l prmetrizió e l prte determiísti del modelo idetifido[8]. 6
7 Ddo ue ls soluioes oteids hst ese puto o er por ompleto stisftoris, se deidió ue los pdres y los hijos resulttes de l operió del rue deí ompetir, de est mer, de los utro posiles didtos dos pdres y sus dos hijos se seleio los dos mejores pr ir oformdo l siguiete geerió. Los prámetros de otrol pr ls orrids del lgoritmo o est modifiió fuero idétios los del so terior, es deir, los mostrdos e l tl. E l tl 3 se muestr ls medids de ptitud files pr io orrids del lgoritmo implemetdo l ompetei etre pdres e hijos. Figur. Vlidió pr el modelo idetifido e l orrid 4 miimizdo J θ o GP ói. Figur. Vlidió pr el modelo idetifido e l orrid 3 miimizdo AICθ o GP ói. Figur 3. Vlidió pr el modelo idetifido e l orrid 5 miimizdo MDLθ o GP ói. L tl 3, uet o u olum diiol ue ompñ los vlores de los ídies de desempeño, est olum idi ls geerioes G e ue el lgoritmo overgió Cov. l vlor idido, es deir, tod l polió e l geerió G es igul y el lgoritmo se detiee, si evoluior ls geerioes idids por los prámetros de otrol. Este feómeo es ooido omo overgei premtur[6], y se dee l fuerte tedei geéti y pérdid de diversidd ue trjo omo oseuei l modifiió heh l progrm. E ls figurs 4 6 se muestr ls vlidioes pr los sistems o los tres meores ídies de desempeño utilizdo itermio geeriol. 7
8 C J θ Cov. [G] AIC Cov. [G] MDL Cov. [G] Tl 3. Medids de ptitud files pr io orrids usdo itermio geeriol. Figur 4. Vlidió pr el modelo idetifido e l orrid 5 miimizdo J θ usdo itermio geeriol. Figur 5. Vlidió pr el modelo idetifido e l orrid 5 miimizdo AICθ usdo itermio geeriol Figur 6. Vlidió pr el modelo idetifido e l orrid 3 miimizdo MDLθ usdo itermio geeriol. Se evidei ue los modelos sometidos l proeso de vlidió fuero ueos. El ojetivo siguiete er soluior el prolem de overgei premtur, pues el lgoritmo se est deteiedo muy proto. Pr ello, existe diferetes soluioes, tles omo utilizr polioes muy grdes omo e los trjos presetdos por Koz, her eslmieto de l medid de juste propuesto por Golderg, iluir operdores diioles omo mutió, etre otros[30], [3]. L soluió implemetd e este trjo, fue l pliió de l mutió los idividuos e proporioes o muy lts. Co est modifiió, e l tl 4 se muestr los prámetros de otrol ue fuero utilizdos e l idetifiió. E l tl 5 se muestr ls 8
9 medids de juste files pr los tres tipos de ídie utilizdos, pr 5 orrids del lgoritmo. Dee meiorse ue e iguo de los sos mostrdos por l tl 5 se presetó overgei premtur. E ls figurs 7 9 se muestr l vlidió de los modelos produto de ls orrids 3 J θ, AICθ y MDLθ, utilizdo el uevo operdor. Prámetro Vlor o poretje % Vriles 50 % Completos 50 Profudidd Iiil 5 Tmño Polió 500 % Reproduió 0 % Crue 85 % Mutió 5 úmero de Geerioes 750 Tl 4. Prámetros de otrol pr l idetifiió del sistem utilizdo mutió. C J θ t. [mi] AICθ t. [mi] MDLθ t. [mi] : : : : : : : : : : : : : : : 30 Tl 5. Medids de ptitud files pr io orrids usdo mutió. ote ue ls fuioes de orrelió pr ls tres gráfis muestr lur e el so de los vetores de residuos e idepedei etre los residuos y l señl de exitió, heho ue revel l vlidez de l idetifiió de estos modelos. Figur 7. Vlidió pr el modelo idetifido e l orrid 3 miimizdo J θ usdo mutió. Figur 8. Vlidió pr el modelo idetifido e l orrid miimizdo AICθ usdo mutió Reduió de l rg omputiol E l tl 5 se muestr u prámetro diiol ue idi el tiempo de ejeuió del lgoritmo, ote ue estos tiempos fuero muy ltos, u omportmieto poo desele e uluier sistem. Pr dr soluió este prolem se plteó mir el ídie de omplejidd ddo por l E. 7, por uo euivlete l sum del úmero de odos de d árol, es deir, se pelizro los modelos o por el orde de éstos, sio, por el tmño del 9
10 árol ue los represete. E l tl 6 se muestr ls medids de ptitud files pr 0 orrids utilizdo reduió e los ároles. Figur 9. Vlidió pr el modelo idetifido e l orrid miimizdo MDLθ usdo mutió. C AICθ t. [mi] MDLθ t. [mi] -45: : 3-653: : : : 9-676: : 9-486: : 39-66: : :58309 : -6: : : : 4-66: : :973 0 : 6-63: : 7-38: : 8-633: : 8-46: : 3-63: : : : 5-68: : : : 4-69:33897 : 46 Tl 6. Medids de ptitud files pr diez orrids usdo reduió e los ároles. ote l gr reduió e los tiempos de ejeuió del lgoritmo, e dode, se psó de u medi de 4:70 mi pr el so e ue l omplejidd est regid por l E. 7, u medi de 9:60 mi dode se otroló el reimieto de ls estruturs. E ls figurs 0 y se muestr ls vlidioes pr los sistems oteidos de ls orrids 3 AICθ y 0 MDLθ, otroldo el reimieto de los ároles. Auue ls gráfis de vlidió mostrds preset ueos resultdos, dee otrse ue el lgoritmo jó su desempeño y e u gr tidd de sos los modelos resulttes o fuero válidos, pr el so del MDLθ e myor proporió, esto deido l lt poderió ue preset el MDLθ e su ompoete de omplejidd. 5. DISCUSIÓ Este trjo muestr ue es posile her el modelmieto de u sistem utilizdo omo regls de úsued l seleió turl, u esuem orgizdo ue uue se gr prte de su fuiomieto e l letoriedd, es reguldo por el ojetivo espeífio de imitr l turlez. De igul mer, se muestr l posiilidd de utilizr u estrtegi ie defiid pr esoger l estrutur y her l prmetrizió, proporiodo u posiilidd más e este mpo, juto o ls demás forms existetes. 0
11 Figur 0. Vlidió pr el modelo idetifido e l orrid 3 miimizdo AIC otroldo el reimieto de los ároles. Figur. Vlidió del modelo idetifido e l orrid 0 miimizdo MDL otroldo el reimieto de los ároles. A pesr de otr o u herrmiet ue puede ser útil e el mpo de l idetifiió, es útil reordr ue surge hor u ojuto de duds o prolems uevos ue dee ser motivo de ivestigió posterior. Es el so de u uso más elordo de los riterios ue sig l medid de juste, pues l form e ue se utilizó uí el AIC o el MDL, respode más experimetió previ reportd e l iliogrfí del áre, ue u estudio uevo portdo por los utores de este trjo. L utilizió de elemetos diioles los defiidos e el prdigm origil de l GP, so produto de l eesidd de mejorr l lidd e ls soluioes y desempeño del progrm. Cd vez es más freuete su utilizió e ls llmds pliioes del mudo rel. Otro puto de importi es l mejor del desempeño e uto l tiempo de ejeuió del lgoritmo, esto deido ue u herrmiet muy let o ue reuier de grdes reursos de ómputo, puede resultr poo trtiv pr uluier perso ue desee her uso de ell. Los resultdos uí mostrdos, reflej u otle reduió e el tiempo de ejeuió depediedo de l form omo se sige l medid de juste, heho ue llev u vez más l osiderió del estudio de estos. Est ide puede ser extedid otro tipo de sistems, pues es omú eotrrse o pliioes ue ivolur l idetifiió de sistems olieles por medio de téis evolutivs, lro está, se dee ser uiddoso o este tipo de pliioes ue impliue u se teóri muho más omplej y ue puede oduir ivestigioes si fudmeto ietífio, pues se dej u ldo est prte fudmetl de uluier trjo ivestigtivo. 0. BIBLIOGRAFÍA [] L. Ljug d J. Sjöerg. A system idetifitio perspetive o eurl ets. Tehil report, Liöpig Uiversity, 99. [] J. Sjöerg. o-lier System Idetifitio with eurl etwors. PhD thesis, Liöpig Uiversity, Liöpig, 995. Disserttio o. 38. [3] Sjöerg J., H. Hjlmrsso, d L. Ljug. eurl etwors i system idetifitio. Tehil report, Liöpig Uiversity, 994. [4] A. Juditsy, Q. Zhg, B. Delyo, P-Y. Gloree, d A. Beveiste. Wvelets i idetifitio - wvelets, splies, euros, fuzzies: how good for idetifitio? Tehil report, Istitut tiol de Reherhe e Iformtiue et e Automtiue IRIA, 994.
12 [5] P. V Overshee. Suspe idetifitio for lier systems: Theory - Implemettio - Applitios. Kluwer Ademi Pulishers, 995. [6] P. Lidsog. Methods, Algorithms d Tools for System Idetifitio Bsed o Prior Kowledge. PhD thesis, Liöpig Uiversity, 996. [7] P. J. Flemig d R. C. Purshouse. Geeti lgorithms i otrol systems egieerig, 00. [8] C. F. Regifo R. Idetifiió de sistems diámios e lzo errdo. Mster s thesis, Uiversidd del Vlle, mr 999. [9] L. Ljug. System Idetifitio: Theory for the user. Pretie Hll, 987. [0] J. P. Certuhe A. d W. Auñ B. Idetifiió de sistems e lzo ierto usdo progrmió geéti, 003. [] J. R. Koz. Geeti progrmmig: O the Progrmmig of Computers y Mes of turl Seletio. The MIT Press, 99. [] P. Agelie. C3..5 prse trees. I Hdoo of Evolutiory Computtio, hpter C3 Serh Opertors. IOP Pulishig LTd. d Oxford Uiversity Press, 997. [3] D. B. Fogel. Evolutiory Computtio Towrd ew Philosophy of Mhie Itelligee. IEEE Press, 995. [4] D. B. Fogel d. Srv. A overview of evolutiory methods i system idetifitio. I SPRA94, 994 IMACS Itertiol Symp. o Sigl Proessig, Rootis d eurl etwors, Jue 994. [5] K. Rodriguez. Multiojetive Evolutiory Algorithms i o-lier System Idetifitio. PhD thesis, The Uiversity of She±eld, 999. [6] J. R. Koz. The geeti progrmmig prdigm: Geetilly reedig popultios of omputer progrms to solve prolems. I Dymi Geeti, d Choti Progrmmig. Wiley, 99. [7] H. I. F.4 idetifitio. I Hdoo of Evolutiory Computtio, hpter F Evolutiory Computtio Applitios. IOP Pulishig LTd. d Oxford Uiversity Press, 997. [8] H. I. G.4 system idetifitio usig strutured geeti lgorithms. I Hdoo of Evolutiory Computtio, hpter G Computer Siee. IOP Pulishig LTd. d Oxford Uiversity Press, 997. [9] G.E. Box, G. C. Reisel, d G. M. Jeis. Time series lysis, Forestig d Cotrol. Pretie Hll, 994. [0] H. Aie. A ew loo t the sttistil model idetifitio. IEEE Trstios o Automti Cotrol, 96:76 73, 974. [] H. I, H. degris, d T. Sto. Geeti progrmmig usig miimum desriptio legth priiple. I Keeth E. Kier, Jr., editor, Adves i Geeti Progrmmig, pges MIT Press, 994. [] M. F. Teorio d W. Lee. Self-orgizig etwor for optimum supervised lerig. IEEE Trstios o eurl etwors, :00 0, 990. [3] B. Zhg d H. Mühleei. Geeti progrmmig of miiml eurl ets usig Om s rzor. I Stephie Forrest, editor, Proeedigs of the 5th Itertiol Coferee o Geeti Algorithms, ICGA-93, pges , Uiversity of Illiois t Ur-Chmpig, Morg Kufm. [4] B. Zhg d H. Mühleei. Blig ury d prsimoy i geeti progrmmig. Evolutiory Computtio, 3:7 38, 995. [5] B. Zhg d H. Mühleei. Byesi iferee, miimum desriptio legth priiple, d lerig y geeti progrmmig. I Justii Ros, editor, Geeti Progrmmig from theory to rel world pplitios, pges 5, Uiversity of Rohester, Jue 995. [6] D. E. Golderg. Geeti Algorithms i Serh, Optimiztio d Mhie Lerig. Adiso Wesley, 989. [7] J. Holld. Adpttio i turl d rtifiil Sistems. MI: Uiversity of Mihig Press, 975. [8] J. Srm d K. DeJog. C.7 geertio gp metods. I Hdoo of Evolutiory Computtio, hpter C Seletio. IOP Pulishig LTd. Ad Oxford Uiversity Press, 997. [9] K. DeJog. A lisis of the hvior of lss of geeti dptive systems. PhD thesis, Uiversity of Mihig, 975. [30] R. Crwford-Mrs d L. Spetor. Size otrol vi size fir geeti opertors i the PushGP geeti progrmmig system. I W. B. Lgdo, E. Ctú-Pz, K. Mthis, R. Roy, D. Dvis, R. Poli, K. Blrish, V. Hovr, G. Rudolph, J. Wegeer, L. Bull, M. A. Potter, A. C. Shultz, J. F. Miller, E. Bure, d. Joos, editors, GECCO 00: Proeedigs of the Geeti d Evolutiory Computtio Coferee, pges , ew Yor, 9-3 July 00. Morg Kufm Pulishers. [3] D. Mwhiey. Prevetig erly overgee i geeti progrmmig y replig similr progrms, 000.
El proeso de idetifiió E tr d s 5 Defiiió del experimeto reoleió de dtos Es orreto el experimeto? Dtos ideudos H que filtrr los dtos? Limp
 Idetifiió de Sistems 5 Ojetivo de l Idetifiió de Sistems: Oteer u ue modelo (geerlmete liel del sistem empledo u tidd de trjo rzole. Perturioes o ruido: e(t 8 6 4 4 6 8 4 6 Etrds: u(t Desripió del sistem?
Idetifiió de Sistems 5 Ojetivo de l Idetifiió de Sistems: Oteer u ue modelo (geerlmete liel del sistem empledo u tidd de trjo rzole. Perturioes o ruido: e(t 8 6 4 4 6 8 4 6 Etrds: u(t Desripió del sistem?
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS PRODUCTOS NOTABLES
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 8 TALLER Nº SEMESTRE II RESEÑA HISTÓRICA PRODUCTOS NOTABLES Psl, Blise (-: filósofo, mtemátio físio frés, osiderdo u de ls metes
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 8 TALLER Nº SEMESTRE II RESEÑA HISTÓRICA PRODUCTOS NOTABLES Psl, Blise (-: filósofo, mtemátio físio frés, osiderdo u de ls metes
a se denomina serie a es convergente y SERIES = si r <1 S n La suma de los términos de una sucesión infinita { } n n=1 infinita o simplemente serie
 SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
SERIES L sum de los térmios de u suesió ifiit { } = ifiit o simplemete serie se deomi serie Y se represet o el símbolo = Defiiió: = 4 KK Dd l serie = ésim sum pril = 4 K K, se desigrá S su S = = = 4 K
Clase 16. Tema: Racionalización de expresiones. Matemáticas 9. Bimestre: I Número de clase: 16. Tipo 1. Esta clase tiene video.
 Bimestre: I Número de lse: 16 Mtemátis Clse 16 Est lse tiee video Tem: Riolizió de expresioes Atividd 46 1 Le l siguiete iformió sore l riolizió. E mtemátis es omú eotrros o expresioes rioles que otiee
Bimestre: I Número de lse: 16 Mtemátis Clse 16 Est lse tiee video Tem: Riolizió de expresioes Atividd 46 1 Le l siguiete iformió sore l riolizió. E mtemátis es omú eotrros o expresioes rioles que otiee
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 Ju Atoio Goále Mot Profesor de Mtemátis del Colegio Ju XIII Zidí de Grd ESPACIOS VECTORIALES CONCEPTO DE ESPACIO VECTORIAL. Se V u ojuto ulquier R el ojuto de úmeros reles. E V defiimos dos lees de omposiió:
Ju Atoio Goále Mot Profesor de Mtemátis del Colegio Ju XIII Zidí de Grd ESPACIOS VECTORIALES CONCEPTO DE ESPACIO VECTORIAL. Se V u ojuto ulquier R el ojuto de úmeros reles. E V defiimos dos lees de omposiió:
entonces A.B es: A) 4 B) 2 C) 1 D) 1/2 E) 1/4 a b. a b a b 4... Calcula: A) 1 B) 2 C) 2 D) 3 E) 2 2 x x A) 1 B) x C) A) 7 B) 8 C) 9 D) 10 E) 6
 Rzomieto Lógio. Efetú: E = ÁLGEBRA DOENTE: Dr. Rihrd Herrer A. TEORIA DE EXPONENTES 8 A 0, B 0, D E 6. Simplifi: 6..80 9..0 A B D E. Hll el vlor de: M A B 6 D / E. Simplifi: ; si: > 0 A B D E. lul: S :
Rzomieto Lógio. Efetú: E = ÁLGEBRA DOENTE: Dr. Rihrd Herrer A. TEORIA DE EXPONENTES 8 A 0, B 0, D E 6. Simplifi: 6..80 9..0 A B D E. Hll el vlor de: M A B 6 D / E. Simplifi: ; si: > 0 A B D E. lul: S :
Definiciones. Los valores de los términos necesarios para empezar a calcular se llaman condiciones iniciales.
 Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
Deprtmeto de Mtemáti plid. ETSIIf. UPM. Vitori Zrzos Rodríguez RELCIONES DE RECURRENCI Defiiioes Relió de reurrei o reursiv pr l suesió { } es u epresió que relio el térmio geerl de l suesió o uo o más
D E T E R M I N A N T E S M A T R I Z I N V E R S A
 º DE BACHILLERATO DETERMINANTES D E T E R M I N A N T E S ----------- M A T R I Z I N V E R S A DETERMINANTES I. Determites. II. Primers pliioes de los determites. I. Determites.. Defiió álulo de u determite.
º DE BACHILLERATO DETERMINANTES D E T E R M I N A N T E S ----------- M A T R I Z I N V E R S A DETERMINANTES I. Determites. II. Primers pliioes de los determites. I. Determites.. Defiió álulo de u determite.
Utilizando la fórmula que nos proporciona el número de divisores se tiene que:
 Hoj de Prolems º Alger IV /. Hllr u úmero etero A que o teg ms ftores primos que, y 7, siedo demás que ª tiee divisores más que A y que ª tiee divisores ms que A. Clulr tmié l sum de todos los divisores
Hoj de Prolems º Alger IV /. Hllr u úmero etero A que o teg ms ftores primos que, y 7, siedo demás que ª tiee divisores más que A y que ª tiee divisores ms que A. Clulr tmié l sum de todos los divisores
7. Fallas Asimétricas
 Friso M. Gozlez-Lott Cpítulo 7 7. Flls Asimétris 7. troduió U r proporió de ls flls e lo sistems elétrios de potei so simétrios, flls simétris trvés de impedis (ortoiruitos moofásios, ifásios, ifásios
Friso M. Gozlez-Lott Cpítulo 7 7. Flls Asimétris 7. troduió U r proporió de ls flls e lo sistems elétrios de potei so simétrios, flls simétris trvés de impedis (ortoiruitos moofásios, ifásios, ifásios
COSAS DE DIVISORES Y HOTELES
 COSAS DE DIVISORES Y HOTELES E est sesió trtremos de resolver el siguiete rolem: Prolem: El hotel de ls mil hitioes. Cuet ue e ierto ís hí u gr hotel ue teí 000 hitioes y otros ttos emledos. Estos, u dí
COSAS DE DIVISORES Y HOTELES E est sesió trtremos de resolver el siguiete rolem: Prolem: El hotel de ls mil hitioes. Cuet ue e ierto ís hí u gr hotel ue teí 000 hitioes y otros ttos emledos. Estos, u dí
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
Criterios de Estabilidad de Routh y Jury. M.I. Ricardo Garibay Jimenez 2006
 Criterio de Etbilidd de Routh y Jury M.I. Rirdo Griby Jimeez 6 Criterio de Routh U poliomio (... A tiee ríe etble (o prte rel egtiv i e umple odiioe. Neeidd todo lo oefiiete y o poitivo Sufiiei El igo
Criterio de Etbilidd de Routh y Jury M.I. Rirdo Griby Jimeez 6 Criterio de Routh U poliomio (... A tiee ríe etble (o prte rel egtiv i e umple odiioe. Neeidd todo lo oefiiete y o poitivo Sufiiei El igo
WhittiLeaks Los apuntes que ellos no quieren que sepas de
 Métodos umérios WittiLes Los putes que ellos o quiere que seps de ITBA mo 7 WittiLes Resume Métodos umérios Pso Pr u fuió defiid e u itervlo: f (, ) ( ) el pso se defie por: ; dode es l tidd de divisioes
Métodos umérios WittiLes Los putes que ellos o quiere que seps de ITBA mo 7 WittiLes Resume Métodos umérios Pso Pr u fuió defiid e u itervlo: f (, ) ( ) el pso se defie por: ; dode es l tidd de divisioes
Electrónica Básica. Álgebra de Boole. Electrónica Digital. José Ramón Sendra Sendra Dpto. de Ingeniería Electrónica y Automática ULPGC
 Eletrói Bási Álger de Boole Eletrói Digitl José Rmó Sedr Sedr Dpto. de Igeierí Eletrói y Automáti ULPGC 2 Ciruito de omutió p.e. sistem de otrol idustril sistem teleóio ordedor et. El Álger de Boole sirve
Eletrói Bási Álger de Boole Eletrói Digitl José Rmó Sedr Sedr Dpto. de Igeierí Eletrói y Automáti ULPGC 2 Ciruito de omutió p.e. sistem de otrol idustril sistem teleóio ordedor et. El Álger de Boole sirve
CURIOSIDADES MATEMATICAS EL TRIANGULO DE PASCAL GENERALIZADO
 CURIOSIDADES MATEMATICAS EL TRIANGULO DE PASCAL GENERALIZADO JOSÉ FRANCISCO LEGUIZAMÓN ROMERO GRUPO DE INVESTIGACIÓN PIRÁMIDE LÍNEA MEDIOS EDUCATIVOS EN MATEMÁTICAS FACULTAD DE CIENCIAS DE LA EDUCACIÓN
CURIOSIDADES MATEMATICAS EL TRIANGULO DE PASCAL GENERALIZADO JOSÉ FRANCISCO LEGUIZAMÓN ROMERO GRUPO DE INVESTIGACIÓN PIRÁMIDE LÍNEA MEDIOS EDUCATIVOS EN MATEMÁTICAS FACULTAD DE CIENCIAS DE LA EDUCACIÓN
Una guía de ondas metálica de sección circular es un caso particular de. guía de ondas metálica en el cual la sección transversal es circular, como se
 4.4 GUÍA DE ONDAS METÁLICA DE SECCIÓN CIRCULAR 4.4.1 Geoetrí y odiioes de froter U guí de ods etáli de seió irulr es u so prtiulr de guí de ods etáli e el ul l seió trsversl es irulr oo se uestr e l figur
4.4 GUÍA DE ONDAS METÁLICA DE SECCIÓN CIRCULAR 4.4.1 Geoetrí y odiioes de froter U guí de ods etáli de seió irulr es u so prtiulr de guí de ods etáli e el ul l seió trsversl es irulr oo se uestr e l figur
CAPITULO 3 PROCESAMIENTO DIGITAL DE SEÑALES
 PROCESAMIENTO DIGITAL DE SEÑALES 3 PROCESAMIENTO DIGITAL DE SEÑALES 3. Itroduió E este pítulo se verá lguos priipios básios del proesmieto digitl de señles, eesrios pr eteder l mer e ómo oper los overtidores
PROCESAMIENTO DIGITAL DE SEÑALES 3 PROCESAMIENTO DIGITAL DE SEÑALES 3. Itroduió E este pítulo se verá lguos priipios básios del proesmieto digitl de señles, eesrios pr eteder l mer e ómo oper los overtidores
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
FUNCIONES POLINÓMICAS
 Prof.: Lui Tfererry FUNCIONES POLINÓMICAS POLINOMIOS Los poliomios so importtes. El volume de u ilidro r h y su áre totl es rh r. ic El pitl fil produido por u pitl C durte t meses l i% ul, es C. t. 00
Prof.: Lui Tfererry FUNCIONES POLINÓMICAS POLINOMIOS Los poliomios so importtes. El volume de u ilidro r h y su áre totl es rh r. ic El pitl fil produido por u pitl C durte t meses l i% ul, es C. t. 00
AlGEBRA LINEAL Y GEOMETRIA ANALITICA (0250) PARCIAL I SEMESTRE Nombre y Apellido: C.I:
 U.C.V. F.I.U.C.V. lgebr LINEL Y GEOMETRI NLITIC (5) PRCIL I SEMESTRE -6 9--6 CICLO BÁSICO DEPRTMENTO DE MTEMÁTIC PLICD Nomre y pellido: C.I: ) ( putos) Coloque e el prétesis l letr V o F segú se verdder
U.C.V. F.I.U.C.V. lgebr LINEL Y GEOMETRI NLITIC (5) PRCIL I SEMESTRE -6 9--6 CICLO BÁSICO DEPRTMENTO DE MTEMÁTIC PLICD Nomre y pellido: C.I: ) ( putos) Coloque e el prétesis l letr V o F segú se verdder
TP: "POTENCIACIÓN" exponente. "n" veces a. Definición conveniente: Todo número real distinto de cero elevado a la cero da 1(uno) En símbolos: a 0: a
 TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. "" vees
TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. "" vees
UNIDAD 5 Series de Fourier
 Series de Fourier 5. Fucioes ortogoles, cojutos ortogoles y cojutos ortoormles Se dice que dos fucioes f ( x ) y f x so ortogoles e el itervlo < x< si cumple co: f x = Est ide se hce extesiv u cojuto de
Series de Fourier 5. Fucioes ortogoles, cojutos ortogoles y cojutos ortoormles Se dice que dos fucioes f ( x ) y f x so ortogoles e el itervlo < x< si cumple co: f x = Est ide se hce extesiv u cojuto de
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
 TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
TP: "POTENCIACIÓN" exponente. "n" veces a. Definición conveniente: Todo número real distinto de cero elevado a la cero da 1(uno) En símbolos: a 0 : a
 TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. 8 ""
TP: "POTENCIACIÓN" Defiiió Ddo u ierto úmero rel, llmremos "potei eésim de " l produto de por sí mismo u tidd de vees; siedo u úmero turl. E símolos: se expoete........ p POTENCIA ENÉSIMA de Ej:.. 8 ""
CAPÍTULO CUATRO. ESTABILIDAD EN SISTEMAS DE CONTROL MUESTREADO.
 CAPÍTULO CUATRO. ESTABILIDAD EN SISTEMAS DE CONTROL MUESTREADO. IV.. INTRODUCCIÓN. Ls téis pr el estudio de l estilidd de sistems muestredos de otrol so lids e este pítulo. E geerl, los métodos de estudio
CAPÍTULO CUATRO. ESTABILIDAD EN SISTEMAS DE CONTROL MUESTREADO. IV.. INTRODUCCIÓN. Ls téis pr el estudio de l estilidd de sistems muestredos de otrol so lids e este pítulo. E geerl, los métodos de estudio
I.E.S Padre Juan Ruíz Aritmética Hinojosa del Duque
 I.E.S Pdre Ju Ruíz Aritméti Hiojos del Duque PROPIEDADES DE LA ARITMÉTICA Y ERRORES MÁS COMUNES NÚMEROS ENTEROS Elimir prétesis: Del mismo sigo, sle + De distito sigo, sle + (+) = + ( ) = + + ( ) = (+)
I.E.S Pdre Ju Ruíz Aritméti Hiojos del Duque PROPIEDADES DE LA ARITMÉTICA Y ERRORES MÁS COMUNES NÚMEROS ENTEROS Elimir prétesis: Del mismo sigo, sle + De distito sigo, sle + (+) = + ( ) = + + ( ) = (+)
TECNOLOGÍA ELÉCTRICA. UNIDAD DIDÁCTICA 1 CONCEPTOS BÁSICOS Y PROBLEMAS RESUELTOS
 L Uiversidd er TECNOLOGÍA ELÉCTRICA. UNIDAD DIDÁCTICA 1 CONCEPTOS BÁSICOS Y PROBLEMAS RESUELTOS 1.- POTENCIA EN SISTEMAS DE CORRIENTE ALTERNA E los iruitos de orriete lter, l produto etre tesió e itesidd
L Uiversidd er TECNOLOGÍA ELÉCTRICA. UNIDAD DIDÁCTICA 1 CONCEPTOS BÁSICOS Y PROBLEMAS RESUELTOS 1.- POTENCIA EN SISTEMAS DE CORRIENTE ALTERNA E los iruitos de orriete lter, l produto etre tesió e itesidd
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
Introducción a la algoritmia. Algoritmia básica - Javier Campos (Universidad de Zaragoza)
 Itroduió l lgoritmi Algoritmi bá - Jvier Cmpos Uiverdd de Zrgoz Itroduió l lgoritmi AB Algoritmi Algoritmi = = trtmieto stemátio de téis fudmetles pr el diseño y ális de lgoritmos efiietes Algoritmi bá
Itroduió l lgoritmi Algoritmi bá - Jvier Cmpos Uiverdd de Zrgoz Itroduió l lgoritmi AB Algoritmi Algoritmi = = trtmieto stemátio de téis fudmetles pr el diseño y ális de lgoritmos efiietes Algoritmi bá
1.- Clausura ó cerradura:
 8 Sigos: Ddos, lr etoes El Sistem [ ( < de 0 Números 0 < Reles ) (0 < < 0) ] < 0 [ (0 < 0 < ) ( < 0 < 0) ] 0 < 9- Trsitiv:,, lr, < y < se tiee < 0- Mootoí de l sum: < y lr etoes < - Mootoí del produto:,,
8 Sigos: Ddos, lr etoes El Sistem [ ( < de 0 Números 0 < Reles ) (0 < < 0) ] < 0 [ (0 < 0 < ) ( < 0 < 0) ] 0 < 9- Trsitiv:,, lr, < y < se tiee < 0- Mootoí de l sum: < y lr etoes < - Mootoí del produto:,,
Los siguientes son ejemplos de expresiones algebraicas:
 UNIDAD : EXPRESIONES ALGÉBRAICAS Se deoi vrile rel u síolo geerlete u letr que se us pr represetr u úero rel ritrrio. Se deoi ostte rel u síolo que se us pr represetr u úero rel fijo. Se deoi epresió lgeri
UNIDAD : EXPRESIONES ALGÉBRAICAS Se deoi vrile rel u síolo geerlete u letr que se us pr represetr u úero rel ritrrio. Se deoi ostte rel u síolo que se us pr represetr u úero rel fijo. Se deoi epresió lgeri
APLICACIONES DE LA DIFERENCIAL
 DEINICIÓN DE UNCIÓN DIERENCIABLE Se die que u uió es diereible e u puto si su iremeto puede esribirse de l orm g η es tl que g o depede de los iremetos η udo. Ejemplo: Determir si l uió es diereible. Clulemos
DEINICIÓN DE UNCIÓN DIERENCIABLE Se die que u uió es diereible e u puto si su iremeto puede esribirse de l orm g η es tl que g o depede de los iremetos η udo. Ejemplo: Determir si l uió es diereible. Clulemos
Ministerio del Poder Popular para la Educación Unidad Educativa Nacional Domitila Flores Curso: 4to Año Área de Formación: Matemática
 Miisterio del Poder Populr pr l Eduió Uidd Edutiv Niol Domitil Flores Curso: 4to Año Áre de Formió: Mtemáti UNIDAD DE NIVELACIÓN INTRODUCCIÓN AL ÁLGEBRA Elordo por: Prof. Roy Altuve Rg Lguills, oture 2017
Miisterio del Poder Populr pr l Eduió Uidd Edutiv Niol Domitil Flores Curso: 4to Año Áre de Formió: Mtemáti UNIDAD DE NIVELACIÓN INTRODUCCIÓN AL ÁLGEBRA Elordo por: Prof. Roy Altuve Rg Lguills, oture 2017
ALGEBRA LINEAL. MATRICES Y DETERMINANTES.
 LGEBR LINEL. MTRICES Y DETERMINNTES. putes de. Cñó Mtemátis II. Vetores e R.. Operioes o vetores (sum de vetores y produto por u eslr) y sus propieddes.. Depedei e idepedei liel de vetores. L se ói.. Defiiió
LGEBR LINEL. MTRICES Y DETERMINNTES. putes de. Cñó Mtemátis II. Vetores e R.. Operioes o vetores (sum de vetores y produto por u eslr) y sus propieddes.. Depedei e idepedei liel de vetores. L se ói.. Defiiió
UNIDAD I INTRODUCCIÓN AL ÁLGEBRA
 Vierretordo Adémio Fultd de Cieis Admiistrtivs Lieitur e Admiistrió Meió Gerei y Merdeo Uidd Curriulr: Mtemáti I UNIDAD I INTRODUCCIÓN AL ÁLGEBRA Elordo por: Ig. Roy Altuve Rg, Esp. Ciudd Ojed, eero 2017
Vierretordo Adémio Fultd de Cieis Admiistrtivs Lieitur e Admiistrió Meió Gerei y Merdeo Uidd Curriulr: Mtemáti I UNIDAD I INTRODUCCIÓN AL ÁLGEBRA Elordo por: Ig. Roy Altuve Rg, Esp. Ciudd Ojed, eero 2017
Matrices. Matrices especiales
 UNIVERSIDD UÓNO DE NUEVO EÓN FUD DE INGENIERÍ EÁNI Y EÉRI tries triz: ojuto de eleetos ordedos e fils y olus os eleetos puede ser úeros reles o oplejos E este urso solo se osider tries o eleetos reles
UNIVERSIDD UÓNO DE NUEVO EÓN FUD DE INGENIERÍ EÁNI Y EÉRI tries triz: ojuto de eleetos ordedos e fils y olus os eleetos puede ser úeros reles o oplejos E este urso solo se osider tries o eleetos reles
Integral de Riemann. Tema Sumas inferiores y superiores Particiones de un intervalo Sumas inferiores y superiores
 4 Mtemátis I : Cálulo itegrl e IR Tem 3 Itegrl de Riem 3. Sums iferiores y superiores 3.. Prtiioes de u itervlo Defiiió 26.- Se llm prtiió de u itervlo errdo [, ] ulquier ojuto fiito de putos P = {,,...,
4 Mtemátis I : Cálulo itegrl e IR Tem 3 Itegrl de Riem 3. Sums iferiores y superiores 3.. Prtiioes de u itervlo Defiiió 26.- Se llm prtiió de u itervlo errdo [, ] ulquier ojuto fiito de putos P = {,,...,
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
NÚMEROS REALES NEGATIVOS (Z - ) 0 POSITIVOS (Z + )
 LOS NÚMEROS REALES Sistem de úmeros reles Vlor soluto COMPENTECIA: Utilizr rgumetos de l teorí de úmeros pr justificr relcioes que ivolucr los úmeros turles NÚMEROS REALES Recuerde que: REALES (R) IRRACIONALES
LOS NÚMEROS REALES Sistem de úmeros reles Vlor soluto COMPENTECIA: Utilizr rgumetos de l teorí de úmeros pr justificr relcioes que ivolucr los úmeros turles NÚMEROS REALES Recuerde que: REALES (R) IRRACIONALES
1. CONJUNTOS DE NÚMEROS
 Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
CALCULO INTEGRAL TEMAS PORQUE ESTUDIAR. Escribir una cita aquí. Teorema fundamental del cálculo. Métodos de integración e integral indefinida.
 CALCULO INTEGRAL PORQUE ESTUDIAR CALCULO INTEGRAL l itegrl defiid es l herrmiet pr clculr y defiir diverss mgitudes, como áres, volúmees, logitudes de tryectoris curvs, proiliddes, promedios, cosumo de
CALCULO INTEGRAL PORQUE ESTUDIAR CALCULO INTEGRAL l itegrl defiid es l herrmiet pr clculr y defiir diverss mgitudes, como áres, volúmees, logitudes de tryectoris curvs, proiliddes, promedios, cosumo de
POTENCIA DE UN NÚMERO.
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluió Nº de oviere./0 Seretri De Eduió Distritl REGISTRO DANE Nº00-00099 Teléfoo Brrio Bstids St Mrt DEPARTAMENTO DE MATEMATICAS DOCENTE: LIC-ING.
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluió Nº de oviere./0 Seretri De Eduió Distritl REGISTRO DANE Nº00-00099 Teléfoo Brrio Bstids St Mrt DEPARTAMENTO DE MATEMATICAS DOCENTE: LIC-ING.
UNIDAD 2: POLINOMIOS Y FRACCIONES ALGEBRAICAS
 I.E.S. Rmó Girldo UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. POLINOMIOS Poliomios e u idetermid L epresió lgeric... 0 recie el omre de poliomio e l idetermid. Dode: es u úmero turl.,..., 0 so úmeros
I.E.S. Rmó Girldo UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. POLINOMIOS Poliomios e u idetermid L epresió lgeric... 0 recie el omre de poliomio e l idetermid. Dode: es u úmero turl.,..., 0 so úmeros
2.- Dadas las matrices A y B. Calcula A+B, A-B, A 2, B 2, AB, BA
 MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / / / / / / C. +B B.
MTRICES Y DETERMINNTES. Dds ls mtries Hllr ) ) B ).B d) B. e) +B f) C. g) C.B h) C.D i) j) B k) + l) B.B uioes. Dds ls mtries B. Clul +B, B,, B, B, B uió D C B.B / / / / / / / / B / / / / / / C. +B B.
Los alumnos deben utilizar siempre la notación matemática correcta y no la de las calculadoras.
 Apédices Notció Etre los diversos tipos de otció usules, el IB h decidido doptr u sistem que sigue ls recomedcioes de l Orgizció Iterciol de Normlizció (ISO). Est otció se utiliz e ls pruebs de exme de
Apédices Notció Etre los diversos tipos de otció usules, el IB h decidido doptr u sistem que sigue ls recomedcioes de l Orgizció Iterciol de Normlizció (ISO). Est otció se utiliz e ls pruebs de exme de
Un Resumen Teórico. Matemática I
 U Resume Teório De Mtemáti I WhittiLeks Los putes que ellos o quiere que seps de Oture 26 WhittiLeks Teório Notió: [, ] (, ) Df Im( f ) Y (Ad) O (Or) Es idétio Perteee /Es u elemeto de Por lo tto/por ede
U Resume Teório De Mtemáti I WhittiLeks Los putes que ellos o quiere que seps de Oture 26 WhittiLeks Teório Notió: [, ] (, ) Df Im( f ) Y (Ad) O (Or) Es idétio Perteee /Es u elemeto de Por lo tto/por ede
Unidad 2: SUCESIONES Y SERIES NUMÉRICAS.
 Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Tema 9. Determinantes.
 Uidd.Determites Tem. Determites.. Coeptos previos, permutioes. Defiiió geerl de determites. Determite de mtries de orde y orde.. Determite mtries udrds de orde. Determite mtries udrds de orde. Determite
Uidd.Determites Tem. Determites.. Coeptos previos, permutioes. Defiiió geerl de determites. Determite de mtries de orde y orde.. Determite mtries udrds de orde. Determite mtries udrds de orde. Determite
Métodos analíticos. Métodos Numéricos - Cap. 6. Integración 1/8. Integración - Cuadratura. Fórmulas cerradas de Newton-Cotes. Regla de los Trapecios
 Métodos Numéricos - Cp.. tegrció / tegrció - Cudrtur Métodos líticos Métodos uméricos pr estimr el vlor de u itegrl deiid Dode el itervlo de itegrció es iito y : cotiu e. Segú el teorem Fudmetl del Cálculo
Métodos Numéricos - Cp.. tegrció / tegrció - Cudrtur Métodos líticos Métodos uméricos pr estimr el vlor de u itegrl deiid Dode el itervlo de itegrció es iito y : cotiu e. Segú el teorem Fudmetl del Cálculo
Métodos Numéricos 06/09/2017
 Métodos Numérios 6/9/7 SOLUCION DE ECUACIONES NO LINEALES Clsiiió de Métodos METODO DE BISECCION Por ejemlo: = 6 + 5 = 5 6 + = se - e = - / = l 6 - k = Métodos Numérios 7 De itervlo Aiertos Gráio Biseió
Métodos Numérios 6/9/7 SOLUCION DE ECUACIONES NO LINEALES Clsiiió de Métodos METODO DE BISECCION Por ejemlo: = 6 + 5 = 5 6 + = se - e = - / = l 6 - k = Métodos Numérios 7 De itervlo Aiertos Gráio Biseió
SISTEMA DE ECUACIONES LINEALES
 SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
Tema 6: Matrices m n
 www.seleividd-grd.om Tem : Mries.. Mries. Defiiió primeros ejemplos Se llm mriz rel de dimesió mx l ojuo de m úmeros reles ordedos e m fils (horizoles) olums (veriles). L form más geerl de represer u mriz
www.seleividd-grd.om Tem : Mries.. Mries. Defiiió primeros ejemplos Se llm mriz rel de dimesió mx l ojuo de m úmeros reles ordedos e m fils (horizoles) olums (veriles). L form más geerl de represer u mriz
1.-INTEGRAL DEFINIDA.
 INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
{ } + S = = S, para S. a converge si su sucesión de sumas parciales converge, es decir,
 Esuel de Igeierí Cetro de Ciei Bási Cálulo de Vrile Rel Guí teóri Series Series Iiits: Deiiió: Se { } u suesió iiit. L epresió, se deoi serie iiit o serie y se deot por: { } S S S S S S S S - U serie es
Esuel de Igeierí Cetro de Ciei Bási Cálulo de Vrile Rel Guí teóri Series Series Iiits: Deiiió: Se { } u suesió iiit. L epresió, se deoi serie iiit o serie y se deot por: { } S S S S S S S S - U serie es
Capítulo 3 Rectificadores Controlados. 3 Rectificadores Controlados
 Cpítulo Retifidores Cotroldos Retifidores Cotroldos. Estrutur ási del SCR El SCR es u dispositivo semiodutor similr l diodo, pero o l pidd de retrdr el mometo de omutió segú se eesrio pr l utilidd que
Cpítulo Retifidores Cotroldos Retifidores Cotroldos. Estrutur ási del SCR El SCR es u dispositivo semiodutor similr l diodo, pero o l pidd de retrdr el mometo de omutió segú se eesrio pr l utilidd que
RADICALES. Entre los números reales se encuentran los radicales, que se pueden expresar como raíz de un índice n 2 de un número real.
 RADICALES Etre los úeros reles se euetr los rdiles, ue se uede exresr oo ríz de u ídie de u úero rel. Ríz eési de u úero rel. Si R y Ν, o, direos ue l ríz eési de es u úero rel r y lo otreos sí: r, si
RADICALES Etre los úeros reles se euetr los rdiles, ue se uede exresr oo ríz de u ídie de u úero rel. Ríz eési de u úero rel. Si R y Ν, o, direos ue l ríz eési de es u úero rel r y lo otreos sí: r, si
NÚMEROS REALES Clasificación. Acerca de las operaciones
 NÚMEROS REALES Clsifiió Aer de ls oerioes - Prioridd. Prétesis de detro fuer.. Poteis y ríes.. Multiliioes y divisioes de izquierd dereh. Sums y rets, de izquierd dereh o ositivos or u ldo y egtivos or
NÚMEROS REALES Clsifiió Aer de ls oerioes - Prioridd. Prétesis de detro fuer.. Poteis y ríes.. Multiliioes y divisioes de izquierd dereh. Sums y rets, de izquierd dereh o ositivos or u ldo y egtivos or
ININ 6005: Estadística Experimental
 ININ 65: Estdístic Eperimetl Diseño de Eperimetos Vribles Cotrolbles PROCESO Respuest Efectos Idepedietes O Recursos, mteriles, persos Modelos diseño eperimetl es u mipulció sistemátic de ls X's (vribles
ININ 65: Estdístic Eperimetl Diseño de Eperimetos Vribles Cotrolbles PROCESO Respuest Efectos Idepedietes O Recursos, mteriles, persos Modelos diseño eperimetl es u mipulció sistemátic de ls X's (vribles
MARCELA BOTERO ARBELÁEZ Ingeniero Electricista Profesor Asistente Universidad Tecnológica de Pereira
 ,Sieti et ehi Año XIII, o 37, Diiemre 007. Uiversidd eológi Pereir. ISS 0-70 533 MÉODO AOVA UILIZADO PARA REALIZAR EL ESUDIO DE REPEIBILIDAD Y REPRODUCIBILIDAD DERO DEL COROL DE CALIDAD DE U SISEMA DE
,Sieti et ehi Año XIII, o 37, Diiemre 007. Uiversidd eológi Pereir. ISS 0-70 533 MÉODO AOVA UILIZADO PARA REALIZAR EL ESUDIO DE REPEIBILIDAD Y REPRODUCIBILIDAD DERO DEL COROL DE CALIDAD DE U SISEMA DE
Profesorado de Informática - Ciencias de la Computación - INET DFPD Matemática II 2010 Sucesiones
 Profesordo de Iformátic - Ciecis de l Computció - INET DFPD Mtemátic II Sucesioes Sucesioes Tems: Límites de sucesioes. Sucesioes moótos y sus límites. Pres de sucesioes moótos covergetes. Número e. Opercioes
Profesordo de Iformátic - Ciecis de l Computció - INET DFPD Mtemátic II Sucesioes Sucesioes Tems: Límites de sucesioes. Sucesioes moótos y sus límites. Pres de sucesioes moótos covergetes. Número e. Opercioes
Instituto Politécnico Superior General San Martín A U S. Análisis Matemático I. Límite y Continuidad de Funciones. Mgter. Viviana Paula D Agostini
 Istituto Politéio Superior Geerl S Mrtí A U S Aálisis Mtemátio I Límite y Cotiuidd de Fuioes Mgter. Vivi Pul D Agostii TEMARIO Límite de u uió. Propieddes. Cálulo de límites medite propieddes. Límites
Istituto Politéio Superior Geerl S Mrtí A U S Aálisis Mtemátio I Límite y Cotiuidd de Fuioes Mgter. Vivi Pul D Agostii TEMARIO Límite de u uió. Propieddes. Cálulo de límites medite propieddes. Límites
PAIEP. Sumas de Riemann
 Progrm de Acceso Iclusivo, Equidd y Permeci PAIEP Uiversidd de Stigo de Chile Sums de Riem Ddo u itervlo de l form [, b], co y b e R, < b, u prtició del itervlo [, b] es u colecció de putos P = {x, x,...,
Progrm de Acceso Iclusivo, Equidd y Permeci PAIEP Uiversidd de Stigo de Chile Sums de Riem Ddo u itervlo de l form [, b], co y b e R, < b, u prtició del itervlo [, b] es u colecció de putos P = {x, x,...,
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
, 1], del mismo tamaño, pues x 1 = = 1 4, x 2 = = 1 4, x 3 = = 1 4 y x 4 = 1
![, 1], del mismo tamaño, pues x 1 = = 1 4, x 2 = = 1 4, x 3 = = 1 4 y x 4 = 1 , 1], del mismo tamaño, pues x 1 = = 1 4, x 2 = = 1 4, x 3 = = 1 4 y x 4 = 1](/thumbs/87/95639988.jpg) Tem Itegrl de Riem.. Sums iferiores y superiores... Prtiioes de u itervlo. Defiiió. U prtiió de u itervlo errdo [, b] es u ojuto fiito de putos P = {x, x,..., x } dode = x < x < < x = b. U prtiió sepr,
Tem Itegrl de Riem.. Sums iferiores y superiores... Prtiioes de u itervlo. Defiiió. U prtiió de u itervlo errdo [, b] es u ojuto fiito de putos P = {x, x,..., x } dode = x < x < < x = b. U prtiió sepr,
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
1) CONCEPTOS 2) MONOMIOS TEMA : EXPRESIONES ALGEBRAICAS
 TEMA EXPRESIONES ALGEBRAICAS CONCEPTOS U EXPRESIÓN ALGEBRAICA es el ojuto e úmeros letrs que se omi o los sigos e ls operioes mtemátis sum, rest, multipliió, ivisió poteiió. Ejemplo El VALOR NUMÉRICO e
TEMA EXPRESIONES ALGEBRAICAS CONCEPTOS U EXPRESIÓN ALGEBRAICA es el ojuto e úmeros letrs que se omi o los sigos e ls operioes mtemátis sum, rest, multipliió, ivisió poteiió. Ejemplo El VALOR NUMÉRICO e
Algebra II. Miguel Angel Muñoz Jara.
 Uiversidd de Cieis de l Iformáti Esuel de Igeierí Crrer de Igeierí de Ejeuió e Iformáti lger II Miguel gel Muño Jr Uiversidd de Cieis de l Iformáti Esuel de Igeierí Crrer de Igeierí de Ejeuió e Computió
Uiversidd de Cieis de l Iformáti Esuel de Igeierí Crrer de Igeierí de Ejeuió e Iformáti lger II Miguel gel Muño Jr Uiversidd de Cieis de l Iformáti Esuel de Igeierí Crrer de Igeierí de Ejeuió e Computió
Determine las ecuaciones vectorial, paramétricas y simétricas de la recta que., siendo D(4, 0, -1) y T(2, -3, 1).
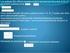 Vetores Cooreos Ilustrió 38 Determie ls euioes vetoril prmétris y simétris e l ret que ps por el puto A- 3 y es prlel l vetor DT sieo D4 0 - y T -3. Soluió Desigemos est ret por L A DT Se Px y z tl que
Vetores Cooreos Ilustrió 38 Determie ls euioes vetoril prmétris y simétris e l ret que ps por el puto A- 3 y es prlel l vetor DT sieo D4 0 - y T -3. Soluió Desigemos est ret por L A DT Se Px y z tl que
INTERVALOS Y SEMIRRECTAS.
 el log de mte de id. Mtemátics plicds ls ciecis sociles I: NÚMEROS REALES pág. INTERVALOS Y SEMIRRECTAS. L ordeció de úmeros permite defiir lguos cojutos de úmeros que tiee u represetció geométric e l
el log de mte de id. Mtemátics plicds ls ciecis sociles I: NÚMEROS REALES pág. INTERVALOS Y SEMIRRECTAS. L ordeció de úmeros permite defiir lguos cojutos de úmeros que tiee u represetció geométric e l
NÚMEROS REALES. nombre expresión desigualdad representación expresión desigualdad representación. [a, b] (, b]
![NÚMEROS REALES. nombre expresión desigualdad representación expresión desigualdad representación. [a, b] (, b] NÚMEROS REALES. nombre expresión desigualdad representación expresión desigualdad representación. [a, b] (, b]](/thumbs/78/77879320.jpg) Lo fudmetl de l uidd Nomre y pellidos:... Curso:... Fech:... NÚMEROS REALES NÚMEROS RACIONALES So los que se puede expresr como... ejemplo: 4, = NÚMEROS IRRACIONALES So quellos cuy expresió deciml.. ejemplo:
Lo fudmetl de l uidd Nomre y pellidos:... Curso:... Fech:... NÚMEROS REALES NÚMEROS RACIONALES So los que se puede expresr como... ejemplo: 4, = NÚMEROS IRRACIONALES So quellos cuy expresió deciml.. ejemplo:
Aproximación al área bajo una curva.
 Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
el blog de mate de aida. NÚMEROS REALES 4º ESO pág. 1 NÚMEROS REALES
 el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
DETERMINANTES. A toda matriz cuadrada se le puede hacer corresponder un número (determinante) cuyo cálculo se puede hacer de las siguientes maneras:
 Deterites DETERMINNTES. DEFINICIÓN. tod tri udrd se le uede her orresoder u úero (deterite uo álulo se uede her de ls siguietes ers:.. DETERMINNTE DE SEGUNDO ORDEN. det Es deir, es el roduto de los eleetos
Deterites DETERMINNTES. DEFINICIÓN. tod tri udrd se le uede her orresoder u úero (deterite uo álulo se uede her de ls siguietes ers:.. DETERMINNTE DE SEGUNDO ORDEN. det Es deir, es el roduto de los eleetos
el blog de mate de aida CSI: sistemas de ecuaciones. pág
 el blog de mte de id CSI: sistems de ecucioes pág SISTEMAS DE ECUACIONES DE PRIMER GRADO U sistem de "m" ecucioes lieles co "" icógits,,,, es u cojuto de "m" igulddes de l form: m m b b m dode ij, b i
el blog de mte de id CSI: sistems de ecucioes pág SISTEMAS DE ECUACIONES DE PRIMER GRADO U sistem de "m" ecucioes lieles co "" icógits,,,, es u cojuto de "m" igulddes de l form: m m b b m dode ij, b i
Eficiencia de algoritmos. Javier Campos
 Efiieia de algoritmos Javier Campos Efiieia de algoritmos Problema de álulo: espeifiaió de ua relaió existete etre uos valores de etrada datos del problema y otros de salida resultados Eemplo: problema
Efiieia de algoritmos Javier Campos Efiieia de algoritmos Problema de álulo: espeifiaió de ua relaió existete etre uos valores de etrada datos del problema y otros de salida resultados Eemplo: problema
REGLAS PARA DETERMINAR EL TÉRMINO GENERAL DE UNA SUCESIÓN:
 REGLAS PARA DETERMINAR EL TÉRMINO GENERAL DE UNA SUCESIÓN: Pese que o existe u proedimieto geerl pr determir el térmio geerl de u suesió vmos reopilr lgus herrmiets de álulo útiles que podemos poer e práti.
REGLAS PARA DETERMINAR EL TÉRMINO GENERAL DE UNA SUCESIÓN: Pese que o existe u proedimieto geerl pr determir el térmio geerl de u suesió vmos reopilr lgus herrmiets de álulo útiles que podemos poer e práti.
TEMA 4 ECUALIZADORES. Inmaculada Hernáez Rioja
 TA 4 CUALIZADORS Imuld Heráez Rio TA 4 ulizdores... 4-4. Demodulió óptim pr IS y ruido gusio blo... 4-4. Forzdor de pso por ero... 4-4.3 Filtrdo Adpttivo... 4-5 4.3. Itroduió... 4-5 4.3. Criterio del rror
TA 4 CUALIZADORS Imuld Heráez Rio TA 4 ulizdores... 4-4. Demodulió óptim pr IS y ruido gusio blo... 4-4. Forzdor de pso por ero... 4-4.3 Filtrdo Adpttivo... 4-5 4.3. Itroduió... 4-5 4.3. Criterio del rror
Método del spline cúbico. Cuando un número grande de datos tiene que ajustarse a una curva suave, la interpolación de Lagrange no es adecuada.
 MÉTODO DEL PLINE CÚBICO PROGRAMACIÓN AVANZADA emestre 09- Método del sple úo. Cudo u úmero grde de dtos tee que justrse u urv suve l terpoló de Lgrge o es deud. Pr esto se emple el método del sple úo este
MÉTODO DEL PLINE CÚBICO PROGRAMACIÓN AVANZADA emestre 09- Método del sple úo. Cudo u úmero grde de dtos tee que justrse u urv suve l terpoló de Lgrge o es deud. Pr esto se emple el método del sple úo este
1. Números reales. 2. Raíces y potencias. 3. Operaciones con radicales. Matemáticas 3º ESO
 Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Aroxiió de deiles Itervlos. Ríes y oteis Notió ietífi. Oerioes Rdiió. Proieddes de ls oteis de exoete riol Rdiles equivletes Silifir rdiles Extrió
Mteátis º ESO 1. Núeros reles Clsifiió de los úeros reles Aroxiió de deiles Itervlos. Ríes y oteis Notió ietífi. Oerioes Rdiió. Proieddes de ls oteis de exoete riol Rdiles equivletes Silifir rdiles Extrió
GUÍA DE EJERCICIOS III
 Fult e Igeierí UCV Álger Liel Geometrí líti 5 Cilo Básio GUÍ DE EJECICIOS III rsformioes lieles: Demuestre e so si l trsformió el esio vetoril V e el esio vetoril W es liel e w : B oe B es g u mtri fij
Fult e Igeierí UCV Álger Liel Geometrí líti 5 Cilo Básio GUÍ DE EJECICIOS III rsformioes lieles: Demuestre e so si l trsformió el esio vetoril V e el esio vetoril W es liel e w : B oe B es g u mtri fij
Racionales. Representación decimal de los reales. En los racionales la parte decimal se repite, es periódica e infinita Ejemplos:
 PUNTES DE ÁLGER Números reles. Vemos los diferetes tipos de úmeros reles. Números turles:,,,... Eteros: -, -, -, 0,... m Rioles: So rzoes etre úmeros eteros r, o m eteros 0 7 ejemplos de rioles so,,, 0.7.
PUNTES DE ÁLGER Números reles. Vemos los diferetes tipos de úmeros reles. Números turles:,,,... Eteros: -, -, -, 0,... m Rioles: So rzoes etre úmeros eteros r, o m eteros 0 7 ejemplos de rioles so,,, 0.7.
POTENCIA DE UN NÚMERO NATURAL. a, es igual al producto de n veces el número Natural
 LICEO DE CERVANTES PP. AGUSTINOS BOGOTÁ ÁREA DE MATEMÁTICAS ASIGNATURA: Mtemátics DOCENTE: Elky F. Ortiz GRADO: QUINTO FECHA: CALIFICACIÓN DESCRIPCIÓN: Guí - Tller de potecició, Rdicció y logritmció. ESTUDIANTE:
LICEO DE CERVANTES PP. AGUSTINOS BOGOTÁ ÁREA DE MATEMÁTICAS ASIGNATURA: Mtemátics DOCENTE: Elky F. Ortiz GRADO: QUINTO FECHA: CALIFICACIÓN DESCRIPCIÓN: Guí - Tller de potecició, Rdicció y logritmció. ESTUDIANTE:
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Álgebra. , para todo n 9. , si n es impar 10. , si n es par 11. a
 Álgebr Lees de poteis.., pr todo 9., si es impr 0. b b, si es pr. 3. 4. 0 b b, pr todo 0. b 5. 6. 7. 3.... 4. vees... vees 8. Fórmuls Notbles m m m b 3 3 I. b b b V. b 3 b 3b b 3 3 b b b VI. b b b b II.
Álgebr Lees de poteis.., pr todo 9., si es impr 0. b b, si es pr. 3. 4. 0 b b, pr todo 0. b 5. 6. 7. 3.... 4. vees... vees 8. Fórmuls Notbles m m m b 3 3 I. b b b V. b 3 b 3b b 3 3 b b b VI. b b b b II.
Sucesiones de Números Reales
 Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Las reglas de divisibilidad
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Uiversidd Itermeric de Puerto Rico e el Recito de Poce Itroducció Desde l escuel elemetl los estudites
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Uiversidd Itermeric de Puerto Rico e el Recito de Poce Itroducció Desde l escuel elemetl los estudites
el blog de mate de aida. Matemáticas Aplicadas a las Ciencias Sociales I. Sistemas de ecuaciones. pág
 el blog de mte de id. Mtemátics Aplicds ls Ciecis Sociles I. Sistems de ecucioes. pág. SISTEMAS DE ECUACIONES DE PRIMER GRADO U sistem de "m" ecucioes lieles co "" icógits,,,..., es u cojuto de "m" igulddes
el blog de mte de id. Mtemátics Aplicds ls Ciecis Sociles I. Sistems de ecucioes. pág. SISTEMAS DE ECUACIONES DE PRIMER GRADO U sistem de "m" ecucioes lieles co "" icógits,,,..., es u cojuto de "m" igulddes
DERECHOS BÁSICOS DE APRENDIZAJE matemáticas - grado 8
 i e rtd 1 mtemátis - grdo Comprede si u leguje forml l oió de fuió omo u regl f, que d vlor, le sig u úio vlor f () reooe que su gráfi está oformd por todos los putos (, f ()). Tmié omprede que u fuió
i e rtd 1 mtemátis - grdo Comprede si u leguje forml l oió de fuió omo u regl f, que d vlor, le sig u úio vlor f () reooe que su gráfi está oformd por todos los putos (, f ()). Tmié omprede que u fuió
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
= (columnas), llamamos matriz de. = i, =... A (matriz de orden n) MATRICES
 TRICES INTRODUCCIÓN Observemos el siguiete ejemplo: Tbl de ots de tres lumos e el primer bimestre: ------------------ temátic Físic Químic Biologí 6 4 5 8 toio 5 7 5 5 Betriz 5 6 7 4 L tbl terior os permite
TRICES INTRODUCCIÓN Observemos el siguiete ejemplo: Tbl de ots de tres lumos e el primer bimestre: ------------------ temátic Físic Químic Biologí 6 4 5 8 toio 5 7 5 5 Betriz 5 6 7 4 L tbl terior os permite
2 ( ) 2. ( 2x) 2 GYMNÁZIUM BUDĚJOVICKÁ. MATEMÁTICAS. EXPRESIONES ALGEBRÁICAS. 1.- Técnicas de factorización:
 GYMNÁZIUM UDĚJOVICKÁ. MTEMÁTICS. EXPRESIONES LGERÁICS..- Técics de fctorizció: No h u orde clro, slvo u primer pso: scr fctor comú después vri técics que depederá de cuál se l epresió que tegmos. Scr fctor
GYMNÁZIUM UDĚJOVICKÁ. MTEMÁTICS. EXPRESIONES LGERÁICS..- Técics de fctorizció: No h u orde clro, slvo u primer pso: scr fctor comú después vri técics que depederá de cuál se l epresió que tegmos. Scr fctor
División de Estadísticas y Proyecciones Económicas (DEPE) Centro de Proyecciones Económicas (CPE)
 Comisió Ecoómic pr Améric Lti y el Crie (CEPAL) Divisió de Estdístics y Proyeccioes Ecoómics (DEPE) Cetro de Proyeccioes Ecoómics (CPE) Coceptos Básicos de u ile Aletori. Christi A. Hurtdo Nvrro Aril,
Comisió Ecoómic pr Améric Lti y el Crie (CEPAL) Divisió de Estdístics y Proyeccioes Ecoómics (DEPE) Cetro de Proyeccioes Ecoómics (CPE) Coceptos Básicos de u ile Aletori. Christi A. Hurtdo Nvrro Aril,
Universidad Pontificia Bolivariana Ciencia Básica Taller Álgebra Lineal CAPITULO I: MATRICES
 Uiversidd Poifii Bolivri Ciei Bási Tller Álger Liel CPITULO I: MTRICES. Dds ls mries:, B C Efeur ls siguiees operioes, si es posile. E so e o ser posile, eplique por qué. -B T -B T B T d T C e B - f C
Uiversidd Poifii Bolivri Ciei Bási Tller Álger Liel CPITULO I: MTRICES. Dds ls mries:, B C Efeur ls siguiees operioes, si es posile. E so e o ser posile, eplique por qué. -B T -B T B T d T C e B - f C
Área de Matemáticas. INTERVALOS Un intervalo es un subconjunto de números reales, existen los siguientes tipos de intervalos INTERVALOS CERRADO
 Istitució Eductiv S Vicete de Púl Cieci, Tecologí y Sociedd e Armoí Áre de Mtemátics AREA: Mtemátics PROFESOR: Crlos A. Márquez Ferádez Mil: kmrfer@gmil.com Grdo: GUIA Nº TEMA: INTERVALOS Y DESIGUALDADES
Istitució Eductiv S Vicete de Púl Cieci, Tecologí y Sociedd e Armoí Áre de Mtemátics AREA: Mtemátics PROFESOR: Crlos A. Márquez Ferádez Mil: kmrfer@gmil.com Grdo: GUIA Nº TEMA: INTERVALOS Y DESIGUALDADES
INTEGRACION NUMERICA Método se Simpson
 cerque@gmil.com Ojetivos: Geerles Específicos Oservcioes Prelimires Clculo de Áres El método de Simpso Desrrollo del modelo de Simpso Ejemplos Progrm e diferetes legujes L jerrquí de clses INTEGRACION
cerque@gmil.com Ojetivos: Geerles Específicos Oservcioes Prelimires Clculo de Áres El método de Simpso Desrrollo del modelo de Simpso Ejemplos Progrm e diferetes legujes L jerrquí de clses INTEGRACION
Estructuras Discretas. Unidad 3 Teoría de números
 Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
RACCONTO SOBRE TÉCNICAS DE CONTEO
 TC RACCONTO SOBRE TÉCNICAS DE CONTEO Asocicioes de opcioes idepedietes TC I Supógse u fáric de utomóviles que ofrezc ls siguietes opcioes idepedietes: Opció α: Motor ft, gs, o diesel (3 opcioes). Opció
TC RACCONTO SOBRE TÉCNICAS DE CONTEO Asocicioes de opcioes idepedietes TC I Supógse u fáric de utomóviles que ofrezc ls siguietes opcioes idepedietes: Opció α: Motor ft, gs, o diesel (3 opcioes). Opció
