PANELES SANDWICH PANELES SANDWICH. Carlos Navarro. Departamento de Mecánica de Medios Continuos y Teoría de Estructuras
|
|
|
- Ricardo San Martín Naranjo
- hace 5 años
- Vistas:
Transcripción
1 PNELES SNDWIH PNELES SNDWIH arlos Navarro Dartamto d Mcáica d Mdios otiuos Toría d Estructuras
2 PNELES SNDWIH (a) Núclo d suma (foam) (b) Núclo d ido d abja (c) Núclo wb (d) Núclo corrugado
3 PNELES SNDWIH z Pil Núclo / Pil
4 PNELES SNDWIH Emlado la Rsistcia d matrials
5 ( ) M N σ ( ) M N σ ( ) Q τ ( ) z R z o ε ε o E N ε ( ) E M R VIGS SNDWIH Tsios ua viga sádwic Dformacios ua viga sádwic z Q M N PNELES SNDWIH
6 ( ) E I E P ( ) ( ) c G G 3 G G G ( ) L EI G L EI P ado π π álculo d flcas giros vigas sádwic arga crítica d ado global ua viga sádwic PNELES SNDWIH
7 PNELES SNDWIH HIPÓTESIS DE ÁLULO:.- El matrial dl úclo rsta u comortamito trasvrsalmt isótroo os u ssor muco más grad qu l d las ils (>>, ).- Las tsios l lao dl úclo (σ, σ, τ ) so dsrciabls 3.- Los dslazamitos l lao dl úclo (u v ) varía lialmt co la coordada z 4.- Los dslazamitos l lao d las ils (u v ) so uiforms a lo largo dl ssor d las ils 5.- Las tsios fura dl lao las ils (τ z, τ z ) so dsrciabls 6.- Los dslazamitos so quños comaració co l ssor dl sadwic 7.- Las dformacios l lao so quñas comaració co la uidad
8 PNELES SNDWIH HIPÓTESIS DE ÁLULO (ot): 8.- El dslazamito trasvrsal w s iddit d la coordada z, or tato, ε z s dsrciabl 9.- Tato los matrials dl úclo d las ils obdc a la l d Hook.- E úclo las ils ti ssor costat
9 PNELES SNDWIH asádoos la 3ª iótsis u v u v (, ) z (, ) (, ) z (, )
10 PNELES SNDWIH v v v v u u u u asádoos la 4ª iótsis Los subídics s rfir a la il surior () a la ifrior ()
11 PNELES SNDWIH asádoos la 8ª iótsis w w(, )
12 PNELES SNDWIH Dformacios l ε ε z z u z v z w w úclo : w w
13 PNELES SNDWIH DEFORMIONES EN EL PLNO MEDIO ε ε γ u v u v
14 PNELES SNDWIH URVTURS κ κ κ
15 PNELES SNDWIH Pil surior () : ε ε ε () () () ε ε ε κ κ κ
16 PNELES SNDWIH Pil ifrior () : ε ε ε ( ) ( ) ( ) ε ε ε κ κ κ
17 PNELES SNDWIH N N N EQUIVLENI FUERZS EN EL PLNO-TENSIONES ( ) σ ( ) ( ) σ ( ) ( ) τ ( ) dz dz dz ( ) σ ( ) ( ) σ ( ) ( ) τ ( ) dz dz dz E l úclo : σ, σ, τ
18 M M M PNELES SNDWIH EQUIVLENI MOMENTOS-TENSIONES ( ) σ ( ) ( ) σ ( ) ( ) τ ( ) zdz zdz zdz ( ) σ ( ) ( ) σ ( ) ( ) τ ( ) zdz zdz zdz E l úclo : σ, σ, τ
19 PNELES SNDWIH EQUIVLENI FUERZS FUER DEL PLNO-TENSIONES Q Q τ τ z z dz dz (Hiótsis 5)
20 PNELES SNDWIH Rlació tsió-dformació l k ésima lámia d la il i σ σ τ ( k ) ( k ) ( k ) Q Q Q ( k ) ( k ) ( k ) ( k ) ( k ) ( k ) ( k ) ( k ) ( k ) 6 Q Q Q 6 Q Q Q ε ε γ ( i ) () i () i ( i, )
21 PNELES SNDWIH Rlació tsios-dformacios l úclo τ τ z z G 3 G 3 γ γ ( ) z ( ) z
22 PNELES SNDWIH D D D D D D D D D M M M N N N κ κ κ γ ε ε
23 D () ( ) [ () ( )] () ( ) [ () ( )] ( ) () ( k ) ( ) ( k ) ( ) Si las dos ils fus idéticas: ( ) ( ) ( ) ( ) Q Q PNELES SNDWIH dz dz D ( ) () ( k ) ( ) ( k ) ( ) ( ) Q Q zdz zdz
24 PNELES SNDWIH w w G G Q Q 3 3 ORTNTE TRNSVERSL L PNEL
25 PNELES SNDWIH PROXIMIÓN: Tratmos a las ils como si stuvis ralizadas d u matrial omogéo : Rigidz fctiva ( k ) k k, D 4 ( ) ( ) ( ) ( )
26 PNELES SNDWIH ( ) ( ) v v v u u u EUIONES DE EQUILIRIO SDS EN DESPLZMIENTOS:
27 PNELES SNDWIH ( ) ( ) v v v u u u
28 PNELES SNDWIH ( ) ( ) w G D D D D D D D v v v u u u
29 PNELES SNDWIH ( ) ( ) w G D D D D D D D v v v u u u
30 PNELES SNDWIH 3 3 q w N w N w N w G w G
31 PNELES SNDWIH t f Pil c Núclo t f Pil a lzado
32 PNELES SNDWIH (úclo d suma) b L t c t Proidads dl úclo: E ρ Módulo d lasticidad aart d la suma dl Dsidad aart d la suma dl úclo úclo
33 PNELES SNDWIH (úclo d suma) E E mat ρ ρ mat G E mat ρ ρ mat E mat ρ mat Módulo d lasticidad dl matrial dl qu stá fabricado la suma Dsidad dl matrial dl qu stá fabricado la suma, 4
34 PNELES SNDWIH (úclo d suma) Proidads d las ils: E ρ Módulo d lasticidad quivalt d la il Dsidad aart d la il
35 PNELES SNDWIH (úclo d suma) Rigidz a flió quivalt dl al sadwic: ( EI ) E bt 3 3 quiv. 6 Ebc E btd El trcr sumado s bastat más grad qu los otros dos. Hacido la iótsis d qu: s obti:: d c ( EI ) quiv. E btc
36 PNELES SNDWIH (úclo d suma) Rigidz a cortat quivalt dl al sadwic: ( G) G bd bcg quiv. c
37 PNELES SNDWIH (úclo d suma) uado l al s cutra somtido a ua carga trior P, su flca máima vi dada or: δ δ δ flió cor tat PL 3 PL ( EI ) ( ) quiv. G quiv.
38 PNELES SNDWIH (úclo d suma) δ δ δ flió cor tat PL 3 PL ( EI ) quiv. ( G) quiv. Modo d carga 3 4 Mésula co carga (P) l trmo 3 Mésula co carga uiformmt distribuida (P/L) 8 Viga flio trs utos co carga ctral (P) Viga flio trs utos co carga uiformmt distribuida (P/L) 384/5 8 8 Viga bimotrada co carga ctral (P) Viga bimotrada co carga uiformmt distribuida (P/L) 384 8
39 PNELES SNDWIH (úclo d suma) FLEXIILIDD: δ l 3 l P E btc bcg PESO: W ρ ρ gblt gblc
40 PNELES SNDWIH (úclo d suma) t/l DISEÑO ÓPTIMO DEL PNEL (ρ ct) t ótimo Rigidz scífica (P/δ) Puto d disño ótimo Rquisito d so t t c urva corrsodit a ua rigidz (P/δ) dada: G t E ( / l) b L ( c / l) ( δ / P) bg ( c / l) c ótimo urva corrsodit a u so (W) dado: Pso 4 6 c/l ( t / l) ( c / l) bl ρ ρ g ρ W
41 PNELES SNDWIH (úclo d suma) RESISTENI L ROTUR DE PNELES SNDWIH Modos d fallo a flió: Rotura d la il traccioada σ f σ f Dsgu il-úclo σ f σ f Pado local d la il a comrsió Idtació d la il l úclo τ c Fallo dl úclo τ c
42 PNELES SNDWIH (úclo d suma) t σ τ c σ τ t Distribució tsioal ral t σ τ c σ τ t Distribució tsioal aroimada
43 PNELES SNDWIH (úclo d suma) Tsios ormals σ MzE ( EI ) quiv M btc Pl btc 3 σ MzE M btc E ( EI ) quiv E 3 E Pl btc E Tsios tagcials τ τ Q bc τ c P bc 4
44 PNELES SNDWIH (úclo d suma) TENSIONES PRINIPLES EN LS PIELES O EN EL NÚLEO: σ τ σ τ σ τ σ σ σ τ σ σ má σ τ (suomos qu o ist tsios sgú z)
45 PNELES SNDWIH (úclo d suma) E las ils, odmos suor qu: s ua catidad quña, or lo qu: E l úclo, odmos suor qu: Es, gral, ua catidad grad, or lo qu: l t 4 3 σ τ τ τ σ σ σ ma E E l t 4 3 σ τ c τ τ τ σ τ σ ma
46 PNELES SNDWIH (úclo d suma) Rotura d la il traccioada σ f σ f MPL/ 3 La il falla cuado la tsió ormal alcaza su rsistcia (tsió d cdcia, ara matrials dúctils tsió d rotura ara matrials frágils) P σ 3btc l
47 PNELES SNDWIH (úclo d suma) Si: /3 ( ) ( ) E E l btc P ν ν ν E E ρ ρ E E l btc P ρ ρ, Pado local d la il a comrsió σ f σ f
48 PNELES SNDWIH (úclo d suma) Núclo d matrial frágil: l tamaño d la célula alogitud d fisura (>4l) a l bc P a K f σ ρ ρ π σ τ σ 3 4 f bc P σ ρ ρ 3 4 Fallo dl úclo τ c τ c
49 PNELES SNDWIH (úclo d suma) Dsgu il-úclo Probablmt st tio d fallo sa l más difícil d aalizar. E gral, ara úclos d suma, las ils s ga al úclo mdiat rsia Eoi, la cual s más furt qu l foam qu costitu l úclo, or tato, l fallo más bi s roduc l roio úclo qu l roio adsivo. El aálisis a qu ralizarlo térmios d rgía.
50 PNELES SNDWIH (úclo d suma) Ergía almacada l al trabajado a flió ura: U M M ( EI) R quiv ( EI) quiv L U M ( EI) L quiv
51 PNELES SNDWIH (úclo d suma) Si suomos la istcia d ua fisura d logitud ª: Surfici d la fisura ab Si la fisura s roagas ua logitud da, la variació d Ergía sría: du b da U Lb ( M EI ) quiv da
52 PNELES SNDWIH (úclo d suma) G Tasa d libració d rgía G du b da M b( EI) quiv Por lo qu: P 3btc L GE t f
53 PNELES SNDWIH (úclo d suma) Idtació d la il l úclo P σ i
PROBLEMAS TEMA 4 EJERCICIO 1 (Ej 9.15 de Fernández Abascal)
 PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
CASO DE ESTUDIO N 8. Análisis de un tornillo de transmisión
 Vrsió 01 CAPITULO POYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIEE CASO DE ESTUDIO N 8 Aálisis u torillo trasmisió Vrsió 01 1. Itroucció Los torillos trasmisió stá somtios a cosirabls solicitacios bias
Vrsió 01 CAPITULO POYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIEE CASO DE ESTUDIO N 8 Aálisis u torillo trasmisió Vrsió 01 1. Itroucció Los torillos trasmisió stá somtios a cosirabls solicitacios bias
2. Utilizando el método adimensional basado en el factor de calidad Q, determine:
 Uivrsidad Simó Bolívar Dpartamto d Covrsió y Trasport d Ergía Autor: Eduardo Albaz. Cart: 06-391 Profsor: J. M. Allr Máquias Eléctricas II CT-311 U motor d iducció coxió strlla d 100 kw, 416 V, rdimito
Uivrsidad Simó Bolívar Dpartamto d Covrsió y Trasport d Ergía Autor: Eduardo Albaz. Cart: 06-391 Profsor: J. M. Allr Máquias Eléctricas II CT-311 U motor d iducció coxió strlla d 100 kw, 416 V, rdimito
Fonones: Cuantización de las vibraciones de la red cristalina.
 Foo: Cuatizació d la ibracio d la rd critalia. Oda d logitud larga Oda lática... Oda d logitud corta λ a o πa tmo qu tr cuta la tructura atómica dl crital. foó logitudial foó traral a mooatómica: Coidrmo
Foo: Cuatizació d la ibracio d la rd critalia. Oda d logitud larga Oda lática... Oda d logitud corta λ a o πa tmo qu tr cuta la tructura atómica dl crital. foó logitudial foó traral a mooatómica: Coidrmo
************************************************************************ *
 1.- Ua barra de secció circular, de 5 mm de diámetro, está sometida a ua fuerza de tracció de 5 kg, que se supoe distribuida uiformemete e la secció. partir de la defiició de vector tesió, determiar sus
1.- Ua barra de secció circular, de 5 mm de diámetro, está sometida a ua fuerza de tracció de 5 kg, que se supoe distribuida uiformemete e la secció. partir de la defiició de vector tesió, determiar sus
! 1 3 <1 la serie converge (y confirma a n! 0 ). a n. x 2 >0; f 0 (x)<0 si x>1; R 1 f (x)dx = 1 2 e x2 1 = 1 2e. ) Convergente. n! 0 ) Convergente.
 Solucios d los roblmas d Matmáticas (07-08) {a } acotada ifriormt or 0 (los a so ositivos) y dcrcit us + + )9líma a ) a a ) a0 Como a + a < la sri covrg (y cofirma a 0 ) a) (a ) / Divrgt (O orqu {a
Solucios d los roblmas d Matmáticas (07-08) {a } acotada ifriormt or 0 (los a so ositivos) y dcrcit us + + )9líma a ) a a ) a0 Como a + a < la sri covrg (y cofirma a 0 ) a) (a ) / Divrgt (O orqu {a
LECCIÓN 11 CÉLULAS SOLARES
 ÓN CÉUAS SOAS NTODUÓN tr los dispositivos basados smicoductors, la célula solar s uo d los más adcuados para tdr cómo las propidads itríscas básicas dl smicoductor, combiació co las propidads tríscas coscucia
ÓN CÉUAS SOAS NTODUÓN tr los dispositivos basados smicoductors, la célula solar s uo d los más adcuados para tdr cómo las propidads itríscas básicas dl smicoductor, combiació co las propidads tríscas coscucia
La distribución canónica y la aproximación clásica. Espacio de fases clásico. Distribución de velocidades de Maxwell. Aplicaciones de la distribución
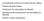 La distibució caóica y la aoiació clásica. Esacio d fass clásico. Distibució d locidads d Mawll. Alicacios d la distibució d locidads d Mawll. Efusió y hacs olculas La distibució caóica sgú la aoiació
La distibució caóica y la aoiació clásica. Esacio d fass clásico. Distibució d locidads d Mawll. Alicacios d la distibució d locidads d Mawll. Efusió y hacs olculas La distibució caóica sgú la aoiació
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica. Determinar si las integrales impropias convergen o divergen.
 Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Cap. II: Principios Fundamentales del Flujo de Tránsito
 Cap. II: Pricipios Fudamtals dl Flujo d Trásito Diagrama Espacio-Timpo Distacia 1 2 Itralo (i) 3 4 5 6 Espaciamito () Timpo Flujo, q Dsidad, Vlocidad, Tasa horaria quialt a la cual trasita los hículos
Cap. II: Pricipios Fudamtals dl Flujo d Trásito Diagrama Espacio-Timpo Distacia 1 2 Itralo (i) 3 4 5 6 Espaciamito () Timpo Flujo, q Dsidad, Vlocidad, Tasa horaria quialt a la cual trasita los hículos
Resistencia de Materiales TRACCIÓN Y COMPRESIÓN
 Resistencia de Materiales TRCCIÓN Y COMRESIÓN Resistencia de Materiales TRCCIÓN Y COMRESIÓN Introducción. Tracción y compresión. Tensiones y alargamientos. Deformaciones de piezas de peso no despreciable.
Resistencia de Materiales TRCCIÓN Y COMRESIÓN Resistencia de Materiales TRCCIÓN Y COMRESIÓN Introducción. Tracción y compresión. Tensiones y alargamientos. Deformaciones de piezas de peso no despreciable.
TEMA 3.4 Tracción y Flexion
 TEA 3.4 Tracción Fleion Física ecánica de las Construcciones Física ecánica de las Construcciones 3.4.1. Introducción γ β α σ σ σ t t t α β α ε γ γ γ ε γ γ γ ε ε ε ε 1 1 1 1 1 1 1 ESTADO TENSIONAL: ESTADO
TEA 3.4 Tracción Fleion Física ecánica de las Construcciones Física ecánica de las Construcciones 3.4.1. Introducción γ β α σ σ σ t t t α β α ε γ γ γ ε γ γ γ ε ε ε ε 1 1 1 1 1 1 1 ESTADO TENSIONAL: ESTADO
UNIVERSIDAD CARLOS III DE MADRID DEPARTAMENTO DE MECÁNICA DE MEDIOS CONTINUOS Y TEORÍA DE ESTRUCTURAS
 UNIRIDAD CARO III D ADRID DPARTANTO D CÁNICA D DIO CONTINUO Y TORÍA D TRUCTURA INNIRÍA INDUTRIA º Curo ATICIDAD Y RITNCIA D ATRIA II CURO /5 FORUARIO ÁICO ICROCÁNICA Ddad d ua láa udroal ρ ρ ρ Cotat láta
UNIRIDAD CARO III D ADRID DPARTANTO D CÁNICA D DIO CONTINUO Y TORÍA D TRUCTURA INNIRÍA INDUTRIA º Curo ATICIDAD Y RITNCIA D ATRIA II CURO /5 FORUARIO ÁICO ICROCÁNICA Ddad d ua láa udroal ρ ρ ρ Cotat láta
5 MECÁNICA ESTADÍSTICA CUÁNTICA DE GASES IDEALES
 ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
III. Campo eléctrico y conductores
 III. ampo léctrico y conductors onductors n quilibrio lctrostático tico Gabril ano Gómz, G 27/8 Dpto. Física F Aplicada III (U. Svilla) ampos Elctromagnéticos ticos Ingniro d Tlcomunicación arga léctrica
III. ampo léctrico y conductors onductors n quilibrio lctrostático tico Gabril ano Gómz, G 27/8 Dpto. Física F Aplicada III (U. Svilla) ampos Elctromagnéticos ticos Ingniro d Tlcomunicación arga léctrica
El transistor bipolar de unión (BJT)
 l rasisor biolar d uió (JT roducció 1948-1949: illia hockly, Joh ard y alr H. raai dscubr s disosiivo y modla su riciio d fucioamio. s l rasisor más uilizado circuios discros. Prsa mayors vlocidad d rsusa
l rasisor biolar d uió (JT roducció 1948-1949: illia hockly, Joh ard y alr H. raai dscubr s disosiivo y modla su riciio d fucioamio. s l rasisor más uilizado circuios discros. Prsa mayors vlocidad d rsusa
Grado en Ingeniería Mecánica EXAMEN FINAL DE MECÁNICA DE SÓLIDOS (20/01/2014) Nombre y Apellidos: NIA:
 Grado en Ingeniería Mecánica EXAMEN FINAL DE MECÁNICA DE SÓLIDOS (20/01/2014) Nombre y Apellidos: NIA: Problema 1 (Duración 45 minutos) (Puntuación máxima: 2.5 puntos) La estructura de la figura está compuesta
Grado en Ingeniería Mecánica EXAMEN FINAL DE MECÁNICA DE SÓLIDOS (20/01/2014) Nombre y Apellidos: NIA: Problema 1 (Duración 45 minutos) (Puntuación máxima: 2.5 puntos) La estructura de la figura está compuesta
Se llama sucesión a un conjunto de números dados ordenadamente de modo que se puedan numerar: primero, segundo, tercero,...
 TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
Consideremos los siguientes experimentos aleatorios
 69 Veremos e lo que sigue uevas variables aleatorias discretas. Estas variables y sus distribucioes se utiliza como modelos e muchas alicacioes estadísticas. Distribució Biomial Cosideremos los siguietes
69 Veremos e lo que sigue uevas variables aleatorias discretas. Estas variables y sus distribucioes se utiliza como modelos e muchas alicacioes estadísticas. Distribució Biomial Cosideremos los siguietes
( ) 1.8 CRITERIOS DE CONVERGENCIA PARA SERIES (1.8_CvR_T_061, Revisión: , C8, C9, C10) INTRODUCCIÓN. Forma general de una serie: + a 1
 .8 CRITERIOS DE COVERGECIA PARA SERIES (.8_CvR_T_6, Revisió: -9-6, C8, C9, C).8.. ITRODUCCIÓ. Forma geeral de ua serie: S = = a = a + a + a +...+ a Suma de térmios. Si es fiito, la suma (S ) tambié es
.8 CRITERIOS DE COVERGECIA PARA SERIES (.8_CvR_T_6, Revisió: -9-6, C8, C9, C).8.. ITRODUCCIÓ. Forma geeral de ua serie: S = = a = a + a + a +...+ a Suma de térmios. Si es fiito, la suma (S ) tambié es
Campo eléctrico en presencia de aislantes.
 Cam léctic scia d aislats. Cmtamit d ls aislats u cam lctstátic (I). i itducims u diléctic t las amaduas d u cdsad la, la dd t las amaduas dismiuy, auqu la caga las amaduas cambia. Q Q d A V 1 V 2 Oy 0
Cam léctic scia d aislats. Cmtamit d ls aislats u cam lctstátic (I). i itducims u diléctic t las amaduas d u cdsad la, la dd t las amaduas dismiuy, auqu la caga las amaduas cambia. Q Q d A V 1 V 2 Oy 0
Complementos de Física -Ingeniería Informática- Boletín 3. Semiconductores intrínsecos
 Coltos d ísia -Igiría Iforátia- oltí Siodutors itrísos 1. A ua barra d G d 10 d logitud y d sió s l alia ua d.d.. d 10 V tr sus xtros. Sabido qu i =,6 10 19 -, = 0,9 /V s y = 0,18 /V s, dtrís: a) la rsistiidad
Coltos d ísia -Igiría Iforátia- oltí Siodutors itrísos 1. A ua barra d G d 10 d logitud y d sió s l alia ua d.d.. d 10 V tr sus xtros. Sabido qu i =,6 10 19 -, = 0,9 /V s y = 0,18 /V s, dtrís: a) la rsistiidad
Ejemplo: 0+0i y -3+0i representan los números reales 0 y 3 respectivamente. Si a=0 se considera un número imaginario puro a 0+bi
 u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
u_miii.doc EL SISTEMA DE LOS NÚMEROS COMPLEJOS: No eiste u úmero real que satisfaga la ecuació +0 Para resolver este tipo de ecuacioes es ecesario itroducir el cocepto de úmero complejo. U úmero complejo
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS
 UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
) = Ln(1 + 1 n ) 1 n. Ln( n ) n tiene términos positivos y si 0 < lím n n bn. < entonces ambas series divergen o bien ambas series convergen
 Criterio de Comparació Si a 0 y b 0. Si existe ua costate C > 0 tal que a Cb etoces la covergecia de b implica la covergecia de a. Ejemplo.- Sabemos que la serie coverge a, pero como (+), etoces la serie
Criterio de Comparació Si a 0 y b 0. Si existe ua costate C > 0 tal que a Cb etoces la covergecia de b implica la covergecia de a. Ejemplo.- Sabemos que la serie coverge a, pero como (+), etoces la serie
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA 1: Problema Nº 5.34 Oppenheim
 SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
Elementos Uniaxiales Sometidos a Carga Axial Pura
 Elementos Uniaiales Sometidos a Carga ial ura Definición: La Tensión representa la intensidad de las fuerzas internas por unidad de área en diferentes puntos de una sección del sólido aislada (Fig. 1a).
Elementos Uniaiales Sometidos a Carga ial ura Definición: La Tensión representa la intensidad de las fuerzas internas por unidad de área en diferentes puntos de una sección del sólido aislada (Fig. 1a).
EJERCICIO Paso a P aso
 h 0.40m INTRFIS LS ON RGS ONNTRS Se tiene un cable fijo en sus extremos, a la misma altura, sometido a cargas concentradas. Para determinar la tensión en cada tramo es necesario conocer las reacciones
h 0.40m INTRFIS LS ON RGS ONNTRS Se tiene un cable fijo en sus extremos, a la misma altura, sometido a cargas concentradas. Para determinar la tensión en cada tramo es necesario conocer las reacciones
1.1. La barra de la figura tiene un incremento de temperatura, Δt, en el tramo BC. Calcular el esfuerzo axil en el tramo AB.
 Nombre: Grupo: jercicio 1. (6 puntos). minutos. l primer ejercicio consta de una serie de problemas teórico prácticos. Sólo se permite el uso de calculadora. NO desgrapar las hojas. IMORTANT: l resultado
Nombre: Grupo: jercicio 1. (6 puntos). minutos. l primer ejercicio consta de una serie de problemas teórico prácticos. Sólo se permite el uso de calculadora. NO desgrapar las hojas. IMORTANT: l resultado
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Capítulo IV. Estadísticas cuánticas.
 Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
2.- Pruebe, la convergencia de las siguientes sucesiones: b n. 4.- Investigar la convergencia de la sucesión dada por la formula recursiva :
 UNIVERSIDAD SIMON BOLIVAR DEPARTAMENTO DE MATEMATICAS APLICADAS MATEMATICAS IV TRIMESTRE Eero- Abril 004 PRACTICA DE SUCESIONES Y SERIES.- Ivestigue si las siguietes sucesioes so o o covergete. Si coverge,
UNIVERSIDAD SIMON BOLIVAR DEPARTAMENTO DE MATEMATICAS APLICADAS MATEMATICAS IV TRIMESTRE Eero- Abril 004 PRACTICA DE SUCESIONES Y SERIES.- Ivestigue si las siguietes sucesioes so o o covergete. Si coverge,
L lim. lim. a n. 5n 1. 2n lim. lim. lim. 1 Calcula: Solución: a) 2
 Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
1. Teorema del Límite Central. Como se dijo varias clases atras si tenemos n variables aleatorias, cada una de. X i = X. n = 1 n.
 1. Teorema del Límite Cetral Teorema: ea Y 1, Y,..., Y variables aleatorias idepedietes idéticamete distribuidas co EY i = µ y V Y i =
1. Teorema del Límite Cetral Teorema: ea Y 1, Y,..., Y variables aleatorias idepedietes idéticamete distribuidas co EY i = µ y V Y i =
MAT2715 VARIABLE COMPLEJA II Ayudantia 8 Rodrigo Vargas
 PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICAS MAT2715 VARIABLE COMPLEJA II Ayudatia 8 Rodrigo Vargas 1. Si Ω es u domiio e C. Demuestre que existe ua sucesió K } de subcojutos compactos
PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICAS MAT2715 VARIABLE COMPLEJA II Ayudatia 8 Rodrigo Vargas 1. Si Ω es u domiio e C. Demuestre que existe ua sucesió K } de subcojutos compactos
Función exponencial y logarítmica:
 MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
Resistencia de Materiales TORSIÓN
 Resistencia de ateriales TORSIÓN Introducción Torsión en perfiles circulares. Tensiones y Giros Energía de deformación. Resolución de problemas hiperestáticos en torsión. Torsión en vigas de sección cualquiera
Resistencia de ateriales TORSIÓN Introducción Torsión en perfiles circulares. Tensiones y Giros Energía de deformación. Resolución de problemas hiperestáticos en torsión. Torsión en vigas de sección cualquiera
TEMA 2 SUCESIONES. Tema 2 Sucesiones Matemáticas I 1º Bach. 1 SUCESIONES Y TÉRMINOS
 Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Resistencia de Materiales FLEXIÓN PLANA I: (Cálculo de tensiones)
 Resistencia de ateriales FLEXIÓN PLANA I: (Cálculo de tensiones) Resistencia de ateriales FLEXIÓN PLANA I: (Cálculo de tensiones). Introducción. Lees diagramas en vigas isostáticas. Tensiones en la barra
Resistencia de ateriales FLEXIÓN PLANA I: (Cálculo de tensiones) Resistencia de ateriales FLEXIÓN PLANA I: (Cálculo de tensiones). Introducción. Lees diagramas en vigas isostáticas. Tensiones en la barra
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
CAPITULO 4. División 1. Cálculo de uniones por pernos Cálculo de uniones por soldadura Cálculo de uniones por pegamento
 CAPITULO 4 Proyecto de elementos de sueción, anclae y cierre División Cálculo de uniones por pernos Cálculo de uniones por soldadura Cálculo de uniones por pegamento Introducción PROYECTO DE UNIONES PERNOS
CAPITULO 4 Proyecto de elementos de sueción, anclae y cierre División Cálculo de uniones por pernos Cálculo de uniones por soldadura Cálculo de uniones por pegamento Introducción PROYECTO DE UNIONES PERNOS
5 Variables aleatorias bidimensionales y de mayor dimension.
 5 Variables aleatorias bidimesioales de maor dimesio. Edgar Acua ESMA 4 Edgar Acua Sea S el esacio muestral de u eerimeto aleatorio. Sea s s dos ucioes que asiga u umero real a cada elemeto s de S. Etoces
5 Variables aleatorias bidimesioales de maor dimesio. Edgar Acua ESMA 4 Edgar Acua Sea S el esacio muestral de u eerimeto aleatorio. Sea s s dos ucioes que asiga u umero real a cada elemeto s de S. Etoces
TEMA 2. ESPACIOS Y OPERADORES LINEALES CONTENIDO
 TEMA. ESPACIOS Y OPERADORES LINEALES CONTENIDO ESPACIOS LINEALES SOBRE UN CAMPO INDEPENDENCIA LINEAL, BASES Y CAMBIOS DE BASES OPERADORES LINEALES Y SUS REPRESENTACIONES SISTEMAS DE ECUACIONES ALGEBRÁICAS
TEMA. ESPACIOS Y OPERADORES LINEALES CONTENIDO ESPACIOS LINEALES SOBRE UN CAMPO INDEPENDENCIA LINEAL, BASES Y CAMBIOS DE BASES OPERADORES LINEALES Y SUS REPRESENTACIONES SISTEMAS DE ECUACIONES ALGEBRÁICAS
PROBLEMAS DE MECANICA DE FRACTURA
 MECANICA AVANZADA DE MATERIALES Dr. Luis A. Godoy 2005 PROBLEMAS DE MECANICA DE FRACTURA Prolema 1: El eséimen de la figura tiene una fisura en el extremo, y uede onsiderarse omo una dole viga en voladizo.
MECANICA AVANZADA DE MATERIALES Dr. Luis A. Godoy 2005 PROBLEMAS DE MECANICA DE FRACTURA Prolema 1: El eséimen de la figura tiene una fisura en el extremo, y uede onsiderarse omo una dole viga en voladizo.
CASTILLA-LA MANCHA / JUNIO 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 CASILLA-LA MANCHA / JUNIO 0. LOGSE / FÍSICA / EXAMEN COMPLEO El aluo dbrá cottar a ua d la do ocio routa A o B. Lo robla utúa 3 uto cada uo y la cutio uto cada ua. S odrá utilizar ua calculadora y ua rgla.
CASILLA-LA MANCHA / JUNIO 0. LOGSE / FÍSICA / EXAMEN COMPLEO El aluo dbrá cottar a ua d la do ocio routa A o B. Lo robla utúa 3 uto cada uo y la cutio uto cada ua. S odrá utilizar ua calculadora y ua rgla.
si G es abierto. La función del conjunto m tiene las siguientes propiedades: de partes de se dice que es una , entonces E.
 LA INTGRAL D LBSGU PARA FUNCIONS D UNA SOLA VARIABL RSULTADOS TÓRICOS LA MDIDA D LBSGU CONJUNTOS MDIBLS Dado u couto abierto o vació G de la recta real, existe ua amilia iita o umerable {V: œl}, ormada
LA INTGRAL D LBSGU PARA FUNCIONS D UNA SOLA VARIABL RSULTADOS TÓRICOS LA MDIDA D LBSGU CONJUNTOS MDIBLS Dado u couto abierto o vació G de la recta real, existe ua amilia iita o umerable {V: œl}, ormada
Análisis de resultados. Independencia de las muestras
 Aálisis de resultados Clase ro. 8 Curso 00 Idepedecia de las muestras Los resultados de ua corrida de simulació, so muestras de algua distribució. Esos resultados los llamamos "respuestas". Las respuestas
Aálisis de resultados Clase ro. 8 Curso 00 Idepedecia de las muestras Los resultados de ua corrida de simulació, so muestras de algua distribució. Esos resultados los llamamos "respuestas". Las respuestas
Cómo se ha de analizar una fuerza dependiendo del movimiento que produce?
 Cómo se ha de aalizar ua fuerza depediedo del movimieto que produce? Tipos de movimietos e fució de la orietació etre la fuerza y la velocidad 1.- Si la fuerza es paralela a la velocidad del objeto sobre
Cómo se ha de aalizar ua fuerza depediedo del movimieto que produce? Tipos de movimietos e fució de la orietació etre la fuerza y la velocidad 1.- Si la fuerza es paralela a la velocidad del objeto sobre
Tema 5: Transistor Bipolar de Unión (BJT)
 Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
3. Modelos Univariantes de Probabilidad. Curso Estadística. Modelos Univariantes
 3. Modlos Uivariats d Probabilidad Curso - Estadística Modlos Uivariats Procso d Broulli El rsultado d u rimto admit dos catgorías: Actabl y Dfctuoso. S rit l rimto vcs. La robabilidad d dfctuoso s la
3. Modlos Uivariats d Probabilidad Curso - Estadística Modlos Uivariats Procso d Broulli El rsultado d u rimto admit dos catgorías: Actabl y Dfctuoso. S rit l rimto vcs. La robabilidad d dfctuoso s la
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
RESISTENCIA DE MATERIALES I CURSO EXAMEN DE JUNIO
 RESISTENI DE MTERILES I URSO 007-08 EXMEN DE JUNIO 6-6-008.- (3 puntos) L plc de l figur (E = 0 G, ν = 0,3) tiene 0 mm de espesor está sometid un estdo tensionl plno homogéneo bjo l solicitción indicd
RESISTENI DE MTERILES I URSO 007-08 EXMEN DE JUNIO 6-6-008.- (3 puntos) L plc de l figur (E = 0 G, ν = 0,3) tiene 0 mm de espesor está sometid un estdo tensionl plno homogéneo bjo l solicitción indicd
Estructuras de Materiales Compuestos
 Estructuras de Materiales Compuestos Análisis de falla progresiva Ing. Gastón Bonet - Ing. Cristian Bottero - Ing. Marco Fontana Estructuras de Materiales Compuestos Análisis de falla progresiva Repaso
Estructuras de Materiales Compuestos Análisis de falla progresiva Ing. Gastón Bonet - Ing. Cristian Bottero - Ing. Marco Fontana Estructuras de Materiales Compuestos Análisis de falla progresiva Repaso
25 EJERCICIOS de RADICALES 4º ESO opc. B
 EJERCICIOS de RADICALES º ESO opc. B RECORDAR: Definición de raíz n-ésima: Consecuencia: n n x n a x x x, y también ( ) n n x n a x Equivalencia con una potencia de exponente fraccionario: Simplificación
EJERCICIOS de RADICALES º ESO opc. B RECORDAR: Definición de raíz n-ésima: Consecuencia: n n x n a x x x, y también ( ) n n x n a x Equivalencia con una potencia de exponente fraccionario: Simplificación
TEMA 5: REGRESION LINEAL
 ESTADÍSTICA, CURSO 008 009 TEMA 5: REGRESION LINEAL REGRESION LINEAL SIMPLE. CORRELACION. REGRESION.. Regresió lieal simple Recta de regresió: y a + b.. Ajuste de ua recta de regresió Método de míimos
ESTADÍSTICA, CURSO 008 009 TEMA 5: REGRESION LINEAL REGRESION LINEAL SIMPLE. CORRELACION. REGRESION.. Regresió lieal simple Recta de regresió: y a + b.. Ajuste de ua recta de regresió Método de míimos
Análisis del caso promedio El plan:
 Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
( ) RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN A + B = 9K B + C = 11 K A + C = 10 K RESOLUCIÓN SEMANA 13 RAZONES Y PROPORCIONES. a b c d.
 SEMANA 1 RAZONES Y PROPORCIONES 1. Si: a b c d y 7 4 1 6 ab + cd 500, halle el valor de (a + c) a c e g K b d f h b + d + e + g 67 a + c + f + h 4 a + c + e + g 88 1 A) 75 B) 80 C) 90 D) 95 E) 100 a b
SEMANA 1 RAZONES Y PROPORCIONES 1. Si: a b c d y 7 4 1 6 ab + cd 500, halle el valor de (a + c) a c e g K b d f h b + d + e + g 67 a + c + f + h 4 a + c + e + g 88 1 A) 75 B) 80 C) 90 D) 95 E) 100 a b
es un proceso de conteo si representa el número de eventos ocurridos hasta el tiempo t.
 PROCESOS ROBABILIDADES ESTOCÁSTICOS (ITEL-3005) (80807) Tema 4. Los Procesos Tema. de Fudametos Poisso y otros de Estadística procesos asociados Descriptiva Semaa Distribució 5 Clase 07 de frecuecias Lues
PROCESOS ROBABILIDADES ESTOCÁSTICOS (ITEL-3005) (80807) Tema 4. Los Procesos Tema. de Fudametos Poisso y otros de Estadística procesos asociados Descriptiva Semaa Distribució 5 Clase 07 de frecuecias Lues
Z = número atómico o número de protones del núcleo Z = 1 (H); 2 (He + ); 3 (Li 2+ ).
 CAPITULO. l átoo d idógo ) Atoo d idógo idogoid Z úo atóico o úo d poto dl úclo Z (H); (H + ); (Li + ). F q q / ε F q q / θ.6-9 cul.8 - u N u cul /( ε ) / φ V() -Z / ( u ) Hˆ Hˆ Hˆ + Ψ (, ) ψ ( )ψit( )
CAPITULO. l átoo d idógo ) Atoo d idógo idogoid Z úo atóico o úo d poto dl úclo Z (H); (H + ); (Li + ). F q q / ε F q q / θ.6-9 cul.8 - u N u cul /( ε ) / φ V() -Z / ( u ) Hˆ Hˆ Hˆ + Ψ (, ) ψ ( )ψit( )
TALLER SOLUCIÓN NUMÉRICA DE ECUACIONES
 . Apliue los métodos de bisecció y de la regla falsa para ecotrar todas las solucioes detro de 0 para 7 + 6 = 0. 5. Apliue el método de bisecció para solucioes eactas detro de 0 para: a. = 0 R: 0.68. Apliue
. Apliue los métodos de bisecció y de la regla falsa para ecotrar todas las solucioes detro de 0 para 7 + 6 = 0. 5. Apliue el método de bisecció para solucioes eactas detro de 0 para: a. = 0 R: 0.68. Apliue
I.T. INDUSTRIAL METODOS ESTADÍSTICOS. FORMULARIO I. ESTADISTICA DESCRIPTIVA Xv.a. Media x = n n i x 2 Varianza poblacional σ 2 i
 I.T. INDUSTRIAL METODOS ESTADÍSTICOS FORMULARIO I. ESTADISTICA DESCRIPTIVA Xv.a k modalidades x 1,x,..., x k ; datos i x i Media x = i x Variaza poblacioal σ i = x i (x i x) Variaza muestral S = 1 (x i
I.T. INDUSTRIAL METODOS ESTADÍSTICOS FORMULARIO I. ESTADISTICA DESCRIPTIVA Xv.a k modalidades x 1,x,..., x k ; datos i x i Media x = i x Variaza poblacioal σ i = x i (x i x) Variaza muestral S = 1 (x i
Asignatura: RESISTENCIA DE MATERIALES (I.T.O.P.) Examen : Enero 2009
 UIVERSIDD DE SLMC Problema 1º signatura: RESISTECI DE MTERILES (I.T.O.P.) Eamen : Enero 009 En la barra indicada en la figura, de sección circular maciza, se pide calcular: 1) Diagrama de esfuerzos de
UIVERSIDD DE SLMC Problema 1º signatura: RESISTECI DE MTERILES (I.T.O.P.) Eamen : Enero 009 En la barra indicada en la figura, de sección circular maciza, se pide calcular: 1) Diagrama de esfuerzos de
[e j N 2 e j N 2 ]...} (22)
![[e j N 2 e j N 2 ]...} (22) [e j N 2 e j N 2 ]...} (22)](/thumbs/68/58319623.jpg) Trasformadores multiseccioales de cuarto de oda. La teoría de reflexioes pequeñas descrita e la secció aterior se puede usar para aalizar trasformadores multiseccioales de u cuarto de oda. Cosidere la
Trasformadores multiseccioales de cuarto de oda. La teoría de reflexioes pequeñas descrita e la secció aterior se puede usar para aalizar trasformadores multiseccioales de u cuarto de oda. Cosidere la
Tema 5: Transistor Bipolar de Unión (BJT)
 Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
(50 minutos) Ejercicio 1 Para el circuito de la figura adjunta, se pide: Datos: L 1 ; R 1 = 10 Ω; U red = 380 V; f = 50 Hz
 EXAMEN FINA DE SEIEMBE DE EECÓNICA DE OENCIA (6/7) Normas d xam El alumo db djar bi visibl sobr la msa ua idtifiaió válida (aré d la sula, DNI ). No s pud usar libros i aputs y, por tato, ua vz mpzado
EXAMEN FINA DE SEIEMBE DE EECÓNICA DE OENCIA (6/7) Normas d xam El alumo db djar bi visibl sobr la msa ua idtifiaió válida (aré d la sula, DNI ). No s pud usar libros i aputs y, por tato, ua vz mpzado
( 3.c) INTRODUCCIÓN A LOS MODELOS NO EXPONENCIALES Y REDES DE COLAS
 (.c) INTRODUCCIÓN A LOS MODELOS NO EXONENCIALES Y REDES DE COLAS INTRODUCCIÓN A LAS REDES DE COLAS. Cocepto de red abierta y cerrada. Redes abiertas y Teorema de Jackso. MODELOS NO EXONENCIALES Cola M/G/:
(.c) INTRODUCCIÓN A LOS MODELOS NO EXONENCIALES Y REDES DE COLAS INTRODUCCIÓN A LAS REDES DE COLAS. Cocepto de red abierta y cerrada. Redes abiertas y Teorema de Jackso. MODELOS NO EXONENCIALES Cola M/G/:
60kN/m 50kNm 50kNm. 60kN/m. 50kNm D D D CC. C C 2 2 m 5 m
 Ejercicio 6.1 Para las vigas de la figura: a) Bosquejar cualitativamente el diagrama momento flector, el diagrama del giro y el diagrama de la deformada. b) Determinar la flecha en C y el ángulo de giro
Ejercicio 6.1 Para las vigas de la figura: a) Bosquejar cualitativamente el diagrama momento flector, el diagrama del giro y el diagrama de la deformada. b) Determinar la flecha en C y el ángulo de giro
Métodos de Análisis Cuantitativo
 Métodos de Aálisis Cuatitativo Fórmulas E este documeto se lista las fórmulas trabajadas e las clases del curso de Métodos de Ivestigació Cuatitativa (GES204) de la Facultad de Gestió y Alta Direcció de
Métodos de Aálisis Cuatitativo Fórmulas E este documeto se lista las fórmulas trabajadas e las clases del curso de Métodos de Ivestigació Cuatitativa (GES204) de la Facultad de Gestió y Alta Direcció de
Competencia Matemática E. Paenza. Sexta Realización 1991
 Competecia Matemática E. Paeza Seta Realizació 99 Resolució de los problemas Participate N : Problema. Sea C u cuadrilátero coveo. Si el área del cada uo de los cuatro triágulos determiados por las dos
Competecia Matemática E. Paeza Seta Realizació 99 Resolució de los problemas Participate N : Problema. Sea C u cuadrilátero coveo. Si el área del cada uo de los cuatro triágulos determiados por las dos
EXAMEN. 16 DE OCTUBRE DE 2014 CURS0 2014/2015 Problema (10 puntos).
 Máquias Eléctricas. Igeiería de Tecologías Idustriales iversidad ey Jua arlos Área de Tecología Electróica EMEN. 16 DE OTBE DE 14 S 14/15 Problema (1 putos). u trasformador trifásico Dy11 de potecia omial
Máquias Eléctricas. Igeiería de Tecologías Idustriales iversidad ey Jua arlos Área de Tecología Electróica EMEN. 16 DE OTBE DE 14 S 14/15 Problema (1 putos). u trasformador trifásico Dy11 de potecia omial
Física y Química 1º Bach.
 Físic Químic º Bch. I.E.S. Elviñ Problems Recuperción del tercer trimestre 8/06/0 Nombre: Tipo A Tipo B. Un muchcho intent hcer psr un pelot sobre un muro situdo 4,0 m de distnci lnzándol con un velocidd
Físic Químic º Bch. I.E.S. Elviñ Problems Recuperción del tercer trimestre 8/06/0 Nombre: Tipo A Tipo B. Un muchcho intent hcer psr un pelot sobre un muro situdo 4,0 m de distnci lnzándol con un velocidd
RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN SEMANA 13 RAZONES Y PROPORCIONES ab + cd = 2500, halle el valor de (a + c) a c e g K.
 SEMANA 1 RAZONES Y PROPORCIONES 1. Si: a b c d y 7 4 1 6 ab + cd = 500, halle el valor de (a + c) A) 75 B) 80 C) 90 D) 95 E) 100 a b ab K K 7 4 8 d e de K K 1 6 7 Luego: 500 100K K = 5 Luego: a = 5, d
SEMANA 1 RAZONES Y PROPORCIONES 1. Si: a b c d y 7 4 1 6 ab + cd = 500, halle el valor de (a + c) A) 75 B) 80 C) 90 D) 95 E) 100 a b ab K K 7 4 8 d e de K K 1 6 7 Luego: 500 100K K = 5 Luego: a = 5, d
Tema 1 Los números reales Matemáticas I 1º Bachillerato 1
 Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Transformada de Laplace
 Transformada de Laplace Definición: La Transformada de Laplace Dada una función f (t) definida para toda t 0, la transformada de Laplace de f es la función F definida como sigue: { f } 0 st F () s = L
Transformada de Laplace Definición: La Transformada de Laplace Dada una función f (t) definida para toda t 0, la transformada de Laplace de f es la función F definida como sigue: { f } 0 st F () s = L
III. Campo eléctrico y conductores
 III. Cmpo léctico y conductos Método d ls imágns Gbil Cno Gómz, G 7/8 Dpto. Físic F Aplicd III (U. Svill) Cmpos Elctomgnéticos ticos Ingnio d Tlcomunicción Gbil Cno G Gómz, 7/8 Sistm cg puntul plno plno
III. Cmpo léctico y conductos Método d ls imágns Gbil Cno Gómz, G 7/8 Dpto. Físic F Aplicd III (U. Svill) Cmpos Elctomgnéticos ticos Ingnio d Tlcomunicción Gbil Cno G Gómz, 7/8 Sistm cg puntul plno plno
CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS:
 CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS: TEMAS: - Demostrar la euaión de la tensión de torsión, su apliaión y diseño de miembros sometidos a tensiones de torsión 5.1. Teoría de torsión simple 5..
CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS: TEMAS: - Demostrar la euaión de la tensión de torsión, su apliaión y diseño de miembros sometidos a tensiones de torsión 5.1. Teoría de torsión simple 5..
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Jueves, 25 de abril. Dificultades de los modelos PNL. Dónde está la solución óptima? Otro ejemplo: Óptima Local frente a Global
 . Jueves, de abril Teoría sobre la programació o lieal Programació separable Dificultades de los modelos PNL PL: Etregas: material de clase PNL: Aálisis gráfico de la programació o lieal e dos dimesioes:
. Jueves, de abril Teoría sobre la programació o lieal Programació separable Dificultades de los modelos PNL PL: Etregas: material de clase PNL: Aálisis gráfico de la programació o lieal e dos dimesioes:
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
PROGRESIONES ARITMETICAS DEF. Se dice que ua serie de úmeros está e progresió aritmética cuado cada uo de ellos (excepto el primero) es igual al aterior más ua catidad costate llamada diferecia de la progresió.
2. - FLUJO LAMINAR. Fig. 36
 . - FLUJO LAMINAR 3.. - Viscosidad. Proidad d un fluido u controla su vlocidad d dforación. Si colocaos un trozo d asfalto sobr una sa forando un volun, oco a oco s dforara hasta alanars, dorando un tio
. - FLUJO LAMINAR 3.. - Viscosidad. Proidad d un fluido u controla su vlocidad d dforación. Si colocaos un trozo d asfalto sobr una sa forando un volun, oco a oco s dforara hasta alanars, dorando un tio
Probabilidad y estadística
 Probabilidad y estadística MEDIDAS DE TENDENCIA CENTRAL, MEDIDAS DE DISPERSIÓN, GRÁFICAS, E INTERPRETANDO RESULTADOS Prof. Miguel Hesiquio Garduño. Est. Mirla Beavides Rojas Depto. De Igeiería Química
Probabilidad y estadística MEDIDAS DE TENDENCIA CENTRAL, MEDIDAS DE DISPERSIÓN, GRÁFICAS, E INTERPRETANDO RESULTADOS Prof. Miguel Hesiquio Garduño. Est. Mirla Beavides Rojas Depto. De Igeiería Química
Práctico 10: Desplazamientos en vigas isostáticas
 Práctico 10: Desplazamientos en vigas isostáticas Ejercicio 1: Una columna telescópica de tres tramos está empotrada en la base y sometida a una carga de 5kN (compresión) en su etremo superior. a longitud
Práctico 10: Desplazamientos en vigas isostáticas Ejercicio 1: Una columna telescópica de tres tramos está empotrada en la base y sometida a una carga de 5kN (compresión) en su etremo superior. a longitud
Desigualdad de Tchebyshev
 Desigualdad de Tchebyshev Si la Esperaza y la variaza de la variable X so fiitas, para cualquier úmero positivo k, la probabilidad de que la variable aleatoria X esté e el itervalo La probabilidad de que
Desigualdad de Tchebyshev Si la Esperaza y la variaza de la variable X so fiitas, para cualquier úmero positivo k, la probabilidad de que la variable aleatoria X esté e el itervalo La probabilidad de que
(Se recogerá a las 17,30 h. aproximadamente)
 Resistencia de Materiales, Elasticidad y Plasticidad. Examen extraordinario 9 de diciembre de 4 Ejercicio. Apellidos..................................... Nombre......................... Nº... Curso 3º
Resistencia de Materiales, Elasticidad y Plasticidad. Examen extraordinario 9 de diciembre de 4 Ejercicio. Apellidos..................................... Nombre......................... Nº... Curso 3º
Variables aleatorias discretas
 Probabilidads y stadística Comutació Facultad d Cicias actas y aturals. Uivrsidad d Buos Airs Aa M. Biaco y la J. Martíz 4 Variabls alatorias discrtas istribució Biomial: Muchos rimtos alatorios satisfac
Probabilidads y stadística Comutació Facultad d Cicias actas y aturals. Uivrsidad d Buos Airs Aa M. Biaco y la J. Martíz 4 Variabls alatorias discrtas istribució Biomial: Muchos rimtos alatorios satisfac
LEE ATENTAMENTE ANTES DE COMENZAR!
 LEE ATENTAMENTE ANTES DE COMENAR! El eamen consta de varios ejercicios, que se repartirán sucesivamente, con un tiempo máimo para la realiación de cada uno. Se hará un descanso de unos minutos hacia la
LEE ATENTAMENTE ANTES DE COMENAR! El eamen consta de varios ejercicios, que se repartirán sucesivamente, con un tiempo máimo para la realiación de cada uno. Se hará un descanso de unos minutos hacia la
TEMA 5: Gráficos de Control por Atributos. 1. Gráfico de control para la fracción de unidades defectuosas
 TEMA 5: Gráficos de Cotrol por Atributos 1 Gráfico de cotrol para la fracció de uidades defectuosas 2 Gráfico de cotrol para el úmero medio de discoformidades por uidad Selecció del tamaño muestral 3 Clasificació
TEMA 5: Gráficos de Cotrol por Atributos 1 Gráfico de cotrol para la fracció de uidades defectuosas 2 Gráfico de cotrol para el úmero medio de discoformidades por uidad Selecció del tamaño muestral 3 Clasificació
El error con ese presupuesto será aproximadamente del 3,1% Ejercicio 8.2
 EJERCICIO 8.1 U ivstigador dispo d 0.000 para ralizar las trvistas d ua custa ua gra ciudad. El custioario s admiistrará mdiat trvistas tlfóicas, sido l cost d cada trvista d 0. Qué marg d rror dbrá asumir
EJERCICIO 8.1 U ivstigador dispo d 0.000 para ralizar las trvistas d ua custa ua gra ciudad. El custioario s admiistrará mdiat trvistas tlfóicas, sido l cost d cada trvista d 0. Qué marg d rror dbrá asumir
2. Estimación de errores de medidas directas
 Estimació de errores y forma de expresar los resultados de las prácticas. Error: Defiició E el laboratorio igua medida tiee ifiita precisió. Por ello, ua parte importate del proceso de medida es la estimació
Estimació de errores y forma de expresar los resultados de las prácticas. Error: Defiició E el laboratorio igua medida tiee ifiita precisió. Por ello, ua parte importate del proceso de medida es la estimació
Práctico 10: Desplazamientos en vigas isostáticas
 Práctico 0: Desplazamientos en vigas isostáticas Ejercicio : Una columna telescópica de tres tramos está empotrada en la base y sometida a una carga de 5kN (compresión) en su etremo superior. a longitud
Práctico 0: Desplazamientos en vigas isostáticas Ejercicio : Una columna telescópica de tres tramos está empotrada en la base y sometida a una carga de 5kN (compresión) en su etremo superior. a longitud
Variable Compleja I Tema 12: El teorema general de Cauchy
 Variable Compleja I Tema 12: El teorema general de Cauchy 1 Índice 2 Cadenas y ciclos 3 Teorema general de Cauchy Índice de un punto con respecto a un camino cerrado Motivación a C, r R +, z C \C(a,r)
Variable Compleja I Tema 12: El teorema general de Cauchy 1 Índice 2 Cadenas y ciclos 3 Teorema general de Cauchy Índice de un punto con respecto a un camino cerrado Motivación a C, r R +, z C \C(a,r)
2.2. Una versión elemental de la ley fuerte de los números grandes
 34 CAÍTULO 2. LEY DE LOS NÚMEROS GRANDES Demostració. or el Teorema 2.0, vemos que basta probar que ( ) 2 2E (X,k E(X,k )) = 0. La esperaza e esta expresió se puede escribir como V ar(x,k ) + or la hipótesis
34 CAÍTULO 2. LEY DE LOS NÚMEROS GRANDES Demostració. or el Teorema 2.0, vemos que basta probar que ( ) 2 2E (X,k E(X,k )) = 0. La esperaza e esta expresió se puede escribir como V ar(x,k ) + or la hipótesis
c) la raíz cuadrada Primero tienes que teclear la raíz cuadrada y después el número. 25 = 5
 Aexo Calculadora La proliferació de las calculadoras e la vida cotidiaa obliga a profesores y padres a replatearse su uso. Los profesores debemos eseñar a los alumos su utilizació. Pero será los profesores
Aexo Calculadora La proliferació de las calculadoras e la vida cotidiaa obliga a profesores y padres a replatearse su uso. Los profesores debemos eseñar a los alumos su utilizació. Pero será los profesores
3.1. Muestreo aleatorio sin reposición Muestreo aleatorio con reposición (muestreo aleatorio simple)
 1 Muestreo Tema 1 1. Muestreo. Muestreo aleatorio 3. Tipos de muestreo aleatorio 3.1. Muestreo aleatorio si reposició 3.. Muestreo aleatorio co reposició (muestreo aleatorio simple) 3.3. Muestreo aleatorio
1 Muestreo Tema 1 1. Muestreo. Muestreo aleatorio 3. Tipos de muestreo aleatorio 3.1. Muestreo aleatorio si reposició 3.. Muestreo aleatorio co reposició (muestreo aleatorio simple) 3.3. Muestreo aleatorio
