Compensación: diseño de Gc. Ejemplo 1: Sea una planta Gs () =
|
|
|
- Vanesa Farías Fidalgo
- hace 5 años
- Vistas:
Transcripción
1 Compenión: ieño e G Ejemplo : Se un plnt G () =, e neeit relimentr l ( + )( + )( + ) plnt. El enor utilio tenú vee l li (G LCBF =) y lo requerimiento el item relimento on lo iguiente: ) Anho e bn, BW=r/eg b) Error en régimen permnente l elón: e = ) Mrgen e fe: M φ =45º ) Reho e perturbión: R r/eg =B Proeimiento: ) Grfir Boe e G p H(j). ) Cumplieno lo requerimiento y tenieno omo refereni el propio Boe e G p H, trr el Boe e GH(j), e eir trr el GH(j) eeo. 3) Do que G p.g.h(j)=gh(j), prtir e l ifereni GH(j) B G p H(j) B, obtener gráfimente G (j). 4) A prtir el Boe e G (j) obtener l expreión e G (). Ej.: Po B 8 Ej.: Po ) Anho e Bn, BW, e refiere l pr el ul l grfi GH ru B, que en nuetro o e r/eg, punto en l gráfi. b) Error en régimen permnente nulo pr entr elón. Impli tener un item tipo, e eir un polo en el origen, iniánolo on b en l gráfi. ) Mrgen e fe= 45º. Exite un relión biunívo entre lo gráfio e móulo y fe. Se puee ber uál v er φ on l ol gráfi e B. Má ún, exiten un prtiulri el grfio el móulo que no revel el M φ. Por ejemplo, M φ =45º uno GH ru B on un mbio e peniente. Má onretmente uno el gráfio viene on peniente y p, o, viever, uno e peniente e p peniente. No bmo en et prtiulri pr trr el GH eeo bieno el M φ, punto e l gráfi. ) Atenuión e perturbione. No pien un reho perturbione e B pr l perturbión e freueni r/eg. E lo mimo que eir que l
2 li e ih perturbión e verá reui o tenu B, e eir A = B. Eto efine el vlor e GH(jr/eg), e eir el punto. A p B b 8 e) Ej.: Po 3 B b G 8 Ej.: Po 4 ( + ) G() = ( + ) 3( + ) Ejemplo : G () = y emá GLCBF ( j ) = 3B B ( + ) Lo requerimiento el item relimento on lo iguiente: ) Anho e bn, BW=r/eg b) Error en régimen permnente l rmp: e = ) Mrgen e fe: M φ 45º ) Reho e perturbión: R,3r/eg =B
3 Ej. : Po B 3 8 G p Ej. : Po B,3 b G.H p 8 Ej. : Po 3 B G,3 b 8
4 Ej. : Po 4 ( + ) G() = ( + ) Ejemplo 3: Compenr el iguiente item: G() = H=. ( + ) Lo requerimiento el item relimento on lo iguiente: e) Error en régimen permnente l elón: e, f) Anho e bn, BW=r/eg g) Mrgen e fe: M φ =45º h) G lo má imple poible. Ej.3: Po B Ej.3: Po ) En unto l epeifiión el error en régimen permnente pr un Kr entr elón, l expreión orreponie nte e: e =. Como K r =, + K entone e puee obtene r K = = 99. Aoptmo K=. e b) BW=r/eg impli que GH(jr/eg)=b. ) Mφ=45º impli que uno GH ru B, ebe exitir un mbio e peniente. ) Aiionlmente, inorpormo un polo en lt freueni pr que el G e fíimente relible; iho polo no fet l performne oliit.
5 B 4 b e) Ej.3: Po 3 B 4 G b Ej.3: Po 4 ( + ) G () = + Ejemplo 4: Íem Ejemplo 3 pero e oliit BW=r/eg en lugr e r/eg. Reolvemo igul que en el Ejemplo 3, pero inrementmo el K e mner e rur B en r/eg. Tmbién mbimo el ero e G r/eg e tl form que exit mbio e peniente juto en el rue por B.
6 B 4 G b El K reultnte urge el iguiente nálii: KB 4 B/ e (log) e = B KB = 4 B / e (log) e = 4 B / e,3e = 5B 5/ logkvee = 5B Kvee = = 4vee 3 El error reultnte e: e = = =,5. <, + K 4 4( + ) G () = + Ejemplo 5: Mimo ejemplo pero hor e oliit mntener e =, y M φ 45º. E eir que hor e exige un K fijo en, on lo ul pr poer umplir on BW=r/eg poemo jugr on el mrgen e fe, y que tenemo libert y que éte puee er menor que 45º y no etritmente igul 45º. L oluión e plnte en l figur iguiente: B 4 G b
7 Ahor hy que obtener el vlor el ero e G. Se puee obtener nlítimente, uno l expreione intóti (proxim) el propio gráfio e Boe, omo e ve ontinuión, one e el ero e G. 4B 4 B / e (log ) e + B / e (log ) e = B = r/ eg 4B 4B log+ Blog Blog = B [ ] = r/ eg 4B 4B log + Blog Blog = B 4B B log Blog = B B,3B ( log) B = B, 7= log = 5 r/ eg Por i U. no reyer en ete proeimiento porque puee reer que e muy proximo, e puee obtener utilino l euione ext, lo que e he ontinuión. 4B log ( + j ) + log + j = B = r/ eg 4B log ( + j) + log + j = B 4 log log + = B 4B 5B + log + = B B log + = B log + =,6 log + =, + =, =, = = 5, r / eg, Finlmente l expreión e G () e: ( + ) G () 5 = +
PROBLEMA RESUELTO DE ESTABILIDAD
 Univeridd Ncionl de Rorio Fcultd de Cienci Exct Ingenierí y Agrimenur Ecuel de Ingenierí Electrónic Deprtmento de Electrónic ELECTRÓNICA III PROBLEMA RESUELTO DE ESTABILIDAD AUTOR: Federico Miyr REVISIÓN:
Univeridd Ncionl de Rorio Fcultd de Cienci Exct Ingenierí y Agrimenur Ecuel de Ingenierí Electrónic Deprtmento de Electrónic ELECTRÓNICA III PROBLEMA RESUELTO DE ESTABILIDAD AUTOR: Federico Miyr REVISIÓN:
Ciclos Termodinámicos
 Cpítulo 5 Cilos Termoinámios 5.1. Cilo e Crnot Consieremos un gs iel sometio l siguiente proeso ílio: b isoterm f ibt ibt o isoterm V V V Figur 5.1: Cilo e Crnot. Proeso b : Aibt reversible El gs se omprime
Cpítulo 5 Cilos Termoinámios 5.1. Cilo e Crnot Consieremos un gs iel sometio l siguiente proeso ílio: b isoterm f ibt ibt o isoterm V V V Figur 5.1: Cilo e Crnot. Proeso b : Aibt reversible El gs se omprime
APUNTE: Matrices. Una matriz de tamaño n x m es un arreglo de números reales colocados en n filas (o renglones) y m columnas, de la siguiente forma:
 PUNE: Mtries UNIVERSIDD NCIONL DE RIO NEGRO signtur: Mtemáti Crrers: Li. en ministrión Profesor: Prof. Mel Chresti Semestre: o ño: 6 Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en
PUNE: Mtries UNIVERSIDD NCIONL DE RIO NEGRO signtur: Mtemáti Crrers: Li. en ministrión Profesor: Prof. Mel Chresti Semestre: o ño: 6 Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en
CUESTIONES RESUELTAS 1. VECTORES Y MATRICES FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA
 CUESTIONES RESUELTS. VECTORES Y MTRICES FUNDMENTOS DE MTEMÁTICS. º GRDO GESTIÓN ERONÚTIC. Se el onjunto e vetores } tl que entones se verifi:. El onjunto M es linelmente inepeniente.. El onjunto M tiene
CUESTIONES RESUELTS. VECTORES Y MTRICES FUNDMENTOS DE MTEMÁTICS. º GRDO GESTIÓN ERONÚTIC. Se el onjunto e vetores } tl que entones se verifi:. El onjunto M es linelmente inepeniente.. El onjunto M tiene
MATRICES: un apunte teórico-práctico
 MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
LOS NÚMEROS REALES. Los número 1,2,3 se denominan números naturales. El conjunto de los números naturales se representan con la letra N, así
 LOS NÚMEROS REALES Los número,, se enominn números nturles. El onjunto e los números nturles se representn on l letr N, sí N {,,K } Si se sumn os números nturles el resulto es otro nturl, pero si se rest
LOS NÚMEROS REALES Los número,, se enominn números nturles. El onjunto e los números nturles se representn on l letr N, sí N {,,K } Si se sumn os números nturles el resulto es otro nturl, pero si se rest
2.3.2 VÉRTICE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN CUADRÁTICA EL VÉRTICE.
 .3. VÉRTICE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN CUADRÁTICA..3.. EL VÉRTICE. El vértie es un punto que form prte de l prábol, el ul tiene omo ordend el vlor mínimo o máimo de l funión. En ese punto se puede
.3. VÉRTICE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN CUADRÁTICA..3.. EL VÉRTICE. El vértie es un punto que form prte de l prábol, el ul tiene omo ordend el vlor mínimo o máimo de l funión. En ese punto se puede
DETERMINANTES. 1. Calcular el valor del determinante. Solución: Determinante tipo Van der Mondem. sustituyendo en la primera expresión
 DETERMINANTES. lulr el vlor el eterminnte ² ² ² Soluión: Sno ftor omún e en lª fil Sno ftor omún e en l ª fil ² ² ² ² ² ² Determinnte tipo Vn er Monem. ² ² ² ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) sustituyeno
DETERMINANTES. lulr el vlor el eterminnte ² ² ² Soluión: Sno ftor omún e en lª fil Sno ftor omún e en l ª fil ² ² ² ² ² ² Determinnte tipo Vn er Monem. ² ² ² ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) sustituyeno
Elipse: Ecuación de la elipse dados ciertos elementos
 Elipse: Euión de l elipse ddos iertos elementos Tinoo, G. (013). Euión de l elipse ddos iertos elementos. [Mnusrito no publido]. Méxio: UAEM. Espio de Formión Multimodl Elipse vertil Si l elipse tiene
Elipse: Euión de l elipse ddos iertos elementos Tinoo, G. (013). Euión de l elipse ddos iertos elementos. [Mnusrito no publido]. Méxio: UAEM. Espio de Formión Multimodl Elipse vertil Si l elipse tiene
Análisis del lugar geométrico de las raíces
 Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el itema tiene una ganania
Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el itema tiene una ganania
, donde a y b son números cualesquiera.
 Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Compensación en atraso-adelanto
 UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FACULAD DE INENIEÍA MECANICA Y ELÉCICA CONOL CLÁSICO M.C. JOSÉ MANUEL OCHA NUÑEZ Compenaión en atrao-elanto Compenor eletrónio en atrao-elanto on amplifiore operaionale
UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FACULAD DE INENIEÍA MECANICA Y ELÉCICA CONOL CLÁSICO M.C. JOSÉ MANUEL OCHA NUÑEZ Compenaión en atrao-elanto Compenor eletrónio en atrao-elanto on amplifiore operaionale
Lugar geométrico de las raíces
 Lugar geométrio de la raíe Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si
Lugar geométrio de la raíe Análii del lugar geométrio de la raíe La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si
REPASO PARA EXAMEN SEMESTRAL DE MATEMÁTICAS III C D
 REPASO PARA EXAMEN SEMESTRAL DE MATEMÁTCAS PRMER PARCAL PARTE A) LUGARES GEOMÉTRCOS ) Grfi ls siguientes funiones (tulr e - ): ) Enuentr tres prejs orens e funión (No grfir): B) DSTANCA ENTRE DOS PUNTOS
REPASO PARA EXAMEN SEMESTRAL DE MATEMÁTCAS PRMER PARCAL PARTE A) LUGARES GEOMÉTRCOS ) Grfi ls siguientes funiones (tulr e - ): ) Enuentr tres prejs orens e funión (No grfir): B) DSTANCA ENTRE DOS PUNTOS
Compensador en adelanto por el método de respuesta en frecuencia
 Copenador en adelanto por el étodo de repueta en freuenia CONROL CLÁSICO Copenador eletrónio en adelanto on aplifiadore operaionale E E 0 ( ( RR R R 4 RC + R4C R C + R C i 3 3 + + RC R C + + + + R4C RC
Copenador en adelanto por el étodo de repueta en freuenia CONROL CLÁSICO Copenador eletrónio en adelanto on aplifiadore operaionale E E 0 ( ( RR R R 4 RC + R4C R C + R C i 3 3 + + RC R C + + + + R4C RC
Teoría de Sistemas y Señales
 Teorí de Sitem y Señle Criterio lgerio de etilidd Criterio de Routh Autor Dr. Jun Crlo Gómez Criterio Algerio de Etilidd pr SE en TC Promo que l ondiión neeri y ufiiente pr que un SE en TC repreentdo por
Teorí de Sitem y Señle Criterio lgerio de etilidd Criterio de Routh Autor Dr. Jun Crlo Gómez Criterio Algerio de Etilidd pr SE en TC Promo que l ondiión neeri y ufiiente pr que un SE en TC repreentdo por
Rama de la termodinámica que estudia la forma en la que los sistemas biológicos adquieren, canalizan y utilizan la energía.
 BIOENERGÉTICA Rm e l termoinámi que estui l form en l que los sistems biológios quieren, nlizn y utilizn l energí. CONCEPTOS BÁSICOS DE BIOENERGÉTICA Sistem es l prte el universo que elegimos pr el estuio.
BIOENERGÉTICA Rm e l termoinámi que estui l form en l que los sistems biológios quieren, nlizn y utilizn l energí. CONCEPTOS BÁSICOS DE BIOENERGÉTICA Sistem es l prte el universo que elegimos pr el estuio.
APUNTE: TRIGONOMETRIA
 APUNTE: TRIGONOMETRIA UNIVERSIDAD NACIONAL DE RIO NEGRO Asigntur: Mtemáti Crrers: Li. en Eonomí Profesor: Prof. Mel S. Chresti Cutrimestre: ero Año: 06 o Coneptos Previos o Definiión de ángulo Un ángulo
APUNTE: TRIGONOMETRIA UNIVERSIDAD NACIONAL DE RIO NEGRO Asigntur: Mtemáti Crrers: Li. en Eonomí Profesor: Prof. Mel S. Chresti Cutrimestre: ero Año: 06 o Coneptos Previos o Definiión de ángulo Un ángulo
AA = Eje menor La elipse.
 3.. L elipse. 3... L elipse omo lugr geométrio. L elipse es el lugr geométrio del onjunto de puntos P(, ) u sum de ls distnis dos puntos fijos llmdos foos equivlen l dole de un onstnte (), l ul represent
3.. L elipse. 3... L elipse omo lugr geométrio. L elipse es el lugr geométrio del onjunto de puntos P(, ) u sum de ls distnis dos puntos fijos llmdos foos equivlen l dole de un onstnte (), l ul represent
CRITERIO DE ESTABILIDAD DE ROUTH
 CRITERIO DE ESTABIIDAD DE ROUTH INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. Criterio e etili e Routh-Hurwitz El prolem má importte e lo item e otrol liel
CRITERIO DE ESTABIIDAD DE ROUTH INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. INGENIERÍA DE CONTRO.C. EIZABETH GPE. ARA HDZ. Criterio e etili e Routh-Hurwitz El prolem má importte e lo item e otrol liel
Diseño de Controladores Adelanto-Atraso. Sistemas de Control Prof. Mariela CERRADA
 Dieño de Controladore Adelanto-Atrao Sitema de Control Prof. Mariela CERRADA G Comenadore no ideale: interretaión en el dominio del tiemo Conideremo la iguiente funión de tranferenia K z So Im Se aumenta
Dieño de Controladore Adelanto-Atrao Sitema de Control Prof. Mariela CERRADA G Comenadore no ideale: interretaión en el dominio del tiemo Conideremo la iguiente funión de tranferenia K z So Im Se aumenta
ANÁLISIS ESTRUCTURAL DE MECANISMOS PLANOS
 ANÁLISIS ESTRUCTURAL DE MECANISMOS PLANOS Cinemáti e Menismos Tem 3 Itzir Mrtij López Mier Loizg Grmeni Deprtmento e Ingenierí Meáni Meknik Ingeniritz Sil 2 ANÁLISIS ESTRUCTURAL DE MECANISMOS PLANOS 1.
ANÁLISIS ESTRUCTURAL DE MECANISMOS PLANOS Cinemáti e Menismos Tem 3 Itzir Mrtij López Mier Loizg Grmeni Deprtmento e Ingenierí Meáni Meknik Ingeniritz Sil 2 ANÁLISIS ESTRUCTURAL DE MECANISMOS PLANOS 1.
Matemática II Tema 4: matriz inversa y determinante
 Mtemáti II Tem 4: mtriz invers y eterminnte 2012 2013 Ínie Mtriz invertile 1 Definiión y propiees 1 Cómputo e l mtriz invers 3 Determinnte e un mtriz 4 Propiees e los eterminntes 4 Cómputo el eterminnte
Mtemáti II Tem 4: mtriz invers y eterminnte 2012 2013 Ínie Mtriz invertile 1 Definiión y propiees 1 Cómputo e l mtriz invers 3 Determinnte e un mtriz 4 Propiees e los eterminntes 4 Cómputo el eterminnte
Eje normal. P(x,y) LLR Eje focal
 . L Hipérol...1 L Hipérol omo lugr geométrio. L hipérol es el lugr geométrio de todos los puntos tles que el vlor soluto de l difereni de sus distnis dos puntos fijos es un onstnte. Los puntos fijos se
. L Hipérol...1 L Hipérol omo lugr geométrio. L hipérol es el lugr geométrio de todos los puntos tles que el vlor soluto de l difereni de sus distnis dos puntos fijos es un onstnte. Los puntos fijos se
Análisis del Lugar Geométrico de las Raíces (LGR) o Método de Evans
 Análii del Lugar Geométrio de la Raíe (LGR) o Método de Evan La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el
Análii del Lugar Geométrio de la Raíe (LGR) o Método de Evan La araterítia báia de la repueta tranitoria de un itema en lazo errado e relaiona etrehamente on la ubiaión de lo polo en lazo errado. Si el
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS
 EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
Compensador de retardo-adelanto de fase
 Compenador de retardo-adelanto de fae La ompenaión de adelanto báiamente aelera la repueta e inrementa la etabilidad del itema. La ompenaión de retardo mejora la preiión en etado etaionario del itema,
Compenador de retardo-adelanto de fae La ompenaión de adelanto báiamente aelera la repueta e inrementa la etabilidad del itema. La ompenaión de retardo mejora la preiión en etado etaionario del itema,
Compensador en atraso-adelanto por el método de respuesta en frecuencia
 FIME COMPENSACIÓN EN AASO-ADELANO PO EL MÉODO DE ESPUESA EN FECUENCIA UANL Copenador en atrao-adelanto por el étodo de repueta en freuenia CONOL CLÁSICO M.C. JOSÉ MANUEL OCHA NUÑEZ FIME COMPENSACIÓN EN
FIME COMPENSACIÓN EN AASO-ADELANO PO EL MÉODO DE ESPUESA EN FECUENCIA UANL Copenador en atrao-adelanto por el étodo de repueta en freuenia CONOL CLÁSICO M.C. JOSÉ MANUEL OCHA NUÑEZ FIME COMPENSACIÓN EN
Unidad 1 Matrices PÁGINA 7 SOLUCIONES. 1. La resolución de los sistemas puede expresarse de la forma siguiente:
 Uni Mtries PÁGINA 7 SOLUCIONES. L resoluión e los sistems puee expresrse e l form siguiente: L segun mtriz proporion l soluión x 5,y 6. L últim mtriz proporion l soluión x, y, z 4. . Vemos que P P. Pr
Uni Mtries PÁGINA 7 SOLUCIONES. L resoluión e los sistems puee expresrse e l form siguiente: L segun mtriz proporion l soluión x 5,y 6. L últim mtriz proporion l soluión x, y, z 4. . Vemos que P P. Pr
Compensación en atraso. por el método de respuesta en frecuencia
 Copenación en atrao por el étodo de repueta en frecuencia Copenación en atrao por el étodo de repueta en frecuencia Copenador electrónico en atrao con aplificadore operacionale E E 0 RR R R 4 + RC + R4C
Copenación en atrao por el étodo de repueta en frecuencia Copenación en atrao por el étodo de repueta en frecuencia Copenador electrónico en atrao con aplificadore operacionale E E 0 RR R R 4 + RC + R4C
BLOQUE III: GEOMETRÍA
 LOQUE III: GEOMETRÍ Depmeno e Memái º hilleo Tem 6: Veoe plno e en el epio..- SES DE UN ESPIO VETORIL { u u u n }... e un e e V i umple o oniione: lo númeo {... } e u epeo e l e..- Son L.I..- u V u u u...
LOQUE III: GEOMETRÍ Depmeno e Memái º hilleo Tem 6: Veoe plno e en el epio..- SES DE UN ESPIO VETORIL { u u u n }... e un e e V i umple o oniione: lo númeo {... } e u epeo e l e..- Son L.I..- u V u u u...
Integrales dobles. divide al rectángulo I ab, cd. , j 1, 2,, m. n m ij i i 1 j j 1
 ntegrles oles NTEGRALES OBLES e l mism mner que el onepto e integrl efini pr funiones e un vrile sirve pr resolver e un moo generl, el prolem e l eterminión e áres e figurs plns, el onepto e integrl ole
ntegrles oles NTEGRALES OBLES e l mism mner que el onepto e integrl efini pr funiones e un vrile sirve pr resolver e un moo generl, el prolem e l eterminión e áres e figurs plns, el onepto e integrl ole
EXAMEN PARCIAL SUBSISTEMAS DE RADIOFRECUENCIA Y ANTENAS DPTO. DE TEORÍA DE LA SEÑAL Y COMUNICACIONES
 Alumno: EXAEN PARCIAL UBIEA DE RADIOFRECUENCIA Y ANENA DPO. DE EORÍA DE LA EÑAL Y COUNICACIONE 5 de noviembre de 0 Problem (hy que entregr l hoj de ete enuncido) PROBLEA de mpliicdore de microond y ocildore
Alumno: EXAEN PARCIAL UBIEA DE RADIOFRECUENCIA Y ANENA DPO. DE EORÍA DE LA EÑAL Y COUNICACIONE 5 de noviembre de 0 Problem (hy que entregr l hoj de ete enuncido) PROBLEA de mpliicdore de microond y ocildore
PROBLEMAS DE GENERADORES SINCRÓNICOS. Asignatura : Conversión Electromecánica de la Energía. Fecha : Agosto Autor : Ricardo Leal Reyes.
 ROBLMA D GNRADOR NCRÓNCO. Aigntur : Converión lectromecánic de l nergí. ech : Agoto200. Autor : Ricrdo Lel Reye. 1. Un generdor incrónico de 6 polo conectdo en etrell, de 480 (), 60 (Hz), 1 (Ω/fe), 60
ROBLMA D GNRADOR NCRÓNCO. Aigntur : Converión lectromecánic de l nergí. ech : Agoto200. Autor : Ricrdo Lel Reye. 1. Un generdor incrónico de 6 polo conectdo en etrell, de 480 (), 60 (Hz), 1 (Ω/fe), 60
DEFINICIÓN 1: Sea G = (V, A) un digrafo conexo y sin lazos. Se dice que G es una RED o RED DE TRANSPORTE si se verifican:
 REDES DE TRANSORTE E un pliión digro ponrdo l lujo irulión un ien un uente un tino ddo. Lo iene puen er por ejemplo litro petróleo que luyen por tuerí llmd teleóni tré un item omuniión et. Oerión: el peo
REDES DE TRANSORTE E un pliión digro ponrdo l lujo irulión un ien un uente un tino ddo. Lo iene puen er por ejemplo litro petróleo que luyen por tuerí llmd teleóni tré un item omuniión et. Oerión: el peo
VECTORES. 4º E.S.O. Académicas VECTOR FIJO EN EL PLANO VECTOR DE POSICIÓN DE UN PUNTO. COORDENADAS DE UN VECTOR
 VECTOR FIJO EN EL PLANO VECTORES 4º E.S.O. Acaémica Un vector fijo e un egmento orientao y quea eterminao por o punto, uno como comienzo A yotro como final B. Se repreenta como AB A AB Móulo: Ditancia
VECTOR FIJO EN EL PLANO VECTORES 4º E.S.O. Acaémica Un vector fijo e un egmento orientao y quea eterminao por o punto, uno como comienzo A yotro como final B. Se repreenta como AB A AB Móulo: Ditancia
. 1. La función de transferencia de una planta es:
 Univeridad de Navarra Nafarroako Unibertitatea Ecuela Superior de Ingeniero Ingeniarien Goi Mailako Ekola ASIGNATURA GAIA Ingeniería de Control I 4º CURSO URTSOA NOMBRE IZENA FECHA DATA 9 de enero de 3
Univeridad de Navarra Nafarroako Unibertitatea Ecuela Superior de Ingeniero Ingeniarien Goi Mailako Ekola ASIGNATURA GAIA Ingeniería de Control I 4º CURSO URTSOA NOMBRE IZENA FECHA DATA 9 de enero de 3
que verifican A 2 = A.
 . Hll ls mtries A que verifin A A.. Do el sistem: m ( m ) m ) Disútelo en funión el vlor e m. ) Resuélvelo en el so m represent gráfimente l situión. 3. Consieremos ls mtries B C Hll un mtri A tl que A
. Hll ls mtries A que verifin A A.. Do el sistem: m ( m ) m ) Disútelo en funión el vlor e m. ) Resuélvelo en el so m represent gráfimente l situión. 3. Consieremos ls mtries B C Hll un mtri A tl que A
Tema 3 Respuesta en Frecuencia
 CIRCUITOS ANALÓGICOS SEGUNDO CURSO Tem 3 Repuet en Frecuenci Sebtián López y Joé Fco. López Intituto Univeritrio de Microelectrónic Aplicd IUMA Univeridd de L Plm de Grn Cnri 357 - L Plm de Grn Cnri Tfno.
CIRCUITOS ANALÓGICOS SEGUNDO CURSO Tem 3 Repuet en Frecuenci Sebtián López y Joé Fco. López Intituto Univeritrio de Microelectrónic Aplicd IUMA Univeridd de L Plm de Grn Cnri 357 - L Plm de Grn Cnri Tfno.
SISTEMA DE COORDENADAS EN EL PLANO
 Mtemáti Diseño Inustril Coorens en el lno Ing. Avil Ing. Moll SISTEMA DE CRDENADAS EN EL LAN SISTEMA UNIDIMENSINAL Es sio que es posile soir los números reles on los puntos e un ret reípromente. Es lo
Mtemáti Diseño Inustril Coorens en el lno Ing. Avil Ing. Moll SISTEMA DE CRDENADAS EN EL LAN SISTEMA UNIDIMENSINAL Es sio que es posile soir los números reles on los puntos e un ret reípromente. Es lo
Compensación en adelanto
 UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FAULAD DE INENIEÍA MEANIA Y ELÉIA ONOL LÁSIO M.. JOSÉ MANUEL OHA NUÑEZ ompenaión en adelanto ompenador eletrónio en adelanto on amplifiadore operaionale () () E E i 0,,
UNIVESIDAD AUÓNOMA DE NUEVO LEÓN FAULAD DE INENIEÍA MEANIA Y ELÉIA ONOL LÁSIO M.. JOSÉ MANUEL OHA NUÑEZ ompenaión en adelanto ompenador eletrónio en adelanto on amplifiadore operaionale () () E E i 0,,
IES CASTELAR BADAJOZ Examen Junio de 2011(Específico) Solución Antonio Mengiano Corbacho UNIVERSIDAD DEL PAÍS VASCO MATEMÁTICAS II
 IES STELR BDJOZ Emen Junio e (Espeífio) ntonio engino orho UIVERSIDD DEL PÍS VSO TEÁTIS II TEÁTIS II Tiempo máimo: hor minutos Instruiones: El lumno elegirá un e ls os opiones propuests un e ls utro uestiones
IES STELR BDJOZ Emen Junio e (Espeífio) ntonio engino orho UIVERSIDD DEL PÍS VSO TEÁTIS II TEÁTIS II Tiempo máimo: hor minutos Instruiones: El lumno elegirá un e ls os opiones propuests un e ls utro uestiones
Reemplazando la salida C(s) en función de R(s) obtenemos, la expresión para el cálculo del error actuante:
 Cátedra: Sitema de Control Reemplaando la alida C( en función de R( obtenemo, la expreión para el cálculo del error actuante: Ea( = R ( + GH ( ( Ete error actuante, podría coniderare como el que e obtendría
Cátedra: Sitema de Control Reemplaando la alida C( en función de R( obtenemo, la expreión para el cálculo del error actuante: Ea( = R ( + GH ( ( Ete error actuante, podría coniderare como el que e obtendría
2.2 Asumiendo un comportamiento ideal, calcular el área ocupada por molécula de butanoico en el límite de concentraciones elevadas del mismo.
 . Se introdue un pilr de rdio.5 mm dentro de un disoluión uos en useni de surftnte ºC onsiguiendo un ltur en el interior del pilr, h 1. A ontinuión se introdue el mismo pilr en un disoluión uos que ontiene
. Se introdue un pilr de rdio.5 mm dentro de un disoluión uos en useni de surftnte ºC onsiguiendo un ltur en el interior del pilr, h 1. A ontinuión se introdue el mismo pilr en un disoluión uos que ontiene
Trabajo Práctico N 9: APLICACIONES A LA GEOMETRÍA
 Fultd Regionl Mendo. UTN Álger Geometrí Anlíti Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni que tiene entro en (- ; 3) que ps por el punto ( ; -). Grfique.
Fultd Regionl Mendo. UTN Álger Geometrí Anlíti Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni que tiene entro en (- ; 3) que ps por el punto ( ; -). Grfique.
CALCULO DE CENTROS DE MASA: PLACAS
 CALCULO DE CENTROS DE MASA: PLACAS Clulr l posiión el entro e mss e l siguiente pl suponieno que su ms está uniformemente istribui por to ell: b b( 1 k 3 ) Soluión: I.T.I. 1,, I.T.T. 1, En primer lugr,
CALCULO DE CENTROS DE MASA: PLACAS Clulr l posiión el entro e mss e l siguiente pl suponieno que su ms está uniformemente istribui por to ell: b b( 1 k 3 ) Soluión: I.T.I. 1,, I.T.T. 1, En primer lugr,
Trabajo Práctico N 9: APLICACIONES A LA GEOMETRÍA
 Fultd Regionl Mendo. UTN Álger Geometrí Anlíti 6 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni siendo que el segmento de etremos (- ; 3) (4; -) es diámetro
Fultd Regionl Mendo. UTN Álger Geometrí Anlíti 6 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni siendo que el segmento de etremos (- ; 3) (4; -) es diámetro
PROBLEMAS DE ÁLGEBRA DE MATRICES
 Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
TEORÍA DE CONTROL PRIMER PARCIAL 13 DE ABRIL 2018
 TEOÍ DE ONTOL PE PL DE BL 8 TEOÍ: Ejercicio Ejercicio Ejercicio punto punto punto El objetivo de lo tem de teorí e exponer u conocimiento teórico obre modeldo de item. Pr ello, derrolle con clridd y conciión
TEOÍ DE ONTOL PE PL DE BL 8 TEOÍ: Ejercicio Ejercicio Ejercicio punto punto punto El objetivo de lo tem de teorí e exponer u conocimiento teórico obre modeldo de item. Pr ello, derrolle con clridd y conciión
Reguladores y Redes de Compensación
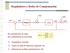 Reguladore y Rede de Compenaión l(t) r(t) e(t) x(t) Reg() G() n(t) y(t) l(t): perturbaión de arga n(t): perturbaión en la medida R ( ) ( + zi ) ( + pi ) Ø Ø Ø Reguladore enillo Seguir la eñal de referenia
Reguladore y Rede de Compenaión l(t) r(t) e(t) x(t) Reg() G() n(t) y(t) l(t): perturbaión de arga n(t): perturbaión en la medida R ( ) ( + zi ) ( + pi ) Ø Ø Ø Reguladore enillo Seguir la eñal de referenia
Competencia Monopolística EJERCICIOS. Profesor Guillermo Pereyra clases.microeconomia.
 Competeni Monopolísti EJERCICIOS Profesor Guillermo Pereyr guillermopereyr@miroeonomi.org www.miroeonomi.org lses.miroeonomi.org 1. Cuál e ls siguientes lterntivs no es rterísti e l ompeteni monopolísti?
Competeni Monopolísti EJERCICIOS Profesor Guillermo Pereyr guillermopereyr@miroeonomi.org www.miroeonomi.org lses.miroeonomi.org 1. Cuál e ls siguientes lterntivs no es rterísti e l ompeteni monopolísti?
A es de 2 2 y tiene dos valores propios distintos, por lo tanto es diagonalizable sobre IR.
 Sergio Ynsen Núñez. Se A 8 3 3 Muestre que A es digonlizle sore IR. Soluión: 8 3 3 6 5 3 Los vlores propios de A sony3 A es de y tiene dos vlores propios distintos, por lo tnto es digonlizle sore IR. Otr
Sergio Ynsen Núñez. Se A 8 3 3 Muestre que A es digonlizle sore IR. Soluión: 8 3 3 6 5 3 Los vlores propios de A sony3 A es de y tiene dos vlores propios distintos, por lo tnto es digonlizle sore IR. Otr
SISTEMAS DE ECUACIONES LINEALES CON DOS INCÓGNITAS
 nstituto Dr. Jun Segundo Fernández Áre y urso: Mtemáti 4º ño. Profesor: Griel Bejr TRABAJO PRÁCTICO Nº. SISTEMAS DE ECUACIONES LINEALES CON DOS INCÓGNITAS RESOLUCIÓN DE SISTEMAS DE ECUACIONES Ténis de
nstituto Dr. Jun Segundo Fernández Áre y urso: Mtemáti 4º ño. Profesor: Griel Bejr TRABAJO PRÁCTICO Nº. SISTEMAS DE ECUACIONES LINEALES CON DOS INCÓGNITAS RESOLUCIÓN DE SISTEMAS DE ECUACIONES Ténis de
Transformadas de Laplace
 Semn 7 - Cle 2. Definicione pr Comenzr Trnformd de Lplce En generl vmo definir un trnformción integrl, F (), de un función, f(t) como F () = b K (, t) f(t)dt = T {f(t)} () donde K (, t) e un función conocid
Semn 7 - Cle 2. Definicione pr Comenzr Trnformd de Lplce En generl vmo definir un trnformción integrl, F (), de un función, f(t) como F () = b K (, t) f(t)dt = T {f(t)} () donde K (, t) e un función conocid
ECUACIÓN DE BERNOULLI
 ECUACIÓN DE BERNOULLI 1. RESUMEN Ete lbortorio trt obre l comprobción de l ecución de Bernoulli. Aquí e intent comprobr l relción que exite entre l velocidd (cbez dinámic), l cbez (cbez etátic) y l cbez
ECUACIÓN DE BERNOULLI 1. RESUMEN Ete lbortorio trt obre l comprobción de l ecución de Bernoulli. Aquí e intent comprobr l relción que exite entre l velocidd (cbez dinámic), l cbez (cbez etátic) y l cbez
Razones y Proporciones
 Rzones y Proporiones 01. L rzón geométri e os números es 1/ y su rzón ritméti es 7. Hllr el myor. ) 117 ) 11 ) 119 ) 118 e) 110 0. L rzón geométri entre l sum e números y su ifereni es :. Hllr l rzón geométri
Rzones y Proporiones 01. L rzón geométri e os números es 1/ y su rzón ritméti es 7. Hllr el myor. ) 117 ) 11 ) 119 ) 118 e) 110 0. L rzón geométri entre l sum e números y su ifereni es :. Hllr l rzón geométri
Taller: Sistemas de ecuaciones lineales
 Deprtmento de ienis ásis Asigntur: Mtemátis I Doente: Vitor Hugo Gil Avendño Apellidos-Nomres: 0 de mrzo de 08 Tller: Sistems de euiones lineles Un sistem de euiones es un onjunto de dos o más euiones
Deprtmento de ienis ásis Asigntur: Mtemátis I Doente: Vitor Hugo Gil Avendño Apellidos-Nomres: 0 de mrzo de 08 Tller: Sistems de euiones lineles Un sistem de euiones es un onjunto de dos o más euiones
Transformaciones Geométricas 3D
 Trnsformciones Geométrics 3D Introucción 3D Cuno nos introucimos l muno 3D, hy que consierr: El fctor e profuni Ls combinciones que se pueen generr sobre 3 ejes L perspectiv e observción Los operores se
Trnsformciones Geométrics 3D Introucción 3D Cuno nos introucimos l muno 3D, hy que consierr: El fctor e profuni Ls combinciones que se pueen generr sobre 3 ejes L perspectiv e observción Los operores se
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
ESTABILIDAD DE SISTEMAS REALIMENTADOS CRITERIO DE ESTABILIDAD DE NYQUIST
 ESTABILIDAD DE SISTEMAS REALIMENTADOS CRITERIO DE ESTABILIDAD DE NYQUIST Condición de etabilidad: G( ) N( ) D( ) p n a 1 b 1 p1 n1...... a b p1 n1 a b n p p n z z... z N () 1 2 p G( ) p n D( ) p p... p
ESTABILIDAD DE SISTEMAS REALIMENTADOS CRITERIO DE ESTABILIDAD DE NYQUIST Condición de etabilidad: G( ) N( ) D( ) p n a 1 b 1 p1 n1...... a b p1 n1 a b n p p n z z... z N () 1 2 p G( ) p n D( ) p p... p
Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte
 chritianq@uninorte.edu.co Departamento de Ingeniería Eléctrica y Electrónica Univeridad del Norte El problema má importante de lo itema de control lineal tiene que ver con la etabilidad. Un itema de control
chritianq@uninorte.edu.co Departamento de Ingeniería Eléctrica y Electrónica Univeridad del Norte El problema má importante de lo itema de control lineal tiene que ver con la etabilidad. Un itema de control
Criterio de Estabilidad de Routh-Hurwitz
 Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e el emiplo
Criterio de Etbilidd de Routh-Hurwitz F Pr l etbilidd BIBO, l ríce de l ecució crcterític, o lo polo de C()/R(), o puede etr loclizdo e el emiplo derecho del plo o e eje j, todo debe quedr e el emiplo
Instituto Tecnológico de Santo Domingo. Área de Ingeniería. Cálculo de esfuerzo axial en las barras de una armadura
 Intituto Tecnológico de Santo Domingo Área de Ingeniería Práctica No. Cálculo de efuerzo aial en la barra de una armadura Realizada por Jairon lberto rancico Mateo Reprobó la aignatura la primera vez en
Intituto Tecnológico de Santo Domingo Área de Ingeniería Práctica No. Cálculo de efuerzo aial en la barra de una armadura Realizada por Jairon lberto rancico Mateo Reprobó la aignatura la primera vez en
Primer Examen Parcial 17/4/2003
 MR990. Control de Proceo Indutriale Salvador Macía Hernández 7730 Primer Examen Parcial 7/4/003 PRIMER INCISO Sea el itema hidráulico/eléctrico iguiente: R q R q L Ct C Generador de voltaje vt () kq()
MR990. Control de Proceo Indutriale Salvador Macía Hernández 7730 Primer Examen Parcial 7/4/003 PRIMER INCISO Sea el itema hidráulico/eléctrico iguiente: R q R q L Ct C Generador de voltaje vt () kq()
SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS
 MATEMÁ TTCAS BÁSICAS SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS Ddos números reles l', b l, b, l Y ' l pr de euiones lx + b,y=l Y x + b y = se denomin un sistem linel de dos euiones en ls dos
MATEMÁ TTCAS BÁSICAS SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS Ddos números reles l', b l, b, l Y ' l pr de euiones lx + b,y=l Y x + b y = se denomin un sistem linel de dos euiones en ls dos
(4, 3, 1) (iii) Defina estrategia débilmente dominada. Qué estrategias están débilmente
 . Conidere el iguiente juego en form norml: (4,, ) (,, ) (, β, ) (, 6, ) (0,, 4) (, 4, ) (i) efin etrtegi. Repreente el juego en form norml. (ii) efin equilirio de N. Oteng lo equilirio de N. (iii) efin
. Conidere el iguiente juego en form norml: (4,, ) (,, ) (, β, ) (, 6, ) (0,, 4) (, 4, ) (i) efin etrtegi. Repreente el juego en form norml. (ii) efin equilirio de N. Oteng lo equilirio de N. (iii) efin
1. PRODUCTO VECTORIAL DE DOS VECTORES LIBRES
 UNIDAD : Produto etoril y mixto. Apliione.. PRODUCTO VECTORIAL DE DOS VECTORES LIBRES Definiión: El produto etoril de do etore lire y, que e not por, e define omo: - Si 0 ó 0 ó y on proporionle, entone
UNIDAD : Produto etoril y mixto. Apliione.. PRODUCTO VECTORIAL DE DOS VECTORES LIBRES Definiión: El produto etoril de do etore lire y, que e not por, e define omo: - Si 0 ó 0 ó y on proporionle, entone
Ingeniería de Control I - Examen 1.II.2001
 ESCUELA SUPERIOR DE INGENIEROS UNIVERSIDAD DE NAVARRA INGENIARIEN GOI MAILAKO ESKOLA NAFARROAKO UNIBERTSITATEA Ingeniería de Control I - Examen.II. Nombre y apellido: Nº de carnet: Se parte de la planta
ESCUELA SUPERIOR DE INGENIEROS UNIVERSIDAD DE NAVARRA INGENIARIEN GOI MAILAKO ESKOLA NAFARROAKO UNIBERTSITATEA Ingeniería de Control I - Examen.II. Nombre y apellido: Nº de carnet: Se parte de la planta
APUNTES DE CRISTALOGRAFÍA: RETÍCULO RECÍPROCO Màrius Vendrell RETÍCULO RECÍPROCO
 RETÍCULO RECÍPROCO A pti el etíulo efinio nteiomente, en el que omo nuo oespone un motivo o llmemos etíulo ieto, es posible efini oto etíulo (que llmemos eípoo) en el ul los tes vetoes funmentles son:
RETÍCULO RECÍPROCO A pti el etíulo efinio nteiomente, en el que omo nuo oespone un motivo o llmemos etíulo ieto, es posible efini oto etíulo (que llmemos eípoo) en el ul los tes vetoes funmentles son:
En el espacio una superficie cuádrica es la gráfica de una ecuación de segundo grado en las variables x, y, z. la forma general de esta ecuación es:
 UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BÁSICAS DEPARTAMENTO DE CIENCIAS BASICAS. SUPERFICIES CUADRICAS 1 SUPERFICIES CUADRICAS En el espio un superfiie uádri es l gráfi de un euión
UNIVERSIDAD FRANCISCO DE PAULA SANTANDER FACULTAD DE CIENCIAS BÁSICAS DEPARTAMENTO DE CIENCIAS BASICAS. SUPERFICIES CUADRICAS 1 SUPERFICIES CUADRICAS En el espio un superfiie uádri es l gráfi de un euión
Calcular los parámetros y los vértices de las siguientes hipérbola equilátera: La hipérbola equilátera es aquella cuyos ejes son iguales a = b
 Problem relizdo por Elen Abd Felip Enunido: Clulr los prámetros y los vérties de ls siguientes hipérbol equiláter: y = 6 ) Según sus síntots b) Según sus ejes Bses teóris: L hipérbol equiláter es quell
Problem relizdo por Elen Abd Felip Enunido: Clulr los prámetros y los vérties de ls siguientes hipérbol equiláter: y = 6 ) Según sus síntots b) Según sus ejes Bses teóris: L hipérbol equiláter es quell
SISTEMAS DE ECUACIONES DE PRIMER GRADO
 el log e me e i: Memáis I. Sisems e euiones. pág. SISTEMAS DE ECUACIONES DE PRIMER GRADO Un sisem e os euiones e primer gro on os inógnis puee esriirse sí: += `+`=` one los oefiienes e ls inógnis los érminos
el log e me e i: Memáis I. Sisems e euiones. pág. SISTEMAS DE ECUACIONES DE PRIMER GRADO Un sisem e os euiones e primer gro on os inógnis puee esriirse sí: += `+`=` one los oefiienes e ls inógnis los érminos
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
ESTABILIDAD. estable, si sometido a una perturbación, éste, luego de un tiempo, vuelve a su
 ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
ESTABIIDAD El álii de lo ite de otrol e e gr prte e el ooiieto de u etilidd olut y reltiv ESTABIIDAD ABSOUTA: u ite liel ivrite e el tiepo e etle, i oetido u perturió, éte, luego de u tiepo, vuelve u odiió
AUTÓMATAS Y SISTEMAS DE CONTROL
 º NGENERÍA TELECOMUNCACÓN 2º TT SSTEMAS ELECTRÓNCOS 2º TT SSTEMAS DE TELECOMUNCACÓN AUTÓMATAS Y SSTEMAS DE CONTROL PROBLEMAS DE SSTEMAS PARTE 2: ERRORES EN REG. PERMANENTE LUGAR DE LAS RACES DSEÑO REGULADORES
º NGENERÍA TELECOMUNCACÓN 2º TT SSTEMAS ELECTRÓNCOS 2º TT SSTEMAS DE TELECOMUNCACÓN AUTÓMATAS Y SSTEMAS DE CONTROL PROBLEMAS DE SSTEMAS PARTE 2: ERRORES EN REG. PERMANENTE LUGAR DE LAS RACES DSEÑO REGULADORES
1. INTEGRALES MÚLTIPLES
 1. INTGALS MÚLTIPLS 1.1. INTGAL OBL SOB UN CTÁNGULO Se f : 2 un funión otd de dos vribles, denid sobre el retángulo = [, b] [, d] = {(x, y) 2 : x b, y d} A ontinuión se onsider un prtiión de en subretángulos.
1. INTGALS MÚLTIPLS 1.1. INTGAL OBL SOB UN CTÁNGULO Se f : 2 un funión otd de dos vribles, denid sobre el retángulo = [, b] [, d] = {(x, y) 2 : x b, y d} A ontinuión se onsider un prtiión de en subretángulos.
BOLETIN DE EJERCICIOS 2: CIRCUITOS COMBINACIONALES
 : OBJETIVO Los ejeriios e este oletín tienen omo ojetivo onsolir los onoimientos reltivos los siguientes oneptos: - L implementión e ls uniones lógis meinte puerts lógis interonets. - Los istintos tipos
: OBJETIVO Los ejeriios e este oletín tienen omo ojetivo onsolir los onoimientos reltivos los siguientes oneptos: - L implementión e ls uniones lógis meinte puerts lógis interonets. - Los istintos tipos
EQUILIBRIO QUÍMICO. Constante de equilibrio K C
 EQUILIBRIO QUÍMIO Un e ls pliiones más importntes e l termoinámi son ls reiones químis en equilibrio. En ls reiones que trnsurren, presión y tempertur onstnte, si G sistem kj / mol, el proeso es reversible
EQUILIBRIO QUÍMIO Un e ls pliiones más importntes e l termoinámi son ls reiones químis en equilibrio. En ls reiones que trnsurren, presión y tempertur onstnte, si G sistem kj / mol, el proeso es reversible
TEMA 5: FRACCIONES. Las fracciones permiten trabajar de manera simbólica con cantidades no enteras.
 Alonso Fernánez Glián TEMA FRACCIONES Ls friones permiten trjr e mner simóli on nties no enters.. CONCEPTO DE FRACCIÓN Un frión es un expresión e l form numeror enominor ( 0) Represent el resulto e iviir
Alonso Fernánez Glián TEMA FRACCIONES Ls friones permiten trjr e mner simóli on nties no enters.. CONCEPTO DE FRACCIÓN Un frión es un expresión e l form numeror enominor ( 0) Represent el resulto e iviir
SR(s)=R(s) + E(s) C(s)
 TEMA: EO EN ÉGIMEN PEMANENTE Un apecto importante a tener en cuenta e el comportamiento de un itema ante divera entrada en régimen permanente. En cualquier itema fíico de control exite un error inherente,
TEMA: EO EN ÉGIMEN PEMANENTE Un apecto importante a tener en cuenta e el comportamiento de un itema ante divera entrada en régimen permanente. En cualquier itema fíico de control exite un error inherente,
Matemáticas aplicadas a las Ciencias Sociales II. ANAYA
 Uni Nº Resoluión e sisems meine eerminnes! PR EPEZR, RELEXION Y RESUELVE Deerminnes e oren! Resuelve uno e los siguienes sisems e euiones lul el eerminne e l mri e los oefiienes: E sumno E E sumno λ,s.c.i.,
Uni Nº Resoluión e sisems meine eerminnes! PR EPEZR, RELEXION Y RESUELVE Deerminnes e oren! Resuelve uno e los siguienes sisems e euiones lul el eerminne e l mri e los oefiienes: E sumno E E sumno λ,s.c.i.,
FILTROS ACTIVOS CAPÍTULO 3
 FILTOS TIOS PÍTULO ealización ctiva en Matlab. Filtro ctivo. Lo filtro activo también tienen en u configuracione elemento paivo como capacitore, reitencia y elemento activo como el mplificador Operacional,
FILTOS TIOS PÍTULO ealización ctiva en Matlab. Filtro ctivo. Lo filtro activo también tienen en u configuracione elemento paivo como capacitore, reitencia y elemento activo como el mplificador Operacional,
SOLUCIONES DE LOS EJERCICIOS DE CORRIENTE CONTINUA -1 er TRIMESTRE-. problemas:11, 12 y 14
 R= SOLUCONES DE LOS PROLEMS DE ELECTRCDD DE C.C. SOLUCONES DE LOS EJERCCOS DE CORRENTE CONTNU - er TRMESTRE-. prolems:, y ª ) Soluionremos este prolem por el método generl de nálisis por lzos ásios, omprondo
R= SOLUCONES DE LOS PROLEMS DE ELECTRCDD DE C.C. SOLUCONES DE LOS EJERCCOS DE CORRENTE CONTNU - er TRMESTRE-. prolems:, y ª ) Soluionremos este prolem por el método generl de nálisis por lzos ásios, omprondo
INGENIERIA DE SISTEMAS Y AUTOMATICA Calcular las antitransformadas de Laplace de las siguientes funciones: - +
 . Concepto báico.. Calcular la antitranformada de Laplace de la iguiente funcione: a) b) c) F ( ) F ( ) F ( ) ( ) 3 ( ) 3 ( )( 6 34).. Encontrar la función de tranferencia M()Y()/X() mediante la implificación
. Concepto báico.. Calcular la antitranformada de Laplace de la iguiente funcione: a) b) c) F ( ) F ( ) F ( ) ( ) 3 ( ) 3 ( )( 6 34).. Encontrar la función de tranferencia M()Y()/X() mediante la implificación
6 La transformada de Laplace
 CAPÍTULO 6 L trnformd de Lplce 6.4.3 Segund propiedd de trlción Et propiedd permitirá reolver ecucione diferencile donde prezcn funcione dicontinu. Pr entenderl e conveniente introducir un función con
CAPÍTULO 6 L trnformd de Lplce 6.4.3 Segund propiedd de trlción Et propiedd permitirá reolver ecucione diferencile donde prezcn funcione dicontinu. Pr entenderl e conveniente introducir un función con
UNIDAD VI LA ELIPSE 6.1. ECUACIÓN EN FORMA COMÚN O CANÓNICA DE LA ELIPSE
 UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
1 - Resolver los siguientes determinantes usando propiedades 1/10
 - Resolver los siguientes determinntes usndo propieddes ) ) / ) d) e) f) / / g) / / / / / / / / / / / / / h) / / / / / / / / / / / / / / / i) / / / / j) / / 8 / k) h k w k w h w h k h k w - Hllr los vlores
- Resolver los siguientes determinntes usndo propieddes ) ) / ) d) e) f) / / g) / / / / / / / / / / / / / h) / / / / / / / / / / / / / / / i) / / / / j) / / 8 / k) h k w k w h w h k h k w - Hllr los vlores
Representar las dos proyecciones y la tercera proyección de los puntos dados a continuación:
 Reeent l o oyeione y l tee oyeión e lo unto o ontinuión: to. lej. ot A + 0 B + = + C + < + D 0 + E - > + F - = + G - > + H - 0 I - > - J - = - K - < - L 0 - M + < - N + = - + > - Lo igno =,> y < e efieen
Reeent l o oyeione y l tee oyeión e lo unto o ontinuión: to. lej. ot A + 0 B + = + C + < + D 0 + E - > + F - = + G - > + H - 0 I - > - J - = - K - < - L 0 - M + < - N + = - + > - Lo igno =,> y < e efieen
Cálculo del tamaño muestral en estudios de casos y controles
 Investigión: Cálulo el tmño muestrl en estuios e sos y ontroles /5 Cálulo el tmño muestrl en estuios e sos y ontroles Pértegs Dí S., Pit Fernáne S. Uni e Eiemiologí Clíni y Bioestísti. Comlexo Hositlrio
Investigión: Cálulo el tmño muestrl en estuios e sos y ontroles /5 Cálulo el tmño muestrl en estuios e sos y ontroles Pértegs Dí S., Pit Fernáne S. Uni e Eiemiologí Clíni y Bioestísti. Comlexo Hositlrio
MATRICES Y DETERMINANTES
 MATRICES Y DETERMINANTES EJERCICIOS RESUELTOS D l triz A, qué relión een gurr ls onstntes pr que se verifique l igul A A. Cluleos A : A. Coo se h e uplir que A A, teneos que:, por tnto se otiene el siguiente
MATRICES Y DETERMINANTES EJERCICIOS RESUELTOS D l triz A, qué relión een gurr ls onstntes pr que se verifique l igul A A. Cluleos A : A. Coo se h e uplir que A A, teneos que:, por tnto se otiene el siguiente
FIGURAS SEMEJANTES. r B CRITERIOS DE SEMEJANZA DE TRIÁNGULOS. Dos triángulos son semejantes si cumplen alguna de las siguientes condiciones:
 Lo fundmentl de l unidd Nombre y pellidos:... urso:... Feh:... FIGURS SEMEJNTES Dos figurs son semejntes si sus ángulos orrespondientes son... y sus distnis... D F D' ' F' ' ' Por ejemplo, si ls figurs
Lo fundmentl de l unidd Nombre y pellidos:... urso:... Feh:... FIGURS SEMEJNTES Dos figurs son semejntes si sus ángulos orrespondientes son... y sus distnis... D F D' ' F' ' ' Por ejemplo, si ls figurs
Trabajo Práctico N 9: APLICACIONES A LA GEOMETRÍA
 Fultd Regionl Mendoz. UTN Álger Geometrí Anlíti 13 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio 1: Hlle l euión norml generl de l irunfereni que tiene por diámetro el segmento de etremos ( - 1,
Fultd Regionl Mendoz. UTN Álger Geometrí Anlíti 13 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio 1: Hlle l euión norml generl de l irunfereni que tiene por diámetro el segmento de etremos ( - 1,
Podemos calcular la suma de las áreas de los rectángulos superiores que es una aproximación por exceso del área R(f; a, b):
 TEMA 6: INTEGRAL DEFINIDA. 6.1 Integrl efini omo límite e sums superiores o inferiores. 6. Propiees e l integrl efini. 6. Regl e Brrow. 6.4 Apliiones e l integrl efini (Áre). 6.1 Integrl efini. Se f un
TEMA 6: INTEGRAL DEFINIDA. 6.1 Integrl efini omo límite e sums superiores o inferiores. 6. Propiees e l integrl efini. 6. Regl e Brrow. 6.4 Apliiones e l integrl efini (Áre). 6.1 Integrl efini. Se f un
Recuerda lo fundamental
 6 L semejnz sus pliiones Reuerd lo fundmentl urso:... Fe:... FIGURS SEMEJNTES Dos figurs son semejntes si sus ángulos orrespondientes son... sus distnis... Por ejemplo, si ls figurs F F' son semejntes,
6 L semejnz sus pliiones Reuerd lo fundmentl urso:... Fe:... FIGURS SEMEJNTES Dos figurs son semejntes si sus ángulos orrespondientes son... sus distnis... Por ejemplo, si ls figurs F F' son semejntes,
REGULACIÓN AUTOMATICA (8)
 REGULACIÓN AUOMAICA 8 Repueta en frecuencia Nyquit Ecuela Politécnica Superior Profeor: Darío García Rodríguez -4.-Dada la función de tranferencia de lazo abierto de un itema con imentación unitaria, para
REGULACIÓN AUOMAICA 8 Repueta en frecuencia Nyquit Ecuela Politécnica Superior Profeor: Darío García Rodríguez -4.-Dada la función de tranferencia de lazo abierto de un itema con imentación unitaria, para
PROBLEMAS DE MOTORES SINCRÓNICOS. Asignatura : Conversión Electromecánica de la Energía Fecha : Agosto-2003 Autor : Ricardo Leal Reyes
 ROMA D MOTOR NRÓNO Aigntur : onverión lectromecánic de l nergí ech : Agoto-200 Autor : Ricrdo el Reye 1. Un motor incrónico trifáico de polo cilíndrico, conectdo en etrell 172 volt entre líne, r 0, 10
ROMA D MOTOR NRÓNO Aigntur : onverión lectromecánic de l nergí ech : Agoto-200 Autor : Ricrdo el Reye 1. Un motor incrónico trifáico de polo cilíndrico, conectdo en etrell 172 volt entre líne, r 0, 10
Plaquitas Fresas de planear Fresas de escuadrar Fresas de disco Fresas helicoidales específicas y Sets Aplicaciones
 www.cneltool.com Metl uro integrl Freo e perfile Apliccione epecífic y Set Fre helicoile Fre e ico Fre e ecurr Fre e plner Plquit Plquit Cóigo Trepnore Informción técnic I.02 I.03 I.04 I.11 I.13 Cono y
www.cneltool.com Metl uro integrl Freo e perfile Apliccione epecífic y Set Fre helicoile Fre e ico Fre e ecurr Fre e plner Plquit Plquit Cóigo Trepnore Informción técnic I.02 I.03 I.04 I.11 I.13 Cono y
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El siguiente diagrama representa una memoria asociativa y su contenido. Calcule los valores del registro de marcas.
 El iguiente dig epeent un eoi oitiv y u ontenido. Clule lo vloe del egito de. 0 0 0 0 guento 0 0 0 á 0 0? 0 0 0 0? 0 0 0 0 0? 0 0 0 0? 0 0 0 0? ontenido El lgoito genel del funioniento de un eoi oitiv
El iguiente dig epeent un eoi oitiv y u ontenido. Clule lo vloe del egito de. 0 0 0 0 guento 0 0 0 á 0 0? 0 0 0 0? 0 0 0 0 0? 0 0 0 0? 0 0 0 0? ontenido El lgoito genel del funioniento de un eoi oitiv
