CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES
|
|
|
- Vicente Salazar Lozano
- hace 8 años
- Vistas:
Transcripción
1 CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: Pedro J. López Cello
2 Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes elemetles: situcioes reles e ls que prece. Composició de fucioes Fucioes dds e form de tls. Iterpolció poliómic. Iterpolció y etrpolció de dtos Limites de fucioes. Cotiuidd y discotiuiddes. Teorem de Bolzo. Rms ifiits Derivd de u fució e u puto. Fució derivd. Derivds sucesivs. Apliccioes Desrrollo de u fució e serie de potecis. Teorem de Tylor. Apliccioes l estudio locl de fucioes El prolem del cálculo del áre. Itegrl defiid Primitiv de u fució. Cálculo de lgus primitivs. Apliccioes de l itegrl l cálculo de mgitudes geométrics Biliogrfí
3 3
4 Itroducció Al escriir este liro se h pretedido presetr los resultdos más importtes del álisis mtemático rel, cocretmete ordmos ls fucioes reles de vrile rel, l cotiuidd de dichs fucioes, el cálculo diferecil e itegrl y l iterpolció uméric. Cd uo de los coceptos priciples del álisis mtemático prece defiido, justificdo los resultdos priciples medite u demostrció. E todos los cpítulos se utiliz u fudmetció clásic del cálculo ifiitesiml de mer que este liro pude ser utilizdo por lumos de primeros ños de estudios superiores de igeierís y ciecis ects. Está tmié recomeddo pr los opositores l profesordo e Educció Secudri. Cometmos, pr termir, que l lector se le supoe úicmete uos ciertos coocimietos de álger y lgus ocioes elemetles de geometrí. 4
5 Cpítulo FUNCIONES REALES DE VARIABLE REAL FUNCIONES ELEMENTALES: SITUACIONES REALES EN LAS QUE APARECEN COMPOSICIÓN DE FUNCIONES f u c i o e s r e l e s d e v r i l e r e l O p e r c i o e s c o f u c i o e s. E s t r u c t u r d e l c o j u t o d e f u c i o e s r e l e s d e v r i l e r e l. F u c i o e s e l e m e t l e s 5
6 . FUNCIONES REALES DE VARIABLE REAL CONCEPTO DE FUNCIÓN REAL DE VARIABLE REAL U fució rel de vrile rel es u correspodeci de u sucojuto o vcío D IR e IR, lo escriiremos f: D IR, que cd elemeto D le soci uo y sólo u elemeto y IR. El sucojuto D se llm domiio de defiició o cmpo de eisteci de f y se escrie Dom(f) = { IR /!f() IR}. El recorrido o imge de u fució es el sucojuto de IR formdo por ls imágees de los elemetos del domiio: Im (f) = Rec(f) = {f() / D}. El úmero represet u elemeto ritrrio del domiio de l fució y se llm vrile idepediete. Al úmero y socido por l fució l vlor de se le llm vrile depediete. REPRESENTACIÓN GRÁFICA U sistem de coordeds crtesis e el plo es u pr ordedo de dos ejes perpediculres etre sí e u puto O. Al eje horizotl se le llm eje de ciss y se desig co OX, y l verticl se le llm eje de ordeds y se desig co OY. Sore OX se sitú l vrile idepediete y sore OY l vrile depediete. Si tommos el sistem de refereci R = { O ; i, j}, u puto culquier del plo P vedrá represetdo por los coeficietes de l comició liel que epres el vector OP e fució de l se { i, j}. Así, u puto P se epresrí como ( o, y o ), siedo o l scis de P e y o l orded de P. L gráfic de u fució es el lugr geométrico de los putos cuys coordeds verific l ecució y = f(). L visulizció de ls gráfics de ls fucioes permite ver más fácilmete sus propieddes. Trslció e l gráfic de u fució. Trslció horizotl Dd l represetció gráfic de u fució f(), si cosidermos l fució g() = f(-), otedremos u fució cuy gráfic estrá trsldd respecto l origil uiddes l derech, pr > ó l izquierd pr <.. Trslció verticl Dd f(), si cosidermos l fució g() = f() +, otedremos u fució cuy gráfic estrá trsldd respecto l origil uiddes hci rri, si > ó hci jo si <. 6
7 PROPIEDADES DE LAS FUNCIONES Pridd U fució rel de vrile rel y = f() es pr si y sólo si se verific que f(-)=f(). L gráfic de u fució pr es simétric respecto l eje de ordeds, y verific que si cotiee l puto (, y), cotedrá l (-, y). Ls fucioes y = cos, y = 4 + so fucioes pres. U fució rel de vrile rel y = f() es impr si y sólo si se verific que f(-) = -f(). L gráfic de u fució impr es simétric respecto l orige de coordeds, y verific que si cotiee l puto (, y), cotedrá l (-, -y). Ejemplos: y = se, y = 3 + so fucioes impres. U fució se dice que o tiee pridd si o es pr i impr. Fució iyectiv U fució rel de vrile rel y = f() es iyectiv si y sólo si se verific que, IR, f( ) = f( ) =. Gráficmete lo veremos cudo ls rects prlels l eje OY cort l fució e u sólo puto. Ls fucioes y = +, y = 3 so iyectivs. Fució soreyectiv U fució rel de vrile rel y = f() es soreyectiv si y sólo si pr culquier y IR D, tl que f() = y. Gráficmete lo veremos cudo Im(f) = IR. Ls fucioes y = +, y = 3 so fucioes soreyectivs. Fució iyectiv U fució rel de vrile rel y = f() es iyectiv si es iyectiv y soreyectiv. Fució periódic U fució rel de vrile rel y = f() es periódic si t IR, o ulo / D se verific f( + t) = f(). A dicho vlor t se le deomi periodo y se verific que todo múltiplo de t tmié es u periodo pr f. So periódics tods ls fucioes trigoométrics. Mootoí U fució rel de vrile rel y = f() es creciete e D si se verific:, D / < f( ) f( ) y es estrictmete creciete si, D / < f( ) < f( ). U fució rel de vrile rel y = f() es decreciete e D si, D / < f( ) f( ) y es estrictmete decreciete si, D / < f( ) > f( ). 7
8 Ls fucioes f ( ) f = so estrictmete crecietes pr > y = y ( ) log estrictmete decrecietes pr < <. Acotció U fució rel de vrile rel y = f() está cotd superiormete si K IR / f() K D. A ese úmero K lo llmremos cot superior y será u máimo si l fució lcz ese vlor. Se dice que está cotd iferiormete si K IR / f() K D y este úmero K se le llmrá cot iferior y será u míimo si lo lcz. Se dice que u fució y = f() está cotd si lo está superior e iferiormete. L fució f ( ) = está cotd, verificádose < f() IR +. OPERACIONES CON FUNCIONES. ESTRUCTURA DEL CONJUNTO DE LAS FUNCIONES REALES DE VARIABLE REAL. Se IF(D,IR) = IF el cojuto de ls fucioes reles de vrile rel co domiio D: IF = {f : D IR}, vmos defiir ls opercioes que podemos relizr co dichs fucioes. SUMA DE FUNCIONES Dds dos fucioes f y g IF, l sum es otr fució rel h = f + g que verific: h() = (f + g)() = f() + g() D. Se verific que Dom(f + g) = Dom(f) Dom(g) = D. Propieddes. Ley de composició iter: L sum verific que si f y g IF, etoces f + g IF.. Asocitiv: (f + g) + h = f + (g + h) f, g, h IF. 3. Comuttiv: f + g = g + f f, g IF 4. Elemeto eutro: Llmremos fució ul l fució: : D IR / () = D. Como se verific que f + = + f = f f IF, dich fució es el elemeto eutro pr l sum de fucioes. 5. Elemeto simétrico. Llmremos fució opuest de f IF l fució: -f : D IR / (- f)() = -f() D. Como se verific que f + f = f + (-f) =, dich fució es el elemeto simétrico pr l sum de fucioes. 8
9 Co tods ls propieddes teriores respecto de l sum podemos firmr que el (IF, +) tiee estructur de grupo elio. Como tod fució tiee opuest, podemos defiir l difereci de dos fucioes f g como l sum de f co l opuest de g: f g = f + (-g), cuyo domiio es Dom(f g) = Dom(f) Dom(g) = D. PRODUCTO DE UN NÚMERO REAL POR UNA FUNCIÓN El producto de u úmero rel por u fució f IF es otr fució f que verific: ( f)() = f() D. Se verific que Dom( f) = Dom(f) = D. Propieddes. Distriutividd respecto l sum de fucioes: (f + g) =. f + g.. Distriutividd respecto l sum de esclres: ( + ') f = f + ' f. 3. Asocitividd mit: ( ') f = (' f) 4. Elemeto eutro: f = f, siedo el elemeto eutro de IR. Co dichs propieddes podemos firmr que ( IF, ),+ es u espcio vectoril. IR PRODUCTO DE FUNCIONES Dds dos fucioes f y g IF, se defie el producto h = f g como l fució rel que verific: h() = (f g)() = f() g() D. Se verific que Dom(f g) = Dom(f) Dom(g). Propieddes. Ley de composició iter: f g IF f, g IF. Asocitiv: (f g) h = f (g h). f, g, h IF 3. Comuttiv: f g = g f. f, g IF 4. Elemeto eutro: Llmmos fució uidd l fució defiid como: : D IR / () = D. Como se verific que f = f = f f IF, dich fució es el elemeto eutro pr el producto de fucioes. 5. Distriutiv respecto l sum: f (g + h) = f g + f h f, g, h IF Co ests propieddes el cojuto (IF,+, ) tiee estructur de illo comuttivo co elemeto uidd. Defiimos l fució recíproc respecto l producto de fucioes como l fució: : D f IR / ( ) =. Se verific que Dom( ) = D { / f() = }. A prtir de est f f ( ) f 9
10 defiició, podemos cosiderr l divisió de dos fucioes f, g IF como el producto de f por l fució recíproc de g: f f f =, verificdo que Dom( ) = Dom(f) Dom( g g g g ). COMPOSICIÓN DE FUNCIONES Se f y g dos fucioes tles que Im(f) Dom(g), se llm fució compuest de f y g l fució go f : Dom(f) Im(g) / go f () = g(f()) Dom(f). Dich fució compuest se lee f compuest co g y se verific: Dom(go f) = Dom(f). Propieddes. L composició de fucioes o es comuttiv.. Es socitiv: ( f g) o h f o ( g o h) o = f, g, h IF 3. Llmmos fució idetidd l fució defiid como: i: D IR / i() = D. Como se verific que io f = fo i = f f IF, dich fució es el elemeto eutro pr l composició de fucioes. FUNCIÓN INVERSA Se f u fució iyectiv co f: Dom(f) Im(f), llmmos fució ivers de f, y lo deotmos por f -, l fució: f - :Im(f) Dom(f) / f - (y) = f() = y. Se verific que Dom(f - ) = Im(f) Propieddes. Si f o es iyectiv, o eiste su fució ivers.. Si f posee fució ivers, se verific f o f = f o f = i. Luego f - es el elemeto simétrico de f respecto de l composició de fucioes. 3. Ls gráfics de u fució y su ivers so simétrics respecto l isectriz del primer cudrte. Así si el pr (,y) perteece l gráfic de f etoces (y,) perteece l gráfic de f FUNCIONES ELEMENTALES. SITUACIONES REALES EN LAS QUE APARECEN. LA FUNCION AFÍN
11 Se dice que u fució es fí si es del tipo f() = +, co, IR, o ulos. Su represetció gráfic correspode u rect que cort l eje OX e el puto / y l eje OY e el puto. Se verific que si > l rect es creciete y si < es decreciete. Eiste umeross situcioes del mudo rel cuyo comportmieto correspode l modelo de l fució fí como por ejemplo e lgus fcturs como ls de teléfoo se cor u cuot iicil fij K y u ctidd costte A pr cd periodo de tiempo por lo que l fució correspodiete serí f() = A + K. LA FUNCIÓN LINEAL Si = teemos y =, que correspode u rect que ps por el orige y cuy pediete y vle. Al ser costte, est fució os descrie situcioes de proporciolidd direct. Se verific que f( ) = f() y f( + y) = f() + f(y). Este tipo de fució prece e umeross situcioes, por ejemplo el coste de u producto segú ls uiddes dquirids, l logitud de u circufereci segú el rdio, el espcio recorrido por u móvil co movimieto uiforme o l deformció de u muelle sometido u fuerz. LA FUNCIÓN CUADRÁTICA Se dice que u fució es cudrátic si es del tipo f() = + + c, co,, c IR, o ulo. Su represetció gráfic correspode co u práol. A prtir de l derivd de l fució podemos deducir que dich práol tiee su vértice e el puto, 4 e el puto (,c) y pr el corte co el eje OX estudimos el sigo del discrimite: si = 4c >, l práol cortrá dicho eje e los putos: + 4c = y 4c = + c. Cort l eje OY si =, l práol cortrá dicho eje e el puto: = si <, l práol o cort dicho eje. A prtir de l derivd segud podemos deducir que si >, l práol es cove y si < es cócv. Además dich fució es simétric respecto l rect =. Este tipo de fucioes prece por ejemplo e el espcio recorrido por u móvil co movimieto uiformemete celerdo o el áre de u círculo e fució del rdio.
12 LA FUNCIÓN DE PROPORCIONALIDAD INVERSA Se dice que u fució es de proporciolidd ivers si se puede escriir como f() =. Su gráfic correspode u hipérol equiláter, curv simétric respecto l isectriz del primer y tercer cudrte si es positivo o simétric respecto l isectriz del segudo y curto cudrte si es egtivo. Aprece e situcioes e ls que dos mgitudes so iversmete proporcioles, por ejemplo e el período y l frecueci de u feómeo periódico, el reprto de u cpitl fijo e fució del úmero de persos o l relció presió o volume y tempertur e l ley de los gses perfectos. FUNCIÓN EXPONENCIAL DE BASE, >. L fució epoecil de se es f ( ) = IR y verific que es cotiu y derivle e todo IR, estrictmete creciete pr > y estrictmete decreciete pr < <. Su gráfic pr > es de l form: L fució epoecil de myor iterés es quell e l que l se es el úmero e, pues est fució prece e prolems relciodos co el crecimieto de u polció. FUNCIÓN LOGARÍTMICA DE BASE, > L fució logrítmic de se es f ( ) = log IR y verific que es cotiu, derivle e todo IR, estrictmete creciete pr > y estrictmete decreciete pr < <. Su gráfic pr > es de l form:
13 L fució logrítmic de myor iterés es quell e l que l se es el úmero e. Se deomi logritmo eperio y se deot por L. Al ser l ivers de l epoecil prece e l resolució de ls ecucioes epoeciles. El ph de u solució se clcul e fució del logritmo e se. 3
14 CAPÍTULO FUNCIONES DADAS EN FORMA DE TABLAS INTERPOLACIÓN POLINÓMICA INTERPOLACIÓN Y EXTRAPOLACIÓN DE DATOS 4
15 .- INTRODUCCIÓN. U prolem clásico e ls Mtemátics, es el de clculr el vlor que tom u fució e u puto cuy epresió descoocemos. Se trt de ecotrr u fució lo más simple posile, de form que coicid co l fució ojeto del prolem e los dtos coocidos. Los vlores que otegmos prtir de est fució será proimcioes de los vlores reles. Se utilizrá los poliomios pr relizr dich costrucció lo que d lugr l iterpolció poliómic..- FUNCIONES EN FORMA DE TABLAS Ls fucioes que más comúmete viee dds e form de tls so ls fucioes trigoométrics, epoeciles y logritmos y ls fucioes de distriucioes de proilidd: Biomil, Poisso o Norml. E ells se epres medite tls los vlores que dichs fucioes tom pr uos determidos vlores más comues de l vrile idepediete. Estos suele estr ordedos de form creciete y equidisttes. 3.- PLANTEAMIENTO DEL PROBLEMA DE LA INTERPOLACIÓN POLINÓMICA. El prolem de l iterpolció plte el siguiete prolem: Se S = {,, L, }, i j, u cojuto llmdo soporte y f : D, co S D, hllr p P [ ] u poliomio de grdo tl que p( ) = f ( ) j =,...,. A p le llmremos poliomio de iterpolció de f socido S. j j Teorem E ls codicioes teriores podemos segurr que eiste u úico poliomio iterpoldor de grdo meor o igul que, de form que Demostrció Se u poliomio p() = p( ) = f( i i) pr i =,,, P []. Al impoer que p( ) = f( i i) pr i =,,, result u sistem de + ecucioes co + icógits,,...,, : 3
16 = y = y = y El determite de l mtriz del sistem result ser de Vdermode, por tto: M M L L O L M = ( ) y que > i i si i i Así pues el sistem es comptile determido y por tto eiste u úic solució segú el teorem de Rouché-Froeius. De este resultdo se deduce que eiste ifiitos poliomios de iterpolció de grdo +. L demostrció terior os d u método pr clculr el poliomio iterpoldor pero tiee el icoveiete de teer que clculr + determites por lo que este procedimieto o se utiliz pr 4. POLINOMIO INTERPOLADOR DE LAGRANGE. Teorem El siguiete teorem d u método costructivo pr hllr u poliomio de iterpolció. Se S = {,, L, }, i j, f : D, co S D, etoces eiste u úico poliomio de iterpolció de f socido S y demás p() = f ( ) L ( ) dode = ( j) L ( ) = so los poliomios -ésimos de Lgrge. ( ) j= j j Demostrció L ( ) P [ ] y por tto p P [ ]. Además L ( ) = y L ( ) =, j, luego j j = p( ) = L ( ) f ( ) j =,..., Es úico pues si eiste q P [ ] que iterpol f, cosidero el poliomio r() = p() q(). r P [ ] y r se ul e + putos por tto dee ser r =. j 4
17 4.- MÉTODOS DE INTERPOLACIÓN MÉTODO DE AITKEN Este método permite clculr el poliomio de iterpolció por recurreci y oteer el vlor de u puto si clculr previmete su epresió lític. Teorem: P Ddo u soporte S = {,, L, } y i, j, i j, i, ( )P i S { } () ( )P j j S { i } () () = { i j } - S, j i j S, etoces Demostrció. P, P so poliomios de grdo + por poseer + putos distitos. Al multiplicrlos S S { } { } i i por u fctor de se otiee u poliomio de grdo +. Se S, i, j, ( i)f( ) ( j)f( ) P ( S { i, } ) = = f ( ) j - j i Se i, (i j)f( i) P ( S { i, } i) = = f ( i ) y álogmete pr j. j - j i Algoritmo Etp Deotmos p j () el poliomio que ps por j, etoces p j () = f( j ), j =,...,. Etp Deotmos por p j () el poliomio que tiee {, j } como soporte, etoces p j () = ( )p j() ( j)p (), j =,..., i j. - Etp j Coocemos p,...,,, j =,...,, etoces p,...,, ( ) = j j ( )p,...,-,j() ( j)p,..., (), pr j = - j +,...,. Etp p,..., ( ) = ( )p () ( )p () -,...,-,,...,
18 METODO DE LAS DIFERENCIAS SUCESIVAS Se S = {,, L, }, i j, u cojuto llmdo soporte, deotmos por p P [ ] poliomio que iterpol f e,...,. Se pretede clculr de form recursiv p (). el Se tiee que p () = f( ) y cosidermos p ( ) p ( ) = f [,..., ] ( )... ( ) dode f [,..., ] es el coeficiete de e p. Como p( ) p( ) = = p ( ) p ( ) = f = [,..., ] ( )... ( ), etoces = + f = p ( ) p ( ) de l form de Newto. [,..., ] ( )... ( ) que se deomi poliomio de iterpolció A l epresió f [,..., ] se le deomi difereci sucesiv de orde socid los putos, f [,..., ] f [,..., ]...,. Se tiee que f [ i ] = f( i ), i =,..., y que f [,..., ] = Deotdo por p,..., P - [] l poliomio de iterpolció socido,...,, el coeficiete que compñ es f [,..., ]. Cosideremos q () = ( )p () ( )p (),...,,...,- - y teemos que p S { i, j} = ( )p () ( )p i S { } j { i }() j S, etoces S = {,..., - } y q () = ps { } - = p, (). El j i coeficiete de f [,..., ] f [,..., ] e p () es f [,..., ] y e q () es. METODO DE LAS DIFERENCIAS FINITAS Se S = { = + h, =,..., } u soporte regulr. Se defie el operdor difereci progresiv de l siguiete mer: f ( i ) = f ( i ), i =,..., ; f ( i ) = f ( i+ ) f ( i ), i =,..., ; f ( ) = f ( ) f ( ) = f ( ) + f ( ), i =,..., ; y e geerl i i+ i i+ i f ( ) = f ( ) f ( ), i =,...,. i i+ i Se tiee que f ( ) =! h f [,..., + ], =,..., y que: f ( i ) = f ( i ) = f[ i ] i i i 6
19 f [, + ] f ( i ) = f ( i+ ) f ( i ) = f[ i+ ] f[ i ] = h i i Supogmos f ( i ) =! h f [ i,..., i + ] y! h f [ i,..., i + ] =! h ( f [ +,..., + + ] f [ i,..., i + ])! h ( + ) h f [ i,..., i + + ]. i i f ( ) = f ( ) f ( ) =! h f [,..., ] + i i+ i = ( ) i+ i+ + -! h f [,..., ] = i+ + i i i+ + E cocreto pr i =, ( ) =! [,..., ], prtir del método de ls diferecis sucesivs f h f se lleg : p ( ) p( ) = + = f! h ( ) ( )... ( ). 5.- ERROR EN LA INTERPOLACIÓN. Siempre que se sustituye culquier fució por u poliomio de iterpolció se comete u error. Dicho error es ievitle, pero se puede cotr. Teorem: Supogmos u fució f C + (,) y p su poliomio de iterpolció de f e el cojuto de putos S = { p() = L } (, ). Etoces [ ],,, ( ) ( ) L ( ) + ) f ( δ ) ( + )! Demostrció. Si = pr lgú i =,,, etoces e() =. i Fijo, δ (, ) tl que e () = f (), pr todo i, cosideremos F(t) = ƒ(t) p(t) i A() (t ) (t ) L (t ), dode l fució A() es tl que F() =, es decir, f () P () A() =. ( ) ( ) L ( ) L fució F es, l meos, + veces derivle y se ul e,, L,, ( + sciss) por costrucció. Estmos e ls codicioes del teorem de Rolle. Además este teorem se puede plicr hst + veces. Al plicrlo dichs + veces, se otiee que δ (, ) de form que F + ) (δ ) =. Derivdo l fució F ( + veces) oteemos: F + ) (δ ) = f + ) (δ ) A() ( + )! 7
20 Así pues, l uir mos resultdos podemos despejr: A() = + ) f ( δ ) ( + )! Por tto teemos que f () P () = f () P () A() = = ( ) ( ) L ( ) + ) f ( δ ) ( + )! ( ) ( ) L ( ) + ) f ( δ ) ( + )! E pricipio δ es descoocido pero podemos oteer u cot del error: M f p ( + )! { } + ( ) ( ) m ( )... ( ), (, ) mer que el ldo derecho o depede de. + ) co M m { f ( ), (, ) } + = de 6.- EXTRAPOLACIÓN DE DATOS. E lguos prolems el ojetivo es clculr el vlor de u fució e u puto o perteeciete l soporte. Este proceso recie el omre de etrpolció. Tiee el icoveiete de que cuto más os lejemos del cojuto S más crecerá el error que cometemos y por tto es meos preciso que l iterpolció. Por tto el vlor utilizdo dee estr t cerc como se posile del soporte. 8
21 CAPÍTULO 3 Limites de fucioes. Cotiuidd y discotiuiddes. Teorem de Bolzo. Rms ifiits. 9
22 .- LÍMITE DE UNA FUNCIÓN Límite fiito e u puto Se I u itervlo de l rect rel, I y f u fució rel defiid e I. Se dice l IR es el límite de f cudo tiede l puto si se verific: ε > δ > / I, < < δ f ( ) l < ε y lo escriiremos como lim f ( ) = l. Oservcioes:. Como se cosider, el vlor f(), si eiste, o ifluye sore el vlor del límite.. Al tomr < < δ, estmos tomdo vlores myores o meores que. El hecho de cosiderr estos u ldo u otro del puto d lugr l cocepto de límites lterles. Limites lterles fiitos Se dice que l es el límite por l derech de l fució f e el puto si se verific: ε > δ > / (, + δ ) I f ( ) l < ε y se deotrá lim f ( ) = l Aálogmete, se dice que l es el límite por l derech de l fució f e el puto si se verific: ε > δ > / ( δ, ) I f ( ) l < ε y se deotrá lim f ( ) = l Propieddes. lim f ( ) = l lim f ( ) = lim f ( ) = l. Si el límite eiste, este es úico f está cotd e el cojuto ( - δ, + δ) I. + Límite ifiito e u puto Se I u itervlo de l rect rel, I y f u fució rel defiid e I. Se dice que f tiede ( + ó ) cudo tiede l puto si se verific: M > δ > / I, < < δ f ( ) > M y lo escriiremos como lim f ( ) =. Límites lterles ifiitos Se dice que el límite por l derech de l fució f es ( + ó ) e el puto si se verific: M > δ > / (, + δ ) I f ( ) > M y se deotrá lim f ( ) =. Se dice que el límite por l izquierd de l fució f es ( + ó ) e el puto si se verific: M > δ > / ( δ, ) I f ( ) > M y se deotrá lim f ( ) =. +
23 Límite fiito l ifiito Se I u cojuto o cotdo superiormete y f u fució rel defiid e I. Se dice que f tiede l IR cudo tiede + si se verific: ε > H > / I, > H f ( ) l < ε y se escrie lim f ( ) = l. + Aálogmete, se I u cojuto o cotdo iferiormete y f u fució rel defiid e I. Se dice que f tiede l IR cudo tiede - si se verific: ε > H > / I, < H f ( ) l < ε y se escrie lim f ( ) = l. Límites ifiitos l ifiito. Se I u cojuto o cotdo superiormete y f u fució rel defiid e I. Se dice que f tiee ( + ó ) cudo tiede + si se verific: M > H > / I, > H f ( ) < M y se escrie lim f ( ) + =. Se I u cojuto o cotdo iferiormete y f u fució rel defiid e I. Se dice que f tiede ( + ó ) cudo tiede - si se verific: M > H > / I, < H f ( ) > M y se escrie lim f ( ) =. Álger de límites Se f y g fucioes reles defiids e I y I, se puede relizr ls siguietes opercioes límites sore dichs fucioes:. Sum:. Si lim f ( ) = l y lim g( ) = l ' etoces lim f ( ) + g( ) = l + l '. Si lim f ( ) = + y lim g( ) = + etoces lim f ( ) + g( ) = + c. Si lim f ( ) = y lim g( ) = etoces lim f ( ) + g( ) = d. Si f() M I y lim g( ) = etoces lim f ( ) + g( ) = e. Si lim f ( ) = + y lim g( ) = etoces lim f ( ) + g( ) d lugr u idetermició.. Producto:. Si lim f ( ) = l y lim g( ) = l ' etoces lim f ( ) g( ) = l l '. Si f() > h > y lim g( ) = etoces lim f ( ) g( ) = c. Si f() M I y lim g( ) = etoces lim f ( ) g( ) =
24 d. Si lim f ( ) = y lim g( ) = etoces lim f ( ) g( ) idetermició 3. Cociete:. Si lim f ( ) = l, lim g( ) = l ' y g() I etoces f ( ) l lim = g ( ) l ' d lugr u. Si f() > h > y lim g( ) = etoces c. Si lim f ( ) =, g() > h > etoces f ( ) lim = g ( ) f ( ) lim = g( ) d. Si f() M I y lim g( ) = etoces f ( ) lim = g( ) e. Si lim f ( ) =, g() M I etoces f. Si lim f ( ) = y lim g( ) = etoces 4. Fució poteci:. Si lim f ( ) = l, lim g( ) = l ' etoces lim f ( ) g = l l f ( ) lim = g ( ) f ( ) lim d lugr u idetermició. g ( ) ( ) '. Si lim f ( ) =, lim g( ) = l ' etoces g ( ) lim f ( ) = si l > y lim f ( ) g ( ) = + si l < c. Si lim f ( ) = +, lim g( ) = + etoces lim f ( ) g ( ) = + d. Si lim f ( ) = +, lim g( ) = l ' etoces lim f ( ) g ( ) = + si l > y g ( ) lim f ( ) = si l <. e. Si lim f ( ) = +, lim g( ) = etoces g ( ) lim f ( ) = f. Si lim f ( ) l [,) =, etoces g ( ) lim f ( ) = si lim g( ) = + y lim f ( ) g ( ) = + si lim g( ) =. g. Si lim f ( ) = l >, etoces lim f ( ) g ( ) = + si lim g( ) = + y g ( ) lim f ( ) = si lim g( ) =. h. Si lim f ( ) = y lim g( ) =, lim f ( ) = + y lim g( ) = o ie lim f ( ) = y lim g( ) = + etoces lim ( ) f ( ) g d lugr u idetermició.
25 Se otedrá los mismos resultdos pr el cso e que I se o cotdo y tied. Ls idetermicioes se resuelve relizdo trsformcioes e ls fucioes que permit llegr l vlor de dicho límite, plicdo ifiitésimos equivletes o plicdo l regl de L Hôpitl..- CONTINUIDAD Y DISCONTINUIDAD Se I u itervlo de l rect rel, I y f u fució rel defiid e I. Se dice f es cotiu e si se verific: ε > δ > / I, < δ f ( ) f ( ) < ε y se escrie lim f ( ) = f ( ). Se dice que f es cotiu l derech de si lim f ( ) = f ( ) y se dice que es cotiu l izquierd de si lim f ( ) = f ( ). Por tto, u fució es cotiu si se verific que lim f ( ) = lim f ( ) = f ( ). + + Se J I, J, se dice que f es cotiu e J si f es cotiu e, J. Oservció Ls fucioes, >, IR;, IR; lg, IR +,, > ; Se y Cos, IR so cotius e los putos dode esté defiids. Propiedd Se f, g : I IR IR, I, f y g cotius e, etoces se verific:. f + g es cotiu e. f g es cotiu e 3. si g() etoces f/g está ie defiid e ( δ, δ ) + I y es cotiu e p De quí se deduce que ls fucioes eters: f ( ) = p p IN, IR, so fucioes cotius e IR, y ls fucioes rcioles: p Q( ) = q q p y ls fucioes trigoométrics tg, Ctg, Sec y Cosec so cotius ecepto dode se ul el deomidor. Composició de fucioes cotius Se f : I IR IR, g : J IR IR, f ( I ) J. Si f es cotiu e I y g es cotiu e f() J, etoces go f es cotiu e Demostrció Hy que pror que 3
26 ε > δ > / I, < δ g( f ( )) g( f ( )) < ε Al ser g cotiu e f(), se verific que ddoε > δ > / y J, y f ( ) < δ g( y) g( f ( )) < ε como f es cotiu e, ddoδ > δ > / I, < δ f ( ) f ( ) < δ y por tto g( f ( )) g( f ( )) < ε Discotiuiddes Se f : I IR IR, I, si f o es cotiu e, se dice que es discotiu. Se puede presetr los siguietes tipos de discotiuiddes:. Discotiuidd evitle, si lim f ( ) f ( ). Discotiuidd ifiit, si lim f ( ) = 3. Discotiuidd de slto fiito o de primer especie, si lim f ( ) lim f ( ) 4. Discotiuidd de slto ifiito, si lim f ( ) o lim f ( ) = Discotiuidd esecil o de segud especie, si o eiste lim f ( ) o lim f ( ). + Propieddes de ls fucioes cotius. Se f : [,] IR cotiu e [,], etoces f lcz sus vlores máimos y míimos e [,].. Se f cotiu e, co f() etoces eiste u etoro de e el que l fució o cmi de sigo: f() f(y) >,, y ( δ, δ ) Se f cotiu e etoces eiste u etoro de e el que l fució está cotd. 3.- TEOREMA DE BOLZANO. Se f : [,] IR cotiu e [,] y f() f() <, etoces eiste (,) tl que f( ) = Demostrció +, Por reducció l surdo, supogmos que f(), [,] y se [, ] + etoces f ( ). 4
27 Deotmos por [, ], [, ] [,] y = + el suitervlo, ó +, e el que se verific que f( ) f( ) < Supuesto defiido [, ] verificdo [, ] [, ]... [,] co = y f( ) f( ) <, hemos defiido u sistem de itervlos cerrdo y ecjdo. Por el Teorem de Ctor teemos que I [, ]. Se I [, ] IN [ ] IN δ > / ( δ, + δ ), f ( ) f ( ) > Pr ese vlor δ, IN / < δ y [, ] ( δ, δ ) el mismo sigo que f( ), pero f( ) f( ) <., f es cotiu e y f( ), etoces + [,], luego f( ) y f( ) tiee El teorem de Bolzo se utiliz pr l úsqued de ríces de ecucioes y el estudio del sigo de u fució. 4.- RAMAS INFINITAS. ASÍNTOTAS Se f() u fució cotiu e u itervlo o cotdo decimos que f() tiee u rm ifiit si eiste putos M = (, f()) cuy distci l orige se myor que culquier úmero prefijdo. Se dice que u fució co rm ifiit posee u sítot si eiste u rect cuy distci de l rect u puto de l rm ifiit se puede hcer t pequeñ como se quier. Se dice que u fució co rm ifiit posee u rm prólic si o posee sítots. Rms ifiits e el ifiito Al hcer lim f ( ), se os puede presetr los siguietes csos: +. Si lim f ( ) = l, etoces l rect y = l es sítot horizotl. +. Si lim f ( ) =, psmos hcer el + lim + f ( ) y podemos oteer los siguietes csos: 5
28 . lim + f ( ) =, l fució tiee u rm prólic e l direcció del eje OX.. lim + f ( ) =, l fució tiee u rm prólic e l direcció del eje OY. c. lim + f ( ) = m, lim f ( ) m =, l fució tiee u rm prólic e l + direcció y = m. d. lim + f ( ) = m, lim f ( ) m =, l rect y = m + es u sítot olicu pr + P( ) f(). Si f ( ) = y grdo(p()) = grdo (Q()) + etoces l sítot olicu Q( ) coicide co el cociete de P() : Q(). U fució o puede teer l vez sítot olicu y horizotl. Rms ifiits e u puto Si lim f ( ) = etoces l rect = es u sítot verticl. Si f ( ) es u fució rciol si ríces comues, ls sítots verticles se ecuetr e los vlores de que so ríces del deomidor. De l mism mer se puede oteer los resultdos pr -. 6
29 CAPÍTULO 4 Derivd de u fució e u puto Fució derivd Derivds sucesivs Apliccioes 7
30 . DERIVADA DE UNA FUNCIÓN EN UN PUNTO límite Se f : S, y S S ', S cojuto de putos de cumulció de S. Si eiste el f ( ) f ( ) lim se dice que f es derivle o diferecile e y el vlor del límite se deot por f ( ) que llmremos derivd de f e. Oservcioes f ( + h) f ( ). Se puede utilizr l otció: f ( ) = lim, dode h =. h h. Se dice que f es derivle e por l derech si derivle e por l izquierd si f ( ) f ( ) = f ( ) f ( ) = lim f '( ) + lim f '( ) + y f es. Si f es derivle por l izquierd y derech de etoces f es derivle e si f '( ) + = f '( ). Si f '( ) + f '( ) se dice que f tiee e u puto guloso. Teorem Se f : S, y S S '. Si f es derivle e etoces f es cotiu e. El recíproco o es cierto, por ejemplo f() = es cotiu y o derivle e. INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA Se f : S, y S S ' y cosidermos el hz de rects r y = m( ) + f ( ). Deomimos tgete l curv y = f() e el puto (, f( )) l rect del hz que verifique f ( ) y lim =. m L tgete es l rect del hz que mejor proim l curv e u etoro de. Pr que eist l tgete se dee cumplir: f ( ) ( m( ) + f ( )) = lim f ( ) f ( ) lim = m. Por 8
31 tto eiste rect tgete u fució f() e u puto si y sólo si f es derivle e y f ( ) = m. L ecució de l rect tgete es: y = f '( ) ( ) + f ( ).. FUNCIÓN DERIVADA. DERIVADAS SUCESIVAS. Se f : S, si f es derivle e, S se dice que f es derivle e S y l fució que cd puto le soci su derivd se deomi fució derivd primer de f y se deot f. Si l fució f es derivle e S S ', l derivd de f e se le deomi derivd segud de f e y se deot f ( ). E geerl si f es veces derivle e S, l fució que cd puto le soci el vlor de l fució derivd veces se deomi fució derivd - ésim y se deot f (). ÁLGEBRA DE DERIVADAS Se f, g : S, y S S '. Si f y g so derivles e etoces:. f ± g es derivle e y (f ± g) ( ) = f ( ) ± g ( ).. f g es derivle e y (f g) ( ) = f ( ) g( ) + f( ) g ( ). 3. Si g( ), f g es derivle e y / f f '( ) g( ) f ( ) g '( ) ( ) = g g ( ) Derivció de l fució compuest (Regl de l cde) Se f : S, g : T, f(s) T. Si f es derivle e y g es derivle e f( ) go f '( ) = g '( f ( )) f '( ). etoces go f es derivle e y ( ) Demostrció Se h : T / h( y) h es cotiu e f( ) pues g( y) g( f ( )) y f ( ) ; y f ( ) = g f y = f '( ( )) ; ( ) lim h( y) = lim y f ( ) y f ( ) y f ( ) g( y) g( f ( )) = g '( f ( )) = h(f( )). Se h( f ( )) g( f ( )) g( f ( )) f ( ) f ( ) ; f ( ) f ( ) = g f f = f '( ( )) ; ( ) ( ) 9
32 f es cotiu e por ser derivle, por tto ho f es cotiu e y lim h( f ( )) = h( f ( )) = g '( f ( )) f ( ) f ( ) se tiee ( f ( ) f ( ) ) h(f()) = g(f()) g(f( )), por tto ( ) h(f()) = g( f ( )) g( f ( )). Tomdo límites pr qued: '( ) f '( ( )) g f = ( ) go f '( ). Derivd de l fució ivers Se f :( r, r) +, si f es cotiu y estrictmete moóto e ( r, r) + y es derivle e, co f ( ) etoces f - es derivle e f( ) y se verific ( f ) '( f ( )) Ejemplo =. f '( ) π π Se :,, [ ] es cotiu y estrictmete creciete por lo que π π π π f :[,], cotiu y derivle e todo puto de, co f ( y) = rcse( y). Por el teorem de l fució ivers: ( f ) '( y) = = = Cos Se y Luego (rcse) = (,) DERIVADA DE LAS FUNCIONES ELEMENTALES f () = f () = f () = f () = f() = e f () = e f() = f () = l 3 f() = l f () = f() = log f () = l f() = se f() = cos f() = cos f() = - se
33 f() = tg f () = sec f() = cotg f () = - cosec f() = rcse f () = f() = rccos f () = f() = rctg f () = + 3. APLICACIONES FUNCIONES CON DERIVADA NO NULA Se f : S, S, se dice que f tiee e u máimo reltivo si δ tl que f() es u máimo de f e ( δ δ ), + S. Aálogmete se dice que tiee u míimo reltivo si f() es u míimo de f e dicho itervlo. Teorem Se f : S, it(s), si f es derivle e y f ( ), etoces δ > tl que:. Si f ( ) > etoces. Si f ( ) < etoces f ( ) < f ( ) si < < + δ f ( ) < f ( ) si δ < < f ( ) > f ( ) si < < + δ f ( ) > f ( ) si δ < < Cosecueci Se f : S, it(s), si f tiee e u etremo reltivo y f es derivle e etoces f ( ) =. Este resultdo d u codició ecesri pr l eisteci de etremos reltivos. E l práctic si f: [,] IR es cotiu, f lcz el máimo y míimo soluto e lguo de los putos:. ó. (,) / o eiste f ( ) 3. (,) / f ( ) = TEOREMA DE ROLLE Y DEL VALOR MEDIO 3
34 Teorem de Rolle Se f: [,] IR cotiu y derivle e (,), etoces:. si f() = f() (, ) / f '( ) =. si f () (, ) f es estrictmete creciete si f() < f() y estrictmete decreciete si f() > f(). Demostrció.- Por reducció l surdo. Supogmos que (, ) / f '( ), etoces el máimo y míimo de f o se lcz e (,). Al ser f cotiu e u compcto f dee lczr su máimo y míimo soluto e [,], etoces mf = mif = f() = f() f es costte y f =.- Supogmos que f() < f(), por el mismo rzomieto terior f() = mi f [, ] y f() = m f. Además f() < f() < f() (, ) y que si f() = f(), por el prtdo terior eistirí (,) / f ( ) = y lo mismo si f() = f(). Se, [,], <. Si = f( ) < f( ) y si < < plicdo el mismo rzomieto e [, ] llegmos que f() < f( ) < f( ). Por tto f es estrictmete creciete. De form álog se puede pror pr f() > f(). [, ] Teorem del vlor medio Se f, g: [,] IR cotius y derivles e (,), etoces (, ) / ( f ( ) f ( )) g '( ) = ( g( ) g( )) f '( ) Teorem del vlor medio de Lgrge Se f: [,] IR cotiu y derivle e (,), etoces (, ) / f ( ) f ( ) = ( ) f '( ) Se otiee prtir del teorem del vlor medio tomdo g() =. Cosecueci Se f: [,] IR cotiu y derivle e (,), se tiee:. f () = (, ) f es costte e [,]. f () > (, ) f es estrictmete creciete e [,] c. f () < (, ) f es estrictmete decreciete e [,] 3
35 REGLA DE L HOPITAL Se f, g: (,) IR derivles e (,), g () e (,) y lim f ( ) = lim g( ) = o. f '( ) Si lim = l o etoces + g '( ) f ( ) lim = l. + g ( ) Se puede oteer de form álog el resultdo cudo Se f, g: (M, + ) IR derivles e (M, + ), g () e (M, + ) y f '( ) lim f ( ) = lim g( ) = o. Si lim = l o etoces g '( ) f ( ) lim = l. + g ( ) Se puede oteer de form álog el resultdo pr el itervlo (-, M). 33
36 CAPÍTULO 5 D E S A R R O L L O D E U N A F U N C I O N E N S E R I E D E P O T E N C I A S T E O R E M A D E T A Y L O R A P L I C A C I O N E S A L E S T U D I O L O C A L D E F U N C I O N E S. DESARROLLO DE UNA FUNCIÓN EN SERIE DE POTENCIAS 34
37 Se,, IR, IN y se f : IR IR / f () = y f () = ( ). Se defie l serie de potecis e como Resultdos ( ). Criterio de l ríz. Se < l serie diverge.,, se lim = L. Si L <, l serie coverge y si L. Criterio de Weierstrss. Se f ( ) serie de fucioes co f( ) U, <, etoces f ( ) es uiformemete covergete e U y solutmete covergete e todo puto de U. Teorem Se ( ) y L = lim, se tiee:. si L = + etoces l serie coverge e =. si < L < + etoces coverge solutmete e, +, uiformemete e todo L L compcto coteido e, + L L y diverge e, +, + L L 3. si L = etoces l serie coverge solutmete e IR y uiformemete e todo compcto coteido e IR. Demostrció Fijo IR, lim = L Si L = +,, lim ( ) ( ) = +, y si =, ( ) =. Si < L < +, por el criterio de l ríz l serie coverge solutmete si y sólo si L <, + L L Si L =, L < IR y l serie es solutmete covergete e IR. 35
38 Se T, + ó IR, l plicció L L T es cotiu e T por lo que eiste T máimo soluto: T y < + pues T. Por el Criterio de Weierstrss ( ) coverge uiformemete. Nots L. A [, ] + se le deomi rdio de covergeci y l itervlo que defie itervlo de covergeci.. E los etremos del itervlo de covergeci l serie puede teer culquier crácter. 3. Utilizdo el Criterio de Stolz teemos que si lim etoces lim Se ( ), ρ el rdio de covergeci, I el itervlo de covergeci. L fució f: I IR / f() = ( ) se deomi fució defiid por l serie de potecis. Se verific que f es cotiu y derivle e I co / f () = ( ). Además f ( ) I y = f ( )! FUNCIONES ELEMENTALES DEFINIDAS COMO SERIE DE POTENCIAS e + = =! + log( + ) = ( ) = + = = = + + Se = ( ) ( + )! + Cos = ( ) = ( )! 36
39 . FÓRMULA DE TAYLOR Se f: (, c) IR y f veces derivle e (, c), IN. El poliomio f '( ) f ( ) + ( ) ! grdo. f ( ) ( ) se deomi poliomio de Tylor de f e el puto de! T () = f() { f '( ) f ( ) f ( ) + ( ) ( ) } se deomi térmio complemetrio o!! f '( ) resto de orde de f e. L fórmul: f() = f ( ) + ( ) ! deomi fórmul de Tylor de orde de f e el puto. f ( ) ( ) + T () se! Teorem de Tylor Se f: (, c) IR, (, c), f es veces derivle e (, c) y veces derivle e, etoces T ( ) lim = ( ) Al ser f cotiu e teemos que lim T ( ) =. T es veces derivle e (,c) por ( ) serlo f sí que podemos plicr l regl de L Hopitl veces, queddo el límite: T lim ( ) ( )... = lim f f f ( ) ( ) ( ) ( ) = ( )! ( ) f ( ) f ( ) lim f ( )! =, eiste pues f es veces derivle e el puto. Se deot T ( ) Θ(( ) ) que se lee ifiitésimo de orde superior ( ) cudo Co el poliomio de Tylor se pretede proimr loclmete fucioes medite poliomios co u grdo ddo. Cudo =, l fórmul de Tylor recie el omre de Fórmul de McLuri: f() = f '() f () ! f () + Θ ( ) y! Θ(( ) ) lim = FORMULA DE McLAURIN DE ALGUNAS FUNCIONES ELEMENTALES. = Θ ( ). e = Θ ( )!! 37
40 3. 3 ( ) log( + ) = Θ ( ) 3 α α α α α + = ( ) + Θ ( ) 5. Se = ( )... + ( + )! Θ ( + ) 6. Cos = + 4 ( ) ( )! Θ ( + ) EXPRESIONES DEL TÉRMINO COMPLEMENTARIO Teorem Se f: (, c) IR,, (, c),, f + veces derivle e (, c), etoces, I(, ) / T () = f ( + )! + ( ) ( ) +, deomid Epresió de Lgrge y T () = f + ( ) ( ) ( )! Demostrció, deomid Epresió de Cuchy. Se F: I[, ] derivle e I(, ), F(t) = f '( t) f ( t) + ( t) ! f ( t) ( t )! F (t) = + f ( t) ( ) t! Se G: I[, ] derivle e I(, ), G(t) = y G, teemos que t I(, ) F() = P (), luego qued: otiee l epresió de Lgrge. ( t) / F '( t )[ G( ) G( ) ] = G '( t )[ F( ) F( ) ] f ( t ) ( ) ( )! +. Aplicdo el teorem del vlor medio F. G() =, F() = f(), + + t = ( + )( t ) (-) T (). Despejdo se Pr oteer l epresió de Cuchy se plic el mismo procedimieto tomdo G() = t. 3. APLICACIÓN AL ESTUDIO DE EXTREMOS RELATIVOS Se f: (, c) IR, si f es derivle e (, c) y f () = se dice que es u puto crítico de f. Si es u puto crítico y o es i u máimo i míimo reltivo se dice que es u puto de ifleió. 38
41 Se f: (, c) IR y f veces derivle e (, c), >, y f () = = f ''( ) =... = f ( ) y f ( ) etoces:. Si es pr y:. f ( ) > etoces f tiee e u míimo reltivo. f ( ) < etoces f tiee e u máimo reltivo. Si es impr, f tiee e u puto de ifleió Demostrció f() = f ( ) + f ( ) ( ) + T ()! f ( ) f ( ) f ( ) T ( ) = + ( )! ( ) T ( ) ( ) o tiee sigo cudo porque tiee, sí que pr ( δ, δ ) +,, f ( ) f ( ) f ( ) δ > / sg( ) = sg( ) ( )! Si es pr, f () > y etoces f() > f(), ( δ, δ ) +, Si es pr, f () < y etoces f() < f(), ( δ, δ ) +, Si es impr, pr < : ( ) < y pr > : ( ) >. Luego f() f() dee cmir de sigo e ( δ, δ ) { } + pr que coicid co f ( ) sg( ).! CONCAVIDAD Y CONVEXIDAD Se f: (, c) IR, f es derivle e (, c), l rect tgete y = f() e tiee por ecució: y = f () ( ) + f(). Si δ que f es cove e. Si δ cócv e. > / ( δ, δ ) > / ( δ, δ ) + f() f () ( ) + f(), se dice + f() f () ( ) + f(), se dice que f es Cócv Teorem Cove 39
42 Se f: (, c) IR y f veces derivle e (, c), >, y f () = = f '''( ) =... = f ( ) y f ( ) etoces:. Si es pr y:. f ( ) > etoces f es cove. f ( ) < etoces f es cócv. Si es impr, f o es i cócv i cove Demostrció f() = f ( ) + f ()( ) + f ( ) ( ) + T ()! f ( ) ( f ( ) f '( )( )) ( ) f ( ) T ( ) = +! ( ) Se sigue los mismos psos que e l demostrció terior. Pr el cso e que se impr se otiee que l rect tgete qued mos ldos de l fució e el itervlo ( δ, δ ) +. 4
43 C A P Í T U L O 6 EL PROBLEMA DEL CÁLCULO DEL ÁREA I N T E G R A L D E F I N I D A 4
44 . EL PROBLEMA DEL CÁLCULO DEL ÁREA Medir el áre de u figur es dr u vlor de su tmño o etesió. Pr hllr el áre de regioes poligoles descompoemos dich regió e triágulos disjutos tomdo como vlor del áre l sum de ls áres de dichos triágulos. Pr otro tipo de figurs utilizremos u reuió de rectágulos disjutos de ldos prlelos. El cocepto de áre dee verificr los cutro siguietes postuldos:. El áre de u figur es u úmero myor o igul que cero.. Dos figurs cogruetes tiee igul áre. 3. El áre de dos figurs disjuts es l sum de ls áres de cd figur. 4. El áre, tl como se defi, dee coicidir co ls fórmuls del áre de ls figurs elemetles. Pr l primer defiició de áre cosiderremos u úmero fiito de rectágulos disjutos de ldos prlelos cuy reuió cotiee y está coteidos e u figur F. Si ddo ε >, ls áres de dichos cojutos difiere meos de ε, etoces se dirá que F tiee áre e el setido de Riem. No tods ls figurs pls cumple est defiició. U segud defiició de áre geerliz ést tomdo u serie ifiit de rectágulos disjutos pr lo que se deomi áre e el setido de Leesgue. E este cso se resuelve prolems e los que prece opercioes co límites o espcios más strctos. Ams defiicioes verific los cutro postuldos teriores. Si u figur tiee áre e el setido de Riem, tmié l tiee e el setido de Leesgue. E l myorí de los csos st co utilizr l primer pr los cojutos que trtremos.. INTEGRAL DEFINIDA. INTEGRAL DE RIEMANN Se [,] IR, u prtició de [,] es u cojuto P ={,,, } tl que = < < < =. Se f : [,] IR cotd y se P ={,,, } u prtició de [,]. 4 Se m i = if{f() / i- i } y M i = sup{f() / i- i }. Se defie l sum iferior de f pr P como S ( f, P ) = mi ( i i ) y l sum superior de f pr P como S ( f, P ) = i= M i ( i i ). i=
45 L codició de que f esté cotd e el itervlo [, ] es fudmetl pr que los m i y M i quede defiidos. Además cosidermos los ífimos y supremos y que f puede o ser cotiu. Ls sums superiores e iferiores verific ls siguietes propieddes:. S ( f, P ) S ( f, P ). Si cosidermos u prtició P tl que P P, oteemos us sums que verific: S ( f, P ) S ( f, P ) y S ( f, P ) S ( f, P ). 3. Ls sums iferiores está cotds superiormete por culquier sum superior, y por tto eiste Sup S ( f, P ). Aálogmete tmié eiste If S ( f, P ). Se defie l Itegrl Superior de Drou como f ( ) d = if{ S (f,p) / P P [,] } Se defie l Itegrl Iferior de Drou como f ( ) d = sup{ S (f,p) / P P [,] } Se verific por l propieddes del ífimo y supremo que f ) d ( f ( ) d. U fució f: [ ] R, cotd, se dice que f es itegrle de Riem e [,] si f ) d ( = f ( ) d. A este úmero se le llm itegrl de Riem de f sore [, ] y se deot por f ( ) d. Además, si f() e [,] pr A = {(,y);, y f()} se defie el áre de A como f ( ) d. Si f() e [,] pr B = {(,y);, f() y } se defie el áre de B como - f ( ) d. Teorem Se f: [ ] R ε P P[ ], fució cotd, co, R. Etoces f es itegrle Riem >,, / S ( f, P) S( f, P) < ε. 43
46 Demostrció: Se f itegrle Riem y ε >. f ( ) d =if{ S (f,p)/p P[,]} f ( ) d es l myor de ls cots iferiores de { S (f,p) / P P [,] } f ( ) d +ε / o es cot iferior del cojuto P P [,] / f ( ) d S (f,p) < f ( ) d +ε / De l mism form, f ( ) d =sup{ S (f,p) / P P [,] } f ( ) d es l meor de ls cots superiores del cojuto{ S (f,p) / P P [,] } f ( ) d -ε / o es cot superior P P [,] / f ( ) d -ε / < S (f,p) f ( ) d. Etoces f ( ) d -ε / < S (f,p) y S (f,p) < f ( ) d +ε /. Restdo, S (f,p) - S (f,p) f ( ) d +ε /- ( f ( ) d -ε / ) = ε 44
47 Se P = P P. Como P P S (f,p) S (f,p) < f ( ) d +ε / Como P P f ( ) d -ε / < S (f,p) S (f,p) Etoces S ( f, P) S( f, P) < ε. Se ε > culquier, P P [,] / S ( f, P) S( f, P) < ε S (f,p) f ( ) d f ( ) d S (f,p) S (f,p) - S (f,p) f ) d ( - f ( ) d ε, ε > f ( ) d = f ( ) d Luego f itegrle Riem. Teorems. Si f : [,] IR es cotiu e [,] etoces f es itegrle Riem e [,].. Si f : [,] IR es cotd y cotiu e [,] ecepto e u cojuto fiito de putos etoces f es itegrle Riem e [,]. 3. Si f : [,] IR es moóto e [,] etoces f es itegrle Riem e [,]. Propieddes 45
48 . f, g itegrles Riem e [, ] f + g es itegrle Riem e [,] y ( f + g) = f + g. f itegrle Riem e [, ] λf es itegrle Riem e [,] y λ f = λ f 3. f, g itegrles Riem e [, ] f.g itegrle Riem e [, ] 4. f itegrle Riem e [, ] y c (,) f itegrle Riem e [, c] y [c,] y f = c f + c f 5. f itegrle Riem e [, ] y e [, c] f itegrle Riem e [, c] y c f = f + c f 6. f, g itegrles Riem e [, ] / f g f g 7. f itegrle Riem e [, ] etoces f itegrle Riem e [, ] y f f 8. f ( ) d = - f ( ) d Teorem Fudmetl del Cálculo Itegrl. Se f : [ ] R, itegrle Riem y F : [,] IR defiid como F() = f. Etoces F es cotiu e [, ]. Además si f es cotiu e [,] etoces F es derivle e y F () = f(). Demostrció: 46
49 F está ie defiid e [.] pues [, ] serlo e [,]. Se [ ), f es itegrle Riem e [,] por, vemos que F es cotiu l derech de. [ ],, F( ) F( ) = f f = f + f f = f f M ( ) siedo M = sup{ f(), [,]} Luego pr + se otiee lim F( ) F( ) =. + Aálogmete, si (,], [, ] se tiee F( ) F( ) = f f = f ( f + f ) = f f M ( ) siedo M = sup{ f(), [,]} Luego pr se otiee lim F( ) F( ) =. Se f cotiu e [,] y [ ),, vemos que lim + F( ) F( ) = f() Ddo ε >, por ser f cotiu e δ > < + δ tl que f ( ) f ( ) < ε F( ) F( ) ( ) ( ) = f = f f f f ( )( ) = f f ( ) f f ( ) < ε (-) = ε Se (,], vemos que F( ) F( ) lim = f() Ddo ε >, por ser f cotiu e δ > δ < tl que f ( ) f ( ) < ε 47
50 F( ) F( ) = f f = f ( f + f ) = f = f F( ) F( ) ( ) ( ) = f = f f f f ( )( ) = f f ( ) f f ( ) < ε (-) = ε Cosecuecis. Si f es cotiu e [,], etoces eiste u primitiv de f e [,]: F : [,] IR, F() = f co F derivle e [,] y F = f. Regl de Brrow. Se f cotiu e [,] y G u primitiv de f e [,], etoces f = G( ) G( ) 3. Se f : [ ] R f = G( ) G( )., itegrle Riem y G u primitiv de f e [,], etoces 48
51 CAPÍTULO 7 PRIMITIVA DE UNA FUNCIÓN CÁLCULO DE ALGUNAS PRIMITIVAS APLICACIONES DE LA INTEGRAL AL CÁLCULO DE MAGNITUDES GEOMÉTRICAS o Primitiv de u fució o Itegrles imedits o Método de sustitució o Itegrció por prtes o Fórmuls recurretes o Itegrció de fucioes rcioles o Método de Hermite o Itegrció de fucioes irrcioles o Itegrles iomis o Itegrció de fucioes trigoométrics o Apliccioes 49
52 .- PRIMITIVA DE UNA FUNCIÓN 5 Dd u fució f(), si eiste u fució F() tl que F () = f() se dice que F() es u primitiv de f() y se escrie F() = f ( ) d. Si l fució f() dmite u primitiv etoces tod fució de l form F() + C, co C costte es tmié u primitiv de f. Propieddes. ( f d) ( ) ' = f ( ) costte. f ( ) d = f ( ) d f ( ) f ( ) d f ( ) d f ( ) d 3. ± = ± Itegrles imedits d = + C - + e d = e + C d = + C l d = l + C 5. Se( ) d = Cos + C 6. Cos( ) d = Se + C 7. d = tg + C Cos 8. Cosec d = Cotg + C 9. tg( ) d = l Cos + C. Cotg( ) d = l Se + C.. d = rcse + C d = rccos + C 3. d = rctg + C +
53 4. Sh( ) d = Ch + C 5. Ch( ) d = Sh + C E geerl, si f ( ) d es u itegrl imedit, etoces f ( + ) d tmié lo es y f ( + ) d = F( + ) + C, dode F es u primitiv de f..- METODO DE SUSTITUCIÓN Este método cosiste e ecotrr u fució g(t) que l sustituirl jo el sigo itegrl, covierte l itegrl e otr más secill co l uev vrile t. Dich fució dee cumplir que se derivle y co derivd o ul y que dmit fució ivers.. Se = g(t), etoces f ( ) d = f ( g( t)) g '( t) dt 3.- INTEGRACIÓN POR PARTES 5 Se u y v dos fucioes de. Aplicdo el diferecil u v, teemos: d(u v) = u dv + v du. Despejdo u dv e itegrdo llegmos : udv = d( uv) vdu = u v - vdu que es l llmd fórmul de itegrció por prtes. Se l itegrl f ( ) g( ) d y tommos u = f() co du = f ()d y dv = g()d, dode G es u primitiv de g, plicdo l itegrció por prte oteemos: udv = f ( ) G ( ) G ( ) f '( ) d. Hemos descompuesto l itegrl como producto de dos fucioes, escogiedo ests de mer que l uev itegrl dee ser más secill. Este método se utiliz geerlmete cudo e l itegrl prece fucioes trigoométrics, epoeciles, logritmos de itegrció imedit y poliomios. Fórmuls recurretes Se utiliz fórmuls de recurreci e itegrles que se resuelve por el método de itegrció por prtes y que cotiee u fució co epoete turl. Por ejemplo l itegrl: I = ( + ) d
54 I = + d = ( + ) ( + ) d d = I + ( ) Hcemos u =, du = d y dv = ( + ) ( ) + I = I ( ) + ( ) ( + ) ( ) ( + ) ( ) ( ) + Luego I = ( + ) d d, v = d = I I ( ) ( ) ( ) I INTEGRACIÓN DE FUNCIONES RACIONALES P( ) Es l itegrció de l form d dode P() y Q() so poliomios. Se dee Q( ) compror que l frcció o se reduce u itegrl de ls y estudids: A. d lugr u logritmo. A. m -, d lugr u fució potecil ( ) m A + B 3. + p + q, dode p 4q <, d lugr u logritmo y u rcotgete. A + B 4. ( + p + q), dode Z + y p 4q <, se descompoe e dos itegrles, l primer se ps u fució potecil medite el cmio t = + p + q y l segud se plic l fórmul de recurreci vist e el ejemplo terior. 5
55 Itegrció de fucioes rcioles P( ) Pr itegrr u fució rciol, coviee hcer ls trsformcioes lgerics Q( ) siguietes:. Si el gr(p()) gr(q()), se dee hcer l divisió de los poliomios, trsformdo l P( ) R( ) frcció de l form = M ( ) +, de mer que gr(r()) < gr(q()) Q( ) Q( ). Descompoer el deomidor e fctores lieles y cudráticos: Q() = ( ) m... ( p q) , dode p 4q <. 3. Descompoer u frcció rciol e elemetos simples: R( ) Q( ) = A ( ) m A ( ) m + Am B + C ( + p + q) B + C ( + p + q) B + C + p + q 4. Se clcul los coeficietes idetermidos A, A,..., A m,..., B, C,..., B, C,..., reduciedo comú deomidor l últim iguldd, iguldo etre sí los coeficietes de potecis igules de e mos miemros y resolviedo el sistem de ecucioes lieles. Los coeficietes tmié se puede oteer ddo l vrile vlores uméricos ritrrios e l idetidd. L itegrció se reduce itegrr u poliomio y frccioes elemetles rcioles. E l descomposició de Q() se puede dr los siguietes csos:. Ríces reles simples. L itegrl v dr logritmos.. Ríces reles múltiples. L itegrl v dr logritmos y fucioes poteciles. c. Ríces complejs simples. V dr logritmos y rcotgetes. d. Ríces reles múltiples. V dr fucioes poteciles, rcotgetes y logritmos. E este cso se suele resolver l itegrl por el Método de Hermite. Método de Hermite Prtimos del cociete de poliomios P( ), dode Q() se puede descompoer e culquier Q( ) P( ) de los 4 csos vistos teriormete. Etoces escriimos l iguldd: Q( ) = d S( ) + D( ) d T ( ) dode T() es u poliomio co ls misms ríces que Q() pero co u uidd meos e el orde de multiplicidd, S() es u poliomio co gr(s()) < gr(t()) y D() es l descomposició de l 53
56 P( ) S( ) frcció cosiderdo ls ríces de Q() como simples. Se deriv l frcció Q( ) T( ), se epres el ldo derecho co deomidor Q(), se igul los umerdores y se clcul los S( ) coeficietes idetermidos. L itegrl qued como: I = T( ) + D( ) d, dode ést últim correspode uo de los tres primeros csos teriores. 5.- INTEGRACIÓN DE FUNCIONES IRRACIONALES. Itegrles del tipo ( ) m m R, +,( + ),... d, dode R es u fució rciol y m,, m,,... so úmeros eteros. L sustitució + = t s, dode s = m.c.m. (,,...) trsform l fució dd e u fució rciol.. Itegrles elis. Se deomi itegrl eli u del tipo Se resuelve medite sustitució, tediedo los tres siguietes csos: R, + + c d.. Si >, etoces tommos. Si c >, etoces tommos c. Si <, etoces tommos + + c = + t + + c = c + t + + c = ( α) t, dode α es u solució de l ecució + + c. Si =, utilizremos l sustitució usdo fucioes trigoométrics. 3. Itegrles del tipo d ( α) p + + c. El cmio t = ( α) p trsform l itegrl e u del tipo terior. 4. Itegrles del tipo P ( ) + + c itegrles se clcul teiedo e cuet l idetidd: P ( ) + + c d = Q - () + + c + λ d, dode P () es u poliomio de grdo. Ests d dode Q - () es u poliomio + + c de grdo - de coeficietes idetermidos y λ u úmero rel. Derivdo dich idetidd y reduciedo comú deomidor el resultdo, se tiee l iguldd de dos poliomios de l que se determirá los coeficietes y λ. 54
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
EL TEOREMA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE. Alberto E. J. Manacorda*
 EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Sucesiones de Números Reales
 Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
1. CONJUNTOS DE NÚMEROS
 Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Profesora: María José Sánchez Quevedo FUNCIÓN DERIVADA
 FUNCIÓN DERIVADA Cosideremos, de etrd, u fució f cotiu, Ituitivmete diremos que l fució f es derivble si es de vrició suve, esto es, que o preset cmbios bruscos como picos o cmbios vertigiosos pediete
FUNCIÓN DERIVADA Cosideremos, de etrd, u fució f cotiu, Ituitivmete diremos que l fució f es derivble si es de vrició suve, esto es, que o preset cmbios bruscos como picos o cmbios vertigiosos pediete
A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS PROPIEDADES.
 CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
1.-INTEGRAL DEFINIDA.
 INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
Unidad 2: SUCESIONES Y SERIES NUMÉRICAS.
 Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
UNIDAD 2: POLINOMIOS Y FRACCIONES ALGEBRAICAS
 I.E.S. Rmó Girldo UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. POLINOMIOS Poliomios e u idetermid L epresió lgeric... 0 recie el omre de poliomio e l idetermid. Dode: es u úmero turl.,..., 0 so úmeros
I.E.S. Rmó Girldo UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. POLINOMIOS Poliomios e u idetermid L epresió lgeric... 0 recie el omre de poliomio e l idetermid. Dode: es u úmero turl.,..., 0 so úmeros
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación RESUMEN TEMA SUCESIONES
 E.T.S.I. Idustriles y Telecomuicció Curso 22-23 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I DEFINICIONES BÁSICAS Existe muchos feómeos que o se comport de mer cotiu, sio que ecesit u determido
E.T.S.I. Idustriles y Telecomuicció Curso 22-23 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I DEFINICIONES BÁSICAS Existe muchos feómeos que o se comport de mer cotiu, sio que ecesit u determido
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
1.4. Sucesión de funciones continuas ( )
 1.4. Sucesió de fucioes cotius (6.1.017) Propiedd: Se {f } u sucesió de fucioes f, defiids e I. Si {f } coverge uiformemete f e I y ls f so cotius e I, etoces f es cotiu e I. Demostrció: Hemos de probr
1.4. Sucesió de fucioes cotius (6.1.017) Propiedd: Se {f } u sucesió de fucioes f, defiids e I. Si {f } coverge uiformemete f e I y ls f so cotius e I, etoces f es cotiu e I. Demostrció: Hemos de probr
La Integral Definida
 Cpítulo 5 L Itegrl Defiid 5.. Prtició U cojuto fiito de putos P = {x, x, x,, x } es u prtició de [, b] si, y solmete si, = x x x x = b. 5.. Sum Superior y Sum Iferior Se y = f(x), u fució cotiu e [, b].
Cpítulo 5 L Itegrl Defiid 5.. Prtició U cojuto fiito de putos P = {x, x, x,, x } es u prtició de [, b] si, y solmete si, = x x x x = b. 5.. Sum Superior y Sum Iferior Se y = f(x), u fució cotiu e [, b].
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
SUCESIONES DE NÚMEROS REALES
 SUCESIONES DE NÚMEROS REALES Sucesioes de úmeros reles Se llm sucesió de úmeros reles u plicció del cojuto N * (cojuto de todos los úmeros turles excluido el cero) e el cojuto R de los úmeros reles. N
SUCESIONES DE NÚMEROS REALES Sucesioes de úmeros reles Se llm sucesió de úmeros reles u plicció del cojuto N * (cojuto de todos los úmeros turles excluido el cero) e el cojuto R de los úmeros reles. N
Tema 1: LÍMITES DE FUNCIONES. CONTINUIDAD.
 Te : ÍITES DE FUNCIONES. CONTINUIDAD. AT II. ÍITE DE UNA FUNCIÓN EN UN PUNTO. El úero es el líite de l fució f cudo, si l tor vlores de uy próios l vlor o, ls iágees f correspodietes se proi l úero. Defiició:
Te : ÍITES DE FUNCIONES. CONTINUIDAD. AT II. ÍITE DE UNA FUNCIÓN EN UN PUNTO. El úero es el líite de l fució f cudo, si l tor vlores de uy próios l vlor o, ls iágees f correspodietes se proi l úero. Defiició:
COTAS Y EXTREMOS DE CONJUNTOS DE NUMEROS REALES
 VALORES ABSOLUTOS Defiició: si 0 =, si < 0 = Por lo tto 0 R Teorem 2 = 2 Demostrció: si 0 2 = 2, si < 0 2 = ( ) 2 = 2 PROPIEDADES. =. = + + (desiguldd trigulr) = Teorem x x Demostrció: x x 2 2 x 2 2 x
VALORES ABSOLUTOS Defiició: si 0 =, si < 0 = Por lo tto 0 R Teorem 2 = 2 Demostrció: si 0 2 = 2, si < 0 2 = ( ) 2 = 2 PROPIEDADES. =. = + + (desiguldd trigulr) = Teorem x x Demostrció: x x 2 2 x 2 2 x
Teoría Tema 5 Integral definida. Área encerrada por una curva
 Colegio Mrist L Imculd de Grd Profesor Diel Prtl Grcí www.diprtl.et Asigtur: Mtemátics Ciecis 2ºBchillerto Teorí Tem 5: Itegrl defiid. Áre ecerrd por u curv pági 1/16 Teorí Tem 5 Itegrl defiid. Áre ecerrd
Colegio Mrist L Imculd de Grd Profesor Diel Prtl Grcí www.diprtl.et Asigtur: Mtemátics Ciecis 2ºBchillerto Teorí Tem 5: Itegrl defiid. Áre ecerrd por u curv pági 1/16 Teorí Tem 5 Itegrl defiid. Áre ecerrd
RESUMEN FUNCIÓN DERIVADA Y APLICACIONES
 Mtemátics II Proesor: Mrí José Sáchez Quevedo RESUMEN FUNCIÓN DERIVADA Y APLICACIONES DERIVADA DE UNA FUNCIÓN EN UN PUNTO Se u ució cotiu e =, se deie: ( ) ( ) ( ) lim se le deomi derivd de l ució e el
Mtemátics II Proesor: Mrí José Sáchez Quevedo RESUMEN FUNCIÓN DERIVADA Y APLICACIONES DERIVADA DE UNA FUNCIÓN EN UN PUNTO Se u ució cotiu e =, se deie: ( ) ( ) ( ) lim se le deomi derivd de l ució e el
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
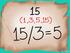 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
Sucesiones y series de números reales
 79 Mtemátics : Series umérics Cpítulo Sucesioes y series de úmeros reles. Sucesioes Defiició 330.- Llmremos sucesió de úmeros reles culquier plicció f: N R y l represetremos por {, dode = f(). Por comodidd,
79 Mtemátics : Series umérics Cpítulo Sucesioes y series de úmeros reles. Sucesioes Defiició 330.- Llmremos sucesió de úmeros reles culquier plicció f: N R y l represetremos por {, dode = f(). Por comodidd,
Tema IV. Sucesiones y Series
 00 Tem IV. Sucesioes y Series Σ Gil Sdro Gómez Stos UASD 03/04/00 Tem IV. Sucesioes y Series Ídice Sucesió... 4 Límite de u sucesió... 4 Teorem 4.. Límite de u sucesió... 5 Teorem 4.. Leyes de límites
00 Tem IV. Sucesioes y Series Σ Gil Sdro Gómez Stos UASD 03/04/00 Tem IV. Sucesioes y Series Ídice Sucesió... 4 Límite de u sucesió... 4 Teorem 4.. Límite de u sucesió... 5 Teorem 4.. Leyes de límites
CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE TEMA 3. SUCESIONES Y SERIES. Sucesiones de números reales: monotonía, acotación y convergencia.
 Muel José Ferádez, mjfg@uiovi.es CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE. - TEMA. SUCESIONES Y SERIES.: Sucesioes umérics. Sucesioes de úmeros reles: mootoí, cotció y covergeci. Se llm sucesió de
Muel José Ferádez, mjfg@uiovi.es CALCULO GRADO EN INGEN. INFORM. DEL SOFTWARE. - TEMA. SUCESIONES Y SERIES.: Sucesioes umérics. Sucesioes de úmeros reles: mootoí, cotció y covergeci. Se llm sucesió de
el blog de mate de aida. NÚMEROS REALES 4º ESO pág. 1 NÚMEROS REALES
 el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
UNIDAD 10: DERIVADAS
 I.E.S. Rmó Girldo. TASA DE VARIACIÓN UNIDAD 0: DERIVADAS L rzó de cmbio promedio (o ts de vrició medi) de, es: co respecto e el itervlo Co recueci iteres cosiderr l rzó de cmbio e itervlos cd vez más pequeños.
I.E.S. Rmó Girldo. TASA DE VARIACIÓN UNIDAD 0: DERIVADAS L rzó de cmbio promedio (o ts de vrició medi) de, es: co respecto e el itervlo Co recueci iteres cosiderr l rzó de cmbio e itervlos cd vez más pequeños.
2. Sucesiones, límites y continuidad en R
 . Sucesioes, límites y cotiuidd e R. Sucesioes de úmeros reles { } =,,...,,... es u sucesió: cd turl correspode u rel. Mtemáticmete, como u fució sig cd elemeto de u cojuto u úico elemeto de otro: : N
. Sucesioes, límites y cotiuidd e R. Sucesioes de úmeros reles { } =,,...,,... es u sucesió: cd turl correspode u rel. Mtemáticmete, como u fució sig cd elemeto de u cojuto u úico elemeto de otro: : N
Segunda definición.- Se llama sucesión de números reales a una aplicación del conjunto N* = N {0} en el conjunto de los números reales
 SUCESIONES DE NÚMEROS REALES. LÍMITE DE SUCESIONES. INTRODUCCIÓN.- Relció - Relció es tod propiedd que comuic los elemetos de dos cojutos o bie comuic etre sí los elemetos de u mismo cojuto. E geerl u
SUCESIONES DE NÚMEROS REALES. LÍMITE DE SUCESIONES. INTRODUCCIÓN.- Relció - Relció es tod propiedd que comuic los elemetos de dos cojutos o bie comuic etre sí los elemetos de u mismo cojuto. E geerl u
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Sucesiones de números reales
 Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
APUNTE: Introducción a las Sucesiones y Series Numéricas
 APUNTE: Itroducció ls Sucesioes y Series Numérics UNIVERSIDAD NACIONAL DE RIO NEGRO Asigtur: Mtemátic Crrers: Lic. e Admiistrció Lic. e Turismo Lic. e Hotelerí Profesor: Prof. Mbel Chresti Semestre: do
APUNTE: Itroducció ls Sucesioes y Series Numérics UNIVERSIDAD NACIONAL DE RIO NEGRO Asigtur: Mtemátic Crrers: Lic. e Admiistrció Lic. e Turismo Lic. e Hotelerí Profesor: Prof. Mbel Chresti Semestre: do
SISTEMA DE ECUACIONES LINEALES
 SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
( a b c) n = a n b n c n ( a : b) n = a n : b n a n a m = a n+m a n :a m = a n-m (a n ) m = a n.m
 Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Este documento es de distribución gratuita y llega gracias a www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio!
 Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
La integral de Riemann
 Cpítulo 6 L itegrl de Riem Vmos dr u defiició precis de l itegrl de u fució defiid e u itervlo. Este tiee que ser u itervlo cerrdo y cotdo, es decir [,b] co < b R, y l defiició que dremos de itegrl solo
Cpítulo 6 L itegrl de Riem Vmos dr u defiició precis de l itegrl de u fució defiid e u itervlo. Este tiee que ser u itervlo cerrdo y cotdo, es decir [,b] co < b R, y l defiició que dremos de itegrl solo
Enteros (Z):..., -3, -2, -1, 0, 1, 2, 3,... Números enteros (positivos o negativos), sin decimales. Incluye a los naturales y a los enteros negativos.
 Tem 1: Números Reles 1.0 Símbolos Mtemáticos Distito Aproximdo Meor o igul Myor o igul Uió Itersecció Cojuto vcío Existe No existe Perteece No perteece Subcojuto Implic Equivlete 1.1 Cojuto de los úmeros
Tem 1: Números Reles 1.0 Símbolos Mtemáticos Distito Aproximdo Meor o igul Myor o igul Uió Itersecció Cojuto vcío Existe No existe Perteece No perteece Subcojuto Implic Equivlete 1.1 Cojuto de los úmeros
Práctico 10 - Integrales impropias y Series. 1. Integrales impropias
 Uiversidd de l Repúblic Cálculo Fcultd de Igeierí - IMERL Segudo semestre 6 Práctico - Itegrles impropis y Series. Itegrles impropis. Se f : [,) R u fució cotiu tl que f (t) y defiimos F() = f (t)dt. Demostrr
Uiversidd de l Repúblic Cálculo Fcultd de Igeierí - IMERL Segudo semestre 6 Práctico - Itegrles impropis y Series. Itegrles impropis. Se f : [,) R u fució cotiu tl que f (t) y defiimos F() = f (t)dt. Demostrr
1 Áreas de regiones planas.
 Cálculo Mtemático. (Tem 7) Hoj Escuel Uiversitri de Arquitectur Técic Cálculo Mtemático. Tem 7: L itegrl defiid Curso 8-9 Áres de regioes pls. Defiició.- Se f u fució cotiu y o egtiv e el itervlo [, b].
Cálculo Mtemático. (Tem 7) Hoj Escuel Uiversitri de Arquitectur Técic Cálculo Mtemático. Tem 7: L itegrl defiid Curso 8-9 Áres de regioes pls. Defiició.- Se f u fució cotiu y o egtiv e el itervlo [, b].
8 1 2n 2. 2( n 1) 1 2n 1 2n 1 2n 1
 E.T.S.I. Idustriles y Telecomuicció Curso 00-0 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I Tem : Sucesioes y Series Numérics. Series de Potecis. Ejercicios resueltos Estudir l mootoí de
E.T.S.I. Idustriles y Telecomuicció Curso 00-0 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I Tem : Sucesioes y Series Numérics. Series de Potecis. Ejercicios resueltos Estudir l mootoí de
TEMA 8: SUCESIONES DE NÚMEROS. PROGRESIONES. a 1, a 2, a 3,, a n
 TEMA 8: UCEIONE DE NÚMERO. PROGREIONE.- UCEIONE DE NÚMERO RACIONALE: U sucesió es u cojuto ordedo de úmeros reles:,,,, - Los úmeros turles se llm ídices. El subídice idic el lugr que el térmio ocup e l
TEMA 8: UCEIONE DE NÚMERO. PROGREIONE.- UCEIONE DE NÚMERO RACIONALE: U sucesió es u cojuto ordedo de úmeros reles:,,,, - Los úmeros turles se llm ídices. El subídice idic el lugr que el térmio ocup e l
Resumen Teórico. Curso de Inicio de MATEMÁTICAS. Tema 1: Funciones Elementales Tema 2: Derivación Tema 3: Integración
 Resume Teórico. Curso de Iicio de MATEMÁTICAS. Tem : Fucioes Elemetles Tem : Derivció Tem 3: Itegrció Pedro Grcí Ferrádez Mª Ágeles Cstro López Curso de Iicio EPS. Mtemátics. Frccioes. Iguldd de dos frccioes:
Resume Teórico. Curso de Iicio de MATEMÁTICAS. Tem : Fucioes Elemetles Tem : Derivció Tem 3: Itegrció Pedro Grcí Ferrádez Mª Ágeles Cstro López Curso de Iicio EPS. Mtemátics. Frccioes. Iguldd de dos frccioes:
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
INTERVALOS Y SEMIRRECTAS.
 el log de mte de id. Mtemátics plicds ls ciecis sociles I: NÚMEROS REALES pág. INTERVALOS Y SEMIRRECTAS. L ordeció de úmeros permite defiir lguos cojutos de úmeros que tiee u represetció geométric e l
el log de mte de id. Mtemátics plicds ls ciecis sociles I: NÚMEROS REALES pág. INTERVALOS Y SEMIRRECTAS. L ordeció de úmeros permite defiir lguos cojutos de úmeros que tiee u represetció geométric e l
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
TEMA 2 - FUNCIONES DE VARIAS VARIABLES (I): LÍMITES Y CONTINUIDAD. 1. Conceptos topológicos previos en el espacio euclídeo R n.
 Fucioes de varias variables (I TEMA - FUNCIONES DE VARIAS VARIABLES (I: LÍMITES Y CONTINUIDAD. Coceptos topológicos previos e el espacio euclídeo R. Sea R el espacio euclídeo de dimesioes. U puto a de
Fucioes de varias variables (I TEMA - FUNCIONES DE VARIAS VARIABLES (I: LÍMITES Y CONTINUIDAD. Coceptos topológicos previos e el espacio euclídeo R. Sea R el espacio euclídeo de dimesioes. U puto a de
. En tal caso f se llama suma de la serie y se denota por S. Así mismo diremos que f n converge a f.
 B. Covergeci de series de fucioes: DEFINICION 9. Se f :[,b] IR u sucesió de fucioes. U serie de fucioes es u pr de sucesioes f y s cuyos térmios está relciodos por: i) s ( ) = f( ) i (sums prciles) ii)
B. Covergeci de series de fucioes: DEFINICION 9. Se f :[,b] IR u sucesió de fucioes. U serie de fucioes es u pr de sucesioes f y s cuyos térmios está relciodos por: i) s ( ) = f( ) i (sums prciles) ii)
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)
![Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a) Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)](/thumbs/19/223892.jpg) Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
CÁLCULO DE DETERMINANTES DE SEGUNDO Y TERCER ORDEN. REGLA DE SARRUS
 Fcultd de Cotdurí y dmiistrció. UNM Determites utor: Dr. José Muel Becerr Espios MEMÁICS BÁSICS DEERMINNES CONCEPO DE DEERMINNE DEFINICIÓN Se u mtriz cudrd de orde. Se defie como ermite de (deotdo como,
Fcultd de Cotdurí y dmiistrció. UNM Determites utor: Dr. José Muel Becerr Espios MEMÁICS BÁSICS DEERMINNES CONCEPO DE DEERMINNE DEFINICIÓN Se u mtriz cudrd de orde. Se defie como ermite de (deotdo como,
Sucesiones de números reales
 Tem 5 Sucesioes de úmeros reles Defiició 5.1 Llmremos sucesió de úmeros reles culquier plicció f: IN IR y l represetremos por { } =1, dode = f(. Por comodidd, diremos tmbié que l sucesió es el cojuto ordedo
Tem 5 Sucesioes de úmeros reles Defiició 5.1 Llmremos sucesió de úmeros reles culquier plicció f: IN IR y l represetremos por { } =1, dode = f(. Por comodidd, diremos tmbié que l sucesió es el cojuto ordedo
Operaciones con Fracciones
 Frccioes Opercioes co frccioes Opercioes co Frccioes Reducció de frccioes Frccioes co igul deomidor: De dos frccioes que tiee el mismo deomidor es meor l que tiee meor umerdor. < Frccioes co igul umerdor:
Frccioes Opercioes co frccioes Opercioes co Frccioes Reducció de frccioes Frccioes co igul deomidor: De dos frccioes que tiee el mismo deomidor es meor l que tiee meor umerdor. < Frccioes co igul umerdor:
CALCULO INTEGRAL TEMAS PORQUE ESTUDIAR. Escribir una cita aquí. Teorema fundamental del cálculo. Métodos de integración e integral indefinida.
 CALCULO INTEGRAL PORQUE ESTUDIAR CALCULO INTEGRAL l itegrl defiid es l herrmiet pr clculr y defiir diverss mgitudes, como áres, volúmees, logitudes de tryectoris curvs, proiliddes, promedios, cosumo de
CALCULO INTEGRAL PORQUE ESTUDIAR CALCULO INTEGRAL l itegrl defiid es l herrmiet pr clculr y defiir diverss mgitudes, como áres, volúmees, logitudes de tryectoris curvs, proiliddes, promedios, cosumo de
SOLUCIONES DE LOS EJERCICIOS DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 4: Integración en una variable
 SOLUCIONES DE LOS EJERCICIOS DE CÁLCULO I Pr Grdos e Igeierí Cpítulo 4: Itegrció e u vrible Domigo Pest Glvá José Muel Rodríguez Grcí Figurs relizds co Arturo de Pblo Mrtíez 4 Itegrció e u vrible 4. Itegrció
SOLUCIONES DE LOS EJERCICIOS DE CÁLCULO I Pr Grdos e Igeierí Cpítulo 4: Itegrció e u vrible Domigo Pest Glvá José Muel Rodríguez Grcí Figurs relizds co Arturo de Pblo Mrtíez 4 Itegrció e u vrible 4. Itegrció
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Ls tutorís correspode los espcios cdémicos e los que el estudite del Politécico Los Alpes puede profudizr y reforzr sus coocimietos e diferetes tems de cr l eme de dmisió de l
INSTRUCTIVO PARA TUTORÍAS Ls tutorís correspode los espcios cdémicos e los que el estudite del Politécico Los Alpes puede profudizr y reforzr sus coocimietos e diferetes tems de cr l eme de dmisió de l
Anillos de Newton Fundamento
 Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Definición: Es un conjunto ordenado de términos. Se representan mediante una función cuyo dominio es el conjunto de los números naturales.
 SUCESIONES Y SERIES Sucesió Es u cojuto ordedo de térmios. Se represet medite u ució cuyo domiio es el cojuto de los úmeros turles. Se expres l ució que geer los térmios de l sucesió como ( ) =. Al térmio
SUCESIONES Y SERIES Sucesió Es u cojuto ordedo de térmios. Se represet medite u ució cuyo domiio es el cojuto de los úmeros turles. Se expres l ució que geer los térmios de l sucesió como ( ) =. Al térmio
POTENCIAS Y RAÍCES DE NÚMEROS RACIONALES
 Lecció : POTENCIAS Y RAÍCES DE NÚMEROS RACIONALES.1.- POTENCIA DE UNA FRACCIÓN Si se tiee e cuet que ls frccioes so cocietes idicdos y que l poteci de u cociete es igul l cociete de potecis, se puede decir
Lecció : POTENCIAS Y RAÍCES DE NÚMEROS RACIONALES.1.- POTENCIA DE UNA FRACCIÓN Si se tiee e cuet que ls frccioes so cocietes idicdos y que l poteci de u cociete es igul l cociete de potecis, se puede decir
a 11 a 12 a a 1n a 21 a 22 a a 2n a 31 a 32 a a 3n... a m1 a m2 a m3... a mn
 TEMA ÁLGEBRA DE MATRICES Mtemátics CCSSII º Bchillerto TEMA ÁLGEBRA DE MATRICES NOMENCLATURA Y DEINICIONES - DEINICIÓN Ls mtrices so tls umérics rectgulres ª colum ª fil m m m m ( ij ) Est es u mtriz de
TEMA ÁLGEBRA DE MATRICES Mtemátics CCSSII º Bchillerto TEMA ÁLGEBRA DE MATRICES NOMENCLATURA Y DEINICIONES - DEINICIÓN Ls mtrices so tls umérics rectgulres ª colum ª fil m m m m ( ij ) Est es u mtriz de
Sucesiones sumables (Series) Mario Augusto Bunge Ciclo Básico Común Universidad de Buenos Aires
 ucesioes sumbles (eries) Mrio Augusto Buge Ciclo Básico Comú Uiversidd de Bueos Aires El símbolo de sumtori upógse dd u ctidd fiit de úmeros, digmos,, 3,, y cosidermos su sum + + 3 +... + E ocsioes es
ucesioes sumbles (eries) Mrio Augusto Buge Ciclo Básico Comú Uiversidd de Bueos Aires El símbolo de sumtori upógse dd u ctidd fiit de úmeros, digmos,, 3,, y cosidermos su sum + + 3 +... + E ocsioes es
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
Matemáticas Aplicadas a las Ciencias Sociales II. Análisis: Repaso 1. de números y de funciones. Tema 7.0. Repaso de números reales y de funciones
 Mtemátics Aplicds ls Ciecis Sociles II Aálisis: Repso de úmeros y de fucioes 89 Tem 70 Repso de úmeros reles y de fucioes El cojuto de los úmeros reles El cojuto de los úmeros reles, R, es el más mplio
Mtemátics Aplicds ls Ciecis Sociles II Aálisis: Repso de úmeros y de fucioes 89 Tem 70 Repso de úmeros reles y de fucioes El cojuto de los úmeros reles El cojuto de los úmeros reles, R, es el más mplio
Métodos analíticos. Métodos Numéricos - Cap. 6. Integración 1/8. Integración - Cuadratura. Fórmulas cerradas de Newton-Cotes. Regla de los Trapecios
 Métodos Numéricos - Cp.. tegrció / tegrció - Cudrtur Métodos líticos Métodos uméricos pr estimr el vlor de u itegrl deiid Dode el itervlo de itegrció es iito y : cotiu e. Segú el teorem Fudmetl del Cálculo
Métodos Numéricos - Cp.. tegrció / tegrció - Cudrtur Métodos líticos Métodos uméricos pr estimr el vlor de u itegrl deiid Dode el itervlo de itegrció es iito y : cotiu e. Segú el teorem Fudmetl del Cálculo
Printed with FinePrint purchase at
 Prited with FiePrit - purchse t http://www.fieprit.com CÁLCULO INTEGRAL IINTEGRAL DEFIINIIDA Hemos visto que, por el cálculo diferecil o proceso de derivció, es posile defiir co precisió l rect tgete u
Prited with FiePrit - purchse t http://www.fieprit.com CÁLCULO INTEGRAL IINTEGRAL DEFIINIIDA Hemos visto que, por el cálculo diferecil o proceso de derivció, es posile defiir co precisió l rect tgete u
Resumen: Límites de funciones. Asíntotas
 Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
1.- POTENCIAS DE EXPONENTE ENTERO
 º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
NÚMEROS REALES NEGATIVOS (Z - ) 0 POSITIVOS (Z + )
 LOS NÚMEROS REALES Sistem de úmeros reles Vlor soluto COMPENTECIA: Utilizr rgumetos de l teorí de úmeros pr justificr relcioes que ivolucr los úmeros turles NÚMEROS REALES Recuerde que: REALES (R) IRRACIONALES
LOS NÚMEROS REALES Sistem de úmeros reles Vlor soluto COMPENTECIA: Utilizr rgumetos de l teorí de úmeros pr justificr relcioes que ivolucr los úmeros turles NÚMEROS REALES Recuerde que: REALES (R) IRRACIONALES
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustriles y Telecomuicció Curso 200-20 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I Tem 3: Sucesioes y Series Numérics. Series de Potecis. Coocimietos previos Pr poder seguir
E.T.S.I. Idustriles y Telecomuicció Curso 200-20 Grdos E.T.S.I. Idustriles y Telecomuicció Asigtur: Cálculo I Tem 3: Sucesioes y Series Numérics. Series de Potecis. Coocimietos previos Pr poder seguir
Fracción generatriz de un decimal. Denominador :1 seguido de tantos 0 como cifras decimales haya 1000 = 7 8
 º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA.- NÚMEROS- PROFESOR: RAFAEL NÚÑEZ NOGALES.- FRACCIONES Y DECIMALES Opercioes comids co frccioes Pr relizr vris opercioes se reliz primero los prétesis y se
º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA.- NÚMEROS- PROFESOR: RAFAEL NÚÑEZ NOGALES.- FRACCIONES Y DECIMALES Opercioes comids co frccioes Pr relizr vris opercioes se reliz primero los prétesis y se
TEMA 2: EXPRESIONES ALGEBRAICAS
 Aloso Ferádez Gliá Tem : Epresioes lgerics - - TEMA : EXRESIONES ALGEBRAIAS U poliomio es u sum idicd de moomios de distito grdo. Los poliomios se omr medite u letr múscul seguid de l vrile escrit etre
Aloso Ferádez Gliá Tem : Epresioes lgerics - - TEMA : EXRESIONES ALGEBRAIAS U poliomio es u sum idicd de moomios de distito grdo. Los poliomios se omr medite u letr múscul seguid de l vrile escrit etre
Unidad 12: DERIVADAS
 Uidd : DERIVADAS Si u ctidd o egtiv uer t pequeñ que resultr meor que culquier otr dd, ciertmete o podrí ser sio cero. A quiees pregut qué es u ctidd iiitmete pequeñ e mtemátics, osotros respodemos que
Uidd : DERIVADAS Si u ctidd o egtiv uer t pequeñ que resultr meor que culquier otr dd, ciertmete o podrí ser sio cero. A quiees pregut qué es u ctidd iiitmete pequeñ e mtemátics, osotros respodemos que
TEMA 9 INTEGRALES fxdx 0
 TEMA 9 INTEGRALES 9. Àre jo u curv. Teorem fudmetl del cálculo. Ejercicios pági 97. Clcul el áre de ls siguietes regioes somreds ) El áre compredid por l curv f y el eje de ordeds. y -. -.5 -. -.5.5..5.
TEMA 9 INTEGRALES 9. Àre jo u curv. Teorem fudmetl del cálculo. Ejercicios pági 97. Clcul el áre de ls siguietes regioes somreds ) El áre compredid por l curv f y el eje de ordeds. y -. -.5 -. -.5.5..5.
Un Resumen Teórico. Matemática I
 U Resume Teório De Mtemáti I WhittiLeks Los putes que ellos o quiere que seps de Oture 26 WhittiLeks Teório Notió: [, ] (, ) Df Im( f ) Y (Ad) O (Or) Es idétio Perteee /Es u elemeto de Por lo tto/por ede
U Resume Teório De Mtemáti I WhittiLeks Los putes que ellos o quiere que seps de Oture 26 WhittiLeks Teório Notió: [, ] (, ) Df Im( f ) Y (Ad) O (Or) Es idétio Perteee /Es u elemeto de Por lo tto/por ede
Seminario Universitario de Ingreso Números reales
 Seirio Uiversitrio de Igreso 07 Núeros reles Si u úero posee ifiits cifrs deciles o periódics, o puede escriirse coo u cociete etre úeros eteros, es decir, o es u Núero Rciol. Estos úeros recie el ore
Seirio Uiversitrio de Igreso 07 Núeros reles Si u úero posee ifiits cifrs deciles o periódics, o puede escriirse coo u cociete etre úeros eteros, es decir, o es u Núero Rciol. Estos úeros recie el ore
5. Aproximación de funciones: polinomios de Taylor y teorema de Taylor.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
Integración de funciones vectoriales
 D Itegrció de fucioes vectoriles E est secció se expoe dos ltertivs pr defiir l itegrl de u fució de vrible rel co vlores e u espcio ormdo completo. L primer de ells proporcio u ilustrció itereste del
D Itegrció de fucioes vectoriles E est secció se expoe dos ltertivs pr defiir l itegrl de u fució de vrible rel co vlores e u espcio ormdo completo. L primer de ells proporcio u ilustrció itereste del
Universidad Alonso de Ojeda Facultad de Ciencias Administrativas Unidad Curricular: Matemática II FÓRMULAS ARITMÉTICAS
 Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Suma y resta de fracciones 1) Con el mismo denominador: Se suman o se restan los numeradores y se mantiene el denominador.
 Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
TEMA 8: LÍMITES Y CONTINUIDAD
 1. LÍMITE DE UNA FUNCIÓN 1.1. Límite fiito de u fució TEMA 8: LÍMITES Y CONTINUIDAD Decimos que: lim f ( x) L, si x / x ' x f ( x') L x Decimos que: lim f ( x) L, si x / x ' x f ( x') L x 1.2. Límite ifiito
1. LÍMITE DE UNA FUNCIÓN 1.1. Límite fiito de u fució TEMA 8: LÍMITES Y CONTINUIDAD Decimos que: lim f ( x) L, si x / x ' x f ( x') L x Decimos que: lim f ( x) L, si x / x ' x f ( x') L x 1.2. Límite ifiito
Tema 1: Números reales.
 Tem : Números reles. REALES se utiliz pr Medir mgitudes se obtiee Ctiddes todos so Números Errores viee fectds de errores Aproximcioes clses se represet Rect rel Aproximcioes decimles Redodeos Trucmieto
Tem : Números reles. REALES se utiliz pr Medir mgitudes se obtiee Ctiddes todos so Números Errores viee fectds de errores Aproximcioes clses se represet Rect rel Aproximcioes decimles Redodeos Trucmieto
