EDO Teoría de la existencia y la prolongabilidad

Transcripción

1 EDO Teorí de l exisenci y l prolongbilidd Conenidos: Teorem de Ascoli Arzelá 2 Teorem de Cuchy Peno 4 Teorem de Picrd Lindelöf 9 Lem de Winner 12 Lem de Gronwll 18 Teorem de ls soluciones proximds 21 Teorem de dependenci Lipschiz de ls condiciones iniciles 23 Teorem de dependenci coninu de prámeros 24 Teorem de diferencibilidd de Peno 26 Teorem de dependenci diferencible de vlores iniciles 28 1

2 A lo lrgo del cpíulo esudiremos l eorí de exisenci y unicidd, l eorí de l prolongbilidd y l dependenci de prámeros. El primer eorem que vemos es el eorem de Cuchy-Peno o Teorem de exisenci Globl. Ide del eorem: En plicción del eorem de Ascoli Arzelá se consruye un sucesión de poligonles de Euler, que son soluciones proximds del PVI. Como vemos que v ser relevne, recordmos el eorem de Ascoli-Arzelá. Pr ello enemos que recordr primero qué significb l equiconinuidd. Definición: Equiconinuidd. Diremos que un sucesión de funciones {f k } C([, b]) es equiconinu si, y sólo si: ε > 0, δ > 0 q x, y [, b], x y < δ f k (x) f k (y) < ε, k N Sl l vis que es un concepo muy similr l de límie (y coninuidd por lo no) en funciones de vrible rel. L ide que represen formlmene es l de que más cerc esén dos punos x, y más cerc esrán sus imágenes, independienemene del miembro de l sucesión de funciones. Algo sí como un coninuidd sobre od l sucesión. Teorem: Ascoli Arzelá. Dd un sucesión {f k } C([, b]). Si es equiconinu y uniformemene cod enonces exise un subsucesión uniformemene convergene en [, b]. Demosrción. Consideremos el conjuno numerble Q [, b], subconjuno de [, b]. Ordenmos dicho conjuno: Se hor: Q [, b] = {x 1, x 2, } =: B {f k (x 1 )} k N R Un sucesión cod de números. Por compcidd podemos exrer un subsucesión convergene. Digmos: Considero hor l sucesión cod: Y exrigo l sucesión convergene: {f k1 (x 1 )} k N {f k (x 1 )} R {f k1 (x 2 )} {f k1 } {f k } R {f k2 (x 2 )} k N {f k1 (x 2 )} k N R 2

3 Repiiendo el proceso recurrenemene enemos: f 11 (x), f 21 (x), f 31 (x), f 12 (x), f 22 (x), f 32 (x), f 13 (x), f 23 (x), f 33 (x), ec. L primer sucesión es convergene en x 1 L segund sucesión es convergene en x 1 por ser subsucesión de f k1 (x 2 ) y en x 2 por consrucción. De form nálog, l ercer sucesión es convergene en x 1, x 2, x 3. Y sí sucesivmene. Aplicmos rgumeno de l digonl. Considermos: f k {f kk (x)} k = f 11 (x), f 22 (x), f 33 (x), Es uniformemene convergene es sucesión? Sí, lo es. Demosrción: Vemos que es de Cuchy uniformemene. Por equiconinuidd se iene que, ddo ε > 0 exise un δ > 0 de form que: x, y: x y < δ f k (x) f k (y) < ε 3, k No: δ depende exclusivmene de ε. Uilizmos l densidd de B = {x 1, x 2, x 3, }. Ddo δ > 0, pr cd x [, b] exise y B de form que: Enonces el siguiene conjuno: x B(y, δ) x y < δ {B(y, δ)} y B Es un recubrimieno de [, b]. Por compcidd, ese recubrimieno dmie un subrecubrimieno finio. Eso es: exisen y 1,, y j B de l mner que: x y i < δ, x, y i Por úlimo, enemos que en dichos punos y i l sucesión f k es convergene. Es decir que exise N i nurl, de l mner que: f n (y i ) f m (y i ) < ε 3, n, m > N i Tomemos: N = mx i=1,,j N i 3

4 Enonces, si n, m > N se iene que f n f m < ε. En efeco: f n (x) f m (x) = f n (x) f n (y j ) + f n (y j ) f m (y j ) + f m (y j ) f m (x) < ε Por lo no f k converge uniformemene en B. QED. Vmos con el eorem de exisenci de Cuchy-Peno. Teorem (Cuchy-Peno): Se F: D = [ 0 T, 0 + T] U R n donde U R n es un enorno biero de ξ 0. Se supone que F es coninu en D y esá cod por M. Eso es, que pr culquier (, x) D se iene F(, x) M. Enonces, pr el PVI { x (s) = F(s, x(s)) x( 0 ) = ξ 0 Exise l menos un solución definid en ( 0 τ, 0 + τ), τ > 0 R n R n U ξ 0 D F M T ( ) 0 R Fig 1. Teorem de Cuchy Peno. Demosrción. Dividiremos l demosrción del eorem en res pres. Pre 1 En primer lugr, dmos un definición previ. Definición: Soluciones proximds. Diremos que y ε : [ 0 τ, o + τ] R n es un solución proximd del problem de vlores iniciles con error ε > 0 si: 4

5 { } 1) (, y ε ()) D cundo [ 0 τ, 0 + τ] 2) y ε es coninu en [ 0 τ, 0 + τ] y iene derivd cod, slvo, como mucho, en un número finio de punos. 3) y ε () F(, y ε ()) ε pr culquier [ 0 τ, 0 + τ] slvo quizás en quellos punos en los que l derivd no esá cod. 4) y ε ( 0 ) = ξ 0 Bueno, vmos ver que ls poligonles de Euler son soluciones proximds del problem de vlores iniciles pr un elección decud del pso h y del inervlo de definición. Proposición 1. Se F coninu en D, y se τ l que B (ξ 0, τ M) U, donde M es un co de F en D. Enonces, pr culquier ε > 0 exise un poligonl de Euler y ε : [ 0 τ, o + τ] R n Que es solución proximd del problem de vlores iniciles con error ε. R n R n U ξ 0 τ M D F M τ { } T 0 R Fig 2. Poligonles de Euler como soluciones proximds Demosrción. Vmos consruir poligonles ε-proximds. Demosrremos, simplemene, que cumplen l definición. Ls consruiremos, demás, en el inervlo [ 0, 0 + τ]. Nurlmene, en l or mid del inervlo es complemene nálogo. Elegiremos como pso de l poligonl h = τ/k, donde k es un nurl que deerminremos coninución. El inervlo qued enonces dividido en k rozos medine k + 1 punos. { 0,, k } Los cules genern oros nos ξ j, definidos por: ξ j ξ j 1 + h F( j 1, ξ j 1 ) 5

6 L poligonl v ser l inerpolción linel enre esos vlores. Probmos que ls poligonles cumplen ls propieddes de ls soluciones proximds. 1) [ 0 τ, 0 + τ] (, y ε ()) D j j 1 = h. Enonces ξ 1 ξ 0 = h F( 0, ξ 0 ) h M. Por inducción: ξ j ξ 0 τ M Se h elegido τ l que B(ξ 0, τ M) U. Por convexidd, ls poligonles de Euler perenecen l dominio. 2) Es obvio que son coninus y demás el vlor siempre es finio porque l imgen de un puno pr ciero es F que esá cod. 3) Fijdo k se iene que el vlor de l poligonl es: P k () = ξ j + F( j, ξ j ) ( j ), [ j, j+1 ] Queremos demosrr que: P k () F(, P k ()) < ε Por l coninuidd uniforme (por compcidd) de F, ddo ε > 0 exise δ > 0 l que: si s < δ y ξ η < δ enonces: F(, ξ) F(s, η) < ε Tomemos k de l mner que: Así, si [ j, j+1 ] enonces: h = τ k δ M P k () F(, P k ()) = F( j, ξ j ) F (, ξ j + F( j, ξ j )( j )) Ddo que j < h δ y ξ j (ξ j + F( j, ξ j )( j )) h M δ qued que: P k () F(, P k ()) < ε, Pre 2 Proposición: Se {ε k } sucesión cod de números posiivos. Enonces l sucesión {y εk } [ 0, 0 + τ] de soluciones ε k -proximds del PVI es equicod y equiconinu. Demosrción: Observmos que, pr un solución proximd y εk que nurlmene cumple ls condiciones 1),2) se sigue, por ierción en los inervlos [ j, j+1 ] del eorem fundmenl del cálculo, que ddo [ 0, 0 + τ]: y εk () = y εk ( 0 ) + y ε (s) ds 0 6

7 Demosrción de equicod: y εk () ξ 0 = y (s) ds 0 Demosrción de equiconinuidd. Por lo no: F (s, y εk (s)) ds + ε k τ τ (M + ε k ) 0 y εk () y εk ( ) = y ε (s) ds y ε () y ε ( ) ε ( ) + F(s, y ε (s)) ds (M + ε) ( ) QED Pre 3 Hllr un solución del PVI es equivlene hllr un x() que sisfg: x() = ξ 0 + F(s, x(s)) ds, (1) 0 Tomemos ls ε k soluciones proximds dds por ls poligonles de Euler. Tomemos y k subsucesión uniformemene convergene dd por el eorem de Ascoli Arzelá. Vemos enonces que su límie uniforme es un solución de (1). Se δ > 0 l que, por l coninuidd uniforme de F, si ξ η < δ enonces: F(, ξ) F(, η) ε/3τ Tomemos k suficienemene grnde como pr que: Y mbién: Enonces: x y k < min (δ, ε/3) ε k < ε/3τ x() ξ 0 F(s, x(s)) ds 0 x() y k () + y k () ξ 0 F(s, y k (s)) ds 0 F(s, x(s)) ds 0 + F(s, y k (s)) ds 0 7

8 ε 3 + ε k τ + ε 3 ε Como ε es n pequeño como se desee, qued probd l convergenci. QED. Tl y como hemos viso, Cuchy Peno sólo nos segur l exisenci de solución, no l unicidd. Vmos ver oro eorem bsdo en los sisems de ecuciones diferenciles que d condiciones suficienes pr l exisenci de solución únic nivel locl. Primero enemos que revisir lgunos concepos. Definición: Lipschizidd locl. Decimos que un función f: R n R m es loclmene Lipschiz si ddo culquier puno x R n exise un enorno suyo en el que f es globlmene Lipschiz. Definición: Lipschizidd globl. Decimos que un función f: R n R m es globlmene Lipschiz si exise un consne L l que: f(x) f(y) L x y, x, y R n Observciones: 1) En priculr, si Df coninu y cod en el dominio D de definición, por el eorem del vlor medio se prueb que f cumple l hipóesis de Lipschizidd locl, y demás: L = n sup{ D i f(x) : x D, i = 1,, n} 2) L consne de Lipschiz permie conrolr l disnci enre soluciones. Eso moiv el siguiene Lem: Lem: Dependenci coninu de ls condiciones iniciles. Sen x, y R n soluciones de x = F(, x), supongmos F función L-lipschizin en un enorno de ls gráfics de x, y pr [ 0, 1 ]. Enonces, si [ 0, 1 ]: Demosrción: Se obiene direcmene derivndo. Enonces: x() y() e L ( 0 ) x( 0 ) y( 0 ) d d x() y() 2 = 2 x() y() F(, x) F(, y) 2L x() y() 2 x() y() e L ( 0 ) x( 0 ) y( 0 ) 8

9 Teorem (Picrd-Lindelöf): Se F: D R R n R n coninu y L-lipschiz con respeco l segund vrible ξ R n en D enorno de ( 0, ξ 0 ). Enonces el PVI: x () = F(, x), x R n Tiene un únic solución en ( δ, + δ), con δ > 0. R n R n ρ ξ 0 U D F M δ 0 T R Fig 3. Teorem de Picrd Lindelöf. Demosrción: F: D R R n R n x: [ δ, + δ] R n x = F(, x) x( 0 ) = ξ 0 Podemos suponer que U = [ 0 T, 0 + T] B (ξ 0, ρ). Uilizremos el eorem del puno fijo de Bnch. Enconrr un solución del PVI es enconrr un x() l que: x() = ξ 0 + F(s, x(s)) ds, [ 0 δ, 0 + δ] 0 Definimos l plicción: φ(y()) = ξ 0 + F(s, x(s)) ds 0 φ: C([ 0 δ, 0 + δ], R n ) C([ 0 δ, 0 + δ], R n ) 9

10 Vmos ver que φ es un plicción conrciv sobre el espcio mérico C([ 0 δ, 0 + δ], R n ) pr un cier elección de δ > 0 y con l norm del supremo con el peso e L. Pr que esé bien definido φ debe ener senido F(s, y(s)) Pr s [ 0 δ, 0 + δ], luego y(s) B(ξ 0, ρ) y ξ 0 < ρ. Por lo no: Tomemos el espcio de funciones: Elegiremos δ pr que: Es decir que: Eso es: sup y(s) ξ 0 < ρ s [ 0 δ, 0 +δ] B = {y C(( 0 δ, 0 + δ)): y ξ 0 < ρ [ 0 δ, 0 + δ]} ξ 0 + F(s, y(s)) ds 0 φ: B B φ(y()) ξ 0 < ρ, [ 0 δ, 0 + δ] ξ 0 F(s, y(s)) ds 0 Con lo cul, hemos de escoger δ l que: = M ( 0 ) Mδ < ρ δ < ρ M No: Seguimos suponiendo F cod l igul que nes, lógicmene. Ahor, sen y, z B vemos que φ conrciv en B pr l siguiene disnci: Veámoslo: φy φz L = sup y z L = sup ( 0 δ, 0 +δ) { e L L y z L ds 0 sup {e L y z } [ o, 0 +δ] {e L F(s, y) F(s, z) ds } 0 } y z L sup{1 e 0 } En efeco, φ es conrciv consne C = 1 e L < 1, con lo cul exise un puno fijo. QED. 10

11 Observciones: 1) Se h probdo que φ(y(s)) ξ 0 + F(s, y(s)) ds es conrciv en el 0 espcio de funciones coninus en ( 0 δ, 0 + δ) que disn de ξ 0 menos que ρ, y que por lo no en dicho enorno, que corresponde l zon rlld en verde en l figur 3, exise un únic solución. 2) El mño δ del inervlo de exisenci-unicidd depende de ρ, definido previmene, y de M co de F. 3) El mño δ es independiene de L consne de Lipschizidd. 4) Se deduce que l solución es prolongble hs un 1 l que 1 0 no exced ni T ni mpoco ρ/m. Recordemos, T es l nchur de U uilizd en Cuchy Peno. 5) Uilizmos l norm con peso exponencil porque sí δ no depende de l consne L. 6) Cuchy Peno supone únicmene l coninuidd de F e implic exisenci. Al exigirle F mbién Lipschizidd podemos segurr unicidd, sin embrgo el inervlo en el que exise solución únic no depende de l consne de Lipschizidd, si no del mño del enorno de ξ 0 = x( 0 ) y de l co de F. Podemos pregunrnos si es posible llevr δ más llá de min(t, ρ/m). Eso moiv l siguiene ep de nuesro esudio. L prolongbilidd de soluciones. 11

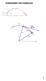
12 Empezmos viendo lguns definiciones previs. Definición: Inervlo de definición y prolongciones. Se x un solución del PVI e I quel inervlo cenrdo en 0 en el cul esá definid. Designremos medine el pr (x, I) dich solución socid l inervlo. Diremos que (x, I ) es prolongción de (x, I) si: 1) I I 2) x = x, I Ambos I, I pueden ser inervlos bieros, cerrdos, semibieros, semicerrdos o semirecs. Definición: Prolongbilidd. Diremos que (x, I) es no prolongble si no exise prolongción de (x, I). Lem: Dd (x, I) siempre exise un prolongción suy (x, I ) que es no prolongble. Demosrción: Se P = {(x α, I α )} α Diremos que (x α, I α ) (x β, I β ) I α I β Se iene que (P, ) es olmene ordendo. Se (x α, I α ) cden de prolongciones. Si defino (x, I) l que I = α I α, l (x, I) es un co superior. Enonces, por le lem de Zorn exise elemeno mximl. Enonces, por definición, dicho mximl consiuye un solución no prolongble. Definición: Puno de cumulción. Diremos que ξ 0 es un puno de cumulción de x() cundo 0 si exise un sucesión { k } 0 de l mner que x( k ) ξ 0. Con és úlim definición quiere decirse, formlmene, que ( 0, ξ 0 ) es un puno de cumulción de l gráfic {(, x()): < 0 }. Es decir que: Ddo ε > 0 exise τ > 0 de l mner que 0 < 0 τ < ε y x( 0 τ) ξ 0 < ε Vemos el primer lem imporne de prolongbilidd. Lem (de Winner): Se F: D R R n R n coninu, con D enorno biero de ( 0, ξ 0 ). Si exise solución de x = F(, x) definid en ( 0 h, 0 ) con h > 0 y ξ 0 es puno de cumulción de x() cundo 0, enonces lim 0 x() = ξ 0. 12

13 Demosrción: Tenemos el cilindro A = [ 0 T, 0 ] B (ξ 0, ε 1 ), suponiendo F coninu en A, que es compco. Se iene F esá cod por M en A. Se ε > 0 que podemos suponer ε < ε 1. Y omemos δ = ε/4m. Tomemos mbién 1 [ 0 T, 0 ] l que 1 0 < δ. Y demás x( 1 ) ξ 0 < ε/2, cos que podemos suponer por ser ξ 0 puno de cumulción en 0. Consideremos: Se r de probr que V = Supongmos que no. V = { ( 1, 0 ): x() ξ 0 > ε} Tommos = inf V. Enonces x() ξ 0 ε < ε 1 culquier que se ( 1, ). Enonces, cundo perenece dicho inervlo x() B(ξ 0, ε 1 ), eso es, en dicho inervlo l gráfic esá en A. Eso no puede psr: Por el eorem del vlor medio, y eniendo en cuen quién es 1 : x( ) ξ 0 x( ) x( 1 ) + x( 1 ) ξ 0 ε + ε 2 = 3 ε < ε 4 Pero l como hemos definido se iene que x( ) ξ 0 ε. Conrdicción. R n QED. ε 1 ξ 0 ε/2 ε/2 A D 0 T 1 δ 0 R Fig 4. Siendo ξ 0 po de cumulción y bjo ls hipóesis, es imposible enconrr punos en l zon verde. 13

14 Observción: L función x no podrí por ejemplo ser un llmdo seno del opólogo porque enonces F en 0, y F es cod por compcidd. Definición: Froner exendid. Se un conjuno D y D = D D su froner opológic definimos l froner exendid como: 1) D { }, si D no codo. 2) D, si D codo. Corolrio (de Winner) PRIMERA VERSIÓN: Se F: D R R n R n coninu con D biero. Se (x, I) solución de x = F(, x) que suponemos no prolongble l derech. Enonces I = [ 0, 1 ) es biero por l derech, y demás, si 1 los punos de cumulción de x esán en l froner exendid de D. Demosrción: R n D D x 1 () x() x 3 () x 2 () R Fig 5. Consecuenci de Winner: Ls siuciones x 1, x 2 son posibles; x 3 no. 14

15 Si I = [ 0, ) rivil. Supongmos que el inervlo es finio (en el senido de: longiud fini). Si lim 1 x() = enones ξ 1 esá en l froner exendid. Si exise un puno de cumulción finio ξ 1 enonces el lem de Winner segur que exise el límie. Dicho puno ξ 1 no puede perenecer l inerior de D porque enonces el problem: { y = F(, x) y( 0 ) = x( 1 ) Tendrí solución y l solución (x, I) serí prolongble, conrdicción. L únic posibilidd es que ξ 1 perenezc l froner opológic. QED. Corolrio (de Winner) SEGUNDA VERSIÓN: Se F: D R R n R n con D biero. Se (x, I) solución de x = F(, x) que suponemos no prolongble l derech. Ddo culquier compco K D l solución escp de K en un k < sup I, quiere decirse: x() K, > k. Demosrción: Supongmos I = (T 0, T 1 ), y un sucesión j T 1 de l mner que ( j, x j ) K. Por definición de compcidd, exise (T 1, ξ) = lim ( j, x j ()) K D. Por el lem de j Winner exise (T 1, ξ) = lim (, x()), un puno inerior de D. L solución (x, I) T1 podrímos prolongrl con un solución locl l derech de del problem con vlor inicil x(t 1 ) = ξ. Conrdicción. R n D D K R Fig 6. Si l solución no escpse de K nes de llegr sup I enonces serí prolongble 15

16 Observción: El compormieno de l solución en 1 no iene por qué ser n simple; puede ser muy diverso (oscilorio, sinóico ). Vemos lgunos ejemplos de odo eso. Ejemplo 1. Considermos el domino D = ( 2,2) ( 2,2) con el PVI: { y () = y() y(0) = 1 Tiene solución y = e, que lcnz froner en ( 2, log(2)) y por el lem de Winner no es prolongble. Ejemplo 2. Consideremos hor D = {(, y): > 0, y > 0} con el problem: Por inegrción elemenl: { y () = y 1 3 y(1) = y y() = (y ( 1)) Enonces pr vlores posiivos de y 0 ls soluciones no prolongbles l izquierd llegn y = 0, y que si y() = 0 iene solución 0 > 0. El límie de l gráfic de ess soluciones no prolongbles l izquierd es el puno ( 0, 0). Ejemplo 3. Se el problem de vlores iniciles con D = {(, y): < 1, y R} y() = 0, y 1 y () = { 1 (1 ) 2 1 y2, y < 1 { y(0) = 1 2 Ls ecuciones sisfcen ls condiciones del eorem de exisenci si 1. Por inegrción elemenl se obiene un solución no prolongble l derech: y() = sin ( π 4 ) Es un ejemplo de solución que oscil en 1 y no iene límie. Los infinios punos de cumulción de l gráfic pr 1 esán en l froner del dominio. Observ que l unicidd fll pr los vlores iniciles y( 0 ) = 1. 16

17 Por úlimo, un resuldo de prolongbilidd. Se D dominio biero de F coninu, l que [ 0, 1 ] R n D. Si F cod por M, enonces culquier solución no prolongble (x, I) del problem del vlor inicil x( 0 ) = ξ lcnz el puno = 1. Bs observr que pr l solución no prolongble x() se iene l coción pr odo I: x() ξ M 0 De quí se deduce que l solución es no prolongble y que iene que bndonr el compco K = [ 0, 1 ] B(ξ, M 1 0 ) en un iempo < sup I y iene que hcerlo por los punos ( 1, x), con lo cul 1 < sup I. Lo que cbmos de uilizr es un comprción enre soluciones de dos ecuciones con mismo do inicil: x = F(, x), x = G(, x). En ese cso, G = M. Esos crierios de comprción pueden uilizrse con ls desigulddes cmbids, pr obligr nuesr solución irse l infinio nes de un iempo. Ls soluciones de l ecución uxilir ls denominmos brrers. Y de eso r el siguiene cpíulo, del crierio de comprción de soluciones. 17

18 Lem (de Gronwll): Sen ls funciones coninus y, f, g: [, b] R con g() 0 les que se cumple: y() f() + g(s) y(s) ds (2) Enonces: y() f() + g(u) f(u) e u g(s) ds du Hcemos lguns observciones nes de demosrrlo. Observción 0: El lem nos d un esimción de y en l que y no prece en el ldo derecho, por lo no nos sirve pr esimr soluciones de un inecución inegrl. Observción 1: El érmino de l derech en (2) es un ierne de Picrd socid l ecución linel homogéne x () = g() x() cuy solución viene dd por x() = k e g(s) ds. L ide pues, es definir h() = g(s) y(s) ds y usr un vrición de prámeros h() = k() e g(s) ds. Observción 2: Si exisiese iguldd: Y si f fuese derivble: y() = f() + g(s) y(s) ds y () = f () + g() y() Que es un ecución linel. Por no, resolviendo l homogéne: y () y() g(s) ds = g() y() = k e L no homogéne l resolverímos omndo y() = k() e g(s) ds. Es ide es usd en l demosrción. Vemos cómo excmene. Demosrción: Escribimos el érmino de l derech de (2). h() = g(s) y(s) ds Derivndo hor ess dos expresiones, por el TFC. = k() e g(s) ds g() y() = k () e g(s) ds + k() e g(s) ds g() (3) 18

19 Uilizndo (2). y() f() + h() h () = g() y() g()f() + g()h() Cos que podemos decir usndo que g() 0 Ahor, por (3) Enonces: k () e g(s) ds + h() g() g()f() + g()h() k () e g(s) ds g()f() k () g()f()e g(s) ds k() g(u)f(u)e u g(s)ds du h() = k() e g(s) ds g(u)f(u)e u g(s)ds du Por no, susiuyendo: = g(u)f(u)e u g(s)ds du y() f() + g(u)f(u)e u g(s)ds du, e g(s) ds = Vemos un cso priculr muy úil. Digmos que f() = C. Enonces se deduce que: Demosrción: Según el eorem: y() C e g(s) ds y() C + C g(u)e u g(s)ds du Observmos que denro de l inegrl enemos un derivd. d du g(s)ds (e u Enonces denominndo, pr simplificr: ) = g(u)e u g(s)ds F(u) = e u g(s)ds 19

20 y() C + C ( F(u)) du = C + C (F() F()) = y() C e g(s) ds En ese corolrio esmos comprndo y() con l solución del problem de vlores iniciles x () = g() x() con do inicil x() = C. Eso sugiere un prueb lerniv del lem de Gronwll bsd en propieddes de monoonicidd del operdor ierne de Picrd. Lem: Se g: [, b] [0, + ) coninu y β: [, b] R coninu. Supongmos que y: [, b] R coninu y verific pr odo [, b]: Enonces: y() (g(s)y(s) + β(s)) ds y() β(u)e u g(s) ds du Demosrción: Pr un función h() C[, b] se definió el ierne de Picrd correspondiene l problem de vlores iniciles: Como: { z = g() z + β() z() = 0 Th() = (g(s)h(s) + β(s)) ds Pues bien, ese operdor es monóono. Suponiendo que h 1 () h 2 () 0 pr culquier del inervlo de definición, enoncesth 1 Th 2 L hipóesis del lem dice que: y() Ty() Aplicndo T repeids veces enemos que: y() Ty() T k y() Y sbemos que l sucesión de iernes converge uniformemene l solución del problem linel. Es decir: y() β(u)e u g(s)ds du 20

21 El lem de Gronwll se obiene de lo nerior con el cmbio y () = y() f(). QED. Observción: β(s) = f(s)g(s) Teorem (de ls soluciones proximds de l ecución): Se F un función L-Lipschiz. Supongmos x 1 (), x 2 () dos soluciones proximds l sisem x () = F(, x), quiere decirse: x 1 F(, x 1 ()) ε 1 x 2 F(, x 2 ()) ε 2 [, b] Con un error δ en el do inicil: x 1 () x 2 () δ Enonces: x 1 () x 2 () δ e L( ) + (ε 1 + ε 2 ) el( ) 1 L Demosrción: Se y() = x 1 () x 2 () Enonces: y() = x 1 () x 2 () = x 1 () + x 1 (s)ds = x 1 () + F(s, x 1 (s))ds δ + F(s, x 1 (s)) F(s, x 2 (s)) ds δ + L y(s) ds x 2 () x 2 (s)ds = x 2 () F(s, x 2 (s))ds + (ε 1 + ε 2 )( ) + (ε 1 + ε 2 )( ) 21

22 Uilizndo el lem de Gronwll en y() : y() δ + (ε 1 + ε 2 )( ) + (δ + (ε 1 + ε 2 )(s )) L e s Ldu ds = Evlundo l inegrl y operndo: = δ e L( ) + (ε 1 + ε 2 ) el( ) 1 L QED. Un ejemplo de eso: l ecución del péndulo. x + λ sin(x) = 0 Donde x() es l desvición ngulr respeco de l posición de equilibrio, pero no sbemos inegrrl. Enonces, suponiendo pequeñs oscilciones de modo que x~sin (x), susiuimos en l fórmul su proximción linel: x + λx = 0 Y eso sí que sbemos inegrrlo. Esmos comprndo ls soluciones de dos ecuciones disins. x + λ sin(x) = 0 y + λy = 0 (1) { x (0) = v 0, (2) { y (0) = v 0 x(0) = x 0 y(0) = x 0 Con mismos dos iniciles pues. Y queremos ver cómo se proxim x y pr iempos pequeños. Esmos buscndo enonces soluciones proximds. El problem se plne como: { x = f 1 (, x) x( 0 ) = ξ 0, { y = f 2 (, x) y( 0 ) = ξ 1 Donde f 2 es un proximción de f 1 y los dos ξ 0, ξ 1 esán próximos: es un error en l medid. Enonces: Cómo de cerc esán x, y? Ejercicio: Usr el eorem de ls soluciones proximds pr esimr el error del cso no linel respeco de l linelizción. 22

23 Vmos esudir hor el problem de l dependenci de prámeros y condiciones iniciles. Vemos un ejemplo que lo ilusr. Consideremos de nuevo l ecución del péndulo. x + λ sin(x) = 0 Aquí, λ es un prámero que depende de l elongción del péndulo. (Más concremene, λ = g/l) Dos iniciles: { x(0) = ξ 0 x (0) = v 0 { x 1() = x() x 2 () = x () { x 1 () = x() x 2 () = x = λ sin (x 1 ) ( x 1 ) x 2 x 2 = ( λ sin(x 1 ) ), (x 1(0) x 2 (0) ) = (ξ 0 ) v 0 L solución x 1 x 2 depende de g, L. Cómo se compor l solución ne cmbios en dichos prámeros? Y ne vriciones en los vlores iniciles? Empezmos con un consecuenci direc del lem de dependenci coninu de ls condiciones iniciles (págin 8): Teorem (de dependenci Lipschiz de los prámeros iniciles): Se F loclmene Lipschiz respeco de ls vribles x en un biero D. Se un solución x del problem de vlores iniciles con do x( 0 ) = ξ 0 en el inervlo [ 0, 1 ]. Enonces exise r > 0 l que l solución del problem con dos iniciles: y( 0 ) = ξ 1, ξ 0 ξ 1 < r Esá definid en el inervlo [ 0, 1 ], y en dicho inervlo verific: x() y() e L( 0 ) ξ 0 ξ 1 Demosrción: Exise un enorno compco K de l gráfic de x conenido en D, de mner que exise ρ > 0 l que {(, B(x(), ρ)) : [ 0, 1 ]} K. Consideremos l consne de Lipschiz L de F en K. L elección r = e L( 1 0) ρ y el lem nos segurn que, l derech de 0 : x() y() e L( 0 ) ξ 0 ξ 1 e L( 1 ) ρ Lo cul quiere decir que y prolongble hs = 1 y su gráfic permnece en K hs el vlor = 1, y sí enemos l esimción en [ 0, 1 ] x() y() e L( 0 ) ξ 0 ξ 1 23

24 R n D ξ 0 ξ 1 2ρ K 0 1 R Fig 7. L perenenci K nos segur que y prolongble hs 1 y plicndo el lem de condiciones iniciles surge l proximción que d el eorem. Teorem (de dependenci coninu con respeco prámeros): Se: F: D R R x n R λ m R n Coninu en D biero, y loclmene Lipschiz respeco de l vrible x en odos los punos de D. Quiere decirse: loclmene exise L de l mner que: F(, x; λ) F(, y; λ) L x y Considermos ls soluciones x(, λ) del problem: P λ { x = F(, x; λ) x( 0 ) = ξ 0 Si exise solución del problem pr λ = λ 0, se x(, λ 0 ) en el inervlo J l derech de 0, J = [ 0, 0 + h], de form que l gráfic (, x(), λ 0 ) D, J. Enonces exise ε > 0 l que si λ λ 0 ε exise solución x(, λ) en J, y demás: lim x(, λ) = x(, λ 0 ) λ λ 0 24

25 Demosrción: Por el eorem de exisenci y unicidd sbemos que x(, λ) esá definid en el inervlo [ 0 δ, 0 + δ]. Trremos de probr un esimción de: x(, λ) x(, λ 0 ) Que usremos pr prolongr l solución l inervlo J omndo ε suficienemene pequeño. Al igul que en el eorem nerior, l gráfic x(, λ 0 ) en [ 0, 0 + h] iene un enorno compco K = {(, ξ): ξ B(x(, λ 0 ), ρ)} l que K B(λ 0, ρ) D. Denomos D λ R R x n l dominio de definición de F λ = F(,, λ). Tods ess funciones son Lipschiz consne L uniforme en K pr odos esos vlores de λ. Se y() = x(, λ) x(, λ 0 ), x (, λ) F(, x(, λ); λ) = x (, λ 0 ) F(, x(, λ 0 ); λ 0 ) = 0 y () = x (, λ) x (, λ 0 ) = F(, x(, λ); λ) F(, x(, λ 0 ); λ 0 ) No podemos segurr que eso iend cero en λ λ 0 porque necesimos conrolr el compormieno de ls soluciones. Usndo es úlim ecución diferencil: sup s [ 0, 0 +h] Que resumimos en: y() F(s, x(s, λ 0 ); λ 0 ) F(s, x(s, λ 0 ); λ) ds + 0 Usndo Gronwll, obenemos: + F(s, x(s, λ 0 ); λ) F(s, x(s, λ); λ) ds 0 F(s, x(s, λ 0 ); λ 0 ) F(s, x(s, λ 0 ); λ) 0 + L y(s) ds y() C(λ) ( 0 ) + L y(s) ds 0 y() C(λ) el( 0 ) 1 L Si λ λ 0 suficienemene pequeño, por coninuidd uniforme de F (por compcidd), podemos hcer C(λ) n pequeño como se quier pr que x(, λ) no slg de K nes de = 0 + h. Eso prueb l prolongbilidd de x(, λ) [ 0, 0 + h]. L convergenci x(, λ) x(, λ 0 ) se deduce de l esimción y que C(λ) 0 en λ λ 0. 0 QED 25

26 R x n K K B(λ 0, ρ) h R λ 0 λ 0 + ρ R λ m Fig 8: De form nálog l oro eorem, se puede probr que si λ, λ 0 esán suficienemene cerc, enonces x(, λ) no sle del compco que gener l solución x(, λ 0 ) que exise loclmene por eorem de unicidd y exisenci y es prolongble 0 + h A coninución se esudi l diferencibilidd respeco prámeros y condiciones iniciles. Teorem (de diferencibilidd de Peno o de dependenci diferencible respeco de prámeros): Supongmos F: D R R x n R λ m R n coninu en un biero D y diferencible respeco de x, λ con derivds prciles coninus. Enonces, si exise solución P λ0 pr λ 0 fijo definid en J = [ 0 h, 0 + h] exise un ε > 0 l que si λ λ 0 < ε enonces l solución de P λ exise en J. Además, dich solución x(, λ) es derivble respeco λ en el puno λ = λ 0 y su derivd prcil Cumple el sisem: D λj x(, λ) = y j () = x λ j () ED { y j () = D x F(, x(, λ 0 ); λ 0 ) y() + D λj F(, x(, λ 0 ); λ 0 ) y j ( 0 ) = 0 26

27 Vemos n sólo de dónde sle ED. Ecución de x(, λ) Si derivmos respeco de λ j : dx (, λ) = F(, x(, λ); λ) d x( 0, λ) = ξ 0 d d (D λ j x(, λ)) = d d y() = D xf(, x(, λ)) D λj x(, λ) + D λj F(, x(, λ); λ) Si hcemos λ = λ 0 en D λ x(, λ) obenemos y(). Vemos un ejemplo de odo eso. P λ { x = 2x + 2λ sin(x) x(0) = 1 1. Considermos l solución en λ = 0 x(, 0) = e 2 2. Clculmos cómo depende de λ lrededor de λ = 0. Pr ello clculmos: x(, λ) λ λ=0 3. x(, λ) esrá definido si λ es pequeño en culquier inervlo codo [ N, N] lrededor de = 0. Llmemos: y() = x(, λ) λ λ=0 Que es solución de l ecución prméric. y () = D x F(, x(, 0); 0) y() + D λ F(, x(, 0); 0) y () = (2 + λ cos(x)) y() + sin (x) Priculrizndo pr x(, 0) = e 2, λ = 0 27

28 Enonces: { y () = 2 y() + sin (e 2 ) y(0) = 0 Que es un ecución linel homogéne que se puede inegrr. Teorem (de dependenci diferencible respeco vlores iniciles): Se F: D R R x n R n con D biero y F iene derivds prciles coninus respeco de l vrible x. Consideremos el problem pr ( 0, ξ) D: x (, ξ) = F(, x(, ξ)) P ξ 1 x( 0 ) = ξ = (ξ ) { ξ n Suponemos que pr ξ = ξ 0 fjo el problem P ξ iene solución únic en el inervlo cerrdo J lrededor de 0. Enonces: 1) Exise ε > 0 l que P ξ iene solución únic en J, digmos x = x(, ξ), siempre que ξ ξ 0 < ε. 2) L solución es diferencible en ξ = ξ 0 3) Si x(, ξ) z j () = ξ j Donde D x F represen l mriz diferencil de F respeco de x, enonces ess derivds prciles cumplen l llmd ecución vricionl: z j () = D x F(, x(, ξ 0 )) z j () { z j ( 0 ) = ( 0) = e j, (j-ésimo vecor cnónico) 28

29 Observciones: 1. Ese eorem es complemene nálogo l de dependenci de prámeros. De hecho el eorem de dependenci de vlores iniciles se puede reducir l de prámeros, y vicevers, medine el cmbio: y(, 0, ξ) = x(, 0, ξ) ξ Así enemos que y(, 0, ξ) es solución del sisem: { y (, ξ) = F(, y(, ξ) + ξ) y( 0 ) = 0 Por el eorem de derivción prméric se iene: Como enemos: Enonces: { y j () ξ j = D x F(, y j (, ξ) + ξ) ( y j() ξ j + e j ) y j () ξ j 0 = 0 y j () + e ξ j = z j () j { z j () = D x F(, x)z j z j ( 0 ) = e j L reducción en el oro senido se reliz inroduciendo los prámeros como nuevs vribles. x n+1 = λ 1,, x n+m = λ m Por consiguiene, se ñdirán ls ecuciones diferenciles: x n+1 = 0,, x n+m = 0 Y el sisem qued pr ls funciones incógnis x = (x 1,, x n+m ): x = F (, x ) ξ 0 λ x ( 0 ) = ( 1 ) { λ m 29

30 Ls úlims m componenes de F: D R R n+m R n+m son evidenemene nuls. 2. L mriz Φ() = D ξ x(, ξ) ξ=ξ0 cuys columns son ls derivds prciles respeco ξ j es solución fundmenl normlizd en = 0 del sisem de n ecuciones diferenciles lineles que, enonces cumple Φ() 0 en odo el inervlo de definición. 3. L plicción ξ R n φ (ξ) = x(, ξ) Cumple que iene diferencil en ξ 0 con deerminne que nunc se nul, por consiguiene, medine el eorem de l función invers, se puede decir que es un plicción loclmene inverible en un enorno de ξ 0. En cso de ser el sisem originl un sisem uónomo F(, x) = F(x) se dice que φ represen el flujo del cmpo de vecores F(x) y es un difeomorfismo locl en un enorno de ξ 0. Es ineresne observr cómo ese difeomorfismo locl cmbi el volumen: d d Φ = rz (D xf(x(, ξ 0 ))) Φ = div(f) Φ Demosrción: Uilizmos el resuldo obenido del eorem de dependenci Lipschiz respeco los dos iniciles (págin 23). Elegimos ε < r en dicho eorem, de mner que nos segurmos l exisenci de solución con do inicil ξ en [ 1, 2 ]. Designemos φ() = x(, ξ 0 ) y consideremos el compco K del menciondo eorem. Observemos l diferencibilidd uniforme de F. Es decir: ddo δ > 0 exise un τ F > 0 de l mner que, pr odo (, x), (, y) K con x y τ F se iene que: En efeco: F(, x) F(, y) D x F(, x)(x y) δ x y F(, x) F(, y) D x F(, x)(x y) = = F(, y) D x F(, x) y (F(, x) D x F(, x) x) = = F(, z) D x F(, x) z z=y (F(, z) D x F(, x) z z=x ) TVM x y sup D x F(, z) D x F(, x) x z y 30

31 Por coninuidd uniforme (por compcidd) podemos enconrr τ F > 0 l que: En x z x y τ F. sup D x F(, z) D x F(, x) δ x z y Consideremos enonces l plicción flujo: x: [ 0, 1 ] B(ξ 0, τ F ) K Definid como x(, ξ) pr l solución con do inicil ξ. Tommos l mriz Φ de l observción 2 y probmos l diferencibilidd de l plicción x respeco de ξ evlud en ξ 0, y que de hecho l diferencil es Φ, solución de l ecución vricionl. Quiere decirse, rmos de probr que: x(, ξ) x(, ξ 0 ) Φ() (ξ ξ 0 ) = o ξ ξ 0 En ξ ξ 0 (noción o pequeñ de Lndu). Uilizmos l siguiene expresión pr l derivd de l invers de un mriz: De donde se deduce: d dφ d Φ 1 1 = Φ d Φ 1 Enonces: dφ 1 d = Φ 1 D x F(, φ()) d (Φ 1 () (x(, ξ) x(, ξ 0 ) Φ() (ξ ξ 0 ))) = d (Φ 1 () (x(, ξ) x(, ξ 0 ))) d d = Φ 1 () (F (, x(, ξ) F(, φ()) D x F(, φ()) (x(, ξ) φ())) Ls mrices Φ, Φ 1 esán cods en K por C debido l diferencibilidd uniforme de F. C ε x(, ξ) φ() Y por el lem de dependenci Lipschiz respeco de los vlores iniciles, omndo ξ ξ 0 lo suficienemene pequeño hcemos l expresión nerior, no myor que: Lo cul prueb que: C ε e L ( 1 0) ξ ξ 0 x(, ξ) x(, ξ 0 ) Φ()(ξ ξ 0 ) C ε e L ( 1 0) ξ ξ 0 ( 0 ) Y, por no, l diferencibilidd de x respeco ξ. 31

32 Probmos hor l coninuidd de Φ respeco ξ. Denomos: Φ 1 = Φ(, ξ 1 ) Φ 2 = Φ(, ξ 2 ) Un cálculo nálogo l nerior demuesr que: d d Φ 2 1 Φ 1 = Φ 2 1 (D x F(, x(, ξ 2 ))) (D x F(, x(, ξ 1 ))) Φ 1 1 L ecución vricionl iene mriz de coeficienes cod por L (co de D x F en K), y por consiguiene: Por no: Φ j () ±1 ε L( 0 ) d d (Φ 2 1 Φ 2 ) e 2L( 1 0 ) D x F(, x(, ξ 2 )) D x F(, x(, ξ 1 )) Finlmene: Φ 1 Φ 2 Φ 2 (Φ 1 2 Φ 1 I) e 3L( 1 0 ) 1 D x F(, x(, ξ 2 )) D x F(, x(, ξ 1 )) d L coninuidd se sigue d el coninuidd e D x F, x(, ξ). 0 QED 32

33 Pblo Esquer Csillo Myo