Números reales. Factorización. a b. Elaborado y Recopilado por: Magístra Alba Castillo de Quiel
|
|
|
- Tomás Jorge Nieto Figueroa
- hace 6 años
- Vistas:
Transcripción
1 ( c) c Fctorizció Números reles Q /, Ζ 0 Elordo Recopildo por: Mgístr Al Cstillo de Quiel
2 CONTENIDO Pági NÚMEROS REALES EXPONENTES 8 Propieddes De Los Epoetes 8 RADICALES 0 Propieddes De Los Rdicles 0 Le Distriutiv 0 Opercioes Co Rdicles Sum Y Rest De Rdicles Multiplicció De Rdicles Multiplicció De Rdicles De Distitos Ídice Divisió De Rdicles Rciolizció De Deomidores PRODUCTOS NOTABLES 7 Biomio Al Cudrdo 7 Triomio Al Cudrdo 8 Biomio Al Cuo 8 Sum Por Difereci (Cojugdos) 8 Producto De L Form ( )( c d ) 9 FACTORIZACIÓN 0 Fctor Comú Fctor Comú Moomio Fctor Comú Poliomio Fctor Comú Por Agrupció De Térmios Triomio Cudrdo Perfecto Difereci De Cudrdos Triomio De L Form c Triomio De L Form c Sum Y Difereci De Cuos Perfectos 7 Poliomio Cuo Perfecto 7 OPERACIONES CON FRACCIONES ALGEBRAICAS 9 Reducció 9 Multiplicció Y Divisió 9 Comició De Frccioes 0 7 FIGURAS GEOMÉTRICAS PLANAS, IDENTIFICACIÓN, CÁLCULO DE PERÍMETRO Y ÁREA 7 Coceptos Geerles Sore Polígoos 7 Elemetos De Los Polígoos 7 Polígoos Regulres 7 El Triágulo 7 Segmetos Notles De U Triágulo Y Putos De Itersecció 8 7 Perímetro De U Triágulo 9 7 Teorem De Pitágors 9 7 Cudriláteros 7 Áre De Cudriláteros
3 7 Coceptos Fudmetles Sore L Circufereci Y El Círculo 7 Elemetos De L Circufereci Y El Círculo 7 Cuerpos Geométricos (Sólidos), Idetificció, Cálculo Del Áre Y Volume 8 CONCEPTOS GENERALES DE LA TRIGONOMETRÍA 8 Sistem De Coordeds Rectgulres O Plo Crtesio 8 Fucioes Trigoométrics Básics 8 8 Fucioes Trigoométrics De Culquier Águlo 9 8 Fucioes Trigoométrics De U Águlo E Posició Norml 0 8 Fucioes Pr Culquier Águlo E Térmios De Fucioes De Águlo Agudo (Águlos De Refereci O Relciodos) 8 Vlores De Ls Fucioes Trigoométrics De Los Águlos Especiles De 0 º, º, 0º Y Sus Múltiplos 87 Fucioes Trigoométrics De Águlos De Cudrtes 88 Águlos Cotermiles 89 Fucioes Trigoométrics Y Sus Gráfics 7 80 Gráfics De Ls Fucioes Trigoométrics 7 BIBLIOGRAFIA 7
4 NÚMEROS REALES El cojuto umérico co el que predemos cotr es el Cojuto de Los Números Nturles N {,,,, } Cudo se trj solmete co este cojuto l sustrcció o siempre es posile, por ejemplo - 8- o tiee respuest e el cojuto de úmeros turles Surge etoces el Cojuto de Números Eteros Z {,,,0,,,, } Este cojuto umérico o es cerrdo pr l divisió porque o siempre l dividir úmeros eteros oteemos como cociete u úmero etero, por ejemplo, l dividir oteemos 7 que es u úmero etero, pero o tiee solució e este cojuto umérico Pr resolver est situció surge el Cojuto de Números Rcioles Q /, Ζ 0 Deemos oservr que todo úmero etero es u úmero rciol, es decir, el cojuto de los úmeros eteros es u sucojuto de los úmeros rcioles, que todo úmero etero se puede escriir como u úmero rciol co deomidor, por l cul Z Q Todo úmero rciol, se puede represetr tmié como u úmero deciml fiito o u úmero deciml periódico, que se otiee l dividir el umerdor etre el deomidor Por ejemplo: ; 0 ; 0,, 0 99 Alguos úmeros o puede represetrse como u cociete de dos úmeros eteros, ellos se les cooce como el Cojuto de Números Irrcioles se represet simólicmete por I Estos úmeros puede represetrse como úmeros decimles ifiitos o periódicos, por ejemplo: π 9 e A l uió del Cojuto de Números Rcioles el Cojuto de Números Irrcioles se le deomi Cojuto de Números Reles R, es decir, u úmero rel puede ser turl, etero, rciol o irrciol; como lo muestr el siguiete esquem Números Reles R Rcioles Q Irrcioles I Eteros Z Negtivos (Opuestos de los Nturles) Cero Nturles N
5 El cojuto de úmeros Reles puede represetrse gráficmete sore los putos de u rect l cul llmremos l rect rel El cojuto de úmeros Reles cumple l relció de orde, l cul estlece que ddos dos úmeros reles culesquier, se cumple u sólo u de ls siguietes firmcioes: < > Es importte oservr que e l rect rel, todo úmero que esté l derech es mor que culquier que este su izquierd E ocsioes ecesitmos trjr co todo el Cojuto de Números Reles o co u sucojuto de él Pr represetr estos cojutos, utilizmos el cocepto de itervlo U itervlo es u cojuto cotiuo de úmeros reles Itervlo Notció de itervlo Notció de cojuto Aierto (, ) { R < < } Cerrdo [, ] { R } Semiiertos (, ] [, ) { R < } { R < } Represetció gráfic (, ) { R < } [, ) { R } Ifiitos (,) (,] (, ) { R < } { R } { R < < }
6 PRÁCTICA Nº I Eprese los siguietes itervlos e otció de cojuto represete gráficmete (,7] [ 8,] (, ),, 8, II Eprese cd uo de los siguietes cojutos e otció de itervlo represete gráficmete R < R { } 7 R < R < R R 7 < < 8 { } III Eprese e otció de cojuto e form de itervlo
7 RESPUESTAS I Prte R < 7 ) { } ) { R 8 } ) R ) R ) R < 8 ) R II Prte ), ) 7, ), ) [,] ), ) ( 7,8) 7
8 EXPONENTES Propieddes de los epoetes ) Epoetes eteros positivos: Los epoetes eteros positivos se soci u úmero rel pr idicr l multiplicció repetid de tl úmero Por ejemplo escriimos, e dode el etero positivo se llm epoete e idic que el úmero rel se repite tres veces como fctor fctores El etero positivo se llm epoete de el úmero rel es l se L epresió es u poteci se lee como " l -ésim poteci " o " l " Teorem : pr todo úmero rel, siedo u etero positivo: Si, > 0, etoces > 0 Si < 0, etoces > 0 si es pr Si <0, etoces <0 si es impr Si 0, etoces 0 Si 0, etoces Ls lees ásics pr los epoetes se estlece lo siguiete: Teorem : pr culesquier, úmeros reles siedo m eteros positivos: m m los epoetes se sum m los epoetes se multiplic m [ ] [ ] 0 Todo úmero rel elevdo 0 m m m m ó Los epoetes se rest m Si m<, etoces: m 7 Ests lees pr los epoetes se puede eteder regls que iclue tres o más m p m p potecis Por ejemplo: Ejemplo : Ecuetre el producto ( )( ) Solució: ( )( ) ( ) 8
9 9 Ejemplo : Ecotrr el producto de ( ) z Solució: ( )( ) ( ) ( ) 9 7 z z Ejemplo : Ecuetre el producto de Solució: 9 9 PRÁCTICA Nº ( )( ) ( ) ( ) ( ) ( ) ( ) z c c 7 7 z z 7 8 ( ) ( ) k k k k 9 ( ) ( ) [ ] ( ) 0 ( ) ( ) [ ] ( ) ( ) [ ] Ejemplo : Eprese ( ) 0 z si epoetes egtivos simplificr Solució: ( ) ( )( ) [ ] [ ] ( )( ) ( )( ) 0 z Ejemplo : Eprese ( ) si epoetes egtivos simplifique Solució: ( ) PRÁCTICA Nº ( ) ( ) 0 d c d c ( ) 0 ( )( ) 7 ( ) ( ) ( )
10 RESPUESTAS PRÁCTICA Nº 7 8 ) ; ) 8 ; ) 7) ; 8) k 8k ; ) ; 9) 7 ; 0) c z ; ) 8 08 z ; ) ; PRÁCTICA Nº c d ; ; ; 7 ; ; 9 RADICALES Ríz es u epresió lgeric que elevd u poteci reproduce l epresió dd Así es l ríz cudrd de por que ( ) Pero tmié es ríz cudrd de porque ( ) Así es ríz cúic de 7 porque ( ) 7 El sigo de ríz es, llmdo sigo rdicl Dejo de este sigo se coloc l ctidd l cul se etre l ríz llmd ctidd surdicl El sigo llev u ídice que idic l poteci que h que elevr l ríz pr que reproduzc l ctidd surdicl Por coveció el ídice se suprime cudo el sigo o llev ídice se etiede que el ídice es Si u ríz idicd es ect, teemos u ctidd rciol Si o tiee ríz ect, es irrciol Así: es u ctidd rciol es u ctidd irrciol, este o tiee ríz ect El grdo de u rdicl lo idic el ídice de l ríz Así: grdo, es u rdicl de tercer grdo es u rdicl de segudo Propieddes de los rdicles Le distriutiv E l rdicció o se cumple est le co relció l sum l rest; esto es: 0
11 o es igul Oserve: ; pero 9 o es igul L rdicció es distriutiv co relció l multiplicció l divisió: E efecto si teemos: c esto es igul c Ejemplo : Simplifique Solució: Es igul porque 00 0 ( )( ) 0 E el cso de l divisió podemos plicr l siguiete relció: si mismo siempre cudo 0 es lo Ejemplo : Simplifique 9 Solució: 9 9 Simplificció de rdicles Es reducir su más simple epresió U rdicl está reducido su más simple epresió, cudo l ctidd surdicl es eter del meor grdo posile E l simplificció de rdicles cosiderremos los dos csos siguietes: Cso : Cudo l ctidd surdicl cotiee fctores cuo epoete es divisile por el ídice Ejemplo : Simplifique 9
12 Solució: 9 Se descompoe el 9 ect l ríz idicd Así que 9 9 e dos fctores tles que uo de ellos pose ríz cudrd Etoces Se sc del rdicl, quellos fctores cuo epoete se divisile por el ídice (dividiedo su epoete por el ídice) Simplifique: PRÁCTICA Nº z 8 CASO : Cudo los fctores de l ctidd surdicl el ídice tiee u divisor comú Ejemplo : Simplifique Solució: Se descompoe se reemplz (teorem ), l ivers teemos: plicdo l tercer regl de los epoetes Simplifique: PRÁCTICA Nº 0 0 m Reducció de rdicles l míimo comú ídice Est operció tiee como ojeto covertir rdicles de distitos ídice e rdicles equivletes que teg el mismo ídice Pr ello, se plic l siguiete regl: Se ecuetr el M C M de los ídices, que será el ídice comú se elev cd ctidd surdicl l poteci que result de dividir el ídice comú etre el ídice de su rdicl Ejemplo : Reduzc l míimo comú ídice:, Solució: El MCM de los ídices:, es Dividiedo etre cd ídice se otiee el epoete de l ctidd surdicl
13 ( ) ( ) 8 9 PRÁCTICA Nº Reduzc l míimo comú ídice:,, m,,,, 8, m Opercioes co rdicles Sum rest de rdicles Se descompoe ls ctiddes surdicles se etre quells ctiddes que se pued scr del rdicl, luego; se reduce los rdicles semejtes cotiució se escrie los rdicles o semejtes co sus propios sigo Ejemplo : Reduzc 80 Solució: 80 Ejemplo 7: Reduzc 8 ( ) ( ) Solució: ( ) ( ) ( ) PRÁCTICA Nº7 Simplifique: 9 9 m 9m m m 0 7 ( )
14 Multiplicció de rdicles Regl: Se multiplic los coeficietes etre sí ls ctiddes surdicles etre sí, colocdo este último producto jo el sigo rdicl comú se simplific el resultdo Así que: m m Ejemplo 8: Multiplique Solució: ( )( ) ( ) ( ) ( ) Simplifique: por PRÁCTICA Nº8 por por por Multiplicció de rdicles de distitos ídice Se reduce los rdicles l míimo ídice, se multiplic, como rdicles del mismo ídice Ejemplo 9: Multiplique por Solució: 7 ( ) ( ) PRÁCTICA Nº9 Simplifique: Divisió de rdicles Divisió de rdicles del mismo ídice
15 Regl: Se divide los coeficietes etre sí ls ctiddes surdicles etre sí, colocdo este último cociete, jo el sigo rdicl comú se simplific el resultdo Ejemplo 0: Divid Solució: 7 8 etre Aplicdo l propiedd distriutiv respecto l divisió pero e form ivers: Resuelv: etre 8 z etre z PRÁCTICA Nº0 8 etre etre Rciolizció de deomidores U frcció que cotiee u rdicl e el deomidor se puede epresr siempre por medio de otr frcció equivlete que o coteg igú rdicl e el deomidor Este proceso se llm Rciolizció de Deomidores Muchs opercioes que comprede rdicles se fcilit si l pricipio se rcioliz todos los deomidores Si el rdicdo es u frcció cuo deomidor es u moomio, o si el deomidor de u frcció tiee u rdicl como fctor, el rdicl se elimi del deomidor, segú el método que se ilustr e los ejemplos siguietes: Ejemplo : Rciolice Solució: Ejemplo : Rciolice Solució: 8 8
16 PRÁCTICA Nº Simplifique: 7 m Al rciolizr el deomidor de u frcció, cudo el deomidor es u iomio que cotiee rdicles de segudo grdo, se multiplic mos térmios de l frcció por l cojugd del deomidor se simplific el resultdo L cojugd de u epresió es que defiere e el sigo que ue sus térmios - c es c Ejemplo : Rciolice Solució: ( )( ) ( )( ) - Simplifique: PRÁCTICA Nº PRÁCTICA Nº 7 ; z 0z PRÁCTICA Nº ; ; 7 ; PRÁCTICA Nº,, 7 RESPUESTAS ; ; ; ; m, 7, ; , 9 m m,,
17 PRÁCTICA Nº7 7 ; m m ; ; 0 ; PRÁCTICA Nº8 ( ) ; ( ) 7 ; ( 0) 8 ; ; PRÁCTICA Nº9 ; 9 ; ; PRÁCTICA Nº0 ; 8 ; ; z PRÁCTICA Nº ; ; ; m m PRÁCTICA Nº -- ; ; ; ( )( ) PRODUCTOS NOTABLES Etre los diversos productos lgericos, h lguos que deido su form recie el omre de Productos Notles E los csos que veremos cotiució ls letrs represet úmeros reles Biomio l Cudrdo ( ± ) ± Pr clculr el cudrdo de u iomio, se elev l cudrdo el primer térmio, más o meos el dole producto del primer térmio por el segudo, más el cudrdo del segudo térmio Ejemplos: ( ) ( ) ( )( ) ( ) 9 7
18 ( ) ( ) Triomio l Cudrdo ( z) z z z El cudrdo de u triomio es igul l sum de los cudrdos de cd uo de sus térmios más el duplo de ls comicioes iris que co ellos puede formrse Est regl se cumple, culquier que se el úmero de térmios del poliomio Ls comicioes iris so los productos tomdos co el sigo que resulte de l multiplicció Osérvese que los cudrdos de todos los térmios so positivos Ejemplo: ( z) ( ) ( ) ( z) ( )( ) ( )( z) ( )( z) Biomio l Cuo 9 z z z ( ± ) ( ) ± ( ) ( ) ( )( ) ± ( ) El cuo de u iomio es igul l cuo del primer térmio más o meos el triple producto del cudrdo del primero por el segudo térmio más el triple producto del primero por el cudrdo del segudo térmio más o meos el cuo del segudo térmio Ejemplos: ( ) ( ) ( ) ( ) ( )( ) ( ) 8 ( ) ( ) ( ) ( ) ( )( ) ( ) 7 8 Sum por Difereci (Cojugdos) ( )( ) El producto de l sum de dos ctiddes por su difereci es igul l cudrdo de l primer ctidd meos el cudrdo de l segud ctidd 8
19 9 Ejemplos: ( )( ) ( ) ( ) 7 ( ) 8 ( )( ) ( ) ( ) 9 9 ( )( ) ( ) [ ] ( ) [ ] m m m m m m m m ( ) ( ) m m m m m Producto de l Form ( )( ) d c ( )( ) ( ) d c d c d c Cso Prticulr si c ( )( ) ( ) d d d Ejemplos: 0 ( 7)( ) (7 ) (7)() 8 ( 8)( ) ( ) ( ) [ ] ( )( ) ( 7)( ) ( ) ( ) [ ] ( )( ) 7 7 ( )( ) ( )( ) ( )( ) ( )( ) [ ] ( )( ) ( )( ) ( )( )( ) ( )( ) ( )( ) [ ] ( )( ) - 0
20 I Resolver los productos idicdos: PRÁCTICA Nº ) ( ) R: ) ( ) 8 R: 0 m 0m R: 009m m m m R: ) ( )( ) ) ( )( ) R: 0 ) ( ) ) ( )( ) 7) ( ) R: R: 8) ( ) 9 9 R: 8 0 R: 0 R: 7 R: 8 9) ( )( ) 0) ( ) ) ( )( ) 9 ) m R: m m 9 ) ( )( ) R: ) ( )( 7) R: 8 7 R: 8 0 R: 7 z r R: z 9r z r z r zr ) ( ) ) ( )( ) 7) ( ) 8) R: 9) ( )( ) R: 0) ( )( ) R: FACTORIZACION L multiplicció cosiste e oteer el producto de dos o más epresioes dds, los cules se llm fctores de ese producto Ahor estudiremos el cso iverso, que cosiste e oteer los fctores de u producto ddo Fctorizr u poliomio sigific epresrlo como u producto de poliomios irreductiles U poliomio co coeficietes e lgú cojuto de úmeros es primo o irreducile sore ese cojuto, si o puede escriirse como producto de dos poliomios co coeficietes e el cojuto de úmeros idicdo 0
21 El máimo fctor comú de u epresió es el producto de los fctores que prece e cd térmio, cd uo elevdo l epoete meor diferete de cero que prezc e culquier térmio Cosideremos lguos csos de fctorizció de poliomios L mor prte de estos tipos de fctorizció tiee su fudmeto e ls fórmuls de productos otles Fctor Comú Fctor Comú Moomio Si cd térmio de u epresió lgeric cotiee u moomio que es fctor comú, ese moomio es u fctor de tod l epresió como cosecueci de l propiedd distriutiv L epresió se descompoe e dos fctores: el fctor comú el formdo por los térmios del poliomio dividido etre el fctor comú ( c) c c c Ejemplos: Descompoer e fctores ( ) m m m m( m m ) 7 7( ) Fctor Comú Poliomio Si los térmios de u epresió lgeric tiee u poliomio como fctor comú, l fctorizció es el producto de dos fctores, el primero es el fctor comú el segudo fctor se otiee co u proceso semejte l cso de fctor comú moomio Ejemplos: Fctorice ( ) ( ) ( )( ) ( ) ( ) ( )( ) ( )( ) ( )( ) ( )( ) ( ) [( ) ( ) ] ( -)( ) ( )() ( )
22 7 ( ) ( ) ( ) ( ) ( ) ( )( ) Fctor Comú por Agrupció de Térmios Se grup los térmios que tiee lgú fctor comú se resuelve como fctor comú moomio luego como fctor comú poliomio Ejemplos: Fctorice ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) ( ) ( )( ) Triomio Cudrdo Perfecto ( ) ( ) ( 9 ) ( ) ( ) ( ) ( )( ) U triomio es Cudrdo Perfecto si se tiee dos térmios cudrdos u tercer térmio epresdo como el dole producto de sus ríces Pr fctorizrlo se etre l ríz cudrd l primero tercer térmios del triomio se sepr ests ríces por el sigo del segudo térmio El iomio formdo se elev l cudrdo ( ) ( ) Ejemplos: Fctorice 9 ( ) ( )( )
23 ( ) ( )( ) 7 9 ( ) ( ) ( ) ( ) 9 m m m m ( )( ) m Difereci de Cudrdos ( )( ) Pr fctorizrlo se etre l ríz cudrd l miuedo sustredo se multiplic l sum de ests ríces cudrds por su difereci Ejemplos: Fctorice ( )( )
24 7 8 9u v u v 8 9 ( u v)( u v) ( 9 )( 9 ) ( ) [ ( ) ] [ ( ) ] ( )( ) Triomio de l Form c Se usc dos úmeros eteros p q cu sum se cuo producto se c fctorizció es el producto de los iomios ( p) ( q) L Ejemplos: Fctorice 9 Buscr dos úmeros eteros p q tles que p q pq ( )( ) Los úmeros so 0 8 p q 8 ( ) ( 8)( ) pq -8 ( 8)( ) 8 ( )( ) ( )( ) p q pq () - Triomio de l Form c Pr fctorizr u triomio de l form c se multiplic divide por el coeficiete de luego se resuelve como el cso del triomio de l form c Ejemplos: Fctorice 0 Solució:
25 Fctorice Solució: Fctorice 0 7 Solució: ( 0) 9 ( ) 0 0 ( 0)( ) ( 0)( ) 0 ( )( ) ( ) ( ) ( ) ( ) ( ) 0 ( )( ) ( )( ) 0(0 7 ) 7 0 (0 ) 7(0 ) 0 0 ( 0 )( 0 8) 0 ( ) ( ) 0 ( )( ) U form ltertiv de fctorizr este triomio es oteer úmeros m,, p q tles que m p se fctores del coeficiete de, q se fctores del térmio costte l sum de los productos mp qr se el coeficiete de Estos úmeros se otiee medite esos c m mp q ( ) qp Dode Ejemplos: Fctorice 0 m mp qr c qp
26 Solució: Los fctores de los coeficietes dee ser: ( )( ) ; 0 ( )( ) Agrupmos: ( )( ) ( )( ) Luego, 0 ( )( ) El térmio - se otiee resolviedo: 0 ( )( 7) 7 7 ( )( ) Sum Difereci de Cuos Perfectos Sum de cuos perfectos ( )( ) L sum de dos cuos perfectos se descompoe e dos fctores: El primer fctor es l sum de sus ríces cúics el segudo fctor se otiee elevdo l cudrdo l primer ríz, meos el producto de ls dos ríces, más el cudrdo de l segud ríz Difereci de cuos perfectos ( )( ) L difereci de dos cuos perfectos se descompoe e dos fctores: El primer fctor es l difereci de sus ríces cúics el segudo fctor se otiee elevdo l cudrdo l primer ríz, más el producto de ls dos ríces, más el cudrdo de l segud ríz
27 7 Ejemplos: Fctorice ( ) ( ) ( )( ) ( ) [ ] ( )( ) ( ) ( ) ( ) ( ) [ ] ( )( ) ( ) ( ) ( )( ) ( ) [ ] ( )( ) ( ) ( ) ( ) ( )( ) [ ] ( )( ) Poliomio Cuo Perfecto ( ) ± ± ± Pr que u poliomio de térmios se el cuo de u iomio dee cumplir ls siguietes codicioes: El primer el último térmio se cuos perfectos Que el segudo térmio se más o meos el triple del cudrdo de l ríz cúic del primer térmio multiplicdo por l ríz cúic del último térmio Que el tercer térmio se más el triple de l ríz cúic del primer térmio por el cudrdo de l ríz cúic del último térmio Si los térmios so positivos se refiere l cuo de l sum de ls ríces cúics de su primero último térmio si so lterdos positivos egtivos, l epresió dd es el cuo de l difereci de dichs ríces Ejemplos: Fctorice ( ) 7 8 ( ) ( ) ( )( )
28 0 0 8 ( ) ( ) ( ) 7 ( )( ) 88 ( ) ( 7 ) ( )( 7 ) 7 ( 7 ) PRÁCTICA Nº I E cd uo de los ejercicios, fctorice l epresió dd 0 00 R: ( ) 9 8 R: ( )( ) R: ( )( ) R: ( 7 )( ) 0 8 R: ( )( ) R: ( ) 7 R: ( )( ) 8 ( ) R: ( )( ) R: ( )( )( ) 7 R: ( )( 9 ) R: ( )( 0 ) R: ( )( )( ) R: ( ) 8 m m 8 R: ( m ) 8 R: ( ) R: ( )( ) 7 m m 8 R: ( )( m) m m m R: ( ) m 8
29 9 0 R: ( ) 0 00 R: ( ) 9 R: ( ) R: 7 c m ( ) ( ) R: ( )( ) ( c) c R: ( )( ) m ( m ) R: ( )( ) OPERACIONES CON FRACCIONES ALGEBRAICAS Reducció L epresió se fctoriz si eistier fctores comues e el umerdor deomidor de l frcció se ccel pr reducir l frcció su epresió más simple Ejemplo: reduzc cd frcció su más simple epresió ( )( ) ) ( )( ) ) c d 0c 0d ( c d ) 0( c d) ( c d)( c d) 0( c d) c d ) 8 0 ( )( ) ( )( ) Multiplicció Divisió Ls regls pr multiplicr dividir frccioes lgerics so los mismos que ls regls ritmétics: Multiplíquese umerdores deomidores: A C AC B D BD A C A D AD Iviértse multiplíquese: Al igul que e ritmétic, primero se B D B C BC ccel o elimi los fctores comues que prece e el umerdor deomidor, tes de multiplicr Ejemplos: Relice ls opercioes idicds: 9
30 0 ) ) ( ) ( 8 ) )( ( 8 m m m m m m m m m m ) ) )( ( ) ( ) ( ) ) ( ) ( ) ( ) )( ( ) ) / ( ) ( 8 8 ) ) ( ) )( ( ) )( ( 9 9 ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) )( ( Comició de frccioes L comició (dició o sustrcció) de frccioes lgerics requiere del coocimieto de comició de frccioes ritmétics de l fctorizció Pr simplificr ls frccioes lgerics se otiee el mcd de ls frccioes se plic l regl fudmetl de ls frccioes: l multiplicr o dividir el umerdos el deomidor por el mismo úmero (diferete de cero) o cmi el vlor de u frcció Ejemplos: Simplifique ls epresioes siguietes: ) ) )( ( 7 7 ) )( ( 7) ( ) ( ) ( ) )( ( ) )( ( 7 9 ) ) ( ) (
31 ) ( ) ( ) ( 0 ) ( ) ) ( 7 ) ( 7 ) )( ( ) 7( ) ()( ) ( ) ( 7 ) ( ) ( ) )( ( PRÁCTICA N Simplifique: ) 8 9 R/ ) R r R r 8 R/ R rr r ) m m R/ m ) 7 0 R/ ) ( ) ( ) R/ ) ( ) 8 R/ ) )( ( ) ( 7) R/ ) ( 8) 0 9 R/ 7 9) R/ 0) R/
32 7 FIGURAS GEOMÉTRICAS PLANAS, IDENTIFICACIÓN, CÁLCULO DE PERÍMETRO Y ÁREA 7 Coceptos geerles sore polígoos: Se llm polígoo l porció de plo limitd por segmetos de rect 7 Elemetos de los polígoos: Ldos: So los segmetos de rect de que está formdo el polígoo Águlos iteros de u polígoo: so los formdos por cd dos ldos cosecutivos Águlos eteriores de u polígoo: so los águlos dcetes los iteros, se otiee prologdo los ldos e u mismo setido Vértice: Es el puto e el cul se cort dos ldos del polígoo Apotem: Es el segmeto de rect perpediculr u ldo del polígoo trzdo desde el cetro Digol: Se llm digol l segmeto determido por dos vértices o cosecutivos 7 Perímetro: El perímetro pr u polígoo es igul l sum de l logitud de sus ldos se epres e medids de logitud (uiddes lieles) 8 Áre: Es l medid de u superficie o se el tmño de ést epresd e uiddes cudrds ( m, cm, pu lg ) 9 Superficie: Es l form de u figur geométric, tles como, trigulres, cudrds, circulres, etc Y coocemos que es u perímetro, u áre u superficie Más delte defiiremos lgus figurs coocids, ésts os servirá pr clculr su perímetro El áre de figurs más complicds es el resultdo de l sum de áres de figurs coocids Los polígoos irregulres so quellos que o tiee águlos i ldos cogruetes Ve figur Los polígoos regulres quellos cuos ldos águlos so igules, es decir so equilátero equiágulo Ve figur Figur : Polígoo irregulr Figur : Polígoo regulr AB BC CD DE EF FC CB D A C B F E
33 Segú el crácter etrte o sliete de sus águlos recie el omre de polígoos coveos cudo todos sus águlos so meores de 80º polígoos cócvos cudo tiee uo o más águlos iteriores mores 80º Sum de los águlos eteros de u polígoo: Teorem : L sum de los águlos eteriores (Se) de todo polígoo es igul 0 Dode Se 0 Teorem : Si los ldos de u águlo so respectivmete perpediculres los ldos del otro, los dos águlos so igules o suplemetrios Ve l figur Figur : Polígoo regulr B C c A D AB BC AD CD etoces el c so suplemetrios 7 Polígoos regulres Clsificció segú el úmero de ldos: De cuerdo co el úmero de ldos los polígoos regulres recie omres especiles El polígoo de meor úmero de ldos es el triágulo NUMEROS DE LADOS NOMBRES Tres triágulo equilátero Cutro cudrdo Cico petágoo regulr Seis heágoo Siete heptágoo regulr Ocho octágoo Nueve oeágoo regulr Diez decágoo Oce edecágoo regulr Doce dodecágoo Quice petdecágoo regulr Veite icoságoo -ldos -ágoo regulr Los polígoos de,,, 7, 8, 9, etc ldos, o recie omres especiles
34 Pricipios reltivos los polígoos regulres: Pricipio : A todo polígoo regulr se le puede circuscriir u circufereci Pricipio : E todo polígoo regulr se puede iscriir u circufereci Pricipio : El cetro de l circufereci circuscrit u polígoo regulr es, tmié, el cetro de su circufereci iscrit Pricipio : Si u polígoo iscrito e u circufereci tiee sus ldos igules, el polígoo es regulr Pricipio : Los rdios de u polígoo regulr so igules Pricipio : Todo rdio de u polígoo regulr es isectriz del águlo por cuo vértice ps Pricipio 7: Ls potems de u polígoo regulr so igules Pricipio 8: Tod potem de u polígoo regulr isec (por ser meditriz), el ldo correspodiete Pricipio 9: E u polígoo regulr de ldos: 0 Cd águlo cetrl " c " es igul Cd águlo itero" i " es igul ( )( 80 ) 0 Cd águlo etero " e " es igul ( ) Números de digoles que puede trzrse e u polígoo: D Número de digoles que puede trzrse desde u vértice de u polígoo: d - Polígoo iscrito: Polígoo regulr es el que tiee todos sus ldos águlos igules, es decir es equilátero equiágulo Ver l figur Polígoo circuscrito: Se llm polígoo circuscrito l que tiee todos sus ldos tgetes u circufereci Ver l figur Figur : Polígoo iscrito Figur : Polígoo circuscrito Cetro del polígoo regulr: Se llm sí l cetro comú de su circufereci iscrit circuscrit Rdio de u polígoo regulr: Es el segmeto que ue el cetro co u vértice del polígoo El rdio del polígoo equivle l rdio de l circufereci circuscrit
35 Águlo cetrl de u polígoo regulr: Es el águlo que form dos rdios que ps por dos vértices cosecutivos Apotem de u polígoo regulr: Es el segmeto perpediculr trzdo desde el cetro del polígoo uo de sus ldos L potem es igul l rdio de l circufereci iscrit 7 El Triágulo El triágulo es u figur pl limitd por tres rects que se cort dos dos Tmié se puede defiir como el polígoo o figur geométric formd por tres ldos que form su vez, etre sí, tres águlos Se puede idicr como ABC (se lee triágulo ABC) Ve l figur Figur : El triágulo Vértices: So los putos de itersecció de los ldos del triágulo E l figur 0, los vértices so A, B C Ldos: So los segmetos cosecutivos del triágulo E l figur 0, los ldos so AB, BC, CA se deot por letr miúscul,, c Todo triágulo determi tres águlos: ABC, BCA BAC Los cules se puede omrr co l letr de los vértices A, B C o se puede utilizr otr omecltur; siempre cudo se especifique e el diujo del triágulo Todo triágulo tiee ldos, vértices águlos E cd vértice de u triágulo se puede oteer dos forms de águlos los cules so suplemetrios etre sí; o se que etre los dos sum 80 Estos so: Águlos iteros: So los águlos que tiee por lo meos u puto iterior del triágulo E l figur 0, el águlo θ es u águlo itero l triágulo ABC Águlos eteros: So los águlos dcetes culquier águlo itero E l figur 0, el águlo γ es u águlo etero del triágulo ABC Teorem : L sum de los tres águlos iteros de u triágulo sum 80 Teorem : L sum de los tres águlos eteros de u triágulo sum 0
36 Teorem : E todo triágulo, u ldo culquier es meor que l sum de los otros dos mor que su difereci Sum de los águlos iteros de u triágulo: Pr demostrr que l sum de los águlos iteros de u triágulo es igul h 80 ; se trz por uo de los vértices del triágulo l prlel l ldo opuesto Ve l figur 7 L rect MN es prlel l rect AC; β porque so lteros iteros etre prlels, α c porque so lteros iteros etre prlels Etoces c 80 porque l sum de los águlos de u rect es igul 80 o se u águlo llo Por tto se demuestr que l sum de los tres águlos iteros de u triágulo es 80 Figur 7: Sum de los águlos iteros de u triágulo Teorem : E todo triágulo, u águlo etero es igul l sum de los águlos iteros o dcetes él Teorem : E todo triágulo, u ldo culquier es meor que l sum de los otros dos mor que su difereci Clsificció de los triágulos: Segú sus ldos: Triágulo isósceles: Es el triágulo que tiee dos ldos igules Tmié dos de sus águlos so igules E l figur 8, l señl e cd ldo sigific que el ldo c Teorem : E todo triágulo isósceles, ldos igules se opoe águlos igules
37 Triágulo equilátero: Es quel el que tiee sus tres ldos sus tres águlos igules E l figur 9, l señl e los tres ldos sigific que c Teorem : Todo triágulo equilátero es equiágulo Triágulo escleo: Es el que tiee sus tres ldos sus tres águlos desigules Ve figur 0 Figur 8: Triágulo isósceles Figur 9: Triágulo equilátero Figur 0: Triágulo escleo Segú sus águlos: Triágulo cutágulo: Es el triágulo que tiee sus tres águlos iteriores gudos, o se, cd uo de sus águlos es meor de 90 Triágulo otuságulo: Es el triágulo que tiee u águlo otuso, es decir, uo de sus águlos es mor de 90 Los triágulos cutágulos otuságulos tmié recie el omre de triágulos olicuágulos Triágulo rectágulo: Es el triágulo que tiee u águlo recto, o se, u águlo igul 90 El triágulo más útil es el triágulo rectágulo, demás de teer u águlo recto, sus otros dos águlos so complemetrios sus ldos recie omres especiles Ve l figur Ctetos: So los ldos, perpediculres etre sí que form el águlo recto Hipoteus: Es el ldo opuesto l águlo recto el ldo más lrgo 7
38 Figur : El triágulo rectágulo 7 Segmetos otles de u triágulo putos de itersecció: Medi: Es el segmeto de rect trzdo desde u vértice hst el puto medio del ldo opuesto Ve l figur Todo triágulo tiee tres medis El puto de itersecció de ls tres medis se llm rícetro, grvicetro o cetroide del triágulo El cetroide es el cetro de grvedd o puto de lceo del triágulo es importte e ls pliccioes ivel de igeierí, por ejemplo costrucció de estructurs Figur : L medi Figur : L ltur BM es l medi correspodiete l ldo AC, BM M es el puto medio de AC Altur: Es el segmeto perpediculr trzdo desde el vértice de u águlo l ldo opuesto o su prologció Eiste tres lturs e cd triágulo el puto de itersecció de ls tres se llm ortocetro Ve l figur Bisectriz: Se llm isectriz de u águlo iterior de u triágulo, l segmeto de rect que isec (divide e dos prtes igules) el águlo lleg hst el ldo opuesto Ve l figur Cosecuetemete h tres isectrices, u pr cd águlo El puto dode se ecuetr ls tres isectrices, se llm icetro 8
39 Figur : L isectriz Figur : L meditriz PM es l meditriz del ldo, BD es l isectriz del águlo B AC e el triágulo ABC El águlo es igul l águlo Meditriz: Es l rect perpediculr u ldo e su puto medio, por ejemplo l figur Se puede trzr tres meditrices e u triágulo Ls tres meditrices cocurre e u puto llmdo circucetro 7 Perímetro de u triágulo El perímetro es igul l sum de l logitud de sus ldos, o se P c Ver figur Áre de u triágulo El áre de u triágulo es igul u medio l se por l ltur, o se figur 7 A h Ver Figur : Perímetro de u triágulo Figur 7: Áre de u triágulo 7 Teorem de Pitágors Uo de los teorems de mor utilidd e l mtemátic, es el Teorem de Pitágors Este teorem fue empledo desde hce más de 000 ños por los grimesores de Biloi Egipto 9
40 Este teorem dice: E u triágulo rectágulo, l sum del cudrdo de los ctetos es igul l cudrdo de l hipoteus Por lo cul c dode so los ctetos c es l hipoteus Ver l figur 8 Figur 8: Teorem de Pitágors Corolrio : E todo triágulo rectágulo, l hipoteus es igul l ríz cudrd de l sum de los cudrdos de los ctetos De l iguldd c ; scdo l ríz cudrd mos miemros de l iguldd, oteemos: c Corolrio : E todo triágulo rectágulo, cd cteto es igul l ríz cudrd del cudrdo de l hipoteus, meos el cudrdo del otro cteto c c c c Pricipio: L medi correspodiete l hipoteus de u triágulo rectágulo es igul l mitd de l hipoteus Ve l figur 9 Figur 9: CD BD BA 0
41 7 Cudriláteros Los cudriláteros so polígoos de cutro ldos sus elemetos so los ldos opuestos, quellos que o tiee igú vértice comú los ldos cosecutivos, quellos que tiee u vértice comú so pres de ldos cosecutivos Los cudriláteros se clsific tediedo l prlelismo de los ldos opuestos e: 7 Áre de cudriláteros Prlelogrmos: So cudriláteros que tiee los ldos opuestos prlelos Etre los prlelogrmos más utilizdos teemos: Rectágulo: prlelogrmo que tiee los cutro águlos igules sus ldos cotiguos desigules Ver l figur 0 Su perímetro es igul l sum de sus ldos, P L, el áre es el producto de l se por l ltur, A L Propieddes: Ls digoles de u rectágulo so igules Ls digoles de u rectágulo form dos pres de triágulos cogruetes Cudrdo: prlelogrmo que tiee los cutros águlos igules los cutros ldos igules, es equilátero equiágulo Ver l figur Su perímetro es igul cutro veces el vlor del ldo, P L su áre es igul l se por l ltur, A L ; como ls digoles so d igules podemos decir que el A Este coserv tods ls propieddes del rectágulo Figur 0: Rectágulo Figur : Cudrdo El cudrdo coserv tods ls propieddes del rectágulo del romo Romo: tiee los cutro ldos igules los águlos cotiguos desigules Su perímetro es l sum de los cutro ldos, P L el áre es igul l multiplicció de ls digoles d divids etre dos, d A, dode d digol meor d digol mor Ver l figur
42 Propieddes: Ls digoles de u romo so isectrices de los águlos de los vértices que ue Ls digoles de u romo so perpediculres etre si se isec mutumete (U es meditriz de l otr) Ver figur Figur : Figur : Trpecio Los trpecios so cudriláteros que tiee dos sólo dos ldos prlelos A los ldos que so prlelos se les llm se como so desigules se le llm se mor se meor A los ldos o prlelos se les llm piers del trpecio l segmeto que ue los putos de ls piers se le deomi prlel medi del trpecio, L L Ver l figur L ltur del trpecio es l distci etre ls ses, o se l perpediculr comú, (h) Ver figur El perímetro equivle l sum de ls logitudes de sus ldos, Perímetro L L su áre es el producto de l semisum de ls ses por l ltur, A h Clsificció de los trpecios: Trpecio rectágulo: So los que tiee dos águlos rectos Trpecio isósceles: So lo que tiee los dos ldos o prlelos igules Trpecio escleo: So los que o so rectgulres i isósceles 7 Coceptos fudmetles sore l circufereci el círculo Circufereci: es el cojuto de todos los putos de u plo que equidist de otro puto llmdo cetro L figur, represet u circufereci de cetro O
43 Círculo: es el cojuto de todos los putos de l circufereci de los iteriores l mism E l figur, se represet u círculo Figur : Circufereci Figur : Círculo 7 Elemetos de l circufereci el círculo Secte: es culquier rect que cort l circufereci e dos putos Ver l figur Rdio: Es culquier segmeto que ue el cetro co u puto de l circufereci Ver l figur Diámetro: Es tod cuerd que ps por el cetro Es igul l sum de dos rdios Ver l figur Cuerd: Es el segmeto determido por dos putos de l circufereci Ver l figur Tgete: Es u rect que toc l circufereci e u solo puto Ver l figur Arco de l circufereci: Es u porció de circufereci Ver l figur 7 Águlo cetrl: Es el que tiee su vértice e el cetro de l circufereci E l figur 7, < AOB, es u águlo cetrl 8 Águlo iscrito: Es quel que tiee su vértice colocdo sore l circufereci sus ldos so dos cuerds Ver l figur 8 9 Segmeto circulr: Es l prte de círculo limitd etre u cuerd su rco, ver l figur 9 0 Sector circulr: Es l prte de círculo limitd por dos rdios el rco compredido, ver l figur 0 Coro circulr: Es l porció de plo limitd por dos circuferecis cocétrics, ver l figur
44 Trpecio circulr: Es l porció de plo limitd por dos circuferecis cocétrics dos rdios, ver l figur Semicircufereci: Es u rco igul l mitd de l circufereci Semicírculo: Es l porció de plo compredid etre u diámetro l semicircufereci Figur : Elemetos de l circufereci Figur 7: Águlo cetrl Figur 8: Águlo iscrito Figur 9: Segmeto circulr Figur 0: Sector circulr Figur : Coro circulr Figur : Trpecio circulr
45 Pricipios: Tod tgete es perpediculr l rdio que ps por el puto de cotcto Si u rect es perpediculr l tgete e el puto de tgeci, ps por el cetro de l circufereci Ls tgetes trzds desde u puto eterior de l circufereci so igules L rect que ue u puto de l circufereci co u puto eterior es isectriz del águlo que form ls tgetes trzds desde ese puto l circufereci Águlos rcos relciodos co circufereci: Águlo cetrl: Como se dijo, es quel que tiee su vértice e el cetro de l circufereci, tl como el < AOB Ver l figur Pricipio: E u mism circufereci o e circuferecis igules, los águlos cetrles so proporcioles sus rcos correspodietes siedo O O' circuferecis igules, ver l figur, teemos que: < AOB AB < MO' N MN Medid del águlo cetrl: L medid de u águlo cetrl es igul l medid del rco que rc, por ejemplo < AOB AB; < BOC BC Figur : Águlo cetrl Águlo Iscrito: Es el águlo que tiee su vértice e l circufereci sus ldos so cuerds de l circufereci E l figur, < CBA es u águlo iscrito Pricipio: Todo águlo iscrito e u semicircufereci es recto Ver figur Águlo Iscrito: Es el águlo que tiee su vértice e l circufereci sus ldos so cuerds de l circufereci E l figur, < CBA es u águlo iscrito Pricipio: Todo águlo iscrito e u semicircufereci es recto Ver figur Medid del águlo iscrito: L medid de todo águlo iscrito es igul l mitd del rco compredido etre sus ldos o se < CBA AC Ver l figur Figur : Águlo iscrito C Figur : Águlo iscrito A o B
46 Águlo semi iscrito: es el águlo formdo por u cuerd u tgete l circufereci es igul l mitd del rco que form Ver figur Figur : Águlo semi-iscrito A B º Figur 7: Águlo iterior C B º P ( AC DB ) Águlo iterior: es el formdo por dos cuerds que se cort e el iterior de l circufereci Ver figur 7 Su medid e igul l semisum de los rcos que rc Águlo eterior es el formdo por: ) Dos sectes que se cort fuer de l circufereci tiee medid igul l semidifereci de los rcos que rc Ver figur 8 () A B o B º Figur 8: Águlo eterior B C º A o º C (AC - DB) C (DA - DB) C (CDA- CA) ( ) ( ) ( c ) ) U secte u tgete que se cort fuer de l circufereci su medid es igul l semidifereci de los rcos que rc Ver figur 8 () c) Dos tgetes tiee como medid l semidifereci de los rcos que rc Ver figur 8 (c) Logitud de l circufereci: El úmero π ( pi ) es l rzó etre l logitud C de l circufereci de culquier círculo su diámetro d ; es decir, o C proimdos de π se tiee ; o se 7 A D P º º c π De quí, C πd o se C πr Como vlores d U circufereci se puede cosiderr como u polígoo regulr de u úmero ifiito de ldos Si u cudrdo se iscrie e u circufereci se duplic cotiumete el C º º D C D A B o B º B
47 úmero de sus ldos (pr formr u octágoo, u goo, etc); los perímetros de los polígoos resulttes se proimrá cd vez más l logitud de l circufereci Áre de u círculo Es el producto del rdio l cudrdo l costte ( pi) π : A π r Logitud de u rco º L logitud del rco de es igul l prte l logitud de l circufereci, o se: 0º º L ( π r) 0º π º r L 80º Áre de u sector circulr º El áre de u sector circulr de es igul l prte del áre del círculo, es decir: 0º º k ( π r ) 0º Áre de u segmeto circulr Él áre de u segmeto circulr es igul l áre del sector correspodiete meos el áre del triágulo que form sus rdios l cuerd que sutiede: º h Asc ( π r ) 0º PRÁCTICA N Cómo se llm el segmeto que ue u vértice de u triágulo el puto medio del ldo opuesto? U águlo etero de u triágulo es igul l: ) Sum de los águlos iteros ) Sum de los águlos iteros o dcetes c) Sum de los otros águlos eteros d) Difereci de los águlos iteros o dcetes U polígoo tiee: ) Ectmete tres ldos ) Tres o más ldos c) Más de tres ldos d) Meos de diez ldos A E el triágulo ABC ddo cotiució, el segmeto CD es: C B 7
48 ) medi ) isectriz c) ltur d) meditriz e) Cómo se llm el polígoo regulr que tiee seis ldos? D E l siguiete figur el vlor del águlo ABC es: C 7 ABC es u triágulo isósceles, dode AC es l se Determie el vlor del águlo "" 0 B A B 0 D A C 8 E u triágulo equilátero, cuál es el vlor del águlo eterior e culquier vértice? (utilice π ) 9 Cuál es l medid de l digol del cudrdo cuos ldos mide cm? 0 E l figur dd, el vlor del águlo "" es de: 90 0 Cuál es l digol del rectágulo cuos ldos mide cm 8 cm? E el prlelogrmo ABCD, el vlor de "" e " ", respectivmete so: A 7 0 B E u triágulo rectágulo, C su hipoteus vle D cm u cteto 9 cm Determie l logitud del otro cteto U escler de 8 0 m de logitud se coloc 8 m de u pred A qué ltur de l pred lleg l escler? E el triágulo IJK el vlor del águlo "" es de: I J K 8
49 El vlor de "" e l figur dd es de: B 0 A C B 0 m 7 El perímetro áre del trpecio de l figur dd es: m A 8 Cómo se llm u polígoo que se l vez equilátero equiágulo? C 7m h E 8m D 9 El perímetro de l figur es: cm cm 9cm 7cm 0 El perímetro de l figur dd es de: m m m m El áre del trpecio isósceles mostrdo e l figur, es de: 0 m m m m m m m El perímetro de l figur dd es de: 7m m Determie el áre somred: 0 m m m m m Hlle el áre somred de l siguiete figur: 0 m 0 m 9
50 Los triágulos ABC DEF so equiláteros El triágulo ABC tiee 8 cm de perímetro DF AB Cuál es el perímetro de l figur somred? ) 7 cm ) cm c) cm d) 99 cm e) B F A C D Cuál es el lugr geométrico de los putos de u plo que está igul distci de u puto fijo? 7 Si del diámetro de u circufereci mide pulg Cuál es l logitud de l circufereci? 8 E l figur dd, el águlo iscrito BCD mide 8 Cuál es el vlor del águlo BAD (tmié iscrito)? A B C 9 Cuál es l logitud del rco AB de l figur mostrd? D 0 Cuál es el áre totl de l siguiete figur? cm R E l figur, AB 0, BC 90 Hlle El águlo <ABC R cm B C Cuál es l logitud del rco AB? Use π A A B 0 R m O 0
51 Cudo el águlo iscrito ABC es Cuál es el vlor del águlo iscrito BCA si BC es el diámetro de l circufereci? A B C Si el rco AC 0 Cuál es el vlor de? E l figur dd, el segmeto AB es: B A B C A O E l figur mostrd, el vlor del águlo "" es: A B C 7 L siguiete figur correspode u circufereci de rdio m el águlo cetrl etre dos rdios es de 0 ; Cuáto mide l logitud de su rco? r r ) 70 ) 0 c) 0 d) 7 e) RESPUESTAS π ) medi; ) ; ) ; ) c; ) heágoo regulr; ) 0 ; 7)00 ; 8) rd 9) 88 cm; 0) 0 ; ) 0 cm; ) d; ) cm; ) cm; ) m; ) 70 ; 7) 90 m 0 m ; 8) triágulo, equilátero o cudrdo; 9) 0 cm ; ; 0) 0 cm ; ) cm ; ) m ; ) m ; ) heágoo regulr, P 8cm ; ) ldos ; ) 7 cm ; 7) 0 ldos ; 8) 70 digoles ; 9) 7 digoles ; 0) circufere ci ; ) 7 8pulg ; ) 80 º ; ) recto ; ) 0 8cm ; ) º ; ) cuerd ; 7) º 7 º ;
52 7 Cuerpos geométricos (sólidos), idetificció, cálculo del áre volume U sólido o cuerpo es u posició cerrd de espcio, limitd por superficies pls o leds Cudo u sólido está limitdo por superficies pls se llm Poliedro Por ejemplo l pirámide el cuo El coo, el cilidro l esfer o lo so porque está limitdos e prte o totlmete por superficies leds Ls superficies que limit u poliedro se llm crs; ls iterseccioes de ls crs se llm rists los putos dode ésts se cort se deomi vértices Todos los cuerpos que os rode so sólidos tridimesioles por ejemplo: los sloes de clses tiee l form de u sólido rectgulr, los tques de depósito de gu tiee form cilídric, ls ols de éisol tiee form esféric, etre lguos ejemplos de sólido Los sólidos tiee áres lterles, ls cules se determi por medio de l sum del áre de cd u ls crs que form el sólido Se d e uiddes cudrds Volume: Se defie como el espcio que ocup u cuerpo Y éste se epres e uiddes cúics, tles como mt, cm, pie, pulg, etc Tmié se puede epresr por el áre de l se por l ltur Cuo: es u sólido rectgulr cus crs so cudrdos igules Ver l figur 9 Áre lterl del cuo: Es igul l áre de cd uo se sus ldos multiplicdos por l ctidd de crs que tiee el cul es de crs, A Volume: Figur 9: Cuo V V L Prlelepípedo o sólido rectgulr: So rectágulos perpediculres etre sí e igules dos dos Ver l figur 0 Áre lterl: es igul l sum del áre de cd u de sus crs o se: Áre lterl A A A c c Volume de u prlelepípedo: V c o áre de l se por l ltur Áre de l se lrgo cho ltur c Figur 0: Prlelepípedo
53 Cilidro: es u cuerpo cus ses so círculos prlelos e igules cus seccioes trsversles so rectágulos Los ldos del cilidro so perpediculres l se Ver l figur Áre lterl de u cilidro circulr recto: Es el producto de l ltur l logitud de l se, dode l logitud de l se es el perímetro de l circufereci A hπ D h π r A πr h ( ) ( ) Not: Est áre lterl solo iclue el áre de sus ldos o l de sus tps (circulres) Volume de u cilidro circulr recto: Es el producto del áre de l se por l ltur V Áredelse ltur Figur : Cilidro V πr h Áre de l se π r Esfer: Es u cuerpo e el cul todos los putos de su superficie está igul distci de u puto fijo que se llm cetro de l esfer L esfer se puede cosiderr egedrd por el giro completo de u semicircufereci lrededor de su diámetro como eje demás tiee u form compct, ver l figur Áre lterl: Es el producto de veces el rdio l cudrdo por π : A πr Volume de l esfer: Es el producto de π el rdio l cuo: V π r Figur : Esfer Coo circulr: es el sólido cu se es u círculo su superficie lterl termi e u puto L secció trsversl que ps por el vértice el cetro de l se es u triágulo isósceles cuos ldos igules so potems (o geertrices g ) del coo Ver l figur
54 Áre lterl del coo circulr recto: Es el producto del rdio por l geertriz por π A π r g Not: El áre lterl solo iclue el áre de sus ldos o l de su tp (o se su se circulr) Volume de coo circulr recto: Es el producto de u tercio del áre de l se por l ltur Áre de l se π r Volume Áre de l se ltur del coo Volume π r h Figur : Coo Pirámide o prism: Es u poliedro cu se es u polígoo de culquier úmero de ldos, cus crs lterles so triágulos que se ecuetr e u puto llmdo vértice de l pirámide L ltur de l pirámide es el segmeto perpediculr ( h ) trzdo desde l se l vértice de l pirámide Se llm pirámide regulr l que tiee por se u polígoo regulr por crs lterles triágulos isósceles igules, cu ltur demás ue l vértice co el cetro de l se Ver l figur Figur : Pirámide Áre lterl de u pirámide: Es l sum de ls áres de ls crs lterles
55 P p A ; dode P perímetro p potem Apotem del polígoo de l se: Segmeto trzdo desde el cetro del polígoo de l se hst uo de sus ldos, siedo perpediculres etre sí Divide e dos l mitd el ldo de l se l isectriz del águlo cetrl del polígoo de l se Volume de u pirámide: Es igul u tercio de producto del áre de l se por l medid de l ltur de l pirámide V Bh El prism se compoe de tres pirámides igules Áre lterl de culquier prism es el producto del perímetro de l se por l ltur del prism A Ph Volume de u prism es igul l producto del áre por l ltur del prism PRÁCTICA N 7 ( Utilice π ) Clcule el áre totl de u cuo, cu rist (ldo) mide 7cm? Si el volume de u coo es de π cm, su ltur es de cm Cuál es l medid del rdio de l se? Clcule el áre el volume del cuo que tiee por ldo 08 cm Si el volume de u coo es de 8 π cm, su rdio es de cm Cuál es l medid de l ltur? Si el áre de u cuo es 8 cm, ecuetre el vlor de l rist (ldo) Determir el volume de u cilidro, cuo diámetro de l se es 8 cm ltur 0 cm 7 Cuál es el volume u cuo, cu rist (ldo) mide 87 pulg? 8 Si el volume de u cilidro circulr recto es de 70π cm su ltur es cm, Cuál es l medid del rdio es? 9 Clcule l rist de u cuo que tiee volume 98 cm 0 Hlle el volume de u coo cuo diámetro de l se es cm su ltur 8 cm Cuál es el rdio de u esfer que tiee u volume de 7 cm, Determie l ltur de u cilidro, cuo diámetro de l se es cm volume 08 cm Ecuetre el volume de u prlelepípedo que tiee pies de cho, l logitud ecede e pies l cho l ltur es de 7 pies Clcule el volume de l pirámide de se cudrd ltur 9 cm Como muestr l figur h cm
56 Cuál es el volume de u cilidro co ltur 9 m, si el perímetro de su se es 7 m? El volume de u pirámide es 0 m el áre de l se es de mts Cuáto mide l ltur? 7 U pirámide de se cudrd tiee u ltur igul l logitud de l digol de su se, ecuetre el volume de l pirámide si el ldo de l se mide 8 pulg 8 Clcule el rdio de u esfer cuo volume es cm 9 El volume de l o formd por u semiesfer seguid por u coo, es? 0 m h m 0 Determie el volume el áre totl de u pirámide que tiee de ltur 9 pies u se cudrd de pies de ldo RESPUESTAS ) 8 cm ) 9 cm ) 87 cm ;,779 cm ) cm ) pulg ) 0 cm 7) pulg 8) 8 cm 9) 8 cm 0) 7π cm ) cm ) 0 cm ) 87 pies ) 89 cm ) 899 cm ) m 7) 0 pulg 8) cm 9) 9 m 0) pies, 8 pies 8 CONCEPTOS GENERALES DE LA TRIGONOMETRÍA L trigoometrí, o geometrí de los triágulos, se cocetr e los triágulos rectágulos que estos so l se pr eteder tods ls clses de triágulos L trigoometrí se h defiido tmié como l cieci de l medid idirect, que trvés de ell se puede clculr distcis imposiles de medir directmete Tl cálculo se hce medite seis rzoes que se llm fucioes trigoométrics cu defiició se drá más delte L defiició de ls fucioes trigoométrics se fud e el sistem de coordeds rectgulres, co ls cules se clcul distci, de segmetos rectilíeos dirigidos de águlos A cotiució estudiremos este sistem 8 Sistem De Coordeds Rectgulres O Plo Crtesio Pr costruir este sistem de coordeds rectgulres, se trz e u plo u rect horizotl u rect verticl, ms dirigids perpediculres etre sí L rect horizotl recie el omre de eje de ls sciss o eje de ls ; l rect verticl el omre de ls ordeds o eje de ls ; el puto de itersecció de ells es el orige
57 Usdo estos ejes como refereci, se locliz putos situdos e el plo, los cules está determidos por dos úmeros deomidos coordeds del puto; represetdos sí P(, ), l primer coorded es l coorded e (o se e el eje ) l segud coorded es l coorded e (o se e el eje ) Es importte destcr que tod coorded l derech del puto llmdo orige es positiv l izquierd de dicho puto es egtiv Tod coorded hci rri llmdo orige es positiv hci jo de dicho puto es egtiv Los ejes de coordeds divide l plo crtesio e cutro regioes llmds cudrtes, ve l figur Figur : E l figur so ls regioes omrds por los úmeros romos I, II, III, IV; demás se idic los sigos de ls coordeds e los diferetes cudrtes Ve el ejemplo Ejemplo : Trzr el puto P ( ), P ( ), P (, ) el (, ),, distci del orige l puto P o se OP P ecotrr l Solució: Pr loclizr cd puto, se mide l distci de l primer coorded sore el eje hci l derech (), hci l izquierd (-) l distci que correspode l segud coorded se mide sore el eje hci rri () hci jo (-) El puto será l itersecció de l medid sore el eje el eje E l figur siguiete se muestr: 7
58 L distci OP se ecuetr por el teorem de Pitágors Siedo que, OP r que es l hipoteus, "" e "" so los ctetos, teemos que r, r Como se oserv OP M es u triágulo rectágulo, dode OM MP so los ctetos los cules so perpediculres o se que form etre sí u águlo de 90 A l distci OP, tmié se le llm rdio vector, el cul es l distci del orige l puto loclizdo o es más que l mgitud de l distci, siempre es positivo si importr e que cudrte se ecuetr Ve el ejemplo Ejemplo : Determie "" si r, - el puto se ecuetr e el tercer cudrte Solució: Pr ecotrr el vlor descoocido deemos utilizr el teorem de Pitágors; e este cso se despej el vlor descoocido r ; r, por lo cul () ( ) 9 ± ; como el puto se ecuetr e el tercer cudrte l "" es egtiv o se que el puto es igul (-, -) 8 Fucioes Trigoométrics Básics Ls fucioes trigoométrics ásics se defie como ls rzoes trigoométrics pr u triágulo rectágulo ( 90º ), segú coicid su ldo termil co el eje o co el eje Co l figur se ecuetr ls fucioes trigoométrics ásics pr el águlo A Figur Ls fucioes trigoométrics ásics pr el águlo A so: ldo opuesto seo de A se A hipoteus c coseo de A cos A ldo dcete hipoteus c ldo opuesto tgete de A ta ldo dcete Ls fucioes trigoométrics recíprocs pr el águlo A so: hipoteus c Cosecte de A csca ldo opuesto sea 8
59 hipoteus c Secte de A es sec A ldo dcete cosa ldo dcete Cotgete de A cot A ldo opuesto t A Ve el ejemplo Ejemplo : Ecuetre ls tres fucioes trigoométrics ásics pr el águlo A el águlo B Solució: El ldo c se ecuetr por el teorem de Pitágors c (8) () 00 0 se A se B cosa cosb ta tb Como se puede oservr e el ejemplo ; sea cosb, cosa seb, t A cot B l cot A t B Esto sucede cudo dos águlos so complemetrios ( A B 90º ) El seo de uo de los águlos es igul l coseo de su complemeto vicevers Por ejemplo se0º cos80º ; se0º cos0º se70º cos0º Esto se verific co ls demás fucioes trigoométrics 8 Fucioes trigoométrics de culquier águlo Por ejemplo se0º Est fució trigoométric se ecuetr utilizdo u clculdor cietífic, sio se cuet co u clculdor cietífic se dee ecotrr co u tl de vlores (Este método csi o se emple, porque result más lrgo meos ecto; o es ecto por que todo los vlores o se ecuetr e ls tls l o ecotrrse se dee iterpolr) Pr los efectos de este liro pr este curso, todos los estudites deerá utilizr u clculdor cietífic Pr ecotrr el se0º e u clculdor cietífic; como el águlo est e decimles de grdo, se coloc l clculdor e el modo de grdo (DEG) co l tecl DRG o co u tecl similr L morí de ls clculdors está e el modo de grdo (DEG) cudo se eciede o es ecesrio oprimir otr tecl Cudo l clculdor est e este modo (DEG) se itroduce el úmero 0 se oprime l tecl de l fució trigoométric: 0 se [ ] 8 8 9
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
( a b c) n = a n b n c n ( a : b) n = a n : b n a n a m = a n+m a n :a m = a n-m (a n ) m = a n.m
 Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Universidad Alonso de Ojeda Facultad de Ciencias Administrativas Unidad Curricular: Matemática II FÓRMULAS ARITMÉTICAS
 Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
1.- POTENCIAS DE EXPONENTE ENTERO
 º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
TEMA Nº 1: NÚMEROS REALES
 Deprtmeto de Mtemátics. I.E.S. Ciudd de Arjo º BAC MCS TEMA Nº : NÚMEROS REALES. NÚMEROS RACIONALES. EXPRESIONES DECIMALES.. NÚMEROS RACIONALES. EXPRESIONES DECIMALES. NÚMEROS IRRACIONALES.. NÚMEROS REALES.
Deprtmeto de Mtemátics. I.E.S. Ciudd de Arjo º BAC MCS TEMA Nº : NÚMEROS REALES. NÚMEROS RACIONALES. EXPRESIONES DECIMALES.. NÚMEROS RACIONALES. EXPRESIONES DECIMALES. NÚMEROS IRRACIONALES.. NÚMEROS REALES.
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
MATEMÁTICAS BÁSICAS RADICALES. 4 x, es exacto. OPERACIONES CON RADICALES. 16x es un radical racional porque su resultado,
 Fcultd de Cotdurí Adiistrció. UNAM Rdicles Autor: Dr. José Muel Becerr Espios MATEMÁTICAS BÁSICAS RADICALES OPERACIONES CON RADICALES U rdicl es culquier rí idicd de u expresió. L rdicció es l operció
Fcultd de Cotdurí Adiistrció. UNAM Rdicles Autor: Dr. José Muel Becerr Espios MATEMÁTICAS BÁSICAS RADICALES OPERACIONES CON RADICALES U rdicl es culquier rí idicd de u expresió. L rdicció es l operció
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
PSU Matemática NM-4 Guía 13: Ángulos y Triángulos
 etro Educciol S rlos de rgó. pto. Mtemátic. Prof. Xime Gllegos H. PSU Mtemátic NM- Guí : Águlos Triágulos Nombre: : urso: Fech: - oteido: Geometrí. predizje Esperdo: Utiliz el método deductivo como herrmiet
etro Educciol S rlos de rgó. pto. Mtemátic. Prof. Xime Gllegos H. PSU Mtemátic NM- Guí : Águlos Triágulos Nombre: : urso: Fech: - oteido: Geometrí. predizje Esperdo: Utiliz el método deductivo como herrmiet
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
CAPÍTULO 2: POTENCIAS Y RAÍCES 1. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES
 CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
Ejercicios: 1. Coloca donde corresponda los siguientes números: N Z Q FRACCIONARIOS I
 TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Enteros (Z) Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto de cero
 www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
Radicación en R - Potencia de exponente racional Matemática
 Rdiccio e R Poteci de eoete rciol Mtemátic º Año Cód. 0- P r o f. V e r ó i c F i l o t t i P r o f. M r í d e l L u j á M r t í e z C o r r e c c i ó : P r o f. S i l v i A m i c o z z i Dto. de M t emátic
Rdiccio e R Poteci de eoete rciol Mtemátic º Año Cód. 0- P r o f. V e r ó i c F i l o t t i P r o f. M r í d e l L u j á M r t í e z C o r r e c c i ó : P r o f. S i l v i A m i c o z z i Dto. de M t emátic
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
5 3 = (5)(5)(5) = 125
 Potecició: Es el resultdo que se obtiee l ultiplicr l bse por si is cuts veces lo idique el expoete: = ( )( )( )... BASE = ()()() = POTENCIA EXPONENTE Bse: Es el úero que se ultiplic por si iso. Expoete:
Potecició: Es el resultdo que se obtiee l ultiplicr l bse por si is cuts veces lo idique el expoete: = ( )( )( )... BASE = ()()() = POTENCIA EXPONENTE Bse: Es el úero que se ultiplic por si iso. Expoete:
Sucesiones de números reales
 Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Los elementos de un polígono son los lados, los vértices, los ángulos interiores, los ángulos exteriores, las diagonales, el perímetro y el área.
 POLÍGONOS. ELEMENTOS DE UN POLÍGONO. Los elementos de un polígono son los ldos, los vértices, los ángulos interiores, los ángulos exteriores, ls digonles, el perímetro y el áre. LADO REGIÓN EXTERIOR A
POLÍGONOS. ELEMENTOS DE UN POLÍGONO. Los elementos de un polígono son los ldos, los vértices, los ángulos interiores, los ángulos exteriores, ls digonles, el perímetro y el áre. LADO REGIÓN EXTERIOR A
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
NÚMEROS REALES (PARTE II)
 NIVELACIÓN MATEMÁTICA SEMANA NÚMEROS REALES (PARTE II Todos los derechos de utor so de l eclusiv propiedd de IACC o de los otorgtes de sus licecis. No está permitido copir, reproducir, reeditr, descrgr,
NIVELACIÓN MATEMÁTICA SEMANA NÚMEROS REALES (PARTE II Todos los derechos de utor so de l eclusiv propiedd de IACC o de los otorgtes de sus licecis. No está permitido copir, reproducir, reeditr, descrgr,
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por co dos opercioes
Podemos decir también que número real es todo número que podemos representar en la recta numérica - 1, ¼ 0,
 Uidd EL NÚMERO REAL E etps sucesivs del estudio de l Mteátic se trbj co cpos uéricos que v pliádose co l icorporció de uevos y distitos tipos de úeros. Así, se coiez lizdo el cpo de los úeros turles (
Uidd EL NÚMERO REAL E etps sucesivs del estudio de l Mteátic se trbj co cpos uéricos que v pliádose co l icorporció de uevos y distitos tipos de úeros. Así, se coiez lizdo el cpo de los úeros turles (
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Neper ( ) Lección 2. Potencias, radicales y logarítmos
 Neer (0-7) Lecció Potecis, rdicles y logrítmos º ESO MATEMÁTICAS ACADÉMICAS Potecis, rdicles y logritmos LECCIÓN. POTENCIAS, RADICALES, LOGARITMOS. Potecis de exoete etero Recuerd l defiició de oteci co
Neer (0-7) Lecció Potecis, rdicles y logrítmos º ESO MATEMÁTICAS ACADÉMICAS Potecis, rdicles y logritmos LECCIÓN. POTENCIAS, RADICALES, LOGARITMOS. Potecis de exoete etero Recuerd l defiició de oteci co
( ) ( ) 10. 18 = y el número 12 también es múltiplo del 3 ya que. 6 = y el número 8 también es múltiplo del 2 ya que. 3.
 Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Estructuras Discretas. Unidad 3 Teoría de números
 Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
16/11/2015. Tema 1: Números reales REALES. Racionales (Q) Irracionales (I) Naturales (N) REALES (I) (Q) (Z) (N)
 rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
CURSO DE INGRESO 2010 CUADERNILLO DE MATEMÁTICAS
 UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO FACULTAD DE AGRONOMIA Y AGROINDUSTRIAS CURSO DE INGRESO 00 CUADERNILLO DE MATEMÁTICAS Autor: Dr. Lucreci L. Chillou Fcultd de Agroomí Agroidustris Mtemátics
UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO FACULTAD DE AGRONOMIA Y AGROINDUSTRIAS CURSO DE INGRESO 00 CUADERNILLO DE MATEMÁTICAS Autor: Dr. Lucreci L. Chillou Fcultd de Agroomí Agroidustris Mtemátics
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
Liceo Marta Donoso Espejo Raíces para Terceros
 . Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
. Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
Tema 2. Operaciones con Números Reales
 Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
APUNTES DE MATEMÁTICAS 1º BACHILLERATO
 APUNTES DE MATEMÁTICAS 1º BACHILLERATO 01-014 Aputes Bchillerto 01-014 Tem 0 1. TEMA 0:NÚMEROS REALES 1.1. CONJUNTOS NUMERICOS... 1.. INTERVALOS Y SEMIRECTAS.... 1.. VALOR ABSOLUTO.... 5 1.4. PROPIEDADES
APUNTES DE MATEMÁTICAS 1º BACHILLERATO 01-014 Aputes Bchillerto 01-014 Tem 0 1. TEMA 0:NÚMEROS REALES 1.1. CONJUNTOS NUMERICOS... 1.. INTERVALOS Y SEMIRECTAS.... 1.. VALOR ABSOLUTO.... 5 1.4. PROPIEDADES
LOS NÚMEROS REALES. La estructura del conjunto de los números reales es: Naturales Enteros { } { }
 LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
El conjunto de los Números Reales
 El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Recuerda: a 0 = 1 1 m = 1 ( 1) m = 1 m par ( 1) n = 1 n impar 0 n = 0
 CAPÍTULO : POTENCIAS Y RAÍCES: º de ESO. OPERACIONES CON POTENCIAS Recuerd que l poteci de se u úero turl epoete turl es u producto de fctores igules l se: =... fctores... > 0) El fctor que se repite es
CAPÍTULO : POTENCIAS Y RAÍCES: º de ESO. OPERACIONES CON POTENCIAS Recuerd que l poteci de se u úero turl epoete turl es u producto de fctores igules l se: =... fctores... > 0) El fctor que se repite es
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Guía Práctica N 12 RAÍCES FUNCIÓN RAÍZ CUADRADA
 Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
PLANIFICACIÓN DE LAS CLASES
 PLANIFICACIÓN DE LAS CLASES Sem N 0 Clse N 0 Tem N 0: Notció Mtemátic Coteido Geerl: el fcilitdor dee relizr u descripció de los símolos mtemáticos más coocidos y su otció Operció Notció Se lee Perteeci
PLANIFICACIÓN DE LAS CLASES Sem N 0 Clse N 0 Tem N 0: Notció Mtemátic Coteido Geerl: el fcilitdor dee relizr u descripció de los símolos mtemáticos más coocidos y su otció Operció Notció Se lee Perteeci
1.6 Perímetros y áreas
 3 1.6 Perímetros y áres Perímetro: es l medid del contorno de un figur. Superficie (pln): es el conjunto de puntos del plno encerrdos por un figur geométric pln. Áre: es l medid de un superficie. Represente
3 1.6 Perímetros y áres Perímetro: es l medid del contorno de un figur. Superficie (pln): es el conjunto de puntos del plno encerrdos por un figur geométric pln. Áre: es l medid de un superficie. Represente
3. Volumen de un sólido.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Itegrales y aplicacioes.. Volume de u sólido. E esta secció veremos cómo podemos utilizar la itegral defiida para calcular volúmees de distitos tipos
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Itegrales y aplicacioes.. Volume de u sólido. E esta secció veremos cómo podemos utilizar la itegral defiida para calcular volúmees de distitos tipos
Anillos de Newton Fundamento
 Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
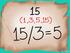 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
Matemáticas Aplicadas a la Ciencias Sociales II SISTEMAS DE ECUACIONES. , a toda ecuación que pueda escribirse de la forma: ...
 Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
SISTEMAS DE ECUACIONES LINEALES
 SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
Tema 1: NÚMEROS REALES.
 I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
NÚMEROS ( 4) ENTEROS RACIONALES 1 + : 2. A) Ordena los siguientes números enteros: 4, B) Calcula: 2) 3) 4) ( ) ( ) 3. A) Calcula:
 NÚMEROS ENTEROS A Orde los siguietes úmeros eteros,,,,, 8, 8 B Clcul 7 ( ( 7 ( ( ( 7 0 ( ( 7 7 ( 0 ( ( 8 7 ( 0 ( 9 8 [ ( 0 7] 0 [ 8 ] ( 7 8 [ ( ] ( ( 8 ( ( ( ( [ ] [ 9 ] ( 7 8 [ ( ] [ ( ] {[ ] [ ( ] }
NÚMEROS ENTEROS A Orde los siguietes úmeros eteros,,,,, 8, 8 B Clcul 7 ( ( 7 ( ( ( 7 0 ( ( 7 7 ( 0 ( ( 8 7 ( 0 ( 9 8 [ ( 0 7] 0 [ 8 ] ( 7 8 [ ( ] ( ( 8 ( ( ( ( [ ] [ 9 ] ( 7 8 [ ( ] [ ( ] {[ ] [ ( ] }
EXPONENTES Y RADICALES
 EXPONENTES Y RADICALES L potecició o otció epoecil es u otció pr revir u ultiplicció: Notció: L, pr u etero positivo 0. veces Se lee coo elevdo l o ás revido: l. es lld l se el epoete o poteci e idic el
EXPONENTES Y RADICALES L potecició o otció epoecil es u otció pr revir u ultiplicció: Notció: L, pr u etero positivo 0. veces Se lee coo elevdo l o ás revido: l. es lld l se el epoete o poteci e idic el
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
ÁLGEBRA APUNTES. EXPONENTES y RADICALES. Ing. Francisco Raúl Ortíz González UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ARAGÓN DIVISIÓN DE LAS CIENCIAS FÍSICO-MATEMÁTICAS Y DE LAS INGENIERÍAS INGENIERÍA MECÁNICA-ELÉCTRICA APUNTES EXPONENTES RADICALES
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ARAGÓN DIVISIÓN DE LAS CIENCIAS FÍSICO-MATEMÁTICAS Y DE LAS INGENIERÍAS INGENIERÍA MECÁNICA-ELÉCTRICA APUNTES EXPONENTES RADICALES
FASE COGNITIVA. LOS NUMEROS REALES Los números reales se conforman por los decimales finitos, decimales infinitos periódicos e infinitos no periódicos
 Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Guía ejercicios resueltos Sumatoria y Binomio de Newton
 Auilir: Igcio Domigo Trujillo Silv Uiversidd de Chile Guí ejercicios resueltos Sumtori y Biomio de Newto Solució: ) Como o depede de j, es costte l sumtori. b) c) d) Auilir: Igcio Domigo Trujillo Silv
Auilir: Igcio Domigo Trujillo Silv Uiversidd de Chile Guí ejercicios resueltos Sumtori y Biomio de Newto Solució: ) Como o depede de j, es costte l sumtori. b) c) d) Auilir: Igcio Domigo Trujillo Silv
BLOQUE III Geometría
 LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
LOQUE III Geometrí 7. Semejnz y trigonometrí 8. Resolución de triángulos rectángulos 9. Geometrí nlític 7 Semejnz y trigonometrí 1. Teorem de Thles Si un person que mide 1,70 m proyect un sombr de 3,40
Matemáticas aplicadas a las Ciencias Sociales
 Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
SOLUCIONES DE LOS PROBLEMAS DE LA OME 49ª. 1. Sean a, b y n enteros positivos tales que a b y ab 1 n. Prueba que
 SOLUCIONES DE LOS PROBLEMAS DE LA OME 49ª Sea a, b y eteros positivos tales que a b y ab Prueba que a b 4 Idica justificadamete cuádo se alcaa la igualdad Supogamos que el resultado a demostrar fuera falso
SOLUCIONES DE LOS PROBLEMAS DE LA OME 49ª Sea a, b y eteros positivos tales que a b y ab Prueba que a b 4 Idica justificadamete cuádo se alcaa la igualdad Supogamos que el resultado a demostrar fuera falso
UNIDAD 3. LA INTEGRAL DEFINIDA
 UNIDAD. LA INTEGRAL DEFINIDA Propósitos: Itroducir el cocepto de itegrl defiid como u fució-áre pr costruir su sigificdo. Relcior los coceptos de derivd e itegrl e l formulció del teorem Fudmetl del Cálculo.
UNIDAD. LA INTEGRAL DEFINIDA Propósitos: Itroducir el cocepto de itegrl defiid como u fució-áre pr costruir su sigificdo. Relcior los coceptos de derivd e itegrl e l formulció del teorem Fudmetl del Cálculo.
Transformaciones lineales
 Trsformcioes lieles [Versió prelimir] Prof. Isbel Arrti Z. 1 Se V y W espcios vectoriles sobre el cuerpo R de los úmeros reles. U trsformció liel o plicció liel de V e W es u fució T : V W que stisfce:
Trsformcioes lieles [Versió prelimir] Prof. Isbel Arrti Z. 1 Se V y W espcios vectoriles sobre el cuerpo R de los úmeros reles. U trsformció liel o plicció liel de V e W es u fució T : V W que stisfce:
UNIVERSIDAD AMERICANA. Curso BAN-03: Matemática I ( Jueves- Noche ) Prof. Edwin Gerardo Acuña Acuña PRÁCTICA DE FACTORIZACIÓN
 UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
EJERCICIOS DE APLICACIÓN
 EJERCICIOS DE APLICACIÓN Uidd. Añde tres térmios cd serie. ; ; ; 9; 6;... b. 7; 7,7;,7;,7;... c. ; ; 0; ; 6;... d. 0; ; 6; ; 0;... e. ; ; ; ;... f. ; 6 ; ; ; ; ;.... Escribe térmios más de l sucesió. ;
EJERCICIOS DE APLICACIÓN Uidd. Añde tres térmios cd serie. ; ; ; 9; 6;... b. 7; 7,7;,7;,7;... c. ; ; 0; ; 6;... d. 0; ; 6; ; 0;... e. ; ; ; ;... f. ; 6 ; ; ; ; ;.... Escribe térmios más de l sucesió. ;
Resumen de las clases teóricas del turno tarde a cargo de la Prof. Alcón.
 Resume de ls clses teórics del turo trde crgo de l Prof. Alcó. 0.1. Complejos. Form de pr ordedo. Opercioes. Form biómic U úmero complejo es u pr ordedo cuys compoetes so úmeros reles. Luego el cojuto
Resume de ls clses teórics del turo trde crgo de l Prof. Alcó. 0.1. Complejos. Form de pr ordedo. Opercioes. Form biómic U úmero complejo es u pr ordedo cuys compoetes so úmeros reles. Luego el cojuto
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 3º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Escuela Pública Eperimetal Descocetrada Nº Dr. Carlos Jua Rodríguez Matemática º Año Ciclo Básico de Secudaria Teoría Nº Primer Trimestre Cojuto de los úmeros racioales Los úmeros racioales so aquellos
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
NATURALES: surgen de la necesidad de contar o de ordenar. Se denotan con la letra N. N={1,2,3,4, }
 1. CONJUNTOS NUMÉRICOS NATURALES: surge de l ecesidd de cotr o de order. Se deot co l letr N. N{1,,3,4, } L su de dos úeros turles es siepre otro úero turl. Pero co l rest o ps lo iso. Eje.: 6-8 ENTEROS:
1. CONJUNTOS NUMÉRICOS NATURALES: surge de l ecesidd de cotr o de order. Se deot co l letr N. N{1,,3,4, } L su de dos úeros turles es siepre otro úero turl. Pero co l rest o ps lo iso. Eje.: 6-8 ENTEROS:
