Sistema de Corrección Atmosférica en Espectro Solar por Métodos Físico-Estadísticos

Tamaño: px

Comenzar la demostración a partir de la página:

Download "Sistema de Corrección Atmosférica en Espectro Solar por Métodos Físico-Estadísticos"

José Ramón Guzmán Villalobos
hace 8 años
Vistas:

1 Sistm d Corrión Atmosféri n Esptro Solr por Métodos Físio-Estdístios Mrtínz, L., Plà, V. y Arbiol, R. Institut Crtogràfi d Ctluny (ICC) Unitt d Tldtió Pr d Montjuï s/n Brlon E-mil: lmrtinz@i.s Plbrs lv: orrión tmosféri, sptro solr, dyni, trnsfrni rditiv, normlizión, multitmporl, suprfiis invrints, MASS, Lndst 7 ETM+. Rsumn: En st trbjo s mustr l Sistm d Corrión Atmosféri ICC, pr snsors d tldtión psiv n l sptro solr, qu rdu l impto d l bsorión gsos, l disprsión d Rylight, l disprsión d Mi y l fto d dyni qu l tmósfr produ n l mdid rdiométri. El método físio s bs n simulions d trnsfrni rditiv, no stá rstringido un pltform onrt y su disño prmit ontmplr l impto d l gomtrí d iluminión y obsrvión, l stdo d l tmósfr, y l topogrfí. L orrión físi s omplmnt mdint un prodiminto d normlizión stdísti bsdo n l rdiomtrí d suprfiis invrints qu posibilit l gnrión d sris multitmporls d imágns ompnsds. El Sistm s h implmntdo pr l orrión d sris d imágns pnromátis Lndst 7 ETM+, mplndo dtos tmosférios dl modlo d prdiión mtorológi MASS. El fto d l orrión tmosféri s nliz sobr suprfiis invrints dtrminds sobr l trnsformión Tssld Cp. L dsviión udráti mdi d l rfltividd d ls suprfiis invrints s rdujo l mitd l plir l método propusto, rspto l rfltividd sin orrgir. 1.Introduión Los snsors d tldtión n l sptro solr midn básimnt l rdini dl Sol rfljd por l sistm suprfii-tmósfr, pusto qu n l rngo sptrl d stos snsors ls misions térmis d l Tirr son dspribls. Ests imágns prsntn divrss distorsions gométris y rdiométris. L orrión d ls distorsions rdiométris s nsri pr modlr dudmnt prámtros físios rlists y onsistnts, bordr studios multitmporls o on imágns d difrnts snsors. L rdini mdid por l snsor dpnd d l rfltividd d l suprfii obsrvd y l gomtrí d iluminión. Est mdid stá prturbd por dos fnómnos tmosférios: l bsorión gsos, y l disprsión por moléuls gsoss y rosols, dnominds disprsión d Rylight y Mi, rsptivmnt. L bsorión s un intrión inlásti y, por tnto, d rátr disrto on l longitud d ond. L disprsión s un intrión lásti d rátr ontinuo on l longitud d ond, qu modifi l dirión d propgión d l rdiión ltromgnéti. D st form l disprsión s rsponsbl dl fto d dyni, por l qu l mdid rdiométri dl ár otd por un píxl s v ontmind por l rdiión qu s propg dsd l ntorno d diho ár, s dir, dsd los píxls próximos. Pr obtnr mdids d l rdini tldtión libr d ftos tmosférios s h dsrrolldo un Sistm d Corrión Atmosféri d Esptro Solr bsdo n un método físio on dtos tmosférios sínronos, sguido d un método d normlizión prtir d suprfiis invrints. Diho método s d rátr modulr y dptbl ulquir tipo d snsor y pltform d sptro solr, y prmit l inorporión d dtos sínronos l imgn pr l obtnión d rfltividds bsoluts mdint simulions d trnsfrni rditiv o l uso d vlors stándr n usni d stos. Un vz rlizd l orrión tmosféri bsolut d d imgn, prmit l dpurdo d un sri multitmporl mdint un método d normlizión stdísti.

Rsumn: En st trbjo s mustr l Sistm d Corrión Atmosféri ICC, pr snsors d tldtión psiv n l sptro solr, qu rdu l impto d l bsorión gsos, l disprsión d Rylight, l disprsión d Mi y l fto d dyni qu l

2 2. Mtodologí dl Sistm 2.1 El método físio El método físio s pli ls rdinis mdids por l snsor o rdini Top Of Atmosphr (TOA), pr obtnr l rfltividd orrgid o rfltividd Bottom Of Atmosphr (BOA). L rdini mdid por l snsor L, pud rlionrs on l rfltividd xtrtrrstr quivlnt, o rfltividd TOA, omo dond: E s s l irdini solr xtrtrrstr. µ s s l osno dl ángulo nitl solr. π L µ Pro, tnindo n unt los fnómnos d intrión on l tmósfr dsritos y sgún Stnz [2], s posibl notr l rdini solr qu lnz un snsor d tldtión obsrvndo un suprfii horizontl omo s E S ( 1 S) + B /( S) L L A / 1 + dond: s l rfltividd orrgid d l suprfii obsrvd. < > s l rfltividd orrgid dl ntorno n l qu s nuntr l suprfii obsrvd. S s l lbdo sfério d l tmósfr. L s l rdini rtrodisprsd por l tmósfr hi l snsor. A y B dn unt dl fto tmosfério sobr l rdiión dirt y difus, rsptivmnt. Así l rfltividd orrgid d l suprfii obsrvd, srá pr d píxl ( L L )( 1 S) Los prámtros A, B, S y L rtrizn tnto l gomtrí y posiión n l tmósfr d snsor y ár obsrvd, omo ls ondiions tmosféris n ls qu s rliz l mdid. Su vlor no dpnd ni d l rfltividd d l suprfii obsrvd ni d l d su ntorno. Así pus, su álulo s rliz prtir d ls mgnituds L g o rdini qu lnz l snsor dsd l suprfii obsrvd, y L p o rdini qu lnz l snsor dsd l ntorno d l suprfii obsrvd y por l tmósfr, qu pr un mdio d rfltividd uniform s notn omo A B L g A L B + L p 1 S 1 S Ambs mgnituds L g y L p pudn obtnrs mdint ódigos d trnsfrni rditiv funionndo n modo dirto, sindo l obtnión dl vlor d A, B, S y L trivil mdint l rsoluión d sistms d uions. En dih simulión d trnsfrni rditiv s dond s introdun l orrión los dtos gométrios y tmosférios sinrónios l obtnión d l imgn. L mgnitud < > o rfltividd orrgid dl mdio n l qu s nuntr l suprfii obsrvd s obtndrá trtndo l onjunto d píxls qu onstituyn l ntorno o vindd, omo un nuvo píxl situdo n un ntorno uniform d rfltividd. Su vlor vndrá ddo por L L A + B + S < > ( L L ) Así l álulo d l rfltividd orrgid pr d píxl s rliz n un prodiminto d dos psos, qu prmit ruprr ontrst prdido dbido l fto d dyni l inorporr n l prodiminto l fto d l rfltividd dl ntorno dl píxl.

π L µ Pro, tnindo n unt los fnómnos d intrión on l tmósfr dsritos y sgún Stnz [2], s posibl notr l rdini solr qu lnz un snsor d tldtión obsrvndo un suprfii horizontl omo s E S ( 1 S) + B /( S) L L A

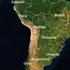
3 2.2 El método stdístio En un sri d imágns orrgids bsolutmnt on l método físio s pud plir d mnr gnrl un método d normlizión sobr suprfiis invrints, pus s h limindo los ftors qu limitn l uso d diho método stdístio. Est prodiminto homogniz l rfltividd d sris multitmporls orrigindo dsviions d l rtrizión tmosféri, drivs dl librdo dl snsor, t [3]. A prtir d l rfltividd d dihs zons s luln los ofiints d ssgo y gnni qu rlionn ls rfltividds ntr ls imágns d l sri. 3. Apliión y rsultdos El Sistm d Corrión s h dptdo pr orrgir tmosférimnt un sri d 6 imágns pnromátis dl snsor Enhnd Thmti Mppr Plus (ETM+) d l pltform Lndst 7. El frgmnto nlizdo s loliz n l ár mtropolitn d Brlon (Figur 1). L fh d dquisiión d ls imágns s: 23-jul-1999, 09-sp-1999, 30-di-1999, 03-mr-2000, 07-jun-2000 y 11-sp L sri stá orintd gométrimnt n un solo bloqu usndo l método gométrio d Plà y Pons [4], y rtifid por vino más próximo n píxls d 15 mtros. Figur 1: Imgn Lndst 7 ETM+ d Brlon sobr l qu s pli l orrión tmosféri L simulión d trnsfrni rditiv pr l método físio s hn rlizdo prtir dl ódigo ): Sond Simultion of th Stllit Signl in th Solr Sptrum (6S) [5], mplndo simulions d l tmósfr dl modlo Msoslr Atmosphri Simultion Systm (MASS) [6] dl Srvi d Mtorologi d Ctluny (SMC) [7], un modlo limtológio stándr d rosols y un modlo d lvión dl trrno (MET) on l mism rsoluión spil qu l imgn. Ls árs invrints pr l método stdístio s hn sogido prtir d l trnsformión Tssld Cp (TC) pr ETM+ sgún Hung [8]. S hn tomdo un totl d 9 zons qu ontbn on un mplio rngo d vlors d l primr omponnt TC o intnsidd, on los mínimos vlors nontrdos pr l sgund omponnt TC o índi d vrdor. Sobr lls s hn rlizdo rgrsions linls on r 2 suprior 0.98 pr l normlizión stdísti rspto l primr imgn d l sri orrspondint 23-jul-1999 (Figur 2).

A prtir d l rfltividd d dihs zons s luln los ofiints d ssgo y gnni qu rlionn ls rfltividds ntr ls imágns d l sri. 3.

4 N ormlizión stdísti 11-st-2000 rspto 23-jul-1999 Rfltividd 11-sp (Rfltividd 23-jul-1999 ) r Rfltividd BOA método físio 11-sp Rfltividd BOA método físio 23-jul-1999 Figur 2: Ejmplo dl método d normlizión stdísti pr l imgn d 11-sp-2000 Como mustr l Tbl 1, l rfltividd TOA d ls árs stblids omo invrints mustrn un dsviión udráti mdi n su rfltividd d y si s pli l método físio s obtin un dsviión udráti mdi d Cundo dspués dl método físio s pli l sri l método stdístio, l rfltividd orrgid d dihs árs rdu su dsviión udráti mdi L rduión d l dsviión udráti mdi logrd on l método físio no s muy lvd. Pro db tnrs n unt qu st proso d obtnión d rfltividds BOA port l imgn otro bnfiio qu s l ruprión d ontrst. Método d orrión tmosféri plido l rfltividd Dsviión udráti mdi d l rfltividd orrgid n árs invrints Ninguno (TOA) Físio Físio + Estdístio Tbl 1: Dsviión udráti mdi d l rfltividd orrgid n árs invrints 4.Conlusions. En st trbjo s h prsntdo l Sistm d Corrión Atmosféri ICC pr snsors d tldtión n l sptro solr, bsdo n l ontnión d un método físio, on simulions d trnsfrni rditiv, más un método stdístio, on rgrsions linls. S h dsrito su mtodologí bási y su pliión un so prátio: un sri d imágns pnromátis Lndst ETM+ dl ár d Brlon. S hn sliondo árs invrints uy rfltividd TOA prsntb un dsviión udráti mdi d Trs l pliión dl método físio l dsviión udráti mdi d l rfltividd BOA r d y s rdujo trs l pliión onsutiv dl método físio y dl método stdístio. Estos rsultdos son stisftorios, más tnindo n unt qu ls zons invrints s nuntrn n un ntorno urbno y, por tnto, son susptibls d prsntr ltrions rdiométris por l fto d ls sombrs. Agrdimintos Los utors dsn xprsr su grtitud Elisu Villr Ribs y Abdlmlik Sirouni dl SMC, por los dtos dl modlo mtorológio MASS.

25 Rfltividd BOA método físio 23-jul-1999 Figur 2: Ejmplo dl método d normlizión stdísti pr l imgn d 11-sp-2000 Como mustr l Tbl 1, l rfltividd TOA d ls árs stblids omo invrints mustrn un dsviión

5 Rfrnis [1] Hung, C., L. Yng, C. Homr, B. Wyli, J. Voglmn nd T. DFli, "At-Stllit Rfltn: A First Ordr Normliztion of Lndst & ETM+ Imgs". USGS. [2] Stnz, K., Willims, D.J. 1997, Rtrivl of Surf Rfltn from Hiprsptrl Dt Using Look-up Tbl Approh. Cndin Journl of Rmot Snsing, Vol 23, nº4, [3] Cslls, V. y Lópz, M.J. (1989): An ltrntiv simpl pproh to stimt tmosphri orrtion in multitmporl studis, Intrntionl Journl of Rmot Snging, vol. 10, pp [4] Plà V. y Pons X. (1995): Inorportion of rlif in polynomil-bsd gomtri orrtions, Photogrmmtri Enginring nd Rmot Snsing, vol. 61, pp [5] Vrmont, E., Tnré, D., Duzé, J.L., Hrmn, M. y Morrtt, J.J. (1997): Sond simultion of th stllit signl in th solr sptrum, 6S: n ovrviw. IEEE Trnstions on Gosin nd Rmot Snsing, 35, [6] [7] Codin, B., Arn, M., Young, S. y Rdño, A. (1997): Prdition of Msosl Convtiv Systm ovr Ctloni (Northstrn Spin) with Nstd Numril Modl. Mtor. Atmos. Phys., 62, [8] Hung, C., Wyli, B., Homr, C., Yng, L., nd Zylstr, G., 2002, Drivtion of Tssld p trnsformtion bsd on Lndst 7 t-stllit rfltn: Intrntionl Journl of Rmot Snsing, v. 23, no. 8, p

$, Hrmn, M. y Morrtt, J.J. (1997): Sond simultion of th stllit signl in th solr sptrum, 6S: n ovrviw. IEEE Trnstions on Gosin nd Rmot Snsing, 35, 675-686. [6] http:\\www.mtot.s [7] Codin, B., Arn, M.$

Documentos relacionados

TRANSFORMADORES EN PARALELO

TRANSFORMADORES EN PARALELO TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio: