26 EJERCICIOS de LOGARITMOS
|
|
|
- José Ángel Montero Ortíz
- hace 8 años
- Vistas:
Transcripción
1 6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto. v) Dominio y rcorrido. vi) Asíntots. vii) lim f() y lim f() - ) f() = 0 y f() = b) f() 0, = y f() = 0, c) f() = y f() = d) f() = y f() = Dfinición d ritmo: N = = N (dond >0, ) Sistms d ritmos más utilizdos: NOMBRE BASE NOTACIÓN DEFINICIÓN N = 0 = N Logritmo dciml =0 N = = N Logritmo nprino = Ln, dond,759 s llm ct. d Eulr; s un númro irrcionl. Dfinición d ritmo:. Utilizndo l dfinición, hllr los siguints ritmos: ) 9 b) c) /9 d) (-9) ) f) g) h) i) 6 j) 0 0,0 k) /6 l) 5 0, m) 56 n) /6 o) 0,5 p) q) 0 r) /6 s) 7 t) (Soluc: ) ; b) ; c) -; d) ; ) /; f) /; g) ; h) /; i) ; j) -; k) -; l) -; m) ; n) -; o) -; p) 0; q) 0; r) -6; s) /; t) ) S rcomind vr tmbién los jrcicios rsultos pág. 5 y 0 pág., y rlizr los jrcicios 9 y 50 d l pág. dl libro.. Clculr los ritmos dcimls d los siguints númros (sin clculdor) y comprobr l rsultdo: ) b) c) 0,00 d) / ) 0 f) 0-7 g) 0 h) (Soluc: ) ; b) 6; c) -; d) -6; ) ; f) -7; g) ; h) 0) S rcomind rlizr tmbién l jrcicio 56 d l pág. dl libro. En honor John Npir (Npr, n ltín), mtmático inglés (550-67) invntor d los ritmos.
2 . Utilizndo l dfinición d ritmo, hllr l vlor d n cd un d ls iguldds siguints: ) = ) = i) = m) 0.0= q) 0.5 = b) /= f) =- j) 6= n) =-/ r) (-6)= c) 00= g) 9= k) 5=- o) /6 = s) 5=- d) = h) = l) /00 00= p) =0 t) )= (Soluc: ) ; b) -; c) ; d) 7; ) ; f) /9; g) 7; h) ; i) ; j) 6; k) /5; l) -; m) 0,; n) /; o) /96; p) ; q) 0,065; r) ; s) /5; t) 0) S rcomind vr tmbién l jrcicio rsulto pág. y rlizr los jrcicios 5 y 5 pág. ( n l bs) Cálculo rítmico: Fórmuls dl cálculo rítmico: p q = p + q p = p - q q n p = n p n p = p n (tods son válids n culquir bs) Csos prticulrs: = = = = = = 0 = = 0 5. Aplicndo ls fórmuls ntriors, clculr: ) 6 6 h) p) 9 w) γ) b) 7 c) d) ) f) 5 6 g) 9 i) j) k) l) m) 6 n) 6 o) 5 q) r) ( ) s) t) 7 u) v) 5 6 ) y) z) α) β) , δ) 7 ε) /5 5 (Soluc: ) -; b) /; c) /; d) -/; ) ; f) -/5; g) /; h) -; i) /; j) /; k) 5/6; l) /; m) 6; n) -; o) /5; p) -/; q) -/; r) ; s) 5/; t) /; u) -9/5; v) -/; w) -5/; ) ; y) -/; z) -/; α) /; β) /; γ) /; δ) -7/; ε) -) S rcomind rlizr tmbién l jrcicio pág. 6 dl libro.
3 6. Eprsr n función d los ritmos dcimls d los siguints númros, y comprobr con l clculdor: ) 6 b) 5 c) /5 d) 0,5 ) 0,65 f) 50 g) /0 6 h) i) 6/5 j) 0, k) 0,0 5 0 l) m) 0,0 (Soluc: ) ; b) - ; c) -+6 ; d) - ; ) - ; f) - ; g) -- ; h) + + j) -+5 ; k) -+ ; l) 5 ; m) ) ; i) -+5 ; 7. Eprsr n función d : ) b) c) d) ) (Soluc: ) ; b) - ; c) - ; d) + ; ) + ). Eprsr n función d y los ritmos siguints, y comprobr con l clculdor: ) 5 b) c) / d) 9/ ) 6 f) 0 g) 6 h),6 i), (Sol: ) - ; b) + ; c) - ; d) - ; ) j) 90 k) 0,7 l) 0,7 m),6 + ; f) + ; g) + ; h) -+ + ; i) -+ + ; j) + ; k) -+ ; l) -+ + ; m) -/+ + ) 9. Eprsr n función d, y 7 los ritmos siguints: ) b) 0, c) 0,5 d), ) 0. Justificr ls siguints iguldds: ) 6 + = b) 5=(- ) c) = 9 ) + = 5 + d) 0 = S rcomind rlizr tmbién l jrcicio 6 pág. dl libro.. Sbindo qu 7,5=0,665..., hllr (sin clculdor): ) 75, b) 0,0075 c) 75. Utilizndo ls fórmuls dl cálculo rítmico, dsrrollr l máimo ls prsions siguints: mnp ) () d) ( ) mn r g) qr i) b) ( ) ) () p c / c) f) h) j) y mn k)
4 l) m) ( -y ) mn n) pq r m n o) m p) m + q) ( 0 ) r) b c5 mp s) ( n y m ) m n t) pq u) c (Sol: ) + ; b) + ; c) + - y; d) + ; ) + ; f) ; m + n g) m+ n+ p- q- r; h) ; i) r m+r n-r p; j) -- ; k) ; l) ; n m - p -r q m + n m n m) (+y)+(-y); n) ; o) ; p) + + b + 5 c m p q) ; r) ; s) n +m y; t) + m+ n- p- q u) ) + m+ + S rcomind vr tmbién l jrcicio rsulto pág. 6 y rlizr l jrcicio 60 pág. dl libro. m m +. Obtnr n ls siguints prsions: = + ) = + b b) + b = b c) Soluc : = 0 ( ) b 6 c + d Soluc : = ( c d ) S rcomind vr tmbién l jrcicio rsulto pág. dl libro, y rlizr l jrcicio 55 pág. dl libro... Sbindo qu =7 y=, utilizr l clculdor pr hllr: ) b) () c) d) (+y) ) + y f) + y g) + y lo g + lo g b = ) Hllr sbindo qu b (Soluc: =9) N b) Si N=, cuánto vl N? Cuánto vl N? (Soluc: -; N=6) S rcomind vr tmbién los jrcicios rsultos y pág. 6, y rlizr los jrcicios y 5 pág. 6, y 57 y 5 pág. dl libro. 6. En qué bs s cumpl qu + =? (Soluc: =6) S rcomind rlizr l jrcicio 6 pág. 9 dl libro. 7. V o F? Rzon l rspust: ) (A+B)= A + B b) (A +B )= A+ B = c) ) = d) AB = C C AB
5 f) El ritmo d un númro simpr d como rsultdo un númro irrcionl. g) Los ritmos dcimls d númros < son ngtivos; n cso contrrio, son positivos. S rcomind rlizr tmbién l jrcicio 6 pág. 9 dl libro.. CURIOSIDAD MATEMÁTICA: Comprobr l vrcidd d l siguint fórmul, dbid l físico británico Pul Dirc (90-9), qu prmit scribir culquir númro N mpdo solmnt trs doss: N= (N rícs) 9. Cuáls son los númros cuyos ritmos dcimls stán comprndidos ntr 0 y? Y ntr 0 y -? (Soluc: y 00; 0,0 y ) Ecucions ponncils: 0. Rsolvr ls siguints cucions ponncils por l método más propido, y comprobr l rsultdo n cd cso: = = 6+ ) (Soluc:,57) w) (Soluc: = =) b) 7 (Soluc: -,759) - = ) (Sol: =, =) + + = 0 = + c) (Soluc: 5,79) y) (Soluc: -7,0) + = = 0 d) (Soluc: =) z) (Soluc: =, =) + + = 6 = 79 ) (Soluc: =) α) (Soluc: =5) = + f) (Soluc: =-6) β) 9 = 7 (Soluc:,5) = 0 +9 = g) (Soluc: =) γ) (Soluc: 5,) = h) (Soluc: soluc.) = δ) (Soluc: =±) 5 = + i) 5 (Soluc: =) 0 = ε) (Soluc: =) = + = j) (Soluc:,055) ζ) (Soluc: =0, =) 00 0 = = k) (Soluc: =) η) + (Soluc: =-, =) / = 76 / = 76 l) (Soluc:,099) θ) + = m) (Soluc: soluc.) = ι) (Soluc: =) +5 = 7 + = 0 n) (Soluc: =) κ) (Soluc: o) = 7 soluc.) + = 0 (Soluc: -,95) λ) (Soluc: =, = / ) = = µ) (Soluc: =) p) (Soluc: =, =) q) ( ) = 9 ν) = (Soluc: =0, =) (Soluc: =) + = ξ) (Soluc: =) + + = 0 r) (Soluc: =) + = = 0 ο) (Soluc: =) s) (Soluc: 0,) = 7 π) (Soluc: =) t) = (Soluc: =-) = 0 u) (Sol: =, =; =) = + v) (Soluc: =) ρ) = 6 σ) 9 = (Soluc:,550) (Soluc: =, = / )
6 τ) = (Soluc: =-) υ) 6 = + (Soluc: =) S rcomind vr tmbién los jrcicios rsultos pág. 7 y 5 pág. 9, y rlizr los siguints jrcicios dl libro: 5c,d y 59,c pág. ; 7 y,b pág. 79; 5, 6 y 7 págs. 9 y 9. Considérs l siguint fórmul: U = P( ρ + V) /D ρ V P D U D Dspjr ρ (Ayud: no s ncsrio utilizr ritmos) (Soluc: = + ). Sin ncsidd d oprr, rzonr qu cucions dl tipo: + = = = 0, tc. no pudn tnr solución. Ecucions rítmics:. Rsolvr ls siguints cucions rítmics, comprobndo l vlidz d ls solucions obtnids: ) - (+6)= (Soluc: =) b) ( +)= 65 (Soluc: =±) c) (Soluc: =±5) + = d) (-)+ (+)= + (-) (Soluc: =5) Soluc : = 0; = 5 0 /0 ) +7-9=0 ( ) f) (-)= - (Soluc: =) g) (+)- (-6)= (Soluc: =7) h) (+9)=+ (Soluc: =/) i) (+)+ (-)=/00 (Soluc: soluc.) = j) (Soluc: =5) k) ( -7+0)= (Soluc: =; =5) l) + (+)= (Soluc: =) m) ( ++6)=+ (+) (Soluc: =; =6) n) + + = (Soluc: =/) o) - (-)= (Soluc: =) p) (-)+ (+6)= (+) (Soluc: =) q) + (-)= (Soluc: =5) r) (+9)- = (Soluc:,) s) (+6)-= (-) (Soluc: =; =/5) t) (+)- = (Soluc: =/0)
7 u) (6-)- (+)= (Soluc: =) v) + =5 (Soluc: =0) S rcomind vr tmbién los jrcicios rsultos pág. 79 y pág. 9 Sistms d cucions ponncils y/o rítmics: S rcomind vr los jmplos b pág. 0 y pág., y rlizr los jrcicios b, c pág. y pág. 9 dl libro. Cmbio d bs: = b b (fórmul dl cmbio d bs). Utilizndo l fórmul dl cmbio d bs s pid: ) Dmostrr qu b b = b) Hllr l rlción ntr l ritmo nprino y l ritmo dciml. c) Eprsr n función d (Soluc: =,9) 5. ) Nustr clculdor sólo dispon d ritmos dcimls. Usndo l fórmul dl cmbio d bs, hllr 5 b) Rzonr qu 5 s irrcionl. 6. Volvr hcr l jrcicio, pro utilizndo st vz l clculdor y l fórmul dl cmbio d bs. S rcomind dmás vr los jrcicios rsultos 5 pág. 6 y 9 pág., y rlizr l jrcicio pág. 6 dl libro.
Función exponencial y logarítmica:
 MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
34 EJERCICIOS de LOGARITMOS
 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
31 EJERCICIOS de LOGARITMOS
 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
Para que exista límite de una f(x) en un punto han de coincidir los límites laterales en dicho punto.
 REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS
 FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
Tema 4: Integrales Impropias
 Prof. Susn López 1 Universidd Autónom de Mdrid Tem 4: Integrles Impropis 1 Integrl Impropi En l definición de un integrl definid f (x) se exigió que el intervlo [, b] fuese finito. Por otro ldo el teorem
Prof. Susn López 1 Universidd Autónom de Mdrid Tem 4: Integrles Impropis 1 Integrl Impropi En l definición de un integrl definid f (x) se exigió que el intervlo [, b] fuese finito. Por otro ldo el teorem
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho UNIVERSIDAD DE EXTREMADURA MATEMÁTICAS II
 IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
IES CASTELAR BADAJOZ Emn Junio d (Gnrl) Antonio ngino Corbcho UNIVERSIDAD DE ETREADURA ATEÁTICAS II ATEÁTICAS II Timpo máimo: hor minutos Instruccions: El lumno lgirá un d ls dos opcions propusts Cd un
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
 IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
SOLUCIONES DE LIMITES
 SOLUCIONES DE LIMITES.. Ln Sustituyndo por obtnmos: INDETERMINADO Ln Como s trt d un indtrminción d tipo L Hopitl, plicmos dich rgl: Ln Ln Rsolvmos prt l it Ln INDETERMINACIÓN d tipo L Hopitl otr vz: 6Ln
SOLUCIONES DE LIMITES.. Ln Sustituyndo por obtnmos: INDETERMINADO Ln Como s trt d un indtrminción d tipo L Hopitl, plicmos dich rgl: Ln Ln Rsolvmos prt l it Ln INDETERMINACIÓN d tipo L Hopitl otr vz: 6Ln
ACTIVIDADES FINALES EJERCICIOS. trino grau fernández. x lím. lím. lím. lím. sen x 1. x 1. lím x 0 sen x x. lím. x lím. sen x. x arcsen x lím 11.
 L Í M I T E S th ls ACTIVIDADES FINALES EJERCICIOS Ln tg sn sn [ ( )] 5 sn 6 cotg 7 sn sn 8 9 sn rcsn sn b sn sn cotg 5 sn cos 6 sn 7 n 8 Ln 9 Ln trino gru frnándz th ls 5 Clculr pr qu s cumpl: π Ln tg
L Í M I T E S th ls ACTIVIDADES FINALES EJERCICIOS Ln tg sn sn [ ( )] 5 sn 6 cotg 7 sn sn 8 9 sn rcsn sn b sn sn cotg 5 sn cos 6 sn 7 n 8 Ln 9 Ln trino gru frnándz th ls 5 Clculr pr qu s cumpl: π Ln tg
REPRESENTACION GRAFICA.
 REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE NAVARRA JUNIO 2012 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
3dx dx 3. dx 1-4x. 7. 3xdx 4+x x 2
 MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES
 3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
TRANSFORMADORES EN PARALELO
 TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
ECUACIONES EXPONENCIALES
 ECUACIONES EXPONENCIALES. Rsolvr ls siguins cucions ponncils ) Eponncils con igul s, s iguln los ponns. ) Los dos érminos s pudn prsr como ponncils d igul s. c) 0' Los dos érminos s pudn prsr como ponncils
ECUACIONES EXPONENCIALES. Rsolvr ls siguins cucions ponncils ) Eponncils con igul s, s iguln los ponns. ) Los dos érminos s pudn prsr como ponncils d igul s. c) 0' Los dos érminos s pudn prsr como ponncils
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
 Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
Derivadas: Teoría y ejercicios DERIVADAS. La derivada de una función f en el punto de abscisa x = a, se define como el siguiente límite, si existe:
 Drivds: Torí jrcicios Bcillrto DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis =, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién ts d vrición instntán.
Drivds: Torí jrcicios Bcillrto DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis =, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién ts d vrición instntán.
Funciones vectoriales de variable vectorial. Son aplicaciones entre espacios eucĺıdeos, IR n, f : X IR n Y IR m
 Funciones vectoriales de variable vectorial Son aplicaciones entre espacios eucĺıdeos, IR n, f : X IR n Y IR m x y x = (x 1, x 2,, x n ), y = (y 1, y 2,, y m ) e y j = f j (x 1, x 2,, x n ), 1 j n n =
Funciones vectoriales de variable vectorial Son aplicaciones entre espacios eucĺıdeos, IR n, f : X IR n Y IR m x y x = (x 1, x 2,, x n ), y = (y 1, y 2,, y m ) e y j = f j (x 1, x 2,, x n ), 1 j n n =
Se llama tasa de variación media (T.V.M.) de una función y = f(x) en un intervalo a. T.V.M. a,b =
 TEMA 7: DERIVADAS 7. Concpto d drivd. Función drivd. 7. Rgls d drivción. 7. CONCEPTO DE DERIVADA. FUNCIÓN DERIVADA. Est concpto mtmático no sólo nos prstrá un yud primordil n l rprsntción d funcions y
TEMA 7: DERIVADAS 7. Concpto d drivd. Función drivd. 7. Rgls d drivción. 7. CONCEPTO DE DERIVADA. FUNCIÓN DERIVADA. Est concpto mtmático no sólo nos prstrá un yud primordil n l rprsntción d funcions y
IES Mediterráneo de Málaga Solución Junio 2014 Juan Carlos Alonso Gianonatti BLOQUE A
 IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti BLOQUE CUESTIÓN.: Sbindo qu, clcul, sin dsrrollr ni utilir l rgl d Srrus, los siguints dtrminnts, indicndo n cd pso qué propidd d los dtrminnts
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti BLOQUE CUESTIÓN.: Sbindo qu, clcul, sin dsrrollr ni utilir l rgl d Srrus, los siguints dtrminnts, indicndo n cd pso qué propidd d los dtrminnts
INTEGRAL INDEFINIDA MÉTODOS ELEMENTALES DE INTEGRACIÓN
 INTEGRAL INDEFINIDA MÉTODOS ELEMENTALES DE INTEGRACIÓN El almán Gottfrid Libniz (66-76), quin, junto con su antagonista l inglés Isaac Nwton (6-77), fu l crador dl cálculo infinitsimal. MATEMÁTICAS II
INTEGRAL INDEFINIDA MÉTODOS ELEMENTALES DE INTEGRACIÓN El almán Gottfrid Libniz (66-76), quin, junto con su antagonista l inglés Isaac Nwton (6-77), fu l crador dl cálculo infinitsimal. MATEMÁTICAS II
LOGARITMOS. John Neper ( ) Henry Briggs ( ) MATEMÁTICAS I 1º Bachillerato Alfonso González IES Fernando de Mena Dpto.
 LOGARITMOS John Neper (550-67) Henry Briggs (56-60) MATEMÁTICAS I º Bchillerto Alfonso González IES Fernndo de Men Dpto. de Mtemátics I) FUNCIÓN EXPONENCIAL de BASE f()= «Es quell función en l que l vrible
LOGARITMOS John Neper (550-67) Henry Briggs (56-60) MATEMÁTICAS I º Bchillerto Alfonso González IES Fernndo de Men Dpto. de Mtemátics I) FUNCIÓN EXPONENCIAL de BASE f()= «Es quell función en l que l vrible
DERIVADAS. La derivada de una función f en el punto de abscisa x = a, se define como el siguiente límite, si existe:
 DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis =, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién ts d vrición instntán. Intrprtción ométric d
DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis =, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién ts d vrición instntán. Intrprtción ométric d
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL
 EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
EJERCICIOS RESUELTOS DE FUNCIONES REALES DE VARIABLE REAL. Calcular los dominios d dfinición d las siguints funcions: a) f( ) 6 b) f( ) c) f( ) ln d) f( ) arctg 3 4 ) f( ) f) f( ) 5 g) f( ) sn 9 h) 4 4
COMPUTACIÓN. Práctica nº 2
 Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
a > 0 y a 1. Si la base es e se llama exponencial natural tiene la forma
 INTRODUCCIÓN A LAS MATEMATICAS SUPERIORES TEMA 6 FUNCIONES LOGARÍTMICAS Un función ponncil d s tin l form f ( pr tod R > 0 y. Si l s s s llm ponncil nturl tin l form dond f (. L.- Con l informción qu cunt
INTRODUCCIÓN A LAS MATEMATICAS SUPERIORES TEMA 6 FUNCIONES LOGARÍTMICAS Un función ponncil d s tin l form f ( pr tod R > 0 y. Si l s s s llm ponncil nturl tin l form dond f (. L.- Con l informción qu cunt
XIV.- ALIMENTACIÓN AL RODETE CÁMARA ESPIRAL
 XIV.- ALIMENTACIÓN AL OETE CÁMAA ESPIAL XIV..- IMENSIONAMIENTO PAA TUBINAS FANCIS (ELECTOCONSULT) c [m/s] 0,44 5,4 nq Figura 4.. Vlocia ntraa n la spiral n función la vlocia spcífica n s. Figura 4.. Esquma
XIV.- ALIMENTACIÓN AL OETE CÁMAA ESPIAL XIV..- IMENSIONAMIENTO PAA TUBINAS FANCIS (ELECTOCONSULT) c [m/s] 0,44 5,4 nq Figura 4.. Vlocia ntraa n la spiral n función la vlocia spcífica n s. Figura 4.. Esquma
Tarea 11. Integral Impropia
 Tr Intgrl Imroi Ers con l límit corrsondint cd un d ls siguints intgrls Mustr un dibujo qu indiqu l ár qu s clculrí (si ist) con l intgrl rsctiv, no clculs l intgrl d ; b) d ; c) d ; d) / cot( ) d En los
Tr Intgrl Imroi Ers con l límit corrsondint cd un d ls siguints intgrls Mustr un dibujo qu indiqu l ár qu s clculrí (si ist) con l intgrl rsctiv, no clculs l intgrl d ; b) d ; c) d ; d) / cot( ) d En los
DERIVABILIDAD.. Intuitivamente: cuando no presenta saltos en ese punto. Toda función derivable en un punto, es continua en ese punto.
 ERIVABILIA.... inir unción continu n un punto. inir unción drivbl n un punto. s posibl ponr un jmplo d un unción qu n s: ) Continu y drivbl. b) rivbl y no continu. c) Continu y no drivbl. y s continu n
ERIVABILIA.... inir unción continu n un punto. inir unción drivbl n un punto. s posibl ponr un jmplo d un unción qu n s: ) Continu y drivbl. b) rivbl y no continu. c) Continu y no drivbl. y s continu n
3º.- Junio i) Producto de matrices: definición, condiciones para su realización. Si A M m n. (la matriz A tiene m filas y n columnas), B M n p
 IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrics dtrinnts Mtrics dtrinnts. Ejrcicios d Slctividd. º.- Junio 99. i) Dfin rngo d un triz. ii) Un triz d trs fils trs coluns tin rngo trs, cóo pud vrir
IES EL PILES SELECTIVIDD OVIEDO DPTO. MTEMÁTICS Mtrics dtrinnts Mtrics dtrinnts. Ejrcicios d Slctividd. º.- Junio 99. i) Dfin rngo d un triz. ii) Un triz d trs fils trs coluns tin rngo trs, cóo pud vrir
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
UNIVERSIDAD DE LA RIOJA JUNIO lim
 IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
Practica Sistemas electrónicas Practica 1: Aplicaciones lineales de los amplificadores operacionales
 Prctic Sistms lctrónics Prctic : Apliccions linls d los mplificdors oprcionls Autor: Profsor rsponsbl: Profsor cuidnd: né Wrnr Ibld Slvdor Brcho dl Pino osrio Csnuv Arpid Objtivo d l práctic: El objtivo
Prctic Sistms lctrónics Prctic : Apliccions linls d los mplificdors oprcionls Autor: Profsor rsponsbl: Profsor cuidnd: né Wrnr Ibld Slvdor Brcho dl Pino osrio Csnuv Arpid Objtivo d l práctic: El objtivo
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)
 IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
105 EJERCICIOS de DERIVABILIDAD 2º BACH.
 105 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad: 1. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
105 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad: 1. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
85 EJERCICIOS de ECUACIONES y SISTEMAS de 1 er y 2 o GRADO
 85 EJERCICIOS de ECUACIONES y SISTEMAS de er y o GRADO. Resolver las siguientes ecuaciones de er grado y comprobar la solución: a) 5[-(+)] -0+0 (Soluc: -) b) -[-(-)] (Soluc: 9) c) [6-5(-)]5-(-5) (Soluc:
85 EJERCICIOS de ECUACIONES y SISTEMAS de er y o GRADO. Resolver las siguientes ecuaciones de er grado y comprobar la solución: a) 5[-(+)] -0+0 (Soluc: -) b) -[-(-)] (Soluc: 9) c) [6-5(-)]5-(-5) (Soluc:
91 EJERCICIOS de DERIVABILIDAD 2º BACH.
 9 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad:. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
9 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad:. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
Integrales impropias.
 IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
IX / 8 UNIVERSIDAD SIMON BOLIVAR MA nro-mrzo d 4 Dprtmnto d Mtmátics Purs y Aplicds. Intgrls impropis. Ejrcicios sugridos pr : los tms d ls clss dl 4 y 9 d mrzo d 4. Tms : Otrs forms indtrminds. Intgrls
Universidad Central de Venezuela Facultad de Farmacia Matemática - Física Prof. J. R. Morales
 Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
1.3.4 Ejercicios resueltos sobre la función exponencial y logarítmica
 .. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
.. Ejrcicios rsultos sobr l función ponncil rítmic. Us ls propidds d l función ponncil (torm ) pr simplificr totlmnt l siguint prsión:. Prub qu Simplifiqu inicilmnt l numrdor l dnomindor d l frcción. Así:
DERIVADAS. La derivada de una función f en el punto de abscisa x = a, se define como el siguiente límite, si existe:
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. DERIVADAS Dinición d drivd. L drivd d un unción n l punto d bscis, s din como l siuint límit, si ist: lím A l drivd d un unción n un punto s l llm tmbién
EJERCICIOS DE INECUACIONES
 EJERCICIOS DE INECUACIONES REPASO DE DESIGUALDADES: 1. Dadas las siguientes desigualdades, indicar si son V o F utilizando la recta real. Caso de ser inecuaciones, indicar además la solución mediante la
EJERCICIOS DE INECUACIONES REPASO DE DESIGUALDADES: 1. Dadas las siguientes desigualdades, indicar si son V o F utilizando la recta real. Caso de ser inecuaciones, indicar además la solución mediante la
( ) 4. Colegio Diocesano Sagrado Corazón de Jesús. MATEMÁTICAS I / 1º Bachillerato C y T LOGARTIMOS. log. log. log. 1 log log 3.
 Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Solución de los Problemas del Capítulo 3
 1. Slccion l rspust corrct y xpliqu por qué. Un lctrón qu tin un n= y m= ) Db tnr un m s =+1/ b) Pud tnr un l= c) Pud tnr un l=, ó 1 d) Db tnr un l=1 L rspust corrct s l c) porqu si n=, los posibls vlors
1. Slccion l rspust corrct y xpliqu por qué. Un lctrón qu tin un n= y m= ) Db tnr un m s =+1/ b) Pud tnr un l= c) Pud tnr un l=, ó 1 d) Db tnr un l=1 L rspust corrct s l c) porqu si n=, los posibls vlors
98 EJERCICIOS de DERIVABILIDAD 2º BACH.
 98 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad: 1. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
98 EJERCICIOS d DERIVABILIDAD º BACH. Drivabilidad y continuidad: 1. Dada si 0 f() si < 0 (Soluc: / f'(0)), s pid: a) Estudiar su drivabilidad n 0 b) Rprsntarla.. Ídm con 4 5 si f() 4 si < n (Soluc: f'()).
I.E.S. RUIZ GIJÓN. Departamento de Física y Química Luis Sánchez López Ejercicios y Cuestiones de Química 2º Bachillerato
 I.E.S. RUIZ GIJÓN Departamento de Física y Química Luis Sánchez López. 2018-2019 Ejercicios y Cuestiones de Química 2º Bachillerato QUÍMICA 2º BACHILLERATO =========================================================
I.E.S. RUIZ GIJÓN Departamento de Física y Química Luis Sánchez López. 2018-2019 Ejercicios y Cuestiones de Química 2º Bachillerato QUÍMICA 2º BACHILLERATO =========================================================
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES
 CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
(Soluc: a) 1/x b) x 6 /36 c)
 EJERCICIOS d INTEGRAL INDEFINIDA º BACH.. Calcular las siguints intgrals potncials (s rcominda hacr la comprobación: a d b d c d d d t t dt d g t dt d i d j d t m d n d o d + d ( t dt l d (Soluc: a / b
EJERCICIOS d INTEGRAL INDEFINIDA º BACH.. Calcular las siguints intgrals potncials (s rcominda hacr la comprobación: a d b d c d d d t t dt d g t dt d i d j d t m d n d o d + d ( t dt l d (Soluc: a / b
Para que exista límite de una f(x) en un punto han de coincidir los límites laterales en dicho punto.
 REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
REPASO LÍMITES º BACH. RECORDAR: Para qu ista límit d una f() n un punto han d coincidir los límits latrals n dicho punto. A fctos dl f() no tnmos n cunta lo qu ocurr actamnt n a, sino n las a proimidads.
Deducción de las reglas de derivación. Partiendo de las derivadas de la función potencial, la función exponencial y la función seno, ( ) ( ) 1
 dmttmtics.wordprss.com Btriz d Otto Lópz Dducción d ls rgls d drivción Prtindo d ls drivds d l función potncil, l función ponncil l función sno, = R = f = =, f = sn = cos, f,, d ls rgls d drivción pr l
dmttmtics.wordprss.com Btriz d Otto Lópz Dducción d ls rgls d drivción Prtindo d ls drivds d l función potncil, l función ponncil l función sno, = R = f = =, f = sn = cos, f,, d ls rgls d drivción pr l
Resolución de circuitos complejos de corriente continua: Leyes de Kirchhoff.
 Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por
CAPÍTULO XII. INTEGRALES IMPROPIAS
 CAPÍTULO XII. INTEGRALES IMPROPIAS SECCIONES A. Integrles impropis de primer especie. B. Integrles impropis de segund especie. C. Aplicciones l cálculo de áres y volúmenes. D. Ejercicios propuestos. 9
CAPÍTULO XII. INTEGRALES IMPROPIAS SECCIONES A. Integrles impropis de primer especie. B. Integrles impropis de segund especie. C. Aplicciones l cálculo de áres y volúmenes. D. Ejercicios propuestos. 9
IV. POSICIONES GEODESICAS
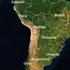 IV. OICIOE GEODEIC Un d ls finlidds principls d l godsi s l cálculo d ls coordnds godésics d puntos sobr l lipsoid. Ests coordnds s dnoinn Ltitud y Longitud y stán sipr rfrids un sist godésico pr-dtrindo.
IV. OICIOE GEODEIC Un d ls finlidds principls d l godsi s l cálculo d ls coordnds godésics d puntos sobr l lipsoid. Ests coordnds s dnoinn Ltitud y Longitud y stán sipr rfrids un sist godésico pr-dtrindo.
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
Determinización: Construcción de Safra
 Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
1.6. BREVE REPASO DE LOGARITMOS.
 .. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
.. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
LOGARITMOS. John Neper ( ) Henry Briggs ( )
 LOGARITMOS John Neper (550-67) Henry Briggs (56-630) MATEMÁTICAS CCSS I º Bchillerto Alfonso González IES Fernndo de Men Dpto. de Mtemátics I) FUNCIÓN EXPONENCIAL de BASE f()= «Es quell función en l que
LOGARITMOS John Neper (550-67) Henry Briggs (56-630) MATEMÁTICAS CCSS I º Bchillerto Alfonso González IES Fernndo de Men Dpto. de Mtemátics I) FUNCIÓN EXPONENCIAL de BASE f()= «Es quell función en l que
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
UNIDAD 9 LÍMITES DE FUNCIONES. CONTINUIDAD.
 IES Pdr Povd (Gudi Mtmátics I UNIDAD 9 LÍMITES DE FUNCIONES CONTINUIDAD Límit d un unción n un punto Límits ltrls Límit d un unción n un punto Límits n l ininito Comportminto d un unción cundo Comportminto
IES Pdr Povd (Gudi Mtmátics I UNIDAD 9 LÍMITES DE FUNCIONES CONTINUIDAD Límit d un unción n un punto Límits ltrls Límit d un unción n un punto Límits n l ininito Comportminto d un unción cundo Comportminto
f (x)dx = f (x) dx. Si la respuesta es afirmativa justifíquese, si es negativa,
 CALCULO INTEGRAL.(97).- Sa f() una función tal qu, para cualquira qu sa > s cumpl qu = Pruébs qu, ntoncs, s vrifica qu f( ) = f(), para todo >. f f..(97).- Sa la función f() = -. S pid: a) Hacr un dibujo
CALCULO INTEGRAL.(97).- Sa f() una función tal qu, para cualquira qu sa > s cumpl qu = Pruébs qu, ntoncs, s vrifica qu f( ) = f(), para todo >. f f..(97).- Sa la función f() = -. S pid: a) Hacr un dibujo
4 3x 2x 3 6x x x x dt d x x dy p dx y
 EJERCICIOS UNIDAD IV.- LA DERIVADA.- Comprub cd un d ls siguints drivds. d ) 8 d t 5 5 bt 5 t 5 bt dt d 6.-Rliz ls siguints drivds ) d.-comprobr cd un d ls siguints drivds. ) d d r d dr d d ( ) p b b b
EJERCICIOS UNIDAD IV.- LA DERIVADA.- Comprub cd un d ls siguints drivds. d ) 8 d t 5 5 bt 5 t 5 bt dt d 6.-Rliz ls siguints drivds ) d.-comprobr cd un d ls siguints drivds. ) d d r d dr d d ( ) p b b b
Matemáticas Empresariales I. Extensiones de la Integral
 Mtemátics Empresriles I Lección 9 Extensiones de l Integrl Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 19 Integrles impropis - Definición Definición Integrl
Mtemátics Empresriles I Lección 9 Extensiones de l Integrl Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 19 Integrles impropis - Definición Definición Integrl
GRIEGO BÍBLICO. Josías Grauman
 GRIEGO BÍBLICO Josías Grauman CONTENIDO INTRODUCCIÓN:... 3 CAPÍTULO 1: EL ALFABETO... 7 CAPÍTULO 2: EL VERBO - PRESENTE INDICATIVO ACTIVO...11 CAPÍTULO 3: EL SUSTANTIVO - LOS CASOS...17 CAPÍTULO 4: LA
GRIEGO BÍBLICO Josías Grauman CONTENIDO INTRODUCCIÓN:... 3 CAPÍTULO 1: EL ALFABETO... 7 CAPÍTULO 2: EL VERBO - PRESENTE INDICATIVO ACTIVO...11 CAPÍTULO 3: EL SUSTANTIVO - LOS CASOS...17 CAPÍTULO 4: LA
Árboles binarios. Árbol: definición. Árbol (del latín arbor oris):
 Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
NÚMEROS REALES 1º Bachillerato CC. SS.
 Números Reles NÚMEROS REALES 1º Bchillerto CC. SS. Reles R Irrcionles I Enteros Rcionles Z Q Nturles Nturles N 1,,,... EnterosZ, 1, 0, 1,... Rcionles Q 7,, 6'... 5 N Irrcionles I π,, 7'114... Números Reles
Números Reles NÚMEROS REALES 1º Bchillerto CC. SS. Reles R Irrcionles I Enteros Rcionles Z Q Nturles Nturles N 1,,,... EnterosZ, 1, 0, 1,... Rcionles Q 7,, 6'... 5 N Irrcionles I π,, 7'114... Números Reles
Opción A ( ) ( ) Examen. 2ª evaluación 4/03/2008. Obtener el valor del siguiente límite: ab entonces la función. t ln 1 4t dt x ln 1 4x ln 1 4x 2
 Eamn. ª valuación //8 Opción A Ejrcicio. Puntuación máima: puntos Obtnr l valor dl siguint límit: lim + t ln t dt 5 Aplicación dl torma fundamntal dl cálculo intgral: Si f s continua n [, ] f t dt s drivabl
Eamn. ª valuación //8 Opción A Ejrcicio. Puntuación máima: puntos Obtnr l valor dl siguint límit: lim + t ln t dt 5 Aplicación dl torma fundamntal dl cálculo intgral: Si f s continua n [, ] f t dt s drivabl
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
51 EJERCICIOS DE VECTORES
 51 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coorens e los vectores fijos e l
51 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coorens e los vectores fijos e l
TÉCNICAS DE INTEGRACIÓN
 C TÉCNICAS DE INTEGRACIÓN C. CONCEPTOS PRELIMINARES C.. Función primitiva Sea f : I R, donde I es un intervalo real. Diremos que la función F : I R es una función primitiva de la función f en I si se cumple
C TÉCNICAS DE INTEGRACIÓN C. CONCEPTOS PRELIMINARES C.. Función primitiva Sea f : I R, donde I es un intervalo real. Diremos que la función F : I R es una función primitiva de la función f en I si se cumple
43 EJERCICIOS de POLINOMIOS
 EJERCICIOS de POLINOMIOS 1. Calcular el valor numérico del polinomio P(x) para el valor de x indicado: a) P(x)x +1, para x1 b) P(x)x +1, para x-1 (Soluc: a) ; b) 0; c) 8; d) -) Ejercicios libro: pág. 1:
EJERCICIOS de POLINOMIOS 1. Calcular el valor numérico del polinomio P(x) para el valor de x indicado: a) P(x)x +1, para x1 b) P(x)x +1, para x-1 (Soluc: a) ; b) 0; c) 8; d) -) Ejercicios libro: pág. 1:
UNIDAD 8 LÍMITES DE FUNCIONES. CONTINUIDAD.
 IES Pdr Povd (Gudi Mtmátics Aplicds ls CCSS I UNIDAD 8 LÍMITES DE FUNCIONES CONTINUIDAD CONCEPTOS PREVIOS: Dcimos qu: y s l tind, si tom vlors cd vz más próimos Ejmplo: L scunci d númros ; ; ; 9; 8; ;
IES Pdr Povd (Gudi Mtmátics Aplicds ls CCSS I UNIDAD 8 LÍMITES DE FUNCIONES CONTINUIDAD CONCEPTOS PREVIOS: Dcimos qu: y s l tind, si tom vlors cd vz más próimos Ejmplo: L scunci d númros ; ; ; 9; 8; ;
1 sen. f Solución: 3 ; 1. sen. 2 sen. f Solución: ; Solución: CONTINUIDAD Y DERIVABILIDAD
 Frnndo Frnádz-Rmos Mrín º.- Clcul l continuidd d ls guints uncions. ) 8 7 ) 8 6 c) d) sn ) º.- Dtrminr l vlor d los prámtros d ls uncions pr qu sn continus n todo ) sn Solución: ) Solución: c) cos sn sn
Frnndo Frnádz-Rmos Mrín º.- Clcul l continuidd d ls guints uncions. ) 8 7 ) 8 6 c) d) sn ) º.- Dtrminr l vlor d los prámtros d ls uncions pr qu sn continus n todo ) sn Solución: ) Solución: c) cos sn sn
(Soluc: 1) 1/x 2) x 6 /36 3)
 INTEGRALES INDEFINIDAS º BACH.. Calcular las siguints intgrals potncials (y comprobar la sombrada: d d d 6 d t t dt d 7 t dt d 9 d 0 d t d d d + d ( t dt d (Soluc: / 6 /6 0 t 7 /7 t 6 /6 8 8 7 t / + 9
INTEGRALES INDEFINIDAS º BACH.. Calcular las siguints intgrals potncials (y comprobar la sombrada: d d d 6 d t t dt d 7 t dt d 9 d 0 d t d d d + d ( t dt d (Soluc: / 6 /6 0 t 7 /7 t 6 /6 8 8 7 t / + 9
Qué son los rangos de usuarios?
 Rangos de usuarios [Rangos de usuarios] Qué son los rangos de usuarios? Los rangos de usuarios son imágenes que aparecen debajo del nombre de los usuarios. Estos rangos se encuentran divididos en tres
Rangos de usuarios [Rangos de usuarios] Qué son los rangos de usuarios? Los rangos de usuarios son imágenes que aparecen debajo del nombre de los usuarios. Estos rangos se encuentran divididos en tres
INTEGRALES IMPROPIAS
 NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES IMPROPIAS Ing. Jun Scerdoti Deprtmento de Mtemátic Fcultd de Ingenierí Universidd de Buenos Aires V INDICE INTEGRALES IMPROPIAS.- PUNTOS SINGULARES
NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES IMPROPIAS Ing. Jun Scerdoti Deprtmento de Mtemátic Fcultd de Ingenierí Universidd de Buenos Aires V INDICE INTEGRALES IMPROPIAS.- PUNTOS SINGULARES
1 Introducción... 2. 2 Distribución exponencial... 2. 3 Distribución Weibull... 6. 4 Distribuciones Gamma y k-erlang... 10
 Asignatura: Ingeniería Industrial Índice de Contenidos 1 Introducción... 2 2 Distribución exponencial... 2 3 Distribución Weibull... 6 4 Distribuciones Gamma y k-erlang... 10 5 Distribución log-normal...
Asignatura: Ingeniería Industrial Índice de Contenidos 1 Introducción... 2 2 Distribución exponencial... 2 3 Distribución Weibull... 6 4 Distribuciones Gamma y k-erlang... 10 5 Distribución log-normal...
Modelos Estadísticos de los Factores de Riesgo: Series de Tiempo
 Contenido Estructura básica análisis de riesgo Ejemplos Distribuciones codicionales y no condicionales Hacia donde vamos?: medidas de riesgo Métodos para deducir la distribución del proceso de pérdidas
Contenido Estructura básica análisis de riesgo Ejemplos Distribuciones codicionales y no condicionales Hacia donde vamos?: medidas de riesgo Métodos para deducir la distribución del proceso de pérdidas
INFORME DE LA PRÁCTICA nº 2: LA RUEDA DE MAXWELL. Fernando Hueso González. Carlos Huertas Barra. (1º Fís.), L1, 21-XI-07 - 0 -
 INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
INFORME DE LA PRÁCTICA nº : LA RUEDA DE MAXWELL Fernndo Hueso González. Crlos Huerts Brr. (1º Fís.), L1, 1-XI-7 - - RESUMEN L práctic de l rued de Mxwell consiste en medir el tiempo que trd en descender
EXPONENCIACIÓN Y LOGARITMACIÓN
 EXPONENCIACIÓN Y LOGARITMACIÓN Se presentn dos funciones de grn importnci en l mtemátic, como son: l función eponencil y l función rítmic. Función eponencil Definición: Se un número rel positivo. L función
EXPONENCIACIÓN Y LOGARITMACIÓN Se presentn dos funciones de grn importnci en l mtemátic, como son: l función eponencil y l función rítmic. Función eponencil Definición: Se un número rel positivo. L función
TEMA 4. LOGARITMOS 1. REPASO DE POTENCIAS 2. DEFINICIÓN DE LOGARITMO. Ejercicio 1. a = 1 = 3 porque 1 = ACCESO UNIVERSIDAD
 TEMA 4. LOGARITMOS. REPASO DE POTENCIAS - Poteci de epoete turl: = ( veces) - Poteci de epoete ulo: 0 = - Poteci de epoete egtivo: - = / - Poteci de epoete frcciorio: Propieddes: - m = +m - : m = -m -
TEMA 4. LOGARITMOS. REPASO DE POTENCIAS - Poteci de epoete turl: = ( veces) - Poteci de epoete ulo: 0 = - Poteci de epoete egtivo: - = / - Poteci de epoete frcciorio: Propieddes: - m = +m - : m = -m -
LOGARITMOS. John Neper ( ) Henry Briggs ( )
 LOGARITMOS John Neper (550-67) Henry Briggs (56-60) MATEMÁTICAS I º Bchillerto CCNN Alfonso González IES Fernndo de Men Dpto. de Mtemátics Mtemátics I LOGARITMOS I) FUNCIÓN EXPONENCIAL de BASE f()= «Es
LOGARITMOS John Neper (550-67) Henry Briggs (56-60) MATEMÁTICAS I º Bchillerto CCNN Alfonso González IES Fernndo de Men Dpto. de Mtemátics Mtemátics I LOGARITMOS I) FUNCIÓN EXPONENCIAL de BASE f()= «Es
Proyecciones ortogonales (diédricas y triédricas)
 Proyccions ortogonls (diédrics y triédrics) Pro. Rúl F. ongiorno S dnominn proyccions ortogonls l sistm d rprsntción qu nos prmit diujr n dirnts plnos un ojto situdo n l spcio. undo hlmos d sistms d rprsntción
Proyccions ortogonls (diédrics y triédrics) Pro. Rúl F. ongiorno S dnominn proyccions ortogonls l sistm d rprsntción qu nos prmit diujr n dirnts plnos un ojto situdo n l spcio. undo hlmos d sistms d rprsntción
Las anteriores fórmulas suelen expresarse matricialmente como
 Capítulo III Teoría de las curvas 1. Clasificación de curvas en R 3 En esta sección veremos que, esencialmente, la curvatura y la torsión determinan las curvas de R 3. Para ello necesitaremos las conocidas
Capítulo III Teoría de las curvas 1. Clasificación de curvas en R 3 En esta sección veremos que, esencialmente, la curvatura y la torsión determinan las curvas de R 3. Para ello necesitaremos las conocidas
Opción A Ejercicio 1 opción A, modelo Septiembre 2011
 IES Fco Ayala d Granada Sptimbr d 0 (Modlo ) Grmán-Jsús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 0-0 MATEMÁTICAS II Opción A Ejrcicio opción A, modlo Sptimbr 0 k si
IES Fco Ayala d Granada Sptimbr d 0 (Modlo ) Grmán-Jsús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 0-0 MATEMÁTICAS II Opción A Ejrcicio opción A, modlo Sptimbr 0 k si
(a+1)x+ay=3 (a+1)x+(a+1)y+(a+2)z=1 (a 2 +a)x+(a 2-1)y+(a 2-2a-8)z=2a+5. a 1. a+1. a+2 a 2-2a a+5 ~1 0. a=-1
 EXTRAORDINARIO DE 4. PROBLEMA A. Estudi l siguint sistm d uions linls dpndint dl prámtro rl y rsuélvlo n los sos n qu s omptil: Aplimos l método d Guss: ~ + + + + + - 3 + --6 - -+3 (+)+y3 (+)+(+)y+(+)z
EXTRAORDINARIO DE 4. PROBLEMA A. Estudi l siguint sistm d uions linls dpndint dl prámtro rl y rsuélvlo n los sos n qu s omptil: Aplimos l método d Guss: ~ + + + + + - 3 + --6 - -+3 (+)+y3 (+)+(+)y+(+)z
I.E.S. Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti PROPUESTA A
 I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
Manual de teoría: Trigonometría Matemática Bachillerato
 Manual de teoría: Trigonometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Trigonometría: José Pablo Flores Zúñiga Página Contenido: 4) Trigonometría 4. Trigonometría Básica 4. Funciones
Manual de teoría: Trigonometría Matemática Bachillerato Realizado por José Pablo Flores Zúñiga Trigonometría: José Pablo Flores Zúñiga Página Contenido: 4) Trigonometría 4. Trigonometría Básica 4. Funciones
Aptitud Matemática ( ) ( ) EDADES RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN. 3x x = 75 3x 5x = 75 x = 15 3(x) = 45. 1 + 2α = 9 + α RPTA.: B RPTA.
 EDADES 1 Teófilo tiene el triple de la edad de Pedro Cuando Pedro tenga la edad de Teófilo, este tendrá 75 años Cuál es la edad de Teófilo? A) 30 B) 35 C) 40 D) 45 E) 50 3 Las edades de tres amigos son
EDADES 1 Teófilo tiene el triple de la edad de Pedro Cuando Pedro tenga la edad de Teófilo, este tendrá 75 años Cuál es la edad de Teófilo? A) 30 B) 35 C) 40 D) 45 E) 50 3 Las edades de tres amigos son
7Soluciones a los ejercicios y problemas PÁGINA 161
 7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
7Soluciones los ejercicios y problems ÁGIN 161 ág. 1 RTI Rzones trigonométrics de un ángulo gudo 1 Hll ls rzones trigonométrics del ángulo en cd uno de estos triángulos: ) b) c) 7 m m 11,6 cm 8 m m 60
IES Mediterráneo de Málaga Solución Septiembre 2010 (Específico) Juan Carlos Alonso Gianonatti OPCIÓN A. 2, se pide determinar:
 IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y

