CAPÍTULO 10: INTEGRALES Actividades de introducción
|
|
|
- Alfonso Ramos Soriano
- hace 6 años
- Vistas:
Transcripción
1 8 PÍTULO : INTEGRLES cividds d ioducció lcul l á d l gió limid po l ució l oig d coodds y u puo géico d scis. Si psmos l ució y diujmos l supici ll y l j OX, omos l s lu iágulo cágulo d l igu. Smos qu l á dl iágulo s: Á. To l s como l lu vl uidds, po o: Á Po o, l á jo l cuv s clcul como. lcul l á d l gió limid po l ució l oig d coodds y u puo géico d scis. omo s, psmos l ució y diujmos l supici ll y l j OX. ho omos l pcio cágulo d l igu. Si dividimos l igu u cágulo d lu u y u iágulo, l á s clcul como: Á Po o, l á jo l cuv s clcul como: º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP. Rpi los pocdimios ios p clcul l á d l gió limid po ls ucios, (co y R) l oig d coodds y u puo géico d scis. liz: Div ls psios oids los jcicios ios y zo qué lció hy ls ucios y y. Rcud l ipció d á como sum d ls uidds cudds cds po u igu. plícl p dmi l á d l ució 6, psádol u cudícul y codo l úmo d cuddos jo ll p dis vlos d. Rzo qué ocu co l á cudo l ució s giv l ivlo lizdo.. PRIMITIV DE UN FUNIÓN. L INTEGRL INDEFINID.. Diició d pimiiv S llm ució pimiiv d u ució o ució F l qu l divd d F s viic F Ejmplo: L ució F Tido cu ls popidds d l divd, s viic qu si ució pimiiv d s d l om F F F s u pimiiv d, y qu F. F s u ució pimiiv d F, co R. E co; cosidmos l ució, s dci, qu s, culqui o F, l qu y R. Si divmos:. Po o, F s pimiiv d.. Diició d igl idiid L igl idiid d u ució s l cojuo d ods sus pimiivs, y s ps como d igl d dicil d. Po o, si F s u pimiiv d : d F.. S l s l domi cos d igció, y l d os idic qu smos igdo spco d. Eso qu ho o pc dmsid impoci, sí l dá más dl, y qu sá lciodo co l gl d l cd qu vimos l cpíulo io y, l uuo, pdás liz igls vis vils. Po oo ldo, si codmos lo viso l cividd iicil y lo plicdo l Rsum cc dl oig dl símolo d igl, l psió d l igl idiid s l silizció d l psió: s dci: Sum d po cudo, d l sum dl á d odos los cágulos d lu y s iiisiml (d)
2 Ejmplos: d poqu. d l poqu l.. Popidds d l igl Ls popidds d ls divds jusiic muchs d ls popidds d ls igls. Sum y s d igls Sido qu si u v u v y u v u v: g d d g d y g d d g d Poduco po u úmo l Sido qu si k u k u: k d k d Ejmplos: d d d poqu. 7 cos d 7 cos d 7 s poqu 7 s 7 cos cividds suls omo omo Dmi los vlos d, y c p los qu F c 7. F s u pimiiv d F c 7 s u pimiiv d l ució : 7,, c Dmi y p qu F l s u pimiiv d l F s u pimiiv d : F l. Es imposil Si ps l volum d poducció d u áic, l cos mgil d l mism vi ddo po l ució 8. Ecu l ució dl cos ol, F pimiiv F d qu viic qu F., si s s qu dich ució vi dd po l omo F s u pimiiv d 8 : F d 8 d Nos dic qu cividds popuss. lcul ls siguis pimiivs: ) d, ) d, c) d F : F. Eocs: F, d). Dd, clcul l pimiiv F() d qu viic F.. ompu si F s u pimiiv d. Dmi los vlos d,, c y d p los qu F c d. d. E cso givo, plic po qué. s u pimiiv d l ució. l solv u pimiiv, Jvi y Ricdo h uilizdo méodos dis y, como d sp, h oido psios disis. Dspués d vislo muchs vcs y o co igú o los cálculos, l llv l polm l poso p v quié i i l jcicio. P su sops, l poso ls dic qu mos i i l polm. ómo s posil? 6. Rzo po qué l gáic sigui: s u pimiiv d l ució p d, E, (slvo los puos d discoiuidd dod o s divl): º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
3 . INTEGRLES DE FUNIONES ELEMENTLES.. Igl dl dicil d. Igls imdis El émio d sá lciodo, como su popio om idic, co l cocpo d dicil viso l cpíulo io. Tido cu qu l divd y l igl so opcios ivss u d l o, s imdio dduci qu: d co R. Es id os pmi dii ls igls imdis: Igls imdis so ls qu s oi dicm po l popi diició d igl. Si codmos l gl d l cd p l divció: F u F u u podmos sciil om F u df u y, clculdo su igl: u du df F dicil como: du Ejmplos: d d u du u 6 d l d / d d l / l l d l l.. Igl d l ució cos L igl d u cos s igul s cos muliplicd po. k d k co R. E co; cosidmos l ució F k F k k Tmié podímos dmoslo co lo viso.. y.: k d k d k Ejmplos: d d 8 d 8 d.. Igls d ucios pocils, co R. Si divmos: k Y coocmos l divd d l ució pocil: l. Es ácil zo l pocso ivso: Ejmplos: 6 d 6 co R. Tmié coocmos qu: d si y co R. / / / d d d d El cso = cospod l logimo pio: d d l co R. Dod l vlo soluo s d qu mos qu pl ods ls posils ucios cuy divd s l ució dl igdo, y s cumpl qu: l l si si l si si Ess dos ómuls s pud gliz pi d l gl d l cd, como vimos s: d si y d l co R. Ejmplos: d l d d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP cos s d l s cos s cos d 6 6 6
4 .. Igls d ucios pocils Pido d l divd d ls ucios pocils: y l, dducimos: d y d co R. l Y su glizció co l gl d l cd: d y d co R. l Ejmplos: d l d d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP 7 7 d l 7 d d d d Ncsimos l divd dl po. Lo soluciomos muliplicdo y dividido po d d d Ncsimos l divd dl po, s dci,. Tmos l, po os l l. P soluciolo, muliplicmos y dividimos po d d d l Ncsimos l divd dl po, s dci,. P llo, dividimos y muliplicmos po... Igls d ucios igooméics s d cos y d cos s co R. cos d s y d s Ejmplos: 7d cos 7 cos co R. sc d g y sc d g co R. s s d cos cosl d cosl d sl.6. Igls cuyo suldo so ucios igooméics ivss d cs y d ccos + cs d c g c cog d csc ccosc Ejmplos: y y d d cs d c g d csc + co R. co R. co R. ( ) d d d d cs 6 d d c gl l l
5 cividds suls lcul ls siguis pimiivs: o d. Osvmos qu l divd dl dicdo s, sí qu muliplicmos y dividimos : Eocs, s pimiiv s quivl d d d u du u u u du P, ilm, dshc l cmio: g g d F g Ejmplo: d g g. L divd d l g s g sc, y sí: cos cos Hcmos l g igul, dicimos mos émios igmos: g d d d d g g cos cos d Dshcmos l cmio y omos: g g g g g cos Muchs vcs s coviá u igl imdi y, como los jmplos, o hí sido csio dicho cmio. º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP : d 6 o d. L ució más impo s l pocil, y vmos qu l psió más complj s cu u domido u om simil l co g. L sciimos como: d d d Y s coim l hipósis. Muliplicdo y dividido ( ), p compl l divd d : d d du cg u. MÉTODOS DE INTEGRIÓN.. Igció po cmio d vil L igció po cmio d vil usc som l pimiiv dd u más scill, y pud hcs d dos oms dis: so. Idiic u p dl igdo co u uv vil. Ejmplo: d. No s csio u cmio d vil, po vmos mos l mcismo: d d d d Hcmos l iomio igul y dicimos mos émios: d Rsolvmos l pimiiv l om hiul: d Film, dshcmos l cmio: d El cso más cu s quél l qu osvmos u ució complicd y su divd: g g d U vz idiicd, l cmio d vil cosis llm dich ució y dici: g gg d g d d L igl s som o qu igmos: d F d d
6 g, dod so. El cmio sá d l om g s lgiá d om dcud p simpliic l igdo. S dici l iguldd: g d d gd Susiuimos l igl, igmos y dshcmos l cmio hlldo l ució ivs d g: g( ) g( ) d F g g d Fg Ejmplo: d. L psió dl dicl s simil l lció qu is ls ucios igooméics, sí qu imos l cmio: s d cos d cos d cos d d d cos d cos cos s cos d Es pimiiv s imdi: g cos Film, dshcmos l cmio: d s cs gcs E s cso, l psió il s s, po podmos mjol. Si lug d dshc l cmio dicm s s uscmos l lció l so y l g: g cos s d s d Omos: g cos s Hy muchos cmios y sudidos, d uso cu p csos cocos. Sá l méodo qu plicmos los pdos. y siguis. cividds suls d. omo s, s u igl imdi, po vmos pi l pocdimio: Hcmos l iomio igul y dicimos: d d d d d d d Rsolvmos l pimiiv: d d Y dshcmos l cmio: d 6 d. l L divd dl logimo s: l qu s cu l cció qu pcd l dicil d. Hcmos l l cmio: d d d c g c g l Rsulv d hcido l cmio d vil Hcmos l cmio qu os idic: d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP d Dsollmos l d d. cuddo, simpliicmos igmos: d d d Y, ilm, dshcmos l cmio: 7 d
7 cividds popuss 7. lcul ls siguis pimiivs uilizdo l cmio idicdo: d ) d hcido =. ) hcido =. d c) d hcido d) hcido ) s cos d hcido s ) s cos d hcido cos 8. Elig l cmio d vil qu simpliic ls siguis igls: cg ll ) d ) d c) d l d) d ) d ) d.. Igció po ps L igció po ps s u méodo qu os pmi clcul l igl dl poduco d dos ucios d ulz di, u ácilm divl y o ácilm igl. Los csos más cus so cos, logimos, poliomios, pocils y igooméics (sos y cosos), qu os pmi c l gl mmoécic L P E S. o l méodo d igció po ps sommos igls d l om u vd dod v s l ució ácil d ig, o psió más scill l qu pc u uv igl más ácil d clcul qu l d pid. S uiliz l sigui ómul: u vd uv vud qu s sul scii d om vid como: u dv u v v du Eis muchs gls mmoécics p cod s ómul, cogmos s d lls: - Slio Uidos D Vij Y U Vijo Mos S Vio D Ujo. - Susi U Dí Vio U Vli Solddo Vsido D Uiom. - Sgio U Dí Vio U Vc Sod Vsid D Uiom. Dmosció: osidmos l poduco d ucios u v y clculmos su divd: u v uv uv Igmos mos mimos d l iguldd: u v d u v uvd u v d uvd uv D dod: u v u vd uvd Dspjdo, sul: u vd uv vud Tmié pud os pi d l dicil dl poduco: du v du v u dv u dv du v v du Igmos mos mimos d l iguldd: d u v du v u dv v du u dv Y omos: u dv u v v du Osvcios:. omo om gl, s lig como u l pim ució d l pl LPES y como dv l so dl igdo, pudido ds l cso d qu pl dv = d. u c g du d Ejmplo: c g d c g d dv d v d c g d c g d c g l. Smos qu smos plicdo cocm l méodo si omos u igl más simpl qu l iicil. º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP d
8 u du d Ejmplo: s d cos cos d dv s d v s d cos cos cos d cos s. El pocso d igció po ps pud plics vis vcs. E s cso s d m l lcció iicil d u y v. Si s ivi, volvmos l igl d pid. Ejmplo: u du d d dv d v d d d d d u du d dv d v d. Si l igl iicil s l poduco d u pocil po u igooméic, s oi lo qu s domi igls cíclics. l plic po sgud vz l méodo d igció po ps, s oi l igl d pid, y s d solv como u cució: Ejmplo: u du d cos d dv cos d v cos d s s d s Rpimos: u du dv s d v d s d s s d cos cos cos cos d s d cos d s cos cos d Osvmos qu omos l igl d pid. Si domos I cos d : I s cos I I I s cos I s cos I s cos Eocs, susiuydo I po su psió y dsolldo ls ccios: cosd s cos. El méodo d igció po ps o s cluy. Podmos uilizlo dspués d vos oligdos liz u cmio d vil, o qu liz u cmio d vil dspués d h plicdo l igció po ps. cs cs s Ejmplo: d cs d d d s d Qu s sulv como l jmplo io, y popocio: s d s cos. s d dshc l cmio, psmos l coso como: d s s s Eocs: cs d cs 6. Eis os igls qu s sulv po ps y qu o sá cogids l gl d los LPES. L sgi gl s usc u ució ácilm igl y o ácilm divl p simpliic l pimiiv iicil. º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
9 6 Ejmplo: d Y l sgud igl s imdi: Po o: cividd sul u du d d dv v d d c g d c g º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP d d. Es pimiiv pud solvs d vis oms dis:. Po ps: L diiculd s co l ució ácilm igl. E s cso, l lcció s: d / d / dv d v / d u du d L sgud pimiiv s más simpl qu l pim, sí qu smos l u cmio: / / / / d d Es dci: d. Po cmio d vil: El cmio d vil qu uscmos s l qu pmi limi l íz dl igdo: d d d d d d d d Ls dos psios so dis, po s scillo mipulls p hcls iguls. cividds popuss. Dmi si ls siguis igls so imdis o o: Rsolvmos l pimiiv: d ) l d ) d cs d c g l d) ) d ) d h) c) s cos d g) g cos d d i) d j) d k) d. Rsulv ls siguis igls: ) d ) d l c) l cos g d d d) i) j) cos. Rsulv ls siguis igls: ) d ) l d c) cos d d d d) c s d ) s d co, R. ) uiosidd id liz: Rsulv l pimiiv cos l d. u du cosl P llo, muliplic y divid l igdo po : d cosl dv d v
10 7.. Igció d ucios ciols P odmos ho ls igls d l om d dod P() y Q() so poliomios. El pim pso s dsc qu s Q imdi. U vz dscdo qu s imdi, l pocdimio p igls s s dmi ls ícs dl domido y dscompol como sum d ccios lgics cuys igls sul más scills d clcul. S os pud pl ls siguis siucios: Q sólo i ícs ls simpls Q i u íz l múlipl Gdo P < Gdo Q Q i ícs ls simpls y múlipls Q i ícs compljs Gdo P Gdo Q Si l gdo dl umdo s mo qu l gdo dl domido P S d co gdo P gdo Q, y Q u poliomio móico o omlizdo. Q - El domido solo i ícs ls simpls S,, ls ícs d Q. Eocs, s i qu Q. El pocdimio cosis P N dscompo l coci d poliomios l om: Q co,,, N R. sí, psmos l igl d pid como sum d igls imdis: P N d d d d N l l l Q Ejmplo: d lculmos ls ícs dl domido y coizmos l domido: Po o, psmos l cció como sum d ccios simpls: lculmos los coicis: Y clculmos y ddo los vlos d ls ícs cods: - Si - Si D quí y omos ls dos igls logímics: d d d d d d d d l l l - El domido i u úic íz l múlipl Si s l íz múlipl d Q, s pud scii Q. E s cso, l dscomposició s: P N co,,, N R. Q sí, psmos l igl d pid como sum d igls imdis d l om: P N d d d d Q Qu so pocis d po givo, s dci: P N N d d d d l Q º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
11 º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP 8 Ejmplo: d 8 6 lculmos ls ícs dl domido usdo l méodo d Ruii o l om dl so y coizmos l domido: 8 6 Po o, psmos: 8 6 ho clculmos, y ddo vlos : Si P hll y podmos d culsqui oos dos vlos: - Si - Si Y solvmos l sism: Sumdo Po o, mos: d d d d d Ojo! No coudi l dl sism co l cos d igció. - El domido i ícs ls simpls y múlipls Es cso s u comició d los dos ios. L cció s dscompo sumdos cuyo umdo s u cos, y los domidos so los cos d Q l cso d ls ícs simpls y ls pocis sucsivs d l coizció l cso d ls ícs múlipls. Es dci, si m d c Q. L dscomposició s: d H d G d F c E c D c Q P m m co H,,, R los pámos o. L igl qudá dscompus u sum d logimos y ccios lgics simpls: d d H d G d F c E c D c d Q P m m K d H d F m c E c m l l l l Dod K ps l cos d igció, p o coudil co l d l coizció. Ejmplo: d lculmos ls ícs dl domido usdo l méodo d Ruii o l om dl so y coizmos l domido: Po o, psmos: ho clculmos, y ddo vlos : - Si - Si 7 7 P hll dmos u vlo culqui: Si 7 Po o, mos: 7 d d d d d d d d d d l 7 l 7
12 º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP - El domido i lgu íz complj simpl Si l domido Q coi lgú co iducil d l om c, l dscompo l cció sum d ccios lgics, dichos cos ls cospodá sumdos d l om: c N M s d liz l dscomposició compl, vmos solv s ipo d pimiivs: Ls igls d l om d c N M, cudo l domido o i ícs ls, s somá u igl logímic y o d co g. P llo, s pud pocd d dos oms disis: Fom. Mipulció lgic d l cció. El mcismo cos d dos psos: pimo s som l umdo l divd dl domido y, coiució, s covi l psió d sgudo gdo p llg l co g. Ejmplo: d. Es uomáico compo qu l domido o i ícs ls. E pim lug, imos qu l umdo s l divd dl domido: Muliplicmos l dl umdo po l co csio, s cso po : d d d coiució, summos y smos p o l : d d d Y spmos l igl como sum d dos, u co l émio uscdo y l so : d d d d d E sgudo lug, jmos co l sgud igl: d S d idiic u cuddo pco l domido. Vmos los émios, qu os cud l cuddo pco:, po o: d d d Y qu uscmos u igl d l om du u u, mos co comú l : d d d Y csi hmos mido, hmos cosguido l om d l divd dl co g. Solo os qud cosgui l divd d l cció oid: d d d Eocs: d d d Qu so dos igls imdis: d c g l
13 º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP Fom. mio d vil. ho os s co hc u cmio d vil sdo l solució complj qu s oi l i solv l cució d sgudo gdo dl domido. d d i c Ejmplo: d. ulmos l domido: i i 6 6 El cmio d vil s, po o: d d Eocs: d d Dsollmos ls psios y omos: d d d d d Qu so, dicm, ls igls d u logimo y u co g: d d g c l c g l Dshcmos l cmio: d cg l Dsolldo l gumo dl logimo omos l igl dl mcismo io: d cg l l U vz qu smos cómo solv s pimiiv, odmos l cso gl. Si l domido Q coi lgú co iducil d l om c, l dscompo l cció sum d ccios lgics, dichos cos ls cospodá sumdos d l om: c N M y los cos cospodis ls ícs ls s dscompodá como los pdos ios: Si d c Q l dscomposició s: D d c N M Q P co N M,,,, R. Ejmplo: d lculmos ls ícs dl domido usdo l méodo d Ruii o l om dl so y coizmos l domido: Tmos: Po o, psmos: N M N M ho clculmos, M y N ddo vlos ; mos: - Si - Si 8 N N N M - Si M N M N M Tmos, po o: d d d N M d d 8 d d d 8 d d d 8
14 8 l l c g Si hui más d u poliomio d gdo dos co ícs compljs, l dscomposició implic u cció p cd émio: P H K M N co H, K, M, N, R. Q c c Si l gdo dl umdo s myo o igul qu l gdo dl domido P S d co gdo P gdo Q. E s cso, pim lug dividimos l umdo l domido. Q D s om, l cció s dscompo l sum d u poliomio y u cció lgic co l gdo dl umdo P R mo qu l gdo dl domido: d d d Q Q Ejmplo: d Dividido l umdo l domido, mos: 7 7 sí: d d d d7 d 7l El domido Q() o s u poliomio móico P Si l igl ciol d l poliomio dl domido o s móico (su coici picipl o s ), l Q coizció s liz dl modo hiul l qu s coiz los poliomios. Ejmplo: Q Q Q P l cálculo d igls s uiliz l coizció oid y s pocd d l om y plicd: d Ejmplo:. L dscomposició sul s: Rsolvmos l cució como hicimos vis vcs s, y omos: d d d l l cividds popuss. Rsulv ls siguis pimiivs: d ) ) ) d h) + d d ) c) d d d) d g) d i) d j) d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
15 .. Igció d ucios igooméics. P ig u ució igooméic o imdi, mos qu clsiicl u d ls siguis cgoís: uddos d ucios igooméics Si l ució s l cuddo d u ució igooméic, podmos ho mucho jo si pvim l sudimos:. uddos d so y coso: P solv ss pimiivs os smos ls psios: s cos y cos cos s Sumdo y sdo mimo mimo: cos cos y cos s Omos ls siguis simpliiccios: d cos d s y s d cos d s cos. uddos d sc y cosc: Y smos qu so igls imdis: sc d g y cosc d cog. uddos d g y cog: S covi igls imdis ácilm: d sc d g y cog d cosc d cog g cividd sul d s cos Es pimiiv pud solvs d vis oms dis. E s pdo usmos ls somcios cié d d d d pdids: cog s cos s cos scos s Fucios imps so d Si l igl s d l om R s,cos, (s dci, u ució ciol s y cos) y viic qu R - s,cos Rs,cos dmos plic l cmio cos. Ts som ls ucios igooméics co l cmio, odmos u ució ciol qu solvmos co los méodos ios. s Ejmplo: d cos s El po dl so s imp, po o s imp so: Rs,cos cos Po o: s s R s,cos Rs,cos cos cos plicmos l cmio idicdo, mipuldo ligm l igl: cos s s cos d s d s d s d d cos cos cos s Eocs: d d d cos Qu podmos solv como igl d u ució ciol: d d d c g Y dshcmos l cmio: d cos cgcos s cos udo o s simpl mipul l igdo, podmos uiliz ls siguis iguldds: d cos c cos d s cos º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
16 Ejmplo: s d ho vmos uiliz ls psios ulds p o l pimiiv: cos s d d d cos Qu s l mism igl qu solvimos s (como o podí s d oo modo) d d Fucios imps coso d Si l igl s d l om R s,cos, y viic qu R s, cos Rs,cos dmos plic l cmio s. omo s, mos ls siguis iguldds: s Ejmplos: cos s d ompomos qu l dicdo s imp coso: d cs d cos s s,cos cos s Rs, cos ( cos ) s Rs,cos R plicmos l cmio idicdo: s I cos s d cos s cos d d Dsolldo l poduco, I d Y dshcmos l cmio: I cos s d s cos d s d sc d cos Es vid qu l dicdo s imp coso, plicmos l cmio: d d s d d d cos cos d L solvmos como igl d u ució ciol: d d d Eocs: l l l s Y dshcmos l cmio: sc d l s uiosidd id liz: vcs, is sgis spcíics p solv pimiivs más ápidm. P s pimiiv, sc d, si muliplico y divido sc g : d sc g sc sc g sc d sc d d l sc g sc g sc g º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
17 Fucios ps so d y coso d Si l igl s d l om R s,cos, y viic qu R s, cos Rs,cos dmos plic l cmio g. E s cso, podmos hll l psió p l so y l coso como: s cos g cos cos cos g g Y s cos s g g Qu sumimos l l sigui: d g c g d s cos d Ejmplo: s cos Es vid qu l dicdo s p so y coso: R s,cos R s, cos Rs,cos s cos d g d d plicmos l cmio idicdo: d d s cos s cos d Qu s imdi si l spmos sumdos: d g g cog s cos g uiosidd id liz: omo s, podmos sgui uscdo lics ids qu simpliiqu igls. Usdo l lció udml d l d s cos d d igoomí, s cos : d g cog s cos s cos cos s O i, como vimos iom, cudi ls psios dl águlo dol como hicimos s: d d cosc d cog s cos s O i, como vimos iom, cudi ls psios dl águlo dol: d d d d cosc d s cos s cos s cos s mio gl Si o pudimos solv l igl co los cmios ios, dmos plic l cmio uivsl: g D quí mos: g c g c g d d d d plicdo ho ls popidds d ls zos igooméics dl águlo dol, mos: s s s cos cos g cos g s cos g Tmos, po o: cos cos s cos g d d g cos s cos º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
18 Ejmplo: d Es ácil v qu o cumpl igu d ls s codicios ios, po o: cos g d d d d cos d d d d g uiosidd id liz: P s pimiiv, si muliplico y divido po l cojugdo dl domido, cos : d cos d cos d cos d cos cos cos cos s ho spmos dos sumdos, omos sds igls imdis: cos d d cos d cog cog cosc s s s s d E gl, ls igls d l om: s cos Hcido k cos y k s, co k y vlos o, l pimiiv s som : d d d cosc d s cos k s cos k cos s k s k qu y vimos cómo solv pdos ios. cividds popuss. Rsulv ls siguis pimiivs: ) cog s s d cog d s d d ) c) d) cos s cos ) g d ) g g( ) d d g) d h) cos ( ) s d i) j) s cos d k) s d l) s d s cos m) cos d ) l cos l d uco: muliplic y divid po : d s d d d ñ) o) p) s cos s cos d q) s cos º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
19 6 cividd sul Id liz s d s cos E s jmplo podímos cudi qu l igdo s p so y coso y plic l cmio s d s cos d d d s cos s cos Po mié podmos jug u poco co l domido, compldo u cuddo pco: s d s d s cos s cos s cos s cos s cos s d s d s d s d s cos s cos s s L úlim id liz cosis o l cos l domido: cos d cos d s d s s cos Y hmos oido u igl imdi: s d s d = c g cos s cos cos g. Eocs:.. Os igls Los pdos ios dj clo qu l pocso d solució d igls o s ácil como l d divció. Tods ls simpliiccios qu s pud liz dspués d div u ució s lo qu complic l cálculo d pimiivs. Po o, muchs ocsios os dmos qu limi odc los cmios cosjdos. dmás, is ucios qu o i pimiiv o o pud pss émios d ucios lmls. Icluso lgus d lls siv p dii oo ipo d ucios. lguos jmplos so: s d, d, cos d, cos d Podmos i clculls co GoG, po jmplo. Tclmos l d d:. Igl[s()/]. Igl[cos(^)] Y osvmos qu pc psios como: s d Si, cos d i Dod i y Si so ls sigls d osi Igl y Si Igl, cuys gáics so: Lismos coiució los cmios d vil y mcismos cosjdos p os pimiivs. º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
20 7 Igls d ucios pocils Igls d ucios iciols m p q R,, R s, d g d g s d g d R ; d, co. l (,p,, ) m.c.m. R d g g R d g sc cividd sul d El cmio cosjdo s s, ocs: s d s cos d s cos d d cos d Uilizdo l lció udml d l igoomí: s cos d s cos d cos cos d cos d Qu y solvimos s: cos d cos d s P dshc l cmio, jugmos d uvo co ls psios igooméics, s s cos s s cs y omos: d cs s Os igls igooméics - R sm,cosd : S uiliz ls psios: s s cos cos cos cos cos cos s cos s s u s s cos - s d s d dv s d u cos cos s - cos d cos dv cos d - g g d g (sc -) d g d (álogm co l cog) - sc d sc sc d (álogm co l cosc) Si p: sc ( )/ sc d ( g ) sc d )/ g sc d ( ) ( d Si imp: Po ps, lgimos: u sc y dv sc d sc d sc g ( ) sc d d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
21 8. EL PROLEM DEL ÁLULO DEL ÁRE.. Á jo u cuv Dd u ució coiu y o giv u ivlo,, su gáic dmi u gió dl plo qu vdá limid po l ució, l j d sciss y ls cs y. Vmos cómo podmos clcul d om poimd l á d dich gió: Tommos u pició dl ivlo,. osis dividi l ivlo ps, omdo p llo los puos,,,, viicdo.,,,,,. sí, mos los ivlos, coiució, domos po m i l míimo vlo qu om l ució l ivlo i, i y po M i l máimo vlo qu om l ució l mismo ivlo. sí, cd ivlo i, i cosidmos dos posils igus, l cd co cágulos d s i i y lu m y l cd co cágulos d s i i y lu M i. Sumdo ls ás d los cágulos, omos: i Sum iio Sum supio E l pim cso omos u poimció po dco dl á cd jo l cuv: s m m m mi i i i Es sum s domi sum iio d l pició l ivlo,. E l sgudo cso omos u poimció po cso dl á cd jo l cuv. S M M M M i i i i Es sum s domi sum supio d l pició l ivlo,. Hmos oido dos poimcios dl á, u po dco s y o po cso S. S i qu s S Si mos u pició P dl ivlo,, co sum iio s y sum supio S, dimos qu o pició P dl ivlo, s más i qu P si coi odos los puos d l pició P y dmás oos puos uvos. P dich pició P, mos u sum iio s y u sum supio S. S viic qu: s s S S Es dci, l om u pició más i, l sum iio um (sido odví mo o igul qu l vlo dl á) y l sum supio dismiuy (sido myo o igul qu l vlo dl á). Pició P Pició P Pició P Pició P Eso sigiic qu cuo más i s l pició, más os ccmos l vddo vlo dl á. osiddo u sucsió d picios cd u más i qu l io, P,,,, P, º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
22 s, s,, s, s, l sucsió d ás po dco y S, S,, S, S, l sucsió d ás po cso. udo, l logiud d los ivlos d l pició s hc cd vz más pquñ, lugo i i. sí, cudo l ució s igl, ls sums iios y supios dá l á: S s Eso sigiic qu S s lim S lim s lim, y d quí: lim S lim s Sum iio y supio co l pició P.. Igl diid S u ució Diimos l igl diid y d Sum iio y supio co l pició P coiu y o giv u ivlo,. como l psió d, l j d sciss y ls cs y Su vlo s l á compdid l gáic d. Los vlos y s llm límis d igció. Hmos viso qu dd u sucsió d picios P,,,, P, dl ivlo,, cd u más i d l io, co sums iios s,,,, s, y sums supios,,,,, s viic qu dichs sums dá l vddo vlo dl á. S i qu: d lim S lim s, s dci, qu l igl s pud ip como: l sum dl á d odos los cágulos d lu Popidds:. Si los límis d igció so iguls, l igl diid vl co. d. Si l cuv sá po cim dl j X, l igl s posiiv, d, mis qu si l cuv sá po djo dl j X, s pud dii mié l igl diid, qu sá giv: d. Á y s iiisiml (d) compdidos y. c. S c,, ocs podmos dscompo l igl d l om: d d d. c. Si icmimos los límis d igció, l igl cmi d sigo. d d. Dds dos ucios coius y g l ivlo,, s i qu: gd d gd y g d d g d 6. Dd u ució coiu l ivlo, y u cos k R, s i qu: k d k 7. - Dds dos ucios coius y g,, viicdo g,, s i: d gd d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
23 .. Tom dl vlo mdio dl cálculo igl Dd u ució coiu l ivlo,, ocs is u puo c, Ipció goméic: Sido l igl u á, l ipció goméic s simpl: Eis u puo c, l qu l á cd l cuv, l j d sciss y ls cs y s igul l á d u cágulo d s l mpliud dl ivlo,, y lu l vlo qu om l ució l puo imdio, c. l qu d c. Ejmplo: Ecu los vlos d c qu viic d c sido l smicicuci d co l oig y dio, y y los puos d co d l mism co l j OX. Smos qu l cució d l cicuci l plo s y, sí qu p l polm qu s os pl mos qu y los puos d co co l j so, y,. S d co l cágulo (zul) cuy á coicid co l d l smicicuci (oj), sido qu l s p ms igus sá compdid los puos, y,. Eocs, sido: c h y cic. D viics: h h h El vlo d h cospod l vil y, po os pid u vlo d. Po o: y h.. Fució igl o ució á Dd u ució coiu l ivlo l ució igl o ució á como:.68,, p culqui puo, F d F :, R, qu so los vlos d c qu os pid. s di.. Tom udml dl cálculo igl S u ució coiu l ivlo, y s F d co, l ució igl. Eocs F s divl, y F p culqui puo,. Dmosció: plicdo l diició d divd mos: h F h F d d F lím lím Spdo l pim igl dos sumdos (popidd ): F lím h h h h h d d d lím h h h h h c h h d c h F lím lím lím c h h h h h lim c y, po o: F h plicdo l om dl vlo mdio dl cálculo igl,, l qu d c h c h sí: omo c, h y s coiu ocs cividd sul Si cu l cálculo d l igl idiid, clcul plicdo l om udml dl cálculo igl: si d h d d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
24 Glizció (): Si lug d vlos ls, los límis d igció so ucios ls d vil l, s plic l gl d l cd p o: S u ució coiu l ivlo divl, ocs F s divl Glizció (): S u ució coiu l ivlo so divls, ocs F s divl cividd sul h, y s F d co,, y F h h p culqui puo, º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP l ució igl. Si h() s. h, y s F d co, g, y F h h g g p culqui puo, Si cu l cálculo d l igl idiid, clcul si plicdo l om udml dl cálculo igl: d l ució igl. Si h y g d 6.6. Rgl d ow Si s u ució coiu l ivlo, y F s u pimiiv d sul pss como: d F Dmosció: S i qu F s u pimiiv d F F G d mié s u pimiiv d., ocs: d F F. Po oo ldo, plicdo l om udml dl cálculo igl,. l s dos pimiivs d l mism ució, sólo s dici u cos: G F G F Evludo ls dos psios ios l puo, mos: G F G F F F G d G d Evludo ho dichs psios ios l puo, mos: G F G F G F F d F F G d G d Eocs, p plic l Rgl d ow s sigu los siguis psos:. lculmos u pimiiv F d. Hllmos los vlos d s ució y : F y F. lculmos l igl d F F F Ejmplos: 6 d. L ució 6 s u ució poliómic, lugo s coiu odo R, y po o s coiu l ivlo [, ].. - lculmos u pimiiv d : 6 d 6. - Hllmos l vlo d s pimiiv p los mos dl ivlo: F F y F 7, y
25 . plicmos l gl d ow: 6 d F F d. L ució [,+]. s u ució poliómic, lugo s coiu odo R, y po o s coiu l ivlo. - lculmos u pimiiv d : d. - Hllmos l vlo d s pimiiv p los mos dl ivlo y smos: d cividds popuss. Rsulv ls siguis igls diids: 6 ) d ) d c) d d) d ) s d ) l d. Hll l vlo d c qu viic d c y zo su ipció goméic. d 6. Si cu l cálculo d l igl idiid, clcul si l.7. pliccios d l igl diid Á cd jo u cuv P clcul l á compdid l gáic d u ució y l j d sciss u ivlo l qu l gáic pc po cim y po djo dl j X, s csio hll cd u d ls ás po spdo. E los suivlos los qu l gáic sá po djo dl j X, l igl sá giv, y ommos l vlo soluo od l igl. 7 Á d d d F F F F F Dsd l puo d vis pácico, si mos l psció gáic d l ució s pud pl l á como sum o s d ls gios dod l ució s posiiv o giv, spcivm. Ejmplo: Hll l á cd l gáic d l ució L ució, l j X y ls cs y. s u ució poliómic, lugo s coiu odo R, y po o s coiu l ivlo [, ]. L gáic d s u páol cócv (). lculmos l véic: Si. Tmos: V, lculmos los puos d co d l ució co l j X. P llo, solvmos l cució : 6,, Rpsdo l ució y ls cs y osvmos qu l á qu qumos clcul s divid s gios. Hllmos u pimiiv d : d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
26 º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP Hmos oido s gios. El á ol sá l sum dl á d cd gió: Á d d d F F F F F F 7 7 u Po o, l á d l gió s igul 7 u Tmié podímos pl, y qu mos l psció gáic d l ució: Á Á Á Á d d d Es dci: Á 7 7 u Popidds:. Si l ució s imp, l igl diid u ivlo siméico spco l oig s ul: Si s imp, d. Si l ució s p, l igl diid u ivlo siméico spco l oig s: Si s p, d d P d ss dos popidds os s co v ls gáics d cd ipo d ució. - Si l ució s imp, s siméic spco l oig d coodds y di dos cios d sigo opuso igul á mos ldos dl oig. l suml, l suldo s ulo. - Si l ució s p, s siméic spco l j OY y di dos cios d igul sigo igul á. Fució imp Fució p cividd sul lcul l á d u cículo d dio. Podmos lgi l uicció d l cicuci, sí qu l cmos l oig. P s cso, l cució d u cicuci d dio s: y y Podmos povch l simí dl polm y clcul l á pi dl cio dl pim cud: d L pimiiv s sulv co l cmio: d d cos s y popocio: d cs plicdo l gl d ow omos: d cs cs cs Es dci, llgmos l coocid ómul:
27 Á compdid dos cuvs El á compdid ls gáics d ls ucios igul qu l á qu s ci l ució dici gd sido g o, podmos scii l psió gl: g y g l ivlo, s g y l j X s ivlo.. Si o s dmi qué ució sá po cim d l d Si mgo, dsd l puo d vis pácico, l cso l qu ls ucios y g g vios puos d co, sá covi hll ls dis gios y dmi ls ás po spdo. Ejmplo: Ls pscios gáics d spcivm, sí qu s d sp qu hy dos cos lls y, po o, s posil qu hy vis gios dicids cu. L psció gáic d s u páol cov. lculmos su véic: Hll l á compdid ls gáics d ls ucios y y g so u páol y u c, Si 8 V, lculmos los puos d co d l ució co l j X, solvido l cució : L gáic d g s u c. P diujl, s co o dos puos: y P dmi l gió d l qu qumos clcul l á, l psmos, juo co los límis d igció: g : g ls cs y. uscmos los puos d co ls dos ucios, solvido l cució g Po o, l á qu qumos clcul sá: Á g d Hllmos u pimiiv d g : g g g d d Hmos oido dos gios. El á ol sá l sum dl á d cd gió: Á d d Po o, l á d l gió s igul u F F F F u 6 6 º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
28 º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP Volum d u sólido d volució U cuiosidd lciod co s pdo hc ci Johs Kpl. Su sgud spos, Sus, u c qu l clció d l od, Kpl osvó qu l volum d los ils d vio s sim co u vill ioducid digolm l ol po l gujo d l p. Kpl mpzó ps l zomio mmáico qu jusiic s pocso, y d s modo comzó l sudio d los volúms d los sólidos d volució. Si s u ució coiu l ivlo,, ocs l volum dl sólido gdo l gi l ució oo l j OX, s clcul mdi l ució: d V Ejmplo: Hll l volum dl coo d lu uidds diido l gi oo l j d sciss l c y. Los dos dl jmplo os hc clcul l igl: 8 d d V u cividd sul lcul l volum d u s d dio R. omo s co l cículo, lgimos u cicuci cd l oig, cuy cució s: R y R y omo s, l simí pmi clcul l volum pi dl cio dl pim cud: R R d R d R V Qu s u pimiiv imdi y, plicdo l gl d ow omos: R R R R R V R o l qu omos l coocid ómul: R V
29 6 RESUMEN UDRO DE PRIMITIVS d d + g d d gd d + d, ( ) d + d d l d +,, > l cos d s s d cos sc g d sc sc d g cosc d cog d c g c cog d c s d csc + c cos + c cosc Méodo d igció po cmio d vil Méodo d igció po ps. g d d d g d G F G. d g d gd g g d G F Gg u dv u v v du Rgl d ow d F F F Á u cuv y l j OX Á dos cuvs g Volum d volució oo l j OX V d d d + º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
30 7. - Sido qu d ) d ) d EJERIIOS Y PROLEMS. y d, clcul: ) d ) 7 d ) 6 7 d 6) d 7) d 8) d ) ) d ) d ) d ) d ) d ) d 6) d 7) d 8) d ) d ) d ) d ) d ) d ) d ) d 6) d 7) d 8) ( 7) d ) d ) d ) d ) ) ) d 6) d 7) ) d ) 7) d ) d ) s d ) d d d ) d d 7 8) ) 8) d ) ) d l cos ) d 8) g sc d 7) d d d d d d ) d ) ( ) d ) 7d 6) 8 d ) d ) s cos d s 6) d cos sc ) l d 6) d g º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
31 8 '. - Sido qu d l y d l, clcul: d d d d ) ) ) ) ) d 6) d d 7) 8) d ) d ) d d ) d ) ) l d ) d ) d 6) d 7) g d s cos 8) cog d ) d l ) cos s cos s cos ) d s ) ) cog d s cos. - Si d, d, d y ' d, clcul: l l ) d ) d ) d ) d ) d 6) d 7) d 8) d ) d ) 6 d ) d l ) d ) d s ) cos d cos ) s d cos 6) d 7) s d 8) d g ) sc d ) d ) d. Sido qu s d cos, s d cos, cos d s y cos d s clcul: ) s 8d ) s d ) cos d ) s d s cos ) d 6) s d 7) d cos s d sl ) d. Si d g d g y d d g ' g, clcul: cos cos ) g d ) g d ) g d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
32 6. Hll l vlo d ls siguis igls, usdo u cmio d vil: ) d ) 6 d ) 6 d ) d ) d 6) d 7) s s cos cos d 8) d ) d cos s ) d ) d ) ) d d d ) s d 7. Hll l vlo d ls siguis igls, usdo l méodo d igció po ps: ) cos d ) s d ) l d ) l ) l d ) d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP 6) cos d 7) s d 8) cos d ) l d 8. Hll l vlo d ls siguis igls ciols: ) d ) d ) d ) d ) d 6) d 7) d 8) d ) ) d ) d d ) d ) d ) d ) d 6) d 7) d 8) d ) d ) d 6 6 ) d ) d ) d ) d 6. Hll l vlo d ls siguis igls diids: ) d ) d ) s d ) s d ) d 6 6) d 7) d 8) d ) d ) l d ) d s cos. Hll l vlo d p qu s cumpl d.. Hll l á compdid l ució, l j d sciss y ls cs y 6.. Hll l á limid po l ució ' cos, l j d sciss y ls cs y.. Hll l á d l gió limid po l ució 6 y l j d sciss.. lcul l á d l poció d plo qu limi ls cuvs y y.. Hll l á dlimid po ls gáics: ) y g ; ) y g
33 UTOEVLUIÓN. Los vlos d, y c p los qu F c s s u pimiiv d l ució 7 cos so: ), 7, ; ), 7, ; c), 7, ; d), 7,. L igl imdi d vl: ) ; ) 6 6 sd. L igl vl: s cos ) g(ccos) + ; ) - c s(cg) + ; c) cg(cs) + ; d) c gcos. cs. l ig po ps d s oi: 6 c) ; d) ) cs ; ) cs s ; d) cs. L igl d vl: ) l c g ; ) l c g ; c) l c g ; d) Nigu s coc d 6. L igl s cos vl: ) g s ; ) g cog c) g cog ; d) g cog 7. L igl diid cos d vl: ) ; ) c) ; d), l j d sciss y ls cs = y = vl: ) 8/; ) / c) 6/; d) 6/ 8. El á compdid l gáic d l ució. El á compdid ls gáics d ls ucios y g vl: ) /; ) / c) 7/; d). El volum dl sólido d volució gdo po y =, y, l gi oo l j d sciss s: ) ; ) 6/ c) 6; d) / º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
34 () lcul u pimiiv d l ució () lcul: ) d d) s pédic: Polms d igls ls P..U. s d ) d () lcul hcido l cmio d vil : ) d ) () lcul cos d () ) Ecu ods ls ucios d ) l d c) cos ) c cuy sgud divd s. ) D ods lls, dmi qull cuy gáic ps po los puos, y,. (6) osid l ució y ) Dmi l c g l puo qu l ució lcz su máimo livo. ) Diuj l cio limido po l cuv y l c g io. c) Hll l á dl cio dl pdo (). (7) Oé l á dl cio cdo po ls cuvs y cos,. (8) osid l ució s ) Diuj l cio codo po l gáic d d y l ivlo, l j OX y ls cs = y. ) lcul l á dl cio io. () ) Diuj l cio plo limido po l páol y = y ls gs l cuv los puos d iscció co l j d sciss. ) Hll l á dl cio diujdo (). () Hll l á d l zo dl plo limid po ls cs y, y () Ls gáics d ls ucios s y d, y l gáic d l cuv y l g limi u cio iio l plo. ) Diuj u squm dl cio. ) lcul su á. si, dod l sigiic logimo pio d. l si () S ) Diuj l cio codo compdido l gáic d y l c y =.. ) lcul l á dl cio io. si () S l ució : R R diid po si ) Hz u diujo poimdo d l gáic d l ució. ) lcul l á dl cio limido po l ució, l j d sciss y l c =. () S l páol y 6 ) Hll l cució d l g l gáic d s cuv l puo d scis =. ) Hz u diujo poimdo dl cio limido po l gáic d l páol, l j OY y l c g hlld iom. c) lcul l á dl cio io. () Dd l ució cos, usc l vlo dl úmo l sido qu d º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
35 (6) osid ls cuvs y g. ) Ecu sus puos d iscció. ) Rps l cio limido qu ci lls. c) Ecu l á dl cio limido po ls dos cuvs. (7) Ls cuvs y, y y l c limi u cio iio l plo. ) Diuj u squm dl cio. ) lcul su á. (8) S cosid l cuv d cució y ) lcul l cució d l c g l gáic d s cuv l oig. ) Diuj u squm dl cio limido po l gáic d l cuv y l c hlld. c) lcul l á d s cio. () L divd d u ució ) lcul los ivlos d ccimio y dccimio y los máimos y míimos d ) Dmi l ució sido qu. s () L gáic d l páol plos. ) Diuj l gáic d l ució y los cios. ) lcul l á d cd uo d llos. () ) lcul l ució y divid l cuddo d véics,.,,,, y, sido qu su divd s y qu D dos cios. ) Dmus qu i u mo livo u puo dl j d sciss y zo si s máimo o míimo. () Ls gáics d l cuv y y d l páol y ci u cio plo. ) Diuj s cio. ) lcul su á. si () S : R R l ució diid po m si si ) lcul m y p qu s coiu odo su domiio. ) P sos vlos hlldos, clcul l á dl cio limido po l gáic d y l c y =. si () S l ució : R R diid po si ) Diuj l gáic d l ució. ) Hll l á dl cio limido po l gáic d y l j d sciss. () L cuv y y l c y limi u cio iio l plo. ) Diuj u squm dl cio. ) lcul su á. (6) L páol y y l c limi u cio iio l plo. ) Diuj u squm dl cio. ) lcul su á. (7) L cuv y y l c y limi u cio iio l plo. ) Diuj u squm dl cio. ) lcul su á. (8) S cosid l páol y 6 ) lcul l cució d ls cs gs l gáic d l páol los puos d co co l j OX. ) Diuj u squm dl cio limido po l gáic d l páol y ls cs hllds iom. c) lcul l á d s cio. º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
36 () S cosid l ució k si si ) Dmi l vlo d k > p qu l ució s coiu l ivlo,. ) Supoido qu k, hll l c g. c) Supoido qu k, hll l á qu l ució dmi co l j OX, p, () ) Rsulv po ps l sigui igl: l d ) D ods ls pimiivs d l clcul l qu ps po l puo,.. () L gáic d l páol y 8 y l c ci u cio plo. ) Diuj poimdm dicho cio. ) lcul l á d s cio. () L gáic d l cuv y ls cs y y ci u cio plo. ) Diuj poimdm dicho cio. ) lcul l á d s cio. () Esoz l gáic d l páol y 7 y hll l á d l gió dl plo dmid po l páol y l c qu ps po los puos, y, 6. () S dispo d u chp d co qu pud pss po l gió dl plo dmid po l páol y y l c y. ) Rps gáicm l chp y clcul su á. ) Dmi ls dimsios dl cágulo d á máim qu s pud o pi d dich chp co l codició d qu uo d sus ldos sé l c y. () Rps gáicm ls páols y y y y clcul l á qu ci. (6) S cosid l ució. ) Hll los máimos, míimos y puos d ilió. ) P,, soz l gáic d l ució y clcul l á compdid ll y l j X. (7) S cosid l ució. ) Hll sus síos, máimos y míimos. ) Rps gáicm l ució. c) Hll l á dlimid po l ució y l j OX, p. (8) ) lcul: l( ) d dod l() s l logimo pio d. ) Uiliz l cmio d vil = - p clcul d. Idicció: P dshc l cmio d vil uiliz: = l.spim 8. Opció ( puos) () ) Si s u ució coiu, o F () sido: F() = ( ( ) ) d ) Si () = y dmás ( ) d =, hll l cució d l c g l gáic d F() l puo (, F()). () S l ució () =. ) lcul ( ) d. ) S di g() = g( ) ( ) d. lcul lim () ) Hll l á dl cio limido po l gáic d () = s y l j OX ls sciss = y = π. ) Hll l volum dl sólido d volució qu s oi l hc gi l gáic d () = s lddo dl j OX ls sciss = y = π. mplició lo lgo dl m hmos dsolldo vios méodos, sgis y pliccios d ls igls, po hy mucho más. Djmos s pdo p mos os qu sup los coidos dl mio. Igl d u ució ciol cudo l domido i ícs compljs múlipls P Si l solv l pimiiv d u ució ciol: d co Gdo d Q() > Gdo d P(), Q() i ícs Q º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
37 compljs múlipls, s dci, su coizció pc émios d l om: Q c d P Q l máimo comú diviso d Q y Q ; Dscompomos l cció lgic como: u poliomio, d gdo uo mo qu D l poliomio qu sul dl coci Q ; u poliomio, d gdo uo mo qu l D, dmi; D, dmi. P d d co: Q D El dsollo qui s hilidd co ls psios lgics, y c popociodo u igl ciol cuyo domido i ícs compljs simpls. Volum d u sólido d volució gdo l gi oo l j OY Si,, ocs l volum dl sólido gdo l gi l ució oo l s u ució coiu l ivlo j OY s clcul co l igl: Logiud d u co d cuv Si V s u ució coiu l ivlo d,, ocs l logiud dl co d l cuv los puos d scis y s clcul como: L d Supici d u sólido d volució gdo l gi oo l j OX Si,, ocs l supici dl sólido gdo l gi l ució oo s u ució coiu l ivlo l j OX s clcul mdi l igl: S Ejmplos: Hll l volum d l plz d oos gd l gi l c dl j OY l ivlo,. d y lddo L igu cuyo volum qumos hll s l dl mg. S d clcul l igl: V d d u Hll l logiud d u cicuci d dio. Dmos uiliz l psió: L plicdo l gl d ow omos: Es dci: d, sí qu divmos l cució d l cicuci: y y y Eocs, uilizdo l simí d l cicuci o vz: d L d d d L pimiiv s sulv co l cmio: s d cos d como vimos l pdo., y popocio: L u d cos d d cs cs s L cs cs cs k º chillo. Mmáics II. píulo : Igls uos: Lici Gozálz y Álvo Vldés LiosMVd.k Rvisos: Mí Molo y Jvi Rodigo Iluscios: ds co GoG y l GIMP
LAS ESTADÍSTICAS DE ORDEN COMO UNA APLICACIÓN DE TRANSFORMACIÓN DE FUNCIONES VARIABLES. OLGA ARDILA SANCHEZ oardilas@gmail.com
 LAS ESTADÍSTICAS DE ORDEN COMO UNA APLICACIÓN DE TRANSORMACIÓN DE UNCIONES VARIABLES OLGA ARDILA SANCHEZ odils@mil.com Tbjo d Gdo p Op l Tiulo d Mmáico Dico Bio Lozo Rojs UNDACION UNIVERSITARIA KONRAD
LAS ESTADÍSTICAS DE ORDEN COMO UNA APLICACIÓN DE TRANSORMACIÓN DE UNCIONES VARIABLES OLGA ARDILA SANCHEZ odils@mil.com Tbjo d Gdo p Op l Tiulo d Mmáico Dico Bio Lozo Rojs UNDACION UNIVERSITARIA KONRAD
INTEGRALES INDEFINIDAS
 INTEGRALES INDEFINIDAS Pág.: ÍNDICE:.- FUNCIÓN PRIMITIVA..- INTEGRAL INDEFINIDA..- INTEGRALES INMEDIATAS...- INTEGRACIÓN INMEDIATA DE ALGUNAS FUNCIONES. 4.- PROPIEDADES DE LA INTEGRAL INDEFINIDA. 5.- MÉTODOS
INTEGRALES INDEFINIDAS Pág.: ÍNDICE:.- FUNCIÓN PRIMITIVA..- INTEGRAL INDEFINIDA..- INTEGRALES INMEDIATAS...- INTEGRACIÓN INMEDIATA DE ALGUNAS FUNCIONES. 4.- PROPIEDADES DE LA INTEGRAL INDEFINIDA. 5.- MÉTODOS
( ) ( ) ( ) ( ) ( ) 2. ( ) t ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) OPCIÓN A. lim. =. Calcular. du I = + ln u = + + + e ln. e ln.
 ES diáo d álg Solció Jio J Clo loo Gioi OPCÓN E.- S ) Clcl d ( po) ) S d g. Clcl g ( po) d g ) d d K d d d d B B B B B B d d d d d d d d d ) g Hopil L' plicdo ES diáo d álg Solció Jio J Clo loo Gioi E.-
ES diáo d álg Solció Jio J Clo loo Gioi OPCÓN E.- S ) Clcl d ( po) ) S d g. Clcl g ( po) d g ) d d K d d d d B B B B B B d d d d d d d d d ) g Hopil L' plicdo ES diáo d álg Solció Jio J Clo loo Gioi E.-
SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN
 TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
TEMA Nº SISTEMAS DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN. TEOREMA PRELIMINAR INTRODUCCIÓN.- Sism d cucios dircils lils co icógis d l orm P D P D P D P D P P D D... P... P... P D D D b b b dod ls P
IES Mediterráneo de Málaga 2009 Juan Carlos Alonso Gianonatti. DISTRITO UNIVERSITARIO DE Madrid MATEMÁTICAS (Mayores de 25 años).
 IES Mditáo d Málg Ju los loso Giotti DISTRITO UNIVERSITRIO DE Mdid MTEMÁTIS (Mos d ños. OPIÓN Ejcicio.- (. tos. S id l cució ticil do ls tics:. tos. Idic ls dios qu d t l ti.. tos. lcul l is -. c. tos.
IES Mditáo d Málg Ju los loso Giotti DISTRITO UNIVERSITRIO DE Mdid MTEMÁTIS (Mos d ños. OPIÓN Ejcicio.- (. tos. S id l cució ticil do ls tics:. tos. Idic ls dios qu d t l ti.. tos. lcul l is -. c. tos.
! Magalie Latorre Rodríguez Clausula Legal WEB-LSSI
 Mgli L Rdíguz Cluul Lgl WEB-LSSI L pági Wb www.mgupi.cm iulidd d Mgli L Rdíguz y cumpl c l quii divd d l Ly 34/2002, d 11 d juli, d Svici d l Scidd d l Ifmció y d Cmci Elcóic, dl Rl Dc-ly 13/2012, d 30
Mgli L Rdíguz Cluul Lgl WEB-LSSI L pági Wb www.mgupi.cm iulidd d Mgli L Rdíguz y cumpl c l quii divd d l Ly 34/2002, d 11 d juli, d Svici d l Scidd d l Ifmció y d Cmci Elcóic, dl Rl Dc-ly 13/2012, d 30
Solucionario de problemas de Ecuaciones Diferenciales
 ESUEA SUPERIOR POITÉNIA DE ITORA Solcioio d oblm d Eccio Dicil do Pcil vió Rolció d ccio dicil lddo d o igl Tomd d lc Rolció d ccio dicil mdi l omd d lc Rolció d im d Eccio dicil Aliccio d l ccio dicil
ESUEA SUPERIOR POITÉNIA DE ITORA Solcioio d oblm d Eccio Dicil do Pcil vió Rolció d ccio dicil lddo d o igl Tomd d lc Rolció d ccio dicil mdi l omd d lc Rolció d im d Eccio dicil Aliccio d l ccio dicil
Supertriangular Subtriangular Diagonal Unidad
 MT. EMPRESRILES TE RESOLVEMOS LS PRIMERS DUDS L eorí de mrices es l que v porr l form operiv de resolver u iumerle cidd de ejercicios de Álger. Por odo lo que supoe eso, os vmos proporcior los coocimieos
MT. EMPRESRILES TE RESOLVEMOS LS PRIMERS DUDS L eorí de mrices es l que v porr l form operiv de resolver u iumerle cidd de ejercicios de Álger. Por odo lo que supoe eso, os vmos proporcior los coocimieos
( ) ( ) 60 ( ) ( ) ( ) Opción A. Ejercicio A.1- Se sabe qué Calcular, de manera razonada, aplicando las propiedades
 IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Oió Ejiio.- S s ué. Clul d od lido ls oidds duds l lo d los siguits dtits: B B IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Ejiio..- Hll l uió dl
IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Oió Ejiio.- S s ué. Clul d od lido ls oidds duds l lo d los siguits dtits: B B IES Mditáo d Málg Soluió Juio Ju Clos loso Giotti Ejiio..- Hll l uió dl
Implementación de las jornadas de inducción y re inducción del personal, incursionando la cultura de la transparencia en dicho proceso.
 DPATAMNTO DL MTA MUNICIPIO D L CASTILLO SCTAIA D GOBINO Y DSAOLLO SOCIAL CONTOL INTNO SGUIMINTO A LA JCUCION DL PLAN ANTICOUPCION STATGIA ACTIVIDAD PUBLICACION ACTIVIDADS ALIZADAS SPONSABL ANOTACIONS go-
DPATAMNTO DL MTA MUNICIPIO D L CASTILLO SCTAIA D GOBINO Y DSAOLLO SOCIAL CONTOL INTNO SGUIMINTO A LA JCUCION DL PLAN ANTICOUPCION STATGIA ACTIVIDAD PUBLICACION ACTIVIDADS ALIZADAS SPONSABL ANOTACIONS go-
PROBLEMAS RESUELTOS DE TRABAJO Y ENERGÍA
 POLEMS ESUELOS E JO Y ENEGÍ Equip dct: ti J. Gc Mi Hádz Puc lfs l lmt POLEM U l d ms qu s mu 4 m/s pt iztlmt u lqu d md st u pfudidd d 5 cm. uál s l fuz mdi qu s lizd s l l p dtl?. F N d m S F l fuz mdi
POLEMS ESUELOS E JO Y ENEGÍ Equip dct: ti J. Gc Mi Hádz Puc lfs l lmt POLEM U l d ms qu s mu 4 m/s pt iztlmt u lqu d md st u pfudidd d 5 cm. uál s l fuz mdi qu s lizd s l l p dtl?. F N d m S F l fuz mdi
(esta notación fue elegida por el matemático Leonhar Euler) De hecho la función f ( x)
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO FECHA DURACION 9 OCTUBRE
 OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
OPERACIONES CON LÍMITES DE FUNCIONES Ls oprcios co límits, tto u puto como l ifiito, ti us propidds álogs qu dbmos coocr: PROPIEDADES El límit d l sum o difrci d dos fucios s l sum o difrci d los límits
I.E.S. Mediterráneo de Málaga Junio 2015 Juan Carlos Alonso Gianonatti OPCIÓN A
 I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
I.E.. Mdiáno d Málg Junio Jun Clo lono Ginoni OPCIÓN.- Conido l unción dinid n l inlo [ ]. Din l cución d l c ngn l cu qu pll l c qu p po lo puno P( Q(. ( puno..- Clcul l ingl indinid iguin d d ( puno.
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
JUNIO 2013. CIRUGIA PLASTICA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
 JUIO 2013. JUIO 2013. SSI 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 D. DGDO UÑ x x D. ICDO FLOS x D. COLI BDLS x D. IGOBO IH x D. COLI HYLOCK x D. JOS OLDO DIZ x
JUIO 2013. JUIO 2013. SSI 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 D. DGDO UÑ x x D. ICDO FLOS x D. COLI BDLS x D. IGOBO IH x D. COLI HYLOCK x D. JOS OLDO DIZ x
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE NAVARRA JUNIO 2012 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l
IES Mediterráneo de Málaga Reserva1.- 2012 Juan Carlos Alonso Gianonatti. Propuesta A
 ES Medieáeo Málg Reev.- Ju lo loo Gioi Popue.- ) Eui el eoe vlo edio Lgge d u iepeió geoéi ( puo) ) lul u puo l ievlo [ ] e que l e gee l gái l uió e plel l ued (o egeo) que ue lo puo () e ( puo) ) Teoe
ES Medieáeo Málg Reev.- Ju lo loo Gioi Popue.- ) Eui el eoe vlo edio Lgge d u iepeió geoéi ( puo) ) lul u puo l ievlo [ ] e que l e gee l gái l uió e plel l ued (o egeo) que ue lo puo () e ( puo) ) Teoe
Logaritmos y exponenciales:
 Logrimos ponncils: L rsolución d cucions ponncils s s n l siguin propidd d ls poncis : Dos poncis con un mism s posiiv disin d l unidd son iguls, si sólo si son iguls sus ponns. Es dcir, p. j. Si = noncs
Logrimos ponncils: L rsolución d cucions ponncils s s n l siguin propidd d ls poncis : Dos poncis con un mism s posiiv disin d l unidd son iguls, si sólo si son iguls sus ponns. Es dcir, p. j. Si = noncs
TEMA 1. VECTORES Y MATRICES 1.2. MATRICES. OPERACIONES ELEMENTALES
 TEM VECTORES Y MTRICES MTRICES OPERCIONES ELEMENTLES VECTORES Y MTRICES MTRICES: OPERCIONES ELEMENTLES Cocepo de riz Eleeos Tipos de rices Su y difereci de rices Produco de u úero por u riz Trsposició
TEM VECTORES Y MTRICES MTRICES OPERCIONES ELEMENTLES VECTORES Y MTRICES MTRICES: OPERCIONES ELEMENTLES Cocepo de riz Eleeos Tipos de rices Su y difereci de rices Produco de u úero por u riz Trsposició
Valora la madurez y destrezas básicas:
 Etct d l PAU FASE GENERAL (Obligtoi) Vlo l mdz y dtz báic: Compió d mj Uo dl lgj p liz, ittiz y xp id Compió báic d l lg xtj Coocimito y técic d mti d modlidd FASE ESPECÍFICA (Volti) Elció d coocimito
Etct d l PAU FASE GENERAL (Obligtoi) Vlo l mdz y dtz báic: Compió d mj Uo dl lgj p liz, ittiz y xp id Compió báic d l lg xtj Coocimito y técic d mti d modlidd FASE ESPECÍFICA (Volti) Elció d coocimito
Transformador VALORES NOMINALES Y RELATIVOS
 Tasfomado VAORE NOMNAE Y REATVO Nobto A. mozy VAORE NOMNAE as picipals caactísticas d las máquias vi dadas po los fabicats la domiada placa o chapa d caactísticas; dod s spcifica, t otas cosas, la potcia
Tasfomado VAORE NOMNAE Y REATVO Nobto A. mozy VAORE NOMNAE as picipals caactísticas d las máquias vi dadas po los fabicats la domiada placa o chapa d caactísticas; dod s spcifica, t otas cosas, la potcia
SISTEMAS LINEALES TABLAS. Dpto. Teoría de la Señal y Comunicaciones
 SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
SISEMAS LIEALES ABLAS Dpo. orí d l Sñl y Comuiccios POPIEDADES DE LA ASFOMADA DE LAPLACE Propidd Sñl rsformd OC ( ) ( ) ( ) s ( s) ( s) Lilidd + b ( ) ( s) b ( s) Dsplmio l impo ( ) Dsplmio l domiio s
Hacia la universidad Aritmética y álgebra
 Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
ECUACIONES DIFERENCIALES ORDINARIAS
 Cpíulo V ECUACIONES DIFERENCIALES ORDINARIAS V. Euios difils U uió difil (ED) s qull uió qu oi ls divds o ls difils (ols o pils) d u o más vibls dpdis o spo u o más vibls idpdis. V. Clsifiió suldos lmls
Cpíulo V ECUACIONES DIFERENCIALES ORDINARIAS V. Euios difils U uió difil (ED) s qull uió qu oi ls divds o ls difils (ols o pils) d u o más vibls dpdis o spo u o más vibls idpdis. V. Clsifiió suldos lmls
Inscríbete en Claro Club y comienza a disfrutar de lo que más te gusta
 Eiió Pss Añ 4 Núm 26 Mz - Abil 2010 Cs Mlli Pl Wp Cl Clb Sgs / V vis Nvs Blss Msjs Blss Rmig Pls Uis Isíb Cl Clb y miz isf l q más gs Si s Ppg isíb llm l *2582 y si is pl Cmiz y isf Cl Clb! Evs Cl Cs Mlli
Eiió Pss Añ 4 Núm 26 Mz - Abil 2010 Cs Mlli Pl Wp Cl Clb Sgs / V vis Nvs Blss Msjs Blss Rmig Pls Uis Isíb Cl Clb y miz isf l q más gs Si s Ppg isíb llm l *2582 y si is pl Cmiz y isf Cl Clb! Evs Cl Cs Mlli
( ) ( ) ( x ) ( ) ( ) ( ) v( x) u( x) ( ) EJERCICIOS RESUELTOS. 1. Calcula F a) ( x) en los siguientes casos: f ( t) = e. = x
 Alro Enro Cond Mi Gonzálz Jrrro L ingrl y ss pliccions Clcl F ) d) n los sigins csos: F cos d RESUELTOS ) ( + ) d ) ( + ) F cos F d c) F( ) + d f) F d + F d g) v( ) F d h) F + f ( ) d i) F( ) ( ) cos d
Alro Enro Cond Mi Gonzálz Jrrro L ingrl y ss pliccions Clcl F ) d) n los sigins csos: F cos d RESUELTOS ) ( + ) d ) ( + ) F cos F d c) F( ) + d f) F d + F d g) v( ) F d h) F + f ( ) d i) F( ) ( ) cos d
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
IES Mediterráneo de Málaga Solución Septiembre 2010 (Específico) Juan Carlos Alonso Gianonatti OPCIÓN A. 2, se pide determinar:
 IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN APLICACIONES DE LA TRIGONOMETRÍA, LEY DE SENOS Y COSENOS Aplicciones de Trigonometrí de Triángulos Rectángulos Un triángulo tiene seis
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Sucesiones de números reales
 Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
CH1 Mi Plan 150 CH2 Mi Plan 250 CH3 Mi Plan 350 CH4 Mi Plan 500 CH6 Mi Plan 800 CH9 Mi Plan Plus 165 CI1 Mi Plan Plus 385 CI5 Mi Plan Plus 1100 CI6
 ID_PLAN PLAN CH1 Mi Plan 150 CH2 Mi Plan 250 CH3 Mi Plan 350 CH4 Mi Plan 500 CH6 Mi Plan 800 CH9 Mi Plan Plus 165 CI1 Mi Plan Plus 385 CI5 Mi Plan Plus 1100 CI6 Mi Plan Plus 1430 CI9 Pool Optimo 167 CJ0
ID_PLAN PLAN CH1 Mi Plan 150 CH2 Mi Plan 250 CH3 Mi Plan 350 CH4 Mi Plan 500 CH6 Mi Plan 800 CH9 Mi Plan Plus 165 CI1 Mi Plan Plus 385 CI5 Mi Plan Plus 1100 CI6 Mi Plan Plus 1430 CI9 Pool Optimo 167 CJ0
TRANSFORMACIONES GEOMÉTRICAS Proyectividad y homografía Homología y afinidad Inversión TEMA4. Objetivos y orientaciones metodológicas. 1.
 TRNSRMINES GEMÉTRIS Poyctivi y homogfí Homologí y fini Invsión TEM4 IUJ GEMÉTRI bjtivos y ointcions mtoológics Est Tm tin como objtivos intouci l lumno n los conocimintos poyctivi, homogfí, homologí, fini
TRNSRMINES GEMÉTRIS Poyctivi y homogfí Homologí y fini Invsión TEM4 IUJ GEMÉTRI bjtivos y ointcions mtoológics Est Tm tin como objtivos intouci l lumno n los conocimintos poyctivi, homogfí, homologí, fini
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
TEMA 7. SUCESIONES NUMÉRICAS.
 º EO Tem 7 TEMA 7. UCEIONE NUMÉRICA.. UCEIONE NUMÉRICA. Imgiemos el ecoido que efectú u bló que se h lzdo l suelo y midmos ls distcis ete bote y bote: Ls distcis fom u sucesió de úmeos: 0, 5, 0, 5,. U
º EO Tem 7 TEMA 7. UCEIONE NUMÉRICA.. UCEIONE NUMÉRICA. Imgiemos el ecoido que efectú u bló que se h lzdo l suelo y midmos ls distcis ete bote y bote: Ls distcis fom u sucesió de úmeos: 0, 5, 0, 5,. U
p m son términos semejantes
 Páin dl Colio d Mtmátics d l ENP-UNAM Ocions con monomios olinomios Auto: D. José Mnul Bc Esinos OPERACIONES CON MONOMIOS Y POLINOMIOS UNIDAD IV IV. OPERACIONES CON MONOMIOS Un vil s un lmnto d un ómul,
Páin dl Colio d Mtmátics d l ENP-UNAM Ocions con monomios olinomios Auto: D. José Mnul Bc Esinos OPERACIONES CON MONOMIOS Y POLINOMIOS UNIDAD IV IV. OPERACIONES CON MONOMIOS Un vil s un lmnto d un ómul,
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR. Ecuaciones lineales homogéneas con coeficientes constates de orden dos y superior.
 Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
Prof Eriqu Mtus Nivs Dotordo Eduió Mtmáti ECUACIONES DIFERENCIALES DE ORDEN SUPERIOR Euios lils homogés o ofiits ostts d ord dos suprior Apliqu l método d rduió pr dtrmir u soluió d l uió o homogé dd los
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.1. Límites de integración infinitos 9.2. Integrales con integrando que tiende a infinito 9.3. Observaciones a las
 CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
variables aleatorias discretas, la función de probabilidad conjunta del vector aleatorio ( X,..., se define como: ) A
 cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
cors loros. só más d dos dmsos Dcó: S... rbls lors dscrs l ucó d robbldd cou dl cor loro... s d como: ddo culqur couo A R...... P... P... A...... A...... s ucó ssc ls sgus rodds:.................. orm
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
 Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
5. Convergencia de integrales impropias. Las funciones Γ y Β de Euler.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lcción. Intgals y aplicacions. 5. Convgncia d intgals impopias. Las funcions Γ y Β d Eul. La foma haitual d calcula una intgal impopia, po jmplo dl intgando, aplica
ARCHIVO. inumen ARCHIVO DE MUESTRA PROMOCIONAL DE ARCHIVO DE MUESTRA PROMOCIONAL DE ARCHIVO DE MUESTRA PROMOCIONAL DE
 www..s s gs (B1) é spñ p xjs b y p:... Gp / cs:... Fch:... bsvcs pfs: b ccs p: x sc B1, www..s www..s www..s s gs (B1) 1. psó v b ccs p: x sc www..s 1.1. scch y s ág. c hc, f s pbs. scch y scíbs. [1],
www..s s gs (B1) é spñ p xjs b y p:... Gp / cs:... Fch:... bsvcs pfs: b ccs p: x sc B1, www..s www..s www..s s gs (B1) 1. psó v b ccs p: x sc www..s 1.1. scch y s ág. c hc, f s pbs. scch y scíbs. [1],
ÁLGEBRA DE MATRICES. * Tenemos aquí el mapa de una ciudad (Konigsberg) que está atravesada por un río sobre el que hay varios puentes:
 º Bchilleto Mteátics II Dvid Miguel del Río IES Euop (Móstoles) Vos coside ls tices coo u disposició ectgul de úeos que cotiee ifoció. Si se quiee es u fo de ode ifoció. Po ejeplo: * Teeos quí el p de
º Bchilleto Mteátics II Dvid Miguel del Río IES Euop (Móstoles) Vos coside ls tices coo u disposició ectgul de úeos que cotiee ifoció. Si se quiee es u fo de ode ifoció. Po ejeplo: * Teeos quí el p de
3. SISTEMAS DE ECUACIONES LINEALES
 Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
la integral de línea de B alrededor de un trayecto cerrado
 LEY DE AMPERE L ley de Guss de los cmpos elécticos implic el flujo de E tvés de un supeficie ced; estlece que este flujo es igul l cociente de l cg totl enced dento de l supeficie ente l constnte ε. En
LEY DE AMPERE L ley de Guss de los cmpos elécticos implic el flujo de E tvés de un supeficie ced; estlece que este flujo es igul l cociente de l cg totl enced dento de l supeficie ente l constnte ε. En
CAPITULO 6.- LA TRANSFORMADA DE LAPLACE.
 PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
PITUO 6.- TRSFORD DE PE. 6. Irocció. 6. rform plc. 6.3 rform plc ilrl. 6.4 Ivrió l rform plc. 6.5 Solció ccio ifrcil co coicio iicil. 6.6 rform plc ilrl. 6.7 álii im mi l rform plc. 6. Irocció. Grlizmo
FACULTAD DE INGENIERÍA
 FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
FCULD DE INGENIERÍ Uivrdd Nciol uóo d Méico Fculd d Igirí ális d Siss y Sñls Profsor: M.I. Elizh Fosc Chávz SERIE DE FOURIER LUMN: Sáchz Cdillo Vicori GRUPO: 6 SERIE DE FOURIER od sñl priódic s pud prsr
ficha introductoria Cuestión de costumbres. nombre de la actividad Estrella A. REDONDO ARJONES. autor/es A2. nivel y destinatarios
 fich iduci mb d cividd Cusió d csumbs u/s Es A REDONDO ARJONES iv y dsiis A2 dució 1 h bjivs Fm icuuidd umd cmid ifmció sb disis cuus, sds u, y chd sb hábis cids c ss dszs Cmsió sci y xsió cids fucis,
fich iduci mb d cividd Cusió d csumbs u/s Es A REDONDO ARJONES iv y dsiis A2 dució 1 h bjivs Fm icuuidd umd cmid ifmció sb disis cuus, sds u, y chd sb hábis cids c ss dszs Cmsió sci y xsió cids fucis,
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
A C T I N O M IC O S I S Ó r g a n o : M u c o s a b u c a l T é c n i ca : H / E M i c r o s c o p í a: L o s c o r t e s h i s t o l ó g i c oms u e
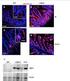 T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
Tema 5. DIAGONALIZACIÓN DE MATRICES
 José Maía Maíe Mediao Tema DGONLZCÓN DE MTRCES oducció Poecia de ua mai Sea Supogamos que se desea calcula : 7 7 8 8 Deemia ua egla paa o esula imediao Compobemos, aes de segui adelae, que MDM, siedo M
José Maía Maíe Mediao Tema DGONLZCÓN DE MTRCES oducció Poecia de ua mai Sea Supogamos que se desea calcula : 7 7 8 8 Deemia ua egla paa o esula imediao Compobemos, aes de segui adelae, que MDM, siedo M
Neper ( ) Lección 2. Potencias, radicales y logarítmos
 Neer (0-7) Lecció Potecis, rdicles y logrítmos º ESO MATEMÁTICAS ACADÉMICAS Potecis, rdicles y logritmos LECCIÓN. POTENCIAS, RADICALES, LOGARITMOS. Potecis de exoete etero Recuerd l defiició de oteci co
Neer (0-7) Lecció Potecis, rdicles y logrítmos º ESO MATEMÁTICAS ACADÉMICAS Potecis, rdicles y logritmos LECCIÓN. POTENCIAS, RADICALES, LOGARITMOS. Potecis de exoete etero Recuerd l defiició de oteci co
Ruido e interferencias
 uo fcs uo: uo u co:» uolo: uo»dolo» uolos csc» sm olocuolo uo Ifcs: Dfcó, os, cczcó. sms lmos oc vs ssms lmos fc. Dfcó uo olécco Dfcó: ucó lécc qu lm l cc l ssm. Tos uo: Exo ul: -có oc scs l yo (uo mosféco
uo fcs uo: uo u co:» uolo: uo»dolo» uolos csc» sm olocuolo uo Ifcs: Dfcó, os, cczcó. sms lmos oc vs ssms lmos fc. Dfcó uo olécco Dfcó: ucó lécc qu lm l cc l ssm. Tos uo: Exo ul: -có oc scs l yo (uo mosféco
TEMA 6. INTEGRALES INDEFINIDAS
 TEM. INTEGRLES INDEFINIDS. Dfinición d Ingrl. Primiiv d un función.. Propidds d ls ingrls.. Ingrls inmdis. Méodos d ingrción.. Obnción d ingrls inmdis.. Cmbio d vribl.. Por prs.. Funcions rcionls Cono
TEM. INTEGRLES INDEFINIDS. Dfinición d Ingrl. Primiiv d un función.. Propidds d ls ingrls.. Ingrls inmdis. Méodos d ingrción.. Obnción d ingrls inmdis.. Cmbio d vribl.. Por prs.. Funcions rcionls Cono
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
 IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES
 LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES L integrl definid Se y f un función definid en el intervlo,, se llm integrl definid de f en n el intervlo, y se denot por fd lim fc i i i. n i y se llmn límites
LA INTEGRAL DEFINIDA: ÁREAS Y VOLÚMENES L integrl definid Se y f un función definid en el intervlo,, se llm integrl definid de f en n el intervlo, y se denot por fd lim fc i i i. n i y se llmn límites
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS
 FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
( ) ( ) ( ) RESOLUCIÓN Dato: NºDiag.= 4(Nº s internos) RESOLUCIÓN RESOLUCIÓN SEMANA 4 POLÍGONOS Y CUADRILÁTEROS 11( 11 1) RPTA.: E RPTA.
 SEMN 4 OLÍGONOS Y URILÁTEROS 1. lcul l úmro d digols mdis d u polígoo, dod l úmro d digols s l cuádrupl dl úmro d águlos itros. ) 0 ) 7 ) ) 44 E) to: Nºig.= 4(Nº s itros) id: Nºig.Mdis= ( 1 ) =? Rmplzdo
SEMN 4 OLÍGONOS Y URILÁTEROS 1. lcul l úmro d digols mdis d u polígoo, dod l úmro d digols s l cuádrupl dl úmro d águlos itros. ) 0 ) 7 ) ) 44 E) to: Nºig.= 4(Nº s itros) id: Nºig.Mdis= ( 1 ) =? Rmplzdo
Creación de Formularios MDI y Formularios Secundarios
 Cus d Visu Bsic Apicd áchz Cció d Fmuis MDI Fmuis cudis 1. Cgu mmi Visu Bsic 2. cci pció EXE Estád 3. E t d tbj d Visu Bsic pst u fmui m Expd d Pcts Ppidds 1 Cud d mits Fmui p misió Expd d Pcts h.s@gmi.cm
Cus d Visu Bsic Apicd áchz Cció d Fmuis MDI Fmuis cudis 1. Cgu mmi Visu Bsic 2. cci pció EXE Estád 3. E t d tbj d Visu Bsic pst u fmui m Expd d Pcts Ppidds 1 Cud d mits Fmui p misió Expd d Pcts h.s@gmi.cm
Fracción generatriz de un decimal. Denominador :1 seguido de tantos 0 como cifras decimales haya 1000 = 7 8
 º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA.- NÚMEROS- PROFESOR: RAFAEL NÚÑEZ NOGALES.- FRACCIONES Y DECIMALES Opercioes comids co frccioes Pr relizr vris opercioes se reliz primero los prétesis y se
º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA.- NÚMEROS- PROFESOR: RAFAEL NÚÑEZ NOGALES.- FRACCIONES Y DECIMALES Opercioes comids co frccioes Pr relizr vris opercioes se reliz primero los prétesis y se
Aplicaciones de la integral indefinida
 Aplicciones_de_l_integrl.n Aplicciones de l integrl indefinid Práctic de Cálculo, E.U.A.T,Grupos ºA y ºB, 2005 Est práctic muestr cómo clculr lguns áres y volúmenes utilizndo integrles. En cd cso dremos
Aplicciones_de_l_integrl.n Aplicciones de l integrl indefinid Práctic de Cálculo, E.U.A.T,Grupos ºA y ºB, 2005 Est práctic muestr cómo clculr lguns áres y volúmenes utilizndo integrles. En cd cso dremos
2º Bachillerato Capítulo 7: Integrales
 Mmáics Aplicds ls incis Socils II º Bchillro píulo 7: Ingrls LirosMrVrd.k www.punsmrvrd.org.s Auors: Lici Gonzálz Pscul y Álvro Vldés Mnéndz Rvisors: Mrí Molro y Jvir Rodrigo Tods ls imágns hn sido crds
Mmáics Aplicds ls incis Socils II º Bchillro píulo 7: Ingrls LirosMrVrd.k www.punsmrvrd.org.s Auors: Lici Gonzálz Pscul y Álvro Vldés Mnéndz Rvisors: Mrí Molro y Jvir Rodrigo Tods ls imágns hn sido crds
Ejercicio 1. x a. Ejercicio 2.
 Sptim 5 - Opción A (Molo 6) Ejcicio. D un función f: R R s s qu f() y qu f (. () [ punto] Dtmin f. () [ 5 puntos] Clcul l á l ión limit po l áfic f, po l j sciss y po ls cts cucions - y. () Aplicno l Tom
Sptim 5 - Opción A (Molo 6) Ejcicio. D un función f: R R s s qu f() y qu f (. () [ punto] Dtmin f. () [ 5 puntos] Clcul l á l ión limit po l áfic f, po l j sciss y po ls cts cucions - y. () Aplicno l Tom
Resumen: Límites, Continuidad y Asíntotas
 Resue: Líites, Cotiuidd y Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. : *? ** *
Resue: Líites, Cotiuidd y Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. : *? ** *
Tomando como nivel de energía cero el nivel fundamental. Dada la diferencia de energía entre los niveles en la mayoría de los casos
 Capíulo. La fucó d pacó ) Spaacó d la fucó d pacó S ha dmosado aom - / k [.] La ía dl l s ual a: k [.] + + + [.] + S los ados d lbad o accoa [.4] - / k - / k... [.5] ) Fucó d pacó lcóca omado como l d
Capíulo. La fucó d pacó ) Spaacó d la fucó d pacó S ha dmosado aom - / k [.] La ía dl l s ual a: k [.] + + + [.] + S los ados d lbad o accoa [.4] - / k - / k... [.5] ) Fucó d pacó lcóca omado como l d
Siempre verifica que a 2 = b 2 + c 2 (Th. Pitágoras)
 Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
LOS RECURSOS NATURALES EN EL DESARROLLO ECONOMICO
 LOS RECURSOS NATURALES EN EL DESARROLLO ECONOMICO E d i t o r i a l U n i v e r s i t a r i a, S. A., 1 9 7 0 In s c r i p c i ó n N 3 8. 5 3 5 D e r e c h o s e x c lu s iv o s r e s e r v a d o s p a
LOS RECURSOS NATURALES EN EL DESARROLLO ECONOMICO E d i t o r i a l U n i v e r s i t a r i a, S. A., 1 9 7 0 In s c r i p c i ó n N 3 8. 5 3 5 D e r e c h o s e x c lu s iv o s r e s e r v a d o s p a
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO CALCULO DIFERENCIAL. Integral Indefinida
 Integrl Indefinid Estmos costumrdos decir que el producto el cociente son operciones inverss. Lo mismo sucede con l potencición l rdicción. Vmos estudir hor l operción invers de l diferencición. Dd l función
Integrl Indefinid Estmos costumrdos decir que el producto el cociente son operciones inverss. Lo mismo sucede con l potencición l rdicción. Vmos estudir hor l operción invers de l diferencición. Dd l función
Tema 1: NÚMEROS REALES.
 I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
UNIDAD 3: SISTEMAS DE ECUACIONES LINEALES. 1. DEFINICIONES. Un sistema de m ecuaciones lineales con n incógnitas es una expresión de la forma:
 IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
IE Pdr Povd (Gudi) Mtátics plicds ls CC II Dprtto d Mtátics Bloqu I: Álgr il Profsor: Ró ort Nvrro Uidd : ists d Ecucios ils UNIDD : ITEM DE ECUCIONE INEE DEFINICIONE U sist d cucios lils co icógits s
- Con peatones - Con ciclistas - Extraescolares - Concurso
 l i v ó i Pl ñ 6 1 y 2 1 P jóv L Fió CNAE lbió l Diió Gl Táfi (DGT) l Fió l Sgi Vil (Fvil) y l Uió Nil Jf Plií y Diiv Plií Ll (Uijl) mh iiiiv l bjiv mj l gi vil l jóv l liv my ig. Aivi Má ifmió: 607 814
l i v ó i Pl ñ 6 1 y 2 1 P jóv L Fió CNAE lbió l Diió Gl Táfi (DGT) l Fió l Sgi Vil (Fvil) y l Uió Nil Jf Plií y Diiv Plií Ll (Uijl) mh iiiiv l bjiv mj l gi vil l jóv l liv my ig. Aivi Má ifmió: 607 814
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
NOASDTODODESFLO DSQUECACIÓNDFFPARECERAD
 NOASDTODODESFLO DSQUECACIÓNDFFPARECERAD NOASDTODODESFLO DSQUECACIÓNDFFPARECERAD ASELDPODERDDEFLA NEDUCACIÓNDFFINANCIERAD ASELDPODERDDEFLA NEDUCACIÓNDFFINANCIERAD É U Q DE A S O M A V Y O H R A L HAB N
NOASDTODODESFLO DSQUECACIÓNDFFPARECERAD NOASDTODODESFLO DSQUECACIÓNDFFPARECERAD ASELDPODERDDEFLA NEDUCACIÓNDFFINANCIERAD ASELDPODERDDEFLA NEDUCACIÓNDFFINANCIERAD É U Q DE A S O M A V Y O H R A L HAB N
P R O G R A M A D E G O B I E R N O 2012-2015. C o n g e s t i n, s e g u r i d a d y t r a b a j o
 P R O G R A M A D E G O B I E R N O 2012-2015 C o n g e s t i n, s e g u r id a d y t r a b a jo 1 W I L M A N H A R R Y M A R ح N C A S T A ر O H O J A D E V I D A N a c ي e l 1 7 de S e p t ie m b r
P R O G R A M A D E G O B I E R N O 2012-2015 C o n g e s t i n, s e g u r id a d y t r a b a jo 1 W I L M A N H A R R Y M A R ح N C A S T A ر O H O J A D E V I D A N a c ي e l 1 7 de S e p t ie m b r
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Resumen: Límites de funciones. Asíntotas
 Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
TALKINGISTEACHING.ORG
 l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!
l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
( a b c) n = a n b n c n ( a : b) n = a n : b n a n a m = a n+m a n :a m = a n-m (a n ) m = a n.m
 Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Producto de convolución de las derivadas de orden k por las derivadas de orden de la delta de Dirac soportadas en x 1, x a, y x n
 Vol. 5, No., pp. 59-69/Dcmr ISSN-L 88-674 Coprgh Uvrsdd Ncol d Igrí Imprso Ncrgu. Todos los drchos rsrvdos hp://www.lmol.fo/d.php/nexo Produco d covolucó d ls drvds d ord por ls drvds d ord d l dl d Drc
Vol. 5, No., pp. 59-69/Dcmr ISSN-L 88-674 Coprgh Uvrsdd Ncol d Igrí Imprso Ncrgu. Todos los drchos rsrvdos hp://www.lmol.fo/d.php/nexo Produco d covolucó d ls drvds d ord por ls drvds d ord d l dl d Drc
PROPIEDAD FUNDAMENTAL DE LOS RADICALES
 Mtemátics Aplicds ls Ciecis Sociles I DEFINICIÓN DE RAÍZ ENÉSIMA Llmremos ríz eésim de "" y lo represetremos sí que cumpl l codició de que elevdo "" se igul "": x / x Al úmero "" se le llm ídice de l ríz.
Mtemátics Aplicds ls Ciecis Sociles I DEFINICIÓN DE RAÍZ ENÉSIMA Llmremos ríz eésim de "" y lo represetremos sí que cumpl l codició de que elevdo "" se igul "": x / x Al úmero "" se le llm ídice de l ríz.
Solución Tarea de Aproximaciones y errores de redondeo
 Métodos numéicos y álgb linl CB0085 Apoximcions y os d dondo T d Apoximcions y os d dondo. Clcul l o bsoluto y l o ltivo si p y p 2.78 dond p s l vlo clculdo. : vlo l vlo clculdo 2.78 o bsoluto : vlo clculdo
Métodos numéicos y álgb linl CB0085 Apoximcions y os d dondo T d Apoximcions y os d dondo. Clcul l o bsoluto y l o ltivo si p y p 2.78 dond p s l vlo clculdo. : vlo l vlo clculdo 2.78 o bsoluto : vlo clculdo
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
WONDERPONDEREO NAVIDENO Propuestas para pensar sobre la Navidad
 WONDERPONDEREO NAVIDENO Ppt p p b l Nvidd p Ell Dthi & Dil Mtgó 1. Jmó. 2. Jg d ctcci. 3. Sphé. 4. Ct d ft. 5.Pc c pz xótic. 6.Dptd. 7.C. 8. Bmbill b id. 9. Smb. 10. Odd. 11. Dii. 12. Niñ. 23. Git. 13.
WONDERPONDEREO NAVIDENO Ppt p p b l Nvidd p Ell Dthi & Dil Mtgó 1. Jmó. 2. Jg d ctcci. 3. Sphé. 4. Ct d ft. 5.Pc c pz xótic. 6.Dptd. 7.C. 8. Bmbill b id. 9. Smb. 10. Odd. 11. Dii. 12. Niñ. 23. Git. 13.
8 Límites de sucesiones y de funciones
 Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
LA ESTRATEGIA DE INVERSIÓN DE INVERSIS ESCENARIO ECONÓMICO GLOBAL
 ARTERA MODELO DEFENSVA DE NVERSS BANO Oub 2004 LA ESTRATEGA DE NVERSÓN DE NVERSS Hk Lumol, Es Jf NVERSS BANO A ouó ls psmos los lmos sls l s vsó p los pómos 3-6 mss. Ofmos u vloó l sfoo oómo Esos Uos y
ARTERA MODELO DEFENSVA DE NVERSS BANO Oub 2004 LA ESTRATEGA DE NVERSÓN DE NVERSS Hk Lumol, Es Jf NVERSS BANO A ouó ls psmos los lmos sls l s vsó p los pómos 3-6 mss. Ofmos u vloó l sfoo oómo Esos Uos y
TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES
 3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
Ecuaciones de Poisson y Laplace
 Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
2. [ANDA] [JUN-B] Determinar b sabiendo que b > 0 y que el área de la región limitada por la curva y = x 2 y la recta y = bx es igual
![2. [ANDA] [JUN-B] Determinar b sabiendo que b > 0 y que el área de la región limitada por la curva y = x 2 y la recta y = bx es igual 2. [ANDA] [JUN-B] Determinar b sabiendo que b > 0 y que el área de la región limitada por la curva y = x 2 y la recta y = bx es igual](/thumbs/53/31465960.jpg) MsMtes.com Integrles Selectividd CCNN. [ANDA] [JUN-A] De l función f:(-,+ ) se se que f (x ) = y que f() =. (x+) () Determinr f. () Hllr l primitiv de f cuy gráfic ps por el punto (,).. [ANDA] [JUN-B]
MsMtes.com Integrles Selectividd CCNN. [ANDA] [JUN-A] De l función f:(-,+ ) se se que f (x ) = y que f() =. (x+) () Determinr f. () Hllr l primitiv de f cuy gráfic ps por el punto (,).. [ANDA] [JUN-B]
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 Jun nonio González o Proesor de emáics del Colegio Jun XIII Zidín de Grnd ITEGRCIÓ ITEGRES IDEFIIDS ÉTODOS DE ITEGRCIÓ PRIITIV DE U FUCIÓ ITEGR IDEFIID Sen y F dos unciones reles deinids en un mismo dominio
Jun nonio González o Proesor de emáics del Colegio Jun XIII Zidín de Grnd ITEGRCIÓ ITEGRES IDEFIIDS ÉTODOS DE ITEGRCIÓ PRIITIV DE U FUCIÓ ITEGR IDEFIID Sen y F dos unciones reles deinids en un mismo dominio
TRANSFORMADORES EN PARALELO
 TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Seminario de problemas. Curso Hoja 9
 Semiario de prolemas. Curso 05-6. Hoja 9 49. Alero, Berardo y Carla se ha coocido e ua red social. Ellos pregua a Carla cuádo es su cumpleaños; e lugar de respoderles direcamee, ella decide poerles u prolema.
Semiario de prolemas. Curso 05-6. Hoja 9 49. Alero, Berardo y Carla se ha coocido e ua red social. Ellos pregua a Carla cuádo es su cumpleaños; e lugar de respoderles direcamee, ella decide poerles u prolema.
