Conocer la definición de derivada y su interpretación geométrica. Calcular derivadas de funciones elementales utilizando las siguientes técnicas:
|
|
|
- Claudia Paz Crespo
- hace 7 años
- Vistas:
Transcripción
1 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable Objetivs: Ccer la defiició de derivada y su iterpretació gemétrica. Calcular derivadas de fucies elemetales utilizad las siguietes técicas: Reglas de derivació (derivada de ua suma, prduct, cciete). Derivada de la fució cmpuesta: Regla de la cadea Derivada de la fució iversa. Derivada de fucies implícitas. Derivada de fucies e paramétricas Derivada eésima. Cmpreder la aprimació lcal que prprcia ls plimis de Taylr Ectrar plimis de Taylr para fucies derivables Utilizar el rest de Lagrage para estimar la precisió de la aprimació. Estudiar lcalmete ua fució (determiació de etrems) Cmpreder la aprimació glbal que prprcia las series de Taylr Calcular el camp de cvergecia de ua serie de ptecias Desarrllar ua fució e serie de ptecias. Isaac Newt G.W. Leibitz Prfesra: Elea Álvarez Sáiz
2 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I DERIVADA: DEFINICIÓN La epresió ( + ) f f que es la fórmula de la pediete de la secate a la gráfica de la fució f que ue ls puts ( +, f ( + )) y (, ) icremetal de f. f, se llama el cciete f(+ ) f() f(+ )-f() + La derivada de f e u put es el límite del cciete icremetal, lim ( + ) f f La derivada represeta la pediete de la tagete a la gráfica de f e el put (, f( )). Se represeta pr f ó dy d ó df d Prfesra: Elea Álvarez Sáiz S 3
3 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable f(+ ) f() α f(+ )-f() α + tgα= lim ( + ) f f TÉCNICAS DE DERIVACIÓN ' Regla del prduct pr ua cstate = ' Regla de la suma f + g = f ' + g ' a f af ', a R ' Regla del prduct f g = f ' g + f g ' Regla del cciete f g ' ' f g ' g f = g Derivada de la fució cmpuesta: Regla de la cadea Si y= f( u) es derivable e u y u g cmpuesta y= ( f g) = f( g ) = es derivable e, etces la fució es derivable e y ( f g)( ) = f ( g ) g dy = d df du d d = du d tambié f g 4 Prfesra: Elea Álvarez Sáiz
4 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I g f g() f(g()) Derivada de la fució iversa y además f f, tambié es derivable e y = f y además Si f es ua aplicació iyectiva y derivable e fució iversa, ' etces la ' ( f )( y) = f ' f f - f() Derivada eésima Si y f = es derivable e u dmii D queda defiida la fució derivada: si esta fució y f ' y ( f ')( ' ) f ' : D R f ' = a su vez es derivable se puede calcular su derivada, =, que recibe el mbre de derivada seguda. Se deta, Prfesra: Elea Álvarez Sáiz S 5
5 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable f '' d y = d Este prces puede ctiuar y se tedría la derivada de rde derivada - ésima que csistiría e derivar la fució veces. Si la fució es y f ( detará: f d y = d = se FÓRMULA DE LEIBNIZ.- Si f y g s derivables hasta el rde etces la fució h f g = es derivable hasta el rde y además ( = = ( h f g = f g f g f g f g ( ( ( ' ( '... RECTA TANGENTE. APROXIMACIÓN LINEAL Defiició (Diferecial).- Sea y f abiert que ctiee al úmer, = ua fució derivable e u iterval - La diferecial de es igual al icremet de, = d - La diferecial de y se defie cm dy= ' f d La diferecial de y para u icremet de, d, crrespde el icremet de la rdeada de la recta tagete crrespdiete a ese icremet. 6 Prfesra: Elea Álvarez Sáiz
6 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I 5 Diferecial y=f() 5 (+h,f(+h) y=f(+h)-f() 5 dy (,f() Recta tagete alfa h Aprimació lieal: Csiderems la gráfica de ua fució y f = derivable e = c. Si dibujams la tagete e el put c, f() c vems que, para u iterval pequeñ de, cetrad e c, ls valres de la fució casi cicide c las rdeadas de ls puts de la curva. Pr esta razó llamams a la ecuació de la tagete a la gráfica de f e el put put. = c ua liealizació de la fució e ese Teied e cueta que la ecuació de la recta tagete e el put c, f() c tiee pr pediete f () c se tedrá que su ecuació es: L()=f(c)+f (c)(-c) f(c) L()-f(c)=f (c)(-c) () () () () y f c = f c c y= f c + f c c Prfesra: Elea Álvarez Sáiz S 7
7 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable y se llama a L f() c f ()( c c) = + la liealizació de f e c POLINOMIOS DE TAYLOR Supgams que f( ) es ua fució derivable veces e el put =a. Se defie el plimi de Taylr de grad crrespdiete a la fució f e el put =a cm ( a) ( k f k T f ; a = a = k= k! f ' a f a f a = f( a) + a + a + + a!!! '' (... E el cas e que a= el plimi se llama de MacLauri. Veams alguas prpiedades que s permitirá bteer plimis de Taylr a partir de trs ccids Sea f y g fucies que admite plimi de Taylr hasta el grad e el put a etces se cumple las prpiedades siguietes: Liealidad: T( αf+ βg; a) = αt ( f; a) + βt ( f; a) Derivació, itegració: T ( f; a ) ' = T ( f '; a ) Otras peracies: Se puede bteer el desarrll de prducts y ccietes de fucies a partir del desarrll de cada ua de las ivlucradas. 8 Prfesra: Elea Álvarez Sáiz
8 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I Defiició (Rest -ésim de Taylr).- Sea f ua fució para la que eiste T f ; a. Se defie el rest -ésim de Taylr crrespdiete a la fució f e el put =a, y l escribirems R f ; a cm = R f ; a f T f ; a ; R f ; a e el put =a. La epresió T f a + se llama fórmula de Taylr de f() de grad E las primidades del put =a se verifica sól que el rest -ésim es pequeñ (ifiitésim) si que se hace pequeñ e cmparació c ifiitésim de rde superir a resultad a (es u a para =a). Est se epresa e el siguiete TEOREMA DE TAYLOR: Si f es derivable veces e el put =a y R f ; a es su crrespdiete rest de Taylr etces ( a) R f ; a lim = a EXPRESIONES DEL RESTO: Sea f es ua fució derivable (+) veces e u iterval abiert I, que ctega al put =a. Si R f ; a es el rest -ésim de Taylr crrespdiete a la fució f e el put =a etces: () Rest de Cauchy () t ( )( ) ( + f R f ; a t a =! sied t u put itermedi etre a y. Prfesra: Elea Álvarez Sáiz S 9
9 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable () Rest de Lagrage ( + f () t ( )! R f ; a a = + sied t u put itermedi etre a y. (3) Rest Itegral () t ( ) + ( + f R f ; a t dt =! a defiid si la derivada (+) de f es itegrable e el iterval I. POLINOMIOS DE TAYLOR: APLICACIONES Cálcul de valres aprimads (ver hja ) Cálcul de límites idetermiads Estudi lcal de ua fució: Determiar máims y míims Cálcul de límites idetermiads E el cálcul de límites de fucies surge las mismas idetermiacies que e el cas de sucesies y se aplica las mismas técicas para su reslució. Defiició (Ifiitésim).- Llamarems ifiitésim para tedied a a cualquier fució que tieda a cer. Es decir, ϕ es u ifiitésim para = si limϕ = Prfesra: Elea Álvarez Sáiz
10 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I PROPOSICION.- (a) (b) La suma, diferecia y prduct de ifiitésims es u ifiitésim. El prduct de u ifiitésim pr ua fució actada e u etr de es u ifiitésim. Defiició (Ifiitésims del mism rde, rde superir y rde iferir).- Se dice que ϕ y µ s ds ifiitésims del mism rde para = si ϕ lim = λ cλ, λ µ E este cas se escribe ϕ O( µ ) ϕ y =. ϕ µ equivaletes para = si lim = µ ϕ es de rde superir a cas se escribe ϕ = ( µ ) µ para = si ϕ lim =. E este µ Defiició (Ifiitésims de rde p).- Decims que u ifiitésim es de rde p para = si ϕ O( ) p = es decir, si ϕ ( ) lim = λ λ, λ p PROPOSICION.- El rde de u ifiitésim varía al sumarle restarle tr de rde superir. Prfesra: Elea Álvarez Sáiz S
11 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable Csiderems ahra ϕ u ifiitésim de rde p para que E este cas se tiee que: ϕ ( ) lim = λ λ, λ p =, est sigifica ( ) = ( ) ϕ = λ( ) + ( ) ϕ λ p p p p Etces al térmi λ( ) p se le llama parte pricipal del ifiitésim ϕ para =. PRINCIPIO DE SUSTITUCION.- Si e ua epresió de u límite se sustituye u factr divisr pr su parte pricipal pr tr equivalete el valr del límite se ve alterad. IMPORTANTE: Cuad ls ifiitésims aparezca cm sumads la sustitució de u ifiitésim pr tr equivalete puede cducir e geeral a errres () Si etces se () Si etces (3) Si etces tg (4) Si (5) Si Tabla de equivalecias cs etces lg + etces lg( k k + ) ( k> ) Prfesra: Elea Álvarez Sáiz
12 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I (6) Si etces a lga (7) Si etces arcse (8) Si etces arctg (9) Si a etces ( ) () Si etces + + a térmi de mer grad P Defiició (Ifiits).- Llamarems ifiit para tedied a a cualquier fució limω ω que tieda a ifiit. Es decir, = ω es u ifiit para = si OBSERVACION.- Td l vist aterirmete para ifiitésims puede aplicarse a ifiits teied e cueta que si ω es u ifiit para = etces ϕ = ω es u ifiitésim para = es u ifiitésim. E particular, la sustitució de ifiits e la epresió de u límite se rige pr las mismas reglas que las de ls ifiitésims. Defiició (Ifiits de rde iferir, superir).- Se dice que ω y ifiits para = se dice que: ω es u ifiit de rde iferir a ω lim = τ para τ ω es u ifiit de rde superir a ω lim τ = τ para = si = si τ ds Prfesra: Elea Álvarez Sáiz S 3
13 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable ω es u ifiit del mism rde que ω lim λ λ, λ τ τ para = = si E el cas particular de que λ etces se dice que s equivaletes. Defiició (Ifiit de rde p).- Decims que u ifiit ω para rde p si ω lim = λ λ, λ ( ) p = es de ctiuació, se da e la tabla ls demiads órdees fudametales de ifiitud. Segú se avace de izquierda a derecha e las clumas ls órdees va decrecied. Ptecial - Epecial Epecial Ptecial Lgaritm a b c a> b> c> ( lg ) q p q> p> APLICANDO POLINOMIOS DE TAYLOR Sea y f = ua fució que es ifiitésim para =a que tiee tdas sus ( k derivadas ulas hasta el rde k- e el put a y que f cumplirá: ( a) k ( ) ( k f k f = a + a k! a, etces se 4 Prfesra: Elea Álvarez Sáiz
14 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I de l que se deduce que el rde del ifiitésim y f ( k f ( a) pricipal es k!. = para =a es k y su parte Estudi lcal de ua fució Csiderems ua fució y f a. Se cumple que: = c derivadas hasta el rde + e el put ( ( ) f '' a f a f f( a) = f '( a)( a) + a a + a!! ( Supgams que f ( a) f ( a) f ( a) ( Si es par y f lcal ( Si es par y f ' = '' =... = =, etces a > etces e el put a la fució tiee u míim a < etces e el put a la fució tiee u máim lcal Si es impar e el put a hay u put de ifleió. SERIES DE POTENCIAS. SERIES DE TAYLOR Ua epresió de la frma... a + a a + a a + = a a = Recibe el mbre de serie de ptecias cetrada e el put a. Ua serie de ptecias puede ser iterpretada cm ua fució de Prfesra: Elea Álvarez Sáiz S 5
15 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable = ( ) f a a = Cvergecia de ua serie de ptecias El dmii de la fució f = a ( a) será el cjut de valres de = dde la serie cverge y el valr de f( ) será precisamete la suma de la serie. Nta: Es evidete que la serie cverge e el put a f a = a a a = a = TEOREMA DE ABEL. Se csidera la serie a( a) afirmacies siguietes: =. Etces se cumple ua y sl ua de las (a) La serie cverge sl e a (b) Eiste u úmer R> de frma que la serie cverge e a < R y cverge e a> R (c) La serie cverge para td R Puede decirse que la serie cverge siempre e u iterval de la frma ( a R, a R) + csiderad que e el cas (a) el valr de R es cer y e el cas (c) el valr de R es ifiit. Al úmer R se le llama radi de cvergecia y al iterval ( a R, a R) + iterval de cvergecia. Es imprtate tar que el terema dice ada sbre la cvergecia e ls etrems de dich iterval. 6 Prfesra: Elea Álvarez Sáiz
16 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I TEOREMA. Si la fució viee defiida pr ua serie de ptecias a( a) cumple ua y sl ua de las afirmacies siguietes: =. Etces se (a) La serie cverge sl e a (b) Eiste u úmer R> de frma que la serie cverge e a < R y cverge e a> R (c) La serie cverge para td R TEOREMA. Si la fució f viee defiida pr ua serie de ptecias a( a) cvergecia R> etces = c radi de (a) f es ctiua e td put iterir al iterval de cvergecia. (b) f es derivable e el iterval de cvergecia y su derivada f '( ) puede bteerse mediate la derivació térmi a térmi: f ' = a ( a) sied el radi de cvergecia de esta serie tambié R. (c) f es itegrable e el iterval de cvergecia y, además, se puede itegrar térmi a térmi: + = = = a f d = a a d = a + k + sied el radi de cvergecia de esta serie tambié R. Prfesra: Elea Álvarez Sáiz S 7
17 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable Desarrll de ua fució e serie de ptecias Ahra aalizams el prblema de ectrar el desarrll e serie de ptecias de ua fució f( ) aalizad qué cdicies debe cumplir ectrarse ua serie de ptecias a( a) que cverja a = f para que pueda f. Recrdems ahra el Terema de Taylr que permitía epresar el valr de ua fució mediate su plimi de Taylr. FÓRMULA DE TAYLOR: Si la fució f es derivable + veces e u iterval ( a R, a R) + etces sied ( ; ) k= = ( ; ) + f T f a R ( a) ( k f k T f a = a el plimi de Taylr de grad de f k! e el put a y R el rest del plimi que cumple: R( ) ( a) lim = a Csiderad la epresió de Lagrage del rest se tedrá: + k () + ( k ( f a f c f = a + a k!! k= c c u put itermedi etre a y. + TEOREMA: Si la fució f es ifiitamete derivable e u iterval I abiert cetrad e a y si R( ) es el rest de la fórmula de Taylr etces: = ( a) ( f f = a lim R =! 8 Prfesra: Elea Álvarez Sáiz
18 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I La serie ( f ( a) ( a) se llama Serie de Taylr de la fució =! f. Imprtate: Puede prbarse que si eiste ua cstate k> de frma que ( f k para td, I etces =! ( a) ( f f = a Ejempls: Teied e cueta ls últims resultads se puede bteer ls siguietes desarrlls e serie de Taylr de alguas fucies elemetales: e = = <!!! = se = = +... <! 3! 5! = ( + ) 4 cs = = +... <!! 4! = ( ) = = < = =... = ( ) = +... < + = ( )( )...( + ) ( ) k k k k k k k + = = + k <!! Prfesra: Elea Álvarez Sáiz S 9
19 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable Teied e cueta la dificultad de ectrar la derivada eésima para muchas fucies y de prbar que el rest eésim tiede a cer cuad tiede a ifiit es frecuete, para ectrar el desarrll de ua fució e serie de ptecias, utilizar fucies de las que ya se cce su desarrll y lueg itegrar, derivar realizar peracies algebraicas cm se idica e el siguiete resultad: Si f = a y g = b e ( R, R) = = f ± g = ( a ± b ) e ( R, R ) = f( k) = a k e, k f( ) = R R k k k = a e k k ( R, R) = sied k> etces DERIVACIÓN IMPLÍCITA Ua ecuació de la frma F(, y ) = defie a la variable y cm fució ( y= f ) e u ciert dmii D si se verifica que para td e D eiste u úic y de frma que F(, y ) =. Cuad, para este tip de fucies se pueda despejar la variable y eplícitamete e térmis de, y se quiere bteer la derivada, dy, se prcede d de la siguiete frma:. Se deriva ambs miembrs de la epresió c respect a, aplicad la regla de la cadea sabied que y es fució de, es decir, y y =. Prfesra: Elea Álvarez Sáiz
20 Tería: Fucies ua variable Igeiería de Telecmuicació Fudamets Matemátics I. Se despeja la epresió dy d. E geeral, el valr bteid para dy d es dy derivar la fució F respect a csiderad y cm cstate = d derivar la fució F respect a y csiderad cm cstate DERIVACIÓN PARAMÉTRICA E alguas casies la ecuació de ua curva está dada e la frma y= f ó F(, y ) = si que está determiada pr u par de ecuacies e térmis de ua misma variable. Pr ejempl, csiderems las ecuacies = y= t+ t t c t R. Se tiee que a cada valr de t le crrespde u put (,y) del pla. E el ejempl aterir, la siguiete tabla de valres: t y s permite hacer la represetació gráfica de la relació de la siguiete maera: Prfesra: Elea Álvarez Sáiz S
21 Igeiería de Telecmuicació Fudamets Matemátics I Tería: Fucies de ua variable () () g t E geeral, las ecuacies =, c g, h fucies ctiuas e u iterval y= h t real I, recibe el mbre de ecuacies paramétricas represetació paramétrica de ua curva e el pla XY. La gráfica de las ecuacies paramétricas está dada pr el cjut de puts del pla XY, que se btiee cuad t, que recibe el mbre de parámetr, tma tds sus valres psibles e el dmii I. TEOREMA: Sea g() t, h() t fucies derivables e u iterval (c, d). Supgams que g tiee ua iversa derivable e ese iterval. Etces e cada put dde g '() t, las ecuacies que y f =, y además () () = g t y= h t implica que eiste ua fució derivable f tal dy dy h ' t = dt = d d g ' t dt () () Nta: Si detectas algú errr errata pte e ctact c la prfesra para su crrecció. Prfesra: Elea Álvarez Sáiz
Apellidos y Nombre: Aproximación lineal. dy f x dx
 INGENIERÍA DE TELECOMUNICACIÓN HOJA 0 Aproximació lieal Defiició (Diferecial).- Sea y = f ( x) ua fució derivable e u itervalo abierto que cotiee al úmero x, - La diferecial de x es igual al icremeto de
INGENIERÍA DE TELECOMUNICACIÓN HOJA 0 Aproximació lieal Defiició (Diferecial).- Sea y = f ( x) ua fució derivable e u itervalo abierto que cotiee al úmero x, - La diferecial de x es igual al icremeto de
Material interactivo con teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguientes enlaces una vez dentro de la asignatura
 E el Aula Virtual se ecuetra dispoible: Material iteractivo co teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguietes elaces ua vez detro de la asigatura Pagia Pricipal >Aputes>4.
E el Aula Virtual se ecuetra dispoible: Material iteractivo co teoría y ejercicios resueltos. Para acceder a ello deberá pulsar sobre los siguietes elaces ua vez detro de la asigatura Pagia Pricipal >Aputes>4.
Capítulo 2. El Teorema de Taylor. 2.1 Introducción.
 Capítul El Terema de Taylr.1 Itrducció. E este capítul estudiarems el Terema de Taylr, el cual s permitirá aprimar pr medi de plimis (las ucies más secillas del Cálcul a ucies que cumple ciertas cdicies
Capítul El Terema de Taylr.1 Itrducció. E este capítul estudiarems el Terema de Taylr, el cual s permitirá aprimar pr medi de plimis (las ucies más secillas del Cálcul a ucies que cumple ciertas cdicies
El Teorema de Taylor
 El Terema de Taylr Itrducció La recta tagete La parábla tagete Ls ceicietes de u plii e térmis de sus derivadas El Terema de Taylr Cálcul de aprimacies y estimació del errr Aplicació a Máims y Míims Ejercicis
El Terema de Taylr Itrducció La recta tagete La parábla tagete Ls ceicietes de u plii e térmis de sus derivadas El Terema de Taylr Cálcul de aprimacies y estimació del errr Aplicació a Máims y Míims Ejercicis
Tema 8. Derivabilidad y reglas de derivación. 8.1 Derivada de una función
 Tema 8 Derivabilidad y reglas de derivació 8. Derivada de ua fució f : I R es derivable e a I si eiste el límite que llamaremos f 0 (a) f() f(a) lim a a Ejercicio 8.. Si f() 3 calcular f 0 () f(a + ) f(a)
Tema 8 Derivabilidad y reglas de derivació 8. Derivada de ua fució f : I R es derivable e a I si eiste el límite que llamaremos f 0 (a) f() f(a) lim a a Ejercicio 8.. Si f() 3 calcular f 0 () f(a + ) f(a)
1. INTRODUCCIÓN Formas diversas de expresión de Funciones. a) Funciones dadas en forma de tabla.
 . INTRODUCCIÓN. Al bservar ls feómes que se prduce e la aturaleza pdems dars cueta que se puede elegir ds magitudes e y etre las cuales eiste ua depedecia fucial que epresa el aspect cuatitativ del feóme
. INTRODUCCIÓN. Al bservar ls feómes que se prduce e la aturaleza pdems dars cueta que se puede elegir ds magitudes e y etre las cuales eiste ua depedecia fucial que epresa el aspect cuatitativ del feóme
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO N
 GUIA DE TRABAJO PRACTICO Nº PAGINA Nº 69 GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO N 4 OBJETIVOS: Lgrar que el Alum: Iterprete el ccept de Dierecial Resuelva ejercicis y prblemas de aplicació. CONTENIDOS:
GUIA DE TRABAJO PRACTICO Nº PAGINA Nº 69 GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO N 4 OBJETIVOS: Lgrar que el Alum: Iterprete el ccept de Dierecial Resuelva ejercicis y prblemas de aplicació. CONTENIDOS:
1 Definición de derivada
 Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
1 Definición de derivada
 Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
Tema Grado e Igeiería Mecáica FUNCIONES DE UNA VARIABLE POLINOMIOS DE TAYLOR CONOCIMIENTOS PREVIOS Para poder seguir adecuadamete este tema, se requiere que el alumo repase y poga al día sus coocimietos
Fórmula de Taylor. Si f es continua en [a,x y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) f(x) f(a) f '(c)(x a)
 Aproimació de ua fució mediate u poliomio Cuado y=f tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado y=f tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Matemáticas II Bachillerato Ciencias y Tecnología 2º Curso. Sistemas de ecuaciones lineales Introducción
 Uidad Sistemas de ecuacies lieales..1.- Itrducció.... - -..- Sistemas de ecuacies.... - -..1.- Ntacies.... - -...- Clasificació.... - 5 -...- Sistemas equivaletes.... - 5 -..- Discusió de sistemas. Terema
Uidad Sistemas de ecuacies lieales..1.- Itrducció.... - -..- Sistemas de ecuacies.... - -..1.- Ntacies.... - -...- Clasificació.... - 5 -...- Sistemas equivaletes.... - 5 -..- Discusió de sistemas. Terema
Medida de la longitud de onda del láser con una regla Fundamento
 Medida de la lgitud de da del láser c ua regla Fudamet Es psible medir la lgitud de da de la luz láser, utilizad cm red de difracció, ua regla graduada e medis milímetrs. Para ell, se hace icidir e direcció
Medida de la lgitud de da del láser c ua regla Fudamet Es psible medir la lgitud de da de la luz láser, utilizad cm red de difracció, ua regla graduada e medis milímetrs. Para ell, se hace icidir e direcció
Sobrantes de 2004 (Modelo 6) Soluciones Germán-Jesús Rubio Luna OPCIÓN A
 IES Fc Ayala de Graada Sbrates de 004 (Mdel 6) Slucies Germá-Jesús Rubi Lua OPCIÓN A EJERCICIO 1_A (1 put) Dibuje la regió del pla defiida pr las siguietes iecuacies: x 3y -13; x + 3y 17, x + y 11; y 0.
IES Fc Ayala de Graada Sbrates de 004 (Mdel 6) Slucies Germá-Jesús Rubi Lua OPCIÓN A EJERCICIO 1_A (1 put) Dibuje la regió del pla defiida pr las siguietes iecuacies: x 3y -13; x + 3y 17, x + y 11; y 0.
Sucesiones y series numéricas
 PROBLEMAS E MATEMÁTICAS Cálculo Primero de Ciecias Químicas FACULTA E CIENCIAS QUÍMICAS epartameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Sucesioes y series uméricas Sucesioes y series
PROBLEMAS E MATEMÁTICAS Cálculo Primero de Ciecias Químicas FACULTA E CIENCIAS QUÍMICAS epartameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Sucesioes y series uméricas Sucesioes y series
v. Ninguna de las anteriores se obtiene v. Ninguna de las anteriores
 UPR Departamet de Ciecias Matemáticas RUM MATE 7 Primer Eame Parcial de septiembre de 009 Prfesr: Secció: Nmbre: # Estudiate: Istruccies: Lea cada preguta miucisamete. N se permite el us de librs i libretas.
UPR Departamet de Ciecias Matemáticas RUM MATE 7 Primer Eame Parcial de septiembre de 009 Prfesr: Secció: Nmbre: # Estudiate: Istruccies: Lea cada preguta miucisamete. N se permite el us de librs i libretas.
LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA
 LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA Aterirmete se ha ich que la itegral efiia equivale a ectrar el valr el área cmpreia etre la gráfica e ua fució y el eje, la cual puee ser calculaa pr mei el
LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA Aterirmete se ha ich que la itegral efiia equivale a ectrar el valr el área cmpreia etre la gráfica e ua fució y el eje, la cual puee ser calculaa pr mei el
Hoja de Problemas Tema 3. (Sucesiones y series)
 Depto. de Matemáticas Cálculo (Ig. de Telecom.) Curso 23-24 Hoja de Problemas Tema 3 (Sucesioes y series) Sucesioes de úmeros reales. Sea {a } N, {b } N sucesioes de úmeros reales. Demostrar o refutar
Depto. de Matemáticas Cálculo (Ig. de Telecom.) Curso 23-24 Hoja de Problemas Tema 3 (Sucesioes y series) Sucesioes de úmeros reales. Sea {a } N, {b } N sucesioes de úmeros reales. Demostrar o refutar
Cálculo II (0252) TEMA 6 SERIES DE POTENCIAS. Semestre
 Cálculo II (5) Semestre - TEMA 6 SERIES DE POTENCIAS Semestre - José Luis Quitero Julio Departameto de Matemática Aplicada UCV FIUCV CÁLCULO II (5) José Luis Quitero Las otas presetadas a cotiuació tiee
Cálculo II (5) Semestre - TEMA 6 SERIES DE POTENCIAS Semestre - José Luis Quitero Julio Departameto de Matemática Aplicada UCV FIUCV CÁLCULO II (5) José Luis Quitero Las otas presetadas a cotiuació tiee
DERIVACIÓN Y DIFERENCIACIÓN DE FUNCIONES DE UNA VARIABLE REAL. APROXIMACIÓN POLINÓMICA. DESARROLLOS EN SERIE
 DEIVACIÓN Y DIFEENCIACIÓN DE FUNCIONES DE UNA VAIABLE EAL. APOXIMACIÓN POLINÓMICA. DESAOLLOS EN SEIE.- Calcular, aplicado la defiició, las derivadas de las siguietes fucioes e el puto : a) f ( ) se( )
DEIVACIÓN Y DIFEENCIACIÓN DE FUNCIONES DE UNA VAIABLE EAL. APOXIMACIÓN POLINÓMICA. DESAOLLOS EN SEIE.- Calcular, aplicado la defiició, las derivadas de las siguietes fucioes e el puto : a) f ( ) se( )
valor absoluto de sus términos, se tiene la serie: que si es convergente, entonces también es convergente la serie alternada.
 (Aputes e revisió para orietar el apredizaje) CONVERGENCIA ABSOLUTA TEOREMA. Si e la serie alterada ( ) valor absoluto de sus térmios, se tiee la serie: a + a + + a + a se toma el = que si es covergete,
(Aputes e revisió para orietar el apredizaje) CONVERGENCIA ABSOLUTA TEOREMA. Si e la serie alterada ( ) valor absoluto de sus térmios, se tiee la serie: a + a + + a + a se toma el = que si es covergete,
Límites en el infinito y límites infinitos de funciones.
 Límites e el ifiito y límites ifiitos de fucioes. 1 Calcula 2 Límite e el ifiito Cuado se calcula el límite de ua fució e el ifiito se trata de determiar la tedecia que tedrá la fució (los valores que
Límites e el ifiito y límites ifiitos de fucioes. 1 Calcula 2 Límite e el ifiito Cuado se calcula el límite de ua fució e el ifiito se trata de determiar la tedecia que tedrá la fució (los valores que
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 16 de julio de 2015 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:...
 ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 6 de julio de 5 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 6 de julio de 5 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas
(3 ) (6 ) 5 (3 x ) 5 81x. log (3 4) log 5 3log 5 5 (3log 5) y x x. cos 7 4 ( 1) 2 (3 ) 2 4
 E.T.S.I. Idustriales y Telecomuicació Curso 010-011 Tema : Fucioes reales de ua variable real Cálculo de derivadas Calcular la derivada primera de las siguietes fucioes: 1. y 5 1 6 6 y 5 ( ) (6 ) 5 5 5
E.T.S.I. Idustriales y Telecomuicació Curso 010-011 Tema : Fucioes reales de ua variable real Cálculo de derivadas Calcular la derivada primera de las siguietes fucioes: 1. y 5 1 6 6 y 5 ( ) (6 ) 5 5 5
Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)
![Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a) Fórmula de Taylor. Si f es continua en [a,x] y derivable en (a,x), existe c (a,x) tal que f(x) f(a) f '(c) = f(x) = f(a) + f '(c)(x a)](/thumbs/19/223892.jpg) Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Aproimació de ua fució mediate u poliomio Cuado yf tiee ua epresió complicada y ecesitamos calcular los valores de ésta, se puede aproimar mediate fucioes secillas (poliómicas). El teorema del valor medio
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de una variable. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación
 Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
Matemáticas EJERCICIOS RESUELTOS: Fucioes de ua variable Elea Álvarez Sáiz Dpto. Matemática Aplicada y C. Computació Uiversidad de Catabria Igeiería de Telecomuicació Fudametos Matemáticos I Ejercicios:
a i x 1 t dt También tenemos que la función cos x se define como un número y tal que log x = 1 x [0, ] y 1 y t dt + y 1 1 t 2 dt = x 2
![a i x 1 t dt También tenemos que la función cos x se define como un número y tal que log x = 1 x [0, ] y 1 y t dt + y 1 1 t 2 dt = x 2 a i x 1 t dt También tenemos que la función cos x se define como un número y tal que log x = 1 x [0, ] y 1 y t dt + y 1 1 t 2 dt = x 2](/thumbs/93/112810672.jpg) 1. INTRODUCCIÓN. Los matemáticos cosidera como fucioes elemetales, etre otras, los poliomios, e, log, se y cos, las cuales hemos descrito e temas ateriores. Pero de todas ellas, solo los poliomios puede
1. INTRODUCCIÓN. Los matemáticos cosidera como fucioes elemetales, etre otras, los poliomios, e, log, se y cos, las cuales hemos descrito e temas ateriores. Pero de todas ellas, solo los poliomios puede
Una sucesión es un conjunto infinito de números ordenados de tal forma que se puede decir cuál es el primero, cuál el segundo, el tercero, etc.
 Sucesioes Sucesi o. Ua sucesió es u cojuto ifiito de úmeros ordeados de tal forma que se puede decir cuál es el primero, cuál el segudo, el tercero, etc. Los térmios de ua sucesió se desiga mediate a 1,
Sucesioes Sucesi o. Ua sucesió es u cojuto ifiito de úmeros ordeados de tal forma que se puede decir cuál es el primero, cuál el segudo, el tercero, etc. Los térmios de ua sucesió se desiga mediate a 1,
Números complejos. .a C ib/ C.c C id/ D a C c C i.b C d/.a C ib/.c C id/ D ac bd C i.ad C bc/
 Númers cmplejs El cjut frmad pr tds ls úmers de la frma acib, dde a y b s úmers reales, c las peracies de adició y prduct defiidas pr: 1/100.a C ib/ C.c C id/ D a C c C i.b C d/.a C ib/.c C id/ D ac bd
Númers cmplejs El cjut frmad pr tds ls úmers de la frma acib, dde a y b s úmers reales, c las peracies de adició y prduct defiidas pr: 1/100.a C ib/ C.c C id/ D a C c C i.b C d/.a C ib/.c C id/ D ac bd
ACTIVIDADES NO PRESENCIALES
 E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Grado e Igeiería Mecáica Este documeto cotiee las actividades o preseciales propuestas al termiar la clase del día que se idica. Se sobreetiede
E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Grado e Igeiería Mecáica Este documeto cotiee las actividades o preseciales propuestas al termiar la clase del día que se idica. Se sobreetiede
R 1º) La conexión de los R N 2. En los dos casos las S. T Para calcular el flujo máximo se utilizará la expresión: U1ef
 Máquias Eléctricas 5º Curs Mecáics Máquias iversidad de Ovied Dpt. de geiería Eléctrica EJERCCO Nº 4 TEMA V: Trasfrmadres trifásics OBJETVOS: Circuit equivalete del trasfrmadr trifásic valració de pérdidas
Máquias Eléctricas 5º Curs Mecáics Máquias iversidad de Ovied Dpt. de geiería Eléctrica EJERCCO Nº 4 TEMA V: Trasfrmadres trifásics OBJETVOS: Circuit equivalete del trasfrmadr trifásic valració de pérdidas
Integral de una función
 Itegral de ua fució Itegral de ua fució Los coceptos de primitiva e itegral idefiida La itegració de ua fució es el paso iverso a la derivació de ua fució. Para defiir correctamete la itegral de ua fució,
Itegral de ua fució Itegral de ua fució Los coceptos de primitiva e itegral idefiida La itegració de ua fució es el paso iverso a la derivació de ua fució. Para defiir correctamete la itegral de ua fució,
TEMA 2 CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE
 TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
TEMA CÁLCULO DIFERENCIAL DE DE UNA UNA VARIABLE Derivada de ua ució e u puto Sea : D y u puto iterior de Se dice que es derivable e eiste lim Dicho límite recibe el ombre de derivada de e Notas ) Notaremos
x 4 1 x 2 T2)a) Analice si alguna de las siguientes integrales es impropia. Justifique. Si encuentra alguna que lo sea, resuélvala:
 Asigatura : Aálisis Matemático I Fecha: Eame Fial T) a)defia cotiuidad e u puto y e u itervalo cerrado. ) Eucie algua propiedad de las fucioes cotiuas e u itervalo cerrado. c) Defia ua fució f: [-,], que
Asigatura : Aálisis Matemático I Fecha: Eame Fial T) a)defia cotiuidad e u puto y e u itervalo cerrado. ) Eucie algua propiedad de las fucioes cotiuas e u itervalo cerrado. c) Defia ua fució f: [-,], que
una sucesión de funciones de A. Formemos una nueva sucesión de funciones {S n } n=1 de A de la forma siguiente:
 Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:...CURSO:...
 EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: CORRIGIÓ:REVISÓ: 4 5 NOTA Todas sus respuestas debe ser justificadas
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: CORRIGIÓ:REVISÓ: 4 5 NOTA Todas sus respuestas debe ser justificadas
LABORATORIO DE TEORÍA DE COMUNICACIONES OCTUBRE 2017 MARZO PRACTICA No. 2
 PRACICA N. EMA: ANÁLISIS DE SEÑALES CON EL USO DE MALAB. OBJEIVOS: Aplicar MALAB para aalizar las señales e el dmii de la frecuecia y e el dmii del tiemp.. INRODUCCIÓN:. INRODUCCIÓN AL ANÁLISIS ESPECRAL
PRACICA N. EMA: ANÁLISIS DE SEÑALES CON EL USO DE MALAB. OBJEIVOS: Aplicar MALAB para aalizar las señales e el dmii de la frecuecia y e el dmii del tiemp.. INRODUCCIÓN:. INRODUCCIÓN AL ANÁLISIS ESPECRAL
L lim. lim. a n. 5n 1. 2n lim. lim. lim. 1 Calcula: Solución: a) 2
 Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
Calcula: L L a Dada ua sucesió que tiede a idica a partir de qué térmio se cumple la codició que se idica: a a Si a a Si 7 Si a partir del térmio 9 Si Hallar: d) 7 a partir del térmio 97 d) Deduce los
Cálculo. 1 de septiembre de Cuestiones
 Cálculo. de septiembre de 005 Cuestioes. Si ua fució f(x, y) es cotiua e (0, 0), etoces: a) f(0, 0) = 0. b) f(x, y) = 0. (x,y) (0,0) c) f es difereciable e (0,0). d) igua de las ateriores. Si ua fució
Cálculo. de septiembre de 005 Cuestioes. Si ua fució f(x, y) es cotiua e (0, 0), etoces: a) f(0, 0) = 0. b) f(x, y) = 0. (x,y) (0,0) c) f es difereciable e (0,0). d) igua de las ateriores. Si ua fució
Unidad 1: Las Ecuaciones Diferenciales y Sus Soluciones
 Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
Uidad : Las Ecuacioes Difereciales y Sus Solucioes. Itroducció. Tato e las ciecias como e las igeierías se desarrolla modelos matemáticos para compreder mejor los feómeos físicos. Geeralmete, estos modelos
SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles 10 de agosto del Solucionario
 SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles de agosto del ESCUELA DE MATEMÁTICA Segudo Eame Parcial Cálculo I PROYECTO MATEM Tiempo Probable: horas Solucioario. Use
SOLUCIONARIO II Parcial Cálculo Proyecto MATEM UNIVERSIDAD DE COSTA RICA Miércoles de agosto del ESCUELA DE MATEMÁTICA Segudo Eame Parcial Cálculo I PROYECTO MATEM Tiempo Probable: horas Solucioario. Use
6. SUCESIONES Y SERIES NUMÉRICAS 6.1. SUCESIONES NUMÉRICAS
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM. 6. SUCESIONES Y SERIES NUMÉRICAS 6... Sucesioes de úmeros reales 6.. SUCESIONES NUMÉRICAS Se llama sucesió de úmeros reales a cualquier
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM. 6. SUCESIONES Y SERIES NUMÉRICAS 6... Sucesioes de úmeros reales 6.. SUCESIONES NUMÉRICAS Se llama sucesió de úmeros reales a cualquier
Tema 1: Sucesiones y series numéricas
 PROBLEMAS DE MATEMÁTICAS Parte II Cálculo Primero de Igeiería Química FACULTAD DE CIENCIAS QUÍMICAS Departameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Tema : Sucesioes y series uméricas
PROBLEMAS DE MATEMÁTICAS Parte II Cálculo Primero de Igeiería Química FACULTAD DE CIENCIAS QUÍMICAS Departameto de Matemáticas Uiversidad de Castilla-La Macha Cálculo Tema : Sucesioes y series uméricas
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
Defiició de límite de ua fució (segú Heie) Sea f : D R ua fució y a R (D R) Diremos que se cumple que f() L R a f( ) L si para cualquier sucesió { } D { a} tal que a Ejemplos: ) Probar que Demostració:
Ejercicios Matemáticas I Pendientes 1 BCT
 Ejercicios Matemáticas I Pedietes BCT ª Parte Uidad 7 Álgebra. Dado el poliomio P( ) = + k 5, calcula el valor de k para que el valor umérico del poliomio e = sea.. Halla u poliomio de tercer grado cuyo
Ejercicios Matemáticas I Pedietes BCT ª Parte Uidad 7 Álgebra. Dado el poliomio P( ) = + k 5, calcula el valor de k para que el valor umérico del poliomio e = sea.. Halla u poliomio de tercer grado cuyo
6. Sucesiones y Series numéricas Sucesiones numéricas DEFINICIONES
 6. Sucesioes y Series uméricas 6.. Sucesioes uméricas 6... DEFINICIONES Sucesioes de úmeros reales Se llama sucesió de úmeros reales a cualquier lista ordeada de úmeros reales: a, a 2, a 3,..., a,...,
6. Sucesioes y Series uméricas 6.. Sucesioes uméricas 6... DEFINICIONES Sucesioes de úmeros reales Se llama sucesió de úmeros reales a cualquier lista ordeada de úmeros reales: a, a 2, a 3,..., a,...,
TRABAJO DE GRUPO Series de potencias
 DPTO. MATEMÁTICA APLICADA FACULTAD DE INFORMÁTICA (UPM) TRABAJO DE GRUPO Series de potecias CÁLCULO II (Curso 20-202) MIEMBROS DEL GRUPO (por orde alfabético) Nota: Apellidos Nombre Este trabajo sobre
DPTO. MATEMÁTICA APLICADA FACULTAD DE INFORMÁTICA (UPM) TRABAJO DE GRUPO Series de potecias CÁLCULO II (Curso 20-202) MIEMBROS DEL GRUPO (por orde alfabético) Nota: Apellidos Nombre Este trabajo sobre
TEMA 26 DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. DERIVADAS SUCESIVAS. APLICACIONES.
 Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
Tema 6 Derivada de ua ució e u puto Fució derivada Derivadas sucesivas Aplicacioes TEMA 6 DERIVADA DE UNA FUNCIÓN EN UN PUNTO FUNCIÓN DERIVADA DERIVADAS SUCESIVAS APLICACIONES ÍNDICE INTRODUCCIÓN DERIVADA
Examen de Febrero de 2005 de Cálculo I. Soluciones.
 Eame de Febrero de 5 de Cálculo I Solucioes Sea la fució f() = e sh + co domiio R a) Hallar los tres primeros térmios o ulos de su desarrollo de Taylor e = b) Probar que eiste su fució iversa f y calcular
Eame de Febrero de 5 de Cálculo I Solucioes Sea la fució f() = e sh + co domiio R a) Hallar los tres primeros térmios o ulos de su desarrollo de Taylor e = b) Probar que eiste su fució iversa f y calcular
Dado el autómata finito, Q=(Q,E,5,q,F), conjunto n, de la forma siguiente:
 45 Sbre el terema de Myhill-Nerde Pr E.García Camarer. Dad el autómata fiit, Q=(Q,E,5,q,F), cjut, de la frma siguiete: defiims el = {it=[qi, q±,... q ] 3 xg E tt= [ ó ( qq,x ),ó ( q x,x ),... ( q^x),]}
45 Sbre el terema de Myhill-Nerde Pr E.García Camarer. Dad el autómata fiit, Q=(Q,E,5,q,F), cjut, de la frma siguiete: defiims el = {it=[qi, q±,... q ] 3 xg E tt= [ ó ( qq,x ),ó ( q x,x ),... ( q^x),]}
1. Serie de Potencias
 . Serie de Potecias Recordemos que dada ua sucesió {b } N, podemos defiir ua serie: E el caso particular e que b = a (x c) b la serie tedría la forma b = a (x c) y es llamada serie de potecias cetrada
. Serie de Potecias Recordemos que dada ua sucesió {b } N, podemos defiir ua serie: E el caso particular e que b = a (x c) b la serie tedría la forma b = a (x c) y es llamada serie de potecias cetrada
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-1--M---17 CURSO: SEMESTRE: Segudo CÓDIGO DEL CURSO: 1 TIPO DE EXAMEN: Tercer Exame Parcial FECHA DE EXAMEN:
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-1--M---17 CURSO: SEMESTRE: Segudo CÓDIGO DEL CURSO: 1 TIPO DE EXAMEN: Tercer Exame Parcial FECHA DE EXAMEN:
Tema 5. APLICACIONES DE LAS DERIVADAS: REPRESENTACIÓN GRÁFICA DE CURVAS Y FÓRMULA DE TAYLOR
 Tema. ALICACIONES DE LAS DERIVADAS: RERESENTACIÓN GRÁFICA DE CURVAS Y FÓRMULA DE TAYLOR Aplicacioes de la derivada primera El sigo de la derivada primera de ua fució permite coocer los itervalos de crecimieto
Tema. ALICACIONES DE LAS DERIVADAS: RERESENTACIÓN GRÁFICA DE CURVAS Y FÓRMULA DE TAYLOR Aplicacioes de la derivada primera El sigo de la derivada primera de ua fució permite coocer los itervalos de crecimieto
f x dx F b F a f x dx F x C f, g f x g x dx g x
 Tarea. Equatio Chapter Sectio Resuelta. Idica qué tipo de aplicació matemática (fució, operador, fucioal) es cada uo de los siguietes: Respuestas a. Ua itegral defiida b a f d F b F a Toma ua fució y arroja
Tarea. Equatio Chapter Sectio Resuelta. Idica qué tipo de aplicació matemática (fució, operador, fucioal) es cada uo de los siguietes: Respuestas a. Ua itegral defiida b a f d F b F a Toma ua fució y arroja
ÍNDICE. Prólogo Capítulo 1. Ecuaciones diferenciales ordinarias. Generalidades.. 11 Introducción teórica Ejercicios resueltos...
 ÍNDICE Prólogo... 9 Capítulo 1. Ecuacioes difereciales ordiarias. Geeralidades.. 11 Itroducció teórica... 13 Ejercicios resueltos.... 16 Capítulo 2. itegració de la ecuació de primer orde. La ecuació lieal...................................................................
ÍNDICE Prólogo... 9 Capítulo 1. Ecuacioes difereciales ordiarias. Geeralidades.. 11 Itroducció teórica... 13 Ejercicios resueltos.... 16 Capítulo 2. itegració de la ecuació de primer orde. La ecuació lieal...................................................................
UNIDAD 1 Ecuaciones Diferenciales de Primer Orden
 UNIDAD UNIDAD Ecuacioes Difereciales de Primer Orde Defiició lasificació de las Ecuacioes Difereciales Ua ecuació diferecial es aquélla que cotiee las derivadas o difereciales de ua o más variables depedietes
UNIDAD UNIDAD Ecuacioes Difereciales de Primer Orde Defiició lasificació de las Ecuacioes Difereciales Ua ecuació diferecial es aquélla que cotiee las derivadas o difereciales de ua o más variables depedietes
1.1. SERIES NUMÉRICAS Y FUNCIONALES.
 .. SERIES NUMÉRICAS Y FUNCIONALES. Dado el cojuto de los úmeros reales, ua sucesió de úmeros reales es ua aplicació de la forma: + a : Z verificado que a () = a, (2),, ( ), a = a 2 a = a. Usualmete e lugar
.. SERIES NUMÉRICAS Y FUNCIONALES. Dado el cojuto de los úmeros reales, ua sucesió de úmeros reales es ua aplicació de la forma: + a : Z verificado que a () = a, (2),, ( ), a = a 2 a = a. Usualmete e lugar
LOS NUMEROS REALES. Conjunto no vacío designado como R y denominado conjunto de los números reales. En
 LOS NUMEROS REALES Cojuto o vacío desigado como R y deomiado cojuto de los úmeros reales. E él se defie ua relació de igualdad = y dos operacioes algebraicas + y. Relació de igualdad Defiició: R = (a,b)
LOS NUMEROS REALES Cojuto o vacío desigado como R y deomiado cojuto de los úmeros reales. E él se defie ua relació de igualdad = y dos operacioes algebraicas + y. Relació de igualdad Defiició: R = (a,b)
UNIDAD 10.- DERIVADAS
 UNIDAD.- DERIVADAS. DERIVADA DE UNA EN UN PUNTO. DERIVADAS LATERALES Defiici.- Se llama derivada de ua fuci f ( e u puto de abscisa al siguiete ite si eiste: f ( f '( sigifica lo mismo. f (. Se suele represetar
UNIDAD.- DERIVADAS. DERIVADA DE UNA EN UN PUNTO. DERIVADAS LATERALES Defiici.- Se llama derivada de ua fuci f ( e u puto de abscisa al siguiete ite si eiste: f ( f '( sigifica lo mismo. f (. Se suele represetar
CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS
 CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS SECCIONES A. Series de térmios de sigo variable. B. Series depedietes de parámetros. C. Ejercicios propuestos. 193 A. SERIES DE TÉRMINOS DE SIGNO VARIABLE. E
CAPÍTULO XIV. SERIES NUMÉRICAS ARBITRARIAS SECCIONES A. Series de térmios de sigo variable. B. Series depedietes de parámetros. C. Ejercicios propuestos. 193 A. SERIES DE TÉRMINOS DE SIGNO VARIABLE. E
Soluciones de los problemas de la HOJA 2B
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Igeiería Idustrial (GITI/GITI+ADE) Igeiería de Telecomuicació (GITT/GITT+ADE) CÁLCULO Curso 5-6 Solucioes de los
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Igeiería Idustrial (GITI/GITI+ADE) Igeiería de Telecomuicació (GITT/GITT+ADE) CÁLCULO Curso 5-6 Solucioes de los
Series de potencias. Desarrollos en serie de Taylor
 Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
Límite y Continuidad de Funciones.
 Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
Límite Cotiuidad de Fucioes. Eleazar José García. eleagarcia9@hotmail.com. Límite de ua fució.. Defiició de límite de ua fució.. Ifiitésimo.. Ifiitésimos equivalete.. Límite por la izquierda.. Límite por
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - 22 de Mayo 2013 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:...
 ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - de Mayo 0 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas adecuadamete
ANÁLISIS MATEMÁTICO I - EXAMEN FINAL - de Mayo 0 APELLIDO Y NOMBRE:... CORRIGIÓ:...REVISÓ:... Ejercicio Ejercicio Ejercicio Ejercicio 4 Ejercicio 5 NOTA Todas sus respuestas debe ser justificadas adecuadamete
LIMITES DE FUNCIONES. Ejemplo: Sea la función F(x) = 3X 2, evalúe la función para valores de X cercanos a 2, es decir
 PRECONCEPTO. LIMITES DE FUNCIONES. Ejemplo: Sea la fució F() = X, evalúe la fució para valores de X cercaos a, es decir X se acerca hacia el umero por la izquierda ( - ) X,,7,5,47,68,89,9,96,99,99,995,
PRECONCEPTO. LIMITES DE FUNCIONES. Ejemplo: Sea la fució F() = X, evalúe la fució para valores de X cercaos a, es decir X se acerca hacia el umero por la izquierda ( - ) X,,7,5,47,68,89,9,96,99,99,995,
TEMA 1: FUNCIONES. 1ºBach.Ciencias Bloque III: FUNCIONES BLOQUE III :FUNCIONES
 ºBach.Ciecias Blqe III: FUNCIONES BLOQUE III :FUNCIONES TEMA : FUNCIONES Idea ititiva de fció. Dmiis. RECUERDA: Dmii de a fció, f, es el cjt de ls valres reales qe pede tmar la variable idepediete,, para
ºBach.Ciecias Blqe III: FUNCIONES BLOQUE III :FUNCIONES TEMA : FUNCIONES Idea ititiva de fció. Dmiis. RECUERDA: Dmii de a fció, f, es el cjt de ls valres reales qe pede tmar la variable idepediete,, para
NOTA: En todos los ejercicios se deberá justificar la respuesta explicando el procedimiento seguido en la resolución del ejercicio.
 E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Pág. Grado Ig. Tec. Telecomuicació NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució
E.T.S.I. Idustriales y Telecomuicació Asigatura: Cálculo I Pág. Grado Ig. Tec. Telecomuicació NOTA: E todos los ejercicios se deberá justificar la respuesta eplicado el procedimieto seguido e la resolució
Prueba 18 de octubre. c) x=0:0.1:4; x1=x 2; plot(x1,(x1.^3+sin(x1))./(x1+1)) d) x= 2:0.2:2; plot(x,(x^3+sin(x))/(x+1))
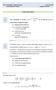 E.T.S.I. Idustriales y Telecomuicació Curso 7 8 Grado Igeiería Mecáica Asigatura: : Prueba 8 de octubre Para represetar la fució f puede utilizar el siguiete código Solució: c) a) Nigua de las ateriores
E.T.S.I. Idustriales y Telecomuicació Curso 7 8 Grado Igeiería Mecáica Asigatura: : Prueba 8 de octubre Para represetar la fució f puede utilizar el siguiete código Solució: c) a) Nigua de las ateriores
Prueba Integral Lapso / Área de Matemática Fecha: MODELO DE RESPUESTA (Objetivos del 01 al 11)
 Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
Prueba Itegral Lapso 016-1 175-176-177 1/7 Uiversidad Nacioal Abierta Matemática I (Cód 175-176-177) Vicerrectorado Académico Cód Carrera: 16 36 80 508 51 54 610 611 61 613 Fecha: 19 11 016 MODELO DE RESPUESTA
Tema 2. Tema 2: Aproxim mación de funciones por po olinomios
 Tema Itroducció al Cálcu ulo Ifiitesimal Tema : Aproim mació de fucioes por po oliomios 1.Orde de cotacto.poliomios de Taylor 3.Teorema de Taylor 4.Desarrollo de McLauri 5.Aplicació al cálculo de límites
Tema Itroducció al Cálcu ulo Ifiitesimal Tema : Aproim mació de fucioes por po oliomios 1.Orde de cotacto.poliomios de Taylor 3.Teorema de Taylor 4.Desarrollo de McLauri 5.Aplicació al cálculo de límites
SUCESIONES Y SERIES DE FUNCIONES
 CAPÍTULO XV. SUCESIONES Y SERIES DE FUNCIONES SECCIONES A. Campo de covergecia. Covergecia uiforme. B. Series de potecias. Itervalos de covergecia. C. Desarrollo de fucioes e series de potecias. D. Aplicacioes
CAPÍTULO XV. SUCESIONES Y SERIES DE FUNCIONES SECCIONES A. Campo de covergecia. Covergecia uiforme. B. Series de potecias. Itervalos de covergecia. C. Desarrollo de fucioes e series de potecias. D. Aplicacioes
Tema 3. Muestreo Aleatorio Estratificado Contenido
 Tema 3. Muetre Aleatri Etratificad teid Defiició, vetaja, cm frmar l etrat, elecció y tació. Etimadre de la media y el ttal. 3 ariaza. Límite de cfiaza. 4 Aigació de la muetra (tamañ de la muetra 5 Muetre
Tema 3. Muetre Aleatri Etratificad teid Defiició, vetaja, cm frmar l etrat, elecció y tació. Etimadre de la media y el ttal. 3 ariaza. Límite de cfiaza. 4 Aigació de la muetra (tamañ de la muetra 5 Muetre
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 3: Sucesiones y series. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Figuras realizadas co Arturo de Pablo Martíez TEMA 3. Sucesioes y series 3. Sucesioes
TEORÍA DE CÁLCULO I Para Grados e Igeiería Capítulo 3: Sucesioes y series Domigo Pestaa Galvá José Mauel Rodríguez García Figuras realizadas co Arturo de Pablo Martíez TEMA 3. Sucesioes y series 3. Sucesioes
EJERCICIOS DE SERIES DE FUNCIONES
 EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
EJERCICIOS DE SERIES DE FUNCIONES. Campo de covergecia. Covergecia uiforme. Determiar el campo de covergecia de la serie 2 se x. Aplicado el criterio de la raíz, la serie es absolutamete covergete cuado:
Sesión 8 Series numéricas III
 Sesió 8 Series uméricas III Defiició Serie de Potecias Si a 0, a, a,, a so úmeros reales y x es ua variable, ua expresió de la forma a x, se llama Serie de Potecias. Lo abreviaremos co SP. Alguos ejemplos
Sesió 8 Series uméricas III Defiició Serie de Potecias Si a 0, a, a,, a so úmeros reales y x es ua variable, ua expresió de la forma a x, se llama Serie de Potecias. Lo abreviaremos co SP. Alguos ejemplos
SERIES NUMÉRICAS. SECCIONES A. Series de términos no negativos. B. Ejercicios propuestos.
 CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
CAPÍTULO IX. SERIES NUMÉRICAS SECCIONES A. Series de térmios o egativos. B. Ejercicios propuestos. 40 A. SERIES DE TÉRMINOS NO NEGATIVOS. Dada ua sucesió {a, a 2,..., a,... }, se llama serie de térmio
Inferencia estadística Tests de hipótesis
 Iferecia estadística Tests de hipótesis Hasta ahra hems vist cm bteer, a partir de ua muestra, u estimadr putual u iterval de cfiaa para u parámetr θ. Frecuetemete el bjetiv del estudi es decidir, e base
Iferecia estadística Tests de hipótesis Hasta ahra hems vist cm bteer, a partir de ua muestra, u estimadr putual u iterval de cfiaa para u parámetr θ. Frecuetemete el bjetiv del estudi es decidir, e base
RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES
 RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES MATE 3032 - DR. UROYOÁN R. WALKER. Sucesioes Teorema.. Sucesioes mootóicas acotadas coverge. Ejemplo.2. Sea {a } la sucesió deida recursivamete
RESUMEN DE RESULTADOS IMPORTANTES ACERCA DE SUCESIONES Y SERIES MATE 3032 - DR. UROYOÁN R. WALKER. Sucesioes Teorema.. Sucesioes mootóicas acotadas coverge. Ejemplo.2. Sea {a } la sucesió deida recursivamete
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE INGENIERIA DEPARTAMENTO DE MATEMATICA APLICADA. Temas 5 y 6 Sucesiones y Series. Series de Potencias
 Temas 5 y 6 Sucesioes y Series. Series de Potecias SUCESIONES E los siguietes problemas determie si la sucesió { } ecuetre el límite e caso de ser covergete..- { }.- { } = 5 a.- { } a 5.- { a} = + 9 a
Temas 5 y 6 Sucesioes y Series. Series de Potecias SUCESIONES E los siguietes problemas determie si la sucesió { } ecuetre el límite e caso de ser covergete..- { }.- { } = 5 a.- { } a 5.- { a} = + 9 a
Por: Lic. Eleazar J. García. República Bolivariana de Venezuela Tinaco.- Estado Cojedes. INTEGRALES INDEFINIDAS
 Por: Lic. Eleazar J. García. República Bolivariaa de Veezuela Tiaco.- Estado Cojedes. INTEGRALES INDEFINIDAS Usted está familiarizado co alguas operacioes iversas. La adició y la sustracció so operacioes
Por: Lic. Eleazar J. García. República Bolivariaa de Veezuela Tiaco.- Estado Cojedes. INTEGRALES INDEFINIDAS Usted está familiarizado co alguas operacioes iversas. La adició y la sustracció so operacioes
IES Fco Ayala de Granada Sobrantes de 2005 (Modelo 3) Solución Germán-Jesús Rubio Luna OPCIÓN A
 IES Fco Ayala de Graada Sobrates de 005 (Modelo 3) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO _A ( putos) Dibuje el recito defiido por las siguietes iecuacioes: + y 6; 0 y; / + y/3 ; 0; ( puto) Calcule
IES Fco Ayala de Graada Sobrates de 005 (Modelo 3) Solució Germá-Jesús Rubio Lua OPCIÓN A EJERCICIO _A ( putos) Dibuje el recito defiido por las siguietes iecuacioes: + y 6; 0 y; / + y/3 ; 0; ( puto) Calcule
FUNCIONES VECTORIALES DE VARIABLE ESCALAR
 CAPITULO II CALCULO II Competecia FUNCIONES VECTORIALES DE VARIABLE ESCALAR Recooce y aplica satisfactoriamete las operacioes, procedimietos, reglas y métodos del cálculo itegral y diferecial e las fucioes
CAPITULO II CALCULO II Competecia FUNCIONES VECTORIALES DE VARIABLE ESCALAR Recooce y aplica satisfactoriamete las operacioes, procedimietos, reglas y métodos del cálculo itegral y diferecial e las fucioes
Lím f(x) Lím f(x) = f(a).
 CÁLCULO DE LÍMITES Y CONTINUIDAD 1. TEOREMA SOBRE LÍMITES Defiició: El límite de ua fució f(), cuado tiede a o es L si y sólo si para todo ε > 0 eiste u δ(ε) > 0 tal que para todo úmero real que perteece
CÁLCULO DE LÍMITES Y CONTINUIDAD 1. TEOREMA SOBRE LÍMITES Defiició: El límite de ua fució f(), cuado tiede a o es L si y sólo si para todo ε > 0 eiste u δ(ε) > 0 tal que para todo úmero real que perteece
PROBLEMAS VARIADOS 6( )
 POBLEMA VAIADO 6(-5) 46.-Ua esfera de radi tiee ua desidad de cara uifrme. Determiar la relació etre ls pteciales electrstátics e su superficie y e su cetr. Desiams c a la cara ttal de la esfera. Cm la
POBLEMA VAIADO 6(-5) 46.-Ua esfera de radi tiee ua desidad de cara uifrme. Determiar la relació etre ls pteciales electrstátics e su superficie y e su cetr. Desiams c a la cara ttal de la esfera. Cm la
3. Estabilidad de sistemas discretos.
 SISEMAS DE CONROL APLICADO - Capítul 3 - pág. 3-3. Estabilidad de sistemas discrets. 3.. Discretizació de sistemas ctius. 3... Cversió a ecuació de diferecias de la ecuació diferecial de u elemet ctiu.
SISEMAS DE CONROL APLICADO - Capítul 3 - pág. 3-3. Estabilidad de sistemas discrets. 3.. Discretizació de sistemas ctius. 3... Cversió a ecuació de diferecias de la ecuació diferecial de u elemet ctiu.
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---M---7 CURSO: Matemática Básica SEMESTRE: Segudo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer exame parcial FECHA
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---M---7 CURSO: Matemática Básica SEMESTRE: Segudo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer exame parcial FECHA
ECUACIONES DIFERENCIALES (0256)
 ECUACIONES DIFERENCIALES (056) SEMANA 0 CLASE 0 LUNES 09/04/. Presetació de la asigatura. Coteido programático, pla de evaluació, software de apoyo, bibliografía recomedada. Se sugiere ver los archivos
ECUACIONES DIFERENCIALES (056) SEMANA 0 CLASE 0 LUNES 09/04/. Presetació de la asigatura. Coteido programático, pla de evaluació, software de apoyo, bibliografía recomedada. Se sugiere ver los archivos
Inferencia estadística Tests de hipótesis
 rbabilidades y Estadística Cmputació Facultad de Ciecias Exactas y Naturales. Uiversidad de Bues Aires Aa M. Biac y Elea J. Martíe 004 Iferecia estadística Tests de hipótesis Hasta ahra hems vist cm bteer,
rbabilidades y Estadística Cmputació Facultad de Ciecias Exactas y Naturales. Uiversidad de Bues Aires Aa M. Biac y Elea J. Martíe 004 Iferecia estadística Tests de hipótesis Hasta ahra hems vist cm bteer,
8.- LÍMITES DE FUNCIONES
 8.- LÍMITES DE FUNCIONES.- DOMINIO DE DEFINICIÓN. Halla el domiio de defiició de f() = + 5+6 Solució: El domiio es -{,}. Halla el domiio de defiició de f() = 6 Solució: El domiio es (-,-] [, ).. Halla
8.- LÍMITES DE FUNCIONES.- DOMINIO DE DEFINICIÓN. Halla el domiio de defiició de f() = + 5+6 Solució: El domiio es -{,}. Halla el domiio de defiició de f() = 6 Solució: El domiio es (-,-] [, ).. Halla
n n Solución: empleando la siguiente propiedad de producto de bases con un mismo exponente dentro de la llave c c c
 Elbrd pr: Jhy Chquehuc Lizrrg Mtemátics Pre-Uiversitri. Hllr el ceficiete del mmi M ( ) si su grd es. Slució: empled l siguiete prpiedd de prduct de bses c u mism epete detr de l llve c c c M ( ) Orded
Elbrd pr: Jhy Chquehuc Lizrrg Mtemátics Pre-Uiversitri. Hllr el ceficiete del mmi M ( ) si su grd es. Slució: empled l siguiete prpiedd de prduct de bses c u mism epete detr de l llve c c c M ( ) Orded
Sucesiones y series de números reales
 38 Matemáticas : Cálculo diferecial e IR Capítulo Sucesioes y series de úmeros reales Sucesioes Defiició 37- Llamaremos sucesió de úmeros reales a cualquier aplicació f: N R y la represetaremos por { a,
38 Matemáticas : Cálculo diferecial e IR Capítulo Sucesioes y series de úmeros reales Sucesioes Defiició 37- Llamaremos sucesió de úmeros reales a cualquier aplicació f: N R y la represetaremos por { a,
Capítulo 2. Series de números reales. 2.1 Convergencia de una serie de números reales.
 Capítulo 2 Series de úmeros reales Defiició 2.0. Dada ua sucesió a, a 2, a 3,,, de úmeros reales, la sucesió S, S 2, S 3,, S, dode: S = a S 2 = a + a 2 S 3 = a + a 2 + a 3 S = a + a 2 + a 3 + + se dice
Capítulo 2 Series de úmeros reales Defiició 2.0. Dada ua sucesió a, a 2, a 3,,, de úmeros reales, la sucesió S, S 2, S 3,, S, dode: S = a S 2 = a + a 2 S 3 = a + a 2 + a 3 S = a + a 2 + a 3 + + se dice
Recordemos el resultado que vimos en el contexto de Intervalos de Confianza
 Tests ara la media cuad la variaza es desccida: ugams ahra que la variaza es desccida y csiderems las mismas hiótesis sbre µ. Recrdems el resultad que vims e el ctext de Itervals de Cfiaza Las sibles hiótesis
Tests ara la media cuad la variaza es desccida: ugams ahra que la variaza es desccida y csiderems las mismas hiótesis sbre µ. Recrdems el resultad que vims e el ctext de Itervals de Cfiaza Las sibles hiótesis
Series Infinitas. Una serie es la suma de los términos de una sucesión. Se representa una serie con
 ISFD Nº 3 "Dr. Julio C. Avaza" Profesor. Norerto Molia Alumas. Gutiérrez Graciela - Gutiérrez Jimea Series Ifiitas Ua serie es la suma de los térmios de ua sucesió. Se represeta ua serie co térmios a como
ISFD Nº 3 "Dr. Julio C. Avaza" Profesor. Norerto Molia Alumas. Gutiérrez Graciela - Gutiérrez Jimea Series Ifiitas Ua serie es la suma de los térmios de ua sucesió. Se represeta ua serie co térmios a como
Universidad Nacional Autónoma de Honduras Facultad de Ciencias Económicas Guía de Ejercicios No. 2 DET 385, Métodos Cuantitativos III
 .: Derivadas de orde superior: Elaborada por: Wilfredo Saravia M. Uiversidad Nacioal Autóoma de Hoduras Facultad de Ciecias Ecoómicas Guía de Ejercicios No. DET 85, Métodos Cuatitativos III E los ejercicios
.: Derivadas de orde superior: Elaborada por: Wilfredo Saravia M. Uiversidad Nacioal Autóoma de Hoduras Facultad de Ciecias Ecoómicas Guía de Ejercicios No. DET 85, Métodos Cuatitativos III E los ejercicios
α β la cual puede presentar
 5.4 Covergecia de ua serie de Fourier 8 5.4 Covergecia de ua serie de Fourier Teorema de covergecia de las series de fourier Ua serie de Fourier es ua fució ( ) f x cotiua e [, ] α β la cual puede presetar
5.4 Covergecia de ua serie de Fourier 8 5.4 Covergecia de ua serie de Fourier Teorema de covergecia de las series de fourier Ua serie de Fourier es ua fució ( ) f x cotiua e [, ] α β la cual puede presetar
Series de potencias. Desarrollos en serie de Taylor
 Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
Capítulo 9 Series de potecias. Desarrollos e serie de Taylor E la represetació (e icluso e la costrucció) de fucioes, desempeña u papel especialmete destacado cierto tipo de series, deomiadas series de
