MOVIMIENTO EN LÍNEA RECTA
|
|
|
- Consuelo Domínguez Ferreyra
- hace 7 años
- Vistas:
Transcripción
1 2 MVIMIENT EN LÍNEA RECTA METAS DE APRENDIZAJE Al esudir ese cpíulo, used prenderá: Cómo describir el moimieno en líne rec en érminos de elocidd medi, elocidd insnáne, celerción medi y celerción insnáne. Cómo inerprer gráfics de posición conr iempo, elocidd conr iempo y celerción conr iempo pr el moimieno en líne rec. Cómo resoler problems que impliquen moimieno en líne rec con celerción consne, incluyendo problems de cíd libre. Cómo nlizr el moimieno en líne rec cundo l celerción no es consne.? Un elocis común celer durne el primer ercio de l crrer y desceler grdulmene en el reso de l compeenci. Es correco decir que un corredor esá celerndo conforme desceler durne los dos ercios finles de l crrer? disnci debe recorrer un ión comercil nes de lcnzr l rpidez de despeje? Cundo lnzmos un pelo de béisbol ericlmene, Qué qué no sube? Cundo se nos resbl un so de l mno, cuáno iempo enemos pr rprlo nes de que choque conr el piso? Ése es el ipo de preguns que used prenderá conesr en ese cpíulo. Inicimos nuesro esudio de físic con l mecánic, que es el esudio de ls relciones enre fuerz, meri y moimieno. En ese cpíulo y el siguiene esudiremos l cinemáic, es decir, l pre de l mecánic que describe el moimieno. Después eremos l dinámic: l relción enre el moimieno y sus cuss. En ese cpíulo nos concenrmos en el ipo de moimieno más simple: un cuerpo que ij en líne rec. Pr describir ese moimieno, inroducimos ls cniddes físics elocidd y celerción, ls cules en físic ienen definiciones sencills; unque son más preciss y lgo disins de ls empleds en el lenguje coidino. Un speco imporne de ls definiciones de elocidd y celerción en físic es que les cniddes son ecores. Como imos en el cpíulo 1, eso signific que ienen no mgniud como dirección. Aquí nos ineres sólo el moimieno recilíneo, por lo que no necesiremos ún od el álgebr ecoril; no obsne, el uso de ecores será esencil en el cpíulo 3, l considerr el moimieno en dos o res dimensiones. Desrrollremos ecuciones sencills pr describir el moimieno recilíneo en el imporne cso en que l celerción es consne. Un ejemplo es el moimieno de un objeo en cíd libre. Tmbién considerremos siuciones en ls que l celerción rí durne el moimieno. En esos csos hbrá que inegrr pr describir el moimieno. (Si no h esudido inegrción ún, l sección 2.6 es opcionl.) 36
2 2.1 Desplzmieno, iempo y elocidd medi Supong que un piloo de uos de rrncones conduce su ehículo por un pis rec (figur 2.1). Pr esudir su moimieno, necesimos un sisem de coordends. Elegimos que el eje y lo lrgo de l ryecori rec del uo, con el origen en l líne de slid. Tmbién elegimos un puno en el uo, digmos su eremo delnero, y represenmos odo el ehículo con ese puno y lo rmos como un prícul. Un form úil de describir el moimieno de l prícul es decir, el puno que represen el uomóil es en érminos del cmbio en su coordend durne un inerlo de iempo. Supong que 1. s después del rrnque el frene del ehículo esá en el puno P 1, 19 m del origen, y que 4. s después del rrnque esá en el puno P 2, 277 m del origen. El desplzmieno de l prícul es un ecor que pun de P l P 2 (ése l sección 1.7). L figur 2.1 muesr que ese ecor pun lo lrgo del eje. L componene del desplzmieno es simplemene el cmbio en el lor de, (277 m 2 19 m) m, que hubo en un lpso de (4. s 2 1. s) 5 3. s. Definimos l elocidd medi del uo durne ese inerlo de iempo como un cnidd ecoril, cuy componene es el cmbio en diidido enre el inerlo de iempo: (258 m)>(3. s) 5 86 m>s. En generl, l elocidd medi depende del inerlo de iempo elegido. Durne un lpso de 3. s nes del rrnque, l elocidd medi fue cero, porque el uo esb en reposo en l líne de slid y uo un desplzmieno cero. Generlicemos el concepo de elocidd medi. En el iempo 1 el uo esá en el puno P l, con l coordend 1, y en el iempo 2 esá en el puno P 2 con l coordend 2. El desplzmieno del uo en el inerlo de 1 2 es el ecor de P l P 2. L componene del desplzmieno, denod con D, es el cmbio en l coordend : 2.1 Desplzmieno, iempo y elocidd medi 37 D (2.1) El uo de rrncones se muee sólo lo lrgo del eje, de mner que ls componenes y y z del desplzmieno son igules cero. CIUDAD El significdo de D Noe que D no es el produco de D y ; es sólo un símbolo que signific el cmbio en l cnidd. Siempre usremos l ler grieg myúscul D (del) pr represenr un cmbio en cier cnidd, clculd resndo el lor inicil del lor finl, y nunc l iners. Asimismo, el inerlo de iempo de 1 2 es D, el cmbio en l cnidd : D (iempo finl menos iempo inicil). L componene de l elocidd promedio, o elocidd medi, es l componene del desplzmieno, D, diidid enre el inerlo de iempo D en el que ocurre el desplzmieno. Usmos el símbolo med- pr represenr elocidd medi (el 2.1 Posiciones de un uo de rrncones en dos insnes durne su recorrido.
3 38 C APÍTUL 2 Moimieno en líne rec subíndice med indic que se r de un lor promedio y el subíndice indic que és es l componene ): med D D (elocidd medi, moimieno recilíneo) (2.2) En el ejemplo del uo de rrncones enímos m, m, s y s, sí que l ecución (2.2) d med m 2 19 m 4. s 2 1. s m 3. s 5 86 m /s L elocidd medi del uo es posii. Eso signific que, durne el inerlo, l coordend umenó y el uo se moió en l dirección 1 ( l derech en l figur 2.1). Si un prícul se muee en l dirección negi durne un inerlo de iempo, su elocidd medi en ese lpso es negi. Por ejemplo, supong que l cmione de un juez se muee hci l izquierd sobre l pis (figur 2.2). L cmione esá en m en s, y en m en s. Enonces, D5 (19 m m) m y D5(25. s s) 5 9. s. L componene de l elocidd medi es med- 5D>D5(2258 m)>(9. s) 5229 m>s. Hy lguns regls sencills pr l elocidd medi. Siempre que se posii y umene o se negi y se uel menos negi, l prícul se muee en l dirección 1 y med- es posii (figur 2.1). Siempre que se posii y disminuy, o se negi y se uel más negi, l prícul se muee en l dirección 2 y med- es negi (figur 2.2). CUIDAD Elección de l dirección posii No sucumb l ención de pensr que un elocidd medi posii implic necesrimene moimieno l derech, como en l figur 2.1, y un elocidd medi negi implic moimieno l izquierd, como en l figur 2.2. Tles conclusiones son correcs sólo si l dirección 1 es hci l derech, como elegimos en ls figurs 2.1 y 2.2. Igulmene podrímos hber decidido que l dirección 1 fuer hci l izquierd, con el origen en l llegd. Enonces, el uo hbrí enido elocidd medi negi; y l cmione del juez, posii. En csi odos los problems, podremos elegir l dirección del eje de coordends. Un ez omd l decisión, deberá omrse en cuen l inerprer los signos de med- y ors cniddes que describen el moimieno! En el moimieno recilíneo por lo generl llmremos D el desplzmieno y med- l elocidd medi. Sin embrgo, no olide que éss son relmene ls componenes de cniddes ecoriles que, en ese cso especil, sólo ienen componenes. En el cpíulo 3, los ecores de desplzmieno, elocidd y celerción endrán dos o res componenes disins de cero. L figur 2.3 es un gráfic de l posición del uo de rrncones en función del iempo, es decir, un gráfic -. L cur de l figur no represen l ryecori del uo; és es un líne rec, como se obser en l figur 2.1. Más bien, l gráfic es un form de represenr isulmene cómo cmbi l posición del uo con el 2.2 Posiciones de l cmione de un juez en dos insnes durne su moimieno. Los punos P 1 y P 2 hor se refieren ls posiciones de l cmione, por lo que son diferenes de ls de l figur 2.1. Posición en s Posición en s SALIDA LLEGADA P 2 P m Es posición es hor 2. D m D D Desplzmieno de 1 2 Cundo l cmione se muee en l dirección 2, D es negio y, por ende, su elocidd medi: 2258 m med m/s 9. s m Es posición es hor 1.
4 2.2 Velocidd insnáne 39 Pis de rrncones (no esá escl) 4 (m) Pr un desplzmieno lo lrgo del eje, l elocidd medi de un objeo med- es igul l pendiene de un líne que conec los punos correspondienes en un gráfic de posición () conr iempo (). 3 P 2 2 p p 1 P 1 1 Pendiene 5 elocidd D D inclinción D Pendiene 5 de l rec 5 D (s) 2.3 L posición de un uo de rrncones en función del iempo. iempo. Los punos p l y p 2 en l gráfic corresponden los punos P 1 y P 2 de l ryecori del uo. L líne p 1 p 2 es l hipoenus de un riángulo recángulo con ceo ericl D y ceo horizonl D Así, l elocidd medi del uo med- 5D>D es igul l pendiene de l líne p 1 p 2, es decir, el cociene del ceo ericl D y el ceo horizonl D. L elocidd medi depende sólo del desplzmieno ol D que se d durne el inerlo D , no en los pormenores de lo que sucede denro de ese inerlo. En el iempo 1 un moocicle podrí hber rebsdo l uo de rrncones en el puno P l de l figur 2.1, pr después reenr el moor y bjr l elocidd, psndo por P 2 en el mismo insne 2 que el uo. Ambos ehículos ienen el mismo desplzmieno en el mismo lpso, sí que ienen l mism elocidd medi. Si epresmos l disnci en meros y el iempo en segundos, l elocidd medi se mide en meros por segundo (m>s). rs uniddes de elocidd comunes son kilómeros por hor (km>h), pies por segundo (f>s), mills por hor (mi>h) y nudos (1 nudo 5 1 mill náuic>h 5 68 f>h). L bl 2.1 muesr lguns mgniudes ípics de elocidd. Elúe su comprensión de l sección 2.1 Cd uno de los siguienes ijes en uomóil dur un hor. L dirección posii es hci el ese. i) El uomóil A ij 5 km l ese. ii) El uomóil B ij 5 km l oese. iii) El uomóil C ij 6 km l ese, luego d uel y ij 1 km l oese. i) El uomóil D ij 7 km l ese. ) El uomóil E ij 2 km l oese, luego d uel y ij 2 km l ese. ) Clsifique los cinco ijes en orden de elocidd medi de más posiio más negio. b) Cuáles ijes, si hy, ienen l mism elocidd medi? c) Pr cuál ije, si hy, l elocidd medi es igul cero? 2.2 Velocidd insnáne Hy ocsiones en que l elocidd medi es lo único que necesimos sber cerc del moimieno de un prícul. Por ejemplo, un crrer en pis rec es en relidd un compeenci pr deerminr quién uo l myor elocidd medi, med-. Se enreg el premio l compeidor que hy recorrido el desplzmieno D de l líne de slid l de me en el inerlo de iempo más coro, D (figur 2.4). Sin embrgo, l elocidd medi de un prícul durne un inerlo de iempo no nos indic con qué rpidez, o en qué dirección, l prícul se esb moiendo en un insne ddo del inerlo. Pr describir el moimieno con myor delle, necesimos definir l elocidd en culquier insne específico o puno específico del cmino. És es l elocidd insnáne, y debe definirse con cuiddo. Tbl 2.1 Mgniudes ípics de elocidd Repr de crcol Andr rápido Hombre más rápido Gueprdo en crrer Auomóil más rápido Moimieno leorio de moléculs de ire Aión más rápido Sélie de comunicción en órbi 3 m/s Elecrón en un áomo de hidrógeno Luz que ij en el cío 1 23 m/s 2 m/s 11 m/s 35 m/s 341 m/s 5 m/s 1 m/s m/s m/s 2.4 El gndor de un crrer de nción de 5 m es el nddor cuy elocidd medi eng l myor mgniud, es decir, quien cubr el desplzmieno D de 5 m en el iempo rnscurrido D más coro. CUIDAD Cuáno iempo dur un insne? Noe que l plbr insne iene un significdo un poco disino en físic que en el lenguje coidino. Podemos uilizr l frse duró sólo un insne pr referirnos lgo que duró un inerlo de iempo muy coro. Sin embrgo, en físic un insne no iene durción; es un solo lor de iempo.
5 4 C APÍTUL 2 Moimieno en líne rec 2.5 Incluso l nzr, l elocidd insnáne de ese ciclis puede ser negi: si esá ijndo en l dirección negi. En culquier problem, nosoros decidimos cuál dirección es posii y cuál es negi. Pr obener l elocidd insnáne del uo de l figur 2.1 en el puno P 1, moemos el segundo puno P 2 cd ez más cerc del primer puno P 1 y clculmos l elocidd medi med- 5D>D pr esos desplzmienos y lpsos cd ez más coros. Tno D yd se hcen muy pequeños; pero su cociene no necesrimene lo hce. En el lenguje del cálculo, el límie de D>D cundo D se cerc cero es l derid de con respeco y se escribe d>d. L elocidd insnáne es el límie de l elocidd medi conforme el inerlo de iempo se cerc cero; es igul l s insnáne de cmbio de posición con el iempo. Usmos el símbolo, sin med en el subíndice, pr l elocidd insnáne en el eje : D 5 lím DS D 5 d d (elocidd insnáne, moimieno recilíneo) (2.3) Siempre suponemos que D es posiio, sí que iene el mismo signo lgebrico que D. Un lor posiio de indic que umen y el moimieno es en l dirección posii; un lor negio de indic que disminuye y el moimieno es en l dirección negi. Un cuerpo puede ener posiio y negi, o l reés; nos dice dónde esá el cuerpo, en no que nos indic cómo se muee (figur 2.5). L elocidd insnáne, igul que l elocidd medi, es un cnidd ecoril. L ecución (2.3) define su componene. En el moimieno recilíneo, ls demás componenes de l elocidd insnáne son cero y, en ese cso, llmremos simplemene elocidd insnáne. (En el cpíulo 3 eremos el cso generl en el que l elocidd insnáne puede ener componenes, y y z disins de cero.) Al usr el érmino elocidd, siempre nos referiremos l elocidd insnáne, no l medi. Los érminos elocidd y rpidez se usn indisinmene en el lenguje coidino; no obsne, en físic ienen diferene significdo. Rpidez deno disnci recorrid diidid enre iempo, con un régimen medio o insnáneo. Usremos el símbolo (sin subíndice) pr denor l rpidez insnáne, que mide qué n rápido se muee un prícul; l elocidd insnáne mide con qué rpidez y en qué dirección se muee. Por ejemplo, un prícul con elocidd insnáne 5 25 m>s y or con 5225 m>s se mueen en direcciones opuess con l mism rpidez insnáne de 25 m>s. L rpidez insnáne es l mgniud de l elocidd insnáne, sí que no puede ser negi. CUIDAD Rpidez medi y elocidd medi L rpidez medi, sin embrgo, no es l mgniud de l elocidd medi. Cundo Alender Popo esbleció un récord mundil en 1994 ndndo 1. m en s, su rpidez medi fue de (1. m)>(46.74 s) m>s. No obsne, como ndó dos eces l longiud de un lberc de 5 m, erminó en el puno de donde prió, con un desplzmieno ol de cero y un elocidd medi de cero! Tno l rpidez medi como l rpidez insnáne son esclres, no ecores, porque no conienen informción de dirección. Ejemplo 2.1 Velociddes medi e insnáne Un gueprdo cech 2 m l ese del escondie de un obserdor (figur 2.6). En el iempo 5, el gueprdo c un nílope y empiez correr en líne rec. Durne los primeros 2. s del que, l coordend del gueprdo rí con el iempo según l ecución 52 m 1 (5. m>s 2 ) 2. ) beng el desplzmieno del gueprdo enre s y s. b) Clcule l elocidd medi en dicho inerlo. c) Clcule l elocidd insnáne en s omndo D5.1 s, luego D5.1 s, luego D5.1 s. d) Deduzc un epresión generl pr l elocidd insnáne en función del iempo, y con ell clcule en 51. s y 52. s.
6 2.2 Velocidd insnáne 41 SLUCIÓN IDENTIFICAR: Ese problem requiere usr ls definiciones de desplzmieno, elocidd medi y elocidd insnáne. El uso de ls dos primers implic álgebr; l úlim requiere cálculo pr derir. PLANTEAR: L figur 2.6b muesr el moimieno del gueprdo. Pr nlizr ese problem, usmos l ecución (2.1) del desplzmieno, l ecución (2.2) de l elocidd medi y l ecución (2.3) de l elocidd insnáne. EJECUTAR: ) En l 5 1. s, l posición l del gueprdo es m m/s s m En s, su posición 2 es m m/s s m El desplzmieno en ese inerlo es D m 2 25 m 5 15 m b) L elocidd medi durne ese inerlo es med m 2 25 m s 2 1. s 5 15 m 1. s 5 15 m /s L elocidd medi durne esos inerlos es med m 2 25 m m/s 1.1 s 2 1. s Sig ese méodo pr clculr ls elociddes medis de los inerlos de.1 s y.1 s. Los resuldos son 1.5 m>s y 1.5 m>s. Al disminuir D, l elocidd medi se cerc 1. m>s, por lo que concluimos que l elocidd insnáne en 51. s es de 1. m>s. d) Al clculr l elocidd insnáne en función del iempo, derie l epresión de con respeco. L derid de un consne es cero, y pr culquier n l derid de n es n n21, sí que l derid de 2 es 2. Por lo no, 5 d d m /s m/s 2 2 En 51. s, 5 1 m>s, como imos en el inciso c). En 52. s, 5 2 m>s. EVALUAR: Nuesros resuldos muesrn que el gueprdo umenó su rpidez de 5 (cundo esb en reposo) 51. s ( 5 1 m>s) 52. s ( 5 2 m>s), lo cul es rzonble: el gueprdo recorrió sólo 5 m durne el inerlo s; sin embrgo, recorrió 15 m en el inerlo 51. s 52. s. c) Con D5.1 s, el inerlo es de s s. En 2, l posición es m m/s s m 2.6 Un gueprdo gzpdo en un rbuso c un nílope. Los nimles no esán l mism escl que el eje.
7 42 C APÍTUL 2 Moimieno en líne rec N L I N E 1.1 Análisis del moimieno usndo digrms bención de l elocidd en un gráfic - L elocidd de un prícul mbién puede obenerse de l gráfic de l posición de l prícul en función del iempo. Supong que queremos conocer l elocidd del uo de l figur 2.1 en P l. En l figur 2.1, conforme P 2 se cerc P 1, el puno p 2 en l gráfic - de ls figurs 2.7 y 2.7b se cerc l puno p 1 y l elocidd medi se clcul en inerlos D cd ez más coros. En el límie D S, ilusrdo en l figur 2.7c, l pendiene de l líne p 1 p 2 es igul l pendiene de l líne ngene l cur en el puno p 1. Así, en un gráfic de posición en función del iempo pr moimieno recilíneo, l elocidd insnáne en culquier puno es igul l pendiene de l ngene l cur en ese puno. Si l ngene l cur - sube hci l derech, como en l figur 2.7c, enonces su pendiene es posii, l elocidd es posii y el moimieno es en l dirección 1. Si l ngene bj hci l derech, l pendiene de l gráfic - y l elocidd son negis, y el moimieno es en l dirección 2. Cundo l ngene es horizonl, l pendiene y l elocidd son cero. L figur 2.8 ilusr ls res posibiliddes. L figur 2.8 muesr el moimieno de un prícul en dos forms: como ) un gráfic - y como b) un digrm de moimieno que muesr l posición de l prícul en diersos insnes, como cudros de un filme o ideo del moimieno de l 2.7 Uso de un gráfic - l ir de ), b) elocidd medi c) elocidd insnáne. En c) obenemos l pendiene de l ngene l cur - diidiendo culquier inerlo ericl (con uniddes de disnci) lo lrgo de l ngene enre el inerlo horizonl correspondiene (con uniddes de iempo). ) b) c) (m) D 5 2. s D 5 15 m med m/s p 2 p 1 D D (s) Cundo l elocidd medi med- es clculd en inerlos cd ez más coros... (m) D 5 1. s D 5 55 m med m/s p 1 p 2 D D su lor med- 5 D/D se cerc l elocidd insnáne. (s) (m) m 4. s 5 4 m/s Pendiene de l ngene 5 elocidd insnáne p 1 4. s 16 m (s) L elocidd insnáne en un iempo ddo es igul l pendiene de l ngene l cur - en ese iempo. 2.8 ) Gráfic - del moimieno de un prícul dd. L pendiene de l ngene en culquier puno es igul l elocidd en ese puno. b) Digrm de moimieno que muesr l posición y elocidd de l prícul en los cinco insnes rouldos en el digrm -. ) Gráfic - b) Moimieno de prículs A Pendiene cero: 5 C B D Pendiene posii:. Pendiene negi:, E A 5 B C D E 5 L prícul esá en, y se muee en l dirección 1. De A B celer, y de B C fren, y se deiene momenánemene en C. De C D celer en l dirección 2, y de D E fren en l dirección 2. Cuno más empind esá l pendiene (posii o negi) de l gráfic - de un objeo, myor será l rpidez del objeo en l dirección posii o negi.
8 2.3 Acelerción medi e insnáne 43 prícul, juno con flechs que represenn l elocidd de l prícul en cd insne. En ese cpíulo, usremos no ls gráfics - como los digrms de moimieno pr yudrle enender el moimieno. Le recomendmos dibujr un gráfic - y un digrm de moimieno como pre de l resolución de culquier problem que implique moimieno. Elúe su comprensión de l sección 2.2 L figur 2.9 es un gráfic - del moimieno de un prícul. ) rdene los lores de l elocidd de l prícul en los punos P, Q, R y S del más posiio l más negio. b) En qué punos es posii? c) En cuáles punos es negi? d) En cuáles es cero? e) rdene los lores de l rpidez de l prícul en los punos P, Q, R y S del más rápido l más leno. 2.9 Un gráfic - pr un prícul. Q P R 2.3 Acelerción medi e insnáne S Así como l elocidd describe l s de cmbio de posición con el iempo, l celerción describe l s de cmbio de elocidd con el iempo. Al igul que l elocidd, l celerción es un cnidd ecoril. En el moimieno recilíneo, su únic componene disin de cero esá sobre el eje en que ocurre el moimieno. Como eremos, en el moimieno recilíneo l celerción puede referirse no umenr l rpidez como disminuirl. Acelerción medi Consideremos or ez el moimieno de un prícul en el eje. Supong que, en el iempo l, l prícul esá en el puno P l y iene un componene de elocidd (insnáne) 1, y en un insne poserior 2 esá en P 2 y iene un componene de elocidd 2. Así, l componene de l elocidd cmbi en D en el inerlo D Definimos l celerción medi de l prícul l moerse de P l P 2 como un cnidd ecoril cuy componene es med- igul D, el cmbio en l componene de l elocidd, diidido enre el inerlo de iempo D: med D D (celerción medi, moimieno recilíneo) (2.4) En el moimieno recilíneo lo lrgo del eje, por lo generl llmremos med- l celerción medi. (Veremos ors componenes del ecor de celerción medi en el cpíulo 3.) Si epresmos l elocidd en meros por segundo y el iempo en segundos, l celerción medi esá en meros por segundo por segundo, o bien (m>s)>s. Eso suele escribirse como m>s 2 y se lee meros por segundo l cudrdo. CUIDAD Acelerción conr elocidd No confund celerción con elocidd! L elocidd describe el cmbio de l posición de un objeo con el iempo; nos indic con qué rpidez y en qué dirección se muee el objeo. L celerción describe cómo cmbi l elocidd con el iempo; es decir, nos dice cómo cmbin l rpidez y l dirección del moimieno. Podrí ser úil recordr l frse celerción es elocidd lo que elocidd es posición. Tmbién yudrí imginrse used mismo yendo en un uomóil con el cuerpo en moimieno. Si el uo celer hci delne y umen su rpidez, used se senirí empujdo hci rás hci su sieno; si celer hci rás y disminuye su rpidez, se senirí empujdo hci delne. Si l elocidd es consne y no hy celerción, no senirí sensción lgun. (Anlizremos l cus de ess sensciones en el cpíulo 4.)
9 44 C APÍTUL 2 Moimieno en líne rec Ejemplo 2.2 Acelerción medi Un sronu sle de un ne espcil en órbi pr probr un unidd personl de mniobrs. Mienrs se muee en líne rec, su compñer bordo mide su elocidd cd 2. s prir del insne 51. s: 1. s 3. s 5. s 7. s Clcule l celerción medi y dig si l rpidez de l sronu umen o disminuye pr cd uno de esos inerlos: ) s s; b) s s; c) s 2 5 l l. s; d) s s. SLUCIÓN.8 m/s 1.2 m/s 1.6 m/s 1.2 m/s IDENTIFICAR: Necesiremos l definición de celerción medi med-. Pr clculr los cmbios en l rpidez, usremos l ide de que l rpidez es l mgniud de l elocidd insnáne. PLANTEAR: L figur 2.1 muesr nuesrs gráfics. Usmos l ecución (2.4) pr deerminr el lor de med- prir del cmbio de elocidd en cd inerlo de iempo. EJECUTAR: En l pre superior de l figur 2.1, grficmos l elocidd en función del iempo. En es gráfic -, l pendiene de l líne que conec los punos inicil y finl de cd inerlo es l celerción medi med- 5D >D pr ese inerlo. En l pre inferior de l figur 2.1, grficmos los lores de med-. benemos: ) med m/s 2.8 m/s2 /1 3. s 2 1. s2 5.2 m/s 2. L rpidez (mgniud de l elocidd insnáne) umen de.8 m>s 1.2 m>s. b) med m/s m/s2 /1 7. s 2 5. s m/s 2. L rpidez disminuye de 1.6 m>s 1.2 m>s. c) med m/s m/s24/1 11. s 2 9. s s 11. s 13. s 15. s 2.4 m/s 21. m/s 21.6 m/s 2.8 m/s 2.1 Nuesr gráfic de elocidd conr iempo (rrib) y celerción medi conr iempo (bjo) pr l sronu. L pendiene de l líne que conec cd pr de punos en l gráfic es igul l celerción medi enre esos punos. 2.3 m/s 2. L rpidez umen de.4 m>s 1. m>s. d) med m/s m/s24/1 15. s s2 5.4 m/s 2. L rpidez disminuye de 1.6 m>s.8 m>s. EVALUAR: Nuesro resuldo indic que cundo l celerción iene l mism dirección (el mismo signo lgebrico) que l elocidd inicil, como en los inerlos ) y c), l sronu se muee más rápidmene; cundo iene l dirección opues (el signo opueso) como en los inerlos b) y d), se fren. De mner que l celerción posii signific ir más rápido si l elocidd es posii [inerlo )], pero frenr si l elocidd es negi [inerlo d)]. Asimismo, celerción negi implic ir más rápido si l elocidd es negi [inerlo c)], pero frenr si l elocidd es posii [inerlo b)]. Acelerción insnáne Y podemos definir l celerción insnáne con el mismo procedimieno que seguimos pr l elocidd insnáne. Como ejemplo, supong que un piloo de crrers cb de enrr en un rec como se muesr en l figur Pr definir l celerción insnáne en P 1, ommos el segundo puno P 2 en l figur 2.11 cd ez más cerc de P 1, de modo que l celerción medi se clcule en inerlos cd ez más coros. L celerción insnáne es el límie de l celerción medi conforme el inerlo de iempo se cerc cero. En el lenguje del cálculo, l celerción insnáne es l s insnáne de cmbio de l elocidd con el iempo. Así, D 5 lím 5 d DS D d (celerción insnáne, moimieno recilíneo) (2.5) 2.11 Vehículo de Grnd Pri en dos punos de l rec. P 1 Rpidez 1 elocidd 1 P 2 Rpidez 2 elocidd 2
10 2.3 Acelerción medi e insnáne 45 bsere que l ecución (2.5) es relmene l definición de l componene del ecor de celerción o l celerción insnáne; en el moimieno recilíneo, ls demás componenes de ese ecor son cero. A prir de quí, l hblr de celerción nos referiremos siempre l celerción insnáne, no l celerción medi. Ejemplo 2.3 Acelerciones medi e insnáne Supong que l elocidd del uo en l figur 2.11 en el iempo esá dd por ) Clcule el cmbio de elocidd del uo en el inerlo enre s y s. b) Clcule l celerción medi en ese inerlo. c) beng l celerción insnáne en s omndo D primero como.1 s, después como.1 s y luego como.1 s. d) Deduzc un epresión pr l celerción insnáne en culquier insne y úsel pr obener l celerción en 5 1. s y 53. s. SLUCIÓN IDENTIFICAR: Ese ejemplo es similr l ejemplo 2.1 de l sección 2.2. (Recomendmos repsr hor ese ejemplo.) Ahí, clculmos l elocidd medi en inerlos cd ez más coros considerndo el cmbio en el desplzmieno, y obuimos l elocidd insnáne diferencindo l posición en función del iempo. En ese ejemplo, deerminremos l celerción medi considerndo cmbios de elocidd en un inerlo de iempo. Asimismo, obendremos l celerción insnáne diferencindo l elocidd en función del iempo. PLANTEAR: Usremos l ecución (2.4) de l celerción medi y l ecución (2.5) de l celerción insnáne. EJECUTAR: ) Primero obenemos l elocidd en cd insne susiuyendo cd lor de en l ecución. En el insne s, m/s m/s s m/s En el insne s, m/s m/s s m/s El cmbio en l elocidd D es 5 6 m/s m/s D m/s m/s 5 4. m/s El inerlo de iempo es D 5 3. s 2 1. s 5 2. s. b) L celerción medi durne ese inerlo es Durne el inerlo de s s, l elocidd y l celerción medi ienen el mismo signo (posiio en ese cso) y el uo celer. c) Cundo D 5.1 s, s y obenemos med- 5 D D Repi ese modelo con D 5.1 s y D 5.1 s; los resuldos son med m>s 2 y med m>s 2, respecimene. Al reducirse D, l celerción medi se cerc 1. m>s 2, por lo que concluimos que l celerción insnáne en 5 1. s es 1. m>s 2. d) L celerción insnáne es 5 d >d. L derid de un consne es cero y l derid de 2 es 2. Con eso, obenemos 5 d d Cundo 51. s, Cundo 53. s, med m /s 5 2. m/s s m/s m/s s m/s D 5.15 m/s 5.15 m /s.1 s m/s 2 5 d d 36 m /s m/s m/s m/s m/s s m/s m/s s m/s 2 EVALUAR: bsere que ninguno de los lores que obuimos en el inciso d) es igul l celerción medi obenid en b). L celerción insnáne del uo rí con el iempo. L s de cmbio de l celerción con el iempo se suele denominr el irón. bención de l celerción en un gráfic - o un gráfic - En l sección 2.2 inerpremos ls elociddes medi e insnáne en érminos de l pendiene de un gráfic de posición conr iempo. Igulmene, podemos enender mejor ls celerciones medi e insnáne grficndo l elocidd insnáne en el eje ericl y el iempo en el eje horizonl, es decir, usndo un gráfic - (figur 2.12). Los punos rouldos p 1 y p 2 corresponden los punos P l y P 2 de l figur L celerción medi med- 5D >D durne ese inerlo es l pendiene de l líne p 1 p 2. Al cercrse P 2 P 1 en l figur 2.11, p 2 se cerc p 1 en l gráfic - de l figur 2.12, y l pendiene de l líne p 1 p 2 se cerc l pendiene de l ngene l cur en el puno p 1. Así, en un gráfic de elocidd en función del iempo, l celerción insnáne en culquier puno es igul l pendiene de l ngene de l cur en ese puno. En l figur 2.12, ls ngenes rzds en
11 46 C APÍTUL 2 Moimieno en líne rec 2.12 Gráfic - del moimieno de l figur Pr un desplzmieno lo lrgo del eje, l celerción medi de un objeo es igul l pendiene de un líne que conec los punos correspondienes en un gráfic de elocidd ( ) conr iempo (). 2 1 p 1 1 Pendiene 5 celerción medi D p 2 2 D Pendiene de l ngene l cur - en un puno ddo 5 celerción insnáne en ese puno. diferenes punos en l cur ienen pendienes diferenes, de mner que l celerción insnáne rí con el iempo. CUIDAD Los signos de celerción y elocidd En sí mismo, el signo lgebrico de l celerción no nos indic si el cuerpo esá celerndo o frenndo; hy que comprr los signos de l elocidd y l celerción. Si y ienen el mismo signo, el cuerpo esá celerndo; si mbs son posiis, el cuerpo se muee en l dirección posii con rpidez creciene. Si mbs son negis, el cuerpo se muee en l dirección negi con elocidd cd ez más negi, y l rpidez umen nuemene. Si y ienen signos opuesos, el cuerpo esá frenndo. Si es posii y negi, el cuerpo se muee en dirección posii con rpidez decreciene; si es negi y posii, el cuerpo se muee en dirección negi con un elocidd cd ez menos negi, y nuemene esá frenndo. L figur 2.13 ilusr lguns de les posibiliddes. Frecuenemene llmmos descelerción un reducción de rpidez. Ddo que eso puede implicr posii o negi, dependiendo del signo de, eiremos ese érmino. Tmbién podemos conocer l celerción de un cuerpo prir de un gráfic de su posición conr iempo. Ddo que 5 d >d y 5 d>d, escribimos? 5 d d 5 d1 d d d2 5 d2 d 2 (2.6) 2.13 ) Gráfic - del moimieno de un prícul diferene de l que se muesr en l figur 2.8. L pendiene de l ngene en culquier puno es igul l celerción en ese puno. b) Digrm de moimieno que indic l posición, elocidd y celerción de l prícul en los insnes rouldos en l gráfic -. Ls posiciones son congruenes con l gráfic -; por ejemplo, de A B l elocidd es negi, sí que en B l prícul esá en un lor más negio de que en A. ) L gráfic - pr un objeo que se muee en el eje b) Posición, elocidd y celerción del objeo en el eje A B Pendiene cero: 5 C Pendiene posii:. Pendiene negi:, Cuno más empind esé l pendiene (posii o negi) de l gráfic - de un objeo, myor será l celerción del objeo en l dirección posii o negi. D E A 5 B C D E El objeo esá en, y se muee en l dirección 2 (, ), frenndo ( y ienen signos opuesos). El objeo esá en,, insnánemene en reposo ( 5 ), y puno de moerse en l dirección 1 (. ). El objeo esá en. y se muee en l dirección 1 (. ); su rpidez no cmbi insnánemene ( 5 ). El objeo esá en., insnánemene en reposo ( 5 ), y puno de moerse en l dirección 2 (, ). El objeo esá en. y se muee en l dirección 2 (, ), celerndo ( y ienen el mismo signo).
12 2.4 Moimieno con celerción consne ) L mism gráfic - de l figur 2.8. L elocidd es igul l pendiene de l gráfic, y l celerción esá dd por su concidd o curur. b) Digrm de moimieno que muesr l posición, elocidd y celerción de l prícul en cd uno de los insnes rouldos en l gráfic -. ) Gráfic - b) Moimieno del objeo A Pendiene cero: 5 Curur hci bjo:, B C D Pendiene negi:, Curur cero: 5 Pendiene posii:. Curur cero: 5 Pendiene posii:. Curur hci rrib:. Pendiene negi:, Curur hci rrib:. Cuno myor se l curur (hci rrib o hci bjo) de l gráfic - de un objeo, myor será l celerción del objeo en l dirección posii o negi. E A 5 B C D E El objeo esá en,, se muee en l dirección 1 (. ) y celer ( y ienen el mismo signo). El objeo esá en 5, se muee en l dirección 1 (. ); l rpidez no cmbi insnánemene ( 5 ). El objeo esá en., insnánemene en reposo ( 5 ) y puno de moerse en l dirección 2 (, ). El objeo esá en., se muee en l dirección 2 (, ); l rpidez no cmbi insnánemene ( 5 ). El objeo esá en., se muee en l dirección 2 (, ) y fren ( y ienen signos opuesos). Es decir, es l segund derid de con respeco. L segund derid de culquier función se relcion direcmene con l concidd o curur de l gráfic de l función. En un puno donde l cur - se cónc hci rrib (curd hci rrib), l celerción es posii y umen; donde l cur - se cónc hci bjo, l celerción es negi y disminuye. Donde l gráfic - no eng curur, como en un puno de infleión, l celerción es cero y l elocidd es consne. Ess res posibiliddes se ilusrn en l figur Eminr l curur de un gráfic - es un mner sencill de decidir qué signo iene l celerción. Es écnic es menos úil pr deerminr lores numéricos de l celerción, y que es difícil medir con eciud l curur de un gráfic. Elúe su comprensión de l sección 2.3 bsere or ez l gráfic - de l figur 2.9 l finl de l sección 2.2. ) En cuál de los punos P, Q, R y S l celerción es posii? b) En cuáles es negi? c) En cuáles prece ser cero? d) En cd puno decid si l rpidez umen, disminuye o se mniene consne. 2.4 Moimieno con celerción consne El moimieno celerdo más sencillo es el recilíneo con celerción consne. En ese cso, l elocidd cmbi l mismo rimo odo el iempo. Se r de un siución muy especil, un cundo ocurre menudo en l nurlez; un cuerpo que ce iene celerción consne si los efecos del ire no son impornes. Lo mismo sucede con un cuerpo que se desliz por un pendiene o sobre un superficie horizonl ásper. El moimieno recilíneo con celerción csi consne se d mbién en l ecnologí, como cundo un je de combe es lnzdo con cpul desde l cubier de un poriones. L figur 2.15 es un digrm de moimieno que muesr l posición, elocidd y celerción de un prícul que se muee con celerción consne. Ls figurs 2.16 y 2.17 represenn ese moimieno con gráfics. Pueso que l celerción es consne, l gráfic - (celerción conr iempo) de l figur 2.16 es un líne horizonl. L gráfic de elocidd conr iempo, -, iene pendiene consne porque l celerción es consne; por lo no, es un líne rec (figur 2.17) Digrm de moimieno pr un prícul que se muee en líne rec en l dirección 1 con celerción posii consne. Se muesrn l posición, elocidd y celerción en cinco insnes equiespcidos. D 2D 3D 4D Si un prícul se muee en líne rec con celerción consne l elocidd cmbi cniddes igules en inerlos igules. Sin embrgo, l posición cmbi cniddes diferenes en inerlos igules porque l elocidd cmbi.
13 48 C APÍTUL 2 Moimieno en líne rec 2.16 Gráfic celerción-iempo ( -) pr moimieno recilíneo con celerción posii consne. Acelerción consne: l gráfic - es un líne horizonl (pendiene 5 ). Cundo l celerción es consne, l celerción medi med- pr culquier inerlo es. Eso uele sencillo derir ls ecuciones pr l posición y l elocidd como funciones del iempo. Pr enconrr un epresión pr primero susiuimos med- por en l ecución (2.4): Sen hor l 5 y 2 culquier insne poserior. Simbolizmos con l componene de l elocidd en el insne inicil 5; l componene de l elocidd en el insne poserior es. Enonces, l ecución (2.7) se coniere en (2.7) El áre bjo l gráfic - es 2 5 cmbio de elocidd del iempo l iempo o 5 1 (sólo con celerción consne) (2.8) 2.17 Gráfic elocidd-iempo ( -) pr moimieno recilíneo con celerción posii consne. L elocidd inicil mbién es posii en ese cso. Acelerción consne: l gráfic - es un rec. Pendiene 5 celerción Durne el inerlo, l elocidd cmbi como 2 5. El áre ol bjo l gráfic - es 2 5 cmbio en l coordend del iempo l iempo. Podemos inerprer l ecución como sigue. L celerción es l s consne de cmbio de elocidd, es decir, el cmbio en l elocidd por unidd de iempo. El érmino es el produco del cmbio en l elocidd por unidd de iempo,, y el inerlo de iempo ; por lo no, es el cmbio ol de l elocidd desde el insne inicil 5 hs un insne poserior. L elocidd en culquier insne es enonces l elocidd inicil (en 5) más el cmbio en l elocidd (ése l figur 2.17). r inerpreción de l ecución (2.8) es que el cmbio de elocidd 2 de l prícul enre 5 y un iempo poserior es igul l áre bjo l gráfic - enre esos dos insnes. En l figur 2.16, el áre bjo l gráfic - es el recángulo erde con ldo ericl y ldo horizonl. El áre del recángulo es, que por l ecución (2.8) es igul l cmbio en elocidd 2. En l sección 2.6 eremos que un cundo l celerción no se consne, el cmbio de elocidd durne un inerlo es igul l áre bjo l cur -, unque en l cso l ecución (2.8) no es álid. Ahor deduciremos un ecución pr l posición en función del iempo cundo l celerción es consne. Pr ello, usmos dos epresiones disins pr l elocidd medi med- en el inerlo de 5 culquier poserior. L primer proiene de l definición de med-, ecución (2.2), que se cumple se consne o no l celerción. L posición inicil es l posición en 5, denod con. L posición en el poserior es simplemene. Así, pr el inerlo D5 2 y el desplzmieno D 5 2, l ecución (2.2) d med- 5 2 (2.9) N L I N E 1.1 Análisis del moimieno con digrms 1.2 Análisis del moimieno con gráfics 1.3 Predicción de un moimieno con bse en gráfics 1.4 Predicción de un moimieno con bse en ecuciones 1.5 Esregis pr resoler problems de cinemáic 1.6 Esquidor en compeenci de descenso Tmbién podemos obener or epresión pr med- que se álid sólo si l celerción es consne, de modo que l gráfic - se un líne rec (como en l figur 2.17) y l elocidd cmbie rimo consne. En ese cso, l elocidd medi en culquier inerlo es sólo el promedio de ls elociddes l principio y l finl del inerlo. Pr el inerlo de, med (sólo con celerción consne) (2.1) (Eso no se cumple si l celerción rí y l gráfic - es un cur, como en l figur 2.13.) Tmbién sbemos que, con celerción consne, l elocidd en un insne esá dd por l ecución (2.8). Susiuyendo es epresión por en l ecución (2.1), med (sólo con celerción consne) (2.11)
14 2.4 Moimieno con celerción consne 49 Por úlimo, igulmos ls ecuciones (2.9) y (2.11) y simplificmos el resuldo: o (sólo con celerción consne) (2.12) Es ecución (2.12) indic que si, en el insne 5, un prícul esá en y iene elocidd, su nue posición en un poserior es l sum de res érminos: su posición inicil, más l disnci que recorrerí si su elocidd fuer consne, y un disnci dicionl 2 2 cusd por el cmbio de elocidd. 1 Un gráfic de l ecución (2.12), es decir, un gráfic - pr moimieno con celerción consne (figur 2.18), siempre es un prábol. L figur 2.18b muesr l gráfic. L cur inersec el eje ericl () en, l posición en 5. L pendiene de l ngene en 5 es, l elocidd inicil, y l pendiene de l ngene en culquier es l elocidd en ese insne. L pendiene y l elocidd umenn coninumene, sí que l celerción es posii. Used puede mbién er eso porque l gráfic de l figur 2.18b es cónc hci rrib (se cur hci rrib). Si es negi, l gráfic - es un prábol cónc hci bjo (iene curur hci bjo). Si hy celerción cero, l gráfic - es un rec; si hy un celerción consne, el érmino dicionl 2 2 en l ecución (2.12) pr en función de cur l 1 gráfic en un prábol (figur 2.19). Podemos nlizr l gráfic - de l mism form. Si hy celerción cero, es gráfic es un líne horizonl (l elocidd es consne); sumr un celerción consne d un pendiene pr l gráfic - (figur 2.19b). N L I N E 1.8 Los cinurones de seguridd sln ids 1.9 Frendo con derrpe 1.1 Auo rrnc y luego se deiene 1.11 Resolución de problems con dos ehículos 1.12 Auo lcnz cmión 1.13 Cómo eir un choque por rás ) Un uo de crrers se muee en l dirección con celerción consne 5 1 Durne el inerlo, l elocidd cmbi como 2 5. b) L gráfic - Pendiene 5 Acelerción consne: l gráfic - es un prábol ) Moimieno recilíneo con celerción consne. b) Un gráfic de posición conr iempo (-) pr ese moimieno (el mismo moimieno que se muesr en ls figurs 2.15, 2.16 y 2.17). En ese cso, l posición inicil, l elocidd inicil y l celerción son ods posiis. Pendiene ) Cómo un celerción consne influye en ) l gráfic - y b) l gráfic - de un cuerpo.
15 5 C APÍTUL 2 Moimieno en líne rec Así como el cmbio de elocidd de l prícul es igul l áre bjo l gráfic -, el desplzmieno (es decir, el cmbio de posición) es igul l áre bjo l gráfic -. Específicmene, el desplzmieno 2 de l prícul enre 5 y culquier insne poserior es igul l áre bjo l cur - enre esos dos insnes. En l figur 2.17 el áre bjo l gráfic se diidió en un recángulo oscuro con ldo ericl, ldo horizonl y un riángulo recángulo clro con ldo ericl y 1 ldo horizonl. El áre del recángulo es, y l del riángulo, , sí que el áre ol bjo l cur - es lo que concuerd con l ecución (2.12). El desplzmieno durne un inerlo siempre puede obenerse del áre bjo l cur -, incluso si l celerción no es consne, unque en l cso l ecución (2.12) no serí álid. (Demosrremos eso en l sección 2.6.) Podemos comprobr si ls ecuciones (2.8) y (2.12) son congruenes con el supueso de celerción consne derindo l ecución (2.12). benemos 5 d d 5 1 que es l ecución (2.8). Diferencindo or ez, enemos simplemene d d 5 que concuerd con l definición de celerción insnáne. Con frecuenci es úil ener un relción enre posición, elocidd y celerción (consne) que no incluy el iempo. Pr obenerl, despejmos en l ecución (2.8), susiuimos l epresión resulne en l ecución (2.12) y simplificmos: Trnsferimos el érmino l miembro izquierdo y muliplicmos l ecución por 2 : Por úlimo, l simplificr obenemos (sólo con celerción consne) (2.13) Podemos obener un relción más úil igulndo dos epresiones pr med-, ecuciones (2.9) y (2.1), y muliplicndo por. Al hcerlo, obenemos (sólo celerción consne) (2.14) bsere que l ecución (2.14) no coniene l celerción. Es ecución es úil cundo es consne pero se desconoce su lor.
16 2.4 Moimieno con celerción consne 51 Ls ecuciones (2.8), (2.12), (2.13) y (2.14) son ls ecuciones del moimieno con celerción consne. Con ells, podemos resoler culquier problem que implique moimieno recilíneo de un prícul con celerción consne. En el cso específico de moimieno con celerción consne ilusrdo en l figur 2.15 y grficdo en ls figurs 2.16, 2.17 y 2.18, los lores de, y son posiios. Vuel dibujr ls figurs pr los csos en que un, dos o ls res cniddes sen negis. Un cso especil de moimieno con celerción consne se d cundo l celerción es cero. L elocidd es enonces consne, y ls ecuciones del moimieno se conieren sencillmene en 5 5 consne 5 1 Esregi pr resoler problems 2.1 Moimieno con celerción consne IDENTIFICAR los concepos perinenes: En csi odos los problems de moimieno recilíneo, used podrá usr ls ecuciones de celerción consne, unque eces se oprá con siuciones en que l celerción no es consne. En les csos, necesirá or esregi (ése l sección 2.6). PLANTEAR el problem siguiendo esos psos: 1. Primero decid dónde esá el origen de ls coordends y cuál dirección es posii. A menudo lo más sencillo es colocr l prícul en el origen en 5; sí, 5. Siempre es úil un digrm de moimieno que muesre ls coordends y lguns posiciones poseriores de l prícul. 2. Recuerde que elegir l dirección posii del eje deermin uomáicmene ls direcciones posiis de l elocidd y l celerción. Si es posii l derech del origen, y mbién serán posiis hci l derech. 3. Replnee el problem con plbrs y luego rduzc su descripción símbolos y ecuciones. Cuándo lleg l prícul ciero puno (es decir, cuáno le )? Dónde esá l prícul cundo iene cier elocidd (eso es, cuáno le cundo iene ese lor)? El ejemplo 2.4 pregun Dónde esá el moociclis cundo su elocidd es de 25 m>s? En símbolos, eso indic Cuáno le cundo 5 25 m>s? 4. Hg un lis de ls cniddes como,,,, y. En generl, lguns serán conocids y ors no. Escrib los lores de ls conocids y decid cuáles de ls ribles son ls incógnis. No pse por lo informción implíci. Por ejemplo, un uomóil esá prdo ne un semáforo implic 5. EJECUTAR l solución: Elij un de ls ecuciones (2.8), (2.12), (2.13) y (2.14) que coneng sólo un de ls incógnis. Despeje l incógni usndo sólo símbolos, susiuy los lores conocidos y clcule el lor de l incógni. A eces endrá que resoler dos ecuciones simulánes con dos incógnis. EVALUAR l respues: Emine sus resuldos pr er si son lógicos. Esán denro del inerlo generl de lores esperdo? Ejemplo 2.4 Cálculos de celerción consne Un moociclis que ij l ese cruz un pequeñ ciudd de Iow y celer pens ps el lerero que mrc el límie de l ciudd (figur 2.2). Su celerción consne es de 4. m>s 2. En 5, esá 5. m l ese del lerero, moiéndose l ese 15 m>s. ) Clcule su posición y elocidd en 52. s. b) Dónde esá el moociclis cundo su elocidd es de 25 m>s? 2.2 Un moociclis que ij con celerción consne. SAGE AW 5 5. m m/s 5 4. m/s AW 5? 5 2. s 5? (ese) SLUCIÓN IDENTIFICAR: El enuncido del problem nos dice que l celerción es consne, sí que podemos usr ls ecuciones pr celerción consne. PLANTEAR: Tommos el lerero como origen de coordends ( 5 ) y decidimos que el eje 1 pun l ese (figur 2.2, que mbién es un digrm de moimieno). En 5, l posición inicil es 5 5. m y l elocidd inicil es 5 15 m>s. L celerción consne es 5 4. m>s 2. Ls ribles desconocids en el inciso ) son los lores de l posición y l elocidd en el insne poserior 52. s; l incógni en el inciso b) es el lor de cundo 5 25 m>s. coninú
17 PLICE hp://libreri-uniersiri.blogspo.com 52 C APÍTUL 2 Moimieno en líne rec EJECUTAR: ) Podemos hllr l posición en 52. s usndo l ecución (2.12) que d l posición en función del iempo : m m/s21 2. s m /s s m Podemos hllr l elocidd en ese insne con l ecución (2.8), que d l elocidd en función del iempo : m/s m/s s m/s b) Queremos enconrr el lor de cundo 5 25 m>s, pero no sbemos el momeno en que el moociclis lle l elocidd. Por lo no, uilizmos l ecución (2.13), que incluye, y pero no incluye : Despejndo y susiuyendo los lores conocidos, obenemos m m /s m/s m m/s 2 2 Un méodo lerno unque más lrgo pr l mim respues serí usr l ecución (2.8) pr erigur primero en qué insne 5 25 m>s: Ddo el iempo, podemos clculr usndo l ecución (2.12): m m/s s m /s s m sí que 5 25 m /s 2 15 m/s 4. m/s s EVALUAR: Son lógicos los resuldos? Según lo que clculmos en el inciso ), el moociclis celer de 15 m>s (uns 34 mi>h o 54 km>h) 23 m>s (uns 51 mi>h o 83 km>h) en 2. s, mienrs recorre un disnci de 38 m (unos 125 f). És es un celerción considerble, pero un moocicle de lo rendimieno bien puede lcnzrl. Al comprr nuesros resuldos del inciso b) con los del inciso ), nomos que el moociclis lcnz un elocidd 5 25 m>s en un insne poserior y después de recorrer un disnci myor, que cundo el moociclis ení 5 23 m>s. Eso suen lógico porque el moociclis iene un celerción posii y, por ende, se incremen su elocidd. Ejemplo 2.5 Dos cuerpos con diferene celerción Un conducor que ij rpidez consne de 15 m>s (uns 34 mi>h) ps por un cruce escolr, cuyo límie de elocidd es de 1 m>s (uns 22 mi>h). En ese preciso momeno, un oficil de policí en su moocicle, que esá prdo en el cruce, rrnc pr perseguir l infrcor, con celerción consne de 3. m>s 2 (figur 2.21). ) Cuáno iempo ps nes de que el oficil de policí lcnce l infrcor? b) A qué rpidez el policí en ese insne? c) Qué disnci ol hbrá recorrido cd ehículo hs hí? SLUCIÓN IDENTIFICAR: El oficil de policí y el conducor se mueen con celerción consne (cero en el cso del conducor), sí que podemos usr ls fórmuls que y dedujimos. PLANTEAR: Tommos como origen el cruce, sí que 5 pr mbos, y ommos como dirección posii l derech. Se P l posición del policí y M l del conducor en culquier insne. Ls elociddes iniciles son P 5 pr el policí y M 5 15 m>s pr el conducor; ls respecis celerciones consnes son P 5 3. m>s 2 y M 5. Nuesr incógni en el inciso ) es el iempo rs el cul el policí lcnz l conducor, es decir, cundo los dos ehículos esán en l mism posición. En el inciso b) nos ineres l rpidez del policí (l mgniud de su elocidd) en el iempo obenido en el inciso ). En el inciso c) nos ineres l posición de culesquier de los ehículos en ese iempo. Por lo no, usremos l ecución (2.12) (que relcion posición y iempo) en los 2.21 ) Moimieno con celerción consne que lcnz moimieno con elocidd consne. b) Gráfic de conr pr cd ehículo. ) CRUCE ESCLAR ficil de policí: inicilmene en reposo, celerción consne. P P 5 3. m/s 2 Conducor: elocidd consne. M M 5 15 m/s b) (m) 8 El policí y el conducor se encuenrn en el insne donde se cruzn sus gráfics -. Conducor 4 Policí (s)
t el espacio recorrido por los dos coches es el mismo t t 300; t 20s (20 10) 600m
 0. Un cuerpo pre del reposo y se muee con celerción consne. En un momeno ddo iene un elocidd de 9,4 m/s, y 48,8 meros más lejos lle un elocidd de 5, m/s. Clcul: ) L celerción. b) El iempo empledo en recorrer
0. Un cuerpo pre del reposo y se muee con celerción consne. En un momeno ddo iene un elocidd de 9,4 m/s, y 48,8 meros más lejos lle un elocidd de 5, m/s. Clcul: ) L celerción. b) El iempo empledo en recorrer
a) en vertical el movimiento es uniforme 400 t 40s b) en ese tiempo, en horizontal e v t 320m c) el ángulo, respecto a la vertical es v v rio
 0. Ls gus de un río de 400 m de nchur se desplzn con un elocidd de 8 m/s. Un brc cruz el río de orill orill, mneniéndose perpendiculr l corriene. L brc se muee con un elocidd consne de 0 m/s. Clculr: )
0. Ls gus de un río de 400 m de nchur se desplzn con un elocidd de 8 m/s. Un brc cruz el río de orill orill, mneniéndose perpendiculr l corriene. L brc se muee con un elocidd consne de 0 m/s. Clculr: )
SOSTENIBILIDAD DE UNA POLÍTICA FISCAL
 1 SOSTENIBILIDAD DE UNA POLÍTICA FISCAL Definición de un políic fiscl sosenible El concepo de políic fiscl sosenible no cep un definición precis. Sin embrgo, un definición generl (unque lgo rivil) es que
1 SOSTENIBILIDAD DE UNA POLÍTICA FISCAL Definición de un políic fiscl sosenible El concepo de políic fiscl sosenible no cep un definición precis. Sin embrgo, un definición generl (unque lgo rivil) es que
Guía de Movimiento Rectilíneo Uniformemente Variado
 Experienci demori DEPARTAMENTO DE FÍSICA Guí de Moimieno Recilíneo Uniformemene Vrido 1) Ver lo ideo que e encuenrn en lo iguiene link pr poder reponder l pregun que e encuenrn coninución hp://www.youube.com/wch?=lmfbwzjyml0
Experienci demori DEPARTAMENTO DE FÍSICA Guí de Moimieno Recilíneo Uniformemene Vrido 1) Ver lo ideo que e encuenrn en lo iguiene link pr poder reponder l pregun que e encuenrn coninución hp://www.youube.com/wch?=lmfbwzjyml0
1. CINEMÁTICA DE LA PARTÍCULA
 . CINEMÁTICA DE LA PARTÍCULA. Moimieno recilíneo.. Poición en función del iempo. L poición de un prícul que decribe un líne rec qued definid medine l epreión = / 9 +, donde i eá en, reul en m. Deermine:
. CINEMÁTICA DE LA PARTÍCULA. Moimieno recilíneo.. Poición en función del iempo. L poición de un prícul que decribe un líne rec qued definid medine l epreión = / 9 +, donde i eá en, reul en m. Deermine:
Concluimos que el concepto de movimiento es relativo. Por lo tanto para describir el movimiento de un cuerpo debemos especificar con respecto a qué.
 CAPÍTULO 1 MOVIMIENTO EN UNA DIMENSIÓN L Mecánic Clásic o Newonin esudi el moimieno de los cuerpos con elociddes mucho menores que l elocidd de l luz. Se diide en dos pres, cinemáic y dinámic. L cinemáic
CAPÍTULO 1 MOVIMIENTO EN UNA DIMENSIÓN L Mecánic Clásic o Newonin esudi el moimieno de los cuerpos con elociddes mucho menores que l elocidd de l luz. Se diide en dos pres, cinemáic y dinámic. L cinemáic
ˆ ˆ. FÍSICA 100 CERTAMEN # 2 Forma R 12 de junio de La pirámide de la figura está definida por los vectores a, b y
 FÍSICA 1 CERAMEN # Form R 1 de junio de 1 A. AERNO A. MAERNO NOMBRE ROL USM - Si su rol comienz con 9 coloque 9 ESE CERAMEN CONSA DE REGUNAS EN 8 ÁGINAS. IEMO: 15 MINUOS SIN CALCULADORA. SIN ELÉFONO CELULAR
FÍSICA 1 CERAMEN # Form R 1 de junio de 1 A. AERNO A. MAERNO NOMBRE ROL USM - Si su rol comienz con 9 coloque 9 ESE CERAMEN CONSA DE REGUNAS EN 8 ÁGINAS. IEMO: 15 MINUOS SIN CALCULADORA. SIN ELÉFONO CELULAR
Fuerza y Movimiento. I. Movimiento de un carro con ventilador ignorando la fricción
 Fuerz y Moimieno I. Moimieno de un crro con enildor ignorndo l fricción En los siguienes experimenos, uilizrá el sensor de moimieno y un crro de bj fricción. L dirección posii es lejándose del sensor.
Fuerz y Moimieno I. Moimieno de un crro con enildor ignorndo l fricción En los siguienes experimenos, uilizrá el sensor de moimieno y un crro de bj fricción. L dirección posii es lejándose del sensor.
PRÁCTICA 3 LEYES DE NEWTON
 Fundmenos Físicos de l Inenierí Inenierí Indusril Prácics de Lbororio PRÁCTIC 3 LEYES DE NEWTON 3 OJETIVO- Deerminr ls leyes que rien l relciones espcio-iempo y velocidd-iempo en movimienos uniformemene
Fundmenos Físicos de l Inenierí Inenierí Indusril Prácics de Lbororio PRÁCTIC 3 LEYES DE NEWTON 3 OJETIVO- Deerminr ls leyes que rien l relciones espcio-iempo y velocidd-iempo en movimienos uniformemene
MOVIMIENTO EN LÍNEA RECTA
 2 MVIMIENT EN LÍNEA RECTA METAS DE APRENDIZAJE Al esudiar ese capíulo, used aprenderá: Cómo describir el moimieno en línea reca en érminos de elocidad media, elocidad insanánea, aceleración media y aceleración
2 MVIMIENT EN LÍNEA RECTA METAS DE APRENDIZAJE Al esudiar ese capíulo, used aprenderá: Cómo describir el moimieno en línea reca en érminos de elocidad media, elocidad insanánea, aceleración media y aceleración
MOVIMIENTO CIRCULAR. r en cualquier punto de su trayectoria. v 2 / R
 MOVIMIENTO CIRCULAR Es un ipo de movimieno en el plno, en el cul l pícul gi un disnci fij lededo de un puno llmdo ceno. El movimieno cicul puede se de dos ipos: Movimieno cicul unifome Movimieno cicul
MOVIMIENTO CIRCULAR Es un ipo de movimieno en el plno, en el cul l pícul gi un disnci fij lededo de un puno llmdo ceno. El movimieno cicul puede se de dos ipos: Movimieno cicul unifome Movimieno cicul
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.1. Límites de integración infinitos 9.2. Integrales con integrando que tiende a infinito 9.3. Observaciones a las
 CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS
 SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
12_02_18_Soluciones unidad 2: Las fuerzas 4º ESO 1
 1_0_18_Soluciones unidd : Ls fuerzs 4º ESO 1 SOLUCIOES UIDAD. LAS UERZAS QUÉ SABES DE ESTO? 1. Se lnz un blón vericlmene y hci rrib. )Cuál de los dos esquems djunos describe mejor ls fuerzs que cún sobre
1_0_18_Soluciones unidd : Ls fuerzs 4º ESO 1 SOLUCIOES UIDAD. LAS UERZAS QUÉ SABES DE ESTO? 1. Se lnz un blón vericlmene y hci rrib. )Cuál de los dos esquems djunos describe mejor ls fuerzs que cún sobre
MATRICES Y DETERMINANTES.
 punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
FUNCIONES VECTORIALES
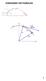 FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
MOVIMIENTO RECTILÍNEO
 MVIMIENT RECTILÍNE 2 BJETIVS DE APRENDIZAJE Al esudiar ese capíulo, used aprenderá: Cómo describir el moimieno recilíneo en érminos de elocidad media, elocidad insanánea, aceleración media y aceleración
MVIMIENT RECTILÍNE 2 BJETIVS DE APRENDIZAJE Al esudiar ese capíulo, used aprenderá: Cómo describir el moimieno recilíneo en érminos de elocidad media, elocidad insanánea, aceleración media y aceleración
Función exponencial y logarítmica
 Fnción eponencil rímic Bchillero Fnción eponencil rímic Repso de poencis Definición: llmmos poenci de bse eponene n, lo denomos por n l prodco n... eces ( ). Pr eponenes negios enemos n n. Pr eponenes
Fnción eponencil rímic Bchillero Fnción eponencil rímic Repso de poencis Definición: llmmos poenci de bse eponene n, lo denomos por n l prodco n... eces ( ). Pr eponenes negios enemos n n. Pr eponenes
Movimiento Rectilíneo Uniformemente Variado
 DEPARTAMENTO DE FÍSICA Moimieno Recilíneo Uniformemene Vrido Preguns pr conesr con el libro Pr conesr ls siguienes preguns e sugerimos leer el libro Físic Concepul de Pul Hewi 1) Qué signific ener elocidd
DEPARTAMENTO DE FÍSICA Moimieno Recilíneo Uniformemene Vrido Preguns pr conesr con el libro Pr conesr ls siguienes preguns e sugerimos leer el libro Físic Concepul de Pul Hewi 1) Qué signific ener elocidd
SISTEMAS DE ECUACIONES LINEALES amn
 Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
Física para todos 1 Carlos Jiménez Huaranga CINEMÁTICA
 ísc pr odos 1 Crlos Jménez Hurng CINEÁTIC CONCEPTOS PREVIOS omeno.- Se dce que un cuerpo esá en momeno cundo su poscón rí respeco un ssem de referenc que se supone fjo. Tryecor.- Es l fgur descr por ls
ísc pr odos 1 Crlos Jménez Hurng CINEÁTIC CONCEPTOS PREVIOS omeno.- Se dce que un cuerpo esá en momeno cundo su poscón rí respeco un ssem de referenc que se supone fjo. Tryecor.- Es l fgur descr por ls
5.1 LÍMITES INFINITOS 5.2 INTEGRANDOS INFINITOS
 MOISES VILLEA MUÑOZ 5 5. LÍMITES IFIITOS 5. ITEGRADOS IFIITOS Objeivo: Se reende que el esudine clcule inegrles sobre regiones no cods y resuelv roblems de licción relciondos con ls inegrles imrois 97
MOISES VILLEA MUÑOZ 5 5. LÍMITES IFIITOS 5. ITEGRADOS IFIITOS Objeivo: Se reende que el esudine clcule inegrles sobre regiones no cods y resuelv roblems de licción relciondos con ls inegrles imrois 97
Integración y Derivación Fraccionaria
 Cpíulo 2 Inegrción y Derivción Frccionri Anes de denrrnos en los operdores de inegrción y derivción generlizdos recordremos lgunos resuldos y nociones del cálculo elemenl que servirán como puno de prid
Cpíulo 2 Inegrción y Derivción Frccionri Anes de denrrnos en los operdores de inegrción y derivción generlizdos recordremos lgunos resuldos y nociones del cálculo elemenl que servirán como puno de prid
MATEMÁTICAS II PRUEBAS DE ACCESO A LA UNIVERSIDAD DE OVIEDO
 MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
Definición de un árbol Rojinegro
 Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí
Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí
CAPITULO II FUNCIONES VECTORIALES
 CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics
CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics
Función exponencial y logarítmica
 Fnción eponencil logrímic Bchillero Inerncionl N-M. Fnción eponencil logrímic Repso de poencis Definición: llmmos poenci de bse ( 0) eponene n, lo denomos por n l prodco n... eces 0 ( 0). Pr eponenes negios
Fnción eponencil logrímic Bchillero Inerncionl N-M. Fnción eponencil logrímic Repso de poencis Definición: llmmos poenci de bse ( 0) eponene n, lo denomos por n l prodco n... eces 0 ( 0). Pr eponenes negios
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
4. Modelos AR(1) y ARI(1,1).
 4. Modelos AR( ARI(,. Los modelos uorregresivos son quellos modelos ARMA(p,q en los que q0. En generl, vmos denorlos por AR(p. En un modelo AR(p en vlor en el momeno de l serie se expres como un combinción
4. Modelos AR( ARI(,. Los modelos uorregresivos son quellos modelos ARMA(p,q en los que q0. En generl, vmos denorlos por AR(p. En un modelo AR(p en vlor en el momeno de l serie se expres como un combinción
INTEGRAL DE RIEMANN-STIELTJES
 Prof. Enrique Meus Nieves Docorndo en Educción Memáic. INTEGRAL DE RIEMANN-STIELTJES L inegrl de Riemnn-Sieljes es un exensión del concepo de Inegrl de Riemnn que permie mplir el poencil de es herrmien.
Prof. Enrique Meus Nieves Docorndo en Educción Memáic. INTEGRAL DE RIEMANN-STIELTJES L inegrl de Riemnn-Sieljes es un exensión del concepo de Inegrl de Riemnn que permie mplir el poencil de es herrmien.
UNIVERSIDAD DEL ZULIA PROGRAMA DE INGENIERÍA NÚCLEO COSTA ORIENTAL DEL LAGO UNIDAD CURRICULAR: FÍSICA I
 UNIVERSIDAD DEL ZULIA PROGRAMA DE INGENIERÍA NÚCLEO COSTA ORIENTAL DEL LAGO UNIDAD CURRICULAR: FÍSICA I INSTRUCTIVO PRÁCTICA Nº 5. MOVIMIENTO RECTILINEO Preparado por. Ing. Ronny J. Chirinos S., MSc prácica
UNIVERSIDAD DEL ZULIA PROGRAMA DE INGENIERÍA NÚCLEO COSTA ORIENTAL DEL LAGO UNIDAD CURRICULAR: FÍSICA I INSTRUCTIVO PRÁCTICA Nº 5. MOVIMIENTO RECTILINEO Preparado por. Ing. Ronny J. Chirinos S., MSc prácica
Hacia la universidad Aritmética y álgebra
 Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
Movimiento rectilíneo uniformemente variado (parte 1)
 Moimieno recilíneo uniformemene ariado Moimieno recilíneo uniformemene ariado Empecemos! A diferencia del MRU cuya elocidad es consane, en nuesra ida diaria obseramos oro ipo de moimieno en el que hay
Moimieno recilíneo uniformemene ariado Moimieno recilíneo uniformemene ariado Empecemos! A diferencia del MRU cuya elocidad es consane, en nuesra ida diaria obseramos oro ipo de moimieno en el que hay
6.7 Teorema de Convolución y la delta de Dirac 409
 6.7 Teorem de Convolución y l del de Dirc 49 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer
6.7 Teorem de Convolución y l del de Dirc 49 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer
Madrid OPOSICIONES AL CUERPO DE PROFESORES DE ENSEÑANZA SECUNDARIA EN LA ESPECIALIDAD DE MATEMÁTICAS
 OPOSICIONES AL CUERPO DE PROFESORES DE ENSEÑANA SECUNDARIA EN LA ESPECIALIDAD DE MATEMÁTICAS Mdrid. Se M el uno medio de un cuerd P Q de un circunferenci. Por M se rzn ors dos cuerds AB y CD: L cuerd AD
OPOSICIONES AL CUERPO DE PROFESORES DE ENSEÑANA SECUNDARIA EN LA ESPECIALIDAD DE MATEMÁTICAS Mdrid. Se M el uno medio de un cuerd P Q de un circunferenci. Por M se rzn ors dos cuerds AB y CD: L cuerd AD
ACTIVIDADES INICIALES
 Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = 001 1 = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
La transformada de Laplace
 CAPÍTULO 6 L rnsformd de Lplce 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer l respues
CAPÍTULO 6 L rnsformd de Lplce 6.7 Teorem de Convolución y l del de Dirc En el nálisis de sisems lineles, como en los sisems vibrorios (mecánicos y elécricos), uno de los objeivos es conocer l respues
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, CONCEPTOS BÁSICOS Y GRÁFICAS
 CINEMÁTICA: MOVIMIENTO RECTILÍNEO, CONCEPTOS BÁSICOS Y GRÁFICAS Dada la dependencia de la velocidad con la posición en un movimieno recilíneo mosrada por la siguiene gráfica, deerminar la dependencia con
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, CONCEPTOS BÁSICOS Y GRÁFICAS Dada la dependencia de la velocidad con la posición en un movimieno recilíneo mosrada por la siguiene gráfica, deerminar la dependencia con
GUÍA DE MOVIMIENTO RECTILÍNEO UNIFORME
 INSTITUTO NACIONAL Deparameno de Física Coordinación Segundo Medio 06. GUÍA DE MOVIMIENTO RECTILÍNEO UNIFORME NOMBRE: CURSO: Caracerísica general de M.R.U: Si una parícula se mueve en la dirección del
INSTITUTO NACIONAL Deparameno de Física Coordinación Segundo Medio 06. GUÍA DE MOVIMIENTO RECTILÍNEO UNIFORME NOMBRE: CURSO: Caracerísica general de M.R.U: Si una parícula se mueve en la dirección del
Signo 2. Signo 1. 9x 6x 8 = 0, se arregla la ecuación así: 3x 1=±
 CAPÍTULO X ECUACIÓN DE º GRADO Y FUNCIÓN CUADRÁTICA 9.. ECUACIÓN DE º GRADO Un ecución de segundo grdo con un incógnit es tod quell que puede ser puest en l form x + bx + c = 0 siendo, b y c coeficientes
CAPÍTULO X ECUACIÓN DE º GRADO Y FUNCIÓN CUADRÁTICA 9.. ECUACIÓN DE º GRADO Un ecución de segundo grdo con un incógnit es tod quell que puede ser puest en l form x + bx + c = 0 siendo, b y c coeficientes
PROBLEMAS DE TEOREMA DE GREEN
 PROBLEMAS E TEOREMA E GREEN ENUNIAO EL TEOREMA Se un curv simple cerrd suve rozos oriend posiivmene se F(; (P;Q un cmpo vecoril cus funciones coordends ienen derivds prciles coninus sore un región ier
PROBLEMAS E TEOREMA E GREEN ENUNIAO EL TEOREMA Se un curv simple cerrd suve rozos oriend posiivmene se F(; (P;Q un cmpo vecoril cus funciones coordends ienen derivds prciles coninus sore un región ier
03) Rapidez de Cambio. 0302) Rapidez de Cambio
 Página 3) Rapidez de Cambio 3) Rapidez de Cambio Desarrollado por el Profesor Rodrigo Vergara Rojas Ocubre 7 Ocubre 7 Página A) Rapidez media de cambio Considere una canidad física (), como la mosrada
Página 3) Rapidez de Cambio 3) Rapidez de Cambio Desarrollado por el Profesor Rodrigo Vergara Rojas Ocubre 7 Ocubre 7 Página A) Rapidez media de cambio Considere una canidad física (), como la mosrada
MOVIMIENTO EN DOS O EN TRES DIMENSIONES
 MVIMIENT EN D EN TRE DIMENINE 3 BJETIV DE APRENDIZAJE Al estudir este cpítulo, usted prenderá: Cómo representr l posición de un cuerpo, usndo ectores, en dos o tres dimensiones.? i un ciclist recorre un
MVIMIENT EN D EN TRE DIMENINE 3 BJETIV DE APRENDIZAJE Al estudir este cpítulo, usted prenderá: Cómo representr l posición de un cuerpo, usndo ectores, en dos o tres dimensiones.? i un ciclist recorre un
el blog de mate de aida.: ECUACIONES 4º ESO pág. 1 ECUACIONES
 el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
el blog de mte de id.: ECUACIONES º ESO pág. ECUACIONES ECUACIONES DE SEGUNDO GRADO Un ecución de segundo grdo tiene l form generl: +b+c=0. (El primer sumndo del primer miembro no puede ser nunc nulo,
Unidad II. Cinemática
 Unidad II. Cinemáica Conenido Definiciones Diagramas de moimieno Marco de referencia Magniudes de la cinemáica Clasificación del moimieno Moimieno recilíneo uniforme Moimieno uniformemene ariado Moimieno
Unidad II. Cinemáica Conenido Definiciones Diagramas de moimieno Marco de referencia Magniudes de la cinemáica Clasificación del moimieno Moimieno recilíneo uniforme Moimieno uniformemene ariado Moimieno
Experimento 3. Análisis del movimiento en una dimensión. Objetivos. Teoría
 Experimeno 3 Análisis del movimieno en una dimensión Objeivos. Esablecer la relación enre la posición y la velocidad de un cuerpo en movimieno 2. Definir la velocidad como el cambio de posición en un inervalo
Experimeno 3 Análisis del movimieno en una dimensión Objeivos. Esablecer la relación enre la posición y la velocidad de un cuerpo en movimieno 2. Definir la velocidad como el cambio de posición en un inervalo
Examen de Física-1, 1 del Grado en Ingeniería Química Examen final. Septiembre de 2012 Cuestiones (Un punto por cuestión).
 Exmen de Físic-1, 1 del Grdo en Ingenierí Químic Exmen finl. Sepiembre de 1 Cuesiones (Un puno por cuesión). Cuesión 1 (Primer prcil): Un rineo se deliz por un superficie horizonl cubier de nieve con un
Exmen de Físic-1, 1 del Grdo en Ingenierí Químic Exmen finl. Sepiembre de 1 Cuesiones (Un puno por cuesión). Cuesión 1 (Primer prcil): Un rineo se deliz por un superficie horizonl cubier de nieve con un
UNIVERSIDAD NACIONAL DE INGENIERIA CENTRO NACIONAL DE ESTUDIOS GENERALES MODALIDAD SABATINA
 UNIVERSIDAD NACINAL DE INGENIERIA CENTR NACINAL DE ESTUDIS GENERALES MDALIDAD SABATINA UNIDAD II CINEMATICA: MVIMIENT DE CAÍDA LIBRE. MVIMIENT BIDIMENSINAL CAIDA LIBRE GUIA DE TRABAJ CLASE PRÁCTICA 4.
UNIVERSIDAD NACINAL DE INGENIERIA CENTR NACINAL DE ESTUDIS GENERALES MDALIDAD SABATINA UNIDAD II CINEMATICA: MVIMIENT DE CAÍDA LIBRE. MVIMIENT BIDIMENSINAL CAIDA LIBRE GUIA DE TRABAJ CLASE PRÁCTICA 4.
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
Tema 10: Descripción física del Universo, Cosmología clásica
 Tem : Descripción físic del Universo, Cosmologí clásic Consulr: An Inroducion o Modern Cosmology, Liddle, libro enero lxies nd Cosmology, Jones & Lmbourne, 7, Cmbridge, ems 5-7 (J&L7). NASA Exrglcic Dbse
Tem : Descripción físic del Universo, Cosmologí clásic Consulr: An Inroducion o Modern Cosmology, Liddle, libro enero lxies nd Cosmology, Jones & Lmbourne, 7, Cmbridge, ems 5-7 (J&L7). NASA Exrglcic Dbse
MOVIMIENTO RECTILÍNEO
 Transparencia Nº 1. CINEMÁTICA. MOVIMIENTO QUÉ ES EL MOVIMIENTO? Cambio de posición de un móvil con el iempo. TIPOS DE MOVIMIENTO Según su rayecoria Todo movimieno es RELATIVO Lo rápido del cambio lo indoca
Transparencia Nº 1. CINEMÁTICA. MOVIMIENTO QUÉ ES EL MOVIMIENTO? Cambio de posición de un móvil con el iempo. TIPOS DE MOVIMIENTO Según su rayecoria Todo movimieno es RELATIVO Lo rápido del cambio lo indoca
Integrales impropias.
 Tem Inegrles impropis.. Inroducción. En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Dom(f) = [, ] es un conjuno codo. f: [, ] IR esá cod en [, ]. Si lgun de ess condiciones
Tem Inegrles impropis.. Inroducción. En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Dom(f) = [, ] es un conjuno codo. f: [, ] IR esá cod en [, ]. Si lgun de ess condiciones
Como podrás observar, los valores de la última columna no son iguales a qué se debe esto, si para una función lineal sí resultaron iguales?
 Razón de cambio de una función cuadráica Ejemplo.5 Un puno se desplaza en el plano describiendo el lugar geomérico correspondiene a la función f ( x x 6x 3. Obén la razón promedio de cambio. Considera
Razón de cambio de una función cuadráica Ejemplo.5 Un puno se desplaza en el plano describiendo el lugar geomérico correspondiene a la función f ( x x 6x 3. Obén la razón promedio de cambio. Considera
TRANSFORMACIONES EN EL ESPACIO (R 2 ) ECUACIONES
 TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
Ecuaciones de 1 er y 2º grado
 Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
Ecuciones de 1 er y º grdo Antes de empezr resolver estos tipos de ecuciones hemos de hcer un serie de definiciones previs, que irán compñds por lgunos ejemplos. Un iguldd lgebric está formd por dos epresiones
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
1º) Si sobre un cuerpo no actúa ninguna fuerza, a qué aceleración está sometido?. Solución: 0 m/s 2
 DINAMICA º) Si obre un cuerpo no cú ningun uerz, qué celerción eá oeido?. Solución: / Por l º Ley de Newon: Si no cú ningun uerz, L únic ner de que un produco e cero e que lguno de lo do uliplicndo e cero.
DINAMICA º) Si obre un cuerpo no cú ningun uerz, qué celerción eá oeido?. Solución: / Por l º Ley de Newon: Si no cú ningun uerz, L únic ner de que un produco e cero e que lguno de lo do uliplicndo e cero.
EXAMEN DE MATEMÁTICAS II (Recuperación)
 º Bchillero Ciencis XN D TÁTICS II Recuperción) ÁLGBR. ), punos) Clsific en función del práero R, el sise de ecuciones: b) puno) Resuélvelo pr, si es posible.. Se un ri cudrd de orden. Si el deerinne de
º Bchillero Ciencis XN D TÁTICS II Recuperción) ÁLGBR. ), punos) Clsific en función del práero R, el sise de ecuciones: b) puno) Resuélvelo pr, si es posible.. Se un ri cudrd de orden. Si el deerinne de
En el tema anterior se ha definido la integral de Riemann con las siguientes hipótesis
 5 Fundmenos de Memáics : Cálculo inegrl en R Cpíulo Inegrles impropis En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] R esá cod en [,
5 Fundmenos de Memáics : Cálculo inegrl en R Cpíulo Inegrles impropis En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] R esá cod en [,
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
FUNCIONES ELEMENTALES.- FUNCIONES POLINÓMICAS.- Funciones Lineles Son funciones cu le es un polinomio de primer grdo, es decir, f() = m + n Sus gráfics son rects pr representrls bst con obtener dos puntos
Relación entre el cálculo integral y el cálculo diferencial.
 Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
Relción entre el cálculo integrl y el cálculo diferencil. Por: Miguel Solís Esquinc Profesor de tiempo completo Universidd Autónom de Chips En est sección presentmos l relción que gurdn l función derivd
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
La Cinemática es la parte de la Física que estudia los movimientos sin preocuparse de la causa que los produce.
 CINEMÁTICA La Cinemáica es la pare de la Física que esudia los moimienos sin preocuparse de la causa que los produce. SISTEMA DE REFERENCIA, POSICIÓN Y TRAYECTORIA Un cuerpo esá en moimieno cuando su posición
CINEMÁTICA La Cinemáica es la pare de la Física que esudia los moimienos sin preocuparse de la causa que los produce. SISTEMA DE REFERENCIA, POSICIÓN Y TRAYECTORIA Un cuerpo esá en moimieno cuando su posición
17532 = Hemos usado el 10 como base, pero podíamos haber usado cualquiera. Por ejemplo el 9, entonces.
 Tem 1.- V de números 1.1.- Números pr contr. Un de ls primers ctividdes intelectules que reliz el ser humno es l de contr: el número de flechs, el número de ovejs, el número de enemigos, etc. En Mtemátics
Tem 1.- V de números 1.1.- Números pr contr. Un de ls primers ctividdes intelectules que reliz el ser humno es l de contr: el número de flechs, el número de ovejs, el número de enemigos, etc. En Mtemátics
Geometría de equilibrio de estructuras en arco
 Geomerí de equilibrio de esrucurs en rco Emilio Corés Deprmeno de Físic, Universidd Auónom Meropolin, Izplp Apdo. Posl 55-534, Méico D.F., 934 Méico E-mil: emil@num.um.m (Recibido el 9 de Febrero de 8;
Geomerí de equilibrio de esrucurs en rco Emilio Corés Deprmeno de Físic, Universidd Auónom Meropolin, Izplp Apdo. Posl 55-534, Méico D.F., 934 Méico E-mil: emil@num.um.m (Recibido el 9 de Febrero de 8;
3.5.1 Trasformada de Laplace de la función escalón unitario
 .5. Trformd de Lplce de l función eclón unirio 0.5. Trformd de Lplce de l función eclón unirio Función Eclón Unirio Tmbién llmd función lo unidd de Heviide, y con frecuenci e uiliz en pliccione que rn
.5. Trformd de Lplce de l función eclón unirio 0.5. Trformd de Lplce de l función eclón unirio Función Eclón Unirio Tmbién llmd función lo unidd de Heviide, y con frecuenci e uiliz en pliccione que rn
PROBLEMAS RESUELTOS SOBRE MOVIMIENTO ARMÓNICO SIMPLE
 PROBLEMS RESUELOS SOBRE MOVIMIENO RMÓNICO SIMPLE L ecución de un M..S. e ( = co,, en l que e l elongción en y en. Cuále on l mpliud, l frecuenci y el período de ee movimieno? En un M..S. l elongción en
PROBLEMS RESUELOS SOBRE MOVIMIENO RMÓNICO SIMPLE L ecución de un M..S. e ( = co,, en l que e l elongción en y en. Cuále on l mpliud, l frecuenci y el período de ee movimieno? En un M..S. l elongción en
En el tema anterior se ha definido la integral de Riemann con las siguientes hipótesis
 59 Memáics I : Cálculo inegrl en IR Tem 5 Inegrles impropis 5. Inroducción En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] IR esá cod
59 Memáics I : Cálculo inegrl en IR Tem 5 Inegrles impropis 5. Inroducción En el em nerior se h definido l inegrl de Riemnn con ls siguienes hipóesis Domf = [, ] es un conjuno codo. f: [, ] IR esá cod
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, OTROS DATOS.
 CINEMÁTICA: MOVIMIENTO RECTILÍNEO, OTROS DATOS. Una parícula se muee en la dirección posiia del eje X, de modo que su elocidad aría según la ley = α donde α es una consane. Teniendo en cuena que en el
CINEMÁTICA: MOVIMIENTO RECTILÍNEO, OTROS DATOS. Una parícula se muee en la dirección posiia del eje X, de modo que su elocidad aría según la ley = α donde α es una consane. Teniendo en cuena que en el
= Δx 2. Escogiendo un sistema de referencia común para ambos móviles x A
 Ejemplos de solución a problemas de Cinemáica de la parícula Diseño en PDF MSc. Carlos Álvarez Marínez de Sanelices, Dpo. Física, Universidad de Camagüey. Carlos.alvarez@reduc.edu.cu Acividad # C1. Un
Ejemplos de solución a problemas de Cinemáica de la parícula Diseño en PDF MSc. Carlos Álvarez Marínez de Sanelices, Dpo. Física, Universidad de Camagüey. Carlos.alvarez@reduc.edu.cu Acividad # C1. Un
( ) 4. Colegio Diocesano Sagrado Corazón de Jesús. MATEMÁTICAS I / 1º Bachillerato C y T LOGARTIMOS. log. log. log. 1 log log 3.
 Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Tema 11: Integrales denidas
 Tem : Integrles denids My 9, 7 Denición y propieddes Denición. Si f ) es un función continu en un intervlo [, b] y denid positiv, f ), l integrl denid en ese intervlo l denimos como: f ). Si f ) > l integrl
Tem : Integrles denids My 9, 7 Denición y propieddes Denición. Si f ) es un función continu en un intervlo [, b] y denid positiv, f ), l integrl denid en ese intervlo l denimos como: f ). Si f ) > l integrl
La elipse es el lugar geométrico de todos los puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante.
 LA ELIPSE DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6., los focos están representdos por los puntos y f.
LA ELIPSE DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6., los focos están representdos por los puntos y f.
1.MATRICES. Definición : Se llama matriz de dimensiones m x n ( m filas y n columnas) a una. colección de datos expresados de la siguiente forma A=.
 .MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
.MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN. Razón de cambio instantánea y la derivada de una función
 RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN Razón de cambio insanánea y la derivada de una función anerior Reomemos nuevamene el problema del proyecil esudiado en la secuencia
RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN Razón de cambio insanánea y la derivada de una función anerior Reomemos nuevamene el problema del proyecil esudiado en la secuencia
4.4 El teorema fundamental del cálculo
 8 CAPÍTULO Inegrción. El eorem undmenl del cálculo Evlur un inegrl deinid uilizndo el eorem undmenl del cálculo. Enender uilizr el eorem del vlor medio pr inegrles. Enconrr el vlor medio de un unción sore
8 CAPÍTULO Inegrción. El eorem undmenl del cálculo Evlur un inegrl deinid uilizndo el eorem undmenl del cálculo. Enender uilizr el eorem del vlor medio pr inegrles. Enconrr el vlor medio de un unción sore
FRACCIONES ALGEBRAICAS
 FRACCIONES ALGEBRAICAS CÓMO ESTAMOS EN EL TEMA?. Cuáno dee ñdirse / r oener l unidd?. De ué número h ue resr / r oener l se re del número?. Qué número sumdo con sus / con sus / es?. Un erson inviere los
FRACCIONES ALGEBRAICAS CÓMO ESTAMOS EN EL TEMA?. Cuáno dee ñdirse / r oener l unidd?. De ué número h ue resr / r oener l se re del número?. Qué número sumdo con sus / con sus / es?. Un erson inviere los
56 CAPÍTULO 2. CÁLCULO ALGEBRAICO. SECCIÓN 2.4 Resolución de Ecuaciones de Segundo Grado
 56 CAPÍTULO. CÁLCULO ALGEBRAICO SECCIÓN.4 Resolución de Ecuciones de Segundo Grdo Introducción Hemos estudido cómo resolver ecuciones lineles, que son quells que podemos escribir de l form x + b = 0. Si
56 CAPÍTULO. CÁLCULO ALGEBRAICO SECCIÓN.4 Resolución de Ecuciones de Segundo Grdo Introducción Hemos estudido cómo resolver ecuciones lineles, que son quells que podemos escribir de l form x + b = 0. Si
Tema 7: ÁLGEBRA DE MATRICES
 ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
La Integral Definida
 Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
BUENA SUERTE! Valor de la aceleración gravitacional = 10 m/s 2. XX Olimpiada Colombiana de Física
 XX Olimpid Colombin de Físic XX OLIMPIADA COLOMBIANA DE FISICA Prueb Clsificori 4 de myo del 2004 INSTRUCCIONES GENERALES 1. NO ABRA ESTE FOLLETO HASTA QUE SE LE INDIQUE. Por fvor le ess insrucciones cuiddosmene.
XX Olimpid Colombin de Físic XX OLIMPIADA COLOMBIANA DE FISICA Prueb Clsificori 4 de myo del 2004 INSTRUCCIONES GENERALES 1. NO ABRA ESTE FOLLETO HASTA QUE SE LE INDIQUE. Por fvor le ess insrucciones cuiddosmene.
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
Es una función exponencial con base 2. Veamos con la rapidez que crece:
 Funciones eponenciles y ritmics Doc. Luis Hernndo Crmon R Funciones Eponenciles Ejemplos: f ( ) Es un función eponencil con bse. Vemos con l rpidez que crece: f () 8 f (0) 0 04 f (0) 0,07,74,84 Funciones
Funciones eponenciles y ritmics Doc. Luis Hernndo Crmon R Funciones Eponenciles Ejemplos: f ( ) Es un función eponencil con bse. Vemos con l rpidez que crece: f () 8 f (0) 0 04 f (0) 0,07,74,84 Funciones
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
Ecuación de la circunferencia de centro el origen C(0, 0) y de
 CÓNICAS EN EL PLANO. CIRCUNFERENCIA, ELIPSE, HIPÉRBOLA Y PARÁBOLA centrds en el origen CIRCUNFERENCIA Aunque segurmente se sep, recordmos que l circunferenci es el conjunto de puntos que distn un cntidd
CÓNICAS EN EL PLANO. CIRCUNFERENCIA, ELIPSE, HIPÉRBOLA Y PARÁBOLA centrds en el origen CIRCUNFERENCIA Aunque segurmente se sep, recordmos que l circunferenci es el conjunto de puntos que distn un cntidd
Funciones de una variable real II Integrales impropias
 Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Solución: El sistema de referencia, la posición del cuerpo en cada instante respecto a dicha referencia, el tiempo empleado y la trayectoria seguida.
 1 Qué es necesario señalar para describir correcamene el movimieno de un cuerpo? El sisema de referencia, la posición del cuerpo en cada insane respeco a dicha referencia, el iempo empleado y la rayecoria
1 Qué es necesario señalar para describir correcamene el movimieno de un cuerpo? El sisema de referencia, la posición del cuerpo en cada insane respeco a dicha referencia, el iempo empleado y la rayecoria
FUNCIONES REALES. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.
 FUNCIONES REALES. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. CONCEPTO DE FUNCIÓN. Llmmos correspondenci entre dos conjuntos A B culquier form de signr lgunos o todos los elementos de A otros elementos de
FUNCIONES REALES. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. CONCEPTO DE FUNCIÓN. Llmmos correspondenci entre dos conjuntos A B culquier form de signr lgunos o todos los elementos de A otros elementos de
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
TEST. Cinemática Respecto al espacio recorrido en el M.R.U.V. podemos afirmar:
 Cineáic TEST.- Siepre que l celerción iene el io enido de l velocidd el oviieno e celerdo. Deplzieno o ryecori e lo io. Siepre que el deplzieno y l celerción ienen l i dirección, el oviieno e celerdo.
Cineáic TEST.- Siepre que l celerción iene el io enido de l velocidd el oviieno e celerdo. Deplzieno o ryecori e lo io. Siepre que el deplzieno y l celerción ienen l i dirección, el oviieno e celerdo.
2 Números racionales positivos
 Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
dx x 2 dx 22. x2 +x-2 dx cos 2 x+cosx senx
 Integrles Clculr l integrl: +e + -+ + sen(+) 6-7 - 8 9 - + ln - 9- + (-)cos 6 ln 7 e 8 sen 9 e - + + + +- +- -6 - ++ () Describir el método de integrción por cmbio de vrible () Usndo el cmbio de vrible
Integrles Clculr l integrl: +e + -+ + sen(+) 6-7 - 8 9 - + ln - 9- + (-)cos 6 ln 7 e 8 sen 9 e - + + + +- +- -6 - ++ () Describir el método de integrción por cmbio de vrible () Usndo el cmbio de vrible
1. Derivadas de funciones de una variable. Recta tangente.
 1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
Física PRUEBA DE ACCESO A LA UNIVERSIDAD 2013 BACHILLERATO FORMACIÓN PROFESIONAL CICLOS FORMATIVOS DE GRADO SUPERIOR. Examen
 PRUEBA DE ACCESO A LA UNIVERSIDAD Físic BACHILLERAO FORMACIÓN PROFESIONAL CICLOS FORMAIVOS DE GRADO SUPERIOR Exmen Crierios e Corrección y Clificción UNIBERSIAERA SARZEKO PROBAK ko UZAILA FISIKA PRUEBAS
PRUEBA DE ACCESO A LA UNIVERSIDAD Físic BACHILLERAO FORMACIÓN PROFESIONAL CICLOS FORMAIVOS DE GRADO SUPERIOR Exmen Crierios e Corrección y Clificción UNIBERSIAERA SARZEKO PROBAK ko UZAILA FISIKA PRUEBAS
Portal Fuenterrebollo XXXVI OLIMPIADA MATEMÁTICA ESPAÑOLA, PALMA DE MALLORCA (2000)
 Portl Fuenterrebollo XXXVI OLIMPIADA MATEMÁTIA ESPAÑOLA, PALMA DE MALLORA (000) Problem. Sen los polinomios: P(x) = x 4 + x + bx + cx + ; Q(x) = x 4 + cx + bx + x +. Hll ls condiciones que deben cumplir
Portl Fuenterrebollo XXXVI OLIMPIADA MATEMÁTIA ESPAÑOLA, PALMA DE MALLORA (000) Problem. Sen los polinomios: P(x) = x 4 + x + bx + cx + ; Q(x) = x 4 + cx + bx + x +. Hll ls condiciones que deben cumplir
