Matemáticas II. 2º Bachillerato. Capítulo 6: Geometría métrica en el espacio LibrosMareaVerde.tk
|
|
|
- Pascual Salazar Vera
- hace 6 años
- Vistas:
Transcripción
1 Memáics II. º Bchillero. Cíulo 6: Geomerí méric en el escio Auores: Leici Gonále Pscul Álro Vldés Menénde Reisor: Milgros Ls Tods ls imágenes hn sido creds or los uores uilindo sofwre libre (GeoGebr GIMP)
2 85 Geomerí méric en el escio Índice. ÁNGULOS EN EL ESPACIO.. ÁNGULO ENTRE DOS RECTAS.. ÁNGULO ENTRE UNA RECTA Y UN PLANO.. ÁNGULO ENTRE DOS PLANOS.4. PARALELISMO PERPENDICULARIDAD Y POSICIONES RELATIVAS. PROYECCIONES ORTOGONALES.. PROYECCIÓN ORTOGONAL DE UN PUNTO SOBRE UNA RECTA.. PROYECCIÓN ORTOGONAL DE UN PUNTO SOBRE UN PLANO.. PROYECCIÓN ORTOGONAL DE UNA RECTA SOBRE UN PLANO. PUNTOS SIMÉTRICOS.. SIMÉTRICO DE UN PUNTO RESPECTO DE OTRO PUNTO.. SIMÉTRICO DE UN PUNTO RESPECTO DE UNA RECTA.. SIMÉTRICO DE UN PUNTO RESPECTO DE UN PLANO.4. POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO 4. DISTANCIAS EN EL ESPACIO 4.. DISTANCIA ENTRE DOS PUNTOS 4.. DISTANCIA DE UN PUNTO A UNA RECTA 4.. DISTANCIA DE UN PUNTO A UN PLANO 4.4. DISTANCIA ENTRE DOS PLANOS 4.5. DISTANCIA ENTRE UNA RECTA Y UN PLANO 4.6. DISTANCIA ENTRE DOS RECTAS Resumen En ese úlimo cíulo de geomerí en dimensión res mos ser cces de resoler roblems de cálculo de disncis de ángulos de roecciones uilindo odo lo rendido en los neriores cíulos de geomerí. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
3 86 Geomerí méric en el escio. ÁNGULOS EN EL ESPACIO.. Ángulo enre dos recs Sbemos ue l dirección de un rec iene dd or su ecor direcor. Con ello odemos deducir: El ángulo ue formn dos recs es el ángulo gudo deermindo or los ecores direcores de dichs recs. Sen ls recs r s con ecores direcores resecios u enemos: u u cos r s rc cos u u Aciidd resuel Hll el ángulo deermindo or ls recs r : s :. 5 De ls ecuciones deducimos fácilmene ue los ecores direcores de r s son resecimene: u 5 Por no: u u u De uí: r s rc cos 78º.. Ángulo enre un rec un lno cos 4 Al conrrio ue en el rdo nerior l dirección del ecor socido l lno (su ecor norml) es erendiculr l roio lno. Por no en ese cso debemos ronr ue: El ángulo ue formn un rec un lno es el comlemenrio del ángulo gudo ue formn el ecor direcor de l rec el ecor norml del lno Se l rec r con ecor direcor u el lno con ecor norml n enemos: u n u n cos r 9º rc cos u n u n º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
4 87 Geomerí méric en el escio Aciidd resuel Hll el ángulo deermindo or l rec r : 4 el lno : 5. n 5 un ecor norml de. Se u un ecor direcor de r Tenemos: u n u n u n 5 5 De uí: r 9º rc cos 9º 74º 6º.. Ángulo enre dos lnos 5 5 cos En ese cso los dos ecores normles son erendiculres los resecios lnos de modo ue: El ángulo formdo or dos lnos es el ángulo gudo deermindo or los ecores normles de dichos lnos. Sen los lnos con ecores normles resecios n n enemos: n n n n cos ' rc cos n n n n Aciidd resuel Hll el ángulo formdo or los lnos : 4 :. Se n un ecor norml de hllmos el ecor norml de con el roduco ecoril de sus ecores direcores: i j k n u 5i j 5k Clculmos: n n 5 5 n n n n Por lo no: rc cos º cos 5 5 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores 5 6 5
5 88 Geomerí méric en el escio.4. Prlelismo erendiculridd osiciones relis En el cíulo nerior nlimos ls osiciones relis de recs lnos enre recs lnos rir de sus ecuciones ero en cd rdo dimos su inerreción geoméric. Podemos relir el mismo esudio rir de sus ecores roechndo lo rendido hs hor eniendo en cuen l oriención reli de los ecores direcores normles socidos dichs recs lnos. Sen ls recs r s consideremos los lnos. Pr definirlos recismos de los siguienes ecores direcores normles de osición: Rec r Rec s Plno Plno Vecor de osición uno A uno B uno P uno Q Vecor direcor u direcor norml n norml n Enonces el esudio de ls osiciones relis enre ellos se reduce los siguienes csos: r s r Coincidenes Prlelos/s Secnes Perendiculres Se crun u u AB u u AB u AB u u u AB u u n n AP u n n AP u n u n n n n PQ n n n PQ n n n n Aciidd roues. Reli en u cuderno los doce dibujos comrueb ls relciones ecoriles descris en l bl nerior: r s coincidenes r s rlels r s secnes r s se crun r coincidenes r rlelos r secnes r erendiculres ' coincidenes ' rlelos ' secnes ' erendiculres º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
6 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores Geomerí méric en el escio 89. PROYECCIONES ORTOGONALES.. Proección orogonl de un uno sobre un rec L roección orogonl de un uno P sobre un rec r será oro uno Q ereneciene l rec l ue el ecor PQ es erendiculr l ecor direcor de l rec. Pr hllr l roección orogonl de un uno sobre un rec dd or l ecución: : r debemos seguir los siguienes sos: Méodo :. Deerminr l ecución del lno erendiculr l rec r ue s or el uno P. Pr ello uilimos el ecor direcor de l rec como ecor norml del lno uilimos l ecución del lno ddo su ecor norml un uno:. El uno ue esmos buscndo (l roección orogonl) es el uno de inersección de l rec con el lno. Resolemos el sisem formdo or ls ecuciones de l rec del lno. de donde hllmos el lor de ue nos ermiirá clculr ls coordends del uno Q: Méodo :. Como Q erenece l rec sus coordends deben erificr l ecución de l rec:. El ecor PQ es erendiculr l rec or no el roduco esclr de dicho ecor con el ecor direcor de l rec es cero: PQ. Resolemos l ecución resulne: de donde hllmos el lor de ue nos ermiirá clculr ls coordends del uno Q:
7 9 Geomerí méric en el escio Aciidd resuel Hll l roección orogonl del uno P sobre l rec r :. En rimer lugr hllmos l ecución del lno erendiculr l rec r ue s or el uno P: El ecor norml de dicho lno será el ecor direcor de l rec: n l ecución del lno es de l form: D Como debe sr or el uno P : D D D Tenemos: : Resolemos el sisem sndo rimero l ecución de l rec su form rméric: Susiuendo el lor de obenemos: Así l roección orogonl del uno P sobre l rec r será el uno Q Proección orogonl de un uno sobre un lno L roección orogonl de un uno P sobre un lno es oro uno Q ereneciene l lno l ue el ecor PQ es erendiculr l lno. Pr hllr l roección orogonl de un uno sobre un lno ddo or l ecución: : A B C D debemos seguir los siguienes sos:. Deerminr l ecución de l rec erendiculr l lno ue s or el uno P. Pr ello uilimos el ecor norml del lno como ecor direcor de l rec: r : A B C. El uno ue esmos buscndo (l roección orogonl) es el uno de inersección de l rec con el lno. Resolemos el sisem formdo or ls ecuciones de l rec del lno. A A B B C C D D A A B B C C 5 7 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
8 9 Geomerí méric en el escio Aciidd resuel Hll l roección orogonl del uno P sobre el lno :. Buscmos l ecución de l rec erendiculr l lno ue coniene l uno P: El ecor direcor de dich rec es el ecor norml del lno: L ecución de l rec ue s or P con ecor direcor es: r : Deerminmos el uno de inersección del lno con l rec: : 4 6 Susiuendo el lor de enemos: Así l roección orogonl del uno P sobre el lno es el uno Q Proección orogonl de un rec sobre un lno L roección orogonl de un rec r sobre un lno es or rec s ue esá conenid en el lno l ue el lno ue coniene ls dos recs es erendiculr l lno. Pr hllr l roección orogonl de un rec sobre un lno hllmos l ecución del lno ue coniene r es erendiculr l lno ddo. L ecución de l rec endrá dd en form imlíci como inersección de los dos lnos. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
9 9 Geomerí méric en el escio Aciidd resuel Hll l roección orogonl de l rec r sobre el lno siendo: r : : Méodo : Obenemos un ecor direcor un uno de l rec: P ecor norml del lno: n. obenemos un A coninución odemos deerminr el lno ue s or el uno P iene como ecores direcores el ecor direcor de l rec el ecor norml del lno: 5 Tenemos el lno : 5 ue coniene l rec r es erendiculr. L rec ue esmos buscndo (l roección orogonl) es enonces: 5 Méodo : Or form de clculr l roección orogonl de un rec sobre un lno ue uede resulr ineresne deendiendo del roblem l ue nos enfrenemos serí: Obener l inersección de l rec r con el lno ue es un uno ue llmremos P. Clculmos l roección orogonl de un uno culuier de r sobre el lno llmémoslo Q. Obenemos l ecución de l rec ue s or esos dos unos P Q. Dich rec será l roección orogonl buscd. Aciidd roues. Hll l roección orogonl del uno. Hll l roección orogonl del uno 4 P sobre l rec r :. 4 P sobre el lno :. 4. Hll l roección orogonl de l rec r sobre el lno siendo: 4 r : : º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
10 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores Geomerí méric en el escio 9. PUNTOS SIMÉTRICOS.. Simérico de un uno reseco de oro uno El simérico de un uno P reseco de oro uno Q es oro uno P de mner ue el uno Q es el uno medio del segmeno ' PP. Y imos en el cíulo 4 cómo deerminr el uno medio del segmeno definido or los unos A B: b b b M Ahor se r de ir l iners ddos un eremo el uno medio obener el oro eremo. Si los unos ienen or coordends P Q reresenmos P or P : QP PQ Igulndo comonenes: P Aciidd resuel Clcul el simérico del uno 4 P reseco del uno 8 5 Q. Se P dicho uno simérico. El uno Q es el uno medio del segmeno P P. El uno medio de P P es 4 luego igulndo enemos: P
11 94 Geomerí méric en el escio.. Simérico de un uno reseco de un rec El simérico de un uno P reseco de un rec r es oro uno P de mner ue l rec r s or el uno medio del segmeno PP el ecor PP es erendiculr l rec r. Pr hllr el simérico de un uno reseco de un rec dd or l ecución: r : debemos seguir los siguienes sos:. Deerminr l roección del uno sobre l rec r r lo ue rocedemos como se indicó en el rdo.. Llmremos ese uno Q.. Deerminmos el uno simérico de P reseco de Q como hicimos en el rdo nerior. Aciidd resuel Clcul el simérico del uno P reseco de l rec r :. En rimer lugr hllmos l roección orogonl del uno P sobre l rec r; eresmos l ecución de l rec en form rméric: r : Ahor buscmos el lno erendiculr l rec r ue s or el uno P. El ecor norml de n l ecución del lno es: dicho lno será el ecor direcor de l rec: 6 L roección orogonl es el uno de inersección de l rec con el lno: 6 6 Susiuendo el lor de en ls ecuciones de r obenemos: Así l roección orogonl del uno P sobre l rec r será el uno Q 6 6 Ahor clculmos el uno simérico de P reseco de l roección Q. Se dicho P. Tenemos: uno De uí el simérico de P reseco de l rec r será: P º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
12 95 Geomerí méric en el escio.. Simérico de un uno reseco de un lno El simérico de un uno P reseco de un lno es oro uno P de mner ue el lno s or el uno medio del segmeno PP ' el ecor PP ' es erendiculr l lno. Pr hllr el simérico de un uno reseco de un lno ddo or l ecución: : A B C D debemos seguir los siguienes sos:. Deerminr l roección del uno sobre el lno r lo ue rocedemos como se indicó en el rdo.. Llmremos ese uno Q.. Deerminmos el uno simérico de P reseco de Q como hicimos en el rdo.. Aciidd resuel Clcul el simérico del uno P reseco del lno : 4. Hllmos l roección orogonl del uno P sobre el lno r ello buscmos l ecución de l rec erendiculr l lno ue s or el uno P. El ecor direcor de dich rec es el ecor norml del lno: n l ecución de l rec es: r : Buscmos el uno de inersección del lno con l rec: Susiuendo el lor de en ls ecuciones de r obenemos: l 9 roección orogonl del uno P sobre el lno será el uno Q. Ahor clculmos el uno simérico de P reseco de l roección Q. Se dicho uno P. Tenemos: De uí el simérico de P reseco de l rec r es: P 4. DISTANCIAS EN EL ESPACIO º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
13 96 Geomerí méric en el escio 4.. Disnci enre dos unos L disnci enre dos unos A B en el escio es el módulo del ecor AB. d A B b b b AB b b b A B AB b b b Aciidd resuel Clcul l disnci del uno A l uno Hllmos el ecor AB su módulo: B. ( ) AB ( ) ( ) 7 AB u Por no: d ( A B) u Deermin ls coordends de los unos ue euidisn de los unos B. Si los unos son de l form P nos dicen ue: d P d P B Elemos l cudrdo oermos simlificmos con lo ue obenemos: u A Que es l ecución de un lno ue es el lugr geomérico edido de los unos ue euidisn de dos unos ddos. Aciidd roues 5. Clcul l disnci del uno A 4 l uno B Deermin ls coordends de los unos ue disn 4 del uno C. 7. Deermin ls coordends de los unos ue disn R del uno C. 8. Deermin ls coordends de los unos ue euidisn de los unos A B. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
14 97 Geomerí méric en el escio 4.. Disnci de un uno un rec Definición: L disnci de un uno P un rec r se define como l menor de ls disncis d(p Q) siendo Q un uno de l rec r. L disnci de un uno P un rec r es l disnci del uno P su roección orogonl sobre dich rec. Méodo : L rimer oción es licr direcmene l definición:. Hllmos l roección del uno sobre l rec el uno Q.. Deerminmos el lno erendiculr r ue coniene P. b. Obenemos el uno Q inersección de r. O bien. Plnemos el uno Q ( ) ue erenece r. b. Eigimos ue el ecor PQ se erendiculr l ecor direcor de l rec es decir su roduco esclr debe ser nulo PQ.. Clculmos l disnci de P Q el módulo del ecor PQ. Méodo : L segund oción es roechr lo ue sbemos de ecores. De l ecución de l rec odemos obener un uno de l mism A su ecor direcor : De l figur deducimos ue l disnci d es l roección del ecor PA sobre el ecor PQ. PERO no conocemos el ecor PQ sí ue no odemos uilir el roduco esclr ero sí el ecoril de cuerdo l siguiene figur: Usndo los unos P A el ecor consruimos el rlelogrmo PABC l lur h de dicho rlelogrmo es recismene l disnci ue esmos inenndo deerminr. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
15 98 Geomerí méric en el escio Usndo l fórmul del áre de un rlelogrmo: Áre Bse Alur h Sbemos ue l inerreción geoméric del roduco ecoril es recismene el áre: Áre AP Igulndo mbs eresiones: AP h AP h Como l lur h coincide con l disnci del uno P l rec r enemos: AP dp r Por no el rocedimieno seguir es:. Deerminmos un uno de l rec A su ecor direcor.. Hllmos el ecor PA (o AP ). Clculmos l disnci con l fórmul: AP dp r Aciidd resuel Clcul l disnci del uno P l rec r :. A rir de l ecución de l rec obengmos un uno un ecor direcor. Es simle er ue son A. Enonces el ecor AP es AP hllmos el roduco ecoril: i j k AP i j k i 4 j k 4 Como: AP dp r Aciidd roues AP 46 AP dp r u Clcul l disnci del uno P l rec r :. 4 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
16 99 Geomerí méric en el escio 4.. Disnci de un uno un lno Definición: L disnci de un uno P un lno se define como l menor de ls disncis d(p Q) siendo Q un uno del lno. L disnci de un uno P un lno es l disnci del uno P su roección orogonl sobre dicho lno. Se el uno siguiene eresión: P el lno : A B C D l disnci de P iene dd or l d P A B A B C C D Demosrción Hllmos l roección del uno P sobre el lno de ecución: : A B C D. Deerminmos l ecución de l rec erendiculr l lno ue s or el uno P con el ecor norml del lno: r : A B C. Resolemos el sisem formdo or ls ecuciones de l rec del lno. A A B B C C D D A B C A B C. L disnci es el módulo del ecor PQ : PQ enonces: A) ( B ) ( C ) A B C A B C ( Y susiuendo or su lor: PQ D A B C A B C PQ A A B B C Alernimene odemos hllr l disnci con l roección del ecor PA sobre el ecor norml del lno siendo A un uno culuier del lno : PA n A B C dp n A B C C d P A B A B C C D º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
17 Geomerí méric en el escio Aciidd resuel Clcul l disnci del uno Alicndo l fórmul: P l lno :. A B C D ( ) 6 d P dp 6 u A B C ( ) 6 Ahor robemos con l roección: Hllmos un uno del lno dndo lores dos de ls ribles: : A Obenemos los ecores PA n : ( ) n Finlmene: PA n ( ) ( ) 6 d P d P A B C ( ) 6 Aciidd roues PA 6. Clcul l disnci del uno 4.4. Disnci enre dos lnos Definición: P l lno : 4. L disnci enre dos lnos se define como l menor de ls disncis d(a B) siendo A B. Ddos dos lnos se ueden resenr los siguienes csos: Si los lnos son coincidenes o secnes: l disnci es cero. Si los lnos son rlelos: l disnci enre ellos será l disnci enre culuier uno de uno de los lnos l oro lno. u º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
18 Geomerí méric en el escio Aciiddes resuels Clcul l disnci enre los lnos : : Anlimos los dos ecores normles: Es ráido er ue NO son rlelos: n n or no los lnos moco son rlelos son secnes l disnci enre ellos es cero. Clcul l disnci enre los lnos : : 4 6 En ese cso emos ue ls ecuciones son roorcionles: 4 6 or no los lnos son coincidenes l disnci enre ellos es cero. Clcul l disnci enre los lnos : : 4 5 A diferenci del ejemlo nerior los coeficienes A B C son roorcionles ero no sí los érminos indeendienes D: 4 5 De modo ue los lnos son rlelos. Hllmos un uno de uno culuier de los lnos: : P usmos l fórmul de l disnci del uno P l lno. A B C D d P dp u. A B C 4 ( ) 4 Aciidd roues. Clcul l disnci enre los lnos: : :.. Clcul l disnci enre los lnos: : ' : 5. Clcul l disnci enre los lnos: : ' : Clcul l disnci enre los lnos: : 4 7 : º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
19 Geomerí méric en el escio 4.5. Disnci enre un rec un lno Definición: L disnci enre un rec r un lno se define como l menor de ls disncis d(a B) siendo A un uno de r B. Dd un rec r un lno se ueden resenr los siguienes csos: Si l rec el lno ienen lgún uno en común: l disnci es cero. Si l rec el lno son rlelos: l disnci enre ellos será l disnci enre culuier uno de l rec el lno. Aciiddes resuels Clcul l disnci enre l rec el lno : l rec r :. L form más ráid de nlir el rlelismo enre lno rec es esudir l osición reli del ecor norml del lno reseco l ecor direcor de l rec: Si r son rlelos n son erendiculres Enonces: n or no: n El roduco esclr NO es nulo r NO son rlelos l disnci enre ellos es nul. Clcul l disnci enre l rec el lno : l rec r :. Procedemos como en el ejemlo nerior: n or no: n El roduco esclr es nulo r son rlelos o coincidenes. Uilimos el uno P ue odemos P r hllr l disnci: obener de ecución de l rec A B C D ( ) 6 d P dp u A B C ( ) 6 Si el lor de l disnci hubier slido cero dirímos ue l rec el lno son coincidenes. Aciidd roues 5. Clcul l disnci enre l rec r : el lno : 5. 4 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
20 Geomerí méric en el escio 4.6. Disnci enre dos recs Definición: L disnci enre dos recs r s se define como l menor de ls disncis d(a B) siendo A r B s. Dds dos recs r s se ueden resenr los siguienes csos: Si ls recs son coincidenes o secnes: l disnci es cero. Si ls recs son rlels: l disnci enre ells será l disnci de un uno de culuier de ls recs l or rec. Si ls recs se crun: l disnci enre ells será l disnci de un de ells l lno rlelo ell ue coniene l or rec. En rinciio deberímos hcer un nálisis de ls osiciones relis de ls recs nes de clculr l disnci enre ells. Sin embrgo eise un ronmieno más simle ue uede relirse nlindo los ecores direcores los ecores de osición de mbs recs. Dds dos recs r s sen los unos A r B s sen demás u un ecor direcor de r un ecor direcor de s. Enonces hllndo el ecor AB : Si u u AB ls recs r s son coincidenes Si u u AB ls recs r s son rlels Si u AB u ls recs r s se corn Si u AB u ls recs r s se crun Enonces un e ue hemos comrobdo ls osiciones relis de ls recs rocedemos según lo elicdo: Si ls recs son rlels: Como hemos obenido los ecores u AB hllmos l disnci con l fórmul: AB u AB dp r o dp r u º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
21 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores Geomerí méric en el escio 4 Si ls recs se crun: En ese cso odemos clculr l disnci enre ells medine l eresión: u AB u s r d Demosrción Considermos el rleleíedo deermindo or los ecores u. Alicndo l fórmul del olumen de un rleleíedo: h u Alur Áre de l bse Volumen Con l inerreción geoméric del roduco mio enemos: AD AC AB Volumen Igulndo mbs eresiones: u AB u u AD AC AB h AD AC AB h u L lur del rleleíedo coincide con l disnci enre ls recs r s luego enemos: u AB u s r d Aciiddes resuels Hll l disnci enre ls recs 4 : r : s. Necesimos un uno un ecor direcor de cd un de ls recs. Como r iene dd como inersección de dos lnos obenemos los ecores normles de mbos lnos: n n r obener el ecor direcor de r como: k j i k j i k j i n n u Obengmos un uno de r r lo ue dmos un lor un rible: : A r Por oro ldo enemos l rec : : s s de l ue obenemos el uno B el ecor direcor o mejor considermos
22 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores Geomerí méric en el escio 5 el ecor r simlificr los cálculos. Ememos hllndo el roduco ecoril r er si son rlels o no: k j i k j i k j i u No obenemos el ecor nulo sí ue r s se corn o se crun. Se el ecor 5 5 AB hllmos su roduco mio con u : u AB El resuldo es disino de cero sí ue r s se crun. Uilimos l eresión r l disnci: u AB u s r d Hllmos el módulo del roduco ecoril de u : 5 u susiuimos: u AB u s r d u. Aciidd roues 6. Hll l disnci enre ls recs 4 : r s :. 7. Hll l disnci enre ls recs : r s :. 8. Hll l disnci enre ls recs : r s :. 9. Hll l disnci enre ls recs : r s 4 :.
23 6 Geomerí méric en el escio CURIOSIDADES. REVISTA Geomerí ruiecur En los libros de Secundri ue cosumbrs usr siemre recen edificios clásicos de l nigu Greci Rom ors culurs nigus. Ho en dí esmos rodedos de edificios con línes mu diferenes sorrendenes lguns de ls cules elorn secos de l geomerí ue hs hce oco no se conocín. Eso no uiere decir ue sólo hblemos de los edificios modernos. Los mocárbes de l Alhmbr en Grnd son un clro ejemlo de cómo jugr con ls res dimensiones l reeición de moios. Mocárbes en l Alhmbr Grnd El Cenro Niemeer de Ailés En oros csos se uilin olúmenes de reolución se consiguen forms sues de seco nurl. Aunue si se r de imir l nurle nd mejor ue er cómo Gudí imió l form de los roncos ls rms en ls columns de l Sgrd Fmili. Sgrd Fmili de Brcelon Monumeno l Consiución Mdrid Se elorn incluso dimensiones sueriores res. El Monumeno l Consiución de Mdrid es el modelo ridimensionl de lo ue se denomin hiercubo un figur de curo dimensiones recibe el nombre de Tesserc. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
24 7 Geomerí méric en el escio RESUMEN Dds ls recs r s los lnos definidos or los siguienes ecores direcores normles de osición: Rec r Rec s Plno Plno Vecor de osición uno A uno B uno P uno Q Vecor direcor u direcor norml n norml n Ángulo enre dos recs r s Ángulos en el escio u rc cos u Ángulo enre rec lno r rc sen u n u n Ángulo enre dos lnos ' rc cos n n n n r s r Prlelismo erendiculridd osiciones relis Coincidenes Prlelos/s Secnes Perendiculres Se crun u u AB u u AB u AB u u u AB u u n n AP u n n AP u n u n n n n PQ n n n PQ n n n n Proecciones orogonles De un uno sobre un rec Pro( P r) Q PQ r De un uno sobre un lno Pro( P ) Q PQ De un rec sobre un lno s Pro( r ) s rs º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
25 8 Geomerí méric en el escio De un uno reseco de oro uno Punos siméricos P PP PQ De un uno reseco de un lno P PP PQ Q Pro( P ) De un uno reseco de un lno Enre dos unos d P PP PQ Q Pro( P r) Disncis A B AB b b b De un uno un lno d P A B A B C C D De un uno un rec dp r AP Enre dos lnos d ' dp ' si P De un rec un lno d r dp r si P r Enre dos recs dr s AB u u º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
26 9 Geomerí méric en el escio EJERCICIOS Y PROBLEMAS.. Esudi l osición reli de ls recs r : s : clcul: ) El uno de inersección. b) L ecución del lno ue ls coniene. c) El ángulo ue formn ls recs.. Ddos los lnos : 6 : 6 se ide: ) Esudir su osición reli. b) Hllr el ángulo ue formn esos dos lnos. c) Hllr l ecución de un rec s ue sndo or el uno N es erendiculr.. Hll l roección ericl del uno A 5 sobre el lno : Hll l roección de l rec r sobre el lno : sí como el ángulo ue formn l rec el lno. 5. Obener ls coordends del uno simérico de 6. Obén ls coordends del uno simérico de 7. Obén ls coordends del uno simérico de ) L rec r : b) El lno : A reseco de l rec r : A reseco del lno : 4. A reseco de: 8. ) Hll l ecución del lno ue s or el uno s or los unos B C. A es erendiculr l rec ue b) Obén ls coordends del uno simérico de C reseco del lno. A l rec r : se ide hllr: ) L ecución de l rec s ue s or el uno A cor erendiculrmene l rec r. b) El uno de inersección de mbs recs r s. c) Ls coordends del uno simérico de A reseco de l rec r. 9. Ddo el uno. Clcul l disnci del uno M : ) Al uno N b) Al lno : c) A l rec r :. Ddos los lnos : 4 : 4 esudi su osición reli clculr l disnci enre ellos. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
27 Geomerí méric en el escio r :. Hllr l osición reli de ls recs 4 clculr l disnci enre ells. s : 4. Dds los res de recs 4 r : ) r : b) s : s : ) Esudi l osición reli. b) Clcul l disnci enre ells. 4. Hll l roección de l rec r sobre el lno : sí como l disnci ue h enre l rec el lno. 5. Dd l rec r : se ide: ) Hll l ecución de l rec s ue sndo or el uno A es rlel l rec r. b) Clcul l disnci ue h enre ells. c) Hll l ecución del lno ue s or el uno M coniene l rec r Hll l ecución de un lno ue coniene l rec r : dis uniddes 9 del origen de coordends. 7. Ddos el lno l rec: : r : ) El uno de inersección de l rec r con el lno. b) El ángulo ue formn l rec r el lno. c) L ecución de un lno ' erendiculr l lno ue coneng l rec r. 8. Ddos los lnos : : 4 se ide: ) Ecución de un rec ue se or el uno A se rlel los lnos. b) Vlor de m n sbiendo ue el uno C m n dis uniddes del lno. 9. Hll el áre del riángulo cuos érices son los unos A el uno de core del lno OYZ con l rec r :. B el ercer érice es. Hll l roección de l rec r : sobre el lno deermindo or el origen B. de coordends los unos A º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
28 Geomerí méric en el escio AUTOEVALUACIÓN 4 ) El ángulo formdo or ls recs r : 5 4 s : es: 4 ) cos ; b) cos ; c) cos ; d) cos ) El ángulo formdo or los lnos : ' : 5 es: 7 ) cos ; b) cos ; c) cos ; d) cos ) L roección orogonl del uno P sobre l rec r : es: ) ) ; b) ) ; c) 9 ) ; d) Ninguno de los neriores ( ( ( ) L roección orogonl del uno 5 P sobre el lno : es: 4 ) 4 4 ) ; b) ( ) 4 ; c) 8 ) ; d) Ninguno de los neriores ( ( ) El simérico del uno P reseco del uno Q es: ) ( 5) ; b) ( ) ; c) ( 4) ; d) Ninguno de los neriores 6) El simérico del uno P reseco de l rec r : es: ) 9 7 ) ; 5 b) ); c) ); d) Ninguno de los neriores ( ( ( ) L disnci del uno A l uno B es: ) 6; b) 6 ; c) ; d) Ninguno de los neriores 8) L disnci del uno ) ; b) ; c) 4 4 9) L disnci del uno A l rec r : es: A l lno : es: ; d) Ninguno de los neriores ) ; b) ; c) ; d) Ninguno de los neriores ) L disnci enre los lnos : ' : 5 es: ) ; b) 5 ; c) ; d) Ninguno de los neriores 4 º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
29 Geomerí méric en el escio Aéndice: Problems de geomerí méric en ls P.A.A.U. () Consider ls recs r : r : ) Esudi l osición reli de r r. b) Encuenr si es osible un lno rlelo r ue coneng r. c) Encuenr l disnci enre r r. () Consider el uno P el lno :. Clcul: ) Ls ecuciones de un rec ue se or el uno P se erendiculr l lno. b) L disnci d del uno P l lno. () Consider los unos A O. ) D l ecución de un lno ue se or A O se erendiculr : 5. b) Encuenr l disnci del uno medio de A O. (4) Considere el lno : el uno P. ) Obén el uno P simérico de P reseco de. b) Hll el uno de core del lno con l rec ue s or P P.. Consider l rec r :. ) Escribe uns ecuciones cresins de l rec s. b) D l osición reli de ls recs r s. c) Obén l disnci enre r s. (5) Se s l rec ue s or los unos A B (6) Consider un moimieno en el escio l ue cd uno de coordends b c uno de coordends b b c b. ) Busc el conjuno de unos ue se mueen l origen de coordends. lo muee l b) D un ecución del lno ue deerminn los unos del rdo () el uno. c) Busc l disnci del origen de coordends l lno. (7) Sen el uno P el lno : 8. Clcul: ) Ls ecuciones de un rec ue se or el uno P se erendiculr l lno. b) L disnci d del uno P l lno. c) L ecución de oro lno rlelo disino de él ue dise de P l mism disnci d. (8) Se considern los unos en el escio A B. ) Hll el uno medio de A B. b) D l ecución del lno reseco l cul A B son unos siméricos. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
30 Geomerí méric en el escio (9) Considere el lno : l rec r :. ) Hll l osición reli de l rec el lno. b) Encuenr un rec erendiculr mbos. c) Busc l mínim disnci enre l rec el lno ddos. () ) Deermin el lor de k r ue los unos A B C D k se encuenren en el mismo lno. b) Hll l disnci del origen de coordends l lno deermindo or los unos A B C. () Ddo el uno O busc un uno O del escio l ue l rec ue s or O O se erendiculr l lno de ecución ls disncis de O de O coincidn. () Se considern l rec lno siguienes: r : 5 5 : : 4 ) Deermin l osición reli de l rec reseco cd uno de los lnos. b) Deermin l osición reli de los dos lnos. c) Clcul l disnci de r l lno. () ) Obén l osición reli de los lnos C ue s or A B 6 C. b) Busc l mínim disnci enre los lnos neriores. (4) Sen el uno P el lno :. Clcul: ) L ecución de un rec ue se or el uno P core l lno. b) L disnci del uno P l lno. (5) Se considern el lno ue s or los unos A ue s or los unos A B ue s or los unos P Q 6 R. Clcul: ) Ls ecuciones generles o imlícis de. b) L osición reli de. c) L disnci enre. (6) Considere los unos A B C. ) D ls ecuciones de l rec r ue s or B C. b) Clcul el lno ue s or A es erendiculr r. c) Hll el uno de core enre r. c) Obén el uno simérico de A reseco de r. B C el lno º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
31 4 Geomerí méric en el escio P l rec r :. Clcul: ) L ecución del lno erendiculr r sndo or P. b) El uno de inersección enre r. c) L disnci del uno P l rec r. (7) Sen el uno (8) Ddo el uno A el lno : 4. ) Clcule l rec r erendiculr l lno ue s or el uno A. b) Hlle el uno de inersección enre r. c) Hlle el uno simérico de A reseco de. (9) Se considern los unos A B. ) Hll los unos C D ue diiden l segmeno AB en res res de igul longiud. b) Hll el lno reseco l cul los unos A B son siméricos. 4 () Se deno or r l rec 6 7 ) Hlle l ecución del lno ue s or P es erendiculr r. b) Hlle el uno de r más róimo P hll l disnci de P r. or P el uno de coordends () Se deno or rs l rec ) Esudi si ls recs r s se corn si se corn hlle el uno de inersección. b) Hll l ecución del lno ue coniene r es rlelo s. c) Hll el uno de r r ue euidis de A B. () Sen ls recs. se s l rec ue s or A r : k s :. ) Esudi si r lgún lor de k ls recs son rlels. b) Esudi si r lgún lor de k ls recs son erendiculres. c) Hll l disnci del uno A l rec s. () Ddos los unos A B C. ) Hll el lno ue coniene los res unos. B. b) Clcul un uno P ue esé disnci de uniddes del lno del uno medio del segmeno AB. c) Considerndo D clcul el olumen del eredro limido or los unos A B C D. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
32 5 Geomerí méric en el escio (4) Se el eredro de l figur formdo or A B C 6 D ) El áre del riángulo limido or los unos A B C. b) L ecución del lno ue s or los unos A B C. c) El lor de r ue el ecor AD se erendiculr l lno. d) Pr 5 el uno D simérico de D reseco l lno. (5) Se el uno A el lno :. Hll: ) L ecución de l rec ue s or A es erendiculr. b) L ecución del lno ' ue s or A no cor. c) L disnci enre los dos lnos. (6) Sen los unos A B. Deermin: ) Ls ecuciones rmérics de l rec r ue une los unos. b) L ecución del lno ue s or A es erendiculr l rec r. c) L disnci del uno B l lno.. Clcul: (7) Se el rism ringulr (riángulos igules rlelos) de l figur con A C A. Clcul: ) L ecución del lno ue s or los unos A B C. b) El lor de r ue el lno ' ue coniene los unos A B C dise un unidd del lno. c) Pr el lno ' el olumen del rism. (8) Los unos A B C D formn un rlelogrmo. Clcule: B ) Ls coordends del érice D oueso B. b) El áre del rlelogrmo. c) L ecución de l rec ue s or el uno medio del segmeno AC es erendiculr l lno ue coniene l rlelogrmo. (9) Se consider el rleleíedo cuos érices de l cr inferior son los unos A B C D con A C érices ouesos. Se A el érice dcene A en l cr suerior. Clcul: ) Ls ecuciones de los lnos ue conienen ls crs inferior suerior. b) Los érices de l cr suerior. c) El olumen del rleleíedo. () Dd l rec r de ecución el uno P. Clcul: 4 ) L ecución de l rec ue s or P es erendiculr r se o en r. b) Ls coordends del uno Q simérico de P reseco r. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
33 6 Geomerí méric en el escio () Se el uno A ereneciene un lno. Clcul: ) L ecución del lno sbiendo ue P erenece l rec erendiculr ue s or el uno A. b) L ecución de un lno cu disnci se de uniddes. c) Un uno B ereneciene l lno ' : ue esá disnci 45 de A. () Se l rec r :. 6 6 ) Clcul ls coordends de los unos P Q ue erenecen l rec disn 5 uniddes del origen de coordends. b) Se M el uno medio del segmeno de eremos P Q. Clcul sus coordends. c) Jusific or ué de odos los unos de l rec r M es el más róimo l origen de coordends. () Los unos P erenece l rec : Q son dos érices coniguos de un recángulo. Un ercer érice r. ) Deermin los érices de un recángulo ue erifiue ls condiciones neriores. b) Qué osición reli deberí ener l rec r l ue coniene l segmeno PQ r ue l solución fuese únic? Ron l resues. (4) Ddo el eredro con un érice O sobre el origen de coordends los oros res A B C sobre los semiejes osiios OX OY OZ resecimene se ide hllr: 8 ) Ls coordends de A B C sbiendo ue el olumen del eredro es u ue ls riss OA OB ienen igul longiud ue l ris OC iene doble longiud ue OA. b) L ecución de l lur del eredro corresondiene l cr ABC. c) L disnci enre ls recs AC OB. d) El ángulo ue formn ls riss AC AB. (5) Ddos los unos A B C se ide: ) Comrobr si esán linedos en cso conrrio clculr el erímero el áre del riángulo. b) Hllr el lor de l lur corresondiene l érice A. c) Clculr el lor del ángulo corresondiene l érice B. d) Hllr l ecución de un de ls res medins. (6) Ddo un riángulo de érices A B 5 C 4 ) El erímero. b) El áre. c) El lor de l lur corresondiene l érice A. d) L ecución de un medin. e) L ecución de un mediri. f) L ecución de un lur. hll: º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
34 7 Geomerí méric en el escio (7) Sbiendo ue l ecución de un lno es : 4 : ) Hll l ecución de un lno ' rlelo l lno ue dise un unidd del uno Q. b) Hll l disnci enre mbos lnos '. c) Hll el áre del riángulo cuos érices son los unos donde el lno cor los ejes de coordends. (8) Ddo el lno : l rec r : el uno ) Hll l ecución de l rec s ue se erendiculr r se or P. b) Hll el uno P simérico de P reseco de r. c) Hll el uno P simérico de P reseco de. P : (9) Se consider el eredro cuos érices son A B C ) Hll el áre del riángulo ABC el olumen del eredro ABCD. b) Clcul l disnci de D l lno deermindo or los unos A B C. c) Hll l disnci enre ls recs AC BD. (4) Sen los unos A 4 B. D. ) Hll ls coordends de los unos P Q ue diiden l segmeno AB en res res igules. b) Si P es el uno del rdo nerior más róimo l uno A deermin l ecución del lno ue coniene P es erendiculr l rec AB. c) Deermin l osición reli del lno l rec r : (4) Hll los unos de l rec: r : cu disnci l lno : 4 4 es igul u. (4) Ddos los unos P Q Q(; ; ) se ide: ) Hll odos los unos R les ue l disnci enre P R se igul l disnci enre Q R. Describe dicho conjuno de unos. b) Hll odos los unos S conenidos en l rec ue s or P Q ue erificn: donde "dis" signific disnci. (4) Ddos el lno : dis P S disq S el uno P se ide: ) Hllr l ecución de l rec r erendiculr l lno ue s or el uno P. b) Hllr el uno Q inersección de con r. c) Hllr el uno R inersección de con el eje OY. d) Hllr el áre del riángulo PQR. º de Bchillero. Memáics II. Cíulo 7: Geomerí méric en el escio Auores: Leici Gonále Álro Vldés Reisor: Milgros Ls Imágenes creds or los uores
OPCIÓN A. 1.A.- Dadas las matrices: a) Determinar la matriz inversa de B. b) Determinar una matriz X tal que A = BX
 IES Medierráneo de Málg Solución Seiembre Jun Crlos lonso Ginoni OPCIÓN..- Dds ls mrices: Deerminr l mri invers de b Deerminr un mri X l que X X X X X dj dj IES Medierráneo de Málg Solución Seiembre Jun
IES Medierráneo de Málg Solución Seiembre Jun Crlos lonso Ginoni OPCIÓN..- Dds ls mrices: Deerminr l mri invers de b Deerminr un mri X l que X X X X X dj dj IES Medierráneo de Málg Solución Seiembre Jun
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
I.E.S. CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE VALENCIA SEPTIEBRE (RESUELTOS por Anonio enguino) ATEÁTICAS II Tiempo máimo: hors Se elegirá el Ejercicio A o el B, del que sólo se hrán
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio, Opción A Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción
Madrid OPOSICIONES AL CUERPO DE PROFESORES DE ENSEÑANZA SECUNDARIA EN LA ESPECIALIDAD DE MATEMÁTICAS
 OPOSICIONES AL CUERPO DE PROFESORES DE ENSEÑANA SECUNDARIA EN LA ESPECIALIDAD DE MATEMÁTICAS Mdrid. Se M el uno medio de un cuerd P Q de un circunferenci. Por M se rzn ors dos cuerds AB y CD: L cuerd AD
OPOSICIONES AL CUERPO DE PROFESORES DE ENSEÑANA SECUNDARIA EN LA ESPECIALIDAD DE MATEMÁTICAS Mdrid. Se M el uno medio de un cuerd P Q de un circunferenci. Por M se rzn ors dos cuerds AB y CD: L cuerd AD
MATRICES Y DETERMINANTES.
 punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
punes de. Cbñó MTRICES Y DETERMINNTES. CONTENIDOS: Definición y erminologí básic. Operciones con mrices: sum y produco. Produco de un mriz por un esclr. Mriz opues. Mriz invers. Epresión mricil de un sisem
MATEMÁTICAS II TEMA 5 Ecuaciones de rectas y planos en el espacio. Posiciones relativas Problemas propuestos
 Geomería del espacio ecuaciones de recas planos; posiciones relaivas MATEMÁTICAS II TEMA Ecuaciones de recas planos en el espacio. Posiciones relaivas Problemas propuesos Ecuaciones de recas planos. Halla,
Geomería del espacio ecuaciones de recas planos; posiciones relaivas MATEMÁTICAS II TEMA Ecuaciones de recas planos en el espacio. Posiciones relaivas Problemas propuesos Ecuaciones de recas planos. Halla,
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (5-M-B-) Consider ls mrices 4 A = y B = 4 ) ( puno) Hll el deerminne de un mriz X que verifique l iguldd X AX = B b)
FRACCIONES ALGEBRAICAS
 FRACCIONES ALGEBRAICAS CÓMO ESTAMOS EN EL TEMA?. Cuáno dee ñdirse / r oener l unidd?. De ué número h ue resr / r oener l se re del número?. Qué número sumdo con sus / con sus / es?. Un erson inviere los
FRACCIONES ALGEBRAICAS CÓMO ESTAMOS EN EL TEMA?. Cuáno dee ñdirse / r oener l unidd?. De ué número h ue resr / r oener l se re del número?. Qué número sumdo con sus / con sus / es?. Un erson inviere los
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 8 Pág. Págin 88 PRACTICA Vectores y puntos Ddos los puntos A 0 B0 C y D hll ls coordends de los vectores AB BC CD DA AC y BD. AB = 0 0 = DA = 0 = BC = 0 = AC = 0 = 7 CD = = 6 BD = 0 = 8 Ls coordends del
8 Pág. Págin 88 PRACTICA Vectores y puntos Ddos los puntos A 0 B0 C y D hll ls coordends de los vectores AB BC CD DA AC y BD. AB = 0 0 = DA = 0 = BC = 0 = AC = 0 = 7 CD = = 6 BD = 0 = 8 Ls coordends del
es incompatible: a) Si m = 1 b) Si m = 2 c) Ninguna de las anteriores. Solución:, siendo r(a) = 2 y r(m) = 3 Sistema incompatible.
 nálisis eáico José rí ríne edino PROBLES DE SITES rouesos en eáenes) Preguns de io es. El sise es incoible: ) Si = b) Si = c) Ningun de ls neriores. 8 si r) =, SCD. Si =,, siendo r) = r) = Sise incoible.
nálisis eáico José rí ríne edino PROBLES DE SITES rouesos en eáenes) Preguns de io es. El sise es incoible: ) Si = b) Si = c) Ningun de ls neriores. 8 si r) =, SCD. Si =,, siendo r) = r) = Sise incoible.
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS
 SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
SISTEMAS DE ECUACIONES LINEALES: MÉTODO DE GAUSS Ejercicio nº.- Pon un ejemplo, cundo se posible, de un sisem de dos ecuciones con res incógnis que se: ) Compible deermindo Compible indeermindo c) Incompible
5.1 LÍMITES INFINITOS 5.2 INTEGRANDOS INFINITOS
 MOISES VILLEA MUÑOZ 5 5. LÍMITES IFIITOS 5. ITEGRADOS IFIITOS Objeivo: Se reende que el esudine clcule inegrles sobre regiones no cods y resuelv roblems de licción relciondos con ls inegrles imrois 97
MOISES VILLEA MUÑOZ 5 5. LÍMITES IFIITOS 5. ITEGRADOS IFIITOS Objeivo: Se reende que el esudine clcule inegrles sobre regiones no cods y resuelv roblems de licción relciondos con ls inegrles imrois 97
ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN 2013
 GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES
 IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
IES Pdre Poved (Gudix) Memáics II EJERCICIOS UNIDADES 5 y 6: MATRICES Y DETERMINANTES (4-M;Jun-B-) (5 punos) Consider ls mrices A = y B = Deermin, si exise, l mriz X que verific AX + B = A + m (4-M-B-)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
TRANSFORMACIONES EN EL ESPACIO (R 2 ) ECUACIONES
 TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR TRNSFORMIONES EN EL ESPIO (R ) EUIONES ONSTRUIR LSIFIR Unidd Docene de Memáics de l E.T.S.I.T.G.. EUIONES DE LOS MOVIMIENTOS, HOMOTEIS Y SEMEJNZS
MATEMÁTICAS II PRUEBAS DE ACCESO A LA UNIVERSIDAD DE OVIEDO
 MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
MTEMÁTCS RUEBS DE CCESO L UNVERSDD DE OVEDO.- MTRCES Y DETERMNNTES.- MODELO DE RUEB roduco de mrices: concepo. Condiciones pr su relición. Es posible que pr dos mrices B no cudrds puedn eisir B B?. b Si
Determinantes y matrices
 emáics SS Deerminnes José rí rínez edino Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los
emáics SS Deerminnes José rí rínez edino Deerminnes mrices. Dds ls mrices:, Hll l invers de, l mriz l que. ; ; djun de De. lcul l mriz invers de l mriz L mriz invers viene dd por, siendo l mriz de los
EJERCICIOS UNIDADES 1 y 2: MATRICES Y DETERMINANTES = 001 1 = A donde ( ) ( ) 2. B calcule la matriz X que verifique.
 ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ES Pdre Poved (Gudi) Memáics plicds ls SS Deprmeno de Memáics loque : Álgebr Linel Profesor: Rmón Lorene Nvrro Uniddes : Mrices Deerminnes EJEROS UNDDES : MTRES Y DETERMNNTES (Jun-96) Encuenre un mriz
ACTIVIDADES INICIALES
 Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
Solucionrio Deerminnes CTIVIDDES INICILES.I. usc ls relciones de dependenci linel enre ls fils columns de ls siguienes mrices e indic el vlor de su rngo. rg() F F Como C C C rg().ii. Comprue que ls siguienes
ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2015
 GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
Hacia la universidad Aritmética y álgebra
 Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
Solucionrio Solucionrio Hci l universidd riméic álger OPIÓN. Dds ls mrices ) lcul ls mrices. ) lcul l mri invers de. c) Resuelve l ecución mricil. ) 8 7 8 9 ) ( ), dj( ) c), [ ] 9 9 8 9. Resuelve el sisem
Definición de un árbol Rojinegro
 Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí
Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí
SOLUCIONES EJERCICIOS MATRICES
 SOLUIONES EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de
SOLUIONES EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.1. Límites de integración infinitos 9.2. Integrales con integrando que tiende a infinito 9.3. Observaciones a las
 CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
CAPÍTULO 9. INTEGRALES IMPROPIAS 9.. Límies de inegrción infinios 9.. Inegrles con inegrndo que iende infinio 9.. Oservciones ls inegrles impropis Cpíulo 9 Inegrles impropis f ( ) f ( ) f f ( ) () f()
Actividades de recuperación
 Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
EJERCICIOS MATRICES. 2 euros/kg. Ejercicio nº 1.-
 EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de queso neriores
EJERIIOS MTRIES Ejercicio nº.- Un hipermercdo quiere oferr res clses de bndejs,. L bndej coniene g de queso mnchego, g de roquefor 8 g de cmember l bndej coniene g de cd uno de los res ipos de queso neriores
SISTEMAS DE ECUACIONES LINEALES amn
 Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
Apunes de A. Cbñó Memáics plicds cc.ss. SISTEMAS DE ECUACIONES LINEALES. CONTENIDOS: Plnemienos de problems lineles. Soluciones de un sisem de ecuciones lineles. Sisems lineles equivlenes. Méodo de reducción
LA RECTA DEL PLANO P O L I T E C N I C O 1 ECUACIÓN VECTORIAL Y ECUACIONES PARAMÉTRICAS
 L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
L Rect del Plno Mtemátic 4º Año Cód. 44-5 P r o f. M r í d e l L u j á n M r t í n e z P r o f. J u n C r l o s B u e P r o f. M i r t R o s i t o P r o f. V e r ó n i c F i l o t t i Dpto. de Mtemátic
Se traza la paralela al lado a y distancia la altura h a.
 Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
Hojs de Problems Geometrí IV 56. Construir un triángulo conocido el ldo, l medin reltiv l ldo b y l ltur reltiv l ldo. Tomndo como ldos de un rectángulo los ldos, b del triángulo nterior clculr los ldos
MATEMÁTICAS II TEMA 3 Sistemas de ecuaciones lineales: Problemas propuestos
 Álgebr: Sisems wwwmemicsjmmmcom José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo
Álgebr: Sisems wwwmemicsjmmmcom José Mrí Mríne Medino MATEMÁTICAS II TEMA Sisems de ecuciones lineles: Problems propuesos Clsificción resolución de sisems por méodos elemenles Resuelve uilindo el méodo
MATRICES Y DETERMINANTES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS. APLICACIONES
 Mtrices. Estudio de l comptibilidd de sistems Abel Mrtín & Mrt Mrtín Sierr MATRICES Y DETERMINANTES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS. APLICACIONES. Actividd propuest Escribe un mtri A de dimensión
Mtrices. Estudio de l comptibilidd de sistems Abel Mrtín & Mrt Mrtín Sierr MATRICES Y DETERMINANTES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS. APLICACIONES. Actividd propuest Escribe un mtri A de dimensión
FRACCIONES ALGEBRAICAS
 FRACCIONES ALGEBRAICAS CÓMO ESTAMOS EN EL TEMA?. Cuáno dee ñdirse / r oener l unidd?. De ué número h ue resr / r oener l se re del número?. Qué número sumdo on sus / on sus / es?. Un erson inviere los
FRACCIONES ALGEBRAICAS CÓMO ESTAMOS EN EL TEMA?. Cuáno dee ñdirse / r oener l unidd?. De ué número h ue resr / r oener l se re del número?. Qué número sumdo on sus / on sus / es?. Un erson inviere los
APLICACIONES DE LAS MATRICES
 PLIIONES DE LS MTRIES Ejercicio nº.- ) Encuenr los vlores de pr los que l ri: no es inversible. Ejercicio nº.- lcul, si es posible, l invers de l ri: Pr los csos en los que. Ejercicio nº.- Hll un ri,,
PLIIONES DE LS MTRIES Ejercicio nº.- ) Encuenr los vlores de pr los que l ri: no es inversible. Ejercicio nº.- lcul, si es posible, l invers de l ri: Pr los csos en los que. Ejercicio nº.- Hll un ri,,
Funciones trigonométricas
 0 Funciones rigonoméricas Tenemos en el plano R² la circunferencia C de radio con cenro (0,0. En ella disinguimos el puno (,0, que es el puno de inersección dec con el semieje de las x posiivas. Si pariendo
0 Funciones rigonoméricas Tenemos en el plano R² la circunferencia C de radio con cenro (0,0. En ella disinguimos el puno (,0, que es el puno de inersección dec con el semieje de las x posiivas. Si pariendo
EJERCICIOS DE GEOMETRÍA
 VECTORES EJERCICIOS DE GEOMETRÍA 1. Hllr un vector unitrio u r r r r de l mism dirección que el vector v = 8i 6j.Clculr otro vector ortogonl v r y de módulo 5.. Normliz los vectores: u r = ( 1, v r = (-4,3
VECTORES EJERCICIOS DE GEOMETRÍA 1. Hllr un vector unitrio u r r r r de l mism dirección que el vector v = 8i 6j.Clculr otro vector ortogonl v r y de módulo 5.. Normliz los vectores: u r = ( 1, v r = (-4,3
Tema 7: ÁLGEBRA DE MATRICES
 ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
ÁLGER DE MTRICES Tem : ÁLGER DE MTRICES Índice. Concepo de mriz... Definición de mriz... Clsificción de ls mrices... Tls, grfos y mrices.. Operciones con mrices... Sum de mrices... Muliplicción de un número
ˆ ˆ. FÍSICA 100 CERTAMEN # 2 Forma R 12 de junio de La pirámide de la figura está definida por los vectores a, b y
 FÍSICA 1 CERAMEN # Form R 1 de junio de 1 A. AERNO A. MAERNO NOMBRE ROL USM - Si su rol comienz con 9 coloque 9 ESE CERAMEN CONSA DE REGUNAS EN 8 ÁGINAS. IEMO: 15 MINUOS SIN CALCULADORA. SIN ELÉFONO CELULAR
FÍSICA 1 CERAMEN # Form R 1 de junio de 1 A. AERNO A. MAERNO NOMBRE ROL USM - Si su rol comienz con 9 coloque 9 ESE CERAMEN CONSA DE REGUNAS EN 8 ÁGINAS. IEMO: 15 MINUOS SIN CALCULADORA. SIN ELÉFONO CELULAR
3º) (Andalucía, Junio, 00) Determina una matriz A simétrica (A coincide con su traspuesta) sabiendo que:
 PROLEMS SORE MTRICES. PROFESOR: NTONIO PIZRRO. http://ficus.pntic.mec.es/pis NDLUCÍ-MTEMÁTICS PLICDS LS CCSSII: º) (ndlucí, Junio, 98) Si son dos mtrices culquier, es correct l siguiente cden de igulddes?:
PROLEMS SORE MTRICES. PROFESOR: NTONIO PIZRRO. http://ficus.pntic.mec.es/pis NDLUCÍ-MTEMÁTICS PLICDS LS CCSSII: º) (ndlucí, Junio, 98) Si son dos mtrices culquier, es correct l siguiente cden de igulddes?:
TEMA 4 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 Te Resolución de sises edine deerinnes Meáics II º chillero TEM RESOLUIÓN DE SISTEMS MEDINTE DETERMINNTES Resolución de sises Regl de rer Teore de Rouché-Froenius EJERIIO Resuelve plicndo l regl de rer
Te Resolución de sises edine deerinnes Meáics II º chillero TEM RESOLUIÓN DE SISTEMS MEDINTE DETERMINNTES Resolución de sises Regl de rer Teore de Rouché-Froenius EJERIIO Resuelve plicndo l regl de rer
UTalca - Versión Preliminar
 1. Definición L hipérbol es el lugr geométrico de todos los puntos del plno cuyo vlor bsoluto de l diferenci de ls distncis dos puntos fijos es constnte. Más clrmente: Ddos (elementos bses de l hipérbol)
1. Definición L hipérbol es el lugr geométrico de todos los puntos del plno cuyo vlor bsoluto de l diferenci de ls distncis dos puntos fijos es constnte. Más clrmente: Ddos (elementos bses de l hipérbol)
TEMA 47. GENERACIÓN DE CURVAS POR ENVOLVENTES
 Tema 47. Generación de curvas por envolvenes. TEMA 47. GENERACIÓN DE CURVAS POR ENVOLVENTES. Inroducción. Una curva o supericie es envolvene de un conjuno de curvas o supericies si es angene en cada puno
Tema 47. Generación de curvas por envolvenes. TEMA 47. GENERACIÓN DE CURVAS POR ENVOLVENTES. Inroducción. Una curva o supericie es envolvene de un conjuno de curvas o supericies si es angene en cada puno
4. PRUEBA DE SELECTIVIDAD-MODELO
 Pruebs de Selectividd de Ciencis PRUEB DE SELECTIVIDD-MODELO-- OPCIÓN : ) Hll l longitud de los ldos del triángulo isósceles de áre máim cuo perímetro se m Perímetro b h h re h ( ) Derivmos : bse crece
Pruebs de Selectividd de Ciencis PRUEB DE SELECTIVIDD-MODELO-- OPCIÓN : ) Hll l longitud de los ldos del triángulo isósceles de áre máim cuo perímetro se m Perímetro b h h re h ( ) Derivmos : bse crece
Espacios vectoriales y Aplicaciones Lineales II: Núcleo e imagen. Diagonalización. Ker(f) = {x V f(x) = 0} Im(f) = {f(x) x V}.
 UNIVERSIDAD DE JAÉN ESCUELA POLITÉCNICA SUPERIOR Deprtmento de Mtemátics (Áre de Álgebr) Curso 28/9 PRÁCTICA Nº Espcios vectoriles y Aplicciones Lineles II: Núcleo e imgen. Digonlizción. NÚCLEO E IMAGEN
UNIVERSIDAD DE JAÉN ESCUELA POLITÉCNICA SUPERIOR Deprtmento de Mtemátics (Áre de Álgebr) Curso 28/9 PRÁCTICA Nº Espcios vectoriles y Aplicciones Lineles II: Núcleo e imgen. Digonlizción. NÚCLEO E IMAGEN
vectores Componentes de un vector
 Vectores Un vector es un segmento orientdo. Está formdo por se representn: - con un flech encim v - en un eje de coordends - el módulo: es l longitud del origen l extremo - l dirección: es l rect que contiene
Vectores Un vector es un segmento orientdo. Está formdo por se representn: - con un flech encim v - en un eje de coordends - el módulo: es l longitud del origen l extremo - l dirección: es l rect que contiene
PROBLEMAS DE TEOREMA DE GREEN
 PROBLEMAS E TEOREMA E GREEN ENUNIAO EL TEOREMA Se un curv simple cerrd suve rozos oriend posiivmene se F(; (P;Q un cmpo vecoril cus funciones coordends ienen derivds prciles coninus sore un región ier
PROBLEMAS E TEOREMA E GREEN ENUNIAO EL TEOREMA Se un curv simple cerrd suve rozos oriend posiivmene se F(; (P;Q un cmpo vecoril cus funciones coordends ienen derivds prciles coninus sore un región ier
Vectores en el espacio 2º Bachillerato. Ana Mª Zapatero
 Vectores en el espcio º Bchillerto An Mª Zptero El conjunto R Es un conjunto de terns ordends de números reles R { ( x, y, z ) / x R, y R, z R } Primer componente Segund componente Tercer componente Iguldd
Vectores en el espcio º Bchillerto An Mª Zptero El conjunto R Es un conjunto de terns ordends de números reles R { ( x, y, z ) / x R, y R, z R } Primer componente Segund componente Tercer componente Iguldd
OPCIÓN A MATEMÁTICAS 2º BACHILLERATO B
 MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
Ejercicios de Análisis Matemático Integrales. Aplicaciones del cálculo integral
 Ejercicios de Análisis Memáico Inegrles. Alicciones del cálculo inegrl. Se f./ e sen. Jusific que f es inegrle en Œ; y se verific l desiguldd 6 f./ d 6 e. Solución. Como 6 sen 6 r odo Œ;, se sigue que
Ejercicios de Análisis Memáico Inegrles. Alicciones del cálculo inegrl. Se f./ e sen. Jusific que f es inegrle en Œ; y se verific l desiguldd 6 f./ d 6 e. Solución. Como 6 sen 6 r odo Œ;, se sigue que
I.E.S. PADRE SUÁREZ Álgebra Lineal 1 TEMA I MATRICES. DETERMINANTES.
 I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
I.E.S. PDRE SUÁREZ Álgebr Linel TEM I. Mtrices.. Operciones con mtrices. Determinnte de un mtriz cudrd.. Mtriz invers de un mtriz cudrd. MTRICES. DETERMINNTES.. MTRICES. Llmmos mtriz de números reles,
1.MATRICES. Definición : Se llama matriz de dimensiones m x n ( m filas y n columnas) a una. colección de datos expresados de la siguiente forma A=.
 .MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
.MATRICES. DEINICION, TERMINOLOGIA, TIPOS DE MATRICES Y OPERACIONES LINEALES: Definición : Se llm mri de dimensiones m n ( m fils n columns) un colección de dos epresdos de l siguiene form A=. m. m..........
1: El producto escalar de un vector consigo mismo coincide con el cuadrado de su módulo
 UNIDAD : Geometrí eclíde. Prodcto esclr. PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores y y se not por l nº rel qe se obtiene de l sigiente form: = es decir el
UNIDAD : Geometrí eclíde. Prodcto esclr. PRODUCTO ESCALAR DE DOS VECTORES LIBRES Definición: Se llm prodcto esclr de los ectores y y se not por l nº rel qe se obtiene de l sigiente form: = es decir el
t el espacio recorrido por los dos coches es el mismo t t 300; t 20s (20 10) 600m
 0. Un cuerpo pre del reposo y se muee con celerción consne. En un momeno ddo iene un elocidd de 9,4 m/s, y 48,8 meros más lejos lle un elocidd de 5, m/s. Clcul: ) L celerción. b) El iempo empledo en recorrer
0. Un cuerpo pre del reposo y se muee con celerción consne. En un momeno ddo iene un elocidd de 9,4 m/s, y 48,8 meros más lejos lle un elocidd de 5, m/s. Clcul: ) L celerción. b) El iempo empledo en recorrer
Vectores. Bases. Solución: a) Los vectores son linealmente independientes pues: λ(1, 2) + µ( 3, 1) = (0, 0) λ 3µ = 0; 2λ + µ = 0 λ = 0 y µ = 0
 Geomeí CTSL Vecoes. Bses. Ddos los vecoes u (, ) v (, ): ) Compueb que u v fomn un bse del espcio vecoil de los vecoes del plno. b) Encuen ls componenes del veco w (, 5) en l bse {u, v }. ) Los vecoes
Geomeí CTSL Vecoes. Bses. Ddos los vecoes u (, ) v (, ): ) Compueb que u v fomn un bse del espcio vecoil de los vecoes del plno. b) Encuen ls componenes del veco w (, 5) en l bse {u, v }. ) Los vecoes
es una matriz de orden 2 x 3.
 TEMA 7: MATRICES. 7.. Introducción l concepto de mtriz. 7.. Tipos de mtrices. 7.. El espcio vectoril de ls mtrices de orden m x n. 7.. INTRODUCCIÓN AL CONCEPTO DE MATRIZ. Se define mtriz de orden m x n
TEMA 7: MATRICES. 7.. Introducción l concepto de mtriz. 7.. Tipos de mtrices. 7.. El espcio vectoril de ls mtrices de orden m x n. 7.. INTRODUCCIÓN AL CONCEPTO DE MATRIZ. Se define mtriz de orden m x n
GUÍA DE EJERCICIOS II
 Faculad de Ingeniería UCV Álgebra ineal Geomería Analíica Ciclo Básico GUÍA DE Encuenre las ecuaciones de la reca que a) iene vecor direcor v (,, ) pasa por el puno P ( 4, 5, ) b) pasa por los punos A
Faculad de Ingeniería UCV Álgebra ineal Geomería Analíica Ciclo Básico GUÍA DE Encuenre las ecuaciones de la reca que a) iene vecor direcor v (,, ) pasa por el puno P ( 4, 5, ) b) pasa por los punos A
55 EJERCICIOS DE VECTORES
 55 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) d = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coordends de los vectores fijos
55 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) d = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coordends de los vectores fijos
Universidad Central de Venezuela Facultad de Farmacia Matemática - Física Prof. J. R. Morales
 Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
Universidd Centrl de Venezuel Fcultd de Frmci Mtemátic - Físic Prof J R Morles Guí de Vectores (Resumen de l Teorí) 1 En físic distinguiremos dos tipos de cntiddes: vectoriles esclres Ls cntiddes vectoriles
C cos x sen x 0 x sen x x cos x x sen x cos x x C 1 x 0. Calculamos la matriz adjunta de C: sen x 0 cox 0 cos x sen x. sen x x 1 x 1 sen x
 Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
TEMA 2. DETERMINANTES
 TEMA. DETERMINANTES A cd mtriz cudrd de orden n se le puede signr un número rel que se obtiene operndo de ciert mner con los elementos de l mtriz. A dicho número se le llm determinnte de l mtriz A, y se
TEMA. DETERMINANTES A cd mtriz cudrd de orden n se le puede signr un número rel que se obtiene operndo de ciert mner con los elementos de l mtriz. A dicho número se le llm determinnte de l mtriz A, y se
UNIDAD 7. PROPORCIONALIDAD, SEMEJANZA Y RELACIONES MÉTRICAS
 UNIDAD 7. PROPORCIONALIDAD, SEMEJANZA Y RELACIONES MÉTRICAS RAZONES Y PROPORCIONES DEFINICIONES RAZÓN: L rzón entre dos números reles y, (0), es el cociente entre y, es decir. Tmién se escrie: /,, :. PROPIEDADES
UNIDAD 7. PROPORCIONALIDAD, SEMEJANZA Y RELACIONES MÉTRICAS RAZONES Y PROPORCIONES DEFINICIONES RAZÓN: L rzón entre dos números reles y, (0), es el cociente entre y, es decir. Tmién se escrie: /,, :. PROPIEDADES
PROBLEMAS DE OPTIMIZACIÓN
 PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
PROBLEMAS DE OPTIMIZACIÓN Plntemiento y resolución de los problems de optimizción Se quiere construir un cj, sin tp, prtiendo de un lámin rectngulr de cm de lrg por de nch. Pr ello se recortrá un cudrdito
TEMA 11: PROBLEMAS MÉTRICOS
 Alonso Fernánde Glián TEMA PROBLEMAS MÉTRICOS Finlmente vmos ocprnos de clclr ánglos distncis entre rects plnos de resolver problems relciondos con estos conceptos.. ÁNGULOS ENTRE RECTAS Y PLANOS Vemos
Alonso Fernánde Glián TEMA PROBLEMAS MÉTRICOS Finlmente vmos ocprnos de clclr ánglos distncis entre rects plnos de resolver problems relciondos con estos conceptos.. ÁNGULOS ENTRE RECTAS Y PLANOS Vemos
Ecuaciones de Segundo Grado II
 Alumno: Fech:. ECUACIONES DE SEGUNDO GRADO II Ecuciones de Segundo Grdo II Nturlez de Ríces depende = b - 4c Discriminnte si Propieddes de ls Ríces sum b x x producto c x. x Formción de l Ecución se debe
Alumno: Fech:. ECUACIONES DE SEGUNDO GRADO II Ecuciones de Segundo Grdo II Nturlez de Ríces depende = b - 4c Discriminnte si Propieddes de ls Ríces sum b x x producto c x. x Formción de l Ecución se debe
PRÁCTICA 3 LEYES DE NEWTON
 Fundmenos Físicos de l Inenierí Inenierí Indusril Prácics de Lbororio PRÁCTIC 3 LEYES DE NEWTON 3 OJETIVO- Deerminr ls leyes que rien l relciones espcio-iempo y velocidd-iempo en movimienos uniformemene
Fundmenos Físicos de l Inenierí Inenierí Indusril Prácics de Lbororio PRÁCTIC 3 LEYES DE NEWTON 3 OJETIVO- Deerminr ls leyes que rien l relciones espcio-iempo y velocidd-iempo en movimienos uniformemene
CAPITULO II FUNCIONES VECTORIALES
 CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics
CAPITULO II FUNCIONES VECTORIALES En el cpíulo nerior, cundo describimos l rec en el espcio, uilizmos un prámero en ls ecuciones pr enconrr ls coordends de los punos que conformn es rec. ecuciones prmérics
Modelo 6 Opción A. Como me dicen que es y = 1 me están dando las condiciones
 Modelo 6 Opción A Ejercicio º [ puntos] Deterin l función f : R R sbiendo que f ( que l rect tngente l gráfic de f en el punto de bscis es l rect. L rect tngente de f( en es " f( f (( " Coo e dicen que
Modelo 6 Opción A Ejercicio º [ puntos] Deterin l función f : R R sbiendo que f ( que l rect tngente l gráfic de f en el punto de bscis es l rect. L rect tngente de f( en es " f( f (( " Coo e dicen que
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID EJERCICIOS PAUS MATEMÁTICAS II (DESDE EL CURSO 07-08 AL 11-12) ÁLGEBRA: TEMAS 1-2-3
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID EJERCICIOS PUS MTEMÁTICS II (DESDE EL CURSO 78 L ) ÁLGEBR: TEMS (Los ejercicios de selectividd resueltos los podéis encontrr en l págin web clsesdepooco) http://wwwclsesdepooco/docuents/es_serch
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID EJERCICIOS PUS MTEMÁTICS II (DESDE EL CURSO 78 L ) ÁLGEBR: TEMS (Los ejercicios de selectividd resueltos los podéis encontrr en l págin web clsesdepooco) http://wwwclsesdepooco/docuents/es_serch
EXAMEN DE MATEMÁTICAS II (Recuperación)
 º Bchillero Ciencis XN D TÁTICS II Recuperción) ÁLGBR. ), punos) Clsific en función del práero R, el sise de ecuciones: b) puno) Resuélvelo pr, si es posible.. Se un ri cudrd de orden. Si el deerinne de
º Bchillero Ciencis XN D TÁTICS II Recuperción) ÁLGBR. ), punos) Clsific en función del práero R, el sise de ecuciones: b) puno) Resuélvelo pr, si es posible.. Se un ri cudrd de orden. Si el deerinne de
2. REPRESENTACIÓN ANALÍTICA Y GRÁFICA DE UN VECTOR
 1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid
Ángulos, distancias. Observación: La mayoría de los problemas resueltos a continuación se han propuesto en los exámenes de Selectividad.
 Geomeía del espacio Ángulos, disancias Obseación: La maoía de los poblemas esuelos a coninuación se han popueso en los eámenes de Seleciidad.. Calcúlese la disancia del oigen al plano que pasa po A(,,
Geomeía del espacio Ángulos, disancias Obseación: La maoía de los poblemas esuelos a coninuación se han popueso en los eámenes de Seleciidad.. Calcúlese la disancia del oigen al plano que pasa po A(,,
EXAMEN RESUELTO Septiembre de 2002
 EXMEN RESUELTO Sepieme de V L{ 45} ë ë Sen los suespcios de R : V ë ë V Hll: Ls dimensiones uns ses de los es suespcios. L dimensión del suespcio VV c Uns ecuciones implícis del suespcio V V. d Compo si
EXMEN RESUELTO Sepieme de V L{ 45} ë ë Sen los suespcios de R : V ë ë V Hll: Ls dimensiones uns ses de los es suespcios. L dimensión del suespcio VV c Uns ecuciones implícis del suespcio V V. d Compo si
TEMA 2. Determinantes Problemas Resueltos
 Memáis II (hillero de Cienis). Soluiones de los prolems propuesos. Tem Clulo de deerminnes TEM. Deerminnes Prolems Resuelos. Hll el vlor de los siguienes deerminnes ) ) ) C Soluión ) Se desrroll por l
Memáis II (hillero de Cienis). Soluiones de los prolems propuesos. Tem Clulo de deerminnes TEM. Deerminnes Prolems Resuelos. Hll el vlor de los siguienes deerminnes ) ) ) C Soluión ) Se desrroll por l
Matemáticas 2º Bachillerato MATRICES. columnas es muy antiguo, pero fue en el siglo XIX cuando J.J. Sylverster ( )
 TRICES emáics º chillero. Inroducción. Definición de mriz El concepo de mriz como un bl ordend de números escrios en fils y columns es muy niguo, pero fue en el siglo XIX cundo J.J. Sylverser (8-897) cuñó
TRICES emáics º chillero. Inroducción. Definición de mriz El concepo de mriz como un bl ordend de números escrios en fils y columns es muy niguo, pero fue en el siglo XIX cundo J.J. Sylverser (8-897) cuñó
FUNCIONES VECTORIALES
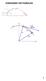 FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
FUNCIONES VECTORIALES v - v e lo c i d d i n i c i l v v v lur inicil v r() P Vecor velocidd r() r Q r(+) INDICE FUNCIONES VECTORIALES FUNCIÓN VECTORIAL 4 Dominio de un función vecoril 5 Operciones con
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 06 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserv, Ejercicio, Opción A Reserv, Ejercicio, Opción B Reserv, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 06 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserv, Ejercicio, Opción A Reserv, Ejercicio, Opción B Reserv, Ejercicio,
CAPÍTULO. La derivada
 CAPÍTULO 5 L derivd 5. L derivd de un función A continución trtremos uno de los concetos fundmentles del cálculo, que es el de l derivd. Este conceto es un ite que está estrecmente ligdo l rect tngente,
CAPÍTULO 5 L derivd 5. L derivd de un función A continución trtremos uno de los concetos fundmentles del cálculo, que es el de l derivd. Este conceto es un ite que está estrecmente ligdo l rect tngente,
MÉTODOS ESTADÍSTICOS DE LA INGENIERÍA SEGUNDA CONVOCATORIA
 Dertmento de Mtemátic Alicd Escuel Universitri de Ingenierí Técnic Industril Universidd del Pís Vsco Plz de l Csill, 48 Bilbo MÉTODOS ESTADÍSTICOS DE LA INGENIERÍA SEGUNDA CONVOCATORIA - EJERCICIO Tres
Dertmento de Mtemátic Alicd Escuel Universitri de Ingenierí Técnic Industril Universidd del Pís Vsco Plz de l Csill, 48 Bilbo MÉTODOS ESTADÍSTICOS DE LA INGENIERÍA SEGUNDA CONVOCATORIA - EJERCICIO Tres
SELECTIVIDAD: MATRICES. B y
 SELETIVIDD: MTRIES EJERIIO. ) Sen dos ries udrds del iso orden que ienen invers. Ron si su produo iene invers. ) Dds ls ries - D, Deerin si D iene invers, en ese so, hálll. EJERIIO. onsider ls ries,. )
SELETIVIDD: MTRIES EJERIIO. ) Sen dos ries udrds del iso orden que ienen invers. Ron si su produo iene invers. ) Dds ls ries - D, Deerin si D iene invers, en ese so, hálll. EJERIIO. onsider ls ries,. )
Tema 5. Trigonometría y geometría del plano
 1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
1 Tem. Trigonometrí y geometrí del plno 1. Rzones trigonométrics de un ángulo gudo Ddo un ángulo culquier, si desde un punto, A, de uno de sus ldos se trz su proyección, A, sobre el otro ldo se obtiene
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
GUÍA DE MATEMÁTICAS V. Ciclo escolar B determina:
 Elbor: Preprtori Págin 1 de 14 Ciclo escolr 014-015 Docente: Fernndo Vivr Mrtínez I) Producto Crtesino, Relciones y Funciones B determin: 1) Ddos los conjuntos A 0,1,,3 y 4,5,6,7 ) El Producto Crtesino
Elbor: Preprtori Págin 1 de 14 Ciclo escolr 014-015 Docente: Fernndo Vivr Mrtínez I) Producto Crtesino, Relciones y Funciones B determin: 1) Ddos los conjuntos A 0,1,,3 y 4,5,6,7 ) El Producto Crtesino
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
 el log de me de id CSII: mrices y deerminnes pág. DEFINICIONES Un cden de iends de elecrodomésicos dispone de curo lmcenes. En un deermindo momeno ls exisencis de lvdors, frigoríficos y cocins son ls siguienes:
el log de me de id CSII: mrices y deerminnes pág. DEFINICIONES Un cden de iends de elecrodomésicos dispone de curo lmcenes. En un deermindo momeno ls exisencis de lvdors, frigoríficos y cocins son ls siguienes:
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho
 IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO Curso / MATERIA MATEMATICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El lumno
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MODELO Curso / MATERIA MATEMATICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El lumno
TEMA 1: MATRICES. Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas ...
 Deprtmento de Mtemátics TEM : MTRICES Un mtriz de orden mxn es un conjunto de m n números reles dispuestos en m fils y n columns... n... n... m m m... mn los números reles ij se les llm elementos de l
Deprtmento de Mtemátics TEM : MTRICES Un mtriz de orden mxn es un conjunto de m n números reles dispuestos en m fils y n columns... n... n... m m m... mn los números reles ij se les llm elementos de l
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
1º (junio 1994) i) Estudiar, para los diferentes valores del parámetro a, la existencia de
 Sistems de ecuciones lineles SISTEMAS DE ECUACIONES LINEALES EJERCICIOS DE SELECTIVIDAD º (junio 994) i) Estudir, pr los diferentes vlores del prámetro, l eistenci de soluciones del sistem resolverlo cundo
Sistems de ecuciones lineles SISTEMAS DE ECUACIONES LINEALES EJERCICIOS DE SELECTIVIDAD º (junio 994) i) Estudir, pr los diferentes vlores del prámetro, l eistenci de soluciones del sistem resolverlo cundo
SOSTENIBILIDAD DE UNA POLÍTICA FISCAL
 1 SOSTENIBILIDAD DE UNA POLÍTICA FISCAL Definición de un políic fiscl sosenible El concepo de políic fiscl sosenible no cep un definición precis. Sin embrgo, un definición generl (unque lgo rivil) es que
1 SOSTENIBILIDAD DE UNA POLÍTICA FISCAL Definición de un políic fiscl sosenible El concepo de políic fiscl sosenible no cep un definición precis. Sin embrgo, un definición generl (unque lgo rivil) es que
dec. per. puros dec. per. mixtos Irracionales dec. inf. cifras no periódicas.
 Cmo numérico. Nurles N Eneros Z Negivos Rcionles Q dec. excos dec. er. uros dec. er. mixos Reles R Frccionrios Irrcionles dec. inf. cifrs no eriódics. Alguns considerciones. Pr sr de un nº en form frccionri
Cmo numérico. Nurles N Eneros Z Negivos Rcionles Q dec. excos dec. er. uros dec. er. mixos Reles R Frccionrios Irrcionles dec. inf. cifrs no eriódics. Alguns considerciones. Pr sr de un nº en form frccionri
ÁlgebrayGeometría. 5. Halla la ecuación de la circunferencia que pasa por (3, 0), ( 1, 0) y (0, 3).
 ÁlgebryGeometrí 1. ) Ddos tres puntos A, B y C en el plno demuestr que l circunferenci de diámetro AC ps por B siysólosielánguloâbc es recto. b) Ddos dos puntos A y B del plno y un rect r, determin, cundo
ÁlgebryGeometrí 1. ) Ddos tres puntos A, B y C en el plno demuestr que l circunferenci de diámetro AC ps por B siysólosielánguloâbc es recto. b) Ddos dos puntos A y B del plno y un rect r, determin, cundo
Resuelve. Unidad 3. Sistemas de ecuaciones. BACHILLERATO Matemáticas II. Los fardos de cereal. Página 89
 Unidd. Sises de ecuciones BCHILLERTO Meáics II Resuelve Págin 9 Los rdos de cerel Resuelve el role chino de los rdos de cerel rocediendo de or siilr coo lo resolvieron ellos. Recuerd el éodo de Guss que
Unidd. Sises de ecuciones BCHILLERTO Meáics II Resuelve Págin 9 Los rdos de cerel Resuelve el role chino de los rdos de cerel rocediendo de or siilr coo lo resolvieron ellos. Recuerd el éodo de Guss que
51 EJERCICIOS DE VECTORES
 51 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coorens e los vectores fijos e l
51 EJERCICIOS DE VECTORES 1. ) Representr en el mismo plno los vectores: = (3,1) b = ( 1,5) c = (, 4) = ( 3, 1) i = (1,0) j = (0,1) e = (3,0) f = (0, 5) b) Escribir ls coorens e los vectores fijos e l
Tema 2. Determinantes
 Memáics plicds ls iencis Sociles II Álger: Deerminnes Deerminne de un mriz Tem Deerminnes Definición de deerminne El deerminne de un mriz cudrd es un número Pr l mriz, su deerminne se deno por de() o por
Memáics plicds ls iencis Sociles II Álger: Deerminnes Deerminne de un mriz Tem Deerminnes Definición de deerminne El deerminne de un mriz cudrd es un número Pr l mriz, su deerminne se deno por de() o por
a) en vertical el movimiento es uniforme 400 t 40s b) en ese tiempo, en horizontal e v t 320m c) el ángulo, respecto a la vertical es v v rio
 0. Ls gus de un río de 400 m de nchur se desplzn con un elocidd de 8 m/s. Un brc cruz el río de orill orill, mneniéndose perpendiculr l corriene. L brc se muee con un elocidd consne de 0 m/s. Clculr: )
0. Ls gus de un río de 400 m de nchur se desplzn con un elocidd de 8 m/s. Un brc cruz el río de orill orill, mneniéndose perpendiculr l corriene. L brc se muee con un elocidd consne de 0 m/s. Clculr: )
Álgebra Vectorial. Matemática
 Álger Vectoril 3º Año Cód. 3-5 P r o f. N o e m í L g r e c P r o f. M i r t R o s i t o P r o f. S u s n S t r z z i u s o Dto. de I- Introducción En diverss oortuniddes nos hemos encontrdo en tems relciondos
Álger Vectoril 3º Año Cód. 3-5 P r o f. N o e m í L g r e c P r o f. M i r t R o s i t o P r o f. S u s n S t r z z i u s o Dto. de I- Introducción En diverss oortuniddes nos hemos encontrdo en tems relciondos
