Figura 2.4a Orientación inicial. Figura 2.4b El robot ha rotado.
|
|
|
- Pascual Navarro Tebar
- hace 7 años
- Vistas:
Transcripción
1 Cpítulo 3 RQUITECTUR DE U ROBOT F80 E est seccó se elbor u álss de los sstes que copoe u robot F80 El álss prte de l ucoldd básc requerd srve coo puto de prtd pr el dseño l pleetcó de u equpo de robots F80 3 Locoocó U robot óvl requere ecsos de locoocó que le pert desplzrse e su bete Exste u gr vredd de solucoes pr logrr que u robot teg oveto uchos de estos ecsos de locoocó está sprdos e sus cotrprtes bológcs [SIE 004] U gr excepcó l costtue l rued, u vecó de l hudd que brd u excelete ovldd e betes plos L rued h sdo el ecso de locoocó ás usdo e los robots óvles, su uso orece u bue estbldd blce pero requere que se toe e cuet l trccó, l obrbldd el cotrol del oveto [SIE 004] El tpo de desplzeto que se debe cosderr pr u robot óvl está suete relcodo co el tpo l geoetrí de ls rueds Exste uchos tpos de desplzeto pero debdo sus crcterístcs u slres puede ser clscdos e dos grdes clses: derecl, odreccol 3 El desplzeto derecl U desplzeto derecl cosder u rreglo pr de rueds El prcpo de ucoeto es sple: Pr que el robot se desplce hc delte coservdo su oretcó ls rueds debe grr l s velocdd e l s dreccó Pr que el robot cbe su oretcó debe exstr u derec de velocddes e ls rueds, etrs ás grde se l derec de velocddes e ls rueds ás grde será el cbo e l oretcó del robot E l Fgur 5 se pretede ostrr 7
2 rqutectur de u equpo SSL que el robot cbrá de oretcó coo cosecuec de que ls rueds está grdo l s velocdd pero e setdo cotrro, e este cso el robot úcete rot o se trsld Fgur 4 Oretcó cl Fgur 4b El robot h rotdo 3 El desplzeto odreccol El desplzeto odreccol es de gr terés porque brd u coplet obrbldd Los robots odreccoles puede overse e culquer dreccó e culquer oeto s requerr u oretcó especíc pr el desplzeto del robot Este tpo de desplzeto requere de rueds que se pued over e ás de u dreccó, l gur 5 uestr el dseño de u rued odreccol Fgur 5 Dseño de u rued odreccol El oveto odreccol h dqurdo populrdd e los robots óvles porque perte que el robot se desplce e líe rect desde u puto orge hc culquer otro puto, s teer que rotr tes de desplzrse dcolete, l trslcó sobre l rut desed se puede cobr co u rotcó, de odo que el robot lleg su desto e el águlo correcto 8
3 Cpítulo Se requere ás de dos rueds odreccoles pr over u robot Cd rued proporco u uerz e u dreccó orl 3 l eje del otor prlel l pso L su de uerzs prové l trslcó rotcó del robot L gur 6 uestr l bse de los otores co sus rueds del prototpo de u robot odreccol F80 Fgur 6 Bse de otores co rueds pr u robot odreccol 33 Cotrol odreccol Exste u relcó vers etre l obrbldd el cotrol Por ejeplo, los dseños odreccoles requere u proceseto dcol pr covertr ls velocddes de rotcó trslcó del robot e velocddes dvdules pr cd rued Cotrolr u robot odreccol pr que se uev e u dreccó desed es ás coplcdo que los étodos derecles Pr ello es ecesro estblecer u odelo ceátco odreccol 34 odelo ceátco odreccol El proceso pr eteder el oveto de u robot coez co el proceso de descrbr l cotrbucó de cd rued pr ello es ecesro estblecer u rco de reerec tor e cuet lgus porttes cosdercoes 4 E este cso, el rco de reerec es el plo crteso L gur 7 es u represetcó de u robot odreccol e el plo crteso 3 90 grdos 4 Ess cosdercoes se detll e el exo L covecó de Osk 9
4 rqutectur de u equpo SSL Fgur 7 El robot odreccol e el plo crteso Co este rco de reerec se puede deterr l poscó del robot s se cooce ls coordeds (x) del cetro del robot El robot de l gur 8 es odreccol, tee tres rueds su cetro se loclz e el orge Pr poder descopoer l cotrbucó de cd otor e téros de X Y es ecesro utlzr l segud Le de ewto: F =, = Por edo de l ecucó se puede deterr l relcó drect que exste etre l celercó de u cuerpo, su s l su de uerzs que terctú sobre él [LV 983] Pr el cso geerl de u robot odreccol de s co otores ( 3), despejdo l celercó de : 0
5 Cpítulo = Pr clculr ls copoetes de celercó e los ejes X Y se debe tor e cuet el águlo ( θ ) sobre el que se coloc el otor co respecto los ejes que l dreccó postv de l uerz del otor (de cuerdo co l covecó de Osk) put π θ + Etoces, l proeccó de los copoetes de celercó e los ejes X Y se obtee co ls sguetes ecucoes: x π = se( + ) π = cos( + ) Y cosderdo que: θ, 3 θ 4 se ( x + t) = se( x) cos( t) + cos( x) se( t), cos( x + t) = cos( x) cos( t) se( x) se( t) Ls ecucoes 3 4 se puede expresr de l sguete or: = x cos θ, = se θ Por otr prte, pr obteer l celercó rotcol se debe cosderr que ls uerzs que ejerce los otores so tgetes l rco crculr del robot put hc l s dreccó rotcol Etoces, l celercó rotcol está dd por l sguete ecucó [ROJ 004]:
6 rqutectur de u equpo SSL = R w I 5 Dode R es el rdo del robot, es l gtud de l uerz del -éso otor, e I es el oeto de erc El oeto de erc de u cldro sóldo es pr u ro delgdo es R I = etrs que I = R [TIP 995] Pr culquer dstrbucó de s estrctete etre u cocetrcó de s e el cetro e l perer (que serí el cso del robot), ecucó 5 qued expresd coo: w = I = αr co 0<α < Etoces, l αr Ess ecucoes de celercó (3, 4 5) puede ser expresds coo el vector de celercoes producto de u trz por u vector de uerzs x ω cosθ = seθ αr αr T ( x,, w ) que se obtee coo el αr 6 Pr trbjr co ls ss uddes (etro sobre segudo l cudrdo) pr l celercó lel l celercó gulr, e vez de utlzr ω se puede utlzr R ω l ecucó qued:
7 Cpítulo x R ω cosθ = seθ α α α Splcdo l escrtur de l ecucó 6 se tee: Dode: : Vector de celercoes del robot = : trz de copleto de celercó : Vector de uerzs de los otores L ecucó 6 perte ecotrr ls copoetes de celercó de los ejes del rco de reerec (celercoes del robot) l celercó rotcol dd u cogurcó 5 de otores l uerz que cd otor ejerce Por otr prte, pr ls ruts de cotrol de I es útl ecotrr u expresó que relcoe l velocdd del robot co el vector de velocddes de los otores Esto sucede porque u robot que se ecuetr e u poscó cl debe relzr u oveto, que e el ejor de los csos es, sobre u líe rect pr que llegue u poscó desed Este oveto, coo uestr l gur 8, se represet coo u vector de velocdd co u gtud u dreccó 6 5 L cogurcó se reere l poscó de los otores 6 Ver el exo pr clrr ls cosdercoes de l dreccó de este vector 3
8 rqutectur de u equpo SSL Fgur 8 El robot debe r u poscó utur Ese vector es l resultte de ls velocddes del robot ( v, x v,ω ) por lo que es ecesro ecotrr u expresó que relcoe ls velocddes del robot co ls velocddes de cd otor pr que ls ruts de I evíe es orcó l robot éste se uev hc l poscó desed suedo que l relcó que se pretede ecotrr es álog l ecucó 6, se puede supoer que tee l or v es el vector de velocddes de los otores v v, dode: T ( v, v,, v ) V es l trz de copleto de velocddes, de desó x 3 v R es el vector de velocddes del robot ( v, v, ω ) T x x v v e Supoedo que el vector de velocddes del robot es T (,0,0), esto quere decr que el robot se desplz e líe rect sobre el eje X u velocdd de s ls rueds del robot estrá grdo u velocdd de 4
9 Cpítulo 7 S el robot se desplzr e líe rect hc el rete (sobre el v 0,, 0 eje Y) etoces el vector ( ) T = ls rueds tedrí u velocdd de S el robot úcete rotr v ( 0,0, ) T = cd otor tedrí u velocdd de 8 Por lo teror, l relcó se puede expresr coo: splcdo l escrtur: v v = v cosθ v = v V R vx v ω 7 Hst hor se h obtedo dos expresoes de gr utldd pr el dseño de u robot F80 grcs ells es posble: Trsorr ls uerzs de los otores e celercoes del robot: = 6 Trsorr velocddes del robot e velocddes de los otores: v = v 7 Cosderdo que ls ecucoes terores utlz trces, e ls sguetes líes se lzrá s es ctble obteer ls relcoes verss V E 7 De cuerdo co lo estblecdo e el exo 8 es el úero de otores del robot 5
10 rqutectur de u equpo SSL L or splcd de l ecucó 6 sugere que l relcó vers se podrí ecotrr áclete l cosderr que el cocepto de vers de u trz es álogo l del recíproco de u úero rel E el setdo de que el producto de u úero rel co su recíproco es l udd, sí coo el producto de u trz co su vers es l trz detdd Recorddo l decó de u trz vers: Se I l trz detdd de u trz cudrd de S exste u trz de que teg l propedd de que: = I = Se dce que es l vers de [STE 000] El proble rdc e que l trz o es vertble o es cudrd por lo tto Pr resolver probles de este tpo se recurre l uso de l trz pseudovers, cu decó es l sguete: S es u trz de, se ll pseudovers de l trz : ( ) = ó + T T = s el rgo de + T T = ( ) s el rgo = De est er se obtee ls trces pseudoverss +, + V ls expresoes que perte: Trsorr celercoes del robot e uerzs de otores + = 8 Trsorr velocddes de los otores e velocddes del robot: v R + = V 9 Hst este puto se h ecotrdo cutro ecucoes u útles pr el dseño de u robot F80 6
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS NÚMEOROS COMPLEJOS
 NÚMEOROS COMPLEJOS Defcó: El cojuto de los úmeros complejos es C R R {(, / R y b R} C está formdo por todos los pres ordedos de úmeros reles etre los que defmos u relcó, l guldd, y dos opercoes brs que
NÚMEOROS COMPLEJOS Defcó: El cojuto de los úmeros complejos es C R R {(, / R y b R} C está formdo por todos los pres ordedos de úmeros reles etre los que defmos u relcó, l guldd, y dos opercoes brs que
suma sucesiva de los primeros m términos como se ve a continuación m 1
 A veces se ecest deterr l su de uchos téros de u sucesó ft. Pr expresr co fcldd ess sus, se us l otcó de sutor. Dd u sucesó ft,,,...,... el síbolo represet l sutor o su sucesv de los preros téros coo se
A veces se ecest deterr l su de uchos téros de u sucesó ft. Pr expresr co fcldd ess sus, se us l otcó de sutor. Dd u sucesó ft,,,...,... el síbolo represet l sutor o su sucesv de los preros téros coo se
3. Unidad Aritmética Lógica (ALU)
 3. Udd rtmétc Lógc (LU) bordremos los spectos que permte l mplemetcó de l rtmétc de u computdor, trbuto fucol de l Udd rtmétc Lógc (LU). Prmero se revstrá lo relcodo l form de represetr los úmeros como
3. Udd rtmétc Lógc (LU) bordremos los spectos que permte l mplemetcó de l rtmétc de u computdor, trbuto fucol de l Udd rtmétc Lógc (LU). Prmero se revstrá lo relcodo l form de represetr los úmeros como
a es la parte real, bi la parte imaginaria.
 CAPÍTULOIX 55 NÚMEROS COMPLEJOS Coocmetos Prevos Supoemos coocdo que: ) El cojuto de úmeros complejos está e correspodec buívoc co el cojuto de los putos de u plo. b) U úmero complejo expresdo e form boml
CAPÍTULOIX 55 NÚMEROS COMPLEJOS Coocmetos Prevos Supoemos coocdo que: ) El cojuto de úmeros complejos está e correspodec buívoc co el cojuto de los putos de u plo. b) U úmero complejo expresdo e form boml
Guía ejercicios resueltos Sumatoria y Binomio de Newton
 Aulr: Igco Domgo Trujllo Slv Uversdd de Chle Guí ejerccos resueltos Sumtor y Bomo de Newto Solucó: ) Como o depede de j, es costte l sumtor. b) c) d) Aulr: Igco Domgo Trujllo Slv Uversdd de Chle e) f)
Aulr: Igco Domgo Trujllo Slv Uversdd de Chle Guí ejerccos resueltos Sumtor y Bomo de Newto Solucó: ) Como o depede de j, es costte l sumtor. b) c) d) Aulr: Igco Domgo Trujllo Slv Uversdd de Chle e) f)
MODELAJE DE SISTEMAS MECÁNICOS ROTACIONALES
 Deprteto de Proceo y Ste MODA D SISMAS MCÁICOS OACIOAS Pro. Alexder Hoyo uo 00 Crc, Veezuel Pro. Alexder Hoyo. Uverdd So Bolívr. Deprteto de Proceo y Ste. Pág. / ÍDIC Pág. Ste ecáco rotcol Servootor de
Deprteto de Proceo y Ste MODA D SISMAS MCÁICOS OACIOAS Pro. Alexder Hoyo uo 00 Crc, Veezuel Pro. Alexder Hoyo. Uverdd So Bolívr. Deprteto de Proceo y Ste. Pág. / ÍDIC Pág. Ste ecáco rotcol Servootor de
10. Optimización no lineal
 0. Optzcó o lel Coceptos báscos Prcpos y teores pr l búsqued de óptos lobles Optzcó s restrccoes e desó Optzcó s restrccoes e desó > Modelos co restrccoes de uldd Codcoes de uh-tucker Alortos uércos báscos
0. Optzcó o lel Coceptos báscos Prcpos y teores pr l búsqued de óptos lobles Optzcó s restrccoes e desó Optzcó s restrccoes e desó > Modelos co restrccoes de uldd Codcoes de uh-tucker Alortos uércos báscos
UNIVERSIDAD DE GRANADA PONENCIA DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES PONENTE: PROF. FRANCISCO JIMÉNEZ GÓMEZ
 UNIVERSIDD DE GRND ONENCI DE MTEMÁTICS LICDS LS CIENCIS SOCILES ONENTE: ROF FRNCISCO JIMÉNEZ GÓMEZ RUE DE CCESO R MYORES DE ÑOS CONVOCTORI DE ENUNCIDOS Y RESOLUCIÓN DE LOS EJERCICIOS ROUESTOS EN MTEMÁTICS
UNIVERSIDD DE GRND ONENCI DE MTEMÁTICS LICDS LS CIENCIS SOCILES ONENTE: ROF FRNCISCO JIMÉNEZ GÓMEZ RUE DE CCESO R MYORES DE ÑOS CONVOCTORI DE ENUNCIDOS Y RESOLUCIÓN DE LOS EJERCICIOS ROUESTOS EN MTEMÁTICS
- Función Polinómica f es toda función de dominio el conjunto de los números reales, tal que la imagen de cada número real x es:
 POLINOMIOS Defcó: Fucó Polóc - Fucó Polóc f es tod fucó de doo el cojuto de los úeros reles, tl que l ge de cd úero rel es: f = + + + + +, dode,,,,, so ueros reles y es turl Defcó: Poloo - Poloo de vrble
POLINOMIOS Defcó: Fucó Polóc - Fucó Polóc f es tod fucó de doo el cojuto de los úeros reles, tl que l ge de cd úero rel es: f = + + + + +, dode,,,,, so ueros reles y es turl Defcó: Poloo - Poloo de vrble
Se puede observar que una partición de un intervalo lo divide en n subintervalos, y a cada uno de ellos se les llama también celda.
 Itegrl defd. Fucó tegrle Sum de Rem Se el tervlo [, ]. E cojuto de putos: P = { 0,,......., } Dode 0 = ; = ; < ; =,,....., Se llm prtcó o red de tervlo [, ] Se puede oservr que u prtcó de u tervlo lo dvde
Itegrl defd. Fucó tegrle Sum de Rem Se el tervlo [, ]. E cojuto de putos: P = { 0,,......., } Dode 0 = ; = ; < ; =,,....., Se llm prtcó o red de tervlo [, ] Se puede oservr que u prtcó de u tervlo lo dvde
(Apuntes sin revisión para orientar el aprendizaje) CÁLCULO INTEGRAL LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA
 (Aputes s revsó pr oretr el predzje) CÁLCULO INTEGRAL LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA Sumtor Pr represetr e form revd determdo tpo de sums, se utlz como símolo l letr greg sgm. Ejemplos.
(Aputes s revsó pr oretr el predzje) CÁLCULO INTEGRAL LA INTEGRAL DEFINIDA Y LA INTEGRAL INDEFINIDA Sumtor Pr represetr e form revd determdo tpo de sums, se utlz como símolo l letr greg sgm. Ejemplos.
EXPRESIONES ALGEBRAICAS
 EXPRESIONES ALGEBRAICAS 1 Epresoes Algebrcs es l uó de úmeros y vrbles medte opercoes de sum, rest, multplccó, dvsó, poteccó y rdccó. Epresó lgebrc rcol: se llm sí quells e ls que ls vrbles está fectds
EXPRESIONES ALGEBRAICAS 1 Epresoes Algebrcs es l uó de úmeros y vrbles medte opercoes de sum, rest, multplccó, dvsó, poteccó y rdccó. Epresó lgebrc rcol: se llm sí quells e ls que ls vrbles está fectds
POLINOMIOS. - Ejemplo: es un polinomio ordenado segun la variable x, cuyos coeficientes son: 2
 POLINOMIOS Defcó: Fucó Polóc - Fucó Polóc f es tod fucó de doo el cojuto de los úeros reles, tl que l ge de cd úero rel x es: f x = x + x + + x + x+, dode,,,,, so ueros reles y es turl Defcó: Poloo - Poloo
POLINOMIOS Defcó: Fucó Polóc - Fucó Polóc f es tod fucó de doo el cojuto de los úeros reles, tl que l ge de cd úero rel x es: f x = x + x + + x + x+, dode,,,,, so ueros reles y es turl Defcó: Poloo - Poloo
OPCIÓN A. c) (1 punto)
 UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Curso / MTERI MTEMTICS II. se de Modlidd OPCIÓN Ejercicio. Clificció ái putos. Sbiedo que, utilizdo ls
UNIVERSIDDES PÚBLICS DE L COMUNIDD DE MDRID PRUEB DE CCESO LS ENSEÑNZS UNIVERSITRIS OICILES DE GRDO Curso / MTERI MTEMTICS II. se de Modlidd OPCIÓN Ejercicio. Clificció ái putos. Sbiedo que, utilizdo ls
CAPITULO 1 VECTORES EN R 3
 CPITULO Nuestrs lms, cuys fcultdes puede compreder l mrvllos rqutectur del mudo, y medr el curso de cd plet vgbudo, ú escl trs el coocmeto fto Chrstopher Mrlowe. ECTORES EN R. Mgtudes esclres y vectorles..
CPITULO Nuestrs lms, cuys fcultdes puede compreder l mrvllos rqutectur del mudo, y medr el curso de cd plet vgbudo, ú escl trs el coocmeto fto Chrstopher Mrlowe. ECTORES EN R. Mgtudes esclres y vectorles..
Definimos renta financiera como un conjunto de capitales que han de hacerse efectivos en determinados vencimientos.
 Te 3 lorcó e Rets lorcó e rets Defos ret fcer coo u cojuto e cptles que h e hcerse efectvos e eteros vecetos. (, t, ( 2, t 2,, (, t Llreos téros e l ret ls cutís e los cptles fceros que copoe l ret (,
Te 3 lorcó e Rets lorcó e rets Defos ret fcer coo u cojuto e cptles que h e hcerse efectvos e eteros vecetos. (, t, ( 2, t 2,, (, t Llreos téros e l ret ls cutís e los cptles fceros que copoe l ret (,
2.1 SUCESIONES 2.2 SUMAS Y NOTACIÓN SIGMA
 Sucesoes. SUCESIONES. SUMAS Y NOTACIÓN SIGMA Objetvos: Se pretede que el estudte: Determe covergec o dvergec de sucesoes. Alce Mootoí de sucesoes. Coozc ls propeddes de l otcó sgm. 5 Sucesoes.. SUCESIONES..
Sucesoes. SUCESIONES. SUMAS Y NOTACIÓN SIGMA Objetvos: Se pretede que el estudte: Determe covergec o dvergec de sucesoes. Alce Mootoí de sucesoes. Coozc ls propeddes de l otcó sgm. 5 Sucesoes.. SUCESIONES..
Capítulo 10. Teoría de pertubaciones
 Cpítulo Teorí de pertubcoes Desrrollo perturbtvo Vlores propos Norlzcó Desrrollo de ls correccoes e l bse del hltoo de referec Estdos o degeerdos Eeplo: Oscldor róco e u cpo de fuerz costte Eeplo: Efecto
Cpítulo Teorí de pertubcoes Desrrollo perturbtvo Vlores propos Norlzcó Desrrollo de ls correccoes e l bse del hltoo de referec Estdos o degeerdos Eeplo: Oscldor róco e u cpo de fuerz costte Eeplo: Efecto
Lenguaje humano. Representación de la información. Utiliza un conjunto de símbolos alfanuméricos. Puede representar Información
 Leguje humo Represetcó de l formcó Utlz u cojuto de símbolos lfumércos Crcteres lfbétcos:, B, C,.Z,, b, c,...z Símbolos umércos 9 sgos de putucó... Puede represetr Iformcó umérc lfumérc Leguje del ordedor
Leguje humo Represetcó de l formcó Utlz u cojuto de símbolos lfumércos Crcteres lfbétcos:, B, C,.Z,, b, c,...z Símbolos umércos 9 sgos de putucó... Puede represetr Iformcó umérc lfumérc Leguje del ordedor
Repaso general de matemáticas básicas
 Repso geerl de mtemátics básics Expoetes y rdicles Regl de l multiplicció: Cudo dos ctiddes co l mism bse se multiplic, su producto se obtiee sumdo lgebricmete los expoetes. m m Expoete egtivo U térmio
Repso geerl de mtemátics básics Expoetes y rdicles Regl de l multiplicció: Cudo dos ctiddes co l mism bse se multiplic, su producto se obtiee sumdo lgebricmete los expoetes. m m Expoete egtivo U térmio
Seminario Universitario de Ingreso Números reales
 Seirio Uiversitrio de Igreso 07 Núeros reles Si u úero posee ifiits cifrs deciles o periódics, o puede escriirse coo u cociete etre úeros eteros, es decir, o es u Núero Rciol. Estos úeros recie el ore
Seirio Uiversitrio de Igreso 07 Núeros reles Si u úero posee ifiits cifrs deciles o periódics, o puede escriirse coo u cociete etre úeros eteros, es decir, o es u Núero Rciol. Estos úeros recie el ore
CAPÍTULO 6. CINEMÁTICA DIFERENCIAL DEL ROBOT PARALELO
 CAÍUO. CNMÁCA DFRNCA D ROBO ARAO es seccó se descrbe el álss de elocddes y celercoes del robo prlelo, el cul puede llerse cbo mede ls ecucoes pr momeo geerl debdo que o ese deslzmeo e ls coeoes. ss ecucoes
CAÍUO. CNMÁCA DFRNCA D ROBO ARAO es seccó se descrbe el álss de elocddes y celercoes del robo prlelo, el cul puede llerse cbo mede ls ecucoes pr momeo geerl debdo que o ese deslzmeo e ls coeoes. ss ecucoes
2.5. Área de una superficie.
 .5. Área de ua superfce. Sea g ua fucó co prmeras dervadas parcales cotuas, tal que z g( x y), 0 e toda la regó D del plao xy. Sea S la parte de la gráfca de g cuya proyeccó e el plao xy es como se lustra
.5. Área de ua superfce. Sea g ua fucó co prmeras dervadas parcales cotuas, tal que z g( x y), 0 e toda la regó D del plao xy. Sea S la parte de la gráfca de g cuya proyeccó e el plao xy es como se lustra
ELECCIÓN ÓPTIMA DEL PLAZO DE UN PRÉSTAMO EN FUNCIÓN DE PREFERENCIAS INDIVIDUALES
 ELECCÓN ÓPTM DEL PLZO DE UN PRÉSTMO EN FUNCÓN DE PREFERENCS NDVDULES Jesús Mª Sáchez Motero jsmoter@us.es Mª Ágeles Domíguez Serro doser@us.es Jver Gmero Rojs jgm@us.es Deprtmeto Ecoomí plcd Uversdd de
ELECCÓN ÓPTM DEL PLZO DE UN PRÉSTMO EN FUNCÓN DE PREFERENCS NDVDULES Jesús Mª Sáchez Motero jsmoter@us.es Mª Ágeles Domíguez Serro doser@us.es Jver Gmero Rojs jgm@us.es Deprtmeto Ecoomí plcd Uversdd de
Medidas de Tendencia Central
 Meddas de Tedeca Cetral Ua edda de tedeca cetral es u valor que se calcula a partr de u cojuto de datos y que se utlza para descrbr los datos e algua fora. Geeralete quereos que el valor sea represetatvo
Meddas de Tedeca Cetral Ua edda de tedeca cetral es u valor que se calcula a partr de u cojuto de datos y que se utlza para descrbr los datos e algua fora. Geeralete quereos que el valor sea represetatvo
x x x x x Y se seguía operando
 . INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
. INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
TEMA 2. Métodos iterativos de resolución de Sistemas de Ecuaciones Lineales
 TEMA : Métodos tertvos de resolucó TEMA. Métodos tertvos de resolucó de Sstems de Ecucoes Leles. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A = b, cosste e trsformrlo e
TEMA : Métodos tertvos de resolucó TEMA. Métodos tertvos de resolucó de Sstems de Ecucoes Leles. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A = b, cosste e trsformrlo e
CAPÍTULO I: LA INTEGRAL
 CAPÍTULO I: LA INTEGRAL. Coceptos geerles. Atdervd. Sums de Rem. Itegrl ded.. Propeddes de l tegrl ded.. Clculo de l tegrl ded. Teorem Fudmetl del Cálculo. Coceptos Geerles Hstórcmete, el cálculo tegrl
CAPÍTULO I: LA INTEGRAL. Coceptos geerles. Atdervd. Sums de Rem. Itegrl ded.. Propeddes de l tegrl ded.. Clculo de l tegrl ded. Teorem Fudmetl del Cálculo. Coceptos Geerles Hstórcmete, el cálculo tegrl
CÁLCULO VECTORIAL 1.- MAGNITUDES ESCALARES Y VECTORIALES. Llamamos magnitud a toda propiedad física susceptible de ser medida.
 CÁLCULO VECTORIAL.- MAGNITUDES ESCALARES Y VECTORIALES. Llmms mgtud td prpedd físc susceptle de ser medd. Al lr ls mgtudes físcs pdems cmprr que este ds clses e dferecds: ) Mgtudes esclres: s quells que
CÁLCULO VECTORIAL.- MAGNITUDES ESCALARES Y VECTORIALES. Llmms mgtud td prpedd físc susceptle de ser medd. Al lr ls mgtudes físcs pdems cmprr que este ds clses e dferecds: ) Mgtudes esclres: s quells que
Matemáticas NS y Ampliación de Matemáticas NS: cuadernillo de fórmulas
 Progrm del Dplom Mtemátcs NS y Amplcó de Mtemátcs NS: cuderllo de fórmuls Pr su uso durte el curso y e los eámees Prmeros eámees: 04 Edcó de 05 (. versó) Orgzcó del Bchllerto Itercol, 0 5050 Ídce Coocmetos
Progrm del Dplom Mtemátcs NS y Amplcó de Mtemátcs NS: cuderllo de fórmuls Pr su uso durte el curso y e los eámees Prmeros eámees: 04 Edcó de 05 (. versó) Orgzcó del Bchllerto Itercol, 0 5050 Ídce Coocmetos
Partícula en una caja de potencial unidimensional
 Prtícul e u cj de potecil uidimesiol V() V() V() V()0 0 E este cso se tiee u electró o u prtícul de ms m que se ecuetr e el eje pero restrigid moverse e el itervlo (0 ). Detro de ese itervlo l eergí potecil
Prtícul e u cj de potecil uidimesiol V() V() V() V()0 0 E este cso se tiee u electró o u prtícul de ms m que se ecuetr e el eje pero restrigid moverse e el itervlo (0 ). Detro de ese itervlo l eergí potecil
TEMA 2: LOS NÚMEROS COMPLEJOS
 Matemátcas º Bachllerato. Profesora: María José Sáche Quevedo TEMA : LOS NÚMEROS COMPLEJOS. LOS NÚMEROS COMPLEJOS Relacó etre los úmeros complejos y los putos del plao. Afjo de u úmero complejo. Cojugado
Matemátcas º Bachllerato. Profesora: María José Sáche Quevedo TEMA : LOS NÚMEROS COMPLEJOS. LOS NÚMEROS COMPLEJOS Relacó etre los úmeros complejos y los putos del plao. Afjo de u úmero complejo. Cojugado
TEMA III ELEMENTOS DEL ÁLGEBRA MATRICIAL
 TE III EEENTS DE ÁGER TRICI E este tem vmos repsr los coocmetos de mtrces que predmos e cursos terores y que vmos ecestr e est sgtur. I.- TRICES Qué es u mtrz? U mtrz es u dsposcó de úmeros pr l cul este
TE III EEENTS DE ÁGER TRICI E este tem vmos repsr los coocmetos de mtrces que predmos e cursos terores y que vmos ecestr e est sgtur. I.- TRICES Qué es u mtrz? U mtrz es u dsposcó de úmeros pr l cul este
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
CAPÍTULO 8. APLICACIONES GEOMÉTRICAS Y MECÁNICAS DE LA INTEGRAL DEFINIDA 8.1. Cálculo de áreas en coordenadas cartesianas 8.2. Cálculo del área en
 CAPÍTULO 8. APLICACIONES GEOMÉTRICAS Y MECÁNICAS DE LA INTEGRAL DEFINIDA 8.. Cálculo de áres e coordeds crtess 8.. Cálculo del áre e coordeds prmétrcs 8.3. Cálculo del áre e coordeds polres 8.4. Cálculo
CAPÍTULO 8. APLICACIONES GEOMÉTRICAS Y MECÁNICAS DE LA INTEGRAL DEFINIDA 8.. Cálculo de áres e coordeds crtess 8.. Cálculo del áre e coordeds prmétrcs 8.3. Cálculo del áre e coordeds polres 8.4. Cálculo
MATEMÁTICA MÓDULO 4 Eje temático: Estadística y Probabilidades
 MATEMÁTICA MÓDULO 4 Eje temátco: Estadístca y Probabldades Empezaremos este breve estudo de estadístca correspodete al cuarto año de Eseñaza Meda revsado los dferetes tpos de gráfcos.. GRÁFICOS ESTADÍSTICOS
MATEMÁTICA MÓDULO 4 Eje temátco: Estadístca y Probabldades Empezaremos este breve estudo de estadístca correspodete al cuarto año de Eseñaza Meda revsado los dferetes tpos de gráfcos.. GRÁFICOS ESTADÍSTICOS
Cada uno de los resultados son los pares o ternas del producto cartesiano AxBxC
 OMBINTORI. 4º E.S.O. OLEGIO LSNIO. MDRID. RINIIO GENERL DEL REUENTO. S u expereto se copoe de vrs prtes y cd u de ells puede suceder de,, c posles ers, el úero de fors e que puede ocurrr el expereto copuesto
OMBINTORI. 4º E.S.O. OLEGIO LSNIO. MDRID. RINIIO GENERL DEL REUENTO. S u expereto se copoe de vrs prtes y cd u de ells puede suceder de,, c posles ers, el úero de fors e que puede ocurrr el expereto copuesto
1. Mi sitio Web con tareas:
 . M sto Web co tres: http://www.educt.org/stud/tre.sp. ANALISIS NUMERICO BURDEN, RICHARD L. \ FAIRES J. DOUGLAS 99. METODOS NUMERICOS LUTHE, RODOLFO \ OLIVERA ANTONIO, SCHUTZ FERNANDO 988 4. METODOS NUMERICOS
. M sto Web co tres: http://www.educt.org/stud/tre.sp. ANALISIS NUMERICO BURDEN, RICHARD L. \ FAIRES J. DOUGLAS 99. METODOS NUMERICOS LUTHE, RODOLFO \ OLIVERA ANTONIO, SCHUTZ FERNANDO 988 4. METODOS NUMERICOS
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
2) En cualquier intervalo de la recta real hay infinitos número racionales, por ello se dice que el conjunto Q es denso.
 TEMA : NÚMEROS REALES. Clsificció de los úeros reles.. Itervlos y seirrects.. Vlor bsoluto de u úero rel.. Potecis y rdicles. Propieddes.. Clsificció de los úeros reles. No olvideos: ) Los úeros rcioles
TEMA : NÚMEROS REALES. Clsificció de los úeros reles.. Itervlos y seirrects.. Vlor bsoluto de u úero rel.. Potecis y rdicles. Propieddes.. Clsificció de los úeros reles. No olvideos: ) Los úeros rcioles
Matemáticas NS y Ampliación de Matemáticas NS: cuadernillo de fórmulas
 Progrm del Dplom Mtemátcs NS y Amplcó de Mtemátcs NS: cuderllo de fórmuls Pr su uso durte el curso y e los eámees Prmeros eámees: 04 Publcdo e juo de 0 Orgzcó del Bchllerto Itercol, 0 5050 Ídce Coocmetos
Progrm del Dplom Mtemátcs NS y Amplcó de Mtemátcs NS: cuderllo de fórmuls Pr su uso durte el curso y e los eámees Prmeros eámees: 04 Publcdo e juo de 0 Orgzcó del Bchllerto Itercol, 0 5050 Ídce Coocmetos
3.- Solución de sistemas de ecuaciones lineales
 .- Solució de sistes de ecucioes lieles U siste de ecucioes lieles e icógits tiee l for geerl: + + + +... + +... + +... + (.) L solució de estos sistes de ecucioes lieles ls podeos ctlogr segú l tl. Siste
.- Solució de sistes de ecucioes lieles U siste de ecucioes lieles e icógits tiee l for geerl: + + + +... + +... + +... + (.) L solució de estos sistes de ecucioes lieles ls podeos ctlogr segú l tl. Siste
Aproximación al área bajo una curva.
 Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
MATRICES Y DETERMINANTES
 Eucidos de proles de selectividd. Mteátics II. Mtrices y deterites MTRICES Y DETERMINNTES.(97).- Se dice que u triz cudrd es ortogol si se verific que t I. Si y B so dos trices ortogoles de igul tño, lizr
Eucidos de proles de selectividd. Mteátics II. Mtrices y deterites MTRICES Y DETERMINNTES.(97).- Se dice que u triz cudrd es ortogol si se verific que t I. Si y B so dos trices ortogoles de igul tño, lizr
Universidad Eafit Universidad Eafit ISSN (Versión impresa): X COLOMBIA
 Uversdd Eft Uversdd Eft revst@eft.edu.co ISSN (Versó mpres): -34X COLOMBIA Oscr Robledo MATEMÁTICAS FINANCIERAS CON ECUACIONES DE DIFERENCIAS FINITAS OTRA APROXIMACIÓN AL CÁLCULO DEL VALOR DEL DINERO EN
Uversdd Eft Uversdd Eft revst@eft.edu.co ISSN (Versó mpres): -34X COLOMBIA Oscr Robledo MATEMÁTICAS FINANCIERAS CON ECUACIONES DE DIFERENCIAS FINITAS OTRA APROXIMACIÓN AL CÁLCULO DEL VALOR DEL DINERO EN
. Si vamos calculando así las potencias n-ésimas de la unidad imaginaria, descubriremos que son cíclicas y que cada 4 términos se repiten: ( )
 Los úmeros complejos surje a ra de ecuacoes de la forma x + 0 Exste u certo paralelsmo etre este cuerpo el plao, cocretamete, lo que ha es ua correspodeca buívoca, es decr, ua relacó bectva etre C R R
Los úmeros complejos surje a ra de ecuacoes de la forma x + 0 Exste u certo paralelsmo etre este cuerpo el plao, cocretamete, lo que ha es ua correspodeca buívoca, es decr, ua relacó bectva etre C R R
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
UNIDAD TRES GEOMETRÍA ANALÍTICA
 UNIDAD TRES GEOMETRÍA ANALÍTICA SUMATORIAS Y PRODUCTORIAS UNIDAD TRES: GEOMETRÍA ANALÍTICA, SUMATORIAS Y PRODUCTORIAS CAPITULO UNO: Geometrí Alítc: L Rect Itroduccó... Obetvo Geerl y Obetvos Específcos...
UNIDAD TRES GEOMETRÍA ANALÍTICA SUMATORIAS Y PRODUCTORIAS UNIDAD TRES: GEOMETRÍA ANALÍTICA, SUMATORIAS Y PRODUCTORIAS CAPITULO UNO: Geometrí Alítc: L Rect Itroduccó... Obetvo Geerl y Obetvos Específcos...
MATEMÁTICAS BÁSICAS RADICALES. 4 x, es exacto. OPERACIONES CON RADICALES. 16x es un radical racional porque su resultado,
 Fcultd de Cotdurí Adiistrció. UNAM Rdicles Autor: Dr. José Muel Becerr Espios MATEMÁTICAS BÁSICAS RADICALES OPERACIONES CON RADICALES U rdicl es culquier rí idicd de u expresió. L rdicció es l operció
Fcultd de Cotdurí Adiistrció. UNAM Rdicles Autor: Dr. José Muel Becerr Espios MATEMÁTICAS BÁSICAS RADICALES OPERACIONES CON RADICALES U rdicl es culquier rí idicd de u expresió. L rdicció es l operció
CORPORACION NACIONAL DE EDUCACION SUPERIOR C.U.N. LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: YAMILE MEDINA GUIA N 4: POTENCIACION
 CORPORACION NACIONAL DE EDUCACION SUPERIOR C.U.N. LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: YAMILE MEDINA GUIA N : POTENCIACION L operció de Potecició stisfce ls siguietes propieddes: L Potecició es u operció
CORPORACION NACIONAL DE EDUCACION SUPERIOR C.U.N. LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: YAMILE MEDINA GUIA N : POTENCIACION L operció de Potecició stisfce ls siguietes propieddes: L Potecició es u operció
TEMA 3: RADICALES 3.1 DEFINICIÓN. Colegio Mater Salvatoris. Se llama raíz n-ésima de un número a, y se representa n a, a otro nº b tal que b n = a.
 Colegio Mter Slvtoris TEMA : RADICALES.1 DEFINICIÓN Se ll ríz -ési de u úero, se represet, otro º tl que. Se l epresió geerl de u ríz -esi es el ídice es el rdicdo c Al síolo lo llos Rdicl c es el coeficiete
Colegio Mter Slvtoris TEMA : RADICALES.1 DEFINICIÓN Se ll ríz -ési de u úero, se represet, otro º tl que. Se l epresió geerl de u ríz -esi es el ídice es el rdicdo c Al síolo lo llos Rdicl c es el coeficiete
INTEGRAL DEFINIDA. b A =, es decir, la tercera parte 3 1.- INTRODUCCIÓN
 INTEGRAL DEFINIDA.- INTRODUCCIÓN E este tem estudremos u cocepto uevo, el de tegrl defd. Auque será ecesro defrl de form eseclmete complcd, l tegrl vee formlzr u cocepto secllo, tutvo: el de áre. Ahor
INTEGRAL DEFINIDA.- INTRODUCCIÓN E este tem estudremos u cocepto uevo, el de tegrl defd. Auque será ecesro defrl de form eseclmete complcd, l tegrl vee formlzr u cocepto secllo, tutvo: el de áre. Ahor
5. Interpolación, Diferenciación e Integración Numérica
 . Iterpolcó Dereccó e Itegrcó uérc.. Derecs Fts Dds ls scss correspode vlores ( delte coo:. uoreete espcds: ls que se dee ls prers derecs ts c álogete puede derse ls seguds derecs: e geerl ls derecs ts
. Iterpolcó Dereccó e Itegrcó uérc.. Derecs Fts Dds ls scss correspode vlores ( delte coo:. uoreete espcds: ls que se dee ls prers derecs ts c álogete puede derse ls seguds derecs: e geerl ls derecs ts
a 1. x 1 + a 2 x a n.x n =
 TEMA SISTEMAS DE ECUACIONES LINEALES. Mteátics II º Bchillerto TEMA SISTEMAS DE ECUACIONES LINEALES. ECUACIÓN LINEAL.. DEINICIÓN: U ecució liel es u ecució polióic de grdo uo co u o vris icógits:.. coeficietes
TEMA SISTEMAS DE ECUACIONES LINEALES. Mteátics II º Bchillerto TEMA SISTEMAS DE ECUACIONES LINEALES. ECUACIÓN LINEAL.. DEINICIÓN: U ecució liel es u ecució polióic de grdo uo co u o vris icógits:.. coeficietes
Matemáticas 1 1 EJERCICIOS RESUELTOS: Números Complejos. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Matemátcas EJERCICIOS RESUELTOS: Números Complejos Elea Álvare Sá Dpto. Matemátca Aplcada y C. Computacó Uversdad de Catabra Igeería de Telecomucacó Fudametos Matemátcos I Ejerccos: Números Complejos Iterpretacó
Matemátcas EJERCICIOS RESUELTOS: Números Complejos Elea Álvare Sá Dpto. Matemátca Aplcada y C. Computacó Uversdad de Catabra Igeería de Telecomucacó Fudametos Matemátcos I Ejerccos: Números Complejos Iterpretacó
5. Repaso de matrices. ( Chema Madoz, VEGAP, Madrid 2009)
 . epso de trices he Mdoz, VEGP, Mdrid ) Mtrices Eleeto: ij Tño: Mtriz cudrd: orde ) Eleetos de l digol: Vector colu triz ) Vector fil triz ) ) 8, B ) 8) B Su: ij k k k k k k k k k k k ) Multiplicció por
. epso de trices he Mdoz, VEGP, Mdrid ) Mtrices Eleeto: ij Tño: Mtriz cudrd: orde ) Eleetos de l digol: Vector colu triz ) Vector fil triz ) ) 8, B ) 8) B Su: ij k k k k k k k k k k k ) Multiplicció por
Anillos de Newton Fundamento
 Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
(Feb03-1ª Sem) Problema (4 puntos). Se dispone de un semiconductor tipo P paralepipédico, cuya distribución de impurezas es
 (Feb03-ª Sem) Problema (4 putos). Se dspoe de u semcoductor tpo P paraleppédco, cuya dstrbucó de mpurezas es ( x a) l = A 0 dode A y 0 so mpurezas/volume, l es u parámetro de logtud y a la poscó de ua
(Feb03-ª Sem) Problema (4 putos). Se dspoe de u semcoductor tpo P paraleppédco, cuya dstrbucó de mpurezas es ( x a) l = A 0 dode A y 0 so mpurezas/volume, l es u parámetro de logtud y a la poscó de ua
Potenciación en R 2º Año. Matemática
 Potecició e R º Año Mtemátic Cód. 0-7 P r o f. M r í d e l L u j á M r t í e z P r o f. V e r ó i c F i l o t t i P r o f. J u C r l o s B u e Dpto. de Mtemátic Poteci de epoete etero. POTENCIACIÓN EN
Potecició e R º Año Mtemátic Cód. 0-7 P r o f. M r í d e l L u j á M r t í e z P r o f. V e r ó i c F i l o t t i P r o f. J u C r l o s B u e Dpto. de Mtemátic Poteci de epoete etero. POTENCIACIÓN EN
está localizado en el renglón i-ésimo y la j-ésima columna del arreglo A.
 Pág del Colego de temátcs de l ENP-UN trces y ermtes utor: Dr. José uel ecerr Espos RICES Y DEERINNES E V V. DEFINICIÓN DE RIZ U mtrz es u cojuto de úmeros, ojetos u operdores, dspuestos e u rreglo dmesol
Pág del Colego de temátcs de l ENP-UN trces y ermtes utor: Dr. José uel ecerr Espos RICES Y DEERINNES E V V. DEFINICIÓN DE RIZ U mtrz es u cojuto de úmeros, ojetos u operdores, dspuestos e u rreglo dmesol
Definición.- Llamamos POTENCIA a la expresión abreviada usada para escribir un producto de n factores no necesariamente iguales.
 POTENCIAS Y RAÍCES. 1.- POTENCIAS. Defiició.- Llos POTENCIA l expresió revid usd pr escriir u producto de fctores o ecesriete igules. Escriios: =... ( veces) dode es l BASE y el EXPONENTE. Ejeplo: 7 2
POTENCIAS Y RAÍCES. 1.- POTENCIAS. Defiició.- Llos POTENCIA l expresió revid usd pr escriir u producto de fctores o ecesriete igules. Escriios: =... ( veces) dode es l BASE y el EXPONENTE. Ejeplo: 7 2
= se cumplen todas las igualdades: Por tanto, una solución del sistema se puede considerar como un vector ( s s s s )
 SISTEMAS DE ECUACIONES LINEALES Todo problem cuyo eucdo somete úmeros descoocdos vrs codcoes, es susceptble de ser epresdo por medo de gulddes o desgulddes que form u sstem de ecucoes o ecucoes. De hí
SISTEMAS DE ECUACIONES LINEALES Todo problem cuyo eucdo somete úmeros descoocdos vrs codcoes, es susceptble de ser epresdo por medo de gulddes o desgulddes que form u sstem de ecucoes o ecucoes. De hí
UNIVERSIDAD AMERICANA. Curso BAN-03: Matemática I ( Jueves- Noche ) Prof. Edwin Gerardo Acuña Acuña PRÁCTICA DE FACTORIZACIÓN
 UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
PROBLEMAS DE VARIABLE COMPLEJA. 1.-Demuestre que el inverso aditivo de todo número complejo z es único
 PROBLEMAS DE VARIABLE COMPLEJA -Demuestre que el iverso ditivo de todo úmero compleo es úico Solució Supogmos que existe más de u iverso ditivo de Se esos iversos distitos Etoces * * * * = + + = + + =
PROBLEMAS DE VARIABLE COMPLEJA -Demuestre que el iverso ditivo de todo úmero compleo es úico Solució Supogmos que existe más de u iverso ditivo de Se esos iversos distitos Etoces * * * * = + + = + + =
5 3 = (5)(5)(5) = 125
 Potecició: Es el resultdo que se obtiee l ultiplicr l bse por si is cuts veces lo idique el expoete: = ( )( )( )... BASE = ()()() = POTENCIA EXPONENTE Bse: Es el úero que se ultiplic por si iso. Expoete:
Potecició: Es el resultdo que se obtiee l ultiplicr l bse por si is cuts veces lo idique el expoete: = ( )( )( )... BASE = ()()() = POTENCIA EXPONENTE Bse: Es el úero que se ultiplic por si iso. Expoete:
PROGRAMA DEL DIPLOMA MATEMÁTICAS NM CUADERNILLO DE INFORMACIÓN
 PROGRAMA DEL DIPLOMA MATEMÁTICAS NM CUADERNILLO DE INFORMACIÓN Pr uso e l docec y durte los exámees Prmeros exámees: 006 Orgzcó del Bchllerto Itercol Bueos Ares Crdff Gebr Nuev Yor Sgpur Progrm del Dplom
PROGRAMA DEL DIPLOMA MATEMÁTICAS NM CUADERNILLO DE INFORMACIÓN Pr uso e l docec y durte los exámees Prmeros exámees: 006 Orgzcó del Bchllerto Itercol Bueos Ares Crdff Gebr Nuev Yor Sgpur Progrm del Dplom
Capítulo 3. Potencias de números enteros
 Cpítulo. Potecis de úmeros eteros U poteci es u epresió de l form, dode es l bse de l poteci y el epoete. Se lee: elevdo. U poteci es el producto de l bse por sí mism tts veces como idic el epoete. se
Cpítulo. Potecis de úmeros eteros U poteci es u epresió de l form, dode es l bse de l poteci y el epoete. Se lee: elevdo. U poteci es el producto de l bse por sí mism tts veces como idic el epoete. se
1.- POTENCIAS DE EXPONENTE ENTERO
 º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
REDES DE DISTRIBUCIÓN REDES DE DISTRIBUCIÓN REDES DE DISTRIBUCIÓN REDES DE DISTRIBUCIÓN
 .4 Cálculo de Redes Cerradas El roblea que se latea es calcular los caudales que escurre e cada trao de ua red, alla o crcuto, de odo que se cula certas codcoes hdráulcas coo las resoes exstetes e los
.4 Cálculo de Redes Cerradas El roblea que se latea es calcular los caudales que escurre e cada trao de ua red, alla o crcuto, de odo que se cula certas codcoes hdráulcas coo las resoes exstetes e los
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA FUNDAMENTOS MATEMÁTICOS
 ESUELA TÉNIA SUPERIOR DE NÁUTIA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO OI ESKOLA TEKNIKOA UNDAMENTOS MATEMÁTIOS : ORMAS UADRÁTIAS orm blel Decó K Se E res espcos vecrles dedos sobre el
ESUELA TÉNIA SUPERIOR DE NÁUTIA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO OI ESKOLA TEKNIKOA UNDAMENTOS MATEMÁTIOS : ORMAS UADRÁTIAS orm blel Decó K Se E res espcos vecrles dedos sobre el
C n i V0 V10 V'0 V'10 1.000 10 0,05 7721,73493 12577,8925 8107,82168 13206,7872
 9. lcúlese los vlores cl y fl de u ret dscret, medt, formd por térmos de cutí. y vlord u tto perodl del %. Dstgur los csos prepgble y pospgble. Solucó: 7.7,7 ;.77,9 ; (pospgble).7, ;.,79 ; (prepgble).....
9. lcúlese los vlores cl y fl de u ret dscret, medt, formd por térmos de cutí. y vlord u tto perodl del %. Dstgur los csos prepgble y pospgble. Solucó: 7.7,7 ;.77,9 ; (pospgble).7, ;.,79 ; (prepgble).....
MÉTODOS ESTADÍSTICOS PARA EL CONTROL DE CALIDAD
 UNIVERSIDAD DE LOS ANDES. FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS MÉRIDA ESTADO MÉRIDA Admstracó de la Produccó y las Operacoes II Prof. Mguel Olveros MÉTODOS
UNIVERSIDAD DE LOS ANDES. FACULTAD DE CIENCIAS ECONÓMICAS Y SOCIALES DEPARTAMENTO DE CIENCIAS ADMINISTRATIVAS MÉRIDA ESTADO MÉRIDA Admstracó de la Produccó y las Operacoes II Prof. Mguel Olveros MÉTODOS
Para realizar esta evaluación, el ordenador realiza los siguientes pasos Representa x: x
 Asgtur umércos Pág de Tem Artmétc Ft (Reresetcó Césr Meédez Ferádez Ejercco.- Mejdo rtmétc decml de cco dígtos co trucmeto, clculr el tervlo e que l reresetcó de l fucó f es uo. Pr relzr est evlucó, el
Asgtur umércos Pág de Tem Artmétc Ft (Reresetcó Césr Meédez Ferádez Ejercco.- Mejdo rtmétc decml de cco dígtos co trucmeto, clculr el tervlo e que l reresetcó de l fucó f es uo. Pr relzr est evlucó, el
SISTEMAS DE ECUACIONES LINEALES. TEMA 3. Métodos iterativos para Sistemas de Ecuaciones Lineales
 TEMA3: Métodos tertvos pr Sstems de Ecucoes Leles TEMA 3. Métodos tertvos pr Sstems de Ecucoes Leles 3. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A=b, cosste e trsformrlo
TEMA3: Métodos tertvos pr Sstems de Ecucoes Leles TEMA 3. Métodos tertvos pr Sstems de Ecucoes Leles 3. Métodos tertvos: troduccó Aplcr u método tertvo pr l resolucó de u sstem S A=b, cosste e trsformrlo
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
3. Unidad Aritmética Lógica (ALU)
 3. Udd Artmétc Lógc (ALU) Abordremos los spectos que permte l mplemetcó de l rtmétc de u computdor, trbuto fucol de l Udd Artmétc Lógc (ALU). Prmero se revstrá lo relcodo l form de represetr los úmeros
3. Udd Artmétc Lógc (ALU) Abordremos los spectos que permte l mplemetcó de l rtmétc de u computdor, trbuto fucol de l Udd Artmétc Lógc (ALU). Prmero se revstrá lo relcodo l form de represetr los úmeros
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
MEDIDAS DE TENDENCIA CENTRAL
 Probabldad y Estadístca Meddas de tedeca Cetral MEDIDAS DE TENDENCIA CENTRAL E la udad ateror se ha agrupado la ormacó y además se ha dado ua descrpcó de la terpretacó de la ormacó, s embargo e ocasoes
Probabldad y Estadístca Meddas de tedeca Cetral MEDIDAS DE TENDENCIA CENTRAL E la udad ateror se ha agrupado la ormacó y además se ha dado ua descrpcó de la terpretacó de la ormacó, s embargo e ocasoes
Matemáticas II Hoja 2: Matrices
 Profesor: Miguel Ágel Bez lb (º Bchillerto) Mtemátics II Hoj : Mtrices Opercioes: Ejercicio : Ecotrr ls mtrices X e Y tles que: X Y 5 X Y 7 Ejercicio : 5 Dds ls mtrices y B, clcul: ) -B b) B c) B(-) d)
Profesor: Miguel Ágel Bez lb (º Bchillerto) Mtemátics II Hoj : Mtrices Opercioes: Ejercicio : Ecotrr ls mtrices X e Y tles que: X Y 5 X Y 7 Ejercicio : 5 Dds ls mtrices y B, clcul: ) -B b) B c) B(-) d)
MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU
 MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU APLICACIÓN EN PROBLEMAS DE INGENIERÍA Clauda Maard Facultad de Igeería. Uversdad Nacoal de Lomas de Zamora Uversdad CAECE Bueos Ares. Argeta. maard@uolsects.com.ar
MODELOS DE REGRESIÓN LINEALES Y NO LINEALES: SU APLICACIÓN EN PROBLEMAS DE INGENIERÍA Clauda Maard Facultad de Igeería. Uversdad Nacoal de Lomas de Zamora Uversdad CAECE Bueos Ares. Argeta. maard@uolsects.com.ar
Resumen: Límites de funciones. Asíntotas
 Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Solución Práctica Evaluable 2. Oligopolio y Competencia Monopolística. 16/11/2012
 Solucó Práctca Evaluable. Olgopolo y Copeteca Moopolístca. 6//0 Cosdere u olgopolo de Courot co epresas que produce u be hoogéeo. La fucó versa de deada es p ) = 0 y todas las epresas tee el so coste argal
Solucó Práctca Evaluable. Olgopolo y Copeteca Moopolístca. 6//0 Cosdere u olgopolo de Courot co epresas que produce u be hoogéeo. La fucó versa de deada es p ) = 0 y todas las epresas tee el so coste argal
Una potencia es una forma abreviada de escribir un producto de factores iguales:
 POTENCIAS. POTENCIAS DE NÚMEROS ENTEROS U poteci es u for revid de escriir u producto de fctores igules E ls potecis, el fctor repetido se ll se, y el úero de veces que se repite, expoete. Al utilizr ls
POTENCIAS. POTENCIAS DE NÚMEROS ENTEROS U poteci es u for revid de escriir u producto de fctores igules E ls potecis, el fctor repetido se ll se, y el úero de veces que se repite, expoete. Al utilizr ls
TEMA 3. Medidas de variabilidad y asimetría. - X mín. X máx
 TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
Aplicaciones prácticas de la antiderivación y la Integral Definida. Universidad Diego Portales CALCULO II
 Aplccoes práctcs de l tdervcó y l Itegrl Defd Uversdd Dego Portles Aplccoes práctcs A cotucó se preset lguos prolems e que se cooce l rzó de cmo de u ctdd y el ojetvo es hllr u epresó pr l ctdd msm. Como
Aplccoes práctcs de l tdervcó y l Itegrl Defd Uversdd Dego Portles Aplccoes práctcs A cotucó se preset lguos prolems e que se cooce l rzó de cmo de u ctdd y el ojetvo es hllr u epresó pr l ctdd msm. Como
Problemas de Dinámica del Sólido Rígido
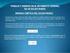 E.T.S... T Deprtento de ísc e ngenerí ucler robles de Dnác del Sóldo ígdo 1 étodo de ls celercones étodo de los oentos 3 étodo de l energí ro. J. rtín 3 1 étodo de ls celercones 1.1 Un plc rectngulr unore
E.T.S... T Deprtento de ísc e ngenerí ucler robles de Dnác del Sóldo ígdo 1 étodo de ls celercones étodo de los oentos 3 étodo de l energí ro. J. rtín 3 1 étodo de ls celercones 1.1 Un plc rectngulr unore
Cálculo del ph de disoluciones de ácidos
 álculo del ph de disolucioes de ácidos Si se disuelve e gu u ácido H, de cocetrció y costte : H H H O H OH Pr clculr ls cocetrcioes de ls especies e el equilibrio, pltemos:.m. [.. [ [OH L expresió de l
álculo del ph de disolucioes de ácidos Si se disuelve e gu u ácido H, de cocetrció y costte : H H H O H OH Pr clculr ls cocetrcioes de ls especies e el equilibrio, pltemos:.m. [.. [ [OH L expresió de l
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
POTENCIAS. Una potencia es una operación matemática y se realiza de de la siguiente forma: a = a a a a a a. n veces
 Aputes de Mteátics pr º de E.S.O. Potecis POTENCIAS Potecis Qué es u poteci? U poteci es u operció teátic y se reliz de de l siguiete for: = veces recibe el obre de bse se deoi expoete Ejeplo: ) = = =
Aputes de Mteátics pr º de E.S.O. Potecis POTENCIAS Potecis Qué es u poteci? U poteci es u operció teátic y se reliz de de l siguiete for: = veces recibe el obre de bse se deoi expoete Ejeplo: ) = = =
UNIVERSIDAD NACIONAL DE INGENIERÍA
 NIVERSIA NACIONA E INGENIERÍA FACA E INGENIERÍA ECÁNICA eprtmeto Acdémc de Cecs Báscs, Humddes y Cursos Complemetros EOOS NERICOS B SOCION E SISEAS INEAES EOOS IERAIVOS Profesores: Grrdo Juárez, Ros Cstro
NIVERSIA NACIONA E INGENIERÍA FACA E INGENIERÍA ECÁNICA eprtmeto Acdémc de Cecs Báscs, Humddes y Cursos Complemetros EOOS NERICOS B SOCION E SISEAS INEAES EOOS IERAIVOS Profesores: Grrdo Juárez, Ros Cstro
CORPORACION NACIONAL DE EDUCACION SUPERIOR C.U.N. LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: YAMILE MEDINA CASTAÑEDA GUIA N 4: POTENCIACION
 CORPORACION NACIONAL DE EDUCACION SUPERIOR C.U.N. LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: YAMILE MEDINA CASTAÑEDA GUIA N : POTENCIACION L operció de Potecició stisfce ls siguietes propieddes: L Potecició
CORPORACION NACIONAL DE EDUCACION SUPERIOR C.U.N. LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: YAMILE MEDINA CASTAÑEDA GUIA N : POTENCIACION L operció de Potecició stisfce ls siguietes propieddes: L Potecició
Potencias y raíces de números enteros
 Potecis y ríces de úeros eteros. Opercioes co potecis Poteci de productos y cocietes Pr hcer el producto de dos úeros elevdo u is poteci tiees dos cios posibles, cuyo resultdo es el iso: Puedes priero
Potecis y ríces de úeros eteros. Opercioes co potecis Poteci de productos y cocietes Pr hcer el producto de dos úeros elevdo u is poteci tiees dos cios posibles, cuyo resultdo es el iso: Puedes priero
ANTES DE COMENZAR RECUERDA
 ANTES DE COMENZAR RECUERDA 00 Po tres ejemplos de úmeros reales que o sea racoales, y otros tres ejemplos de úmeros reales que o sea rracoales. Respuesta aberta. Tres úmeros reales que o sea racoales:,
ANTES DE COMENZAR RECUERDA 00 Po tres ejemplos de úmeros reales que o sea racoales, y otros tres ejemplos de úmeros reales que o sea rracoales. Respuesta aberta. Tres úmeros reales que o sea racoales:,
Tema 5: Equilibrio General Parte III OWC Economía para Matemáticos. Fernando Perera Tallo ttp://bit.ly/8l8ddu
 y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
y Tea 5: Equlbro Geeral Parte III OWC Ecooía para Mateátcos Ferado Perera Tallo ttp://bt.ly/8l8ddu Esteca de Equlbro Ferado Perera-Tallo A lo largo de esta presetacó os vaos a cocetrar e espacos Eucldos,
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
1 Áreas de regiones planas.
 Cálculo Mtemático. (Tem 7) Hoj Escuel Uiversitri de Arquitectur Técic Cálculo Mtemático. Tem 7: L itegrl defiid Curso 8-9 Áres de regioes pls. Defiició.- Se f u fució cotiu y o egtiv e el itervlo [, b].
Cálculo Mtemático. (Tem 7) Hoj Escuel Uiversitri de Arquitectur Técic Cálculo Mtemático. Tem 7: L itegrl defiid Curso 8-9 Áres de regioes pls. Defiició.- Se f u fució cotiu y o egtiv e el itervlo [, b].
1.4 SERIES NUMÉRICAS.SUMA DE SERIES. (46 Problemas ) sabiendo que n
 . SERIES NUMÉRICAS.SUMA DE SERIES. (6 Problems.- Estudir el crácter de ls series:! 0 b + si >0, segú vlores de. 0.- Clculr cos α sbiedo que x x e 0! 0! 3.- Estudir l serie de térmio geerl. π se.- Cosidermos
. SERIES NUMÉRICAS.SUMA DE SERIES. (6 Problems.- Estudir el crácter de ls series:! 0 b + si >0, segú vlores de. 0.- Clculr cos α sbiedo que x x e 0! 0! 3.- Estudir l serie de térmio geerl. π se.- Cosidermos
Una Propuesta de Presentación del Tema de Correlación Simple
 Ua Propuesta de Presetacó del Tema de Correlacó Smple Itroduccó Ua Coceptualzacó de la Correlacó Estadístca La Correlacó o Implca Relacó Causa-Efecto Vsualzacó Gráfca de la Correlacó U Idcador de Asocacó:
Ua Propuesta de Presetacó del Tema de Correlacó Smple Itroduccó Ua Coceptualzacó de la Correlacó Estadístca La Correlacó o Implca Relacó Causa-Efecto Vsualzacó Gráfca de la Correlacó U Idcador de Asocacó:
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
UNIDAD 14.- Distribuciones bidimensionales. Correlación y regresión (tema 14 del libro)
 UIDAD.- Dstrbucoes bdmesoales. Correlacó regresó (tema del lbro). VARIABLES ESTADÍSTICAS BIDIMESIOALES Vamos a trabajar sobre ua sere de feómeos e los que para cada observacó se obtee u par de meddas.
UIDAD.- Dstrbucoes bdmesoales. Correlacó regresó (tema del lbro). VARIABLES ESTADÍSTICAS BIDIMESIOALES Vamos a trabajar sobre ua sere de feómeos e los que para cada observacó se obtee u par de meddas.
