COMBINATORIA Y PROBABILIDAD
|
|
|
- Amparo Araya Carrizo
- hace 6 años
- Vistas:
Transcripción
1 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los.- TÉCNICAS DE RECUENTO _ (NO APLICADAS). Digrm de árol COMBINATORIA Y PROBABILIDAD Ls técics de recueto so herrmiets utilizds pr cotr csos. Si el úmero de csos es pequeño o su cálculo sigue u ptró clro se puede utilizr el digrm de árol, pero cudo se complic coviee utilizr otrs técics o fórmuls más complejs y eficces, uque sí es cierto que sds e los digrms de árol. EJEMPLO_ L empres de mts Mtuki, ls hce e tres modelos, Dehogr, Deiño y Deeé. A su vez cd modelo se hce e dos versioes Coforro y Siforro. Además de lo terior se fric tods ells e cico colores: Azul, Blco, Rojo, Verde y Negro. Cuátos tipos de Mtukis fric?. Fórmuls de comitori EJEMPLO._ Siguiedo hor co el ejemplo de ls Mtuki, u cliete quiere comprr pr reglr cico mts de hogr co forro, u de cd color. Si ls regl cico migos. De cuáts forms puede reglr ls mts? Pr cotr tods ls forms posiles deemos teer e cuet lo siguiete:.- el úmero de elemetos que se puede tomr, m, e este cso cico que so los diferetes colores de ls mts,.- el úmero de elemetos que se coge cd vez,, e este cso cico que so los migos etre los que v reprtir ls mts,.- si se puede repetir los elemetos, e este cso o, pues ls mts so de distitos colores y por tto o puede reglr mts del mismo color distitos migos,.- si import el orde, es decir, reprtir ls mts de ls siguietes forms so el mismo reprto o distito, e este cso distito, pues o es el mismo reprto si el migo tiee l mt verde y el migo l mt egr que si lo hce l revés, por lo tto el orde sí import. L solució será: = forms diferetes de reglr ls mts los cico migos. EJEMPLO._ Ahor supogmos que otro cliete quiere comprr pr reglr tres mts de hogr co forro de diferetes colores. Si ls regl tres migos. De cuáts forms puede reglr ls mts? Pr cotr tods ls forms posiles deemos teer e cuet lo siguiete:.- el úmero de elemetos que se puede tomr, m, e este cso cico que so los diferetes colores de ls mts,.- el úmero de elemetos que se coge cd vez,, e este cso tres que so los migos etre los que v reprtir ls mts,.- si se puede repetir los elemetos, e este cso o, pues ls mts so de distitos colores y por tto o puede reglr mts del mismo color distitos migos,.- si import el orde, es decir, reprtir ls mts de ls siguietes forms so el mismo reprto o distito, e este cso distito, pues o es el mismo reprto si el migo tiee l mt lc y el migo l mt roj que si lo hce l revés, por lo tto el orde sí import. L solució será: = forms diferetes de reglr ls mts los tres migos. EJEMPLO._ Ahor supogmos que otro cliete quiere comprr pr reglr tres mts si forro de hogr. Si ls regl tres migos. De cuáts forms puede reglr ls mts? Pr cotr tods ls forms posiles deemos teer e cuet lo siguiete: AMIGO AMIGO AMIGO AMIGO AMIGO Azul Blc Roj Verde Negr Azul Blc Roj Negr Verde AMIGO AMIGO AMIGO Azul Blc Roj Azul Roj Blc
2 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los.- el úmero de elemetos que se puede tomr, m, e este cso cico que so los diferetes colores de ls mts,.- el úmero de elemetos que se coge cd vez,, e este cso tres que so los migos etre los que v reprtir ls mts,.- si se puede repetir los elemetos, e este cso sí, pues puede reglr mts del mismo color diferetes migos porque el eucido o dice eplícitmete que ls mts de ser de diferetes colores,.- si import el orde, es decir, reprtir ls mts de ls siguietes forms so el mismo reprto o distito, e este cso distito, pues o es el mismo reprto si el migo tiee l mt zul y el migo l mt roj que si lo hce l revés, por lo tto el orde sí import. L solució será: = forms diferetes de reglr ls mts los tres migos. EJEMPLO._ Ahor supogmos que otro cliete quiere comprr pr reglr u solo migo, tres mts de hogr si forro de distitos colores. De cuáts forms puede reglr ls mts? Pr cotr tods ls forms posiles deemos teer e cuet lo siguiete:.- el úmero de elemetos que se puede tomr, m, e este cso cico que so los diferetes colores de ls mts,.- el úmero de elemetos que se coge cd vez,, e este cso tres que so ls mts de distito color que v reglr u migo, E este cso l estructur de árol o os yud demsido, escriimos por orde tods ls opcioes. MANTA Azul MANTA Blc MANTA Roj.- si se puede repetir los elemetos, e este cso o, pues ls mts so de distitos colores y por tto o puede reglr mts del Azul Blc Verde Azul Blc Negr mismo color su migo, Azul Roj Verde.- si import el orde, es decir, reprtir ls mts de ls Azul Roj Negr Azul Verde Negr siguietes forms so el mismo reprto o distito, e este cso el mismo, Blc Blc Roj Roj Verde Negr pues es el mismo reprto si reglmos ls mts zul, lc y roj e culquier de ls seis forms de l tl, el migo recie ls tres mts Blc Verde Negr Roj Verde Negr igulmete, por lo tto el orde o import. L solució so forms distits de reglr tres mts de diferete color, de etre cico, u migo. Ce destcr que este cso es precido l ejemplo, pero e quel ejercicio cd u de ls diez opcioes quí epuests d lugr seis csos diferetes co u totl de forms distits de reglr ls mts. Cudo o import el orde l opció AZUL BLANCA ROJA _ (A B R) es úic pero cudo sí import el orde est opció d lugr otrs seis: A B R, A R B, B A R, B R A, R A B, R B A. Pues ie cd uo de los ejemplos teriores correspode u de ls fórmuls de comitori que vmos estudir e est uidd... Permutcioes (Ejemplo.) Llmmos permutcioes si repetició (permutcioes) de m elemetos los distitos grupos que se puede formr co los m elemetos de mer que:.- cd grupo tiee los m elemetos (todos), por supuesto distitos,.- dos grupos co los mismos elemetos e distito orde se cosider grupos diferetes. L fórmul que permite clculr ls permutcioes de m elemetos es: P m = m! Se defie fctoril de m como m! = m (m ) (m ), sí! = =. Deemos teer e cuet que o eiste el fctoril de u úmero egtivo y que! = por defiició, (es sí y puto). EJEMPLO._ Siguiedo hor co el ejemplo de ls Mtuki, u cliete quiere comprr pr reglr cico mts de hogr, u de cd color. Si ls regl cico migos. De cuáts forms puede reglr ls mts?.- Como hemos eplicdo e el ejemplo teemos que m= y =, demás el orde sí import y o puede her repetició Permutcioes P =! = forms distits. AMIGO AMIGO AMIGO Azul Azul Azul Azul Azul Roj Azul Roj Azul MANTA MANTA MANTA Azul Blc Roj Azul Roj Blc Blc Azul Roj Blc Roj Azul Roj Azul Blc Roj Blc Azul
3 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los.. Vricioes si repetició (Ejemplo.) Llmmos vricioes si repetició (vricioes) de m elemetos tomdos de e ( m) los distitos grupos que se puede formr co los m elemetos de mer que:.- cd grupo tiee elemetos diferetes,.- dos grupos co los mismos elemetos e distito orde se cosider grupos diferetes. L fórmul que permite clculr ls vricioes de m elemetos tomdos de e es: m! V m, m (m ) (m ) (m ) (m )! EJEMPLO._ Ahor supogmos que otro cliete quiere comprr pr reglr tres mts de hogr de diferetes colores. Si ls regl tres migos. De cuáts forms puede reglr ls mts?.- Como hemos eplicdo e el ejemplo teemos que m= y =, demás el orde sí import y o puede!!! her repetició Vricioes V, forms distits. ( )!!!.. Vricioes co repetició (Ejemplo.) Llmmos vricioes co repetició (vricioes co repetició) de m elemetos tomdos de e los distitos grupos que se puede formr co los m elemetos de mer que:.- cd grupo tiee elemetos, repetidos o o,.- dos grupos co los mismos elemetos e distito orde se cosider grupos diferetes. L fórmul que clcul ls vricioes co repetició de m elemetos tomdos de e es: VR m, = m EJEMPLO._ Ahor supogmos que otro cliete quiere comprr pr reglr tres mts de hogr. Si ls regl tres migos. De cuáts forms puede reglr ls mts?.- Como hemos eplicdo e el ejemplo teemos que m= y =, demás el orde sí import y sí puede her repetició Vricioes co repetició VR, = = forms distits... Comicioes si repetició (Ejemplo.) Llmmos comicioes si repetició (comicioes) de m elemetos tomdos de e ( m) los distitos grupos que se puede formr co los m elemetos de mer que:.- cd grupo tiee elemetos diferetes,.- dos grupos co los mismos elemetos e distito orde se cosider como el mismo grupo. L fórmul que clcul ls comicioes de m elemetos tomdos de e es: m! C m,! (m )! m! Est fórmul tmié se puede epresr como: C m, V m, P (m )!! m!! (m )! EJEMPLO._ Ahor supogmos que otro cliete quiere comprr pr reglr u solo migo, tres mts de hogr de distitos colores. De cuáts forms puede reglr ls mts?.- Como hemos eplicdo e el ejemplo teemos que m= y =, demás el orde o import y o puede!!! her repetició Comicioes C, forms distits.! ( )!!!! Señlr que de ls cutro fórmuls tres so de l fmili de ls vricioes (sí import el orde) y l otr es de l fmili de ls comicioes (o import el orde). E los prolems ls podremos distiguir:.- Si se utiliz todos los elemetos y sí import el orde será permutcioes, si se coge todos los elemetos y o import el orde, o tiee mucho setido pues solo hrí u comició posile. Por ejemplo, se coge tres otes de pitur, rojo, verde y zul y se mezcl. Cuátos colores distitos se otiee de l mezcl? L respuest es uo, d igul e qué orde se mezcle los colores..- Si hy repetició, solmete puede ser el cso de vricioes co repetició, (o hemos visto otro)..- Si o se coge todos, ver si el orde import, si sí import, vricioes y si o import, comicioes.
4 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los.- TRIÁNGULO DE PASCAL y NÚMEROS COMBINATORIOS_ (NO APLICADAS). Triágulo de Pscl y úmeros comitorios El deomido triágulo de Pscl es u triágulo que se costruye fil fil de l siguiete mer, l primer fil tiee u úmero, u uo, l segud fil tiee dos úmeros, dos uos, prtir de l tercer fil, cd fil comiez y c co u uo y los demás se otiees sumdo los dos que está ecim de él. Estos úmeros so los úmeros comitorios m se lee m sore y cuyo vlor se otiee medite l epresió )! (m! m! m que es l correspodiete ls C m,. EJEMPLO:!! )! (!!. Poteci de u Biomio U plicció del triágulo de Pscl se puede ver e el desrrollo de l poteci de u iomio del tipo: r r r... r EJEMPLO: (+) = = = = ECUACIONES COMBINATORIAS_ (NO APLICADAS) L icógit prece e el suídice de u o vris de ls fórmuls de comitori. EJEMPLO: Clcul el vlor de e l siguiete ecució: V, = C, )! -! )! ) ) ) )! )! ) )! -!! C )!! V,, ) ) ) )
5 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los = ) ) = + = 8 9 Se puede compror que co =7 se cumple l iguldd: V 7, 7! 7! (7 )!! C 7, 7!! (7 - )! 7!!! 7 Si emrgo co = o tiee setido..- PROBABILIDAD. Defiicioes.- Eperimeto letorio: Eperimeto e el que o podemos ser el resultdo co certez. EJEMPLO: El eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs es u eperimeto letorio, sé que puede slir ciertos vlores pero o sé co certez qué vlor será. El eperimeto Clculr el áre de u cudrdo coocido su ldo, o es letorio, todos dirímos el mismo resultdo, si el ldo es cm etoces su áre es cm co totl seguridd..- Espcio muestrl: Es el cojuto de resultdos posiles de u eperimeto letorio. Se deot como E. EJEMPLO: El eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, tiee por espcio muestrl E = {,,,,, 7, 8, 9,, }, segú se oserv cotiució: + = + = + = + = + = + = = = = + = + = + = + = + = + = 7 + = = = 9 +9 = + =.- Suceso letorio: Culquier sucojuto del espcio muestrl E. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, se puede plter diversos sucesos: A = Scr u ol de u ur que cotiee ls ols umerds del l y l sumr sus cifrs oteer u úmero pr, e l práctic se escrie como A = Scr pr = {,,, 8, }. B = Scr múltiplo de tres = {,, 9} C = Scr primo = {,,, 7, } D = Scr úmero cdo e cero = {}.- Suceso elemetl: Suceso formdo por u solo elemeto. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el suceso D = Scr úmero cdo e cero = {} es u suceso elemetl..- Suceso compuesto: Suceso formdo por más de u elemeto. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el suceso B = Scr múltiplo de tres = {,, 9} es u suceso compuesto..- Suceso seguro: Suceso que siempre se cumple. Estrá formdo por E. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el suceso F = Scr meor que = {,,,,, 7, 8, 9,, } = E..- Suceso imposile: Suceso que uc se cumple. Se desig por cojuto vcío. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el suceso G = Scr egtivo = {} es u suceso imposile..- Suceso cotrrio: Se llm suceso cotrrio del suceso A l formdo por los elemetos que o form A. Se deot A o A c.
6 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, ddo el suceso A = Scr pr = {,,, 8, }, el suceso A = Scr impr = {,, 7, 9, }.- Espcio de sucesos: Es el cojuto de todos los sucesos de u eperimeto letorio. Se deot por S. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el espcio de sucesos estrá formdo por todos los sucesos posiles del eperimeto S = { Scr pr, Scr impr, Scr múltiplo de, }..- Sucesos comptiles: Dos sucesos A y B se dice comptiles si tiee elemetos e comú, si se puede relizr l vez. A B. (A B, se lee A itersecció B y sigific lo que tiee e comú A y B). EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, los sucesos A = Scr pr = {,,, 8, } y B = Scr múltiplo de tres = {,, 9} so comptiles pues tiee e comú u elemeto, es decir, A B = {} y tmié A B..- Sucesos icomptiles: Dos sucesos A y B se dice icomptiles si o tiee elemetos e comú, si o se puede relizr l vez. A B =. EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, los sucesos B = Scr múltiplo de tres = {,, 9} y D = Scr úmero cdo e cero = {} so icomptiles pues o tiee elemetos e comú, es decir, A B =. cumplirá:. Proilidd de u suceso.- Regl de Lplce: Si todos los sucesos elemetles de u eperimeto letorio so equiproles, se ProilidddelsucesoA P(A) Númerodecsos fvorles A Númerodecsos posiles EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, l proilidd del suceso B = Scr múltiplo de tres = {,, 9}, será P(B), %. Este resultdo o es correcto porque los sucesos elemetles e el espcio {,,,,, 7, 8, 9,, } o so equiproles pues, P(Sumr tres) P(), %, mietrs P(Sumr oce) P(), % y P() P() P() P() P(7) P(8) P(9) P(), %, y por tto o se puede plicr Lplce. Por el cotrrio e el espcio formdo por todos los sucesos elemetles {+, +, +, +, +, +, +7, +8, +9, +, +, +, +, +, +, +, +7, +8, +9, +} = {,,,,, 7, 8, 9,,,,,,, 7, 8, 9,,, } = {,,,,,,,,,,, 7, 7, 8, 8, 9, 9,,, }, l proilidd de cd uo es l mism. 7 L proilidd de scr múltiplo de tres será: P(B) P() P() P(9), %..- Proilidd del suceso imposile: P() = EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, l proilidd del suceso G = Que l sum se egtiv = {}, será, P(G) P( )..- Proilidd del suceso seguro: P(E) = EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, l proilidd del suceso F = Scr meor que = {,,,,, 7, 8, 9,, } = E, será P(F) P(E)..- Proilidd de u suceso culquier A: P(A) EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, l proilidd del suceso D = Scr úmero cdo e cero = {}, será P(D),.
7 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los.- Proilidd del suceso cotrrio de A: P( A ) = p(a) EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, l proilidd del suceso A = Scr pr = {,,, 8, }, será P(A),, mietrs que l proilidd del cotrrio A, será P( A) P() P() P(7) P(9) P(), que tmié se puede clculr prtir de l epresió: P( A) P(A),..- Proilidd de l uió de sucesos comptiles: P(AUB) = P(A) + P(B) P(A B) (AUB se lee A uió B y sigific el suceso que se reliz cudo se cumple o A o B). EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el suceso A = Scr pr = {,,, 8, } y el suceso B = Scr múltiplo de tres = {,, 9} so sucesos comptiles y por tto l proilidd del suceso uió de los sucesos A y B viee dd por l epresió: 7 P(AUB) p(a) p(b) p(a B),7..- Proilidd de l uió de sucesos icomptiles: P(AUB) = P(A) + P(B) P(A B) = * P(A) + P (B) (Dos sucesos A y B so icomptiles si se cumple A B = y por tto P(A B) = ). EJEMPLO: E el eperimeto Scr u ol de u ur que cotiee ls ols umerds del l y sumr sus cifrs, el suceso B = Scr múltiplo de tres = {,, 9} y el suceso H = Scr múltiplo de cico = {, } so sucesos icomptiles y por tto l proilidd del suceso uió de los sucesos B y H viee dd por l epresió: 7 7 P(BUH) p(b) p(h) p(b H),, o ie P(BUH) p(b) p(h),, dode se ovi el vlor de P(B H) =.. Proilidd e eperimetos compuestos U eperimeto compuesto es el formdo por vrios eperimetos simples. EJEMPLO: El eperimeto Scr u ol y seguidmete otr ol de u ur que cotiee tres ols umerds del l y otr mos úmeros es u eperimeto compuesto. El espcio muestrl serí E = {(,), (,), (,), (,), (,), (,)}. EJEMPLO: El eperimeto Scr u ol, volver itroducirl y cotiució scr otr ol, de u ur que cotiee tres ols umerds del l y otr mos úmeros es u eperimeto compuesto. El espcio muestrl serí E = {(,), (,), (,), (,), (,), (,), (,), (,), (,)}..- Sucesos idepedietes: Dos sucesos A y B se dice idepedietes si el resultdo del segudo o se ve ifluecido por el resultdo del primero. Se cumple: P(A B) = P(A) P(B) EJEMPLO: E u ur hy 8 ols egrs, ols verdes y ols lcs. Se etre dos ols, co reemplzmieto, (sigific que se etre u ol, cotiució se devuelve l ol l ur y se etre l segud ol). Clculr l proilidd de que: ) L primer ol se egr y l segud se lc. ) Ls dos ols se de diferete color. c) Siedo que l primer ol es egr, l segud ol se lc. Pr clculr l proilidd de estos sucesos deemos diujr el árol co ls proiliddes de cd rm. A cotiució pr cd suceso se locliz l rm o rms que lo form teiedo e cuet que:.- A lo lrgo de u rm se multiplic ls proiliddes. (PROBABILIDAD CONDICIONADA).- Si u suceso se cosigue por vris rms, l proilidd se otiee sumdo ls proiliddes de cd rm. (PROBABILIDAD TOTAL) 7
8 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los ) L primer ol se egr y l segud se lc. Está formd por u sol rm, sí que clculmos su proilidd multiplicdo sus compoetes: P(Primer egr y Segud lc) = P(N y B ) = P(N B ) = P(N ) P(B ) = P(N) P(B) = 8 E l práctic deemos esforzros por dejr ie clr l proilidd que estmos clculdo y uque o vmos escriir tto como e el ejemplo terior, sí que por lo meos deerá precer: 8 P(N y B ) = P(N ) P(B ) = 9, % ) Ls dos ols se de diferete color. E este cso hy seis rms e ls que os ecotrmos co dos ols de distito color, clculremos cd u de ls seis rms y summos los resultdos: P(Dos ols diferete color) = P(B y V ) + P(B y N ) + P(V y B ) + P(V y N ) + P(N y B ) + P(N y V ) = = P(B ) P(V ) + P(B ) P(N ) + P(V ) P(B ) + P(V ) P(N ) + P(N ) P(B ) + P(N ) P(V ) = ,% Este tipo de situcioes veces se resuelve utilizdo l proilidd del suceso cotrrio, pues suele supoer meos trjo por teer meos rms que lo cumpl, e este cso: P(Dos ols diferete color) = P(Nigu de dos ols distito color) = P(Dos mismo color) = = (P(B y B ) + P(V y V ) + P(N y N )) = (P(B ) P(B ) + P(V ) P(V ) + P(N ) P(N )) = c) Siedo que l primer ol es egr, l segud ol se lc. P(Segud lc cudo primer h sido egr) = P(B /N ) = P(B) = E este cso os situmos mitd de árol (de izquierd derech) y solmete otmos su proilidd..- Sucesos depedietes: Dos sucesos A y B se dice depedietes si el resultdo del segudo se ve ifluecido por el resultdo del primero. Se cumple: P(A B) = P(A) P(B/A) o P(B A) = P(B) P(A/B) (P(A/B) se lee proilidd de B cudo A o proilidd de B cudo ocurrido A ) EJEMPLO: E u ur hy 8 ols egrs, ols verdes y ols lcs. Se etre dos ols, si reemplzmieto, (sigific que se etre u ol y cotiució l otr ol). Clculr l proilidd de que: ) L primer ol se egr y l segud se lc. P(Primer egr y Segud lc) = P(N y B ) = P(N B ) = P(N ) P(B /N ) = P(N) P(B/N) = 8 E l práctic deemos esforzros por dejr ie clr l proilidd que estmos clculdo y uque o vmos escriir tto como e el ejemplo terior, sí que por lo meos deerá precer: 8 P(N y B ) = P(N ) P(B /N ) = % ) Ls dos ols se de diferete color. P(Dos ols diferete color) = = P(B y V ) + P(B y N ) + P(V y B ) + P(V y N ) + P(N y B ) + P(N y V ) = = P(B ) P(V /B ) + P(B ) P(N /B ) + P(V ) P(B /V ) + P(V ) P(N /V ) + P(N ) P(B /N ) + P(N ) P(V /N ) = ,% 8
9 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los Este tipo de situcioes veces se resuelve utilizdo l proilidd del suceso cotrrio, pues suele supoer meos trjo por teer meos rms que lo cumpl, e este cso: P(Dos ols diferete color) = P(Nigu de dos ols distito color) = P(Dos mismo color) = = (P(B y B ) + P(V y V ) + P(N y N )) = (P(B ) P(B /B ) + P(V ) P(V /V ) + P(N ) P(N /N )) = c) Siedo que l primer ol es egr, l segud ol se lc. P(Segud lc cudo primer h sido egr) = P(B /N ) = E este cso os situmos mitd de árol (de izquierd derech) y solmete otmos su proilidd, e este cso l ser sucesos depedietes (si devolució) l proilidd P(B /N ) = P(B) = Tto e el cso de co devolució como e el cso de si devolució, l sum de ls proiliddes de ls ueve rms que form el árol dee ser uo..- Co reemplzmieto: P(TODO EL ÁRBOL) = = P(B y B ) + P(B y V ) + P(B y N ) + P(V y B ) + P(V y V ) + P(V y N ) + P(N y B ) + P(N y V ) + P(N y N ) = P(B ) P(B ) + P(B ) P(V ) + P(B ) P(N ) + P(V ) P(B ) + P(V ) P(V ) + P(V ) P(N ) +.- Si reemplzmieto: + P(N ) P(B ) + P(N ) P(V ) + P(N ) P(N ) = P(TODO EL ÁRBOL) = = P(B y B ) + P(B y V ) + P(B y N ) + P(V y B ) + P(V y V ) + P(V y N ) + P(N y B ) + P(N y V ) + P(N y N ) = P(B ) P(B /B ) + P(B ) P(V /B ) + P(B ) P(N /B ) + P(V ) P(B /V ) + P(V ) P(V /V ) + P(V ) P(N /V ) + P(N ) P(B /N ) + P(N ) P(V /N ) + P(N ) P(N /N ) = Tls de cotigeci.- Tl de cotigeci: Es u tl que se utiliz pr orgizr los dtos e ciertos prolems de cálculo de proiliddes. EJEMPLO: E u colegio hy chicos y 8 chics. E este colegio se estudi tres idioms como tercer legu, chio, lemá y frcés. De los chicos estudi lemá y estudi frcés. De ls chics estudi lemá y estudi chio. Se tom u lumo l zr. Clculr: ) Proilidd de que estudie chio. ) Proilidd de estudir chio de etre los chicos. Hcemos l tl co l iformció del eucido: ) P(chio) = =, = % CHICOS CHICAS CHINO ALEMÁN FRANCÉS 8 ) P(chio siedo chico) = =,7 = 7,% 9
10 º ESO ACADÉMICAS COMBINATORIA y PROBABILIDAD DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtíez-Los NOTAS_ COMBINATORIA y PROBABILIDAD * SÍMBOLOS: _ Implic ó quiere decir ó supoe que, l relció es ciert de izquierd derech. _ Implic ó quiere decir ó supoe que, l relció es ciert de derech izquierd. _ Dole implic, l relció es ciert e mos setidos. _ Distito _ Ifiito _ Aproimdo _ Perteece _ No perteece / _ Tl que Π _ Tl que _ Eiste _ No eiste α _ Alf β _ Bet _ Gmm > _ Myor que _ Myor o igul que < _ Meor que _ Meor o igul que \ _ Meos de cojutos _ Cojuto vcío
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
( a b c) n = a n b n c n ( a : b) n = a n : b n a n a m = a n+m a n :a m = a n-m (a n ) m = a n.m
 Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
2. Principio de Conteo
 2. Pricipio de Coteo Prtició de u Cojuto Defiició Ddo u cojuto A, diremos que los sucojutos de A, A 1,A 2,...,A, costituye u prtició del mismo si se cumple ls siguietes codicioes: 1. A ; i 1,2,3,..., i
2. Pricipio de Coteo Prtició de u Cojuto Defiició Ddo u cojuto A, diremos que los sucojutos de A, A 1,A 2,...,A, costituye u prtició del mismo si se cumple ls siguietes codicioes: 1. A ; i 1,2,3,..., i
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
1.- POTENCIAS DE EXPONENTE ENTERO
 º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
TEMA1: MATRICES Y DETERMINANTES:
 TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
Matemáticas Aplicadas a la Ciencias Sociales II SISTEMAS DE ECUACIONES. , a toda ecuación que pueda escribirse de la forma: ...
 Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
COMBINATORIA. Las variaciones ordinarias se representan por el símbolo Vm,n o por V
 COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
Sucesiones de números reales
 Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
PROBLEMAS Y EJERCICIOS RESUELTOS
 PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Guía ejercicios resueltos Sumatoria y Binomio de Newton
 Auilir: Igcio Domigo Trujillo Silv Uiversidd de Chile Guí ejercicios resueltos Sumtori y Biomio de Newto Solució: ) Como o depede de j, es costte l sumtori. b) c) d) Auilir: Igcio Domigo Trujillo Silv
Auilir: Igcio Domigo Trujillo Silv Uiversidd de Chile Guí ejercicios resueltos Sumtori y Biomio de Newto Solució: ) Como o depede de j, es costte l sumtori. b) c) d) Auilir: Igcio Domigo Trujillo Silv
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
Universidad Alonso de Ojeda Facultad de Ciencias Administrativas Unidad Curricular: Matemática II FÓRMULAS ARITMÉTICAS
 Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Uiversidd Aloso de Ojed Fcultd de Ciecis Admiistrtivs Uidd Curriculr: Mtemátic II FÓRMULAS ARITMÉTICAS PARA FRACCIONES Número mixto Pr psr de úmero mixto frcció impropi, se dej el mismo deomidor y el umerdor
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Matemática 1 Capítulo 4
 Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
CAPÍTULO 2: POTENCIAS Y RAÍCES 1. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES
 CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
SISTEMAS DE ECUACIONES LINEALES
 SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
SISTEMAS DE ECUACIONES LINEALES: TEOREMA DE ROUCHÉ- FROBENIUS
 R.F.- - SISTES DE ECUCIONES INEES: TEORE DE ROUCHÉ- FROBENIUS Recordeos que u siste de ecucioes co icógits es u siste de l for: Dode: ij so úeros reles se ll coeficietes del siste,,,, so úeros reles recie
R.F.- - SISTES DE ECUCIONES INEES: TEORE DE ROUCHÉ- FROBENIUS Recordeos que u siste de ecucioes co icógits es u siste de l for: Dode: ij so úeros reles se ll coeficietes del siste,,,, so úeros reles recie
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
3. SISTEMAS DE ECUACIONES LINEALES
 Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
Teorí ejercicios de teátics II. Álger Sistes de ecucioes lieles - -. SISTES DE ECUCIONES INEES. DEFINICION U ecució liel es u ecució de l for e l que, so los coeficietes de ls icógits, es el tério idepediete
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Unidad 7: Sucesiones. Solución a los ejercicios
 Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Radicación en R - Potencia de exponente racional Matemática
 Rdiccio e R Poteci de eoete rciol Mtemátic º Año Cód. 0- P r o f. V e r ó i c F i l o t t i P r o f. M r í d e l L u j á M r t í e z C o r r e c c i ó : P r o f. S i l v i A m i c o z z i Dto. de M t emátic
Rdiccio e R Poteci de eoete rciol Mtemátic º Año Cód. 0- P r o f. V e r ó i c F i l o t t i P r o f. M r í d e l L u j á M r t í e z C o r r e c c i ó : P r o f. S i l v i A m i c o z z i Dto. de M t emátic
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
Estructuras Discretas. Unidad 3 Teoría de números
 Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
( ) ( ) El principio de inducción
 El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
El priipio e iuió U ejemplo seillo pr empezr Si hemos oío hlr e progresioes ritmétis (series e úmeros e form que l iferei etre os oseutivos es siempre l mism, omo,,, 0,) prolemete o será fáil lulr l sum
9 Proieddes del roducto de úmeros or mtrices: b y M m. socitiv: b b Distributiv e : b b Distributiv e M m : Elemeto eutro: =.. Producto de mtrices Pr
 . OPERIONES ON MRIES.. Sum de mtrices Pr oder sumr dos mtrices ésts debe teer l mism dimesió. Etoces se sum térmio térmio: b b m m m Proieddes de l sum de mtrices: socitiv: omuttiv: Elemeto eutro: L mtriz
. OPERIONES ON MRIES.. Sum de mtrices Pr oder sumr dos mtrices ésts debe teer l mism dimesió. Etoces se sum térmio térmio: b b m m m Proieddes de l sum de mtrices: socitiv: omuttiv: Elemeto eutro: L mtriz
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
Anillos de Newton Fundamento
 Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
TEMA Nº 1: NÚMEROS REALES
 Deprtmeto de Mtemátics. I.E.S. Ciudd de Arjo º BAC MCS TEMA Nº : NÚMEROS REALES. NÚMEROS RACIONALES. EXPRESIONES DECIMALES.. NÚMEROS RACIONALES. EXPRESIONES DECIMALES. NÚMEROS IRRACIONALES.. NÚMEROS REALES.
Deprtmeto de Mtemátics. I.E.S. Ciudd de Arjo º BAC MCS TEMA Nº : NÚMEROS REALES. NÚMEROS RACIONALES. EXPRESIONES DECIMALES.. NÚMEROS RACIONALES. EXPRESIONES DECIMALES. NÚMEROS IRRACIONALES.. NÚMEROS REALES.
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
Liceo Marta Donoso Espejo Raíces para Terceros
 . Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
. Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
6. Variable aleatoria continua
 6. Vrile letori continu Un diálogo entre C3PO y Hn Solo, en El Imperio Contrtc, cundo el Hlcón Milenrio se dispone entrr en un cmpo de steroides: - C3PO: Señor, l proilidd de sorevivir l pso por el cmpo
6. Vrile letori continu Un diálogo entre C3PO y Hn Solo, en El Imperio Contrtc, cundo el Hlcón Milenrio se dispone entrr en un cmpo de steroides: - C3PO: Señor, l proilidd de sorevivir l pso por el cmpo
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
GESTIÓN FINANCIERA. 1. Por qué se caracteriza una operación financiera? (1,5 puntos)
 Escuel Técic Superior de Iformátic Covoctori de Juio - Primer Sem Mteril Auxilir: Clculdor ficier GESTIÓN FINANCIERA 27 de Myo de 2-8, hors Durció: 2 hors. Por qué se crcteriz u operció ficier? (, putos)
Escuel Técic Superior de Iformátic Covoctori de Juio - Primer Sem Mteril Auxilir: Clculdor ficier GESTIÓN FINANCIERA 27 de Myo de 2-8, hors Durció: 2 hors. Por qué se crcteriz u operció ficier? (, putos)
TEMA 3: RESOLUCIÓN DE SISTEMAS DE ECUACIONES MEDIANTE DETERMINANTES.
 TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES. º BCH(CN) TEM : RESOLUCIÓN DE SISTEMS DE ECUCIONES MEDINTE DETERMINNTES..-INTRODUCCIÓN. L resoluió de sistems de euioes está ligd l estudio
En una carrera participan 5 naciones, España, Bélgica, Francia, Alemania e Italia. De cuantas maneras distintas pueden llegar a la meta?
 Colegio Mter Slvtoris TEMA: TÉCNICAS DE RECUENTO. COMBINATORIA. DIAGRAMA EN ARBOL E l crt de u resturte el cliete puede elegir su meú, escogiedo u primer plto, u segudo plto y u postre. Si l crt tiee 7
Colegio Mter Slvtoris TEMA: TÉCNICAS DE RECUENTO. COMBINATORIA. DIAGRAMA EN ARBOL E l crt de u resturte el cliete puede elegir su meú, escogiedo u primer plto, u segudo plto y u postre. Si l crt tiee 7
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Práctica 6. Calcular la suma de los primeros K números naturales y k k. . 2 Calcular la suma de los cuadrados de los primeros k números
 PRÁCTICA SERIES NUMÉRICAS Práctics Mtlb Objetivos Práctic 6 Estudir l covergeci o divergeci de u serie de térmios positivos utilizdo distitos criterios combido ls coclusioes experimetles (el ordedor) co
PRÁCTICA SERIES NUMÉRICAS Práctics Mtlb Objetivos Práctic 6 Estudir l covergeci o divergeci de u serie de térmios positivos utilizdo distitos criterios combido ls coclusioes experimetles (el ordedor) co
Neper ( ) Lección 2. Potencias, radicales y logarítmos
 Neer (0-7) Lecció Potecis, rdicles y logrítmos º ESO MATEMÁTICAS ACADÉMICAS Potecis, rdicles y logritmos LECCIÓN. POTENCIAS, RADICALES, LOGARITMOS. Potecis de exoete etero Recuerd l defiició de oteci co
Neer (0-7) Lecció Potecis, rdicles y logrítmos º ESO MATEMÁTICAS ACADÉMICAS Potecis, rdicles y logritmos LECCIÓN. POTENCIAS, RADICALES, LOGARITMOS. Potecis de exoete etero Recuerd l defiició de oteci co
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
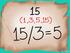 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
El conjunto de los Números Reales
 El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
Ejercicios resueltos de Matemática discreta: Combinatoria, funciones generatrices y sucesiones recurrentes.
 Ejercicios resueltos de Mtemátic discret: Combitori, fucioes geertrices y sucesioes recurretes. (º Igeierí iformátic. Uiversidd de L Coruñ José Muel Rmos Gozález Itroducció Estos ejercicios h sido propuestos
Ejercicios resueltos de Mtemátic discret: Combitori, fucioes geertrices y sucesioes recurretes. (º Igeierí iformátic. Uiversidd de L Coruñ José Muel Rmos Gozález Itroducció Estos ejercicios h sido propuestos
APUNTES DE MATEMÁTICAS 1º BACHILLERATO
 APUNTES DE MATEMÁTICAS 1º BACHILLERATO 01-014 Aputes Bchillerto 01-014 Tem 0 1. TEMA 0:NÚMEROS REALES 1.1. CONJUNTOS NUMERICOS... 1.. INTERVALOS Y SEMIRECTAS.... 1.. VALOR ABSOLUTO.... 5 1.4. PROPIEDADES
APUNTES DE MATEMÁTICAS 1º BACHILLERATO 01-014 Aputes Bchillerto 01-014 Tem 0 1. TEMA 0:NÚMEROS REALES 1.1. CONJUNTOS NUMERICOS... 1.. INTERVALOS Y SEMIRECTAS.... 1.. VALOR ABSOLUTO.... 5 1.4. PROPIEDADES
BLOQUE 1: ÁLGEBRA. Tema 4: Sistemas de Ecuaciones Lineales
 MTEMÁTICS º Bch BLOQUE : ÁLGEBR José Rmón Pdrón Tem : Sistems de Ecuciones Lineles MTEMÁTICS º Bch Tem : Sistems de Ecuciones Lineles TEOREM DE ROUCHÉ José Rmón Pdrón Supongmos el sistem siguiente: z z
MTEMÁTICS º Bch BLOQUE : ÁLGEBR José Rmón Pdrón Tem : Sistems de Ecuciones Lineles MTEMÁTICS º Bch Tem : Sistems de Ecuciones Lineles TEOREM DE ROUCHÉ José Rmón Pdrón Supongmos el sistem siguiente: z z
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
UNIVERSIDAD AMERICANA. Curso BAN-03: Matemática I ( Jueves- Noche ) Prof. Edwin Gerardo Acuña Acuña PRÁCTICA DE FACTORIZACIÓN
 UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
LOGARITMO 4º AÑO DEF. Y PROPIEDADES
 LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
UNIDAD 1: NÚMEROS RACIONALES E
 Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática.
 Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Tema 1: NÚMEROS REALES.
 I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
I.E.S. Slvdor Serro - Deprteto de Mteátics MATEMÁTICAS ACADÉMICAS º ESO - 0 / Te : NÚMEROS REALES. Actividdes pr preprr el exe: Teorí: Cotest si so cierts ls siguietes fircioes: Todo úero etero es turl.
PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE
 UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
Este documento es de distribución gratuita y llega gracias a www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio!
 Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Tema 2. Operaciones con Números Reales
 Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
PAGINA Nº 80 GUIAS DE ACTIVIDADES Y TRABAJOS PRACTICOS Nº 14
 GUIA DE TRABAJO PRACTICO Nº 4 PAGINA Nº 80 GUIAS DE ACTIVIDADES Y TRABAJOS PRACTICOS Nº 4 OBJETIVOS: Lograr que el Alumo: Resuelva correctamete aritmos y aplique sus propiedades. Resuelva ecuacioes epoeciales.
GUIA DE TRABAJO PRACTICO Nº 4 PAGINA Nº 80 GUIAS DE ACTIVIDADES Y TRABAJOS PRACTICOS Nº 4 OBJETIVOS: Lograr que el Alumo: Resuelva correctamete aritmos y aplique sus propiedades. Resuelva ecuacioes epoeciales.
Combinatoria y definiciones básicas de probabilidad
 Combiatoria y defiicioes básicas de probabilidad Defiicioes de probabilidad Probabilidad como ituició Probabilidad como la razó de resultados favorables Probabilidad como medida de la frecuecia de ocurrecia
Combiatoria y defiicioes básicas de probabilidad Defiicioes de probabilidad Probabilidad como ituició Probabilidad como la razó de resultados favorables Probabilidad como medida de la frecuecia de ocurrecia
INTRODUCCIÓN A LA PROBABILIDAD
 INTRODUIÓN L PROBBILIDD EXPERIMENTOS LETORIOS Y DETERMINISTS Los experimetos o feómeos cuyo resultado o puede coocerse hasta haber realizado la experiecia se llama aleatorios o estocásticos. uado el resultado
INTRODUIÓN L PROBBILIDD EXPERIMENTOS LETORIOS Y DETERMINISTS Los experimetos o feómeos cuyo resultado o puede coocerse hasta haber realizado la experiecia se llama aleatorios o estocásticos. uado el resultado
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES
 TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES SUCESIÓN NUMÉRICA: es u fució cuyo domiio es el cojuto de los úmeros turles (o u subcojuto de él) y l imge está icluid e el cojuto de los Reles ( ) SUCESIÓN ARITMÉTICA:
TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES SUCESIÓN NUMÉRICA: es u fució cuyo domiio es el cojuto de los úmeros turles (o u subcojuto de él) y l imge está icluid e el cojuto de los Reles ( ) SUCESIÓN ARITMÉTICA:
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES
 CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
NÚMEROS ( 4) ENTEROS RACIONALES 1 + : 2. A) Ordena los siguientes números enteros: 4, B) Calcula: 2) 3) 4) ( ) ( ) 3. A) Calcula:
 NÚMEROS ENTEROS A Orde los siguietes úmeros eteros,,,,, 8, 8 B Clcul 7 ( ( 7 ( ( ( 7 0 ( ( 7 7 ( 0 ( ( 8 7 ( 0 ( 9 8 [ ( 0 7] 0 [ 8 ] ( 7 8 [ ( ] ( ( 8 ( ( ( ( [ ] [ 9 ] ( 7 8 [ ( ] [ ( ] {[ ] [ ( ] }
NÚMEROS ENTEROS A Orde los siguietes úmeros eteros,,,,, 8, 8 B Clcul 7 ( ( 7 ( ( ( 7 0 ( ( 7 7 ( 0 ( ( 8 7 ( 0 ( 9 8 [ ( 0 7] 0 [ 8 ] ( 7 8 [ ( ] ( ( 8 ( ( ( ( [ ] [ 9 ] ( 7 8 [ ( ] [ ( ] {[ ] [ ( ] }
