Departamento de Diseño Mecánico Elementos de Máquinas AJUSTES Y TOLERANCIAS
|
|
|
- Juan José Camacho Espejo
- hace 8 años
- Vistas:
Transcripción
1 Depatament de Dseñ Mecánc AJUSTES Y TOLERANCIAS
2 Depatament de Dseñ Mecánc. TOLERANCIAS Tleanca se puede defn cm la vaacón ttal admsble del val de una dmensón. Las tleancas dmensnales fjan un ang de vales pemtds paa las ctas funcnales de la peza. Se utlzaá la sguente temnlgía en el estud de este tp de pblemas Eje: element mach del acplament. Aguje: element hemba en el acplament Dmensón: Es la cfa que expesa el val numéc de una lngtud de un ángul. Dmensón nmnal (dn paa ejes, DN paa agujes): es el val teóc que tene una dmensón, espect al que se cnsdean las meddas límtes. Dmensón efectva:(de paa eje, De paa agujes): es el val eal de una dmensón, que ha sd delmtada mdend sbe la peza ya cnstuda. Dmensnes límtes (máxma, dm paa ejes, DM paa agujes; mínma, dm paa ejes, Dm paa agujes): sn ls vales extems que puede tma la dmensón efectva. Dmensnes límtes (máxma, dm paa ejes, DM paa agujes; mínma, dm paa ejes, Dm paa agujes): sn ls vales extems que puede tma la dmensón efectva. Desvacón dfeenca: es la dfeenca ente una dmensón y la dmensón nmnal. Dfeenca efectva: es la dfeenca efectva ente la medda efectva y la dmensón nmnal. Dfeenca supe nfe: es la dfeenca ente la dmensón máxma/mínma y la dmensón nmnal cespndente.
3 Depatament de Dseñ Mecánc Dfeenca fundamental: es una cualquea de las desvacnes límtes (supe nfe) elegda cnvenentemente paa defn la pscón de la zna de tleanca en elacón a la línea ce. Línea de efeenca línea ce: es la línea ecta que sve de efeenca paa las desvacnes dfeencas y que cespnde a la dmensón nmnal. Tleanca (t paa ejes, T paa agujes): es la vaacón máxma que puede tene la medda de la peza. Vene dada p la dfeenca ente las meddas límtes, y cncde cn la dfeenca ente las desvacnes supe e nfe. Zna de la tleanca: es la zna cuya ampltud es el val de la tleanca Tleanca fundamental: es la tleanca que se detemna paa cada gup de dmensnes y paa cada caldad de tabaj.
4 Depatament de Dseñ Mecánc Las tleancas dmensnales se pueden epesenta en ls dbujs de vaas fmas: Cn su medda nmnal seguda de las desvacnes límtes. Cn ls vales máxm y mínm. Cn la ntacón nmalzada ISO. Pueden se a su vez: a) Blateales, cuand la dmensón de una peza puede se may men que la dmensón dada, b) Unlateal, cuand la dmensón de una peza puede se sl may, sl men, que la dmensón dada. Las undades de las desvacnes sn las msmas que las de la dmensón nmnal. Nmalmente seán mlímets. El núme de cfas decmales debe se el msm en las ds dfeencas, salv que una de ellas sea nula. Ls símbls ISO utlzads paa epesenta las tleancas dmensnales tenen tes cmpnentes: Medda nmnal.
5 Depatament de Dseñ Mecánc Una leta epesentatva de la dfeenca fundamental en val y en sgn (mnúscula paa eje, mayúscula paa aguje), que ndca la pscón de la zna de tleanca. Un núme epesentatv de la anchua de la zna de tleanca (Caldad de la tleanca). P ejempl en un plan se tendá: Vales paa el ajuste cn jueg 50 F8/g6
6 Depatament de Dseñ Mecánc S ls vales están lmtads en máxm y mínm es sufcente cn pne ls vales límte.. Caldad de la tleanca El sstema de tleancas y ajustes ISA tene cm fundament las sguentes pemsas:
7 Depatament de Dseñ Mecánc º) La tempeatua de efeenca es de 0ºC º) El Sstema ISO de tleancas ( Nma ISO 86(I)-6) paa dmensnes nmnales cmpenddas ente 0 y 500mm ealza una patcón en gups de dámets dent de cuys límtes las magntudes nmnales de las tleancas pemanecen cnstantes. Ls dámets ncluds sn de 0 a 500mm. 3º) Dcha nma dstngue decch caldades ( decch gads de tleanca clases de pecsón) desgnads cm IT0, IT0, IT,, IT6, y se calculan las tleancas que se llaman fundamentales. 4º)Paa cada gup de dámets y cada caldad, la tleanca, llamada fundamental, pemanecó cnstante. 5º)Las tleancas fundamentales, paa las caldades 5 a 6, se detemnan en funcón de la undad de tleanca ntenacnal, send: =0,45D /3 +0,00D, dnde se expesa en mcnes y D es la medda gemétca de ls dámets límtes del gup, expesada en mm. La caldad índce de caldad es un cnjunt de tleancas que se cespnde cn un msm gad de pecsón paa cualque gup de dámets. Cuant may sea la caldad de la peza, men seá la tleanca. De esta fma, las caldades 0 a 3 paa ejes y 0 a 4 paa agujes se usan paa calbes y pezas de alta pecsón. Las caldades 4 a paa ejes y 5 a paa agujes, están pevstas paa pezas que van a esta smetdas a ajustes. P últm, las caldades supees a se usan paa pezas elements aslads que n equeen un acabad tan fn. En la tabla se muestan ls vales fundamentales en mcas paa cada una de las decch caldades y paa cada un de ls tece gups de dmensnes de la see pncpal.
8 Depatament de Dseñ Mecánc Gups de CALIDADES Dámets IT IT IT IT IT IT IT IT IT IT IT IT IT IT IT IT IT IT (mm) d < d < d < d < d < d < d < d < d < d < d < d < d Ultape- -csón Calbe y pezas de gan pecsón Pezas elements destnads a ajusta Pezas elements que n han de ajusta Tabla I. Vales numécs de ampltudes de znas de tleanca.3 Pscón de la zna de tleanca El sstema ISO de tleancas defne ventch pscnes dfeentes paa las znas de tleanca, stuadas espect a la línea ce, según puesde vese en la Fg..
9 Depatament de Dseñ Mecánc Se defnen medante unas letas (mayúsculas paa agujes y mnúsculas paa ejes), según se muesta a cntnuacón: Agujes: A, B, C, CD, D, E, EF, F, FG, G, H, J, Js, K, M, N, P, R, S, T, U, V, X, Y, Z, ZA, ZB, ZC EJES : a, b, c, cd, d, e, ef, f, fg, g, h, j, js, k, m, n, p,, s, t, u, v, x, y, z, za, zb, zc. En la tabla II se muestan las dfeencas fundamentales paa ejes expesadas en mcas. La dfeenca fundamental es gual a la supe ds paa las pscnes a hasta h, y la nfe paa las pscnes j hasta zc. La ta dfeenca fundamental se puede calcula a tavés de las elacnes: d = ds t ó ds = d +t En la tabla III se muestan las dfeencas fundamentales paa agujes expesadas en mcas. La dfeenca fundamental es la nfe D paa las pscnes A hasta H, y la supe paa las pscnes J hasta ZC. La ta dfeenca fundamental se puede calcula a tavés de las elacnes: Ds = D + T ó D = Ds - T
10 Depatament de Dseñ Mecánc
11 Fg. Pscnes de las znas de tleanca Depatament de Dseñ Mecánc
12 Depatament de Dseñ Mecánc
13 Depatament de Dseñ Mecánc Dad que paa cada gup de dámets nmnales se pueden eleg un núme elevad de znas de tleanca y de gads de caldad, se ecmenda utlza slamente algunas znas de tleanca, llamadas znas de tleanca pefeentes. Znas de tleanca pefeentes paa Agujes G6 H6 Js6 K6 M6 N6 P6 R6 S6 T6 F7 G7 H7 Js7 K7 M7 N7 P7 R7 S7 T7 E8 F8 H8 Js8 K8 M8 N8 P8 R8 D9 E9 F9 H9 D0 E0 H0 A B C D H Znas de tleanca pefeentes paa Ejes g5 h5 js5 k5 m5 n5 p5 5 s5 t5 f6 g6 h6 js6 k6 m6 n6 p6 6 s6 t6 f7 h7 js7 k7 m7 n7 p7 7 t7 t7 u7 d8 e8 f8 h8 d9 e9 h9 d0 a b c h.4 Ajustes Se denmna ajuste a la dfeenca ente las meddas antes del mntaje de ds pezas que han de acpla. Según la zna de tleanca de la medda nte y exte, el ajuste puede se:
14 Depatament de Dseñ Mecánc Ajuste móvl cn jueg. Ajuste ndetemnad. Ajuste fj cn apete. Apete (A) es la dfeenca ente las meddas efectvas de eje y aguje, antes del mntaje, cuand ésta es pstva, es dec, cuand la dmensón eal del eje es may que la del aguje: A = de - De > 0
15 Depatament de Dseñ Mecánc Apete máxm (AM) es el val de la dfeenca ente la medda máxma del eje y la medda mínma del aguje: AM = dm - Dm Apete mínm (Am) es el val de la dfeenca ente la medda mínma del eje y la máxma del aguje: Am = dm - DM Se llama tleanca del Apete (TA) a la dfeenca ente ls apete máxm y mínm, que cncde cn la suma de las tleancas del aguje y del eje: TA = AM - Am = T + t
16 Depatament de Dseñ Mecánc Sstema Aguje Base: En este sstema se tma sempe cm element fj paa el ajuste la pscón del aguje H, y a pat de ahí, se usan ls dats de Apet Máxm, Apet Mínm, Tleanca del Aguje y Tleanca del Eje paa btene las dfeencas nfees máxma y mínma paa la pscón del eje que vefcan las cndcnes del ajuste. Sstema Eje Base: En este sstema se tma sempe cm element fj paa el ajuste la pscón del eje h, y a pat de ahí, se usa ls dats de Apet Máxm, Apet Mínm, Tleanca del Aguje y Tleanca del Eje paa btene las dfeencas supees máxmas y mínmas paa la pscón del aguje que vefcan las cndcnes del ajuste:
17 Depatament de Dseñ Mecánc.5 Jueg (u Hlgua) Se denmna jueg (J) a la dfeenca ente las meddas del aguje y del eje, antes del mntaje, cuand ésta es pstva, es dec, cuand la dmensón eal del eje es men que la del aguje: J = De - de > 0 Jueg máxm (JM) es la dfeenca que esulta ente la medda máxma del aguje y la mínma del eje: JM = DM - dm Jueg mínm (Jm) es la dfeenca ente la medda mínma del aguje y la máxma del eje: Jm = Dm - dm Se llama tleanca del jueg (TJ) a la dfeenca ente ls juegs máxm y mínm, que cncde cn la suma de las tleancas del aguje y del eje: TJ = JM - Jm = T + t
18 Depatament de Dseñ Mecánc Se denmna ajuste ndetemnad (I) a un tp de ajuste en el que la dfeenca ente las meddas efectvas de aguje y eje puede esulta pstva negatva, dependend de cada mntaje cncet: I = De - de < 0 ó > 0 JM = DM - dm AM = dm - Dm Se llama tleanca del ajuste ndetemnad (TI) a la suma del jueg máxm y del apet máxm, que cncde cn la suma de las tleancas del aguje y del eje: TI = JM + AM = T + t Tenend en cuenta las pscnes y tamañs elatvs ente las tleancas de ejes y agujes, se pueden da tes cass, cm se muestan en las fguas a cntnuacón:
19 Depatament de Dseñ Mecánc El val del Jueg máxm supea al Apete máxm El apete máxm es gual al jueg máxm. El apete máxm es supe al jueg máxm. Paa detemna ls juegs límtes se tendá en cuenta que: Se debe evta td exces de pecsón.
20 Depatament de Dseñ Mecánc Se debe adpta sempe que sea psble may tleanca paa el eje que paa el aguje. Se deben eleg las tleancas de fma que las caldades del eje y del aguje n vaíen en más de ds índces. Se debe tene en cuenta la expeenca en ajustes análgs. Mntaje de las pezas. Al fja ls juegs límtes de un acplament se deben tene en cuenta: Estad supefcal. Natualeza del mateal. Velcdad de funcnament. Natualeza, ntensdad, deccón, sentd, vaacón y pdad de ls esfuezs. Engase. Desgaste. Gemetía del cnjunt.
21 Depatament de Dseñ Mecánc
22 .6 Nma ASA Standad B Depatament de Dseñ Mecánc
23 Depatament de Dseñ Mecánc
24 Depatament de Dseñ Mecánc
25 .7 Pcess de manufactua y acabads supefcales Depatament de Dseñ Mecánc
26 Depatament de Dseñ Mecánc Tabla XX Rugsdad según ls dstnts pcess de manufactua
27 Depatament de Dseñ Mecánc Smblgía paa las caacteístcas bjet de tleancas
28 Depatament de Dseñ Mecánc. INTERCAMBIABILIDAD El cntnu avance de la técnca exge mecansms cada vez más pecss y a csts aznables; ell tae apaejad un aument de la caldad de la pduccón y una elevacón del endment de ls pcess ndustales. Ests ds aspects se hallan fmemente ascads a la ntecambabldad de pezas, ya que sn su cncus, pc se puede ealza de l ante, pues debems tene pesente que, en geneal, se está habland de pcess en ls que ntevenen un cnjunt de pezas paa ntega una máquna un mecansm, y n de elements aslads. Ls dvess elements ntegantes de máqunas pates de éstas se hallan vnculads de maneas peestablecdas y deben ealza mvments detemnads, cm se el de tacón de desplazament, y en ts cass deben mantene una elatva pscón, nvaable a tavés del temp, cn el fn de asegua la gdez de víncul que ealzan. Vems entnces que pdems establece ds gandes gups de vnculacnes que sn (Fg.) las fjas y las móvles. Es evdente que el eje B pdá se ntducd cn jueg en el aguje A, cuand el dámet del aguje sea may que el dámet del eje. En el cas de se el dámet del eje may que el del aguje, tendems que, p ntduccón del eje en el aguje ambas pezas se defmaán, btenéndse una vnculacón fja. Al espect se debe aclaa que el caácte de la unón de las pezas debe pemanece cnstante a pesa de las vaacnes que puedan cu de las cndcnes de tabaj, cm se vaacnes de ls esfuezs, de las velcdades de tacón de la tempeatua de la msma. La unón fja móvl del ábl cn el aguje puede btenese medante la aplcacón de dscepancas en las dmensnes del dámet del eje y del aguje, las que se tman espect a la llamada
29 Depatament de Dseñ Mecánc dmensón nmnal de la unón, que es la que se ndca en ls plans. Cada un de ls vínculs pyectads de esta manea puede tene dstntas pecsnes de acabad. Antguamente exstía la tendenca de mantene la dmensón nmnal cn la may pecsón psble y en fma ndependente de la funcón que cumple el mecansm. Est d mtv a que la elabacón fuea sumamente e nnecesaamente cstsa e hz mpescndble la utlzacón de man de ba calfcada; mas aún, la ealzacón de ds vínculs guales n ajaba el msm ajuste, p la nevtable vaacón que ntduce el acabad manual. Pe había alg que ea much más gave que td es y cnsstía en el hech de que las pezas ntegantes de mecansms cnstuds de tal manea n pdían se dectamente eemplazadas, sn pev ajuste. De l expuest suge enseguda la cnsdeacón de la mpsbldad de tene pezas de epuest paa un ápd ntecamb. El cnstuct debeá fja de anteman las dscepancas de las dmensnes nmnales de las pezas a fabca y peve ls límtes de pecsón admsbles duante la ejecucón, cmpatbles cn la natualeza y caacteístcas de funcnament de la vnculacón, la psbldad de su ealzacón en funcón del equp dspnble y las necesaas cndcnes ecnómcas de btencón de pezas a csts aznables. De este md se psblta la taea de fabcacón y mntaje de pezas de una manea acnal y ealzada p peas, nclusve pc calfcads. Llamaems pezas ntecambables a las que pueden se eemplazadas dectamente, sn nngún ajuste pste y sn que ell nfluya en el funcnament del mecansm La ntecambabldad es de captal mptanca paa el usua de una máquna, ya que psblta el ecamb ápd de la peza a un cst elatvamente baj y cn man de ba cente, en el pe de ls cass debeá ealza la epaacón un talle especalzad pe se habá evtad tene que emt la máquna al fabcante, csa páctcamente n vable, tatándse de elements de mptacón fuea de catálg en el país de gen. El cst y la pecsón sn factes puests en la entabldad de una pduccón (Fg.): a men tleanca, may cst de mecanzad.
30 Depatament de Dseñ Mecánc Fg. Cst elatv en funcón de la tleanca Resulta ben cla que eleva las exgencas de pecsón, más allá de l que el pces cente de fabcacón pemte, hace cmplca y encaece nnecesaamente la pduccón. P l tant se debe psee un cla cncept de la detemnacón de fmas de pezas, emplea dmensnes nmnales nmalzadas, tleancas de ejecucón y ugsdad de supefces cm así tambén desalla métds de medcón y cntl de pezas que gaantcen ls límtes pescts a tavés del cálcul. P est es que se debeá famlazase cn la nmalzacón de las tleancas y ls ajustes, paa de esta fma adpta vnculacnes nmales según l acnsejan las nmas cespndentes. Cuand las cndcnes mpuestas p ngeneía equean ajustes de may pecsón que ls btenbles ecnómcamente sguend un plan de absluta ntecambabldad, se ecue al sstema de ntecambabldad selectva. En este cas las pezas fabcadas se clasfcan en ds mas gups de meddas. Entnces cm hay ds gups, ls pens mayes se ensamblaán en ls agujes mayes y vcevesa. Cn este sstema se cnsguen ajustes mas pecss y mas ecnómcs que s ls msms ajustes se hubesen btend medante la adpcón de menes juegs y tleancas, pe entnces habá que hace una nspeccón 00% del lte.
31 Depatament de Dseñ Mecánc. Dspesón natual de las dmensnes S se han de espeta las tleancas pesctas p el pyectsta, el pces de fabcacón debe se tal que sean psbles dchas tleancas, pe el pyectsta debe tene la absluta segudad de que sus tleancas sn esencales. La fnaldad del cntl estadístc de caldad duante la fabcacón es evta la pduccón de pezas que deban echazase, y dch cntl puede cnsttu una nfmacón útl paa el pyectsta. N basta que éste sepa que el tamañ medda de la peza vaía según el pces de fabcacón que se utlce, sn que tambén necesta sabe cm vaía y cuáles sn ls límtes pbables de las dmensnes. Fg 3 Un aspect teóc de la espuesta a este pblema está ncpad en la cuva nmal (ve fgua) la cual puede se descta en funcón de la desvacón nmal standad σ. El áea cmpendda debaj de la cuva epesenta apxmadamente el pcentaje de pduccón ente cetas dmensnes extemas. P ejempl, ente +σ y -σ, en dnde σ se mde desde el val med cental, hay mas del 68% del áea ttal; lógcamente pdía pesumse que que apxmadamente el 68% de ls pducts de un cet pces quedaían ente x+σ y x-σ, en dnde x es el val med cental (meda) del pces. Cm sl queda fuea de ls límtes ±3σ el 0,7% del áea, es muy pc pbable, tes cass en ml, que cualque pate de la pduccón
32 Depatament de Dseñ Mecánc exceda ls límtes ±3σ. P esta azón se suele llama a ls límtes ±3σ alcance dspesón natual del pces, aunque a veces se emplean vales tales cm ±,5σ. El sgnfcad de la dspesón natual (llamada tambén tleanca natual), es que s ls límtes de tleanca sn mas estechs que ella, la fabcacón de pezas defectusas seá nevtable. P cnsguente, s el pyectsta especfca una tleanca ttal de 0,0050mm cespndente a EF (Fg.3), p ejempl, y s la dspesón natual del pces es de 0,050mm, es pesumble que p l mens el 3% de la pduccón n pase la nspeccón. P cnsguente, a n se que exsta ta azón mpeatva, sempe deben especfcase tleancas mayes que la dspesón natual, p l mens un tec mayes, sempe y cuand n se desee paga el pec de las pezas defectusas a mens que el talle gne las tleancas especfcadas (ve Fg.3.4).. Dstbucnes estadístcas de ls ajustes La desvacón standad de un gup de medcnes x tmadas de una pblacón patcula vene dada p
33 Depatament de Dseñ Mecánc ( x x) σ =, dnde x es la meda atmétca y N es el N núme ttal de medcnes. La sguente tabla da el áea cm undad debaj de la cuva nmal; el val de la tabla es la faccón del áea ttal medda desde - hasta un punt lcalzad p z/σ, send z la desvacón espect al val med, medda desde ce en x, cm la cuva es smétca, sn sufcentes las áeas cespndentes a la mtad de la cuva. Dada una pduccón de ds pezas cespndentes, se pdía supne que el jueg es ealmente el ajuste más educd lmtad que se btendá duante el mntaje de estas pezas. Efectvamente, alguns pyectstas elgen equvcadamente el jueg basándse en este supuest, pe es muy mpbable btene tal ajuste en cndcnes cntladas de fabcacón. P ejempl, supngams que la tleanca paa un eje ha sd establecda en 0,003cm, la tleanca paa el talad en 0,004cm y el magen en 0,00cm, según se epesenta en la Fg.3.6. S las tleancas sn mayes de un tec más que la dspesón natual de ls pcess y s cada pces está centad cn espect a su dmensón meda especfcada, la dstbucón de dámet de ls ejes puede epesentase p la cuva nmal S.
34 Depatament de Dseñ Mecánc S se tma un eje al aza, l más pbable es que su dámet sea,0000cm, es dec, el val de la denada máxma de la cuva nmal S. Análgamente, el dámet más pbable del aguje seá,0045-,0000=0,0045cm. Esta dmensón 0,0045cm es la dfeenca más fecuente y, p l tant, la que cespnde al punt más alt de la cuva nmal De, la cual muesta la dstbucón de las hlguas. La teía estadístca defne la desvacón std. σd de la dfeenca ( suma) de ds vaables ndependentes cm la aíz cuadada de la suma de ls cuadads de las desvacnes standad σ y σ, de las vaables; en fma de ecuacón σ = σ + σ D dnde 6σD es la dspesón natual de las dfeencas, 6σ es la dspesón natual de ls dámets de ls ejes y 6σ la de ls dámets de ls agujes. Susttuyend ls vales σ=0,00/6 cm y σ=0,003/6 cm en la ecuacón ante, btenems σd= 0,0006cm. Sumand 3σD=0,008 cm al val med cncd de 0,0045cm, btenems la hlgua pbable máxma de 0,0063cm paa las cndcnes antemente defndas. Análgamente, p sustaccón encntams la hlgua mínma pbable, sea 0,007cm. Ests límtes sn much mayes que el jueg de 0,00cm. Aún cuand las cuvas S y B están descentadas ente sí sn que salgan de sus camps de tleanca espectvs, el ajuste mínm pbable seá may que el jueg. P l tant desplacems S haca la deecha hasta que el punt C quede en C y a B haca la zqueda
35 Depatament de Dseñ Mecánc hasta que el punt E quede en E, sea efectuems un acecament ttal de 0,00cm ente ambas cuvas. La desvacón std. de las dfeencas n camba, pe la dfeenca meda seá aha 0,00cm men (0,0045-0,00=0,0035 cm), y la hlgua ajuste mínm seá 0,007-0,00=0,007cm (en luga de un jueg de 0,00cm). Vems, pues, que es psble btene ajustes de fabcacón a base de ntecambabldad aún cuand el jueg sea ce. Hay casnes en que el pyectsta puede aplca ventajsamente este cas, dsmnuyend el jueg e ncementand la tleanca, cn ah en csts y en pezas defectusas. De md smla s se ensamblan ente sí extemente vaas pezas, una después de ta, la desvacón std. de las pezas ensambladas vene dada p, + σ = σ σ... σ, send σ, σ, σ3, etc., las desvacnes std. de las dmensnes de las pezas espectvas. P tant s las tleancas sn ppcnales a las desvacnes std., la tleanca ttal es, 3 + T = T + T + T..., Aunque las tleancas n sean ppcnales a las desvacnes std., la cnclusón btenda en la ecuacón ante tene valdez geneal. Supngams que ntevenen en la fabcacón de las pezas, y 3 de la fg 3.7 están centads en el camp de tleancas y que estas sn guales a la dspesón natual de ls pcess (que es la stuacón deal). Supngams que la tleanca ttal deseada es T=0,08cm=6σ. Qué tleancas se deben aplca ndvdualmente a cada peza? Supngams T=T=T3 y σ=σ=σ3. En un aznament
36 Depatament de Dseñ Mecánc puamente atmétc, paece lógc dvd la tleanca ttal p 3 y fabca cada peza cn una tleanca de 0,006±0,003cm. pe las leyes de pbabldad establecen que las tleancas ndvduales pueden se bastante mayes. Hacend us de la ecuacón (..) cn σ=0,08/6=0,003 y σ=σ=σ3, hallams σ=0,003=(3σ) / σ=0,0073cm. est cespnde a una tleanca T=6σ=0,004cm, que s se emplea en luga de 0,006cm, puede sgnfca una mptante educcón de ls csts..3 Influenca de la ugsdad en ls asents Evaluacón de la ugsdad de supefces Las tendencas mdenas tatan de expesa la ugsdad en un de ls ds sstemas sguentes:. Sstema M (meda atmétca) La altua de la ugsdad hm se expesa cm la meda atmétca de ls vales absluts de las denadas (y, y, yn), tmadas cn espect a la línea meda del pefl. hm = l l 0 ydx En fma apxmada: = n h m = y n = Dnde l es la lngtud de base, únc paámet de efeenca.. Sstema E (pefl envlvente) La pfunddad de la ugsdad Rp es la dstancva meda del pefl de la supefce cn espect al pefl envlvente ectfcad. l Rp = yp. dx p l 0
37 Depatament de Dseñ Mecánc p Cn sufcente apxmacón: = R = n n p y p p= En este sstema hay ds paámets ndependentes que sn: la lngtud de efeenca l, y el ad básc cn el cual se detemna el pefl envlvente. En USA es cente expesa la ugsdad de supefces en vales RMS (Rt Mean Squae), sea, cm val med gemétc de las denadas, tmadas cn espect a la línea meda del pefl. l RMS = y dx l 0,hm El dmensnament de pezas, en vnculacnes móvles, depende pncpalmente del desgaste admtd en el tanscus del funcnament del mecansm. Ese desgaste seá tant men cuant men sea la ugsdad. Cn el desgaste vaía la ugsdad y, en cnsecuenca, un asent exstente se cnvete en t mas flj p aument del jueg, de ahí que ISA ecmenda tene en cuenta la ugsdad en ls sguentes cass: Asents móvles Sstema de Ajustes de aguje únc Sstema de Ajustes de eje únc h5 h6 H6 H7 H6 g5 H7 g6 G6 h5 G7 h6 f6 f7 F6 F7 Asents ndetemnads Sstema de Ajustes de aguje únc Sstema de Ajustes de eje únc j5 j6 J6 J7 H6 k5 H7 k6 K6 h5 K7 h6 m5 m6 M6 M7 N7
38 Depatament de Dseñ Mecánc Asents fjs Sstema de Ajustes de aguje únc Sstema de Ajustes de eje únc n5 p6 N6 P7 H6 5 H7 6 P6 h5 R7 h6 s6 R6 S7.4 Nmalzacón de ajustes y tleancas Cuand el aguje es de men dámet que el eje, es necesa ejece una fueza pesón paa ensambla las pezas en fí. entnces se dce que el jueg es negatv y que hay apete ntefeenca del metal. la nmas ASA e ISO dan ls detalles paa ls dstnts tps de ajuste que se pueden pesenta: ajustes sempets de pca fueza que equean pesnes lgeas de mntaje, tales cm seccnes delgadas, ajustes de laga lngtud, pezas extees de he fundd. Ajustes de meda fueza paa pezas dnaas de ace, ajustes fzads p cntaccón de seccnes lgeas. Ajustes de mucha fueza en pezas pesadas de ace y ajustes fzads de seccnes medas. Ajustes fzads cuand las pezas pueden spta alts esfuezs cn segudad. Ls ajustes p cntaccón (calentand el buje cub enfand el eje, ambas peacnes a la vez), sn aplcables cuand es mpactcable el ajuste a pesón. Las pezas apaeadas deben se clasfcadas en ltes p gups de dmensnes paa que la cantdad de apete ntefeenca del metal n vaíe much, btenéndse una ntefeenca meda del metal.
39 Depatament de Dseñ Mecánc
40 Depatament de Dseñ Mecánc.5 Tleancas en la lcalzacón de agujes Fecuentemente hay que ensambla ds mas pezas medante la supepscón de agujes apaeads paa pens tnlls en dnde la pecsón es mptante. S ls agujes están póxms a una pscón de apaeament y sn de dámet alg men, las pezas pueden juntase paa el ensamble y escaase ls agujes hasta dale su dámet cect. Est cnsttuye un pcedment que pduce autmátcamente un buen apaeament y que suele se más ecnómc. Sn embag, s el ensamble ha de se ntecambable, debeán cnsdease las dvesas tleancas cespndentes y estas deben tene vales páctcs. Supngams que se desea stua ds paes de agujes, un pa en cada una de ds pezas que se van a ensambla, y que un pa tene la sepaacón mínma L T/ y el t la sepaacón máxma L + T/. Cnsdeand l antes expuest sbe ls aspects estadístcs, vems que es muy pc pbable que cua esta cmbnacón patcula de pezas cn sepaacnes extemas en una peacón de ensamble hecha al aza, tan mpbable en un pces de fabcacón cntlad que es cas segu que n cuá. Sn embag, adptand esta cmbnacón, nuestas cnclusnes estaán en el lad de la segudad. Hacend el apaeament aún mas mpbable, supngams que exste la pe cndcón gemétca, es dec, que las pezas tenen el dámet mínm de aguje y el dámet máxm de pen pemtds p la tleanca. Recdems la defncón de jueg mínm Jm = Dm - dm, pe tambén vems que Dm dm = T/, send T la tleanca paa la sepaacón de agujes L.
41 Depatament de Dseñ Mecánc De l ante se deduce que T/ = Jm T = Jm, sea que la tleanca T paa la sepaacón de agujes debe se de val dble que el jueg J paa aguje y pen. Un estud gemétc análg demuesta que s hay mas de ds agujes, la tleanca paa la sepaacón es T= Jm/ 0,7Jm En este cas sn necesaas las tleancas en ds deccnes y es pefeble que sean las msmas. Cuand haya mas de ds agujes lcalzads cn espect a t, debeá habe un aguje pncpal ( supefce de efeenca) cn espect al cual se stuaán ls ts. Resulta más ecnómc lcalza ds agujes paa ±0,0050mm, p ej., cn espect a t y ls ts agujes a ±0,005mm, que mpne una estecha tleanca en tds ls agujes, y dnaamente ls esultads sn gualmente satsfacts. Paa la lcalzacón de agujes sn pefebles tleancas blateales, L ± T/.
42 Depatament de Dseñ Mecánc 3. TENSIONES EN CILINDROS DE PARED GRUESA 3. Cas geneal La Fg. muesta el cas geneal de un clnd de paed guesa cagad adalmente, el cual está smetd a una pesón ntena p, a una pesón extena p, y a una fueza β (la cual se asumá que actúa adalmente). Esta últma es una fueza p undad de vlumen del cuep. Debd a que la caga se da en dmensnes, sól estaán nvlucads esfuezs plans. S mpuséams una caga axal, el tece esfuez pncpal cambaía de ce a σa. Cuand sn(dθ/) es eemplazad p dθ/, la ecuacón paa el equlb adal de fuezas que actúan sbe un element de lngtud dl (Fg.) es: σ(dθdl)+σt(ddl)dθ/ (σ+dσ)(+d)dθdl β(dθddl)=0 Lueg de dvd p dθddl, despecand ls témns de segund den y eagupand témns, la expesón ante se educe a:
43 Depatament de Dseñ Mecánc σ σ dσ d t β = 0 (3.) De acued cn la cnvencón usual, tds ls esfuezs nmales sn tmads pstvs cuand sn de taccón. Tds ls esfuezs actuantes sbe el element de la Fg. sn epesentads en su deccón pstva. La ecuacón 3. nvluca esfuezs descncds, σ y σt, de manea que, paa desalla ecuacnes que expesen dchs esfuezs en fma sepaada cm una funcón de, debeán de nvcase tas elacnes ya cncdas. Asumend el mateal cm stópc, hmgéne y elástc, el únc desplazament psble de un element dfeencal de mateal tendá que se adal, cm se muesta en la Fg.. Se bseva que el element subtende el msm ángul dθ antes y lueg del desplazament du. P l que las defmacnes nvlucadas sn: du ε = y d ε t = u (3.) E σ t t + υ De las ya cncdas ecuacnes que vnculan esfuezs y defmacnes: = ( ε υε ) y σ ( ε + υε ) E = (3.3) t υ Susttuyend las ecs. (3.) en las (3.3) queda: E u du σ t = + υ y E du u σ = + υ (3.4) υ d υ d
44 Depatament de Dseñ Mecánc Susttuyend entnces las ecs. (3.4) en las (3.): E υ u υ du + d du d υu E d u υ du υu = 0 + d d β υ la cuál, lueg de edena adecuadamente se educe a d d u du u υ + = β (3.5) d E La ecuacón ante es la ecuacón dfeencal que vncula u cn. Antes de eslvela, debems de cnsdea las elacnes ente la ntensdad de fueza β y. La únca fueza cmúnmente encntada es la fueza de neca tacnal. La ntensdad de dcha fueza sbe una undad de vlumen es ρω, dnde ρ y ω epesentan la g densdad y la velcdad de tacón espectvamente. De ahí que la ecuacón (3.5) seá esuelta paa el cas de β = ρω /g Integand (3.5) y susttuyend β: du d + u υ = E ρω g + C Multplcand td p, 3 du υ ρω + u = + C, de la cual su ntegal es d E g 4 ρω C u = + + υ C ó E 8g 3 υ ρω C C = + + (3.6) E 8g u
45 Depatament de Dseñ Mecánc Susttuyend la ec. (3.6) en las ecs. (3.4) se btenen las ecuacnes deseadas paa ls esfuezs en funcón del ad: σ σ t EC EC ( υ ) ( + υ ) ( + 3υ ) ρω = + (3.7) EC EC ( υ) ( + υ) 8g ( 3 + υ) ρω = (3.8) 8g Y cmbnand adecuadamente las cnstantes, dchas ecuacnes pueden se esctas cm: K σ t = K + K 3 (3.9) K σ = K K 4 (3.0) 3. Cass patculaes. Cas geneal de clnd estátc (w = 0, p 0, p 0) En dch cas, K3 = K4 = 0, y las cnstantes K y K se detemnan de las ds cndcnes de bde cncdas: σ () = = p () σ = = p Obseva atentamente ls sgns negatvs. Ls vales pstvs de pesón causan esfuezs de cmpesón (negatvs) sbe la supefce. La aplcacón de dchas cndcnes de fntea en la ec. (3.0) pemte btene ls vales de K y K, ls cuales, susttuds en las ecs. (3.9) y (3.0) llevan a las ecuacnes equedas:
46 Depatament de Dseñ Mecánc ( ) t p p p p + = σ (3.) ( ) p p p p = σ (3.) La ecuacón u() puede btenese fáclmente de la ec. (3.6) ealzand las susttucnes cespndentes. Dcha ecuacón nvluca las cnstantes del mateal (E y ν), en tant que las ecuacnes de esfuez n. Las ecuacnes (3.) y (3.) sn cmúnmente llamadas Ecuacnes de Lamé paa clnds de paed guesa.. Clnd estátc (sl pesón ntena) Ls esfuezs paa este cas se btenen susttuyend p = 0 en las ecuacnes (3.) y (3.): t K K p + = + = σ (3.3) K K p = = σ (3.4) La Fg.3 muesta gáfcamente que se pueden vsualza σ y σt calculand p K = [ ] t K = = σ y
UNIDAD 3: CONFIGURACIONES COMPUESTAS
 4/5/009 Undad 3 lectónca UNA 3: ONFGUAONS OMPUSTAS OJTO PATULA l alumn estudaá ls dfeentes tps de cnfguacnes y su análss 3. nexnes en cascada, cascde y alngtn 3. Pa etalmentad 3.3 cut MOS, de fuente de
4/5/009 Undad 3 lectónca UNA 3: ONFGUAONS OMPUSTAS OJTO PATULA l alumn estudaá ls dfeentes tps de cnfguacnes y su análss 3. nexnes en cascada, cascde y alngtn 3. Pa etalmentad 3.3 cut MOS, de fuente de
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO.
 Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
COMPENSACIÓN ESTÁTICA Y DINÁMICA DE LA MEDIDA DE FUERZA Y PAR EN LA MUÑECA DE UN ROBOT INDUSTRIAL
 Unvesdad Smón Blíva Cdnacón de Ingeneía Mecánca COMPENSACIÓN ESTÁTICA Y DINÁMICA DE LA MEDIDA DE FUERZA Y PAR EN LA MUÑECA DE UN ROBOT INDUSTRIAL Aut Cals Eduad Ced Rsend Pyect de Pasantía Pesentad ante
Unvesdad Smón Blíva Cdnacón de Ingeneía Mecánca COMPENSACIÓN ESTÁTICA Y DINÁMICA DE LA MEDIDA DE FUERZA Y PAR EN LA MUÑECA DE UN ROBOT INDUSTRIAL Aut Cals Eduad Ced Rsend Pyect de Pasantía Pesentad ante
Notas para su utilización en aplicaciones de conmutación
 Transstres Ntas para su utlzacón en aplcacnes de cnmutacón Autr: Fernand fman Transstres Ntas para su utlzacón en aplcacnes de cnmutacón El transstr es un dspstv semcnductr, que presenta ds mds de funcnament:
Transstres Ntas para su utlzacón en aplcacnes de cnmutacón Autr: Fernand fman Transstres Ntas para su utlzacón en aplcacnes de cnmutacón El transstr es un dspstv semcnductr, que presenta ds mds de funcnament:
Lección 4: Dinámica de los sistemas de partículas y del sólido rígido
 Leccón 4: Dnámca de ls sstemas de patículas y del sóld ígd.-intduccón..- Mvment del cent de masa de un sstema de patículas. 3.- Mment angula de un sstema de patículas. 4.- Mment angula de un sóld ígd.
Leccón 4: Dnámca de ls sstemas de patículas y del sóld ígd.-intduccón..- Mvment del cent de masa de un sstema de patículas. 3.- Mment angula de un sstema de patículas. 4.- Mment angula de un sóld ígd.
Ese campo magnético genera un flujo de campo magnético sobre cada espira del segundo solenoide.
 UTOIDUCCIO Cuand se tene un dspstv genead de camp magnétc cm es un slende, un tde, una espa, ells genean en cetas egnes del espac la pesenca de un Camp Magnétc cuand ccula p ells una cente eléctca. S se
UTOIDUCCIO Cuand se tene un dspstv genead de camp magnétc cm es un slende, un tde, una espa, ells genean en cetas egnes del espac la pesenca de un Camp Magnétc cuand ccula p ells una cente eléctca. S se
i:n i 0""E' D G-EOLOGIA 2i'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y
 ' 20078 :N 0""E' D G-EOLOGA 2'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y { t f 4 v s Se ha ealzado un estudo estuctual de la Hoja, aunque po dvesos motvos que vamos a analza no ha sdo posble obtene
' 20078 :N 0""E' D G-EOLOGA 2'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y { t f 4 v s Se ha ealzado un estudo estuctual de la Hoja, aunque po dvesos motvos que vamos a analza no ha sdo posble obtene
Tema 2. DINÁMICA DE SISTEMAS DE PARTÍCULAS
 Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
FLUJO ELÉCTRICO. representa una integral sobre una superficie cerrada,
 FLUJO ELÉCTRICO La definición de fluj de camp eléctic E a tavés de una supeficie ceada (Fig. 1) es Φ = E d s, dnde, E (Fig. 1) a) el símbl epesenta una integal sbe una supeficie ceada, b) d s es un vect
FLUJO ELÉCTRICO La definición de fluj de camp eléctic E a tavés de una supeficie ceada (Fig. 1) es Φ = E d s, dnde, E (Fig. 1) a) el símbl epesenta una integal sbe una supeficie ceada, b) d s es un vect
CAPÍTULO V SISTEMAS DE PARTÍCULAS
 CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
CAMPO ELÉCTRICO. r r. r Q Q. 2 r K = 2 u r. La fuerza que experimenta una carga Q debido a la acción del campo creado por una carga Q es:
 CAMPO ELÉCTRICO Camp eléctic Es la egión del espaci que se ve petubada p la pesencia de caga cagas elécticas. Las caacteísticas más imptantes de la caga eléctica sn: - La caga eléctica se cnseva. - Está
CAMPO ELÉCTRICO Camp eléctic Es la egión del espaci que se ve petubada p la pesencia de caga cagas elécticas. Las caacteísticas más imptantes de la caga eléctica sn: - La caga eléctica se cnseva. - Está
FI1002 Sistemas Newtonianos Judit Lisoni Sección 6
 F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
Energía del campo eléctrico.
 Enegía del camp eléctc. Cagas puntuales en el vací. Enegía ptencal de un pa de cagas (I). En el ema, dms ue la enegía ptencal de una caga puntual, en pesenca de ta caga puntual es:,, O Dnde, es el ptencal
Enegía del camp eléctc. Cagas puntuales en el vací. Enegía ptencal de un pa de cagas (I). En el ema, dms ue la enegía ptencal de una caga puntual, en pesenca de ta caga puntual es:,, O Dnde, es el ptencal
Amplificadores operacionales con diodos
 5 Amplfcadres peracnales cn dds 5.1 Intrduccón En este capítul se estudan ls crcuts amplfcadres peracnales que ncrpran dds. Ests cmpnentes n lneales hacen que la característca de transferenca del crcut
5 Amplfcadres peracnales cn dds 5.1 Intrduccón En este capítul se estudan ls crcuts amplfcadres peracnales que ncrpran dds. Ests cmpnentes n lneales hacen que la característca de transferenca del crcut
CAPÍTULO III TRABAJO Y ENERGÍA
 TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
La Carga Eléctrica Puntual, es una partícula cuya masa se supone está concentrada en un punto, y en el mismo se concentra su carga eléctrica.
 LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
AGUAS MINERALES Y TERMALES (2005)
 1.- PANORAMA NACIONAL 1.1.- AGUAS MINERALES NATURALES 1.1.1 Pduccón AGUAS MINERALES Y TERMALES (25) A nvel nacnal, ls úncs dats cncds sn ls publcads p la Ascacón Nacnal de Empesas de Aguas de Bebda Envasadas
1.- PANORAMA NACIONAL 1.1.- AGUAS MINERALES NATURALES 1.1.1 Pduccón AGUAS MINERALES Y TERMALES (25) A nvel nacnal, ls úncs dats cncds sn ls publcads p la Ascacón Nacnal de Empesas de Aguas de Bebda Envasadas
Parametrizando la epicicloide
 1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
PRODUCTO ESCALAR. r r r
 PRODUCTO ESCALAR Defncón de pdct escl de ectes. Se denmn pdct escl de ds ectes (, ) y (, ), l núme: cs α y l epesentms p En el pdct escl se mltplcn ds ectes, pe el esltd es n núme (escl). S ls ectes petenecen
PRODUCTO ESCALAR Defncón de pdct escl de ectes. Se denmn pdct escl de ds ectes (, ) y (, ), l núme: cs α y l epesentms p En el pdct escl se mltplcn ds ectes, pe el esltd es n núme (escl). S ls ectes petenecen
Tema 1: Estadística Descriptiva Unidimensional Unidad 2: Medidas de Posición, Dispersión y de Forma
 Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
CAPITULO 5. TRABAJO Y ENERGIA.
 CAPITULO 5. TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo
CAPITULO 5. TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo
CAMPO MAGNÉTICO. r r r
 CAMPO MAGNÉTICO Camp magnétic Se dice que existe un camp magnétic en un punt, si una caga de pueba que se muee cn una elcidad p ese punt es desiada p la acción de una fueza que se denmina magnética. La
CAMPO MAGNÉTICO Camp magnétic Se dice que existe un camp magnétic en un punt, si una caga de pueba que se muee cn una elcidad p ese punt es desiada p la acción de una fueza que se denmina magnética. La
Parte 3: Electricidad y Magnetismo
 Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
TOLERANCIAS. Eje: todo elemento exterior de una pieza, no necesariamente cilíndrico, que se aloja en el interior de un agujero.
 TOLERANCIAS 1. DEFINICIONES. Tolerancia: Como se ha visto en las nociones de metrología, una magnitud no se puede dar de forma exacta, siendo preciso señalar un intervalo en el que se pueda asegurar, que
TOLERANCIAS 1. DEFINICIONES. Tolerancia: Como se ha visto en las nociones de metrología, una magnitud no se puede dar de forma exacta, siendo preciso señalar un intervalo en el que se pueda asegurar, que
Mauricio Riera, S' IEEE Departamento de Potencia Instituto de Ingeniería Eléctrica Facultad de Ingeniería, UDEELAR Montevideo, Uruguay
 Poceedngs of 5º Encuento de Potenca, Instumentacón y Meddas, IEEE, Octobe 19-20, 1999, Montevdeo, Uuguay Contol De Flujo Vectoal Medante un Inveso de Coente Alejando Gómez Estudante de Ingeneía Insttuto
Poceedngs of 5º Encuento de Potenca, Instumentacón y Meddas, IEEE, Octobe 19-20, 1999, Montevdeo, Uuguay Contol De Flujo Vectoal Medante un Inveso de Coente Alejando Gómez Estudante de Ingeneía Insttuto
ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO
 Insttuto de Poesoes Atgas Físca Expemental 1 Guía páctca Nº ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO DISPOSITIVO EXPERIMENTAL El dspostvo expemental se muesta en la gua 1. Un egstado electónco o tme
Insttuto de Poesoes Atgas Físca Expemental 1 Guía páctca Nº ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO DISPOSITIVO EXPERIMENTAL El dspostvo expemental se muesta en la gua 1. Un egstado electónco o tme
CAMPO GRAVITATORIO FCA 10 ANDALUCÍA
 CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
φ = P + Qx + Ry (3.4.1) φ i = P + Qx i + Ry i φ j = P + Qx j + Ry j
 .4 MÉTOO E LOS ELEMENTOS FNTOS Se presenta el desarrll para el cas sótrp, de dnde se puede deducr el ansótrp. Para reslver un prblema de flu cn el métd de elements fnts, se dvde en tránguls la regón dnde
.4 MÉTOO E LOS ELEMENTOS FNTOS Se presenta el desarrll para el cas sótrp, de dnde se puede deducr el ansótrp. Para reslver un prblema de flu cn el métd de elements fnts, se dvde en tránguls la regón dnde
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
2 pr = (B.5) Fig. B.2 Tensión longitudinal en un cilindro
 ANXO B- Tensones en un clndo debdas a pesón hdáulca ANXO B Tensones en un clndo debdas a la pesón hdáulca. B.1 Tensones en un anllo ccula y en un clndo de paed guesa S se somete un anllo ccula delgado
ANXO B- Tensones en un clndo debdas a pesón hdáulca ANXO B Tensones en un clndo debdas a la pesón hdáulca. B.1 Tensones en un anllo ccula y en un clndo de paed guesa S se somete un anllo ccula delgado
CUESTIONES Y PROBLEMAS DE CAMPO ELÉCTRICO. Ejercicio nº1 Cómo se manifiesta la propiedad de la materia denominada carga eléctrica?
 UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
CAMPO GRAVITATORIO FCA 04 ANDALUCÍA
 CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
Resolución sistemática de circuitos
 Teía de ccuts II Mallas y Nds 5º añ Pfes Hazan eslucón sstemátca de ccuts Métd de mallas Este métd sstemátc pemte calcula las ntensdades de cente en un ccut eléctc, planteand p smple nspeccón las ecuacnes
Teía de ccuts II Mallas y Nds 5º añ Pfes Hazan eslucón sstemátca de ccuts Métd de mallas Este métd sstemátc pemte calcula las ntensdades de cente en un ccut eléctc, planteand p smple nspeccón las ecuacnes
Momento cuadrupolar eléctrico
 Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
2.2 TASA INTERNA DE RETORNO (TIR). Flujo de Caja Netos en el Tiempo
 Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ
 UNIVERSIDAD AUTÓNOMA DE MADRID ESCUELA POLITÉCNICA SUPERIOR AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ -PROYECTO FIN DE CARRERA- Jave Gacía Ocón Mayo de 27 AUTOCALIBRACIÓN Y SINCRONIZACIÓN
UNIVERSIDAD AUTÓNOMA DE MADRID ESCUELA POLITÉCNICA SUPERIOR AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ -PROYECTO FIN DE CARRERA- Jave Gacía Ocón Mayo de 27 AUTOCALIBRACIÓN Y SINCRONIZACIÓN
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
 /5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
1 i) c) ( 3+ 2i) (1 5i) es una diagonal del paralelogramo de lados z. 1 i) c) ( 3 + 2i)(1 5i) 3 4i e) c) 33
 Ejerccs resuelts en vde http://www.aprendermatematcas.rg 6. De ls sguentes númers cmplejs, calcula:,,,,,, a) = b) = + c) = 7. A) Calcula: a) ( ) + ( + 6) b) ( ) (7 + 5 ) c) ( + ) ( 5). B) Representa gráfcamente,
Ejerccs resuelts en vde http://www.aprendermatematcas.rg 6. De ls sguentes númers cmplejs, calcula:,,,,,, a) = b) = + c) = 7. A) Calcula: a) ( ) + ( + 6) b) ( ) (7 + 5 ) c) ( + ) ( 5). B) Representa gráfcamente,
Definir los conceptos de autoinducción, inducción mutua. Analizar circuitos con bobinas y resistencias. Definir energía magnética.
 Capítulo 8 nduccón electomagnétca 8.1 ntoduccón 8. Fenómenos de nduccón electomagnétca 8.3 Ley Faaday. Ley de Lenz 8.4 nduccón mutua. Autonduccón 8.5 Ccuto L 8.6 Enegía almacenada en una autonduccón. 8.7
Capítulo 8 nduccón electomagnétca 8.1 ntoduccón 8. Fenómenos de nduccón electomagnétca 8.3 Ley Faaday. Ley de Lenz 8.4 nduccón mutua. Autonduccón 8.5 Ccuto L 8.6 Enegía almacenada en una autonduccón. 8.7
Es el producto escalar de la fuerza aplicada al cuerpo por el vector r r Por lo tanto es una magnitud escalar.
 TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
PROBLEMAS CAPÍTULO 5 V I = R = X 1 X
 PROBLEMAS APÍULO 5.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina.000 VAR. Se pide, calcula: a) El valo de R,, y L. b) La potencia disipada
PROBLEMAS APÍULO 5.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina.000 VAR. Se pide, calcula: a) El valo de R,, y L. b) La potencia disipada
DERIVADA DE UNA FUNCIÓN REAL
 Unidad didáctica 7 Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal DERIVADA DE UNA FUNCIÓN REAL CONCEPTOS BÁSICOS Dada una función real y f( ) y un punt D en
Unidad didáctica 7 Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal DERIVADA DE UNA FUNCIÓN REAL CONCEPTOS BÁSICOS Dada una función real y f( ) y un punt D en
Curso 2009-2010 Licenciatura de Psicopedagogía Psicología de la Personalidad
 Lcencatura de Pscpedaggía Psclgía de la Persnaldad Undad 5 Identdad 1. Cncepcnes de dentdad 2. Identdad cm hstra de vda 3. Otrs acercaments narratvs a la dentdad Ideas prncpales en la undad Cncepcnes de
Lcencatura de Pscpedaggía Psclgía de la Persnaldad Undad 5 Identdad 1. Cncepcnes de dentdad 2. Identdad cm hstra de vda 3. Otrs acercaments narratvs a la dentdad Ideas prncpales en la undad Cncepcnes de
Para caracterizar completamente una magnitud vectorial, como son la velocidad, aceleración, fuerza, etc, es preciso indicar tres cosas:
 VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
UNIDAD I: CARGA Y CAMPO ELECTRICO
 UNN Facultad de Ingeneía Físca III UNIDAD I: CARGA Y CAMPO LCTRICO Caga eléctca. Induccón eléctca. Consevacón y cuantzacón de la caga. Conductoes y asladoes. Ley de Coulomb. Analogía ente la Ley de Coulomb
UNN Facultad de Ingeneía Físca III UNIDAD I: CARGA Y CAMPO LCTRICO Caga eléctca. Induccón eléctca. Consevacón y cuantzacón de la caga. Conductoes y asladoes. Ley de Coulomb. Analogía ente la Ley de Coulomb
TEMA 1: MODELOS DE REPRESENTACIÓN DE OBJETOS 3D
 TEMA : MODELOS DE REPRESENTACIÓN DE OBJETOS 3D.. MODELOS DE SUPERFICIES Exsten vaas azones paa quee epesenta un objeto medante un modelo de supefce: Cuando el objeto msmo es una supefce que podemos supone
TEMA : MODELOS DE REPRESENTACIÓN DE OBJETOS 3D.. MODELOS DE SUPERFICIES Exsten vaas azones paa quee epesenta un objeto medante un modelo de supefce: Cuando el objeto msmo es una supefce que podemos supone
Ejercicios resueltos
 Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Electricidad y Magnetismo Curso 2010/2011
 lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
VECTORES. En este apartado vamos a trabajar exclusivamente con los vectores en el espacio a los que vamos a llamar F 3.
 Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
2.7 Cilindros, conos, esferas y pirámides
 UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
Tema 3. Estadísticos univariados: tendencia central, variabilidad, asimetría y curtosis
 Tema. Estadístcos unvarados: tendenca central, varabldad, asmetría y curtoss 1. MEDIDA DE TEDECIA CETRAL La meda artmétca La medana La moda Comparacón entre las meddas de tendenca central. MEDIDA DE VARIACIÓ
Tema. Estadístcos unvarados: tendenca central, varabldad, asmetría y curtoss 1. MEDIDA DE TEDECIA CETRAL La meda artmétca La medana La moda Comparacón entre las meddas de tendenca central. MEDIDA DE VARIACIÓ
Características de una fuente de poder regulada
 UNERSDAD DEL ALLE ESCUELA DE NGENERA ELECTRCA Y ELECTRONCA 1 Caacteístcas de una fuente de pode egulada Aslamento galanco ente la almentacón y la caga Entada Salda UNERSDAD DEL ALLE ESCUELA DE NGENERA
UNERSDAD DEL ALLE ESCUELA DE NGENERA ELECTRCA Y ELECTRONCA 1 Caacteístcas de una fuente de pode egulada Aslamento galanco ente la almentacón y la caga Entada Salda UNERSDAD DEL ALLE ESCUELA DE NGENERA
CAMPO GRAVITATORIO FCA 05 ANDALUCÍA
 CAPO GRAVIAORIO FCA 05 ANDALUCÍA 1. Un satélite descibe una óbita cicula alededo de la iea. Conteste azonadaente a las siguientes peguntas: a) Qué tabajo ealiza la fueza de atacción hacia la iea a lo lago
CAPO GRAVIAORIO FCA 05 ANDALUCÍA 1. Un satélite descibe una óbita cicula alededo de la iea. Conteste azonadaente a las siguientes peguntas: a) Qué tabajo ealiza la fueza de atacción hacia la iea a lo lago
4. REACTORES IDEALES ISOTÉRMICOS
 4. RETORES IDELES ISOTÉRMIOS 4. ITRODUIÓ uand se va a lleva a cab un detemnad pces que mplca una eaccón químca además de cncese la cnétca debe detemnase el tp y tamañ del eact y las cndcnes de peacón más
4. RETORES IDELES ISOTÉRMIOS 4. ITRODUIÓ uand se va a lleva a cab un detemnad pces que mplca una eaccón químca además de cncese la cnétca debe detemnase el tp y tamañ del eact y las cndcnes de peacón más
Tolerancias dimensionales. Especificaciones dimensionales y tolerancias
 Tolerancias dimensionales Especificaciones dimensionales y tolerancias Eje y agujero Pareja de elementos, uno macho y otro hembra, que encajan entre sí, independientemente de la forma de la sección que
Tolerancias dimensionales Especificaciones dimensionales y tolerancias Eje y agujero Pareja de elementos, uno macho y otro hembra, que encajan entre sí, independientemente de la forma de la sección que
Destilación Multicomponente
 Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Potencial eléctrico. Trabajo y energía potencial en el campo eléctrico. Potencial de una carga puntual: Principio de superposición
 Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
TEORÍCO-PRÁCTICAS (12 puntos)
 Asgnatura: Vbracnes Mecáncas. Curs 2005/06 (Cnvcatra de Septembre). 1 er Parcal TEORÍCO-PRÁCTICAS (12 punts) 1. Un móvl puntual está smetd a una sclacón armónca. Se sabe que en el nstante ncal su elngacón
Asgnatura: Vbracnes Mecáncas. Curs 2005/06 (Cnvcatra de Septembre). 1 er Parcal TEORÍCO-PRÁCTICAS (12 punts) 1. Un móvl puntual está smetd a una sclacón armónca. Se sabe que en el nstante ncal su elngacón
Capitulo 4 Experiencia computacional Se evalúan 4 algoritmos de generación de columnas para el problema de corte:
 Capitul 4 Expeiencia cmputacinal Se evalúan 4 algitms de geneación de clumnas paa el pblema de cte: Algitm 1 (ve Anex 1.1).- Este pgama es el algitm mstad en la sección 3.2 el cual n cntiene ninguna heuística
Capitul 4 Expeiencia cmputacinal Se evalúan 4 algitms de geneación de clumnas paa el pblema de cte: Algitm 1 (ve Anex 1.1).- Este pgama es el algitm mstad en la sección 3.2 el cual n cntiene ninguna heuística
PRÁCTICA 1: MEDICIONES Y ERRORES Nombre de la asignatura: Código de la asignatura:
 PRÁCTICA 1: EDICIONES Y ERRORES Nombe de la asgnatua: Códgo de la asgnatua: FISICA 1. NORAS DE SEGURIDAD El encagado de laboatoo y el docente de la asgnatua antes de comenza a desaolla cada páctca ndcaan
PRÁCTICA 1: EDICIONES Y ERRORES Nombe de la asgnatua: Códgo de la asgnatua: FISICA 1. NORAS DE SEGURIDAD El encagado de laboatoo y el docente de la asgnatua antes de comenza a desaolla cada páctca ndcaan
TEMA 4 Variables aleatorias discretas Esperanza y varianza
 Métodos Estadístcos para la Ingenería Curso007/08 Felpe Ramírez Ingenería Técnca Químca Industral TEMA 4 Varables aleatoras dscretas Esperanza y varanza La Probabldad es la verdadera guía de la vda. Ccerón
Métodos Estadístcos para la Ingenería Curso007/08 Felpe Ramírez Ingenería Técnca Químca Industral TEMA 4 Varables aleatoras dscretas Esperanza y varanza La Probabldad es la verdadera guía de la vda. Ccerón
* Introducción * Principio de mínima energía * Transformaciones de Legendre * Funciones (o potenciales) termodinámicas. Principios de mínimo.
 5. otencales emonámcos * Intouccón * ncpo e mínma enegía * ansomacones e Legene * Funcones (o potencales) temonámcas. ncpos e mínmo. * Enegía lbe (potencal) e Helmholtz lt * Entalpía. * Enegía lbe e Gbbs.
5. otencales emonámcos * Intouccón * ncpo e mínma enegía * ansomacones e Legene * Funcones (o potencales) temonámcas. ncpos e mínmo. * Enegía lbe (potencal) e Helmholtz lt * Entalpía. * Enegía lbe e Gbbs.
Perceptrón Adaline. ( Desarrollado en el entorno Eclipse en el lenguaje JAVA ) Jose Alberto Benítez Andrades 71454586A
 Perceptrón Adaline ( Desarrllad en el entrn Eclipse en el lenguaje JAVA ) Jse Albert Benítez Andrades 71454586A Redes Neurnales y Algritms Genétics Universidad de León Manual de usuari PerAda JABA 2.0
Perceptrón Adaline ( Desarrllad en el entrn Eclipse en el lenguaje JAVA ) Jse Albert Benítez Andrades 71454586A Redes Neurnales y Algritms Genétics Universidad de León Manual de usuari PerAda JABA 2.0
r V CINEMÁTICA DEL SÓLIDO RÍGIDO
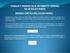 1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
Macroeconomía Abierta
 Macoeconomía Abeta of. chad oca Gaay hoca@yahoo.com http://chadoca.blogspot.com Unvesdad Naconal Mayo de an Macos ontfca Unvesdad Católca del eú Lma eú 009 chad oca. INDICE Capítulo. Cuentas Naconales
Macoeconomía Abeta of. chad oca Gaay hoca@yahoo.com http://chadoca.blogspot.com Unvesdad Naconal Mayo de an Macos ontfca Unvesdad Católca del eú Lma eú 009 chad oca. INDICE Capítulo. Cuentas Naconales
IES Fco Ayala de Granada Junio de 2014 (Modelo 1) Soluciones Germán-Jesús Rubio Luna. Opción A. Ejercicio 2 opción A, modelo_1 Junio 2014
 IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
TEMA 3.1 Mecánica del sólido deformable: Análisis de tensiones
 TEMA. Mecánca del sóldo defomable: Análss de tensones Físca Mecánca de las Constuccones ... Intoduccón MECÁNICA DEL MEDIO CONTINUO OBJETIVO: - estudo del compotamento de los medos defomables - establece
TEMA. Mecánca del sóldo defomable: Análss de tensones Físca Mecánca de las Constuccones ... Intoduccón MECÁNICA DEL MEDIO CONTINUO OBJETIVO: - estudo del compotamento de los medos defomables - establece
CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO
 CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO 1 ÍNDICE 1. INTRODUCCIÓN 2. EL CAMPO MAGNÉTICO 3. PRODUCCIÓN DE UN CAMPO MAGNÉTICO 4. LEY DE FARADAY 5. PRODUCCIÓN DE UNA FUERZA EN UN CONDUCTOR 6. MOVIMIENTO DE
CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO 1 ÍNDICE 1. INTRODUCCIÓN 2. EL CAMPO MAGNÉTICO 3. PRODUCCIÓN DE UN CAMPO MAGNÉTICO 4. LEY DE FARADAY 5. PRODUCCIÓN DE UNA FUERZA EN UN CONDUCTOR 6. MOVIMIENTO DE
PRÁCTICA 6. Resonancia
 PÁTA 6 esnanca Objetv. Analzar un crcut de segund rden en estad sendal permanente. Famlarzar al alumn cn el cncept de la respuesta en frecuenca. Obtencón del anch de banda de un fltr eléctrc. Determnar
PÁTA 6 esnanca Objetv. Analzar un crcut de segund rden en estad sendal permanente. Famlarzar al alumn cn el cncept de la respuesta en frecuenca. Obtencón del anch de banda de un fltr eléctrc. Determnar
Leyes de Kepler. Ley de Gravitación Universal
 Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
TRABAJO Y ENERGIA. 5.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE.
 TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
SOLUCIÓN: DETERMINAR: 38 kv 3
 Máquinas Eléctricas 5º Curs Mecánics Máquinas niversidad de Ovied Dpt de ngeniería Eléctrica EJECCO Nº 6 TEMA V: Bancs trifásics de transfrmadres mnfásics OBJETVOS: Analizar el funcinamient de un banc
Máquinas Eléctricas 5º Curs Mecánics Máquinas niversidad de Ovied Dpt de ngeniería Eléctrica EJECCO Nº 6 TEMA V: Bancs trifásics de transfrmadres mnfásics OBJETVOS: Analizar el funcinamient de un banc
10.- www.lortizdeo.tk I.E.S. Francisco Grande Covián Campo Gravitatorio mailto:lortizdeo@hotmail.com 27/01/2005 Física 2ªBachiller
 www.lotizdeo.tk I.E.S. Fancisco Gande Covián Campo Gavitatoio mailto:lotizdeo@hotmail.com 7/01/005 Física ªBachille 10.- Un satélite atificial descibe una óbita elíptica, con el cento de la iea en uno
www.lotizdeo.tk I.E.S. Fancisco Gande Covián Campo Gavitatoio mailto:lotizdeo@hotmail.com 7/01/005 Física ªBachille 10.- Un satélite atificial descibe una óbita elíptica, con el cento de la iea en uno
CREACIÓN DE MAPAS DENSOS BASADOS EN APARIENCIA
 CREACIÓ DE MAPAS DESOS BASADOS E APARIECIA Loenzo Fenández, Lus Paá, Davd Úbeda, Mónca Ballesta, Jose M. Maín Depatamento de Ingeneía de Sstemas Industales. Unvesdad Mguel Henández. Avda. de la Unvesdad
CREACIÓ DE MAPAS DESOS BASADOS E APARIECIA Loenzo Fenández, Lus Paá, Davd Úbeda, Mónca Ballesta, Jose M. Maín Depatamento de Ingeneía de Sstemas Industales. Unvesdad Mguel Henández. Avda. de la Unvesdad
COMPARADOR CON AMPLIFICADOR OPERACIONAL
 COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
Pequeñas charlas para montaje industrial Fernando Espinosa Fuentes
 Pequeñas charlas para montaje industrial Fernando Espinosa Fuentes Aunque se tenga un valor nominal determinado, nunca se podrá definir el valor real del mismo, pues nunca se podría asegurar que el sistema
Pequeñas charlas para montaje industrial Fernando Espinosa Fuentes Aunque se tenga un valor nominal determinado, nunca se podrá definir el valor real del mismo, pues nunca se podría asegurar que el sistema
Ley de Gauss. Frecuentemente estamos interesados en conocer el flujo del campo eléctrico a través de una superficie cerrada, que viene dado por.
 Ley de Gauss La ley de Gauss elacina el fluj del camp eléctic a tavés de una supeficie ceada cn la caga neta incluida dent de la supeficie. sta ley pemite calcula fácilmente ls camps eléctics que esultan
Ley de Gauss La ley de Gauss elacina el fluj del camp eléctic a tavés de una supeficie ceada cn la caga neta incluida dent de la supeficie. sta ley pemite calcula fácilmente ls camps eléctics que esultan
CAMPO GRAVITATORIO FCA 08 ANDALUCÍA
 CAMPO GRAVIAORIO FCA 08 ANDALUCÍA. L atélite metelógic n un medi paa btene infmación be el etad del tiemp atmféic. Un de et atélite, de 50 kg, gia aleded de la iea a una altua de 000 km en una óbita cicula.
CAMPO GRAVIAORIO FCA 08 ANDALUCÍA. L atélite metelógic n un medi paa btene infmación be el etad del tiemp atmféic. Un de et atélite, de 50 kg, gia aleded de la iea a una altua de 000 km en una óbita cicula.
Decodificador: el código binario generado por las n entradas activa una de entre 2 n salidas.
 Tema 4 FUNCIONES DE RUTA DE DATOS 41 INTRODUCCIÓN Hems vst en el tema anterr que medante chps MSI pdíams mplementar funcnes artmétcas y lógcas cn un únc crcut ntegrad En este tema verems que cn ests chps
Tema 4 FUNCIONES DE RUTA DE DATOS 41 INTRODUCCIÓN Hems vst en el tema anterr que medante chps MSI pdíams mplementar funcnes artmétcas y lógcas cn un únc crcut ntegrad En este tema verems que cn ests chps
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
clasificación digital
 clasfcacón dgtal leccón 3 sumao Intoduccón. Conceptos estadístcos. Fase de entenamento. Fase de clasfcacón. Contol de caldad. La es un poceso de genealzacón temátca que, medante categozacón, convete la
clasfcacón dgtal leccón 3 sumao Intoduccón. Conceptos estadístcos. Fase de entenamento. Fase de clasfcacón. Contol de caldad. La es un poceso de genealzacón temátca que, medante categozacón, convete la
DEPARTAMENTO DE INGENIERÍA MECÁNICA DISEÑO MECÁNICO INGENIERÍA INDUSTRIAL
 DEPARTAMENTO DE INGENIERÍA MECÁNICA DISEÑO MECÁNICO INGENIERÍA INDUSTRIAL Higinio Rubio Alonso INTRODUCCIÓN! Evolución tecnológica Necesidad de piezas más precisas! Creación de normas! Estandarización
DEPARTAMENTO DE INGENIERÍA MECÁNICA DISEÑO MECÁNICO INGENIERÍA INDUSTRIAL Higinio Rubio Alonso INTRODUCCIÓN! Evolución tecnológica Necesidad de piezas más precisas! Creación de normas! Estandarización
PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medida del índice de refracción de una lámina de vidrio
 Coodnacón EVAU. Páctcas cuso 2017-18 P2 Objetvo: Detemna el índce de efaccón de un vdo. Fundamento: PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medda del índce de efaccón de una lámna de vdo La ley de la efaccón,
Coodnacón EVAU. Páctcas cuso 2017-18 P2 Objetvo: Detemna el índce de efaccón de un vdo. Fundamento: PRÁCTICA 2. LEY DE LA REFRACCIÓN. Medda del índce de efaccón de una lámna de vdo La ley de la efaccón,
Elementos de Aritmética de Computadoras Parte I
 Elementos de Atmétca de Computadoas Pate I M. Vázquez, E. Todoovch, M. Tosn Aqutectua I - Cuso 3 UNICEN Cómputo Atmétco Las peguntas de fondo cuando se aboda el tema de la atmétca de computadoas son: Cómo
Elementos de Atmétca de Computadoas Pate I M. Vázquez, E. Todoovch, M. Tosn Aqutectua I - Cuso 3 UNICEN Cómputo Atmétco Las peguntas de fondo cuando se aboda el tema de la atmétca de computadoas son: Cómo
DISEÑO TERMOHIDRÁULICO DE INTERCAMBIADORES DE CALOR DE CARCASA Y TUBOS, UN MÉTODO CORTO
 Nº5 Marz 0 IEÑO ERMOHIRÁULICO E INERCMBIORE E CLOR E CRC Y UBO, UN MÉOO CORO Rbert Carrzales Martínez Labratr de Ingenería Químca, Facultad de Cencas Químcas Unversdad utónma de an Lus tsí rcarrza@uaslp.mx
Nº5 Marz 0 IEÑO ERMOHIRÁULICO E INERCMBIORE E CLOR E CRC Y UBO, UN MÉOO CORO Rbert Carrzales Martínez Labratr de Ingenería Químca, Facultad de Cencas Químcas Unversdad utónma de an Lus tsí rcarrza@uaslp.mx
DECLARACIÓN DEL TESTIGO REDOUAN AGMIR
 DECLARACIÓN DEL TESTIGO REDOUAN AGMIR Fecha de la declaración : 17-05-2007 Orden en la sesión : 17 En cursiva azul, las preguntas del Ministeri Fiscal y ls abgads. En nrmal negr, las respuestas. Ls cmentaris
DECLARACIÓN DEL TESTIGO REDOUAN AGMIR Fecha de la declaración : 17-05-2007 Orden en la sesión : 17 En cursiva azul, las preguntas del Ministeri Fiscal y ls abgads. En nrmal negr, las respuestas. Ls cmentaris
dq de x r CAMPO DE UN ANILLO CON CARGA UNIFORME r α P de y de x
 y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
TEMA 5.- SISTEMAS TRIFÁSICOS
 DPTO. INGENIERIA EECTRICA ESCUEA DE INGENIERÍAS INDUSTRIAES EECTROTECNIA TEMA 5.- SISTEMAS TRIFÁSICOS 5.1.- En la red trifásica de la figura 5.1, la tensión cmpuesta al final de la línea es de 380V. a
DPTO. INGENIERIA EECTRICA ESCUEA DE INGENIERÍAS INDUSTRIAES EECTROTECNIA TEMA 5.- SISTEMAS TRIFÁSICOS 5.1.- En la red trifásica de la figura 5.1, la tensión cmpuesta al final de la línea es de 380V. a
CÁLCULO VECTORIAL 1.- MAGNITUDES ESCALARES Y VECTORIALES. 2.- VECTORES. pág. 1
 CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES
 Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES CRECIMIENTO Y DECRECIMIENTO Dada una función real
Unidad didáctica 7. Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES CRECIMIENTO Y DECRECIMIENTO Dada una función real
Análisis de Regresión y Correlación
 1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
Tema 4B. Inecuaciones
 1 Tema 4B. Inecuacines 1. Intrducción Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines
1 Tema 4B. Inecuacines 1. Intrducción Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines
Potencial electroestático
 Ptencial electestátic Jsé Jesús MNA DGADIO Una ppiedad mu imptante de td camp electestátic, cespnde al hech de que el camp eléctic es cnsevativ, es deci, eiste una función escala que depende de un punt
Ptencial electestátic Jsé Jesús MNA DGADIO Una ppiedad mu imptante de td camp electestátic, cespnde al hech de que el camp eléctic es cnsevativ, es deci, eiste una función escala que depende de un punt
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA
 PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
PROBLEMAS DE ELECTRÓNICA ANALÓGICA (Diodos)
 PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
www.fisicaeingenieria.es Vectores y campos
 www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
