TEMA 1: MODELOS DE REPRESENTACIÓN DE OBJETOS 3D
|
|
|
- Juan Nieto Giménez
- hace 8 años
- Vistas:
Transcripción
1 TEMA : MODELOS DE REPRESENTACIÓN DE OBJETOS 3D.. MODELOS DE SUPERFICIES Exsten vaas azones paa quee epesenta un objeto medante un modelo de supefce: Cuando el objeto msmo es una supefce que podemos supone sn goso (po ejemplo, la chapa metálca del capó de un vehículo). Este tpo de epesentacón nos pemte vsualza supefces abetas, mentas que los sóldos se caactezaán po tene su supefce necesaamente ceada sobe sí msma. Cuando tan sólo nos nteesa vsualza su aspecto vsual exteno, sn detalles sobe su estuctua ntena, aunque el objeto ocupe un ceto volumen. Cuando deseamos ealza una vsualzacón en tempo eal, y paa ello utlzamos hadwae o softwae gáfco que está sólo pepaado paa vsualza polígonos. En cualquea de estos casos es convenente utlza una epesentacón de la supefce del objeto. En pncpo la nfomacón sobe una supefce debe da cuenta de su geometía, de sus popedades vsuales (cómo se compota fente a la luz ) y quzás tambén de alguna popedad físca (como la elastcdad) s se va a efectua una smulacón físca sobe el objeto. S la totaldad del objeto consta de dfeentes pates (po ejemplo, vaos polígonos o vaos tozos defndos po dfeentes ecuacones), entonces podemos añad tambén nfomacón topológca, es dec, sobe cómo estas dfeentes pates se conectan ente sí paa foma la supefce. Con esta nfomacón adconal el modelo se conoce como una epesentacón de fontea del objeto (b-ep: bounday epesentaton). Esta epesentacón de fontea se utlza fecuentemente en combnacón con un modelo sóldo, ya que una de ellas se puede econstu a pat de la ota. En geneal, las dfeentes epesentacones no se excluyen ente sí, y muchos pogamas suelen combnalas, pasando de una a ota según convenga. Una caacteístca que suele exgse a las supefces epesentadas es que sean vaedades bdmensonales (en nglés: supefces -manfold), es dec, que no exstan puntos sngulaes donde la supefce se ntesecte consgo msma o se aba en vaas hojas. Ve fgua. Fgua..: Ejemplo de una supefce que NO es -manfold Además de la nfomacón geométca y topológca, es fecuente añad a la epesentacón de los objetos datos adconales equedos paa su vsualzacón (como el colo, las popedades vsuales del mateal, textua, etc.) o paa efectua pocesos de smulacón físca (dstbucón de densdad, tempeatua, composcón). Ve el modelo Luz-Supefce 5
2 Tema : Modelos de epesentacón de objetos 3D... MODELO POLIÉDRICO Consste en defn el objeto a tavés de una supefce fomada po polígonos que compaten sus astas y vétces, es dec, de un poledo, que puede se abeto o ceado. La exgenca de que sea una vaedad bdmensonal se taduce, en este caso, en la estccón de que los polígonos no se ntesecten ente sí excepto en las astas, y que en una asta no puedan conflu más de dos polígonos. En un vétce pueden concd cualque númeo de polígonos. Además, una buena epesentacón polgonal debe tene en cuenta: Evta la degeneacón de los polígonos,que se poduce po ejemplo, s uno de sus lados tene longtud ceo. Los tángulos degeneados son especalmente poblemátcos, ya que esulta un objeto de áea nula, nomalmente nvsble, peo que puede povoca eoes en cetos algotmos. Evta los vétces en T ya que puede povoca poblemas a la hoa de ellena el colo po ntepolacón ente los vétces y otas snguladades en cetos algotmos. Vétce en T Utlza en lo posble pmtvas polgonales que pemtan especfca el objeto sn epet vaas veces los vétces que petenezcan a vaos polígonos. La epesentacón basada en polígonos tene la ventaja de que pemte hace una vsualzacón muy ápda, poque úncamente se deben ealza una see de opeacones lneales muy efcentes, tanto paa la poyeccón sobe la pantalla como paa el posteo ellenado de los polígonos, gacas a lo cual es muy adecuada paa epesentacones en tempo eal 3. Como veemos después, su vsualzacón medante tazado de ayos, en conceto el cálculo de nteseccones 4 tambén esulta especalmente smple. Sn embago, hay tambén desventajas: los objetos complejos o de ogen natual aas veces están fomados po polígonos exactos, po lo que en su epesentacón se deben ealza apoxmacones, hacendo que la supefce apaezca fomada po tozos no suaves cuyo aspecto atfcal es vsble.... Repesentacón po Polígonos Aslados En este caso un poledo se epesenta medante una lsta de polígonos, sendo cada uno de éstos una lsta de vétces o de astas (ve el anexo paa una caactezacón matemátca más completa). Hay que tene cudado a la hoa de defn polígonos con más de tes puntos, ya que cuato puntos no tenen poqué se coplanaos en el espaco de tes dmensones, y al poyectalos paa foma una magen bdmensonal los esultados pueden no esta ben defndos (ve un ejemplo en la fgua...a). Fgua...A.: Ejemplo de bowte (bow=aco, te=pajata), una fgua fomada po cuato puntos no coplanaos cuya poyeccón en D puede tene dfeentes aspectos ( pajata en este caso) Ve apatado...: Pmtvas polgonales 3 Ve Tema 3: Sstemas de Vsualzacón en Tempo Real 4 Ve Tema 4: Modelos de Ilumnacón Global. Tazado de Rayos 6
3 Paa pode ncopoa nfomacón topológca, de elacón de vecndad ente los polígonos, hay que constu una estuctua de datos en la que se especfquen las efeencas adecuadas. Vamos a ve un pa de fomas de epesenta un conjunto de polígonos aslados en foma de tabla, de manea que sea posble extae nfomacón topológca. La pmea foma contendía: V A 6 V 5 A A P P A 5 V A V 3 3 A 4 V 4 Una lsta de vétces, una de astas y una de polígonos. Tabla de Vétces Tabla de Astas Tabla de Polígonos V : X Y Z V 5 : X 5 Y 5 Z 5 A : V V A : V V 3.. P : A A A 3 P : A A 4 A 5 A 6. Paa cada vétce, defndo po tes coodenadas, tendíamos efeencas a las astas que lo utlzan y (opconalmente) a los polígonos que lo contenen. Paa cada asta, tendíamos los dos vétces que la foman y, s se desea, los dos polígonos que la compaten. Paa cada polígono guadaíamos las astas que lo foman. A esto se le suele denomna epesentacón doblemente ndexada. Con esta estuctua seá muy sencllo, po ejemplo, compoba s dos polígonos se tocan, pues debeán compat al menos una asta. O ben podíamos smplfca la epesentacón elmnando las astas: Tabla Tabla de de Polígonos Vétces Tabla de Polígonos Vétces P : V V V 3 P : V V 3 V 4 V 5. V : X Y Z. V 5 : X 5 Y 5 Z 5 (INDEXADA) Una lsta de vétces y una de polígonos. Paa cada polígono los vétces que lo defnen. O tambén podíamos dectamente pone las coodenadas de los vétces que foman cada polígono, aunque estas se eptan en los vétces compatdos. 7
4 Tema : Modelos de epesentacón de objetos 3D Tabla de Polígonos P : X Y Z X Y Z X 3 Y 3 Z 3 P : (NO INDEXADA) Estas epesentacones se pueden modfca de dvesas fomas, elmnando nfomacón edundante, o añadendo más nfomacón paa faclta la búsqueda de elacones ente los dfeentes elementos. Apaece po tanto, la necesdad de un compomso ente la cantdad de almacenamento equeda, la complejdad de la estuctua de datos y la apdez de acceso a la nfomacón geométca y topológca. Un msmo vétce puede foma pate de dfeentes polígonos. S guadamos la nfomacón de cada vétce (poscón, vecto nomal, colo, etc.) una sola vez y luego, cuando descbamos los polígonos de los que foma pate, hacemos efeenca a él medante su índce en la tabla de vétces entonces se dce que estamos descbendo el objeto de foma ndexada. S, po el contao, cada vez que un vétce apaece en la descpcón de algún polígono epetmos toda la nfomacón coespondente al vétce, entonces estamos tabajando con una estuctua no ndexada o explcta. La estuctua ndexada tene la ventaja de ahoa espaco de almacenamento. Sus desventajas son que no pemte la dscontnudad de colo u ota magntud asocada a los vétces, ya que dos polígonos que compaten el msmo vétce tenen necesaamente el msmo colo en ese punto. Esto poduce un efecto de suavzado del colo de la supefce que a veces esulta eal (ve Fgua...B). Ota desventaja es que se poduce un lgeo aumento en el tempo necesao paa una consulta de datos sobe los vétces, ya que pmeo debe aveguase el índce y luego busca la nfomacón deseada en la tabla. En caso de emplea una lsta no ndexada, se puede epesenta un poledo con una únca lsta de polígonos, defndos po las coodenadas de cada uno de los vétces que lo componen. Al no se necesaa la consulta de una tabla de vétces, se consgue accede de foma mucho más ápda a las coodenadas, lo que puede se un ahoo de coste mpotante en aplcacones de tempo eal. Sn embago, tene el nconvenente de aumenta consdeablemente el espaco de almacenamento necesao, ya que las coodenadas de los vétces apaecen epetdas cada vez que un msmo vétce petenece a vaos polígonos dstntos.... Consdeacones geométcas de los modelos Polgonales. Una caacteístca mpotante que tenemos que tene en cuenta a la hoa de tabaja con modelos polgonales seá el oden en el cual se especfcan los vétces que lo componen. Este oden nfluye en algunos algotmos que se emplean paa elmnacón de supefces ocultas. El cteo de la egla del sacacochos es el que defne el cteo de especfcacón de vétces, o sea la pate extena de un polígono es aquella obtenda ecoendo sus vétces en sentdo anthoao: º 3º Pate Intena 4º º Pate Extena 5º 5º 4º Pate Extena 3º º Pate Intena º Oto punto mpotante a tene en cuenta a la hoa de tabaja con polígonos la obtencón del plano sobe el cual cae el polígono (ya que hemos comentado que los todos los vétces de un polígono deben se coplanaos). Paa el cálculo de la ecuacón del plano que ocupa un polígono y compoba que todos los 8
5 vétces son coplanaos bastaá con eleg tes de sus vétces (que no estén alneados) y calcula el vecto nomal al plano como el poducto vectoal de las dos astas defndas po dchos vétces: º V º N V 5º N = v v Y la ecuacón del Plano seá de la Foma: A x + B y + C z + D = Donde A=Nx, B=Ny y C=Nz y la D puede obtenese al susttu cualquea de los vetces en la ecuacón del plano y despeja. El oden del poducto vectoal tambén afecta a la deccón de la nomal y es necesao tenelo en cuenta. La egla que se aplca es la msma que la vsta paa el oden de los vetces. Tenendo la ecuacón del plano y según el cteo de que la nomal apunta haca fuea del polígono ahoa paa un punto cualquea P (x,y,z), s susttumos sus coodenadas en la ecuacón del plano que cotene al polígono y el esultado es mayo que ceo demos que el punto esta fuea del plano (o delante) y s el valo es negatvo demos que esta dento (o detás). Este tpo de compobacones nos seván en métodos de patcón especal basados en supefces planas. Comenta fnalmente que el cálculo de nomales a los polígonos es mpotante paa los modelos de lumnacón que tataemos en el tema y en el tema Pmtvas Polgonales Las pmtvas polgonales son gupos de polígonos que se descben de foma conjunta paa ahoa espaco de almacenamento y coste de vsualzacón en tempo eal, azón po la cual son amplamente utlzadas. Algunas de las pmtvas más utlzadas son: Ta de cuadláteos: los pmeos cuato vétces defnen el pme cuadláteo, y cada nuevo pa defne oto cuadláteo fomado po éste pa de vétces y el anteo. Podemos ve que este tpo de pmtva ahoa, especto de la especfcacón de polígonos aslados, cas la mtad de espaco. Sn embago, tene el nconvenente de que no se gaantza que en cada cuadláteo los vétces sean coplanaos. V V V 4 V k V V 3 V 5 V k+ Ta de tángulos: con los tes pmeos puntos se constuye un tángulo y los demás se foman añadendo sucesvos puntos. Cada nuevo tángulo se foma po los tes últmos vétces añaddos, de tal foma que con N puntos se obtenen N- tángulos. v v v 4 v v 3 v 5 9
6 Tema : Modelos de epesentacón de objetos 3D Abanco (Fan): se da un pme punto y luego el esto sguendo un abanco. Apaecen N- tángulos fomados po el pme vétce y los vétces, + ( dfeente de ). Se emplea paa consegu fomas mposbles de loga con la ta de tángulos. Esta pmtva, al gual que la anteo, tene la ventaja de que no es necesao compoba la coplanaedad. V V V 5 V 4 V V 3 Malla ectangula. Se utlza dectamente una matz de n po m vétces. Malla tangula. Apenas se emplea. En ealdad, la mayo pate de aplcacones y lbeías gáfcas descomponen posteomente todas estas pmtvas en tángulos duante el poceso de vsualzacón Modelo de Repesentacón Polígonal sobe OpenGL. La lbeía gáfca OpenGL es po natualeza una lbeía oentada al tabajo con modelos polédcos, po tanto nos seá fácl ealza epesentacón de esta natualeza. Puntualzaemos que se tata de una lbeía de funcones oentada pncpalmente a modelos nteactvos, po ello se pema la apdez fente al espaco, el tpo de epesentacón polgonal que empleaa seá po tanto explícta. Las defncones de pmtvas polgonales en OpenGL se encean ente las llamadas a las funcones: glbegn(glenum tpo_pmtva) y glend(vod). Ente dchas funcones debeemos especfca la lsta de vétces que componen nuesto polígono. La funcón paa pasa las coodenadas de cada vétce es glvetex3fv(glfloat *coo), donde coo es un vecto que contene las tes coodenadas del vétce. Los valoes nomales paa el tpo de pmtva son las constantes: Valo de la Cte GL GL_POINTS GL_LINES GL_LINE_STRIP GL_LINE_LOOP GL_POLYGON GL_TRIANGLES GL_TRIANGLE_STRIP GL_QUADS GL_QUAD_STRIP GL_TRIANGLE_FAN Tpo de Pmtva Polgonal Puntos aslados Líneas de dos vétces Línea de cualque numeo de vétces Línea Ceada. Polígono de Cualque tpo Polígonos de tes lados Ta de Tangulos Polígonos de cuato vetces Ta de Cuadlateos. Abanco de tangulos. Tabla de Pmtvas Gáfcas OpenGL
7 Po ejemplo la defncón de un tangulo en OpenGL sea: float mtan[3][3]={{,,,{,,,{,,; /*.*/ glbegn(gl_triangles); glvetex3fv(mtan[]); glvetex3fv(mtan[]); glvetex3fv(mtan[]); glend(); /*.*/... SUPERFICIES CURVAS La ventaja de las epesentacones polédcas es que son más adecuadas paa la vsualzacón en tempo eal, cuyas técncas se basan la poyeccón y ellenado de tángulos. El poblema que plantean es que la mayoía de los objetos no son ealmente poledos, sno que están compuestos po supefces contnuas y cuvadas. Paa epesenta un objeto complejo se puede utlza una descomposcón de la supefce en tozos o paches (patches) tangulaes o cuadangulaes, cada uno de los cuales se suele modela con supefces paamétcas (supefces de Beze, NURBS...). Esta epesentacón pemte modfca la foma de la supefce con mucha facldad: en luga de camba las coodenadas de un gan númeo de vétces, solo necestamos camba unos cuantos paámetos en las ecuacones. Una vez temnado el modelado s queemos hace una vsualzacón en tempo eal sempe esultaá posble convet estas supefces en una apoxmacón polgonal. Exsten otos métodos de vsualzacón, como el tazado de ayos, que sí pueden tabaja dectamente con una epesentacón exacta. Los poblemas que plantea la epesentacón contínua a tozos son, po una pate, la dfcultad de contola que la foma de la supefce sea exactamente la que queemos y, po oto, la complejdad de mantene las estccones (contnudad, devabldad) en las nteseccones de los tozos. Paa defn una supefce cuvada y suave de foma exacta debemos ecu a una epesentacón analítca, es dec, medante ecuacones. Dependendo de la foma de las ecuacones habá que evalua la supefce (halla sus puntos) utlzando dstntos métodos. En geneal tenemos los sguentes tpos: Ec. mplícta : f( x, y, z) = Ec. explícta : p.ej. y = f( x, z) Ec. paamétca : p.ej. una supefce ( x, y, z) = f( u, v) En tes dmensones una ecuacón explícta sempe puede tansfomase en paamétca, como podemos ve en el sguente ejemplo: S z = f( x, y) es la ecuacón en foma explícta, entonces la ecuacón paamétca podemos defnla como : x = u z = f z ( u, v) y = v ( x, y, z) = ( u, v, f ( u, v)) = f ( u, v)... Supefces Implíctas : Cuádcas, Isosupefces y Supefces Equpotencales. Cuadcas: Comenzaemos po evsa el modelado de fomas desctas en base a funcones matemátcas de tpo cuadátco que se expesan de foma mplctas. En este caso las expesón geneal que dentfcaía a dchas supefces seía: z
8 Tema : Modelos de epesentacón de objetos 3D ax + by + cz + dxy + eyz + fxz + gx + hx + jz + k = Ahoa en funcón de los valoes de estos paámetos tenemos dstntos de cuádcas: Esfea: En este caso los coefcente no nulos son a,b,c y el temno ndependente epesenta el cuadado del ado de las esfea. En algunos caso se suele hace un cambo en la epesentacón de la cuádca paa faclta su evaluacón, elegendo epesentacón paamétcas,en el caso de la esfea se suele epesenta en coodenadas polaes, sendo los ángulos de bado los paámetos. z ax + by + cz = Ec. Implcta de la Esfea. π π x = cosφ cosθ, φ y = cosφ snθ, π θ π z = snφ x θ φ y Repesentacón pola de la esfea Ejemplo OpenGL. Veamos en el sguente ejemplo como constu la epesentacón de una cuadca de tpo esféco basada en una descomponscón polígonal que utlce las tas de tangulos de OpenGL. La funcón ejemplo ecbá como paámetos el ado de la esfea y las dvsones en lattud (φ) y longtud(θ) vod Esfea_T_Stp(float ado, nt nlattud, nt nlongtud) { float nct,ncf; nt,j; float vetce[3]; nct=*pi/nlongtud; ncf=pi/nlattud; fo(=;<nlattud;++) { glbegn(gl_triangle_strip); vetce[]=vetce[]=; vetce[]=-ado; glvetex3fv(vetce); fo(j=;j<nlongtud-;j++) { vetce[]=ado*cos(*nct)*cos(j*ncf-.5*pi); vetce[]=ado*cos(*nct)*cos(j*ncf-.5*pi); vetce[]=ado*sn(j*ncf-.5*pi); glvetex3fv(vetce); vetce[]=ado*cos((+)*nct)*cos(j*ncf-.5*pi); vetce[]=ado*sn((+)*nct)*cos(j*ncf-.5*pi); glvetex3fv(vetce); vetce[]=vetce[]=; vetce[]=ado; glvetex3fv(vetce);
9 3 Ellpsode: En este caso la foma de expesón de los paametos es algo más compleja y se puede obtene al desaolla la sguente expesón mplcta: = + + z y x z y x Ec. Implcta de un Elpsode En este caso tambén tenemos la expesón paamétca coespondente: Ec. Paamétca del Elpsode Oto ejemplo común de cuadíca es el too. Supecuadcas: Se tata de una genealzacón de las cuádcas donde se añaden paámetos adconales que afectan al gado de la ecuacón mplícta, con ello se obtenen vaacones ntesantes de la foma. Po ejemplo el Supeellpsode seía una vaante del elpsode anteo donde se añade un paámeto s y s que afectan al gado de la ecuacón. En la fgua se pueden obseva los efectos de los cambos en s y s. = + + s z s s s y s x z y x Ec. Implcta de un Supeelpsode. Isosupefces y Supefces Equpotencales. Oto método de modelado especal de supefces consste en defnlas como funcones en foma mplícta, es dec, en la foma F(x,y,z)= y luego busca alguna manea de vsualzalas. Esto es equvalente a defn un campo escala en el espaco y luego toma todos los puntos x,y,z en los que esa magntud toma un valo constante. De esta foma, a pat de una funcón ( ) ( ) g x y z T umbal o theshold,, =, podemos defn ota funcón en foma mplícta equvalente, sn más que hace : ( ) ( ) f xyz gxyz T,,,, = = Este tpo de objeto se denomna tambén sosupefce. S el campo escala vaía de foma suave (exste su gadente o devada especto a la poscón) entonces se denomna potencal (como el geneado po un campo de fueza en físca). En ese caso la sosupefce se denomna supefce equpotencal. x x φ π θ π θ φ π φ π θ φ sn z sn sn y x z y x = = =,, cos cos x θ φ y z
10 Tema : Modelos de epesentacón de objetos 3D Ejemplo: un campo escala (las tes dmensones han sdo educdas a una) ceado po dos objetos dfeentes de ados y. En este caso la supefce equpotencal seían puntos aslados, que se hallaían sumando las dos contbucones y buscando aquellos puntos de altua umbal T. Una foma de pode contola la foma de esas supefces paa utlzalas en el modelado de objetos es hace que la funcón F(x,y,z) ó g(x,y,z) sea la suma de vaas contbucones geneadas po dfeentes objetos báscos nstancados en la escena, nomalmente esfeas o elpsodes. El síml físco seía que cada uno de esos objetos genea un ceto campo de fueza (gavtatoo, eléctco...), un potencal a su alededo, en cada punto del espaco. La supefce equpotencal envolveá a los objetos báscos como una película elástca de aspecto suave. Es po ello que estos objetos globulaes (blobs o blobby objects) que se utlzan amplamente paa epesenta fomas ogáncas, en las que la pel o la concha ecuben las estuctuas ntenas (esqueleto, músculos). Un ejemplo popula de esta apoxmacón es la combnacón de funcones gaussanas en las que el potencal en cada punto poducdo po cada una de las componentes es una cuva nomal o gaussana. De este modo s paa cada punto se defne : σ b x ( σ ) Entonces podemos defn el potencal en cada punto como : f x, b, = be ( ) x poscon b fueza = altua desvacon tpca x x De foma que la supefce equpotencal quedaía como sgue : x x fxyz (,, ) = be = T Este tpo de objetos se conoce tambén como blobs en algunos paquetes de anmacón. Oto tpo son las metaballs, defndas medante polnomos, y po tanto más fácles de evalua, como podemos ve en su ecuacón geneal (ve fgua...). 4
11 ( ) [ ] ( ) [ ] b 3 d s, d 3 d d/3 d/3 d f ( ) = 3 b d s d 3, d s > d Con = ( x x ) el tamaño de la componente. y b la fueza, la dstanca ente un punto y el cento y d el ado, es dec, Ota posbldad son los soft objects. En los que la ecuacón geneal es : - f ( ) = d + 7 d d s s > d [, d] f() d d Fgua...: Ejemplo de supefce equpotencal geneada con tes esfeas 5
12 Tema : Modelos de epesentacón de objetos 3D Vsualzacón de Isosupefces: Machng Cubes La vsualzacón de cualque sosupefce puede ealzase báscamente po dos métodos dfeentes, ben po geneacón de polígonos Machng Cubes o po tazado de ayos 5. Tambén pueden dbujase cetas apoxmacones duante la fase de modelado, que equee una vsualzacón ápda Apoxmacones duante la edcón 6. El algotmo del machng cubes nos descbá la supefce en foma de polígonos desctos po las nteseccones de la supefce a evalua con una descomposcón del espaco en unas fomas geométcas base. El algotmo clásco comenza ealzando una descomposcón del espaco afectado po la supefce en cubos de un tamaño detemnado (geometías base), estos cubos se suele denomna voxel po analogía a los pxel bdmensonales (en otos puntos de este tema los volveemos a nomba). Dada la descomposcón en voxels, cada uno de estos voxel puede encontase en una de estas tes stuacones: Completamente fuea de la supefce. Completamente dento de la supefce Pacalmente dento o sea ntesectado po la supefce. El algotmo después de ealza esta clasfcacón se dedcaa a la detemna la foma del polígono de nteseccón ente la ecuacón de la supefce y el cubo ntesectado. El numeo de posbles fomas de nteseccón esta lmtado. Veamos un ejemplo sencllo en D y luego lo genealzaemos a 3D. En la magen se obseva una cuva sobe un plano dvddo en una etícula. La cuva lmta un espaco dento de cuadados nteoes oto de exteoes y un espaco de cuadados ntesectados. En este caso lo que vamos a hace es segmenta la cuva en tamos ectos, que defnen los puntos de nteseccón de la cuva con los cuadados: Cuva eal sobe la muesta tomadas de la msma. Cuva polgonal geneada de la muestas. El tpo de nteseccones esta lmtado como hemos comentado anteomente a unas cuantas posbldades, en el caso D las fomas de nteseccón cuva-celdas se lmta a cnco posbldades (dos de ellas no mplcan nteseccón). El poblema seá detecta el punto de cote exacto, esto se puede hace po un método de ntepolacón ente el valo de la funcón que defne la cuva en el punto nteo (azul y en exteo (ojo) paa cada segmento de celta ntesectado. El esultado de esta epesentacón como en toda dscetzacón dependea de la pecsón elegda, que en esta caso es funcón del tamaño de las celdas. La genealzacón a tes dmensones es elatvamente senclla de compende, aunque la mplementacón es bastante más laboosa. En este caso las nteseccones en luga de se segmentos ectos son polígonos y la casuístca de nteseccón se complca exstendo 6 posbldades dstntas: 5 Ve Tema 3: Modelos de Ilumnacón Global. Tazado de Rayos 6 Ve anexo 8 6
13 Posbldades Topologcamente dstntas de nteseccón ente uan supefce y un cubo. Aplcado a un ejemplo smla a la cuva peo en 3D: Supefce ntepolada. Exsten codfcacones especales en la numeacón de los vétces, etc, paa optmza las clasfcacones de las nteseccones, etc, no obstante suele tatase de un algotmo lento y paa ealzalo off-lne y muchas veces los esultados no son excesvamente buenos pudendo sug algunos poblemas de desconexón en la malla polgonal que ya se pueden ntu de las fomas de nteseccón pesentadas.... Supefces Paamétcas : Supefces de Contol. Vamos a examna alguna de las fomas de pocede con una supefce paamétca, que mostaán lo smple que esulta su utlzacón en cetos algotmos y su vsualzacón. S se emplean las ecuacones paamétcas paa defn una supefce, es posble halla puntos que petenezcan a ella (po ejemplo, paa pode dbujala) sn más que dando valoes a los paámetos u y v, de tal foma que se ecoe la supefce de foma exhaustva. En muchas epesentacones se nomalza la ecuacón de manea que los paámetos u y v solamente tomen valoes en el ango [,]. Además se pueden calcula muy fáclmente algunos paámetos nteesantes (ve Anexo ), como: Los vectoes tangentes paa los paámetos u, v y el vecto nomal a la supefce. Calcula la dstanca ecoda en un camno a lo lago de la supefce. Calcula la cuvatua (elaconada con las segundas devadas) en un punto cualquea de la supefce. Calcula los paámetos u,v de un punto desconocdo (po ejemplo, el punto donde una ecta ntesecta a la supefce) medante apoxmacones sucesvas dando valoes a u y v. El poblema de esta apoxmacón es que la complejdad de las ecuacones suele aumenta enomemente cuando mponemos muchas estccones (po ejemplo, que la supefce pase po más y más puntos que nos nteesan). Tambén apaecen efectos ndeseados; las supefces esultantes pueden tene una foma extaña aunque les focemos a pasa po cetos puntos de contol, como puede vese en el sguente dbujo. Puntos de contol 7
14 Tema : Modelos de epesentacón de objetos 3D Al apaece odenadoes capaces de epesenta gáfcos, y comenza su aplcacón en el Dseño Asstdo po Odenado (CAD), sugeon gupos de nvestgacón en empesas de automóvles que desaollaon la teoía y la aplcacón de cetas supefces paamétcas cuya foma se podía defn de manea senclla a tavés de puntos de contol, gaantzándose que su foma no sufa vaacones ncontolables. Las cuvas más nteesantes son constudas a pat de polnomos y cumplen con la sguente popedad: s defnmos el cee convexo de un conjunto de puntos como el mínmo polígono convexo (en D) o poledo convexo (en 3D) que los contene, entonces se cumple que la cuva o supefce detemnada po un conjunto de puntos de contol no se sale del cee convexo de estos puntos. No vamos a especfca aquí en detalle los dfeentes tpos de supefces paamétcas polnómcas con puntos de contol. Las más empleadas son las supefces de Bèze 7, las B_Splnes y las NURBS (ve Fgua...). Su foma geneal seía: Fgua...: Ejemplo de supefce dseñada con NURBS Dento de estas nocones geneales de epesentacón paamétca exsten dos apoxmacones pncpales a la hoa de aboda el modelado de estas supefces o cuvas: Cuvas o supefces de ntepolacón Cuvas o supefces de apoxmacón. Paamétcas de Intepolacón. Las pmeas ofecen un contol más nmedato del modelado y nos pemten asegua que las cuvas o supefces pasan po el conjunto de puntos de contol. Esto puede paece una ventaja peo paa el modelado geométco supone que las estccones e nfomacón que hemos de ofece hagan que las supefces de ntepolacón sean complejas de utlza. Se emplean sobe todo paa ntepolacón de tayectoas donde s que necestamos asegua unos puntos de paso. El ejemplo más común de las paamétcas de apoxmacón lo consttuyen las splnes natuales, estas cuvas petenecen a la famla de las splnes las cuales se basan en defn la cuva a pat de cuvas polnomales a tozos, nomalmente el gado de los tozos se seleccón de gado cúbco. Las cuvas (y po extensón supefces) tenen el aspecto de contnudad y suavdad po que se les exgen condcones de contnudad y devabldad en los puntos de unón. En el caso de la splnes natuales se exge contnudad C lo que sgnfca pmeas y segundas devadas contnuas. Estas condcones nos seván paa detemna los paámetos que defnen las cuva. La foma de cada uno de estos tozos de cuva es: 7 Paa más detalles sobe las supefces de Bèze ve el anexo 3 8
15 C( u) = a u C 3 = u 3 ( u) = a + au + au + au Es mpotante puntualza que esta es la foma geneal paa cada una de las tes dmensones, sendo el paámeto la u, po tanto tendíamos una ecuacón de este tpo paa x, ota paa y y ota paa z El numeo de tozos de cuva que necestamos paa defn una splne natual depende del numeo de puntos po los que queamos foza el paso, el numeo de tozos es equvalente al numeo de puntos de paso menos : P P3 P5 P P4 C C C3 C4 Po ejemplo en el caso de la fgua el númeo de cúbcas que tenemos que combna es cuato. Cada una de las cúbcas vene defnda po cuato paámetos (del a al a3), po tanto paa defn completamente las cuva necestamos sabe el valo de 4*(n-) paámetos. Paa detemna esos paámetos se establece un sstema de 4n 4 ecuacones (sempe n es el numeo de puntos) donde las ncógntas son los paámetos. De las condcones de contnudad de las devadas pmea y segunda en los puntos medos y del paso po los puntos contol podemos obtene 4n-6 ecuacones y las otas ecuacones se consguen asgnando unos valoes de tangenca en los extemos, estos valoes de tangenca detemnan tambén en buena medda la foma fnal de la splne natual. Veamos esto en un ejemplo smple con solo tes puntos de paso (n=3) P,P, y P3. El numeo de cuvas seá de dos y po tanto necesto 4*3-4 paámetos o sea 8, 4 po cuva como hemos ndcado. Las ecuacones se obtenen de la sguente foma: Sabemos que en el punto ncal la cuva C pasa po P po tanto:. C () = P En el Punto medo la cuva C pasa po P, esto coesponde al valo de su paámeto de evaluacón. po contnudad C en su valo de paámeto tamben pasa po P po tanto tenemos dos nuevas ecuacones:. C ()=P 3. C ()=P Ota ecuacón la obtenemos de la condcón de paso de C po el punto P3 en su valo de paámeto. 4. C ()=P3 Otas *n- ecuacones salen de las condcones de contnudad de la pmea devada y segunda devada en los puntos de unón, en este caso seán dos ecuacones: 5. C ()=C () 6. C ()=C () Las dos ecuacones que nos faltan las sacamos como hemos comentado anteomente de asgna un valo de tangenca en los extemos o sea un P y un P3 7. C ()=P 8. C ()=P3 La foma fnal de las ecuacones segun la foma de las cuvas vsta anteomente seía:. a =P. a +a +a +a 3 =P 3. a =P 4. a +a +a +a 3 =P3 5. a +a +3a 3 =a 6. a +6a 3 = a 9
16 Tema : Modelos de epesentacón de objetos 3D 7. a =P 8. a +a + 3a 3 =P3 Este desaollo se debeá hace paa cada una de las coodenas ya que P,P y P3 tenen una componente x, y, z, po tanto las ecuacones que esolvemos ealmente son el tple de las comentadas. Las splnes natuales tenen poblemas de contol local ya que las ecuacones que escbmos hacen que exstan dependencas que se tasmten de unos puntos de contol a otos. Po oto lado exste un poblemas mpotante confome aumenta el numeo de puntos ya que el sstema de ecuacones al esolve cece de una foma bastante mpotante. Exsten algunas mejoas de estas cuvas de ntepolacón como po ejemplo las splnes cadnales, o las ntepolacones de hemte que se basan en deas paacdas a las funcones base del tpo que comentaemos en el sguente apatado de splnes de apoxmacón, en todos los casos se tata de mnmza los poblemas apuntados en el páafo anteo. Cuvas y Supefces Paámetcas de Apoxmacón En este caso como hemos comentado el polnomo de contol no foma pate de la cuva o supefce s no que es un modo de poduc las defomacones en la msma. Ota caacteístca que es habtual en estas cuvas el utlza unas funcones polnómcas base que se combnan paa foma la cuva que se vsualza. El tpo y natualeza de estas funcones base se emplea nomalmente paa clasfca dstntas categoías de supefces y cuvas de apoxmacón. Vamos a epasa bevemente un pa de tpos las cuvas de Beze y las B-Splnes. Cuvas y Supefces de Beze. En la cuvas de Beze se cumple que la cuva pasa po los puntos extemos del polnomo del contol y se apoxma al esto. En este caso las funcones base son los polnomos de Besten y la foma que toma la cuva es: C( u) = con B, n n = B, n ( u) P n! ( u) = u ( u)!( n )! u n con n = B, n ( u) = u P P P3 P P4 Donde la B son los polnomos de Besten y las P son los puntos de contol, n es el numeo de puntos. No obstante esta foma de las cuvas de Beze tene el poblema que el gado del polnomo base depende del numeo de puntos. Paa evta esto se suelen emplea paa el modelado de cuvas tozos de cuvas de Beze con hasta 4 puntos en el polnomo de contol y a los cuales se les exgen condcones de contnudad paa genea cuvas con más puntos de contol. La pncpal caacteístca que deben cumpl estas cuvas es que el últmo punto de la pmea cuva α(t) sea el pme punto de la segunda cuva β(t), es dec, los tozos deben defnse de tal modo que las cuvas esultantes sean contínuas. Sean dos cuvas polnómcas de Bèze: 3 [ ] ( ) P ( ) 3 [ ] ( ) Q ; ( ) α:, R α = ; α = P β:, R β = β = Q n n
17 La cuva esultante se defne como: αo β:, t [ ] 3 R α () t t β( t ) t que estaá ben defnda sempe que P Q n = Cuvas de beze medante el algotmo de Casteljau La dea de Casteljau es aplca el método de ntepolacón lneal ecusvamente paa defn la cuva paamétca. Dados dos puntos cualesquea P,P se consdea la cuva: 3 α =, R Supongamos que tenemos los sguentes puntos P,P,P,P 3,...,P n se defnía la cuva del sguente modo: con t, : P P P n () t = () t = () t = P P P n ' P = ( ) P + P ' () t = ( t) () t + t () t t () t t () t P () t = ( t) + P () t t P() t P P () t P () t = ( t) + P () t t P () t () t t () t t () t () ( ) () () n n n P t = t n P t + t n P t n P ' P = ( ) P + P Así sucesvamente hasta llega: n n n P ( t) = ( t) P ( t) + t P ( t) Este útmo polmono se epesenta po α( t ) y se denomna CURVA DE BEZIER asocada a los PUNTOS DE CONTROL { P,P,P,P 3,...,P n. Matemátcamente tenemos. Pt () = P P () t = =,.., n () t t () t t () t =,..., n + P = ( ) P + P Fnalmente Indcaemos que paa pasa de cuvas a supefces de Beze es necesao añad un segundo paámeto a la descpcón de la cuva, el polígono de contol estaá fomado ahoa po una matz bdmensonal de puntos. La foma de la ecuacón es la sguente: S beze ( u, v) n m = = j= B, n( u) B j, m( v) Pj u Cuvas y Supefces B-Splnes. Se tata de una genealzacón de las cuvas de apoxmacón defndas a tozos, en este caso se han buscado unos polnomos base que pemtan un contol local todavía mas adecuado que en el caso de los polnomos de Beze, paa sepaa y agega este contol local se añaden una see de puntos de uptua en el paámeto base el cual es dvddo en un conjunto de ntevalos. Este conjunto de ntevalos ecbe el nombe de vecto de nodos o knots. La expesón que defne a una B-Splne es la sguente:
18 Tema : Modelos de epesentacón de objetos 3D C( u) = N con N, n = ( u) =, d su ( u) P u u u + enotocaso mn < u < u N, d max, d n + u u ( u) = N u u + d, d u ( u) + u + d + d u u + N +, d El temno d que apaece en la expesón de la B-Splne hace efeenca al gado de los polnomos base N que vamos a utlza, mentas que P son los puntos de contol. Como vemos una pmea dfeenca mpotante con las Beze es que el gado del polnomo base no depende del numeo de puntos de contol y que ndependentemente de ese numeo podemos selecconalo en cada caso. Oto aspecto nteesante es la defncón de los polnomos base N, los cuales se defnen de foma ecusva y como hemos comentado se evalúan en dfeentes ntevalos del paámeto u, los ntevalos venen defndos po el vecto de knots. El numeo de elementos del vecto de knots po la expesón ecusva debe se del númeo de puntos mas el d selecconado. La seleccón del vecto de knots es mpotante ya que con él se gestona en gan medda el contol local de la cuva. En funcón de la dstbucón del vecto de knots se tenen dstntas clasfcacones de ls B- Splnes: Unfomes: el vecto de knots se dstbuye unfomemente ente el mínmo y el máxmo. No Unfomes: Esta dstbucó no es unfome,etc. Un ejemplo de la nfluenca del vecto de knots puede vese en el hecho de que po ejemplo s queemos foza a que la cuva pase po los puntos extemos del polígono de contol debemos epet el valo ncal y fnal de los knots el msmo numeo de veces que el gado de los polnomos base, esto es, d veces. Po ejemplo un vecto de knots tpco paa una B-Splne con cnco puntos de contol, gado 3 y que pase po los puntos extemos podía se: {,,,,,3,3,3. Como vemos tene 5+d valoes y se epten 3 veces los de los extemos. B-Splnes Raconales. Se tata de una vaante de las B-Splnes donde las cuvas se defnen a pat de un cocente o azón ente una dos expesones basada en los polnomos base, además se añada asocado a cada punto de contol una cantdad o peso que epesenta el pode de ataccón de ese punto sobe la cuva. Esto pemte mejoa el gado de contol local de la cuva. La expesón de las Bsplnes aconales es: C( u) n = = n = w N w N, d, d ( u) P En esta expesón w epesentan los pesos asocadas a cada punto de contol el esto de témnos tene el msmo sgnfcado que en el caso de la Bsplnes. Dento de las Bsplnes Raconales tambén podemos tene una dstbucón unfome o no unfome del vecto de knots. Cuando la dstbucón es no unfome estamos dento de un conjunto muy conocdo de cuvas y supefces se tata de las NURBS (Non Unfom Ratonal B-Splnes). Las pncpales ventajas de las B-Splnes Raconales sobe las nomales es que pemten epesenta de foma exacta a las fomas cuadcas, esto pemte utlza en los paquetes de modelado un únco tpo de pmtva de modelado de supefce. Como sucedía en el caso de las cuvas de Beze pasaa supefces B-Splne equee genealza las expesones anteoes añadendo un segundo paámeto. S BSplne ( u, v) = n m = j= N ( u) j, l ( v) N, d ( u) Vsualzacón de cuvas y supefces paamétcas. Paa ealza la vsualzacón de estas supefces pmeo habá que evalua los polnomos que apaecen en su expesón analítca. Ya hemos vsto que una foma de dbuja la supefce seía dando valoes a los paámetos u y v. Otas fomas de optmza estos cálculos se basan en el calculo de P j ( u)
19 ncementos a pat de un pme punto cálculo de ncementos dfeencales 8 o en la ealzacón de sucesvas subdvsones de foma adaptatva métodos de subdvsón 9. Cuvas y Supefces Paámetcas en OpenGL Paa tabaja con cuvas y supefces en OpenGL podemos utlza una descomposcón de la cuva o supefce en polígonos y epesentalos sguendo los métodos vstos en puntos anteoes, la ota foma es utlza las pmtvas de este tpo que posee la OpenGL. Cuvas y Supefces de Beze en OpenGL: En este caso tenemos un conjunto de funcones que nos pemten genea los valoes de la cuva de Beze. La pmea funcon necesaa es glmap se tata de una funcon que defne evaluacones paamétcas de una dmenson (cuvas) o dos dmensones (supefces). Los paámetos e la funcón haán efeenca al tpo de vétce a genea, valoes de los extemos de los paámetos, numeo de puntos de contol, valoes y valoes de los puntos de contol. Po ejemplo: glmapf(gl_map_vertex_3,.,., 3,, puntos_contol); Paa que esta funcón se hablte es necesao emplea el glenable(gl_map_vertex_3). Además de hace esta habltacón y el mapeo anteo ahoa seá necesao añad las funcón de ecogda de las saldas y de dbuja. El sguente ejemplo dbuja una cuva de beze, el contono del polígono de contol y los puntos de contol vod dbuja_cuvas_beze() { nt,j; /** Defncon del Mapeo */ glmapf(gl_map_vertex_3,.,.,3,n_pc_c_beze,&pc_c_beze[] ); /*Habltacon del mapeo a vetces 3D */ glenable(gl_map_vertex_3); /* Especfcacón del numeo de evaluacones del mapeo ( en los valoes y del paámeto*/ glmapgdd(,,.); /*Dbujado de los puntos de la cuva de beze */ glevalmesh(gl_line,,); /* Dbujado de la pollnea de contol*/ glbegn(gl_line_strip); fo(j=;j<n_pc_c_beze;j++) glvetex3fv(pc_c_beze[j]); glend(); /* Dbujado de los puntos de contol */ glpontsze(5.); glbegn(gl_points); fo(j=;j<n_pc_c_beze;j++) glvetex3fv(pc_c_beze[j]); glend(); Paa el caso de las supefces de Beze es necesao emplea la funcon glmapf y evlau la mesh en dos dmensones glevalmesh. En el sguente ejemplo se dbuja la supefce de beze y el polnomo de contol y los puntos de contol. vod dbuja_s_beze() { nt,j,k; gldsable(gl_lighting); 8 Paa ve como funcona este método ve el anexo 5 9 Este método se explca en el anexo 6 3
20 Tema : Modelos de epesentacón de objetos 3D gllnewdth(.); glmapf(gl_map_vertex_3,,5,3,n_pc_s_beze[],,5,3, n_pc_s_beze[],&pc_s_beze[]); glenable(gl_map_vertex_3); // glenable(gl_auto_normal); // glshademodel(gl_smooth); /** Evaluacon de la Mesh con 5 dvsones en cada paameto de a 5 */ glmapgdf(5,,5,5,,5); /*Dbujado de la supefce de beze */ glevalmesh(gl_line,,5,,5); /*Dbujado del polgono de contol y de los puntos de contol*/ gllnewdth(.); glcolo3f(,,); fo(j=;j<n_pc_s_beze[];j++) { glbegn(gl_line_strip); fo(k=;k<n_pc_s_beze[];k++) glvetex3fv(pc_s_beze[j][k]); glend(); glcolo3f(,,); fo(j=;j<n_pc_s_beze[];j++) { glbegn(gl_line_strip); fo(k=;k<n_pc_s_beze[][];k++) glvetex3fv(pc_s_beze[k][j]); glend(); glpontsze(5.); glcolo3f(,,); glbegn(gl_points); fo(j=;j<n_pc_s_beze[];j++) fo(k=;k<n_pc_s_beze[];k++) glvetex3fv(pc_s_beze[j][k]); glend(); NURBS en OpenGL En este caso la cosa es algo más complcada debéndose defn un objeto de descpcón de la Bsplne o NURB. En el sguente ejemplo se muestan los pasos necesaos paa una supefce NURB vod dbujanubs() { nt,j; float ctlptos[4][4][3]; float knots[8]={,,,,,,,; GLUnubsObj *pnub=null; // Declaacón de la vaable de objeto NURB /* Rellenado de unos puntos de contol smples*/ fo(=;<4;++) fo(j=;j<4;j++) { ctlptos[][j][]=; ctlptos[][j][]=j; ctlptos[][j][]=; fo(=;<4;++) ctlptos[][][]=; gldsable(gl_lighting); /* Ceacon del Objeto NURB */ pnub=glunewnubsrendee(); glenable(gl_auto_normal); //glshademodel(gl_smooth); 4
21 /* Cambo de las popedaddes del objeto, en este caso la toleaca de eo se pone en pxel, esto mplca mas o menos polgonzacón en la vsualzacón*/ glunubspopety(pnub,glu_sampling_tolerance,.); /* Establecemos que quemos ve la NURB en modo alambe*/ glunubspopety(pnub, GLU_DISPLAY_MODE,GLU_OUTLINE_POLYGON); /* Incamos el dbujado de la supefce NURB*/ glubegnsuface(pnub); /*Damos los valoes de descpcon de la NURB, en este caso 8 knots y gado de los polnomos 4*/ glunubssuface(pnub,8,knots,8,knots,4*3,3,&ctlptos,4,4,gl_map _VERTEX_3); gluendsuface(pnub); /* Elmnamos el objeto nub que ceamos*/ gludeletenubsrendee(pnub);.. MODELO DE SÓLIDOS Debeemos epesenta nuestos objetos con un modelo de sóldo cuando: No sólo nos nteesa la apaenca extena del objeto sno tambén dscen ente el espaco ocupado po el objeto y el exteo. Debemos guada nfomacón efeente a alguna magntud que vaía en el nteo de objeto paa posteomente epesentala gáfcamente. Po ejemplo, esto sucede con los datos médcos obtendos con algun sstema de scanne tdmensonal, como el TAC. Debemos efectua detemnadas opeacones (po ejemplo la unón o la nteseccón) ente objetos o aplca cetos algotmos que esultan más efcentes epesentándolos como sóldos. Exsten dos tpos báscos de epesentacones: Repesentacones de fontea (bounday ep o b-ep). Se descbe la fontea del objeto utlzando un modelo de supefce con nfomacón topológca, tal como vmos en el apatado anteo, tenendo en cuenta que esta supefce debeá sempe se ceada. Repesentacones sóldas o de volumen. No se emplea la supefce sno que se efectúa una descomposcón del espaco msmo, ndcando qué pates caen dento o fuea del objeto. Estos métodos pemten además asgna popedades no solo a la supefce (po ejemplo, cómo esponde a la lumnacón), sno tambén al nteo del objeto. Son los que vamos a estuda en este apatado. Al gual que en las supefces fomadas po polígonos podían plantea stuacones no egulaes, tambén las epesentacones de volumen pueden da luga a snguladades (p. ej. objetos de volumen nulo) o ncoheencas (p. ej. autonteseccones en las que una msma pate del objeto se epesenta dos veces). Sea cual sea el modelo que eljamos paa epesenta los sóldos, éste debe pemtnos ealza las llamadas opeacones booleanas (unón, nteseccón, esta o negacón). La esta y la negacón son ntedefnbles, es dec, que podemos defn una a pat de la ota del sguente modo: A B = A ( B). Estas opeacones deben defnse de foma que sean egulaes: su esultado debe se sempe un sóldo eal (deben tatase con cudado los casos en que la nteseccón es sólo un plano, ecta o punto, o 5
22 Tema : Modelos de epesentacón de objetos 3D cuando el esultado puede se nulo, po ejemplo al esta un objeto a sí msmo). Estas opeacones son muy útles paa el modelado geométco 3D, ya que podemos cea nuevos objetos añadendo o qutando pates sóldas mantenendo la undad del objeto como entdad. Debemos tene sempe pesente que cada método de epesentacón tene cetas ventajas e nconvenentes, po lo que se suelen combna en las aplcacones páctcas. Po ejemplo, se puede usa uno duante la fase de modelado, oto paa una smulacón físca y oto paa la vsualzacón ealsta, efectuándose las convesones apopadas. Los objetos de patda pueden genease po dfeentes métodos, sea cual sea el método de epesentacón ntena elegdo. Los más sencllos son la nstancacón de pmtvas, es dec, de objetos pedefndos, y la geneacón po desplazamento de supefces o sóldos. El bado o desplazamento puede se utlzado tambén como una epesentacón de cetos objetos. Po ejemplo, cuando tasladamos una fgua plana a lo lago de un eje defnmos una foma tdmensonal po extusón (ve fgua...) y cuando gamos una supefce o línea en el espaco alededo de un eje defnmos un sóldo de evolucón.... MODELOS DE BARRIDO Tpos a) Extusón de una supefce (genea un volumen) Ex. paalela ecta Ex. paalela cuva Paalelepípedo Ex. de poyeccón: convegente o dvegente Dvegente Convegente Ex. Genealzada 6
23 x= (u,v) f x = f ( u,v ) b) Extusón de una línea Exsten los msmos tpos que en el caso anteo. La línea puede se abeta o ceada dependendo de lo cual se geneaá una supefce abeta o ceada (que envuelve un volumen). 7
24 Tema : Modelos de epesentacón de objetos 3D c) Rotacón de una línea sobe su eje Genea una supefce o un sóldo de evolucón dependendo de s la línea se cea sobe su eje (ve fgua...) Fgua...: Geneacón de un objeto po extusón y po otacón Vsualzacón El mecansmo de bado se suele emplea paa constu los objetos, peo a la hoa de vsualzalos lo habtual es pasa a oto tpo de epesentacón (paamétca o polgonal). Sn embago, tambén es posble hace un tazado de ayos con bastante facldad.... Dseño de Sóldos. Geometía Sólda Constuctva ( Constuctve Sold Geomety : CSG ) Este es uno de los paadgmas domnantes en el modelado de sóldos. Se tata de nstanca objetos pmtvos y combnalos medante opeacones booleanas ( unón, nteseccón, esta,...). La epesentacón de un objeto complejo es un ábol en el que fguan las opeacones y objetos pmtvos que defnen la foma del objeto (ve fgua...). De esta foma tan senclla se epesenta un objeto en la memoa o en una base de datos. En el ábol CSG se ncluyen dstntos tpos de nodos : Nodos de pmtvas : seán las hojas del ábol. Nodos de opeacones : unón, nteseccón y dfeenca (o negacón). Nodos de tansfomacón de coodenadas ( pueden ncluse en los nodos de pmtvas). La cuestón sguente es cómo vsualzalo. Exsten algotmos que sven paa vsualza dectamente el objeto a pat del ábol CSG. medante tazado de ayos o pocesamento de tpo áste. Otos métodos se basan en el paso de la epesentacón CSG a oto tpo (supefce o patcón espacal) que faclte el uso de algotmos de vsualzacón. Ve Tema 4: Modelos de Ilumnacón Global. Tazado de ayos 8
25 Fgua...: Constuccón de un sóldo medante un ábol CSG Como otos métodos de epesentacón del volumen, el sstema CSG esulta tambén adecuado paa añad a los objetos popedades físcas, ya que se está epesentando dectamente su volumen, y pemte ealza la compobacón de petenenca al objeto de los puntos en el espaco, como vamos a ve ahoa. El modelo CSG esulta muy adecuado cuando los objetos a epesenta se foman po combnacón de fomas báscas sencllas (paalelepípedos, esfeas, clndos, etc.), peo puede esulta muy nefcente paa oto tpo de objetos. C.S.G. como método de patcón espacal Los métodos de patcón espacal dstnguen ente aquellas egones del espaco que contenen puntos del objeto y aquellas que no lo contenen. La evaluacón de puntos esulta muy senclla en un ábol CSG po medo de un poceso ecusvo. El algotmo sguente muesta una posble mplementacón paa este algotmo ecusvo suponendo que la estuctua NODO tene una see de campos específcos como son, nodo_tpo que ndca el tpo de opeacón booleana, s es un nodo de opeacón, o el tpo de objeto en caso de que se tate de un nodo de pmtvas. Además contene dos campos adconales entenddos como dos punteos a cada uno de sus posbles hjos, que seán de nuevo una estuctua nodo. esta_dento (nodo, punto) { swtch (nodo_tpo) { caso UNION : esta_dento esta_dento (nodo.hjo) OR esta_dento(nodo.hjo) caso INTERSEC :esta_dento esta_dento(nodo.hjo) AND esta_dento(nodo.hjo) caso RESTA: esta_dento esta_dento (nodo.hjo) AND NO esta_dento(nodo.hjo)... caso CUBO :... esta_dento compoba_cubo(punto)..3. MODELOS DE PARTICIÓN ESPACIAL Aunque la geometía sólda constuctva nduce una dvsón del espaco, no puede hablase popamente de una patcón, ya que po defncón ésta estaía fomada po elementos que no tenen nteseccón ente sí. Defncón de patcón espacal: Conjunto de volúmenes { V, que pemte caacteza qué pate del espaco está dento del objeto y qué pate está fuea. Debe cumpl: 9
26 Tema : Modelos de epesentacón de objetos 3D V 3, j V V j = U {V = Espaco ( R ) Algunas de las utldades del empleo de este método de epesentacón son: Clasfcacón de puntos : paa dscen cuáles son los puntos del espaco ocupados po el objeto y cuáles no {V : V k Objeto, V j Objeto Infomacón sobe popedades de puntos en el espaco. Cada volumen de la patcón puede además contene nfomacón adconal sobe alguna popedad del objeto en esa pate del espaco (densdad, colo, pesón, composcón ). Clasfcacón de objetos dento de la escena : en este caso no se tataía de descb la foma de un objeto detemnado, sno de agupa los objetos de una escena compleja en pates paa optmza los métodos de vsualzacón. Las patcones pueden dvdse en no jeáqucas, cuando exste un únco conjunto de volúmenes que foman la patcón, y no tene elacones ntenas de nclusón, o ben patcones jeáquca y que consstán en sucesvas patcones de más y más detalle, cuyos volúmenes están ncludos en una patcón de nvel nfeo, y que se foma medante opeacones sucesvas de dvsón Patcones No Jeáqucas En este caso la patcón no se foma po opeacones sucesvas de dvsón, sno que se da dectamente todo el conjunto de volúmenes en los que se ha dvddo el espaco de patda. No exsten elacones de nclusón, ente los volúmenes. Descomposcón en celdas En este caso los volúmenes de la patcón son celdas contguas delmtadas po caas que pueden se planas o cuvas, y que pueden tene asocados datos escalaes o vectoales sobe la pate del objeto que epesentan. Las dfeentes celdas se encuentan pegadas ente sí sn ntesectase, y pueden tene dfeente foma y tamaño. Fecuentemente esta epesentacón se usa paa efectua el llamado análss po elementos fntos (FEA: Fnte Element Analyss), que smula efectos físcos en un objeto sóldo o fludo (cambos de tempeatua, pesón, velocdad de flujo, etc.) utlzando una descomposcón en celdas que nteactúan ente sí. celda Aunque se tata de una estuctua de datos senclla, tene el nconvenente de eque gan volumen de almacenamento. Ve Tema 3: Smulacón en Tempo Real y el Tema 4: Modelos de Ilumnacón Global. 3
VECTORES. En este apartado vamos a trabajar exclusivamente con los vectores en el espacio a los que vamos a llamar F 3.
 Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
CAPÍTULO III TRABAJO Y ENERGÍA
 TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO.
 Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
6 Sistemas Autoorganizativos
 6 Sstemas Autooganzatvos 6.1 Intoduccón Las edes de neuonas atfcales con apendzae no supevsado se han aplcado con éxto a poblemas de econocmento de patones y deteccón de señales. Estas edes constuyen clases
6 Sstemas Autooganzatvos 6.1 Intoduccón Las edes de neuonas atfcales con apendzae no supevsado se han aplcado con éxto a poblemas de econocmento de patones y deteccón de señales. Estas edes constuyen clases
Para caracterizar completamente una magnitud vectorial, como son la velocidad, aceleración, fuerza, etc, es preciso indicar tres cosas:
 VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
clasificación digital
 clasfcacón dgtal leccón 3 sumao Intoduccón. Conceptos estadístcos. Fase de entenamento. Fase de clasfcacón. Contol de caldad. La es un poceso de genealzacón temátca que, medante categozacón, convete la
clasfcacón dgtal leccón 3 sumao Intoduccón. Conceptos estadístcos. Fase de entenamento. Fase de clasfcacón. Contol de caldad. La es un poceso de genealzacón temátca que, medante categozacón, convete la
Tema 2. DINÁMICA DE SISTEMAS DE PARTÍCULAS
 Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ
 UNIVERSIDAD AUTÓNOMA DE MADRID ESCUELA POLITÉCNICA SUPERIOR AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ -PROYECTO FIN DE CARRERA- Jave Gacía Ocón Mayo de 27 AUTOCALIBRACIÓN Y SINCRONIZACIÓN
UNIVERSIDAD AUTÓNOMA DE MADRID ESCUELA POLITÉCNICA SUPERIOR AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ -PROYECTO FIN DE CARRERA- Jave Gacía Ocón Mayo de 27 AUTOCALIBRACIÓN Y SINCRONIZACIÓN
Parametrizando la epicicloide
 1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
CREACIÓN DE MAPAS DENSOS BASADOS EN APARIENCIA
 CREACIÓ DE MAPAS DESOS BASADOS E APARIECIA Loenzo Fenández, Lus Paá, Davd Úbeda, Mónca Ballesta, Jose M. Maín Depatamento de Ingeneía de Sstemas Industales. Unvesdad Mguel Henández. Avda. de la Unvesdad
CREACIÓ DE MAPAS DESOS BASADOS E APARIECIA Loenzo Fenández, Lus Paá, Davd Úbeda, Mónca Ballesta, Jose M. Maín Depatamento de Ingeneía de Sstemas Industales. Unvesdad Mguel Henández. Avda. de la Unvesdad
i:n i 0""E' D G-EOLOGIA 2i'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y
 ' 20078 :N 0""E' D G-EOLOGA 2'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y { t f 4 v s Se ha ealzado un estudo estuctual de la Hoja, aunque po dvesos motvos que vamos a analza no ha sdo posble obtene
' 20078 :N 0""E' D G-EOLOGA 2'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y { t f 4 v s Se ha ealzado un estudo estuctual de la Hoja, aunque po dvesos motvos que vamos a analza no ha sdo posble obtene
ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO
 Insttuto de Poesoes Atgas Físca Expemental 1 Guía páctca Nº ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO DISPOSITIVO EXPERIMENTAL El dspostvo expemental se muesta en la gua 1. Un egstado electónco o tme
Insttuto de Poesoes Atgas Físca Expemental 1 Guía páctca Nº ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO DISPOSITIVO EXPERIMENTAL El dspostvo expemental se muesta en la gua 1. Un egstado electónco o tme
* Introducción * Principio de mínima energía * Transformaciones de Legendre * Funciones (o potenciales) termodinámicas. Principios de mínimo.
 5. otencales emonámcos * Intouccón * ncpo e mínma enegía * ansomacones e Legene * Funcones (o potencales) temonámcas. ncpos e mínmo. * Enegía lbe (potencal) e Helmholtz lt * Entalpía. * Enegía lbe e Gbbs.
5. otencales emonámcos * Intouccón * ncpo e mínma enegía * ansomacones e Legene * Funcones (o potencales) temonámcas. ncpos e mínmo. * Enegía lbe (potencal) e Helmholtz lt * Entalpía. * Enegía lbe e Gbbs.
Mauricio Riera, S' IEEE Departamento de Potencia Instituto de Ingeniería Eléctrica Facultad de Ingeniería, UDEELAR Montevideo, Uruguay
 Poceedngs of 5º Encuento de Potenca, Instumentacón y Meddas, IEEE, Octobe 19-20, 1999, Montevdeo, Uuguay Contol De Flujo Vectoal Medante un Inveso de Coente Alejando Gómez Estudante de Ingeneía Insttuto
Poceedngs of 5º Encuento de Potenca, Instumentacón y Meddas, IEEE, Octobe 19-20, 1999, Montevdeo, Uuguay Contol De Flujo Vectoal Medante un Inveso de Coente Alejando Gómez Estudante de Ingeneía Insttuto
OPTIMIZACIÓN DE LOS GRÁFICOS DE CONTROL ESTADÍSTICO DE PROCESOS EWMA Y MEWMA MEDIANTE ALGORITMOS GENÉTICOS
 27 Congeso Naconal de Estadístca e Investgacón Opeatva Lleda, 8- de abl de 2003 OPTIMIZACIÓN DE LOS GRÁFICOS DE CONTROL ESTADÍSTICO DE PROCESOS EWMA Y MEWMA MEDIANTE ALGORITMOS GENÉTICOS J.C. Gacía-Díaz,
27 Congeso Naconal de Estadístca e Investgacón Opeatva Lleda, 8- de abl de 2003 OPTIMIZACIÓN DE LOS GRÁFICOS DE CONTROL ESTADÍSTICO DE PROCESOS EWMA Y MEWMA MEDIANTE ALGORITMOS GENÉTICOS J.C. Gacía-Díaz,
La Carga Eléctrica Puntual, es una partícula cuya masa se supone está concentrada en un punto, y en el mismo se concentra su carga eléctrica.
 LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
IES Fco Ayala de Granada Junio de 2014 (Modelo 1) Soluciones Germán-Jesús Rubio Luna. Opción A. Ejercicio 2 opción A, modelo_1 Junio 2014
 IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
SIMULACIÓN DE PRESIÓN NO ESTÁTICA EN YACIMIENTOS MEDIANTE SOLUCIONES FUNDAMENTALES
 FARAUTE Cens. y Tec., 3(): 4-5, 8. ISSN 698-748 Depósto Legal PP4CA67 SIMULACIÓN DE PRESIÓN NO ESTÁTICA EN YACIMIENTOS MEDIANTE SOLUCIONES FUNDAMENTALES Smulaton Of Tansent Resevo Pessue Based On Fundamental
FARAUTE Cens. y Tec., 3(): 4-5, 8. ISSN 698-748 Depósto Legal PP4CA67 SIMULACIÓN DE PRESIÓN NO ESTÁTICA EN YACIMIENTOS MEDIANTE SOLUCIONES FUNDAMENTALES Smulaton Of Tansent Resevo Pessue Based On Fundamental
11. COMPENSACIÓN DEL RADIO
 Capítlo 3: Desaollo del poama. COMPENSACIÓN DEL RADIO. Intodccón Los pntos tomados dectamente po palpacón sobe la spece de la peza en cestón no son pntos eales de dcha spece, ya qe el pnto ecodo tene las
Capítlo 3: Desaollo del poama. COMPENSACIÓN DEL RADIO. Intodccón Los pntos tomados dectamente po palpacón sobe la spece de la peza en cestón no son pntos eales de dcha spece, ya qe el pnto ecodo tene las
www.fisicaeingenieria.es Vectores y campos
 www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
Potencial eléctrico. Trabajo y energía potencial en el campo eléctrico. Potencial de una carga puntual: Principio de superposición
 Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
2.7 Cilindros, conos, esferas y pirámides
 UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
CUESTIONES Y PROBLEMAS DE CAMPO ELÉCTRICO. Ejercicio nº1 Cómo se manifiesta la propiedad de la materia denominada carga eléctrica?
 UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
UNIDAD I: CARGA Y CAMPO ELECTRICO
 UNN Facultad de Ingeneía Físca III UNIDAD I: CARGA Y CAMPO LCTRICO Caga eléctca. Induccón eléctca. Consevacón y cuantzacón de la caga. Conductoes y asladoes. Ley de Coulomb. Analogía ente la Ley de Coulomb
UNN Facultad de Ingeneía Físca III UNIDAD I: CARGA Y CAMPO LCTRICO Caga eléctca. Induccón eléctca. Consevacón y cuantzacón de la caga. Conductoes y asladoes. Ley de Coulomb. Analogía ente la Ley de Coulomb
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
CAPITULO 5. TRABAJO Y ENERGIA.
 CAPITULO 5. TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo
CAPITULO 5. TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
 /5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
CAMPO GRAVITATORIO FCA 10 ANDALUCÍA
 CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
Momento cuadrupolar eléctrico
 Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
MAGNITUDES VECTORIALES:
 Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
Profesor Francisco R. Villatoro 15 de Noviembre de 1999 SOLUCIONES. Soluciones de los ejercicios de la tercera relación de problemas.
 Tecea elacón de poblemas Técncas Numécas Pofeso Fancsco R. Vllatoo 5 de Novembe de 999 SOLUCIONES Solucones de los ejeccos de la tecea elacón de poblemas.. Se defne la taza de la matz cuadada A como la
Tecea elacón de poblemas Técncas Numécas Pofeso Fancsco R. Vllatoo 5 de Novembe de 999 SOLUCIONES Solucones de los ejeccos de la tecea elacón de poblemas.. Se defne la taza de la matz cuadada A como la
Tema 1: Estadística Descriptiva Unidimensional Unidad 2: Medidas de Posición, Dispersión y de Forma
 Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Parte 3: Electricidad y Magnetismo
 Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES
 PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
6.5 ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS
 6.. Gáficas de ectas usando m b Po ejemplo, paa gafica la ecta Maca el valo de b (odenada al oigen) sobe el eje, es deci el punto (0,). A pati de ese punto, como la pendiente es, se toma una unidad a la
6.. Gáficas de ectas usando m b Po ejemplo, paa gafica la ecta Maca el valo de b (odenada al oigen) sobe el eje, es deci el punto (0,). A pati de ese punto, como la pendiente es, se toma una unidad a la
+ + h. 8 v A. = = 2026 m s 1 3 1,3 10 6 m
 m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
DISEÑO Y MODIFICACION DE MOLDE INVERSO PARA PROTESIS MEDIANTE HERRAMIENTAS COMPUTACIONALES
 ONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA DISEÑO Y MODIFICACION DE MOLDE INVERSO ARA ROTESIS MEDIANTE HERRAMIENTAS COMUTACIONALES MARÍA CONSUELO DÍAZ WICHMANN Tess aa ota al gado de
ONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA DISEÑO Y MODIFICACION DE MOLDE INVERSO ARA ROTESIS MEDIANTE HERRAMIENTAS COMUTACIONALES MARÍA CONSUELO DÍAZ WICHMANN Tess aa ota al gado de
GEOMETRÍA. punto, la recta y el plano.
 MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
r V CINEMÁTICA DEL SÓLIDO RÍGIDO
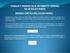 1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA
 PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
PRÁCTICA DE LABORATORIO Nº 7 ÓPTICA GEOMÉTRICA ExpeencaNº : Reflexón A- Ojetvo de la Expeenca Deduc la elacón ente el ángulo de ncdenca y el de eflexón. B- Fundamentos teócos Expuesto con detalle en el
X X 1. MECÁNICA GENERAL 1.4. FUNDAMENTOS DE ANÁLISIS TENSORIAL. 1.4.1. Introducción
 Fndmentos y eoís Físcs ES Aqtect. MECÁNCA GENERAL.4. FUNDAMENOS DE ANÁLSS ENSORAL.4.. ntodccón L myoí de ls mgntdes físcs y elcones mtemátcs ente ls msms qedn pefectmente defnds tbjndo con escles y ectoes.
Fndmentos y eoís Físcs ES Aqtect. MECÁNCA GENERAL.4. FUNDAMENOS DE ANÁLSS ENSORAL.4.. ntodccón L myoí de ls mgntdes físcs y elcones mtemátcs ente ls msms qedn pefectmente defnds tbjndo con escles y ectoes.
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Definir los conceptos de autoinducción, inducción mutua. Analizar circuitos con bobinas y resistencias. Definir energía magnética.
 Capítulo 8 nduccón electomagnétca 8.1 ntoduccón 8. Fenómenos de nduccón electomagnétca 8.3 Ley Faaday. Ley de Lenz 8.4 nduccón mutua. Autonduccón 8.5 Ccuto L 8.6 Enegía almacenada en una autonduccón. 8.7
Capítulo 8 nduccón electomagnétca 8.1 ntoduccón 8. Fenómenos de nduccón electomagnétca 8.3 Ley Faaday. Ley de Lenz 8.4 nduccón mutua. Autonduccón 8.5 Ccuto L 8.6 Enegía almacenada en una autonduccón. 8.7
Histogramas: Es un diagrama de barras pero los datos son siempre cuantitativos agrupados en clases o intervalos.
 ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
La fuerza gravitatoria entre dos masas viene dada por la ley de gravitación universal de Newton, cuya expresión vectorial es
 LGUNS CUESTIONES TEÓICS SOE LOS TEMS Y.. azone si las siuientes afimaciones son vedadeas o falsas a) El tabajo que ealiza una fueza consevativa sobe una patícula que se desplaza ente dos puntos, es meno
LGUNS CUESTIONES TEÓICS SOE LOS TEMS Y.. azone si las siuientes afimaciones son vedadeas o falsas a) El tabajo que ealiza una fueza consevativa sobe una patícula que se desplaza ente dos puntos, es meno
APÉNDICE 1 1. Sistemas de coordenadas
 APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas
Macroeconomía Abierta
 Macoeconomía Abeta of. chad oca Gaay hoca@yahoo.com http://chadoca.blogspot.com Unvesdad Naconal Mayo de an Macos ontfca Unvesdad Católca del eú Lma eú 009 chad oca. INDICE Capítulo. Cuentas Naconales
Macoeconomía Abeta of. chad oca Gaay hoca@yahoo.com http://chadoca.blogspot.com Unvesdad Naconal Mayo de an Macos ontfca Unvesdad Católca del eú Lma eú 009 chad oca. INDICE Capítulo. Cuentas Naconales
TRABAJO Y ENERGIA. 5.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE.
 TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
Bibliografía. Bibliografía. Fundamentos Físicos de la Ingeniería. Tema 3 Mc Graw Hill. - Tipler. "Física". Cap. 23. Reverté.
 Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Kronotek: Configuración de Red para VoIP
 Konotek: Configuación de Red paa VoIP Contenido 1. Intoducción... 2 2. Impotancia de la Configuación de Red... 2 3. Pasos Pevios: Cálculo del númeo de líneas de voz... 3 Pime paso: obtención del ancho
Konotek: Configuación de Red paa VoIP Contenido 1. Intoducción... 2 2. Impotancia de la Configuación de Red... 2 3. Pasos Pevios: Cálculo del númeo de líneas de voz... 3 Pime paso: obtención del ancho
Reflexión y Refracción
 eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
DEFINICIÓN DE INDICADORES
 DEFINICIÓN DE INDICADORES ÍNDICE 1. Notacón básca... 3 2. Indcadores de ntegracón: comerco total de benes... 4 2.1. Grado de apertura... 4 2.2. Grado de conexón... 4 2.3. Grado de conexón total... 5 2.4.
DEFINICIÓN DE INDICADORES ÍNDICE 1. Notacón básca... 3 2. Indcadores de ntegracón: comerco total de benes... 4 2.1. Grado de apertura... 4 2.2. Grado de conexón... 4 2.3. Grado de conexón total... 5 2.4.
Capítulo 4 CORRIENTE ELÉCTRICA
 Capítulo 4 CORRIENTE ELÉCTRICA 4. Coente eléctca y movmento de cagas. (5.) 4. Resstenca y Ley de Ohm. (5.) 4. La enegía en los ccutos eléctcos. (5.) 4.4 Combnacones de esstencas. (5.4) BIBLIOGRAFÍA. Conduccón
Capítulo 4 CORRIENTE ELÉCTRICA 4. Coente eléctca y movmento de cagas. (5.) 4. Resstenca y Ley de Ohm. (5.) 4. La enegía en los ccutos eléctcos. (5.) 4.4 Combnacones de esstencas. (5.4) BIBLIOGRAFÍA. Conduccón
Coordenadas Generales.
 oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
Solución a los ejercicios de vectores:
 Tema 0: Solución ejecicios de intoducción vectoes Solución a los ejecicios de vectoes: Nota : Estas soluciones pueden tene eoes eatas (es un ollo escibios las soluciones bonitas con el odenado), así que
Tema 0: Solución ejecicios de intoducción vectoes Solución a los ejecicios de vectoes: Nota : Estas soluciones pueden tene eoes eatas (es un ollo escibios las soluciones bonitas con el odenado), así que
CAMPO GRAVITATORIO FCA 05 ANDALUCÍA
 CAPO GRAVIAORIO FCA 05 ANDALUCÍA 1. Un satélite descibe una óbita cicula alededo de la iea. Conteste azonadaente a las siguientes peguntas: a) Qué tabajo ealiza la fueza de atacción hacia la iea a lo lago
CAPO GRAVIAORIO FCA 05 ANDALUCÍA 1. Un satélite descibe una óbita cicula alededo de la iea. Conteste azonadaente a las siguientes peguntas: a) Qué tabajo ealiza la fueza de atacción hacia la iea a lo lago
FI1002 Sistemas Newtonianos Judit Lisoni Sección 6
 F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
F00 Sstemas Newtonanos Ju Lson Seccón 6 Undad 4C Sóldos ígdos: Toque y momento angula Undad 4D Sóldos ígdos: Rodadua o oda sn esbala Contendos Undad 4C.Foma otaconal de la segunda ley de Newton: momento
CAMPO GRAVITATORIO FCA 04 ANDALUCÍA
 CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA. La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros.
 QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
Leyes de Kepler. Ley de Gravitación Universal
 Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
FIELD ORIENTED VECTOR CONTROL OF AN INDUCTION MOTOR WITH AN ADAPTABLE FUZZY LOGIC CONTROLLER APPLIED TO MACHINES TOOL
 ISSN: 692-7257 Volumen 2 Númeo 6 año - 25 FIELD ORIENTED VECTOR CONTROL OF AN INDUCTION MOTOR WITH AN ADAPTABLE FUZZY LOGIC CONTROLLER APPLIED TO MACHINES TOOL CONTROL VECTORIAL POR CAMPO ORIENTADO DE
ISSN: 692-7257 Volumen 2 Númeo 6 año - 25 FIELD ORIENTED VECTOR CONTROL OF AN INDUCTION MOTOR WITH AN ADAPTABLE FUZZY LOGIC CONTROLLER APPLIED TO MACHINES TOOL CONTROL VECTORIAL POR CAMPO ORIENTADO DE
Ejercicios resueltos
 Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Elementos de la geometría plana
 Elementos de la geometía plana Elementos de la geometía plana El punto Los elementos básicos de la geometía plana El punto es el elemento mínimo del plano. Los otos elementos geométicos están fomados po
Elementos de la geometía plana Elementos de la geometía plana El punto Los elementos básicos de la geometía plana El punto es el elemento mínimo del plano. Los otos elementos geométicos están fomados po
Índice INTRODUCCIÓN... 11 1.1 MARCO DE LA TESIS...11 1.1.1 ALCANCE DE LA TESIS...12 1.2 OBJETIVOS...13 1.3 ESTRUCTURA DE LA TESIS...
 Índce INTRODUCCIÓN.... MARCO DE LA TESIS..... ALCANCE DE LA TESIS.... OBJETIVOS...3.3 ESTRUCTURA DE LA TESIS...4 PROBLEMÁTICA DE LA INSPECCIÓN VISUAL AUTOMATIZADA... 7. LA INSPECCIÓN INDUSTRIAL...8.. TAXONOMÍA
Índce INTRODUCCIÓN.... MARCO DE LA TESIS..... ALCANCE DE LA TESIS.... OBJETIVOS...3.3 ESTRUCTURA DE LA TESIS...4 PROBLEMÁTICA DE LA INSPECCIÓN VISUAL AUTOMATIZADA... 7. LA INSPECCIÓN INDUSTRIAL...8.. TAXONOMÍA
1.1 Ejercicios Resueltos Tema 1
 .. EJERCICIOS RESUELTOS TEMA. Ejerccos Resueltos Tema Ejemplo: Probarque ++3+ + n 3 + 3 +3 3 + + n 3 n (n +) Ã n (n +)! - Para n es certa, tambén lo comprobamos para n, 3,... ( + ) + 3 (+) supuesto certa
.. EJERCICIOS RESUELTOS TEMA. Ejerccos Resueltos Tema Ejemplo: Probarque ++3+ + n 3 + 3 +3 3 + + n 3 n (n +) Ã n (n +)! - Para n es certa, tambén lo comprobamos para n, 3,... ( + ) + 3 (+) supuesto certa
UNIDAD 3: CONFIGURACIONES COMPUESTAS
 4/5/009 Undad 3 lectónca UNA 3: ONFGUAONS OMPUSTAS OJTO PATULA l alumn estudaá ls dfeentes tps de cnfguacnes y su análss 3. nexnes en cascada, cascde y alngtn 3. Pa etalmentad 3.3 cut MOS, de fuente de
4/5/009 Undad 3 lectónca UNA 3: ONFGUAONS OMPUSTAS OJTO PATULA l alumn estudaá ls dfeentes tps de cnfguacnes y su análss 3. nexnes en cascada, cascde y alngtn 3. Pa etalmentad 3.3 cut MOS, de fuente de
El Espacio Afín. I. E. S. Siete Colinas (Ceuta) Departamento de Matemáticas
 I. E. S. Siete Colinas (Ceuta) Depatamento de Matemáticas Matemáticas de º de Bachilleato El Espacio Afín Po Javie Caoquino CaZas Catedático de matemáticas del I.E.S. Siete Colinas Ceuta 005 El Espacio
I. E. S. Siete Colinas (Ceuta) Depatamento de Matemáticas Matemáticas de º de Bachilleato El Espacio Afín Po Javie Caoquino CaZas Catedático de matemáticas del I.E.S. Siete Colinas Ceuta 005 El Espacio
Análisis de la Envoltura de Datos Usos y Aplicaciones. Palabras Clave: Análisis de la Envoltura de Datos, DEA, Análisis de Eficiencia
 Títlo: Ato: Análss de la Envolta de Datos Usos y Aplcacones Davd Güemes Castoena, D.Sc. Fecha: Jlo del 2004 Palabas Clave: Análss de la Envolta de Datos, DEA, Análss de Efcenca Resmen Este atíclo se enfoca
Títlo: Ato: Análss de la Envolta de Datos Usos y Aplcacones Davd Güemes Castoena, D.Sc. Fecha: Jlo del 2004 Palabas Clave: Análss de la Envolta de Datos, DEA, Análss de Efcenca Resmen Este atíclo se enfoca
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
UNIVERSIDAD CARLOS III DE MADRID Ingeniería Informática Examen de Investigación Operativa 21 de enero de 2009
 UNIVERSIDAD CARLOS III DE MADRID Ingenería Informátca Examen de Investgacón Operatva 2 de enero de 2009 PROBLEMA. (3 puntos) En Murca, junto al río Segura, exsten tres plantas ndustrales: P, P2 y P3. Todas
UNIVERSIDAD CARLOS III DE MADRID Ingenería Informátca Examen de Investgacón Operatva 2 de enero de 2009 PROBLEMA. (3 puntos) En Murca, junto al río Segura, exsten tres plantas ndustrales: P, P2 y P3. Todas
Electricidad y Magnetismo Curso 2010/2011
 lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
lectcdad y Magnetsmo Cuso / lectostátca Defncón Los conductoes en electostátca. Campo de una caga puntual. Aplcacones de la Ley de Gauss Integales de supeposcón. Potencal electostátco Defncón e Intepetacón.
WICC 2012 202 ALGORITMO CON COBERTURA MUESTRAL EN DATA MINING APLICADO AL ESTUDIO DE LA BIODIVERSIDAD
 WICC 202 202 ALGORITMO CON COBERTURA MUETRAL EN DATA MINING APLICADO AL ETUDIO DE LA BIODIVERIDAD Cstóbal R. anta Maía Depatamento de Ingeneía UNLAM Macelo oa Facultad de Agonomía Cáteda de Mcobología
WICC 202 202 ALGORITMO CON COBERTURA MUETRAL EN DATA MINING APLICADO AL ETUDIO DE LA BIODIVERIDAD Cstóbal R. anta Maía Depatamento de Ingeneía UNLAM Macelo oa Facultad de Agonomía Cáteda de Mcobología
Comprensión conceptual y el uso de tecnología. César Cristóbal Escalante Verónica Vargas Alejo Universidad de Quintana Roo Julio 2013
 Compensión conceptual y el uso de tecnología Césa Cistóbal Escalante Veónica Vagas Alejo Univesidad de Quintana Roo Julio 203 Qué significa tene conocimiento de un concepto? Conoce su definición? Conoce
Compensión conceptual y el uso de tecnología Césa Cistóbal Escalante Veónica Vagas Alejo Univesidad de Quintana Roo Julio 203 Qué significa tene conocimiento de un concepto? Conoce su definición? Conoce
RECTAS Y ÁNGULOS. SEMIRRECTA.- Un punto de una recta la divide en dos semirrectas. La semirrecta tiene principio pero no tiene fin.
 RECTAS Y ÁNGULOS 5º de E. Pimaia RECTAS Y ÁNGULOS -TEMA 5 RECTA.- Es una sucesión infinita de puntos que tienen la misma diección. La ecta no tiene ni pincipio ni fin. Po dos puntos del plano pasa una
RECTAS Y ÁNGULOS 5º de E. Pimaia RECTAS Y ÁNGULOS -TEMA 5 RECTA.- Es una sucesión infinita de puntos que tienen la misma diección. La ecta no tiene ni pincipio ni fin. Po dos puntos del plano pasa una
MOVIMIENTO DE UNA PARTICULA EN EL CAMPO GRAVITACIONAL REAL
 MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
Smoothed Particle Hydrodynamics Animación Avanzada
 Smoothed Partcle Hydrodynamcs Anmacón Avanzada Iván Alduán Íñguez 03 de Abrl de 2014 Índce Métodos sn malla Smoothed partcle hydrodynamcs Aplcacón del método en fludos Búsqueda de vecnos Métodos sn malla
Smoothed Partcle Hydrodynamcs Anmacón Avanzada Iván Alduán Íñguez 03 de Abrl de 2014 Índce Métodos sn malla Smoothed partcle hydrodynamcs Aplcacón del método en fludos Búsqueda de vecnos Métodos sn malla
UNIVERSIDAD DE CHILE
 UNIVERSIDAD DE CHILE FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS ESCUELA DE POSTGRADO PLAN PARA ENFOCAR LAS CAMPAÑAS BANCARIAS UTILIZANDO DATAMINING MAURICIO PASCUAL DE LUCA VENEGAS MIEMBROS DE LA COMISIÓN
UNIVERSIDAD DE CHILE FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS ESCUELA DE POSTGRADO PLAN PARA ENFOCAR LAS CAMPAÑAS BANCARIAS UTILIZANDO DATAMINING MAURICIO PASCUAL DE LUCA VENEGAS MIEMBROS DE LA COMISIÓN
TEMA 4 Variables aleatorias discretas Esperanza y varianza
 Métodos Estadístcos para la Ingenería Curso007/08 Felpe Ramírez Ingenería Técnca Químca Industral TEMA 4 Varables aleatoras dscretas Esperanza y varanza La Probabldad es la verdadera guía de la vda. Ccerón
Métodos Estadístcos para la Ingenería Curso007/08 Felpe Ramírez Ingenería Técnca Químca Industral TEMA 4 Varables aleatoras dscretas Esperanza y varanza La Probabldad es la verdadera guía de la vda. Ccerón
Material realizado por J. David Moreno y María Gutiérrez. Asignatura: Economía Financiera
 Tema - MATEMÁTICAS FINANCIERAS Materal realzado por J. Davd Moreno y María Gutérrez Unversdad Carlos III de Madrd Asgnatura: Economía Fnancera Apuntes realzados por J. Davd Moreno y María Gutérrez Advertenca
Tema - MATEMÁTICAS FINANCIERAS Materal realzado por J. Davd Moreno y María Gutérrez Unversdad Carlos III de Madrd Asgnatura: Economía Fnancera Apuntes realzados por J. Davd Moreno y María Gutérrez Advertenca
CAPÍTULO V SISTEMAS DE PARTÍCULAS
 CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
CAPÍTULO V SISTEAS DE PARTÍCULAS 3 SISTEAS DE PARTÍCULAS La mayo pate de los objetos físcos no pueden po lo geneal tatase como patículas. En mecánca clásca, un objeto enddo se consdea como un sstema compuesto
UNIDAD Nº 2 VECTORES Y FUERZAS
 UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE FISICA FISICA EXPERIMENTAL PLAN ANUAL INGENIERIA FISICA 1 e SEMESTRE 2012 UNIDAD Nº 2 VECTORES Y FUERZAS OBJETIVOS Medi el módulo de un vecto fueza usando
UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE FISICA FISICA EXPERIMENTAL PLAN ANUAL INGENIERIA FISICA 1 e SEMESTRE 2012 UNIDAD Nº 2 VECTORES Y FUERZAS OBJETIVOS Medi el módulo de un vecto fueza usando
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO
 PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
Comparación entre distintos Criterios de decisión (VAN, TIR y PRI) Por: Pablo Lledó
 Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
Destilación Multicomponente
 Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Destlacón Multcomponente Componentes Clave: pueden se o no aquellos cuyas sepaacones se han especfcados Componente Clave Lgeo: Es el componente mas pesado ente los componentes lvanos Componente Clave Pesado:
Matemática Financiera Sistemas de Amortización de Deudas
 Matemátca Fnancera Sstemas de Amortzacón de Deudas 7 Qué aprendemos Sstema Francés: Descomposcón de la cuota. Amortzacones acumuladas. Cálculo del saldo. Evolucón. Representacón gráfca. Expresones recursvas
Matemátca Fnancera Sstemas de Amortzacón de Deudas 7 Qué aprendemos Sstema Francés: Descomposcón de la cuota. Amortzacones acumuladas. Cálculo del saldo. Evolucón. Representacón gráfca. Expresones recursvas
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
Universidad de Tarapacá Facultad de Ciencias Departamento de Física
 Univesidad de Taapacá Facultad de Ciencias Depatamento de Física Aplica el álgea de vectoes: Poducto escala Poducto vectoial Magnitudes físicas po su natualeza Escalaes Vectoiales Es un escala que se
Univesidad de Taapacá Facultad de Ciencias Depatamento de Física Aplica el álgea de vectoes: Poducto escala Poducto vectoial Magnitudes físicas po su natualeza Escalaes Vectoiales Es un escala que se
Trabajo y Energía Cinética
 Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
PROBLEMAS DE ELECTROESTÁTICA
 PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
2.2 TASA INTERNA DE RETORNO (TIR). Flujo de Caja Netos en el Tiempo
 Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
Evaluacón Económca de Proyectos de Inversón 1 ANTECEDENTES GENERALES. La evaluacón se podría defnr, smplemente, como el proceso en el cual se determna el mérto, valor o sgnfcanca de un proyecto. Este proceso
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
1. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA. Definición del álgebra geométrica del espacio-tiempo
 EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
Optica I. seni nsenr seni nsenr nsen(90 i) ncos i seni tg i n 1,5 i 56,30º cosi. nseni sen90 1 seni 0,66 i 41,30º.
 01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
01. Dos espejos planos están colocados pependculamente ente sí. Un ayo que se desplaza en un plano pependcula a ambos espejos es eflejado pmeo en uno y después en el oto espejo. Cuál es la deccón fnal
INDUCCIÓN ELECTROMAGNÉTCA Y ENERGÍA DEL CAMPO MAGNÉTICO
 NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
E 1 E 2 E 2 E 3 E 4 E 5 2E 4
 Problemas resueltos de Espacios Vectoriales: 1- Para cada uno de los conjuntos de vectores que se dan a continuación estudia si son linealmente independientes, sistema generador o base: a) (2, 1, 1, 1),
Problemas resueltos de Espacios Vectoriales: 1- Para cada uno de los conjuntos de vectores que se dan a continuación estudia si son linealmente independientes, sistema generador o base: a) (2, 1, 1, 1),
Campo eléctrico. Introducción a la Física Ambiental. Tema 7. Tema 7.- Campo eléctrico.
 Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
