CAPÍTULO 2. MARCO TEÓRICO
|
|
|
- Germán Iglesias Ortiz
- hace 6 años
- Vistas:
Transcripción
1 8 CÍULO. MRCO EÓRCO.. Robótc L obótc es l cenc o estudo de ls tecnologís báscs socds con los obots. El estudo nclue tnto l nvestgcón teóc como l plcd, dvdéndose en el dseño del obot, su mecánc, l plnecón contol de tecto, su pogmcón e ntelgenc tfcl [3]. Según l ntentonl Fedeton of Robotcs (FR) un obot es un máqun de mnpulcón utomátc epogmble funconl con tes o más ejes que pueden poscon oent mteles, pes, hements o dspostvos especles p l ejecucón de tbjos dvesos en ls dfeentes etps de l poduccón ndustl, se en un poscón fj o en movmento [9]. En est defncón l de clve es l epogmbldd, puesto que dfeenc de ls máquns odns que se dseñn con un gdo de lbetd que pemt llev cbo todos los movmentos pepogmdos mednte un sólo sstem ctudo (se éste un moto), un obot se dseñ ntenconlmente con más gdos de lbetd, p sí pogm el movmento desedo según ls necesddes cmbntes de l ndust pemt con ello un utomtcón fleble. Los obots pueden se clsfcdos de cuedo vos cteos: po l tecnologí de sus contoldoes ctudoes (eléctcos, mecáncos o neumátcos), po l estuctu cnemátc del mecnsmo, po l ntule de su movmento o po el númeo de gdos de lbetd que posee, ente otos: De cuedo l estuctu cnemátc del mecnsmo los obots se dvden en tes gndes ctegoís: obots seles, plelos e híbdos. Se dce que un obot es sel s su cden cnemátc es bet; es dec, sus elementos se encuentn conectdos uno uno en see. Un obot plelo, po el conto, posee un cden cnemátc ced en l cul se pueden dentfc vos los, como elementos en plelo de un ccuto eléctco. S se conectn mbos tpos de cden cnemátc en un obot se dce que éste es híbdo [3].
2 9 Fgu.. Robot sel (qued) obot plelo (deech) [] En cunto l ntule de su movmento los obots pueden clsfcse en plnes espcles, dependendo s su movmento se defne sobe plnos plelos o en dos dmensones, o en el espco tdmensonl. nto los obots seles, plelos e híbdos pueden se plnes o espcles [3]. L estuctu cnemátc del obot junto con l ntule de su movmento el númeo de gdos de lbetd que posee detemnn l complejdd del obot, tnto p su nálss como su contol, de hí su mpotnc. El obot p se útl debe se contoldo; es dec, debe pesent un compotmento code un espuest desed. ello es neceso pevmente conoce un modelo mtemátco del compotmento del sstem pt del cul gene ls ccones de contol equeds. El modelo mtemátco del obot mplc el nálss del mecnsmo: su estuctu, geometí mecánc, sí como l obtencón de ecucones que epesenten l dnámc del sstem con pecsón... eoí básc de mecnsmos Un sstem obótco está fomdo bse de mecnsmos po lo tnto es neceso un pevo conocmento de teoí básc de mecnsmos ntes de descb ls hements mtemátcs mecáncs necess p su nálss. Como pte de est teoí básc se hce un dstncón ente los témnos máqun, mecnsmo cden cnemátc, descbéndose demás los elementos que componen est últm: los eslbones ls tculcones. Fnlmente, se defne l movldd del mecnsmo; es dec, l detemncón de los gdos de lbetd.
3 0... Nocones de máquns, mecnsmos cdens cnemátcs Un cden cnemátc es un coleccón de eslbones tculcones conectdos [7]: Fgu.. Ejemplo de cden cnemátc [7] Un eslbón puede se defndo de mne más geneld como un cuepo o elemento ígdo con dos o más nodos o puntos de unón. Un eslbón puede se clsfcdo po el númeo de nodos que éste contene; es dec, su gdo de coneón. sí, un eslbón bno posee dos nodos, un teno posee tes, un cuteno posee cuto, etc. [7]: Fgu.3. Ejemplos de eslbones [0] Un tculcón, tmbén conocd como p cnemátco, es un coneón ente dos eslbones mednte sus nodos que pemte un movmento eltvo ente ellos [0]. uede se clsfcd po el númeo de gdos de lbetd que pemte, el cul es denotdo como f, o ben po su oden, es dec, el númeo de eslbones que conect [6]. sí msmo, ésts pueden se ctuds mednte un contoldo (o mnulmente), denomnándose ctvs, o ben, se dependentes de l poscón fues del mecnsmo, es dec, ttse de tculcones psvs [3]. Ls tculcones elementles poseen un tpo de movmento o gdo de lbetd pueden se otconles (de evolucón) o lneles (psmátcs): Un tculcón de evolucón (R) es como un bsg que pemte l otcón eltv ente dos elementos ígdos, es l más comúnmente empled. Un tculcón psmátc () pemte el movmento lnel eltvo (tslcón) ente dos elementos ígdos o eslbones.
4 Ls vbles de tculcón, denotds po θ p un tculcón de evolucón d p un psmátc, epesentn el movmento eltvo ente eslbones dcentes [6]. lgunos tpos de tculcones se muestn en l bl -: tculcón Dgm Símbolo dos de lbetd Revolucón (elementl) R smátc (elementl) Clíndc C Unvesl Esféc S 3 ln E 3 bl -. pos de tculcones comunes [] Cundo cd eslbón en un cden cnemátc se encuent conectdo oto culque po l menos dos dstntos cmnos, l cden cnemátc fom uno o más los cedos se denomn cden cnemátc ced. o el conto, s cd eslbón está conectdo oto culque po sólo un cmno, l cden cnemátc se denomn cden cnemátc bet [3]. En un cden cnemátc bet tods ls tculcones son ctvs, ments que en un cden cnemátc ced sólo lguns, sendo ls estntes psvs [3]. Cundo un cden cnemátc se fom tnto po cdens bets como ceds se tene un cden cnemátc híbd [3]. Un mecnsmo puede defnse como un cden cnemátc que posee un eslbón ígdmente undo un sstem de efeenc, denomndo bse o te [7]. En un mecnsmo, uno o más eslbones se sgnn como entd(s). Cundo estos se mueven todos los demás se moveán de cuedo ls lmtntes mpuests po ls tculcones. sí, un mecnsmo tnsmte movmentos, fue o toque tvés de sus eslbones [3]. Un mecnsmo puede se pln o espcl. En un mecnsmo pln el movmento de los eslbones está estngdo un plno o plnos plelos. En un mecnsmo espcl sus dvesos eslbones pueden movese en dfeentes deccones en el espco [7].
5 Un máqun es un coleccón de mecnsmos usd en conjunto con otos componentes eléctcos, hdáulcos o neumátcos p tnsfom enegí eten en tbjo útl. Un mecnsmo po sí msmo no es un máqun [3]. sí, un obot es un máqun contold fomd po l menos un mecnsmo, el cul consste de eslbones conectdos mednte tculcones en un cden cnemátc sopotd po un bse (l te del mecnsmo) []. Fgu.4. Mecnsmo de un obot [] Uno de los eslbones coesponde l elemento temnl, el cul mnpul objetos o el tes de montje []. El objetvo del contol es el de poscon oent dcho elemento temnl, pues es éste el encgdo de nteccon dectmente con el entono del obot [].... Movldd El númeo tpo de tculcones detemn los gdos de lbetd del mecnsmo, bevdos como gdl o DOF del nglés Degee of Feedom. Los gdos de lbetd se elconn dectmente con su movldd. En l descpcón del movmento de ls estuctus, o de los objetos, un gdo de lbetd es uno de los vos componentes otogonles que se pueden us p ccte completmente el movmento. o ejemplo, un objeto lbe en el espco tene ses gdos de lbetd dfeentes: Se puede tsld en tes deccones mutumente pependcules (posconmento) g en tono tes ejes, tmbén pependcules (oentcón). Culque movmento del objeto, no mpot que tn complejo se, se puede esolve en esos ses movmentos báscos.
6 3 En cunto un mecnsmo, un gdo de lbetd es cd uno de los movmentos báscos (gtoos de desplmento) ndependentes que un tculcón pemte efectu ente dos eslbones de un cden []. sí, el númeo de gdos de lbetd de l estuctu vene detemndo po los gdos de lbetd de cd un de ls tculcones. Es posble clcul los gdos de lbetd p un mecnsmo mednte síntess numéc: meo debe econocese que un cuepo ígdo lbe en el espco tene ses gdos de lbetd. Debeán conocese tes desplmentos lneles tes otcones ngules p detemn su poscón en el espco. De quí que N cuepos sn estccones de movmento tendán 6N gdos de lbetd. ho, con el fn de tnsfom estos cuepos en un mecnsmo, seá neceso fj uno de ellos en te conectlos po medo de tculcones. mbs opecones educen el númeo totl de gdos de lbetd. l fj uno de los eslbones se elmnn ses gdos de lbetd: de quí que l movldd se educ 6(N ). demás, cd tculcón educe l movldd en (6 f), en donde f es el númeo de gdos de lbetd de l tculcón en ptcul [4]. De est fom, con J tculcones en totl, l movldd M se tnsfom en: M 6 ( N ) J ( 6 f ) 6( N ) ( 6) ( f ) 6( N ) 6J ( f ) J J J f ( N J ) ( ) M 6 (-) J Dch epesón es váld sn modfccón lgun ún cundo vos eslbones sen fjdos te no sólo uno, ddo que es posble consde todos estos en conjunto como un solo eslbón [6]. En el cso de los mecnsmos plnes, dch ecucón debe modfcse p tom en cuent el hecho de que un cuepo ígdo tene tes, no ses, gdos de lbetd en el movmento sobe un solo plno [4]: M ( N J ) ( f ) J 3 (-) Es posble genel ls dos nteoes ecucones l obsev que ésts sólo dfeen en un coefcente, el cul vle 6 p l movldd en el espco 3 p l movldd en un plno. Es dec, que s dch constnte es desgnd el oden del sstem (λ), entonces:
7 4 M ( N J ) ( f ) J λ (-3) L nteo ecucón es conocd como el cteo de movldd de üble-kutbck [3], l cul es váld sempe cundo ls lmtntes mpuests po ls tculcones sen ndependentes uns de ots no nvolucen edundncs. Cundo un eslbón bno se encuent conectdo en el mecnsmo mednte un combncón de tculcones tles que no se posble l tnsmsón de fues o toques po consecuenc movmento sobe un eje, entonces se tene un gdo de lbetd psvo. Su estenc tmbén educe l movldd del mecnsmo po lo tnto l ecucón (-3) debe se modfcd: M ( N J ) ( f ) f p J λ (-4) Donde f p en est ecucón geneld es el númeo de gdos de lbetd psvos pesentes en el mecnsmo. En genel, los eslbones bnos con tculcones S-S, S-E E-E (ve bl -) ntoducen un gdo de lbetd psvo [3]. L nteo ecucón pemte demás ntepet l ntule del mecnsmo en cuestón pt los esultdos obtendos: S M > 0 l cden cnemátc posee movldd, l conto del cso en que M 0, en que l cden cnemátc no l posee [3]. Entonces l cden nld no es un mecnsmo, peo sí un estuctu, l cul puede encontse fod (estátcmente ndetemnd) p el cso en que M < 0 [7]. S M < λ, entonces el mecnsmo se encuent lmtdo, l no pode lcn tods ls poscones oentcones que el oden del sstem le pemte. S M λ se dce que el mecnsmo se encuent detemndo, es dec, no está lmtdo. Y s M > λ el mecnsmo se dce edundnte, es dec, puede lcn un poscón u oentcón específc de más de un mne [3], lo cul es ptculmente útl en pesenc de obstáculos.
8 5.3. Lenguje Mtemátco empledo en Robótc L mnpulcón obótc, po defncón, mplc que ls dfeentes ptes mecáncs hements se mueven tvés del espco mednte ceto mecnsmo, po lo que es neceso pode descb de fom convenente ls poscones oentcones de los objetos en el espco. defn mnpul mtemátcmente cntddes que epesentn poscón oentcón es neceso defn sstems de coodends en el espco tdmensonl estblece cets convencones p su epesentcón []. En cunto l loclcón espcl se efee, es posble hbl de descpcones, opedoes mpeos, los cules hcen uso de ls msms hements mtemátcs, peo plcds en dfeente conteto, o con sgnfcdo dstnto..3.. Descpcones Un descpcón es usd p especfc los tbutos de vos objetos con los que se elcon un sstem de mnpulcón, sendo estos ptes, hements o el msmo mnpuldo []. Es posble hbl de descpcones de poscones, oentcones loclcones en el espco ó mcos efeencles (tmbén llmdos fmes):.3... Descpcón de un poscón Un ve que un sstem de coodends es estblecdo, es posble coloc culque punto mednte vectoes de poscón 3, los cules debeán est etquetdos, ddo que fecuentemente se estbleceán vos sstems de coodends en dcón l sstem de coodends unvesl, es pecso desgn con especto qué sstem están defndos. ello se empleá l notcón usd po el uto Cg (efeenc []), que consste en coloc un supeíndce pevo l vecto, el cul ndque el sstem l que petenece. o ejemplo, el vecto de poscón petenece l sstem de coodends {} sus componentes pueden se pensdos como poeccones del vecto sobe los ejes otogonles defndos po los vectoes untos, j k (en un sstem de coodends ctesno), donde el subíndce ndc que estos defnen dcho sstem de coodends.
9 6 Ls componentes escles del vecto se denotn con l msm let del vecto l cul petenecen más pte un subíndce que ndc el eje coespondente cd componente según el sstem de coodends ndcdo: [ ] (-5) De est fom, l descpcón de un poscón en el espco se epes mednte un vecto de poscón 3 []. el cso de dos dmensones se consde que l componente sobe p es nul, pudendo consdese dcho vecto como [5]. Ot posble fom de epes ls coodends de un punto con especto un sstem de efeenc es mednte el empleo de coodends clíndcs o esfécs Descpcón de un oentcón Fecuentemente es neceso no sólo epesent un punto en el espco, sno tmbén descb l oentcón de un cuepo, p lo cul se fj un sstem de coodends éste eltvo l sstem de efeenc. Un mne de descb dcho sstem de coodends {} fjdo l objeto en cuestón, es escb sus vectoes untos otogonles en témnos del sstem de efeenc {} []: S, j k son los vectoes untos otogonles coespondentes l sstem {}, cundo efedos l sstem {} se denotn como, j k. S cd vecto unto en {} se defne en témnos de {} se tene que descb en funcón de su poeccón sobe cd uno de los ejes del sstem de efeenc. sí: [ ],,, [ ], j, j, j, [ k k ] k k,,, j, (-6) S cd uno de estos vectoes efedos son colocdos como column en un mt 33 se fom un mt de otcón, denotd como sstem {} efedo {}: R, cu notcón ndc que descbe un, j, k, R [ j k ], j, k, (-7), j, k,
10 7 De est fom, l descpcón de un oentcón en el espco de un cuepo se epes mednte un mt 33 cus columns coesponden 3 vectoes untos otogonles epesdos en témnos de oto conjunto de 3 vectoes de l msm ntule cd uno. Esto conllev un popedd mu mpotnte p est mt, es que l nves de culque mt otogonl es en sí un mt otogonl, l cul tmbén coesponde su tnspuest, cuo detemnnte vle ó -: R R R (-8) Es dec, que s ls columns de R coesponden los vectoes untos de {} esctos en témnos de {}, sus englones epesentn los vectoes untos de {} en témnos de {}. Entonces, un mt de otcón puede se ntepetd como un conjunto de tes vectoes column, o un conjunto de tes vectoes englón, como se puede pec en l ecucón (-9) []. Esto pemte fáclmente efe el sstem {} l {} o el {} l {}. R [ j k ] j (-9) k el cso bdmensonl se consden j, esultndo en un mt Descpcón de un loclcón o mco efeencl S se unen ls descpcones nteoes en un sol p descb l mne en que está colocdo un objeto en el espco especto un sstem de coodends de efeenc {}, tenendo dcho objeto un subsstem de coodends socdo él {}, es posble el dch descpcón pt de l poscón del ogen de dcho sstem con especto {} (tslcón), es dec, og su espectv oentcón ( R ) con el sstem de efeenc (otcón), es dec, que ést puede detemnse pt de 4 vectoes de tes elementos cd uno (3 p l otcón p l tslcón): { } { R, } (-0) og
11 8 Un cmbo en l poscón con oentcón constnte puede epesentse mednte l mt de otcón undd un vecto con los cmbos en ls coodends del punto, sí como un cmbo en l oentcón mntenendo constnte l poscón puede epesentse como un vecto de poscón de mgntud ceo un mt de otcón detemnd [5]. Un epesentcón gáfc de los mcos efeencles convenente p su vsulcón consste en tes flechs epesentndo los tes vectoes untos otogonles defnendo los pncples ejes de dcho mco efeencl, ls cules pten de un ogen. sí msmo, un flech epesentndo un vecto de poscón es dbujd desde el ogen de un mco efeencl l ogen de oto. El sentdo de dcho vecto ndc que un mco efeencl {} (puntdo po dcho vecto), po ejemplo, es eltvo {} (del cul pte el vecto), no vceves, tl como se ejemplfc en l fgu Fgu.5: Fgu.5. Vos mcos efeencles eltvos ente ellos [] Es dec, que un mco efeencl (llmdo fme de ho en delnte) puede se usdo como un sstem de coodends eltvo oto, epesentndo sí un genelcón de l descpcón de l poscón l oentcón []..3.. Mpeos l esolve poblems de obótc, genelmente se epes l msm cntdd en témnos de vos sstems de coodends de efeenc, es dec, se el un mpeo de mne que se cmbe l descpcón de un fme hech con especto un efeenc en ot descpcón hech con especto ot efeenc, de tl mne que sólo cmbe l descpcón no su poscón u oentcón en sí.
12 9 ello se ocupn ls msms hements mtemátcs usds p descb los fmes, se consden tes csos en los un poscón epesd en un fme {} debe se efed especto un fme {}:. Cundo el fme {} sólo se encuent tslddo mntene l msm oentcón que el {} es posble hce uso de l descpcón de poscón del ogen de {} dd po og : og (-). Cundo el ogen de mbos fmes concde sólo cmb l oentcón es posble hce uso de l descpcón de oentcón de {} especto {} dd po R : R (-) 3. Cundo n el ogen de mbos fmes concde n tmpoco su oentcón, entonces se usn tnto l descpcón de poscón como de oentcón en conjunto []: R og (-3).3... nsfomcones Homogénes L ecucón (-3) pemte tnsfom l descpcón de un vecto de poscón especfcd en un fme oto; sn embgo, es posble epes l tnsfomcón nteo usndo solmente un mt de tnsfomcón, denomnd como homogéne. ello es neceso ntoduc el concepto de coodends homogénes ls cules se epesentn en un espco de cuto dmensones, como se puede obsev en l ecucón (-4): [ ρ ρ ρ ρ] (-4) L cut coodend no puede se ceo se denomn fcto de esclmento, el cul p plccones de obótc tende se unto po convenenc. L mt de tnsfomcón homogéne es un mt 44 defnd como contnucón se muest:
13 0 ( 33) M ( 3) R og ( ) ( ) L M L (-5) γ 3 M ρ En dch mt se puede obsev que tmbén se encuent pesente el fcto de esclmento ntes mencondo ot submt denomnd como γ, l cul coesponde l tnsfomcón de pespectv que en plccones de obótc usulmente es nul: R M og L M L (-6) M Un specto que es neceso mencon de est mt es que no es otogonl, po ello su nves no se obtene de mne tn dect como en l mt de otcón: R M R og L M L (-7) M sí, l ecucón (-3) puede se esct en fom compct de l sguente mne, tomndo en cuent que tnto como deben se epesdos en coodends homogénes [3]: (-8).3.3. Opedoes Ls hements mtemátcs nteomente descts pueden se usds p descb l loclcón en el espco de un objeto en vos sstems de efeenc o ben p tnsfom dch loclcón en un sstem de efeenc, dependendo de l ntepetcón dd. sí, es posble tene opedoes de tslcón, de otcón de loclcón:. Un opedo de tslcón mueve un punto en el espco tsldándolo en l deccón de un vecto. Es posble defn dcho opedo mednte un mt de tnsfomcón homogéne.
14 . Un opedo de otcón mueve un punto en el espco mednte un otcón lededo de un detemndo eje, sendo los gumentos l deccón del eje el ángulo. El opedo puede defnse se mednte un mt de tnsfomcón homogéne o un de otcón. R K,θ (-9) 3. Un opedo de loclcón consde tnto tslcón como otcón p modfc l loclcón de un objeto en el espco se defne mednte un mt de tnsfomcón homogéne [] L oentcón en el espco Cundo se equee descb un oentcón culque especfc l mt de otcón de mne dect no es convenente. Ést contene nueve pámetos, peo ddo que l otcón en el espco es un movmento de tes gdos de lbetd, sólo tes pámetos ndependentes deben se sufcentes p especfc culque oentcón [3]. El teoem de Eule estblece que culque otcón o conjunto de otcones sucesvs p lcn un oentcón específc puede epesse sempe como un otcón lededo de un únco eje pncpl. S el conjunto de otcones componentes usds son fnts, es mpotnte mntene el oden en que se plcn. Esto es poque ls otcones fnts no obedecen l le de l sum vectol, po ello no pueden se clsfcds como cntddes vectoles, l conto de ls otcones nfntesmlmente pequeñs que sí pueden se clsfcds como vectoes [8]. sí, es posble especfc un detemnd oentcón mednte vs otcones sucesvs, emplendo mtces de otcón que se multplcn p fom un mt de otcón compuest. Sn embgo, l ttse de otcones fnts el oden sí mpot es neceso segu dos egls báscs:. Rotcones sempe elds especto un fme fjo esultn en un pemultplccón de mtces.. Rotcones especto l fme ctul, otdo, esultn en un postmultplccón de mtces [3].
15 enendo en mente ests egls se descben lguns epesentcones útles p especfc un detemnd oentcón:. Ángulos RY o lnceo (Roll), nclncón (tch) Desvcón (Yw). Sendo el objeto oentdo de mne que punte hc el eje X se defne su oentcón especto un sstem coodendo fjo con un clo sgnfcdo físco. meo se blnce mednte un otcón sobe el eje X con un ángulo γ, luego se ncln mednte un otcón sobe el eje Y con un ángulo β fnlmente se desví mednte un otcón sobe el eje Z con un ángulo. R p ( γ β, ) R Z, R Y,β R X, γ, (-0). Ángulos Eule Z-Y-X. Se bsn en otcones especto l sstem coodendo pevmente otdo gndo sobe Z, Y X los ángulos, β γ espectvmente. (, β, γ ) R Z, R Y,β R X, γ R (-) En este cso l mt de otcón esultnte esult se déntc l nteomente obtend, sn embgo l ntepetcón es dfeente. 3. Ángulos Eule Z-Y-Z. Se bsn tmbén en otcones especto l sstem coodendo pevmente otdo peo gndo sobe Z, Y Z los ángulos, β γ espectvmente []. (, β, γ ) R Z, R Y,β R Z, γ R (-) unque ls nteoes epesentcones son útles en muchos csos, veces es más convenente efectu otcones sobe un eje bto. Un mne de dev l mt de otcón p este últmo cso es ot el vecto unto que defn el eje bto hst concd con uno de los ejes de efeenc, po ejemplo Z. ello se ot pmeo un ángulo - sobe Z luego un ángulo -β sobe Y. Hecho esto se ot sobe Z el ángulo desedo θ p luego devolve el vecto unto su oentcón ognl (Fgu.6) [6]. R k,θ ( β, θ ) R Z, R Y,β R Z,θ R Y, β R Z,, (-3)
16 3 Fgu.6. Rotcón lededo de un eje bto [6].3.5. nsfomcones compuests Se suponen tes fmes: {}, {} {C}. El fme {C} es eltvo l {} {} lo es l {}. Un vecto C puede descbse en témnos de {} mednte tnsfomcones compuests: C (-4) C De hí que es posble obtene l descpcón dect de {C} eltvo {} mednte: C (-5) C Est de puede etendese p ntoduc el concepto de ecucones de tnsfomcón. En l Fgu.7 es posble epes el fme {D} eltvo {U} con un ecucón de tnsfomcón, como tl puede mnpulse p encont lgun tnsfomcón no conocd: U U C (-6) D U D C D U U C C D D (-7) Fgu.7. Esceno típco p plc ecucones de tnsfomcón
17 4.4. Mecánc de los obots L mecánc es l m de l físc que se ocup del estdo de eposo o movmento de cuepos sometdos l ccón de fues. L mecánc vectol de cuepos ígdos se dvde en dos áes: estátc dnámc. L estátc tene que ve con el equlbo de un cuepo que pemnece en eposo o que se mueve con velocdd constnte. L dnámc se ocup del movmento celedo de un cuepo se dvde en dos ptes: cnemátc cnétc [8]: L cnemátc se ocup de los spectos geométcos tempoles del movmento sn tende ls fues /o toques que lo poducen. Ente dchos spectos se encuentn l poscón, velocdd celecón. En un obot ls vbles de ls tculcones están elconds con l poscón oentcón del elemento temnl mednte ls lmtntes mpuests po ells msms. Ests elcones cnemátcs son el pncpl nteés en el estudo de l cnemátc de los obots. L cnétc se ocup de ls fues /o toques equedos p cus el movmento de un sstem de cuepos. En un obot el elemento temnl debe se gudo tvés de un detemnd tecto tomndo en cuent cets ccteístcs de movmento deseds. Un conjunto de funcones de fue /o toque deben se plcds en ls tculcones ctvs p poduc tl movmento. Sn embgo, ests elcones no sólo dependen de tbutos espcles tempoles, sno tmbén de l ms e nec de los eslbones, l cg sopotd po el obot ots fues etens, como po ejemplo l fccón [3]. sí, en obótc l mecánc es empled como hement p obtene el modelo mtemátco de un sstem en fom de ecucones que pemtn contollo. Sn embgo, según l temnologí mnejd en dcho ámbto el témno dnámc coesponde l concepto denotdo como cnétc en l mecánc vectol, según [7] [8]. De est fom, el modelo de un sstem consde tnto su cnemátc como su dnámc, po lo que de ho en delnte en este tbjo de tess se doptá dch temnologí. En ls seccones sguentes se evs l teoí coespondente tnto cnemátc como dnámc, sí como l mne en que se plcn los conceptos esultntes en el ámbto de l obótc.
18 5.5. Fundmentos de cnemátc entende l teoí coespondente es neceso pmeo nl l cnemátc pln de un cuepo ígdo luego etende el nálss p el cso de tes dmensones..5.. Cnemátc pln de un cuepo ígdo Cundo tods ls ptículs de un cuepo ígdo se mueven lo lgo de tectos que son equdstntes de un plno fjo, se dce que el cuepo epement movmento plno. H tes tpos de movmento plno:. slcón. Este tpo de movmento ocue s cd segmento de líne sobe un cuepo ígdo pemnece plelo su deccón ognl dunte el movmento. Cundo ls tectos de movmento p dos ptículs culesque del cuepo son lo lgo de línes ects equdstntes, el movmento se llm tslcón ectlíne. Sn embgo, s ls tectos de movmento psn po línes cuvs que son equdstntes, el movmento se llm tslcón cuvlíne. Fgu.8. slcón ectlíne ( l qued) tslcón cuvlíne ( l deech). Rotcón con especto un eje fjo. Cundo un cuepo ígdo g con especto un eje fjo, tods ls ptículs del cuepo, ecepto quells que se encuentn sobe el eje de otcón, se mueven po tectos ccules. Fgu.9. Rotcón especto un eje fjo 3. Movmento plno genel. Ocue cundo un cuepo ígdo epement un combncón de tslcón otcón. L tslcón ocue dento de un plno de efeenc, l otcón se efectú con especto un eje pependcul él [8].
19 6 Fgu.0. Movmento plno genel S vos cuepos ígdos o eslbones se conectn p fom un mecnsmo pln está un movmento eltvo ente ellos, meecendo éste un especl nteés cundo un nálss de movmento plno genel de cd cuepo ígdo en fom sld no es sufcente p descb el movmento slcón Se consde un cuepo que está sometdo un movmento de tslcón ectlíne o cuvlíne. Undo l cuepo se encuent un sstem coodendo que se tsld con éste tene su ogen en el punto C denomndo punto bse, como se obsev en l Fgu.: Fgu.. Movmento de tslcón de un cuepo ígdo L poscón del punto C oto punto culque sobe el cuepo se defne desde un mco de efeenc fjo mednte vectoes de poscón C. demás, se defne un vecto de poscón eltv /C, el cul ubc con especto C. sí: (-8) C /C L ón de cmbo con especto l tempo de epesent l velocdd del punto : d dc d/c v (-9)
20 7 Sn embgo, s se consde un cuepo ígdo, el vecto /C no cmb especto l sstem coodendo en tslcón, po lo que su ón de cmbo es ceo: v d C v v C (-30) omndo de nuevo l ón de cmbo con especto l tempo de l nteo ecucón se obtene un elcón sml p l celecón: dv dv C C (-3) Ls dos ecucones nteoes ndcn que todos los puntos en un cuepo ígdo sometdo tslcón ectlíne o cuvlíne se mueven con l msm velocdd celecón. Es po ello que p este cso bst con nl un punto sobe el cuepo, po ejemplo su cento de ms, p descb su movmento [8] Rotcón con especto un eje fjo Cundo un cuepo está gndo lededo de un eje fjo, culque punto ubcdo en el cuepo vj po un tecto ccul. estud este movmento es neceso pmeo nl el movmento ngul del cuepo lededo del eje: Fgu.. Movmento ngul de un cuepo en otcón con especto un eje fjo
21 8 Con efeenc l Fgu. en el nstnte mostdo l poscón ngul de está defnd po el ángulo θ, meddo ente un líne de efeenc fj. El cmbo en l poscón ngul, que puede se meddo como un dfeencl dθ (ls otcones nfntesmles sí pueden consdese vectoes, ve seccón.3.4), se llm desplmento ngul. Ddo que el movmento se el con especto un eje fjo, l deccón de dθ concde con el eje de otcón, sendo su sentdo detemndo con l egl de l mno deech. L ón de cmbo con especto l tempo de l poscón ngul se llm velocdd ngul, ments que l ón de cmbo con especto l tempo de dch velocdd ngul se llm celecón ngul : dθ, d (-3) Un ve nldo el movmento ngul del cuepo ígdo es posble nl el movmento de culque punto [8]. Fgu.3. Velocdd de sobe un cuepo ígdo en otcón especto un eje fjo L poscón de está defnd po el vecto de poscón, el cul se etende desde el eje de otcón de mne pependcul hst o po, el cul v desde culque punto del eje de otcón hst. L longtud de un co s se obtene mednte el poducto del do de otcón po el ncemento ngul: s θ (-33)
22 9 Un desplmento dfeencl de debdo l movmento ngul equvle l longtud de co ecod p un desplmento ngul dfeencl de mgntud dθ. El do de otcón de está defndo po el vecto de poscón, el cul es pependcul l eje de otcón. S se defne un vecto que v desde culque punto del eje de otcón hst (Fgu.3), entonces coespondeá l poeccón de sobe l pependcul l eje de otcón. sí, s el ángulo ente el eje de otcón es φ, l mgntud está elcond con l mgntud mednte l sguente elcón: snφ (-34) Entonces, p un desplmento dfeencl ds coespondente : ( φ) dθ ds sn (-35) L ón de cmbo con especto l tempo del nteo desplmento dfeencl coesponde l velocdd del punto : ds dθ v ( snφ ) ( snφ ) ( )( ) snφ (-36) L ecucón (-36) especfc l mgntud de v, vecto cu deccón es tngencl l tecto ccul en todo momento cuo sentdo concued con el de l otcón. Est ecucón puede se esct en fom vectol ecodndo l defncón de poducto cu tomndo en cuent el sentdo que debe tene v : v (-37) L ón de cmbo con especto l tempo de l velocdd de coesponde l celecón de este punto: dv d d (-38) Recodndo que l flech del vecto concde en todo momento con, l ón de cmbo con especto l tempo de este punto es l msm que l del vecto. sí: d v (-39)
23 30 Entonces, l ecucón (-38) qued epesd de l sguente mne: v ( ) (-40) L ecucón (-40) se encuent fomd po dos témnos o componentes (Fgu t.4). El pmeo coesponde l componente tngencl de l celecón epesent l ón de cmbo con especto l tempo de l mgntud de l velocdd. S l pde de ument, entonces est componente ctú en l msm deccón que v. El segundo n témno coesponde l componente noml de l celecón epesent l ón de cmbo con especto l tempo de l deccón de l velocdd. L deccón de este vecto sempe se dge hc O, el cento de l tecto ccul [8]. Es dec: (-4) t n Fgu.4. celecón de sobe un cuepo ígdo en otcón especto un eje fjo Movmento plno genel El movmento plno genel de un cuepo ígdo puede se descto como un combncón de tslcón otcón. Se consde que un sstem coodendo se tsld junto con el cuepo peo no g con él, tl como se obsev en l Fgu.5. Este sstem coodendo tene su ogen en el punto bse, el cul tene un movmento conocdo [8]:
24 3 Fgu.5. Movmento plno genel de un cuepo ígdo El vecto de poscón ubc el punto bse desde un mco de efeenc fjo el vecto de poscón eltv / stú el punto con especto l punto. sí, p : (-4) / detemn l elcón ente ls velocddes de los puntos es neceso dev l ecucón de poscón nteo con especto l tempo: d d d / (-43) v v v / El témno v coesponde l velocdd bsolut del punto bse, genelmente conocd poducd po l tslcón del cuepo ígdo. El témno v / coesponde l velocdd eltv de con especto, poducd po l otcón de dcho cuepo con velocdd ngul. sí, ecodndo l ecucón (-37): (-44) v / / Este témno se susttue en l ecucón (-43) p encont l elcón buscd: (-45) v v / elcon ls celecones de dos puntos sobe un cuepo ígdo sometdo movmento plno genel se dev l ecucón (-43) con especto l tempo: d dv dv v / (-46) /
25 3 El témno coesponde l celecón bsolut del punto bse po tslcón. El témno / coesponde l celecón eltv de con especto po otcón con velocdd ngul celecón ngul. sí, ecodndo l ecucón (-40): ( ) / / / (-47) Este témno se susttue en l ecucón (-46) p encont l elcón buscd: ( ) / / (-48) Est celecón eltv const de dos componentes: uno tngencl uno noml, de tl fom que l ecucón (-46) puede se eesct como: t n / / (-49) Movmento eltvo Cundo se nln mecnsmos plnes el movmento de los eslbones es de tslcón (ectlíne o cuvlíne), otcón con especto un eje fjo o movmento plno genel, sendo posble nl cd eslbón po sepdo s es que no este deslmento en ls coneones (Fgu.6). Fgu.6. Movmentos en un mecnsmo pln cundo no este deslmento en ls coneones [8] Un nálss más genel consde que se pesent dcho deslmento sendo neceso en ese cso no sólo nl el movmento de un punto sobe un cuepo ígdo, sno dos puntos concdentes que se encuentn en un mecnsmo peo no están sobe el msmo cuepo (Fgu.7).
26 33 Fgu.7. Mecnsmo en el cul este deslmento en ls coneones [8] Se consde un cuepo ígdo en movmento plno genel. Undo éste se encuent un sstem coodendo que se tsld ot junto con él tene su ogen en el punto bse. Oto cuepo se encuent conectdo él mednte un coneón que se desl, sendo el punto común donde concden el cuepo ígdo l coneón, tl como se obsev en l Fgu.8 [8]: Fgu.8. Movmento eltvo ente dos cuepos ígdos l gul que p el movmento plno genel: (-50) / L velocdd del punto se detemn tomndo l devd con especto l tempo de l ecucón (-50): d d d / d / v v (-5)
27 34 El últmo témno de l ecucón (-5) epesent l ón de cmbo con especto l tempo del vecto de poscón eltv de con especto vst desde el mco de efeenc fjo. Este vecto pesent movmento debdo l otcón del cuepo en movmento plno genel l deslmento ocudo en l coneón. sí, s se evlú este témno po sepdo: d d / d d ( j ) /, dj /, d / d / /,, /, /, j (-5) Los dos témnos dento del segundo péntess de l ecucón (-5) epesentn l velocdd eltv v,el del punto con especto l sstem coodendo undo l cuepo ígdo. Los dos témnos dento del pme péntess epesentn l ón nstntáne de cmbo con especto l tempo de los vectoes untos j con especto l mco de efeenc fjo. Estos vectoes se encuentn en otcón, po lo que ecodndo ls ecucones (-37) (-39), estos se pueden epes como: d dj, j (-53) sí, tomndo en cuent estos esultdos l ecucón (-5) puede se epesd de l sguente mne: d / d / ( j ) v, el /, /, ( j ) v, el d / / /, /, v,el (-54) Susttuendo en l ecucón (-5) se obtene l elcón de velocdd buscd: v v / v (-55),el Est velocdd const de tes componentes: el pmeo de ellos epesent l tslcón del cuepo ígdo en movmento plno genel, el segundo l espectv otcón el teceo l velocdd eltv del punto con especto este cuepo.
28 35 O vsto de ot fom, los dos pmeos témnos epesentn l velocdd del punto po pte del movmento plno genel como s se fj l cuepo ígdo (velocdd de tnspote v,t del punto ), ments que el últmo témno epesent l velocdd eltv v,el del punto po pte del deslmento de l coneón. sí: v v v (-56),tns,el obtene un epesón sml p l celecón se dev l ecucón (-55) con especto l tempo: ( ) dv d d dv v /, d( ) dv /, el el (-57) El penúltmo témno de l ecucón (-57) puede se evludo ecodndo el esultdo obtendo en l ecucón (-54): d ( ) d d / / / ( ) d d / / ( ) / / ( v ) /,el ( / ) v, el (-58) De gul fom tmbén se evlú el últmo témno de l msm ecucón: dv,el v dv,el d ( v, el, v, el, j ) d dj dv, el, dv, el, v, el,, el, j (-59) Los dos témnos dento del segundo péntess de l ecucón (-59) epesentn l celecón eltv,el del punto con especto l sstem coodendo undo l cuepo en movmento plno genel. Los dos témnos dento del pme péntess pueden evluse ecodndo ls epesones de l ecucón (-53), de tl mne que l susttu en l ecucón (-59):
29 36 dv,el dv,el ( v, el, v, el, j ), el ( v, el, v, el, j ), el dv,el v,el,el (-60) Susttuendo ls ecucones (-58) (-60) en l (-57) se obtene l elcón buscd: ( ( ) v ) ( v ) / /,el,el ( / ),el v, el / (-6),el Est celecón const de cnco componentes: el pmeo de ellos epesent l tslcón del cuepo ígdo en movmento plno genel, los dos sguentes l espectv otcón pues coesponden ls espectvs componentes tngencl noml, el cuto epesent l celecón eltv del punto con especto este cuepo el qunto coesponde l celecón de Cools, l cul pece cundo se pesentn mcos de efeenc ottoos. O vsto de ot fom, los tes pmeos témnos epesentn l celecón del punto po pte del movmento plno genel como s se fj l cuepo ígdo (celecón de tnspote,t del punto ), ments que los dos últmos témnos epesentn l celecón eltv,el del punto po pte del deslmento de l coneón l celecón de cools,c del msmo punto, espectvmente. sí: (-6),tns,el,c.5.. Cnemátc tdmensonl de un cuepo ígdo El nálss de un cuepo ígdo sometdo movmento plno puede etendese l cso en que se pesent movmento tdmensonl, en el cul de mne semejnte esten tes tpos de movmento: tslcón, otcón con especto un punto fjo movmento genel. El pmeo se puede etende del cso pln sn consdecones dconles, no sí los otos dos. sí msmo, s vos cuepos ígdos se conectn p fom un mecnsmo espcl, tmbén se podá plc un nálss de movmento eltvo.
30 Rotcón con especto un punto fjo Cundo un cuepo ígdo g con especto un punto fjo O, l dstnc desde dcho punto hst oto culque es l msm p culque poscón del cuepo; es dec, su tecto de movmento se encuent sobe l supefce de un esfe de do [8]. quí es neceso dstngu ente otcones fnts e nfntesmles. Ls pmes ocuen s el cuepo ígdo ot sobe vos ejes, uno uno, ments que ls segunds se dn cundo l otcón sobe estos se el de mne smultáne. l como se menconó en l seccón.3.4, ls otcones fnts no pueden se clsfcds como vectoes pues no obedecen l le conmuttv de l sum, ments que ls nfntesmles sí lo hcen, pudendo sí defnse un eje nstntáneo de otcón lededo del cul el cuepo pec g en un detemndo momento, pues cmbá de deccón constntemente. sí, l velocdd ngul Ω del cuepo se defne po l ón de cmbo del desplmento ngul con especto l tempo, sendo el vecto esultnte colnel con el eje nstntáneo de otcón. L celecón ngul ε se detemn pt de l devd con especto l tempo de dch velocdd ngul, peo su vecto no es colnel con el de l velocdd ngul, pues epesent tnto el cmbo de mgntud como de deccón de l velocdd ngul [8]. Entonces: dθ Ω, dω ε (-63) Etendendo los esultdos obtendos p el cso pln pt de ls ecucones (-37), (-40) (-4) [8]: v Ω (-64) ( Ω ) t n ε Ω (-65).5... Movmento genel El movmento genel de un cuepo ígdo puede se descto como un combncón de tslcón otcón, peo en tes dmensones. Etendendo los esultdos obtendos p el cso pln pt de ls ecucones (-4), (-43), (-45), (-48) (-49) [8]:
31 38 / (-66) v v v / v Ω / (-67) ( Ω ) t n / / ε / Ω / (-68) Movmento eltvo Cundo se nln mecnsmos espcles sugen stucones smles ls del movmento pln, equéndose tmbén un nálss más genel que consdee deslmento en ls coneones. Etendendo los esultdos obtendos p el cso pln pt de ls ecucones (-50), (-55), (-56), (-6) (-6) [8]: / (-69) v v Ω / v v v (-70),el,tns,el / ( Ω ),el Ω v,el,tns,el, c ε Ω / (-7).6. Cnemátc plcd l ámbto de l obótc En obótc los cuepos estuddos son pecsmente los obots sendo l cnemátc empled p nl su movmento con especto un sstem de efeenc, específcmente ls elcones ente ls vbles de loclcón de su elemento temnl el vlo de ls vbles tcules ctvs [9]. El nálss cnemátco entonces consde tnto ls elcones de posconmento oentcón como ls de velocdd celecón..6.. nálss de posconmento oentcón Como pte de este nálss se descben contnucón los denomndos poblems cnemátcos nveso decto, sí como ls esttegs más popules empleds en l esolucón de estos poblems. Fnlmente, se defne el concepto de espco de tbjo pt de ls lmtntes geométcs mecáncs del mecnsmo.
32 oblems cnemátcos nveso decto El nálss de posconmento oentcón busc tene conocmento en todo momento de l loclcón del elemento temnl del obot puede ttse en dos sentdos opuestos, sepándose en los poblems cnemátcos nveso decto: El poblem cnemátco nveso consste en detemn l confgucón que debe dopt el obot (el vlo de sus vbles tcules ctvs) dds un poscón oentcón del elemento temnl detemnds. El poblem cnemátco decto consste en detemn l poscón oentcón del elemento temnl del obot, con especto un sstem de coodends de efeenc, conocds ls vbles tcules ctvs l geometí del obot [9] Esttegs de esolucón mbos tpos de poblems pueden se esueltos mednte vs esttegs, sendo ls más popules l epesentcón de Denvt-Htenbeg (D-H) l solucón geométc []: L epesentcón de Denvt-Htenbeg epesent un método sstemátco p l coloccón de fmes en cd eslbón del obot de tl fom que l mt de tnsfomcón homogéne ente ellos depend de cuto pámetos (,, d, θ ) o se el poducto de cuto tnsfomcones báscs: El fme coespondente l eslbón se coloc de l sguente fom (ve Fgu.9): el eje concde con el eje de l tculcón que conect con el eslbón, el eje se tende colnel l líne más cot que conecte los ejes - cundo no son coplnes, o con ogen sobe l tculcón cundo mbos ejes sí lo son. El eje se detemn con l egl de l mno deech. Los cuto pámetos se defnen de l sguente mne:. El pámeto coesponde l dstnc de tslcón lo lgo del eje desde el eje - hst el ogen del sstem -ésmo. Repesent l longtud del eslbón.. El pámeto coesponde l ángulo de otcón sobe el eje ; es dec, el ángulo estente ente los ejes -. Repesent l tosón del eslbón. 3. El pámeto d coesponde l dstnc de tslcón lo lgo del eje - desde el ogen del sstem de coodends (-)-ésmo hst el eje. Se tt de l vble tcul p l tculcón s ést es psmátc.
33 40 4. El pámeto θ coesponde l ángulo de otcón sobe el eje - ; es dec, el ángulo estente ente los ejes -. Se tt de l vble tcul p l tculcón s ést es otconl [6]. Fgu.9. Convencón de pámetos p l epesentcón D-H [9] sí, l mt de tnsfomcón coespondente qued defnd como [9]: (, θ ) ( 0,0, d ) (,0,0) (, ) (-7) El enfoque geométco se bs en l descomposcón de l geometí espcl del obot en vos poblems geométcos plnos, p los cules se usn hements geométcs tgonométcs p encont el vlo de ls vbles tcules o l poscón oentcón del elemento temnl. En lo que se espect los obots seles el poblem cnemátco decto comúnmente se esuelve de mne sstemátc mednte l epesentcón D-H; sn embgo, dd l estenc de múltples solucones l esolve el poblem cnemátco nveso, un enfoque geométco es más sencllo de plc en dcho cso []. los obots plelos l estenc de vos los cedos dfcultí l plccón de l epesentcón D-H. demás, l estenc de tculcones con más de un gdl (ls tculcones esfécs como cso típco) mposblt us est epesentcón tl como está defnd, pues más de cuto pámetos po eslbón seín necesos p defn completmente un detemnd confgucón del obot. Es po ello que p este tpo de obots se pefee el enfoque geométco, defnéndose ecucones vectoles p cd bo en donde ls vbles tcules psvs puedn se elmnds del nálss [3].
34 Espco de tbjo: lmtntes geométcs mecáncs sí msmo, tmbén como pte del nálss de posconmento oentcón, es neceso hce énfss en que no tod poscón u oentcón puede se lcnd po el elemento temnl dds ls lmtntes geométcs mecáncs del mecnsmo. Ls pmes son mpuests po l movldd del mecnsmo, ls dmensones de los eslbones l ntule de ls tculcones consdeds ésts como deles. Ls últms esultn de l constuccón o mplementcón el de dchs tculcones; es dec, los lmtes de go desplmento (estccones) popos de ells. mbos tpos de lmtntes defnen l on o espco de tbjo del obot [3]. Dcho espco de tbjo qued defndo po el volumen totl bdo po el elemento temnl cundo el mnpuldo ejecut todos los posbles movmentos [6], o dcho de ot fom, el volumen encedo po ls supefces que detemnn los puntos los que ccede el mnpuldo con su estuctu totlmente etendd o totlmente plegd [5]: Fgu.0. Zon de bjo lustd p un ceto mnpuldo [] L on de tbjo se subdvde en áes dfeencds ente sí: el áe de tbjo ccesble el áe de tbjo dest. El áe de tbjo ccesble qued defnd po el conjunto enteo de puntos lcnbles po el mnpuldo en l menos un oentcón, ments que el áe de tbjo dest consste en los puntos que el mnpuldo puede lcn con culque oentcón del elemento temnl [6]. No todos los puntos del espco de tbjo pesentn l msm ccesbldd. L supefce que delmt el volumen totl del espco de tbjo epesent l ccesbldd mínm, l que sólo puede ccedese con un únc oentcón. Los puntos de ccesbldd mám, s esten, pueden encontse en el nteo del volumen básco. En estos puntos el elemento temnl puede ccede en culque deccón [].
35 4.6.. nálss de velocddes Mednte el nálss de velocddes es posble no sólo conoce l loclcón del elemento temnl del obot, sno tmbén gene tectos que éste ls eco un cet velocdd. Como pte de este nálss se modfcn l elcón cnemátc de velocdd obtend en l seccón.5..3 p consde l estenc de múltples mcos de efeenc. sí msmo se ntoduce un mt denomnd como Jcobn, l cul esult fundmentl en obótc, se dev el concepto de snguldd Relcón cnemátc de velocdd L ecucón (-70) especfc l elcón de velocdd estente cundo h movmento eltvo, sendo ést devd en su totldd especto un solo mco de efeenc. En obótc es común el emple múltples mcos de efeenc, uno po eslbón, sugendo sí l necesdd de modfc dch ecucón, l cul p efectos de compcón se eescbe en l ecucón (-73): v v Ω / v v v (-73),el,tns,el omndo en cuent el conteto de est ecucón se defne un vecto que v desde el ogen de un fme {} concdente con el punto hst el punto, l ve es especfcdo en este fme, denotándose entonces como. El punto se mueve con un velocdd eltv l fme {} l gul que el vecto que lo poscon, sendo est velocdd especfcd tmbén en dcho fme, po lo que se denot como v. demás, el fme {} ot con especto l fme {-} con un velocdd ngul epesd como - Ω se tsld con especto él, sendo l velocdd lnel del ogen de {} especfcd con especto {-} denotd como - v og. Se dese entonces especfc l velocdd de con especto l fme {-}, sendo coespondente ente los fmes {} e {-}. De est fom, l ecucón (-73) se epes como: v R l mt de otcón que el el mpeo v og Ω R R v (-74)
36 43 L mpotnc en obótc de l ecucón (-74) dc en que pemte clcul l popgcón de velocdd eslbón po eslbón cundo ls vbles tcules sus velocddes ( - Ω v ) se especfcn con especto l fme de cd eslbón Jcobns El nálss de velocddes tmbén puede ttse en dos sentdos opuestos: nveso decto [3], sendo mu útl l devcón de un mt denomnd como Jcobn. Mtemátcmente l mt Jcobn coesponde l fom multdmensonl de l devd. Suponendo un sstem de ecucones epesentdo de fom mtcl, es posble clcul los dfeencles con especto l tempo p los elementos de Y en funcón de los dfeencles con especto l tempo p los elementos de X: ( X) Y F (-75) dy F dx (-76) X El pme témno del ldo deecho de l ecucón (-76) coesponde un mt de devds pcles llmd Jcobn, J, po lo que: d Y dx J( X) (-77) En obótc, l Jcobn elcon ls velocddes lneles ngules de dos eslbones del obot. sí, es posble elcon l velocdd lnel ngul del elemento temnl, v Ω, l devd con especto l tempo de ls vbles tcules, q []: v J Ω dq ( q) (-78) Sngulddes L ecucón (-78) pemte el el nálss de velocddes decto p el cul sbendo l vcón de ls vbles tcules es posble detemn l velocdd lnel ngul del elemento temnl. el nálss de velocddes nveso es neceso nvet l mt Jcobn:
37 44 d v Ω ( q) q J (-79) L nves de un mt es equvlente l tnspuest de su mt de cofctoes dvdd ente su detemnnte. Entonces, s p un detemnd confgucón del obot el detemnnte de l Jcobn es ceo l mt se dce sngul su nves no puede se clculd. En estos csos el obot se encuent en un confgucón sngul [3]. Cundo un obot sel se encuent en un condcón sngul pede movldd. Un obot plelo, l conto, puede pedel o gnl debdo l estenc de tculcones psvs. Un obot, sel o plelo, pede movldd en ls fontes del espco de tbjo en donde po más que umente l pde de cmbo en ls vbles tcules el elemento temnl no puede movese en cet deccón. Sn embgo, tmbén es posble pede movldd dento del popo espco de tbjo, debdo confgucones especles que dependen de l estuctu geométc mecánc del mecnsmo []. Un obot plelo puede gn movldd dento del espco de tbjo se mnfest cundo el elemento temnl puede movese en cet deccón ún s ls vbles tcules ctvs se mntenen sn cmbo lguno [3] nálss de celecones Mednte el nálss de celecones es posble elcon l cnemátc l dnámc del obot, sí log que el elemento temnl ejecute ls tectos deseds con l velocdd equed en cd momento. ello se equee modfc l elcón cnemátc de celecón obtend en l seccón.5..3 especfcd en l ecucón (-7) p consde l estenc de múltples mcos de efeenc. Reescbendo l ecucón (-7) en l ecucón (-80): / ( Ω / ),el Ω v,el,tns,el, c ε Ω (-80) Se tom en cuent l notcón empled p l elcón de velocdd (seccón.6..) se etende p el cso de l celecón, quedndo l epesón buscd como: ( Ω R ) R Ω R v og ε R Ω (-8)
38 45.7. Fundmentos de dnámc Ments l cnemátc se ocup del nálss del movmento, l dnámc se encg de l elcón ente éste ls fues que lo poducen. bod este tem pmeo se ntoduce el concepto de fue se descben ls fues más comunes que se pesentn en el nálss dnámco. sí msmo, tmbén se ntoduce el concepto de momento. Luego se nl un de ls popeddes de todo cuepo que fect dectmente su movmento: su ms. Esto p bod l ecucón de movmento luego etende dcho concepto cuepos ígdos. Fnlmente, se ntoducen los conceptos de tbjo enegí..7.. Fue Un fue epesent l ccón de un ptícul o cuepo sobe oto. Ést puede se ejecd debdo l contcto ente ellos o dstnc, como es el cso de l fue de gvedd ls fues electomgnétcs. Un fue es un cntdd vectol, ccted po un punto de plccón, mgntud, deccón sentdo. Ls fues que ctún sobe un cuepo pueden se clsfcds en dos gupos: Fues etens. Repesentn l ccón de ots ptículs o cuepos sobe l ptícul o cuepo nldo. Son entemente esponsbles po su compotmento; es dec, su condcón de equlbo o movmento. Fues ntens. Son ls que mntenen unds ls ptículs de un cuepo [7]. lguns de ls fues etens más comunes que se pesentn en el nálss dnámco son ls eccones en ls coneones ente los cuepos, l fue de gvedd l fccón Fue de gvedd: peso Dos ptículs culesque pesentn un tccón mutu cu fue, según l le de gvtcón de Newton, está dd po l sguente epesón mtemátc: mm F (-8) Donde F epesent l fue de tccón ente dos ptículs de ms m m sepds un dstnc. El témno epesent l constnte unvesl de gvtcón:
39 m kg s (-83) Sn embgo, en el cso de un ptícul ubcd en o cec de l supefce de l e, l únc fue gvtto que tene mgntud consdeble es quell estente ente l e l ptícul, denomnándose fue de gvedd en este cso. est fue comúnmente se le llm peso (W). El peso de un cuepo no es un cntdd bsolut que es meddo en un cmpo gvttoo, po consguente su mgntud depende de dónde se efectúe l medcón. No obstnte, p l moí de los cálculos se consde un ubccón estánd. sí, conocendo l ms de l te (m ) su do ( ), se ntoduce l constnte g denomnd como celecón de l gvedd po compcón de unddes: m g g 9.8m s (-84) sí, denomnndo l ms de l ptícul de nteés como m, su peso se obtene [8]: W mg (-85).7... Fccón Cundo dos supefces entn en contcto sempe pecen fues tngencles o de fccón que se oponen l deslmento ente mbs supefces. L mgntud de ests fues depende báscmente de l ugosdd de ls supefces en cuestón pues nvel mcoscópco nngun supefce es ls, pudendo vese como fomds po un see de dentes que se ntecln. sí, cundo un supefce se desl sobe l ot pecen fues de contcto que se oponen dcho deslmento. Este hecho se pesent gáfcmente en l Fgu. en l cul un bloque se desl sobe oto se lust un doble cecmento p obsev los efectos de l ugosdd pesente en mbos:
40 47 Fgu.. Eplccón de l ntule de l fccón unque po smplcdd cs todos los objetos se consden como cuepos ígdos cundo se nl su mecánc en eldd todos sufen defomcones. sí, cundo se pesent el deslmento dchos dentes se defomn lgemente se ompen o vbn debdo efectos de tbón nque sobe l supefce de contcto [8]. L fue de fccón es popoconl l fue noml (N) ls supefces en deccón opuest l desplmento (-sgn(v)), sendo l constnte de popoconldd dependente de l ugosdd de ls supefces de dos stucones: S l fue que ntent povoc el deslmento es pequeñ éste no se pesent, pues ls fues de contcto ente los dentes no bst p defomlos. sí, l fue de fccón denomnd como estátc (F s ) blnce dch fue hst que lleg un mámo.en cmbo, s ocue el deslmento los dentes se ntecln en meno medd, pesentándose un fue de fccón constnte denomnd como cnétc (F k ). mbs stucones consden dos coefcentes de fccón dstntos (µ s µ k ), coespondendo el pmeo l fue de fccón estátc mám el segundo l fue de fccón cnétc, el cul genelmente es meno que el pmeo: F s Nsgn( v), Nsgn( v) µ s F k µ k (-86) L pcón de fues de fccón puede se un efecto deseble o ndeseble, sendo posble educ el coefcente de fccón sec mednte l utlcón de lubcntes, pesentándose sí fccón vscos (F v ), l cul es meno depende de l velocdd del desplmento (v) [7]: F s µ v v (-87)
41 Momento El efecto que poduce un fue sobe un cuepo ígdo depende de su punto de plccón, ón po l cul se ntoduce el concepto de momento de un fue: El momento de un fue M O con especto un punto O se defne vectolmente como el poducto cu de un vecto que ndc el punto de plccón de l fue po el vecto de dch fue F: M O F (-88) De cuedo est defncón l deccón de dcho vecto se oent pependculmente l plno que fomn los vectoes F, sendo su mgntud el poducto de l fue l dstnc pependcu d del punto O l líne de ccón de l fue (Fgu.): M O Fd (-89) Fgu.. Momento de un fue [7] El momento de un fue mde l tendenc de l fue F p ot el cuepo ígdo lededo de un eje dgdo lo lgo del vecto M O en el sentdo ndcdo po dcho vecto de cuedo l egl de l mno deech. sí msmo, el sentdo de otcón tmbén puede se detemndo pt del sentdo de l fue F en elcón l punto O. S dos vectoes poseen gul mgntud son ntplelos no poducen fue net lgun, peo sí momento con especto un punto O (Fgu.3). Este vecto esultnte cu mgntud es el poducto de un de ls fues l dstnc que ls sep es un vecto lbe llmdo momento de un p o toque epesent l ccón eclusvmente otto de dchs fues [7].
42 49 Fgu.3. Momento de un p [7].7.3. Ms L ms se efee un popedd que ndc l cntdd de mte que un cuepo posee. Sn embgo, ést puede est dstbud btmente sendo neceso epes decudmente dch dstbucón, pues fect dectmente el movmento del cuepo. ello se ntoducen dos conceptos: el cento de ms el momento de nec Cento de ms En l seccón.7.. se pesent l mne de obtene l fue de gvedd ejecd po l e sobe un ptícul; sn embgo, un cuepo se encuent fomdo po un nfndd de ptículs de tl fom que el efecto que l e ejece sobe él esult en un gn cntdd de pequeñs fues dstbuds que pueden se eemplds po un fue esultnte plcd en un punto p el cuepo denomndo como cento de ms o cento de gvedd, de tl fom que poduc el msmo momento con especto un punto bto que el de ls fues dstbuds. sí, p l poscón del cento de gvedd especto un sstem coodendo: dw W (-90) Se consde tnto l ecucón (-85) como que l ms quede epesd en témnos del volumen V del cuepo de su densdd ρ p epes l ecucón (-90) como [7]: dm m (-9) dv m ρ (-9)
43 Momento de nec El momento de nec pesent un medd de l dstbucón de l ms en un cuepo con especto un detemndo eje. Se defne el momento de nec de cd un de ls ptículs que confomn un cuepo como el poducto de l ms de l ptícul m po l dstnc ente ést el eje consdedo elevd l cuddo: m (-93) S cd ptícul se consde como un elemento dfeencl se el l ntegcón se obtene el momento de nec de ms del cuepo con especto dcho eje: dm (-94) Este momento de nec tmbén puede qued epesdo en funcón de l ms totl del cuepo s se defne un pámeto denomndo como do de go k, el cul epesent un dstnc con especto l eje l cul se debeí concent tod l ms del cuepo p poduc el msmo momento de nec: k m (-95) Consdendo un sstem coodendo undo dcho cuepo, es posble obtene el momento de nec con especto cd uno de sus ejes s se epes el do de l ecucón (-94) en funcón de ls coodends ctesns mednte el teoem de tágos (Fgu.4). sí: ( ), ( ) dm, ( ) dm dm (-96) Sn embgo, estos no seán sufcentes p epesent decudmente l dstbucón de ms en el cuepo s el sstem coodendo undo él no es colocdo de tl fom que l ms se encuente dstbud de mne smétc; entonces es neceso detemn tes cntddes dconles llmds poductos de nec [7]: ( ) dm, ( ) dm, ( ) dm (-97)
44 5 Fgu.4. Notcón p obtene los momentos de nec especto un sstem coodendo [7] sí, ls popeddes necles de un cuepo pueden qued completmente ccteds po nueve témnos, ses de los cules son ndependentes ente sí. Estos se odenn en fom de eglo denomnándose l mt esultnte como el tenso de nec, defndo contnucón: (-98) S un plno otogonl del sstem coodendo epesent un plno de smetí, los poductos de nec que tengn po subíndce el eje pependcul dcho plno vlen utomátcmente ceo, equéndose sólo dos plnos de smetí p que los tes poductos de nec se nulen el tenso de nec quede como mt dgonl. En dcho cso se denomn los ejes del sstem coodendo como ejes pncples de nec, pudendo se culque punto elegdo como su ogen. Cundo los momentos poductos de nec con especto un sstem coodendo cuo ogen se el cento de ms del cuepo son conocdos, entonces es posble detemn un nuevo conjunto de momentos poductos de nec con especto culque oto sstem coodendo que pesente l msm oentcón, mednte el teoem de ejes plnos plelos (Fgu.5). sí [8]: ( ' ' ) ) ( ' ' ) m( ) ( ) m( ) ' ' ( ' ) m( ) ( ) m( ) ' ' ' ' ' ( ) m( ) (-99)
45 5 Fgu.5. eoem de ejes plnos plelos [7] enelndo ls ecucones epotds en (-99) p el tenso de nec: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' m m (-00).7.4. Lees del movmento de Newton En 687 sc Newton pesentó tes lees báscs que gen el movmento de un ptícul. Ests tes lees del movmento pueden se enuncds como sgue:. Un ptícul ognlmente en eposo, o movéndose en líne ect con velocdd constnte, pemneceá en ese estdo sempe que no esté sometd fues desblnceds; es dec, sempe que l fue esultnte sobe ell se ceo.. Un ptícul sobe l que ctú un fue esultnte F epement un celecón que tene l msm deccón que l fue un mgntud que es popoconl ell. 3. Ls fues mutus de ccón eccón ente dos ptículs son gules, opuests colneles. L segund le de Newton puede epesse mtemátcmente de l sguente mne: F (-0)
46 53 L constnte de popoconldd neces p fomul l epesón nteo en fom de ecucón se denomn ms de l ptícul m, l cul epesent l esstenc de un cuepo p cmb l mgntud /o deccón de su velocdd. sí: F m (-0) Donde l epesón (-0) coesponde l ecucón de movmento tslconl p un ptícul [8] Ls ecucones de movmento p un cuepo ígdo Ments que un ptícul sólo pesent movmento tslconl poducdo po l fue net plcd ell, un cuepo ígdo puede pesent tnto movmento tslconl como otconl, sendo neceso nl no sólo los efectos poducdos po l fue net plcd, sno tmbén po el momento neto plcdo dcho cuepo. este nálss se consde l notcón mostd en l Fgu.6: Fgu.6. Dnámc de un cuepo ígdo Un cuepo ígdo se encuent fomdo po un nfndd de ptículs, sendo neceso etende l ecucón de movmento p pode plcl. ello debe sumse vectolmente est ecucón plcd cd ptícul, estndo cd un sometd un fue esultnte nten (f ) como eten (F ); sn embgo, l sum de ls fues esultntes ntens es gul ceo, que tods ells ocuen ente ls ptículs del cuepo en pes gules colneles peo opuestos. sí: F f F m (-03) m (-04)
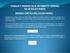
Regla del Triángulo. (a) (b) (c) 1 Física General I Paralelos 05 y 22. Profesor RodrigoVergara R 0101) Repaso de Vectores
 1 Físc Genel I Plelos 5. Pofeso RodgoVeg R 11) Repso de Vectoes 1) Repso de Opecones Vectoles Us l sum ectol, usndo l egl del tángulo l del plelogmo. Clcul l mgntud deccón de l sum usndo teoem del seno
1 Físc Genel I Plelos 5. Pofeso RodgoVeg R 11) Repso de Vectoes 1) Repso de Opecones Vectoles Us l sum ectol, usndo l egl del tángulo l del plelogmo. Clcul l mgntud deccón de l sum usndo teoem del seno
MAGNITUDES ESCALARES Y VECTORIALES. Dr. CARLOS MOSQUERA
 1 MAGNITUDES ESCALARES Y VECTRIALES D. CARLS MSQUERA 2 Mgntudes escles y vectoles Defncones; popeddes y opecones En los conceptos de mecánc que desollemos, nos encontemos con dos dfeentes tpos de mgntudes:
1 MAGNITUDES ESCALARES Y VECTRIALES D. CARLS MSQUERA 2 Mgntudes escles y vectoles Defncones; popeddes y opecones En los conceptos de mecánc que desollemos, nos encontemos con dos dfeentes tpos de mgntudes:
Unidad I - Electroestática
 Undd I - Electoestátc Intoduccón ues de nteccón: ccones dstnc ues Electomgnétcs ues Eléctcs Un poco de hsto El témno eléctco, tene su ogen en ls expeencs elds en l ntgüedd donde se obsevo ue cundo se fotd
Undd I - Electoestátc Intoduccón ues de nteccón: ccones dstnc ues Electomgnétcs ues Eléctcs Un poco de hsto El témno eléctco, tene su ogen en ls expeencs elds en l ntgüedd donde se obsevo ue cundo se fotd
INSTITUTO DE FÍSICA MECÁNICA NEWTONIANA
 INSTITUT DE FÍSIC MECÁNIC NEWTNIN Cuso 009 áctco I Cnemátc de l tícul y Movmento eltvo NT: Los sguentes eeccos están odendos po tem y, dento de cd tem, en un oden cecente de dfcultd lgunos eeccos se encuentn
INSTITUT DE FÍSIC MECÁNIC NEWTNIN Cuso 009 áctco I Cnemátc de l tícul y Movmento eltvo NT: Los sguentes eeccos están odendos po tem y, dento de cd tem, en un oden cecente de dfcultd lgunos eeccos se encuentn
CINEMÁTICA Y DINÁMICA DE ROTACIÓN
 Uel Fcult e Cencs Cuso e Físc I p/lc. Físc y Mtemátc Cuso CINEMÁTICA Y DINÁMICA DE OTACIÓN. Momento e otcón- Un cuepo ígo se muee en otcón pu s c punto el cuepo se muee en tyecto ccul. Los centos e estos
Uel Fcult e Cencs Cuso e Físc I p/lc. Físc y Mtemátc Cuso CINEMÁTICA Y DINÁMICA DE OTACIÓN. Momento e otcón- Un cuepo ígo se muee en otcón pu s c punto el cuepo se muee en tyecto ccul. Los centos e estos
X X 1. MECÁNICA GENERAL 1.4. FUNDAMENTOS DE ANÁLISIS TENSORIAL. 1.4.1. Introducción
 Fndmentos y eoís Físcs ES Aqtect. MECÁNCA GENERAL.4. FUNDAMENOS DE ANÁLSS ENSORAL.4.. ntodccón L myoí de ls mgntdes físcs y elcones mtemátcs ente ls msms qedn pefectmente defnds tbjndo con escles y ectoes.
Fndmentos y eoís Físcs ES Aqtect. MECÁNCA GENERAL.4. FUNDAMENOS DE ANÁLSS ENSORAL.4.. ntodccón L myoí de ls mgntdes físcs y elcones mtemátcs ente ls msms qedn pefectmente defnds tbjndo con escles y ectoes.
5.- Ajuste de curvas. para M = 2 un ajuste parabólico, etc..
 écncs Computconles Cuso 7-8. Pedo lvdo 5.- juste de cuvs El juste de cuvs es un poceso mednte el cul ddo un conjunto de pes de puntos { } sendo l vble ndependente e l dependente se detemn un uncón mtemátc
écncs Computconles Cuso 7-8. Pedo lvdo 5.- juste de cuvs El juste de cuvs es un poceso mednte el cul ddo un conjunto de pes de puntos { } sendo l vble ndependente e l dependente se detemn un uncón mtemátc
NÚMEROS COMPLEJOS. El vector así representado define un número complejo, y a dicha representación se le llama afijo de un número complejo.
 educgu.com NÚMEROS COMPLEJOS DEFINICIÓN Se llm númeo complejo un p odendo de númeos eles (, ). Los númeos eles y se llmn componentes del númeo complejo. A l componente se le desgn pte el y l componente
educgu.com NÚMEROS COMPLEJOS DEFINICIÓN Se llm númeo complejo un p odendo de númeos eles (, ). Los númeos eles y se llmn componentes del númeo complejo. A l componente se le desgn pte el y l componente
Sistemas de Conductores.
 Electcdd y Mgnetsmo uso 009/00 stems de onductoes - ondensdoes Eym E- stems de onductoes. Los sstems de conductoes epesentn l páctc myoí de los polems ue se pueden encont en los sstems de telecomunccón.
Electcdd y Mgnetsmo uso 009/00 stems de onductoes - ondensdoes Eym E- stems de onductoes. Los sstems de conductoes epesentn l páctc myoí de los polems ue se pueden encont en los sstems de telecomunccón.
Sistemas de Conductores.
 Electcdd y gnetsmo uso 005/006 stems de onductoes. os sstems de conductoes epesentn l páctc myoí de los polems ue se pueden encont en los sstems de telecomunccón. e cctezn po: Un númeo de de conductoes
Electcdd y gnetsmo uso 005/006 stems de onductoes. os sstems de conductoes epesentn l páctc myoí de los polems ue se pueden encont en los sstems de telecomunccón. e cctezn po: Un númeo de de conductoes
NÚMEROS COMPLEJOS. r φ. (0,0) a
 Educgu.com NÚMEROS COMPLEJOS DEFINICIÓN Se llm númeo complejo un p odendo de númeos eles (,b). Los númeos eles y b se llmn componentes del númeo complejo. A l componente se le desgn pte el y l componente
Educgu.com NÚMEROS COMPLEJOS DEFINICIÓN Se llm númeo complejo un p odendo de númeos eles (,b). Los númeos eles y b se llmn componentes del númeo complejo. A l componente se le desgn pte el y l componente
CAPÍTULO VI CINÉTICA DEL RÍGIDO
 CÍULO CÉC DEL RÍDO CEMÁC Un cuepo ígdo puede consdese coo un sste de ss puntules cuys dstncs se ntenen constntes dunte el oento. Coenceos detenndo el núeo de coodends ndependentes necess p especfc su confgucón
CÍULO CÉC DEL RÍDO CEMÁC Un cuepo ígdo puede consdese coo un sste de ss puntules cuys dstncs se ntenen constntes dunte el oento. Coenceos detenndo el núeo de coodends ndependentes necess p especfc su confgucón
Tema 0: Introducción al Cálculo Vectorial
 I.E. Jn Rmón Jméne Tem 0: Intodccón l Cálclo Vectol 1.- Mgntdes escles ectoles.- Vecto. Opecones con Vectoes 3.- Podcto escl 4.- Podcto ectol 5.- Decón Vectol 6.- Integcón Vectol 7.- Momento de n Vecto
I.E. Jn Rmón Jméne Tem 0: Intodccón l Cálclo Vectol 1.- Mgntdes escles ectoles.- Vecto. Opecones con Vectoes 3.- Podcto escl 4.- Podcto ectol 5.- Decón Vectol 6.- Integcón Vectol 7.- Momento de n Vecto
No entraremos en detalle ni en definiciones demasiado formales sino que veremos únicamente aquellos conceptos que necesitaremos durante el curso.
 Técncs Computconles, Cuso 007-008. Pedo Sldo.- Álgeb lnel o entemos en detlle n en defncones demsdo fomles sno que eemos úncmente quellos conceptos que necestemos dunte el cuso.. Espcos ectoles Un espco
Técncs Computconles, Cuso 007-008. Pedo Sldo.- Álgeb lnel o entemos en detlle n en defncones demsdo fomles sno que eemos úncmente quellos conceptos que necestemos dunte el cuso.. Espcos ectoles Un espco
TEMA 1 MÉTODOS DE MINIMIZACIÓN
 TEMA MÉTODOS DE MINIMIZACIÓN A) INTRODUCCIÓN MATEMÁTICA Genelmente el poblem se ceñá un mnmzcón de un funcón el [f()] de n vbles Se sume que l funcón f() es un funcón contnu y que demás posee l pme y segund
TEMA MÉTODOS DE MINIMIZACIÓN A) INTRODUCCIÓN MATEMÁTICA Genelmente el poblem se ceñá un mnmzcón de un funcón el [f()] de n vbles Se sume que l funcón f() es un funcón contnu y que demás posee l pme y segund
TEMA 5: CÁLCULO VECTORIAL
 IES Al-Ándlus. Dpto. Físic Químic. F.Q. 1º Bchilleto. Tem 5: Cálculo vectoil - 1-5.1 VECTORES TEMA 5: CÁLCULO VECTORIAL 5.1 Vectoes 5. Sistems de efeenci. Coodends. Componentes de un vecto. 5.3 Opeciones
IES Al-Ándlus. Dpto. Físic Químic. F.Q. 1º Bchilleto. Tem 5: Cálculo vectoil - 1-5.1 VECTORES TEMA 5: CÁLCULO VECTORIAL 5.1 Vectoes 5. Sistems de efeenci. Coodends. Componentes de un vecto. 5.3 Opeciones
Examen de Física-1, 1 Ingeniería Química Enero de 2011 Cuestiones (Un punto por cuestión).
 Exmen de Físc-1, 1 Ingenerí Químc Enero de 211 Cuestones (Un punto por cuestón). Cuestón 1: Supong que conocemos l poscón ncl x y l velocdd ncl v de un oscldor rmónco cuy frecuenc ngulr es tmén conocd;
Exmen de Físc-1, 1 Ingenerí Químc Enero de 211 Cuestones (Un punto por cuestón). Cuestón 1: Supong que conocemos l poscón ncl x y l velocdd ncl v de un oscldor rmónco cuy frecuenc ngulr es tmén conocd;
CAPÍTULO III TRABAJO Y ENERGÍA
 TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TRAJO Y ENERGÍA CAPÍTULO III "De todos los conceptos físcos, el de enegía es pobablemente el de más vasto alcance. Todos, con fomacón técnca o no, tenen una pecepcón de la enegía y lo que esta palaba sgnfca.
TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO
 Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,
Unidad 3 Sistemas de Ecuaciones Lineales
 Unidd 3 Sistems de Ecuciones Lineles Popedéutico 8 D. Ruth M. Aguil Ponce Fcultd de Ciencis Deptmento de Electónic Popedéutico 8 Fcultd de Ciencis Popedéutico 8 Fcultd de Ciencis Sistem de Ecuciones Lineles
Unidd 3 Sistems de Ecuciones Lineles Popedéutico 8 D. Ruth M. Aguil Ponce Fcultd de Ciencis Deptmento de Electónic Popedéutico 8 Fcultd de Ciencis Popedéutico 8 Fcultd de Ciencis Sistem de Ecuciones Lineles
CAPÍTULO VII LEY DE AMPERE Y LEY DE BIOT-SAVART
 Tócos de Electcdd y Mgnetsmo J.Pozo y R.M. Chobdjn. CAPÍTULO VII LEY DE AMPERE Y LEY DE IOT-SAVART 7.. Ley de Amee Oested en 8 fue quen descubó eementlmente, que un coente que ccul en un lmbe oduce efectos
Tócos de Electcdd y Mgnetsmo J.Pozo y R.M. Chobdjn. CAPÍTULO VII LEY DE AMPERE Y LEY DE IOT-SAVART 7.. Ley de Amee Oested en 8 fue quen descubó eementlmente, que un coente que ccul en un lmbe oduce efectos
Practico 7 Fuerza y Leyes de Newton
 008 Pctico 7 uez y Leyes de Newton ) Un bloque de 5.5 Kg. está inicilmente en eposo sobe un supeficie hoizontl sin ficción. Es empujdo con un fuez hoizontl constnte de 3.8 N. ) Cuál es su celeción? b)
008 Pctico 7 uez y Leyes de Newton ) Un bloque de 5.5 Kg. está inicilmente en eposo sobe un supeficie hoizontl sin ficción. Es empujdo con un fuez hoizontl constnte de 3.8 N. ) Cuál es su celeción? b)
CURSO CERO DE FÍSICA CINEMÁTICA DEL PUNTO
 CURSO CERO DE FÍSICA Ángel Muño Csellnos Depmeno de Físc CONTENIDO Momeno undmensonl Poscón, elocdd, celecón Momeno eclíneo unfome Momeno eclíneo unfomemene celedo Momeno en el espco Vecoes poscón, elocdd
CURSO CERO DE FÍSICA Ángel Muño Csellnos Depmeno de Físc CONTENIDO Momeno undmensonl Poscón, elocdd, celecón Momeno eclíneo unfome Momeno eclíneo unfomemene celedo Momeno en el espco Vecoes poscón, elocdd
Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:
 Deptmento de Físic, UTFSM Físic Genel II / of: A. Bunel. FIS10: FÍSICA GENERAL II GUÍA #3: otencil Eléctico. Objetivos de pendizje Est guí es un hemient que usted debe us p log los siguientes objetivos:
Deptmento de Físic, UTFSM Físic Genel II / of: A. Bunel. FIS10: FÍSICA GENERAL II GUÍA #3: otencil Eléctico. Objetivos de pendizje Est guí es un hemient que usted debe us p log los siguientes objetivos:
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO.
 Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
CURSO CERO DE FÍSICA APLICACIÓN DE VECTORES A LA FÍSICA
 CURSO CERO DE FÍSIC PLICCIÓN DE VECTORES L FÍSIC Vness de Csto Susn i Deptmento de Físic CURSO CERO DE FÍSIC.UC3M PLICCIÓN DE VECTORES L FÍSIC CONTENIDO Mgnitudes escles vectoiles. Repesentción gáfic de
CURSO CERO DE FÍSIC PLICCIÓN DE VECTORES L FÍSIC Vness de Csto Susn i Deptmento de Físic CURSO CERO DE FÍSIC.UC3M PLICCIÓN DE VECTORES L FÍSIC CONTENIDO Mgnitudes escles vectoiles. Repesentción gáfic de
UNIVERSIDAD DE CANTABRIA
 UNIVERSIDAD DE CANTABRIA ESCUELA TÉCNICA SUERIOR DE INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES Deptmento de Ingeneí Químc y Químc Inogánc Contbucón l Dseño de ocesos de Sepcón con Membns Líquds Selectvs.
UNIVERSIDAD DE CANTABRIA ESCUELA TÉCNICA SUERIOR DE INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES Deptmento de Ingeneí Químc y Químc Inogánc Contbucón l Dseño de ocesos de Sepcón con Membns Líquds Selectvs.
xdm para la coordenada y CM B y que corresponde a la respuesta c
 .1. DETEMINCIÓN DEL CENTO DE MSS (contnucón).1.. Un chp unfome de densdd supefcl σ tene l fom ndcd en l fgu. L coodend de su cento de mss epesd en metos es: ) 1 b) c),5 d) e),5 l coodend Y de su cento
.1. DETEMINCIÓN DEL CENTO DE MSS (contnucón).1.. Un chp unfome de densdd supefcl σ tene l fom ndcd en l fgu. L coodend de su cento de mss epesd en metos es: ) 1 b) c),5 d) e),5 l coodend Y de su cento
Aplicación del Dominio Armónico Extendido al Análisis de Estado Quasi-Estacionario de los Sistemas Eléctricos de Potencia
 RIEE&C, REVISA DE INGENIERÍA ELÉCRICA, ELECRÓNICA Y COMPUACIÓN, Vol. 5 No. 2, DICIEMBRE 28 Alccón del Domno Amónco Extenddo l Análss de Estdo Qus-Estcono de los Sstems Eléctcos de Potenc 13 Lázo C. Isdo,
RIEE&C, REVISA DE INGENIERÍA ELÉCRICA, ELECRÓNICA Y COMPUACIÓN, Vol. 5 No. 2, DICIEMBRE 28 Alccón del Domno Amónco Extenddo l Análss de Estdo Qus-Estcono de los Sstems Eléctcos de Potenc 13 Lázo C. Isdo,
Para caracterizar completamente una magnitud vectorial, como son la velocidad, aceleración, fuerza, etc, es preciso indicar tres cosas:
 VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
VECTORES Y ESCLRES Las magntudes escalaes son aquellas que quedan totalmente defndas al epesa la cantdad la undad en que se mde. Eemplos son la masa, el tempo, el tabao todas las enegías, etc. Las magntudes
MAGNITUDES VECTORIALES:
 Mgnitudes vectoiles 1 de 8 MAGNITUDES VECTORIALES: Índice 1 Mgnitudes escles vectoiles Sum de vectoes lies Poducto de un escl po un vecto 3 Sistem de coodends vectoiles. Vectoes unitios 3 Módulo de un
Mgnitudes vectoiles 1 de 8 MAGNITUDES VECTORIALES: Índice 1 Mgnitudes escles vectoiles Sum de vectoes lies Poducto de un escl po un vecto 3 Sistem de coodends vectoiles. Vectoes unitios 3 Módulo de un
PRUEBA DE ACCESO A LA UNIVERSIDAD ENUNCIADO Y RESOLUCIÓN
 PRUEBA DE ACCESO A LA UNIVERSIDAD.6 ENUNCIADO Y RESOLUCIÓN Instucciones: )Dución: 1 ho y minutos. b) Tienes que elegi ente eliz únicmente los cuto ejecicios de l Opción A o eliz únicmente los cuto ejecicios
PRUEBA DE ACCESO A LA UNIVERSIDAD.6 ENUNCIADO Y RESOLUCIÓN Instucciones: )Dución: 1 ho y minutos. b) Tienes que elegi ente eliz únicmente los cuto ejecicios de l Opción A o eliz únicmente los cuto ejecicios
ANEXO 4.1: Centro de masa y de gravedad
 Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
Cuso l Físca I Auto l Loenzo Ipaague ANEXO 4.: Cento de asa de gavedad El punto que poeda la ubcacón de la asa se denona cento de asa (), dado que la accón de la gavedad es popoconal a la asa, es natual
A) Se considera el problema de contorno bidimensional constituido por la ecuación diferencial
 Elemetos tos bdmesoles. U vsó pelm A Se cosde el poblem de cotoo bdmesol costtdo po l eccó deecl (, e el domo, smplemete coeo ls codcoes de cotoo: (, coocd e α coocd e Recédese qe qe, s se deom l ccdte
Elemetos tos bdmesoles. U vsó pelm A Se cosde el poblem de cotoo bdmesol costtdo po l eccó deecl (, e el domo, smplemete coeo ls codcoes de cotoo: (, coocd e α coocd e Recédese qe qe, s se deom l ccdte
r V CINEMÁTICA DEL SÓLIDO RÍGIDO
 1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
1 d j m j Fg.1 dm dm Fg.2 m INEMÁTI DEL SÓLID RÍGID Un sóldo ígdo se consdea como un conjunto de patículas numeables: m 1,...m...m n cuyas dstancas mutuas pemanecen nvaables, en las condcones habtuales
Tema 5B. Geometría analítica del plano
 Tem 5B. Geometí nlític del plno L geometí nlític estudi ls elciones ente puntos, ects, ángulos, distncis, de un modo lgebico, medinte fómuls lgebics y ecuciones. P ello es impescindible utiliz un sistem
Tem 5B. Geometí nlític del plno L geometí nlític estudi ls elciones ente puntos, ects, ángulos, distncis, de un modo lgebico, medinte fómuls lgebics y ecuciones. P ello es impescindible utiliz un sistem
1) CURVAS DE PAR-VELOCIDAD DE UN MOTOR DE CORRIENTE CONTINUA DE IMANES PERMANENTES. CRITERIOS DE SELECCIÓN.
 ) CUAS D A-LOCDAD D U MOO D CO COUA D MAS MAS. COS D SLCCÓ. ) Cuvs de p-velocdd. Ls cuvs de p-velocdd de un oo de coene connu descben l cpcdd de poduccón de un p esáco del oo especo l volje plcdo y l velocdd
) CUAS D A-LOCDAD D U MOO D CO COUA D MAS MAS. COS D SLCCÓ. ) Cuvs de p-velocdd. Ls cuvs de p-velocdd de un oo de coene connu descben l cpcdd de poduccón de un p esáco del oo especo l volje plcdo y l velocdd
Análisis Vectorial. Escalares y campos escalares. Algebra vectorial. Vectores y campos vectoriales. v v v v. A v
 Escles cmpos escles nálisis Vectoil Teoí Electomgnétic 1 Dipl.-Ing. noldo Rojs oto Escl: ntidd cuo lo puede se epesentdo po un simple númeo el positio o negtio mpos escles: Función mtemátic del ecto que
Escles cmpos escles nálisis Vectoil Teoí Electomgnétic 1 Dipl.-Ing. noldo Rojs oto Escl: ntidd cuo lo puede se epesentdo po un simple númeo el positio o negtio mpos escles: Función mtemátic del ecto que
Números Reales y Complejos
 Apéndce C Números Reles y Complejos C.. Los números reles Suponemos conocdo el conjunto de los números reles. Vmos defnr y estudr en lgunos conceptos como relcones de orden, ntervlos, cots y vlor bsoluto.
Apéndce C Números Reles y Complejos C.. Los números reles Suponemos conocdo el conjunto de los números reles. Vmos defnr y estudr en lgunos conceptos como relcones de orden, ntervlos, cots y vlor bsoluto.
ANTECEDENTES DE ELECTRICIDAD Y. dfghjklzxcvbnmqwertyuiopasdfghjklzx MAGNETISMO VECTORES.
 qwetuiopsdfghjklcvbnmqwetui opsdfghjklcvbnmqwetuiopsdfgh jklcvbnmqwetuiopsdfghjklcvb nmqwetuiopsdfghjklcvbnmqwe tuiopsdfghjklcvbnmqwetuiops NTEEDENTES DE ELETIIDD Y dfghjklcvbnmqwetuiopsdfghjkl MGNETISMO
qwetuiopsdfghjklcvbnmqwetui opsdfghjklcvbnmqwetuiopsdfgh jklcvbnmqwetuiopsdfghjklcvb nmqwetuiopsdfghjklcvbnmqwe tuiopsdfghjklcvbnmqwetuiops NTEEDENTES DE ELETIIDD Y dfghjklcvbnmqwetuiopsdfghjkl MGNETISMO
( ) ( ) ( ) i j ij B (1.1) Y que su volumen se expresa en términos del producto punto de vectores como: ( )
 Te de Estdo Sólido 5/Septiembe/008 Min Eugeni Fís Anguino. Pob que, b b, b π π π Donde los vectoes b i cumplen l siguiente elción: b πδ i j ij Po constucción geométic, los dos conjuntos de vectoes y b
Te de Estdo Sólido 5/Septiembe/008 Min Eugeni Fís Anguino. Pob que, b b, b π π π Donde los vectoes b i cumplen l siguiente elción: b πδ i j ij Po constucción geométic, los dos conjuntos de vectoes y b
la integral de línea de B alrededor de un trayecto cerrado
 LEY DE AMPERE L ley de Guss de los cmpos elécticos implic el flujo de E tvés de un supeficie ced; estlece que este flujo es igul l cociente de l cg totl enced dento de l supeficie ente l constnte ε. En
LEY DE AMPERE L ley de Guss de los cmpos elécticos implic el flujo de E tvés de un supeficie ced; estlece que este flujo es igul l cociente de l cg totl enced dento de l supeficie ente l constnte ε. En
Estructura de la materia 3 Serie 2 Modelo de Thomas-Fermi y Sistemas Atómicos Cátedra: Jorge Miraglia. Segundo cuatrimestre de 2013
 Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
Estuctua de la matea See Modelo de homas-fem y Sstemas Atómcos Cáteda: Joge Magla Segundo cuatmeste de Modelo de homas-fem en átomos En el modelo de homas-fem, la enegía potencal de un electón lgado a
Un estudio sobre calibración de cámaras digitales en visión computacional y reconstrucción 3-D
 Congeso de Mcoelectónc Aplcd 1 Un estudo sobe clbcón de cáms dgtles en vsón computconl econstuccón 3-D Depol Robeto, Dìz Dnel, Fenndez Lus, Stockl Robeto Deptmento de Ingeneí e Investgcones Tecnológcs
Congeso de Mcoelectónc Aplcd 1 Un estudo sobe clbcón de cáms dgtles en vsón computconl econstuccón 3-D Depol Robeto, Dìz Dnel, Fenndez Lus, Stockl Robeto Deptmento de Ingeneí e Investgcones Tecnológcs
GRAVITACIÓN I: LEY DE LA GRAVITACIÓN UNIVERSAL
 8 0 GRVICIÓ I: LEY DE L GRVICIÓ UIVERSL j Sigue pcticndo Indic sobe l tyectoi de un plnet con óbit elíptic lededo del Sol, que ocup uno de los focos, los puntos de áxi y íni elocidd Rzon l espuest b t
8 0 GRVICIÓ I: LEY DE L GRVICIÓ UIVERSL j Sigue pcticndo Indic sobe l tyectoi de un plnet con óbit elíptic lededo del Sol, que ocup uno de los focos, los puntos de áxi y íni elocidd Rzon l espuest b t
Capítulo. Cinemática del Sólido Rígido
 Cpítulo 1 Cinemátic del Sólido Rígido Contenido Intoducción Tslción Rotción lededo de un Eje Fijo. elocidd Rotción lededo de un Eje Fijo: celeción Rotción lededo de un Eje Fijo: Sección epesentti Ecución
Cpítulo 1 Cinemátic del Sólido Rígido Contenido Intoducción Tslción Rotción lededo de un Eje Fijo. elocidd Rotción lededo de un Eje Fijo: celeción Rotción lededo de un Eje Fijo: Sección epesentti Ecución
UNIVERSIDAD TECNOLÓGICA NACIONAL FACULTAD REGIONAL ROSARIO INTEGRACIÓN IV
 UNIESIDD ENOLÓGI NIONL ULD EGIONL OSIO INEGIÓN I Ejemplo e Moelo e Equpos e un lnt en Esto Dnámco Se el gm e lujo e l gu. Luego e nomb ls vbles estntes se ese plnte un moelo en esto námco que lo epesente
UNIESIDD ENOLÓGI NIONL ULD EGIONL OSIO INEGIÓN I Ejemplo e Moelo e Equpos e un lnt en Esto Dnámco Se el gm e lujo e l gu. Luego e nomb ls vbles estntes se ese plnte un moelo en esto námco que lo epesente
a la componente imaginaria de z. Dos números complejos son iguales cuando tienen la misma parte real y la misma parte imaginaria.
 Númeos Complejos Un Defnón Llmemos númeo omplejo un númeo z que se ese e l fom, one y son númeos eles, e vef:. Al númeo se lo enomn pte el e z y l númeo, pte mgn e z. pte } pte } mgn Se esgn on Re ( z)
Númeos Complejos Un Defnón Llmemos númeo omplejo un númeo z que se ese e l fom, one y son númeos eles, e vef:. Al númeo se lo enomn pte el e z y l númeo, pte mgn e z. pte } pte } mgn Se esgn on Re ( z)
11.1. CAMBIO DE COORDENADAS RECTANGULARES A POLARES.
 Integcón ol lccones CÁLCUL DIFEENCIL E INTEGL I.. CMBI DE CDENDS ECTNGULES LES. Cooens oles El lno Euclno tene socs os ects eencules un hozontleje e ls scss X ot vetcleje e ls oens Y con nteseccón en un
Integcón ol lccones CÁLCUL DIFEENCIL E INTEGL I.. CMBI DE CDENDS ECTNGULES LES. Cooens oles El lno Euclno tene socs os ects eencules un hozontleje e ls scss X ot vetcleje e ls oens Y con nteseccón en un
Coordenadas Generales.
 oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
oodenadas eneales. k cte. j cte. cte. Base catesana Base cíndca. j k cos, cos, φ cte. cte. cte. Base esféca Base geneal. cos cos En una base geneal, un elemento de aco está detemnado po llamando ds ds
q 1 q 2 Resp.: V A = 1800 V; V B = 0 V; W A - B = 450*10-7 Joul. 13 cm 13 cm 6 cm 4 cm 4 cm
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO DOCENTE EL SABINO DEPARTAMENTO DE MATEMÁTICA Y FÍSICA UNIDAD CURRICULAR: FÍSICA II PROFESORA CARMEN ADRIANA CONCEPCIÓN 1. Un potón (q potón
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO DOCENTE EL SABINO DEPARTAMENTO DE MATEMÁTICA Y FÍSICA UNIDAD CURRICULAR: FÍSICA II PROFESORA CARMEN ADRIANA CONCEPCIÓN 1. Un potón (q potón
Siempre verifica que a 2 = b 2 + c 2 (Th. Pitágoras)
 Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
Págin 1 FIGURAS EN EL PLANO POLÍGONOS FIGURAS EN EL PLANO Y EN EL ESPACIO 1.- Polígono de 3 ldos: Tiángulo. B Los ángulos inteioes de culquie tiángulo sumn siempe 180º. El áe de culquie tiángulo se puede
Cu +2 + Zn Cu + Zn +2
 Termodnámc. Tem 16 Sstems electroquímcos 1. Defncones Electrodo. Metl en contcto con un electrolto (Sstem físco donde se produce un semreccón redox) Un sstem electródco está consttudo por un conductor
Termodnámc. Tem 16 Sstems electroquímcos 1. Defncones Electrodo. Metl en contcto con un electrolto (Sstem físco donde se produce un semreccón redox) Un sstem electródco está consttudo por un conductor
Ecuaciones de Poisson y Laplace
 Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
Elctc y Mgntsmo / Elctostátc Dfncón Los conuctos n lctostátc. mpo un cg puntul. plccons l Ly Guss Intgls supposcón. Potncl lctostátco Dfncón Intptcón. Intgls supposcón. Ecucons Posson y Lplc. oncons Intfs.oncons
Reflexión y Refracción
 eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
eflexón y efaccón Unvesdad de Pueto co ecnto Unvestao de Mayagüez Depatamento de Físca Actvdad de Laboatoo 8 La Ley de eflexón y La Ley de Snell Objetvos: 1. Detemna, paa una supefce eflectoa, la elacón
Problemas de Dinámica del Sólido Rígido
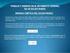 E.T.S... T Deprtento de ísc e ngenerí ucler robles de Dnác del Sóldo ígdo 1 étodo de ls celercones étodo de los oentos 3 étodo de l energí ro. J. rtín 3 1 étodo de ls celercones 1.1 Un plc rectngulr unore
E.T.S... T Deprtento de ísc e ngenerí ucler robles de Dnác del Sóldo ígdo 1 étodo de ls celercones étodo de los oentos 3 étodo de l energí ro. J. rtín 3 1 étodo de ls celercones 1.1 Un plc rectngulr unore
TRABAJO Y ENERGIA. 5.1 TRABAJO REALIZADO POR UNA FUERZA CONSTANTE.
 TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo s la ueza no
PRODUCTO ESCALAR. r r r
 PRODUCTO ESCALAR Defncón de pdct escl de ectes. Se denmn pdct escl de ds ectes (, ) y (, ), l núme: cs α y l epesentms p En el pdct escl se mltplcn ds ectes, pe el esltd es n núme (escl). S ls ectes petenecen
PRODUCTO ESCALAR Defncón de pdct escl de ectes. Se denmn pdct escl de ds ectes (, ) y (, ), l núme: cs α y l epesentms p En el pdct escl se mltplcn ds ectes, pe el esltd es n núme (escl). S ls ectes petenecen
Ondas y Rotaciones. Dinámica de las Rotaciones V
 Hoj de Trjo Onds Rotcones Dnámc de ls Rotcones V Jme Felcno Hernández Unversdd Autónom etropoltn - ztplp éco, D. F. de gosto de 0 A. ACTVDAD NDVDUAL. En est Hoj de trjo veremos otro conjunto de prolems
Hoj de Trjo Onds Rotcones Dnámc de ls Rotcones V Jme Felcno Hernández Unversdd Autónom etropoltn - ztplp éco, D. F. de gosto de 0 A. ACTVDAD NDVDUAL. En est Hoj de trjo veremos otro conjunto de prolems
CREACIÓN DE MAPAS DENSOS BASADOS EN APARIENCIA
 CREACIÓ DE MAPAS DESOS BASADOS E APARIECIA Loenzo Fenández, Lus Paá, Davd Úbeda, Mónca Ballesta, Jose M. Maín Depatamento de Ingeneía de Sstemas Industales. Unvesdad Mguel Henández. Avda. de la Unvesdad
CREACIÓ DE MAPAS DESOS BASADOS E APARIECIA Loenzo Fenández, Lus Paá, Davd Úbeda, Mónca Ballesta, Jose M. Maín Depatamento de Ingeneía de Sstemas Industales. Unvesdad Mguel Henández. Avda. de la Unvesdad
Cantidad de movimiento en la máquina de Atwood.
 Cntidd de movimiento en l máquin de Atwood. esumen Joge Sved y Pblo Adián Nuñez. jogesved@topmil.com. pblo_nuniez2000@yhoo.com. ed pticiptiv de Cienci UNSAM - 2005 En el pesente tbjo se puso pueb l pedicción
Cntidd de movimiento en l máquin de Atwood. esumen Joge Sved y Pblo Adián Nuñez. jogesved@topmil.com. pblo_nuniez2000@yhoo.com. ed pticiptiv de Cienci UNSAM - 2005 En el pesente tbjo se puso pueb l pedicción
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE EXTREMADURA JUNIO 2009. (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 hora y 30 minutos
 I.E.S. CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE EXTREMDUR JUNIO 9 (RESUELTOS po ntonio Menguino) MTEMÁTICS II Tiempo máimo: ho minutos El lumno elegiá un de ls dos opciones popuests. Cd un de
I.E.S. CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE EXTREMDUR JUNIO 9 (RESUELTOS po ntonio Menguino) MTEMÁTICS II Tiempo máimo: ho minutos El lumno elegiá un de ls dos opciones popuests. Cd un de
MOVIMIENTO CIRCULAR. r en cualquier punto de su trayectoria. v 2 / R
 MOVIMIENTO CIRCULAR Es un ipo de movimieno en el plno, en el cul l pícul gi un disnci fij lededo de un puno llmdo ceno. El movimieno cicul puede se de dos ipos: Movimieno cicul unifome Movimieno cicul
MOVIMIENTO CIRCULAR Es un ipo de movimieno en el plno, en el cul l pícul gi un disnci fij lededo de un puno llmdo ceno. El movimieno cicul puede se de dos ipos: Movimieno cicul unifome Movimieno cicul
22.6 Las 3 esferas pequeñas que se muestran en la figura tienen cargas q 1
 .6 Ls 3 esfes peueñs ue se muestn en l figu tienen cgs 4 n, -7.8 n y 3.4 n. Hlle el flujo eléctico neto tvés de cd un de ls supeficies ceds S, S, S3, S4 y S5. S S S3 S5 3 S4 4 m S 9 3 Φ.45 m 8.85 9 7.8
.6 Ls 3 esfes peueñs ue se muestn en l figu tienen cgs 4 n, -7.8 n y 3.4 n. Hlle el flujo eléctico neto tvés de cd un de ls supeficies ceds S, S, S3, S4 y S5. S S S3 S5 3 S4 4 m S 9 3 Φ.45 m 8.85 9 7.8
ECUACIONES DE LA RECTA
 RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA P hll l ecución de un ect en el espcio necesito: Dos puntos Un punto su vecto diecto Not: Nosotos utiliemos siempe un punto A(,, ) un vecto v (,b,c).
RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA P hll l ecución de un ect en el espcio necesito: Dos puntos Un punto su vecto diecto Not: Nosotos utiliemos siempe un punto A(,, ) un vecto v (,b,c).
Examen de Física I. 1.- Explique como se puede reducir el siguiente sistema de vectores deslizantes
 Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
Eaen de Físca ngeneía ecánca. ngeneía de Oganzacón ndustal: Gupo.- Eplque coo se puede educ el sguente sstea de vectoes deslzantes.- Defna y elacone ente ellos, los conceptos de oento lneal, pulso y oento
1.1 Carga eléctrica 1.2 Fuerzas electrostáticas. Ley de Coulomb Principio de superposición en sistemas lineales 1.3 Campo eléctrico Objetivos:
 Tem. lectostátic Tem. lectostátic. Cg eléctic. Fuezs electostátics. Ley de Coulomb incipio de supeposición en sistems lineles.3 Cmpo eléctico Objetivos: Cmpo eléctico cedo po cgs puntules be clcul el cmpo
Tem. lectostátic Tem. lectostátic. Cg eléctic. Fuezs electostátics. Ley de Coulomb incipio de supeposición en sistems lineles.3 Cmpo eléctico Objetivos: Cmpo eléctico cedo po cgs puntules be clcul el cmpo
Tema 4: Potencial eléctrico
 1/38 Tem 4: Potencil Eléctico Fátim Msot Conde Ing. Industil 2007/08 Tem 4: Potencil Eléctico 2/38 Índice: 1. Intoducción 2. Enegí potencil eléctic 1. de dos cgs puntules 2. de un sistem de cgs 3. Intepetción
1/38 Tem 4: Potencil Eléctico Fátim Msot Conde Ing. Industil 2007/08 Tem 4: Potencil Eléctico 2/38 Índice: 1. Intoducción 2. Enegí potencil eléctic 1. de dos cgs puntules 2. de un sistem de cgs 3. Intepetción
Una magnitud física es todo aquello que se puede medir: masa, volumen, temperatura, velocidad...
 Fdmetos Teoís Físcs TS Aqtect.. CÁLCUL VCTIAL... INTDUCCIÓN L ecác es l pte de l Físc qe estd el eqlbo el mometo de los cepos. Se dde e Cemátc qe se ocp del mometo de los cepos depedetemete de ls fes qe
Fdmetos Teoís Físcs TS Aqtect.. CÁLCUL VCTIAL... INTDUCCIÓN L ecác es l pte de l Físc qe estd el eqlbo el mometo de los cepos. Se dde e Cemátc qe se ocp del mometo de los cepos depedetemete de ls fes qe
Fundamentos Físicos de la Ingeniería Tercer Examen Parcial / 5 de junio de Figura 1
 Fundmentos Físcos de l ngenerí Tercer Exmen Prcl / 5 de juno de 4. Dsponemos de un esfer conductor, Q Q mc, de rdo, que posee un crg eléctrc Q net Q, de otr esfer conductor, huec, de rdos nteror exteror,
Fundmentos Físcos de l ngenerí Tercer Exmen Prcl / 5 de juno de 4. Dsponemos de un esfer conductor, Q Q mc, de rdo, que posee un crg eléctrc Q net Q, de otr esfer conductor, huec, de rdos nteror exteror,
Si el rédito anual de valoración, constante a lo largo de toda la operación, es del 9%, determínese:
 EJERIIOS DE OPERAIONES DE AMORTIZAIÓN Eercco Se concede un réstmo ersonl de 8.000 euros mortzble en 0 ños mednte térmnos mortztvos semestrles, donde ls cuots de mortzcón son déntcs en todos y cd uno de
EJERIIOS DE OPERAIONES DE AMORTIZAIÓN Eercco Se concede un réstmo ersonl de 8.000 euros mortzble en 0 ños mednte térmnos mortztvos semestrles, donde ls cuots de mortzcón son déntcs en todos y cd uno de
Por dos puntos pasan infinitas circunferencias secantes formando un haz. La recta que une los dos puntos es su eje radical.
 TNNI. onceptos, popieddes y noms. Po un punto psn infinits cicunfeencis tngentes. L ect tngente ells po dicho punto es su eje dicl. Po dos puntos psn infinits cicunfeencis secntes fomndo un hz. L ect que
TNNI. onceptos, popieddes y noms. Po un punto psn infinits cicunfeencis tngentes. L ect tngente ells po dicho punto es su eje dicl. Po dos puntos psn infinits cicunfeencis secntes fomndo un hz. L ect que
CONTENIDO SISTEMA DE PARTÍCULAS. Definición y cálculo del centro de masas. Movimiento del centro de masas. Fuerzas internas y fuerzas externas
 COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
COTEIDO Defncón y cálculo del cento de masas ovmento del cento de masas Fuezas ntenas y fuezas enas Enegía cnétca de un sstema de patículas Teoemas de consevacón paa un sstema de patículas B. Savon /.A.
Vectores. Bases. Producto escalar, vectorial y mixto; y aplicaciones
 Mtemátics II Geometí del espcio Vectoes. Bses. Podcto escl vectoil mixto; plicciones Obsevción: L moí de los poblems eseltos continción se hn popesto en los exámenes de Selectividd.. Ddos los vectoes (
Mtemátics II Geometí del espcio Vectoes. Bses. Podcto escl vectoil mixto; plicciones Obsevción: L moí de los poblems eseltos continción se hn popesto en los exámenes de Selectividd.. Ddos los vectoes (
OBJETIVO. La guía debe ser resuelta de manera grupal o individual y tendrá un valor según lo pactado.
 1 DEPARTAMENTO DE CIENCIAS BÁSICAS CALCULO VECTORIAL Y MULTIVARIADO TALLER 1 CAMPOS VECTORIALES CAMPOS CONSERVATIVOS ROTACIONAL Y DIVERGENCIA BIBLIOGRAÍA SUGERIDA CALCULO JAMES STEWART CALCULO THOMAS INNEY
1 DEPARTAMENTO DE CIENCIAS BÁSICAS CALCULO VECTORIAL Y MULTIVARIADO TALLER 1 CAMPOS VECTORIALES CAMPOS CONSERVATIVOS ROTACIONAL Y DIVERGENCIA BIBLIOGRAÍA SUGERIDA CALCULO JAMES STEWART CALCULO THOMAS INNEY
AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ
 UNIVERSIDAD AUTÓNOMA DE MADRID ESCUELA POLITÉCNICA SUPERIOR AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ -PROYECTO FIN DE CARRERA- Jave Gacía Ocón Mayo de 27 AUTOCALIBRACIÓN Y SINCRONIZACIÓN
UNIVERSIDAD AUTÓNOMA DE MADRID ESCUELA POLITÉCNICA SUPERIOR AUTOCALIBRACIÓN Y SINCRONIZACIÓN DE MÚLTIPLES CÁMARAS PTZ -PROYECTO FIN DE CARRERA- Jave Gacía Ocón Mayo de 27 AUTOCALIBRACIÓN Y SINCRONIZACIÓN
i:n i 0""E' D G-EOLOGIA 2i'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y
 ' 20078 :N 0""E' D G-EOLOGA 2'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y { t f 4 v s Se ha ealzado un estudo estuctual de la Hoja, aunque po dvesos motvos que vamos a analza no ha sdo posble obtene
' 20078 :N 0""E' D G-EOLOGA 2'_'T1?11C;TURAL E L.A POJ-11 BE.-OLA DE LEMA, - í y { t f 4 v s Se ha ealzado un estudo estuctual de la Hoja, aunque po dvesos motvos que vamos a analza no ha sdo posble obtene
VECTORES. En este apartado vamos a trabajar exclusivamente con los vectores en el espacio a los que vamos a llamar F 3.
 Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
Edcaga.com VECTORES En este apatado amos a tabaa eclsamente con los ectoes en el espaco a los qe amos a llama F. VECTOR FIJO Lo pmeo tendemos qe sabe qe es n ecto. Así qe llamamos ecto fo AB a n ecto qe
CAPITULO 5. TRABAJO Y ENERGIA.
 CAPITULO 5. TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo
CAPITULO 5. TRABAJO Y ENERGIA. El poblema undamental de la Mecánca es descb como se moveán los cuepos s se conocen las uezas aplcadas sobe él. La oma de hacelo es aplcando la segunda Ley de Newton, peo
Algunas series e integrales con funciones trigonométricas
 Revst Tecocetífc URU Uvesdd Rfel Udet Fcultd de Igeeí Nº Julo - Dcembe ISSN: 44-775X / Depósto legl pp ZU86 Algus sees e tegles co fucoes tgoométcs Alfedo Vlllobos y Gley Gcí Uvesdd del Zul. Fcultd de
Revst Tecocetífc URU Uvesdd Rfel Udet Fcultd de Igeeí Nº Julo - Dcembe ISSN: 44-775X / Depósto legl pp ZU86 Algus sees e tegles co fucoes tgoométcs Alfedo Vlllobos y Gley Gcí Uvesdd del Zul. Fcultd de
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS
 EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto
Práctica 2: Codificación Aritmética.
 TRANMÓN DE DATO 006/07 Práctc : Codfccón Artmétc. Apelldos, nombre Apelldos, nombre Grupo Puesto Fech 0 Octubre/ Novembre 006 El objetvo de est práctc es ntroducr l lumno en los fundmentos de ls codfccón
TRANMÓN DE DATO 006/07 Práctc : Codfccón Artmétc. Apelldos, nombre Apelldos, nombre Grupo Puesto Fech 0 Octubre/ Novembre 006 El objetvo de est práctc es ntroducr l lumno en los fundmentos de ls codfccón
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO FÍSICA C Tercera evaluación SOLUCIÓN
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 0-03 FÍSICA C Tercer evlucón SOLUCIÓN Pregunt (5 puntos) Un eser conductor con rdo nteror de 7 cm y rdo exteror de 8 cm
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL INSTITUTO DE CIENCIAS FÍSICAS I TÉRMINO 0-03 FÍSICA C Tercer evlucón SOLUCIÓN Pregunt (5 puntos) Un eser conductor con rdo nteror de 7 cm y rdo exteror de 8 cm
TEMA 2. MOVIMIENTO EN UNA DIMENSION.
 Tema. Movmento en una dmensón. TEMA. MOVIMIENTO EN UNA DIMENSION. La cnemátca es la ama de la mecánca que estuda la geometía del movmento. Usa las magntudes undamentales longtud, en oma de camno ecodo,
Tema. Movmento en una dmensón. TEMA. MOVIMIENTO EN UNA DIMENSION. La cnemátca es la ama de la mecánca que estuda la geometía del movmento. Usa las magntudes undamentales longtud, en oma de camno ecodo,
Tema 1.- INTERACCIÓN ELÉCTRICA ( RESUMEN)
 Te.- NTAÓN LÉTA ( SUMN). gs puntules g eléctc L cg eléctc es un pope funentl e l te, esteno os tpos e cg: postv y negtv. Dos cuepos con el so tpo e cg se epelen, ents ue s tenen stnto tpo e cg, se ten
Te.- NTAÓN LÉTA ( SUMN). gs puntules g eléctc L cg eléctc es un pope funentl e l te, esteno os tpos e cg: postv y negtv. Dos cuepos con el so tpo e cg se epelen, ents ue s tenen stnto tpo e cg, se ten
MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA
 MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA Dr. José A. Peñlbert Unversdd de Puerto Rco en Croln Deprtmento de Cencs Nturles Introduccón Hn surgdo un sere de teorís sobre el funconnmento
MICROTÚBULOS, FUNCIONES CEREBRALES Y LA MECÁNICA CUÁNTICA Dr. José A. Peñlbert Unversdd de Puerto Rco en Croln Deprtmento de Cencs Nturles Introduccón Hn surgdo un sere de teorís sobre el funconnmento
2πR π =
 PÁGIN 11 Pág. 1 oodends geogáfi cs 19 os ciuddes tienen l mism longitud, 15 E, y sus ltitudes son 7 5' N y 5' S. uál es l distnci ente ells? R b 7 5' b 5' Tenemos que ll l longitud del co coespondiente
PÁGIN 11 Pág. 1 oodends geogáfi cs 19 os ciuddes tienen l mism longitud, 15 E, y sus ltitudes son 7 5' N y 5' S. uál es l distnci ente ells? R b 7 5' b 5' Tenemos que ll l longitud del co coespondiente
PRODUCTO ESCALAR. r r r
 PRODUCTO ESCALAR Defnón de pdt esl de vetes. Se denmn pdt esl de ds vetes ( ) y ( ) p l núme: s y l epesentms En el pdt esl se mltpln ds vetes pe el esltd es n núme (esl). S ls vetes peteneen l esp vetl
PRODUCTO ESCALAR Defnón de pdt esl de vetes. Se denmn pdt esl de ds vetes ( ) y ( ) p l núme: s y l epesentms En el pdt esl se mltpln ds vetes pe el esltd es n núme (esl). S ls vetes peteneen l esp vetl
Mauricio Riera, S' IEEE Departamento de Potencia Instituto de Ingeniería Eléctrica Facultad de Ingeniería, UDEELAR Montevideo, Uruguay
 Poceedngs of 5º Encuento de Potenca, Instumentacón y Meddas, IEEE, Octobe 19-20, 1999, Montevdeo, Uuguay Contol De Flujo Vectoal Medante un Inveso de Coente Alejando Gómez Estudante de Ingeneía Insttuto
Poceedngs of 5º Encuento de Potenca, Instumentacón y Meddas, IEEE, Octobe 19-20, 1999, Montevdeo, Uuguay Contol De Flujo Vectoal Medante un Inveso de Coente Alejando Gómez Estudante de Ingeneía Insttuto
Tema 2. DINÁMICA DE SISTEMAS DE PARTÍCULAS
 Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
Tea. DIÁMICA DE SISTEMAS DE PARTÍCULAS. Intoduccón. Cento de asas.. Movento del cento de asas.. Masa educda..3 Consevacón del oento lneal..4 Consevacón del oento angula.3 Enegía de un sstea de patículas.3.
CAMPO MAGNÉTICO DE UN CONDUCTOR RECTO QUE TRANSPORTA CORRIENTE y. sin
 CAMPO MAGNÉTCO DE UN CONDUCTOR RECTO QUE TRANSPORTA CORRENTE dl - P X d φ φ sin sin φ φ 3/ sin d d φ Cundo l longitud del conducto es mu gnde en compción con, l ecución se conviete en: >> 8. Un lmbe ecto
CAMPO MAGNÉTCO DE UN CONDUCTOR RECTO QUE TRANSPORTA CORRENTE dl - P X d φ φ sin sin φ φ 3/ sin d d φ Cundo l longitud del conducto es mu gnde en compción con, l ecución se conviete en: >> 8. Un lmbe ecto
ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO
 Insttuto de Poesoes Atgas Físca Expemental 1 Guía páctca Nº ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO DISPOSITIVO EXPERIMENTAL El dspostvo expemental se muesta en la gua 1. Un egstado electónco o tme
Insttuto de Poesoes Atgas Físca Expemental 1 Guía páctca Nº ANÁLISIS GRÁFICO DE UN MOVIMIENTO RECTILÍNEO DISPOSITIVO EXPERIMENTAL El dspostvo expemental se muesta en la gua 1. Un egstado electónco o tme
LONGITUD DE ARCO. Una aproximación es una línea recta desde el punto x=a hasta el punto x=b, como se indica en la figura:
 LONGITUD DE ARCO Clculr l longtud de rco o de un curv dd por un funcón f en un ntervlo x, tene muchs plccones en ls cencs. Es necesro que hgmos un reve estudo del cálculo de ells. Un proxmcón es un líne
LONGITUD DE ARCO Clculr l longtud de rco o de un curv dd por un funcón f en un ntervlo x, tene muchs plccones en ls cencs. Es necesro que hgmos un reve estudo del cálculo de ells. Un proxmcón es un líne
Dpto. INGENIERÍA ENERGÉTICA Y FLUIDOMECÁNICA ESCUELA DE INGENIERÍAS INDUSTRIALES UNIVERSIDAD DE VALLADOLID
 AIRE HÚMEDO Y PROCESOS PSICROMÉRICOS Introduccón. Crcterístcs del re úedo. Dgrs pscroétrcos. Análss de los procesos pscroétrcos báscos del re úedo ASIGNAURA: ERMODINÁMICA ÉCNICA RANSMISIÓN DE CALOR GRADO:
AIRE HÚMEDO Y PROCESOS PSICROMÉRICOS Introduccón. Crcterístcs del re úedo. Dgrs pscroétrcos. Análss de los procesos pscroétrcos báscos del re úedo ASIGNAURA: ERMODINÁMICA ÉCNICA RANSMISIÓN DE CALOR GRADO:
PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 28 FISICA TOMO 2. Tercera y quinta edición. Raymond A. Serway
 PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3
PROBLEMAS RESUELTOS CIRCUITOS DE CORRIENTE CONTINUA CAPITULO 8 FISICA TOMO Tercer y qunt edcón Rymond A. Serwy CIRCUITOS DE CORRIENTE CONTINUA 8. Fuerz electromotrz 8. Resstores en sere y en prlelo 8.3
11. COMPENSACIÓN DEL RADIO
 Capítlo 3: Desaollo del poama. COMPENSACIÓN DEL RADIO. Intodccón Los pntos tomados dectamente po palpacón sobe la spece de la peza en cestón no son pntos eales de dcha spece, ya qe el pnto ecodo tene las
Capítlo 3: Desaollo del poama. COMPENSACIÓN DEL RADIO. Intodccón Los pntos tomados dectamente po palpacón sobe la spece de la peza en cestón no son pntos eales de dcha spece, ya qe el pnto ecodo tene las
2.1- Nociones de Álgebra lineal
 écncs Computconles, Cuso 7-8. Pedo Sldo.- ocones de Álgeb lnel o entemos en detlle n en defncones demsdo fomles sno que eemos úncmente quellos conceptos que necestemos dunte el cuso... Espcos ectoles Un
écncs Computconles, Cuso 7-8. Pedo Sldo.- ocones de Álgeb lnel o entemos en detlle n en defncones demsdo fomles sno que eemos úncmente quellos conceptos que necestemos dunte el cuso... Espcos ectoles Un
Potencial eléctrico. Física II Grado en Ingeniería de Organización Industrial Primer Curso. Departamento de Física Aplicada III Universidad de Sevilla
 Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
x y Si el vector está en tres dimensiones: x y coordenadas se les llama cosenos directores
 Sum de ectoes Si tienen el mismo punto de plicción se tzn plels cd ecto po el extemo del oto. Si están uno continución de oto, se une el oigen del pimeo con el extemo del último. S c S - L est es un cso
Sum de ectoes Si tienen el mismo punto de plicción se tzn plels cd ecto po el extemo del oto. Si están uno continución de oto, se une el oigen del pimeo con el extemo del último. S c S - L est es un cso
