TEMA 38. Trigonometría Plana. Resolución de triángulos. Aplicaciones
|
|
|
- María Carmen Giménez Godoy
- hace 7 años
- Vistas:
Transcripción
1 TEMA 8. Trigonometrí Pn. Resouión de triánguos. Apiiones. Introduión. E origen de pr trigonometrí es de origen griego ( trigo-triánguo, metron-medid). Así medinte e estudio de trigonometrí podemos estudir s reiones entre os 6 eementos que o formn ( ánguos y dos). Como veremos on sóo eementos de os 6 (siempre que uno menos se un do) podemos determinr e vor de os otros. E triánguo y sus propieddes son sin ningun dud e poígono más estudido, su importni reside en que todo poígono se puede desomponer en triánguos. Destr e impuso geometrí, y en prtiur geometrí de triánguo en Grei ási de mnos de mtemátios importntes omo Pitágors, Tes o Ptoomeo. Ls rzones trigonométris de os triánguos retánguos ern y onoids en Grei ási, Ptoomeo tení ts de vores de s misms respeto os ánguos undo estos umentn de medio en medio grdo. En Ed Modern trigonometrí tuvo grn importni de mnos de stronomí, surge sí e onepto de funión trigonométri. Copérnio en su iro fundment dedi e primer pítuo trigonometrí. En tuidd s funiones trigonométris son utiizds en muos mpos de físi y ingenierí: meáni, inéti, y en gener en tods s mgnitudes vetories trigonometrí es ási pr desomposiión vetori de vetor.. E ánguos. Definiión y distints uniddes de medid... Definiión de ánguos Dds dos semirrets on origen en omún e ánguo que formn es e espio omprendido entre ms, definiendo sí dos ánguos: - Interior: ánguo menor (menos prte de pnno) - Exterior: ánguo myor (myor prte de pno) Los ánguos tiene sentido, sí e sentido positivo es e ntiorrio, siendo negtivo e orrio... Uniddes de medi de os ánguos. Pr medir os ánguos se usn tres ess de medid, tods sds en irunfereni:. Grdos sexgesimes: e vor de un ánguo en grdos sexgesimes se sn en e signr e ánguo de un irunfereni e vor de 60 o. Pr ur e ánguo formdo por dos semirrets se e por proporionidd entre superfiie de setor irur y e iruo de mismo rdio: α60 o resetor reiruo. Grdos entesimes: en est es irunfereni form un ánguo de 400 o g. A igu que os grdos sexgesimes se ur por proporionidd on e áre de setor que oup y e de íruo de mismo rdio: α400 o resetor g reiruo Jose Luis Lorente (preprdor oposiiones seundri
2 . Rdines: un rdin es e ánguo que e que e ro que oup e ánguo se igu rdio de irunfereni. En un irunfereni y π rd, uego podemos ur de form equivente os sos nteriores os grdos en rdines omo resetor απ reiruo Pr onvertir uns uniddes en otrs st on usr equiveni 60 o 400 o gπ rd... Rngo de os ánguos. Desde un punto de vist geométrio os ánguos definidos entre e ánguo nuo, definid omo e interior de dos semirrets oinidentes(0 o 0 o g0rd) y e ánguo rdo por tod irunfereni, exterior de s nteriores dos semirrets (60 o 400 o gπrd). Si e estudio se e desde un punto de vist nítio (funiones irures) e ánguo puede tomr uquier vor re, α R. Si queremos definir un ánguo fuer de rngo [0,60 o ) de mner geométri no tenemos más que tomr móduo 60, es deir quedrnos on e resto de dividir e vor de α entre 60 o. Ejempo: 760 O 40 O.. Propieddes fundmentes de os triánguos. En este prtdo veremos dos propieddes fundmentes (teorems) pr resouión de os triánguos: Teorem de Pitágors y Teorem de os ánguos de un triánguo. Teorem de Pitágors: En todo triánguo retánguo (un ánguo reto o de 90 o ) e udrdo de ipotenus (e opuesto ánguo reto) es igu sum de os udrdos de os tetos (os otros dos dos). + Demostrión: es uno de os teorems más demostrdos y de más diferentes forms. En est demostrión usremos un de s más ásis sd en e áuo de áre de un udrdo dividió en 4 triánguos y un udrdo más pequeño de do igu ipotenus. áre tot t udrdo grnde (+) + + re totre udrdo pequeño +4 tringuo +4 / + Igundo: + + +, despejndo + Teorem de os ánguos: sum de os ánguos de todo triánguo es 80 o : o A ˆ + Bˆ + Cˆ 80 Demostrión: trzmos por un vértie de triánguo un ret pre do opuesto, formándose trs ánguos que por preismo son igues os de triánguo, y por tnto sum un ánguo no, es deir 80 o : Jose Luis Lorente (preprdor oposiiones seundri
3 4. Rzones trigonométris. Definiión y propieddes. 4. Definiión de rzones prtir de triánguos (ánguos gudos) Los triánguos retánguos semejnz se umpe si tienen entre sí un ánguo omún (demás de ánguo reto). Como semos os dos de os triánguos semejntes son proporiones, por tnto siendo e ánguo de este triánguo retánguo quedrn determinds os vores de s reiones de os dos de uquier triánguo retánguo on este ánguo fijdo. Ests rzones entre os dos se mn rzones trigonométris: α sen( os( tg( teto opuesto ipotenus teto ontiguo ipotenus teto opuesto teto ontiguo Es importnte drse uent que e vor de s rzones trigonométris depende de ánguo y no de triánguo. E ánguo en est definiión umpe α (0 o,90 o ) Como semos prtir de teorem de Pitágors e vor de ipotenus () de un triánguo es myor que e de os dos tetos ( y ), por tnto se umpe que:0<sen(<, 0<os(< undo α (0,90º). A prtir de ests rzones trigonométris fundmentes podemos definir s siguientes: se( os( ose( sen( ipotenus teto opuesto ipotenus teto ontiguo tetoontiguo otg( tg( tetoopuesto Jose Luis Lorente (preprdor oposiiones seundri
4 4.. Rzones trigonométris de uquier ánguo. Pr poder definir s rzones de ánguos de más de 90 o tenemos que definir primermen- te irunfereni goniométri: siendo irunfereni entrd en e origen de rdio unidd (x +y ), de form que d punto de mism define un ánguo midiéndose on reión eje positivo de siss. De est form I udrnte α [0,90 o ], II udrnte α [90 o,80 0 ], III udrnte α [80 0, 70 o ], IV udrnte α[70 o,60 o ]. Sore est irunfereni podemos definir e seno, oseno y tngente de uquier ánguo de siguiente form: sen(coordend y de puntop y os(coordend x de puntop x tg(p y /P x A prtir de est definiión podemos representr tngente y s demás rzones trigo- nométris prtir de definiión y usndo triánguos semejntes donde e denomindor de s rzones trigonométris se g igu. Vemos en os 4 udrntes. Signo de s rzones trigonométris: sen( os( tg( I Cudrnte + + II Cudrnte + - III Cudrnte - - IV Cudrnte Not: si α>60 o se divide entre 60 o y se tom e resto (o que ddo después de n vuets) Jose Luis Lorente (preprdorr oposiiones seundri 4
5 4.. Propieddes eementes. A prtir de definiión de s rzones trigonométri, es deir que P(os(,sen() es un punto de irunfereni se umpen s siguientes propieddes que reionn s rzones trigonométris. Propiedd : se umpe que seno y oseno ven entre y -: - sen(, - os( -. Propiedd : reión fundment, sen (+os (. Not: sen ((sen() Propiedd : Reión on tngente. Propiedd 4: +, + Demostriones: Propiedd : omo sen( y os( son oordends de os puntos de irunfereni de rdio unidd se umpe que siempre serán menores o igues (extremos) unidd Propiedd : ser P(os(, sen() perteneiente irunfereni unidd se umpe euión irunfereni x +y sen (+os ( Propiedd : Por definiión de tngente tg(p y /P x Propiedd 4: +tg (+ 5. Rzones trigonométris en ánguos notes. α0,90 o, 80 o, 70 o : α0 o 0 rd: P(,0) α90 o π/rd:p(0,) α80 o π rd: P(-,0) α70 o π/rd: P(0,-) sen( os( 0-0 tg( 0 0 α0 o, 45 o, 60 o : α0 o π/6 rd α45 o π/4rd α60 o π/ rd sen( os( tg( Demostrión 0 o y 60 o prtir de triánguo equiátero: 0 o 60 o + ( ) sen(0)os(60) / sen(60)os(0) Jose Luis Lorente (preprdor oposiiones seundri 5
6 Demostrión de 45 o prtir de triánguo isósees retánguo: 45 o sen(45 o )os(45 o ) 45 o 6. Pso primer udrnte. En este prtdo vmos reionr s riones trigonométris situds en os udrntes II, III y IV on s rzones situds en e I udrnte. ) Ánguos ompementrios (α +α 90 o π/ rd) Se umpe s siguientes reiones: os 90 sen 90 otg 90 ) Ánguos supementrios (α +α 80 o π rd). De II I udrnte sen 80 os 80 tg 80 Jose Luis Lorente (preprdor oposiiones seundri 6
7 ) Ánguos que difieren 80 o (α α + 80 o ). De III I udrnte sen 80+ os 80+ tg 80+ 4) Ánguos que sumn 60 o (α +α 60 o ). De IV I udrnte sen 60 os 60 tg Rzones trigonométris ánguos sum, difereni doe y mitd. 7.. Rzones trigonométris ánguo sum. En este prtdo vmos ver s rzones trigonométris de os ánguos sum: () sen(α+β)sen( os(β)+os( sen(β) () os(α+β)os( os(β)-sen( sen(β) () tg(α+β) β β Demostrión: Pr demostrr () y () nos poyremos en siguiente figur, donde tenemos tres triánguos retánguos. β β sen(α+β) + os +sen( os( sen(β)+sen( os(β) os(α+β) os β os β Jose Luis Lorente (preprdor oposiiones seundri 7
8 Pr ur tngente o remos en funión de sen(α+β) y os(α+β): β β β β β β β β +β β β β β β β 7.. Rzones trigonométris ánguo difereni. En este prtdo vmos ver s rzones trigonométris de os ánguos difereni: () sen(α-β)sen( os(β)-os( sen(β) () os(α-β)os( os(β)+sen( sen(β) () tg(α-β) β β Demostrión: sen(α-β)sen(α+(-β)) y os(α+(-β)) y utiizndo que sen(-β)-sen(β), os(-β)os(β), tg(-β)-tg(β) 7.. Rzones trigonométris ánguo doe Ls rzones de os ánguos does es: () sen( sen( os( () os(os (-sen ( () tg( Demostrión: sin más que pir s rzones trigométris de ánguo sum sen(sen(α+, os(os(α+ y tg(tg(α Rzones trigonométris ánguo mitd. Rzones trigonométris de ánguo mitd: () sen( () os( () tg( os( + os( os( + os( Demostrión: en e prtdo nterior en e os( renomrmos α omo α, y entones α será α/: os(os (α/)-sen (α/)- sen (α/). Despejndo sen(α/) tenemos igudd primer. Pr otener segund no tenemos más que poner e sen (-os ( y despejr e oseno. L tngente se otiene dividiendo () entre (). Jose Luis Lorente (preprdor oposiiones seundri 8
9 8. Trnsformiones rzones trigonométris sums en produto. Mus vees resut interesnte expresr un sum de rzones trigonométris, de igu o diferente rgumento, omo un produto de otrs rzones trigonométris. E ejempo más rifidor de su utiidd es resouión de un euión trigonométri donde trnsformr sum en produto otendremos un euión ftorizd. Ls trnsformiones son: A+ B A B () sen( A) + sen( B) sen os A+ B A B () sen( A) sen( B) os sen A+ B A B () os( A) + os( B) os os A+ B A B (4) os( A) os( B) sen sen () sen( x) os( () os( x) sen( () os( x) os( (4) sen( x) sen( ( sen( x+ + sen( x ) ( sen( x+ sen( x ) ( os( x+ + os( x ) ( os( x+ os( x ) Demostrión: demostrremos s iguddes de udro de dere pues os de izquierd se deduen de nterior, mndo Ax+y, Bx-y. L demostrión se e prtir de ánguo sum y rest de seno y de oseno: () sen(x+sen(x)os(+os(x)sen( () os(x+os(x)os(-sen(x)sen( () sen(x-sen(x)os(-os(x)sen( (d) os(x+os(x)os(+sen(x)sen( ()+() ()sen(x++sen(x- sen(x)os(; ()-()(); ()+(d)() y ()-(d)(4) 9. Resouión de triánguos retánguos E triánguo retánguo es que que tiene un ánguo reto, de 90 o. En este triánguo e do opuesto ánguo reto se m ipotenus,, y os otros dos dos tetos, y. Podemos pir en estos triánguos: () Sum de ánguos ( + 90) () Teorem de Pitágors: + () Rzones trigonométris. Pr resover un triánguo retánguo neesitmos tener dos dtos (uno un do).. Conoido os dos tetos ( y ): +, Bˆ rtg, Cˆ 90 o Bˆ. Conoido un teto y ipotenus ( y ):, Bˆ rsen, Cˆ 90 o Bˆ. Conoido ánguo e ipotenus (Bˆ y ): sen(bˆ ), os(bˆ ), Cˆ 90 o Bˆ 4. Conoido ánguo y teto ontiguo (Bˆ y ): tg(bˆ ), /os(bˆ ), Cˆ 90 o Bˆ 5. Conoido ánguo y teto opuesto (Bˆ y ): /tg(bˆ ), /sen(bˆ ), Cˆ 90 o Bˆ Jose Luis Lorente (preprdor oposiiones seundri 9
10 0. Resouión de triánguos no retánguos. 0.. Teorems de seno y oseno. Pr resover triánguos no retánguos no podemos pir Pitágors ni rzones trigoteorems nuevos: nométris, sóo e teorem de sum de os tres ánguos. Se neesitn dos Teorem de oseno o de Pitágors generizdo: () + - os(a) () + - os(b) () + - os(c) Demostrión: A Si A90 o () T. de Pitágors, ()os(b)/,() os(c)/ x sen(c) y os(c) x x +(- sen (C)+ + os (C)- os(c) + - os(c) C y B Teorem de seno: sen( A) sen( B) Demostrión: sen ( ) R on Rrdio irunfereni irunsrit. Ddo e triánguo ABC, denotmos por O su irunentro y diuj- Proongndo e segmen- mos su irunfereni irunsrit. to BO st ortr irunfereni, se otiene un diámetro BP. Aor, e triánguo PBC es reto, puesto que BP es un diámetro, y demás os ánguos A y P son igues, porque mos son ánguos insritos que ren e segmento BC (Vése definiión de ro - seno, se pz). Por definiión de funión trigonométri tiene: sen(a)sen(p) BC BP R 0.. Resouión triánguos no retánguos. Tenemos vrios sos:. Conoemos os tres + - os(a) + - os(b) C80-B-A Podemos er o mismo sore os dos y : sen(b)/r y sen(c)/r. Despejndo R otenemos e teorem dos:,,. Aros(( + - )/( )) Bros(( + - )/( )) Se umpe que siempre existirá souión, C>0, si e do myor menor que sum de os otros dos y e menor myor que rest de os otros dos. Jose Luis Lorente (preprdorr oposiiones seundri 0
11 . Conoemos un do y dos ánguos: A80-B-C sen(b)/sen(a) sen(c)/sen(a) Siempre un souión.. Conoemos dos dos y ánguo omprendido (por ejempo,, C) ( + - os(c)) / Brsen( sen(c)/) A80-B-C Siempre un souión. 4. Conoemos dos dos y e ánguo opuesto uno de eos (por ejempo,,a) Este so es e más ompejo, pudiendo e proem no tener souión, un o inuso dos: Brsen( sen(a)/) < sen(a) : entonesnosouión o ) Si < opiones: sen(a) :B90 y e proemunsouión B > AyC 80 B > sen(a) :sen(b)<dossouiones: B 80 B, C 80 B ) Si entones BA y C80 o -A (no souión si A 90 ο ) ) > souión úni: Brsen( sen(a)/) on souión que g B<A y C80-B-A.. Apiiones geométris. Ls piiones geométris de s rzones trigonométris y de os teorems de seno y oseno son muy mpis, pues todo proem métrio que pued identifirse on un triánguo se puede resover on ests expresiones omo emos visto en os prtdos nteriores. Ejempo : Cáuo de tur de un edifiio onoido un ánguo y distni orizont: d tg( d α Jose Luis Lorente (preprdor oposiiones seundri
12 90 o -α' Si se no esie (dtos α, β y d) d α' α Sistem: (d+x) tg( x tg(β) Operndo β β α x d Ejempo : áuo áre de poígono regur de n dos de ongitud α60/n80/n tg( / p α re. Conusiones L trigonometrí es fundment pr resouión de proems métrios, sí omo pr desomposiión de vetores. Su piión ene e mundo de s ienis e ingenierí es muy mpio. En e urríuo de 4º ESO (s dos opiones) se ord trigonometrí, sí omo resouión de triánguos retánguos. En º de Bierto de Cienis trigonometrí es tmién otr unidd didáti, en este so demás de repsr o visto en e urso nterior tmién se trj os teorems de seno y oseno y resouión de triánguos uesquier, no sóo retánguos. Jose Luis Lorente (preprdor oposiiones seundri
Colegio Nuestra Señora de Loreto TRIGONOMETRÍA 4º E.S.O.
 TRIGONOMETRÍ 4º E.S.O. Frniso Suárez Bluen TRIGONOMETRÍ PREVIOS. Teorem de Tles (Semejnz) Si ortmos dos rets por un serie de rets prlels, los segmentos determindos en un de ells son proporionles los segmentos
TRIGONOMETRÍ 4º E.S.O. Frniso Suárez Bluen TRIGONOMETRÍ PREVIOS. Teorem de Tles (Semejnz) Si ortmos dos rets por un serie de rets prlels, los segmentos determindos en un de ells son proporionles los segmentos
DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS
 7 REPSO Y POYO OJETIVO DISTINGUIR LS RZONES TRIGONOMÉTRICS Nomre: Curso: Feh: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
7 REPSO Y POYO OJETIVO DISTINGUIR LS RZONES TRIGONOMÉTRICS Nomre: Curso: Feh: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
NOMBRE: CURSO: FECHA: coseno. a (cateto contiguo dividido entre hipotenusa) cos α = c a = 4 5
 00 _ 00-06.qd 9/7/0 9:7 Págin RAZONES OBJETIVO TRIGONOMÉTRICAS Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen = (teto opuesto dividido entre ipotenus)
00 _ 00-06.qd 9/7/0 9:7 Págin RAZONES OBJETIVO TRIGONOMÉTRICAS Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen = (teto opuesto dividido entre ipotenus)
DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS
 7 REPASO Y APOYO OBJETIVO DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS Nomre: Curso: Fe: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
7 REPASO Y APOYO OBJETIVO DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS Nomre: Curso: Fe: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
TRIGONOMETRÍA. 1. ÁNGULOS 1.1. Ángulo en el plano Criterios de orientación de ángulo Sistema de medida de ángulos. Sistema sexagesimal
 . ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
. ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
APUNTE: TRIGONOMETRIA
 APUNTE: TRIGONOMETRIA UNIVERSIDAD NACIONAL DE RIO NEGRO Asigntur: Mtemáti Crrers: Li. en Eonomí Profesor: Prof. Mel S. Chresti Cutrimestre: ero Año: 06 o Coneptos Previos o Definiión de ángulo Un ángulo
APUNTE: TRIGONOMETRIA UNIVERSIDAD NACIONAL DE RIO NEGRO Asigntur: Mtemáti Crrers: Li. en Eonomí Profesor: Prof. Mel S. Chresti Cutrimestre: ero Año: 06 o Coneptos Previos o Definiión de ángulo Un ángulo
TRIGONOMETRÍA (4º OP. A)
 SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
1 RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
 T3: TRIGONOMETRÍ 1º T 1 RESOLUIÓN DE TRIÁNGULOS RETÁNGULOS Resolver un triángulo es llr ls longitudes de sus ldos y ls mplitudes de sus ángulos. Ls fórmuls que se plin son: ) Ls rzones trigonométris: ˆ
T3: TRIGONOMETRÍ 1º T 1 RESOLUIÓN DE TRIÁNGULOS RETÁNGULOS Resolver un triángulo es llr ls longitudes de sus ldos y ls mplitudes de sus ángulos. Ls fórmuls que se plin son: ) Ls rzones trigonométris: ˆ
1.- MEDIDA DE ÁNGULOS. - El sistema sexagesimal que usa como unidad de medida el grado. Un grado es la 90-ava parte del ángulo recto.
 º Bhillerto Mtemátis I Dpto de Mtemátis- I.E.S. Montes Orientles (Iznlloz)-Curso 0/0 TEMAS 4 y 5.- RESOLUCIÓN DE TRIÁNGULOS. FUNCIONES FÓRMULAS TRIGONOMÉTRICAS Pr medir ángulos se suelen usr dos sistems
º Bhillerto Mtemátis I Dpto de Mtemátis- I.E.S. Montes Orientles (Iznlloz)-Curso 0/0 TEMAS 4 y 5.- RESOLUCIÓN DE TRIÁNGULOS. FUNCIONES FÓRMULAS TRIGONOMÉTRICAS Pr medir ángulos se suelen usr dos sistems
UNIDAD 2 Geometría 2.2 Triángulos 10
 UNI Geometrí. Triánguos 10. Triánguos OJETIVOS ur e áre e perímetro de triánguos. Otener os dos ánguos de triánguos utiizndo s reiones entre otros ánguos en figurs geométris. ur os dos de un triánguo usndo
UNI Geometrí. Triánguos 10. Triánguos OJETIVOS ur e áre e perímetro de triánguos. Otener os dos ánguos de triánguos utiizndo s reiones entre otros ánguos en figurs geométris. ur os dos de un triánguo usndo
TRIGONOMETRÍA. 4º E.S.O. Académicas AB = OA
 ÁNGULO. GRDO. TRIGONOMETRÍ El grdo es l medid de d uno de los ángulos que resultn l dividir el ángulo reto en 90 prtes igules. Su símolo es el º. 4º E.S.O. démis IRUNFERENI GONIOMÉTRI ÁNGULO. RDIÁN. 90º
ÁNGULO. GRDO. TRIGONOMETRÍ El grdo es l medid de d uno de los ángulos que resultn l dividir el ángulo reto en 90 prtes igules. Su símolo es el º. 4º E.S.O. démis IRUNFERENI GONIOMÉTRI ÁNGULO. RDIÁN. 90º
TEMA 39. Geometría del triángulo.
 TEM 9. Geometrí del triángulo. TEM 9. Geometrí del triángulo.. Introduión. El triángulo es el polígono ms estudido, su importni reside en ls múltiples propieddes que estos tienen y que todos los polígonos
TEM 9. Geometrí del triángulo. TEM 9. Geometrí del triángulo.. Introduión. El triángulo es el polígono ms estudido, su importni reside en ls múltiples propieddes que estos tienen y que todos los polígonos
α A TRIGONOMETRÍA PLANA
 TRIGONOMETRÍ PLN El origen de l plr trigonometrí puede enontrrse en el griego, trígono triángulo y metrí medid. L trigonometrí justmente trt de eso, l mediión y resoluión de situiones donde se preten triángulos.
TRIGONOMETRÍ PLN El origen de l plr trigonometrí puede enontrrse en el griego, trígono triángulo y metrí medid. L trigonometrí justmente trt de eso, l mediión y resoluión de situiones donde se preten triángulos.
22. Trigonometría, parte II
 22. Trigonometrí, prte II Mtemátis II, 202-II 22. Trigonometrí, prte II Extensión del dominio Se P un punto sore l irunfereni x 2 + 2 =. Est irunfereni tiene rdio entro el origen O(0, 0). Denotmos por
22. Trigonometrí, prte II Mtemátis II, 202-II 22. Trigonometrí, prte II Extensión del dominio Se P un punto sore l irunfereni x 2 + 2 =. Est irunfereni tiene rdio entro el origen O(0, 0). Denotmos por
1. Definición de Semejanza. Escalas
 Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS
 TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS L trigonometrí es l prte de ls mtemátis que estudi ls reliones métris entre los elementos de un tringulo. A) RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS L trigonometrí es l prte de ls mtemátis que estudi ls reliones métris entre los elementos de un tringulo. A) RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
7 Semejanza. y trigonometría. 1. Teorema de Thales
 7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
Tema 5. Semejanza. Tema 5. Semejanza
 Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
TRIGONOMETRÍA II = = ; procediendo igual que antes, pero con h : longitudes de los lados son proporcionales a los senos de los ángulos opuestos).
 TEMA: 1. TEOREMA DE LOS SENOS despejndo h de ms igulddes: En generl tendremos que resolver triángulos no retángulos, y, en ellos, no es posile plir ls definiiones de ls rzones trigonométris de sus ángulos.
TEMA: 1. TEOREMA DE LOS SENOS despejndo h de ms igulddes: En generl tendremos que resolver triángulos no retángulos, y, en ellos, no es posile plir ls definiiones de ls rzones trigonométris de sus ángulos.
Semejanza. 2. Relación entre perímetros, áreas y volúmenes de figuras semejantes 51
 Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
I.E.S. Ciudad de Arjona Departamento de Matemáticas. 1º BAC
 I.E.S. Ciudd de Arjon Deprtmento de Mtemátis. º BAC UNIDAD : TRIGONOMETRÍA. MEDIDAS DE ÁNGULOS. GRADOS: Un grdo sexgesiml es el ángulo orrespondiente un de ls 60 prtes en que se divide el ángulo entrl
I.E.S. Ciudd de Arjon Deprtmento de Mtemátis. º BAC UNIDAD : TRIGONOMETRÍA. MEDIDAS DE ÁNGULOS. GRADOS: Un grdo sexgesiml es el ángulo orrespondiente un de ls 60 prtes en que se divide el ángulo entrl
MATEMÁTICA MÓDULO 3 Eje temático: Geometría
 MATEMÁTICA MÓDULO 3 Eje temátio: Geometrí 1. SEGMENTOS PROPORCIONALES EN EL TRIÁNGULO RECTÁNGULO En el ABC retángulo en C de l figur: Se pueden estbleer ls siguientes semejnzs: 1) De est semejnz, se obtienen
MATEMÁTICA MÓDULO 3 Eje temátio: Geometrí 1. SEGMENTOS PROPORCIONALES EN EL TRIÁNGULO RECTÁNGULO En el ABC retángulo en C de l figur: Se pueden estbleer ls siguientes semejnzs: 1) De est semejnz, se obtienen
TRIGONOMETRÍA. =60 ; 1 = de 1 1 =60 60
 TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS Pr medir ángulos se utilizn: 1. Sistem sexgesiml: L unidd de medid en este sistem es el grdo sexgesiml Un ángulo mide un grdo sexgesiml (1 0 ) si su ro entrl
TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS Pr medir ángulos se utilizn: 1. Sistem sexgesiml: L unidd de medid en este sistem es el grdo sexgesiml Un ángulo mide un grdo sexgesiml (1 0 ) si su ro entrl
Departamento: Física Aplicada III
 Fund mentos Físi os de l Ingenierí. (Ind ustri les) Prlelogrmo insrito en trpezoide Ddo un trpezoide (udrilátero irregulr que no tiene ningún ldo prlelo otro), demuestre, usndo el álger vetoril, que los
Fund mentos Físi os de l Ingenierí. (Ind ustri les) Prlelogrmo insrito en trpezoide Ddo un trpezoide (udrilátero irregulr que no tiene ningún ldo prlelo otro), demuestre, usndo el álger vetoril, que los
02) Mediciones. 0204) Geometría Básica
 Págin 1 0) Mediciones 004) Geometrí Básic Desrrodo por e Profesor Rodrigo Vergr Rojs Octubre 007 Octubre 007 Págin A) Ánguos Grdo Sexgesim Si se divide un circunferenci de rdio R en 360 sectores igue (ver
Págin 1 0) Mediciones 004) Geometrí Básic Desrrodo por e Profesor Rodrigo Vergr Rojs Octubre 007 Octubre 007 Págin A) Ánguos Grdo Sexgesim Si se divide un circunferenci de rdio R en 360 sectores igue (ver
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 03 - Ministerio de Eduión Universidd Tenológi Nionl Fultd Regionl Rosrio
1. Razones trigonométricas en triángulos rectángulos. (Ángulos agudos)
 Trigonometrí (I). Rzones trigonométris en triángulos retángulos. (Ángulos gudos).... Reliones trigonométris fundmentles.... Rzones trigonométris de 0º, 45º y 60º... 4 4. Resoluión de triángulos retángulos....
Trigonometrí (I). Rzones trigonométris en triángulos retángulos. (Ángulos gudos).... Reliones trigonométris fundmentles.... Rzones trigonométris de 0º, 45º y 60º... 4 4. Resoluión de triángulos retángulos....
Haga clic para cambiar el estilo de título
 Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
Definiciones de seno, coseno OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Definiciones de seno, coseno y tangente.
 89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
Trigonometría Ing. Avila Ing. Moll
 Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de un triángulo o de un figur
Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de un triángulo o de un figur
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA
 SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 007 - Noiones de Trigonometrí: L trigonometrí se dedi l estudio de ls reliones que existen entre ls medids de los ángulos y ldos de un triángulo.
SECRETARÍA ACADÉMICA ÁREA DE INGRESO MATEMÁTICA - Septiemre de 007 - Noiones de Trigonometrí: L trigonometrí se dedi l estudio de ls reliones que existen entre ls medids de los ángulos y ldos de un triángulo.
Unidad didáctica 4. Trigonometría plana
 Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS. Para medir ángulos se utilizan:
 TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS Pr medir ángulos se utilizn:. Sistem sexgesiml: L unidd de medid en este sistem es el grdo sexgesiml Un ángulo mide un grdo sexgesiml ( 0 ) si su ro entrl orrespondiente,
TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS Pr medir ángulos se utilizn:. Sistem sexgesiml: L unidd de medid en este sistem es el grdo sexgesiml Un ángulo mide un grdo sexgesiml ( 0 ) si su ro entrl orrespondiente,
Matemática Diseño Industrial Trigonometría Ing. Avila Ing. Moll
 Mtemáti Diseño Industril Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de
Mtemáti Diseño Industril Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de
TRIGONOMETRIA. Diremos que un ángulo tiene medida positiva si la medición se realiza en sentido antihorario y negativo en sentido horario.
 TRIGONOMETRI. Introduión. Medids de ángulos Ángulos orientdos. onsiderremos los ejes rtesinos, y representremos sore ellos los ángulos de tl form que el vértie oinid on el origen de oordends, y uno de
TRIGONOMETRI. Introduión. Medids de ángulos Ángulos orientdos. onsiderremos los ejes rtesinos, y representremos sore ellos los ángulos de tl form que el vértie oinid on el origen de oordends, y uno de
Geometría. Ángulos. Complementarios y suplementarios. Clasificación de los ángulos. Lados paralelos. Lados perpendiculares
 Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. Jesús Grcí de Jón de Fuente IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios
Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. Jesús Grcí de Jón de Fuente IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 7 Pág. Págin 66 PRTI Rzones trigonométris de un ángulo gudo Hll ls rzones trigonométris del ángulo en d uno de estos triángulos: ) ) ), m, m,6 m 8, m m 8, m ) sen, 0, os 0, 0,89 tg 0, 0,, 0,89 ) tg,6,
7 Pág. Págin 66 PRTI Rzones trigonométris de un ángulo gudo Hll ls rzones trigonométris del ángulo en d uno de estos triángulos: ) ) ), m, m,6 m 8, m m 8, m ) sen, 0, os 0, 0,89 tg 0, 0,, 0,89 ) tg,6,
Lados Vértice complementarios CONVEXO CÓNCAVO suplementarios
 Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios CÓNCAVO CONVEXO Dos ánguos
Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios CÓNCAVO CONVEXO Dos ánguos
Una condición necesaria y suficiente para que el triangulo PBP sea equilátero es que el ángulo HBP sea 30º. b que es la relación buscada.
 Hoj de Prolems Geometrí III 49. Dd l elipse, si tommos el etremo B de ordend positiv del eje menor omo entro, se desrie un irunfereni de rdio igul diho eje menor, ortr l elipse en dos punto P P. Determinr
Hoj de Prolems Geometrí III 49. Dd l elipse, si tommos el etremo B de ordend positiv del eje menor omo entro, se desrie un irunfereni de rdio igul diho eje menor, ortr l elipse en dos punto P P. Determinr
Razones trigonométricas de un ángulo agudo. Relaciones fundamentales
 B C Mtemátis I - º Billerto Rzones trigonométris de un ángulo gudo. Reliones fundmentles En todo triángulo retángulo BC ls rzones trigonométris (seno, oseno y tngente) de uno de sus ángulos gudos, en este
B C Mtemátis I - º Billerto Rzones trigonométris de un ángulo gudo. Reliones fundmentles En todo triángulo retángulo BC ls rzones trigonométris (seno, oseno y tngente) de uno de sus ángulos gudos, en este
Razones trigonome tricas de un a ngulo agudo. Relaciones fundamentales
 Rzones trigonome tris de un ngulo gudo. Reliones fundmentles En todo triángulo retángulo C ls rzones trigonométris (seno, oseno y tngente) de uno de sus ángulos gudos, en este so, se definen de l siguiente
Rzones trigonome tris de un ngulo gudo. Reliones fundmentles En todo triángulo retángulo C ls rzones trigonométris (seno, oseno y tngente) de uno de sus ángulos gudos, en este so, se definen de l siguiente
2 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R
 1 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R MEDICIONES Semn 04 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R Equivenci entre rdines y grdos sexgesimes 1) Ánguos Definir os conceptos:
1 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R MEDICIONES Semn 04 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R Equivenci entre rdines y grdos sexgesimes 1) Ánguos Definir os conceptos:
c c a c a b b a c a A estas razones numéricas se les da el nombre: Si en cambio consideramos γ, resulta: Comparando (1), (2), (3), (4) obtenemos:
 TRIGONOMETRIA NOCIONES PREVIAS Si onsidermos tres vrills,, tles que puede onstruirse on ells un triángulo (siempre que se umpl que l medid de d vrill se menor que l sum de ls otrs dos mor que l difereni)
TRIGONOMETRIA NOCIONES PREVIAS Si onsidermos tres vrills,, tles que puede onstruirse on ells un triángulo (siempre que se umpl que l medid de d vrill se menor que l sum de ls otrs dos mor que l difereni)
Dados dos triángulos rectángulos PQR y P QR, se dice que son semejantes si tienen un mismo ángulo α en el vértice Q RQ R'Q RQ R'Q PQ P'Q
 1..Coneptos sore trigonometrí. 1.1. Definiión. 1.. Rzones de ángulos omplementrios. 1.3. Otr definiión de rzón trigonométri. 1.4. Rzones de ángulos otusos. 1.5. ngulos suplementrios 1.6. Ángulos que difieren
1..Coneptos sore trigonometrí. 1.1. Definiión. 1.. Rzones de ángulos omplementrios. 1.3. Otr definiión de rzón trigonométri. 1.4. Rzones de ángulos otusos. 1.5. ngulos suplementrios 1.6. Ángulos que difieren
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
UNIDAD VI LA ELIPSE 6.1. ECUACIÓN EN FORMA COMÚN O CANÓNICA DE LA ELIPSE
 UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
Áreas y perímetros. Egipcios y babilonios demostraron una cierta destreza calculando áreas de polígonos y volúmenes de
 13 Áres y perímetros GRUPO ANAYA, S.A. Mtemátics 1. ESO. Mteri fotocopie utorizdo. Egipcios y ionios demostrron un ciert destrez ccundo áres de poígonos y voúmenes de gunos cuerpos ( esto o mn cutur de
13 Áres y perímetros GRUPO ANAYA, S.A. Mtemátics 1. ESO. Mteri fotocopie utorizdo. Egipcios y ionios demostrron un ciert destrez ccundo áres de poígonos y voúmenes de gunos cuerpos ( esto o mn cutur de
11La demostración La demostración en matemáticas (geometría)
 L demostrión en mtemátis (geometrí) ág. 1 Tl vez los lumnos y lumns hyn demostrdo, en lgun osión, lgun fórmul o lgun propiedd mtemáti, o hyn ontempldo su demostrión. omo semos, pr ellos, el proeso no es
L demostrión en mtemátis (geometrí) ág. 1 Tl vez los lumnos y lumns hyn demostrdo, en lgun osión, lgun fórmul o lgun propiedd mtemáti, o hyn ontempldo su demostrión. omo semos, pr ellos, el proeso no es
INTRODUCCIÒN Solución de triángulos rectángulos
 INTRODUIÒN omo se vio en l unidd 1, l trigonometrí, se encrg de enseñr l relción entre los ldos y los ángulos de un tringulo. Es de sum importnci y que nos yud encontrr ls respuests en l físic, pr medir
INTRODUIÒN omo se vio en l unidd 1, l trigonometrí, se encrg de enseñr l relción entre los ldos y los ángulos de un tringulo. Es de sum importnci y que nos yud encontrr ls respuests en l físic, pr medir
PB' =. Además A PB = APB por propiedad de
 limpid de Mtemátis, Querétro GEMETRÍ: Trigonometrí, Áres, ílios, Ptolomeo Rosrio Velázquez 0 y de Junio, 005 PRLEM EL EXMEN ESTTL P es ulquier punto del interior de un triángulo. Sen, y los puntos medios
limpid de Mtemátis, Querétro GEMETRÍ: Trigonometrí, Áres, ílios, Ptolomeo Rosrio Velázquez 0 y de Junio, 005 PRLEM EL EXMEN ESTTL P es ulquier punto del interior de un triángulo. Sen, y los puntos medios
OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Rectas y puntos notables en un triángulo.
 Figurs pns INTRODUCCIÓN Ls figurs pns y e cácuo de áres son y conocidos por os umnos de cursos nteriores. Conviene, sin embrgo, señr presenci de s figurs pns en distintos contextos rees y destcr importnci
Figurs pns INTRODUCCIÓN Ls figurs pns y e cácuo de áres son y conocidos por os umnos de cursos nteriores. Conviene, sin embrgo, señr presenci de s figurs pns en distintos contextos rees y destcr importnci
Visualización de triángulos. Curso de Matemáticas para Física. Trigonometría. Trigonometría. Física I, Internet A b.
 Visulizión de triángulos Curso de Mtemátis pr Físi Curso de Mtemátis pr Físi Físi I, vi@ Internet 2004 B A C Físi I, vi@ Internet 2004 Visulizión de triángulos Fijémonos en un triángulo ulquier. Curso
Visulizión de triángulos Curso de Mtemátis pr Físi Curso de Mtemátis pr Físi Físi I, vi@ Internet 2004 B A C Físi I, vi@ Internet 2004 Visulizión de triángulos Fijémonos en un triángulo ulquier. Curso
Resumen creado por Hernán Verdugo Fabiani, profesor de Matemática y Física, abril 2011.
 Reliones métris en un triángulo Resumen redo or Hernán Verdugo Fini, rofesor de Mtemáti y Físi, ril 011. El estudio de un triángulo siemre revestido interés y or ello es ue existen un serie de desriiones,
Reliones métris en un triángulo Resumen redo or Hernán Verdugo Fini, rofesor de Mtemáti y Físi, ril 011. El estudio de un triángulo siemre revestido interés y or ello es ue existen un serie de desriiones,
AMPLIACIÓN DE TRIGONOMETRÍA
 Alonso Fernández Glián 1. EL TEOREMA DEL SENO AMPLIACIÓN DE TRIGONOMETRÍA 1.1. OTRA DEMOSTRACIÓN DEL TEOREMA DEL SENO 1.. MEDIDA DE UN ÁNGULO INSCRITO EN UNA CIRCUNFERENCIA 1.3. UN COROLARIO DEL TEOREMA
Alonso Fernández Glián 1. EL TEOREMA DEL SENO AMPLIACIÓN DE TRIGONOMETRÍA 1.1. OTRA DEMOSTRACIÓN DEL TEOREMA DEL SENO 1.. MEDIDA DE UN ÁNGULO INSCRITO EN UNA CIRCUNFERENCIA 1.3. UN COROLARIO DEL TEOREMA
Trigonometría. Prof. María Peiró
 Trigonometrí Prof. Mrí Peiró Trigonometri Funciones Trigonométrics Ls funciones trigonométrics son rzones o cocientes entre dos ldos de un triángulo rectángulo. Hy seis funciones trigonométrics: Directs
Trigonometrí Prof. Mrí Peiró Trigonometri Funciones Trigonométrics Ls funciones trigonométrics son rzones o cocientes entre dos ldos de un triángulo rectángulo. Hy seis funciones trigonométrics: Directs
U.T.N. F.R.C.U. Seminario Universitario Matemática. Módulo 6. Trigonometría
 U.T.N. F.R.C.U. Seminrio Universitrio Mtemáti Módulo 6 Trigonometrí L mtemáti ompr los más diversos fenómenos y desubre ls nlogís serets que los unen Joseph Fourier TRIGONOMETRÍA Pr omenzr trbjr on trigonometrí
U.T.N. F.R.C.U. Seminrio Universitrio Mtemáti Módulo 6 Trigonometrí L mtemáti ompr los más diversos fenómenos y desubre ls nlogís serets que los unen Joseph Fourier TRIGONOMETRÍA Pr omenzr trbjr on trigonometrí
F(x,y,z)=0 (2) Es decir la superficie S está formada por dos planos paralelos al plano coordenado xy
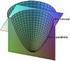 Estudio de Curvs Superfiies Euiones de superfiies: L superfiie más simpe sido motivo de nuestro estudio e es e pno L euión de mismo referido un sistem de oordends rtesino ortogon es ine en s vries ; es
Estudio de Curvs Superfiies Euiones de superfiies: L superfiie más simpe sido motivo de nuestro estudio e es e pno L euión de mismo referido un sistem de oordends rtesino ortogon es ine en s vries ; es
cos α sen α sen 0º 30º 45º 60º 90º cos 90º 60º 45º 30º 0º
 Preuniversitrio Populr Vítor Jr 7.. TRIGONOMETRÍA L trigonoetrí (del griego, trigono = tres ldos o triángulo, y etrí = edid) es l r de ls teátis que estudi ls reliones entre los ldos y los ángulos de triángulos,
Preuniversitrio Populr Vítor Jr 7.. TRIGONOMETRÍA L trigonoetrí (del griego, trigono = tres ldos o triángulo, y etrí = edid) es l r de ls teátis que estudi ls reliones entre los ldos y los ángulos de triángulos,
4º ESO ACADÉMICAS - APLICADAS TRIGONOMETRÍA DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa TRIGONOMETRÍA
 º ESO ACADÉMICAS - APLICADAS TRIGONOMETRÍA DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtínez-Los TRIGONOMETRÍA El polígono más senillo es el de tres ldos, el triángulo, es por ello que el estudio
º ESO ACADÉMICAS - APLICADAS TRIGONOMETRÍA DEPARTAMENTO DE MATEMÁTICAS. COPIRRAI_Julio Césr Ad Mrtínez-Los TRIGONOMETRÍA El polígono más senillo es el de tres ldos, el triángulo, es por ello que el estudio
OBJETIVO 1 DETERMINAR LAS RECTAS Y PUNTOS NOTABLES EN TRIÁNGULOS
 OJETIVO 1 DETERMINR LS RETS Y PUNTOS NOTLES EN TRIÁNULOS NOMRE: URSO: EH: RETS Y PUNTOS NOTLES DE UN TRIÁNULO Ls medins de un triánguo son s rects que unen cd uno de os vértices de triánguo con e punto
OJETIVO 1 DETERMINR LS RETS Y PUNTOS NOTLES EN TRIÁNULOS NOMRE: URSO: EH: RETS Y PUNTOS NOTLES DE UN TRIÁNULO Ls medins de un triánguo son s rects que unen cd uno de os vértices de triánguo con e punto
MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA
 MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA CURSO 4 TRIGONOMETRIA Y TRANSFORMACIONES GEOMETRICAS EN EL PLANO CARTA DIDÁCTICA Desripión: Con este
MINISTERIO DE EDUCACION CURSO DE POSTGRADO TERCER CICLO DE EDUCACION BASICA ESPECIALIDAD EN MATEMATICA CURSO 4 TRIGONOMETRIA Y TRANSFORMACIONES GEOMETRICAS EN EL PLANO CARTA DIDÁCTICA Desripión: Con este
Qué tienes que saber?
 Trigonometrí Qué tienes que sber? QUÉ tienes que sber? tividdes Finles Ten en uent Rzones trigonométris de un ángulo gudo, α: teto opuesto sen α hipotenus teto dyente os α hipotenus teto opuesto tgα teto
Trigonometrí Qué tienes que sber? QUÉ tienes que sber? tividdes Finles Ten en uent Rzones trigonométris de un ángulo gudo, α: teto opuesto sen α hipotenus teto dyente os α hipotenus teto opuesto tgα teto
- Aplicar la ley de Ohm en los circuitos puros de corriente alterna.
 9. CIRCUITOS SIMPLES DE CORRIENTE ALTERNA Conoidos los omponentes, hor se prenderá ómo se omportn de form individul l estr onetdos un fuente de limentión de orriente ltern. El onoimiento de l ley de Ohm
9. CIRCUITOS SIMPLES DE CORRIENTE ALTERNA Conoidos los omponentes, hor se prenderá ómo se omportn de form individul l estr onetdos un fuente de limentión de orriente ltern. El onoimiento de l ley de Ohm
GEOMETRÍA TRIÁNGULOS. 1. DEFINICIÓN: Si A, B y C son tres puntos no colineales entonces la unión de los segmentos
 MISIÓN 2011-2 ONGRUENI E TRIÁNGULOS GEOMETRÍ TRIÁNGULOS 1. EFINIIÓN: Si, y son tres puntos no oinees entones unión de os segmentos, y se denomin triánguo y se denot omo. = /, y son puntos no oinees 1.1.
MISIÓN 2011-2 ONGRUENI E TRIÁNGULOS GEOMETRÍ TRIÁNGULOS 1. EFINIIÓN: Si, y son tres puntos no oinees entones unión de os segmentos, y se denomin triánguo y se denot omo. = /, y son puntos no oinees 1.1.
SenB. SenC. c SenC = 3.-
 TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
TRIANGULOS OBLICUANGULOS Se llmn oliuángulos por que los ldos son oliuos on relión uno l otro, no formndo nun ángulos retos. Hy seis elementos fundmentles en un tringulo: los tres ldos y los tres ángulos,
4 Trigonometría UNIDAD
 UNIDAD 4 Trigonometrí ÍNDICE DE CONTENIDOS 1. Ángulos............................................ 77 1.1. Sistem sexgesiml................................. 77 1.2. Rdines........................................
UNIDAD 4 Trigonometrí ÍNDICE DE CONTENIDOS 1. Ángulos............................................ 77 1.1. Sistem sexgesiml................................. 77 1.2. Rdines........................................
Los triángulos se clasifican según la magnitud de sus lados y de sus ángulos internos. SEGÚN SUS LADOS EQUILÁTERO ISÓSCELES ESCALENO
 Unidd uno Geometrí y Trigonometrí 4. TRIÁNGULOS 4.1 Definiión y notión de triángulos El triángulo es un polígono de tres ldos. Los puntos donde se ortn se llmn vérties. Los elementos de un triángulo son:
Unidd uno Geometrí y Trigonometrí 4. TRIÁNGULOS 4.1 Definiión y notión de triángulos El triángulo es un polígono de tres ldos. Los puntos donde se ortn se llmn vérties. Los elementos de un triángulo son:
UNIDAD Nº 1: LAS RELACIONES TRIGONOMETRICAS Y SUS APLICACIONES, GUIA 2 DOCENTE: LIC ROSMIRO FUENTES ROCHA
 REPUBLICA DE COLOMBIA SECRETARIA DE EDUCACION DISTRITAL DE SANTA MARTA INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluión Nº 88 de noviemre.8/ Emnd de l Seretri De Eduión Distritl DANE Nº7-99
REPUBLICA DE COLOMBIA SECRETARIA DE EDUCACION DISTRITAL DE SANTA MARTA INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resoluión Nº 88 de noviemre.8/ Emnd de l Seretri De Eduión Distritl DANE Nº7-99
TEMA 6: INTEGRAL DEFINIDA. APLICACIONES.
 TEMA 6: INTEGRAL DEFINIDA. APLICACIONES.. Áre jo un urv El prolem que pretendemos resolver es el álulo del áre limitd por l gráfi de un funión f() ontinu y positiv, el eje X y ls siss = y =. Si l gráfi
TEMA 6: INTEGRAL DEFINIDA. APLICACIONES.. Áre jo un urv El prolem que pretendemos resolver es el álulo del áre limitd por l gráfi de un funión f() ontinu y positiv, el eje X y ls siss = y =. Si l gráfi
UNIDAD DE APRENDIZAJE IV
 UNIDAD DE APRENDIZAJE IV Seres procedimentles 1. Utiliz correctmente el lenguje lgerico, geométrico y trigonométrico.. Identific l simologí propi de l geometrí y l trigonometrí. 3. Identific ls uniddes
UNIDAD DE APRENDIZAJE IV Seres procedimentles 1. Utiliz correctmente el lenguje lgerico, geométrico y trigonométrico.. Identific l simologí propi de l geometrí y l trigonometrí. 3. Identific ls uniddes
GYMNÁZIUM BUDĚJOVICKÁ. MATEMÁTICAS. TRIGONOMETRÍA. EJERCICIOS IV: RESOLUCIÓN DE TRIÁNGULOS. PROBLEMAS.
 GYMNÁZIUM BUDĚJOVICKÁ MATEMÁTICAS TRIGONOMETRÍA EJERCICIOS IV: RESOLUCIÓN DE TRIÁNGULOS PROBLEMAS - Determinr ls longitudes de los ldos y los tmños de los ángulos interiores del triángulo ABC si semos:
GYMNÁZIUM BUDĚJOVICKÁ MATEMÁTICAS TRIGONOMETRÍA EJERCICIOS IV: RESOLUCIÓN DE TRIÁNGULOS PROBLEMAS - Determinr ls longitudes de los ldos y los tmños de los ángulos interiores del triángulo ABC si semos:
( ) X 100% Var = σ = X X. σ = X X. 0201) Información de. Mediciones. Valor Medido. Parámetros de Desviación. Generalidades. Promedio.
 Bsd en Oservción Experimentción Oservción en condiciones controds Percepciones Acción Cuittiv Cienci Se otienen Mediciones Acción Cuntittiv Vor Representtivo Indic Exctitud de conjunto de mediciones Por
Bsd en Oservción Experimentción Oservción en condiciones controds Percepciones Acción Cuittiv Cienci Se otienen Mediciones Acción Cuntittiv Vor Representtivo Indic Exctitud de conjunto de mediciones Por
BLOQUE 1.TRIGONOMETRIA. RESOLUCIÓN DE TRIÁNGULOS. 1ª Parte :Trigonometría:Resolución de triángulos.
 BLOQUE 1.TRIGONOMETRIA. RESOLUCIÓN DE TRIÁNGULOS 1ª Prte :Trigonometrí:Resolución de triángulos. 1.-Medid de ángulos. Un ángulo se puede medir en : )Grdos sexgesimles (DEG ó D) : 1º=60,1 =60. = 90º, =180º
BLOQUE 1.TRIGONOMETRIA. RESOLUCIÓN DE TRIÁNGULOS 1ª Prte :Trigonometrí:Resolución de triángulos. 1.-Medid de ángulos. Un ángulo se puede medir en : )Grdos sexgesimles (DEG ó D) : 1º=60,1 =60. = 90º, =180º
5. RECTA Y PLANO EN EL ESPACIO
 Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
XVI Encuentro Departamental de Matemáticas: La innovación en el proceso docente educativo en Matemáticas a partir de diferentes medios de aprendizaje
 XVI Enuentro Deprtmentl de Mtemátis: L innovión en el proeso doente edutivo en Mtemátis prtir de diferentes medios de prendizje y I Enuentro Deprtmentl de GeoGer Netmente intuitivos. Inextitud de los
XVI Enuentro Deprtmentl de Mtemátis: L innovión en el proeso doente edutivo en Mtemátis prtir de diferentes medios de prendizje y I Enuentro Deprtmentl de GeoGer Netmente intuitivos. Inextitud de los
a vectores a y b se muestra en la figura del lado derecho.
 Produto ruz o produto vetoril Otr form nturl de definir un produto entre vetores es trvés del áre del prlelogrmo determindo por dihos vetores. El prlelogrmo definido por los h vetores y se muestr en l
Produto ruz o produto vetoril Otr form nturl de definir un produto entre vetores es trvés del áre del prlelogrmo determindo por dihos vetores. El prlelogrmo definido por los h vetores y se muestr en l
DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE
 DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE ESPECIALISTA EN LA ENSEÑANZA DE LAS MATEMÁTICAS U de A INTRODUCCIÓN En el desrrollo de l geometrí
DETERMINACIÓN DE LOS PUNTOS NOTABLES DE UN TRIÁNGULO EN TÉRMINOS DE SUS LADOS HERNAN DARIO ORTIZ ALZATE ESPECIALISTA EN LA ENSEÑANZA DE LAS MATEMÁTICAS U de A INTRODUCCIÓN En el desrrollo de l geometrí
RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS
 Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
ECUACIONES DE PRIMER Y SEGUNDO GRADO
 UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
Lección 10: TRIÁNGULOS. Un triángulo es un polígono de tres ángulos y tres lados. También tiene tres vértices.
 1.- QUÉ ES UN TRIÁNGULO? Leión 10: TRIÁNGULOS Un triángulo es un polígono de tres ángulos y tres ldos. Tmién tiene tres vérties. ELEMENTOS DE UN TRIÁNGULO Ldo: Cd uno de los tres segmentos que limitn l
1.- QUÉ ES UN TRIÁNGULO? Leión 10: TRIÁNGULOS Un triángulo es un polígono de tres ángulos y tres ldos. Tmién tiene tres vérties. ELEMENTOS DE UN TRIÁNGULO Ldo: Cd uno de los tres segmentos que limitn l
CAPÍTULO 22: INTRODUCCIÓN A LA TRIGONOMETRÍA ESFÉRICA (III)
 CAPÍTULO 22: INTRODUCCIÓN A LA TRIGONOMETRÍA ESFÉRICA (III) Dnte Guerrero-Chnduví Piur, 2015 FACULTAD DE INGENIERÍA Áre Deprtmentl de Ingenierí Industril y de Sistems CAPÍTULO 22: INTRODUCCIÓN A LA TRIGONOMETRÍA
CAPÍTULO 22: INTRODUCCIÓN A LA TRIGONOMETRÍA ESFÉRICA (III) Dnte Guerrero-Chnduví Piur, 2015 FACULTAD DE INGENIERÍA Áre Deprtmentl de Ingenierí Industril y de Sistems CAPÍTULO 22: INTRODUCCIÓN A LA TRIGONOMETRÍA
FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL
 FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL El prolem de l práol horizontl Qué relión h entre ls propieddes nlítis de l funión udráti ls propieddes geométris de l práol horizontl? Como
FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL El prolem de l práol horizontl Qué relión h entre ls propieddes nlítis de l funión udráti ls propieddes geométris de l práol horizontl? Como
Elipse: Ecuación de la elipse dados ciertos elementos
 Elipse: Euión de l elipse ddos iertos elementos Tinoo, G. (013). Euión de l elipse ddos iertos elementos. [Mnusrito no publido]. Méxio: UAEM. Espio de Formión Multimodl Elipse vertil Si l elipse tiene
Elipse: Euión de l elipse ddos iertos elementos Tinoo, G. (013). Euión de l elipse ddos iertos elementos. [Mnusrito no publido]. Méxio: UAEM. Espio de Formión Multimodl Elipse vertil Si l elipse tiene
TRIGONOMETRÍA RESOLUCIÓN de TRIÁNGULOS
 TRIGONOMETRÍA RESOLUCIÓN de TRIÁNGULOS MATEMÁTICAS I º Bhillerto CCNN Alfonso González IES Fernndo de Men Dpto. de Mtemátis Mtemátis I TRIGONOMETRÍA REPASO de TRIGONOMETRÍA ELEMENTAL I.) Grdos y rdines:
TRIGONOMETRÍA RESOLUCIÓN de TRIÁNGULOS MATEMÁTICAS I º Bhillerto CCNN Alfonso González IES Fernndo de Men Dpto. de Mtemátis Mtemátis I TRIGONOMETRÍA REPASO de TRIGONOMETRÍA ELEMENTAL I.) Grdos y rdines:
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Trabajo Práctico N 9: APLICACIONES A LA GEOMETRÍA
 Fultd Regionl Mendo. UTN Álger Geometrí Anlíti 6 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni siendo que el segmento de etremos (- ; 3) (4; -) es diámetro
Fultd Regionl Mendo. UTN Álger Geometrí Anlíti 6 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni siendo que el segmento de etremos (- ; 3) (4; -) es diámetro
MAT I RESOLUCIÓN DE TRIÁNGULOS. «Mi pereza no me deja tiempo libre para nada» Escritor MATERIAL ÍNDICE:
 4 «Mi perez no me dej tiempo lire pr nd» Esritor MT I RESOLUIÓN DE TRIÁNGULOS ÍNDIE: MTERIL 1. RZONES TRIGONOMÉTRIS DE UN ÁNGULO GUDO (0º 90º). RZONES TRIGONOMÉTRIS DE UN ÁNGULO ULQUIER (0º 360º) 3. RZONES
4 «Mi perez no me dej tiempo lire pr nd» Esritor MT I RESOLUIÓN DE TRIÁNGULOS ÍNDIE: MTERIL 1. RZONES TRIGONOMÉTRIS DE UN ÁNGULO GUDO (0º 90º). RZONES TRIGONOMÉTRIS DE UN ÁNGULO ULQUIER (0º 360º) 3. RZONES
PROBLEMAS DE OLIMPIADAS MATEMÁTICAS SOBRE GEOMETRÍA El triángulo
 . PROLEMS DE OLIMPIDS MTEMÁTIS SORE GEOMETRÍ El triángulo ELISETH GONZÁLEZ FUENTES Máster de Mtemátis Universidd de Grnd. 014 Prolems sore triángulos Trjo Fin de Máster presentdo en el Máster Interuniversitrio
. PROLEMS DE OLIMPIDS MTEMÁTIS SORE GEOMETRÍ El triángulo ELISETH GONZÁLEZ FUENTES Máster de Mtemátis Universidd de Grnd. 014 Prolems sore triángulos Trjo Fin de Máster presentdo en el Máster Interuniversitrio
MAT I RESOLUCIÓN DE TRIÁNGULOS. «Mi pereza no me deja tiempo libre para nada» Escritor MATERIAL ÍNDICE:
 4 «Mi perez no me dej tiempo lire pr nd» Esritor MT I RESOLUIÓN DE TRIÁNGULOS ÍNDIE: MTERIL 1. RZONES TRIGONOMÉTRIS DE UN ÁNGULO GUDO (0º 90º). RZONES TRIGONOMÉTRIS DE UN ÁNGULO ULQUIER (0º 360º) 3. RZONES
4 «Mi perez no me dej tiempo lire pr nd» Esritor MT I RESOLUIÓN DE TRIÁNGULOS ÍNDIE: MTERIL 1. RZONES TRIGONOMÉTRIS DE UN ÁNGULO GUDO (0º 90º). RZONES TRIGONOMÉTRIS DE UN ÁNGULO ULQUIER (0º 360º) 3. RZONES
NOCIONES DE TRIGONOMETRÍA
 Ejeiios de Tigonometí http://pi-tgos.esp.st NOCIONES DE TRIGONOMETRÍA L Tigonometí tiene po ojeto l esoluión de tiángulos, es dei, onoe los vloes de sus tes ldos de sus tes ángulos. P esolve un tiángulo
Ejeiios de Tigonometí http://pi-tgos.esp.st NOCIONES DE TRIGONOMETRÍA L Tigonometí tiene po ojeto l esoluión de tiángulos, es dei, onoe los vloes de sus tes ldos de sus tes ángulos. P esolve un tiángulo
Propuesta sobre la enseñanza de los números racionales Geovany Sanabria Brenes
 Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
Geovny Snri B. Propuest sore l enseñnz de los números rionles Geovny Snri Brenes Un mner de ordr los números rionles es trvés del onoimiento previo de rzones. En l tulidd, ls friones en primri no son vists
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
TRIGONOMETRÍA ETIMOLÓGICAMENTE: Lado Final o Terminal Vértice. Lado Inicial
 TRIGONOMETRÍ ETIMOLÓGICMENTE: Trigonometrí, es l prte de l mtemáti que estudi ls reliones que eisten entre los ángulos internos y los ldos de un triángulo, y pli dihs reliones l álulo del vlor o medid
TRIGONOMETRÍ ETIMOLÓGICMENTE: Trigonometrí, es l prte de l mtemáti que estudi ls reliones que eisten entre los ángulos internos y los ldos de un triángulo, y pli dihs reliones l álulo del vlor o medid
Eje normal. P(x,y) LLR Eje focal
 . L Hipérol...1 L Hipérol omo lugr geométrio. L hipérol es el lugr geométrio de todos los puntos tles que el vlor soluto de l difereni de sus distnis dos puntos fijos es un onstnte. Los puntos fijos se
. L Hipérol...1 L Hipérol omo lugr geométrio. L hipérol es el lugr geométrio de todos los puntos tles que el vlor soluto de l difereni de sus distnis dos puntos fijos es un onstnte. Los puntos fijos se
TRIGONOMETRÍA CONTENIDO TRIGONOMETRÍA
 CONTENIDO TRIGONOMETRÍA Tem. Pág. Coneptos y definiiones. Ángulos. Grdos. Aros. Rdines 4 Polígonos y irunfereni. 5 4 Sistems oordendos. Retngulres. Polres. 6 5 Triángulos. Definiión. Clsifiión. 7 6 Círulo
CONTENIDO TRIGONOMETRÍA Tem. Pág. Coneptos y definiiones. Ángulos. Grdos. Aros. Rdines 4 Polígonos y irunfereni. 5 4 Sistems oordendos. Retngulres. Polres. 6 5 Triángulos. Definiión. Clsifiión. 7 6 Círulo
Unidad 5-. Trigonometría II 1
 Unidd - Trigonometrí II ACTIVIDADES FINALES EJERCICIOS Y PROBLEMAS Sbiendo que sen - / y tg b /7, y que 70 < < 0 y 80 < b < 70, clcul: sen ( b bb cos ( b cc tg ( b Hllmos el resto de rzones trigonométrics
Unidd - Trigonometrí II ACTIVIDADES FINALES EJERCICIOS Y PROBLEMAS Sbiendo que sen - / y tg b /7, y que 70 < < 0 y 80 < b < 70, clcul: sen ( b bb cos ( b cc tg ( b Hllmos el resto de rzones trigonométrics
La elipse. coordenadas de los vértices, y la longitud del eje mayor que es #+Þ. coordenadas de los extremos del eje menor, cuya longitud es #,Þ
 Definiión. L elipse Est Guí tiene..todas...ls respuests MALAS Se llm elipse, l lugr geométrio de los puntos de un plno u sum de distnis dos puntos fijos del mismo plno es onstnte. Los puntos fijos se ostumrn
Definiión. L elipse Est Guí tiene..todas...ls respuests MALAS Se llm elipse, l lugr geométrio de los puntos de un plno u sum de distnis dos puntos fijos del mismo plno es onstnte. Los puntos fijos se ostumrn
