5 Procedimiento general para obtener el esquema equivalente de un transformador
|
|
|
- José Manuel Murillo Castro
- hace 8 años
- Vistas:
Transcripción
1 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado 45 5 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado En este capítulo se encontaá el esquema equivalente de un tansfomado con cualquie númeo de devanados y, en paticula, el del tansfomado de dos devanados (monofásico) con pédidas en el núcleo, de una foma mucho más sencilla que la empleada en los apatados 4.3 y 4.4. Paa ello, seá necesaio educi ambas ecuaciones mediante una base común. La demostación ealizada en el capítulo 4 paa enconta las ecuaciones y el esquema equivalente del tansfomado monofásico es un caso paticula de la que se utilizaá aquí. La difeencia es que allí se ha ealizado la educción al pimaio sin decilo, mientas que aquí se educe a una base cualquiea (no tiene po qué se al pimaio). 5. Esquema equivalente de un tansfomado de vaios devanados c k i (t) k R k L d,k u (t) k u (t) i,k Nk k' Fig. 5. Devanado k-ésimo de un tansfomado con n devanados Sea un tansfomado de n devanados. La ecuación eléctica paa el devanado k-ésimo (Ec. 4.0) es:
2 46 Tansfomadoes di k u k R k i k u i,k R k i k L d,k dt N d c k dt (5.) y la ecuación magnética (Ec. 4.): N k i k H Fe l Fe c c (5.) Estas ecuaciones se pueden epesenta mediante los esquemas equivalentes de la figua 5.. Fig. 5. Esquemas equivalentes que epesentan la ecuación eléctica del devanado k-ésimo, y la ecuación magnética de un tansfomado con n devanados Se obseva que el esquema equivalente del cicuito eléctico de cada devanado tiene una fuente de tensión de valo N k d c dt Como nos planteamos la posibilidad de junta todos los esquemas equivalentes en uno solo, si esta fuente de tensión fuea igual paa todos ellos, se podían coloca en paalelo. Dividiendo la ecuación 5. po el númeo de espias obtenemos (5.3) u k R k ( N N k N k i k ) L d,k k N k d ( N k i k ) dt d c dt (5.4) donde la intensidad se ha escito como N k i k po analogía con la ecuación 5.. Aquí suge la necesidad de educi a una base común, ya que en luga de tabaja con vaiables multiplicadas po constantes (como u k/n ko i k N) k esulta mucho más cómodo defini nuevas vaiables. Definamos unos valoes base de tensión, coiente, pulsación, flujo y eluctancia magnética. Obsevando
3 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado 47 la ecuación 5.4 se deduce como han de se estas bases: U b N... U bk N k... b b (5.5) N I b... N k I bk... b b Nomalmente se elige =. La impedancia e inductancia bases se obtienen a pati de las anteioes: b Z bk U bk I bk, L bk U bk I bk b U bk I bk (5.6) Dividiendo cada magnitud po su coespondiente valo base, se llega a la ecuación eléctica del devanado k-ésimo educida u k R k i k L di k d,k d c dt dt (5.7) y a la ecuación magnética educida i k c c (5.8) Si el cicuito magnético es lineal su eluctancia magnética, c, seá constante y po lo tanto independiente del flujo, c. En las ecuaciones 5.7 apaece la deivada del flujo. Deivando la ecuación 5.8 y despejando la deivada del flujo, obtenemos c c i k d c dt d dt c i k (5.9) La deivada d /dt se ha epesentado en el esquema equivalente de la figua 5. como una fuente de c tensión dependiente, aunque también se puede utiliza una bobina si ealizamos los cambios de vaiable siguientes: i k i µ M µ c c M µ i µ (5.0)
4 48 Tansfomadoes Esto significa que hay una elación ente el flujo y una coiente i µ. Esta coiente se llama coiente magnetizante, y es la coiente necesaia paa que se establezca el flujo c en el núcleo. Si el cicuito es lineal, M µ seá constante, y entonces d c M µ dt di µ dt (5.) Fig. 5.3 Esquema equivalente educido de un tansfomado de n devanados La figua 5.3 muesta el esquema equivalente que cumple las ecuaciones elécticas y magnética del tansfomado. Se ha de ecoda que todas las magnitudes están educidas. Es impotante ecoda que las ecuaciones 5. y 5. son válidas paa núcleos lineales o no líneales. En el caso no lineal se llega al mismo esquema equivalente de la figua 5.3, peo donde la inductancia M µ no es lineal (no es constante), y se epesenta gáficamente como muesta la figua 5.4. La deivada del flujo (Ec. 5.) en este caso es d c dt d dt ( M µ i µ ) (5.) Fig. 5.4 Inductancia magnetizante no lineal
5 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado Esquema equivalente del tansfomado monofásico con pédidas en el cicuito magnético A la vista de los esultados del apatado anteio, esulta muy sencillo el estudio de un tansfomado monofásico consideando las pédidas magnéticas. Fig. 5.5 Tansfomado monofásico con devanado cotocicuitado en el núcleo Las ecuaciones de los dos devanados son: di u R i u i, R i L d, dt N d c dt di u R i u i, R i L d, dt N d c dt (5.3) Asociaemos las pédidas magnéticas a las que se poduzcan en un tece devanado cotocicuitado embebido en el núcleo magnético, como el de la figua 5.5. Po esta cotocicuitado, su tensión es nula. Tampoco tiene flujo de dispesión al esta integado en el núcleo. Suponiendo que tiene una sola espia, la ecuación eléctica de este devanado es: Y la ecuación magnética: 0 R 3 i 3 u i,3 R 3 i 3 d c dt N k i k H Fe l Fe c c (5.4) (5.5)
6 50 Tansfomadoes Paa educi las ecuaciones, se eligen las bases mostadas en la ecuación 5.5: U b N U b N U b3 b b (5.6) N I b N I b I b3 b b Se obseva que las tensiones y coientes base cumplen la elación de tansfomación, al igual que en el esto de educciones ealizadas en estos apuntes, U b U b I b I b N N t (5.7) Tomaemos =. Reduciendo las ecuaciones: b u R i L di d, d c dt dt u R i L di d, d c dt dt (5.8) 0 R 3 i 3 d c dt i i i 3 c c M µ i µ y si se supone que el núcleo es lineal, la inductancia M µ seá constante. Estas ecuaciones educidas están epesentadas en el siguiente esquema equivalente: Fig. 5.6 Esquema educido del tansfomado monofásico incluyendo las pédidas en el hieo Compaando con el esquema de la figua 4.9 se pueden identifica los paámetos del hieo: R 3 R Fe, i 3 i Fe (5.9)
7 Tansfomado monofásico en égimen pemanente senoidal 5 6 Tansfomado monofásico en égimen pemanente senoidal El tansfomado se alimenta nomalmente con tensión senoidal, po lo que todas las magnitudes esultan senoidales en égimen pemanente. En ealidad la coiente de vacío del tansfomado no lo es, debido a la satuación, peo ya se ha comentado que se acepta la apoximación de núcleo lineal (aunque edefiniendo los paámetos del mismo, R Fe ' y M µ '). Po ello, las ecuaciones (y cicuitos) que se utilizan son las de égimen pemanente senoidal. Estas ecuaciones se obtienen pasando las expesiones tempoales a notación fasoial (la deivada se conviete en el opeado j). Paa deduci en los capítulos 4 y 5 las ecuaciones que igen el compotamiento del tansfomado en el dominio del tiempo, el tansfomado se ha consideado con tensiones y coientes de ambos devanados hacia su inteio. Cuando el tansfomado se alimenta a tavés de una fuente de tensión po el pimaio y se conecta en su secundaio una caga, la diección eal de la intensidad del secundaio va en sentido contaio al dibujado. Po ello, a pati de ahoa, i (t) siempe se dibujaá en diección contaia, sin pede po ello ninguna genealidad en las expesiones (donde haya i habá que pone -i ). 6. Tansfomado monofásico ideal I I En las ecuaciones del tansfomado monofásico ideal no afecta el hecho de tabaja con fasoes o con magnitudes tempoales, ya que no hay deivadas. Recodémoslas: U U U N N U I I N N t (6.) ' ' m: = N /N t Po se ideal, no consume intenamente potencia activa ni eactiva, y po ello se cumple que Fig. 6. Tansfomado monofásico ideal en égimen pemanente senoidal S U I U I (6.)
8 5 Tansfomadoes 6. Tansfomado monofásico eal A pati del cicuito de la figua 4.9 se obtiene el siguiente esquema equivalente del tansfomado monofásico eal paa égimen pemanente senoidal: Fig. 6. Esquema equivalente del tansfomado monofásico eal paa égimen pemanente senoidal donde: R = esistencia del devanado pimaio en, X = eactancia de dispesión del devanado pimaio en (L ), d R = esistencia del devanado secundaio en, X = eactancia de dispesión del devanado secundaio en (Ld ), - G ' = conductancia de pédidas en el hieo vista desde el pimaio en (/R '), Fe - B' µ = susceptancia de magnetización vista desde el pimaio en (/X µ ' = /(M µ ')). En ealidad, cuando un tansfomado monofásico eal se alimenta con tensión senoidal pua, no todas las magnitudes son senoidales. Debido a la satuación del núcleo, la coiente de vacío no lo es (figua A3.b del anexo 3). Como en vacío las pédidas en el cobe son despeciables fente a las del hieo, lo que se hace es defini una intensidad senoidal, I o', que poduzca las mismas pédidas en una esistencia ficticia R Fe' que las que se poducen en el hieo (paa ello ha de tene el mismo valo eficaz que la intensidad de vacío eal). Es la llamada senoide equivalente (Anexo 3). A pati de esta I o' senoidal se calculan la esistencia e inductancia ficticias R Fe ' y M'. µ Las impedancias de la figua 6. se pueden agupa como: Fe Z R jx Z R jx Y o Z o G Fe jb µ R Fe jx µ (6.3)
9 Tansfomado monofásico en égimen pemanente senoidal 53 Al contaio de lo que sucede con la esistencia y eactancia de los devanados, la conductancia G Fe' y la susceptancia B µ ' no petenecen a ninguno de los dos devanados sino que son popias del tansfomado. Po ello, estamos hablando de conductancia y susceptancia vistas desde uno de los devanados (en la figua 6. se han denotado con el supeíndice ': vistas po el pimaio). Las ecuaciones del esquema de la figua 6. son: U R I jx I Z o ( I I ) (6.4) U R I jx I Z o ( I I ) N N I I N N
10 Valoes nominales. Placa de caacteísticas 55 7 Valoes nominales. Placa de caacteísticas En este capítulo se comentaán los paámetos paa los cuales se ha diseñado un tansfomado monofásico. Conceptualmente son idénticos paa el tansfomado tifásico, aunque paa conceta las difeencias véase el capítulo Valoes nominales Los valoes nominales de una máquina eléctica son aquellos paa los cuales ha sido diseñada. Los más impotantes de un tansfomado diseñado paa tabaja en égimen senoidal son: - potencia nominal, - tensión nominal de pimaio y secundaio, - intensidad nominal de pimaio y secundaio, - elación de tansfomación, y - fecuencia nominal. Al igual que en otas máquinas elécticas, la potencia máxima que puede suminista el tansfomado está limitada po la calidad de sus aislantes, que se pueden deteioa po un exceso de tensión o po un exceso de tempeatua: - la tensión máxima del aislante fija la tensión máxima del tansfomado; - la tempeatua máxima del aislante, junto con la capacidad de disipación de calo del tansfomado, fija las pédidas máximas que se pueden poduci en su inteio (pédidas en el hieo y en el cobe). Paa una tensión deteminada (pédidas en el hieo constantes) y una sección de conducto deteminada (esistencia constante, R = l / S), la tempeatua máxima del aislante fija una intensidad máxima en el tansfomado. Potencia nominal, S n Es la potencia apaente (VA, kva o MVA) que se obtiene a pati de la tensión nominal y la coiente nominal de ambos devanados del tansfomado. Paa el tansfomado monofásico se calcula como: S n U n I n U n I n (7.)
11 56 Tansfomadoes Salvando las pédidas, indica la potencia activa máxima que podía suminista el secundaio del tansfomado con caga esistiva y égimen pemanente sin que se poduzca un calentamiento excesivo. En condiciones intemitentes de funcionamiento (conexiones y desconexiones peiódicas), el tansfomado puede suminista hasta,5 veces la potencia nominal. El motivo es que duante el tiempo de desconexión el tansfomado se enfiaá hasta la tempeatua ambiente (u ota intemedia ente la de funcionamiento y la ambiente), y un tansfomado fío puede suminista una potencia supeio a la nominal mientas se calienta hasta alcanza su tempeatua máxima. Tensión nominal, U n, Un Es la tensión que se debe aplica a los devanados del tansfomado paa que funcione coectamente en égimen pemanente sin deteioo del mismo. En condiciones intemitentes de funcionamiento, se pueden admiti sobetensiones de,05 veces la tensión nominal. Intensidad nominal, I n, In Es la intensidad máxima que puede cicula po los devanados del tansfomado sin deteioo de los mismos. En condiciones intemitentes se pueden admiti sobecagas. Relación de tansfomación, t Es la elación ente tensiones de pimaio y secundaio cuando el tansfomado tabaja en vacío. En el tansfomado monofásico se suele toma como la elación ente númeos de espias de pimaio y secundaio o, lo que es lo mismo, ente U n y U n: t N N U n U n (7.) Fecuencia nominal, f n Es la fecuencia a la que coesponden el esto de valoes nominales. Los valoes nominales de un tansfomado son unos valoes de funcionamiento, peo también puede funciona coectamente con otos valoes difeentes. Po ejemplo: - puede suminista potencias infeioes a la nominal (las potencias están fijadas po la caga), o lo que es lo mismo, puede suminista intensidades infeioes a la nominal, que es lo que nomalmente sucede; - puede tabaja a tensiones infeioes a la nominal, aunque no podá suminista entonces la potencia máxima (sí podá suminista la intensidad máxima); - puede tabaja a ota fecuencia, aunque si es supeio se poducián mayoes pédidas en el hieo, con lo que la potencia máxima seá infeio a la nominal.
12 Valoes nominales. Placa de caacteísticas Placa de caacteísticas La placa de caacteísticas de un tansfomado contiene, ente otos, los siguientes valoes: - potencia nominal, S, n - tensiones nominales de pimaio y secundaio, U n y U n, - intensidades nominales de pimaio y secundaio, I n e I n, - elación de tansfomación,, t - fecuencia nominal, f, n - datos de los ensayos en vacío y en cotocicuito (Cap. 7): potencia en valo eal y coiente y tensión en p.u., W, i, W y. o o cc cc
13 Reducción de cicuitos con tansfomadoes ideales 59 8 Reducción de cicuitos con tansfomadoes ideales 8. Cicuitos con un tansfomado ideal Cuando se tiene un cicuito con un tansfomado ideal (po ejemplo un cicuito con un tansfomado eal, ya que su esquema equivalente contiene un tansfomado ideal -Fig. 6.-), en ealidad se tienen dos cicuitos sepaados elécticamente y elacionados mediante las ecuaciones del tansfomado ideal: U U I I N N t (8.) I Z I U G + U N N U Z ' Tansfomado ideal t m: = N /N ' Fig. 8. Cicuito con un tansfomado ideal El tabajo con cicuitos de este tipo puede esulta engooso, po lo que nomalmente se opta po elimina el tansfomado ideal. Un tansfomado ideal se podía supimi si fuea de elación de tansfomación unitaia o, lo que es lo mismo, si las tensiones o coientes de ambos lados del mismo fuean iguales. Un tansfomado así se puede sustitui po dos hilos que unan con y ' con '. Paa consegui esto hay que educi el esquema. Reduci un esquema es dividi todas las magnitudes del
14 60 Tansfomadoes mismo po unos valoes base deteminados. Los valoes base necesaios paa pode pescindi del tansfomado ideal no pueden se cualesquiea, sino que han de cumpli: - que la potencia base (S b) sea única paa todo el cicuito; - que las tensiones base de cada lado del tansfomado (U b, U b) cumplan la elación de tansfomación del tansfomado ideal (U b/u b=). t A pati de la potencia y tensiones base elegidas, se obtienen las coientes e impedancias base de cada lado del tansfomado. También se pueden calcula las admitancias base. S b (VA) U b (V) U b U b t U b (V) I b S b U b (A) I b S b U b (A) Z b U b S b () Z b U b S b () Y b Z b S b U b ( ) Y b Z b S b U b ( ) Ejemplo.- Vamos a educi el cicuito de la figua 8. paa elimina el tansfomado ideal. Las ecuaciones del cicuito son: U G Z I U U Z I U U I I t (8.) Elegimos una potencia base S b y unas tensiones base U b y U b tal que U b / U b = t (Fig. 8.a) y dividimos la pimea ecuación po U b y la segunda po U b: U G U b Z I U b U U b U U b Z I U b (8.3)
15 Reducción de cicuitos con tansfomadoes ideales 6 Fig. 8. Cicuito con un tansfomado ideal: (a) elección de valoes base, y (b) cicuito educido Como las tensiones base cumplen la elación de tansfomación, se tiene que: U U U b U b t U U b U U b (8.4) po lo que se pueden junta ambas ecuaciones, esultando: U G U b Z I U b Z I U b (8.5) Cambiando la tensión base po el poducto de impedancia base po coiente base se obtiene: U G U b Z I Z b I b Z I Z b I b (8.6) A cada magnitud eal dividida po la base se le denomina magnitud educida, y se indica po una leta minúscula (el supeíndice indica que se ha ealizado la educción ): u G z i z i, donde: u U G, z G U Z, i b Z I, z b I Z, i b Z I b I b (8.7)
16 6 Tansfomadoes Como las intensidades también cumplen la elación de tansfomación: I I I b I b t I I b I I b i i i (8.8) se tiene la ecuación (educida): u G z i z i (8.9) que se puede epesenta mediante el cicuito (educido) de la figua 8.b, en el que ha desapaecido el tansfomado ideal (se puede intepeta que se ha convetido en dos hilos). Como se puede compoba, con la educción se han igualado las tensiones en ambos lados del tansfomado, y como sigue cumpliendo que u i = u i, también se igualan las intensidades de pimaio y secundaio. U U b U U b u u u i i i (8.0) Fig. 8.3 Tansfomado ideal educido Se puede deci entonces que al educi de esta foma un cicuito que contiene un tansfomado ideal, éste desapaece, o lo que es lo mismo, se conviete en dos hilos (Fig. 8.3). Todas las vaiables (potencias, tensiones, intensidades e impedancias) y todos los componentes (fuentes de tensión o de coiente, impedancias, cagas) de cada lado del tansfomado se han dividido po su coespondiente valo base. De esta foma, la fuente de tensión situada en el pimaio del tansfomado de la figua 8.a, U G, se educe dividiendo su tensión po la tensión base del pimaio, con lo cual se conviete en u G en la figua 8.b. Po este motivo, las magnitudes educidas no tienen dimensiones. Al da un valo educido se añade p.u. que quiee deci valo po unidad y, además, debe indicase la base a la que está efeido.
17 Reducción de cicuitos con tansfomadoes ideales Cicuitos con vaios tansfomadoes ideales Si el cicuito contiene vaios tansfomadoes ideales (o eales) se tienen igualmente cicuitos sepaados elécticamente y elacionados mediante las ecuaciones de los tansfomadoes ideales. Paa eliminalos hay que educi el cicuito: - se elige una potencia base (S ) única paa todo el cicuito, y b - se eligen tantas tensiones base como niveles de tensión haya, de foma que cumplan las elaciones de tansfomación ente niveles de tensión. Las educciones de cicuitos con vaios tansfomadoes ideales no tienen un nombe especial, y se llaman en geneal educciones a p.u. Como en cualquie ota educción, al da los datos en p.u. también hay que especifica la base a la que están efeidos. Como ejemplo de que se pueden elegi tantas bases como se desee al educi un cicuito, en el de la figua 8.4 también se podían habe elegido: - base efeida a los valoes nominales de la caga y del tansfomado elevado: S = MVA, b U = kv, b - ídem a los del tansfomado educto: S = MVA, U = 8 kv, b b - otas combinaciones. Geneado Tansfo. Línea Tansfo. Caga ideal ideal elevado educto MVA MVA.5 kv /0 kv Z L 8/.5 kv cos=0.8 S b= MVA U =.5 kv U b =.5/(/0) =5 kv U b3 =.5 =5/(8/.5) b kv (a) z L i u G + ( p.u.) s c (0.5 p.u. cos=0.8) (b) Fig. 8.4 Cicuito con vaios tansfomadoes ideales: (a) elección de las bases, y (b) cicuito educido
18 El tansfomado eal educido 65 9 El tansfomado eal educido Como el tansfomado eal contiene un tansfomado ideal, la educción de un cicuito con un tansfomado eal es idéntica a la comentada en el capítulo anteio en cuanto a la eliminación del tansfomado ideal. Peo como el tansfomado eal contiene, además del tansfomado ideal, unas esistencias y eactancias, éstas también quedan educidas. El esquema educido del tansfomado eal pemite ealiza una apoximación que es muy utilizada. Sea el tansfomado monofásico eal de la figua 9.. Elegimos una potencia y unas tensiones base adecuadas (que cumplan la elación de tansfomación) paa pode educi el esquema y elimina el tansfomado ideal. I R X X R I I ' o U B ' µ I ' µ G ' Fe I Fe ' N N ' ' U U b I b= S b/ub Z b= (U b)/sb Tansfomado ideal t m: = N /N S b (U b/u b= t ) U b I b= S b/ub Z b= (U b)/sb Fig. 9. Tansfomado monofásico eal. Potencia, tensión, coiente e impedancias base La figua 9. muesta el esquema del tansfomado eal educido. Todas las vaiables (potencias, tensiones, intensidades e impedancias) y todos los componentes (fuentes de tensión o de coiente,
19 66 Tansfomadoes impedancias, cagas) de cada lado del tansfomado se han dividido po su coespondiente valo base. De esta foma, la tensión U del pimaio del tansfomado se ha educido dividiendo su valo po la tensión base del pimaio, y se ha convetido en u. Po oto lado las impedancias R y X, que se encuentan físicamente situadas en el secundaio del tansfomado de la figua 9., se han educido utilizando la impedancia base del secundaio. El esquema que se obtiene se denomina esquema en T. Fig. 9. Tansfomado monofásico eal con sus valoes educidos (esquema en T) En la páctica, dado el pequeño eo que se comete, se juntan las esistencias y eactancias de ambos devanados del tansfomado eal en una sola, situada nomalmente (po convenio) en el lado de alta tensión (AT), de valo la suma de ambas ( y x son mucho más pequeñas que /g Fe y /b µ ), con lo que esulta el esquema en L de la figua 9.3: x x x (9.) ( Cuidado! Estas esistencias sólo se pueden junta cuando estén educidas: no se puede hace R = R + R en la figua 9..) Fig. 9.3 Tansfomado monofásico eal con, x, y x unidas en la misma ama (esquema en L)
20 El tansfomado eal educido 67 Se ha de señala que en la mayoía de los ejemplos utilizados a pati de este momento se hace efeencia a tansfomadoes eductoes (AT/BT), po lo que el subíndice coesponde al lado de alta tensión. Paa un tansfomado elevado (BT/AT), el subíndice seía paa el lado de baja tensión, y el esquema seía como el que se muesta en la figua 9.4 (con y x situadas siempe en el lado de AT). Fig. 9.4 Tansfomado elevado (BT/AT) con sus valoes educidos La última simplificación que se ealiza en el esquema educido del tansfomado es despecia la ama del hieo (que es lo mismo que supone que el núcleo es ideal). Cuando se cumpla que: i» i o (9.) entonces se podá despecia la ama del hieo del esquema equivalente, ya que, i i (9.3) i i x u u Fig. 9.5 Esquema educido del tansfomado despeciando la ama del hieo (la intensidad es tal que se puede considea i i ) La ecuación 9. seá cieta cuando la impedancia de la caga que alimente el secundaio cumpla: z caga ( jx ) «y o (9.4)
21 68 Tansfomadoes Es deci que cuando el tansfomado no está en vacío (ni póximo a él) se puede despecia la ama del hieo. Este esquema educido se utiliza paa calcula tensiones y coientes en ambos lados del tansfomado, peo no paa calcula endimientos, ya que, al se genealmente del mismo oden que las del hieo, las pédidas en el cobe se han de tene en cuenta. Paa calcula estas pédidas de una foma apoximada con este esquema se puede supone que g Fe tiene en bones una tensión u si es un tansfomado AT/BT o una tensión u si es BT/AT.
22 Bases empleadas en la educción de cicuitos con un solo tansfomado eal 69 0 Bases más empleadas en la educción de cicuitos con un solo tansfomado eal De ente todas las bases posibles que se pueden utiliza paa educi cicuitos con un solo tansfomado ideal, hay algunas más utilizadas, sobe todo cuando se tata de educi un tansfomado eal. Son las llamadas bases efeidas al popio tansfomado, y son: - educción en la base efeida a los valoes nominales del tansfomado (S, U y U ) n n n conocida como educción a valoes en p.u. (po unidad), - educción al pimaio, y - educción al secundaio. Ya se ha comentado que cualquie educción educe a valoes en p.u., aunque la que se efiee a los valoes nominales del tansfomado haya tomado el nombe. En ealidad es la más utilizada con difeencia. A continuación se pasa a descibi estas tes educciones.
23 70 Tansfomadoes 0. Reducción a valoes en p.u. (po unidad) Se eligen las siguientes potencia y tensiones base: S p.u. b S n (VA) (potencia nominal del tansfomado) U p.u. b U n (V) U p.u. b (tensión nominal del pimaio) U p.u. b t U p.u. b U n (V) (tensión nominal del secundaio) I p.u. b S n U n I n (A) I p.u. b S n U n I n (A) b U n () Z p.u. b U n S n Z p.u. S n () Los valoes educidos en p.u.: - se denotan po letas minúsculas, no se acostumba a pone ningún supeíndice, y - como cualquie oto valo educido no tienen dimensiones, y nomalmente se añade al final de los mismos la expesión p.u., po ejemplo, = 0.3 p.u. i x i u b µ g Fe u AT/BT u =U /U i =I /I p.u. =R /Z +R /Z n b n p.u. x=x /Z +X /Z b p.u. b p.u. b ' p.u. b =B /Y µ µ b ' g =G /Y Fe Fe p.u. b u =U /U i =I /I n n Fig. 0. Tansfomado monofásico eal con valoes educidos a p.u.
24 Bases empleadas en la educción de cicuitos con un solo tansfomado eal 7 0. Reducción al pimaio Se eligen las siguientes potencia y tensiones base: S b (VA) U b (V) U b t U b U b t U n U n (V) I b (A) I b t U n U n (A) Z b () Z b t U n U n () Los valoes educidos al pimaio: - se denotan con letas mayúsculas y una pima ('), y - no tienen dimensiones, como cualquie oto valo educido. I ' R ' X ' I ' U ' B ' µ G ' Fe U ' AT/BT U =U ' ' I =I ' R =R +R *( ) X ' =X +X *( ) t t ' B =B ' µ µ ' ' G Fe=G Fe U =U * ' ' I =I / t t Fig. 0. Tansfomado monofásico eal con valoes educidos al pimaio
25 7 Tansfomadoes Con esta educción, una impedancia del secundaio vista po el pimaio se conviete en ( t) Z, como sucede con el tansfomado ideal de la figua 0.3 (ve la ecuación 3.5). Fig. 0.3 Reducción al pimaio de una impedancia en el secundaio de un tansfomado monofásico ideal 0.3 Reducción al secundaio Se eligen las siguientes potencia y tensiones base: S b (VA) U b t U n U n (V) U b U b t U b (V) I b t U n U n (A) I b (A) Z b ( t ) U n U n () Z b () Los valoes educidos al secundaio: - se denotan con letas mayúsculas y una doble pima ("), y - no tienen dimensiones, como cualquie oto valo educido.
26 Bases empleadas en la educción de cicuitos con un solo tansfomado eal 73 I " R " X " I " U " B " µ G " Fe U " AT/BT U =U / " " I =I * t t " R =R /( )+R X " =X /( )+X t t B " =B * µ µ ' " Fe t ' G =G * Fe t U =U " " I =I Fig. 0.4 Tansfomado monofásico eal con valoes educidos al secundaio Como consecuencia de esta educción, una impedancia del pimaio vista po el secundaio se conviete en Z /( t), como sucede con el tansfomado ideal de la figua 0.5. Fig. 0.5 Reducción de una fuente de tensión y una impedancia al secundaio de un tansfomado monofásico ideal 0.4 Relaciones ente las tes bases efeidas al popio tansfomado Estas tes bases se denominan bases efeidas al popio tansfomado po esta efeidas: - a los valoes nominales del tansfomado, S, U y U, o n n n - al pimaio del tansfomado, o - al secundaio del tansfomado.
27 74 Tansfomadoes En el caso de cicuitos con vaios tansfomadoes nomalmente no seá posible utiliza bases efeidas a todos los tansfomadoes a la vez (po ejemplo, poque las potencias nominales de los tansfomadoes pueden se distintas o poque hay vaios pimaios y vaios secundaios). Cada una de estas bases tiene sus peculiaidades. Debido a su sencillez, la educción a p.u. es la más utilizada. Además, algunos datos de la placa caacteística del tansfomado suelen esta efeidos a esta base (i oy cc). p.u. Reducc. al º x x U ' b U " b Z ' b Z " b I ' b I " b Reducc. al º Fig. 0.6 Relaciones ente las tes educciones La ventaja de la educción al pimaio/secundaio es que no se ha de educi el cicuito del lado pimaio/secundaio (las potencias, tensiones, coientes e impedancias no cambian). Con esta educción se "conviete" todo el cicuito que se encuenta en el secundaio/pimaio del tansfomado (que tiene un nivel de tensión deteminado) en un cicuito que sea equivalente (peo a la tensión del pimaio/secundaio). A veces es necesaio pasa unos valoes educidos en una base a educidos en ota. El paso más común es de valoes en p.u. a valoes educidos al pimaio o al secundaio, paa ello se ha de multiplica po las coespondientes bases en p.u. del pimaio o del secundaio espectivamente. En el capítulo se explican con detalle los cambios de base.
28 Reducción de cicuitos con vaios tansfomadoes eales 75 Reducción de cicuitos con vaios tansfomadoes eales En la educción de cicuitos con vaios tansfomadoes eales vale todo lo dicho paa cicuitos con vaios tansfomadoes ideales: - Se ha de elegi una potencia base paa todo el cicuito, y tantas tensiones base como niveles de tensión haya en el mismo. Evidentemente, los valoes base de tensión deben cumpli las elaciones de tansfomación ente niveles de tensión. - Se dice que se tabaja en p.u. Como son posibles tantas educciones como se desee (se puede elegi cualquie potencia base y cualquie tensión base inicial), al da los datos en p.u. también hay que especifica la base a la que están efeidos. - En este tipo de cicuitos no tiene sentido habla de educción al pimaio o al secundaio, ya que habá tantos pimaios y secundaios como tansfomadoes. La figua. muesta una ed eléctica, compuesta po altenado, tansfomadoes, línea y caga, con tes niveles de tensión, que se ha educido a p.u. utilizando la base indicada. En el estudio de edes elécticas en caga, se suele utiliza el cicuito equivalente apoximado del tansfomado que despecia la ama del hieo (Fig. 9.5), aunque paa calcula el endimiento hay que tenela en cuenta. Como ejemplo de que se pueden elegi tantas bases como se desee al educi un cicuito, en el de la figua. también se podían habe elegido: - base efeida a los valoes nominales del tansfomado elevado: S b=. MVA, U b = kv, - ídem a los del tansfomado educto: S b =.8 MVA, U b= 8 kv, - otas combinaciones.
29 76 Tansfomadoes Geneado Tansfo. Línea Tansfo. elevado educto MVA.5 kv E. MVA.8 MVA /0 kv Z L 8/.5 kv R Caga MVA cos=0.8 U =.5 kv b E E S = MVA b U =.5/(/0) b (a) =5 kv z L R R x x U b3=5/(8/.5) =.5 kv i c u G ( p.u.) + b µe g Fe E b µr g Fe R s c (0.5 p.u. cos=0.8) (b) E x E z L R x R i u G ( p.u.) + s c (0.5 p.u. cos=0.8) (c) Fig.. Red eléctica con vaios niveles de tensión: (a) elección de las bases, (b) cicuito educido a p.u., y (c) cicuito educido utilizando el esquema simplificado de los tansfomadoes que despecia la ama del hieo
30 Cambios de base 77 Cambios de base La potencia base en la educción de cicuitos con vaios tansfomadoes es única. Po ello, los paámetos de los tansfomadoes eales (que nomalmente están efeidos a sus popias bases) se tienen que pasa a la base común. Este poceso se llama cambio de base. Paa ealiza un cambio de base se ha de tene en cuenta que el valo eal (valo al deshace la educción) es el mismo. Po ejemplo, se desea ealiza un cambio de base a una impedancia situada en el pimaio Z eal, cuyo valo educido en la base A es z A. Paa halla el valo educido en la base B, z B, se ha de cumpli que: Z eal z A Z A b z B Z B b (.) Si la impedancia hubiea estado en el secundaio: Z eal z A Z A b z B Z B b (.) Y en geneal, el nuevo valo educido de la impedancia se calcula como: z B i z A i Z A bi Z B bi (.3) Si se tuviea que ealiza un cambio de base a una tensión, coiente o potencia se pocede de la misma foma: (Valo educido) B i (Valo educido) A i (Valo base) A i (.4) (Valo base) B i Casos paticulaes de cambio de base son los mostados en la figua 0.6: son cambios de base ente bases que están efeidas al popio tansfomado.
31 78 Tansfomadoes Ejemplo.- Se tiene una tensión del pimaio que está en p.u., secundaio, U : u p.u., y se desea conoce su valo educido al U u p.u. U p.u. b U b u p.u. U n (U n /U n ) u p.u. U p.u. b (.5) este esultado es el que indica la figua 0.6 paa el paso de valoes en p.u. a valoes educidos al secundaio. Lo mismo sucedeá con impedancias: sea una impedancia del secundaio en p.u., desea conoce su valo educido al pimaio, Z : z p.u., de la que se Z z p.u. Z p.u. b Z b z p.u. (U n /S n ) (U n /U n ) z p.u. Z p.u. b (.6)
Adaptación de impedancias
 .- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
.- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
PROBLEMAS CAPÍTULO 5 V I = R = X 1 X
 PROBLEMAS APÍULO 5.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina.000 VAR. Se pide, calcula: a) El valo de R,, y L. b) La potencia disipada
PROBLEMAS APÍULO 5.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina.000 VAR. Se pide, calcula: a) El valo de R,, y L. b) La potencia disipada
www.fisicaeingenieria.es Vectores y campos
 www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
Instrumentación Nuclear Conf. # 2 Tema I. Procesamiento y Conformación de Pulsos.
 Instumentación Nuclea onf. # 2 Tema I. Pocesamiento y onfomación de Pulsos. Sumaio: aacteísticas geneales de los pulsos. oncepto de Ancho de Banda y su elación con el tiempo de subida de un pulso. Objetivo
Instumentación Nuclea onf. # 2 Tema I. Pocesamiento y onfomación de Pulsos. Sumaio: aacteísticas geneales de los pulsos. oncepto de Ancho de Banda y su elación con el tiempo de subida de un pulso. Objetivo
MAGNITUDES VECTORIALES:
 Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
INDUCCIÓN ELECTROMAGNÉTCA Y ENERGÍA DEL CAMPO MAGNÉTICO
 NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
Kronotek: Configuración de Red para VoIP
 Konotek: Configuación de Red paa VoIP Contenido 1. Intoducción... 2 2. Impotancia de la Configuación de Red... 2 3. Pasos Pevios: Cálculo del númeo de líneas de voz... 3 Pime paso: obtención del ancho
Konotek: Configuación de Red paa VoIP Contenido 1. Intoducción... 2 2. Impotancia de la Configuación de Red... 2 3. Pasos Pevios: Cálculo del númeo de líneas de voz... 3 Pime paso: obtención del ancho
Potencial eléctrico. Trabajo y energía potencial en el campo eléctrico. Potencial de una carga puntual: Principio de superposición
 Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
CUESTIONES Y PROBLEMAS DE CAMPO ELÉCTRICO. Ejercicio nº1 Cómo se manifiesta la propiedad de la materia denominada carga eléctrica?
 UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
Parametrizando la epicicloide
 1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
 /5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
CAMPO GRAVITATORIO FCA 04 ANDALUCÍA
 CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO
 PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
Tablas y formulas prácticas
 Tablas y fomulas pácticas ECCÓN Automation Technology Poducts Tablas y fómulas pácticas NDCE Tabla de esquemas típicos en sistemas de conmutación (tansfeencias)... Tabla de potencias y coientes nominales...
Tablas y fomulas pácticas ECCÓN Automation Technology Poducts Tablas y fómulas pácticas NDCE Tabla de esquemas típicos en sistemas de conmutación (tansfeencias)... Tabla de potencias y coientes nominales...
Parte 3: Electricidad y Magnetismo
 Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
+ + h. 8 v A. = = 2026 m s 1 3 1,3 10 6 m
 m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
CAMPO GRAVITATORIO FCA 10 ANDALUCÍA
 CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
Escuela 4-016 Ing. Marcelo Antonio Arboit - Junín
 Un transformador se compone de dos arrollamientos aislados eléctricamente entre sí y devanados sobre un mismo núcleo de hierro. Una corriente alterna que circule por uno de los arrollamientos crea en el
Un transformador se compone de dos arrollamientos aislados eléctricamente entre sí y devanados sobre un mismo núcleo de hierro. Una corriente alterna que circule por uno de los arrollamientos crea en el
Ejercicios resueltos
 Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Tema 3. Campo eléctrico
 Tema 3 Campo eléctico Pogama 1. Inteacción eléctica. Campo eléctico.. Repesentación mediante líneas de campo. Flujo eléctico: Ley de Gauss. 3. Enegía y potencial elécticos. Supeficies equipotenciales.
Tema 3 Campo eléctico Pogama 1. Inteacción eléctica. Campo eléctico.. Repesentación mediante líneas de campo. Flujo eléctico: Ley de Gauss. 3. Enegía y potencial elécticos. Supeficies equipotenciales.
Leyes de Kepler. Ley de Gravitación Universal
 Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
Leyes de Keple y Ley de Gavitación Univesal J. Eduado Mendoza oes Instituto Nacional de Astofísica Óptica y Electónica, México Pimea Edición onantzintla, Puebla, México 009 ÍNDICE 1.- PRIMERA LEY DE KEPLER
La fuerza gravitatoria entre dos masas viene dada por la ley de gravitación universal de Newton, cuya expresión vectorial es
 LGUNS CUESTIONES TEÓICS SOE LOS TEMS Y.. azone si las siuientes afimaciones son vedadeas o falsas a) El tabajo que ealiza una fueza consevativa sobe una patícula que se desplaza ente dos puntos, es meno
LGUNS CUESTIONES TEÓICS SOE LOS TEMS Y.. azone si las siuientes afimaciones son vedadeas o falsas a) El tabajo que ealiza una fueza consevativa sobe una patícula que se desplaza ente dos puntos, es meno
IES Fco Ayala de Granada Junio de 2014 (Modelo 1) Soluciones Germán-Jesús Rubio Luna. Opción A. Ejercicio 2 opción A, modelo_1 Junio 2014
 IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
Física Universitaria 2 5 de junio 2006 Enrique Sánchez y Aguilera, Rodolfo Estrada Guerrero, Abraham Vilchis CONSTANTE DIELÉCTRICA RELATIVA
 CONSTANTE DIELÉCTRICA RELATIVA OBJETIVO: El alumno podá detemina la constante dieléctica elativa de divesos mateiales dielécticos mediante la medición de la capacitancia de un condensado de placas paalelas.
CONSTANTE DIELÉCTRICA RELATIVA OBJETIVO: El alumno podá detemina la constante dieléctica elativa de divesos mateiales dielécticos mediante la medición de la capacitancia de un condensado de placas paalelas.
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES
 PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
Aplicación 2: Diversificación de las inversiones (problema de selección de cartera)
 Aplicación : Divesificación de las invesiones (poblema de selección de catea) Hecho empíico: Cuanto mayo es el valo espeado (endimiento) de una invesión NO es cieto que sea más apetecible. (Si invesoes
Aplicación : Divesificación de las invesiones (poblema de selección de catea) Hecho empíico: Cuanto mayo es el valo espeado (endimiento) de una invesión NO es cieto que sea más apetecible. (Si invesoes
6.5 ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS
 6.. Gáficas de ectas usando m b Po ejemplo, paa gafica la ecta Maca el valo de b (odenada al oigen) sobe el eje, es deci el punto (0,). A pati de ese punto, como la pendiente es, se toma una unidad a la
6.. Gáficas de ectas usando m b Po ejemplo, paa gafica la ecta Maca el valo de b (odenada al oigen) sobe el eje, es deci el punto (0,). A pati de ese punto, como la pendiente es, se toma una unidad a la
GEOMETRÍA. punto, la recta y el plano.
 MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
TRABAJO DE LABORATORIO Nº 2: Potencial Eléctrico Mapa de Campo Eléctrico
 Univesidad Nacional del Nodeste Facultad de Ingenieía Cáteda: Física III Pofeso Adjunto: Ing. Atuo Castaño Jefe de Tabajos Pácticos: Ing. Cesa Rey Auiliaes: Ing. Andés Mendivil, Ing. José Epucci, Ing.
Univesidad Nacional del Nodeste Facultad de Ingenieía Cáteda: Física III Pofeso Adjunto: Ing. Atuo Castaño Jefe de Tabajos Pácticos: Ing. Cesa Rey Auiliaes: Ing. Andés Mendivil, Ing. José Epucci, Ing.
PROBLEMAS DE ELECTROESTÁTICA
 PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
El Espacio Afín. I. E. S. Siete Colinas (Ceuta) Departamento de Matemáticas
 I. E. S. Siete Colinas (Ceuta) Depatamento de Matemáticas Matemáticas de º de Bachilleato El Espacio Afín Po Javie Caoquino CaZas Catedático de matemáticas del I.E.S. Siete Colinas Ceuta 005 El Espacio
I. E. S. Siete Colinas (Ceuta) Depatamento de Matemáticas Matemáticas de º de Bachilleato El Espacio Afín Po Javie Caoquino CaZas Catedático de matemáticas del I.E.S. Siete Colinas Ceuta 005 El Espacio
Almacenan energía magnética generada como consecuencia de las variaciones de corriente. Suelen ser fabricados a medida por el propio diseñador.
 6. nductancias Almacenan enegía magnética geneada como consecuencia de las vaiaciones de coiente. Suelen se fabicados a medida po el popio diseñado. Pincipios de la teoía electomagnética Magnitudes a utiliza:
6. nductancias Almacenan enegía magnética geneada como consecuencia de las vaiaciones de coiente. Suelen se fabicados a medida po el popio diseñado. Pincipios de la teoía electomagnética Magnitudes a utiliza:
ENSAYO de TRANSFORMADORES
 NTRODCCÓN ENSAYO de TRANSFORMADORES Nobeto A. Lemozy La veificación del coecto funcionamiento de cualquie equipo es de suma impotancia, en paticula cuando se tata de unidades gandes y de mucho costo, y
NTRODCCÓN ENSAYO de TRANSFORMADORES Nobeto A. Lemozy La veificación del coecto funcionamiento de cualquie equipo es de suma impotancia, en paticula cuando se tata de unidades gandes y de mucho costo, y
INTERACCIÓN ELECTROMAGNÉTICA ELECTROMAGNETISMO. Campo magnético creado por un conductor
 TERACCÓ ELECTROMAGÉTCA ELECTROMAGETSMO ES La Magdalena. Avilés. Astuias La unión electicidad-magnetismo tiene una fecha: 180. Ese año Oested ealizó su famoso expeimento (ve figua) en el cual hacía cicula
TERACCÓ ELECTROMAGÉTCA ELECTROMAGETSMO ES La Magdalena. Avilés. Astuias La unión electicidad-magnetismo tiene una fecha: 180. Ese año Oested ealizó su famoso expeimento (ve figua) en el cual hacía cicula
Universidad de Tarapacá Facultad de Ciencias Departamento de Física
 Univesidad de Taapacá Facultad de Ciencias Depatamento de Física Aplica el álgea de vectoes: Poducto escala Poducto vectoial Magnitudes físicas po su natualeza Escalaes Vectoiales Es un escala que se
Univesidad de Taapacá Facultad de Ciencias Depatamento de Física Aplica el álgea de vectoes: Poducto escala Poducto vectoial Magnitudes físicas po su natualeza Escalaes Vectoiales Es un escala que se
Apéndice 4. Introducción al cálculo vectorial. Apéndice 2. Tabla de derivadas y de integrales inmediatas. Ecuaciones de la trigonometría
 Apéndices Apéndice 1. Intoducción al cálculo vectoial Apéndice. Tabla de deivadas y de integales inmediatas Apéndice 3. Apéndice 4. Ecuaciones de la tigonometía Sistema peiódico de los elementos Apéndice
Apéndices Apéndice 1. Intoducción al cálculo vectoial Apéndice. Tabla de deivadas y de integales inmediatas Apéndice 3. Apéndice 4. Ecuaciones de la tigonometía Sistema peiódico de los elementos Apéndice
FORMACIÓN DE IMÁGENES EN ÓPTICA ADAPTATIVA
 Univesidad de Cantabia Tesis Doctoal FORMACIÓN DE IMÁGENES EN ÓPTICA ADAPTATIVA Vidal Fenández Canales Capítulo 1 LA TURBULENCIA ATMOSFÉRICA La atmósfea no se compota como un medio homogéneo paa la popagación
Univesidad de Cantabia Tesis Doctoal FORMACIÓN DE IMÁGENES EN ÓPTICA ADAPTATIVA Vidal Fenández Canales Capítulo 1 LA TURBULENCIA ATMOSFÉRICA La atmósfea no se compota como un medio homogéneo paa la popagación
Elementos de la geometría plana
 Elementos de la geometía plana Elementos de la geometía plana El punto Los elementos básicos de la geometía plana El punto es el elemento mínimo del plano. Los otos elementos geométicos están fomados po
Elementos de la geometía plana Elementos de la geometía plana El punto Los elementos básicos de la geometía plana El punto es el elemento mínimo del plano. Los otos elementos geométicos están fomados po
TEMA 9 POTENCIA EN SISTEMAS TRIFÁSICOS.
 TEMA 9 POTENCIA EN SISTEMAS TRIFÁSICOS. 9.. Potencias en sistemas equilibrados y simétricos en tensiones Un sistema trifásico puede considerarse como circuitos monofásicos, por lo que la potencia total
TEMA 9 POTENCIA EN SISTEMAS TRIFÁSICOS. 9.. Potencias en sistemas equilibrados y simétricos en tensiones Un sistema trifásico puede considerarse como circuitos monofásicos, por lo que la potencia total
Deflexión de rayos luminosos causada por un cuerpo en rotación
 14 Defleión de ayos luminosos causada po un cuepo en otación 114 Intoducción Cuando un ayo luminoso pasa po la cecanía de un cuepo se ve obligado a abandona su tayectoia ectilínea y cuvase más o menos
14 Defleión de ayos luminosos causada po un cuepo en otación 114 Intoducción Cuando un ayo luminoso pasa po la cecanía de un cuepo se ve obligado a abandona su tayectoia ectilínea y cuvase más o menos
Examen de Selectividad de Física. Septiembre 2008. Soluciones.
 Depatamento de Física y Química. I. E.. Atenea (.. Reyes, Madid) Examen de electividad de Física. eptiembe 2008. oluciones. Pimea pate Cuestión 1. Calcule el módulo del momento angula de un objeto de 1000
Depatamento de Física y Química. I. E.. Atenea (.. Reyes, Madid) Examen de electividad de Física. eptiembe 2008. oluciones. Pimea pate Cuestión 1. Calcule el módulo del momento angula de un objeto de 1000
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
Principio del Transformador
 Transformadores Oil tank High voltage bushing Low voltage bushing Profesor: Ing. César Chilet Cooling radiators Principio del Transformador La bobina primaria crea un flujo magnético variable, que circula
Transformadores Oil tank High voltage bushing Low voltage bushing Profesor: Ing. César Chilet Cooling radiators Principio del Transformador La bobina primaria crea un flujo magnético variable, que circula
E 1 E 2 E 2 E 3 E 4 E 5 2E 4
 Problemas resueltos de Espacios Vectoriales: 1- Para cada uno de los conjuntos de vectores que se dan a continuación estudia si son linealmente independientes, sistema generador o base: a) (2, 1, 1, 1),
Problemas resueltos de Espacios Vectoriales: 1- Para cada uno de los conjuntos de vectores que se dan a continuación estudia si son linealmente independientes, sistema generador o base: a) (2, 1, 1, 1),
P9: ENSAYO DE VACÍO Y CORTOCIRCUITO DEL TRANSFORMADOR MONOFÁSICO FUNDAMENTOS DE TECNOLOGÍA ELÉCTRICA
 ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
1.1. Sección del núcleo
 1. CALCULO ANALÍTICO DE TRANSFORMADORES DE PEQUEÑA POTENCIA Los transformadores tienen rendimiento muy alto; aunque éste no lo sea tanto en la pequeña potencia, podemos considerar que la potencia del primario
1. CALCULO ANALÍTICO DE TRANSFORMADORES DE PEQUEÑA POTENCIA Los transformadores tienen rendimiento muy alto; aunque éste no lo sea tanto en la pequeña potencia, podemos considerar que la potencia del primario
ANALISIS DE RIESGO E INCERTIDUMBRE. Evaluacion de Proyectos Jose Fuentes Valdes
 ANALISIS DE RIESGO E INCERTIDUMBRE Análisis Deteministico V/S Análisis de Riesgo e Incetidumbe Valoes Únicos y Conocidos Valoes Vaiables y Desconocidos ANALISIS DETERMINISTICO Pecio Cantidad Invesión EVALUACION
ANALISIS DE RIESGO E INCERTIDUMBRE Análisis Deteministico V/S Análisis de Riesgo e Incetidumbe Valoes Únicos y Conocidos Valoes Vaiables y Desconocidos ANALISIS DETERMINISTICO Pecio Cantidad Invesión EVALUACION
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Es el producto escalar de la fuerza aplicada al cuerpo por el vector r r Por lo tanto es una magnitud escalar.
 TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
ELECTRICIDAD MODULO 2
 .Paniagua Física 20 ELECTRICIDD MODULO 2 Enegía Potencial Eléctica nalicemos la siguiente situación física: una patícula q 0 cagada elécticamente se mueve desde el punto al punto B. Estos puntos están
.Paniagua Física 20 ELECTRICIDD MODULO 2 Enegía Potencial Eléctica nalicemos la siguiente situación física: una patícula q 0 cagada elécticamente se mueve desde el punto al punto B. Estos puntos están
VII.- EQUILIBRIO DE LAS TRANSFORMACIONES REALES pfernandezdiez.es
 VII.- EQUILIBRIO DE LAS RANSFORMACIONES REALES VII..- SISEMAS ERMODINÁMICOS La masa de los sistemas que evolucionan puede veni en moles, kg, etc., y po eso indicamos los potenciales temodinámicos con mayúsculas.
VII.- EQUILIBRIO DE LAS RANSFORMACIONES REALES VII..- SISEMAS ERMODINÁMICOS La masa de los sistemas que evolucionan puede veni en moles, kg, etc., y po eso indicamos los potenciales temodinámicos con mayúsculas.
Solución a los ejercicios de vectores:
 Tema 0: Solución ejecicios de intoducción vectoes Solución a los ejecicios de vectoes: Nota : Estas soluciones pueden tene eoes eatas (es un ollo escibios las soluciones bonitas con el odenado), así que
Tema 0: Solución ejecicios de intoducción vectoes Solución a los ejecicios de vectoes: Nota : Estas soluciones pueden tene eoes eatas (es un ollo escibios las soluciones bonitas con el odenado), así que
a < b y se lee "a es menor que b" (desigualdad estricta) a > b y se lee "a es mayor que b" (desigualdad estricta)
 Desigualdades Dadas dos rectas que se cortan, llamadas ejes (rectangulares si son perpendiculares, y oblicuos en caso contrario), un punto puede situarse conociendo las distancias del mismo a los ejes,
Desigualdades Dadas dos rectas que se cortan, llamadas ejes (rectangulares si son perpendiculares, y oblicuos en caso contrario), un punto puede situarse conociendo las distancias del mismo a los ejes,
SISTEMA MONOFÁSICO Y TRIFÁSICO DE C.A Unidad 1 Magnetismo, electromagnetismo e Inducción electromagnética.
 SISTEMA MONOFÁSICO Y TRIFÁSICO DE C.A Unidad 1 Magnetismo, electromagnetismo e Inducción electromagnética. A diferencia de los sistemas monofásicos de C.A., estudiados hasta ahora, que utilizan dos conductores
SISTEMA MONOFÁSICO Y TRIFÁSICO DE C.A Unidad 1 Magnetismo, electromagnetismo e Inducción electromagnética. A diferencia de los sistemas monofásicos de C.A., estudiados hasta ahora, que utilizan dos conductores
Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices Estructura del tema. Conceptos básicos y ejemplos Operaciones básicas con matrices Método de Gauss Rango de una matriz Concepto de matriz regular y propiedades Determinante asociado a una
Tema 1 Matrices Estructura del tema. Conceptos básicos y ejemplos Operaciones básicas con matrices Método de Gauss Rango de una matriz Concepto de matriz regular y propiedades Determinante asociado a una
Problemas resueltos. Consideramos despreciable la caída de tensión en las escobillas, por lo que podremos escribir:
 Problemas resueltos Problema 1. Un motor de c.c (excitado según el circuito del dibujo) tiene una tensión en bornes de 230 v., si la fuerza contraelectromotriz generada en el inducido es de 224 v. y absorbe
Problemas resueltos Problema 1. Un motor de c.c (excitado según el circuito del dibujo) tiene una tensión en bornes de 230 v., si la fuerza contraelectromotriz generada en el inducido es de 224 v. y absorbe
PROGRAMA IEM-212 Unidad II: Circuitos acoplados Magnéticamente.
 PROGRAMA IEM-212 Unidad II: Circuitos acoplados Magnéticamente. 2.1 Inductancia Mutua. Inductancia mutua. Sabemos que siempre que fluye una corriente por un conductor, se genera un campo magnético a través
PROGRAMA IEM-212 Unidad II: Circuitos acoplados Magnéticamente. 2.1 Inductancia Mutua. Inductancia mutua. Sabemos que siempre que fluye una corriente por un conductor, se genera un campo magnético a través
Un sencillo medidor vectorial de impedancias eléctricas para el laboratorio Fernando Valcarce Codes
 Enseñanza Un sencillo medido vectoial de impedancias elécticas paa el laboatoio Fenando Valcace Codes An aangement fo vectoial electical-impedance measuements is descibed which is pecise and accuate enough
Enseñanza Un sencillo medido vectoial de impedancias elécticas paa el laboatoio Fenando Valcace Codes An aangement fo vectoial electical-impedance measuements is descibed which is pecise and accuate enough
a = G m T r T + h 2 a = G r T
 www.clasesalacata.com Ley de la Gavitación Univesal 0.- Gavitación Univesal y Campo Gavitatoio Esta ley fomulada po Newton, afima que la fueza de atacción que expeimentan dos cuepos dotados de masa es
www.clasesalacata.com Ley de la Gavitación Univesal 0.- Gavitación Univesal y Campo Gavitatoio Esta ley fomulada po Newton, afima que la fueza de atacción que expeimentan dos cuepos dotados de masa es
Tema 3. Espacios vectoriales
 Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Matrices equivalentes. El método de Gauss
 Matrices equivalentes. El método de Gauss Dada una matriz A cualquiera decimos que B es equivalente a A si podemos transformar A en B mediante una combinación de las siguientes operaciones: Multiplicar
Matrices equivalentes. El método de Gauss Dada una matriz A cualquiera decimos que B es equivalente a A si podemos transformar A en B mediante una combinación de las siguientes operaciones: Multiplicar
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
Tema. Sistemas consevativos Tecea pate: Fueza gavitatoia A Campo gavitatoio Una masa M cea en su vecindad un campo de fuezas, el campo gavitatoio E, dado po E u siendo u el vecto unitaio adial que sale
TRANSFORMADORES EN PARALELO
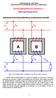 UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
1. Dominio, simetría, puntos de corte y periodicidad
 Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
2.7 Cilindros, conos, esferas y pirámides
 UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
Sistemas de numeración
 Sistemas de numeración Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. Los sistemas de numeración actuales son sistemas posicionales, que se caracterizan
Sistemas de numeración Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. Los sistemas de numeración actuales son sistemas posicionales, que se caracterizan
SISTEMAS DE NUMERACIÓN. Sistema de numeración decimal: 5 10 2 2 10 1 8 10 0 =528 8 10 3 2 10 2 4 10 1 5 10 0 9 10 1 7 10 2 =8245,97
 SISTEMAS DE NUMERACIÓN Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. La norma principal en un sistema de numeración posicional es que un mismo símbolo
SISTEMAS DE NUMERACIÓN Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar datos numéricos. La norma principal en un sistema de numeración posicional es que un mismo símbolo
UNIVERSIDAD DE ZARAGOZA
 Reflectometía en el dominio del tiempo UNIERIDAD DE ZARAGOZA FACUTAD DE CIENCIA DEPARTAMENTO DE FIICA APICADA AREA DE EECTROMAGNETIMO CARACTERIZACIÓN DIEÉCTRICA POR T. D. R. DE UNA MEZCA REINA EPOXY TITANATO
Reflectometía en el dominio del tiempo UNIERIDAD DE ZARAGOZA FACUTAD DE CIENCIA DEPARTAMENTO DE FIICA APICADA AREA DE EECTROMAGNETIMO CARACTERIZACIÓN DIEÉCTRICA POR T. D. R. DE UNA MEZCA REINA EPOXY TITANATO
Resolución paso a paso de problemas de máquinas eléctricas
 Resolución paso a paso de problemas de máquinas eléctricas Mario Ortiz García Sergio Valero Verdú Carolina Senabre Blanes Título: Autor: Resolución paso a paso de problemas de máquinas eléctricas 2ed Mario
Resolución paso a paso de problemas de máquinas eléctricas Mario Ortiz García Sergio Valero Verdú Carolina Senabre Blanes Título: Autor: Resolución paso a paso de problemas de máquinas eléctricas 2ed Mario
Tema 2. Espacios Vectoriales. 2.1. Introducción
 Tema 2 Espacios Vectoriales 2.1. Introducción Estamos habituados en diferentes cursos a trabajar con el concepto de vector. Concretamente sabemos que un vector es un segmento orientado caracterizado por
Tema 2 Espacios Vectoriales 2.1. Introducción Estamos habituados en diferentes cursos a trabajar con el concepto de vector. Concretamente sabemos que un vector es un segmento orientado caracterizado por
MATEMÁTICA DE LAS OPERACIONES FINANCIERAS II
 Facultad de iencias Económicas onvocatoia de Junio Pimea Semana Mateial Auxilia: alculadoa financiea MATEMÁTIA DE LAS OPERAIONES FINANIERAS II 2 de Mayo de 202 hoas Duación: 2 hoas. Péstamos a) Teoía:
Facultad de iencias Económicas onvocatoia de Junio Pimea Semana Mateial Auxilia: alculadoa financiea MATEMÁTIA DE LAS OPERAIONES FINANIERAS II 2 de Mayo de 202 hoas Duación: 2 hoas. Péstamos a) Teoía:
Tema 3: Producto escalar
 Tema 3: Producto escalar 1 Definición de producto escalar Un producto escalar en un R-espacio vectorial V es una operación en la que se operan vectores y el resultado es un número real, y que verifica
Tema 3: Producto escalar 1 Definición de producto escalar Un producto escalar en un R-espacio vectorial V es una operación en la que se operan vectores y el resultado es un número real, y que verifica
VECTORES EN EL ESPACIO. 1. Determina el valor de t para que los vectores de coordenadas sean linealmente dependientes.
 VECTORES EN EL ESPACIO. Determina el valor de t para que los vectores de coordenadas (,, t), 0, t, t) y(, 2, t) sean linealmente dependientes. Si son linealmente dependientes, uno de ellos, se podrá expresar
VECTORES EN EL ESPACIO. Determina el valor de t para que los vectores de coordenadas (,, t), 0, t, t) y(, 2, t) sean linealmente dependientes. Si son linealmente dependientes, uno de ellos, se podrá expresar
C. VALENCIANA / SEPTIEMBRE 04. LOGSE / FÍSICA / EXAMEN COMPLETO
 . VALENANA / SEPEMBRE 04. LOGSE / FÍSA / EXAMEN EXAMEN El alumno ealizaá una opción de cada uno de los bloques La puntuación máxima de cada poblema es de puntos, y la de cada cuestión es de,5 puntos. BLOQUE
. VALENANA / SEPEMBRE 04. LOGSE / FÍSA / EXAMEN EXAMEN El alumno ealizaá una opción de cada uno de los bloques La puntuación máxima de cada poblema es de puntos, y la de cada cuestión es de,5 puntos. BLOQUE
Comprensión conceptual y el uso de tecnología. César Cristóbal Escalante Verónica Vargas Alejo Universidad de Quintana Roo Julio 2013
 Compensión conceptual y el uso de tecnología Césa Cistóbal Escalante Veónica Vagas Alejo Univesidad de Quintana Roo Julio 203 Qué significa tene conocimiento de un concepto? Conoce su definición? Conoce
Compensión conceptual y el uso de tecnología Césa Cistóbal Escalante Veónica Vagas Alejo Univesidad de Quintana Roo Julio 203 Qué significa tene conocimiento de un concepto? Conoce su definición? Conoce
INTRODUCCION AL ANALISIS VECTORIAL
 JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
Tipos de instalaciones
 Tipos de instalaciones Existen este infinidad de configuraciones, pero como técnicos debemos referirnos a las normalizadas por la NTE, la cual diferencia cinco tipos basados en número de circuitos y programas,
Tipos de instalaciones Existen este infinidad de configuraciones, pero como técnicos debemos referirnos a las normalizadas por la NTE, la cual diferencia cinco tipos basados en número de circuitos y programas,
UNIDAD Nº 2 VECTORES Y FUERZAS
 UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE FISICA FISICA EXPERIMENTAL PLAN ANUAL INGENIERIA FISICA 1 e SEMESTRE 2012 UNIDAD Nº 2 VECTORES Y FUERZAS OBJETIVOS Medi el módulo de un vecto fueza usando
UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE FISICA FISICA EXPERIMENTAL PLAN ANUAL INGENIERIA FISICA 1 e SEMESTRE 2012 UNIDAD Nº 2 VECTORES Y FUERZAS OBJETIVOS Medi el módulo de un vecto fueza usando
D.1.- Considere el movimiento de una partícula de masa m bajo la acción de una fuerza central del tipo. n ˆ
 Cuso Mecánica (FI-1A), Listado de ejecicios. Edito: P. Aceituno 34 Escuela de Ingenieía. Facultad de Ciencias Físicas y Matemáticas. Univesidad de Chile. D: FUERZAS CENTRALES Y MOVIMIENTOS PLANETARIOS
Cuso Mecánica (FI-1A), Listado de ejecicios. Edito: P. Aceituno 34 Escuela de Ingenieía. Facultad de Ciencias Físicas y Matemáticas. Univesidad de Chile. D: FUERZAS CENTRALES Y MOVIMIENTOS PLANETARIOS
Ejercicios. 4. Para el transformador del problema 2 repetir las partes (a) y (b) del problema 3.
 Ejercicios 1. Se usa un autotransformador elevador para suministrar 3 kv a partir de una línea de alimentación de 2,4kV. Si la carga del secundario es de 50 A, calcular (despreciando las pérdidas y la
Ejercicios 1. Se usa un autotransformador elevador para suministrar 3 kv a partir de una línea de alimentación de 2,4kV. Si la carga del secundario es de 50 A, calcular (despreciando las pérdidas y la
Los transformadores. Inducción en una bobina
 Los transformadores Los transformadores eléctricos han sido uno de los inventos más relevantes de la tecnología eléctrica. Sin la existencia de los transformadores, sería imposible la distribución de la
Los transformadores Los transformadores eléctricos han sido uno de los inventos más relevantes de la tecnología eléctrica. Sin la existencia de los transformadores, sería imposible la distribución de la
Subespacios vectoriales en R n
 Subespacios vectoriales en R n Víctor Domínguez Octubre 2011 1. Introducción Con estas notas resumimos los conceptos fundamentales del tema 3 que, en pocas palabras, se puede resumir en técnicas de manejo
Subespacios vectoriales en R n Víctor Domínguez Octubre 2011 1. Introducción Con estas notas resumimos los conceptos fundamentales del tema 3 que, en pocas palabras, se puede resumir en técnicas de manejo
TEMA3: CAMPO ELÉCTRICO
 FÍIC º BCHILLERTO. CMPO ELÉCTRICO. TEM3: CMPO ELÉCTRICO o Natualeza eléctica de la mateia. o Ley de Coulomb vs Ley de Newton. o Pincipio de supeposición. o Intensidad del campo elético. o Líneas del campo
FÍIC º BCHILLERTO. CMPO ELÉCTRICO. TEM3: CMPO ELÉCTRICO o Natualeza eléctica de la mateia. o Ley de Coulomb vs Ley de Newton. o Pincipio de supeposición. o Intensidad del campo elético. o Líneas del campo
App para realizar consultas al Sistema de Información Estadística de Castilla y León
 App para realizar consultas al Sistema de Información Estadística de Castilla y León Jesús M. Rodríguez Rodríguez rodrodje@jcyl.es Dirección General de Presupuestos y Estadística Consejería de Hacienda
App para realizar consultas al Sistema de Información Estadística de Castilla y León Jesús M. Rodríguez Rodríguez rodrodje@jcyl.es Dirección General de Presupuestos y Estadística Consejería de Hacienda
Unidad Didáctica. Transformadores Trifásicos
 Unidad Didáctica Transformadores Trifásicos Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION
Unidad Didáctica Transformadores Trifásicos Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION
4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA
 4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA Una ecuación con una incógnita es de segundo grado si el exponente de la incógnita es dos. Ecuaciones de segundo grado con una incógnita son: Esta última ecuación
4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA Una ecuación con una incógnita es de segundo grado si el exponente de la incógnita es dos. Ecuaciones de segundo grado con una incógnita son: Esta última ecuación
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN
 Física P.A.U. GRAVIACIÓN 1 GRAVIACIÓN INRODUCCIÓN MÉODO 1. En geneal: Se dibujan las fuezas que actúan sobe el sistema. Se calcula la esultante po el pincipio de supeposición. Se aplica la ª ley de Newton
Física P.A.U. GRAVIACIÓN 1 GRAVIACIÓN INRODUCCIÓN MÉODO 1. En geneal: Se dibujan las fuezas que actúan sobe el sistema. Se calcula la esultante po el pincipio de supeposición. Se aplica la ª ley de Newton
by Tim Tran: https://picasaweb.google.com/lh/photo/sdo00o8wa-czfov3nd0eoa?full-exif=true
 by Tim Tran: https://picasaweb.google.com/lh/photo/sdo00o8wa-czfov3nd0eoa?full-exif=true I. FUNDAMENTOS 3. Representación de la información Introducción a la Informática Curso de Acceso a la Universidad
by Tim Tran: https://picasaweb.google.com/lh/photo/sdo00o8wa-czfov3nd0eoa?full-exif=true I. FUNDAMENTOS 3. Representación de la información Introducción a la Informática Curso de Acceso a la Universidad
Campo eléctrico. Introducción a la Física Ambiental. Tema 7. Tema 7.- Campo eléctrico.
 Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
Ejercicios de Trigonometría
 Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
Modelos de líneas de transmisión en estado estacionario... 2
 Modelos de líneas de transmisión en estado estacionario Prof Ing Raúl ianchi Lastra Cátedra: CONTENIDO Modelos de líneas de transmisión en estado estacionario Introducción Constantes del cuadripolo Modelos
Modelos de líneas de transmisión en estado estacionario Prof Ing Raúl ianchi Lastra Cátedra: CONTENIDO Modelos de líneas de transmisión en estado estacionario Introducción Constantes del cuadripolo Modelos
0.2.4 Producto de un escalar por un vector. Vector unitario. 0.3 Vectores en el sistema de coordenadas cartesianas.
 VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
ACCIONES Y OTROS TÍTULOS DE INVERSIÓN
 ACCIONES Y OTROS TÍTULOS DE INVERSIÓN TASAS EFECTIVAS DE RENDIMIENTO ANUAL Y MENSUAL: Es aquélla que se emplea en la compraventa de algunos valores en el Mercado Bursátil o Bolsa de Valores. Estas tasas
ACCIONES Y OTROS TÍTULOS DE INVERSIÓN TASAS EFECTIVAS DE RENDIMIENTO ANUAL Y MENSUAL: Es aquélla que se emplea en la compraventa de algunos valores en el Mercado Bursátil o Bolsa de Valores. Estas tasas
Introducción ELECTROTECNIA
 Introducción Podríamos definir la Electrotecnia como la técnica de la electricidad ; desde esta perspectiva la Electrotecnia abarca un extenso campo que puede comprender desde la producción, transporte,
Introducción Podríamos definir la Electrotecnia como la técnica de la electricidad ; desde esta perspectiva la Electrotecnia abarca un extenso campo que puede comprender desde la producción, transporte,
TEMA PRELIMINAR. Los sistemas de representación son objeto de estudio en la geometría descriptiva, la cual se fundamenta en la geometría proyectiva.
 TEMA PRELIMINAR 1. Sistemas de Repesentación y Geometía. En esta pate de la intoducción, se tata de encuada el estudio de los sistemas de epesentación dento de lo que es la geometía. Paa ello se va a intenta
TEMA PRELIMINAR 1. Sistemas de Repesentación y Geometía. En esta pate de la intoducción, se tata de encuada el estudio de los sistemas de epesentación dento de lo que es la geometía. Paa ello se va a intenta
FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO
 FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO Determinar la capacidad de un regulador según la placa de datos:
FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO Determinar la capacidad de un regulador según la placa de datos:
