Estas son una clase particularmente importante de series de funciones: Definición 1.1 Una serie de la forma

Transcripción

1 Cítulo Series de Fourier En est sección vmos trbjr con funciones de vrible e imgen rel, o se f (t, con f : R R. Más delnte extenderemos los resultdos r funciones de imgen comlej, es decir, r funciones f : R C. Si tenemos un función f : R R que se lo suficientemente derivble, se sbe de Análisis I que odemos roximr f loclmente usndo olinomios de Tylor, ero dich roximción tiene muchs limitciones: necesit que l función teng derivds (mientrs más derivds teng, más osibilidd de que l roximción se buen, y d un roximción locl, o se buen cerc de un unto refijdo. Vmos ver cá otr form de hcer esto... Introducción: Series de Potencis Ests son un clse rticulrmente imortnte de series de funciones: Definición. Un serie de l form n (t n = + (t + (t + n= se l llm serie de otencis centrd en. t n Ejemlo.. es un serie de otencis centrd en cero, con n = n n! n! n= N {}.. ( n (t n es un serie de otencis centrd en, con n = ( n n N ( =. 9

2 Series de Fourier Un gruo esecilmente imortnte de series de otencis son ls de l form n= f (n ( n! (t n donde f es lgun función que tiene derivds de todos los órdenes en ; est serie recibe el nombre de series de tylor r f en. Est definición deriv de l de olinomio de Tylor: N si f (, f (, f (,..., f (N f (n ( ( existen tods, luego P N, (t = (t n es el n! n= olinomio de Tylor de grdo N r f en. Se one R N, (t = f (t P N, (t (el resto, de form tl que f (t = P N, (t + R N, (t = N n= f (n ( n! (t n + R N, (t. f (n ( De est exresión se deduce inmeditmente que l serie (t n converge f (t n! n= si y solo sí R N, (t. Notr que P N, (t = S N (t, l N-ésim sum rcil de l serie de N Tylor. Ejemlo.3 Vmos encontrr l serie de Tylor r f (t = t lrededor de t =. Tenemos: en generl f( = f (t = t f ( = f (t = t 3 f ( = f (t = 6 t 4 f ( = 6 f iv (t = 4 t 5 f iv ( = 4 f (n (t = ( n n! t n+ f (n ( = ( n n! r n N. luego l serie buscd es: n= ( n n! n! (t n = ( n (t n. Est cuent no demuestr que dich serie se convergente, y menos que converj f(t, ero odemos ver esto usndo l serie geométric: n= n= t = ( t = ( t n = ( n (t n, donde l segund igundd vle si t < (y l serie diverge r t >. n=

3 Series de Fourier L siguiente roosición, de demostrción inmedit si se disone de l Regl de L Hoitl, nos dice cun bien roxim el olinomio de Tylor de un función en un entorno del centro : Proosición.4 Si f : ( ε, + ε R tiene n derivds en, entonces f (t P n, (t lím t (t n = Demostrción. Ejercicio, licr l regl de L Hoitl n veces. A est ltur conocemos dos fórmuls exlícits r el resto: Proosición.5 Si f : ( ε, + ε R y I es el intervlo de extremos y t, entonces:. Si f (n+ existe en I, entonces R n, (t = f (n+ (ξ (n +! (t n+ r lgún ξ I.. Si f (n+ es integrble en I, entonces R n, (t = t f (n+ (u n! (t u n du. Ejemlo.6 Dd f (t = cos (t y =, f tiene derivds de todos los órdenes en. Clculndo obtenemos f( = f (t = sin (t f ( = f (t = cos (t f ( = f (t = sin (t f ( = A rtir de l curt derivd, los resultdos se reiten de mner cíclic, or lo que result que l serie de Tylor r cos (t en cero es t + t4 4! t6 6! + + ( n t n (n! + R n,o(t (notr que tods ls otencis de t que recen son res. Como f (n+ (ξ n, ξ, se tiene que Entonces, hemos robdo que R n, (t tn+ (n +! n (ejercicio. cos (t = ( n t n (n! n= r todo t R.

4 Series de Fourier De mner bsolutmente nálog se uede ver que y sin (t = n= ex (t = ( n t n+ (n +! n= t n n! r todo t R, r todo t R. Al comenzr el estudio de series, nos concentrmos en l convergenci o no de ls misms. Cundo se trbj con serie de otencis, o en generl con series de términos vribles, el foco debe onerse en cules son los vlores que uede tomr l vrible t r que l serie resultnte se convergente. Pr cd vlor de t en el que l serie de otencis converge, l serie reresent el número que es l sum de l serie. Por tnto, un serie de otencis en t define un función que tiene como dominio todos los vlores de t r los cules l serie de otenci converge. Teorem.7 Si l serie de otencis n (t n converge en t = t, entonces converge n= bsolutmente t tl que t < t. Es decir, si r = t entonces l serie converge bsolutmente t ( r, + r. Demostrción. Puesto que l serie que n (t n converge, l condición del resto nos dice n= lím n (t n =, n y entonces M tl que n (t n M n. Si tommos t tl que t < r, tendremos ( n (t n t n = n r n M t n r r. Puesto que l serie t r converge (or ser geométric de rzón menor que, or comrción concluimos que n= n n (t n converge bsolutmente. El resultdo nterior nos ermite definir el conceto de rdio de convergenci de un serie de otencis: consideremos l serie n (t n, que siemre converge ( cero cundo n= t =. Llmemos R =, y exloremos dos osibiliddes:. Si existe t tl que t > R y tl que l serie n= n (t n se convergente, llmemos R = t (notr R > R. En tl cso l Proosición nterior nos dice que l serie converge bsolutmente t ( R, + R. n=

5 Series de Fourier 3. Si no existe t tl que t > R y l serie n= n (t n se convergente, llmmos R = R =, y l serie converge solo en t =. En el cso., seguimos itertivmente de l siguiente mner:. Si existe t tl que t > R y tl que l serie n= n (t n se convergente, llmemos R = t (notr R > R. En tl cso l Proosición nterior nos dice que l serie converge bsolutmente t ( R, + R.. Si no existe t tl que t > R y l serie n= n (t n se convergente, llmmos R = R, y l serie converge bsolutmente t ( R, + R y diverge t {t : t > R}. Este roceso itertivo nos ermite construir un sucesión creciente {R n } n= cuyo límite ( se llm el rdio de convergenci de l serie de otencis, y or su construcción tiene l roiedd de que l serie converge bsolutmente t ( R, + R = {t : t < R} y diverge t {t : t > R}. No sbemos que s en {t : t = R}, es decir, en t = ± R. Ejemlo.8 Determine los vlores de t r los cules l serie de otencis es convergente: ( n+ n n3 n tn n= Si exresmos l serie dd de l form n= t n, entonces t n = ( n+ n t n n3 n y t n+ = ( n+ n+ t n+ (n + 3 n+ de modo que lím n + t n+ t n = lím n + = lím n + = 3 t n+ t n+ n3 n (n + 3 n+ n t n 3 t n n + Por tnto l serie de otencis es bsolutmente convergente cundo 3 t < o, equivlentemente, cundo t < 3. L serie es divergente cundo 3 t > o, equivlentemente, cundo t > 3. Es decir, el rdio de convergenci de est serie es R = 3. Cundo 3 t = (es decir cundo t = ± 3, el criterio del cociente no d informción. Cundo t = 3, l serie de otencis dd se convierte en l serie rmónic lternnte ( n+ n + l cuál es convergente. Cundo t = 3 se tiene 3 4 n

6 4 Series de Fourier l cul es (un multilo de l serie rmónic, que es divergente. Por tnto, se concluye que l serie de otenci dd es bsolutmente convergente cundo y es condicionlmete convergente cundo 3 < t < 3 t = 3. Si l serie es divergente. t 3 ó t > 3,.. Series de funciones reles De l mism form que ensmos en sucesiones de números reles {x n } n N, donde tenímos un número rel r cd nturl n, odemos ensr en un sucesión de funciones {f n } n N, donde cd f n (t es un función rel definid en cierto dominio (o se, tenemos un función de vrible r cd número nturl n. Por ejemlo si llmmos f n (t = n cos(nt, entonces {f n } n N es un sucesión de funciones reles, cd un de ls funciones de l sucesión est definid en todo R, y l n-ésim función de l sucesión es nt. Suongmos que tenemos un sucesión de funciones {f n } n N, y tomemos un número t fijo que esté en el dominio de tods ls funciones f n, entonces {f n (t} n N es un sucesión de números reles, sí que tiene sentido lnter l serie f (t + f (t + f 3 (t + = f n (t. Pr decidir si un serie de este tio converge, se uede licr culquier de los criterios vistos, ues se trt de un serie norml de números reles. Pero estmos interesdos en ver el roblem desde otro unto de vist: dd un sucesión de funciones {f n } n N, queremos encontrr los números reles t r los cules l serie numéric f n (t es convergente (si es que hy lguno. Suoniendo que l serie f n (t converge r todo t de cierto conjunto I R, llmmos N S (t = lím f n (t = f n (t, N y esto define un nuev función S (t en I (l función que sign cd t de I el vlor de l serie numéric f n (t. Este hecho se suele denotr omitiendo l vrible: S = lím N N f n = f n,

7 Series de Fourier 5 y se dice que l serie de funciones f n converge l función S. L definición de convergenci qued sí: Definición.9 Dd un sucesión de funciones {f n } n N, diremos que f n converge en un conjunto I si f n (t converge r todo t I (notr que, necesrimente I Dom (f n n, es decir, los untos donde l serie converge son, necesrimente, untos del dominio de ls funciones f n. Análogmente, diremos que l serie f n converge bsolutmente en I si l serie f n (t converge r todo t I (o se si l serie f n (t converge bsolutmente r todo t I. L región de convergenci de l serie f n es el conjunto { } t R : f n (t converge, es decir, el myor conjunto donde l serie converge. Ejemlo. Tomr f n (t = t n, con n N (es decir, f (t = t, f (t = t, f 3 (t = t 3, etc., y queremos ver r qué vlores de t odemos clculr f (t + f (t + f 3 (t + (notr que cd función f n está definid en todo R. Llmndo S n (t = f (t + f (t + f 3 (t + + f n (t y hciendo l mism cuent que r l serie geométric, concluimos que r t vle S n (t = t tn+. t Entonces, r t con t < tenemos que f n (t = lím n S n (t = t t, y r t con t l serie no converge ues los términos no tienden cero. Es decir, l serie f n converge en el conjunto I = {t : t < }. Los criterios usules r series numérics quedn hor sí: Si f n y g n son series de funciones, f n converge f en I f R, y g n converge g en I g R, y α es un número rel, entonces l serie de funciones (αf n + g n converge l función αf + g en I f I g. Si f n converge en I R entonces lím f n (t = t I. n L serie f n converge en I si y solo si l serie R N = n=n+ f n converge en I r todo N, y en tl cso lím R N(t = t I. N

8 6 Series de Fourier Si f n converge bsolutmente en I R, entonces converge en I (es decir, si f n (t converge r todo t en I entonces f n (t converge r todo t en I. Si h n (t f n (t t I y f n converge en I, entonces h n converge en I (y entonces h n converge en I. Si {f n } n N es un sucesión con f n (t t I y n N (donde N es lgún nturl y lím f n+ (t n f n (t = l t, entonces l serie f n converge bsolutmente en I si l t < t I, (y diverge r los vlores de t tles que l t >. Si {f n } n N es un sucesión y lím n n fn (t = l t, entonces l serie f n converge bsolutmente en I si l t < t I, (y diverge r los vlores de t tles que l t >. Ejemlo. Tomemos f n (t = ( t n t + (o se que cd f n está definid en R { }, buscmos l región de convergenci de f n. Por el ejemlo nterior, sbemos que necesitmos ( t <, t + y entonces ( t < t < t + t < (t + t + t < t + t + < t, es decir, l serie converge en el intervlo (,. En generl, uno retende que l función definid or un serie de funciones convergentes teng ls misms roieddes de suvidd que ls funciones sumds. Esto en generl no es sí, ero tenemos los siguientes resultdos: Teorem. Si {f n } n N es un sucesión de funciones continus en [, b] y {M n } n N es un sucesión de números reles ositivos tles que. r cd n N, vle que f n (t M n t [, b], y. l serie M n converge.

9 Series de Fourier 7 Entonces l serie f n converge bsolutmente un función continu S(t, y d c S (t dt = d c f n (t dt [c, d] [, b]. Demostrción. Primero notr que or comrción l serie f n(t converge (bsolutmente r todo t [, b]. Llmemos S(t = f n(t. Además, R N (t = f n (t f n (t M n, N n=n+ n=n+ y entonces ddo ε > uedo encontrr n N tl que n=n+ R n (t < ε 3 t [, b] Doy un t fijo en [, b], quiero ver que uedo hcer S (t S (t chico tomndo t suficientemente róximo t, es decir, doy ε > y quiero ver que hy un δ > tl que Llmemos S n (t = n j= f j (t, entonces S (t S (t < ε si t t < δ. S (t S (t = S (t S n (t + S n (t S n (t + S n (t S (t S (t S n (t + S n (t S n (t + S n (t S (t = = R n (t + S n (t S n (t + R n (t < < ε 3 + S n (t S n (t. (. Ahor tomo δ tl que S n (t S n (t < ε 3 si t t < δ (. (que existe ues l función S n (t es continu en t ues es l sum de n funciones continus. Combinndo (. con (., vemos que tl δ es el que estábmos buscndo. En cunto l integrl, queremos ver que l serie numéric d c f n (t dt converge l número d c S (t dt. Rzonndo como rrib, ddo ε > existe N N tl que R n (t ε b r todo t [, b] si n N. Entonces d n d d n d S (t dt f j (t dt = S (t f j (t dt c c c n S (t f j (t c dt = j= que es lo que querímos robr. = d c j= R n (t dt ε (d c < ε n N, b j= Ejemlo.3 Considerr l serie cos (nt n.

10 8 Series de Fourier Puesto que cos(nt n r todo t R, y n convege, concluimos que dich serie n converge un función continu S(t en R. Además, π cos (nt n dt = π cos (nt n dt =. S t Notr que, rtir de l gráfic de S, no es obvio que l integrl vlg cero. Más delnte encontrremos un fórmul r S en términos de funciones elementles. Teorem.4 Si {f n } n N es un sucesión de funciones con derivd continu en [, b] tles que f n(t converge en [, b] S(t, y {M n } n N es un sucesión de números reles ositivos tles que. r cd n N, vle que f n (t M n t [, b], y. l serie M n converge. Entonces S(t tiene derivd continu S (t = f n (t dt. Demostrción. Llmemos g (t = f n (t, quiero ver que S es derivble y que S (t = g (t t (, b. Por el Teorem Fundmentl del Cálculo, f n (t f n ( = Alicndo el Teorem nterior, vemos que t t g (x dx = f n (x dx = = t [ t f n (x dx, ] f n (x dx = f n (t f n ( = S (t S (. [f n (t f n (] = Pero sbemos del Teorem nterior que g es continu, or lo que el Teorem Fundmentl del Cálculo nos dice que [ d t ] g (x dx = g (t, dt que comrndo con l iguldd nterior nos ermite deducir que S es derivble y S (t = g (t. Que S es continu se deduce del Teorem nterior.

11 Series de Fourier 9 Ejemlo.5 (Alicción Series de Potencis Vmos extender los resultdos del Teorem.7. Si S(t = n (t n, n= es un serie de otencis que converge en t, tomemos culquier < r < t, y M tl que n (t n M (que existe or l convertenci en t. Entonces r todo t ( r, +r se tiene n (t n n (t n r n t n M rn t n = M n, y n n (t n nn (t n r n t n M nrn t n = M n. Ests dos cots (que vlen r todo t ( r, + r imlicn (licndo los Teorems. y.4 que S(t se uede integrr término término, y un rimitiv de S(t es t S(xdx = t n (x n dx = n= y demás es derivble en ( r, + r y S (t = n= d dt n (t n = n= n n + (t n, (.3 n n (t n. (.4 Eligiendo convenientemente t y r, se uede ver que ls tres series de otencis tienen el mismo rdio de convergenci, y que ls fórmuls (.3 y (.4 vlen en tod l región de convergenci. Dicho corto: ls series de otencis se ueden integrr y derivr término término. Se dej como ejercicio licr esto ls series de Tylor encontrds, y utilizr el mismo r encontrr l serie de Tylor de otrs funciones (or ejemlo, l de ln integrndo l serie de /t..3. Funciones eriódics Hremos cá un reconto de ls roieddes que necesitmos de ls funciones de vrible rel eriódics. Definición.6 Un función f : R R (ó f : R C se dice eriódic de eríodo T si f (t = f (t + T r todo t R. Cundo existe un menor T ositivo con est roiedd se lo llm eríodo fundmentl de f. Por ejemlo, l función cos (t es eriódic de eríodo kπ, k N, y su eríodo fundmentl es π; or lo tnto si n N y >, l función ( f (t = cos

12 Series de Fourier es eriódic de eríodo k n, y su eríodo fundmentl es n. En rticulr, culquier se el número n, f tiene eríodo. Ls funciones constntes son eriódics con culquier eríodo, y no tienen eríodo fundmentl. Si f tiene eríodo T entonces f tiene eríodo kt r culquier k N (ejercicio, y ls funciones eriódics de eríodo T quedn bsolutmente determinds or su vlor en culquier intervlo de l form [, +T, ues si conozco f en un intervlo sí y quiero sber cunto vle f (t r cierto t, bst con buscr k Z tl que t + kt [, + T. De est form se uede construir funciones eriódics rtir de funciones definids en lgún intervlo: si conozco f en [, b y digo que f tiene eríodo T = b, entonces tengo definid en todo R un función eriódic de eríodo T. En rticulr, se us mucho tener un función definid en un intervlo simétrico [, y eriódic de eríodo. T T T b Si summos funciones de eríodo T obtenemos un nuev función que tmbién tiene eríodo T (ojo, no estmos hblndo del eríodo fundmentl, solo de lgún eríodo, y tmbién si tenemos un sucesión de funciones {f n } n N tods de eríodo T y l serie f n converge, entonces converge un función de eríodo T. Así, l función S N (t = N + ( ( n cos + b n sin es eriódic de eríodo ues es sum de funciones de eríodo (se uede verificr fácilmente, demás, que S N (t = S N (t +, y si l serie + ( ( n cos + b n sin converge, entonces converge un función de eríodo. Si f es eriódic de eríodo T, e integrble (en el sentido de Riemnn, entonces r todo R se tiene que T f (t dt = +T f (t dt, es decir que cd vez que integro sobre un intervlo de longitud T obtengo el mismo resultdo. Esto uede verse fácilmente de mner gráfic, recortndo el áre bjo f en [, + T y

13 Series de Fourier recomodándol r que quede como el áre bjo f en [.T T + T.4. Aroximción or medio de olinomios trigonométricos Sbemos que odemos roximr cierts funciones f (t con olinomios (t usndo Tylor (Análisis I. Lo que se le ide l función es que teng suficientes derivds en un entorno de un unto t, y el criterio de roximción que se tom es hcer l desvición máxim f (t (t lo más chic osible en cierto intervlo [, b] que contiene t (es decir, (t roxim bien f (t en [, b] si l diferenci máxim entre sus gráfics es equeñ. Al usr Tylor, construimos un olinomio de grdo n, n f (j (t n (t = (t t j, j! j= y r mejorr l roximción debímos umentr n, y r que l roximción se tn buen como quermos necesitmos que f teng derivds de todos los órdenes en t y demás que el resto n f f (j (t (t (t t j j! j= tiend cero cundo n tiende infinito r todo t de [, b], lo cul no ocurre siemre. ( t f( t t Ahor vmos trtr de roximr funciones f (t eriódics de eríodo, y r eso usremos olinomios trigonométricos de grdo N y eríodo, que son funciones de l form S N (t = N + ( n cos + b n sin (,

14 Series de Fourier donde es un número rel fijo y,,..., N, b,..., b N son números (reles o comlejos, deendiendo de que f ser rel o comlej que elegiremos r stisfcer cierto criterio de roximción. Notr que cd término de S N (t es un función eriódic de eríodo, or lo tnto S N (t es un función eriódic de eríodo. Entonces S N v ser bueno r roximr funciones de eríodo, o lo que es lo mismo, funciones definids en lgún intervlo de longitud (ues si tengo un función definid en un intervlo de longitud uedo construir un función eriódic de eríodo definiendo f (t = f (t + r todo t rel, y vicevers. De cá en delnte sumimos eso: vmos trbjr con funciones definids en un intervlo de longitud y extendids eriódicmente todo R. En cunto l criterio r roximr, vmos usr el que se llm de l medi cudrátic mínim, y r motivr este criterio vmos suoner que f : R R. Si, con l notción que tremos, llmmos δ N (t = f (t S N (t, entonces el criterio usdo con olinomios de Tylor er hcer chico δ N (t, y si mirmos ls gráfics bjo, con ese criterio, es mejor roximción de f que f( t f( t Pero el áre que qued entre f y en el intervlo [, ] es más grnde que l que qued entre y f, y ese es otro criterio que odrímos usr r decir que un función roxim f. Como dich áre es δ N (t dt, deberímos elegir los coeficientes (reles, ues f lo es,,..., N, b,..., b N de S N r hcer δ N (t dt lo más chico osible. Pero esto resent comlicciones teórics y tiene lgunos resultdos indesebles, sí que vmos tomr como criterio de elección de los coeficientes de S N, minimizr δ N (t dt con l esernz de que se más o menos lo mismo (notr que en este cso δ N (t = δ N (t ues tods ls cntiddes involucrds son reles. Not imortnte.7 Puesto que ests oerciones involucrn l integrción de funciones, de cá en delnte sumiremos que ls funciones involucrds son cotds e integrbles en el sentido de Riemnn. Se uede extender l teorí funciones no cotds (cuy integrl imroi en el intervlo [, ] converge, ero dich generlidd esc l lcnce de ests nots.

15 Series de Fourier 3 Definición.8 Si f (t, g (t y g (t son funciones (de imgen rel o comlej cotds e integrbles en [, b], diremos que g roxim mejor f que g en [, b] en el sentido de l medi cudrátic si b f (t g (t dt b f (t g (t dt. Seguimos hor con el roblem de encontrr los coeficientes,,..., N, b,..., b N de S N, es decir, tomemos un f : [, ] R y busquemos los números reles,,..., N, b,..., b N de S N de form tl que S N roxime lo mejor osible f en el sentido de l medi cudrátic en [, ]. Como tods ls cntiddes involucrds son reles, tenemos que elegir,,..., N, b,..., b N de modo que I N = δ N (t dt = ( [ N f (t + ( ( ] n cos + b n sin dt (.5 se lo más chico osible, es decir, odemos ensr I N (,,..., N, b,..., b N como un función de N + vribles, y tenemos que minimizrl. Pr hcer esto, clculremos I N (or más doloroso que se, y luego derivremos, con l esernz de encontrr un unto crítico que se mínimo. Pr ello vmos utilizr ls siguientes relciones: se tiene que ( cos ( sin ( cos cos sin sin ( kπt ( kπt ( kπt dt = dt = { si n = k si n k, { si n = k si n k, (.6 dt = k, n, y ( cos dt = sin ( dt =. (.7 Desrrollndo el integrndo en (.5 qued ( [ N f (t + ( n cos N [ ( = f (t f (t n cos + b n sin ( ] f (t + b n sin ( ( N + + ( n cos Integrndo el último término de (.8 y usndo (.7 obtenemos ] f (t + (.8 + b n sin (

16 4 Series de Fourier ( [ N + ( ( ] n cos + b n sin dt = = 4 dt + N ( ( n cos dt + b n sin dt + }{{}}{{} [ N ( ( ] + n cos + b n sin dt = N + [ n + b ] n, donde est últim iguldd vle ues cundo hcemos [ N ( ( ] n cos + b n sin obtenemos l sum de tods ls combinciones del tio ( n cos m cos ( mπt, n cos ( b m sin ( mπt, y b n sin ( b m sin ( mπt con n, m N, sí que cundo integrmos (usndo ls relciones (.6 resultn distinto de cero únicmente los términos con solo cosenos o solo senos y con m = n, y en tl cso l integrl vle multilicdo or el cudrdo del resectivo coeficiente. Finlmente, integrndo los otros dos términos de (.8 obtenemos, I N = N ( f (t ( ] dt f (t dt [ n cos f (t dt + b n sin f (t dt + + N + [ n + b ] n. (.9 (notr que es un form cudrátic en,,..., N, b,..., b N. Derivndo, obtenemos que I N = I N k = I N b k = f (t dt +, ( kπt cos ( kπt sin f (t dt + k, (. f (t dt + b k,

17 Series de Fourier 5 que l igulrls cero nos dice que deberímos tomr = k = b k = f (t dt ( kπt f (t cos ( kπt f (t sin Pero derivndo de nuevo en (. obtenemos dt r k dt r k. I N I N =, = I N k b = r k, k y como tods ls derivds cruzds dn cero, result que l mtriz Hessin de I N es l mtriz digonl.....,..... de donde concluimos que efectivmente obtenemos un mínimo eligiendo los coeficientes de es form. El trbjo hecho hst hor nos ermite decir como debemos elegir los coeficientes de S N r obtener l mejor roximción de f en el sentido de l medi cudrátic, ero todví no sbemos cómo de buen es es roximción (unque se l mejor uede ser mlísim, sí que or hor no tenemos teorems ero sí un definición: Definición.9 Si f es un función eriódic de eríodo, cotd e integrble en el intervlo [, ] (en el sentido de Riemnn, definimos sus coeficientes de Fourier or n,f = ( f (t cos dt y b n,f = ( f (t sin dt, y el olinomio trigonométrico S N f (t =,f N + ( ( n,f cos + b n,f sin formdo usndo los coeficientes de Fourier de f se llm l roximción N-ésim de Fourier de f (los subíndices que indicn l función entorecen extremdmente l notción, or lo cul no los utilizremos slvo que se estrictmente necesrio. Seguimos l cuent: evlundo I N en,f,,f,..., N,f, b,f,..., b N,f (ver.9 y teniendo en cuent l definición nterior, obtenemos ( N I N,f = I N (,f,,f,..., N,f, b,f,..., b N,f = f (t,f dt + [ n,f + b ] n,f, de donde odemos scr ls siguientes conclusiones:

18 6 Series de Fourier. Puesto que (,f + [ ] N n,f + b n,f crece cundo N crece (ues sumo más términos ositivos, l roximción mejor cundo N crece, ues. L serie I N,f = f (t dt ( N,f + [ n,f + b ] n,f.,f + [ n,f + b ] n,f converge ues es creciente (es decir, mientrs más grnde N más grnde es l sum y r todo N vle que,f N + [ n,f + b ] n,f f (t dt es decir, es cotd. Esto dice que b n,f n, y entonces n,f [ ] n,f + b n,f y b n,f. n n, y entonces n n,f y n Desués de todo este trbjo hemos demostrdo el siguiente teorem: Teorem. Se f : R R un función eriódic de eríodo, cotd e integrble en el sentido de Riemnn en [, ], y llmemos S N (t = N + ( n cos + b n sin ( Entonces l mejor roximción de f or S N en el sentido de l medi cudrátic se obtiene l elegir n = ( f (t cos dt, n N {}, y b n = ( f (t sin dt, n N (es decir, los coeficientes de Fourier de f. Con est elección, l roximción mejor medid que N crece, y l serie [ n + b n ] converge, resultndo N + [ n + b n] f (t dt.. Además, lím f (t cos n ( dt = lím f (t sin n ( dt =.

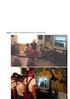
19 Series de Fourier 7 Se uede ver que más que lo que dice el teorem es cierto: en 896 el mtemático Liunoff demostró que lím N I N =, de donde se deduce que vle l iguldd + [ n + b n] = f (t dt r culquier función cotd (e incluso r funciones no cotds ero tles que l integrl imroi f (t dt se convergente. Est iguldd se llm iguldd de Prcevl y l desiguldd del teorem se llm desiguldd de Bessel. Not imortnte. Cundo uno exmin con cuiddo lo hecho, se d cuent de que los coeficientes de Fourier no deenden del grdo de l roximción N. Esto es muy imortnte orque signific que si uno no está conforme con l roximción logrd con ciert cntidd de términos, entonces uedo gregr términos sin tener que reclculr los rimeros coeficientes. Es decir, si r cierto roblem usmos l 3r roximción de Fourier y no estmos conformes con los resultdos, r usr l 4t sólo necesitmos clculr dos nuevos coeficientes: 4 y b 4. Ejemlo.. Tomemos f (t = t en el intervlo [ π, π] (es decir, estmos ensndo en l función eriódic de eríodo π que coincide con t en el intervlo [ π, π]. Los coeficientes de Fourier son n = π π π t cos (nt dt y b n = π π π t sin (nt dt, y como l función t sin (nt es imr, result que tods ls integrles que definen b n son cero, es decir, b n = n, y si n qued n = π t cos (nt dt = π t cos (nt dt = [ ] t sin (nt t=π π sin (nt dt = π π π π n t= π n = [ ] cos (nt t=π π n = { si n es r [cos (nπ ] = t= πn 4 si n es imr. πn Por otro ldo, = π tdt = [ ] t t=π = π, π π t= y entonces l roximción N-ésim r N imr de f qued S N f (t = π 4 π 4 4 cos (t cos (3t π9 πn y si N es r qued S N f (t = S N f (t. Además, π π t dt = π = π donde el último igul vle or Prsevl. cos (Nt, ( π + 6, π (n S 3 S 3 S

20 8 Series de Fourier En el segundo gráfico se uede ver cuál será el orte del tercer término en S 3.. Tomemos l función de eríodo tl que { si t < f (t = t si t <, entonces los coeficientes de Fourier de f son: r n n = = = y y or último f (t cos ( dt = [ t t sin ( cos ( dt = nπ cos (nπ n π = ( n n π, = f (t dt = f (t cos ( dt + sin ( n 3 π 3 t dt = 3 + f (t cos ( dt ] t= t cos ( n π t= b n = = f (t sin ( dt = t sin ( dt = f (t sin ( dt + [ t cos ( cos ( + nπ n 3 π 3 + cos (nπ cos (nπ = + nπ n 3 π 3 n 3 π 3 = ( n+ { nπ = nπ si n es r nπ 4 si n es imr. n 3 π 3 Así l sext roximción de Fourier de f es S 6 f (t = 6 ( π cos (πt + π 4 π 3 sin (πt + ( cos (3πt + 9π 3π 4 7π 3 sin (3πt. f (t sin ( dt = ] t= t sin ( n π = t= + ( n n 3 π 3 n 3 π 3 = cos (πt sin (πt π π.5.5 S S S Puede verse clrmente, demás, que l función nterior er más fácil de roximr, y que sumndo menos términos conseguímos lgo más recido f.

21 Series de Fourier 9.5. Convergenci untul de series de Fourier Hst hor no hemos dicho nd cunto se rece untulmente f su N-ésim roximción de Fourier, es decir no sbemos que relción hy, r cd t, entre f (t y S N (t, y tmoco sbemos que s con S N (t cundo N tiende infinito. Pr estudir eso, introducimos l siguiente definición: Definición.3 Si f (t es un función eriódic de eríodo e integrble en el intervlo [, ], l serie de Fourier de f es + ( ( n cos + b n sin donde los coeficientes { n } n N {} y {b n } n N son los coeficientes de Fourier de f (ver definición.9. A veces denotremos f + ( ( n cos + b n sin r indicr cuál es l serie de Fourier de f. Notr que no sbemos si dich serie converge r lgún vlor de t, ero si tenemos f en ls condiciones de l definición odemos construirl. Por suuesto que nos gustrí mucho que l serie de Fourier de f converj f, lo cul lmentblemente no ocurre. Pero tenemos el siguiente teorem, que demostró Dirichlet en 89 (este es el rimer resultdo de convergenci untul de series de Fourier. Teorem.4 (Dirichlet Si f (t es un función rel de eríodo (definid en todo R, cotd en [, ], con un número finito de discontinuiddes en [, ] y con un número finito de máximos y mínimos (extremos locles en [, ], entonces l serie de Fourier de f converge r todo t l vlor [f (t+ + f (t ], es decir, + ( ( n cos + b n sin = [ ( f t + + f ( t ]. Entendmos qué ide el teorem y qué d: ls condiciones edids f (demás de ser eriódic de eríodo se llmn ls condiciones de Dirichlet en [, ]. Anlicemos que iden ests condiciones: rimero, con extremos locles nos referimos untos t tles que f(t f(t r todo t róximo t (o en lugr de. Que teng un número finito de máximos y mínimos en [, ] nos segur que f no oscil demsido, or ejemlos l función eriódic de eríodo tl que { t sin (/t si < t < f (t = si t =

22 3 Series de Fourier no cumle con es condición (grficr f y ver!. Que teng un número finito de discontinuiddes en [, ] está clro que signific, y or ejemlo l función de eríodo f (t = { si t Q si t R Q no cumle con es condición. Ls tres condiciones junts (que ide Dirichlet dicen lgo muy imortnte: que el intervlo [, ] se uede dividir de form tl que l gráfic de f en cd subintervlo es l de un función creciente o decreciente, y demás, or ser cotd, los límites f ( t + = lím t t + f (t y f ( t = lím t t f (t existen r todo t en [, ]. Pr convencerse de eso, mrcr en [, ] rimero tods ls discontinuiddes, y desués estudir en cd subintervlo un función continu con finitos extremos locles (y l hor de grficr recordr que f es cotd. Notr que si f es continu en t entonces f (t = f (t + = f (t, y si f es discontinu en t entonces debe tener un slto en t (o un discontinuidd evitble, y que or ls crcterístics de f, sbemos que existen límites lterles en ls discontinuiddes, y entonces [f (t+ + f (t ] es el romedio del vlor de f en el slto; es decir [ ( f t + + f ( t ] { = f (t romedio del slto si f es continu en t si f no es continu en t Notr, or último, que en ests condiciones sbemos que f es integrble en [, ]. En cunto lo que el teorem d, nos segur que l serie de Fourier de f converge r todo t, ero no necesrimente f, ues tenemos que + ( ( n cos + b n sin = [ ( f t + + f ( t ], es decir que l serie de Fourier de f converge f (t en los t s donde f es continu, y l romedio del slto en los t s donde f es discontinu. O se, r insistir y que quede bien clro, l iguldd f (t = + ( ( n cos + b n sin vle solo r los vlores de t donde f es continu. El hecho de que l serie de Fourier de f no converge f en ls discontinuiddes de f es bsolutmente rzonble: notr que si tommos t o [, ] y fbricmos un nuev función { g (t = f (t si t t f (t 7 si t = t, entonces f y g tienen l mism serie de Fourier (y dich serie no uede converger en t f (t y g (t..

23 Series de Fourier 3 Demostrción. Veremos un ide de l demostrción, r un función ligermente mejor que Dirichlet en [, ]: le ediremos demás que teng derivds lterles en todos los untos. Tommos t fijo S N f(t = N + ( ( n cos + b n sin = = N ( ( nπx f (x dx+ f (x cos dx cos = [ N f (x + ( ( nπx cos cos Llmemos Usndo sin (( n + u sin (( n se ve que L función D N (t stisfce: i D N (t = + N = + sin + f (x sin ( ( nπx f (x ( nπ cos t [ sin + N u = sin (nu cos ( u + cos (nu sin ( u D N (t = + N ( ( nπx dx sin ] dx ( ] nπ cos (t x dx sin (nu cos ( u cos (nu sin ( u = cos (nu sin ( u ( nπ cos t = sin ( (N + sin ( πt πt. D N (tdt =, ii D N es r, iii tiene eríodo Usndo ests últims dos roieddes se ve que y entonces S N f(t f(t+ f(t = S N f(t = f (x + t D N (xdx [f (x + t f(t ]D N (xdx+ vemos que cd uno de ellos tiende cero, vemos un (l otr es igul: sin ( (N + [f (x + t f(t + ]D N (xdx, πx [f (x + t f(t + ]D N (xdx = [f (x + t f(t + ] ( dx = sin πx = ( Nπx g (x sin dx + ( Nπx g (x cos dx = b g N + g N

24 3 Series de Fourier donde g y g son ls funciones de eríodo tles que ( [f (x + t f(t + ] cos πx ( sin πx < x < g (x = π f ( + x = < x < g (x = { [f (x + t f(t+ ] < x < x < Puesto que g y g son integrbles (cotds en [, ], sus coeficientes de Fourier tienden cero, con lo cul concluye l demostrción. Ejemlo.5 Si considermos l función de eríodo tl que { si t < f (t = t si t < (del ejemlo nterior, entonces el teorem nos dice que su serie de Fourier converge l función g (t de eríodo tl que / t = g (t = si < t <, t si t < Not.6 (comrtiv Con Fourier, si tenemos un función Dirichlet en [, ] y continu (y eriódic de eríodo, entonces usndo roximciones N-ésims de Fourier odemos, vlg l redundnci, roximr f tnto como quermos, diferenci de lo que ocurrí con olinomios de Tylor que edí que f teng derivds de todos los ordenes. De todos modos, volvemos reclcr que ls series y olinomios de Fourier solo sirven r funciones eriódics, or ejemlo no sirven r l función f (x = e x, y Tylor con est hce un trbjo mrvilloso. Not.7 (y ejercicio. Si f y g son eriódics de eríodo e integrbles en [, ], y sus series de Fourier son f,f + ( n,f cos + b n,f sin ( g,g + ( n,g cos y + b n,g sin (,

25 Series de Fourier 33 entonces r culquier número rel α, l serie de Fourier de l función αf + g es αf + g α,f +,g ( ( + [α n,f + n,g ] cos + [αb n,f + b n,g ] sin.. Si f es eriódic de eríodo e integrble en [, ], y f,f + ( n,f cos + ( b n,f sin (o se el miembro de l derech es l serie de Fourier de f, y α R, entonces l función g (t = f (αt es eriódic de eríodo /α e integrble en [ /α, /α], y g,f + ( ( nπαt nπαt n,f cos + b n,f sin (es decir tiene los mismos coeficientes que f. ( + 3. Si f es eriódic de eríodo e integrble en [, ], y f,f + n,f cos, y α R, entonces l función g (t = f (t α es eriódic de eríodo e ( b n,f sin integrble en [, ], y sus coeficientes de Fourier son ( ( nπα nπα n,g = n,f cos b n,f sin, y ( nπα b n,g = n,f sin + b n,f cos ( nπα 4. Si (t es un olinomio trigonométrico, entonces él es su serie de Fourier.. Unicidd y esectro: un regunt un oco delntd es: si f y g son eriódics de eríodo y tienen los mismos coeficientes de Fourier, tiene que vler f (t = g (t t? Est regunt no es tn fácil de contestr, ero si es fácil cundo nos restringimos funciones como ls del teorem de Dirichlet: en ese cso, f y g deben ser igules, slvo osiblemente en ls discontinuiddes de mbs ues si {x,..., x n } son ls discontinuiddes de f en [, ] y {y,..., y m } son ls de g, como f y g tienen l mism serie de Fourier y tl serie converge f y g donde son continus, tendremos que r todo t [, ] {x,..., x n, y,..., y m } vle f (t = + ( ( n cos + b n = g (t. }{{} serie de Fourier de f y g Esto es muy imortnte orque nos dice que un función (eriódic de eríodo y Dirichlet en [, ] está unívocmente determind or sus coeficientes de Fourier (slvo en ls discontinuiddes, es decir, si quiero trnsortr informción uedo clculr los coeficientes de Fourier de f, tirr f y quedrme con los coeficientes, trnquilo de que f es l únic función con dichos coeficientes y de que uedo recuerrl cundo quier (de nuevo, slvo or ls discontinuiddes. Por rzones físics l conjunto de todos los coeficientes de Fourier se llmn el esectro de f, y l cntidd totl. ( + [ n + b n ] (que es igul f (t dt l energí (esectrl

26 34 Series de Fourier.6. Orden de los coeficientes de Fourier Sbemos que los coeficientes de Fourier { n, b n } de un función (rzonble stisfcen n n y b n n, ero no sbemos cun ráido lo hcen. Pr oder medir velocidd de convergenci tenemos que fijr rámetros, y lo hcemos de l siguiente mner: vmos usr r comrr ls sucesiones {/n} n N, { /n } n N, { /n 3}, etc., teniendo en cuent que, or ejemlo, l n N segund converge más ráido cero que l rimer, en el sentido de que /n /n n. En generl, si tenemos {/n m } n N y { /n k} n N segund si m > k. entonces l rimer decrece más ráido que l Not(ción.8 Si f (t es eriódic de eríodo y continu, uede sr que f (t exist en todo (, slvo en finitos untos {t,..., t n }. En este cso, denotremos or f tl función (eriódic de eríodo, dejándol sin definir en los untos que no exist (que serán infinitos en R. Esto no tendrá imortnci ues estmos interesdos en los coeficientes de Fourier de f, y ls integrles no se dn cuent si f no está definid en un cntidd finit de untos. En lgunos csos, cundo quermos remrcr est situción, diremos que f existe en csi todo unto. Así, or ejemlo, l función de eríodo tl que f (t = t si t [, tiene derivd eriódic de eríodo y { f si < t < (t = si < t <, y f no está definid en los t Z. ft ( f ( t En ls condiciones nteriores, o se si f es continu -eriódic y f existe en csi todo unto, si demás f es integrble en [, ], vle que f (tdt = f ( f (. Se suele oner f ( f ( + en lugr de f ( f ( cundo no se sbe que f se continu en y/o. Vmos ver un lem técnico r clculr integrles:

27 Series de Fourier 35 Lem.9 (teorem del vlor medio r integrles Si f : [, b] R es monóton en [, b] (es decir, creciente o decreciente y g es integrble en el sentido de Riemnn en [, b], entonces existe ξ (, b tl que b f (t g (t dt = f ( ξ g (t dt + f (b b ξ g (t dt. Demostrción. L omitimos, es un resultdo clásico unque no inmedito. Tomemos hor un función -eriódic y Dirichlet en [, ]. Como f tiene un cntidd finit de máximos y mínimos en [, ] odemos dividir dicho intervlo en un cntidd finit de subintervlos de form tl que f se monóton en cd uno de ellos. Consecuentemente, n = ( f (t cos dt uede exresrse como un sum finit de integrles del tio b ( f (t cos dt con f monóton en [, b]. Alicándole el lem nterior est integrl tenemos que b ( ξ ( b ( f (t cos dt = f ( cos dt + f (b cos dt = ξ [ ( ( ] [ ( ( ] f ( nπξ nπ f (b nπb nπξ = sin sin + sin sin. nπ nπ Ahor, como f es cotd existe M tl que f (t M r todo t, y entonces cotndo l sum nterior qued b ( f (t cos dt 4M nπ. Por último, como el coeficiente er un sum finit de integrles de este tio, concluimos que existe un constnte c (que no deende de n tl que n c n n N. Análogmente, se rueb que en ests condiciones existe un constnte c tl que b n c n n N. Suongmos hor que f es -eriódic, continu y Dirichlet en [, ], y que existe f en csi todo unto y es Dirichlet en [, ], entonces clculmos los coeficientes de Fourier de f integrndo or rtes (notr que f result cotd e integrble or ser Dirichlet: n = = ( f (t cos ( nπ dt = ( f (t sin [ ( ] f (t sin ( f (t sin dt = nπ nπ dt (.

28 36 Series de Fourier ues sin ( nπ = sin (nπ =. Pero ( f (t sin dt = b n = coeficiente de f, y como f está dentro del rzonmiento nterior, sbemos que existe c tl que n c n y b n c n n N (estmos denotndo con los coeficientes de f, sí que tomndo módulo rrib qued ( c n = nπ b n π n. Análogmente, usndo que f es continu y que f ( = f (, se ve que existe un constnte c tl que b n c n n N. Motivdos or todo este cuenterio, onemos l siguiente definición: Definición.3 Si {c n } n N es un sucesión que converge cero, diremos que es de orden /n k si existe un constnte M tl que c n M n k r todo n. Otr form de decir esto es que {c n } n N decrece l menos como (l sucesión { /n k } n N. Est no es l definición de orden más recis ni l form de determinr velocidd de convergenci más justd (or ejemlo, or qué quedrnos con k nturl en lugr de usr culquier otro exonente? ero lcnz r lo que nosotros queremos estblecer. Ejemlo.3 Si c n = { 4 πn si n es r si n es imr, entonces {c n } n N es de orden /n ero no de orden /n 3. Pr seguir con el rzonmiento que trímos, vmos oner todo en un teorem: Teorem.3 Se f (t un función de eríodo, entonces:. Si f es Dirichlet en [, ], entonces sus coeficientes de Fourier son mbos de orden (l menos /n (es decir, existe M tl que n M/n y b n M/n n. Si f tiene discontinuiddes no evitbles (es decir, sltos or ser f Dirichlet, entonces sus coeficientes de Fourier no ueden decrecer mbos más ráido que /n (decrecer más ráido en el sentido de l demostrción, ver.

29 Series de Fourier 37. Si f es Dirichlet en [, ] y continu, y existe f en csi todo unto y es Dirichlet en [, ], entonces los coeficientes de Fourier de f son mbos de orden (l menos /n (es decir, existe M tl que n M/n y b n M/n n. Si f tiene discontinuiddes, entonces los coeficientes de Fourier de f no ueden decrecer mbos más ráido que /n. 3. En generl, si f es Dirichlet en [, ] y continu, y f, f,..., f (k existen tods, son Dirichlet en [, ] y continus, y f (k+ existe en csi todo unto y es Dirichlet en [, ], entonces sus coeficientes de Fourier son mbos de orden (l menos /n k+ (es decir, existe M tl que n M/n k+ y b n M/n k+ n. Si f (k+ tiene discontinuiddes, entonces los coeficientes de Fourier de f no ueden decrecer mbos más ráido que /n k+. Demostrción.. Que los coeficientes de Fourier de f decrecen l menos como /n y lo robmos, vemos que no ueden decrecer más ráido mbos: r eso, suongmos que si, o se que existe M y α > tl que n M n +α y b n M n +α n N. Llmo g (t = + ( ( n cos + b n sin (el miembro de l derech es l serie de Fourier de f, que converge r todo t ero no necesrimente f, entonces y como l serie ( n cos + b n sin ( M n +α = M n +α M n +α t R, converge (ues ( /t +α dt = /α, es decir, l integrl converge, el Teorem. me dice que g es continu en R. Pero f (t = g (t en todos los t s donde f es continu, y esto quiere decir que f es continu o tiene discontinuiddes evitbles (ensr, lo cul contrdice nuestrs hiótesis.. Que los coeficientes de Fourier de f decrecen l menos como /n y lo robmos, vemos que no ueden decrecer más ráido mbos: r eso, suongmos que si, o se que existe M y α > tl que n M n +α y b n M n +α n N. Como f es continu, tenemos que f (t = + ( n cos + b n sin (,

30 38 Series de Fourier y si miro l serie derivd término término, tenemos que y ( ( ( n cos + b n sin = nπ n y como l serie ( sin + nπ n cos πm ( nπ n nπ πm = n+α ( sin M πm = n+α n +α + nπ n cos ( n +α t R,, (. converge, el Teorem.4 nos dice que f tiene derivd continu, lo cul contrdice nuestrs hiótesis. 3. Se rueb usndo inducción en n y los dos untos nteriores. Not.33 (sutil Fijrse que en el enuncido de ( dice Si f tiene discontinuiddes no evitbles, en cmbio en ( dice Si f tiene discontinuiddes, esto es orque hy un teorem que dice que ls funciones derivds no ueden tener discontinuiddes evitbles, ver Sivk g. 6. Ejemlo.34. Si f (t es l función de eríodo π tl que f (t = t si t [ π, π, y clculmos sus coeficientes de Fourier y nos dio b n = n, = π, y n = { 4 πn si n es imr si n es r, es decir que son de orden /n ero no más, y eso es orque f es continu ero f es discontinu.. Si f es tl que sus coeficientes de Fourier son n = 7 πn 3 y b n = n n +, entonces n = 7 n, y πn 3 b n n, de donde se deduce que mbos son de orden n n /n 3 y no más, es decir que f tiene derivd continu y derivd segund discontinu.

31 Series de Fourier Derivción e integrción de series de Fourier Tod l sección nterior, demás de ser útil r sber cuntos términos debemos usr r obtener un buen roximción, nos ermite sosechr que v sr cundo integremos y/o derivemos un serie de Fourier. De Análisis I, uno sbe que en generl l integrr un función obtenemos un función mejor, y que l derivrl obtenemos un función eor (or ejemlo, en cunto cunts derivds tiene. Est situción tmbién se observ en ls series de Fourier: suongmos que tenemos un función -eriódic y Dirichlet en [, ], y construimos su serie de Fourier f + ( n cos + b n sin ( Si derivmos término término, obtenemos l serie trigonométric ( nπn sin ( + nπb n cos ( cuyos coeficientes decrecen más lentmente, y or lo tnto l serie converge eor (si es que converge. Por otro ldo, si integrmos término término obtenemos t = t + = t + π., dx + t ( nπx t ( nπx n cos dx + b n sin ( n nπ sin b ( ( n cos nπ t nπ b n n + n nπ sin ( b n nπ cos ( dx = que es un serie (no trigonométric, slvo que = que converge mejor (y efectivmente, converge. Más ún, con f como tommos nosotros, se uede ver que est serie converge un función continu en R, ues los coeficientes { n, b n } n N, son de orden /n. Pr estudir formlmente esto, comenzmos con un resultdo y robdo : Lem.35 Se f : R R un función de eríodo,continu, Dirichlet en [, ], y existe f en csi todo unto y es Dirichlet en [, ]. Entonces los coeficientes de Fourier de f y los de f se relcionn de l siguiente mner:, n,f = nπ b n,f y b n,f = nπ n,f Demostrción. L segund iguldd fue robd en el desrrollo de (., cundo estudiábmos el orden de los coeficientes. L otr se demuestr de mner bsolutmente nálog (ejercicio. Est sencill observción nos ermite robr el siguiente teorem:

32 4 Series de Fourier Teorem.36 Se f : R R un función eriódic de eríodo, continu, Dirichlet en [, ], y tl que existe f en csi todo unto y es Dirichlet en [, ]. Entonces l serie de Fourier de f se uede encontrr derivndo término término l serie de Fourier de f; más recismente, [ ( ( ] f d n cos + b n sin. dt donde {, n, b n } n N son los coeficientes de Fourier de f. Demostrción. Primero, notr que,f = f (tdt = (f( f( = (ues f es continu. Derivndo término término l serie de Fourier de f obtenemos ( ( nπn sin + nπb ( n cos, y teniendo en cuent el clculo nterior y el Lem.35, est es l serie de Fourier de f. Notr que en l demostrción nterior, no hemos eldo ningún resultdo de convergenci que nos ermit derivr término término. Directmente lo hemos hecho, y luego consttmos que el resultdo obtenido es un objeto conocido (l serie de Fourier de f. En rticulr, eso signific que en nuestrs hiótesis dich serie converge r todo t. L situción con resecto integrr resent l siguiente singulridd: si f es un función eriódic, no es cierto que un rimitiv de f tmbién lo se, de hecho, ni siquier es cierto que f teng rimitivs eriódics. Observción.37. Si f : R R es un función integrble de eríodo, R, y definimos F (t = t f, entonces g es eriódic de eríodo si y sólo si f =, ues r todo t R vle F (t + F (t = t+ f t f = t+ Es decir, F es eriódic si y sólo si,f = (el coeficiente de Fourier constte de f.. En ls condiciones del unto nterior, si h = f,f entonces f y h tienen los mismos coeficientes de Fourier, slvo osiblemente or,h, que vle cero. Es decir, t f =,h =, n,h = n,f, b n,h = b n,f n N. Esto se deduce inmeditmente de (.7. Teorem.38 Se f (t un función eriódic de eríodo, y Dirichlet en [, ], y denotemos {, n, b n } n N sus coeficientes de Fourier. Entonces l integrl de f se uede clculr integrndo término término su serie de Fourier; más recismente, t t f (x dx = dx + t [ ( ( ] nπx nπx n cos + b n sin dx. f.

33 Series de Fourier 4 En rticulr, el miembro de l derech es l serie de Fourier de l función F (t = t f (x dx, cundo est es eriódic (sii = según l observción nterior. Demostrción. Primero suongmos que = y definmos F (t = t f (es decir, suonemos =. Entonces F es eriódic de eríodo, continu, y F = f en todos los untos donde f es continu (es decir, slvo finitos untos en. Eso me dice demás que F es Dirichlet en [, ]: cotd ues es continu y eriódic, y con un cntidd finit de extremos locles en [, ] y que dichos extremos ueden estr en untos donde F no existe (finitos en [, ] o donde f =, y estos últimos tmbién son finitos en [, ] y que f es Dirichlet en [, ] (no es intención oner tnto énfsis en este hecho tmoco. Con todo esto, el teorem nterior nos dice que n,f = nπ b n y b n,f = nπ n, n N, de donde odemos concluir (or el teorem de Dirichlet,.4 que F (t =,F + ( ( nπ b n cos nπ t + ( nπ n sin, (.3 en rticulr l serie converge r todo t, y = F ( =,F π bn n converge ues los coeficientes b n son de orden /n. Es decir, (notr que est serie,f = b n π n (.4 Por otro ldo, si integrmos término término l serie de Fourier de f y usndo (.4 y (.3 en ese orden, obtenemos t [ ( ( ] nπx nπx ( n n cos + b n sin dx = nπ sin b ( ( n cos nπ t = nπ = = F (t. n nπ sin ( b n nπ cos ( nπ t +,F Si, licmos lo hecho l función h (t = f (t, y utilizndo l observción concluimos que es decir t t ( f (x dx = f (x dx = t + Por último, si, usr que t t t f = [ n cos [ n cos ( nπx ( nπx + b n sin + b n sin ( nπx ( nπx ] dx, ] dx. y que lo hecho nos dice que ess dos integrles se ueden clculr término término. t f f, =

34 4 Series de Fourier Ejemlo.39 Tomemos l función de eríodo π tl que f (t = t si t [ π, π, º ft ( 3º º º º º 3º º entonces los coeficientes de Fourier de f son n = π π π t cos (nt dt = n ues es l integrl de un función imr en el intervlo [ π, π], y b n = π π π t sin (nt dt = n cos (nπ = ( n+ n. Los coeficientes son de orden /n or ser f discontinu, l serie de Fourier de f es f y converge l función ( n+ sin (nt = [sin (t n sin (t + 3 ] sin (3t, g (t = { f (t si (n π < t < (n + π r lgún entero n si t = (n π r lgún entero n. L función h (t = t f (x dx es eriódic de eríodo ues f =, y r t [ π, π] vle h (t = t f (x dx = t xdx = t.

35 Series de Fourier 43 Además el teorem nterior nos dice que h (t = = t ( n+ sin (nx dx = n ( n+ n + ( n n cos (nt + ( n+ n = ( n cos (nt, n de donde concluimos que est últim es l serie de Fourier de h, y or lo tnto ( n+ n = π es decir, l serie de Fourier de h es π 6 + π π h (t dt = π π π ( n cos (nt, n t dt = π 6, lo cul es coherente con nuestros conocimientos, ues es es l serie de Fourier de un función r, continu y con derivd discontinu. Finlmente, si derivmos término término l serie de f, obtenemos [cos (t cos (t + cos (3t ], que diverge r todo t (notr, sin embrgo, que f es eriódic (de eríodo π, ues es cierto que f (t = f (t + π, es decir este es un cso donde l serie de Fourier de l derivd no uede clculrse derivndo l serie de f, y esto no contrdice el teorem, orque el roblem está en que f no es continu..8. Exnsiones de medio rngo, efectos de l simetrí Hemos visto en lgunos ejemlos, que cundo un función es r su serie de Fourier no tiene senos, y cundo es imr no tiene cosenos; en está sección vmos ver que efectos tienen lguns simetrís en los coeficientes de Fourier. Lem.4 Si f es un función integrble de eríodo entonces sus coeficientes de Fourier quedn determindos de l siguiente mner:. Si f es r, entonces r todo n vle n = ( f (t cos dt y b n =.. Si f es imr, entonces r todo n vle n = y b n = ( f (t sin dt.

36 44 Series de Fourier Demostrción. Ejercicio muy simle. L rincil utilidd del lem nterior no es solo horrrse clculr lgunos coeficientes que obvimente ern cero (y cuyo cálculo innecesrio es un frecuente fuente de errores, sino que nos ermite, en lguns circunstncis, encontrr desrrollos de Fourier que contengs solo senos o solo cosenos. El cso tíico es el siguiente: suongmos que tenemos un función f definid solo en el intervlo [,, y queremos logrr l iguldd f (t = ( b n sin r todo t [,, o r l myor cntidd de t s osibles (or ejemlo difícilmente logremos iguldd en los t s donde f es discontinu. Entonces hcemos lo siguiente: definimos f (t = f ( t r t (, (recordr que comenzmos con f solmente definid en [,, y sí extendid, f es imr en [,, y hor definimos f en todo R r que se eriódic de eríodo, es decir onemos f (t = f (t + t R. 3 3 Así, hemos construido un función eriódic de eríodo e imr, que coincide con mi función originl en el intervlo [,, or lo tnto su serie de Fourier tendrá solo senos, y si or ejemlo, tenemos f continu en (,, hbremos conseguido f (t = ( b n sin t (,. Además, notr que en relidd l extensión de f l hcemos virtulmente, es decir, no necesitmos clculr exlícitmente cunto vle f en todo t, orque r clculr los coeficientes b n necesitmos conocer f solo en el intervlo (,, según el lem nterior. Ejemlo.4 Queremos encontrr un serie de Fourier que converge l función f (t = t en el intervlo (, y que conteng solo senos, entonces el rzonmiento nterior nos dice que debemos tomr b n = t sin ( dt = ( n nπ + 4( n n 3 π 3 4 n 3 π 3, y con eso nomás estmos seguros de que t = [ ( n nπ + 4( n n 3 π 3 4 n 3 π 3 ] sin ( t (,.